We present a new approach to graph limit theory that unifies and generalizes the two most well-developed directions, namely dense graph limits (even the more general $L^p$ limits) and Benjamini–Schramm limits (even in the stronger local-global setting). We illustrate by examples that this new framework provides a rich limit theory with natural limit objects for graphs of intermediate density. Moreover, it provides a limit theory for bounded operators (called P-operators) of the form $L^\infty (\Omega )\to L^1(\Omega )$ for probability spaces $\Omega $ . We introduce a metric to compare P-operators (for example, finite matrices) even if they act on different spaces. We prove a compactness result, which implies that, in appropriate norms, limits of uniformly bounded P-operators can again be represented by P-operators. We show that limits of operators, representing graphs, are self-adjoint, positivity-preserving P-operators called graphops. Graphons, $L^p$ graphons, and graphings (known from graph limit theory) are special examples of graphops. We describe a new point of view on random matrix theory using our operator limit framework.

All non-negative, continuous, $\text{SL}(n)$, and translation invariant valuations on the space of super-coercive, convex functions on $\mathbb{R}^{n}$ are classified. Furthermore, using the invariance of the function space under the Legendre transform, a classification of non-negative, continuous, $\text{SL}(n)$, and dually translation invariant valuations is obtained. In both cases, different functional analogs of the Euler characteristic, volume, and polar volume are characterized.

We give a complete description of a basis of the extension spaces between indecomposable string and quasi-simple band modules in the module category of a gentle algebra.

In this work, we obtain a local maximum principle along the Ricci flow $g(t)$ under the condition that $\mathrm {Ric}(g(t))\le {\alpha } t^{-1}$ for $t>0$ for some constant ${\alpha }>0$ . As an application, we will prove that under this condition, various kinds of curvatures will still be nonnegative for $t>0$ , provided they are non-negative initially. These extend the corresponding known results for Ricci flows on compact manifolds or on complete noncompact manifolds with bounded curvature. By combining the above maximum principle with the Dirichlet heat kernel estimates, we also give a more direct proof of Hochard’s [15] localized version of a maximum principle by Bamler et al. [1] on the lower bound of different kinds of curvatures along the Ricci flows for $t>0$ .

We explicate the combinatorial/geometric ingredients of Arthur’s proof of the convergence and polynomiality, in a truncation parameter, of his noninvariant trace formula. Starting with a fan in a real, finite dimensional, vector space and a collection of functions, one for each cone in the fan, we introduce a combinatorial truncated function with respect to a polytope normal to the fan and prove the analogues of Arthur’s results on the convergence and polynomiality of the integral of this truncated function over the vector space. The convergence statements clarify the important role of certain combinatorial subsets that appear in Arthur’s work and provide a crucial partition that amounts to a so-called nearest face partition. The polynomiality statements can be thought of as far reaching extensions of the Ehrhart polynomial. Our proof of polynomiality relies on the Lawrence–Varchenko conical decomposition and readily implies an extension of the well-known combinatorial lemma of Langlands. The Khovanskii–Pukhlikov virtual polytopes are an important ingredient here. Finally, we give some geometric interpretations of our combinatorial truncation on toric varieties as a measure and a Lefschetz number.

We introduce the tracial Rokhlin property for a conditional expectation for an inclusion of unital ${{\text{C}}^{*}}$-algebras $P\,\subset \,A$ with index finite, and show that an action $\alpha$ from a finite group $G$ on a simple unital ${{\text{C}}^{*}}$- algebra $A$ has the tracial Rokhlin property in the sense of N. C. Phillips if and only if the canonical conditional expectation $E:\,A\,\to \,{{A}^{G}}\,$ has the tracial Rokhlin property. Let $\mathcal{C}$ be a class of infinite dimensional stably finite separable unital ${{\text{C}}^{*}}$-algebras that is closed under the following conditions:

(1) If $A\,\in \,\mathcal{C}$ and 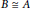$B\,\cong \,A$, then $B\,\in \,\mathcal{C}$.

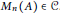(2) If $A\,\in \,\mathcal{C}$ and $n\,\in \,\mathbb{N}$, then ${{M}_{n}}\left( A \right)\,\in \,\mathcal{C}$.

(3) If $A\,\in \,\mathcal{C}$ and $p\,\in \,A$ is a nonzero projection, then 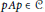$pAp\,\in \,\mathcal{C}$.

Suppose that any ${{\text{C}}^{*}}$-algebra in $\mathcal{C}$ is weakly semiprojective. We prove that if $A$ is a local tracial ${{\text{C}}^{*}}$-algebra in the sense of Fan and Fang and a conditional expectation $E:\,A\,\to \,P$ is of index-finite type with the tracial Rokhlin property, then $P$ is a unital local tracial $\mathcal{C}$-algebra.

The main result is that if $A$ is simple, separable, unital nuclear, Jiang–Su absorbing and $E:\,A\,\to \,P$ has the tracial Rokhlin property, then $P$ is Jiang–Su absorbing. As an application, when an action α from a finite group $G$ on a simple unital ${{\text{C}}^{*}}$-algebra $A$ has the tracial Rokhlin property, then for any subgroup $H$ of $G$ the fixed point algebra 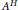${{A}^{H}}$ and the crossed product algebra $A{{\rtimes }_{{{\alpha }_{|H}}}}$$H$ is Jiang–Su absorbing. We also show that the strict comparison property for a Cuntz semigroup 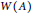$W\left( A \right)$ is hereditary to $W\left( P \right)$ if $A$ is simple, separable, exact, unital, and $E:\,A\,\to \,P$ has the tracial Rokhlin property.

We demonstrate how exact structures can be placed on the additive category of right operator modules over an operator algebra in order to discuss global dimension for operator algebras. The properties of the Haagerup tensor product play a decisive role in this.

We discuss the notion of optimal polynomial approximants in multivariable reproducing kernel Hilbert spaces. In particular, we analyze difficulties that arise in the multivariable case which are not present in one variable, for example, a more complicated relationship between optimal approximants and orthogonal polynomials in weighted spaces. Weakly inner functions, whose optimal approximants are all constant, provide extreme cases where nontrivial orthogonal polynomials cannot be recovered from the optimal approximants. Concrete examples are presented to illustrate the general theory and are used to disprove certain natural conjectures regarding zeros of optimal approximants in several variables.

Associated with every $2n\times 2n$ real positive definite matrix $A,$ there exist n positive numbers called the symplectic eigenvalues of $A,$ and a basis of $\mathbb {R}^{2n}$ called the symplectic eigenbasis of A corresponding to these numbers. In this paper, we discuss differentiability and analyticity of the symplectic eigenvalues and corresponding symplectic eigenbasis and compute their derivatives. We then derive an analogue of Lidskii’s theorem for symplectic eigenvalues as an application.

We initiate the program of extending to higher-rank graphs (k-graphs) the geometric classification of directed graph $C^*$ -algebras, as completed in Eilers et al. (2016, Preprint). To be precise, we identify four “moves,” or modifications, one can perform on a k-graph $\Lambda $ , which leave invariant the Morita equivalence class of its $C^*$ -algebra $C^*(\Lambda )$ . These moves—in-splitting, delay, sink deletion, and reduction—are inspired by the moves for directed graphs described by Sørensen (Ergodic Th. Dyn. Syst. 33(2013), 1199–1220) and Bates and Pask (Ergodic Th. Dyn. Syst. 24(2004), 367–382). Because of this, our perspective on k-graphs focuses on the underlying directed graph. We consequently include two new results, Theorem 2.3 and Lemma 2.9, about the relationship between a k-graph and its underlying directed graph.

Motivated by works on extension sets in standard domains, we introduce a notion of the Carathéodory set that seems better suited for the methods used in proofs of results on characterization of extension sets. A special stress is put on a class of two-dimensional submanifolds in the tridisc that not only turns out to be Carathéodory but also provides examples of two-dimensional domains for which the celebrated Lempert Theorem holds. Additionally, a recently introduced notion of universal sets for the Carathéodory extremal problem is studied and new results on domains admitting (no) finite universal sets are given.

In this paper, we completely solve the $L^{2}\to L^{r}$ extension conjecture for the zero radius sphere over finite fields. We also obtain the sharp $L^{p}\to L^{4}$ extension estimate for non-zero radii spheres over finite fields, which improves the previous result of the first and second authors significantly.

We study immersed surfaces in ${\mathbb R}^3$ that are critical points of the Willmore functional under boundary constraints. The two cases considered are when the surface meets a plane orthogonally along the boundary and when the boundary is contained in a line. In both cases we derive weak forms of the resulting free boundary conditions and prove regularity by reflection.

We prove $L^{p}$ -boundedness of oscillating multipliers on symmetric spaces of noncompact type of arbitrary rank, as well as on a wide class of locally symmetric spaces.

We observe an inductive structure in a large class of Artin groups of finite real, complex and affine types and exploit this information to deduce the Farrell–Jones isomorphism conjecture for these groups.

Involution Schubert polynomials represent cohomology classes of K-orbit closures in the complete flag variety, where K is the orthogonal or symplectic group. We show they also represent $\mathsf {T}$ -equivariant cohomology classes of subvarieties defined by upper-left rank conditions in the spaces of symmetric or skew-symmetric matrices. This geometry implies that these polynomials are positive combinations of monomials in the variables $x_i + x_j$ , and we give explicit formulas of this kind as sums over new objects called involution pipe dreams. Our formulas are analogues of the Billey–Jockusch–Stanley formula for Schubert polynomials. In Knutson and Miller’s approach to matrix Schubert varieties, pipe dream formulas reflect Gröbner degenerations of the ideals of those varieties, and we conjecturally identify analogous degenerations in our setting.

We show that the Mallows measure on permutations of $1,\dots ,n$ arises as the law of the unique Gale–Shapley stable matching of the random bipartite graph with vertex set conditioned to be perfect, where preferences arise from the natural total ordering of the vertices of each gender but are restricted to the (random) edges of the graph. We extend this correspondence to infinite intervals, for which the situation is more intricate. We prove that almost surely, every stable matching of the random bipartite graph obtained by performing Bernoulli percolation on the complete bipartite graph $K_{{\mathbb Z},{\mathbb Z}}$ falls into one of two classes: a countable family $(\sigma _n)_{n\in {\mathbb Z}}$ of tame stable matchings, in which the length of the longest edge crossing k is $O(\log |k|)$ as $k\to \pm \infty $ , and an uncountable family of wild stable matchings, in which this length is $\exp \Omega (k)$ as $k\to +\infty $ . The tame stable matching $\sigma _n$ has the law of the Mallows permutation of ${\mathbb Z}$ (as constructed by Gnedin and Olshanski) composed with the shift $k\mapsto k+n$ . The permutation $\sigma _{n+1}$ dominates $\sigma _{n}$ pointwise, and the two permutations are related by a shift along a random strictly increasing sequence.

A new characterization of $\text {CMO}(\mathbb R^n)$ is established replying upon local mean oscillations. Some characterizations of iterated compact commutators on weighted Lebesgue spaces are given, which are new even in the unweighted setting for the first order commutators.