Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T18:18:50.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur le comportement, par torsion, des facteurs epsilon de paires

Published online by Cambridge University Press:  20 November 2018

Colin J. Bushnell  and
Guy Henniart
Colin J. Bushnell
Affiliation:
Department of Mathematics, King's College, Strand, London WC2R 2LS, United Kingdom. e-mail: bushnell@mth.kcl.ac.uk
Guy Henniart
Affiliation:
Département de Mathématiques, UMR 8628 du CNRS, Bâtiment 425, Université de Paris-Sud, 91405 Orsay cedex, France. e-mail: Guy.Henniart@math.u-psud.fr
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soient 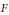$F$ un corps commutatif localement compact non archimédien et 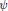$\psi$ un caractère additif non trivial de 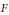$F$. Soient 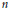$n$ et 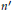${n}'$ deux entiers distincts, supérieurs à 1. Soient $\pi$ et 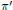${\pi }'$ des représentations irréductibles supercuspidales de 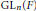$\text{G}{{\text{L}}_{n}}\left( F \right)$, $\text{G}{{\text{L}}_{{{n}'}}}\left( F \right)$ respectivement. Nous prouvons qu’il existe un élément 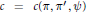$c=c\left( \pi ,{\pi }',\psi \right)$ de 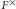${{F}^{\times }}$ tel que pour tout quasicaractère modéré 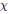$\mathcal{X}$ de 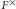${{F}^{\times }}$ on ait $\mathcal{E}\left( \chi \pi \times {\pi }',s,\psi \right)=\chi {{\left( c \right)}^{-1}}\mathcal{E}\left( \pi \times {\pi }',s,\psi \right)$. Nous examinons aussi certains cas où 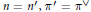$n={n}',{\pi }'={{\pi }^{\text{v}}}$. Les résultats obtenus forment une étape vers une démonstration de la conjecture de Langlands pour 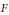$F$, qui ne fasse pas appel à la géométrie des variétés modulaires, de Shimura ou de Drinfeld.

Abstract

Abstract

Let 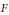$F$ be a non-Archimedean local field, and 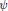$\psi $ a non-trivial additive character of 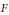$F$. Let 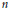$n$ and 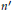${n}'$ be distinct positive integers. Let $\pi $, 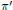${\pi }'$ be irreducible supercuspidal representations of 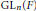$\text{G}{{\text{L}}_{n}}\left( F \right)$, $\text{G}{{\text{L}}_{{{n}'}}}\left( F \right)$ respectively. We prove that there is 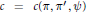$c=c\left( \pi ,{\pi }',\psi \right)$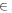$\in $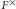${{F}^{\times }}$ such that for every tame quasicharacter 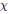$\mathcal{X}$ of 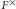${{F}^{\times }}$ we have $\mathcal{E}\left( \chi \pi \times {\pi }',s,\psi \right)=\chi {{\left( c \right)}^{-1}}\mathcal{E}\left( \pi \times {\pi }',s,\psi \right)$. We also treat some cases where 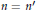$n={n}'$ and 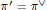${\pi }'={{\pi }^{\text{V}}}$. These results are steps towards a proof of the Langlands conjecture for 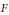$F$, which would not use the geometry of modular—Shimura or Drinfeld—varieties.

Keywords

22E50corps localcorrespondance de Langlands localefacteurs epsilon de paires
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 6 , 01 December 2001 , pp. 1141 - 1173
Copyright
Copyright © Canadian Mathematical Society 2001

References

Références

[1] Arthur, J. and Clozel, L., Simple algebras, base change, and the advanced theory of the trace formula. Ann. of Math. Studies 120, Princeton University Press, 1989.Google Scholar
[2] Bushnell, C. J. Hereditary orders, Gauss sums and supercuspidal representations of GL(n) . J. Reine Angew. Math. 375/376(1987), 184–210.Google Scholar
[3] Bushnell, C. J., Gauss sums and local constants for GL(N) . In: L-functions and Arithmetic, (eds., Coates, J., Taylor, M. J.), London Math. Soc. Lecture Notes 153, Cambridge University Press, 1991, 61–73.Google Scholar
[4] Bushnell, C. J. and Henniart, G., Local tame lifting for GL(n) I: simple characters. Inst. Hautes Études Sci. Publ. 83(1996), 105–233.Google Scholar
[5] Bushnell, C. J. and Henniart, G., Local tame lifting for GL(n) II: wildly ramified supercuspidals. Astérisque 254(1999),Google Scholar
[6] Bushnell, C. J. and Henniart, G., Supercuspidal representations of GL n: explicit Whittaker functions. J. Algebra 209(1998), 270–287.Google Scholar
[7] Bushnell, C. J. and Henniart, G., Calculs de facteurs epsilon de paires pour GL n sur un corps local I. Bull. London Math. Soc. 31(1999), 534–542.Google Scholar
[8] Bushnell, C. J. and Henniart, G., Davenport-Hasse relations and an explicit Langlands correspondence. J. Reine Angew. Math. 519(2000), 171–199.Google Scholar
[9] Bushnell, C. J. and Henniart, G., Davenport-Hasse relations and an explicit Langlands correspondence II: twisting conjectures. J. Th. Nombres Bordeaux 12(2000), 309–347.Google Scholar
[10] Bushnell, C. J., Henniart, G. and Kutzko, P. C., Local Rankin-Selberg convolutions for GL n: explicit conductor formula. J. Amer. Math. Soc. 11(1998), 703–730.Google Scholar
[11] Bushnell, C. J., Henniart, G. and Kutzko, P. C., Correspondance de Langlands locale pour GL n et conducteurs de paires. Ann. Sci. École Norm. Sup. (4) 31(1998), 537–560.Google Scholar
[12] Bushnell, C. J. and Kutzko, P. C., The admissible dual of GL(N) via compact open subgroups. Ann. of Math. Studies 129, Princeton University Press, 1993.Google Scholar
[13] Deligne, P., Les constantes des équations fonctionnelles des fonctions L. In: Modular forms of one variable II, Lecture Notes in Math. 349, Springer, Berlin, 501–597, 1974.Google Scholar
[14] Deligne, P. and Henniart, G., Sur la variation, par torsion, des constantes locales d’équations fonctionnelles des fonctions L. Invent. Math. 64(1981), 89–118.Google Scholar
[15] Godement, R. and Jacquet, H., Zeta functions of simple algebras. Lecture Notes in Math. 260, Springer, Berlin, 1972.Google Scholar
[16] Harris, M. and Taylor, R., On the geometry and cohomology of some simple Shimura varieties. Prépublication, 1999.Google Scholar
[17] Henniart, G., Représentations du groupe de Weil d’un corps local. Enseign. Math. 26(1980), 155–172.Google Scholar
[18] Henniart, G., Galois ε-factors modulo roots of unity. Invent. Math. 78(1984), 117–126.Google Scholar
[19] Henniart, G., Une preuve simple des conjectures de Langlands pour GL n sur un corps p-adique. Invent. Math. 139(2000), 439–455.Google Scholar
[20] Henniart, G. and Herb, R., Automorphic induction for GL(n) (over local non-Archimedean fields). Duke Math. J. 78(1995), 131–192.Google Scholar
[21] Jacquet, H., Principal L-functions of the linear group. In: Automorphic forms, representations and L-functions, (eds., Borel, A. and Casselman, W.), Proc. Symposia Pure Math. (2) 33(1979), Amer. Math. Soc., 63–87.Google Scholar
[22] Jacquet, H., Piatetskii-Shapiro, I. and Shalika, J., Rankin-Selberg convolutions. Amer. J. Math. 105(1983), 367–483.Google Scholar
[23] Laumon, G., Rapoport, M. and Stuhler, U., D-elliptic sheaves and the Langlands correspondence. Invent. Math. 113(1993), 217–338.Google Scholar
[24] Sauvageot, F., Principe de densité pour les groupes réductifs. Compositio Math. 108(1997), 151–184.Google Scholar
[25] Shahidi, F., Fourier transforms of intertwining operators and Plancherel measures for GL(n) . Amer. J. Math. 106(1984), 67–111.Google Scholar
[26] Tate, J., Number theoretic background. In: Automorphic forms, representations and L-functions, (eds., Borel, A. and Casselman, W.), Proc. Symposia Pure Math. (2) 33(1979), Amer. Math. Soc. 3–26.Google Scholar