For integers 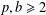 $p,b\geq 2$, let
$p,b\geq 2$, let  $D=\{0,1,\ldots ,b-1\}$ be a set of consecutive digits. It is known that the Cantor measure
$D=\{0,1,\ldots ,b-1\}$ be a set of consecutive digits. It is known that the Cantor measure  $\unicode[STIX]{x1D707}_{pb,D}$ generated by the iterated function system
$\unicode[STIX]{x1D707}_{pb,D}$ generated by the iterated function system 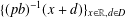 $\{(pb)^{-1}(x+d)\}_{x\in \mathbb{R},d\in D}$ is a spectral measure with spectrum
$\{(pb)^{-1}(x+d)\}_{x\in \mathbb{R},d\in D}$ is a spectral measure with spectrum  $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(pb,S)=\bigg\{\mathop{\sum }_{j=0}^{\text{finite}}(pb)^{j}s_{j}:s_{j}\in S\bigg\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(pb,S)=\bigg\{\mathop{\sum }_{j=0}^{\text{finite}}(pb)^{j}s_{j}:s_{j}\in S\bigg\},\end{eqnarray}$$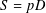 $S=pD$. We give conditions on
$S=pD$. We give conditions on 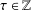 $\unicode[STIX]{x1D70F}\in \mathbb{Z}$ under which the scaling set
$\unicode[STIX]{x1D70F}\in \mathbb{Z}$ under which the scaling set 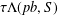 $\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6EC}(pb,S)$ is also a spectrum of
$\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6EC}(pb,S)$ is also a spectrum of  $\unicode[STIX]{x1D707}_{pb,D}$. These investigations link number theory and spectral measures.
$\unicode[STIX]{x1D707}_{pb,D}$. These investigations link number theory and spectral measures.
 $q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
$q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE