No CrossRef data available.
Published online by Cambridge University Press: 02 October 2020
Suppose that
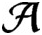 $\mathcal {A}$
is a unital subhomogeneous C*-algebra. We show that every central sequence in
$\mathcal {A}$
is a unital subhomogeneous C*-algebra. We show that every central sequence in
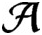 $\mathcal {A}$
is hypercentral if and only if every pointwise limit of a sequence of irreducible representations is multiplicity free. We also show that every central sequence in
$\mathcal {A}$
is hypercentral if and only if every pointwise limit of a sequence of irreducible representations is multiplicity free. We also show that every central sequence in
 $\mathcal {A}$
is trivial if and only if every pointwise limit of irreducible representations is irreducible. Finally, we give a nice representation of the latter algebras.
$\mathcal {A}$
is trivial if and only if every pointwise limit of irreducible representations is irreducible. Finally, we give a nice representation of the latter algebras.