In 2003, Ozsváth, Szabó and Rasmussen introduced the 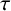$\tau $ invariant for knots, and in 2011, Sarkar [‘Grid diagrams and the Ozsváth–Szabó tau-invariant’, Math. Res. Lett. 18(6) (2011), 1239–1257] published a computational shortcut for the $\tau $ invariant of knots that can be represented by diagonal grid diagrams. Previously, the only knots known to have diagonal grid diagram representations were torus knots. We prove that all such knots are positive knots and we produce an example of a knot with a diagonal grid diagram representation which is not a torus knot.

Each metric graph has canonically associated to it a polarized real torus called its tropical Jacobian. A fundamental real-valued invariant associated to each polarized real torus is its tropical moment. We give an explicit and efficiently computable formula for the tropical moment of a tropical Jacobian in terms of potential theory on the underlying metric graph. We show that there exists a universal linear relation between the tropical moment, a certain capacity called the tau invariant, and the total length of a metric graph. To put our formula in a broader context, we relate our work to the computation of heights attached to principally polarized abelian varieties.