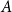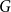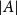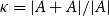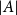For a subset $A$ of an abelian group $G$, given its size $|A|$, its doubling $\kappa =|A+A|/|A|$, and a parameter $s$ which is small compared to $|A|$, we study the size of the largest sumset 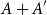$A+A'$ that can be guaranteed for a subset 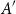$A'$ of 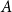$A$ of size at most $s$. We show that a subset 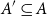$A'\subseteq A$ of size at most $s$ can be found so that 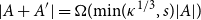$|A+A'| = \Omega (\!\min\! (\kappa ^{1/3},s)|A|)$. Thus, a sumset significantly larger than the Cauchy–Davenport bound can be guaranteed by a bounded size subset assuming that the doubling $\kappa$ is large. Building up on the same ideas, we resolve a conjecture of Bollobás, Leader and Tiba that for subsets 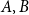$A,B$ of 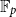$\mathbb{F}_p$ of size at most 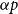$\alpha p$ for an appropriate constant $\alpha \gt 0$, one only needs three elements 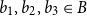$b_1,b_2,b_3\in B$ to guarantee 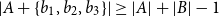$|A+\{b_1,b_2,b_3\}|\ge |A|+|B|-1$. Allowing the use of larger subsets 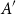$A'$, we show that for sets 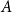$A$ of bounded doubling, one only needs a subset 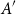$A'$ with 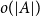$o(|A|)$ elements to guarantee that 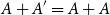$A+A'=A+A$. We also address another conjecture and a question raised by Bollobás, Leader and Tiba on high-dimensional analogues and sets whose sumset cannot be saturated by a bounded size subset.

Let G be a $\sigma $ -finite abelian group, i.e., $G=\bigcup _{n\geq 1} G_n$ where $(G_n)_{n\geq 1}$ is a nondecreasing sequence of finite subgroups. For any $A\subset G$ , let $\underline {\mathrm {d}}( A ):=\liminf _{n\to \infty }\frac {|A\cap G_n|}{|G_n|}$ be its lower asymptotic density. We show that for any subsets A and B of G, whenever $\underline {\mathrm {d}}( A+B )<\underline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B )$ , the sumset $A+B$ must be periodic, that is, a union of translates of a subgroup $H\leq G$ of finite index. This is exactly analogous to Kneser’s theorem regarding the density of infinite sets of integers. Further, we show similar statements for the upper asymptotic density in the case where $A=\pm B$ . An analagous statement had already been proven by Griesmer in the very general context of countable abelian groups, but the present paper provides a much simpler argument specifically tailored for the setting of $\sigma $ -finite abelian groups. This argument relies on an appeal to another theorem of Kneser, namely the one regarding finite sumsets in an abelian group.

Let $\mathcal{A}$ and $\mathcal{B}$ be large subsets of $\{1,\,.\,.\,.\,,\,N\}$. We study the number of pairs $\left( a,b \right)\,\in \,\mathcal{A}\,\times \,\mathcal{B}$ such that the sum of binary digits of $a\,+\,b$ is fixed.

We prove some new bounds for the size of the maximal dissociated subset of structured (having small sumset, large energy and so on) subsets of an abelian group.

Sets of integers form a monoid, where the product of two sets A and B is defined as the set containing a+b for all $a\in A$ and $b\in B$. We give a characterization of when a family of finite sets is a code in this monoid, that is when the sets do not satisfy any nontrivial relation. We also extend this result for some infinite sets, including all infinite rational sets.

Suppose that G is an abelian group and that A ⊂ G is finite and contains no non-trivial three-term arithmetic progressions. We show that |A+A| »ε|A|(log|A|)⅓−ε.