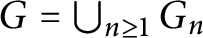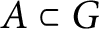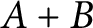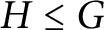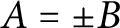1 Introduction and statement of the results
Let A be a subset of an abelian group G,
$\mu $
be a measure on G and
$C>0$
be a real number. Inverse results in additive number theory refer to those in which starting from the small doubling condition
$\mu (A+A)< C\mu (A)$
, it is possible to deduce structural information on A and its sumset
$A+A$
. For finite sets A, the measure of A can be its cardinality. More generally for infinite sets in a locally compact group,
$\mu (A)$
can be chosen as the Haar measure of A. For infinite sets in a discrete semigroup, we may use various notions of density instead of measure.
One of the most popular inverse result is Kneser’s theorem. In an abelian group with
$\mu (\cdot )=|\cdot |$
, the counting measure, and
$C \le 2$
it provides mainly a periodical structure for sumsets
$A+B$
such that
$|A+B|<|A|+|B|-1$
, yielding also a partial structure for
$A,B$
themselves.
In the particular semigroup
$\mathbb {N}$
of positive integers with
$\mu =\underline {\mathrm {d}}$
being the lower asymptotic density, there exists again such a result due to Kneser when
$\underline {\mathrm {d}}(A+B)< \underline {\mathrm {d}}(A)+\underline {\mathrm {d}}(B)$
(see [Reference Hamidoune and Rödseth8] or [Reference Halberstam and Roth3]); basically,
$A+B$
is then a union of residue classes modulo some integer q. When
$\mu $
is the upper asymptotic density or the upper Banach density, some structural information is still available (see [Reference Bihani and Jin1, Reference Kneser7]).
Our goal is to investigate the validity of similar results in abelian
$\sigma $
-finite groups. A group G is said to be
$\sigma $
-finite if it is infinite and admits an exhausting sequence, that is a nondecreasing sequence
$(G_n)_{n\ge 1}$
of finite subgroups such that
$G=\bigcup _{n\ge 1}G_n.$
As examples we have the polynomial ring
$\mathbb {F}_{p^r}[t]$
for any prime p and integer
$r\geq 1$
. More generally, let
$(C_n)_{n\geq 1}$
be a sequence of finite groups,
$G_{\mathbb {N}}=\prod _{n\in \mathbb {N}}C_n$
and
$G_n=\prod _{i\leq n} C_i\leq G_{\mathbb {N}}$
. Then
$G=\bigcup _{n\geq 1} G_n$
is
$\sigma $
-finite. Another class of
$\sigma $
-finite groups is given by the p-Prüfer groups
$\mathbb {Z}(p^\infty )=\bigcup _{r\ge 1}\mathbb {U}_{p^{r}}$
where p is a prime number and
$\mathbb {U}_{q}$
denotes the group of complex qth roots of unity. Further, if
$(d_n)$
is a sequence of integers satisfying
$d_n\mid d_{n+1}$
and
$G_n=\mathbb {U}_{d_n}$
, then
$G=\bigcup _{n\geq 1} G_n$
is
$\sigma $
-finite.
For any
$A\subset G$
, we define its lower and upper asymptotic densities as
$$ \begin{align*}\underline{\mathrm{d}}( A ):=\liminf_{n\to\infty}\frac{|A\cap G_n|}{|G_n|}\quad\text{and}\quad \overline{\mathrm{d}}( A ):=\limsup_{n\to\infty}\frac{|A\cap G_n|}{|G_n|}, \end{align*} $$
respectively. We observe that this definition implicitly requires a particular exhausting sequence to be fixed. If both limits coincide, we denote by
${\mathrm {d}}( A )$
their common value. This type of groups and densities were already studied in the additive combinatorics literature; Hamidoune and Rödseth [Reference Hegyvári4] proved that if
$\langle A\rangle =G$
and
$\alpha =\overline {\mathrm {d}}( A )>0$
, then
$hA=G$
for some
$h=O(\alpha ^{-1})$
. Hegyvári [Reference Hegyvári and Hennecart5] showed that then
$h(A-A)=\langle A-A\rangle $
for some
$h=O(\log \alpha ^{-1})$
, where again
$\alpha =\overline {\mathrm {d}}( A )>0$
; this was improved by Hegyvári and the second author [Reference Jin6].
For a subset X of an abelian group G, we denote by
$\mathrm {Stab}_G(X)$
(or simply
$\mathrm {Stab}(X)$
when no ambiguity is possible) the period or stabilizer of X, i.e., the subgroup
$\{g\in G : \forall x\in X,\, g+x\in X\}$
.
Theorem 1.1 Let G be a
$\sigma $
-finite abelian group and
$(G_n)_{n\geq 1}$
a fixed exhausting sequence. Let
$A\subset G$
and
$B\subset G$
satisfy one of the following hypotheses:
-
(1)
$\underline {\mathrm {d}}( A+B )< \underline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B )$
; -
(2)
$\overline {\mathrm {d}}( A+B )< \overline {\mathrm {d}}( A )+\overline {\mathrm {d}}( B )$
and
$A=B$
or
$A=-B$
; and -
(3)
$\overline {\mathrm {d}}( A+B )< \overline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B ).$
Then
$H=\mathrm {Stab}(A+B)$
has finite index q and admits a density equal to
$q^{-1}$
. Moreover, the numbers
$a,b,c$
of cosets of H met by
$A,B,A+B$
respectively satisfy
$c=a+b-1$
.
We will refer to the statements obtained with hypotheses 1, 2, or 3 as Theorems 1, 2, or 3, respectively.
Let
$A,B,a,b,c$
be as in Theorem 1. Then
$A+B$
admits a density which is rational, namely
$c/q$
. Further, let
$\epsilon = 1-\frac {{\mathrm {d}}( A+B )}{\underline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B )}$
. Then we have
$$ \begin{align*}(1-\epsilon)\frac{a+b}{q}\geq (1-\epsilon)(\underline{\mathrm{d}}( A )+\underline{\mathrm{d}}( B )) = {\mathrm{d}}( A+B )=\frac{a+b-1}{q}. \end{align*} $$
Therefore,
$a+b\leq \epsilon ^{-1}$
. We also get
$$ \begin{align*}q\leq ((\underline{\mathrm{d}}( A )+\underline{\mathrm{d}}( B ))\epsilon)^{-1}=(\underline{\mathrm{d}}( A )+\underline{\mathrm{d}}( B )-{\mathrm{d}}( A+B ))^{-1}.\end{align*} $$
We point out that a slightly weaker conclusion was obtained under a similar hypothesis with the upper Banach density in the general setting of countable abelian groups, by Griesmer [Reference Griesmer2]. To state his theorem, recall that a Følner sequence for an additive group G is a sequence
$\Phi =(F_n)_{n\ge 1}$
of finite subsets in G such that
$$ \begin{align*}\lim_{n\to \infty}\frac{|(g+F_n)\Delta F_n|}{|F_n|}=0,\quad \text{for all }g\in G, \end{align*} $$
where
$\Delta $
is the symmetric difference operator. We let
$$ \begin{align*}{\mathrm{d}}^*( A ):=\sup_{\Phi}\limsup_{n\to\infty}\frac{|A\cap F_n|}{|F_n|} \end{align*} $$
be the upper Banach density of A, where the supremum ranges over Følner sequences
$\Phi $
. Under the hypothesis
${\mathrm {d}}^*( A+B )< {\mathrm {d}}^*( A )+{\mathrm {d}}^*( B )$
, Griesmer obtained that
${\mathrm {d}}^*( A+B )={\mathrm {d}}^*( A+B+H )$
for some subgroup H of finite index. The value of the present paper resides, besides the stronger conclusion that
$A+B=A+B+H$
, in the simplicity and brevity of our elementary argument, in contrast to Griesmer’s involved, ergodic-theoretic method. We make full use of the
$\sigma $
-finiteness property in order to reduce the problem to passing to the limit in Kneser’s theorem for finite sets.
Remark 1.2 In our theorem, the lower asymptotic density may not be replaced by the upper asymptotic nor upper Banach density without any extra hypothesis. Indeed, let G be a
$\sigma $
-finite abelian group. Let
$(G_n)_{n\geq 0}$
be an exhausting sequence of finite subgroups such that
$\left \lvert G_{n+1} \right \rvert /\left \lvert G_n \right \rvert \rightarrow \infty $
. Let
$A=\bigcup _{n\geq 1} G_{2n}\backslash G_{2n-1}$
and
$B=\bigcup _{n\geq 0} G_{2n+1}\backslash G_{2n}$
. Then
$\overline {\mathrm {d}}( A )=\overline {\mathrm {d}}( B )=1$
, therefore
$\overline {\mathrm {d}}( A+B )=1$
and
${\mathrm {d}}^*( A )={\mathrm {d}}^*( B )={\mathrm {d}}^*( A+B )=1$
. Yet it is easy to see that
$A+B=A\cup B=G\backslash G_0$
since
$G_n\backslash G_{n-1}+G_m\backslash G_{m-1}=G_n\backslash G_{n-1}$
whenever
$n>m$
. Hence, the stabilizer of
$A+B$
is
$G_0$
, which is a finite group, in particular it is not of finite index. We are thankful to the anonymous referee for this construction.
However, the fact that the extra hypothesis
$B=\pm A$
suffices for the upper asymptotic density Kneser theorem is in contrast with the situation in the integers, cf [Reference Kneser7]. Further, there exists a
$\sigma $
-finite group G and a set
$A\subset G$
such that
${\mathrm {d}}^*( A+A )<2{\mathrm {d}}^*( A )$
but
$\mathrm {Stab}(A+A)$
is finite. Here is our construction. Let G be a
$\sigma $
-finite abelian group. Assume that G admits an exhausting sequence of finite subgroups
$(G_n)_{n\geq 0}$
satisfying that none of the quotients
$G_{n+1}/G_n$
have exponent 2; this is the case of
$G=\mathbb {F}_3[t]$
for instance. For any
$n\ge 1$
, let
$x_n\in G_{n+1}\backslash G_n$
such that
$2x_n\not \in G_n$
. Let
$$ \begin{align*}A=\bigcup_{n\ge1}(x_n+G_n). \end{align*} $$
Then
$$ \begin{align*}A+A=\bigcup_{n\ge1}(\{x_n,2x_n\}+G_n). \end{align*} $$
Since the sequence
$(x_n+G_n)_{n\in \mathbb {N}}$
is a Følner sequence, we see that
${\mathrm {d}}^*( A )={\mathrm {d}}^*( A+A )=1$
so
${\mathrm {d}}^*( A+A )<2{\mathrm {d}}^*( A )$
. Now, we prove that
$\mathrm {Stab}(A+A)=G_0$
, a finite subgroup.Footnote
1
Indeed, let
$x\in G\backslash G_0$
, thus
$x\in G_{k+1}\backslash G_{k}$
for some
$k\ge 0$
. For any
$g\in G_k$
, we have
$ x+x_k+g\in G_{k+1}\backslash G_k. $
Assume for a contradiction that
$x+(\{x_k,2x_k\}+G_k)\subset A+A$
. In particular,
$x+x_k+g\in A+A$
and
$x+2x_k+g\in A+A$
for some
$g\in G_k$
. Then
$x+x_k+g=x_k+g'$
or
$x+x_k+g=2x_k+g'$
, and
$x+2x_k+g=2x_k+g''$
or
$x+2x_k+g=x_k+g''$
for some
$g',g''\in G_k$
. Since
$x\not \in G_k$
, it follows that
$x+x_k+g=2x_k+g'$
and
$x+2x_k+g=x_k+g''$
. Therefore,
$x=x_k+g'-g\in A$
and
$x=-x_k+g''-g\in -A$
. But
$A\cap (-A)=\emptyset $
, whence the contradiction. We infer that
$x\not \in \mathrm {Stab}(A+A)$
. Thus
$$ \begin{align*}\mathrm{Stab}(A+A)\le G_0. \end{align*} $$
It is easy to check that
$G_0\le \mathrm {Stab}(A+A)$
thus
$\mathrm {Stab}(A+A) = G_0$
as announced. This remark shows that even in the context of
$\sigma $
-finite groups, a small doubling in Banach density of a set A does not imply that
$A+A$
is periodic, thus Griesmer’s weaker structural conclusion is optimal.
Remark 1.3 If G has no proper subgroup of finite index, which is the case of
$\mathbb {Z}(p^\infty )$
for instance, the conclusion implies that
$A+B=G$
, so
$\underline {\mathrm {d}}( A+B )<\underline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B )$
is impossible except in the trivial case
$\underline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B )>1$
.
2 Proofs
We detail the proof of Theorem 1.1. Theorems 2 and 3 will be deduced straightforwardly by the same arguments.
Proof of Theorem 1.1 Let
$\alpha :=\underline {\mathrm {d}}( A )$
and
$\beta :=\underline {\mathrm {d}}( B )$
. Let us assume that
$\underline {\mathrm {d}}( A+B )<\alpha +\beta $
. Therefore,
$\alpha +\beta>0$
and there exists
$\epsilon>0$
such that
$$ \begin{align*}\underline{\mathrm{d}}( A+B )<(1-\epsilon)(\alpha+\beta). \end{align*} $$
By definition of the lower limit, there exists an increasing sequence
$(n_i)_{i\geq 1}$
of integers such that
$$ \begin{align*}|(A+B)\cap G_{n_i}|<(1-\epsilon/2)|G_{n_i}|(\alpha+\beta). \end{align*} $$
Furthermore, denoting
$A_n=A\cap G_n$
and
$B_n=B\cap G_n$
, for any i large enough, we have
$$ \begin{align*}|A_{n_i}|+|B_{n_i}|>(\alpha+\beta) |G_{n_i}|(1-\epsilon/2)/(1-\epsilon/3).\end{align*} $$
Combining these two bounds together with the fact that
$A_{n_i}+B_{n_i}\subset (A+B)\cap G_{n_i}$
, and reindexing the sequence
$(n_i)$
if necessary, we have
$$ \begin{align} |A_{n_i}+B_{n_i}|<(1-\epsilon/3)(|A_{n_i}|+|B_{n_i}|) \end{align} $$
for all
$i\geq 1$
. In particular
$|A_{n_i}+B_{n_i}|<|A_{n_i}|+|B_{n_i}|-1$
for i large enough (by reindexing if necessary, for any
$i\geq 1$
), since
$|A_{n_i}|+|B_{n_i}|\rightarrow \infty $
as a consequence of
$\alpha +\beta>0$
.
We are now able to apply Kneser’s theorem in the finite abelian group
$G_{n_i}$
. Let
$H_i=\mathrm {Stab}_{G_{n_i}}(A_{n_i}+B_{n_i})$
. We obtain that
$H_i\neq \{0\}$
for each
$i\geq 1$
and letting
$a_i,b_i,c_i$
be the number of cosets of
$H_i$
met by
$A_{n_i},B_{n_i},A_{n_i}+B_{n_i}$
respectively, we get
$c_i=a_i+b_i-1$
. Reformulating inequality (2.1) in terms of these quantities yields
$$ \begin{align*} (1-\epsilon/3)(a_i+b_i)|H_i| &\ge (1-\epsilon/3) (|A_{n_i}|+|B_{n_i}|)\\ &>|A_{n_i}+B_{n_i}|= (a_{i}+b_{i}-1)|H_{i}| \end{align*} $$
from which we infer that
$a_{i}+b_{i}<3/\epsilon $
. Moreover,
$$ \begin{align*}(\alpha+\beta)|G_{n_i}|/2<|A_{n_i}|+|B_{n_i}|\le (a_{i}+b_{i})|H_{i}| \end{align*} $$
so
$[G_{n_i}:H_i]=|G_{n_i}|/|H_i|<2\frac {a_i+b_i}{\alpha +\beta }< 6/((\alpha +\beta )\epsilon )$
. By the pigeonhole principle, upon extracting again a suitable subsequence of
$(n_i)$
, one may assume that
$[G_{n_i}:H_i]=k$
for any
$i\geq 1$
and some fixed
$k<6/((\alpha +\beta )\epsilon )$
.
Let us set
$$ \begin{align*}\mathcal{A}_i=\{K< G_{n_i}\,:\, [G_{n_i}:K]=k\}. \end{align*} $$
Thus,
$H_{i}\in \mathcal {A}_{i}$
for any
$n\geq 1$
.
Lemma 2.1 Let
$i\geq 1$
. If
$L\in \mathcal {A}_{i+1}$
, there exists
$K\in \mathcal {A}_{i}$
such that
$K\subset L$
.
Proof Let
$L\in \mathcal {A}_{i+1}$
. Let us set
$K'=L\cap G_{n_i}$
. Thus
$$ \begin{align*}G_{n_i}/K'\simeq (L+G_{n_i})/L\leq G_{n_{i+1}}/L, \end{align*} $$
so
$[G_{n_i}:K']$
divides k. Let us write
$$ \begin{align*}|G_{n}|=kg,\ [G_{n_i}:K']=\frac{k}{h},\ |K'|=gh \end{align*} $$
for some positive integers g and h. Since
$K'$
is abelian and h divides
$ |K'|$
, there exists a subgroup K of
$K'$
of index h. It satisfies
$$ \begin{align*}[G_{n_i}:K]=[G_{n_i}:K']\times [K':K]=k.\end{align*} $$
We draw from the lemma the following corollary by an easy induction.
Corollary For all pairs of integers
$j>i \geq 1$
, there exists a sequence of subgroups
$K_\ell \in \mathcal {A}_\ell $
for
$\ell \in [i,j]$
such that
$K_\ell \leq K_{\ell +1}$
for all
$\ell \in [i,j)$
and
$K_j=H_j$
.
Borrowing terminology from graph theory, for
$K\in \mathcal {A}_i$
and
$L\in \mathcal {A}_j$
where
$i\leq j$
, we call a path from K to L any non decreasing sequence of subgroups
$K_\ell \in \mathcal {A}_\ell ,\ell \in [i,j]$
for which
$K_i=K$
and
$K_j=L$
. With this terminology, the conclusion of the corollary is that there exists a path from
$K_i$
to
$H_j$
.
We shall construct inductively a nondecreasing subsequence of subgroups
$K_i\in \mathcal {A}_{i}$
for
$i\geq 1$
such that for any i, the set of integers
$j\geq i$
for which there exists a path from
$K_i$
to
$H_j$
is infinite.
To construct
$K_1\in \mathcal {A}_1$
with the desired property, let us observe that
$\mathcal {A}_1$
is finite and invoke the corollary and the pigeonhole principle.
Suppose that
$K_1,\ldots ,K_i$
are already constructed for some
$i\geq 1$
; one constructs
$K_{i+1}$
by observing again that
$\mathcal {A}_{i+1}$
is finite and applying the pigeonhole principle. Indeed, there are infinitely many
$j>i$
such that a path from
$K_i$
to
$H_j$
exists, but only finitely many
$K\in \mathcal {A}_{i+1}$
through which these paths may pass, so there exists
$K\in \mathcal {A}_{i+1}$
having the property that there exist infinitely many
$j> i$
such that a path from
$K_i$
to
$H_j$
over
$K\in \mathcal {A}_{i+1}$
exists. One then selects
$K_{i+1}$
to be such a subgroup K.
The sequence
$(K_i)_{i\geq 1}$
being non decreasing, the union
$$ \begin{align*}K=\bigcup_{i\ge 1}K_{i} \end{align*} $$
is a subgroup of G. In fact,
$K\leq \mathrm {Stab}(A+B)=:H$
; indeed, let
$g\in K$
and
$x=a+b\in A+B$
where
$(a,b)\in A\times B$
. Let i satisfy
$g\in K_i$
and
$x\in A_{n_i}+B_{n_i}$
. Since
$K_i$
is included in
$H_j$
for infinitely many
$j\geq 1$
, there exists in particular some
$j\geq i$
for which
$K_i\leq H_j$
. Thus,
$x+g\in A_{n_j}+B_{n_j}$
so
$g\in H$
.
Since
$K_{i}\subset H\cap G_{n_i}$
, the indices
$[G_{n_i}:H\cap G_{n_i}]$
divide
$k=[G_{n_i}:K_{i}]$
. Now
$$ \begin{align*}G_{n_i}/(H\cap G_{n_i})\simeq(G_{n_i}+H)/H, \end{align*} $$
and
$((G_{n_i}+H)/H)_{i\in \mathbb {N}}$
is a non decreasing sequence of subgroups of bounded indices of
$G/H$
, whose union is
$G/H$
. It is therefore stationary, so
$(G_{n_i}+H)/H=G/H$
for any large enough i. It follows that
$[G:H]$
divides k, in particular
$ [G:H]\le k <6/((\alpha +\beta )\epsilon ).$
Furthermore, if i is large enough, we have
$$ \begin{align*}\frac{\left\lvert H\cap G_{n_i} \right\rvert}{|G_{n_i}|}= \left\lvert (G_{n_i}+H)/H \right\rvert^{-1}=\left\lvert G/H \right\rvert^{-1}, \end{align*} $$
whence we deduce that
${\mathrm {d}}( H )$
exists and equals
$q^{-1}=[G:H]^{-1}$
.
Let
$C,D$
and F be the projections of
$A,B$
, and
$A+B$
, respectively, in
$G/H$
. Then
$F=C+D$
. In view of the previous paragraph and the inequality
$\underline {\mathrm {d}}( A+B )<\underline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B )$
, we obtain that
$|C+D|<|C|+|D|$
. Now
$|C+D|\geq |C|+|D|-1$
, since otherwise by Kneser’s theorem applied in the finite abelian group
$G/H$
, the set F would admit a non trivial period and
$\mathrm {Stab}(A+B)$
would be strictly larger than H. Therefore
$|C+D|= |C|+|D|-1$
, and we conclude.
We now prove the same result with the upper asymptotic density in place of the lower one in the case
$B=\pm A$
, that is, Theorem 2. Let
$\alpha :=\overline {\mathrm {d}}( A )=\overline {\mathrm {d}}( B )=\beta $
and suppose that
$\overline {\mathrm {d}}( A+B )<2\alpha (1-\epsilon )$
for some
$\epsilon>0$
. Then on the one hand we have for any large enough n
$$ \begin{align*}|A_n+B_n|\le |(A+B)\cap G_n|<2\alpha(1-\epsilon/2)|G_n|. \end{align*} $$
On the other hand, since
$\left \lvert A_n \right \rvert =\left \lvert B_n \right \rvert $
for all n, there exist infinitely many n such that
$$ \begin{align} |A_n|+|B_n|>\frac{1-\epsilon/2}{1-\epsilon/3}(\alpha+\beta)|G_n|. \end{align} $$
Hence, equation (2.1) holds along some increasing sequence
$(n_i)$
. From there, we are in position to conclude as in the proof of Theorem 1.1. The reader may observe that equation (2.2) fails for general A and B.
Finally, we prove Theorem 3. Let
$\alpha :=\overline {\mathrm {d}}( A )$
and
$\beta =\underline {\mathrm {d}}( B )$
and suppose that
$\overline {\mathrm {d}}( A+B )<(\alpha +\beta )(1-\epsilon )$
for some
$\epsilon>0$
. Then, on the one hand, we have for any large enough n
$$ \begin{align*}|A_n+B_n|\le |(A+B)\cap G_n|<(\alpha+\beta)(1-\epsilon/2)|G_n| \end{align*} $$
and
$$ \begin{align*}|B_n|>\frac{1-\epsilon/2}{1-\epsilon/3}\beta|G_n|. \end{align*} $$
On the other hand, there exist infinitely many n such that
$$ \begin{align*} |A_n|>\frac{1-\epsilon/2}{1-\epsilon/3}\alpha|G_n|. \end{align*} $$
Hence, again we recover equation (2.1) along some subsequence and can conclude.
