For any real polynomial $p(x)$ of even degree k, Shapiro [‘Problems around polynomials: the good, the bad and the ugly$\ldots $’, Arnold Math. J. 1(1) (2015), 91–99] proposed the conjecture that the sum of the number of real zeros of the two polynomials $(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)$ and $p(x)$ is larger than 0. We prove that the conjecture is true except in one case: when the polynomial $p(x)$ has no real zeros, the derivative polynomial $p{'}(x)$ has one real simple zero, that is, $p{'}(x)=C(x)(x-w)$, where $C(x)$ is a polynomial with $C(w)\ne 0$, and the polynomial $(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$ has no real zeros.

In this paper, we prove the well-known Erdős–Lax inequality [4] in a sharpened form. As a consequence, another widely used inequality due to Ankeny and Rivlin [1] gets sharpened. These results may be useful in various applications that required the Erdős–Lax and the Ankeny–Rivlin inequalities.

Classical results about peaking from complex interpolation theory are extended to polynomials on a closed disk, and on the complement of its interior. New results are obtained concerning interpolation by univalent polynomials on a Jordan domain whose boundary satisfies certain smoothness conditions.

The Fermat type functional equations $(*)\, f_1^n+f_2^n+\cdots +f_k^n=1$, where n and k are positive integers, are considered in the complex plane. Our focus is on equations of the form (*) where it is not known whether there exist non-constant solutions in one or more of the following four classes of functions: meromorphic functions, rational functions, entire functions, polynomials. For such equations, we obtain estimates on Nevanlinna functions that transcendental solutions of (*) would have to satisfy, as well as analogous estimates for non-constant rational solutions. As an application, it is shown that transcendental entire solutions of (*) when n = k(k − 1) with k ≥ 3, would have to satisfy a certain differential equation, which is a generalization of the known result when k = 3. Alternative proofs for the known non-existence theorems for entire and polynomial solutions of (*) are given. Moreover, some restrictions on degrees of polynomial solutions are discussed.

Floriculture value exceeds $5.8 billion in the United States. Environmental challenges, market trends, and diseases complicate breeding priorities. To inform breeders’ and geneticists’ research efforts, we set out to gather consumers’ preferences in the form of willingness to pay (WTP) for different rose attributes in a discrete choice experiment. The responses are modeled in WTP space, using polynomials to account for heterogeneity. Consumer preferences indicate that heat and disease tolerance were the most important aspects for subjects in the sample, followed by drought resistance. To the best of our knowledge, this is the first study to identify breeding priorities in rosaceous plants from a consumer perspective.

Given $f\in \mathbb{Z}[t]$ of positive degree, we investigate the existence of auxiliary polynomials $g\in \mathbb{Z}[t]$ for which $f(g(t))$ factors as a product of polynomials of small relative degree. One consequence of this work shows that for any quadratic polynomial $f\in \mathbb{Z}[t]$ and any $\unicode[STIX]{x1D700}>0$, there are infinitely many $n\in \mathbb{N}$ for which the largest prime factor of $f(n)$ is no larger than $n^{\unicode[STIX]{x1D700}}$.

We give a lower bound of the Mahler measure on a set of polynomials that are ‘almost’ reciprocal. Here ‘almost’ reciprocal means that the outermost coefficients of each polynomial mirror each other in proportion, while this pattern may break down for the innermost coefficients.

The elasticity of an atomic integral domain is, in some sense, a measure of how far the domain is from being a half-factorial domain. We consider the relationship between the elasticity of a domain R and the elasticity of its polynomial ring R[x]. For example, if R has at least one atom, a sufficient condition for the polynomial ring R[x] to have elasticity 1 is that every non-constant irreducible polynomial f ∈ R[x] be irreducible in K[x]. We will determine the integral domains R whose polynomial rings satisfy this condition.

The Chowla conjecture states that if $t$ is any given positive integer, there are infinitely many prime positive integers $N$ such that $\text{Per}\left( \sqrt{N} \right)\,=\,t$, where $\text{Per}\left( \sqrt{N} \right)$ is the period length of the continued fraction expansion for $\sqrt{N}$. C. Friesen proved that, for any $k\,\in \,\mathbb{N}$, there are infinitely many square-free integers $N$, where the continued fraction expansion of $\sqrt{N}$ has a fixed period. In this paper, we describe all polynomials $Q\,\in \,{{\mathbb{F}}_{q}}\left[ X \right]$ for which the continued fraction expansion of $\sqrt{Q}$ has a fixed period. We also give a lower bound of the number of monic, non-squares polynomials $Q$ such that $\deg \,Q=\,2d$ and $Per\sqrt{Q}\,=\,t$.

The classical Remez inequality [‘Sur une propriété des polynomes de Tchebycheff’, Comm. Inst. Sci. Kharkov13 (1936), 9–95] bounds the maximum of the absolute value of a real polynomial 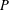$P$ of degree 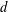$d$ on 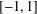$[-1,1]$ through the maximum of its absolute value on any subset 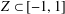$Z\subset [-1,1]$ of positive Lebesgue measure. Extensions to several variables and to certain sets of Lebesgue measure zero, massive in a much weaker sense, are available (see, for example, Brudnyi and Ganzburg [‘On an extremal problem for polynomials of $n$ variables’, Math. USSR Izv.37 (1973), 344–355], Yomdin [‘Remez-type inequality for discrete sets’, Israel. J. Math.186 (2011), 45–60], Brudnyi [‘On covering numbers of sublevel sets of analytic functions’, J. Approx. Theory162 (2010), 72–93]). Still, given a subset 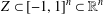$Z\subset [-1,1]^{n}\subset \mathbb{R}^{n}$, it is not easy to determine whether it is ${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming (here 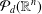${\mathcal{P}}_{d}(\mathbb{R}^{n})$ is the space of real polynomials of degree at most 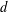$d$ on $\mathbb{R}^{n}$), that is, satisfies a Remez-type inequality: 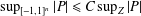$\sup _{[-1,1]^{n}}|P|\leq C\sup _{Z}|P|$ for all 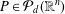$P\in {\mathcal{P}}_{d}(\mathbb{R}^{n})$ with $C$ independent of $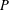P$. (Although 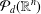${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming sets are precisely those not contained in any algebraic hypersurface of degree 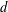$d$ in 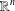$\mathbb{R}^{n}$, there are many apparently unrelated reasons for 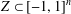$Z\subset [-1,1]^{n}$ to have this property.) In the present paper we study norming sets and related Remez-type inequalities in a general setting of finite-dimensional linear spaces 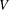$V$ of continuous functions on 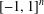$[-1,1]^{n}$, remaining in most of the examples in the classical framework. First, we discuss some sufficient conditions for $Z$ to be $V$-norming, partly known, partly new, restricting ourselves to the simplest nontrivial examples. Next, we extend the Turán–Nazarov inequality for exponential polynomials to several variables, and on this basis prove a new fewnomial Remez-type inequality. Finally, we study the family of optimal constants 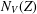$N_{V}(Z)$ in the Remez-type inequalities for 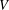$V$, as the function of the set 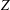$Z$, showing that it is Lipschitz in the Hausdorff metric.

We obtain an asymptotic formula for the number of square-free integers in $N$ consecutive values of polynomials on average over integral polynomials of degree at most $k$ and of height at most $H$, where $H\,\ge \,{{N}^{k-1+\varepsilon }}$ for some fixed $\varepsilon \,>\,0$. Individual results of this kind for polynomials of degree $k\,>\,3$, due to A. Granville (1998), are only known under the $ABC$-conjecture.

In the spectrum of the algebra of symmetric analytic functions of bounded type on ℓp, 1 ≤ p < +∞, and along the same lines as the general non-symmetric case, we define and study a convolution operation and give a formula for the ‘radius’ function. It is also proved that the algebra of analytic functions of bounded type on ℓ1 is isometrically isomorphic to an algebra of symmetric analytic functions on a polydisc of ℓ1. We also consider the existence of algebraic projections between algebras of symmetric polynomials and the corresponding subspace of subsymmetric polynomials.

Let f be a polynomial of degree n≥2 with f(0)=0 and f′(0)=1. We prove that there is a critical point ζ of f with ∣f(ζ)/ζ∣≤1/2 provided that the critical points of f lie in the sector {reiθ:r>0,∣θ∣≤π/6}, and ∣f(ζ)/ζ∣<2/3 if they lie in the union of the two rays {1+re±iθ:r≥0}, where 0<θ≤π/2.

Let $N$ be a zero-symmetric near-ring with identity, and let $\sGa$ be a faithful tame $N$-group. We characterize those ideals of $\sGa$ that are the range of some idempotent element of $N$. Using these idempotents, we show that the polynomials on the direct product of the finite $\sOm$-groups $V_1,V_2,\dots,V_n$ can be studied componentwise if and only if $\prod_{i=1}^nV_i$ has no skew congruences.

AMS 2000 Mathematics subject classification: Primary 16Y30. Secondary 08A40

In this paper, we consider a system of nonlinear delay-differential equations(DDEs) which models the dynamics of the interaction between chronic myelogenousleukemia (CML), imatinib, and the anti-leukemia immune response. Because of thechaotic nature of the dynamics and the sparse nature of experimental data, welook for ways to use computation to analyze the model without employing directnumerical simulation. In particular, we develop several tools usingLyapunov-Krasovskii analysis that allow us to test the robustness of the modelwith respect to uncertainty in patient parameters. The methods developed in thispaper are applied to understanding which model parameters primarily affect thedynamics of the anti-leukemia immune response during imatinib treatment. Thegoal of this research is to aid the development of more efficient modelingapproaches and more effective treatment strategies in cancer therapy.

Given a Banach space $E$ and positive integers $k$ and $l$ we investigate the smallest constant $C$ that satisfies $\|P\|\hskip1pt\|Q\|\le C\|PQ\|$ for all $k$-homogeneous polynomials $P$ and $l$-homogeneous polynomials $Q$ on $E$. Our estimates are obtained using multilinear maps, the principle of local reflexivity and ideas from the geometry of Banach spaces (type and uniform convexity). We also examine the analogous problem for general polynomials on Banach spaces.

The original Gelfond–Schnirelman method, proposed in 1936, uses polynomials with integer coefficients and small norms on [0, 1] to give a Chebyshev-type lower bound in prime number theory. We study a generalization of this method for polynomials in many variables. Our main result is a lower bound for the integral of Chebyshev's $\psi $-function, expressed in terms of the weighted capacity. This extends previous work of Nair and Chudnovsky, and connects the subject to the potential theory with external fields generated by polynomial-type weights. We also solve the corresponding potential theoretic problem, by finding the extremal measure and its support.

Building on the work of Davenport and Schmidt, we mainly prove two results. The first one is a version of Gel'fond's transcendence criterion which provides a sufficient condition for a complex or p-adic number $\xi$ to be algebraic in terms of the existence of polynomials of bounded degree taking small values at $\xi$ together with most of their derivatives. The second one, which follows from this criterion by an argument of duality, is a result of simultaneous approximation by conjugate algebraic integers for a fixed number $\xi$ that is either transcendental or algebraic of sufficiently large degree. We also present several constructions showing that these results are essentially optimal.