Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T01:59:38.772Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Continued Fraction Expansion of Fixed Period in Finite Fields

Published online by Cambridge University Press:  20 November 2018

Hela Benamar ,
Amara Chandoul  and
M. Mkaouar
Hela Benamar
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisie e-mail: hela.benamar@issatgb.rnu.tnmohamed.mkaouar@fss.rnu.tn
Amara Chandoul
Affiliation:
163, avenue de Luminy-case, 907-13288, Marseille Cedex 9, France e-mail: chandoul@iml.univ-mrs.fr
M. Mkaouar
Affiliation:
Faculté des Sciences de Sfax, BP 1171, Sfax 3000, Tunisie e-mail: hela.benamar@issatgb.rnu.tnmohamed.mkaouar@fss.rnu.tn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Chowla conjecture states that if $t$ is any given positive integer, there are infinitely many prime positive integers 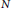$N$ such that 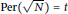$\text{Per}\left( \sqrt{N} \right)\,=\,t$, where 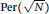$\text{Per}\left( \sqrt{N} \right)$ is the period length of the continued fraction expansion for $\sqrt{N}$. C. Friesen proved that, for any 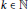$k\,\in \,\mathbb{N}$, there are infinitely many square-free integers 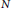$N$, where the continued fraction expansion of $\sqrt{N}$ has a fixed period. In this paper, we describe all polynomials 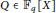$Q\,\in \,{{\mathbb{F}}_{q}}\left[ X \right]$ for which the continued fraction expansion of $\sqrt{Q}$ has a fixed period. We also give a lower bound of the number of monic, non-squares polynomials $Q$ such that 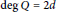$\deg \,Q=\,2d$ and 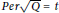$Per\sqrt{Q}\,=\,t$.

Keywords

11A5513J05continued fractionspolynomialsformal power series
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 704 - 712
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Baum, L. E. and Sweet, M. M., Continued fraction of algebraic power series in characteristic 2 Ann. of Math. 103(1976), 593–610. http://dx.doi.Org/10.2307/1970953 Google Scholar
[2] Bertin, M. J., Decomps-Guilloux, A., Grandet-Hugot, M., Pathiaux-Deleosse, M., and Schreiber, J. P., Pisot and Salem numbers. Birkhâuser Verlag, Basel, 1992.Google Scholar
[3] Chowla, P. and Chowla, S., Problems on periodic simple continued fraction. Proc. Nat. Acad. Sci. U.S.A 69(1972), 3745. http://dx.doi.Org/10.1073/pnas.69.12.3745Google Scholar
[4] Friesen, C., On continued fraction of given period. Proc. Amer. Math. Soc. 103(1988), 9–14. http://dx.doi.Org/10.1090/S0002-9939-1988-0938635-4 Google Scholar
[5] Li, B. and Wu, J., Beta-expansion and continued fraction expansion over formal laurent series. Finite Fields Appl. 14(2008), no. 3, 635–647.Google Scholar
[6] Mahler, K., On a theorem ofLiouville infields of positive characteristic. Canad. J. Math. 1(1949), 397–400.Google Scholar
[7] Mkaouar, M., Sur les fractions continues des séries formelles quadratiques sur Wq[X]. Acta Arith. 97(2001), 241–251. http://dx.doi.Org/10.4064/aa97-3-4 Google Scholar
[8] Schmidt, W. M., On continued fractions and Diophantine approximation in power series fields. Acta Arith. 95(2000), 139–166.Google Scholar
[9] Thakur, D. S., Diophantine approximation exponents and continued fractions for algebraic power series. J. Number Theory 79(1999), no. 2, 284–291. http://dx.doi.Org/10.1006/jnth.1999.2413 Google Scholar
[10] Thakur, D. S., Transcendence of gamma values for Fq[T]. Ann. of Math. 144(1996), 181–188. http://dx.doi.Org/10.2307/2118588 Google Scholar
[11] Thakur, D. S., Exponential and continued fractions. J. Number Theory 59(1996), 248–261.Google Scholar