Let X be a complex Banach space and B be a closed linear operator with domain $\mathcal{D}(B) \subset X,\,\, a,b,c,d\in\mathbb{R},$ and $0 \lt \beta \lt \alpha.$ We prove that the problem

\begin{equation*}u(t) -(aB+bI)(g_{\alpha-\beta}\ast u)(t) -(cB+dI)(g_{\alpha}\ast u)(t) = h(t), \quad t\geq 0,\end{equation*}

where $g_{\alpha}(t)=t^{\alpha-1}/\Gamma(\alpha)$ and $h:\mathbb{R}_+\to X$ is given, has a unique solution for any initial condition on $\mathcal{D}(B)\times X$ as long as the operator B generates an ad-hoc Laplace transformable and strongly continuous solution family $\{R_{\alpha,\beta}(t)\}_{t\geq 0} \subset \mathcal{L}(X).$ It is shown that such a solution family exists whenever the pair $(\alpha,\beta)$ belongs to a subset of the set $(1,2]\times(0,1]$ and B is the generator of a cosine family or a C0-semigroup in $X.$ In any case, it also depends on certain compatibility conditions on the real parameters $a,b,c,d$ that must be satisfied.

Well-posedness in time-weighted spaces of certain quasilinear (and semilinear) parabolic evolution equations $u'=A(u)u+f(u)$ is established. The focus lies on the case of strict inclusions $\mathrm{dom}(f)\subsetneq \mathrm{dom}(A)$ of the domains of the nonlinearities $u\mapsto f(u)$ and $u\mapsto A(u)$. Based on regularizing effects of parabolic equations it is shown that a semiflow is generated in intermediate spaces. In applications this allows one to derive global existence from weaker a priori estimates. The result is illustrated by examples of chemotaxis systems.

The article studies an initial boundary valueproblem (ibvp) for the radial solutions of the nonlinear Schrödinger (NLS) equation in a radially symmetric region $\Omega\in \mathbb R^n$ with boundaries. All such regions can be classified into three types: a ball Ω0 centred at origin, a region Ω1 outside a ball, and an n-dimensional annulus Ω2. To study the well-posedness of those ibvps, the function spaces for the boundary data must be specified in terms of the solutions in appropriate Sobolev spaces. It is shown that when $\Omega = \Omega_1$, the ibvp for the NLS equation is locally well-posed in $ C( [0, T^*]; H^s(\Omega_1))$ if the initial data is in $H^s(\Omega_1)$ and boundary data is in $ H^{\frac{2s+1}{4}}(0, T)$ with $s \geq 0$. This is the optimal regularity for the boundary data and cannot be improved. When $\Omega = \Omega_2$, the ibvp is locally well-posed in $ C( [0, T^*]; H^s(\Omega_2))$ if the initial data is in $ H^s(\Omega_2)$ and boundary data is in $ H^{\frac{s+1}{2}}(0, T)$ with $s \geq 0$. In this case, the boundary data requires $1/4$ more derivative compared to the case when $\Omega = \Omega_1$. When $\Omega = \Omega_0$ with n = 2 (the case with n > 2 can be discussed similarly), the ibvp is locally well-posed in $ C( [0, T^*]; H^s(\Omega_0))$ if the initial data is in $ H^s(\Omega_0)$ and boundary data is in $ H^{\frac{s+1}{2}}(0, T)$ with s > 1 (or $s \gt n/2$). Due to the lack of Strichartz estimates for the corresponding boundary integral operator with $ 0 \leq s \leq 1$, the local well-posedness can only be achieved for s > 1. It is noted that the well-posedness results on Ω0 and Ω2 are the first ones for the ibvp of NLS equations in bounded regions of higher dimension.

We study global-in-time dynamics of the stochastic nonlinear beam equations (SNLB) with an additive space-time white noise, posed on the four-dimensional torus. The roughness of the noise leads us to introducing a time-dependent renormalization, after which we show that SNLB is pathwise locally well-posed in all subcritical and most of the critical regimes. For the (renormalized) defocusing cubic SNLB, we establish pathwise global well-posedness below the energy space, by adapting a hybrid argument of Gubinelli-Koch-Oh-Tolomeo (2022) that combines the I-method with a Gronwall-type argument. Lastly, we show almost sure global well-posedness and invariance of the Gibbs measure for the stochastic damped nonlinear beam equations in the defocusing case.

We consider the discrete Safronov-Dubovskiĭ aggregation equation associated with the physical condition, where particle injection and extraction take place in the dynamical system. In application, this model is used to describe the aggregation of particle-monomers in combination with sedimentation of particle-clusters. More precisely, we prove well-posedness of the considered model for a large class of aggregation kernel with source and efflux coefficients. Furthermore, over a long time period, we prove that the dynamical model attains a unique equilibrium solution with an exponential rate under a suitable condition on the forcing coefficient.

In this paper, we mainly investigate the well-posedness of the four-order degenerate differential equation ($P_4$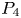): $(Mu)''''(t) + \alpha (Lu)'''(t) + (Lu)''(t)$ 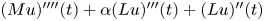$=\beta Au(t) + \gamma Bu'(t) + Gu'_t + Fu_t + f(t),\,( t\in [0,\,2\pi ])$ 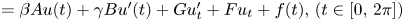in periodic Lebesgue–Bochner spaces $L^p(\mathbb {T}; X)$ 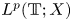and periodic Besov spaces $B_{p,q}^s\;(\mathbb {T}; X)$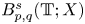, where $A$, $B$, $L$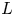 and $M$ 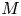are closed linear operators on a Banach space $X$ 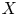such that $D(A)\cap D(B)\subset D(M)\cap D(L)$ 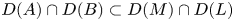and $\alpha,\,\beta,\,\gamma \in \mathbb {C}$, $G$ and $F$ are bounded linear operators from $L^p([-2\pi,\,0];X)$ (respectively $B_{p,q}^s([-2\pi,\,0];X)$) into $X$, $u_t(\cdot ) = u(t+\cdot )$ 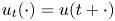and $u'_t(\cdot ) = u'(t+\cdot )$ 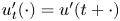are defined on $[-2\pi,\,0]$ for $t\in [0,\, 2\pi ]$. We completely characterize the well-posedness of ($P_4$) in the above two function spaces by using known operator-valued Fourier multiplier theorems.

In this work we study the Cauchy problem in Gevrey spaces for a generalized class of equations that contains the case $b=0$ of the $b$-equation. For the generalized equation, we prove that it is locally well-posed for initial data in Gevrey spaces. Moreover, as we move to global well-posedness, we show that for a particular choice of the parameter in the equation the local solution is global analytic in both time and spatial variables.

A system of mutually interacting superprocesses with migration is constructed as the limit of a sequence of branching particle systems arising from population models. The uniqueness in law of the superprocesses is established using the pathwise uniqueness of a system of stochastic partial differential equations, which is satisfied by the corresponding system of distribution function-valued processes.

When a liquid fills the semi-infinite space between two concentric cylinders which rotate at different steady speeds, how about the shape of the free surface on top of the fluid? The different fluids will lead to a different shape. For the Newtonian fluid, the meniscus descends due to the centrifugal forces. However, for the certain non-Newtonian fluid, the meniscus climbs the internal cylinder. We want to explain the above phenomenon by a rigorous mathematical analysis theory. In the present paper, as the first step, we focus on the Newtonian fluid. This is a steady free boundary problem. We aim to establish the well-posedness of this problem. Furthermore, we prove the convergence of the formal perturbation series obtained by Joseph and Fosdick in Arch. Ration. Mech. Anal. 49 (1973), 321–380.

In this study, we investigate the intial value problem (IVP) for a time-fractional fourth-order equation with nonlinear source terms. More specifically, we consider the time-fractional biharmonic with exponential nonlinearity and the time-fractional Cahn–Hilliard equation. By using the Fourier transform concept, the generalized formula for the mild solution as well as the smoothing effects of resolvent operators are proved. For the IVP associated with the first one, by using the Orlicz space with the function $\Xi (z)={\textrm {e}}^{|z|^{p}}-1$ and some embeddings between it and the usual Lebesgue spaces, we prove that the solution is a global-in-time solution or it shall blow up in a finite time if the initial value is regular. In the case of singular initial data, the local-in-time/global-in-time existence and uniqueness are derived. Also, the regularity of the mild solution is investigated. For the IVP associated with the second one, some modifications to the generalized formula are made to deal with the nonlinear term. We also establish some important estimates for the derivatives of resolvent operators, they are the basis for using the Picard sequence to prove the local-in-time existence of the solution.

We extend previous weak well-posedness results obtained in Frigeri et al. (2017, Solvability, Regularity, and Optimal Control of Boundary Value Problems for PDEs, Vol. 22, Springer, Cham, pp. 217–254) concerning a non-local variant of a diffuse interface tumour model proposed by Hawkins-Daarud et al. (2012, Int. J. Numer. Method Biomed. Engng.28, 3–24). The model consists of a non-local Cahn–Hilliard equation with degenerate mobility and singular potential for the phase field variable, coupled to a reaction–diffusion equation for the concentration of a nutrient. We prove the existence of strong solutions to the model and establish some high-order continuous dependence estimates, even in the presence of concentration-dependent mobilities for the nutrient variable in two spatial dimensions. Then, we apply the new regularity results to study an inverse problem identifying the initial tumour distribution from measurements at the terminal time. Formulating the Tikhonov regularised inverse problem as a constrained minimisation problem, we establish the existence of minimisers and derive first-order necessary optimality conditions.

We study the stochastic cubic nonlinear Schrödinger equation (SNLS) with an additive noise on the one-dimensional torus. In particular, we prove local well-posedness of the (renormalized) SNLS when the noise is almost space–time white noise. We also discuss a notion of criticality in this stochastic context, comparing the situation with the stochastic cubic heat equation (also known as the stochastic quantization equation).

Using known operator-valued Fourier multiplier results on vector-valued Hölder continuous function spaces ${{C}^{\alpha }}(\mathbb{R};\,X)$, we completely characterize the ${{C}^{\alpha }}$-well-posedness of the first order degenerate differential equations with finite delay $(Mu{)}'(t)\,=\,Au(t)\,+\,F{{u}_{t}}\,+\,f(t)$ for $t\,\in \,\mathbb{R}$ by the boundedness of the $(M,\,F)$-resolvent of A under suitable assumption on the delay operator $F$, where $A,M$ are closed linear operators on a Banach space $X$ satisfying $D(A)\,\cap \,D(M)\,\ne \,\{0\}$, the delay operator $F$ is a bounded linear operator from $C([-r,0];X)$ to $X$, and $r\,>\,0$ is fixed.

A fully discrete A-ϕ finite element scheme for a nonlinear model of type-II superconductors is proposed and analyzed. The nonlinearity is due to a field dependent conductivity with the regularized power-law form. The challenge of this model is the error estimate for the nonlinear term under the time derivative. Applying the backward Euler method in time discretisation, the well-posedness of the approximation problem is given based on the theory of monotone operators. The fully discrete system is derived by standard finite element method. The error estimate is suboptimal in time and space.

We derive a class of Navier–Stokes–Cahn–Hilliard systems that models two-phase flows with mass transfer coupled to the process of chemotaxis. These thermodynamically consistent models can be seen as the natural Navier–Stokes analogues of earlier Cahn–Hilliard–Darcy models proposed for modelling tumour growth, and are derived based on a volume-averaged velocity, which yields simpler expressions compared to models derived based on a mass-averaged velocity. Then, we perform mathematical analysis on a simplified model variant with zero excess of total mass and equal densities. We establish the existence of global weak solutions in two and three dimensions for prescribed mass transfer terms. Under additional assumptions, we prove the global strong well-posedness in two dimensions with variable fluid viscosity and mobilities, which also includes a continuous dependence on initial data and mass transfer terms for the chemical potential and the order parameter in strong norms.

A well-posedness theory for the initial-value problem for hydroelastic waves in two spatial dimensions is presented. This problem, which arises in numerous applications, describes the evolution of a thin elastic membrane in a two-dimensional (2D) potential flow. We use a model for the elastic sheet that accounts for bending stresses and membrane tension, but which neglects the mass of the membrane. The analysis is based on a vortex sheet formulation and, following earlier analyses and numerical computations in 2D interfacial flow with surface tension, we use an angle–arclength representation of the problem. We prove short-time well-posedness in Sobolev spaces. The proof is based on energy estimates, and the main challenge is to find a definition of the energy and estimates on high-order non-local terms so that an a priori bound can be obtained.

We analyse a nonlinear hierarchical size-structured population model with time-dependent individual vital rates. The existence and uniqueness of nonnegative solutions to the model are shown via a comparison principle. Our investigation extends some results in the literature.

In this paper, we first discuss the well-posedness of linearizing equations, and then study the stability and unstability of the 3-D compressible Euler Equation, by analysing the existence of saddle point. In addition, we give the existence of local solutions of the compressible Euler equation.

We consider a non-local version of the Cahn–Hilliard equation characterized by the presence of a fractional diffusion operator, and which is subject to fractional dynamic boundary conditions. Our system generalizes the classical system in which the dynamic boundary condition was used to describe any relaxation dynamics of the order-parameter at the walls. The proposed fractional dynamic boundary condition appears to be more general in the sense that it incorporates non-local effects which were completely ignored in the classical approach. We aim to deduce well-posedness and regularity results as well as to establish the existence of finite-dimensional attractors for this system.