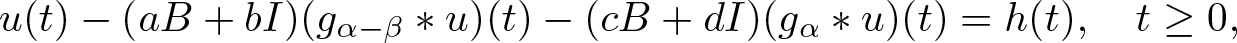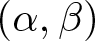1. Introduction
This article deals with the study of well-posedness and existence of solutions for the following inhomogeneous strongly damped abstract Cauchy problem of fractional order
\begin{equation}
\begin{cases}&\tau D_t^{\alpha}u(t)-(aB+bI)D_{t}^{\beta}u(t)-(cB+dI)u(t)=f(t),\\
&u(0)={x \in X,}\\
&u'(0)={y \in X,}
\end{cases}
\end{equation} with τ ≠ 0, 
$a, b,\, c,\, d\in \mathbb{R}$ and 
$0 \lt \beta\leqslant 1 \lt \alpha\leqslant 2$, where B is a closed linear operator defined in a complex Banach space X and 
$D_{t}^{\gamma}$ denotes the Caputo fractional derivative of order γ > 0.
In the integer case α = 2 and 
$\beta =1,$ the well-posedness for the homogeneous Cauchy problem (1.1), that is the existence of a strongly continuous family of bounded and linear operators 
$\{W(t)\}_{t\geq 0}$ that solves (1.1) in case 
$f\equiv0$, was settled by Neubrander [Reference Neubrander28, theorem 11]. In such case, it was proved in [Reference Neubrander28, corollary 18] that for 
$x,y\in \mathcal{D}(B)$ the unique strict solution of (1.1) is given by
\begin{equation}
u(t)= W'(t)x + W(t)[y- \frac{1}{\tau}(aB+bI)x] + \frac{1}{\tau}\int_0^t W(t-s)f(s)ds
\end{equation}where W(t) is formally the inverse Laplace transform of
\begin{equation*}
\lambda \to \dfrac{\tau}{a\lambda+c}\bigg(\dfrac{\tau\lambda^{2}-b\lambda -d}{a\lambda+c}-B\bigg)^{-1}.
\end{equation*} Several works in the literature have dealt with the investigation of Eq. (1.1) in the integer case 
$(\alpha,\beta)=(2,1).$ It corresponds to a second order Cauchy problem and is named, in applications, as the strongly damped linear Klein–Gordon equation, or strongly damped wave equation, among others. See, e.g., [Reference Aviles and Sandefur5–Reference Avrin7, Reference Ding and Yang12, Reference Neubrander28, Reference Pang and Yang29, Reference Sandefur32]. For example, for 
$\tau=1,\, d=0$, it is the linear part of the perturbed sine-equation [Reference Carvalho, Cholewa and Dlotko10] and for 
$\tau=1,\, b=d=0$ it corresponds to the linear part of the viscous Cahn–Hilliard equation [Reference Carvalho, Cholewa and Dlotko10] or the Kuznetsov equation [Reference Kuznetsov22].
In the fractional case, Kirane and Tatar [Reference Kirane and Tatar20] consider a semilinear model that include (1.1) for 
$\alpha=2, a=d=0, c=1, b=-1$, and 
$0 \lt \beta \lt 2.$ Agarwal et al. [Reference Agarwal, Jleli and Samet2] and more recently Zhou and He [Reference Zhou and He36] studied Eq. (1.1) for 
$b=d=0$ and 
$0 \lt \beta \lt 1 \lt \alpha \lt 2.$ An interesting review can be found for instance in [Reference Stojanovic and Gorenflo33]. Equation (1.1) with 
$\alpha=2\beta$ is known as the time-fractional telegraph equation. The special case 
$\beta=1/2$ can be interpreted as the heat equation subject to a damping effect represented by the 
$1/2$-order time-derivative. In all of these cases, 
$B=\Delta$ the Laplacian operator.
In the abstract case, Eq. (1.1) with 
$(\alpha,\beta)=(2,1)$ has been studied by Ikehata, Todorova, and Yordanov [Reference Ikehata, Todorova and Yordanov14]. These authors consider (1.1) with 
$b=d=0,$ 
$f\equiv 0$ and B being a nonnegative self-adjoint operator defined in a Hilbert space with a dense domain. They prove existence and uniqueness of mild solutions based on semigroup theory [Reference Ikehata, Todorova and Yordanov14, proposition 2.1]. Several authors have proposed generalizations to models more general than (1.1) in the integer case, see, e.g., [Reference Melnikova and Filinkov27, Reference Neubrander28, Reference Tijun and Jin34]. Typically, these authors consider the model
\begin{equation*}
u''(t) +Bu'(t)+Au(t)=f(t),
\end{equation*}where A and B are closed linear operators defined in a complex Banach space. However, due to its generality, this approach lacks the possibility of distinguishing its dynamics by means of an eventual combination of the physical parameters of the equation, and it also loses the special features that could be obtained by an explicit description of the solution in terms of a unique strongly continuous family of operators and by means of a kind of variation of parameter formula like (1.2), which is very useful for exploring associated semi linear problems. The same happens in the fractional model proposed in this article, and of which the authors are unaware of previous studies.
Let 
$\alpha, \beta \gt 0$ be given and we define
\begin{equation}
W_{\alpha,\beta}(t):= \int_0^t R_{\alpha,\beta}(s)ds,
\end{equation} where 
$R_{\alpha,\beta}(t)$ is formally the Laplace transform of
\begin{equation*}
\lambda \to \dfrac{\tau\lambda^{\alpha-1}}{a\lambda^{\beta}+c}\bigg(\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}+c}-B\bigg)^{-1}.
\end{equation*} Consider 
$g_{\alpha}(t):=t^{\alpha-1}/\Gamma(\alpha),\, t \gt 0,$ which is the Gelfand–Shilov function. Using Laplace transform methods, we can prove that 
$\{R_{\alpha,\beta}(t)\}_{t\geq 0}$ is a solution family of (1.1), in the sense that a formal solution of (1.1) must have the form
\begin{align}
u(t)&= W'_{\alpha,\beta}(t)x+ \int_0^t R_{\alpha,\beta}(t-s)[ y - \frac{1}{\tau} g_{\alpha-\beta}(s) (aB+bI)x ]ds\nonumber\\ &\quad + \frac{1}{\tau}\int_0^tR_{\alpha,\beta}(t-s) (g_{\alpha-1}*f)(s)] ds
\end{align} which exactly coincides with (1.2) in case α = 2 and β = 1. However, because of the new terms 
$g_{\alpha-1}(t)$ and 
$g_{\alpha-\beta}(t)$ appearing in (1.4), we cannot expect differentiability of u(t) in general, and therefore (1.4) fails to be a strict solution for (1.1). The following natural question arises:
(Q) Is (1.4) the solution of (1.1) in some extent?
In this article, we are able to solve this problem proving that, for any 
$x\in \mathcal{D}(B)$ and 
$y\in X,$ (1.4) is a solution of the following integrated version of (1.1)
\begin{align}
& \tau u(t) -(aB+bI)(g_{\alpha-\beta}\ast u)(t) -(cB+dI)(g_{\alpha}\ast u)(t) \nonumber \\
& \qquad = (g_{\alpha}*f)(t) + \tau(x+ty) - \displaystyle g_{\alpha-\beta+1}(t)(aB+bI)x,
\end{align}under appropriate conditions.
We note that solutions for integrated versions of (1.1) in the integer case 
$\alpha=2,\,\beta=1$ were previously considered by Neubrander [Reference Neubrander28, proposition 19]. The study of this kind of solutions is already known because, in applications, it is useful to find a notion of a weaker solution where 
$x,y$ can be less regular than when considering strict solutions. See also [Reference Stojanovic and Gorenflo33, Section 2.2 and Section 2.3] for an explicit fundamental formula of integrated solutions of (1.1) with 
$a=d=0$ and 
$B=\Delta,$ the Laplacian operator.
In this article, assuming that B is the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq 0}$, we show that existence of a unique solution for the integrated problem (1.5) can be assured in the sector 
$0 \lt \beta \lt \alpha, \, 1 \lt \alpha \leq 2,$ see theorem 5.4.
In some special subsets of the sector described above, we are able to show that the existence of solutions for the integrated problem can be guaranteed, under the stronger hypothesis that B is the generator of a C 0-semigroup or a strongly continuous cosine family. However, some restrictions are needed. More precisely, we first consider the set
\begin{equation}
\Omega_{\alpha,\beta} :=\{(\alpha,\beta): 0 \lt \beta \leq 1 \lt \alpha \lt 2\},
\end{equation} and we show that, for c = 0 in (1.5), there exists a solution family, and hence we have well-posedness, if B is the generator of a cosine family. See theorem 3.7 (b). Then, we decompose 
$\Omega_{\alpha,\beta}$ in two complementary subsets:
\begin{align*}
\Omega_{\alpha,\beta}^1& :=\{(\alpha,\beta): 0 \lt \beta \leq 1 \lt \alpha \lt 1 +\beta \leq 2\}, \quad\\ \Omega_{\alpha,\beta}^2& :=\{(\alpha,\beta): 0 \lt \beta\leq 1 \lt 1+\beta \lt \alpha \leq 2\}.
\end{align*} For 
$\Omega_{\alpha,\beta}^1$ we need 
$c=0, a\neq0,\ \tau\neq 0 \, ,b,d\in\mathbb{R},$ and B generator of a C 0-semigroup for well-posedness, while for 
$\Omega_{\alpha,\beta}^2$ we need 
$b=d=0$, 
$a,c \geq 0 ,\,\, \tau \gt 0$ and B generator of a cosine family. See theorem 3.7 (a) and theorem 3.9, respectively.
To achieve our results, we will use subordination methods and Laplace transform theory, together with a strong application of a criterion due to Prüss [Reference Prüss31, theorem 4.3, p. 104] for the existence of resolvent families under the assumption B is the generator of a cosine family, plus certain specific conditions in the associated kernel.
This article is organized as follows: In §2, we give the necessary preliminaries useful for following the main text of the article. Section 3 is dedicated to defining the notion of solution family that we will use and its relationship with the best known theory of (a, k)-regularized families, proving that solutions families are a particular case of the latter when the parameters satisfy 
$b\geq 0$ and τ > 0. In §4, we define our notions of mild and well-posed solution for the homogeneous problem, proving that under the hypothesis of existence of a solution family, well-posedness can be guaranteed. Then, the existence and uniqueness of mild solutions for the inhomogeneous problem can be proved. In §5, we prove our main results in this article. First, we observe that in the entire case, that is, 
$(\alpha,\beta)=(2,1),$ well-posedness follows under the subordination hypothesis that A is the generator of a C 0-semigroup. Then, we show that under certain constraints on the pair 
$(\alpha,\beta)$ we can distinguish two situations: 
$1 \lt \alpha \lt 1 +\beta \leq 2, 0 \lt \beta \leq 1$ and 
$1+\beta \lt \alpha\leq 2, 0 \lt \beta \leq 1.$ In the first case, if c = 0, the leading term in the equation (1.1) is 
$D^{\alpha}_t u$ and the solution family is subordinate to B being the generator of a C 0-semigroup. In the second case, if 
$b=d=0$, the leading term is 
$D^{\beta}_t u$ and the solution family is subordinated to B being a generator of a cosine family. These conclusions provide new insights into how fractional terms influence the class of abstract evolution equation (1.1). Finally, some examples to illustrate our abstract results are given.
2. Preliminaries
In this section, we provide some of the fundamental concepts that we will need.
Definition 2.1. ([Reference Alvarez and Lizama3], definition 1, p. 5)
Let X be a complex Banach space. Let 
$f: \mathbb{R}_+\longrightarrow X$ be an integrable function (as a Bochner integral) and let 
$T: \mathbb{R}_+\longrightarrow \mathcal{L}(X,Y)$ be strongly continuous. Then the convolution of T and f is defined by
\begin{equation*}(T\ast f)(t)=\int_{0}^{t}T(t-s)f(s)\,ds,\ t\in\mathbb{R}_+.\end{equation*}Theorem 2.2 (Titchmarsh’s Theorem). ([Reference Titchmarsh35], theorem VIII, p. 286), ([Reference Arendt, Batty, Hieber and Neubrander4], corollary 2.8.4)
Let 
$k\in L^1[0,T]$ with 
$0\in supp(k)$ and 
$f\in L^1([0,T],X)$. If
\begin{equation*}(k\ast f)(t)=\int_{0}^{t}k(t-s) f(s)ds=0\end{equation*} on 
$[0,T],$ then 
$f\equiv 0.$
Let 
$u\in C(\mathbb{R}_+;X)$ and 
$v\in C^1(\mathbb{R}_+,X)$. Then for every 
$t\geqslant 0$,
\begin{equation}
\dfrac{d}{dt}[(u\ast v)(t)]=u(t)v(0)+(u\ast v')(t).
\end{equation} The Laplace transform of a function 
$f\in L^{1}(\mathbb{R}_+,X)$ is defined by
\begin{equation*}\mathcal{L}\big(f\big)(\lambda)=\widehat{f}(\lambda):=\int_{0}^{\infty}e^{-\lambda t}f(t)dt=\lim_{T\to\infty}\int_{0}^{T}e^{-\lambda t}f(t)dt,\ \text{Re}(\lambda) \gt w.
\end{equation*} Let α > 0, 
$m=\lceil \alpha \rceil$ and 
$u:[0,\infty)\longrightarrow C^m(\mathbb{R}_+;X)$ be a function. The Caputo fractional derivative of u of order α is defined by
\begin{equation*}
D_{t}^{\alpha}u(t):=\int_{0}^{t}g_{m-\alpha}(t-s)u^{(m)}(s)ds,\ t \gt 0\
\end{equation*}where
\begin{equation*}g_{\beta}(t):=\dfrac{t^{\beta-1}}{\Gamma(\beta)},\ t \gt 0,\ \beta \gt 0,\end{equation*} is the Gelfand–Shilov function. If α = 0, we denote 
$D_{t}^{0}u(t):=u(t)$. In particular,
\begin{equation}
\widehat{D_{t}^{\alpha}f}(\lambda)=\lambda^{\alpha}\widehat{f}(\lambda)-\sum_{k=0}^{m-1}f^{(k)}(0)\lambda^{\alpha-1-k}.
\end{equation}The Riemann–Liouville fractional integral of order α > 0 is defined as follows
\begin{equation*}J_{t}^{\alpha}f(t):=(g_{\alpha}\ast f)(t),\ f\in L^1_{loc}(\mathbb{R}_+),\ t \gt 0.
\end{equation*}Moreover, the Riemann–Liouville fractional derivative of order α > 0 is given by
\begin{equation*}\mathbf{D}_{t}^{\alpha}f(t):=D_t^m(g_{m-\alpha}\ast f)(t)=D_t^mJ_t^{m-\alpha}f(t).\end{equation*}The two-parametric Mittag–Leffler function [Reference Gorenflo, Kilbas and Mainardi13, Section 4.1, p. 64] is defined as follows
\begin{equation*}E_{\alpha,\beta}(z):=\sum_{k=0}^{\infty}\dfrac{z^k}{\Gamma(\alpha k+\beta)},\ \text{Re}(\alpha) \gt 0,\ \beta\in\mathbb{C},\ z\in\mathbb{C}.\end{equation*}Some interesting properties of these functions can be found in the book by Bateman and Erdelyi [Reference Bateman and Erdélyi8, Section 18.1, p. 206].
The following Laplace transform that involves the Mittag–Leffler function is obtained in [Reference Podlubny30, Section 1.2.2, p. 21]:
\begin{align}
\int_{0}^{\infty}e^{-pt}t^{\alpha k+\beta-1}E_{\alpha,\beta}^{(k)}(\pm at^{\alpha})dt=\dfrac{k!p^{\alpha-\beta}}{(p^{\alpha}\mp a)^{k+1}},\quad \alpha \gt 0,\ \beta \gt 0,\ \text{Re}(p) \gt |a|^{\frac{1}{\alpha}}.\nonumber\\
\end{align}We recall the following definition that corresponds to a slight modification of [Reference Lizama and N’Guérékata25, definition 2.1].
Definition 2.3. Let 
$k\in C(\mathbb{R}_+)$, k ≠ 0 and let 
$a\in L_{loc}^{1}(\mathbb{R}_+)$, a ≠ 0. Let A be a linear operator with domain 
$\mathcal{D}(A)\subset X$. A strongly continuous family 
$\{R(t)\}_{t\geqslant 0}\subset \mathcal{L}(X)$ is called an (a, k)-regularized resolvent family on X (or simply (a, k)-regularized family) having A as a generator if the following properties hold.
(i)
$\lim\limits_{t\to 0}\dfrac{R(t)}{k(t)}=I$ if
$k(0)\in\overline{\mathbb{C}}\backslash\{0\}$ and
$R(0)=0$ if
$k(0)=0$;(ii)
$R(t)x\in\mathcal{D}(A)$ and
$R(t)Ax=AR(t)x$, for all
$x\in\mathcal{D}(A)$ and
$t\geqslant 0$;(iii)
$R(t)x=k(t)x+\int_{0}^{t}a(t-s)AR(s)x\,ds$,
$t\geqslant 0$,
$x\in\mathcal{D}(A)$.
Remark 2.4. Note that in case 
$k(t)=g_{\beta}(t),$ the above definition coincides with [Reference Lizama, Kochubei and Luchko23, definition 1.9]. And, in case 
$k(t)\equiv 1$, definition 
$2.3$ coincides with the definition of a resolvent family [Reference Prüss31, definition 1.3, p. 32].
Remark 2.5. If 
$\{R(t)\}_{t\geq0}$ is an (a, k)-regularized family having A as a generator, then by [Reference Lizama24, lemma 2.2, p. 281], if 
$x\in X$ then 
$\int_{0}^{t}a(t-s)R(s)xds\in\mathcal{D}(A)$ and 
$R(t)x=k(t)x+A\int_{0}^{t}a(t-s)R(s)xds$.
Remark 2.6. Let A be a closed linear operator and let 
$\{{R(t)}\}_{t\geq 0}$ be an exponentially bounded and strongly continuous operator family in 
$\mathcal{L}(X)$ such that the Laplace transform 
$\widehat{R}(\lambda)$ exists for 
$\lambda \gt \omega$. It was proved in [Reference Lizama and N’Guérékata25, p. 3] that R(t) is an (a, k)-regularized family with generator A if and only if for every 
$\lambda \gt \omega$, 
$(I-\widehat{a}(\lambda)A)^{-1}$ exists in 
$\mathcal{L}(X)$ and
\begin{equation*}\dfrac{\widehat{k}(\lambda)}{\widehat{a}(\lambda)}\bigg(\dfrac{1}{\widehat{a}(\lambda)}-A\bigg)^{-1}=\int_{0}^{\infty}e^{-\lambda s}R(s)x\,ds.\end{equation*} In the particular case of definition 2.3 with 
$a(t)=g_{\alpha}(t)$ and 
$k(t)=g_{\beta}(t)$, we obtain the following equivalent definition.
Definition 2.7. ([Reference Lizama, Kochubei and Luchko23], definition 1.9, p. 4)
Let X be a Banach space and α > 0, β > 0. A one parameter family 
$\{S_{\alpha,\beta}(t)\}_{t\geq 0}\subset\mathcal{L}(X)$ is called an 
$(\alpha,\beta)$-resolvent family if the following conditions are satisfied:
(a)
$\lim\limits_{t\to0}t^{1-\beta}S_{\alpha,\beta}(t)=\dfrac{1}{\Gamma(\beta)}I$ if
$0 \lt \beta \lt 1$,
$S_{\alpha,1}(0)=I$ and
$S_{\alpha,\beta}(0)=0$ if β > 1;(b)
$S_{\alpha,\beta}(s)S_{\alpha,\beta}(t)=S_{\alpha,\beta}(t)S_{\alpha,\beta}(s)$, for all
$s,t \gt 0$;(c) The functional equation
\begin{equation*}S_{\alpha,\beta}(s)J_{t}^{\alpha}S_{\alpha,\beta}(t)-J_{s}^{\alpha}S_{\alpha,\beta}(s)S_{\alpha,\beta}(t)=g_{\beta}(s)J_{t}^{\alpha}S_{\alpha,\beta}(t)-g_{\beta}(t)J_{s}^{\alpha}S_{\alpha,\beta}(s),\end{equation*}holds for all
$t,s \gt 0$.
We recall [Reference Lizama and N’Guérékata25, p. 3] that a family 
$\{{R(t)}\}_{t\geq 0} \subset \mathcal{L}(X)$ is said to be exponentially bounded or of type 
$(M,\omega)$ if there exist constants M > 0 and 
$\omega\in\mathbb{R}$ such that
\begin{equation*}\|R(t)\|\leq Me^{\omega t}\quad \text{for all}\ t\geq 0.\end{equation*}We recall the following subordination result.
Theorem 2.8. [Reference Lizama, Kochubei and Luchko23], theorem 2.5
Let 
$0 \lt \eta_1\leq2,\ 0 \lt \eta_2$. If A generates an exponentially bounded 
$(\eta_1,\eta_2)$-resolvent family 
$\{S_{\eta_1,\eta_2}(t)\}_{t \gt 0}$, then for each 
$\beta' \geq 0$ and 
$0 \lt \alpha' \lt 1$ we have that A generates an exponentially bounded 
$(\alpha' \eta_1,\alpha' \eta_2+\beta')$-resolvent family given by
\begin{equation*}S_{\alpha' \eta_1,\alpha' \eta_2+\beta'}(t)=\int_{0}^{\infty}\psi_{\alpha',\beta'}(t,s)S_{\eta_1,\eta_2}(s)ds,\ t \gt 0,\end{equation*}where
\begin{equation*}\psi_{\alpha',\beta'}(t,s):=t^{\beta'-1}\sum_{n=0}^{\infty}\dfrac{(-st^{-\alpha'})^n}{n!\Gamma(-\alpha' n+\beta')}\end{equation*}is called the scaled Wright function [1].
We recall the following definition.
Definition 2.9. ([Reference Prüss31], definition 4.4, p. 94)
A function 
$a:(0,\infty)\to\mathbb{R}$ is called a creep function if a(t) is nonnegative, nondecreasing, and concave. A creep function a(t) has the standard form
\begin{equation}
a(t)=a_0+a_{\infty}t+\int_{0}^{t}a_1(\tau)d\tau,\ t \gt 0,
\end{equation} where 
$a_0=a(0+)\geq 0$, 
$a_{\infty}=\lim\limits_{t\to\infty}\dfrac{a(t)}{t}=\inf_{t \gt 0}\dfrac{a(t)}{t}\geq 0$ and 
$a_1(t)=a'(t)-a_{\infty}$ is nonnegative, nonincreasing, 
$\lim\limits_{t\to\infty}a_1(t)=0$.
We introduce the following definition.
Definition 2.10. Let 
$\beta \gt 0,\ \alpha \geq 1,\ a,b,c,d,\tau\in\mathbb{R}, \, \tau \neq 0,$ where 
$(a,c)\neq (0,0).$ A closed linear operator B is said to generate a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}\subseteq\mathcal{L}(X)$ if 
$R_{\alpha,\beta}(t)$ is strongly continuous of type 
$(M,\omega)$, the set 
$\Big\{\mu \in \mathbb{C} : \mu= \dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}+c}\Big\} \subset \rho(B)$ and
\begin{equation*}\widehat{R_{\alpha,\beta}}(\lambda)=\dfrac{\tau\lambda^{\alpha-1}}{a\lambda^{\beta}+c}\bigg(\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}+c}-B\bigg)^{-1}, \quad Re(\lambda) \gt \omega.\end{equation*}Some examples of solution families are given in the following.
(a) If
$\beta=1,$
$a=b=d=0$, and
$c=\tau=1$, then for each
$\alpha \geq 1$,
$\{R_{\alpha,1}(t)\}_{t\geq0}$ is an
$(\alpha,1)$-resolvent family for the equation
$D_{t}^{\alpha}u(t)=Bu(t)$ because in this case
\begin{equation*}\widehat{R_{\alpha,1}}(\lambda)= \lambda^{\alpha-1}(\lambda^{\alpha}-B)^{-1}, \quad Re(\lambda) \gt \omega,\end{equation*}see [Reference Bazhlekova9, p. 215]. If α = 2,
$\{R_{2,1}(t)\}_{t\geq0}$ is a strongly continuous cosine family, see [Reference Arendt, Batty, Hieber and Neubrander4, proposition 3.14.4]. In the border case α = 1,
$\{R_{1,1}(t)\}_{t\geq0}$ is a C 0-semigroup, see [Reference Arendt, Batty, Hieber and Neubrander4, theorem 3.1.7].(b) If
$\alpha\geq 1,\ 0 \lt \beta\leq 1,\ a=d=0, \tau=c=1$, and
$b\leq 0$, then
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$ is a
$(\alpha-1,\beta)_{-b}$-regularized family as defined in [Reference Keyantuo, Lizama and Warma18, definition 2.4].(c) If α = 1,
$0 \lt \beta \lt 1$,
$a=\tau=1$,
$b=c=0$, and
$d=-1$, then
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$ is a (a, k) regularized resolvent family with
$a(t)=t^{-\beta}E_{1,1-\beta}(t)$ and
$k(t)=e^{-t}$. In this case
\begin{equation*}\widehat{R_{1,\beta}}(\lambda)= \dfrac{1}{\lambda^{\beta}}\bigg(\dfrac{\lambda+1}{\lambda^{\beta}}-B\bigg)^{-1}, \quad Re(\lambda) \gt \omega,\end{equation*}see [Reference Lizama and Prado26, p. 138].
The following result is contained in [Reference Prüss31, theorem 4.3, p. 104].
Theorem 2.12.
Let A generate a cosine family and assume that a(t) is a creep function with 
$a_1(t)$ log-convex. Then A generates an 
$(a,1)$-resolvent family.
We finish this section with an interesting property of (a, k)-regularized families that will be repeatedly used.
Lemma 2.13. Let 
$\{R(t)\}_{t\geq 0}$ be an (a, k)-regularized family having A as a generator and satisfying with 
$(1\ast a)(t)\neq 0$, for all t > 0. If 
$b\in L_{loc}^{1}(\mathbb{R}_+),$ then 
$(b\ast R)(t)x\in\mathcal{D}(A)$ for all 
$x\in X,\ t\geq 0$.
Proof. Since R(t) is an (a, k)-regularized family by [Reference Lizama24, remark 2.4 (4)], 
$(b\ast R)(t)$ is an 
$(a,b\ast k)$-regularized family. Define 
$S(t):=(b\ast R)(t).$ By [Reference Lizama24, remark 2.2], 
$(a\ast S)(t)x\in\mathcal{D}(A)$ for every 
$x\in X$. Let 
$\lambda\in\rho(A)$ and 
$x\in X$ be fixed. Define 
$y=(\lambda-A)^{-1}x\in\mathcal{D}(A)$ and let 
$z:=(b\ast R)(t)x$. We have
\begin{align*}
z=(b\ast R)(t)(\lambda-A)y=\lambda(b\ast R)(t)y-(b\ast R)(t)Ay.
\end{align*}Then, convolving with the kernel a(t), we obtain
\begin{align*}
& (1\ast a)(t)z =\lambda(a\ast b\ast R)(t)y-(a\ast b\ast R)(t)Ay =\lambda(a\ast S)(t)y \\
& \qquad -(a\ast S)(t)Ay\in\mathcal{D}(A).
\end{align*}3. Sufficient conditions for existence of solution families
In this section, we want to give conditions on a closed operator B so that it is a generator of a solution family.
Proposition 3.1.
Let 
$0 \lt \beta \lt \alpha \lt 2+\beta$ and B generator of a cosine family 
$\{C(t)\}_{t \gt 0}$. Then B generates an exponentially bounded 
$(\alpha-\beta,\alpha)$-resolvent family.
Proof. Recall that B being a generator of a cosine family 
$\{C(t)\}_{t \gt 0}$ is equivalent to saying that B is generator of an exponentially bounded 
$(2,1)$-resolvent family. By theorem 2.8, choosing 
$\eta_1=2,\ \eta_2=1$ and 
$\alpha'=\dfrac{\alpha-\beta}{2},\ \beta'=\dfrac{\alpha+ \beta}{2},$ and using the hypothesis, we obtain 
$0 \lt \dfrac{\alpha-\beta}{2} \lt 1.$ We conclude that B is the generator of an exponentially bounded 
$(\alpha'\eta_1,\alpha'\eta_2+\beta')=(\alpha-\beta,\alpha)$-resolvent family 
$\{S_{\alpha-\beta,\alpha}(t)\}_{t \gt 0}$. Furthermore,
\begin{equation*}S_{\alpha-\beta,\alpha}(t)x=\int_{0}^{\infty}\psi_{\frac{\alpha-\beta}{2},\frac{\alpha+\beta}{2}}(t,s)C(s){x\,ds.}\end{equation*}Our next result assumes B as generator of a C 0-semigroup instead a cosine family.
Proposition 3.2.
Let 
$0 \lt \beta \lt \alpha \lt 1 +\beta $ and B generator of a C 0-semigroup 
$\{T(t)\}_{t \gt 0}$. Then B generates an exponentially bounded 
$(\alpha-\beta,\alpha)$-resolvent family.
Proof. Since B generates a C 0-semigoup 
$\{T(t)\}_{t \gt 0}$, it is an exponentially bounded 
$(1,1)$-resolvent family 
$\{S_{1,1}(t)\}_{t \gt 0}$. Define 
$\eta_1=\eta_2=1$ and 
$\alpha'=\alpha-\beta,\ \beta'=\beta.$ By hypothesis, we obtain 
$0 \lt \alpha-\beta \lt 1.$ Therefore, by theorem 2.8, we obtain that B generates an exponentially bounded 
$(\alpha'\eta_1,\alpha'\eta_2+\beta')=(\alpha-\beta,\alpha)$-resolvent family 
$\{S_{\alpha-\beta,\alpha}(t)\}_{t \gt 0}$. Furthermore,
\begin{equation*}S_{\alpha-\beta,\alpha}(t)x=\int_{0}^{\infty}\psi_{\alpha-\beta,\beta}(t,s)T(s)x ds.\end{equation*}Remark 3.3. We recall from [Reference Arendt, Batty, Hieber and Neubrander4, theorem 3.14.17, p. 215] that if an operator B generates a cosine family, then it generates a C 0-semigroup.
Corollary 3.4. Let 
$0 \lt \beta \lt \alpha \lt 1 +\beta$ and B generator of a cosine family. Then B generates an exponentially bounded 
$(\alpha-\beta,\alpha)$-resolvent family.
Remark. By [Reference Abadias and Miana1, theorem 12], the following equality holds:
\begin{equation*}S_{\alpha-\beta,\alpha}(t)x=(g_{\beta}\ast S_{\alpha-\beta,\alpha-\beta})(t)x.\end{equation*}The following is an auxiliary result for our main result of this section.
Lemma 3.6. Suppose that 
$a\neq0,\ \tau\neq0,\ \dfrac{a}{\tau} \gt 0,\ c=0,\ \tau,a,b,d\in\mathbb{R},$ and assume any of the following.
(i) 
$0 \lt \beta \lt \alpha \lt 1 +\beta $ and B generator of a C 0-semigroup;
(ii) 
$0 \lt \beta \lt \alpha \lt 2+\beta$ and B generator of a cosine family.
Then the set 
$\Big\{\mu\in\mathbb{C}\, \, : \, \, \mu=\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}}\Big\}\subseteq\rho(B)$ and there exist a strongly continuous family 
$\{Q(t)\}_{t\geq0} \subset \mathcal{L}(X),$ exponentially bounded, such that
\begin{equation*}\widehat{Q(\lambda)}= ( \tau\lambda^{\alpha}-(aB+bI)\lambda^{\beta}-d)^{-1}, \quad Re(\lambda) \gt \omega.\end{equation*}Proof. Since B generates a C 0-semigroup (resp. cosine family) then 
$\dfrac{a}{\tau}B+\dfrac{b}{\tau}I$ also generates a C 0-semigroup (resp. cosine family), see [Reference Arendt, Batty, Hieber and Neubrander4]. Then, by proposition 3.2 (resp. proposition 3.1), we obtain in any case that 
$\dfrac{a}{\tau}B+\dfrac{b}{\tau}I$ generates an exponentially bounded 
$(\alpha-\beta,\alpha)$-resolvent family. Then, we conclude that 
$\Big\{\mu\in\mathbb{C}\, : \, \mu=\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}}{a\lambda^{\beta}}\Big\}\subseteq\rho(B)$. Furthermore, since 
$\{S_{\alpha-\beta,\alpha}(t)\}_{t\geq 0}$ is an exponentially bounded family, say 
$\|S_{\alpha-\beta,\alpha}(t)\|\leq Me^{\omega t},\ \omega\in\mathbb{R}_+,\ t\geq 0$, then using induction we easily obtain
\begin{equation*}
\|S_{\alpha-\beta,\alpha}^{\ast (k+1)}(t)\|\leq M^{k+1}e^{\omega t}\dfrac{t^{k}}{k!},\ k\in\mathbb{N}.
\end{equation*} Now, for each 
$t\geq0$ and 
$x\in X,$ we define
\begin{equation*}Q(t)x:=\sum\limits_{k=0}^{\infty}d^kS_{\alpha-\beta,\alpha}^{\ast (k+1)}(t)x.\end{equation*}It is clear that Q(t) is strongly continuous. Moreover,
\begin{align*}
\|Q(t)\|&=\bigg\|\sum\limits_{k=0}^{\infty}d^kS_{\alpha-\beta,\alpha}^{\ast (k+1)}(t)\bigg\|\leq \sum\limits_{k=0}^{\infty}|d^k|\,\|S_{\alpha-\beta,\alpha}^{\ast (k+1)}(t)\|\leq \sum\limits_{k=0}^{\infty}|d^k|M^{k+1}e^{\omega t}\dfrac{t^{k}}{k!}\\
&=e^{\omega t}\sum\limits_{k=0}^{\infty}|d^k|M\,M^{k}\dfrac{t^{k}}{k!}=Me^{\omega t}\sum\limits_{k=0}^{\infty}\dfrac{(|d|Mt)^k}{k!}=Me^{\omega t}e^{|d|Mt}=Me^{(\omega+|d|M)t}.
\end{align*} It proves that Q(t) is well-defined and exponentially bounded. Taking the Laplace transform of 
$Q(t),$ we obtain by continuity of the Laplace transform
\begin{align*}
\widehat{Q}(\lambda)&=\mathcal{L}\bigg(\sum\limits_{k=0}^{\infty}d^kS_{\alpha-\beta,\alpha}^{\ast (k+1)}(t)\bigg)(\lambda)=\sum\limits_{k=0}^{\infty}d^k\mathcal{L}\big(S_{\alpha-\beta,\alpha}^{\ast (k+1)}(t)\big)(\lambda)\\
&=\sum\limits_{k=0}^{\infty}d^k\mathcal{L}\big(S_{\alpha-\beta,\alpha}^{\ast (k)}(t)\big)(\lambda)\widehat{S_{\alpha-\beta,\alpha}}(\lambda)=\widehat{S_{\alpha-\beta,\alpha}}(\lambda)\sum\limits_{k=0}^{\infty}\big[d\widehat{S_{\alpha-\beta,\alpha}}(\lambda)\big]^k.
\end{align*} Since 
$\widehat{S_{\alpha-\beta,\alpha}}(\lambda)=\dfrac{\lambda^{-\beta}}{\tau}(\lambda^{\alpha-\beta}-(\frac{a}{\tau}B+\frac{b}{\tau}I))^{-1}=\lambda^{-\beta}(\tau\lambda^{\alpha-\beta}-(aB+bI))^{-1}$, and 
$\alpha \gt \beta$, we obtain, for Re
$(\lambda)$ sufficiently large, that
\begin{align}
\widehat{S_{\alpha-\beta,\alpha}}(\lambda)\sum\limits_{k=0}^{\infty}\big[d\widehat{S_{\alpha-\beta,\alpha}}(\lambda)\big]^k&=\lambda^{-\beta}(\tau\lambda^{\alpha-\beta}-(aB+bI))^{-1}\nonumber\\ &\quad\times\sum\limits_{k=0}^{\infty}\big[d\lambda^{-\beta}(\tau\lambda^{\alpha-\beta}-(aB+bI))^{-1}\big]^k.
\end{align} Since 
$\|d\lambda^{-\beta}(\tau\lambda^{\alpha-\beta}-(aB+bI))^{-1}\| \lt 1$ for λ large enough we obtain, using the Neumann series, that 
$\Big\{\mu;\mu=\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}}\Big\}\subseteq\rho(B)$. Moreover, (3.1) equals to
\begin{align*}
&\lambda^{-\beta}(\tau\lambda^{\alpha-\beta}-(aB+bI))^{-1}\big[1-d\lambda^{-\beta}\big(\tau\lambda^{\alpha-\beta}-(aB+bI)\big)^{-1}\big]^{-1}\\
&=\dfrac{1}{\lambda^{\beta}}(\tau\lambda^{\alpha-\beta}-(aB+bI)-d\lambda^{\beta})^{-1}=( \tau\lambda^{\alpha}-(aB+bI)\lambda^{\beta}-d)^{-1},
\end{align*}proving the theorem.
The following main result give our first practical condition for generation of a solution family. It focuses on two sectors illustrated below:
Theorem 3.7.
Let 
$ a,b,c,d,\tau\in\mathbb{R}$ where 
$a\neq0,\ \tau\neq0,\ c=0,$ and assume any of the following.
(a) 
$0 \lt \beta \leq 1 \lt \alpha \lt 1 +\beta \leq 2 $ and B generator of a C 0-semigroup;
(b) 
$0 \lt \beta \leq 1 \lt \alpha \lt 2 $ and B generator of a cosine family.
Then B generates a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}.$
Figure 1. Sectors for (a) and (b) as given in Theorem 3.7.
Proof. By lemma 3.6, there exists a strongly continuous family Q(t) satisfying 
$\widehat{Q(\lambda)}= ( \tau\lambda^{\alpha}-(aB+bI)\lambda^{\beta}-d)^{-1}, \, Re(\lambda) \gt \omega$. Note that
\begin{equation*}\widehat Q(\lambda)=(\tau\lambda^{\alpha}-a\lambda^{\beta}B-b\lambda^{\beta}-d)^{-1}=\dfrac{1}{a\lambda^{\beta}}\bigg(\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}}-B\bigg)^{-1}.\end{equation*} Since 
$1 \lt \alpha \lt 2$ we can define 
$R_{\alpha,\beta}(t):= \frac{d}{dt}(g_{2-\alpha}*Q)(t),$ which corresponds to the fractional derivative of order 
$\alpha-1$ in the sense of Riemann Liouville for Q(t). We obtain that
\begin{equation*} \widehat{R_{\alpha,\beta}}(\lambda)= \lambda \frac{1}{\lambda^{2-\alpha}}\widehat{Q}(\lambda)=\dfrac{\tau\lambda^{\alpha-1}}{a\lambda^{\beta}}\bigg(\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}}-B\bigg)^{-1}.
\end{equation*} Finally, definition 2.10 shows that 
$R_{\alpha,\beta}(t)$ is a solution family generated by B.
We will repeatedly use the following remark.
Remark 3.8. The function 
$g_{\gamma}(t)$ is nonincreasing for 
$0 \lt \gamma \lt 1$ and increasing for γ > 1. Moreover, 
$g_{\gamma}'(t)= \displaystyle \frac{\gamma-1}{t}g_{\gamma}(t), \, t \gt 0.$
In case c ≠ 0, we have the next theorem that aims to the sector illustrated below.
Theorem 3.9.
Let 
$ a,b,c,d,\tau\in\mathbb{R}$ where 
$b=d=0$, 
$a,c \geq 0 ,\,\, \tau \gt 0$ and let B be the generator of a cosine family. Suppose that 
$ 0 \lt \beta\leq 1 \lt 1+\beta \lt \alpha \leq 2.$ Then B generates a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$.
Proof. First, note that since 
$b=d=0$, then if such solution family exists, it must verify
\begin{align*}
\widehat{R_{\alpha,\beta}}(\lambda)=\dfrac{1}{\lambda\widehat{a}(\lambda)}\bigg(\dfrac{1}{\widehat{a}(\lambda)}-B\bigg)^{-1}=\dfrac{\tau\lambda^{\alpha-1}}{a\lambda^{\beta}+c}\bigg(\dfrac{\tau\lambda^{\alpha}}{a\lambda^{\beta}+c}-B\bigg)^{-1}.
\end{align*} Therefore, 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$ is an 
$(a,1)$-regularized family, that is, a resolvent family (see remark 2.4) with 
$a(t)=\dfrac{a}{\tau}g_{\alpha-\beta}(t)+\dfrac{c}{\tau}g_{\alpha}(t)$. Our strategy for the proof is to use theorem 2.12.
Figure 2. Sector 
$0 \lt \beta\leq 1 \lt 1+\beta \lt \alpha \leq 2$.
We claim that a(t) is a creep function (see definition 2.9). In fact, let us define 
$a_1(t):=\dfrac{a}{\tau}g_{\alpha-\beta-1}(t)+\dfrac{c}{\tau}g_{\alpha-1}(t)$. Note that we can rewrite 
$a_1(t)$ as
\begin{align*}
a(t)&=\dfrac{a}{\tau}g_{\alpha-\beta}(t)+\dfrac{c}{\tau}g_{\alpha}(t)=a_0+a_{\infty}t+\int_{0}^{t}a_1(s)ds,
\end{align*} where 
$a_0=0$, 
$a_{\infty}:=\lim\limits_{t\to\infty}\dfrac{a(t)}{t}=\lim\limits_{t\to\infty}\dfrac{1}{t}\Big[\dfrac{a}{\tau}g_{\alpha-\beta}(t)+\dfrac{c}{\tau}g_{\alpha}(t)\Big]=\lim\limits_{t\to\infty}\bigg[\dfrac{a}{\tau}\dfrac{t^{\alpha-\beta-2}}{\Gamma(\alpha-\beta)}+\dfrac{c}{\tau}\dfrac{t^{\alpha-2}}{\Gamma(\alpha)}\bigg]=0$ and 
$a_1(t)=a'(t)-a_{\infty}$. Moreover, since 
$a,c\geq 0$ and τ > 0 it is clear that 
$a_1(t)$ is nonnegative, 
$\lim_{t\to \infty} a_1(t)=0$ and since by hypothesis 
$0 \lt \alpha-\beta -1 \lt 1$ and 
$0 \lt \alpha-1 \lt 1$, by remark 3.8 we obtain that 
$a_1(t)$ is nonincreasing. By definition 2.9, we conclude that a(t) is a creep function, proving the claim.
Next, we claim that 
$a_1(t):=\dfrac{a}{\tau}g_{\alpha-\beta-1}(t)+\dfrac{c}{\tau}g_{\alpha-1}(t)$ is log-convex. Indeed, consider 
$f(t)=\log(a_1(t))$ then 
$f''(t)=\dfrac{a''_1(t)a_1(t)-a'_1(t)a'_1(t)}{a^2_1(t)}$ where, using remark 3.8, we obtain
\begin{equation*}
a'_1(t)=\dfrac{a}{\tau}(\alpha-\beta-2)t^{-1}g_{\alpha-\beta-1}(t)+\dfrac{c}{\tau}(\alpha-2)t^{-1}g_{\alpha-1}(t)
\end{equation*}and
\begin{equation*}
a''_1(t)=\dfrac{a}{\tau}(\alpha-\beta-2)(\alpha-\beta-3)t^{-2}g_{\alpha-\beta-1}(t)+\dfrac{c}{\tau}(\alpha-2)(\alpha-3)t^{-2}g_{\alpha-1}(t).
\end{equation*} We will to show that 
$a''_1(t)a_1(t)\geq a'_1(t)a'_1(t)$. We have that
\begin{align*}
a''_1(t)& a_1(t)=\!\bigg[\!\dfrac{a}{\tau}(\alpha-\beta-2)(\alpha-\beta-3)t^{-2}g_{\alpha-\beta-1}(t)\!+\!\dfrac{c}{\tau}(\alpha-2)(\alpha-3)t^{-2}g_{\alpha-1}(t)\!\bigg] \times
\end{align*}
\begin{align*}
&\qquad\quad\qquad\qquad
\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\times \bigg[\dfrac{a}{\tau}g_{\alpha-\beta-1}(t)+\dfrac{c}{\tau}g_{\alpha-1}(t)\bigg]
\end{align*}
\begin{align*}
&=\dfrac{a^2}{\tau^2}(\alpha-\beta-2)(\alpha-\beta-3)t^{-2}g_{\alpha-\beta-1}^{2}(t)+\dfrac{ac}{\tau^2}(\alpha-\beta-2)(\alpha-\beta-3)t^{-2}\\ &\quad\times g_{\alpha-\beta-1}(t)g_{\alpha-1}(t)
\end{align*}
\begin{align*}
&\quad +\dfrac{ac}{\tau^2}(\alpha-2)(\alpha-3)t^{-2}g_{\alpha-1}(t)g_{\alpha-\beta-1}(t)+\dfrac{c^2}{\tau^2}(\alpha-2)(\alpha-3)t^{-2}g_{\alpha-1}^2(t)
\end{align*}
\begin{align*}
&=\dfrac{a^2}{\tau^2}(\alpha-\beta-2)(\alpha-\beta-3)t^{-2}g_{\alpha-\beta-1}^{2}(t)
\end{align*}
\begin{align}
&\quad+\dfrac{ac}{\tau^2}t^{-2}g_{\alpha-\beta-1}(t)g_{\alpha-1}(t)\big[(\alpha-\beta-2)(\alpha-\beta-3)+(\alpha-2)(\alpha-3)\big]
\end{align}
\begin{align*}
&\quad+\dfrac{c^2}{\tau^2}(\alpha-2)(\alpha-3)t^{-2}g_{\alpha-1}^2(t)
\end{align*}and
\begin{align*}
a'_{1}(t)a'_{1}(t)&=\bigg[\dfrac{a}{\tau}(\alpha-\beta-2)t^{-1}g_{\alpha-\beta-1}(t)+\dfrac{c}{\tau}(\alpha-2)t^{-1}g_{\alpha-1}(t)\bigg]^2
\end{align*}
\begin{align}
&=\dfrac{a^2}{\tau^2}(\alpha-\beta-2)^2t^{-2}g_{\alpha-\beta-1}^{2}(t)+\dfrac{ac}{\tau^2}t^{-2}g_{\alpha-\beta-1}(t)g_{\alpha-1}(t)[2(\alpha-\beta-2)(\alpha-2)]
\end{align}
\begin{align*}
&\quad+\dfrac{c^2}{\tau^2}(\alpha-2)^2t^{-2}g_{\alpha-1}^{2}(t).
\end{align*} By hypothesis, we immediately have 
$(\alpha-\beta-2)(\alpha-\beta-3) \gt (\alpha-\beta-2)^2$, 
$(\alpha-2)(\alpha-3) \gt (\alpha-2)^2.$ On the other hand, from the identity
\begin{align*}
(\alpha-\beta-2)(\alpha-\beta-3)+(\alpha-2)(\alpha-3)=2(\alpha-2)^2-2\beta(\alpha-2)-2(\alpha-2)+\beta^2+\beta
\end{align*} and since by hypothesis 
$-2(\alpha-2) \gt 0$, we obtain
\begin{align*}
2(\alpha-2)^2-2\beta(\alpha-2)-2(\alpha-2)+\beta^2+\beta&\geq 2(\alpha-2)^2-2\beta(\alpha-2)\\ &=2(\alpha-\beta-2)(\alpha-2).
\end{align*} Comparing 
$(3.2)$ with 
$(3.3)$, and taking into account that 
$ac\geq 0,$ we obtain that 
$a''_1(t)a_1(t)\geq a'_1(t)a'_1(t)$ and hence 
$f''(t)\geq 0$ for all t > 0. Therefore, 
$a_1(t)$ is log-convex, proving the claim and the theorem.
4. A particular (a, k)-regularized family
The following main theorem shows that under some conditions on the parameters, a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$ is a particular case of an (a, k)-regularized family, and therefore many properties can be available from the general theory, see, e.g., [Reference Kostic21, Reference Lizama24, Reference Lizama and N’Guérékata25].
Theorem 4.1.
Let 
$a,b, c,d, \tau \in\mathbb{R}$ be given with 
$b\geq 0,\, \tau \gt 0,\, (a,c)\neq (0,0)$ and let B be the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$. Then 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$ is an (a, k)-regularized family with
(I)
$a(t)=aD^{\beta}_tp_{\alpha,\beta}(t)+cp_{\alpha,\beta}(t)$ and
$k(t)=\tau D^{\alpha-1}_tp_{\alpha,\beta}(t)$, if
$0 \lt \beta \leq 1 \lt \alpha \lt 2$.(II)
$a(t)=aD^{\beta}_tp_{1,\beta}(t)+\dfrac{a}{\tau}g_{1-\beta}(t)+cp_{1,\beta}(t)$ and
$k(t)=\tau p_{1,\beta}(t)$, if
$0 \lt \beta \leq 1=\alpha$,
where
\begin{equation}
p_{\alpha,\beta}(t)=\sum\limits_{k=0}^{\infty}\dfrac{d^k}{\tau^{k+1}}\bigg[t^{\alpha-1}E_{\alpha-\beta,\alpha}\Big(\dfrac{b}{\tau}t^{\alpha-\beta}\Big)\bigg]^{\ast(k+1)}.
\end{equation}Proof. From definition 2.10, 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$ is an exponentially bounded family of strongly continuous operators. From remark 2.6, it follows that 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$ is a (a, k)-regularized family with generator B if we can find a(t) and k(t) Laplace transformable functions such that
\begin{equation}
\widehat{R_{\alpha,\beta}}(\lambda)=\dfrac{\tau\lambda^{\alpha-1}}{a\lambda^{\beta}+c}\bigg(\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}+c}-B\bigg)^{-1}=\dfrac{\widehat{k}(\lambda)}{\widehat{a}(\lambda)}\bigg(\dfrac{1}{\widehat{a}(\lambda)}-B\bigg)^{-1},
\end{equation} for all 
$\lambda\in\mathbb{C}$, Re
$(\lambda) \gt \omega$.
For 
$0 \lt \beta \leq 1 \lt \alpha \lt 2, $ we define 
$p_{\alpha,\beta}(t)$ as in (4.1). We first prove that 
$p_{\alpha,\beta}(t)$ is well-defined and exponentially bounded. In fact, by [Reference Podlubny30, theorem 1.6, p. 35], for all t > 0 and since 
$b\geq0,\ \tau \gt 0$, we have
\begin{align*}
\Big|t^{\alpha-1}E_{\alpha-\beta,\alpha}\Big(\dfrac{b}{\tau}t^{\alpha-\beta}\Big)\Big|&\leq t^{\alpha-1}\dfrac{C}{1+\dfrac{b}{\tau}t^{\alpha-\beta}}=t^{\alpha-1}C\dfrac{\tau}{\tau+bt^{\alpha-\beta}}\leq t^{\alpha-1}C.
\end{align*} Note that 
$t^{\alpha-1}=g_{\alpha}(t)\Gamma(\alpha)$ and since 
$1\leq\alpha \lt 2$, 
$\Gamma(\alpha)\leq1$. Then
\begin{align*}
\Big|t^{\alpha-1}E_{\alpha-\beta,\alpha}\Big(\dfrac{b}{\tau}t^{\alpha-\beta}\Big)\Big|\leq g_{\alpha}(t)C.
\end{align*}Using induction, we obtain
\begin{align*}
\bigg|\dfrac{d^k}{\tau^{k+1}}\bigg[t^{\alpha-1}E_{\alpha-\beta}\Big(\frac{b}{\tau}t^{\alpha-\beta}\Big)\bigg]^{\ast(k+1)}\bigg|\leq\dfrac{|d|^kC^{k+1}}{\tau^{k+1}}g_{(k+1)\alpha}(t),\ \text{for all}\ k\in \mathbb{N}_0.
\end{align*}Hence,
\begin{align*}
|p_{\alpha,\beta}(t)|&=\bigg|\sum\limits_{k=0}^{\infty}\dfrac{d^k}{\tau^{k+1}}\bigg[t^{\alpha-1}E_{\alpha-\beta,\alpha}\Big(\dfrac{b}{\tau}t^{\alpha-\beta}\Big)\bigg]^{\ast(k+1)}\bigg|\\
&\leq \dfrac{C}{\tau}\sum_{k=0}^{\infty}\dfrac{|d|^kC^k}{\tau^k}\dfrac{t^{\alpha k+\alpha-1}}{\Gamma(\alpha k+\alpha)}=\dfrac{C}{\tau}t^{\alpha-1}\sum_{k=0}^{\infty}\dfrac{\bigg(\dfrac{|d|C}{\tau}t^{\alpha}\bigg)^k}{\Gamma(\alpha k+\alpha)}\\ &=\dfrac{C}{\tau}t^{\alpha-1}E_{\alpha,\alpha}\bigg(\dfrac{|d|C}{\tau}t^{\alpha}\bigg).
\end{align*} It proves that 
$p_{\alpha,\beta}(t)$ is well-defined for each t > 0, and Laplace transformable. Taking the Laplace transform of 
$p_{\alpha,\beta}(t)$, we have that
\begin{align*}
\widehat{p_{\alpha,\beta}}(\lambda)&=\mathcal{L}\Bigg(\sum\limits_{k=0}^{\infty}\dfrac{d^k}{\tau^{k+1}}\bigg[t^{\alpha-1}E_{\alpha-\beta,\alpha}\Big(\dfrac{b}{\tau}t^{\alpha-\beta}\Big)\bigg]^{\ast(k+1)}\Bigg)(\lambda)\\
&=\sum\limits_{k=0}^{\infty}\dfrac{d^k}{\tau^{k+1}}\bigg[\mathcal{L}\bigg(t^{\alpha-1}E_{\alpha-\beta,\alpha}\Big(\dfrac{b}{\tau}t^{\alpha-\beta}\Big)\bigg)(\lambda)\bigg]^{k+1}\\
&=\sum\limits_{k=0}^{\infty}d^k\bigg[\dfrac{1}{\tau}\mathcal{L}\bigg(t^{\alpha-1}E_{\alpha-\beta,\alpha}\Big(\dfrac{b}{\tau}t^{\alpha-\beta}\Big)\bigg)(\lambda)\bigg]^{k+1}=\sum\limits_{k=0}^{\infty}d^k\Bigg[\frac{\lambda^{-\beta}}{\tau\Big(\lambda^{\alpha-\beta}-\frac{b}{\tau}\Big)}\Bigg]^{k+1}\\
&=\sum\limits_{k=0}^{\infty}d^k\Bigg[\frac{\lambda^{-\beta}}{\tau\lambda^{\alpha-\beta}-b}\Bigg]^{k+1}=\sum\limits_{k=0}^{\infty}\dfrac{d^k\lambda^{-\beta k-\beta}}{(\tau\lambda^{\alpha-\beta}-b)^{k+1}}\\ &=\dfrac{\lambda^{-\beta}}{(\tau\lambda^{\alpha-\beta}-b)}\sum\limits_{k=0}^{\infty}\dfrac{d^k\lambda^{-\beta k}}{(\tau\lambda^{\alpha-\beta}-b)^k}.
\end{align*} Since 
$\frac{d\lambda^{-\beta}}{\tau \lambda^{\alpha-\beta}-b} \to 0$ as 
$\lambda \to \infty$, we obtain for λ sufficiently large
\begin{equation}
\widehat{p_{\alpha,\beta}}(\lambda)=\dfrac{\lambda^{-\beta}}{(\tau\lambda^{\alpha-\beta}-b)}\dfrac{1}{\bigg[1-\dfrac{d\lambda^{-\beta}}{\tau\lambda^{\alpha-\beta}-b}\bigg]}=\dfrac{1}{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}.
\end{equation} An application of [Reference Prüss31, theorem 0.4] with k = 1 and 
$g(\lambda)=\dfrac{1}{\tau\lambda^{\alpha}-b\lambda^{\beta}-d},$ together with the uniqueness of the Laplace transform, shows that 
$p'_{\alpha,\beta}(t)$ exists. We distinguish the following cases:
(I)
$0 \lt \beta \leq 1 \lt \alpha \lt 2.$ We define
$a(t)=a(g_{1-\beta}*p'_{\alpha,\beta})(t)+cp_{\alpha,\beta}(t)$ and
$k(t)=\tau (g_{2-\alpha}*p'_{\alpha,\beta})(t).$ From (4.3) and using the initial value theorem for the Laplace transform, we obtain
\begin{equation*}p_{\alpha,\beta}(0)=\lim\limits_{|\lambda|\to\infty}\lambda\widehat{p_{\alpha,\beta}}(\lambda)=\lim\limits_{|\lambda|\to\infty}\dfrac{1}{\lambda^{\alpha-1}\Big(\tau-\dfrac{b}{\lambda^{\alpha-\beta}}-\dfrac{d}{\lambda^{\alpha}}\Big)}=0.
\end{equation*}Therefore, taking the Laplace transform of a(t), we have
\begin{align*}
\widehat{a}(\lambda)&=a\lambda^{\beta}\widehat{p_{\alpha,\beta}}(\lambda)-\lambda^{\beta-1}p_{\alpha,\beta}(0)+c\widehat{p_{\alpha,\beta}}(\lambda)=\dfrac{a\lambda^{\beta}+c}{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}.
\end{align*}Analogously, taking the Laplace transform of k(t), we obtain
\begin{align*}
\widehat{k}(\lambda)=\tau\lambda^{\alpha-1}\widehat{p_{\alpha,\beta}}(\lambda)-\lambda^{\alpha-2}p_{\alpha,\beta}(0)=\dfrac{\tau\lambda^{\alpha-1}}{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}.
\end{align*}By
$(4.2)$, we conclude that
$\{R_{\alpha,\beta}(t)\}_{t\geq 0}$ is an (a, k)-regularized family.(II)
$0 \lt \beta \lt \alpha =1.$ We define
$a(t)=a(g_{1-\beta}*p'_{1,\beta})(t)+\dfrac{a}{\tau}g_{1-\beta}(t)+cp_{1,\beta}(t)$ and
$k(t)=\tau p_{1,\beta}(t)$. In this case, using the initial value theorem of Laplace transform, we obtain
\begin{equation*}p_{1,\beta}(0)=\lim\limits_{|\lambda|\to\infty}\lambda\widehat{p_{1,\beta}}(\lambda)=\lim\limits_{|\lambda|\to\infty}\dfrac{1}{\Big(\tau-\dfrac{b}{\lambda^{1-\beta}}-\dfrac{d}{\lambda}\Big)}=\dfrac{1}{\tau}.\end{equation*}Therefore, taking the Laplace transform of a(t), we have
\begin{align*}
\widehat{a}(\lambda)&=a\lambda^{\beta}\widehat{p_{1,\beta}}(\lambda)-a\lambda^{\beta-1}p_{1,\beta}(0)+\dfrac{a}{\tau}\dfrac{1}{\lambda^{1-\beta}}+c\widehat{p_{1,\beta}}(\lambda)\\ & =a\lambda^{\beta}\widehat{p_{1,\beta}}(\lambda)+c\widehat{p_{1,\beta}}(\lambda)=\dfrac{a\lambda^{\beta}+c}{\tau\lambda-b\lambda^{\beta}-d}.
\end{align*}Furthermore, taking the Laplace transform of k(t), we have
\begin{align*}
\widehat{k}(\lambda)=\tau\widehat{p_{1,\beta}}(\lambda)=\tau\dfrac{1}{\tau\lambda-b\lambda^{\beta}-d}=\dfrac{\tau}{\tau\lambda-b\lambda^{\beta}-d}.
\end{align*}
It proves the claim and finishes the proof.
We finish this section with the following lemma that will be useful in the next section.
Lemma 4.2. Let 
$0 \lt \beta\leq 1\leq\alpha \lt 2,$ 
$a,b,c,d,\tau\in\mathbb{R}, \, \tau \neq 0,$ where 
$(a,c)\neq (0,0).$ Let B be the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$. Then for each γ > 0, the family 
$\{(g_{\gamma}\ast R_{\alpha,\beta})(t)\}_{t\geq \rm{0}}$ is exponentially bounded and, for each 
$x\in X, \,\, (g_{\gamma}*R_{\alpha,\beta})(t)x\in \mathcal{D}(B)$.
Proof. By definition 2.10, the family 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$ is exponentially bounded and then for t > 0 and 
$x\in X$ we have
\begin{align*}
\|(g_{\gamma}\ast R_{\alpha,\beta})(t)x\|&\leq\int_{0}^{t}|g_{\gamma}(t-s)|\,\|R_{\alpha,\beta}(s)\|\|x\|ds \leq\int_{0}^{t}g_{\gamma}(t-s)Me^{\omega s}ds\|x\| \\ & =M\int_{0}^{t}g_{\gamma}(s)e^{\omega(t-s)}ds\|x\|\leq Me^{\omega t}\int_{0}^{\infty}g_{\gamma}(s)e^{-\omega s}ds\|x\|\\ &=\dfrac{M}{\omega^{\gamma}}e^{\omega t}\|x\|.
\end{align*} Since by theorem 4.1, 
$\{R_{\alpha,\beta}(t)\}_{t\geq 0}$ is an (a, k)-regularized family, then by lemma 2.13 we have that 
$(g_{\gamma}\ast R_{\alpha,\beta})(t)x\in\mathcal{D}(B)$ for each 
$x\in X$ and γ > 0.
We continue with the following result.
Lemma 4.3. Let 
$0 \lt \beta\leq 1\leq\alpha \lt 2,$ 
$ a,b,c,d,\tau\in\mathbb{R}, \, \tau \neq 0,$ where 
$(a,c)\neq (0,0),$ and let B be the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$. Then for all 
$x\in X$
\begin{align}
(g_{\alpha-1}*R_{\alpha,\beta})(t)x&=\dfrac{(aB+bI)}{\tau}(g_{2\alpha-\beta-1}*R_{\alpha,\beta})(t)x
+\dfrac{(cB+dI)}{\tau}\nonumber\\ &\quad\times (g_{2\alpha-1}*R_{\alpha,\beta})(t)x+g_{\alpha}(t)x.
\end{align}Proof. By theorem 4.1, 
$\{R_{\alpha,\beta}(t)\}_{t\geq 0}$ is an (a, k)-regularized family then by lemma 2.13, 
$(g_{\gamma}\ast R_{\alpha,\beta})(t)x\in\mathcal{D}(B)$ for each 
$x\in X$ and γ > 0. In addition, since 
$R_{\alpha,\beta}(t)$ and 
$(g_{\gamma}\ast R_{\alpha,\beta})(t)$, γ > 0 are exponentially bounded by definition 2.10 and lemma 4.2, taking the Laplace transform we obtain for any 
$x\in X$ and λ sufficiently large:
\begin{align*}
&\widehat{R_{\alpha,\beta}}(\lambda)\widehat{g_{\alpha-1}}(\lambda)x-\dfrac{1}{\tau}(aB+bI)\widehat{g_{2\alpha-\beta-1}}(\lambda)\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{1}{\tau}(cB+dI)\widehat{g_{2\alpha-1}}(\lambda)\\ &\times\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\dfrac{1}{\lambda^{\alpha-1}}\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{(aB+bI)}{\tau}\dfrac{1}{\lambda^{2\alpha-\beta-1}}\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{(cB+dI)}{\tau}\dfrac{1}{\lambda^{2\alpha-1}}\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\dfrac{\tau\lambda^{\alpha}}{\tau\lambda^{\alpha}}\dfrac{1}{\lambda^{\alpha-1}}\widehat{R_{\alpha,\beta}}(\lambda)x-(aB+bI)\dfrac{\lambda^{\beta}}{\tau\lambda^{\alpha}\lambda^{\alpha-1}}\widehat{R_{\alpha,\beta}}(\lambda)x-(cB+dI)\dfrac{1}{\tau\lambda^{\alpha}\lambda^{\alpha-1}}\\ &\times\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\dfrac{1}{\lambda^{\alpha}}\dfrac{1}{\tau\lambda^{\alpha-1}}\big[\tau\lambda^{\alpha}-\lambda^{\beta}(aB+bI)-(cB+dI)\big]\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\dfrac{1}{\lambda^{\alpha}}\dfrac{1}{\tau\lambda^{\alpha-1}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-a\lambda^{\beta}B-cB\big]\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\dfrac{1}{\lambda^{\alpha}}\dfrac{1}{\tau\lambda^{\alpha-1}}\bigg(\tau\lambda^{\alpha}-b\lambda^{\beta}-d-(a\lambda^{\beta}+c)B\bigg)\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\dfrac{1}{\lambda^{\alpha}}\dfrac{(a\lambda^{\beta}+c)}{\tau\lambda^{\alpha-1}}\bigg(\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{a\lambda^{\beta}+c}-B\bigg)\widehat{R_{\alpha,\beta}}(\lambda)x=\dfrac{x}{\lambda^{\alpha}}=\widehat{g_{\alpha}}(\lambda)x.
\end{align*}Hence, by uniqueness of the Laplace transform, we obtain (4.4).
We have the next lemma.
Lemma 4.4. Let 
$0 \lt \beta\leq 1\leq\alpha \lt 2,$ 
$ a,b,c,d,\tau\in\mathbb{R}, \, \tau \neq 0,$ where 
$(a,c)\neq (0,0),$ and let B be the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$. Then for all 
$x\in \mathcal{D}(B)$
\begin{align*}
&\tau R_{\alpha,\beta}(t)x-(aB+bI)\big(g_{\alpha-\beta}*R_{\alpha,\beta}\big)(t)x-\tau x-(aB+bI)\big(g_{\alpha-\beta}*R_{\alpha,\beta}\big)(t)x
\end{align*}
\begin{align}
&\quad+\dfrac{1}{\tau}(aB+bI)\big(g_{2\alpha-2\beta}*R_{\alpha,\beta}\big)(t)(aB+bI)x+g_{\alpha-\beta+1}(t)(aB+bI)x
\end{align}
\begin{align*}
&\quad-(cB+dI)\big(g_{\alpha}\ast R_{\alpha,\beta}\big)(t)x+\dfrac{1}{\tau}(cB+dI)\big(g_{2\alpha-\beta}\ast R_{\alpha,\beta}\big)(t)(aB+bI)x=0.
\end{align*}Proof. Note that by theorem 4.1 and lemma 2.13, for each 
$x\in X$, 
$(g_{\gamma} \ast R_{\alpha,\beta} )(t)x\in\mathcal{D}(B),\ \gamma \gt 0$, and since 
$x\in\mathcal{D}(B)$ we have that 
$(aB+bI)x\in X$ and 
$(g_{\gamma}\ast R_{\alpha,\beta})(t)(aB+bI)x\in\mathcal{D}(B)$, for each 
$x\in\mathcal{D}(B)$. Proceeding as in lemma 4.3, and taking the Laplace transform of (4.5), we obtain
\begin{align*}
&\tau \widehat{R_{\alpha,\beta}}(\lambda)x-(aB+bI)\widehat{R_{\alpha,\beta}}(\lambda)\widehat{g_{\alpha-\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x-(aB+bI)\widehat{R_{\alpha,\beta}}(\lambda)\widehat{g_{\alpha-\beta}}(\lambda)x\\
&\qquad+\dfrac{1}{\tau}(aB+bI)\widehat{R_{\alpha,\beta}}(\lambda)\widehat{g_{2\alpha-2\beta}}(\lambda)(aB+bI)x+(aB+bI)\widehat{g_{2\alpha-\beta+1}}(\lambda)x\\ \nonumber
&\qquad-(cB+dI)\widehat{g_{\alpha}}(\lambda)\widehat{R_{\alpha,\beta}}(\lambda)x+\dfrac{1}{\tau}(cB+dI)\widehat{g_{2\alpha-\beta}}(\lambda)\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&=\tau\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{(aB+bI)}{\lambda^{\alpha-\beta}}\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x-\dfrac{1}{\lambda^{\alpha-\beta}}\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&\qquad+\dfrac{1}{\tau}(aB+bI)\dfrac{1}{\lambda^{2\alpha-2\beta}}\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x+(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta+1}}x\\
&\qquad-(cB+dI)\dfrac{1}{\lambda^{\alpha}}\widehat{R_{\alpha,\beta}}(\lambda)x+\dfrac{1}{\tau}\dfrac{(cB+dI)}{\lambda^{2\alpha-\beta}}\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&=\bigg[\tau-\dfrac{1}{\lambda^{\alpha-\beta}}(aB+bI)-(cB+dI)\dfrac{1}{\lambda^{\alpha}}\bigg]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x+\dfrac{(aB+bI)}{\lambda^{\alpha-\beta+1}}x\\
&\qquad+\bigg[-\dfrac{1}{\lambda^{\alpha-\beta}}+\dfrac{1}{\tau}\dfrac{1}{\lambda^{2\alpha-2\beta}}(aB+bI)+\dfrac{1}{\tau\lambda^{2\alpha-\beta}}(cB+dI)\bigg]\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&=\bigg[\tau-\dfrac{\lambda^{\beta}}{\lambda^{\alpha}}(aB+bI)-(cB+dI)\dfrac{1}{\lambda^{\alpha}}\bigg]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x+\dfrac{(aB+bI)}{\lambda^{\alpha-\beta+1}}x\\
&\qquad+\bigg[-\dfrac{1}{\lambda^{\alpha-\beta}}+\dfrac{1}{\tau}\dfrac{\lambda^{\beta}}{\lambda^{2\alpha-\beta}}(aB+bI)+\dfrac{1}{\tau\lambda^{2\alpha-\beta}}(cB+dI)\bigg]\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&=\dfrac{1}{\lambda^{\alpha}}\big[\tau\lambda^{\alpha}-\lambda^{\beta}(aB+bI)-(cB+dI)\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x+(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta+1}}x\\
&\qquad+\bigg[-\dfrac{1}{\lambda^{\alpha-\beta}}\dfrac{\tau\lambda^{\alpha-1}}{\tau\lambda^{\alpha-1}}+\dfrac{1}{\tau}\dfrac{\lambda^{\beta}\lambda^{-1}}{\lambda^{\alpha-1}\lambda^{\alpha-\beta}}(aB+bI)\\
&\qquad\qquad+\dfrac{\lambda^{-1}}{\tau\lambda^{\alpha-1}\lambda^{\alpha-\beta}}(cB+dI)\bigg]\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&=\dfrac{1}{\lambda^{\alpha}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-a\lambda^{\beta}B-cB\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x+(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta+1}}x\\
&\qquad-\dfrac{1}{\lambda^{\alpha-\beta+1}}\dfrac{1}{\tau\lambda^{\alpha-1}}\big[\tau\lambda^{\alpha}-\lambda^{\beta}(aB+bI)-(cB+dI)\big]\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&=\dfrac{1}{\lambda^{\alpha}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-a\lambda^{\beta}B-cB\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x+(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta+1}}x\\
&\qquad-\dfrac{1}{\lambda^{\alpha-\beta+1}}\dfrac{1}{\tau\lambda^{\alpha-1}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-a\lambda^{\beta}B-cB\big]\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x \\ &=\dfrac{1}{\lambda^{\alpha}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-(a\lambda^{\beta}+c)B\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x+(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta+1}}x\\
&\qquad-\dfrac{1}{\lambda^{\alpha-\beta+1}}\dfrac{1}{\tau\lambda^{\alpha-1}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-(a\lambda^{\beta}+c)B\big]\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x \end{align*}
\begin{align*}
&=\dfrac{\tau\lambda^{-1}}{\tau\lambda^{-1}}\dfrac{(a\lambda^{\beta}+c)}{\lambda^{\alpha}}\bigg[\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{(a\lambda^{\beta}+c)}-B\bigg]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda}x+(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta+1}}x\\
&\qquad-\dfrac{1}{\lambda^{\alpha-\beta+1}}\dfrac{(a\lambda^{\beta}+c)}{\tau\lambda^{\alpha-1}}\bigg[\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{(a\lambda^{\beta}+c)}-B\bigg]\widehat{R_{\alpha,\beta}}(\lambda)(aB+bI)x\\
&=\tau\lambda^{-1}x-\dfrac{\tau}{\lambda}x+(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta+1}}x-\dfrac{1}{\lambda^{\alpha-\beta+1}}(aB+bI)x=0.
\end{align*}Hence, the claim follows by uniqueness of the Laplace transform.
We finally prove the following result.
Lemma 4.5. Let 
$0 \lt \beta\leq 1\leq\alpha \lt 2,$ 
$ a,b,c,d,\tau\in\mathbb{R}, \, \tau \neq 0,$ where 
$(a,c)\neq (0,0),$ and let B be the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$. Then for all 
$x\in X$, we have
\begin{align}&
\tau (g_1\ast R_{\alpha,\beta})(t)x-t\tau x-(aB+bI)(g_{\alpha-\beta}\ast g_1\ast R_{\alpha,\beta})(t)x-(cB+dI)\nonumber\\ &\quad\times(g_\alpha\ast g_1\ast R_{\alpha,\beta})(t)x=0.
\end{align}Proof. We have
\begin{align*}
&\dfrac{\tau}{\lambda} \widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda^2}x-(aB+bI)\widehat{g_{\alpha-\beta}}(\lambda)\dfrac{1}{\lambda}\widehat{R_{\alpha,\beta}}(\lambda)x-(cB+dI)\widehat{g_\alpha}(\lambda)\dfrac{1}{\lambda}\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\dfrac{\tau}{\lambda}\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda^2}x-(aB+bI)\dfrac{1}{\lambda^{\alpha-\beta}}\dfrac{1}{\lambda}\widehat{R_{\alpha,\beta}}(\lambda)x-(cB+dI)\dfrac{1}{\lambda^{\alpha}}\dfrac{1}{\lambda}\widehat{R_{\alpha,\beta}}(\lambda)x\\
&=\bigg[\dfrac{\tau}{\lambda}-\dfrac{\lambda^{\beta}}{\lambda^{\alpha}}\dfrac{1}{\lambda}(aB+bI)-\dfrac{1}{\lambda^{\alpha}}\dfrac{1}{\lambda}(cB+dI)\bigg]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda^2}x\\
&=\dfrac{1}{\lambda^{\alpha}}\dfrac{1}{\lambda}\big[\tau\lambda^{\alpha}-\lambda^{\beta}(aB+bI)-(cB+dI)\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda^2}x\\
&=\dfrac{1}{\lambda^{\alpha}}\dfrac{1}{\lambda}\dfrac{\tau\lambda^{-1}}{\tau\lambda^{-1}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-a\lambda^{\beta}B-cB\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda^2}x\\
&=\dfrac{\tau\lambda^{-1}}{\lambda\tau\lambda^{\alpha-1}}\big[\tau\lambda^{\alpha}-b\lambda^{\beta}-d-(a\lambda^{\beta}+c)B\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda^2}x\\
&=\dfrac{\tau\lambda^{-1}}{\lambda}\dfrac{(a\lambda^{\beta}+c)}{\tau\lambda^{\alpha-1}}\bigg[\dfrac{\tau\lambda^{\alpha}-b\lambda^{\beta}-d}{(a\lambda^{\beta}+c)}-\big]\widehat{R_{\alpha,\beta}}(\lambda)x-\dfrac{\tau}{\lambda^2}x\\
&=\dfrac{\tau}{\lambda^2}x-\dfrac{\tau}{\lambda^2}x=0.
\end{align*}5. Well-posedness and sufficient conditions
Let B be a closed operator on a complex Banach space X. We consider the abstract Cauchy problem
\begin{equation}
\begin{cases}&\tau D_t^{\alpha}u(t)-(aB+bI)D_{t}^{\beta}u(t)-(cB+dI)u(t)=0,\\
&u(0)={x \in X,}\\
&u'(0)={y \in X,}\end{cases}
\end{equation} with τ ≠ 0, 
$a, b,\, c,\, d\in \mathbb{R}$ and 
$0 \lt \beta\leqslant 1 \lt \alpha\leqslant 2$, where 
$D_{t}^{\gamma}$ denotes the Caputo derivative of order γ > 0.
By a strict solution of (5.1), we understand a function 
$u\in C^2(\mathbb{R}_+;X)\cap C^1(\mathbb{R}_+;\mathcal{D}(B))$ such that 
$u(t)\in \mathcal{D}(B)$ for all 
$t\geq 0$ and (5.1) holds. If a strict solution exists, then it follows that 
$x,y \in \mathcal{D}(B).$ In applications, it is useful to find a weaker notion of solution where 
$x,y$ may be arbitrary. This can be done by integrating the equation. Assume that u is a strict solution. Since B is closed, it follows from [Reference Arendt, Batty, Hieber and Neubrander4, proposition 1.1.7] that 
$(g_{\alpha-\beta}*u)(t)\in \mathcal{D}(B),$ 
$(g_{\alpha}*u)(t)\in \mathcal{D}(B)$ and
\begin{align}
&\tau u(t) -(aB+bI)(g_{\alpha-\beta}\ast u)(t)-(cB+dI)(g_{\alpha}\ast u)(t) =\tau(x+ty) - \displaystyle g_{\alpha-\beta+1}(t)\nonumber\\ &\quad\times (aB+bI)x,\ t \gt 0.
\end{align}We introduce the following definition.
Definition 5.1. Let 
$0 \lt \beta \lt \alpha.$ A function 
$u\in C(\mathbb{R}_+;X)$ is called a mild solution of (5.1) if 
$(g_{\alpha-\beta}*u)(t)\in \mathcal{D}(B),$ 
$(g_{\alpha}*u)(t)\in \mathcal{D}(B)$ for all t > 0 and (5.2) holds.
It is clear that mild and strict solutions differ merely by regularity.
Definition 5.2. We say that (5.1) is well-posed if for each 
$x\in \mathcal{D}(B)$ and each 
$y\in X$ there exists a unique mild solution.
We observe that this notion of well-posedness has been considered by other authors, see, e.g., references [Reference Arendt, Batty, Hieber and Neubrander4, Reference Keyantuo, Lizama, Amann, Arendt, Hieber, Neubrander, Nicaise and von Below16, Reference Keyantuo, Lizama and Poblete17] where it is named mildly well-posedness. Our first main result in this section is the following.
Theorem 5.3.
Let 
$0 \lt \beta \lt \alpha$, 
$(a,c)\neq (0,0)$. Let B the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$ on 
$X.$ Then (5.1) is well-posed.
Proof. Uniqueness: Let 
$u_1, u_2 \in C(\mathbb{R}_+;X)$ be two mild solutions of (5.1). Then 
$u:=u_1-u_2\in C(\mathbb{R}_+;X)$ and 
$\tau u(t) -(aB+bI)(g_{\alpha-\beta}\ast u)(t)-(cB+dI)(g_{\alpha}\ast u)(t) =0, $ for all 
$t\geq 0$. Hence
\begin{equation*}
(\tau g_{\beta} -(aB+bI)g_{\alpha}-(cB+dI)g_{\alpha+\beta})\ast u(t) =0.
\end{equation*} Therefore, by Titchmarch’s theorem, it follows that 
$u \equiv 0.$
Existence: Let 
$x\in \mathcal{D}(B)$ and 
$y\in X$. We define
\begin{align}
u(t)& = R_{\alpha,\beta}(t)x+ \int_0^t R_{\alpha,\beta}(t-s)\Big[ y - \frac{1}{\tau} g_{\alpha-\beta}(s) (aB+bI)x \Big]ds, \quad t\geq 0.
\end{align}We divide the proof in three steps.
Step 1: When y = 0 we define
\begin{equation}
u_1(t)=R_{\alpha,\beta}(t)x-\dfrac{1}{\tau}(g_{\alpha-\beta}\ast R_{\alpha,\beta})(t)(aB+bI)x.
\end{equation} Now, we will to show that 
$(5.4)$ satisfies the expression 
$(5.2)$. In fact, it is enough to show that
\begin{align*}
&\tau\big(u_1(t)-x\big)-(aB+bI)\big[(g_{\alpha-\beta}\ast u_1)(t)-g_{\alpha-\beta+1}(t)x\big] -(cB+dI)(g_{\alpha}\ast u_1)(t)=0.
\end{align*} By theorem 4.1 and lemma 2.13, for each 
$x\in X$, 
$(g_{\gamma}\ast R_{\alpha,\beta})(t)x\in\mathcal{D}(B),\ \gamma \gt 0$, and since 
$x\in\mathcal{D}(B)$ for a ≠ 0, we have that 
$(aB+bI)x\in X$ and 
$(g_{\gamma}\ast R_{\alpha,\beta})(t)(aB+bI)x\in\mathcal{D}(B)$, for each 
$x\in\mathcal{D}(B)$. Hence 
$(g_{\alpha-\beta}*u_1)(t)\in \mathcal{D}(B)$ and 
$(g_{\alpha}*u_1)(t)\in \mathcal{D}(B).$ Using (5.4) and lemma 4.4, we obtain that
\begin{align*}
&\tau R_{\alpha,\beta}(t)x-\big(g_{\alpha-\beta}\ast R_{\alpha,\beta}\big)(t)(aB+bI)x-\tau x-(aB+bI)\big(g_{\alpha-\beta}\ast R_{\alpha,\beta}\big)(t)x\\
&\quad+\dfrac{1}{\tau}(aB+bI)\big(g_{2\alpha-2\beta}\ast R_{\alpha,\beta}\big)(t)(aB+bI)x+(aB+bI)g_{\alpha-\beta+1}(t)x\\
&\quad-(cB+dI)\big(g_{\alpha}\ast R_{\alpha,\beta}\big)(t)x+\dfrac{1}{\tau}(cB+dI)\big(g_{2\alpha-\beta}\ast R_{\alpha,\beta}\big)(t)(aB+bI)x\\
&=\bigg[\tau R_{\alpha,\beta}(t)-\big(g_{\alpha-\beta}\ast R_{\alpha,\beta}\big)(t)(aB+bI)-\tau-(aB+bI)\big(g_{\alpha-\beta}\ast R_{\alpha,\beta}\big)(t)\\
&\quad+\dfrac{1}{\tau}(aB+bI)\big(g_{2\alpha-2\beta}\ast R_{\alpha,\beta}\big)(t)(aB+bI)+(aB+bI)g_{\alpha-\beta+1}(t)\\
&\quad-(cB+dI)\big(g_{\alpha}\ast R_{\alpha,\beta}\big)(t)+\dfrac{1}{\tau}(cB+dI)\big(g_{2\alpha-\beta}\ast R_{\alpha,\beta}\big)(t)(aB+bI)\bigg]x=0,
\end{align*} proving that 
$u_1(t)$ satisfies (5.2).
Step 2: When x = 0 we define
\begin{equation}
u_2(t)=(g_1\ast R_{\alpha,\beta})(t)y.
\end{equation} By lemma 2.13, it is clear that 
$(g_{\alpha-\beta}*u_2)(t)\in \mathcal{D}(B)$ and 
$(g_{\alpha}*u_2)(t)\in \mathcal{D}(B).$ We will show that
\begin{align*}
&\tau\big(u_2(t)-ty\big)-(aB+bI)\big[(g_{\alpha-\beta}\ast u_2)(t)\big]-(cB+dI)(g_{\alpha}\ast u_2)(t)=0.
\end{align*}In fact, using (5.5), we obtain that the left hand side of the above identity equals to
\begin{align*}
&\tau (g_1\ast R_{\alpha,\beta})(t)y-t\tau y-(aB+bI)(g_{\alpha-\beta}\ast g_1\ast R_{\alpha,\beta})(t)y-(cB+dI)\\ &\quad\times (g_{\alpha}\ast g_1\ast R_{\alpha,\beta})(t)y
\end{align*}being this expression zero by lemma 4.5, as desired.
Step 3: By steps 1 and 2, we obtain that
\begin{align*}
u(t)=u_1(t)+u_2(t)
\end{align*}satisfy (5.2). This proves the theorem.
Now we consider the non-homogeneous abstract Cauchy problem. Let B be a closed operator and let 
$f\in L^1([0,T],X)$ where T > 0. For 
$0 \lt \beta\leq 1 \lt \alpha\leq 2$ we consider the problem
\begin{equation}
\begin{cases}&\tau D_t^{\alpha}u(t)-(aB+bI)D_{t}^{\beta}u(t)-(cB+dI)u(t)=f(t),\quad t\in [0,T],\\
&u(0)=x,\\
&u'(0)=y,\end{cases}
\end{equation} where 
$x\in \mathcal{D}(B)$ and 
$y \in X.$ A function 
$u\in C([0,T],X)$ is called a mild solution of (5.6) if 
$(g_{\alpha-\beta}*u)(t)\in \mathcal{D}(B),$ 
$(g_{\alpha}*u)(t)\in \mathcal{D}(B)$ and
\begin{equation}\begin{aligned}
& \tau u(t) -(aB+bI)(g_{\alpha-\beta}\ast u)(t)-(cB+dI)(g_{\alpha}\ast u)(t) = (g_{\alpha}*f)(t) + \tau(x+ty)\\ &\quad - \displaystyle g_{\alpha-\beta+1}(t)(aB+bI)x, \quad t\in [0,T].
\end{aligned}\end{equation}Our main theorem in this section show that in the case when B generates a solution family there always exists a mild solution.
Theorem 5.4.
Let 
$0 \lt \beta \lt \alpha ,\ \alpha \gt 1,$ 
$ a,b,c,d,\tau\in\mathbb{R}, \, \tau \neq 0,$ where 
$(a,c)\neq (0,0).$ Let B be the generator of a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geqslant0}$ on 
$X.$ Then for every 
$f\in L^1([0,T],X)$ the problem (5.6) has a unique mild solution u given by
\begin{align}
u(t)& = R_{\alpha,\beta}(t)x+ \int_0^t R_{\alpha,\beta}(t-s)\Big[ y - \frac{1}{\tau} g_{\alpha-\beta}(s) (aB+bI)x \Big]ds\nonumber\\ &\quad + \frac{1}{\tau}\int_0^tR_{\alpha,\beta}(t-s) (g_{\alpha-1}*f)(s)] ds.
\end{align}Proof. Uniqueness is proven as in theorem 5.3. For existence, we have seen that
\begin{equation*}
R_{\alpha,\beta}(t)x+ \int_0^t R_{\alpha,\beta}(t-s)\Big[ y - \frac{1}{\tau} g_{\alpha-\beta}(s) (aB+bI)x \Big]ds
\end{equation*}is a mild solution of the homogeneous problem. It remains to show that
\begin{equation}
u_1(t)=\dfrac{1}{\tau}(g_{\alpha-1}\ast R_{\alpha,\beta}\ast f)(t)
\end{equation} is a mild solution of (5.6) with initial value 
$x=y=0.$ Extending f by 0 to 
$\mathbb{R}_+$, we have that 
$u_1 \in C([0,T];X).$ Note that 
$(g_{\alpha-\beta}*u_1)(t)\in \mathcal{D}(B)$ and 
$(g_{\alpha}*u_1)(t)\in \mathcal{D}(B)$ thanks to lemma 2.13. Using 
$(5.9)$ and lemma 4.3, we obtain that
\begin{align*}
&\tau u_1(t)-(aB+bI)(g_{\alpha-\beta}\ast u_1)(t)-(cB+dI)(g_{\alpha}\ast u_1)(t)-(g_{\alpha}\ast f)(t) \\ & =
\tau\big(\dfrac{1}{\tau}(g_{\alpha-1}\ast R_{\alpha,\beta}\ast f)(t)\big)-(aB+bI)\big[(g_{\alpha-\beta}\ast \dfrac{1}{\tau} g_{\alpha-1}\ast R_{\alpha,\beta}\ast f)(t)\big]\\
&\quad-(cB+dI)(g_{\alpha}\ast \dfrac{1}{\tau}g_{\alpha-1}\ast R_{\alpha,\beta}\ast f)(t)-(g_{\alpha}\ast f)(t)\\
&=(g_{\alpha-1}\ast R_{\alpha,\beta}\ast f)(t)-\dfrac{(aB+bI)}{\tau}(g_{2\alpha-\beta-1}\ast R_{\alpha,\beta}\ast f)(t)\\
&\quad-\dfrac{(cB+dI)}{\tau}(g_{2\alpha-1}\ast R_{\alpha,\beta}\ast f)(t)-(g_{\alpha}\ast f)(t)\\
&=\bigg(\bigg[(g_{\alpha-1}\ast R_{\alpha,\beta})(t)-\dfrac{(aB+bI)}{\tau}(g_{2\alpha-\beta-1}\ast R_{\alpha,\beta})(t)\\
&\quad-\dfrac{(cB+dI)}{\tau}(g_{2\alpha-1}\ast R_{\alpha,\beta})(t)\bigg]\ast f\bigg)(t)-(g_{\alpha}\ast f)(t)\\
&=(g_{\alpha}\ast f)(t)-(g_{\alpha}\ast f)(t)=0
\end{align*} proving that 
$u_1(t)$ satisfies (5.7). This proves the claim.
6. Examples
We finish this work illustrating some special cases where our abstract results apply.
6.1. Linear Kuznetsov equation
The Kuznetsov equation [Reference Kuznetsov22] models propagation of non-linear acoustic waves in thermoviscous elastic media. This equation is treated in different works, for example, see [Reference Dekkers and Rozanova-Pierrat11, Reference Kaltenbacher, Lasiecka and Marchand15].
We consider the following linear version of de Kuznetsov equation, with fractional order in time, and Dirichlet boundary conditions
\begin{equation}
\begin{cases}&u_{tt}(t,x)-c^2\Delta u(t,x)-\dfrac{\delta}{p_0}\Delta D^{\beta}_t u(t,x)=f(t,x),\ \, t \gt 0,\,\, x\in(0,1)\\
& u(t,0)=u(t,1)=0,\, \ u(0,x)=u_0(x),\ u_t(0,x)=u_1(x),
\end{cases}
\end{equation} where 
$0 \lt \beta \lt 1,$ where 
$u(x,0)=u_0(x),\ u_t(x,0)=u_1(x)$ and 
$c,\ p_0,\ \gamma,\ \delta$ are the velocity of the sound, the density, the ratio of the specific heats, and the viscosity of the medium, respectively.
Choose 
$X=L^p(0,1),\ 1\leq p \lt \infty$. Consider 
$B=\Delta$ be the Dirichlet Laplacian on 
$L^p(0,1)$, with
\begin{equation*}\mathcal{D}(B):=W_{0}^{2,p}(0,1)=\{v\in W^{2,p}(0,1);\, v(0)=v(1)=0\}.\end{equation*} Then, by [Reference Keyantuo and Warma19, lemma 2.3], for every 
$1\leq p \lt \infty,$ B generates a bounded cosine family in X. Therefore, using theorems 3.9 and 5.4, we obtain the following result.
Theorem 6.1.
Let 
$0 \lt \beta \lt 1,\ \leq p \lt \infty,$ 
$f\in L_{loc}^{1}(\mathbb{R}_+;L^p(0,1))$ be such that 
$\int_{0}^{\infty}e^{-\omega t}\|f(t)\|dt \lt \infty$ for some ω > 0. Then for all 
$u_0\in W_{0}^{2,p}(0,1)$ and 
$u_1 \in L^p(0,1)$, there is a unique 
$u\in C(\mathbb{R}_+;L^p(0,1))$ satisfying
\begin{align*}
&\tau\big(u(t,x)-u_0(x)-tu_1(x)\big)-\frac{\delta}{p_0\Gamma(2-\beta)}\Delta \int_{0}^{t}(t-s)^{1-\beta}u(s,x)ds\\ &\quad + \frac{\delta}{p_0\Gamma(3-\beta)} t^{2-\beta} \Delta u_0(x) \\ & \quad \qquad \qquad \qquad -c^2\Delta\int_{0}^{t}(t-s)u(s,x)ds =\int_{0}^{t}(t-s)f(s,x)ds,\ t\geq0, \,\, x\in (0,1).
\end{align*}Proof. Note that Eq. 
$(6.1)$ is a particular case of 
$(1.1)$ when we consider 
$\tau=1,\ \alpha=2,\ 0 \lt \beta \lt 1,\ a=\dfrac{\delta}{p_0} \gt 0,\ c=c^2 \gt 0,\ B=\Delta,\ b=d=0$, and 
$f\in L_{loc}^{1}(\mathbb{R}_+;L^2(\Omega))$.
Consider the abstract model
\begin{equation}
u''(t)-aBD^{\beta}_t u(t)-cBu(t)=f(t),\,\qquad t\geq 0,
\end{equation} where 
$0 \lt \beta \lt 1,$ 
$a,c \gt 0,$ 
$u(0)\in \mathcal{D}(B)$ and 
$u'(0) \in X$. Using theorems 3.9 and 5.4, we obtain the following general result.
Theorem 6.2.
Let B be the generator of a cosine family, then, for each 
$f\in L_{loc}^{1}(\mathbb{R}_+;X)$ such that 
$\int_{0}^{\infty}e^{-\omega t}\|f(t)\|dt \lt \infty,\ \omega \gt 0$, the model (6.2) has a unique mild solution.
6.2. Linear Klein–Gordon equation
Let 
$\Omega\subset\mathbb{R}^N$ be an open bounded set with sufficiently smooth boundary 
$\partial\Omega.$ We consider the following fractional version of the Klein–Gordon equation
\begin{equation}
\begin{cases}&D^{\alpha}_t \varphi(t,x)- a \Delta D^{\beta}_t \varphi(t,x)- bD^{\beta}_t \varphi(t,x)-\Delta\varphi(t,x)-d\varphi(t,x)=f(t,x),\\ &\quad (t,x)\in\mathbb{R}_+\times\Omega\\
&\varphi(t,x)=0,\ (t,x)\in\mathbb{R}_+\times\partial\Omega\\
&\varphi(0,x)=\varphi_0(x),\ \varphi_t(0, x) = \varphi_1(x),\ x \in\Omega,
\end{cases}
\end{equation} where 
$a \gt 0,\,\, b \lt 0$ and 
$d\in \mathbb{R},$ see [Reference Aviles and Sandefur5, Section 1] in case α = 2 and β = 1.
Let 
$X=L^2(\Omega).$ We define 
$(Bv)(x)=(\Delta v)(x)$, 
$x\in\Omega$, 
$v\in\mathcal{D}(B)$ and
\begin{equation}
\mathcal{D}(B):=\{v\in H_{0}^{1}(\Omega); Bv\in L^2(\Omega)\}.
\end{equation}Using theorem 5.4, we obtain the following result.
Theorem 6.3.
Let 
$a \gt 0,\,\, b \lt 0,\ 0 \lt \beta \lt \alpha,$ α > 1, and 
$f\in L^{1}([0,T], L^2(\Omega)).$ Suppose that the Laplacian operator 
$B:=\Delta$ generates a solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq0}$ on 
$L^2(\Omega)$. Then, for all 
$\varphi_0 \in \mathcal{D}(B) $ and 
$\varphi_1\in L^{2}(\Omega)$, there exists a unique 
$u\in C([0,T], L^2(\Omega))$ such that
\begin{align*}
&\varphi(t,x)-\varphi_0(x)-t\varphi_1(x) -(a\Delta+bI)\bigg[\int_{0}^{t}g_{\alpha-\beta}(t-s)u(s,x)ds-g_{\alpha-\beta+1}(t)x\bigg]\\
&\qquad-(\Delta+dI)\int_{0}^{t}g_{\alpha}(t-s)u(s,x)ds=\int_{0}^{t}g_{\alpha}(t-s)f(s,x)ds,\ t\geq0.
\end{align*} For example, in case α = 2 and β = 1, we know by [Reference Arendt, Batty, Hieber and Neubrander4, example 7.2.1, p. 424] that B is the generator of a C 0-semigroup on 
$L^2(\Omega)$ and therefore, by [Reference Neubrander28, corollary 13], a solution family 
$\{R_{2,1}(t)\}_{t\geq0}$ on 
$L^2(\Omega)$ always exists and is given by
\begin{equation}
R_{2,1}(t)v: = W'(t)v, \quad v \in \mathcal{D}(B),
\end{equation} where 
$\{W(t)\}_{t\geq 0}\subset \mathcal{L}(L^2(\Omega))$ is a strongly differentiable family, see [Reference Neubrander28, corollary 13].
Acknowledgements
J. A. is partially supported by National Council for Scientific Technological Development (CNPq, Brazil) process number 200454/2022-6 and partially supported by CAPES. C. L. is partially supported by CONICYT under FONDECYT grant number 1220036.
