We generalise the properties $\mathsf {OP}$, $\mathsf {IP}$, k-$\mathsf {TP}$, $\mathsf {TP}_{1}$, k-$\mathsf {TP}_{2}$, $\mathsf {SOP}_{1}$, $\mathsf {SOP}_{2}$, and $\mathsf {SOP}_{3}$ to positive logic, and prove various implications and equivalences between them. We also provide a characterisation of stability in positive logic in analogy with the one in full first-order logic, both on the level of formulas and on the level of theories. For simple theories there are the classically equivalent definitions of not having $\mathsf {TP}$ and dividing having local character, which we prove to be equivalent in positive logic as well. Finally, we show that a thick theory T has $\mathsf {OP}$ iff it has $\mathsf {IP}$ or $\mathsf {SOP}_{1}$ and that T has $\mathsf {TP}$ iff it has $\mathsf {SOP}_{1}$ or $\mathsf {TP}_{2}$, analogous to the well-known results in full first-order logic where $\mathsf {SOP}_{1}$ is replaced by $\mathsf {SOP}$ in the former and by $\mathsf {TP}_{1}$ in the latter. Our proofs of these final two theorems are new and make use of Kim-independence.

We obtain an array of consistency results concerning trees and stationary reflection at double successors of regular cardinals $\kappa $ , updating some classical constructions in the process. This includes models of $\mathsf {CSR}(\kappa ^{++})\wedge {\sf TP}(\kappa ^{++})$ (both with and without ${\sf AP}(\kappa ^{++})$ ) and models of the conjunctions ${\sf SR}(\kappa ^{++}) \wedge \mathsf {wTP}(\kappa ^{++}) \wedge {\sf AP}(\kappa ^{++})$ and $\neg {\sf AP}(\kappa ^{++}) \wedge {\sf SR}(\kappa ^{++})$ (the latter was originally obtained in joint work by Krueger and the first author [9], and is here given using different methods). Analogs of these results with the failure of $\sf {SH}(\kappa ^{++})$ are given as well. Finally, we obtain all of our results with an arbitrarily large $2^\kappa $ , applying recent joint work by Honzik and the third author.

We present an alternative proof that from large cardinals, we can force the tree property at $\kappa ^+$ and $\kappa ^{++}$ simultaneously for a singular strong limit cardinal $\kappa $ . The advantage of our method is that the proof of the tree property at the double successor is simpler than in the existing literature. This new approach also works to establish the result for $\kappa =\aleph _{\omega ^2}$ .

In the first part of the article, we show that if 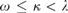$\omega \le \kappa < \lambda$ are cardinals, 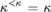${\kappa ^{ < \kappa }} = \kappa$, and λ is weakly compact, then in 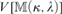$V\left[M {\left( {\kappa ,\lambda } \right)} \right]$ the tree property at $$\lambda = \left( {\kappa ^{ + + } } \right)^{V\left[ {\left( {\kappa ,\lambda } \right)} \right]} $$ is indestructible under all 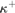${\kappa ^ + }$-cc forcing notions which live in 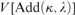$V\left[ {{\rm{Add}}\left( {\kappa ,\lambda } \right)} \right]$, where 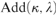${\rm{Add}}\left( {\kappa ,\lambda } \right)$ is the Cohen forcing for adding λ-many subsets of κ and 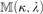$\left( {\kappa ,\lambda } \right)$ is the standard Mitchell forcing for obtaining the tree property at $\lambda = \left( {\kappa ^{ + + } } \right)^{V\left[ {\left( {\kappa ,\lambda } \right)} \right]} $. This result has direct applications to Prikry-type forcing notions and generalized cardinal invariants. In the second part, we assume that λ is supercompact and generalize the construction and obtain a model 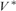${V^{\rm{*}}}$, a generic extension of V, in which the tree property at ${\left( {{\kappa ^{ + + }}} \right)^{{V^{\rm{*}}}}}$ is indestructible under all ${\kappa ^ + }$-cc forcing notions living in $V\left[ {{\rm{Add}}\left( {\kappa ,\lambda } \right)} \right]$, and in addition under all forcing notions living in 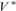${V^{\rm{*}}}$ which are ${\kappa ^ + }$-closed and “liftable” in a prescribed sense (such as ${\kappa ^{ + + }}$-directed closed forcings or well-met forcings which are 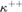${\kappa ^{ + + }}$-closed with the greatest lower bounds).

We construct a model in which the tree property holds in ${\aleph _{\omega + 1}}$ and it is destructible under $Col\left( {\omega ,{\omega _1}} \right)$. On the other hand we discuss some cases in which the tree property is indestructible under small or closed forcings.

We show that from large cardinals it is consistent to have the tree property simultaneously at ${\aleph _{{\omega ^2} + 1}}$ and ${\aleph _{{\omega ^2} + 2}}$ with ${\aleph _{{\omega ^2}}}$ strong limit.

Three central combinatorial properties in set theory are the tree property, the approachability property and stationary reflection. We prove the mutual independence of these properties by showing that any of their eight Boolean combinations can be forced to hold at ${\kappa ^{ + + }}$, assuming that $\kappa = {\kappa ^{ < \kappa }}$ and there is a weakly compact cardinal above κ.

If in addition κ is supercompact then we can force κ to be ${\aleph _\omega }$ in the extension. The proofs combine the techniques of adding and then destroying a nonreflecting stationary set or a ${\kappa ^{ + + }}$-Souslin tree, variants of Mitchell’s forcing to obtain the tree property, together with the Prikry-collapse poset for turning a large cardinal into ${\aleph _\omega }$.

A narrow system is a combinatorial object introduced by Magidor and Shelah in connection with work on the tree property at successors of singular cardinals. In analogy to the tree property, a cardinal κ satisfies the narrow system property if every narrow system of height κ has a cofinal branch. In this paper, we study connections between the narrow system property, square principles, and forcing axioms. We prove, assuming large cardinals, both that it is consistent that ℵω+1 satisfies the narrow system property and $\square _{\aleph _\omega , < \aleph _\omega } $ holds and that it is consistent that every regular cardinal satisfies the narrow system property. We introduce natural strengthenings of classical square principles and show how they can be used to produce narrow systems with no cofinal branch. Finally, we show that the Proper Forcing Axiom implies that every narrow system of countable width has a cofinal branch but is consistent with the existence of a narrow system of width ω1 with no cofinal branch.

We show that from infinitely many supercompact cardinals one can force a model of ZFC where both the tree property and the stationary reflection hold at אω2+1.

Assuming ω supercompact cardinals we force to obtain a model where the tree property holds both at אω+1, and at אn for all 2 ≤ n < ω. A model with the former was obtained by Magidor–Shelah from a large cardinal assumption above a huge cardinal, and recently by Sinapova from ω supercompact cardinals. A model with the latter was obtained by Cummings–Foreman from ω supercompact cardinals. Our model, where the two hold simultaneously, is another step toward the goal of obtaining the tree property on increasingly large intervals of successor cardinals.

An inaccessible cardinal is strongly compact if, and only if, it satisfies thestrong tree property. We prove that if there is a model of ZFC with infinitelymany supercompact cardinals, then there is a model of ZFC where ${\aleph _{\omega + 1}}$ has the strong tree property. Moreover, we prove that everysuccessor of a singular limit of strongly compact cardinals has the strong treeproperty.

We study the consequences of stationary and semi-stationary set reflection. We show that the semi-stationary reflection principle implies the Singular Cardinal Hypothesis, the failure of the weak square principle, etc. We also consider two cardinal tree properties introduced recently by Weiss, and prove that they follow from stationary and semi-stationary set reflection augmented with a weak form of Martin’s Axiom. We also show that there are some differences between the two reflection principles, which suggests that stationary set reflection is analogous to supercompactness, whereas semi-stationary set reflection is analogous to strong compactness.

An inaccessible cardinal κ is supercompact when (κ, λ)-ITP holds for all λ ≥ κ. We prove that if there is a model of ZFC with infinitely many supercompact cardinals, then there is a model of ZFC where for every n ≥ 2 and μ ≥ ℕn, we have (ℕn, μ)-ITP.