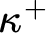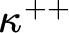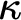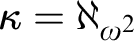1 Introduction
A regular uncountable cardinal
![]() $\kappa $
has the tree property if every
$\kappa $
has the tree property if every
![]() $\kappa $
-tree has a cofinal branch, or equivalently there are no
$\kappa $
-tree has a cofinal branch, or equivalently there are no
![]() $\kappa $
-Aronszajn trees. The tree property belongs to a family of compactness properties which are of great interest in combinatorial set theory. Compactness is the phenomenon where if some property holds for every strictly smaller substructure of an object, it holds for the entire object. Like other compactness properties such as stationary reflection, the tree property is a property of “large cardinal type” which can consistently hold at certain small regular cardinals.
$\kappa $
-Aronszajn trees. The tree property belongs to a family of compactness properties which are of great interest in combinatorial set theory. Compactness is the phenomenon where if some property holds for every strictly smaller substructure of an object, it holds for the entire object. Like other compactness properties such as stationary reflection, the tree property is a property of “large cardinal type” which can consistently hold at certain small regular cardinals.
An old question due to Magidor asks whether the tree property can consistently hold simultaneously at all regular
![]() $\kappa> \aleph _1$
. There are several obstacles to obtaining a positive consistency result for this problem:
$\kappa> \aleph _1$
. There are several obstacles to obtaining a positive consistency result for this problem:
-
• Specker showed that if
 $\tau ^{<\tau } = \tau $
, then there is a special
$\tau ^{<\tau } = \tau $
, then there is a special
 $\tau ^+$
-Aronszajn tree. So a positive result requires a model where there are no strongly inaccessible cardinals and the GCH fails everywhere. In particular the SCH must fail at every singular strong limit cardinal.
$\tau ^+$
-Aronszajn tree. So a positive result requires a model where there are no strongly inaccessible cardinals and the GCH fails everywhere. In particular the SCH must fail at every singular strong limit cardinal. -
• Jensen showed that the weak square principle
 $\square ^*_\tau $
is equivalent to the existence of a special
$\square ^*_\tau $
is equivalent to the existence of a special
 $\tau ^+$
-Aronszajn tree. Results from inner model theory show that the failure of
$\tau ^+$
-Aronszajn tree. Results from inner model theory show that the failure of
 $\square ^*_\tau $
for any singular
$\square ^*_\tau $
for any singular
 $\tau $
requires very substantial large cardinal hypotheses.
$\tau $
requires very substantial large cardinal hypotheses.
A test question which exposes some of the main difficulties asks whether there can exist a singular strong limit cardinal
![]() $\kappa $
such that both
$\kappa $
such that both
![]() $\kappa ^+$
and
$\kappa ^+$
and
![]() $\kappa ^{++}$
have the tree property. This question was resolved positively by Sinapova [Reference Sinapova5], and in subsequent work Sinapova and Unger [Reference Sinapova and Unger6] showed that the singular cardinal
$\kappa ^{++}$
have the tree property. This question was resolved positively by Sinapova [Reference Sinapova5], and in subsequent work Sinapova and Unger [Reference Sinapova and Unger6] showed that the singular cardinal
![]() $\kappa $
can consistently be
$\kappa $
can consistently be
![]() $\aleph _{\omega ^2}$
.
$\aleph _{\omega ^2}$
.
In [Reference Sinapova5], the main forcing was diagonal Prikry forcing interleaved into a Mitchell style poset. The proof of the tree property at
![]() $\kappa ^{++}$
generalized an argument of Cummings and Foreman [Reference Cummings and Foreman1]; this form of argument also appears in work of Unger [Reference Unger7]. The hardest point in the argument of [Reference Sinapova5] was to show the tree property at
$\kappa ^{++}$
generalized an argument of Cummings and Foreman [Reference Cummings and Foreman1]; this form of argument also appears in work of Unger [Reference Unger7]. The hardest point in the argument of [Reference Sinapova5] was to show the tree property at
![]() $\kappa ^+$
, which required a complicated argument. One disadvantage to interleaving the Prikry forcing inside the Mitchell poset is that the construction is not amenable to including collapses to make
$\kappa ^+$
, which required a complicated argument. One disadvantage to interleaving the Prikry forcing inside the Mitchell poset is that the construction is not amenable to including collapses to make
![]() $\kappa $
small; in particular this approach is not suited to make
$\kappa $
small; in particular this approach is not suited to make
![]() $\kappa $
into
$\kappa $
into
![]() $\aleph _{\omega ^2}$
.
$\aleph _{\omega ^2}$
.
That motivated the construction in [Reference Sinapova and Unger6], where the main forcing is a two step iteration, with a Mitchell’s forcing poset followed by diagonal Prikry forcing. In that case one can incorporate collapses between the Prikry points. However, the argument for the tree property at the double successor of the singular cardinal became much more complicated. The hardest technical issue was “branch preservation” with respect to a quotient forcing of the form
![]() $j(\text {Mitchell}*\text {Prikry})/\text {Mitchell}*\text {Prikry}$
, where j is an appropriate elementary embedding.
$j(\text {Mitchell}*\text {Prikry})/\text {Mitchell}*\text {Prikry}$
, where j is an appropriate elementary embedding.
Here we present a simpler construction for the results of [Reference Sinapova5] and [Reference Sinapova and Unger6]. More precisely, we give an alternative proof that forcing with certain iterations of the form
![]() $\text {Mitchell}*\text {Prikry}$
yields the tree property at
$\text {Mitchell}*\text {Prikry}$
yields the tree property at
![]() $\kappa ^{++}$
. Our argument avoids dealing with the above-mentioned quotient poset, and so bypasses all the technical issues connected with that poset.
$\kappa ^{++}$
. Our argument avoids dealing with the above-mentioned quotient poset, and so bypasses all the technical issues connected with that poset.
2 The forcing posets
In this section, we describe the two main posets in our construction: a Mitchell style forcing and a diagonal Prikry forcing.
We will use the following version of the Mitchell forcing from [Reference Mitchell3]. Given regular cardinals
![]() $\kappa ,\, \mu ,\, \lambda $
where
$\kappa ,\, \mu ,\, \lambda $
where
![]() $\kappa < \mu < \lambda $
,
$\kappa < \mu < \lambda $
,
![]() $\kappa ^{<\kappa } = \kappa $
and
$\kappa ^{<\kappa } = \kappa $
and
![]() $\lambda $
is strongly inaccessible, we define a forcing poset
$\lambda $
is strongly inaccessible, we define a forcing poset
![]() $\mathbb M = {\mathbb M}(\kappa ,\, \mu ,\, \lambda )$
. Conditions are pairs
$\mathbb M = {\mathbb M}(\kappa ,\, \mu ,\, \lambda )$
. Conditions are pairs
![]() $(p,\, q)$
such that:
$(p,\, q)$
such that:
-
1.
 $p \in \operatorname {\mathrm {Add}}(\kappa ,\, \lambda )$
.
$p \in \operatorname {\mathrm {Add}}(\kappa ,\, \lambda )$
. -
2. q is a partial function on
 $\lambda $
such that
$\lambda $
such that
 $\vert q \vert < \mu $
.
$\vert q \vert < \mu $
. -
3. For all
 $\alpha \in \operatorname {\mathrm {dom}}(q)$
,
$\alpha \in \operatorname {\mathrm {dom}}(q)$
,
 $q(\alpha )$
is an
$q(\alpha )$
is an
 $ \operatorname {\mathrm {Add}}(\kappa ,\, \alpha )$
-name for a condition in
$ \operatorname {\mathrm {Add}}(\kappa ,\, \alpha )$
-name for a condition in
 $ \operatorname {\mathrm {Add}}(\mu ,\, 1)$
.
$ \operatorname {\mathrm {Add}}(\mu ,\, 1)$
.
The ordering is given by
![]() $(p_1,\, q_1) \le (p_0,\, q_0)$
iff
$(p_1,\, q_1) \le (p_0,\, q_0)$
iff
![]() $p_1 \le p_0$
,
$p_1 \le p_0$
,
![]() $ \operatorname {\mathrm {dom}}(q_0) \subseteq \operatorname {\mathrm {dom}}(q_1)$
, and
$ \operatorname {\mathrm {dom}}(q_0) \subseteq \operatorname {\mathrm {dom}}(q_1)$
, and
![]() $p_1 \upharpoonright \alpha \operatorname {\mathrm {\Vdash }} q_1(\alpha ) \le q_0(\alpha )$
for all
$p_1 \upharpoonright \alpha \operatorname {\mathrm {\Vdash }} q_1(\alpha ) \le q_0(\alpha )$
for all
![]() $\alpha \in \operatorname {\mathrm {dom}}(q_0)$
.
$\alpha \in \operatorname {\mathrm {dom}}(q_0)$
.
We refer the reader to [Reference Cummings and Foreman1] for a detailed account of the properties of
![]() $\mathbb M$
. We will use the following facts:
$\mathbb M$
. We will use the following facts:
-
•
 $\mathbb M$
is
$\mathbb M$
is
 $\kappa $
-directed closed and
$\kappa $
-directed closed and
 $\lambda $
-cc.
$\lambda $
-cc. -
•
 $\mathbb M$
is the projection of
$\mathbb M$
is the projection of
 $ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ) \times {\mathbb R}$
, where
$ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ) \times {\mathbb R}$
, where
 $\mathbb R$
is
$\mathbb R$
is
 $\mu $
-closed.Footnote
1
$\mu $
-closed.Footnote
1
-
• All
 $<\mu $
-sequences of ordinals in the generic extension by
$<\mu $
-sequences of ordinals in the generic extension by
 $\mathbb M$
lie in the subextension by
$\mathbb M$
lie in the subextension by
 $ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda )$
.
$ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda )$
. -
•
 $\mathbb M$
preserves all cardinals except those in the interval
$\mathbb M$
preserves all cardinals except those in the interval
 $(\mu ,\, \lambda )$
, which are collapsed to
$(\mu ,\, \lambda )$
, which are collapsed to
 $\mu $
.
$\mu $
. -
•
 $\mathbb M$
forces
$\mathbb M$
forces
 $2^\kappa = \lambda = \mu ^+$
.
$2^\kappa = \lambda = \mu ^+$
.
If
![]() $\lambda $
is measurableFootnote
2
then
$\lambda $
is measurableFootnote
2
then
![]() $\lambda $
still has the tree property in the extension by
$\lambda $
still has the tree property in the extension by
![]() $\mathbb M$
. The key points are that if
$\mathbb M$
. The key points are that if
![]() $j: V \rightarrow M$
is an embedding with critical point
$j: V \rightarrow M$
is an embedding with critical point
![]() $\lambda $
into a model M such that
$\lambda $
into a model M such that
![]() ${}^\lambda M \subseteq M$
, then:
${}^\lambda M \subseteq M$
, then:
-
• In M,
 $\mathbb M$
is an initial segment of
$\mathbb M$
is an initial segment of
 $j(\mathbb M)$
.
$j(\mathbb M)$
. -
•
 $j \restriction {\mathbb M}$
is a complete embedding of
$j \restriction {\mathbb M}$
is a complete embedding of
 ${\mathbb M}$
into
${\mathbb M}$
into
 $j({\mathbb M})$
.
$j({\mathbb M})$
. -
• If G is
 $\mathbb M$
-generic then in
$\mathbb M$
-generic then in
 $M[G]$
the quotient forcing
$M[G]$
the quotient forcing
 $j({\mathbb M})/G$
is the projection of a product
$j({\mathbb M})/G$
is the projection of a product
 ${\mathbb A} \times {\mathbb Q}$
, where
${\mathbb A} \times {\mathbb Q}$
, where
 $\mathbb A = \operatorname {\mathrm {Add}}(\kappa ,\, j(\lambda ) - \lambda )$
.
$\mathbb A = \operatorname {\mathrm {Add}}(\kappa ,\, j(\lambda ) - \lambda )$
. -
• In
 $V[G]$
,
$V[G]$
,
 $\mathbb A$
is
$\mathbb A$
is
 $\kappa ^+$
-Knaster and
$\kappa ^+$
-Knaster and
 $\mathbb Q$
is
$\mathbb Q$
is
 $\mu $
-closed.
$\mu $
-closed.
Next, we describe the diagonal supercompact Prikry forcing
![]() $\mathbb {P}$
. This forcing was first defined by Gitik and Sharon [Reference Gitik and Sharon2] to prove the consistency of failure of SCH at
$\mathbb {P}$
. This forcing was first defined by Gitik and Sharon [Reference Gitik and Sharon2] to prove the consistency of failure of SCH at
![]() $\kappa $
with failure of
$\kappa $
with failure of
![]() $\square ^*_\kappa $
, and then modified by Neeman [Reference Neeman4] to prove the consistency of failure of SCH at
$\square ^*_\kappa $
, and then modified by Neeman [Reference Neeman4] to prove the consistency of failure of SCH at
![]() $\kappa $
with the tree property holding at
$\kappa $
with the tree property holding at
![]() $\kappa ^+$
.
$\kappa ^+$
.
Let
![]() $\langle \kappa _n \mid n < \omega \rangle $
be an increasing sequence of regular cardinals. Let
$\langle \kappa _n \mid n < \omega \rangle $
be an increasing sequence of regular cardinals. Let
![]() $\kappa =\kappa _0$
and assume that
$\kappa =\kappa _0$
and assume that
![]() $\kappa $
is a supercompact cardinal. Let
$\kappa $
is a supercompact cardinal. Let
![]() $\mu = (\text {sup}_n\kappa _n)^+$
. Let U be a normal measure on
$\mu = (\text {sup}_n\kappa _n)^+$
. Let U be a normal measure on
![]() $\mathcal {P}_\kappa (\mu )$
, and for every n let
$\mathcal {P}_\kappa (\mu )$
, and for every n let
![]() $U_n$
be the projection of U to
$U_n$
be the projection of U to
![]() $\mathcal {P}_\kappa (\kappa _n)$
. The measure
$\mathcal {P}_\kappa (\kappa _n)$
. The measure
![]() $U_n$
concentrates on x such that
$U_n$
concentrates on x such that
![]() $x \cap \kappa $
is an inaccessible cardinal: we only consider
$x \cap \kappa $
is an inaccessible cardinal: we only consider
![]() $x \in P_\kappa (\kappa _n)$
with this property, and write
$x \in P_\kappa (\kappa _n)$
with this property, and write
![]() $\kappa _x$
for
$\kappa _x$
for
![]() $x \cap \kappa $
.
$x \cap \kappa $
.
Conditions in
![]() $\mathbb {P}$
are of the form
$\mathbb {P}$
are of the form
![]() $p =\langle x_0,\, \ldots ,\, x_{n-1},\, A_n,\, A_{n+1} \ldots \rangle $
, where each
$p =\langle x_0,\, \ldots ,\, x_{n-1},\, A_n,\, A_{n+1} \ldots \rangle $
, where each
![]() $x_i \in \mathcal {P}_\kappa (\kappa _i)$
,
$x_i \in \mathcal {P}_\kappa (\kappa _i)$
,
![]() $x_i\prec x_{i+1}$
(i.e.
$x_i\prec x_{i+1}$
(i.e.
![]() $x_i\subseteq x_{i+1}$
and
$x_i\subseteq x_{i+1}$
and
![]() $|x_i|<\kappa _{x_{i+1}}$
), and each
$|x_i|<\kappa _{x_{i+1}}$
), and each
![]() $A_k \in U_k$
. We say that
$A_k \in U_k$
. We say that
![]() $ \operatorname {\mathrm {lh}}(p) = n$
and the stem of p is
$ \operatorname {\mathrm {lh}}(p) = n$
and the stem of p is
![]() $ \operatorname {\mathrm {s}}(p)= \langle x_0,\, \ldots ,\, x_{n-1} \rangle $
.
$ \operatorname {\mathrm {s}}(p)= \langle x_0,\, \ldots ,\, x_{n-1} \rangle $
.
The ordering is given by
![]() $q\leq p$
iff:
$q\leq p$
iff:
-
•
 $ \operatorname {\mathrm {lh}}(q) \ge \operatorname {\mathrm {lh}}(p)$
.
$ \operatorname {\mathrm {lh}}(q) \ge \operatorname {\mathrm {lh}}(p)$
. -
• For all i with
 $i < \operatorname {\mathrm {lh}}(p)$
,
$i < \operatorname {\mathrm {lh}}(p)$
,
 $x^q_i = x^p_i$
.
$x^q_i = x^p_i$
. -
• For all i with
 $ \operatorname {\mathrm {lh}}(p) \leq i< \operatorname {\mathrm {lh}}(q)$
,
$ \operatorname {\mathrm {lh}}(p) \leq i< \operatorname {\mathrm {lh}}(q)$
,
 $x^q_i \in A^p_i$
.
$x^q_i \in A^p_i$
. -
• For all i with
 $ \operatorname {\mathrm {lh}}(q) \le i$
,
$ \operatorname {\mathrm {lh}}(q) \le i$
,
 $A^q_i\subseteq A^p_i$
.
$A^q_i\subseteq A^p_i$
.
We say that q is a direct extension of p, and write
![]() $q \leq ^* p$
, if
$q \leq ^* p$
, if
![]() $q \leq p$
and they have the same length,
$q \leq p$
and they have the same length,
The following are standard facts about
![]() $\mathbb {P}$
:
$\mathbb {P}$
:
-
1.
 $\mathbb {P}$
has the Prikry property: for any statement in the forcing language
$\mathbb {P}$
has the Prikry property: for any statement in the forcing language
 $\phi $
and any
$\phi $
and any
 $p\in \mathbb {P}$
, there is
$p\in \mathbb {P}$
, there is
 $q \leq ^* p$
deciding
$q \leq ^* p$
deciding
 $\phi $
. In particular
$\phi $
. In particular
 $\mathbb P$
adds no bounded subsets of
$\mathbb P$
adds no bounded subsets of
 $\kappa $
.
$\kappa $
. -
2. Conditions with the same stem are compatible, and so
 $\mathbb {P}$
has the
$\mathbb {P}$
has the
 $\mu $
-chain condition.
$\mu $
-chain condition. -
3.
 $\mathbb {P}$
forces that
$\mathbb {P}$
forces that
 $ \operatorname {\mathrm {cf}}(\kappa _n)=\omega $
for all
$ \operatorname {\mathrm {cf}}(\kappa _n)=\omega $
for all
 $n\geq 0$
.
$n\geq 0$
. -
4.
 $\mathbb {P}$
preserves
$\mathbb {P}$
preserves
 $\kappa $
and
$\kappa $
and
 $\mu $
, and forces that
$\mu $
, and forces that
 $\mu =\kappa ^+$
.
$\mu =\kappa ^+$
.
Given a formula
![]() $\phi $
and a stem h, we will say that
$\phi $
and a stem h, we will say that
![]() $h\Vdash ^*\phi $
if there is a condition p with stem h which forces
$h\Vdash ^*\phi $
if there is a condition p with stem h which forces
![]() $\phi $
. Note that by the Prikry property, for every
$\phi $
. Note that by the Prikry property, for every
![]() $\phi ,\, h$
either we have
$\phi ,\, h$
either we have
![]() $h\Vdash ^*\phi $
or
$h\Vdash ^*\phi $
or
![]() $h\Vdash ^*\neg \phi $
.
$h\Vdash ^*\neg \phi $
.
3 The main construction
Let
![]() $\langle \kappa _n \mid n < \omega \rangle $
be an increasing sequence of indestructible supercompact cardinals with limit
$\langle \kappa _n \mid n < \omega \rangle $
be an increasing sequence of indestructible supercompact cardinals with limit
![]() $\kappa _\omega $
. Let
$\kappa _\omega $
. Let
![]() $\mu =\kappa _\omega ^+$
and
$\mu =\kappa _\omega ^+$
and
![]() $\kappa = \kappa _0$
. Suppose also that
$\kappa = \kappa _0$
. Suppose also that
![]() $\lambda $
is a measurable cardinal above
$\lambda $
is a measurable cardinal above
![]() $\mu $
. Let
$\mu $
. Let
![]() $\mathbb {M}$
be the Mitchell forcing
$\mathbb {M}$
be the Mitchell forcing
![]() ${\mathbb M}(\kappa ,\, \mu ,\, \lambda )$
from the last section, and G be
${\mathbb M}(\kappa ,\, \mu ,\, \lambda )$
from the last section, and G be
![]() $\mathbb {M}$
-generic. Since
$\mathbb {M}$
-generic. Since
![]() $\mathbb M$
is
$\mathbb M$
is
![]() $\kappa $
-directed closed,
$\kappa $
-directed closed,
![]() $\kappa $
is still supercompact in
$\kappa $
is still supercompact in
![]() $V[G]$
.
$V[G]$
.
In
![]() $V[G]$
let
$V[G]$
let
![]() $\mathbb {P}$
be the diagonal Prikry forcing described in the preceding section, built using normal measures
$\mathbb {P}$
be the diagonal Prikry forcing described in the preceding section, built using normal measures
![]() $U_n$
on
$U_n$
on
![]() $\mathcal {P}_\kappa (\kappa _n)$
for
$\mathcal {P}_\kappa (\kappa _n)$
for
![]() $n<\omega $
. Let H be
$n<\omega $
. Let H be
![]() $\mathbb {P}$
-generic over
$\mathbb {P}$
-generic over
![]() $V[G]$
. In
$V[G]$
. In
![]() $V[G][H]$
,
$V[G][H]$
,
![]() $\kappa $
is preserved,
$\kappa $
is preserved,
![]() $ \operatorname {\mathrm {cf}}(\kappa )=\omega $
,
$ \operatorname {\mathrm {cf}}(\kappa )=\omega $
,
![]() $\kappa ^+=\mu $
,
$\kappa ^+=\mu $
,
![]() $\kappa ^{++}=\lambda =2^\kappa $
.
$\kappa ^{++}=\lambda =2^\kappa $
.
Theorem 3.1. The tree property holds at
![]() $\lambda $
in
$\lambda $
in
![]() $V[G][H]$
.
$V[G][H]$
.
Proof In
![]() $V[G]$
let
$V[G]$
let
![]() $\dot {T}$
be
$\dot {T}$
be
![]() $\mathbb {P}$
-name for a
$\mathbb {P}$
-name for a
![]() $\lambda $
-tree that is forced to be a counterexample. As usual assume that for
$\lambda $
-tree that is forced to be a counterexample. As usual assume that for
![]() $\alpha <\lambda $
, the levels
$\alpha <\lambda $
, the levels
![]() $\dot {T}_\alpha $
are simply
$\dot {T}_\alpha $
are simply
![]() $\{\alpha \}\times \mu $
.
$\{\alpha \}\times \mu $
.
Let
![]() $j:V \rightarrow M$
be the ultrapower map by a normal measure on
$j:V \rightarrow M$
be the ultrapower map by a normal measure on
![]() $\lambda $
. Lift it to
$\lambda $
. Lift it to
![]() $j:V[G]\rightarrow M[G^*]$
in
$j:V[G]\rightarrow M[G^*]$
in
![]() $V[G][K\times A]$
, where K is generic for a
$V[G][K\times A]$
, where K is generic for a
![]() $\mu $
-closed forcing
$\mu $
-closed forcing
![]() $\mathbb {Q}$
and A is generic for a
$\mathbb {Q}$
and A is generic for a
![]() $\kappa ^+$
-Knaster forcing
$\kappa ^+$
-Knaster forcing
![]() $\mathbb {A}$
. Of course we could have lifted j working in
$\mathbb {A}$
. Of course we could have lifted j working in
![]() $V[G^*]$
, but
$V[G^*]$
, but
![]() ${\mathbb Q} \times {\mathbb A}$
is more tractable than
${\mathbb Q} \times {\mathbb A}$
is more tractable than
![]() $j({\mathbb M})/G$
.
$j({\mathbb M})/G$
.
Lemma 3.2. In
![]() $V[G]$
there exist an unbounded set
$V[G]$
there exist an unbounded set
![]() $J\subseteq \lambda $
, a stem h, and a function
$J\subseteq \lambda $
, a stem h, and a function
![]() $f:J\rightarrow \mu $
, such that for all
$f:J\rightarrow \mu $
, such that for all
![]() $\alpha <\beta $
both in J,
$\alpha <\beta $
both in J,
Proof Work in
![]() $V[G][K\times A]$
. Let
$V[G][K\times A]$
. Let
![]() $u = \langle \lambda ,\, 0 \rangle $
, so that u is a node on the
$u = \langle \lambda ,\, 0 \rangle $
, so that u is a node on the
![]() $\lambda $
-th level of
$\lambda $
-th level of
![]() $j(\dot {T})$
. Then for all
$j(\dot {T})$
. Then for all
![]() $\alpha < \lambda $
there exist
$\alpha < \lambda $
there exist
![]() $p_\alpha \in j(\mathbb {P})$
and
$p_\alpha \in j(\mathbb {P})$
and
![]() $\xi _\alpha <\mu $
such that
$\xi _\alpha <\mu $
such that
 $p_\alpha \Vdash \langle \alpha ,\, \xi _\alpha \rangle <_{j(\dot {T})}u$
. Let
$p_\alpha \Vdash \langle \alpha ,\, \xi _\alpha \rangle <_{j(\dot {T})}u$
. Let
![]() $h_\alpha $
be the stem of
$h_\alpha $
be the stem of
![]() $p_\alpha $
, and note that
$p_\alpha $
, and note that
![]() $h_\alpha $
is a stem in the original forcing
$h_\alpha $
is a stem in the original forcing
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Since there are only
![]() $\kappa _\omega $
-many stems and the cofinality of
$\kappa _\omega $
-many stems and the cofinality of
![]() $\lambda $
is
$\lambda $
is
![]() $\mu $
in
$\mu $
in
![]() $M[G^*]$
, there exist an unbounded
$M[G^*]$
, there exist an unbounded
![]() $J\subseteq \lambda $
and a stem
$J\subseteq \lambda $
and a stem
![]() $\bar {h}$
, such that for all
$\bar {h}$
, such that for all
![]() $\alpha \in J$
we have
$\alpha \in J$
we have
![]() $\bar {h}=h_\alpha $
. For all
$\bar {h}=h_\alpha $
. For all
![]() $\alpha <\lambda $
, if
$\alpha <\lambda $
, if
![]() $\alpha \in J$
then
$\alpha \in J$
then
 $\bar {h}\Vdash ^* \langle \alpha ,\,\xi _\alpha \rangle <_{j(\dot {T})} u$
. Increasing J if needed we may assume that the converse also holds.
$\bar {h}\Vdash ^* \langle \alpha ,\,\xi _\alpha \rangle <_{j(\dot {T})} u$
. Increasing J if needed we may assume that the converse also holds.
Define
![]() $f:J\rightarrow \mu $
by
$f:J\rightarrow \mu $
by
![]() $f(\alpha )=\xi _\alpha $
. Then if
$f(\alpha )=\xi _\alpha $
. Then if
![]() $\beta \in J$
, we have that for all
$\beta \in J$
, we have that for all
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $\alpha \in J$
if and only if there is some
$\alpha \in J$
if and only if there is some
![]() $\xi <\mu $
such that
$\xi <\mu $
such that
 $\bar {h}\Vdash ^*\langle \alpha ,\,\xi \rangle <_{\dot {T}}\langle \beta ,\, f(\beta )\rangle $
, and in this case
$\bar {h}\Vdash ^*\langle \alpha ,\,\xi \rangle <_{\dot {T}}\langle \beta ,\, f(\beta )\rangle $
, and in this case
![]() $\xi _\alpha $
is the unique
$\xi _\alpha $
is the unique
![]() $\xi $
with this property. This implies that for all
$\xi $
with this property. This implies that for all
![]() $\gamma < \lambda $
both
$\gamma < \lambda $
both
![]() $J \cap \gamma $
and
$J \cap \gamma $
and
![]() $f \restriction \gamma $
are in
$f \restriction \gamma $
are in
![]() $V[G]$
.
$V[G]$
.
Next we want to find such a J and f in
![]() $V[G]$
. Since
$V[G]$
. Since
![]() $\mathbb {A}^2$
has the
$\mathbb {A}^2$
has the
![]() $\kappa ^+$
-approximation property in
$\kappa ^+$
-approximation property in
![]() $V[G][K]$
, it is easy to see that the versions of J and f which we just constructed lie in
$V[G][K]$
, it is easy to see that the versions of J and f which we just constructed lie in
![]() $V[G][K]$
. In
$V[G][K]$
. In
![]() $V[G][K\times A]$
, for every stem h extending
$V[G][K\times A]$
, for every stem h extending
![]() $\bar {h}$
, let
$\bar {h}$
, let
 $J_h = \{\alpha \in J\mid \exists \xi (h\Vdash ^* \langle \alpha ,\, \xi \rangle <_{j(\dot {T})}u)\}$
and define
$J_h = \{\alpha \in J\mid \exists \xi (h\Vdash ^* \langle \alpha ,\, \xi \rangle <_{j(\dot {T})}u)\}$
and define
![]() $f_h:J_h\rightarrow \mu $
by setting
$f_h:J_h\rightarrow \mu $
by setting
![]() $f_h(\alpha )$
to be the unique
$f_h(\alpha )$
to be the unique
![]() $\xi $
witnessing that
$\xi $
witnessing that
![]() $\alpha \in J_h$
. As above, if
$\alpha \in J_h$
. As above, if
![]() $J_h$
is unbounded then
$J_h$
is unbounded then
![]() $J_h$
and
$J_h$
and
![]() $f_h$
are in
$f_h$
are in
![]() $V[G][K]$
. Let
$V[G][K]$
. Let
![]() $\bar {\alpha }<\lambda $
be forced by
$\bar {\alpha }<\lambda $
be forced by
![]() $\mathbb A$
to be a bound for all
$\mathbb A$
to be a bound for all
![]() $J_h$
which are bounded in
$J_h$
which are bounded in
![]() $\lambda $
.
$\lambda $
.
For each h, let
![]() $\dot {J}_h,\,\dot {f}_h\in V[G][K]$
be
$\dot {J}_h,\,\dot {f}_h\in V[G][K]$
be
![]() $\mathbb {A}$
-names for
$\mathbb {A}$
-names for
![]() $J_h,\,f_h$
. In
$J_h,\,f_h$
. In
![]() $V[G][K]$
let
$V[G][K]$
let
![]() $\mathcal {C}_h =\{ C\subseteq \lambda \mid C \setminus \bar {\alpha }\neq \emptyset ,\, \exists b\in \mathbb {A}(b\Vdash C=\dot {J}_h)\}$
. Then by the above remark and since
$\mathcal {C}_h =\{ C\subseteq \lambda \mid C \setminus \bar {\alpha }\neq \emptyset ,\, \exists b\in \mathbb {A}(b\Vdash C=\dot {J}_h)\}$
. Then by the above remark and since
![]() $\mathbb {A}$
is
$\mathbb {A}$
is
![]() $\kappa ^+$
-Knaster, if
$\kappa ^+$
-Knaster, if
![]() $J_h$
is unbounded in
$J_h$
is unbounded in
![]() $\lambda $
, we have that
$\lambda $
, we have that
![]() $1\leq |\mathcal {C}_h|\leq \kappa $
. Enumerate
$1\leq |\mathcal {C}_h|\leq \kappa $
. Enumerate
![]() $\mathcal {C}_h$
as
$\mathcal {C}_h$
as
![]() $\langle C_{h,\,\eta } \mid \eta <\kappa \rangle $
(possibly with repetitions) when it is not empty. For every
$\langle C_{h,\,\eta } \mid \eta <\kappa \rangle $
(possibly with repetitions) when it is not empty. For every
![]() $\eta <\kappa $
pick some
$\eta <\kappa $
pick some
![]() $b_\eta \in \mathbb {A}$
forcing that
$b_\eta \in \mathbb {A}$
forcing that
 $C_{h,\,\eta }=\dot {J}_h$
, and let
$C_{h,\,\eta }=\dot {J}_h$
, and let
![]() $f_{h,\,\eta } : C_{h,\,\eta } \rightarrow \mu $
be defined by setting
$f_{h,\,\eta } : C_{h,\,\eta } \rightarrow \mu $
be defined by setting
![]() $f_{h,\,\eta }(\alpha )$
equal to the unique
$f_{h,\,\eta }(\alpha )$
equal to the unique
![]() $\xi $
witnessing
$\xi $
witnessing
![]() $\alpha \in C_{h,\,\eta }$
as forced by
$\alpha \in C_{h,\,\eta }$
as forced by
![]() $b_\eta $
. That is to say,
$b_\eta $
. That is to say,
 $b_\eta \Vdash _{\mathbb {A}}^{V[G][K]} (h \Vdash ^* \langle \alpha ,\, \xi \rangle <_{j(\dot {T})} u)$
.
$b_\eta \Vdash _{\mathbb {A}}^{V[G][K]} (h \Vdash ^* \langle \alpha ,\, \xi \rangle <_{j(\dot {T})} u)$
.
Working in
![]() $V[G]$
, for each h such that
$V[G]$
, for each h such that
![]() $\dot {\mathcal {C}}_h$
is not the empty set and for each
$\dot {\mathcal {C}}_h$
is not the empty set and for each
![]() $\eta <\kappa $
, fix
$\eta <\kappa $
, fix
![]() ${\mathbb Q}$
-names
${\mathbb Q}$
-names
 $\dot {C}_{h,\,\eta }$
and
$\dot {C}_{h,\,\eta }$
and
 $\dot {f}_{h,\, \eta }$
. We want to show that for some h and
$\dot {f}_{h,\, \eta }$
. We want to show that for some h and
![]() $\eta $
the pair
$\eta $
the pair
 $(\dot {C}_{h,\,\eta },\, \dot {f}_{h,\,\eta })$
can be forced to be in
$(\dot {C}_{h,\,\eta },\, \dot {f}_{h,\,\eta })$
can be forced to be in
![]() $V[G]$
. Towards a contradiction, suppose that for all h and
$V[G]$
. Towards a contradiction, suppose that for all h and
![]() $\eta $
we have
$\eta $
we have
 $1_{\mathbb {Q}}\Vdash (\dot {C}_{h,\,\eta },\, \dot {f}_{h,\,\eta })\notin V[G]$
.
$1_{\mathbb {Q}}\Vdash (\dot {C}_{h,\,\eta },\, \dot {f}_{h,\,\eta })\notin V[G]$
.
We say that
![]() $q_0,\, q_1$
in
$q_0,\, q_1$
in
![]() $\mathbb {Q}$
force contradictory information about
$\mathbb {Q}$
force contradictory information about
 $\dot {f}_{h,\,\eta }(\alpha )$
if
$\dot {f}_{h,\,\eta }(\alpha )$
if
![]() $q_0,\, q_1$
both decide “
$q_0,\, q_1$
both decide “
 $\alpha \in \dot {C}_{h,\,\eta }$
” with at least one of them forcing a positive decision, and
$\alpha \in \dot {C}_{h,\,\eta }$
” with at least one of them forcing a positive decision, and
 $(q_0,\, q_1)\Vdash _{\mathbb {Q}\times \mathbb {Q}}\ \dot {f}_{h,\,\eta }[\dot {G}_L](\alpha )\neq \dot {f}_{h,\,\eta }[\dot {G}_R](\alpha )$
.
$(q_0,\, q_1)\Vdash _{\mathbb {Q}\times \mathbb {Q}}\ \dot {f}_{h,\,\eta }[\dot {G}_L](\alpha )\neq \dot {f}_{h,\,\eta }[\dot {G}_R](\alpha )$
.
Since we have assumed that each
 $\dot {f}_{h,\,\eta }$
is forced to be new, we have the following in
$\dot {f}_{h,\,\eta }$
is forced to be new, we have the following in
![]() $V[G]$
:
$V[G]$
:
Claim 3.3. Suppose that
![]() $q_0,\, q_1\in \mathbb {Q}$
, h is a stem extending
$q_0,\, q_1\in \mathbb {Q}$
, h is a stem extending
![]() $\bar {h}$
,
$\bar {h}$
,
![]() $\eta <\kappa $
, and
$\eta <\kappa $
, and
![]() $\alpha <\lambda $
. Then there are
$\alpha <\lambda $
. Then there are
![]() $\alpha '>\alpha $
and
$\alpha '>\alpha $
and
![]() $q_0'\leq q_0,\, q^{\prime }_1\leq q_1$
, forcing contradictory information about
$q_0'\leq q_0,\, q^{\prime }_1\leq q_1$
, forcing contradictory information about
 $\dot {f}_{h,\,\eta }(\alpha ')$
.
$\dot {f}_{h,\,\eta }(\alpha ')$
.
Working in
![]() $V[G]$
we build a binary tree of conditions in
$V[G]$
we build a binary tree of conditions in
![]() $\mathbb Q$
, forcing contradictory information about
$\mathbb Q$
, forcing contradictory information about
![]() $f_{h,\, \eta }$
for every pair
$f_{h,\, \eta }$
for every pair
![]() $(h,\,\eta )$
at every splitting. More precisely we build
$(h,\,\eta )$
at every splitting. More precisely we build
 $\langle q_\sigma ,\, \alpha _{\sigma ,\, h,\,\eta } \mid \sigma \in 2^{<\kappa },\, h\text { a stem },\, h\sqsupseteq \bar {h},\, \eta <\kappa \rangle $
, such that for all
$\langle q_\sigma ,\, \alpha _{\sigma ,\, h,\,\eta } \mid \sigma \in 2^{<\kappa },\, h\text { a stem },\, h\sqsupseteq \bar {h},\, \eta <\kappa \rangle $
, such that for all
![]() $(\sigma ,\, h,\, \eta )$
the conditions
$(\sigma ,\, h,\, \eta )$
the conditions
![]() $q_{\sigma ^\frown 0}$
and
$q_{\sigma ^\frown 0}$
and
![]() $q_{\sigma ^\frown 1}$
force contradictory information about
$q_{\sigma ^\frown 1}$
force contradictory information about
![]() $f_{h,\,\eta }(\alpha _{\sigma ,\, h,\,\eta })$
. We build this tree by induction on
$f_{h,\,\eta }(\alpha _{\sigma ,\, h,\,\eta })$
. We build this tree by induction on
![]() $|\sigma |$
, and at every stage we apply Claim 3.3 repeatedly for each h and
$|\sigma |$
, and at every stage we apply Claim 3.3 repeatedly for each h and
![]() $\eta $
. We use that
$\eta $
. We use that
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\mu $
-closed and the number of pairs
$\mu $
-closed and the number of pairs
![]() $(h,\,\eta )$
is
$(h,\,\eta )$
is
![]() $\kappa _\omega $
.
$\kappa _\omega $
.
Let
![]() $\alpha ^*=\text {sup}_{\sigma ,\, h,\,\eta }\alpha _{\sigma ,\, h,\,\eta }$
. For each
$\alpha ^*=\text {sup}_{\sigma ,\, h,\,\eta }\alpha _{\sigma ,\, h,\,\eta }$
. For each
![]() $i\in 2^\kappa $
, let
$i\in 2^\kappa $
, let
![]() $q_i\leq q_{i\upharpoonright \eta }$
for all
$q_i\leq q_{i\upharpoonright \eta }$
for all
![]() $\eta <\kappa $
. Now let
$\eta <\kappa $
. Now let
![]() $q^{\prime }_i\leq q_i$
be such that there are
$q^{\prime }_i\leq q_i$
be such that there are
![]() $h_i$
,
$h_i$
,
![]() $\eta _i<\kappa $
,
$\eta _i<\kappa $
,
![]() $\xi _i<\mu $
and
$\xi _i<\mu $
and
![]() $b\in \mathbb {A}$
such that:
$b\in \mathbb {A}$
such that:
-
•
 ,
, -
•
 $(q^{\prime }_i,\,b)\Vdash _{\mathbb {Q}\times \mathbb {A}}\dot {C}_{h_i,\,\eta _i}=\dot {J}_{h_i},\, \dot {f}_{h_i}=\dot {f}_{h_i,\,\eta _i}$
Footnote
3
(and so
$(q^{\prime }_i,\,b)\Vdash _{\mathbb {Q}\times \mathbb {A}}\dot {C}_{h_i,\,\eta _i}=\dot {J}_{h_i},\, \dot {f}_{h_i}=\dot {f}_{h_i,\,\eta _i}$
Footnote
3
(and so
 $q^{\prime }_i\Vdash \alpha ^*\in \dot {C}_{h_i,\,\eta _i}$
).
$q^{\prime }_i\Vdash \alpha ^*\in \dot {C}_{h_i,\,\eta _i}$
).
Note that for all
![]() $\alpha <\alpha ^*$
,
$\alpha <\alpha ^*$
,
 $q^{\prime }_i\Vdash \dot {f}_{h_i,\,\eta _i}(\alpha )=\delta $
iff
$q^{\prime }_i\Vdash \dot {f}_{h_i,\,\eta _i}(\alpha )=\delta $
iff
![]() $h_i\Vdash ^*\langle \alpha ,\, \delta \rangle <_{\dot {T}}\langle \alpha ^*,\, \xi _i\rangle $
.
$h_i\Vdash ^*\langle \alpha ,\, \delta \rangle <_{\dot {T}}\langle \alpha ^*,\, \xi _i\rangle $
.
Since
![]() $2^\kappa =\lambda>\mu $
, there exist distinct
$2^\kappa =\lambda>\mu $
, there exist distinct
![]() $i,\, j \in 2^\kappa $
and
$i,\, j \in 2^\kappa $
and
![]() $(h,\, \eta ,\, \xi )$
such that
$(h,\, \eta ,\, \xi )$
such that
![]() $h_i=h_j = h$
,
$h_i=h_j = h$
,
![]() $\eta _i = \eta _j = \eta $
and
$\eta _i = \eta _j = \eta $
and
![]() $\xi _i = \xi _j = \xi $
. Let
$\xi _i = \xi _j = \xi $
. Let
![]() $\sigma $
be the node where i and j split. By construction the conditions
$\sigma $
be the node where i and j split. By construction the conditions
![]() $q_i$
and
$q_i$
and
![]() $q_j$
cannot force contradictory information about
$q_j$
cannot force contradictory information about
 $\dot {f}_{h,\,\eta }(\alpha _{h,\,\sigma ,\,\eta })$
. This is a contradiction, so in
$\dot {f}_{h,\,\eta }(\alpha _{h,\,\sigma ,\,\eta })$
. This is a contradiction, so in
![]() $V[G]$
we may find a stem h, set J and function f as required.⊣
$V[G]$
we may find a stem h, set J and function f as required.⊣
Let
![]() $J,\, f,\,h$
be given by Lemma 3.2, and let
$J,\, f,\,h$
be given by Lemma 3.2, and let
![]() $n=|h|$
. As above, let
$n=|h|$
. As above, let
![]() $\xi _\alpha = f(\alpha )$
.
$\xi _\alpha = f(\alpha )$
.
Lemma 3.4. There are
![]() $\rho <\lambda $
and
$\rho <\lambda $
and
![]() $U_n$
-measure one sets
$U_n$
-measure one sets
![]() $\langle A_\alpha \mid \alpha \in J\setminus \rho \rangle $
in
$\langle A_\alpha \mid \alpha \in J\setminus \rho \rangle $
in
![]() $V[G]$
, such that for all
$V[G]$
, such that for all
![]() $x\in A_\alpha \cap A_\beta $
,
$x\in A_\alpha \cap A_\beta $
,
![]() $h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
.
$h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
.
Proof By the same ideas as in [Reference Neeman4], such measure one sets exist in
![]() $V[G][K]$
. We go over the proof for completeness:
$V[G][K]$
. We go over the proof for completeness:
Claim 3.5. There are
![]() $\langle A^*_\alpha \mid \alpha \in J\setminus \rho \rangle $
in
$\langle A^*_\alpha \mid \alpha \in J\setminus \rho \rangle $
in
![]() $V[G][K]$
, satisfying the conclusion of Lemma 3.4.
$V[G][K]$
, satisfying the conclusion of Lemma 3.4.
Proof For every
![]() $x\in \mathcal {P}_\kappa (\kappa _n)$
let
$x\in \mathcal {P}_\kappa (\kappa _n)$
let
 $J_x = \{\alpha \in J\mid h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{j(\dot {T})}u \}$
. Let
$J_x = \{\alpha \in J\mid h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{j(\dot {T})}u \}$
. Let
![]() $\bar {\alpha }<\lambda $
be such that if
$\bar {\alpha }<\lambda $
be such that if
![]() $J_x$
is bounded in
$J_x$
is bounded in
![]() $\lambda $
, then
$\lambda $
, then
![]() $J_x\subseteq \bar {\alpha }$
. Here we use that the number of x’s is less than
$J_x\subseteq \bar {\alpha }$
. Here we use that the number of x’s is less than
 $\mu = \operatorname {\mathrm {cf}}^{M[G^*]}\lambda $
.
$\mu = \operatorname {\mathrm {cf}}^{M[G^*]}\lambda $
.
Redefine
 $J_x = \{\alpha \in J\setminus \bar {\alpha }\mid h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{j(\dot {T})}u \}$
Then each
$J_x = \{\alpha \in J\setminus \bar {\alpha }\mid h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{j(\dot {T})}u \}$
Then each
![]() $J_x$
is either empty or unbounded. In particular each
$J_x$
is either empty or unbounded. In particular each
![]() $J_x\in V[G][K]$
, since
$J_x\in V[G][K]$
, since
![]() $\mathbb {A}$
has the
$\mathbb {A}$
has the
![]() $\kappa ^+$
-approximation property. In
$\kappa ^+$
-approximation property. In
![]() $V[G][K]$
, define
$V[G][K]$
, define
![]() $\mathcal {C}_x$
to be the set of possible values for
$\mathcal {C}_x$
to be the set of possible values for
![]() $J_x$
. Then it is routine to show:
$J_x$
. Then it is routine to show:
-
•
 $|\mathcal {C}_x| \leq \kappa $
.
$|\mathcal {C}_x| \leq \kappa $
. -
• For all
 $C \in \mathcal {C}_x$
and for all
$C \in \mathcal {C}_x$
and for all
 $\alpha <\beta $
both in C,
$\alpha <\beta $
both in C,
 $h^\frown x \Vdash ^* \langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}} \langle \beta ,\, \xi _\beta \rangle $
.
$h^\frown x \Vdash ^* \langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}} \langle \beta ,\, \xi _\beta \rangle $
. -
• Distinct elements C and
 $C'$
of
$C'$
of
 $\mathcal {C}_x$
are disjoint on a final segment of
$\mathcal {C}_x$
are disjoint on a final segment of
 $\lambda $
.
$\lambda $
.
Fix
![]() $\rho <\lambda $
such that
$\rho <\lambda $
such that
![]() $\bar {\alpha }<\rho $
, and
$\bar {\alpha }<\rho $
, and
![]() $C \cap C' \subseteq \rho $
for all x and all pairs of distinct elements C and
$C \cap C' \subseteq \rho $
for all x and all pairs of distinct elements C and
![]() $C'$
in
$C'$
in
![]() $\mathcal {C}_x$
. Let
$\mathcal {C}_x$
. Let
![]() $\alpha _0 = \min (J\setminus \rho )$
, and define
$\alpha _0 = \min (J\setminus \rho )$
, and define
![]() $f(x,\,\alpha )$
to be the unique
$f(x,\,\alpha )$
to be the unique
![]() $C \in \mathcal {C}_x$
such that
$C \in \mathcal {C}_x$
such that
![]() $\alpha \in C$
, if such exists. Then let
$\alpha \in C$
, if such exists. Then let
![]() $A^*_\alpha =\{x \mid f(x,\,\alpha ) = f(x,\,\alpha _0)\}$
, where the equality means that the values
$A^*_\alpha =\{x \mid f(x,\,\alpha ) = f(x,\,\alpha _0)\}$
, where the equality means that the values
![]() $f(x,\, \alpha )$
and
$f(x,\, \alpha )$
and
![]() $f(x,\, \alpha _0)$
are defined and equal. It is clear that
$f(x,\, \alpha _0)$
are defined and equal. It is clear that
![]() $A^*_\alpha \in U_n$
.⊣
$A^*_\alpha \in U_n$
.⊣
Fix
![]() $\langle A^*_\alpha \mid \alpha \in J\setminus \rho \rangle $
as in Claim 3.5. By construction, we have that for all
$\langle A^*_\alpha \mid \alpha \in J\setminus \rho \rangle $
as in Claim 3.5. By construction, we have that for all
![]() $\alpha <\beta $
both in
$\alpha <\beta $
both in
![]() $J\setminus \rho $
and for all
$J\setminus \rho $
and for all
 $x\in A^*_\beta $
,
$x\in A^*_\beta $
,
![]() $x\in A^*_\alpha $
if and only if
$x\in A^*_\alpha $
if and only if
![]() $h^\frown x\Vdash ^* \langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}} \langle \beta ,\, \xi _\beta \rangle $
.
$h^\frown x\Vdash ^* \langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}} \langle \beta ,\, \xi _\beta \rangle $
.
Working in
![]() $V[G][K]$
, for each x we let
$V[G][K]$
, for each x we let
![]() $b_x = \{\alpha \in J \setminus \rho \mid x\in A^*_\alpha \}$
. By increasing
$b_x = \{\alpha \in J \setminus \rho \mid x\in A^*_\alpha \}$
. By increasing
![]() $\rho $
, we may assume that each
$\rho $
, we may assume that each
![]() $b_x$
is unbounded in
$b_x$
is unbounded in
![]() $\lambda $
or empty. We say that
$\lambda $
or empty. We say that
![]() $\dagger _x$
holds if
$\dagger _x$
holds if
![]() $b_x$
is unbounded and
$b_x$
is unbounded and
![]() $b_x\in V[G]$
. Let
$b_x\in V[G]$
. Let
![]() $A = \{x\in \mathcal {P}_\kappa (\kappa _n) \mid \dagger _x\text { holds }\}$
. Then
$A = \{x\in \mathcal {P}_\kappa (\kappa _n) \mid \dagger _x\text { holds }\}$
. Then
![]() $A \in V[G]$
since
$A \in V[G]$
since
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\mu $
-closed.
$\mu $
-closed.
Claim 3.6.
![]() $A \in U_n$
.
$A \in U_n$
.
Proof Suppose otherwise. Then
![]() $A^c =\mathcal {P}_\kappa (\kappa _n) \setminus A\in U_n$
. Find
$A^c =\mathcal {P}_\kappa (\kappa _n) \setminus A\in U_n$
. Find
![]() $q_0$
and
$q_0$
and
![]() $q_1$
in
$q_1$
in
![]() $\mathbb {Q}$
with the following property: for all
$\mathbb {Q}$
with the following property: for all
![]() $x\in A^c$
such that
$x\in A^c$
such that
![]() $\dot {b}_x$
is not forced to be empty, there is
$\dot {b}_x$
is not forced to be empty, there is
![]() $\alpha _x <\lambda $
such that
$\alpha _x <\lambda $
such that
![]() $q_0$
and
$q_0$
and
![]() $q_1$
decide “
$q_1$
decide “
![]() $\alpha _x\in \dot {b}_x$
” in opposite ways. Let
$\alpha _x\in \dot {b}_x$
” in opposite ways. Let
![]() $\beta \geq \text {sup}_x\alpha _x$
with
$\beta \geq \text {sup}_x\alpha _x$
with
![]() $\beta \in J$
.
$\beta \in J$
.
Extend each condition
![]() $q_i$
to
$q_i$
to
![]() $q^{\prime }_i$
such that for each
$q^{\prime }_i$
such that for each
![]() $x\in A^c$
,
$x\in A^c$
,
 $q_i'\parallel x\in \dot {A}^*_\beta $
. This is possible by the closure of
$q_i'\parallel x\in \dot {A}^*_\beta $
. This is possible by the closure of
![]() $\mathbb {Q}$
. Let
$\mathbb {Q}$
. Let
 $A_i = \{ x \in A^c \mid q_i' \Vdash x\in \dot {A}^*_\beta \}$
, then
$A_i = \{ x \in A^c \mid q_i' \Vdash x\in \dot {A}^*_\beta \}$
, then
![]() $A_i \in U_n$
because
$A_i \in U_n$
because
![]() $A^c \in U_n$
.
$A^c \in U_n$
.
Take
![]() $x\in A_0\cap A_1$
and let
$x\in A_0\cap A_1$
and let
![]() $\alpha =\alpha _x$
. Then both
$\alpha =\alpha _x$
. Then both
![]() $q^{\prime }_0,\, q^{\prime }_1$
force that
$q^{\prime }_0,\, q^{\prime }_1$
force that
 $x\in \dot {A}^*_\beta $
. Then
$x\in \dot {A}^*_\beta $
. Then
![]() $\dot {b}_x$
is forced to be nonempty, so
$\dot {b}_x$
is forced to be nonempty, so
![]() $q_0'$
and
$q_0'$
and
![]() $q_1'$
decide “
$q_1'$
decide “
![]() $\alpha \in \dot {b}_x$
” in opposite ways. Without loss of generality:
$\alpha \in \dot {b}_x$
” in opposite ways. Without loss of generality:
-
1.
 $q^{\prime }_0\Vdash \alpha \in \dot {b}_x$
.
$q^{\prime }_0\Vdash \alpha \in \dot {b}_x$
. -
2.
 $q^{\prime }_1\Vdash \alpha \notin \dot {b}_x$
.
$q^{\prime }_1\Vdash \alpha \notin \dot {b}_x$
.
The first item implies that
 $q^{\prime }_0\Vdash x\in \dot {A}^*_\alpha \cap \dot {A}^*_\beta $
, and so
$q^{\prime }_0\Vdash x\in \dot {A}^*_\alpha \cap \dot {A}^*_\beta $
, and so
![]() $h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. But then since
$h^\frown x\Vdash ^*\langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. But then since
 $q^{\prime }_1\Vdash x\in \dot {A}^*_\beta $
, we get that
$q^{\prime }_1\Vdash x\in \dot {A}^*_\beta $
, we get that
 $q^{\prime }_1\Vdash \alpha \in \dot {b}_x$
. Contradiction.⊣
$q^{\prime }_1\Vdash \alpha \in \dot {b}_x$
. Contradiction.⊣
So, we have
![]() $A\in U_n$
. By the closure of
$A\in U_n$
. By the closure of
![]() $\mathbb {Q}$
, the sequence
$\mathbb {Q}$
, the sequence
![]() $\langle b_x\mid x \in A\rangle $
is also in
$\langle b_x\mid x \in A\rangle $
is also in
![]() $V[G]$
. Let
$V[G]$
. Let
![]() $A_\alpha = \{x \in A \mid \alpha \in b_x\}$
. Since each
$A_\alpha = \{x \in A \mid \alpha \in b_x\}$
. Since each
![]() $A_\alpha =A\cap A^*_\alpha $
and
$A_\alpha =A\cap A^*_\alpha $
and
![]() $A^*_\alpha \in j(U_n)$
, we get that
$A^*_\alpha \in j(U_n)$
, we get that
![]() $A_\alpha \in U_n$
. This completes the lemma.⊣
$A_\alpha \in U_n$
. This completes the lemma.⊣
We can now apply this lemma inductively as in [Reference Neeman4] to get conditions
![]() $\langle p_\alpha \mid \alpha \in J\setminus \rho \rangle $
so that for all
$\langle p_\alpha \mid \alpha \in J\setminus \rho \rangle $
so that for all
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $p_\alpha \land p_\beta \Vdash \langle \alpha ,\,\xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. By the
$p_\alpha \land p_\beta \Vdash \langle \alpha ,\,\xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. By the
![]() $\mu $
chain condition, there are unboundedly many
$\mu $
chain condition, there are unboundedly many
![]() $\alpha $
’s such that
$\alpha $
’s such that
![]() $p_\alpha $
is forced into a generic for
$p_\alpha $
is forced into a generic for
![]() $\mathbb {P}$
. This gives a branch.⊣
$\mathbb {P}$
. This gives a branch.⊣
Remark 3.7. The above arguments can also be carried out by assuming that
![]() $\lambda $
is weakly compact.
$\lambda $
is weakly compact.
The arguments of [Reference Sinapova and Unger6, Section 3] can be used to show that
![]() $\mu $
has the tree property in
$\mu $
has the tree property in
![]() $V[G][H]$
. The setting here is rather simpler and we just outline the argument. Let
$V[G][H]$
. The setting here is rather simpler and we just outline the argument. Let
![]() $\dot T \in V[G]$
be a
$\dot T \in V[G]$
be a
![]() $\mathbb P$
-name for a
$\mathbb P$
-name for a
![]() $\mu $
-tree. Recalling that
$\mu $
-tree. Recalling that
![]() $\mathbb M$
can be written as a projection of
$\mathbb M$
can be written as a projection of
![]() $ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ) \times {\mathbb R}$
for a suitable term forcing
$ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ) \times {\mathbb R}$
for a suitable term forcing
![]() $\mathbb R$
, we force to obtain
$\mathbb R$
, we force to obtain
![]() $V[G] \subseteq V[A \times B]$
where
$V[G] \subseteq V[A \times B]$
where
![]() $A \times B$
is
$A \times B$
is
![]() $ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ) \times {\mathbb R}$
-generic. The Prikry poset
$ \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ) \times {\mathbb R}$
-generic. The Prikry poset
![]() $\mathbb P$
has the same definition in
$\mathbb P$
has the same definition in
![]() $V[A \times B]$
as in
$V[A \times B]$
as in
![]() $V[G]$
, and in this model the cardinals
$V[G]$
, and in this model the cardinals
![]() $\kappa _n$
are generically supercompact via reasonably nice forcing. We can use this to argue as in [Reference Neeman4] that T has a branch in
$\kappa _n$
are generically supercompact via reasonably nice forcing. We can use this to argue as in [Reference Neeman4] that T has a branch in
![]() $V[A \times B][H]$
, and then use the arguments of [Reference Sinapova and Unger6, Lemma 3.6] and [Reference Sinapova and Unger6, Lemma 3.8] to get a branch of T in
$V[A \times B][H]$
, and then use the arguments of [Reference Sinapova and Unger6, Lemma 3.6] and [Reference Sinapova and Unger6, Lemma 3.8] to get a branch of T in
![]() $V[G][H]$
.
$V[G][H]$
.
We have therefore given a new proof of the main theorem of [Reference Sinapova5].
Theorem 3.8. From
![]() $\omega $
many supercompact cardinals and a weakly compact
$\omega $
many supercompact cardinals and a weakly compact
![]() $\lambda $
above them, it is consistent to have the tree property at both
$\lambda $
above them, it is consistent to have the tree property at both
![]() $\kappa ^+$
and
$\kappa ^+$
and
![]() $\kappa ^{++}$
for a singular strong limit cardinal
$\kappa ^{++}$
for a singular strong limit cardinal
![]() $\kappa $
.
$\kappa $
.
Next, we use the above arguments to give another proof of the main theorem of [Reference Sinapova and Unger6].
Theorem 3.9. From
![]() $\omega $
many supercompact cardinals and a weakly compact
$\omega $
many supercompact cardinals and a weakly compact
![]() $\lambda $
above them, it is consistent to have the tree property at both
$\lambda $
above them, it is consistent to have the tree property at both
![]() $\aleph _{\omega ^2+1}$
and
$\aleph _{\omega ^2+1}$
and
![]() $\aleph _{\omega ^2+2}$
, where
$\aleph _{\omega ^2+2}$
, where
![]() $\aleph _{\omega ^2}$
is strong limit.
$\aleph _{\omega ^2}$
is strong limit.
Proof We use the same forcing as in [Reference Sinapova and Unger6]. Namely, we prepare the ground model V, so that:
-
1.
 $\kappa _n=\kappa ^{+n}$
, and
$\kappa _n=\kappa ^{+n}$
, and
 $\kappa _n$
is generically supercompact.
$\kappa _n$
is generically supercompact. -
2. After we force with
 $\mathbb {M}\times \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ^+\setminus \lambda )$
, for each n we have normal measures
$\mathbb {M}\times \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ^+\setminus \lambda )$
, for each n we have normal measures
 $U_n$
on
$U_n$
on
 $\mathcal {P}_\kappa (\kappa _n)$
, and “guiding generics”
$\mathcal {P}_\kappa (\kappa _n)$
, and “guiding generics”
 $K_n$
, for
$K_n$
, for
 $Col(\kappa ^{+\omega +3}, <j_{U_n}(\kappa ))$
over the ultrapower by
$Col(\kappa ^{+\omega +3}, <j_{U_n}(\kappa ))$
over the ultrapower by
 $U_n$
.
$U_n$
. -
3. The guiding generics above are for a
 $\lambda ^+=\mu ^{++}$
-closed forcing since, they are pulled back from a generic for a
$\lambda ^+=\mu ^{++}$
-closed forcing since, they are pulled back from a generic for a
 $Col(\kappa ^{+\omega +3}, <j^*(\kappa ))$
where
$Col(\kappa ^{+\omega +3}, <j^*(\kappa ))$
where
 $j^*$
is a
$j^*$
is a
 $\lambda $
-supercompact embedding with critical point
$\lambda $
-supercompact embedding with critical point
 $\kappa $
, and there the ultrapower is closed under
$\kappa $
, and there the ultrapower is closed under
 $\lambda $
-sequences. For more details, see Section 2 of [Reference Sinapova and Unger6].
$\lambda $
-sequences. For more details, see Section 2 of [Reference Sinapova and Unger6].
Let G be
![]() $\mathbb {M}\times \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ^+\setminus \lambda )$
-generic. In
$\mathbb {M}\times \operatorname {\mathrm {Add}}(\kappa ,\, \lambda ^+\setminus \lambda )$
-generic. In
![]() $V[G]$
define the diagonal Prikry forcing
$V[G]$
define the diagonal Prikry forcing
![]() $\mathbb {P}$
with interleaved collapses to make
$\mathbb {P}$
with interleaved collapses to make
![]() $\kappa =\aleph _{\omega ^2}$
as follows. Conditions are of the form
$\kappa =\aleph _{\omega ^2}$
as follows. Conditions are of the form
![]() $p=\langle d,\, x_0,\, c_o,\, \ldots ,\, x_{n-1},\, c_{n-1},\, A_n,\, C_n,\,\ldots \rangle $
, where,
$p=\langle d,\, x_0,\, c_o,\, \ldots ,\, x_{n-1},\, c_{n-1},\, A_n,\, C_n,\,\ldots \rangle $
, where,
-
1.
 $\langle x_0,\, \ldots ,\, x_{n-1},\, A_n\ldots \rangle $
is in the diagonal Prikry forcing defined from the measures
$\langle x_0,\, \ldots ,\, x_{n-1},\, A_n\ldots \rangle $
is in the diagonal Prikry forcing defined from the measures
 $\langle U_i\mid i<\omega \rangle $
, as defined in Section 2,
$\langle U_i\mid i<\omega \rangle $
, as defined in Section 2, -
2.
 $d\in Col(\omega ,\,\kappa _{x_0}^{+\omega })$
,
$d\in Col(\omega ,\,\kappa _{x_0}^{+\omega })$
, -
3. for
 $i<n-1$
,
$i<n-1$
,
 $c_i\in Col(\kappa _{x_i}^{+\omega +3},\, <\kappa _{x_{i+1}})$
,
$c_i\in Col(\kappa _{x_i}^{+\omega +3},\, <\kappa _{x_{i+1}})$
,
 $c_{n-1}\in Col(\kappa _{x_{n-1}}^{+\omega +3}, <\kappa )$
,
$c_{n-1}\in Col(\kappa _{x_{n-1}}^{+\omega +3}, <\kappa )$
, -
4. for
 $i\geq n$
,
$i\geq n$
,
 $ \operatorname {\mathrm {dom}}(C_i)=A_i$
, each
$ \operatorname {\mathrm {dom}}(C_i)=A_i$
, each
 $C_i(x)\in Col(\kappa _x^{+\omega +3}, <\kappa )$
,
$C_i(x)\in Col(\kappa _x^{+\omega +3}, <\kappa )$
,
 $[C_i]_{U_i}\in K_i$
.
$[C_i]_{U_i}\in K_i$
.
Let H be
![]() $\mathbb {P}$
-generic over
$\mathbb {P}$
-generic over
![]() $V[G]$
. In
$V[G]$
. In
![]() $V[G][H]$
,
$V[G][H]$
,
![]() $\kappa =\aleph _{\omega ^2}$
,
$\kappa =\aleph _{\omega ^2}$
,
![]() $\mu =\aleph _{\omega ^2+1},\, \lambda =\aleph _{\omega ^2+2},\, 2^\kappa =\aleph _{\omega ^2+3}$
. By the arguments of [Reference Sinapova and Unger6, Section 3], which we already sketched above in the setting of Theorem 3.1, we have the tree property at
$\mu =\aleph _{\omega ^2+1},\, \lambda =\aleph _{\omega ^2+2},\, 2^\kappa =\aleph _{\omega ^2+3}$
. By the arguments of [Reference Sinapova and Unger6, Section 3], which we already sketched above in the setting of Theorem 3.1, we have the tree property at
![]() $\mu =\aleph _{\omega ^2+1}$
.
$\mu =\aleph _{\omega ^2+1}$
.
To prove the tree property at
![]() $\aleph _{\omega ^2+2}$
, we use the same approach as in Theorem 3.1. Note that we still have that the number of stems is
$\aleph _{\omega ^2+2}$
, we use the same approach as in Theorem 3.1. Note that we still have that the number of stems is
![]() $\kappa _\omega $
. Also, any two conditions with the same stem are compatible, as witnessed by a common lower bound with that same stem. So
$\kappa _\omega $
. Also, any two conditions with the same stem are compatible, as witnessed by a common lower bound with that same stem. So
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\mu $
-chain condition, and we can define as before the notion of
$\mu $
-chain condition, and we can define as before the notion of
![]() $h\Vdash ^*\phi $
.
$h\Vdash ^*\phi $
.
Let
![]() $j:V\rightarrow M$
be an elementary embedding with critical point
$j:V\rightarrow M$
be an elementary embedding with critical point
![]() $\lambda $
. As in Theorem 3.1, we lift j to
$\lambda $
. As in Theorem 3.1, we lift j to
![]() $j:V[G]\rightarrow M[G^*]$
in
$j:V[G]\rightarrow M[G^*]$
in
![]() $V[G][K\times A]$
, where K is generic for a
$V[G][K\times A]$
, where K is generic for a
![]() $\mu $
-closed forcing
$\mu $
-closed forcing
![]() $\mathbb {Q}$
and A is generic for a
$\mathbb {Q}$
and A is generic for a
![]() $\kappa ^+$
-Knaster forcing. The critical point is still above any fixed condition
$\kappa ^+$
-Knaster forcing. The critical point is still above any fixed condition
![]() $p\in \mathbb {P}$
, that is to say
$p\in \mathbb {P}$
, that is to say
![]() $j(p)=p$
. So we have the analogue of Lemma 3.2: in
$j(p)=p$
. So we have the analogue of Lemma 3.2: in
![]() $V[G]$
, there is an unbounded
$V[G]$
, there is an unbounded
![]() $J\subseteq \lambda $
, a stem h, and a function
$J\subseteq \lambda $
, a stem h, and a function
![]() $f:J\rightarrow \mu $
, such that for all
$f:J\rightarrow \mu $
, such that for all
![]() $\alpha <\beta $
both in J,
$\alpha <\beta $
both in J,
Next we prove the following analogue of Lemma 3.4.
Lemma 3.10. There are
![]() $\rho <\lambda $
and a sequence
$\rho <\lambda $
and a sequence
![]() $\langle A_\alpha ,\, C_\alpha \mid \alpha \in J\setminus \rho \rangle $
in
$\langle A_\alpha ,\, C_\alpha \mid \alpha \in J\setminus \rho \rangle $
in
![]() $V[G]$
, such that:
$V[G]$
, such that:
-
•
 $A_\alpha \in U_n$
,
$A_\alpha \in U_n$
,
 $ \operatorname {\mathrm {dom}}(C_\alpha )=A_\alpha $
,
$ \operatorname {\mathrm {dom}}(C_\alpha )=A_\alpha $
,
 $C_\alpha (x)\in Col(\kappa _x^{+\omega +3}, <\kappa )$
for all
$C_\alpha (x)\in Col(\kappa _x^{+\omega +3}, <\kappa )$
for all
 $x \in A_\alpha $
, and
$x \in A_\alpha $
, and
 $[C_\alpha ]$
is in the guiding generic
$[C_\alpha ]$
is in the guiding generic
 $K_n$
.
$K_n$
. -
• For all
 $x \in A_\alpha \cap A_\beta $
, if
$x \in A_\alpha \cap A_\beta $
, if
 $C_\alpha (x)$
and
$C_\alpha (x)$
and
 $C_\beta (x)$
are compatible, then
$C_\beta (x)$
are compatible, then  $$ \begin{align*} h^\frown \langle x,\, C_\alpha(x)\cup C_\beta(x) \rangle \Vdash^* \langle \alpha,\, \xi_\alpha\rangle <_{\dot{T}} \langle \beta,\, \xi_\beta \rangle.\end{align*} $$
$$ \begin{align*} h^\frown \langle x,\, C_\alpha(x)\cup C_\beta(x) \rangle \Vdash^* \langle \alpha,\, \xi_\alpha\rangle <_{\dot{T}} \langle \beta,\, \xi_\beta \rangle.\end{align*} $$
Proof For every
![]() $\alpha <\beta $
both in J, let
$\alpha <\beta $
both in J, let
![]() $r_{\alpha ,\,\beta } \in \mathbb {P}$
be a condition with stem h, such that
$r_{\alpha ,\,\beta } \in \mathbb {P}$
be a condition with stem h, such that
![]() $r_{\alpha ,\,\beta }\Vdash \langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. Denote
$r_{\alpha ,\,\beta }\Vdash \langle \alpha ,\, \xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. Denote
![]() $r_{\alpha ,\,\beta }=h^\frown (A_{\alpha ,\,\beta },\, C_{\alpha ,\,\beta })^\frown r_{\alpha ,\,\beta }\upharpoonright [n+1,\, \omega )$
. Since each
$r_{\alpha ,\,\beta }=h^\frown (A_{\alpha ,\,\beta },\, C_{\alpha ,\,\beta })^\frown r_{\alpha ,\,\beta }\upharpoonright [n+1,\, \omega )$
. Since each
![]() $[C_{\alpha ,\, \beta }]$
belongs to a
$[C_{\alpha ,\, \beta }]$
belongs to a
![]() $\mu ^{++}$
-closed guiding generic
$\mu ^{++}$
-closed guiding generic
![]() $K_n$
, there is a lower bound
$K_n$
, there is a lower bound
![]() $[C]$
in
$[C]$
in
![]() $K_n$
for all of them. So we may assume that
$K_n$
for all of them. So we may assume that
![]() $ \operatorname {\mathrm {dom}}(C)=\mathcal {P}_\kappa (\kappa _n)$
and that
$ \operatorname {\mathrm {dom}}(C)=\mathcal {P}_\kappa (\kappa _n)$
and that
![]() $C_{\alpha ,\,\beta }=C \upharpoonright A_{\alpha ,\,\beta }$
for all
$C_{\alpha ,\,\beta }=C \upharpoonright A_{\alpha ,\,\beta }$
for all
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, by shrinking measure one sets and extending values of
$\beta $
, by shrinking measure one sets and extending values of
![]() $C_{\alpha ,\, \beta }(x)$
as needed. It follows that for every
$C_{\alpha ,\, \beta }(x)$
as needed. It follows that for every
![]() $\alpha <\beta $
both in J, for
$\alpha <\beta $
both in J, for
![]() $U_n$
-many x,
$U_n$
-many x,
The rest of the proof is exactly as in Lemma 3.4, only we replace instances of
![]() $h^\frown x$
with
$h^\frown x$
with
![]() $h^\frown \langle x,\, C(x)\rangle $
.⊣
$h^\frown \langle x,\, C(x)\rangle $
.⊣
Now we can apply Lemma 3.10 inductively, exactly as we applied Lemma 3.4 in the proof of Theorem 3.1. We construct conditions
![]() $\langle p_\alpha \mid \alpha \in J\setminus \rho \rangle $
so that for all
$\langle p_\alpha \mid \alpha \in J\setminus \rho \rangle $
so that for all
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $p_\alpha \land p_\beta \Vdash \langle \alpha ,\,\xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. By the
$p_\alpha \land p_\beta \Vdash \langle \alpha ,\,\xi _\alpha \rangle <_{\dot {T}}\langle \beta ,\, \xi _\beta \rangle $
. By the
![]() $\mu $
chain condition, there are unboundedly many
$\mu $
chain condition, there are unboundedly many
![]() $\alpha $
’s such that
$\alpha $
’s such that
![]() $p_\alpha $
is forced into a generic for
$p_\alpha $
is forced into a generic for
![]() $\mathbb {P}$
. This gives a branch.⊣
$\mathbb {P}$
. This gives a branch.⊣
Acknowledgments
The results in this paper were conceived and proved during a series of visits to the American Institute of Mathematics, as part of the Institute’s SQuaRE collaborative research program. The authors are deeply grateful to Brian Conrey, Estelle Basor and all the staff at AIM for providing an ideal working environment.
Cummings was partially supported by the National Science Foundation, DMS-1500790. Hayut was partially supported by FWF Lise Meitner grant 2650-N35. Neeman was partially supported by the National Science Foundation, DMS-1764029. Sinapova was partially supported by the National Science Foundation, Career-1454945. Unger was partially supported by the National Science Foundation, DMS-1700425.