We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For any positive integers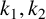 
$k_1,k_2$ and any set 
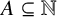$A\subseteq \mathbb {N}$, let 
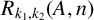$R_{k_1,k_2}(A,n)$ be the number of solutions of the equation 
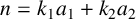$n=k_1a_1+k_2a_2$ with 
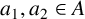$a_1,a_2\in A$. Let g be a fixed integer. We prove that if 
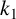$k_1$ and 
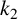$k_2$ are two integers with 
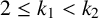$2\le k_1<k_2$ and 
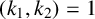$(k_1,k_2)=1$, then there does not exist any set 
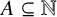$A\subseteq \mathbb {N}$ such that 
$R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb {N}\setminus A,n)=g$ for all sufficiently large integers n, and if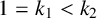 
$1=k_1<k_2$, then there exists a set A such that 
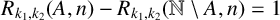$R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb {N}\setminus A,n)=1$ for all positive integers n.
Let 
$\mathbb{N}$ be the set of all nonnegative integers. For any set 
$A\subset \mathbb{N}$, let 
$R(A,n)$ denote the number of representations of 
$n$ as 
$n=a+a^{\prime }$ with 
$a,a^{\prime }\in A$. There is no partition 
$\mathbb{N}=A\cup B$ such that 
$R(A,n)=R(B,n)$ for all sufficiently large integers 
$n$. We prove that a partition 
$\mathbb{N}=A\cup B$ satisfies 
$|R(A,n)-R(B,n)|\leq 1$ for all nonnegative integers 
$n$ if and only if, for each nonnegative integer 
$m$, exactly one of 
$2m+1$ and 
$2m$ is in 
$A$.
