We prove a difference analogue of the celebrated Tumura–Hayman–Clunie theorem. Let f be a transcendental entire function, let c be a nonzero constant and let n be a positive integer. If f and $\Delta _c^n f$ omit zero in the whole complex plane, then either $f(z)=\exp (h_1(z)+C_1 z)$, where $h_1$ is an entire function of period c and $\exp (C_1 c)\neq 1$, or $f(z)=\exp (h_2(z)+C_2 z)$, where $h_2$ is an entire function of period $2c$ and $C_2$ satisfies

$$ \begin{align*} \bigg(\frac{1+\exp(C_2c)}{1-\exp(C_2 c)}\bigg)^{2n}=1. \end{align*} $$

In this work, we consider the first-order difference equation with general argument

\[ \varDelta x(n)+p(n)x\left( \tau (n)\right) =0,\quad n\geq 0, \]

$(p(n))$

$(\tau (n))$

$\tau (n)< n$

$\ n\in \mathbf {N},\,$

$\ \lim _{n\rightarrow \infty }\tau (n)=\infty.$

We compactify and regularise the space of initial values of a planar map with a quartic invariant and use this construction to prove its integrability in the sense of algebraic entropy. The system has certain unusual properties, including a sequence of points of indeterminacy in $\mathbb {P}^{1}\!\times \mathbb {P}^{1}$ . These indeterminacy points lie on a singular fibre of the mapping to a corresponding QRT system and provide the existence of a one-parameter family of special solutions.

Let P and Q be relatively prime integers greater than 1, and let f be a real valued discretely supported function on a finite dimensional real vector space V. We prove that if $f_{P}(x)=f(Px)-f(x)$ and $f_{Q}(x)=f(Qx)-f(x)$ are both $\Lambda $ -periodic for some lattice $\Lambda \subset V$ , then so is f (up to a modification at $0$ ). This result is used to prove a theorem on the arithmetic of elliptic function fields. In the last section, we discuss the higher rank analogue of this theorem and explain why it fails in rank 2. A full discussion of the higher rank case will appear in a forthcoming work.

We study solutions of difference equations in the rings of sequences and, more generally, solutions of equations with a monoid action in the ring of sequences indexed by the monoid. This framework includes, for example, difference equations on grids (for example, standard difference schemes) and difference equations in functions on words. On the universality side, we prove a version of strong Nullstellensatz for such difference equations under the assumption that the cardinality of the ground field is greater than the cardinality of the monoid and construct an example showing that this assumption cannot be omitted. On the undecidability side, we show that the following problems are undecidable:

In this note, we prove a uniqueness theorem for finite-order meromorphic solutions to a class of difference equations of Malmquist type. Such solutions $f$ are uniquely determined by their poles and the zeros of $f-e_{j}$ (counting multiplicities) for two finite complex numbers $e_{1}\neq e_{2}$.

In this paper, some criteria for the existence of positive solutions of a class of systems of impulsive dynamic equations on time scales are obtained by using a fixed point theorem in cones.

Consider the second order superlinear dynamic equation

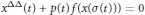$$(*)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}^{\Delta \Delta }}(t)+p(t)f(x(\sigma (t)))=0$$

where 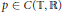$p\,\in \,C(\mathbb{T},\,\mathbb{R})$, $\mathbb{T}$ is a time scale, 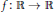$f\,:\,\mathbb{R}\,\to \,\mathbb{R}$ is continuously differentiable and satisfies 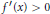${{f}^{'}}(x)>0$, and 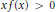$x\,f\,(x)\,>\,0$ for 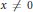$x\,\ne \,0$. Furthermore, $f(x)$ also satisfies a superlinear condition, which includes the nonlinear function 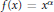$f(x)\,=\,{{x}^{\alpha }}$ with 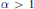$\alpha \,>\,1$, commonly known as the Emden–Fowler case. Here the coefficient function 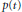$p(t)$ is allowed to be negative for arbitrarily large values of $t$. In addition to extending the result of Kiguradze for 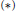$\left( * \right)$ in the real case 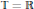$\mathbb{T}\,=\,\mathbb{R}$, we obtain analogues in the difference equation and $q$-difference equation cases.

We present a systematic construction of the discrete KP hierarchy in terms of Sato–Wilson-type shift operators. Reductions of the equations in this hierarchy to 1+1-dimensional integrable lattice systems are considered, and the problems that arise with regard to the symmetry algebra underlying the reduced systems as well as the ultradiscretizability of these systems are discussed. A scheme for constructing ultradiscretizable reductions that give rise to Yang–Baxter maps is explained in two explicit examples.

We describe a family of integrable lattice maps related to the known quad maps Q4. The integrability criterion we use is the vanishing of the algebraic entropy. The family has the advantage of being parametrized rationally: all its parameters are unconstrained.

In this paper, we are computing asymptotic formulas for a base of solutions of the second-order difference equations in the double root case. Two methods are presented.

In this paper, existence criteria for multiple solutions of periodic boundary value problems for the first-order difference equation are established by using the Leggett–Williams multiple fixed point theorem and fixed point theorem of cone expansion and compression. Two examples are also given to illustrate the main results.

This paper is devoted to the study of Wirtinger-type inequalities for the Lebesgue $\Delta$-integral on an arbitrary time scale $\mathbb{T}$. We prove a general inequality for a class of absolutely continuous functions on closed subintervals of an adequate subset of $\mathbb{T}$. By using this expression and by assuming that $\mathbb{T}$ is bounded, we deduce that a general inequality is valid for every absolutely continuous function on $\mathbb{T}$ such that its $\Delta$-derivative belongs to $L_{\Delta }^{2}\,([a,\,b)\,\cap \,\mathbb{T})$ and at most it vanishes on the boundary of $\mathbb{T}$.

The main goal of the paper is to find the discrete analogue of the Bianchi system in spaces of arbitrary dimension together with its geometric interpretation. We show that the proper geometric framework for such generalization is the language of dual quadrilateral lattices and of dual congruences. After introducing the notion of the dual Koenigs lattice in a projective space of arbitrary dimension, we define the discrete dual congruences and we present, as an important example, the normal dual discrete congruences. Finally, we introduce the dual Bianchi lattice as a dual Koenigs lattice allowing for a conjugate normal dual congruence, and we find its characterization in terms of a system of integrable difference equations.

By means of generalized Riccati transformation techniques and generalized exponential functions, some oscillation criteria are given for the nonlinear dynamic equation \[ (p(t)x^{\Delta} (t))^{\Delta}+q(t)(f\circ x^{\sigma})=0 \] on time scales. The results are also applied to linear and nonlinear dynamic equations with damping, and some sufficient conditions are obtained for the oscillation of all solutions.

We present a general recurrence model which provides a conceptual framework for well-known problems such as ascents, peaks, turning points, Bernstein's urn model, the Eggenberger–Pólya urn model and the hypergeometric distribution. Moreover, we show that the Frobenius-Harper technique, based on real roots of a generating function, can be applied to this general recurrence model (under simple conditions), and so a Berry–Esséen bound and local limit theorems can be found. This provides a simple and unified approach to asymptotic theory for diverse problems hitherto treated separately.

It was shown by Edgar and Rosenblatt that f ∈ Lp (ℝn), 1 ≤ p < 2n/ (n-1), and f ≠0, then f has linearly independent translates. Using a result of Hömander, it is shown here that the same theorem holds if p = 2n / (n−1). This gives a sharp result because for n ≥2, there exists f ∈C0 (ℝn), f ≠0, which is simultaneously in all Lp (ℝn), p > 2n/(n−1), that has a linear dependence relation among its translates. References and some discussion are included.

The Neumann operator is an operator on the boundary of a smooth manifold which maps the boundary value of a harmonic function to its normal derivative. The spectrum of the Neumann operator is studied on the curves bounding a family of Riemann surfaces. The Neumann operator is shown to be isospectral to a direct sum of symmetric Jacobi matrices, each acting on l2(ℤ). The Jacobi matrices are shown to be isospectral to generators of bilateral, linear birth-death processes. Using the connection between Jacobi matrices and continued fractions, it is shown that the eigenvalues of the Neumann operator must solve a certain equation involving hypergeometric functions. Study of the equation yields uniform bounds on the eigenvalues and also the asymptotics of the eigenvalues as the curves degenerate into a wedge of circles.

We examine the convergence and analytic properties of a continued fraction of Ramanujan and its connection to the orthogonal polynomials of Meixner-Pollaczek.

Let a ≧ 0, Ia = ﹛a, a + 1, …﹜ and consider the nth order linear difference m ∈ Ia, α0(m) = 1 on Ia. Summability conditions are placed on the coefficients αj(m), 1 ≦ j ≦ n, such that the equation Pu(m) = 0 is eventually disconjugate. Conditions for eventual right disfocality are also given.