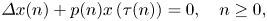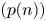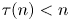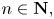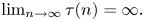1. Introduction
For a long time, the oscillation theory of differential and difference equations has attracted many researchers. In recent years, there has been much research activity concerning the oscillation and non-oscillation of solutions of delay differential and difference equations. For these oscillatory and non-oscillatory results, we refer, for instance [Reference Braverman and Karpuz1–Reference Zhang and Tian19].
Consider the retarded difference equation
where $(p(n))$![]() is a sequence of non-negative real numbers, $(\tau (n))$
is a sequence of non-negative real numbers, $(\tau (n))$![]() is a sequence of integers such that
is a sequence of integers such that
$\varDelta$![]() denotes the forward difference operator $\varDelta x(n)=x(n+1)-x(n).$
denotes the forward difference operator $\varDelta x(n)=x(n+1)-x(n).$![]() Define
Define
By a solution of the difference equation (1.1), we mean a sequence of real numbers $(x(n))$![]() which satisfies (1.1) for all $n\geq 0$
which satisfies (1.1) for all $n\geq 0$![]() . It is clear that, for each choice of real numbers $c_{-k},\,c_{-k+1},\ldots,\,c_{-1},\,c_{0},$
. It is clear that, for each choice of real numbers $c_{-k},\,c_{-k+1},\ldots,\,c_{-1},\,c_{0},$![]() there exists a unique solution $(x(n))$
there exists a unique solution $(x(n))$![]() of (1.1) which satisfies the initial conditions $x(-k)=c_{-k},\,\ x(-k+1)=c_{-k+1},\,\ldots,\,\ x(-1)=c_{-1},\,\ x(0)=c_{0}.$
of (1.1) which satisfies the initial conditions $x(-k)=c_{-k},\,\ x(-k+1)=c_{-k+1},\,\ldots,\,\ x(-1)=c_{-1},\,\ x(0)=c_{0}.$![]()
A solution $(x(n))$![]() of the difference equation (1.1) is called oscillatory, if the terms $x(n)$
of the difference equation (1.1) is called oscillatory, if the terms $x(n)$![]() of the sequence are neither eventually positive nor eventually negative. Otherwise, the solution is said to be non-oscillatory.
of the sequence are neither eventually positive nor eventually negative. Otherwise, the solution is said to be non-oscillatory.
When $\tau (n)=n-l$![]() where $l\geq 0$
where $l\geq 0$![]() an integer number$,$
an integer number$,$![]() then Equation (1.1) reduces to
then Equation (1.1) reduces to
Strong interest in the delay difference equation (1.1) is motivated by the fact that it represents a discrete analogue of the delay differential equation
where $p(t)\in C( [t_{0},\,\infty ),\,[0,\,\infty )) ,\,\ \tau (t)\in C( [t_{0},\,\infty ),\,\mathbb {R}) ,\,\ \tau (t)\leq t$![]() and$\ \lim _{t\rightarrow \infty }\tau (t)=\infty.$
and$\ \lim _{t\rightarrow \infty }\tau (t)=\infty.$![]()
In particular, the delay difference equation (1.3) represents a discrete analogue of the (first-order) delay differential equation
where $T$![]() is a positive real constant. For Equations (1.4) and (1.5), see [Reference Erbe, Kong and Zhang8, Reference Györi and Ladas10, Reference Ladde, Lakshmikantham and Zhang13].
is a positive real constant. For Equations (1.4) and (1.5), see [Reference Erbe, Kong and Zhang8, Reference Györi and Ladas10, Reference Ladde, Lakshmikantham and Zhang13].
The problem of establishing sufficient conditions for the oscillation of all solutions of the difference equations (1.1) and (1.3) has been the subject of many investigations, for instance, in 1989, Erbe and Zhang [Reference Erbe and Zhang7] proved that each one of the conditions
or

is sufficient for all solutions of (1.3) to be oscillatory. In the same year, 1989, Ladas, Philos and Sficas [Reference Ladas, Philos and Sficas12] established that all solutions of (1.3) are oscillatory if

Clearly, the condition (1.8) improves the condition (1.6).
We now turn to the general case of the delay difference equation (1.1). The condition (1.7) can be extended to Equation (1.1). More precisely, if the sequence $( \tau (n))$![]() is assumed to be increasing, then from Chatzarakis et al. [Reference Chatzarakis, Koplatadze and Stavroulakis3], it follows that all solutions of (1.1) are oscillatory if
is assumed to be increasing, then from Chatzarakis et al. [Reference Chatzarakis, Koplatadze and Stavroulakis3], it follows that all solutions of (1.1) are oscillatory if

In 1991, Philos [Reference Philos14] extended the oscillation criterion (1.8) to the general case of Equation (1.1), by establishing that, if the sequence $( \tau (n))$![]() is non-decreasing, then the condition
is non-decreasing, then the condition

suffices for the oscillation of all solutions of Equation (1.1).
In 1998, Zhang and Tian [Reference Zhang and Tian19] obtained that if$\ (\tau (n))$![]() is non-decreasing,
is non-decreasing,
and

then all solutions of (1.1) are oscillatory.
In 1998, Zhang and Tian [Reference Zhang and Tian18] obtained that if$\ (\tau (n))$![]() is not necessarily monotone and
is not necessarily monotone and

then all solutions of (1.1) oscillate.
In 2008, Chatzarakis et al. [Reference Chatzarakis, Koplatadze and Stavroulakis2, Reference Chatzarakis, Koplatadze and Stavroulakis3], when $(\tau (n))$![]() is not necessarily monotone, studied Equation (1.1) and proved that, if one of the following conditions
is not necessarily monotone, studied Equation (1.1) and proved that, if one of the following conditions

or

is satisfied, then all solutions of (1.1) oscillate.
Set,

Clearly,
In 2006, W. Yan, Q. Meng and J. Yan [Reference Yan, Meng and Yan17] obtained that if$\ (\tau (n))$![]() is non-decreasing and
is non-decreasing and

then all solutions of (1.1) are oscillatory.
Observe that, it is easy to see that

and therefore the condition (1.17) is better than the condition (1.12).
In 2016, Öcalan [Reference Öcalan15], when $(\tau (n))$![]() is not necessarily monotone, established the following result; if
is not necessarily monotone, established the following result; if

where $h(n)=\max _{0\leq s\leq n}\tau (s)$![]() , $n\geq 0$
, $n\geq 0$![]() , then all solutions of (1.1) are oscillatory.
, then all solutions of (1.1) are oscillatory.
In 2011, Braverman and Karpuz [Reference Braverman and Karpuz1] proved that if $(\tau (n))$![]() is not necessarily monotone and
is not necessarily monotone and

then all solutions of (1.1) oscillate. Evidently, condition (1.19) has improved condition (1.14).
In [Reference Öcalan16], Öcalan proved that if $(\tau (n))$![]() is not necessarily monotone and
is not necessarily monotone and

then all solutions of (1.1) oscillate. It can be seen immediately that if $(\tau (n))$![]() is non-decreasing, then condition (1.20) returns to condition (1.15). However, if $(\tau (n))$
is non-decreasing, then condition (1.20) returns to condition (1.15). However, if $(\tau (n))$![]() is strictly non-monotone, then condition (1.20) has improved condition (1.15).
is strictly non-monotone, then condition (1.20) has improved condition (1.15).
The main aim of this paper is to improve, involving only upper and only lower limit conditions, the all known results for Equation (1.1) in the literature.
Throughout this paper, we are going to use the following notation:

2. Main results
We present some new sufficient conditions for the oscillation of all solutions of Equation (1.1), under the assumption that the arguments $(\tau (n))$![]() is not necessarily monotone.
is not necessarily monotone.
Let,
Clearly, $h(n)$![]() is non-decreasing and $\tau (n)\leq h(n)$
is non-decreasing and $\tau (n)\leq h(n)$![]() for all $n\geq 0.$
for all $n\geq 0.$![]()
The following Lemma was given in [Reference Chatzarakis, Koplatadze and Stavroulakis3], which is needed to prove our next theorem.
Lemma 2.1 Assume that (1.2) holds and $p(n)\geq 0$![]() . Thus, we have
. Thus, we have

where $(h(n))$![]() is defined by (2.1).
is defined by (2.1).
Theorem 2.2 Assume that (1.2) holds and $p(n)\geq 0$![]() . Furthermore, assume that
. Furthermore, assume that

where $(h(n))$![]() is defined by (2.1). If $\lim _{n\rightarrow \infty }(n-h(n))=\infty$
is defined by (2.1). If $\lim _{n\rightarrow \infty }(n-h(n))=\infty$![]() or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N},$
or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N},$![]() then all solutions of Equation (1.1) oscillate.
then all solutions of Equation (1.1) oscillate.
Proof. Assume, for the sake of contradiction, that $(x(n))$![]() be an eventually positive solution of Equation (1.1). Let $n_{1}\geq -k$
be an eventually positive solution of Equation (1.1). Let $n_{1}\geq -k$![]() be an integer such that $x(n),\,x(\tau (n))>0$
be an integer such that $x(n),\,x(\tau (n))>0$![]() for all $n\geq n_{1}.$
for all $n\geq n_{1}.$![]() Thus, from Equation (1.1), we have
Thus, from Equation (1.1), we have
which means that the sequence $(x(n))$![]() is eventually non-increasing. In view of this and taking into account that $\tau (n)< n$
is eventually non-increasing. In view of this and taking into account that $\tau (n)< n$![]() , Equation (1.1) gives
, Equation (1.1) gives
If we apply the discrete Grönwall inequality to this inequality, we obtain

On the other hand, we know from Lemma 2.1 that

Now, we define

Thus, by (2.2), it follows that there exists a constant $d$![]() such that
such that

Now, in view of (2.4), and for all large $n,$![]() there exists $n^{\ast }\in \lbrack h(n),\,n)$
there exists $n^{\ast }\in \lbrack h(n),\,n)$![]() such that
such that

From the fact that $(h(n))$![]() is non-decreasing and $(x(n))$
is non-decreasing and $(x(n))$![]() is non-increasing, summing up (1.1) from $h(n)$
is non-increasing, summing up (1.1) from $h(n)$![]() to $n^{\ast }$
to $n^{\ast }$![]() and applying the discrete Grönwall inequality, we obtain
and applying the discrete Grönwall inequality, we obtain

and

Also, summing up Equation (1.1) from $n^{\ast }$![]() to $n,$
to $n,$![]() and using the discrete Grönwall inequality, will yield
and using the discrete Grönwall inequality, will yield

By omitting the first terms in (2.6) and (2.7) and by using (2.5), we obtain
and
Thus, we have
and so
On the other hand, by (1.1), we obtain
Applying the discrete Grönwall inequality to (2.9), we obtain

Set
then (2.11) yields,

Now, using the well-known inequality between the arithmetic and geometric means, we find that

So, using the inequality
inequality (2.13) gives

Let $\liminf _{n\rightarrow \infty }\sum \nolimits \limits _{j=h(n)}^{n-1}y(j)=c.$![]() We know that
We know that

and

From (2.10) and (2.15), we have

Now, from (2.16) we get

where $\varepsilon$![]() is an arbitrary real number with $0<\varepsilon < c.$
is an arbitrary real number with $0<\varepsilon < c.$![]() So, from (2.14) and (2.17), we have
So, from (2.14) and (2.17), we have

Summing up (2.18) from $h(n)$![]() to $n-1,$
to $n-1,$![]() we have
we have

Thus, by (2.19), we obtain

and as $\varepsilon \rightarrow 0,$![]() the above inequality yields
the above inequality yields

which contradicts to (2.2). The proof of the theorem is complete.
Remark 2.1 It can be seen immediately that if $\tau (n)< n,\,\ \lim _{n\rightarrow \infty }(n-h(n))=\infty$![]() or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N}$
or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N}$![]() , then
, then

and therefore condition (2.2) is better than condition (1.20).
Moreover, when $(\tau (n))$![]() is strictly non-monotone and $\prod _{i=\tau (j)}^{h(j)-1}\frac {1}{1-p(i)}=1,$
is strictly non-monotone and $\prod _{i=\tau (j)}^{h(j)-1}\frac {1}{1-p(i)}=1,$![]() since
since

Theorem 2.3 Assume that (1.2) holds. Moreover, we suppose that

where $(h(n))$![]() is defined by (2.1). If $\lim _{n\rightarrow \infty }(n-h(n))=\infty$
is defined by (2.1). If $\lim _{n\rightarrow \infty }(n-h(n))=\infty$![]() or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N},$
or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N},$![]() then all solutions of Equation (1.1) oscillate.
then all solutions of Equation (1.1) oscillate.
Proof. Assume, for the sake of contradiction, that $(x(n))$![]() be an eventually positive solution of Equation (1.1). Let $n_{1}\geq -k$
be an eventually positive solution of Equation (1.1). Let $n_{1}\geq -k$![]() be an integer such that $x(n),\,x(\tau (n))>0$
be an integer such that $x(n),\,x(\tau (n))>0$![]() for all $n\geq n_{1}.$
for all $n\geq n_{1}.$![]() Thus, by equation (1.1), we have
Thus, by equation (1.1), we have
which means that the sequence $(x(n))$![]() is non-increasing. It is clear that if $\tau (n)< n$
is non-increasing. It is clear that if $\tau (n)< n$![]() and $\lim _{n\rightarrow \infty }(n-h(n))=\infty,\,~$
and $\lim _{n\rightarrow \infty }(n-h(n))=\infty,\,~$![]() or $h(n)=n-$
or $h(n)=n-$![]() $m$
$m$![]() with $m\geq 1\in \mathbb {N}\mathbf {,\,}$
with $m\geq 1\in \mathbb {N}\mathbf {,\,}$![]() then
then
From Equation (1.1), we have
Now, we assume that $\tau (n)< n$![]() and $\lim _{n\rightarrow \infty }(n-h(n))=\infty.$
and $\lim _{n\rightarrow \infty }(n-h(n))=\infty.$![]() Summing up (2.21) from $h(n)$
Summing up (2.21) from $h(n)$![]() to $n,$
to $n,$![]() we obtain
we obtain

Applying the discrete Grönwall inequality to (2.22), we obtain

and from the fact that $(h(n))$![]() is non-decreasing and $(x(n))$
is non-decreasing and $(x(n))$![]() is non-increasing, we have
is non-increasing, we have

or

So, from (2.24), we obtain

and

Since $\lim _{n\rightarrow \infty }(n-h(n))=\infty,$![]() we have $\lim _{n\rightarrow \infty }s(h(n))=e.$
we have $\lim _{n\rightarrow \infty }s(h(n))=e.$![]() So, by (2.26), we obtain
So, by (2.26), we obtain

which contradicts to (2.20).
Now, we assume that $h(n)=n-m,\,\ m\geq 1\in \mathbb {N}.$![]() So, condition (2.20) is equivalent to
So, condition (2.20) is equivalent to

In view of (2.23), we have

On the other hand, since $\lim _{n\rightarrow \infty }x(n)=l\geq 0,$![]() we can find a constant $c>0$
we can find a constant $c>0$![]() such that
such that
Thus, from (2.28) and (2.29), we obtain

or

or

and

So, by (2.30), we obtain

which contradicts to (2.20). The proof of theorem is complete.
Remark 2.2 Observe that, it is easy to see that if $\tau (n)< n,\,\ \lim _{n\rightarrow \infty }(n-h(n))=\infty$![]() or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N}$
or $h(n)=n-m,\,\ m\geq 1\in \mathbb {N}$![]() , then
, then

and therefore condition (2.20) is better than condition (1.19).
Now, we present two examples to show the significance of our results. The first example is for comparing $\lim \sup$![]() conditions.
conditions.
Example 2.1 Consider the following difference equation
Let us first show that the $\lim \sup$![]() tests mentioned in the introduction fail for this equation. Clearly,
tests mentioned in the introduction fail for this equation. Clearly,

which means that the condition (1.14) is not applicable for this equation. Moreover,

which means that the condition (1.19) is not applicable for this equation. However,

That is, condition (2.20) of Theorem 2.3 is satisfied. Therefore, all solutions of (2.31) oscillate.
The second example is for comparing $\lim \inf$![]() conditions.
conditions.
Example 2.2 Consider the following difference equation
with
Here, it is clear that (1.2) is satisfied and $(\tau (n))$![]() is strictly non-monotone. Also, by (2.1), we have
is strictly non-monotone. Also, by (2.1), we have
Let us first show that the $\lim \inf$![]() tests mentioned in the introduction fail for this equation. Clearly,
tests mentioned in the introduction fail for this equation. Clearly,

which means that condition (1.15) is not applicable for this equation. Moreover,

which means that condition (1.20) is not applicable for this equation. Also,

which means that condition (1.18) is not applicable for this equation. However,

That is, condition (2.2) of Theorem 2.2 is satisfied. Therefore, all solutions of (2.32) oscillate.