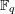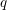1 Introduction
One of the useful tools in complex algebraic geometry is the Kodaira vanishing theorem, which is generalised to the Kawamata–Viehweg vanishing theorem and the Nadel vanishing theorem. For instance, these vanishing theorems yield the following consequences.
 $(1)_{0}$
$(1)_{0}$If
 $X$ is a smooth projective variety over
$X$ is a smooth projective variety over  $\mathbb{C}$ such that
$\mathbb{C}$ such that  $-K_{X}$ is ample, then
$-K_{X}$ is ample, then  $H^{i}(X,{\mathcal{O}}_{X})=0$ for
$H^{i}(X,{\mathcal{O}}_{X})=0$ for  $i>0$.
$i>0$. $(2)_{0}$
$(2)_{0}$If
 $(X,\unicode[STIX]{x1D6E5})$ is a projective klt pair over
$(X,\unicode[STIX]{x1D6E5})$ is a projective klt pair over  $\mathbb{C}$ such that
$\mathbb{C}$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, then
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, then  $H^{i}(X,{\mathcal{O}}_{X})=0$ for
$H^{i}(X,{\mathcal{O}}_{X})=0$ for  $i>0$.
$i>0$. $(3)_{0}$
$(3)_{0}$If
 $(X,\unicode[STIX]{x1D6E5})$ is a projective log pair over
$(X,\unicode[STIX]{x1D6E5})$ is a projective log pair over  $\mathbb{C}$ such that
$\mathbb{C}$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, then
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, then  $H^{i}(X,{\mathcal{J}}(X,\unicode[STIX]{x1D6E5}))=0$ for
$H^{i}(X,{\mathcal{J}}(X,\unicode[STIX]{x1D6E5}))=0$ for  $i>0$, where
$i>0$, where  ${\mathcal{J}}(X,\unicode[STIX]{x1D6E5})$ denotes the multiplier ideal sheaf of
${\mathcal{J}}(X,\unicode[STIX]{x1D6E5})$ denotes the multiplier ideal sheaf of  $(X,\unicode[STIX]{x1D6E5})$.
$(X,\unicode[STIX]{x1D6E5})$.
Indeed,  $(1)_{0}$,
$(1)_{0}$,  $(2)_{0}$ and
$(2)_{0}$ and  $(3)_{0}$ follow from the Kodaira, Kawamata–Viehweg and Nadel vanishing theorems, respectively (cf. [Reference Kawamata, Matsuda and MatsukiKMM87, Theorem 1-2-5], [Reference Kollár and MoriKM98, Corollary 2.68] and [Reference LazarsfeldLaz04, Corollary 9.4.15]).
$(3)_{0}$ follow from the Kodaira, Kawamata–Viehweg and Nadel vanishing theorems, respectively (cf. [Reference Kawamata, Matsuda and MatsukiKMM87, Theorem 1-2-5], [Reference Kollár and MoriKM98, Corollary 2.68] and [Reference LazarsfeldLaz04, Corollary 9.4.15]).
Although the Kodaira vanishing is known to fail in positive characteristic (cf. [Reference RaynaudRay78]), similar vanishing still holds in positive characteristic in terms of Witt vectors. The first result in this direction was given by Esnault in [Reference EsnaultEsn03].
 $(1)_{p}$
$(1)_{p}$If
 $X$ is a smooth projective variety over a perfect field of characteristic
$X$ is a smooth projective variety over a perfect field of characteristic  $p>0$ such that
$p>0$ such that  $-K_{X}$ is ample, then
$-K_{X}$ is ample, then  $H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for
$H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Then it is natural to seek a positive-characteristic analogue of  $(2)_{0}$. Indeed, this is partially established by Gongyo and the authors [Reference Gongyo, Nakamura and TanakaGNT19].
$(2)_{0}$. Indeed, this is partially established by Gongyo and the authors [Reference Gongyo, Nakamura and TanakaGNT19].
 $(2)_{p}$
$(2)_{p}$If
 $(X,\unicode[STIX]{x1D6E5})$ is a projective klt pair over a perfect field of characteristic
$(X,\unicode[STIX]{x1D6E5})$ is a projective klt pair over a perfect field of characteristic  $p>5$ such that
$p>5$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample and
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample and  $\dim X\leqslant 3$, then
$\dim X\leqslant 3$, then  $H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for
$H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
The main theorem of this paper is a positive-characteristic analogue of  $(3)_{0}$ for the three-dimensional case of characteristic
$(3)_{0}$ for the three-dimensional case of characteristic  $p>5$. Furthermore, we treat a relative setting as follows.
$p>5$. Furthermore, we treat a relative setting as follows.
Theorem 1.1 ( $=$ Theorem 4.10).
$=$ Theorem 4.10).
Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a projective
$f:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$. Assume that
$Z$. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Then the equation
$f$-big. Then the equation
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ holds for  $i>0$, where
$i>0$, where  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ denotes the reduced closed subscheme of
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ denotes the reduced closed subscheme of  $X$ consisting of the non-klt points of
$X$ consisting of the non-klt points of  $(X,\unicode[STIX]{x1D6E5})$ and
$(X,\unicode[STIX]{x1D6E5})$ and  $I_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})}$ is the coherent ideal sheaf on
$I_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})}$ is the coherent ideal sheaf on  $X$ corresponding to
$X$ corresponding to  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ (cf. Remark 2.2).
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ (cf. Remark 2.2).
As a consequence of Theorem 1.1, we obtain the Kollár–Shokurov connectedness theorem.
Theorem 1.2 ( $=$ Theorem 4.12).
$=$ Theorem 4.12).
Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a projective
$f:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective scheme
$k$-morphism to a quasi-projective scheme  $Z$ over
$Z$ over  $k$ such that
$k$ such that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$. Assume that
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. If
$f$-big. If  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ denotes the reduced closed subscheme of
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ denotes the reduced closed subscheme of  $X$ consisting of the non-klt points of
$X$ consisting of the non-klt points of  $(X,\unicode[STIX]{x1D6E5})$ and we let
$(X,\unicode[STIX]{x1D6E5})$ and we let  $g:\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ be the induced morphism, then the fibre
$g:\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ be the induced morphism, then the fibre  $g^{-1}(z)$ over an arbitrary point
$g^{-1}(z)$ over an arbitrary point  $z$ of
$z$ of  $f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ is geometrically connected over the residue field
$f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ is geometrically connected over the residue field  $k(z)$ at
$k(z)$ at  $z$.
$z$.
We note that Birkar proved a weaker version of this theorem in the case when  $f$ is birational and the coefficients of
$f$ is birational and the coefficients of  $\unicode[STIX]{x1D6E5}$ are at most one [Reference BirkarBir16, Theorem 1.8].
$\unicode[STIX]{x1D6E5}$ are at most one [Reference BirkarBir16, Theorem 1.8].
Also, we have applications of Theorem 1.1 to rational points on varieties over finite fields. The starting point is the following theorem by Esnault [Reference EsnaultEsn03], which is a consequence of  $(1)_{p}$ and a Lefschetz trace formula for
$(1)_{p}$ and a Lefschetz trace formula for  $W{\mathcal{O}}_{X,\mathbb{Q}}$.
$W{\mathcal{O}}_{X,\mathbb{Q}}$.
 $(1)_{p}^{\prime }$
$(1)_{p}^{\prime }$If
 $X$ is a geometrically connected smooth projective variety over a finite field
$X$ is a geometrically connected smooth projective variety over a finite field  $k$ such that
$k$ such that  $-K_{X}$ is ample, then
$-K_{X}$ is ample, then  $\#X(k)\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\#k)$.
$\#X(k)\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\#k)$.
In [Reference Gongyo, Nakamura and TanakaGNT19], Gongyo and the authors prove that the same formula still holds for Fano threefolds with klt singularities.
 $(2)_{p}^{\prime }$
$(2)_{p}^{\prime }$If
 $(X,\unicode[STIX]{x1D6E5})$ is a three-dimensional geometrically connected projective klt pair over a finite field
$(X,\unicode[STIX]{x1D6E5})$ is a three-dimensional geometrically connected projective klt pair over a finite field  $k$ of characteristic
$k$ of characteristic  $p>5$ such that
$p>5$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, then
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, then  $\#X(k)\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\#k)$.
$\#X(k)\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\#k)$.
Then it is natural to seek an application of Theorem 1.1 to the number of the rational points on a non-klt Fano threefold. In this direction, we show that the number of the rational points on the klt-locus is divisible by  $\#k$.
$\#k$.
Theorem 1.3 ( $=$ Corollary 5.2).
$=$ Corollary 5.2).
Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional geometrically connected projective log pair over a finite field
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional geometrically connected projective log pair over a finite field  $k$ of characteristic
$k$ of characteristic  $p>5$. Assume that
$p>5$. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big and that
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big and that  $(X,\unicode[STIX]{x1D6E5})$ is not klt. Then the congruence
$(X,\unicode[STIX]{x1D6E5})$ is not klt. Then the congruence
 $$\begin{eqnarray}\displaystyle \#X(k)\equiv \#V(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#X(k)\equiv \#V(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$ holds, where  $V$ denotes the closed subset of
$V$ denotes the closed subset of  $X$ consisting of the non-klt points of
$X$ consisting of the non-klt points of  $(X,\unicode[STIX]{x1D6E5})$.
$(X,\unicode[STIX]{x1D6E5})$.
An interesting point is that this theorem is not true if we drop the assumption that  $(X,\unicode[STIX]{x1D6E5})$ is not klt (cf.
$(X,\unicode[STIX]{x1D6E5})$ is not klt (cf.  $(2)_{p}^{\prime }$). On the other hand, the following theorem gives a common generalisation of
$(2)_{p}^{\prime }$). On the other hand, the following theorem gives a common generalisation of  $(2)_{p}^{\prime }$ and Theorem 1.3. Moreover, we treat a relative setting.
$(2)_{p}^{\prime }$ and Theorem 1.3. Moreover, we treat a relative setting.
Theorem 1.4 ( $=$ Theorem 5.1).
$=$ Theorem 5.1).
Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over a finite field
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over a finite field  $k$ of characteristic
$k$ of characteristic  $p>5$. Let
$p>5$. Let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Y$ such that
$Y$ such that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. Assume that
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Then the congruence
$f$-big. Then the congruence
 $$\begin{eqnarray}\displaystyle \#X(k)-\#V(k)\equiv \#Y(k)-\#f(V)(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#X(k)-\#V(k)\equiv \#Y(k)-\#f(V)(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$ holds, where  $V$ denotes the closed subset of
$V$ denotes the closed subset of  $X$ consisting of the non-klt points of
$X$ consisting of the non-klt points of  $(X,\unicode[STIX]{x1D6E5})$.
$(X,\unicode[STIX]{x1D6E5})$.
Furthermore, we shall show that some hypersurfaces  $D$ on smooth Fano threefolds contain rational points even if
$D$ on smooth Fano threefolds contain rational points even if  $D$ is not klt. It can be seen as a variation of the Ax–Katz theorem (cf. [Reference AxAx64, Reference KatzKat71]).
$D$ is not klt. It can be seen as a variation of the Ax–Katz theorem (cf. [Reference AxAx64, Reference KatzKat71]).
Theorem 1.5 (cf. Theorem 5.3).
Let  $X$ be a three-dimensional projective geometrically connected variety with klt singularities over a finite field
$X$ be a three-dimensional projective geometrically connected variety with klt singularities over a finite field  $k$ of characteristic
$k$ of characteristic  $p>5$. Let
$p>5$. Let  $D$ be a non-zero effective
$D$ be a non-zero effective  $\mathbb{Q}$-Cartier Weil divisor on
$\mathbb{Q}$-Cartier Weil divisor on  $X$. Assume that:
$X$. Assume that:
(i)
 $-K_{X}$ is ample; and
$-K_{X}$ is ample; and(ii)
 $-(K_{X}+D)$ is ample.
$-(K_{X}+D)$ is ample.
Then the congruence
 $$\begin{eqnarray}\displaystyle \#D(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#D(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$ holds. In particular, there exists a  $k$-rational point on
$k$-rational point on  $D$.
$D$.
In Theorem 5.3, we work in a more general setting.
1.1 Description of the proof
We now overview some of the ideas of the proof of Theorem 1.1. In the following, we work over a perfect field  $k$ of characteristic
$k$ of characteristic  $p>5$. Roughly speaking, the argument consists of two steps.
$p>5$. Roughly speaking, the argument consists of two steps.
(A) Now, let us give an overview of how to prove Theorem 3.11. Given a three-dimensional klt pair  $(X,\unicode[STIX]{x1D6E5})$ and a projective morphism
$(X,\unicode[STIX]{x1D6E5})$ and a projective morphism  $f:X\rightarrow Z$ such that
$f:X\rightarrow Z$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-ample and
$f$-ample and  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$, we want to prove that
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$, we want to prove that  $R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for any
$R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for any  $i>0$. We further divide the proof of Theorem 3.11 into four cases depending on the dimension of
$i>0$. We further divide the proof of Theorem 3.11 into four cases depending on the dimension of  $Z$. Since the cases
$Z$. Since the cases  $\dim Z=0$ and
$\dim Z=0$ and  $\dim Z=3$ have been settled already in [Reference Gongyo, Nakamura and TanakaGNT19], it is enough to assume that either:
$\dim Z=3$ have been settled already in [Reference Gongyo, Nakamura and TanakaGNT19], it is enough to assume that either:
(A1) We first treat the case when  $\dim Z=1$. In this case, the generic fibre
$\dim Z=1$. In this case, the generic fibre  $X_{K(Z)}$ of
$X_{K(Z)}$ of  $f$ is a log del Pezzo surface over an imperfect field. One of the significant steps is to show that
$f$ is a log del Pezzo surface over an imperfect field. One of the significant steps is to show that  $(X_{K(Z)}\times _{K(Z)}\overline{K(Z)})_{\operatorname{red}}$ is a rational surface (Proposition 2.26). Indeed, this result enables us to use a result by Chatzistamatiou–Rülling (Theorem 3.2) after taking suitable purely inseparable covers of
$(X_{K(Z)}\times _{K(Z)}\overline{K(Z)})_{\operatorname{red}}$ is a rational surface (Proposition 2.26). Indeed, this result enables us to use a result by Chatzistamatiou–Rülling (Theorem 3.2) after taking suitable purely inseparable covers of  $X$ and
$X$ and  $Z$ (cf. Proposition 3.6), which in turn implies what we want.
$Z$ (cf. Proposition 3.6), which in turn implies what we want.
(A2) We now treat the case when  $\dim Z=2$. The crucial part of this case is to prove that
$\dim Z=2$. The crucial part of this case is to prove that  $Z$ has
$Z$ has  $W{\mathcal{O}}$-rational singularities (Theorem 3.8). To this end, we first reduce the problem to the case when
$W{\mathcal{O}}$-rational singularities (Theorem 3.8). To this end, we first reduce the problem to the case when  $k=\overline{\mathbb{F}}_{p}$. Assume that
$k=\overline{\mathbb{F}}_{p}$. Assume that  $k=\overline{\mathbb{F}}_{p}$. In order to prove that
$k=\overline{\mathbb{F}}_{p}$. In order to prove that  $Z$ has
$Z$ has  $W{\mathcal{O}}$-rational singularities, we compute, for sufficiently divisible
$W{\mathcal{O}}$-rational singularities, we compute, for sufficiently divisible  $e\in \mathbb{Z}_{{>}0}$, the numbers of
$e\in \mathbb{Z}_{{>}0}$, the numbers of  $\mathbb{F}_{p^{e}}$-rational points on the models
$\mathbb{F}_{p^{e}}$-rational points on the models  $X^{\prime }$ and
$X^{\prime }$ and  $Z^{\prime }$ over
$Z^{\prime }$ over  $\mathbb{F}_{p^{e}}$ of
$\mathbb{F}_{p^{e}}$ of  $X$ and
$X$ and  $Z$, respectively (cf. Step 1 in the proof of Theorem 3.8).
$Z$, respectively (cf. Step 1 in the proof of Theorem 3.8).
(B) We now overview how to prove Theorem 1.1. For simplicity, we treat only the case when  $Z=\operatorname{Spec}\,k$ and
$Z=\operatorname{Spec}\,k$ and  $k$ is an algebraically closed field. Taking a dlt modification of
$k$ is an algebraically closed field. Taking a dlt modification of  $(X,\unicode[STIX]{x1D6E5})$ (Proposition 2.10), we may assume that
$(X,\unicode[STIX]{x1D6E5})$ (Proposition 2.10), we may assume that  $X$ is
$X$ is  $\mathbb{Q}$-factorial,
$\mathbb{Q}$-factorial,  $(X,\unicode[STIX]{x1D6E5}^{\wedge 1})$ is dlt (for the definition of
$(X,\unicode[STIX]{x1D6E5}^{\wedge 1})$ is dlt (for the definition of  $(-)^{\wedge 1}$, see § 2.1) and
$(-)^{\wedge 1}$, see § 2.1) and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample (cf. Lemma 4.8). By the ampleness of
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample (cf. Lemma 4.8). By the ampleness of  $-(K_{X}+\unicode[STIX]{x1D6E5})$, we can find an effective
$-(K_{X}+\unicode[STIX]{x1D6E5})$, we can find an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6FA}$ on
$\unicode[STIX]{x1D6FA}$ on  $X$ such that:
$X$ such that:
(i)
 $(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt;
$(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt;(ii)
 $K_{X}+\unicode[STIX]{x1D6FA}{\sim}_{\mathbb{R}}0$;
$K_{X}+\unicode[STIX]{x1D6FA}{\sim}_{\mathbb{R}}0$;(iii)
 $\unicode[STIX]{x1D6FA}$ is big;
$\unicode[STIX]{x1D6FA}$ is big;(iv)
 $\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{>}1}$; and
$\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{>}1}$; and(v)
 $\operatorname{Supp}\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=\operatorname{Supp}\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$.
$\operatorname{Supp}\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=\operatorname{Supp}\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$.
Then it suffices to prove the vanishing of  $H^{i}(X,WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})})=0$ for
$H^{i}(X,WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})})=0$ for  $i>0$. Furthermore, we may assume that
$i>0$. Furthermore, we may assume that  $\operatorname{Supp}\,\unicode[STIX]{x1D6FA}^{{>}1}\neq \emptyset$, since the assertion is nothing but [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 1.3] when
$\operatorname{Supp}\,\unicode[STIX]{x1D6FA}^{{>}1}\neq \emptyset$, since the assertion is nothing but [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 1.3] when  $(X,\unicode[STIX]{x1D6E5})$ is klt.
$(X,\unicode[STIX]{x1D6E5})$ is klt.
The first step is to run a  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-MMP in order to reduce the problem to the end result (cf. Proposition 4.1). In Proposition 4.1, it is proved that the cohomologies are preserved under this MMP.
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-MMP in order to reduce the problem to the end result (cf. Proposition 4.1). In Proposition 4.1, it is proved that the cohomologies are preserved under this MMP.
Replacing  $X$ by the end result, let us assume that
$X$ by the end result, let us assume that  $X$ itself is the end result of this MMP. By (ii) and
$X$ itself is the end result of this MMP. By (ii) and  $\operatorname{Supp}\,\unicode[STIX]{x1D6FA}^{{>}1}\neq \emptyset$,
$\operatorname{Supp}\,\unicode[STIX]{x1D6FA}^{{>}1}\neq \emptyset$,  $X$ has a
$X$ has a  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-Mori fibre space structure
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-Mori fibre space structure  $g:X\rightarrow W$. Then the problem is reduced to vanishing of cohomologies for dlt Mori fibre spaces (Lemma 4.7). By induction on the number of the irreducible components of
$g:X\rightarrow W$. Then the problem is reduced to vanishing of cohomologies for dlt Mori fibre spaces (Lemma 4.7). By induction on the number of the irreducible components of  $\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ for
$\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ for  $\unicode[STIX]{x1D6EF}:=\unicode[STIX]{x1D6FA}^{\wedge 1}$, Lemma 4.7 is proved by using the
$\unicode[STIX]{x1D6EF}:=\unicode[STIX]{x1D6FA}^{\wedge 1}$, Lemma 4.7 is proved by using the  $W{\mathcal{O}}$-vanishing for klt Mori fibre spaces (Theorem 3.11).
$W{\mathcal{O}}$-vanishing for klt Mori fibre spaces (Theorem 3.11).
2 Preliminaries
2.1 Notation
In this subsection, we summarise the notation used in this paper.
∙ We will freely use the notation and terminology in [Reference HartshorneHar77] and [Reference KollárKol13].
∙ For a scheme
 $X$, its reduced structure
$X$, its reduced structure  $X_{\operatorname{red}}$ is the reduced closed subscheme of
$X_{\operatorname{red}}$ is the reduced closed subscheme of  $X$ such that the induced closed immersion
$X$ such that the induced closed immersion  $X_{\operatorname{red}}\rightarrow X$ is surjective.
$X_{\operatorname{red}}\rightarrow X$ is surjective.∙ A morphism
 $f:X\rightarrow Y$ of schemes has connected fibres if
$f:X\rightarrow Y$ of schemes has connected fibres if  $X\times _{Y}\operatorname{Spec}\,L$ is either empty or connected for any field
$X\times _{Y}\operatorname{Spec}\,L$ is either empty or connected for any field  $L$ and any morphism
$L$ and any morphism  $\operatorname{Spec}\,L\rightarrow Y$.
$\operatorname{Spec}\,L\rightarrow Y$.∙ For an integral scheme
 $X$, we define the function field
$X$, we define the function field  $K(X)$ of
$K(X)$ of  $X$ as
$X$ as  ${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$ for the generic point
${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$ for the generic point  $\unicode[STIX]{x1D709}$ of
$\unicode[STIX]{x1D709}$ of  $X$.
$X$.∙ For a field
 $k$, we say that
$k$, we say that  $X$ is a variety over
$X$ is a variety over  $k$ or a
$k$ or a  $k$-variety if
$k$-variety if  $X$ is an integral scheme that is separated and of finite type over
$X$ is an integral scheme that is separated and of finite type over  $k$. We say that
$k$. We say that  $X$ is a curve over
$X$ is a curve over  $k$ or a
$k$ or a  $k$-curve (respectively a surface over
$k$-curve (respectively a surface over  $k$ or a
$k$ or a  $k$-surface, respectively a threefold over
$k$-surface, respectively a threefold over  $k$) if
$k$) if  $X$ is a
$X$ is a  $k$-variety of dimension one (respectively two, respectively three).
$k$-variety of dimension one (respectively two, respectively three).∙ For a field
 $k$, let
$k$, let  $\overline{k}$ be an algebraic closure of
$\overline{k}$ be an algebraic closure of  $k$. If
$k$. If  $k$ is of characteristic
$k$ is of characteristic  $p>0$, then we set
$p>0$, then we set  $k^{1/p^{\infty }}:=\bigcup _{e=0}^{\infty }k^{1/p^{e}}=\bigcup _{e=0}^{\infty }\{x\in \overline{k}\,|\,x^{p^{e}}\in k\}$.
$k^{1/p^{\infty }}:=\bigcup _{e=0}^{\infty }k^{1/p^{e}}=\bigcup _{e=0}^{\infty }\{x\in \overline{k}\,|\,x^{p^{e}}\in k\}$.∙ Let
 $f:X\rightarrow Y$ be a projective morphism of noetherian schemes. Let
$f:X\rightarrow Y$ be a projective morphism of noetherian schemes. Let  $M$ be an
$M$ be an  $\mathbb{R}$-Cartier
$\mathbb{R}$-Cartier  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $M$ on
$M$ on  $X$. We say that
$X$. We say that  $M$ is
$M$ is  $f$-ample if we can write
$f$-ample if we can write  $M=\sum _{i=1}^{r}a_{i}M_{i}$ for some
$M=\sum _{i=1}^{r}a_{i}M_{i}$ for some  $r\geqslant 1$, positive real numbers
$r\geqslant 1$, positive real numbers  $a_{i}$ and
$a_{i}$ and  $f$-ample Cartier divisors
$f$-ample Cartier divisors  $M_{i}$. We say that
$M_{i}$. We say that  $M$ is
$M$ is  $f$-big if we can write
$f$-big if we can write  $M=A+E$ for some
$M=A+E$ for some  $f$-ample
$f$-ample  $\mathbb{R}$-Cartier
$\mathbb{R}$-Cartier  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $A$ and effective
$A$ and effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $E$. We can define
$E$. We can define  $f$-nef
$f$-nef  $\mathbb{R}$-divisors in the same way as in [Reference KollárKol13, Definition 1.4]. We say that
$\mathbb{R}$-divisors in the same way as in [Reference KollárKol13, Definition 1.4]. We say that  $M$ is
$M$ is  $f$-numerically-trivial, denoted by
$f$-numerically-trivial, denoted by  $M\equiv _{f}0$, if both
$M\equiv _{f}0$, if both  $M$ and
$M$ and  $-M$ are
$-M$ are  $f$-nef.
$f$-nef.∙ Let
 $\unicode[STIX]{x1D6E5}=\sum r_{i}D_{i}$ be an
$\unicode[STIX]{x1D6E5}=\sum r_{i}D_{i}$ be an  $\mathbb{R}$-divisor, where
$\mathbb{R}$-divisor, where  $D_{i}$ are distinct prime divisors. We define
$D_{i}$ are distinct prime divisors. We define  $\unicode[STIX]{x1D6E5}^{{\geqslant}1}:=\sum _{r_{i}\geqslant 1}r_{i}D_{i}$ and
$\unicode[STIX]{x1D6E5}^{{\geqslant}1}:=\sum _{r_{i}\geqslant 1}r_{i}D_{i}$ and  $\unicode[STIX]{x1D6E5}^{\wedge 1}:=\sum r_{i}^{\prime }D_{i}$, where
$\unicode[STIX]{x1D6E5}^{\wedge 1}:=\sum r_{i}^{\prime }D_{i}$, where  $r_{i}^{\prime }:=\min \{r_{i},1\}$. We also define
$r_{i}^{\prime }:=\min \{r_{i},1\}$. We also define  $\unicode[STIX]{x1D6E5}^{{>}1}$ and
$\unicode[STIX]{x1D6E5}^{{>}1}$ and  $\unicode[STIX]{x1D6E5}^{{<}1}$ similarly. Moreover, we denote
$\unicode[STIX]{x1D6E5}^{{<}1}$ similarly. Moreover, we denote  $\{\unicode[STIX]{x1D6E5}\}=\unicode[STIX]{x1D6E5}-\lfloor \unicode[STIX]{x1D6E5}\rfloor$.
$\{\unicode[STIX]{x1D6E5}\}=\unicode[STIX]{x1D6E5}-\lfloor \unicode[STIX]{x1D6E5}\rfloor$.∙ A sub-log pair
 $(X,\unicode[STIX]{x1D6E5})$ over a field
$(X,\unicode[STIX]{x1D6E5})$ over a field  $k$ consists of a normal variety
$k$ consists of a normal variety  $X$ over
$X$ over  $k$ and an
$k$ and an  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}$ such that
$\unicode[STIX]{x1D6E5}$ such that  $K_{X}+\unicode[STIX]{x1D6E5}$ is
$K_{X}+\unicode[STIX]{x1D6E5}$ is  $\mathbb{R}$-Cartier. A log pair
$\mathbb{R}$-Cartier. A log pair  $(X,\unicode[STIX]{x1D6E5})$ is a sub-log pair such that
$(X,\unicode[STIX]{x1D6E5})$ is a sub-log pair such that  $\unicode[STIX]{x1D6E5}\geqslant 0$.
$\unicode[STIX]{x1D6E5}\geqslant 0$.∙ For a closed subscheme
 $V$ of a scheme
$V$ of a scheme  $X$, we denote by
$X$, we denote by  $I_{V}$ the quasi-coherent ideal sheaf corresponding to
$I_{V}$ the quasi-coherent ideal sheaf corresponding to  $V$. For an effective
$V$. For an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $D$ on a normal variety
$D$ on a normal variety  $X$ over a field, we denote
$X$ over a field, we denote  $I_{D}:=I_{{\mathcal{D}}}$, where
$I_{D}:=I_{{\mathcal{D}}}$, where  ${\mathcal{D}}$ denotes the closed subscheme of
${\mathcal{D}}$ denotes the closed subscheme of  $X$ corresponding to the coherent ideal sheaf
$X$ corresponding to the coherent ideal sheaf  ${\mathcal{O}}_{X}(-\ulcorner D\urcorner )$ on
${\mathcal{O}}_{X}(-\ulcorner D\urcorner )$ on  $X$.
$X$.∙ For terminology on derived category, we refer to [Reference WeibelWei94]. Especially, for morphisms
 $X\xrightarrow[{}]{f}Y\xrightarrow[{}]{g}Z$ of
$X\xrightarrow[{}]{f}Y\xrightarrow[{}]{g}Z$ of  $\mathbb{Z}/p\mathbb{Z}$-schemes and a
$\mathbb{Z}/p\mathbb{Z}$-schemes and a  $W{\mathcal{O}}_{X}$-module
$W{\mathcal{O}}_{X}$-module  $M$, we shall frequently use the isomorphism
$M$, we shall frequently use the isomorphism  $Rg_{\ast }\circ Rf_{\ast }(M)\simeq R(g\circ f)_{\ast }(M)$ (cf. [Reference WeibelWei94, Corollary 10.8.10]).
$Rg_{\ast }\circ Rf_{\ast }(M)\simeq R(g\circ f)_{\ast }(M)$ (cf. [Reference WeibelWei94, Corollary 10.8.10]).
2.2 Results on minimal model program
Definition 2.1. Let  $k$ be a field.
$k$ be a field.
(i) We say that
 $(X,\unicode[STIX]{x1D6E5})$ is a sub-klt pair over
$(X,\unicode[STIX]{x1D6E5})$ is a sub-klt pair over  $k$ if
$k$ if  $(X,\unicode[STIX]{x1D6E5})$ is a sub-log pair over
$(X,\unicode[STIX]{x1D6E5})$ is a sub-log pair over  $k$ such that
$k$ such that  $(X,\unicode[STIX]{x1D6E5})$ is klt in the sense of [Reference KollárKol13, Definition 2.8]. Given a point
$(X,\unicode[STIX]{x1D6E5})$ is klt in the sense of [Reference KollárKol13, Definition 2.8]. Given a point  $x$ of
$x$ of  $X$, we say that
$X$, we say that  $(X,\unicode[STIX]{x1D6E5})$ is sub-klt around
$(X,\unicode[STIX]{x1D6E5})$ is sub-klt around  $x$ if there exists an open neighbourhood
$x$ if there exists an open neighbourhood  $X^{\prime }$ of
$X^{\prime }$ of  $x\in X$ such that
$x\in X$ such that  $(X^{\prime },\unicode[STIX]{x1D6E5}|_{X^{\prime }})$ is sub-klt.
$(X^{\prime },\unicode[STIX]{x1D6E5}|_{X^{\prime }})$ is sub-klt.(ii) We say that
 $(X,\unicode[STIX]{x1D6E5})$ is klt (respectively log canonical) if
$(X,\unicode[STIX]{x1D6E5})$ is klt (respectively log canonical) if  $(X,\unicode[STIX]{x1D6E5})$ is a log pair such that
$(X,\unicode[STIX]{x1D6E5})$ is a log pair such that  $(X,\unicode[STIX]{x1D6E5})$ is klt (respectively log canonical) in the sense of [Reference KollárKol13, Definition 2.8].
$(X,\unicode[STIX]{x1D6E5})$ is klt (respectively log canonical) in the sense of [Reference KollárKol13, Definition 2.8].(iii) Given a point
 $x$ of
$x$ of  $X$, we say that
$X$, we say that  $x$ is a non-klt point of
$x$ is a non-klt point of  $(X,\unicode[STIX]{x1D6E5})$ if
$(X,\unicode[STIX]{x1D6E5})$ if  $(X,\unicode[STIX]{x1D6E5})$ is not sub-klt around
$(X,\unicode[STIX]{x1D6E5})$ is not sub-klt around  $x$. We define
$x$. We define  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$, called the non-klt locus of
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$, called the non-klt locus of  $(X,\unicode[STIX]{x1D6E5})$, as the subset of
$(X,\unicode[STIX]{x1D6E5})$, as the subset of  $X$ that consists of all the non-klt points. Note that
$X$ that consists of all the non-klt points. Note that  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ is a closed subset of
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ is a closed subset of  $X$, as its complement is an open subset of
$X$, as its complement is an open subset of  $X$ by definition. We equip
$X$ by definition. We equip  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ with the reduced scheme structure.
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ with the reduced scheme structure.
Remark 2.2. For coherent ideal sheaves  $I,J\subset {\mathcal{O}}_{X}$ with
$I,J\subset {\mathcal{O}}_{X}$ with  $\sqrt{I}=\sqrt{J}$, it follows that
$\sqrt{I}=\sqrt{J}$, it follows that  $WI_{\mathbb{Q}}=WJ_{\mathbb{Q}}$ (cf. [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 2.1]). Hence, we need not care about the scheme structure of
$WI_{\mathbb{Q}}=WJ_{\mathbb{Q}}$ (cf. [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 2.1]). Hence, we need not care about the scheme structure of  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ when we consider
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ when we consider  $WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}$. By the same reason, if
$WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}$. By the same reason, if  $X$ is a non-reduced noetherian scheme and
$X$ is a non-reduced noetherian scheme and  $j:X_{\operatorname{red}}\rightarrow X$ denotes the closed immersion from its reduced structure
$j:X_{\operatorname{red}}\rightarrow X$ denotes the closed immersion from its reduced structure  $X_{\operatorname{red}}$, then the induced homomorphism
$X_{\operatorname{red}}$, then the induced homomorphism  $W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow j_{\ast }W{\mathcal{O}}_{X_{\operatorname{red}},\mathbb{Q}}$ is an isomorphism. See Lemma 2.17 for a generalisation.
$W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow j_{\ast }W{\mathcal{O}}_{X_{\operatorname{red}},\mathbb{Q}}$ is an isomorphism. See Lemma 2.17 for a generalisation.
Definition 2.3. A log pair  $(X,\unicode[STIX]{x1D6E5})$ is called dlt if the coefficients of
$(X,\unicode[STIX]{x1D6E5})$ is called dlt if the coefficients of  $\unicode[STIX]{x1D6E5}$ are at most one and there exists a log resolution
$\unicode[STIX]{x1D6E5}$ are at most one and there exists a log resolution  $g:Y\rightarrow X$ of
$g:Y\rightarrow X$ of  $(X,\unicode[STIX]{x1D6E5})$ with the condition that
$(X,\unicode[STIX]{x1D6E5})$ with the condition that  $a_{E}(X,\unicode[STIX]{x1D6E5})>0$ holds for any
$a_{E}(X,\unicode[STIX]{x1D6E5})>0$ holds for any  $g$-exceptional prime divisor
$g$-exceptional prime divisor  $E$ on
$E$ on  $Y$.
$Y$.
Definition 2.4. Given a field  $k$ and a projective
$k$ and a projective  $k$-morphism
$k$-morphism  $f:X\rightarrow Z$ from a normal
$f:X\rightarrow Z$ from a normal  $k$-variety
$k$-variety  $X$ to a quasi-projective
$X$ to a quasi-projective  $k$-scheme
$k$-scheme  $Z$, we say that
$Z$, we say that  $X$ is of Fano type over
$X$ is of Fano type over  $Z$ if there exists an effective
$Z$ if there exists an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}$ on
$\unicode[STIX]{x1D6E5}$ on  $X$ such that
$X$ such that  $(X,\unicode[STIX]{x1D6E5})$ is klt and
$(X,\unicode[STIX]{x1D6E5})$ is klt and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big.
$f$-big.
Definition 2.5. Given a field  $k$, a log pair
$k$, a log pair  $(X,\unicode[STIX]{x1D6E5})$ over
$(X,\unicode[STIX]{x1D6E5})$ over  $k$ and projective
$k$ and projective  $k$-morphisms
$k$-morphisms  $X\xrightarrow[{}]{f_{1}}Z_{1}\rightarrow Z_{2}$ of quasi-projective
$X\xrightarrow[{}]{f_{1}}Z_{1}\rightarrow Z_{2}$ of quasi-projective  $k$-schemes, we say that
$k$-schemes, we say that  $f_{1}:X\rightarrow Z_{1}$ is a
$f_{1}:X\rightarrow Z_{1}$ is a  $(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space over
$(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space over  $Z_{2}$ if
$Z_{2}$ if  $\dim X>\dim Z_{1}$,
$\dim X>\dim Z_{1}$,  $(f_{1})_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z_{1}}$,
$(f_{1})_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z_{1}}$,  $\unicode[STIX]{x1D70C}(X/Z_{1})=1$ and
$\unicode[STIX]{x1D70C}(X/Z_{1})=1$ and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f_{1}$-ample. If
$f_{1}$-ample. If  $Z_{2}=\operatorname{Spec}\,k$, then
$Z_{2}=\operatorname{Spec}\,k$, then  $f_{1}:X\rightarrow Z_{1}$ is simply called a
$f_{1}:X\rightarrow Z_{1}$ is simply called a  $(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space.
$(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space.
Lemma 2.6. Let  $k$ be a field and let
$k$ be a field and let  $f:X\rightarrow Y$ be a projective birational
$f:X\rightarrow Y$ be a projective birational  $k$-morphism of normal varieties over
$k$-morphism of normal varieties over  $k$. Let
$k$. Let  $(Y,\unicode[STIX]{x1D6E5}_{Y})$ be a sub-log pair and let
$(Y,\unicode[STIX]{x1D6E5}_{Y})$ be a sub-log pair and let  $\unicode[STIX]{x1D6E5}$ be the
$\unicode[STIX]{x1D6E5}$ be the  $\mathbb{R}$-divisor defined by
$\mathbb{R}$-divisor defined by  $K_{X}+\unicode[STIX]{x1D6E5}=f^{\ast }(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})$. Then the following hold.
$K_{X}+\unicode[STIX]{x1D6E5}=f^{\ast }(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})$. Then the following hold.
(i) Let
 $x$ be a closed point of
$x$ be a closed point of  $X$. If
$X$. If  $x$ is a non-klt point of
$x$ is a non-klt point of  $(X,\unicode[STIX]{x1D6E5})$, then
$(X,\unicode[STIX]{x1D6E5})$, then  $f(x)$ is a non-klt point of
$f(x)$ is a non-klt point of  $(Y,\unicode[STIX]{x1D6E5}_{Y})$.
$(Y,\unicode[STIX]{x1D6E5}_{Y})$.(ii) Let
 $y$ be a closed point of
$y$ be a closed point of  $Y$. If
$Y$. If  $y$ is a non-klt point of
$y$ is a non-klt point of  $(Y,\unicode[STIX]{x1D6E5}_{Y})$, then there exists a closed point
$(Y,\unicode[STIX]{x1D6E5}_{Y})$, then there exists a closed point  $x$ of
$x$ of  $X$ such that
$X$ such that  $f(x)=y$ and
$f(x)=y$ and  $x$ is a non-klt point of
$x$ is a non-klt point of  $(X,\unicode[STIX]{x1D6E5})$.
$(X,\unicode[STIX]{x1D6E5})$.
In particular, there exists a commutative diagram consisting of projective morphisms:

where the horizontal arrows are the induced closed immersions and  $f^{\prime }$ is a projective surjective morphism. In particular,
$f^{\prime }$ is a projective surjective morphism. In particular,  $f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})$.
$f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})$.
Proof. Both of the assertions follow from the fact that  $(U,\unicode[STIX]{x1D6E5}|_{U})$ is sub-klt if and only if
$(U,\unicode[STIX]{x1D6E5}|_{U})$ is sub-klt if and only if  $(f^{-1}(U),\unicode[STIX]{x1D6E5}_{Y}|_{f^{-1}(U)})$ is sub-klt for any open subset
$(f^{-1}(U),\unicode[STIX]{x1D6E5}_{Y}|_{f^{-1}(U)})$ is sub-klt for any open subset  $U\subset X$ (cf. [Reference Kollár and MoriKM98, Lemma 2.30]).◻
$U\subset X$ (cf. [Reference Kollár and MoriKM98, Lemma 2.30]).◻
Proposition 2.7. Let  $(X,\unicode[STIX]{x1D6E5})$ be a
$(X,\unicode[STIX]{x1D6E5})$ be a  $\mathbb{Q}$-factorial sub-log pair over a field such that
$\mathbb{Q}$-factorial sub-log pair over a field such that  $(X,(\unicode[STIX]{x1D6E5}^{{>}0})^{{<}1})$ is klt. Then it holds that
$(X,(\unicode[STIX]{x1D6E5}^{{>}0})^{{<}1})$ is klt. Then it holds that
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})=\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}^{{>}0})=\operatorname{Supp}\unicode[STIX]{x1D6E5}^{{\geqslant}1}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})=\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}^{{>}0})=\operatorname{Supp}\unicode[STIX]{x1D6E5}^{{\geqslant}1}. & & \displaystyle \nonumber\end{eqnarray}$$Proof. The second equality follows from the fact that  $(X,(\unicode[STIX]{x1D6E5}^{{>}0})^{{<}1})$ is klt. Clearly, the inclusion
$(X,(\unicode[STIX]{x1D6E5}^{{>}0})^{{<}1})$ is klt. Clearly, the inclusion  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\subset \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}^{{>}0})$ holds. It suffices to prove the opposite one. Let
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\subset \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}^{{>}0})$ holds. It suffices to prove the opposite one. Let  $D$ be a prime divisor contained in
$D$ be a prime divisor contained in  $\operatorname{Supp}\unicode[STIX]{x1D6E5}^{{\geqslant}1}$. Since
$\operatorname{Supp}\unicode[STIX]{x1D6E5}^{{\geqslant}1}$. Since  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ is a closed subset containing general closed points of
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ is a closed subset containing general closed points of  $D$, we have that
$D$, we have that  $D\subset \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$. In particular,
$D\subset \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$. In particular,  $\operatorname{Supp}\unicode[STIX]{x1D6E5}^{{\geqslant}1}\subset \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$.◻
$\operatorname{Supp}\unicode[STIX]{x1D6E5}^{{\geqslant}1}\subset \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$.◻
Lemma 2.8. Let  $\mathbb{K}\in \{\mathbb{Q},\mathbb{R}\}$. Let
$\mathbb{K}\in \{\mathbb{Q},\mathbb{R}\}$. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$. Let
$p>0$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a quasi-projective dlt pair over
$(X,\unicode[STIX]{x1D6E5})$ be a quasi-projective dlt pair over  $k$ with
$k$ with  $\dim X\leqslant 3$. Let
$\dim X\leqslant 3$. Let  $A$ be an ample
$A$ be an ample  $\mathbb{K}$-Cartier
$\mathbb{K}$-Cartier  $\mathbb{K}$-divisor on
$\mathbb{K}$-divisor on  $X$. Then there exists an effective
$X$. Then there exists an effective  $\mathbb{K}$-Cartier
$\mathbb{K}$-Cartier  $\mathbb{K}$-divisor
$\mathbb{K}$-divisor  $A^{\prime }$ on
$A^{\prime }$ on  $X$ such that
$X$ such that  $A{\sim}_{\mathbb{K}}A^{\prime }$ and
$A{\sim}_{\mathbb{K}}A^{\prime }$ and  $(X,\unicode[STIX]{x1D6E5}+A^{\prime })$ is dlt.
$(X,\unicode[STIX]{x1D6E5}+A^{\prime })$ is dlt.
Proof. If  $k$ is an infinite field, then the proof of [Reference BirkarBir16, Lemma 9.2] works without any changes. Assume that
$k$ is an infinite field, then the proof of [Reference BirkarBir16, Lemma 9.2] works without any changes. Assume that  $k$ is a finite field. Thanks to [Reference PoonenPoo04, Theorem 1.1], we can still make use of Bertini’s theorem. Hence, we can apply the same argument as in [Reference BirkarBir16, Lemma 9.2].◻
$k$ is a finite field. Thanks to [Reference PoonenPoo04, Theorem 1.1], we can still make use of Bertini’s theorem. Hence, we can apply the same argument as in [Reference BirkarBir16, Lemma 9.2].◻
The existence of a minimal model program is known for log canonical threefolds. For terminology appearing in the following theorem, we refer to [Reference Hashizume, Nakamura and TanakaHNT17, § 2.4].
Theorem 2.9. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional  $\mathbb{Q}$-factorial log canonical pair over
$\mathbb{Q}$-factorial log canonical pair over  $k$, where
$k$, where  $\unicode[STIX]{x1D6E5}$ is an
$\unicode[STIX]{x1D6E5}$ is an  $\mathbb{R}$-divisor. Let
$\mathbb{R}$-divisor. Let  $f:X\rightarrow Z$ be a projective
$f:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$. Then there exists a
$Z$. Then there exists a  $(K_{X}+\unicode[STIX]{x1D6E5})$-MMP over
$(K_{X}+\unicode[STIX]{x1D6E5})$-MMP over  $Z$ that terminates. In other words, there is a sequence of birational maps of three-dimensional normal varieties:
$Z$ that terminates. In other words, there is a sequence of birational maps of three-dimensional normal varieties:
 $$\begin{eqnarray}\displaystyle X=:X_{0}\overset{\unicode[STIX]{x1D711}_{0}}{{\dashrightarrow}}X_{1}\overset{\unicode[STIX]{x1D711}_{1}}{{\dashrightarrow}}\cdots \overset{\unicode[STIX]{x1D711}_{\ell -1}}{{\dashrightarrow}}X_{\ell } & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X=:X_{0}\overset{\unicode[STIX]{x1D711}_{0}}{{\dashrightarrow}}X_{1}\overset{\unicode[STIX]{x1D711}_{1}}{{\dashrightarrow}}\cdots \overset{\unicode[STIX]{x1D711}_{\ell -1}}{{\dashrightarrow}}X_{\ell } & & \displaystyle \nonumber\end{eqnarray}$$ such that if  $\unicode[STIX]{x1D6E5}_{i}$ denotes the proper transform of
$\unicode[STIX]{x1D6E5}_{i}$ denotes the proper transform of  $\unicode[STIX]{x1D6E5}$ on
$\unicode[STIX]{x1D6E5}$ on  $X_{i}$, then the following properties hold.
$X_{i}$, then the following properties hold.
(i) For any
 $i\in \{0,\ldots ,\ell \}$,
$i\in \{0,\ldots ,\ell \}$,  $(X_{i},\unicode[STIX]{x1D6E5}_{i})$ is a
$(X_{i},\unicode[STIX]{x1D6E5}_{i})$ is a  $\mathbb{Q}$-factorial log canonical pair which is projective over
$\mathbb{Q}$-factorial log canonical pair which is projective over  $Z$.
$Z$.(ii) For any
 $i\in \{0,\ldots ,\ell -1\}$,
$i\in \{0,\ldots ,\ell -1\}$,  $\unicode[STIX]{x1D711}_{i}:X_{i}{\dashrightarrow}X_{i+1}$ is either a
$\unicode[STIX]{x1D711}_{i}:X_{i}{\dashrightarrow}X_{i+1}$ is either a  $(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$-divisorial contraction over
$(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$-divisorial contraction over  $Z$ or a
$Z$ or a  $(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$-flip over
$(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$-flip over  $Z$.
$Z$.(iii) If
 $K_{X}+\unicode[STIX]{x1D6E5}$ is pseudo-effective over
$K_{X}+\unicode[STIX]{x1D6E5}$ is pseudo-effective over  $Z$, then
$Z$, then  $K_{X_{\ell }}+\unicode[STIX]{x1D6E5}_{\ell }$ is nef over
$K_{X_{\ell }}+\unicode[STIX]{x1D6E5}_{\ell }$ is nef over  $Z$.
$Z$.(iv) If
 $K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective over
$K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective over  $Z$, then there exists a
$Z$, then there exists a  $(K_{X_{\ell }}+\unicode[STIX]{x1D6E5}_{\ell })$-Mori fibre space
$(K_{X_{\ell }}+\unicode[STIX]{x1D6E5}_{\ell })$-Mori fibre space  $X_{\ell }\rightarrow Y$ over
$X_{\ell }\rightarrow Y$ over  $Z$.
$Z$.
Proof. See [Reference Hashizume, Nakamura and TanakaHNT17, Theorem 1.1]. ◻
Proposition 2.10. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional quasi-projective log pair over a perfect field
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional quasi-projective log pair over a perfect field  $k$ of characteristic
$k$ of characteristic  $p>5$. Then there exists a projective birational morphism
$p>5$. Then there exists a projective birational morphism  $f:Y\rightarrow X$ that satisfies the following conditions:
$f:Y\rightarrow X$ that satisfies the following conditions:
(i)
 $a_{F}(X,\unicode[STIX]{x1D6E5})\leqslant 0$ holds for any
$a_{F}(X,\unicode[STIX]{x1D6E5})\leqslant 0$ holds for any  $f$-exceptional prime divisor
$f$-exceptional prime divisor  $F$;
$F$;(ii)
 $(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1})$ is a
$(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1})$ is a  $\mathbb{Q}$-factorial dlt pair, where
$\mathbb{Q}$-factorial dlt pair, where  $\unicode[STIX]{x1D6E5}_{Y}$ is the
$\unicode[STIX]{x1D6E5}_{Y}$ is the  $\mathbb{R}$-divisor defined by
$\mathbb{R}$-divisor defined by  $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$ (see § 2.1 for the definition of
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$ (see § 2.1 for the definition of  $\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}$);
$\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}$);(iii)
 $\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})=f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ holds.
$\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})=f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ holds.
Proof. See [Reference Hashizume, Nakamura and TanakaHNT17, Proposition 3.5]. ◻
For later use, we establish the following result on plt centres.
Proposition 2.11. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional plt pair over a perfect field
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional plt pair over a perfect field  $k$ of characteristic
$k$ of characteristic  $p>5$. Set
$p>5$. Set  $S:=\llcorner \unicode[STIX]{x1D6E5}\lrcorner$. Then the normalisation
$S:=\llcorner \unicode[STIX]{x1D6E5}\lrcorner$. Then the normalisation  $\unicode[STIX]{x1D708}:S^{N}\rightarrow S$ of
$\unicode[STIX]{x1D708}:S^{N}\rightarrow S$ of  $S$ is a universal homeomorphism.
$S$ is a universal homeomorphism.
Proof. Let  $f:Y\rightarrow X$ and
$f:Y\rightarrow X$ and  $\unicode[STIX]{x1D6E5}_{Y}$ be as in Proposition 2.10. Since
$\unicode[STIX]{x1D6E5}_{Y}$ be as in Proposition 2.10. Since  $(X,\unicode[STIX]{x1D6E5})$ is plt, it follows from Proposition 2.10(ii) that
$(X,\unicode[STIX]{x1D6E5})$ is plt, it follows from Proposition 2.10(ii) that  $(Y,\unicode[STIX]{x1D6E5}_{Y})$ is also plt. For
$(Y,\unicode[STIX]{x1D6E5}_{Y})$ is also plt. For  $S_{Y}:=\llcorner \unicode[STIX]{x1D6E5}_{Y}\lrcorner$, we have that
$S_{Y}:=\llcorner \unicode[STIX]{x1D6E5}_{Y}\lrcorner$, we have that  $f^{-1}(S)=f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})=S_{Y}$, where the second equality holds by Proposition 2.10(iii). Hence, the induced morphism
$f^{-1}(S)=f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})=S_{Y}$, where the second equality holds by Proposition 2.10(iii). Hence, the induced morphism  $S_{Y}\rightarrow S$ has connected fibres. Since
$S_{Y}\rightarrow S$ has connected fibres. Since  $Y$ is
$Y$ is  $\mathbb{Q}$-factorial and
$\mathbb{Q}$-factorial and  $(Y,\unicode[STIX]{x1D6E5}_{Y})$ is plt,
$(Y,\unicode[STIX]{x1D6E5}_{Y})$ is plt,  $S_{Y}$ is normal (cf. [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 2.11]). Therefore,
$S_{Y}$ is normal (cf. [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 2.11]). Therefore,  $S_{Y}\rightarrow S$ factors through the normalisation
$S_{Y}\rightarrow S$ factors through the normalisation  $\unicode[STIX]{x1D708}:S^{N}\rightarrow S$:
$\unicode[STIX]{x1D708}:S^{N}\rightarrow S$:
 $$\begin{eqnarray}\displaystyle S_{Y}\rightarrow S^{N}\xrightarrow[{}]{\unicode[STIX]{x1D708}}S. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{Y}\rightarrow S^{N}\xrightarrow[{}]{\unicode[STIX]{x1D708}}S. & & \displaystyle \nonumber\end{eqnarray}$$ Then  $\unicode[STIX]{x1D708}$ is a finite morphism and has connected fibres and hence
$\unicode[STIX]{x1D708}$ is a finite morphism and has connected fibres and hence  $\unicode[STIX]{x1D708}$ is a universal homeomorphism.◻
$\unicode[STIX]{x1D708}$ is a universal homeomorphism.◻
2.3 Connectedness theorem for the birational case
The purpose of this subsection is to establish the three-dimensional Kollár–Shokurov connectedness theorem for the birational case (Theorem 2.15). A key result is Proposition 2.14. To prove this proposition, we show Lemma 2.13 (cf. [Reference BirkarBir16, Theorem 1.8]). We start with the following auxiliary result.
Lemma 2.12. Let  $X$ be a noetherian topological space (for the definition, see [Reference HartshorneHar77, p. 5]). Let
$X$ be a noetherian topological space (for the definition, see [Reference HartshorneHar77, p. 5]). Let  $F$ be a closed subset of
$F$ be a closed subset of  $X$ and let
$X$ and let  $\{{N_{i}\}}_{i\in I}$ be a set of closed subsets of
$\{{N_{i}\}}_{i\in I}$ be a set of closed subsets of  $X$, where
$X$, where  $I$ is a finite set. Set
$I$ is a finite set. Set  $N:=\bigcup _{i\in I}N_{i}$. Assume that the following hold.
$N:=\bigcup _{i\in I}N_{i}$. Assume that the following hold.
(i)
 $N_{i}\,\cap \,F$ is connected for any
$N_{i}\,\cap \,F$ is connected for any  $i\in I$ (
$i\in I$ ( $N_{i}\,\cap \,F$ is possibly empty).
$N_{i}\,\cap \,F$ is possibly empty).(ii)
 $N\,\cap \,U$ is connected for any sufficiently small open neighbourhood
$N\,\cap \,U$ is connected for any sufficiently small open neighbourhood  $U$ in
$U$ in  $X$ of
$X$ of  $F$. In other words, there exists an open subset
$F$. In other words, there exists an open subset  $U_{0}$ of
$U_{0}$ of  $X$ such that
$X$ such that  $F\subset U_{0}$ and, if
$F\subset U_{0}$ and, if  $U$ is an open subset of
$U$ is an open subset of  $X$ satisfying
$X$ satisfying  $F\subset U\subset U_{0}$, then
$F\subset U\subset U_{0}$, then  $N\,\cap \,U$ is connected.
$N\,\cap \,U$ is connected.
Then  $N\,\cap \,F$ is connected.
$N\,\cap \,F$ is connected.
Proof. We first reduce the problem to the case when  $N_{i}\,\cap \,F\neq \emptyset$ for any
$N_{i}\,\cap \,F\neq \emptyset$ for any  $i\in I$. Set
$i\in I$. Set  $I^{\prime }:=\{i\in I\,|\,N_{i}\,\cap \,F\neq \emptyset \}$ and
$I^{\prime }:=\{i\in I\,|\,N_{i}\,\cap \,F\neq \emptyset \}$ and
 $$\begin{eqnarray}\displaystyle U_{0}^{\prime }:=U_{0}\bigg\backslash\biggl(\mathop{\bigcup }_{i\in I\setminus I^{\prime }}N_{i}\biggr)=U_{0}\cap \biggl(\mathop{\bigcap }_{i\in I\setminus I^{\prime }}(X\setminus N_{i})\biggr), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U_{0}^{\prime }:=U_{0}\bigg\backslash\biggl(\mathop{\bigcup }_{i\in I\setminus I^{\prime }}N_{i}\biggr)=U_{0}\cap \biggl(\mathop{\bigcap }_{i\in I\setminus I^{\prime }}(X\setminus N_{i})\biggr), & & \displaystyle \nonumber\end{eqnarray}$$ where  $U_{0}$ is as in (2). Then we have
$U_{0}$ is as in (2). Then we have  $F\subset U_{0}^{\prime }$. If
$F\subset U_{0}^{\prime }$. If  $U$ is an open subset of
$U$ is an open subset of  $X$ such that
$X$ such that  $F\subset U\subset U_{0}^{\prime }$, then (2) implies that
$F\subset U\subset U_{0}^{\prime }$, then (2) implies that  $N\,\cap \,U$ is connected. Therefore, the problem can be reduced to the case when
$N\,\cap \,U$ is connected. Therefore, the problem can be reduced to the case when  $N_{i}\,\cap \,F\neq \emptyset$ for any
$N_{i}\,\cap \,F\neq \emptyset$ for any  $i\in I$. In what follows, we assume that
$i\in I$. In what follows, we assume that  $N_{i}\,\cap \,F\neq \emptyset$ for any
$N_{i}\,\cap \,F\neq \emptyset$ for any  $i\in I$.
$i\in I$.
Take the decomposition into connected components of  $N\,\cap \,F$:
$N\,\cap \,F$:
 $$\begin{eqnarray}\displaystyle N\cap F=\coprod _{j\in J}\unicode[STIX]{x1D6E4}_{j}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N\cap F=\coprod _{j\in J}\unicode[STIX]{x1D6E4}_{j}. & & \displaystyle \nonumber\end{eqnarray}$$ We also have  $N\,\cap \,F=\bigcup _{i\in I}(N_{i}\,\cap \,F)$. We first show that:
$N\,\cap \,F=\bigcup _{i\in I}(N_{i}\,\cap \,F)$. We first show that:
(iii) for any
 $i\in I$, there exists an index
$i\in I$, there exists an index  $j_{i}\in J$ such that
$j_{i}\in J$ such that  $N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j_{i}}\neq \emptyset$ and
$N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j_{i}}\neq \emptyset$ and  $N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j}=\emptyset$ for any
$N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j}=\emptyset$ for any  $j\in J\setminus \{j_{i}\}$. In particular, it holds that
$j\in J\setminus \{j_{i}\}$. In particular, it holds that  $N_{i}\,\cap \,F=N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j_{i}}$ for any
$N_{i}\,\cap \,F=N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j_{i}}$ for any  $i\in I$.
$i\in I$.
Fix  $i\in I$. We have
$i\in I$. We have
 $$\begin{eqnarray}\displaystyle N_{i}\cap F=\coprod _{j\in J}(N_{i}\cap \unicode[STIX]{x1D6E4}_{j}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{i}\cap F=\coprod _{j\in J}(N_{i}\cap \unicode[STIX]{x1D6E4}_{j}). & & \displaystyle \nonumber\end{eqnarray}$$ Since  $N_{i}\,\cap \,F$ is non-empty and connected, (iii) holds.
$N_{i}\,\cap \,F$ is non-empty and connected, (iii) holds.
For  $j\in J$, set
$j\in J$, set  $I_{j}:=\{i\in I\,|\,N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j}\neq \emptyset \}$ and
$I_{j}:=\{i\in I\,|\,N_{i}\,\cap \,\unicode[STIX]{x1D6E4}_{j}\neq \emptyset \}$ and  $N_{I_{j}}:=\bigcup _{i\in I_{j}}N_{i}$. Then (iii) implies that
$N_{I_{j}}:=\bigcup _{i\in I_{j}}N_{i}$. Then (iii) implies that  $I=\coprod _{j\in J}I_{j}$. In particular, we obtain
$I=\coprod _{j\in J}I_{j}$. In particular, we obtain  $N=\bigcup _{j\in J}N_{I_{j}}$. Set
$N=\bigcup _{j\in J}N_{I_{j}}$. Set
 $$\begin{eqnarray}\displaystyle U_{1}:=\mathop{\bigcap }_{j,j^{\prime }\in J,j\neq j^{\prime }}X\setminus (N_{I_{j}}\cap N_{I_{j^{\prime }}}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U_{1}:=\mathop{\bigcap }_{j,j^{\prime }\in J,j\neq j^{\prime }}X\setminus (N_{I_{j}}\cap N_{I_{j^{\prime }}}), & & \displaystyle\end{eqnarray}$$ which is an open subset of  $X$.
$X$.
We now show that  $F\subset U_{1}$. Pick
$F\subset U_{1}$. Pick  $j,j^{\prime }\in J$ such that
$j,j^{\prime }\in J$ such that  $j\neq j^{\prime }$. For
$j\neq j^{\prime }$. For  $i\in I_{j}$ and
$i\in I_{j}$ and  $i^{\prime }\in I_{j^{\prime }}$, we have
$i^{\prime }\in I_{j^{\prime }}$, we have
 $$\begin{eqnarray}\displaystyle N_{i}\cap N_{i^{\prime }}\cap F=(N_{i}\cap F)\cap (N_{i^{\prime }}\cap F)\subset \unicode[STIX]{x1D6E4}_{j_{i}}\cap \unicode[STIX]{x1D6E4}_{j_{i^{\prime }}}=\unicode[STIX]{x1D6E4}_{j}\cap \unicode[STIX]{x1D6E4}_{j^{\prime }}=\emptyset , & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{i}\cap N_{i^{\prime }}\cap F=(N_{i}\cap F)\cap (N_{i^{\prime }}\cap F)\subset \unicode[STIX]{x1D6E4}_{j_{i}}\cap \unicode[STIX]{x1D6E4}_{j_{i^{\prime }}}=\unicode[STIX]{x1D6E4}_{j}\cap \unicode[STIX]{x1D6E4}_{j^{\prime }}=\emptyset , & & \displaystyle \nonumber\end{eqnarray}$$where the inclusion follows from (iii). Hence, we have
 $$\begin{eqnarray}\displaystyle N_{I_{j}}\cap N_{I_{j^{\prime }}}\cap F=\mathop{\bigcup }_{i\in I_{j},i^{\prime }\in I_{j^{\prime }}}(N_{i}\cap N_{i^{\prime }}\cap F)=\emptyset , & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{I_{j}}\cap N_{I_{j^{\prime }}}\cap F=\mathop{\bigcup }_{i\in I_{j},i^{\prime }\in I_{j^{\prime }}}(N_{i}\cap N_{i^{\prime }}\cap F)=\emptyset , & & \displaystyle \nonumber\end{eqnarray}$$ i.e.  $F\subset X\setminus (N_{I_{j}}\,\cap \,N_{I_{j^{\prime }}})$. Hence, (2.12.1) implies that
$F\subset X\setminus (N_{I_{j}}\,\cap \,N_{I_{j^{\prime }}})$. Hence, (2.12.1) implies that  $F\subset U_{1}$.
$F\subset U_{1}$.
Set  $U:=U_{0}\,\cap \,U_{1}$, where
$U:=U_{0}\,\cap \,U_{1}$, where  $U_{0}$ is as in (ii). Since
$U_{0}$ is as in (ii). Since  $F\subset U_{0}\,\cap \,U_{1}=U$, (ii) implies that
$F\subset U_{0}\,\cap \,U_{1}=U$, (ii) implies that  $N\,\cap \,U$ is connected. We have
$N\,\cap \,U$ is connected. We have
 $$\begin{eqnarray}\displaystyle N\cap U=\mathop{\bigcup }_{j\in J}(N_{I_{j}}\cap U)=\coprod _{j\in J}(N_{I_{j}}\cap U), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N\cap U=\mathop{\bigcup }_{j\in J}(N_{I_{j}}\cap U)=\coprod _{j\in J}(N_{I_{j}}\cap U), & & \displaystyle \nonumber\end{eqnarray}$$ where the last equality follows from (2.12.1). For  $j\in J$, we have that
$j\in J$, we have that
 $$\begin{eqnarray}\displaystyle N_{I_{j}}\cap U\supset N_{I_{j}}\cap F\neq \emptyset . & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{I_{j}}\cap U\supset N_{I_{j}}\cap F\neq \emptyset . & & \displaystyle \nonumber\end{eqnarray}$$ Since  $N\,\cap \,U$ is connected, we obtain
$N\,\cap \,U$ is connected, we obtain  $|J|=1$, i.e.
$|J|=1$, i.e.  $N\,\cap \,F$ is connected.◻
$N\,\cap \,F$ is connected.◻
Lemma 2.13. Let  $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic  $p>5$. Let
$p>5$. Let  $(X,D)$ be a three-dimensional
$(X,D)$ be a three-dimensional  $\mathbb{Q}$-factorial dlt pair over
$\mathbb{Q}$-factorial dlt pair over  $k$ and let
$k$ and let  $f:X\rightarrow Y$ be a projective birational
$f:X\rightarrow Y$ be a projective birational  $k$-morphism to a normal threefold
$k$-morphism to a normal threefold  $Y$ over
$Y$ over  $k$. If
$k$. If  $f$ is either a
$f$ is either a  $(K_{X}+D)$-divisorial contraction or a
$(K_{X}+D)$-divisorial contraction or a  $(K_{X}+D)$-flipping contraction, then the induced morphism
$(K_{X}+D)$-flipping contraction, then the induced morphism  $\operatorname{Nklt}(X,D)\rightarrow Y$ has connected fibres.
$\operatorname{Nklt}(X,D)\rightarrow Y$ has connected fibres.
Proof. Set  $S:=\llcorner D\lrcorner$ and let
$S:=\llcorner D\lrcorner$ and let  $S=\sum _{i\in I}S_{i}$ be the irreducible decomposition. We have
$S=\sum _{i\in I}S_{i}$ be the irreducible decomposition. We have  $\operatorname{Nklt}(X,D)=\bigcup _{i\in I}S_{i}$.
$\operatorname{Nklt}(X,D)=\bigcup _{i\in I}S_{i}$.
For any sufficiently small open neighbourhood  $U$ in
$U$ in  $X$ of
$X$ of  $f^{-1}(y)$, it follows from [Reference BirkarBir16, Theorem 1.8] that
$f^{-1}(y)$, it follows from [Reference BirkarBir16, Theorem 1.8] that  $\operatorname{Nklt}(X,D)\,\cap \,U$ is connected. We apply Lemma 2.12 to
$\operatorname{Nklt}(X,D)\,\cap \,U$ is connected. We apply Lemma 2.12 to  $N_{i}:=S_{i}$ and
$N_{i}:=S_{i}$ and  $F:=f^{-1}(y)$. Then it is enough to prove that
$F:=f^{-1}(y)$. Then it is enough to prove that  $S_{i}\,\cap \,F$ is connected. Therefore, after perturbing coefficients of
$S_{i}\,\cap \,F$ is connected. Therefore, after perturbing coefficients of  $D$, we may assume that
$D$, we may assume that  $S=S_{i}$, i.e.
$S=S_{i}$, i.e.  $(X,D)$ is plt.
$(X,D)$ is plt.
From now on, we treat the case when  $\llcorner D\lrcorner =S$ is a prime divisor. In this case, we have
$\llcorner D\lrcorner =S$ is a prime divisor. In this case, we have  $\operatorname{Nklt}(X,D)=S$. If
$\operatorname{Nklt}(X,D)=S$. If  $S\subset \operatorname{Ex}(f)$, then
$S\subset \operatorname{Ex}(f)$, then  $f$ is a
$f$ is a  $(K_{X}+D)$-divisorial contraction such that
$(K_{X}+D)$-divisorial contraction such that  $S=\operatorname{Ex}(f)$. Then the assertion is clear because
$S=\operatorname{Ex}(f)$. Then the assertion is clear because  $f$ has connected fibres. Thus, we may assume that
$f$ has connected fibres. Thus, we may assume that  $S\not \subset \operatorname{Ex}(f)$. Since
$S\not \subset \operatorname{Ex}(f)$. Since  $-(K_{X}+D)$ is
$-(K_{X}+D)$ is  $f$-ample, there exists an effective
$f$-ample, there exists an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $A$ on
$A$ on  $X$ such that
$X$ such that  $A{\sim}_{\mathbb{R},f}-(K_{X}+D)$ and
$A{\sim}_{\mathbb{R},f}-(K_{X}+D)$ and  $(X,D+A)$ is plt. Since
$(X,D+A)$ is plt. Since  $K_{X}+D+A{\sim}_{\mathbb{R},f}0$, we have
$K_{X}+D+A{\sim}_{\mathbb{R},f}0$, we have  $K_{X}+D+A=f^{\ast }(K_{Y}+D_{Y}+A_{Y})$ for
$K_{X}+D+A=f^{\ast }(K_{Y}+D_{Y}+A_{Y})$ for  $D_{Y}:=f_{\ast }D$ and
$D_{Y}:=f_{\ast }D$ and  $A_{Y}:=f_{\ast }A$. In particular,
$A_{Y}:=f_{\ast }A$. In particular,  $(Y,D_{Y}+A_{Y})$ is plt. Then the induced morphism
$(Y,D_{Y}+A_{Y})$ is plt. Then the induced morphism  $g:S\rightarrow S_{Y}:=f(S)$ has connected fibres by Proposition 2.11. Since
$g:S\rightarrow S_{Y}:=f(S)$ has connected fibres by Proposition 2.11. Since  $\operatorname{Nklt}(X,D)\,\cap \,f^{-1}(y)=S\,\cap \,f^{-1}(y)=g^{-1}(y)$ for any
$\operatorname{Nklt}(X,D)\,\cap \,f^{-1}(y)=S\,\cap \,f^{-1}(y)=g^{-1}(y)$ for any  $y\in f(S)=S_{Y}$,
$y\in f(S)=S_{Y}$,  $\operatorname{Nklt}(X,D)\rightarrow Y$ has connected fibres.◻
$\operatorname{Nklt}(X,D)\rightarrow Y$ has connected fibres.◻
Proposition 2.14. Let  $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic  $p>5$. Let
$p>5$. Let  $(V,\unicode[STIX]{x1D6E5})$ be a three-dimensional quasi-projective
$(V,\unicode[STIX]{x1D6E5})$ be a three-dimensional quasi-projective  $\mathbb{Q}$-factorial log pair over
$\mathbb{Q}$-factorial log pair over  $k$. Let
$k$. Let  $\unicode[STIX]{x1D711}:U\rightarrow V$ be a log resolution of
$\unicode[STIX]{x1D711}:U\rightarrow V$ be a log resolution of  $(V,\unicode[STIX]{x1D6E5})$. Let
$(V,\unicode[STIX]{x1D6E5})$. Let  $\unicode[STIX]{x1D6E5}_{U}$ be the
$\unicode[STIX]{x1D6E5}_{U}$ be the  $\mathbb{R}$-divisor defined by
$\mathbb{R}$-divisor defined by  $K_{U}+\unicode[STIX]{x1D6E5}_{U}=\unicode[STIX]{x1D711}^{\ast }(K_{V}+\unicode[STIX]{x1D6E5})$. Then the induced morphism
$K_{U}+\unicode[STIX]{x1D6E5}_{U}=\unicode[STIX]{x1D711}^{\ast }(K_{V}+\unicode[STIX]{x1D6E5})$. Then the induced morphism  $\operatorname{Nklt}(U,\unicode[STIX]{x1D6E5}_{U})\rightarrow V$ has connected fibres.
$\operatorname{Nklt}(U,\unicode[STIX]{x1D6E5}_{U})\rightarrow V$ has connected fibres.
Proof. Let  $F$ be the sum of the
$F$ be the sum of the  $\unicode[STIX]{x1D711}$-exceptional prime divisors
$\unicode[STIX]{x1D711}$-exceptional prime divisors  $F^{\prime }$ on
$F^{\prime }$ on  $U$ whose log discrepancies are positive:
$U$ whose log discrepancies are positive:  $a_{F^{\prime }}(V,\unicode[STIX]{x1D6E5})>0$. Let
$a_{F^{\prime }}(V,\unicode[STIX]{x1D6E5})>0$. Let  $G$ be the sum of the
$G$ be the sum of the  $\unicode[STIX]{x1D711}$-exceptional prime divisors
$\unicode[STIX]{x1D711}$-exceptional prime divisors  $G^{\prime }$ on
$G^{\prime }$ on  $U$ whose log discrepancies are non-positive:
$U$ whose log discrepancies are non-positive:  $a_{G^{\prime }}(V,\unicode[STIX]{x1D6E5})\leqslant 0$. We set
$a_{G^{\prime }}(V,\unicode[STIX]{x1D6E5})\leqslant 0$. We set
 $$\begin{eqnarray}\displaystyle D_{U}:=\unicode[STIX]{x1D711}_{\ast }^{-1}\unicode[STIX]{x1D6E5}^{\wedge 1}+(1-\unicode[STIX]{x1D716})F+G & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{U}:=\unicode[STIX]{x1D711}_{\ast }^{-1}\unicode[STIX]{x1D6E5}^{\wedge 1}+(1-\unicode[STIX]{x1D716})F+G & & \displaystyle \nonumber\end{eqnarray}$$ for a sufficiently small positive real number  $\unicode[STIX]{x1D716}$. Then it holds that:
$\unicode[STIX]{x1D716}$. Then it holds that:
(i)
 $(U,D_{U})$ is dlt; and
$(U,D_{U})$ is dlt; and(ii)
 $\operatorname{Supp}\unicode[STIX]{x1D6E5}_{U}^{{\geqslant}1}=\operatorname{Supp}D_{U}^{=1}$.
$\operatorname{Supp}\unicode[STIX]{x1D6E5}_{U}^{{\geqslant}1}=\operatorname{Supp}D_{U}^{=1}$.
By Theorem 2.9, there is a  $(K_{U}+D_{U})$-MMP over
$(K_{U}+D_{U})$-MMP over  $V$ that terminates:
$V$ that terminates:
 $$\begin{eqnarray}\displaystyle U=:X_{0}{\dashrightarrow}\cdots {\dashrightarrow}X_{\ell }. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U=:X_{0}{\dashrightarrow}\cdots {\dashrightarrow}X_{\ell }. & & \displaystyle\end{eqnarray}$$ For any  $i\in \{0,\ldots ,\ell \}$, we define
$i\in \{0,\ldots ,\ell \}$, we define  $\unicode[STIX]{x1D6E5}_{X_{i}}$,
$\unicode[STIX]{x1D6E5}_{X_{i}}$,  $F_{X_{i}}$,
$F_{X_{i}}$,  $G_{X_{i}}$ and
$G_{X_{i}}$ and  $D_{X_{i}}$ as the push-forwards of
$D_{X_{i}}$ as the push-forwards of  $\unicode[STIX]{x1D6E5}_{U}$,
$\unicode[STIX]{x1D6E5}_{U}$,  $F$,
$F$,  $G$ and
$G$ and  $D_{U}$ on
$D_{U}$ on  $X_{i}$, respectively. Then it holds that
$X_{i}$, respectively. Then it holds that  $K_{X_{i}}+\unicode[STIX]{x1D6E5}_{X_{i}}=\unicode[STIX]{x1D713}_{i}^{\ast }(K_{V}+\unicode[STIX]{x1D6E5})$, where
$K_{X_{i}}+\unicode[STIX]{x1D6E5}_{X_{i}}=\unicode[STIX]{x1D713}_{i}^{\ast }(K_{V}+\unicode[STIX]{x1D6E5})$, where  $\unicode[STIX]{x1D713}_{i}:X_{i}\rightarrow V$ denotes the induced morphism. Moreover, for any
$\unicode[STIX]{x1D713}_{i}:X_{i}\rightarrow V$ denotes the induced morphism. Moreover, for any  $i\in \{0,\ldots ,\ell \}$, we get:
$i\in \{0,\ldots ,\ell \}$, we get:
 $(\text{i})^{\prime }$
$(\text{i})^{\prime }$ $(X_{i},D_{X_{i}})$ is dlt; and
$(X_{i},D_{X_{i}})$ is dlt; and $(\text{ii})^{\prime }$
$(\text{ii})^{\prime }$ $\operatorname{Supp}\unicode[STIX]{x1D6E5}_{X_{i}}^{{\geqslant}1}=\operatorname{Supp}D_{X_{i}}^{=1}$.
$\operatorname{Supp}\unicode[STIX]{x1D6E5}_{X_{i}}^{{\geqslant}1}=\operatorname{Supp}D_{X_{i}}^{=1}$.
Step 1. For any  $i\in \{0,\ldots ,\ell \}$, it holds that
$i\in \{0,\ldots ,\ell \}$, it holds that
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})=\operatorname{Nklt}(X_{i},D_{X_{i}})=\operatorname{Supp}\unicode[STIX]{x1D6E5}_{X_{i}}^{{\geqslant}1}=\operatorname{Supp}D_{X_{i}}^{=1}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})=\operatorname{Nklt}(X_{i},D_{X_{i}})=\operatorname{Supp}\unicode[STIX]{x1D6E5}_{X_{i}}^{{\geqslant}1}=\operatorname{Supp}D_{X_{i}}^{=1}. & & \displaystyle \nonumber\end{eqnarray}$$Proof of Step 1.
Fix  $i\in \{0,\ldots ,\ell \}$. We obtain
$i\in \{0,\ldots ,\ell \}$. We obtain
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},D_{X_{i}})=\operatorname{Supp}D_{X_{i}}^{=1}=\operatorname{Supp}\unicode[STIX]{x1D6E5}_{X_{i}}^{{\geqslant}1}\subset \operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},D_{X_{i}})=\operatorname{Supp}D_{X_{i}}^{=1}=\operatorname{Supp}\unicode[STIX]{x1D6E5}_{X_{i}}^{{\geqslant}1}\subset \operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}}), & & \displaystyle \nonumber\end{eqnarray}$$ where the first equality holds by (i)′ and the second one follows from (ii)′. Hence, it is sufficient to show that  $\operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})\subset \operatorname{Supp}D_{X_{i}}^{=1}$. For sufficiently large
$\operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})\subset \operatorname{Supp}D_{X_{i}}^{=1}$. For sufficiently large  $b>0$, the
$b>0$, the  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor
 $$\begin{eqnarray}\displaystyle A_{X_{i}}:=(\unicode[STIX]{x1D713}_{i}^{-1})_{\ast }\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D716})F_{X_{i}}+bG_{X_{i}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{X_{i}}:=(\unicode[STIX]{x1D713}_{i}^{-1})_{\ast }\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D716})F_{X_{i}}+bG_{X_{i}} & & \displaystyle \nonumber\end{eqnarray}$$ satisfies  $\unicode[STIX]{x1D6E5}_{X_{i}}\leqslant A_{X_{i}}$. Therefore, we get
$\unicode[STIX]{x1D6E5}_{X_{i}}\leqslant A_{X_{i}}$. Therefore, we get
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})\subset \operatorname{Nklt}(X_{i},A_{X_{i}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})\subset \operatorname{Nklt}(X_{i},A_{X_{i}}). & & \displaystyle \nonumber\end{eqnarray}$$ Since  $A_{X_{i}}^{\wedge 1}=D_{X_{i}}$, we have
$A_{X_{i}}^{\wedge 1}=D_{X_{i}}$, we have  $A_{X_{i}}^{{<}1}=D_{X_{i}}^{{<}1}$ and hence
$A_{X_{i}}^{{<}1}=D_{X_{i}}^{{<}1}$ and hence  $(X,A_{X_{i}}^{{<}1})$ is klt by (i)′. Thus, it follows from Proposition 2.7 that
$(X,A_{X_{i}}^{{<}1})$ is klt by (i)′. Thus, it follows from Proposition 2.7 that
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},A_{X_{i}})=\operatorname{Supp}A_{X_{i}}^{{\geqslant}1}=\operatorname{Supp}D_{X_{i}}^{=1}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},A_{X_{i}})=\operatorname{Supp}A_{X_{i}}^{{\geqslant}1}=\operatorname{Supp}D_{X_{i}}^{=1}. & & \displaystyle \nonumber\end{eqnarray}$$ Thus, we obtain the desired inclusion  $\operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})\subset \operatorname{Supp}D_{X_{i}}^{=1}$. This completes the proof of Step 1.◻
$\operatorname{Nklt}(X_{i},\unicode[STIX]{x1D6E5}_{X_{i}})\subset \operatorname{Supp}D_{X_{i}}^{=1}$. This completes the proof of Step 1.◻
Step 2. Let  $g:X_{i}\rightarrow X_{i+1}$ be a divisorial contraction appearing in the MMP (2.14.1). If
$g:X_{i}\rightarrow X_{i+1}$ be a divisorial contraction appearing in the MMP (2.14.1). If  $\operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow V$ has connected fibres, then so does
$\operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow V$ has connected fibres, then so does  $\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow V$.
$\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow V$.
Proof of Step 2.
It follows from Lemma 2.13 that  $\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow \operatorname{Nklt}(X_{i+1},D_{X_{i+1}})$ has connected fibres. This completes the proof of Step 2.◻
$\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow \operatorname{Nklt}(X_{i+1},D_{X_{i+1}})$ has connected fibres. This completes the proof of Step 2.◻
Step 3. Let  $h:X_{i}{\dashrightarrow}X_{i+1}$ be a flip appearing in the MMP (2.14.1). If
$h:X_{i}{\dashrightarrow}X_{i+1}$ be a flip appearing in the MMP (2.14.1). If  $\operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow V$ has connected fibres, then so does
$\operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow V$ has connected fibres, then so does  $\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow V$.
$\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow V$.
Proof of Step 3.
Assume that  $\operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow V$ has connected fibres. Let
$\operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow V$ has connected fibres. Let  $\unicode[STIX]{x1D711}_{i}:X_{i}\rightarrow Y$ be the flipping contraction and let
$\unicode[STIX]{x1D711}_{i}:X_{i}\rightarrow Y$ be the flipping contraction and let  $\unicode[STIX]{x1D711}_{i+1}:X_{i+1}\rightarrow Y$ and
$\unicode[STIX]{x1D711}_{i+1}:X_{i+1}\rightarrow Y$ and  $\unicode[STIX]{x1D713}_{Y}:Y\rightarrow V$ be the induced morphisms. Set
$\unicode[STIX]{x1D713}_{Y}:Y\rightarrow V$ be the induced morphisms. Set  $N_{Y}:=\unicode[STIX]{x1D711}_{i}(\operatorname{Nklt}(X_{i},D_{X_{i}}))$ and
$N_{Y}:=\unicode[STIX]{x1D711}_{i}(\operatorname{Nklt}(X_{i},D_{X_{i}}))$ and  $N_{V}:=\unicode[STIX]{x1D713}_{Y}(N_{Y})$. It follows from Step 1 that
$N_{V}:=\unicode[STIX]{x1D713}_{Y}(N_{Y})$. It follows from Step 1 that  $N_{Y}=\unicode[STIX]{x1D711}_{i+1}(\operatorname{Nklt}(X_{i+1},D_{X_{i+1}}))$. By assumption, it holds that the composite morphism
$N_{Y}=\unicode[STIX]{x1D711}_{i+1}(\operatorname{Nklt}(X_{i+1},D_{X_{i+1}}))$. By assumption, it holds that the composite morphism
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow N_{Y}\rightarrow N_{V} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i+1},D_{X_{i+1}})\rightarrow N_{Y}\rightarrow N_{V} & & \displaystyle \nonumber\end{eqnarray}$$ is a surjective morphism with connected fibres. In particular,  $N_{Y}\rightarrow N_{V}$ has connected fibres. Since
$N_{Y}\rightarrow N_{V}$ has connected fibres. Since  $\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow N_{Y}$ has connected fibres by Lemma 2.13, their composition
$\operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow N_{Y}$ has connected fibres by Lemma 2.13, their composition
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow N_{Y}\rightarrow N_{V} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{i},D_{X_{i}})\rightarrow N_{Y}\rightarrow N_{V} & & \displaystyle \nonumber\end{eqnarray}$$also has connected fibres. This completes the proof of Step 3. ◻
Step 4. The induced morphism  $\operatorname{Nklt}(X_{\ell },D_{\ell })\rightarrow V$ has connected fibres.
$\operatorname{Nklt}(X_{\ell },D_{\ell })\rightarrow V$ has connected fibres.
Proof of Step 4.
We have
 $$\begin{eqnarray}\displaystyle B_{\ell }:=(\unicode[STIX]{x1D713}_{\ell }^{-1})_{\ast }\unicode[STIX]{x1D6E5}^{\wedge 1}+(1-\unicode[STIX]{x1D716})F_{X_{\ell }}+G_{X_{\ell }}-\unicode[STIX]{x1D6E5}_{X_{\ell }}{\sim}_{V,\mathbb{R}}K_{X_{\ell }}+D_{X_{\ell }}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{\ell }:=(\unicode[STIX]{x1D713}_{\ell }^{-1})_{\ast }\unicode[STIX]{x1D6E5}^{\wedge 1}+(1-\unicode[STIX]{x1D716})F_{X_{\ell }}+G_{X_{\ell }}-\unicode[STIX]{x1D6E5}_{X_{\ell }}{\sim}_{V,\mathbb{R}}K_{X_{\ell }}+D_{X_{\ell }}. & & \displaystyle \nonumber\end{eqnarray}$$ Then  $B_{\ell }$ is nef over
$B_{\ell }$ is nef over  $V$. The push-forward of
$V$. The push-forward of  $-B_{\ell }$ on
$-B_{\ell }$ on  $V$, which is nothing but the push-forward of
$V$, which is nothing but the push-forward of  $\unicode[STIX]{x1D6E5}_{X_{\ell }}-(\unicode[STIX]{x1D713}_{\ell }^{-1})_{\ast }\unicode[STIX]{x1D6E5}^{\wedge 1}$, is effective. Hence, it turns out by the negativity lemma that
$\unicode[STIX]{x1D6E5}_{X_{\ell }}-(\unicode[STIX]{x1D713}_{\ell }^{-1})_{\ast }\unicode[STIX]{x1D6E5}^{\wedge 1}$, is effective. Hence, it turns out by the negativity lemma that  $-B_{\ell }$ itself is effective. Since
$-B_{\ell }$ itself is effective. Since  $\unicode[STIX]{x1D716}$ is sufficiently small, it follows that
$\unicode[STIX]{x1D716}$ is sufficiently small, it follows that  $F_{X_{\ell }}=0$, that is, any
$F_{X_{\ell }}=0$, that is, any  $\unicode[STIX]{x1D711}_{\ell }$-exceptional prime divisor
$\unicode[STIX]{x1D711}_{\ell }$-exceptional prime divisor  $E$ satisfies
$E$ satisfies  $a_{E}(V,\unicode[STIX]{x1D6E5})\leqslant 0$. Since
$a_{E}(V,\unicode[STIX]{x1D6E5})\leqslant 0$. Since  $V$ is
$V$ is  $\mathbb{Q}$-factorial, it holds that
$\mathbb{Q}$-factorial, it holds that
 $$\begin{eqnarray}\displaystyle \operatorname{Ex}(\unicode[STIX]{x1D711}_{\ell })\subset \operatorname{Nklt}(X_{\ell },\unicode[STIX]{x1D6E5}_{X_{\ell }}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Ex}(\unicode[STIX]{x1D711}_{\ell })\subset \operatorname{Nklt}(X_{\ell },\unicode[STIX]{x1D6E5}_{X_{\ell }}). & & \displaystyle \nonumber\end{eqnarray}$$ In particular,  $\operatorname{Nklt}(X_{\ell },\unicode[STIX]{x1D6E5}_{X_{\ell }})\,\cap \,\unicode[STIX]{x1D711}_{\ell }^{-1}(v)=\unicode[STIX]{x1D711}_{\ell }^{-1}(v)$ holds and this is connected for any closed point
$\operatorname{Nklt}(X_{\ell },\unicode[STIX]{x1D6E5}_{X_{\ell }})\,\cap \,\unicode[STIX]{x1D711}_{\ell }^{-1}(v)=\unicode[STIX]{x1D711}_{\ell }^{-1}(v)$ holds and this is connected for any closed point  $v$ of
$v$ of  $V$. This completes the proof of Step 4.◻
$V$. This completes the proof of Step 4.◻
Step 2, Step 3 and Step 4 complete the proof of Proposition 2.14. ◻
Theorem 2.15. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $f:X\rightarrow V$ be a projective birational
$f:X\rightarrow V$ be a projective birational  $k$-morphism of normal quasi-projective threefolds over
$k$-morphism of normal quasi-projective threefolds over  $k$. Let
$k$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a sub-log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a sub-log pair over  $k$ such that
$k$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f_{\ast }\unicode[STIX]{x1D6E5}$ is effective. Then the induced morphism
$f_{\ast }\unicode[STIX]{x1D6E5}$ is effective. Then the induced morphism  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow V$ has connected fibres.
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow V$ has connected fibres.
Proof. Taking the base change to the algebraic closure of  $k$, we may assume that
$k$, we may assume that  $k$ is an algebraically closed field. We now reduce the problem to the case when
$k$ is an algebraically closed field. We now reduce the problem to the case when  $K_{X}+\unicode[STIX]{x1D6E5}{\sim}_{\mathbb{R},f}0$. Since
$K_{X}+\unicode[STIX]{x1D6E5}{\sim}_{\mathbb{R},f}0$. Since  $f$ is birational,
$f$ is birational,  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. After replacing
$f$-big. After replacing  $\unicode[STIX]{x1D6E5}$, we may assume that
$\unicode[STIX]{x1D6E5}$, we may assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-ample. Then there exists an effective
$f$-ample. Then there exists an effective  $\mathbb{R}$-Cartier
$\mathbb{R}$-Cartier  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $A$ such that
$A$ such that  $A{\sim}_{\mathbb{R},f}-(K_{X}+\unicode[STIX]{x1D6E5})$ and
$A{\sim}_{\mathbb{R},f}-(K_{X}+\unicode[STIX]{x1D6E5})$ and  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})=\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}+A)$. Thus, we may assume that
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})=\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}+A)$. Thus, we may assume that  $K_{X}+\unicode[STIX]{x1D6E5}{\sim}_{\mathbb{R},f}0$. In particular, for
$K_{X}+\unicode[STIX]{x1D6E5}{\sim}_{\mathbb{R},f}0$. In particular, for  $\unicode[STIX]{x1D6E5}_{V}:=f_{\ast }\unicode[STIX]{x1D6E5}$, it holds that
$\unicode[STIX]{x1D6E5}_{V}:=f_{\ast }\unicode[STIX]{x1D6E5}$, it holds that  $(V,\unicode[STIX]{x1D6E5}_{V})$ is a log pair and
$(V,\unicode[STIX]{x1D6E5}_{V})$ is a log pair and  $K_{X}+\unicode[STIX]{x1D6E5}=f^{\ast }(K_{V}+\unicode[STIX]{x1D6E5}_{V})$.
$K_{X}+\unicode[STIX]{x1D6E5}=f^{\ast }(K_{V}+\unicode[STIX]{x1D6E5}_{V})$.
Let  $\unicode[STIX]{x1D711}:V_{1}\rightarrow V$ be a dlt modification of
$\unicode[STIX]{x1D711}:V_{1}\rightarrow V$ be a dlt modification of  $(V,\unicode[STIX]{x1D6E5}_{V})$ such that
$(V,\unicode[STIX]{x1D6E5}_{V})$ such that  $\operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})=\unicode[STIX]{x1D711}^{-1}(\operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V}))$ (Proposition 2.10). In particular,
$\operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})=\unicode[STIX]{x1D711}^{-1}(\operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V}))$ (Proposition 2.10). In particular,  $\operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})\rightarrow \operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V})$ has connected fibres. Let
$\operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})\rightarrow \operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V})$ has connected fibres. Let $f_{1}:X_{1}\rightarrow V_{1}$ be a log resolution of
$f_{1}:X_{1}\rightarrow V_{1}$ be a log resolution of  $(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})$ that factors through
$(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})$ that factors through  $X$. By Proposition 2.14,
$X$. By Proposition 2.14, $\operatorname{Nklt}(X_{1},\unicode[STIX]{x1D6E5}_{X_{1}})\rightarrow \operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})$ has connected fibres. Thus, the composite morphism
$\operatorname{Nklt}(X_{1},\unicode[STIX]{x1D6E5}_{X_{1}})\rightarrow \operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})$ has connected fibres. Thus, the composite morphism
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{1},\unicode[STIX]{x1D6E5}_{X_{1}})\rightarrow \operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})\rightarrow \operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X_{1},\unicode[STIX]{x1D6E5}_{X_{1}})\rightarrow \operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})\rightarrow \operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V}) & & \displaystyle \nonumber\end{eqnarray}$$ has connected fibres and factors through  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$. In particular, also
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$. In particular, also  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow \operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V})$ has connected fibres.◻
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow \operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V})$ has connected fibres.◻
Remark 2.16. When we apply Proposition 2.14 in the above proof, we only use the properties that  $V_{1}$ is
$V_{1}$ is  $\mathbb{Q}$-factorial and
$\mathbb{Q}$-factorial and  $\operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})=\unicode[STIX]{x1D711}^{-1}(\operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V}))$, whilst we do not use the fact that
$\operatorname{Nklt}(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}})=\unicode[STIX]{x1D711}^{-1}(\operatorname{Nklt}(V,\unicode[STIX]{x1D6E5}_{V}))$, whilst we do not use the fact that  $(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}}^{\wedge 1})$ is dlt.
$(V_{1},\unicode[STIX]{x1D6E5}_{V_{1}}^{\wedge 1})$ is dlt.
2.4 Results on the Witt vector cohomologies
For the definition of the Witt vector cohomology and its properties, we refer to [Reference Gongyo, Nakamura and TanakaGNT19] and [Reference Chatzistamatiou and RüllingCR12]. Our goal of this subsection is to show Propositions 2.22 and 2.23. As far as the authors know, it is an open problem whether  $R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})$ commute with base changes. Such a problem occurs because inverse limits do not commute with tensor products. We start by showing some auxiliary results.
$R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})$ commute with base changes. Such a problem occurs because inverse limits do not commute with tensor products. We start by showing some auxiliary results.
Lemma 2.17. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$. Let
$p>0$. Let  $f:X\rightarrow Y$ be a proper surjective
$f:X\rightarrow Y$ be a proper surjective  $k$-morphism of separated schemes of finite type over
$k$-morphism of separated schemes of finite type over  $k$. Then the following conditions are equivalent:
$k$. Then the following conditions are equivalent:
(i)
 $f$ has connected fibres;
$f$ has connected fibres;(ii) the induced homomorphism
 $W{\mathcal{O}}_{Y,\mathbb{Q}}\rightarrow f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}$ is an isomorphism.
$W{\mathcal{O}}_{Y,\mathbb{Q}}\rightarrow f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}$ is an isomorphism.
Proof. It follows from [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.22] that (i) implies (ii).
It is enough to show that (ii) implies (i). Assume (ii). Taking the Stein factorisation, the problem is reduced to the case when  $f$ is a finite surjective morphism. Since the problem is local on
$f$ is a finite surjective morphism. Since the problem is local on  $Y$, we may assume that
$Y$, we may assume that  $X=\operatorname{Spec}\,B$ and
$X=\operatorname{Spec}\,B$ and  $Y=\operatorname{Spec}\,A$. For the induced ring homomorphism
$Y=\operatorname{Spec}\,A$. For the induced ring homomorphism  $A\rightarrow B$, we have that
$A\rightarrow B$, we have that  $W(A)_{\mathbb{Q}}\rightarrow W(B)_{\mathbb{Q}}$ is an isomorphism. Fix a maximal ideal
$W(A)_{\mathbb{Q}}\rightarrow W(B)_{\mathbb{Q}}$ is an isomorphism. Fix a maximal ideal  $\mathfrak{m}$ of
$\mathfrak{m}$ of  $A$. We have the following commutative diagram of ring homomorphisms.
$A$. We have the following commutative diagram of ring homomorphisms.

By a diagram chase,  $\unicode[STIX]{x1D713}:W(A/\mathfrak{m})_{\mathbb{Q}}\rightarrow W(B/\mathfrak{m}B)_{\mathbb{Q}}$ is surjective. On the other hand,
$\unicode[STIX]{x1D713}:W(A/\mathfrak{m})_{\mathbb{Q}}\rightarrow W(B/\mathfrak{m}B)_{\mathbb{Q}}$ is surjective. On the other hand,  $W(A/\mathfrak{m})_{\mathbb{Q}}$ is a field and hence
$W(A/\mathfrak{m})_{\mathbb{Q}}$ is a field and hence  $\unicode[STIX]{x1D713}$ is an isomorphism. In particular,
$\unicode[STIX]{x1D713}$ is an isomorphism. In particular,  $f^{-1}(\mathfrak{m})$ consists of one point
$f^{-1}(\mathfrak{m})$ consists of one point  $\mathfrak{n}$. By
$\mathfrak{n}$. By  $W(A/\mathfrak{m})_{\mathbb{Q}}\simeq W(B/\mathfrak{m}B)_{\mathbb{Q}}$ and
$W(A/\mathfrak{m})_{\mathbb{Q}}\simeq W(B/\mathfrak{m}B)_{\mathbb{Q}}$ and  $W(B/\mathfrak{n})_{\mathbb{Q}}\simeq W(B/\mathfrak{m}B)_{\mathbb{Q}}$, we have
$W(B/\mathfrak{n})_{\mathbb{Q}}\simeq W(B/\mathfrak{m}B)_{\mathbb{Q}}$, we have  $W(A/\mathfrak{m})_{\mathbb{Q}}\simeq W(B/\mathfrak{n})_{\mathbb{Q}}$. Hence, the finite extension
$W(A/\mathfrak{m})_{\mathbb{Q}}\simeq W(B/\mathfrak{n})_{\mathbb{Q}}$. Hence, the finite extension  $W(A/\mathfrak{m}){\hookrightarrow}W(B/\mathfrak{n})$ of discrete valuation rings is also an isomorphism. Taking modulo
$W(A/\mathfrak{m}){\hookrightarrow}W(B/\mathfrak{n})$ of discrete valuation rings is also an isomorphism. Taking modulo  $p$ reduction, we have that
$p$ reduction, we have that  $A/\mathfrak{m}\rightarrow B/\mathfrak{n}$ is an isomorphism. Thus, (i) holds.◻
$A/\mathfrak{m}\rightarrow B/\mathfrak{n}$ is an isomorphism. Thus, (i) holds.◻
We often use the following exact sequences, which we call the Mayer–Vietoris exact sequences.
Lemma 2.18. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$. Let
$p>0$. Let  $V$ be a scheme of finite type over
$V$ be a scheme of finite type over  $k$. Let
$k$. Let  $X,X_{1}$ and
$X,X_{1}$ and  $X_{2}$ be closed subschemes of
$X_{2}$ be closed subschemes of  $V$ such that the set-theoretic equation
$V$ such that the set-theoretic equation  $X=X_{1}\cup X_{2}$ holds. Let
$X=X_{1}\cup X_{2}$ holds. Let  $X_{1}\,\cap \,X_{2}$ be the scheme-theoretic intersection. Let
$X_{1}\,\cap \,X_{2}$ be the scheme-theoretic intersection. Let  $I_{X},I_{X_{1}},I_{X_{2}}$ and
$I_{X},I_{X_{1}},I_{X_{2}}$ and  $I_{X_{1}\cap X_{2}}$ be the corresponding coherent ideal sheaves on
$I_{X_{1}\cap X_{2}}$ be the corresponding coherent ideal sheaves on  $V$. Then there exist the exact sequences:
$V$. Then there exist the exact sequences:
(i)
 $0\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X_{1},\mathbb{Q}}\oplus W{\mathcal{O}}_{X_{2},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X_{1}\cap X_{2},\mathbb{Q}}\rightarrow 0$; and
$0\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X_{1},\mathbb{Q}}\oplus W{\mathcal{O}}_{X_{2},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X_{1}\cap X_{2},\mathbb{Q}}\rightarrow 0$; and(ii)
 $0\rightarrow WI_{X,\mathbb{Q}}\rightarrow WI_{X_{1},\mathbb{Q}}\oplus WI_{X_{2},\mathbb{Q}}\rightarrow WI_{X_{1}\cap X_{2},\mathbb{Q}}\rightarrow 0$.
$0\rightarrow WI_{X,\mathbb{Q}}\rightarrow WI_{X_{1},\mathbb{Q}}\oplus WI_{X_{2},\mathbb{Q}}\rightarrow WI_{X_{1}\cap X_{2},\mathbb{Q}}\rightarrow 0$.
Proof. By using Remark 2.2 and the fact that the functor  $(-)_{\mathbb{Q}}$ is exact, we obtain the exact sequence (i) by the same argument as in [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 2.2]. The exact sequence (ii) is obtained by (i) and the snake lemma.◻
$(-)_{\mathbb{Q}}$ is exact, we obtain the exact sequence (i) by the same argument as in [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 2.2]. The exact sequence (ii) is obtained by (i) and the snake lemma.◻
Lemma 2.19. Let  $k\subset k^{\prime }$ be an extension of perfect fields of characteristic
$k\subset k^{\prime }$ be an extension of perfect fields of characteristic  $p>0$. Let
$p>0$. Let  $X$ be a proper scheme over
$X$ be a proper scheme over  $k$ and set
$k$ and set  $X^{\prime }:=X\times _{k}k^{\prime }$. Then the induced
$X^{\prime }:=X\times _{k}k^{\prime }$. Then the induced  $W(k^{\prime })_{\mathbb{Q}}$-linear map
$W(k^{\prime })_{\mathbb{Q}}$-linear map
 $$\begin{eqnarray}\displaystyle H^{0}(X,W{\mathcal{O}}_{X,\mathbb{Q}})\otimes _{W(k)_{\mathbb{Q}}}W(k^{\prime })_{\mathbb{Q}}\rightarrow H^{0}(X^{\prime },W{\mathcal{O}}_{X^{\prime },\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{0}(X,W{\mathcal{O}}_{X,\mathbb{Q}})\otimes _{W(k)_{\mathbb{Q}}}W(k^{\prime })_{\mathbb{Q}}\rightarrow H^{0}(X^{\prime },W{\mathcal{O}}_{X^{\prime },\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$is bijective.
Proof. Taking the Stein factorisation of the structure morphism  $X\rightarrow \operatorname{Spec}\,k$, we may assume that
$X\rightarrow \operatorname{Spec}\,k$, we may assume that  $X$ is of dimension zero. Replacing
$X$ is of dimension zero. Replacing  $X$ by a connected component, we may assume that
$X$ by a connected component, we may assume that  $X=\operatorname{Spec}\,L$, where
$X=\operatorname{Spec}\,L$, where  $L$ is a finite extension of
$L$ is a finite extension of  $k$. Then the assertion is clear.◻
$k$. Then the assertion is clear.◻
To prove Proposition 2.23, we first show the following weaker statement.
Lemma 2.20. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$ and let
$p>0$ and let  $X$ be a one-dimensional smooth projective scheme over
$X$ be a one-dimensional smooth projective scheme over  $k$. Then the following are equivalent:
$k$. Then the following are equivalent:
(i)
 $H^{1}(X,{\mathcal{O}}_{X})=0$;
$H^{1}(X,{\mathcal{O}}_{X})=0$;(ii)
 $H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for some
$H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for some  $n\in \mathbb{Z}_{{>}0}$;
$n\in \mathbb{Z}_{{>}0}$;(iii)
 $H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for any
$H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for any  $n\in \mathbb{Z}_{{>}0}$;
$n\in \mathbb{Z}_{{>}0}$;(iv)
 $H^{1}(X,W{\mathcal{O}}_{X})=0$;
$H^{1}(X,W{\mathcal{O}}_{X})=0$;(v)
 $H^{1}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$.
$H^{1}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$.
Proof. Clearly, we may assume that  $X$ is connected. By the exact sequence
$X$ is connected. By the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow W_{n}{\mathcal{O}}_{X}\xrightarrow[{}]{V}W_{n+1}{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow W_{n}{\mathcal{O}}_{X}\xrightarrow[{}]{V}W_{n+1}{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ and the fact that  $X$ is one dimensional, it holds that (i), (ii) and (iii) are equivalent. By [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.19], (iii) implies (iv). Moreover, by the exact sequence
$X$ is one dimensional, it holds that (i), (ii) and (iii) are equivalent. By [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.19], (iii) implies (iv). Moreover, by the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{X}\xrightarrow[{}]{V}W{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{X}\xrightarrow[{}]{V}W{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ and the fact that  $X$ is one dimensional, (iv) implies (i).
$X$ is one dimensional, (iv) implies (i).
The equivalence between (iv) and (v) follows from the fact that  $H^{1}(X,W{\mathcal{O}}_{X})$ is a free
$H^{1}(X,W{\mathcal{O}}_{X})$ is a free  $W(k)$-module [Reference IllusieIll79, ch. II, Proposition 2.19].◻
$W(k)$-module [Reference IllusieIll79, ch. II, Proposition 2.19].◻
Lemma 2.21. Let  $k\subset k^{\prime }$ be an extension of perfect fields of characteristic
$k\subset k^{\prime }$ be an extension of perfect fields of characteristic  $p>0$. Let
$p>0$. Let  $X$ be a proper one-dimensional scheme over
$X$ be a proper one-dimensional scheme over  $k$. Then the following are equivalent:
$k$. Then the following are equivalent:
(i)
 $H^{1}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$;
$H^{1}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$;(ii)
 $H^{1}(X\times _{k}k^{\prime },W{\mathcal{O}}_{X\times _{k}k^{\prime },\mathbb{Q}})=0$.
$H^{1}(X\times _{k}k^{\prime },W{\mathcal{O}}_{X\times _{k}k^{\prime },\mathbb{Q}})=0$.
Proof. For simplicity, we denote  $K=W(k)_{\mathbb{Q}}$,
$K=W(k)_{\mathbb{Q}}$,  $K^{\prime }=W(k^{\prime })_{\mathbb{Q}}$ and
$K^{\prime }=W(k^{\prime })_{\mathbb{Q}}$ and  $Y^{\prime }=Y\times _{k}k^{\prime }$ for a
$Y^{\prime }=Y\times _{k}k^{\prime }$ for a  $k$-scheme
$k$-scheme  $Y$. We may assume that
$Y$. We may assume that  $X$ is reduced. Let
$X$ is reduced. Let
 $$\begin{eqnarray}\displaystyle X^{N}\rightarrow X & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X^{N}\rightarrow X & & \displaystyle \nonumber\end{eqnarray}$$ be the normalisation of  $X$. Thanks to Lemma 2.20, if one of (i) and (ii) holds, then it follows that
$X$. Thanks to Lemma 2.20, if one of (i) and (ii) holds, then it follows that
 $$\begin{eqnarray}\displaystyle H^{1}(X^{N},W{\mathcal{O}}_{X,\mathbb{Q}})=H^{1}(X^{\prime N},W{\mathcal{O}}_{X^{\prime N},\mathbb{Q}})=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{1}(X^{N},W{\mathcal{O}}_{X,\mathbb{Q}})=H^{1}(X^{\prime N},W{\mathcal{O}}_{X^{\prime N},\mathbb{Q}})=0. & & \displaystyle \nonumber\end{eqnarray}$$ For the conductor subschemes  $C$ and
$C$ and  $D$ of
$D$ of  $X$ and
$X$ and  $X^{N}$, respectively, we have a commutative diagram with exact horizontal sequences:
$X^{N}$, respectively, we have a commutative diagram with exact horizontal sequences:

where  $(-)_{K^{\prime }}$ denotes the tensor product
$(-)_{K^{\prime }}$ denotes the tensor product  $(-)\otimes _{K}K^{\prime }$. As both
$(-)\otimes _{K}K^{\prime }$. As both  $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and  $\unicode[STIX]{x1D6FD}$ are isomorphisms by Lemma 2.19, so is
$\unicode[STIX]{x1D6FD}$ are isomorphisms by Lemma 2.19, so is  $\unicode[STIX]{x1D6FE}$ by the five lemma, as desired.◻
$\unicode[STIX]{x1D6FE}$ by the five lemma, as desired.◻
Proposition 2.22. Let  $k\subset k^{\prime }$ be an extension of perfect fields of characteristic
$k\subset k^{\prime }$ be an extension of perfect fields of characteristic  $p>0$. Let
$p>0$. Let  $X$ be a normal surface over
$X$ be a normal surface over  $k$. Then the following are equivalent:
$k$. Then the following are equivalent:
(i)
 $X$ has
$X$ has  $W{\mathcal{O}}$-rational singularities;
$W{\mathcal{O}}$-rational singularities;(ii)
 $X\times _{k}k^{\prime }$ has
$X\times _{k}k^{\prime }$ has  $W{\mathcal{O}}$-rational singularities.
$W{\mathcal{O}}$-rational singularities.
Proof. We may assume that  $Q$ is a unique non-regular point of
$Q$ is a unique non-regular point of  $X$. Let
$X$. Let  $f:Y\rightarrow X$ be a resolution of singularities such that
$f:Y\rightarrow X$ be a resolution of singularities such that  $f(\operatorname{Ex}(f))=Q$. For
$f(\operatorname{Ex}(f))=Q$. For  $E:=\operatorname{Ex}(f)$, we have the exact sequence
$E:=\operatorname{Ex}(f)$, we have the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{E,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{Y,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{E,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{E,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{Y,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{E,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$ Thanks to the vanishing of  $R^{i}f_{\ast }(WI_{E,\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(WI_{E,\mathbb{Q}})=0$ for  $i>0$ [Reference Berthelot, Bloch and EsnaultBBE07, Theorem 2.4], it holds that
$i>0$ [Reference Berthelot, Bloch and EsnaultBBE07, Theorem 2.4], it holds that
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(W{\mathcal{O}}_{Y,\mathbb{Q}})\simeq H^{i}(E,W{\mathcal{O}}_{E,\mathbb{Q}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(W{\mathcal{O}}_{Y,\mathbb{Q}})\simeq H^{i}(E,W{\mathcal{O}}_{E,\mathbb{Q}}). & & \displaystyle \nonumber\end{eqnarray}$$Therefore, it follows from Lemma 2.21 that (i) and (ii) are equivalent. ◻
Proposition 2.23. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$ and let
$p>0$ and let  $X$ be a reduced projective scheme over
$X$ be a reduced projective scheme over  $k$ such that:
$k$ such that:
(a) any irreducible component of
 $X$ is one dimensional; and
$X$ is one dimensional; and(b) any non-regular point
 $x$ of
$x$ of  $X$ is an ordinary double point.
$X$ is an ordinary double point.
Then the following are equivalent:
(i)
 $H^{1}(X,{\mathcal{O}}_{X})=0$;
$H^{1}(X,{\mathcal{O}}_{X})=0$;(ii)
 $H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for some
$H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for some  $n\in \mathbb{Z}_{{>}0}$;
$n\in \mathbb{Z}_{{>}0}$;(iii)
 $H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for any
$H^{1}(X,W_{n}{\mathcal{O}}_{X})=0$ for any  $n\in \mathbb{Z}_{{>}0}$;
$n\in \mathbb{Z}_{{>}0}$;(iv)
 $H^{1}(X,W{\mathcal{O}}_{X})=0$;
$H^{1}(X,W{\mathcal{O}}_{X})=0$;(v)
 $H^{1}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$;
$H^{1}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$;(vi) any connected component of
 $X\times _{k}\overline{k}$ is a tree of smooth rational curves.
$X\times _{k}\overline{k}$ is a tree of smooth rational curves.
Proof. We may assume that  $X$ is connected. Moreover, replacing
$X$ is connected. Moreover, replacing  $k$ by
$k$ by  $k^{\prime }$ for the Stein factorisation
$k^{\prime }$ for the Stein factorisation  $X\rightarrow \operatorname{Spec}\,k^{\prime }\rightarrow \operatorname{Spec}\,k$, we may assume that
$X\rightarrow \operatorname{Spec}\,k^{\prime }\rightarrow \operatorname{Spec}\,k$, we may assume that  $X$ is geometrically connected.
$X$ is geometrically connected.
We now show that the assertions (i), (ii), (iii) and (iv) are equivalent. By the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow W_{n}{\mathcal{O}}_{X}\xrightarrow[{}]{V}W_{n+1}{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow W_{n}{\mathcal{O}}_{X}\xrightarrow[{}]{V}W_{n+1}{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ and the fact that  $X$ is one dimensional, it holds that (i), (ii) and (iii) are equivalent. We have that (iii) implies (iv) by [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.19]. Moreover, by the exact sequence
$X$ is one dimensional, it holds that (i), (ii) and (iii) are equivalent. We have that (iii) implies (iv) by [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.19]. Moreover, by the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{X}\xrightarrow[{}]{V}W{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{X}\xrightarrow[{}]{V}W{\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{X}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ and the fact that  $X$ is one dimensional, (iv) implies (i). Thus, (i), (ii), (iii) and (iv) are equivalent.
$X$ is one dimensional, (iv) implies (i). Thus, (i), (ii), (iii) and (iv) are equivalent.
Thanks to [Reference KollárKol96, ch. II, Lemma 7.5], it holds that (vi) implies (i). Further, (iv) clearly implies (v). Thus, it suffices to show that (v) implies (vi). Lemma 2.21 allows us to replace  $X\rightarrow \operatorname{Spec}\,k$ by the base change
$X\rightarrow \operatorname{Spec}\,k$ by the base change  $X\times _{k}\overline{k}\rightarrow \operatorname{Spec}\,\overline{k}$. Then it follows from [Reference Chatzistamatiou and RüllingCR12, the second last paragraph of § 4.6] that (v) implies (vi), as desired.◻
$X\times _{k}\overline{k}\rightarrow \operatorname{Spec}\,\overline{k}$. Then it follows from [Reference Chatzistamatiou and RüllingCR12, the second last paragraph of § 4.6] that (v) implies (vi), as desired.◻
2.5 Geometric rationality of del Pezzo surfaces over imperfect fields
In this subsection, we prove Proposition 2.26. To this end, we start with the following lemma.
Lemma 2.24. Let  $k$ be a separably closed field of characteristic
$k$ be a separably closed field of characteristic  $p>0$ which is not algebraic over a finite field. Let
$p>0$ which is not algebraic over a finite field. Let  $X$ be a projective normal
$X$ be a projective normal  $\mathbb{Q}$-factorial surface over
$\mathbb{Q}$-factorial surface over  $k$ with
$k$ with  $k=H^{0}(X,{\mathcal{O}}_{X})$. If there is an
$k=H^{0}(X,{\mathcal{O}}_{X})$. If there is an  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}$ such that
$\unicode[STIX]{x1D6E5}$ such that  $0\leqslant \unicode[STIX]{x1D6E5}<1$ and
$0\leqslant \unicode[STIX]{x1D6E5}<1$ and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big, then
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big, then  $(X\times _{k}\overline{k})_{\operatorname{red}}$ is a rational surface.
$(X\times _{k}\overline{k})_{\operatorname{red}}$ is a rational surface.
Proof. Replacing  $\unicode[STIX]{x1D6E5}$, we may assume that
$\unicode[STIX]{x1D6E5}$, we may assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample. If
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample. If  $X\rightarrow X^{\prime }$ is a birational
$X\rightarrow X^{\prime }$ is a birational  $k$-morphism of projective normal varieties with
$k$-morphism of projective normal varieties with  $k=H^{0}(X,{\mathcal{O}}_{X})=H^{0}(X^{\prime },{\mathcal{O}}_{X^{\prime }})$, then also
$k=H^{0}(X,{\mathcal{O}}_{X})=H^{0}(X^{\prime },{\mathcal{O}}_{X^{\prime }})$, then also  $(X\times _{k}\overline{k})_{\operatorname{red}}\rightarrow (X^{\prime }\times _{k}\overline{k})_{\operatorname{red}}$ is birational. Thus, we may replace
$(X\times _{k}\overline{k})_{\operatorname{red}}\rightarrow (X^{\prime }\times _{k}\overline{k})_{\operatorname{red}}$ is birational. Thus, we may replace  $(X,\unicode[STIX]{x1D6E5})$ by the end result of a
$(X,\unicode[STIX]{x1D6E5})$ by the end result of a  $(K_{X}+\unicode[STIX]{x1D6E5})$-MMP [Reference TanakaTan18b, Theorem 1.1]. Hence, we may assume that one of the following conditions holds:
$(K_{X}+\unicode[STIX]{x1D6E5})$-MMP [Reference TanakaTan18b, Theorem 1.1]. Hence, we may assume that one of the following conditions holds:
(a)
 $\unicode[STIX]{x1D70C}(X)=1$;
$\unicode[STIX]{x1D70C}(X)=1$;(b) there is a
 $(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space
$(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space  $\unicode[STIX]{x1D70B}_{1}:X\rightarrow B_{1}$ onto a regular projective curve
$\unicode[STIX]{x1D70B}_{1}:X\rightarrow B_{1}$ onto a regular projective curve  $B_{1}$ with
$B_{1}$ with  $(\unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{B_{1}}$.
$(\unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{B_{1}}$.
In what follows, we denote by  $Y$ the normalisation of
$Y$ the normalisation of  $(X\times _{k}\overline{k})_{\operatorname{red}}$ and denote by
$(X\times _{k}\overline{k})_{\operatorname{red}}$ and denote by  $f:Y\rightarrow X$ the composite morphism. By applying [Reference TanakaTan18a, Theorem 1.1] to the regular locus of
$f:Y\rightarrow X$ the composite morphism. By applying [Reference TanakaTan18a, Theorem 1.1] to the regular locus of  $X$, we can write
$X$, we can write
 $$\begin{eqnarray}\displaystyle K_{Y}+D=f^{\ast }K_{X} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{Y}+D=f^{\ast }K_{X} & & \displaystyle \nonumber\end{eqnarray}$$ for some effective  $\mathbb{Z}$-divisor
$\mathbb{Z}$-divisor  $D$.
$D$.
Suppose (a). Then  $Y$ is a projective normal
$Y$ is a projective normal  $\mathbb{Q}$-factorial surface such that
$\mathbb{Q}$-factorial surface such that  $\unicode[STIX]{x1D70C}(Y)=1$ [Reference TanakaTan18a, Proposition 2.4(2)]. Since
$\unicode[STIX]{x1D70C}(Y)=1$ [Reference TanakaTan18a, Proposition 2.4(2)]. Since  $-K_{Y}$ is ample,
$-K_{Y}$ is ample,  $Y$ is a ruled surface. Assume that
$Y$ is a ruled surface. Assume that  $Y$ is not rational; let us derive a contradiction. Let
$Y$ is not rational; let us derive a contradiction. Let  $\unicode[STIX]{x1D707}:Z\rightarrow Y$ be the minimal resolution of
$\unicode[STIX]{x1D707}:Z\rightarrow Y$ be the minimal resolution of  $Y$. Since
$Y$. Since  $Z$ is an irrational ruled surface, there is a projective morphism
$Z$ is an irrational ruled surface, there is a projective morphism  $\unicode[STIX]{x1D70B}:Z\rightarrow B$ onto a smooth projective irrational curve whose general fibres are
$\unicode[STIX]{x1D70B}:Z\rightarrow B$ onto a smooth projective irrational curve whose general fibres are  $\mathbb{P}^{1}$. Since
$\mathbb{P}^{1}$. Since  $\overline{k}\neq \overline{\mathbb{F}}_{p}$, it follows from [Reference TanakaTan14, Theorem 3.20] that
$\overline{k}\neq \overline{\mathbb{F}}_{p}$, it follows from [Reference TanakaTan14, Theorem 3.20] that  $\unicode[STIX]{x1D70B}$ factors through
$\unicode[STIX]{x1D70B}$ factors through  $\unicode[STIX]{x1D707}$:
$\unicode[STIX]{x1D707}$:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:Z\xrightarrow[{}]{\unicode[STIX]{x1D707}}Y\rightarrow B. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:Z\xrightarrow[{}]{\unicode[STIX]{x1D707}}Y\rightarrow B. & & \displaystyle \nonumber\end{eqnarray}$$ This is a contradiction to  $\unicode[STIX]{x1D70C}(Y)=1$. Thus, we are done for the case (a).
$\unicode[STIX]{x1D70C}(Y)=1$. Thus, we are done for the case (a).
Suppose (b). Since  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, there exists an extremal ray
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is ample, there exists an extremal ray  $R$ of
$R$ of  $\overline{\text{NE}}(X)$ not corresponding to
$\overline{\text{NE}}(X)$ not corresponding to  $\unicode[STIX]{x1D70B}_{1}$. By [Reference TanakaTan18b, Theorem 4.4], the extremal ray
$\unicode[STIX]{x1D70B}_{1}$. By [Reference TanakaTan18b, Theorem 4.4], the extremal ray  $R$ induces either a birational morphism or another
$R$ induces either a birational morphism or another  $(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space
$(K_{X}+\unicode[STIX]{x1D6E5})$-Mori fibre space  $X\rightarrow B_{2}$ onto a curve
$X\rightarrow B_{2}$ onto a curve  $B_{2}$. If the former case occurs, then the problem is reduced to the case (a). Therefore, we may assume that there exist two Mori fibre space structures
$B_{2}$. If the former case occurs, then the problem is reduced to the case (a). Therefore, we may assume that there exist two Mori fibre space structures  $\unicode[STIX]{x1D70B}_{1}:X\rightarrow B_{1}$ and
$\unicode[STIX]{x1D70B}_{1}:X\rightarrow B_{1}$ and  $\unicode[STIX]{x1D70B}_{2}:X\rightarrow B_{2}$ onto curves
$\unicode[STIX]{x1D70B}_{2}:X\rightarrow B_{2}$ onto curves  $B_{1}$ and
$B_{1}$ and  $B_{2}$. In particular, any fibre of
$B_{2}$. In particular, any fibre of  $\unicode[STIX]{x1D70B}_{i}$ dominates
$\unicode[STIX]{x1D70B}_{i}$ dominates  $B_{3-i}$. Let
$B_{3-i}$. Let  $\unicode[STIX]{x1D70B}_{i}^{\prime }:Y\rightarrow B_{i}^{\prime }$ be the Stein factorisation of the composite morphism:
$\unicode[STIX]{x1D70B}_{i}^{\prime }:Y\rightarrow B_{i}^{\prime }$ be the Stein factorisation of the composite morphism:
 $$\begin{eqnarray}\displaystyle Y\rightarrow X\times _{k}\overline{k}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}\times _{k}\overline{k}}B_{i}\times _{k}\overline{k}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y\rightarrow X\times _{k}\overline{k}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{i}\times _{k}\overline{k}}B_{i}\times _{k}\overline{k}. & & \displaystyle \nonumber\end{eqnarray}$$ Then any fibre of  $\unicode[STIX]{x1D70B}_{i}^{\prime }$ dominates
$\unicode[STIX]{x1D70B}_{i}^{\prime }$ dominates  $B_{3-i}^{\prime }$. Since
$B_{3-i}^{\prime }$. Since  $-K_{Y}$ is big, a general fibre of each
$-K_{Y}$ is big, a general fibre of each  $\unicode[STIX]{x1D70B}_{i}^{\prime }$ is isomorphic to
$\unicode[STIX]{x1D70B}_{i}^{\prime }$ is isomorphic to  $\mathbb{P}^{1}$. In particular,
$\mathbb{P}^{1}$. In particular,  $B_{1}^{\prime }\simeq \mathbb{P}^{1}$ and
$B_{1}^{\prime }\simeq \mathbb{P}^{1}$ and  $Y$ is rational.◻
$Y$ is rational.◻
Remark 2.25. The statement of Lemma 2.24 does not hold if we drop the assumption on the base field  $k$. Indeed, if
$k$. Indeed, if  $k=\overline{\mathbb{F}}_{p}$, then any normal surface is
$k=\overline{\mathbb{F}}_{p}$, then any normal surface is  $\mathbb{Q}$-factorial (e.g. see [Reference TanakaTan14, Theorem 4.5]). Thus, the cone
$\mathbb{Q}$-factorial (e.g. see [Reference TanakaTan14, Theorem 4.5]). Thus, the cone  $X$ over an elliptic curve over
$X$ over an elliptic curve over  $\overline{\mathbb{F}}_{p}$ is
$\overline{\mathbb{F}}_{p}$ is  $\mathbb{Q}$-factorial and
$\mathbb{Q}$-factorial and  $-K_{X}$ is ample.
$-K_{X}$ is ample.
Proposition 2.26. Let  $(X,\unicode[STIX]{x1D6E5})$ be a projective two-dimensional klt pair over a field
$(X,\unicode[STIX]{x1D6E5})$ be a projective two-dimensional klt pair over a field  $k$ of characteristic
$k$ of characteristic  $p>0$ such that
$p>0$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big. Assume that
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big. Assume that  $k=H^{0}(X,{\mathcal{O}}_{X})$. Then
$k=H^{0}(X,{\mathcal{O}}_{X})$. Then  $(X\times _{k}\overline{k})_{\operatorname{red}}$ is a rational surface. In particular,
$(X\times _{k}\overline{k})_{\operatorname{red}}$ is a rational surface. In particular,  $X$ is rationally connected over
$X$ is rationally connected over  $k$.
$k$.
Proof. We may assume that  $k$ is separably closed. Since the assertion is well known if
$k$ is separably closed. Since the assertion is well known if  $k$ is an algebraically closed field (cf. [Reference TanakaTan15, Fact 3.4 and Theorem 3.5]), the problem is reduced to the case when
$k$ is an algebraically closed field (cf. [Reference TanakaTan15, Fact 3.4 and Theorem 3.5]), the problem is reduced to the case when  $k$ is an imperfect field. In particular,
$k$ is an imperfect field. In particular,  $k$ is not algebraic over a finite field. As
$k$ is not algebraic over a finite field. As  $X$ is
$X$ is  $\mathbb{Q}$-factorial [Reference TanakaTan18b, Corollary 4.11], the assertion follows from Lemma 2.24.◻
$\mathbb{Q}$-factorial [Reference TanakaTan18b, Corollary 4.11], the assertion follows from Lemma 2.24.◻
3  $W{\mathcal{O}}$-vanishing for log Fano contractions
$W{\mathcal{O}}$-vanishing for log Fano contractions
In this section, we prove a vanishing theorem for log Fano contractions (Theorem 3.11). We shall divide the proof into cases depending on the dimension of the base scheme  $Z$. The cases
$Z$. The cases  $\dim Z=1$ and
$\dim Z=1$ and  $\dim Z=2$ are treated in § 3.1 and § 3.2, respectively. The remaining cases
$\dim Z=2$ are treated in § 3.1 and § 3.2, respectively. The remaining cases  $\dim Z=0$ and
$\dim Z=0$ and  $\dim Z=3$ have been already settled in [Reference Gongyo, Nakamura and TanakaGNT19] (cf. the proof of Theorem 3.11).
$\dim Z=3$ have been already settled in [Reference Gongyo, Nakamura and TanakaGNT19] (cf. the proof of Theorem 3.11).
Before starting the case study, we summarise some results used repeatedly in the proof of Theorem 3.11.
Theorem 3.1. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Then the following hold.
$p>5$. Then the following hold.
(i) If
 $(X,\unicode[STIX]{x1D6E5})$ is a three-dimensional klt pair over
$(X,\unicode[STIX]{x1D6E5})$ is a three-dimensional klt pair over  $k$, then
$k$, then  $X$ has
$X$ has  $W{\mathcal{O}}$-rational singularities.
$W{\mathcal{O}}$-rational singularities.(ii) If
 $X$ is a three-dimensional projective variety of Fano type over
$X$ is a three-dimensional projective variety of Fano type over  $k$, then
$k$, then  $H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for
$H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Proof. When  $\unicode[STIX]{x1D6E5}$ is a
$\unicode[STIX]{x1D6E5}$ is a  $\mathbb{Q}$-divisor, both (i) and (ii) follow from [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 1.4] and [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 1.3], respectively. Thanks to [Reference FujinoFuj17, Lemma 4.6.1], the general case is reduced to this case.◻
$\mathbb{Q}$-divisor, both (i) and (ii) follow from [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 1.4] and [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 1.3], respectively. Thanks to [Reference FujinoFuj17, Lemma 4.6.1], the general case is reduced to this case.◻
Theorem 3.2. Let  $f:X\rightarrow Y$ be a projective morphism between integral schemes with
$f:X\rightarrow Y$ be a projective morphism between integral schemes with  $W{\mathcal{O}}$-rational singularities. Suppose that
$W{\mathcal{O}}$-rational singularities. Suppose that  $Y$ is normal and that the generic fibre
$Y$ is normal and that the generic fibre  $X_{K(Y)}$ of
$X_{K(Y)}$ of  $f$ is smooth and rationally chain connected. Then
$f$ is smooth and rationally chain connected. Then  $R^{i}f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}=0$ holds for
$R^{i}f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}=0$ holds for  $i>0$.
$i>0$.
Proof. This is a special case of [Reference Chatzistamatiou and RüllingCR12, Theorem 4.8.1]. ◻
Lemma 3.3. Let  $k$ be a field of characteristic
$k$ be a field of characteristic  $p>0$. Let
$p>0$. Let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism of normal
$k$-morphism of normal  $k$-varieties such that
$k$-varieties such that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. Then there exists a commutative diagram
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. Then there exists a commutative diagram

of projective  $k$-morphisms of normal
$k$-morphisms of normal  $k$-varieties that satisfies the following properties.
$k$-varieties that satisfies the following properties.
(i) Both
 $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and  $\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms.
$\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms.(ii)
 $f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}={\mathcal{O}}_{Y^{\prime }}$.
$f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}={\mathcal{O}}_{Y^{\prime }}$.(iii) The generic fibre
 $X_{K(Y^{\prime })}^{\prime }$ of
$X_{K(Y^{\prime })}^{\prime }$ of  $f^{\prime }$ is geometrically normal over
$f^{\prime }$ is geometrically normal over  $K(Y^{\prime })$.
$K(Y^{\prime })$.(iv) The induced morphism
 $X_{K(Y^{\prime })}^{\prime }\rightarrow (X\times _{Y}K(Y^{\prime }))_{\operatorname{red}}$ is a finite birational morphism. In particular, this morphism coincides with the normalisation of
$X_{K(Y^{\prime })}^{\prime }\rightarrow (X\times _{Y}K(Y^{\prime }))_{\operatorname{red}}$ is a finite birational morphism. In particular, this morphism coincides with the normalisation of  $(X\times _{Y}K(Y^{\prime }))_{\operatorname{red}}$.
$(X\times _{Y}K(Y^{\prime }))_{\operatorname{red}}$.
Proof. We set  $K:=K(Y)$. Let
$K:=K(Y)$. Let  $\unicode[STIX]{x1D708}_{0}:X_{0}^{\prime }\rightarrow (X\times _{Y}K^{1/p^{\infty }})_{\operatorname{red}}$ be the normalisation of
$\unicode[STIX]{x1D708}_{0}:X_{0}^{\prime }\rightarrow (X\times _{Y}K^{1/p^{\infty }})_{\operatorname{red}}$ be the normalisation of  $(X\times _{Y}K^{1/p^{\infty }})_{\operatorname{red}}$. Since
$(X\times _{Y}K^{1/p^{\infty }})_{\operatorname{red}}$. Since  $\unicode[STIX]{x1D708}_{0}$ is a finite universal homeomorphism by [Reference TanakaTan18a, Lemma 2.2], we have that
$\unicode[STIX]{x1D708}_{0}$ is a finite universal homeomorphism by [Reference TanakaTan18a, Lemma 2.2], we have that  $X_{0}^{\prime }$ is geometrically connected and projective over a perfect field
$X_{0}^{\prime }$ is geometrically connected and projective over a perfect field  $K^{1/p^{\infty }}$ and hence
$K^{1/p^{\infty }}$ and hence  $K^{1/p^{\infty }}=H^{0}(X_{0}^{\prime },{\mathcal{O}}_{X_{0}^{\prime }})$. There exist an intermediate field
$K^{1/p^{\infty }}=H^{0}(X_{0}^{\prime },{\mathcal{O}}_{X_{0}^{\prime }})$. There exist an intermediate field  $L$ between
$L$ between  $K$ and
$K$ and  $K^{1/p^{\infty }}$ satisfying
$K^{1/p^{\infty }}$ satisfying  $[L:K]<\infty$ and a projective normal
$[L:K]<\infty$ and a projective normal  $L$-variety
$L$-variety  $X_{1}^{\prime }$ such that
$X_{1}^{\prime }$ such that  $X_{1}^{\prime }\times _{L}K^{1/p^{\infty }}=X_{0}^{\prime }$ with the following commutative diagram, where
$X_{1}^{\prime }\times _{L}K^{1/p^{\infty }}=X_{0}^{\prime }$ with the following commutative diagram, where  $\unicode[STIX]{x1D708}_{1}$ is birational.
$\unicode[STIX]{x1D708}_{1}$ is birational.

In particular, it follows that  $L=H^{0}(X_{1}^{\prime },{\mathcal{O}}_{X_{1}^{\prime }})$ and
$L=H^{0}(X_{1}^{\prime },{\mathcal{O}}_{X_{1}^{\prime }})$ and  $\unicode[STIX]{x1D708}_{1}$ is a finite universal homeomorphism. Since
$\unicode[STIX]{x1D708}_{1}$ is a finite universal homeomorphism. Since  $\unicode[STIX]{x1D708}_{1}$ is a finite birational morphism and
$\unicode[STIX]{x1D708}_{1}$ is a finite birational morphism and  $X_{1}^{\prime }$ is normal,
$X_{1}^{\prime }$ is normal,  $\unicode[STIX]{x1D708}_{1}$ is nothing but the normalisation of
$\unicode[STIX]{x1D708}_{1}$ is nothing but the normalisation of  $(X\times _{Y}L)_{\operatorname{red}}$. Furthermore,
$(X\times _{Y}L)_{\operatorname{red}}$. Furthermore,  $X_{1}^{\prime }$ is geometrically normal, since
$X_{1}^{\prime }$ is geometrically normal, since  $X_{0}^{\prime }$ is normal and
$X_{0}^{\prime }$ is normal and  $K^{1/p^{\infty }}$ is perfect.
$K^{1/p^{\infty }}$ is perfect.
Let  $X^{\prime }$ (respectively
$X^{\prime }$ (respectively  $Y^{\prime }$) be the normalisation of
$Y^{\prime }$) be the normalisation of  $X$ (respectively
$X$ (respectively  $Y$) in
$Y$) in  $K(X_{1}^{\prime })$ (respectively
$K(X_{1}^{\prime })$ (respectively  $L$). Then we get the commutative diagram as in the statement and the properties (i), (iii) and (iv) follow from the construction.
$L$). Then we get the commutative diagram as in the statement and the properties (i), (iii) and (iv) follow from the construction.
Let us show (ii). Since  ${\mathcal{O}}_{Y^{\prime }}\rightarrow f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}$ is an isomorphism on some non-empty open subset of
${\mathcal{O}}_{Y^{\prime }}\rightarrow f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}$ is an isomorphism on some non-empty open subset of  $Y^{\prime }$, it holds that
$Y^{\prime }$, it holds that  $Y^{\prime \prime }\rightarrow Y^{\prime }$ is a finite birational morphism for the Stein factorisation
$Y^{\prime \prime }\rightarrow Y^{\prime }$ is a finite birational morphism for the Stein factorisation
 $$\begin{eqnarray}\displaystyle f^{\prime }:X^{\prime }\rightarrow Y^{\prime \prime }\rightarrow Y^{\prime } & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f^{\prime }:X^{\prime }\rightarrow Y^{\prime \prime }\rightarrow Y^{\prime } & & \displaystyle \nonumber\end{eqnarray}$$ of  $f^{\prime }$. As
$f^{\prime }$. As  $Y^{\prime }$ is normal, we have that
$Y^{\prime }$ is normal, we have that  $Y^{\prime \prime }\rightarrow Y^{\prime }$ is an isomorphism and hence (ii) holds.◻
$Y^{\prime \prime }\rightarrow Y^{\prime }$ is an isomorphism and hence (ii) holds.◻
3.1 Del Pezzo fibrations
In this subsection, we establish the  $W{\mathcal{O}}$-vanishing for del Pezzo fibrations (Proposition 3.6). A key result is the following.
$W{\mathcal{O}}$-vanishing for del Pezzo fibrations (Proposition 3.6). A key result is the following.
Lemma 3.4. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$. Let
$p>0$. Let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism such that:
$k$-morphism such that:
(i)
 $X$ is a normal threefold over
$X$ is a normal threefold over  $k$ that has
$k$ that has  $W{\mathcal{O}}$-rational singularities;
$W{\mathcal{O}}$-rational singularities;(ii)
 $Y$ is a smooth
$Y$ is a smooth  $k$-curve;
$k$-curve;(iii)
 $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$; and
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$; and(iv) the geometric generic fibre
 $X_{\overline{K(Y)}}$ of
$X_{\overline{K(Y)}}$ of  $f$ is a normal rational surface.
$f$ is a normal rational surface.
Then  $R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Proof. We divide the proof into two steps.
Step 1. The assertion of Lemma 3.4 holds if there exists a projective birational  $K(Y)$-morphism
$K(Y)$-morphism
 $$\begin{eqnarray}\displaystyle g_{0}:Z_{0}\rightarrow X_{K(Y)} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{0}:Z_{0}\rightarrow X_{K(Y)} & & \displaystyle \nonumber\end{eqnarray}$$ from a smooth projective  $K(Y)$-surface
$K(Y)$-surface  $Z_{0}$.
$Z_{0}$.
Proof of Step 1.
Killing the denominators of all the elements of  $K(Y)$ defining
$K(Y)$ defining  $g_{0}$, we can find a non-empty open subset
$g_{0}$, we can find a non-empty open subset  $Y^{\prime }$ of
$Y^{\prime }$ of  $Y$ and morphisms
$Y$ and morphisms
 $$\begin{eqnarray}\displaystyle h^{\prime }:Z^{\prime }\xrightarrow[{}]{g^{\prime }}X^{\prime }:=f^{-1}(Y^{\prime })\xrightarrow[{}]{f|_{f^{-1}(Y^{\prime })}}Y^{\prime } & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{\prime }:Z^{\prime }\xrightarrow[{}]{g^{\prime }}X^{\prime }:=f^{-1}(Y^{\prime })\xrightarrow[{}]{f|_{f^{-1}(Y^{\prime })}}Y^{\prime } & & \displaystyle \nonumber\end{eqnarray}$$ whose base changes by  $(-)\times _{Y^{\prime }}\operatorname{Spec}\,K(Y)$ are the same as
$(-)\times _{Y^{\prime }}\operatorname{Spec}\,K(Y)$ are the same as
 $$\begin{eqnarray}\displaystyle Z_{0}\xrightarrow[{}]{g_{0}}X_{K(Y)}\rightarrow \operatorname{Spec}\,K(Y). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{0}\xrightarrow[{}]{g_{0}}X_{K(Y)}\rightarrow \operatorname{Spec}\,K(Y). & & \displaystyle \nonumber\end{eqnarray}$$Furthermore, we may assume that:
∙
 $Z^{\prime }$ is an integral scheme;
$Z^{\prime }$ is an integral scheme;∙
 $g^{\prime }$ is a projective birational morphism; and
$g^{\prime }$ is a projective birational morphism; and∙ the composite morphism
 $h^{\prime }$ is smooth.
$h^{\prime }$ is smooth.
In particular,  $Z^{\prime }$ is a smooth threefold over
$Z^{\prime }$ is a smooth threefold over  $k$. Let
$k$. Let  $g:Z\rightarrow X$ be a smooth projective compactification of the induced morphism
$g:Z\rightarrow X$ be a smooth projective compactification of the induced morphism
 $$\begin{eqnarray}\displaystyle Z^{\prime }\xrightarrow[{}]{g_{1}}X^{\prime }=f^{-1}(Y^{\prime }){\hookrightarrow}X, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z^{\prime }\xrightarrow[{}]{g_{1}}X^{\prime }=f^{-1}(Y^{\prime }){\hookrightarrow}X, & & \displaystyle \nonumber\end{eqnarray}$$i.e. there are morphisms
 $$\begin{eqnarray}\displaystyle g^{\prime }:Z^{\prime }\xrightarrow[{}]{j}Z\xrightarrow[{}]{g}X & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g^{\prime }:Z^{\prime }\xrightarrow[{}]{j}Z\xrightarrow[{}]{g}X & & \displaystyle \nonumber\end{eqnarray}$$ such that  $j$ is an open immersion,
$j$ is an open immersion,  $g$ is projective and
$g$ is projective and  $Z$ is an integral scheme smooth over
$Z$ is an integral scheme smooth over  $k$. In particular,
$k$. In particular,  $Z$ is a smooth threefold over
$Z$ is a smooth threefold over  $k$ which is projective over
$k$ which is projective over  $X$ and hence over
$X$ and hence over  $Y$. We get the composite morphism
$Y$. We get the composite morphism
 $$\begin{eqnarray}\displaystyle h:Z\xrightarrow[{}]{g}X\xrightarrow[{}]{f}Y & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h:Z\xrightarrow[{}]{g}X\xrightarrow[{}]{f}Y & & \displaystyle \nonumber\end{eqnarray}$$ whose geometric generic fibre  $Z\times _{Y}\overline{K(Y)}$ satisfies the following isomorphisms:
$Z\times _{Y}\overline{K(Y)}$ satisfies the following isomorphisms:
 $$\begin{eqnarray}\displaystyle Z\times _{Y}\overline{K(Y)}\simeq Z^{\prime }\times _{Y^{\prime }}\overline{K(Y)}\simeq Z_{0}\times _{K(Y)}\overline{K(Y)}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z\times _{Y}\overline{K(Y)}\simeq Z^{\prime }\times _{Y^{\prime }}\overline{K(Y)}\simeq Z_{0}\times _{K(Y)}\overline{K(Y)}. & & \displaystyle \nonumber\end{eqnarray}$$ In particular,  $Z\times _{Y}\overline{K(Y)}$ is a smooth projective rational surface over
$Z\times _{Y}\overline{K(Y)}$ is a smooth projective rational surface over  $\overline{K(Y)}$.
$\overline{K(Y)}$.
Therefore, we have that
 $$\begin{eqnarray}\displaystyle Rf_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})\simeq Rf_{\ast }Rg_{\ast }(W{\mathcal{O}}_{Z,\mathbb{Q}})\simeq Rh_{\ast }(W{\mathcal{O}}_{Z,\mathbb{Q}})\simeq W{\mathcal{O}}_{Y,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})\simeq Rf_{\ast }Rg_{\ast }(W{\mathcal{O}}_{Z,\mathbb{Q}})\simeq Rh_{\ast }(W{\mathcal{O}}_{Z,\mathbb{Q}})\simeq W{\mathcal{O}}_{Y,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$where the first isomorphism follows from the assumption (i) and the third follows from Theorem 3.2. This completes the proof of Step 1. ◻
Step 2. The assertion of Lemma 3.4 holds without any additional assumptions.
Proof of Step 2.
Let  $K(Y)^{1/p^{\infty }}$ be the purely inseparable closure of
$K(Y)^{1/p^{\infty }}$ be the purely inseparable closure of  $K(Y)$ in the algebraic closure
$K(Y)$ in the algebraic closure  $\overline{K(Y)}$ of
$\overline{K(Y)}$ of  $K(Y)$. We fix a projective birational
$K(Y)$. We fix a projective birational  $K(Y)^{1/p^{\infty }}$-morphism
$K(Y)^{1/p^{\infty }}$-morphism
 $$\begin{eqnarray}\displaystyle g_{1}:Z_{1}\rightarrow X\times _{Y}K(Y)^{1/p^{\infty }} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{1}:Z_{1}\rightarrow X\times _{Y}K(Y)^{1/p^{\infty }} & & \displaystyle \nonumber\end{eqnarray}$$ from a regular  $K(Y)^{1/p^{\infty }}$-surface
$K(Y)^{1/p^{\infty }}$-surface  $Z_{1}$. Note that
$Z_{1}$. Note that  $Z_{1}$ is smooth over
$Z_{1}$ is smooth over  $K(Y)^{1/p^{\infty }}$, since
$K(Y)^{1/p^{\infty }}$, since  $K(Y)^{1/p^{\infty }}$ is a perfect field. Then there exist a finite purely inseparable extension
$K(Y)^{1/p^{\infty }}$ is a perfect field. Then there exist a finite purely inseparable extension  $L$ of
$L$ of  $K(Y)$ and a projective normal
$K(Y)$ and a projective normal  $L$-surface
$L$-surface  $Z_{2}$ with the following projective birational
$Z_{2}$ with the following projective birational  $L_{0}$-morphism:
$L_{0}$-morphism:
 $$\begin{eqnarray}\displaystyle g_{2}:Z_{2}\rightarrow X\times _{Y}L, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{2}:Z_{2}\rightarrow X\times _{Y}L, & & \displaystyle \nonumber\end{eqnarray}$$ whose base change by  $(-)\times _{L}K(Y)^{1/p^{\infty }}$ is isomorphic to
$(-)\times _{L}K(Y)^{1/p^{\infty }}$ is isomorphic to  $g_{1}$. In particular,
$g_{1}$. In particular,  $Z_{2}$ is a smooth projective surface over
$Z_{2}$ is a smooth projective surface over  $L$.
$L$.
Let  $Y_{2}$ be the normalisation of
$Y_{2}$ be the normalisation of  $Y$ in
$Y$ in  $L$ and let
$L$ and let  $X_{2}$ be the normalisation of
$X_{2}$ be the normalisation of  $(X\times _{Y}Y_{2})_{\operatorname{red}}$. We get the following commutative diagram of normal
$(X\times _{Y}Y_{2})_{\operatorname{red}}$. We get the following commutative diagram of normal  $k$-varieties.
$k$-varieties.

Claim 3.5. The following hold.
(a) There exists a non-empty open subset
 $Y_{3}$ of
$Y_{3}$ of  $Y_{2}$ such that the induced morphism is an isomorphism.
$Y_{2}$ such that the induced morphism is an isomorphism. $$\begin{eqnarray}\displaystyle X_{3}:=f_{2}^{-1}(Y_{3})\rightarrow X\times _{Y}Y_{3} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{3}:=f_{2}^{-1}(Y_{3})\rightarrow X\times _{Y}Y_{3} & & \displaystyle \nonumber\end{eqnarray}$$(b) The generic fibre of
 $f_{2}:X_{2}\rightarrow Y_{2}$ is isomorphic to
$f_{2}:X_{2}\rightarrow Y_{2}$ is isomorphic to  $X\times _{Y}L$.
$X\times _{Y}L$.(c)
 $\unicode[STIX]{x1D6FC}$ is a finite universal homeomorphism.
$\unicode[STIX]{x1D6FC}$ is a finite universal homeomorphism.(d)
 $\unicode[STIX]{x1D6FD}$ is a finite universal homeomorphism.
$\unicode[STIX]{x1D6FD}$ is a finite universal homeomorphism.(e)
 $(f_{2})_{\ast }{\mathcal{O}}_{X_{2}}={\mathcal{O}}_{Y_{2}}$.
$(f_{2})_{\ast }{\mathcal{O}}_{X_{2}}={\mathcal{O}}_{Y_{2}}$.
Proof of Claim 3.5.
Note that the generic fibre of  $X\times _{Y}Y_{2}\rightarrow Y_{2}$ is normal by the geometric normality of
$X\times _{Y}Y_{2}\rightarrow Y_{2}$ is normal by the geometric normality of  $X_{K(Y)}$ (the assumption (iv)). Therefore, (a) holds, since
$X_{K(Y)}$ (the assumption (iv)). Therefore, (a) holds, since  $X_{2}\rightarrow (X\times _{Y}Y_{2})_{\operatorname{red}}$ is the normalisation. It is clear that (b) follows from (a). As
$X_{2}\rightarrow (X\times _{Y}Y_{2})_{\operatorname{red}}$ is the normalisation. It is clear that (b) follows from (a). As  $K(Y)\subset L$ is a purely inseparable extension, the assertion (d) holds.
$K(Y)\subset L$ is a purely inseparable extension, the assertion (d) holds.
Let us show (c). It follows from the construction that  $\unicode[STIX]{x1D6FC}:X_{2}\rightarrow X$ is a finite surjective morphism of normal schemes. In particular,
$\unicode[STIX]{x1D6FC}:X_{2}\rightarrow X$ is a finite surjective morphism of normal schemes. In particular,  $X_{2}$ coincides with the normalisation of
$X_{2}$ coincides with the normalisation of  $X$ in
$X$ in  $K(X_{2})$. Therefore, it suffices to show that the field extension
$K(X_{2})$. Therefore, it suffices to show that the field extension  $K(X)\subset K(X_{2})$ is purely inseparable, which in turn follows from the following equation:
$K(X)\subset K(X_{2})$ is purely inseparable, which in turn follows from the following equation:
 $$\begin{eqnarray}\displaystyle K(X_{2})=K(X_{2}\times _{Y_{2}}K(Y_{2}))=K(X\times _{Y}L), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K(X_{2})=K(X_{2}\times _{Y_{2}}K(Y_{2}))=K(X\times _{Y}L), & & \displaystyle \nonumber\end{eqnarray}$$where the second equality follows from (b). Thus, (c) holds.
Let us show (e). Let  $f_{2}:X_{2}\rightarrow Y_{2}^{\prime }\rightarrow Y_{2}$ be the Stein factorisation of
$f_{2}:X_{2}\rightarrow Y_{2}^{\prime }\rightarrow Y_{2}$ be the Stein factorisation of  $f_{2}$. By (a), there exists a non-empty open subset
$f_{2}$. By (a), there exists a non-empty open subset  $Y_{4}$ of
$Y_{4}$ of  $Y_{2}$ such that the induced homomorphism
$Y_{2}$ such that the induced homomorphism
 $$\begin{eqnarray}\displaystyle {\mathcal{O}}_{Y_{2}}|_{Y_{4}}\rightarrow (f_{2})_{\ast }{\mathcal{O}}_{X_{2}}|_{Y_{4}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{O}}_{Y_{2}}|_{Y_{4}}\rightarrow (f_{2})_{\ast }{\mathcal{O}}_{X_{2}}|_{Y_{4}} & & \displaystyle \nonumber\end{eqnarray}$$ is an isomorphism. In particular,  $Y_{2}^{\prime }\rightarrow Y_{2}$ is a finite birational morphism of integral
$Y_{2}^{\prime }\rightarrow Y_{2}$ is a finite birational morphism of integral  $k$-varieties. As
$k$-varieties. As  $Y_{2}$ is normal, it holds that
$Y_{2}$ is normal, it holds that  $Y_{2}^{\prime }\rightarrow Y_{2}$ is an isomorphism and hence we obtain (e). This completes the proof of Claim 3.5.◻
$Y_{2}^{\prime }\rightarrow Y_{2}$ is an isomorphism and hence we obtain (e). This completes the proof of Claim 3.5.◻
Let us go back to the proof of Step 2. Thanks to (c), (d), (e) and (b) of Claim 3.5, also  $f_{2}$ satisfies the same properties (i), (ii), (iii) and (iv) for
$f_{2}$ satisfies the same properties (i), (ii), (iii) and (iv) for  $f_{2}$, respectively. By Step 1, it holds that
$f_{2}$, respectively. By Step 1, it holds that  $R^{i}(f_{2})_{\ast }(W{\mathcal{O}}_{X_{2},\mathbb{Q}})=0$ for
$R^{i}(f_{2})_{\ast }(W{\mathcal{O}}_{X_{2},\mathbb{Q}})=0$ for  $i>0$. Thanks to (c) and (d) of Claim 3.5, we have that
$i>0$. Thanks to (c) and (d) of Claim 3.5, we have that  $R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for  $i>0$. This completes the proof of Step 2.◻
$i>0$. This completes the proof of Step 2.◻
Proposition 3.6. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional klt pair over
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional klt pair over  $k$ and let
$k$ and let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism to a smooth
$k$-morphism to a smooth  $k$-curve
$k$-curve  $Y$ such that
$Y$ such that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. If
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. If  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big, then
$f$-big, then  $R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Proof. Applying Lemma 3.3 to  $f$, we obtain a commutative diagram
$f$, we obtain a commutative diagram

that satisfies the properties listed in Lemma 3.3. Since  $X$ has
$X$ has  $W{\mathcal{O}}$-rational singularities and
$W{\mathcal{O}}$-rational singularities and  $\unicode[STIX]{x1D6FC}$ is a finite universal homeomorphism, it holds that
$\unicode[STIX]{x1D6FC}$ is a finite universal homeomorphism, it holds that  $X^{\prime }$ has
$X^{\prime }$ has  $W{\mathcal{O}}$-rational singularities. Furthermore, the geometric generic fibre
$W{\mathcal{O}}$-rational singularities. Furthermore, the geometric generic fibre  $X_{\overline{K(Y^{\prime })}}$ of
$X_{\overline{K(Y^{\prime })}}$ of  $f^{\prime }$ is normal (Lemma 3.3(iii)) and hence it is a normal rational surface by Proposition 2.26. Therefore, it follows from Lemma 3.4 that
$f^{\prime }$ is normal (Lemma 3.3(iii)) and hence it is a normal rational surface by Proposition 2.26. Therefore, it follows from Lemma 3.4 that  $Rf_{\ast }^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})=W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$. Thus, we get
$Rf_{\ast }^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})=W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$. Thus, we get
 $$\begin{eqnarray}\displaystyle Rf_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})\simeq Rf_{\ast }R\unicode[STIX]{x1D6FC}_{\ast }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq R\unicode[STIX]{x1D6FD}_{\ast }(W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})\simeq Rf_{\ast }R\unicode[STIX]{x1D6FC}_{\ast }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq R\unicode[STIX]{x1D6FD}_{\ast }(W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$ where the first and last isomorphisms hold because  $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and  $\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms (Lemma 3.3(i)) and the second isomorphism follows from
$\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms (Lemma 3.3(i)) and the second isomorphism follows from  $Rf_{\ast }^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})=W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$.◻
$Rf_{\ast }^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})=W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$.◻
3.2 Conic bundles
In this subsection, we prove the  $W{\mathcal{O}}$-vanishing for conic bundles (Proposition 3.9). To this end, we show that their base schemes have
$W{\mathcal{O}}$-vanishing for conic bundles (Proposition 3.9). To this end, we show that their base schemes have  $W{\mathcal{O}}$-rational singularities (Theorem 3.8). Let us start by recalling the following basic fact.
$W{\mathcal{O}}$-rational singularities (Theorem 3.8). Let us start by recalling the following basic fact.
Lemma 3.7. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$. Let
$p>0$. Let  $f:X\rightarrow Y$ be a proper birational
$f:X\rightarrow Y$ be a proper birational  $k$-morphism of normal
$k$-morphism of normal  $k$-surfaces. If
$k$-surfaces. If  $Y$ has
$Y$ has  $W{\mathcal{O}}$-rational singularities, then so does
$W{\mathcal{O}}$-rational singularities, then so does  $X$.
$X$.
Proof. Fix a resolution of singularities of  $X$:
$X$:  $\unicode[STIX]{x1D711}:V\rightarrow X$. We have the following exact sequence induced by the corresponding Grothendieck spectral sequence:
$\unicode[STIX]{x1D711}:V\rightarrow X$. We have the following exact sequence induced by the corresponding Grothendieck spectral sequence:
 $$\begin{eqnarray}\displaystyle 0\rightarrow R^{1}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}}) & \rightarrow & \displaystyle R^{1}(f\circ \unicode[STIX]{x1D711})_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})\rightarrow f_{\ast }R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle R^{2}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow R^{1}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}}) & \rightarrow & \displaystyle R^{1}(f\circ \unicode[STIX]{x1D711})_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})\rightarrow f_{\ast }R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle R^{2}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}}).\nonumber\end{eqnarray}$$ We obtain  $R^{1}(f\circ \unicode[STIX]{x1D711})_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})=0$, since
$R^{1}(f\circ \unicode[STIX]{x1D711})_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})=0$, since  $Y$ has
$Y$ has  $W{\mathcal{O}}$-rational singularities. Moreover, we have that
$W{\mathcal{O}}$-rational singularities. Moreover, we have that  $R^{2}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$, as the fibres of
$R^{2}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$, as the fibres of  $f$ are at most one dimensional (cf. [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.20]). Therefore, it holds that
$f$ are at most one dimensional (cf. [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.20]). Therefore, it holds that  $f_{\ast }R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})=0$. Thanks to the fact that
$f_{\ast }R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})=0$. Thanks to the fact that  $\operatorname{Supp}\,R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})$ is zero dimensional, we get
$\operatorname{Supp}\,R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})$ is zero dimensional, we get  $R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})=0$.◻
$R^{1}\unicode[STIX]{x1D711}_{\ast }(W{\mathcal{O}}_{V,\mathbb{Q}})=0$.◻
Theorem 3.8. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism of normal
$k$-morphism of normal  $k$-varieties with
$k$-varieties with  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$ which satisfies the following properties:
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$ which satisfies the following properties:
(i)
 $\dim X=3$ and
$\dim X=3$ and  $\dim Y=2$;
$\dim Y=2$;(ii) there exists an effective
 $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}$ on
$\unicode[STIX]{x1D6E5}$ on  $X$ such that
$X$ such that  $(X,\unicode[STIX]{x1D6E5})$ is klt and
$(X,\unicode[STIX]{x1D6E5})$ is klt and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big.
$f$-big.
Then  $Y$ has
$Y$ has  $W{\mathcal{O}}$-rational singularities.
$W{\mathcal{O}}$-rational singularities.
Proof. Replacing  $\unicode[STIX]{x1D6E5}$, we may assume that
$\unicode[STIX]{x1D6E5}$, we may assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-ample.
$f$-ample.
Step 1. The assertion of Theorem 3.8 holds if  $k=\overline{\mathbb{F}}_{p}$.
$k=\overline{\mathbb{F}}_{p}$.
Proof of Step 1.
In this proof,  $X(\mathbb{F}_{p^{e}})$ denotes the number of
$X(\mathbb{F}_{p^{e}})$ denotes the number of  $\mathbb{F}_{p^{e}}$-rational points on a model
$\mathbb{F}_{p^{e}}$-rational points on a model  $X_{0}$ of
$X_{0}$ of  $X$ over
$X$ over  $\mathbb{F}_{p^{e}}$, i.e.
$\mathbb{F}_{p^{e}}$, i.e.  $X_{0}$ is a projective
$X_{0}$ is a projective  $\mathbb{F}_{p^{e}}$-scheme such that
$\mathbb{F}_{p^{e}}$-scheme such that  $X_{0}\times _{\mathbb{F}_{p^{e}}}k\simeq X$. We can define
$X_{0}\times _{\mathbb{F}_{p^{e}}}k\simeq X$. We can define  $X(\mathbb{F}_{p^{e}})$ if
$X(\mathbb{F}_{p^{e}})$ if  $e$ is a sufficiently divisible positive integer and we fix a model
$e$ is a sufficiently divisible positive integer and we fix a model  $X_{0}$ (this number possibly depends on the choice of a model
$X_{0}$ (this number possibly depends on the choice of a model  $X_{0}$).
$X_{0}$).
We may assume that  $Y$ has a unique singular point
$Y$ has a unique singular point  $y$. Let
$y$. Let  $g:Y^{\prime }\rightarrow Y$ be a log resolution such that
$g:Y^{\prime }\rightarrow Y$ be a log resolution such that  $g(\operatorname{Ex}(g))=\{y\}$. Set
$g(\operatorname{Ex}(g))=\{y\}$. Set  $C:=\operatorname{Ex}(g)=g^{-1}(y)$. Let
$C:=\operatorname{Ex}(g)=g^{-1}(y)$. Let  $\unicode[STIX]{x1D711}:W\rightarrow X$ be a log resolution of
$\unicode[STIX]{x1D711}:W\rightarrow X$ be a log resolution of  $(X,\unicode[STIX]{x1D6E5})$ that admits a morphism to
$(X,\unicode[STIX]{x1D6E5})$ that admits a morphism to  $Y^{\prime }$. Then
$Y^{\prime }$. Then  $f^{-1}(y)$ is rationally chain connected [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 4.1]. Hence, by [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 4.8], also
$f^{-1}(y)$ is rationally chain connected [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 4.1]. Hence, by [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 4.8], also  $(f\circ \unicode[STIX]{x1D711})^{-1}(y)$ is rationally chain connected. Therefore, its image on
$(f\circ \unicode[STIX]{x1D711})^{-1}(y)$ is rationally chain connected. Therefore, its image on  $Y^{\prime }$, which is nothing but
$Y^{\prime }$, which is nothing but  $C$, is a union of rational curves. In order to prove that
$C$, is a union of rational curves. In order to prove that  $Y$ has
$Y$ has  $W{\mathcal{O}}$-rational singularities, it is suffices to show that
$W{\mathcal{O}}$-rational singularities, it is suffices to show that  $C$ forms a tree by Proposition 2.23 and [Reference Chatzistamatiou and RüllingCR12, Corollary 4.6.4]. Let
$C$ forms a tree by Proposition 2.23 and [Reference Chatzistamatiou and RüllingCR12, Corollary 4.6.4]. Let  $s$ be the number of the vertices and let
$s$ be the number of the vertices and let  $t$ be the number of the edges of the dual graph of
$t$ be the number of the edges of the dual graph of  $C$. Note that since
$C$. Note that since  $C$ is connected and simple normal closing, the condition that
$C$ is connected and simple normal closing, the condition that  $C$ forms a tree is equivalent to the condition that
$C$ forms a tree is equivalent to the condition that  $s=t+1$. Then, for a sufficiently divisible
$s=t+1$. Then, for a sufficiently divisible  $e$,
$e$,
 $$\begin{eqnarray}\displaystyle C(\mathbb{F}_{p^{e}})=s(p^{e}+1)-t & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C(\mathbb{F}_{p^{e}})=s(p^{e}+1)-t & & \displaystyle \nonumber\end{eqnarray}$$ holds because we may assume that each component of  $C$ and their intersection are defined over
$C$ and their intersection are defined over  $\mathbb{F}_{p^{e}}$. Hence, the condition
$\mathbb{F}_{p^{e}}$. Hence, the condition  $s=t+1$ is equivalent to the condition that
$s=t+1$ is equivalent to the condition that
 $$\begin{eqnarray}\displaystyle C(\mathbb{F}_{p^{e}})\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C(\mathbb{F}_{p^{e}})\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e} & & \displaystyle \nonumber\end{eqnarray}$$ for sufficiently divisible  $e$. Therefore, it suffices to show that
$e$. Therefore, it suffices to show that
 $$\begin{eqnarray}\displaystyle Y^{\prime }(\mathbb{F}_{p^{e}})\equiv Y(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y^{\prime }(\mathbb{F}_{p^{e}})\equiv Y(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e} & & \displaystyle \nonumber\end{eqnarray}$$ for any sufficiently divisible positive integer  $e$.
$e$.
Let  $E$ be the sum of all the
$E$ be the sum of all the  $\unicode[STIX]{x1D711}$-exceptional prime divisors. We run a
$\unicode[STIX]{x1D711}$-exceptional prime divisors. We run a  $(K_{W}+\unicode[STIX]{x1D711}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+E)$-MMP over
$(K_{W}+\unicode[STIX]{x1D711}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+E)$-MMP over  $Y^{\prime }$ that terminates. Since
$Y^{\prime }$ that terminates. Since  $K_{W}+\unicode[STIX]{x1D711}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+E$ is generically anti-ample over
$K_{W}+\unicode[STIX]{x1D711}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+E$ is generically anti-ample over  $Y^{\prime }$, we end with a Mori fibre space
$Y^{\prime }$, we end with a Mori fibre space  $X_{1}\rightarrow Y_{1}$ over
$X_{1}\rightarrow Y_{1}$ over  $Y^{\prime }$. Note that the induced morphism
$Y^{\prime }$. Note that the induced morphism  $Y_{1}\rightarrow Y^{\prime }$ is birational and hence
$Y_{1}\rightarrow Y^{\prime }$ is birational and hence  $Y_{1}$ has
$Y_{1}$ has  $W{\mathcal{O}}$-rational singularities by Lemma 3.7.
$W{\mathcal{O}}$-rational singularities by Lemma 3.7.
Take an arbitrary divisible positive integer  $e$. We obtain
$e$. We obtain
 $$\begin{eqnarray}\displaystyle Y_{1}(\mathbb{F}_{p^{e}})\equiv Y^{\prime }(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y_{1}(\mathbb{F}_{p^{e}})\equiv Y^{\prime }(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}, & & \displaystyle \nonumber\end{eqnarray}$$ since  $Y_{1}$ and
$Y_{1}$ and  $Y^{\prime }$ are birational and have
$Y^{\prime }$ are birational and have  $W{\mathcal{O}}$-rational singularities [Reference Chatzistamatiou and RüllingCR12, Corollary 4.4.16]. Furthermore, it follows from [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.1] that
$W{\mathcal{O}}$-rational singularities [Reference Chatzistamatiou and RüllingCR12, Corollary 4.4.16]. Furthermore, it follows from [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.1] that
 $$\begin{eqnarray}\displaystyle X(\mathbb{F}_{p^{e}})\equiv W(\mathbb{F}_{p^{e}})\equiv X_{1}(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X(\mathbb{F}_{p^{e}})\equiv W(\mathbb{F}_{p^{e}})\equiv X_{1}(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}. & & \displaystyle \nonumber\end{eqnarray}$$ On the other hand,  $X$ and
$X$ and  $X_{1}$ are of Fano type over
$X_{1}$ are of Fano type over  $Y$ and
$Y$ and  $Y_{1}$, respectively. Hence, by [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.4], we obtain
$Y_{1}$, respectively. Hence, by [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.4], we obtain
 $$\begin{eqnarray}\displaystyle X(\mathbb{F}_{p^{e}})\equiv Y(\mathbb{F}_{p^{e}}),\quad X_{1}(\mathbb{F}_{p^{e}})\equiv Y_{1}(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X(\mathbb{F}_{p^{e}})\equiv Y(\mathbb{F}_{p^{e}}),\quad X_{1}(\mathbb{F}_{p^{e}})\equiv Y_{1}(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}. & & \displaystyle \nonumber\end{eqnarray}$$To summarise, we get
 $$\begin{eqnarray}\displaystyle Y(\mathbb{F}_{p^{e}})\equiv Y^{\prime }(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y(\mathbb{F}_{p^{e}})\equiv Y^{\prime }(\mathbb{F}_{p^{e}})\hspace{0.6em}{\rm mod}\hspace{0.2em}p^{e}. & & \displaystyle \nonumber\end{eqnarray}$$This completes the proof of Step 1. ◻
Step 2. The assertion of Theorem 3.8 holds if  $k$ is algebraically closed.
$k$ is algebraically closed.
Proof of Step 2.
We fix a closed point  $y\in Y$ and we may assume that
$y\in Y$ and we may assume that  $y$ is a unique singularity of
$y$ is a unique singularity of  $Y$. Let
$Y$. Let  $g:Z\rightarrow Y$ be a log resolution such that
$g:Z\rightarrow Y$ be a log resolution such that  $g(\operatorname{Ex}(g))=y$. By Proposition 2.23,
$g(\operatorname{Ex}(g))=y$. By Proposition 2.23,  $Y$ has
$Y$ has  $W{\mathcal{O}}$-rational singularities if and only if
$W{\mathcal{O}}$-rational singularities if and only if  $\operatorname{Ex}(g)$ is a tree of smooth rational curves. We take a model over some finitely generated
$\operatorname{Ex}(g)$ is a tree of smooth rational curves. We take a model over some finitely generated  $\overline{\mathbb{F}}_{p}$-algebra
$\overline{\mathbb{F}}_{p}$-algebra  $R$ of a diagram
$R$ of a diagram  $X\rightarrow Y\leftarrow Z$, i.e. an intermediate ring
$X\rightarrow Y\leftarrow Z$, i.e. an intermediate ring  $\overline{\mathbb{F}}_{p}\subset R\subset k$ that is a finitely generated
$\overline{\mathbb{F}}_{p}\subset R\subset k$ that is a finitely generated  $\overline{\mathbb{F}}_{p}$-algebra, and
$\overline{\mathbb{F}}_{p}$-algebra, and  $R$-morphisms of projective schemes over
$R$-morphisms of projective schemes over  $R$
$R$
 $$\begin{eqnarray}\displaystyle \mathfrak{X}\rightarrow \mathfrak{Y}\leftarrow \mathfrak{Z} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{X}\rightarrow \mathfrak{Y}\leftarrow \mathfrak{Z} & & \displaystyle \nonumber\end{eqnarray}$$ whose base changes by  $(-)\,\times _{R}\,k$ are the same as
$(-)\,\times _{R}\,k$ are the same as  $X\rightarrow Y\leftarrow Z$. Then the base change
$X\rightarrow Y\leftarrow Z$. Then the base change  $\mathfrak{X}_{\unicode[STIX]{x1D707}}\overset{f_{\unicode[STIX]{x1D707}}}{\rightarrow }\mathfrak{Y}_{\unicode[STIX]{x1D707}}\overset{g_{\unicode[STIX]{x1D707}}}{\leftarrow }\mathfrak{Z}_{\unicode[STIX]{x1D707}}$ by a general closed point
$\mathfrak{X}_{\unicode[STIX]{x1D707}}\overset{f_{\unicode[STIX]{x1D707}}}{\rightarrow }\mathfrak{Y}_{\unicode[STIX]{x1D707}}\overset{g_{\unicode[STIX]{x1D707}}}{\leftarrow }\mathfrak{Z}_{\unicode[STIX]{x1D707}}$ by a general closed point  $\unicode[STIX]{x1D707}\in \operatorname{Spec}\,R$ satisfies the same properties as
$\unicode[STIX]{x1D707}\in \operatorname{Spec}\,R$ satisfies the same properties as  $X\rightarrow Y\leftarrow Z$. Therefore,
$X\rightarrow Y\leftarrow Z$. Therefore,  $\operatorname{Ex}(g_{\unicode[STIX]{x1D707}})$ is a tree of smooth rational curves by Step 1 and hence so is
$\operatorname{Ex}(g_{\unicode[STIX]{x1D707}})$ is a tree of smooth rational curves by Step 1 and hence so is  $\operatorname{Ex}(g)$ by Proposition 2.23 and the upper semicontinuity of cohomologies [Reference HartshorneHar77, ch. III, Theorem 12.11]. This completes the proof of Step 2.◻
$\operatorname{Ex}(g)$ by Proposition 2.23 and the upper semicontinuity of cohomologies [Reference HartshorneHar77, ch. III, Theorem 12.11]. This completes the proof of Step 2.◻
Step 3. The assertion of Theorem 3.8 holds without any additional assumptions.
Proposition 3.9. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism of normal
$k$-morphism of normal  $k$-varieties with
$k$-varieties with  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$ which satisfies the following properties:
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$ which satisfies the following properties:
(i)
 $\dim X=3$ and
$\dim X=3$ and  $\dim Y=2$;
$\dim Y=2$;(ii) there exists an effective
 $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}$ on
$\unicode[STIX]{x1D6E5}$ on  $X$ such that
$X$ such that  $(X,\unicode[STIX]{x1D6E5})$ is klt and
$(X,\unicode[STIX]{x1D6E5})$ is klt and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big.
$f$-big.
Then  $R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for all
$R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for all  $i>0$.
$i>0$.
Proof. By Lemma 3.3, there exists a commutative diagram

of projective  $k$-morphisms of normal
$k$-morphisms of normal  $k$-varieties which satisfies the properties listed in Lemma 3.3 (for an alternative argument, see Remark 3.10). Since
$k$-varieties which satisfies the properties listed in Lemma 3.3 (for an alternative argument, see Remark 3.10). Since  $(X,\unicode[STIX]{x1D6E5})$ is klt,
$(X,\unicode[STIX]{x1D6E5})$ is klt,  $X$ has
$X$ has  $W{\mathcal{O}}$-rational singularities (Theorem 3.1(i)). By Theorem 3.8, also
$W{\mathcal{O}}$-rational singularities (Theorem 3.1(i)). By Theorem 3.8, also  $Y$ has
$Y$ has  $W{\mathcal{O}}$-rational singularities. Since
$W{\mathcal{O}}$-rational singularities. Since  $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and  $\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms (Lemma 3.3(i)), also
$\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms (Lemma 3.3(i)), also  $X^{\prime }$ and
$X^{\prime }$ and  $Y^{\prime }$ have
$Y^{\prime }$ have  $W{\mathcal{O}}$-rational singularities. Since the generic fibre of
$W{\mathcal{O}}$-rational singularities. Since the generic fibre of  $f^{\prime }$ is smooth and will be a rational curve after taking the base change to the algebraic closure, it follows from Theorem 3.2 that
$f^{\prime }$ is smooth and will be a rational curve after taking the base change to the algebraic closure, it follows from Theorem 3.2 that  $Rf_{\ast }^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$. Therefore, we get
$Rf_{\ast }^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$. Therefore, we get
 $$\begin{eqnarray}\displaystyle Rf_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})\simeq Rf_{\ast }R\unicode[STIX]{x1D6FC}_{\ast }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq R\unicode[STIX]{x1D6FD}_{\ast }(W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})\simeq Rf_{\ast }R\unicode[STIX]{x1D6FC}_{\ast }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq R\unicode[STIX]{x1D6FD}_{\ast }(W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$ where the first and the last isomorphisms follow because  $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and  $\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms (Lemma 3.3(i)) and the second isomorphism follows from
$\unicode[STIX]{x1D6FD}$ are finite universal homeomorphisms (Lemma 3.3(i)) and the second isomorphism follows from  $Rf^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$.◻
$Rf^{\prime }(W{\mathcal{O}}_{X^{\prime },\mathbb{Q}})\simeq W{\mathcal{O}}_{Y^{\prime },\mathbb{Q}}$.◻
Remark 3.10. In the situation of Proposition 3.9, the generic fibre is a conic curve in  $\mathbb{P}_{K(Y)}^{2}$ (cf. [Reference KollárKol13, Lemma 10.6(3)]). Hence, the assumption
$\mathbb{P}_{K(Y)}^{2}$ (cf. [Reference KollárKol13, Lemma 10.6(3)]). Hence, the assumption  $p>2$ implies that the generic fibre of
$p>2$ implies that the generic fibre of  $f$ is generically smooth. Thus,
$f$ is generically smooth. Thus,  $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and  $\unicode[STIX]{x1D6FD}$ in the proof can be assumed to be isomorphisms and we can avoid using Lemma 3.3. We adopt the above argument, as it is less dependent on the assumption on the characteristic
$\unicode[STIX]{x1D6FD}$ in the proof can be assumed to be isomorphisms and we can avoid using Lemma 3.3. We adopt the above argument, as it is less dependent on the assumption on the characteristic  $p$.
$p$.
3.3 Proof of  $W{\mathcal{O}}$-vanishing for log Fano contractions
$W{\mathcal{O}}$-vanishing for log Fano contractions
We now prove the main theorem of this section.
Theorem 3.11. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism of normal
$k$-morphism of normal  $k$-varieties. Assume that
$k$-varieties. Assume that  $\dim X\leqslant 3$ and there exists an effective
$\dim X\leqslant 3$ and there exists an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}$ such that
$\unicode[STIX]{x1D6E5}$ such that  $(X,\unicode[STIX]{x1D6E5})$ is klt and
$(X,\unicode[STIX]{x1D6E5})$ is klt and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Then
$f$-big. Then  $R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(W{\mathcal{O}}_{X,\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Proof. Taking the Stein factorisation of  $f$, we may assume that
$f$, we may assume that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. If
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. If  $\dim Y=0$, then the assertion follows from Theorem 3.1(ii). If
$\dim Y=0$, then the assertion follows from Theorem 3.1(ii). If  $\dim Y=3$, then we have that also
$\dim Y=3$, then we have that also  $(Y,\unicode[STIX]{x1D6E5}_{Y})$ is klt for some effective
$(Y,\unicode[STIX]{x1D6E5}_{Y})$ is klt for some effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}_{Y}$ and hence the assertion holds by Theorem 3.1(i). If
$\unicode[STIX]{x1D6E5}_{Y}$ and hence the assertion holds by Theorem 3.1(i). If  $\dim Y=1$ (respectively
$\dim Y=1$ (respectively  $\dim Y=2$), then the assertion follows from Proposition 3.6 (respectively Proposition 3.9).◻
$\dim Y=2$), then the assertion follows from Proposition 3.6 (respectively Proposition 3.9).◻
4 A Nadel vanishing theorem for Witt multiplier ideal sheaves
In this section, we prove the main theorem of this paper (Theorem 4.10). Our strategy is to run a suitable minimal model program, which enables us to replace the given variety  $X$ by the end result. In § 4.1, we study the behaviour of Witt vector cohomologies under such minimal model programs. In § 4.2, we prove Theorem 4.10 for dlt Mori fibre spaces with an extra assumption (Lemma 4.7). In § 4.3, we give a proof of Theorem 4.10. Furthermore, we also give a generalisation of Theorem 4.10 (Theorem 4.11) and the Kollár–Shokurov connectedness theorem (Theorem 4.12).
$X$ by the end result. In § 4.1, we study the behaviour of Witt vector cohomologies under such minimal model programs. In § 4.2, we prove Theorem 4.10 for dlt Mori fibre spaces with an extra assumption (Lemma 4.7). In § 4.3, we give a proof of Theorem 4.10. Furthermore, we also give a generalisation of Theorem 4.10 (Theorem 4.11) and the Kollár–Shokurov connectedness theorem (Theorem 4.12).
4.1 Witt vector cohomologies under MMP
The purpose of this subsection is to prove the following.
Proposition 4.1. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6FA})$ be a three-dimensional
$(X,\unicode[STIX]{x1D6FA})$ be a three-dimensional  $\mathbb{Q}$-factorial log pair over
$\mathbb{Q}$-factorial log pair over  $k$ and let
$k$ and let  $h:X\rightarrow Z$ be a projective
$h:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$. Suppose that:
$Z$. Suppose that:
∙
 $(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt; and
$(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt; and∙
 $K_{X}+\unicode[STIX]{x1D6FA}{\sim}_{Z,\mathbb{R}}0$.
$K_{X}+\unicode[STIX]{x1D6FA}{\sim}_{Z,\mathbb{R}}0$.
Let
 $$\begin{eqnarray}\displaystyle X=:X_{0}\rightarrow X_{1}\rightarrow X_{2}\rightarrow \cdots \rightarrow X_{r}\rightarrow \cdots & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X=:X_{0}\rightarrow X_{1}\rightarrow X_{2}\rightarrow \cdots \rightarrow X_{r}\rightarrow \cdots & & \displaystyle \nonumber\end{eqnarray}$$ be a  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-MMP over
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-MMP over  $Z$ with the induced morphism
$Z$ with the induced morphism  $h_{r}:X_{r}\rightarrow Z$. Set
$h_{r}:X_{r}\rightarrow Z$. Set  $\unicode[STIX]{x1D6FA}_{r}$ to be the push-forward of
$\unicode[STIX]{x1D6FA}_{r}$ to be the push-forward of  $\unicode[STIX]{x1D6FA}$ on
$\unicode[STIX]{x1D6FA}$ on  $X_{r}$. Then the isomorphism
$X_{r}$. Then the isomorphism
 $$\begin{eqnarray}\displaystyle R^{i}h_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\simeq R^{i}(h_{r})_{\ast }WI_{\unicode[STIX]{x1D6FA}_{r}^{{\geqslant}1},\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}h_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\simeq R^{i}(h_{r})_{\ast }WI_{\unicode[STIX]{x1D6FA}_{r}^{{\geqslant}1},\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$ holds for any  $i\geqslant 0$ and
$i\geqslant 0$ and  $r\geqslant 0$.
$r\geqslant 0$.
Proof. By induction, it is sufficient to prove the case when  $r=1$. We have the following properties.
$r=1$. We have the following properties.
(1)
 $(X_{1},\unicode[STIX]{x1D6FA}_{1})$ satisfies the same conditions as in the statement, i.e.
$(X_{1},\unicode[STIX]{x1D6FA}_{1})$ satisfies the same conditions as in the statement, i.e.  $(X_{1},\unicode[STIX]{x1D6FA}_{1})$ is a
$(X_{1},\unicode[STIX]{x1D6FA}_{1})$ is a  $\mathbb{Q}$-factorial log pair such that
$\mathbb{Q}$-factorial log pair such that  $(X_{1},\unicode[STIX]{x1D6FA}_{1}^{\wedge 1})$ is dlt and
$(X_{1},\unicode[STIX]{x1D6FA}_{1}^{\wedge 1})$ is dlt and  $K_{X_{1}}+\unicode[STIX]{x1D6FA}_{1}{\sim}_{Z,\mathbb{R}}0$.
$K_{X_{1}}+\unicode[STIX]{x1D6FA}_{1}{\sim}_{Z,\mathbb{R}}0$.(2) Given projective birational morphisms
 $\unicode[STIX]{x1D713}_{0}:Y\rightarrow X$ and
$\unicode[STIX]{x1D713}_{0}:Y\rightarrow X$ and  $\unicode[STIX]{x1D713}_{1}:Y\rightarrow X_{1}$, it holds that
$\unicode[STIX]{x1D713}_{1}:Y\rightarrow X_{1}$, it holds that  $\unicode[STIX]{x1D713}_{0}^{\ast }(K_{X}+\unicode[STIX]{x1D6FA}){\sim}_{Z,\mathbb{R}}\unicode[STIX]{x1D713}_{1}^{\ast }(K_{X_{1}}+\unicode[STIX]{x1D6FA}_{1}){\sim}_{Z,\mathbb{R}}0$.
$\unicode[STIX]{x1D713}_{0}^{\ast }(K_{X}+\unicode[STIX]{x1D6FA}){\sim}_{Z,\mathbb{R}}\unicode[STIX]{x1D713}_{1}^{\ast }(K_{X_{1}}+\unicode[STIX]{x1D6FA}_{1}){\sim}_{Z,\mathbb{R}}0$.(3)
 $\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}$ and
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}$ and  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}_{1})=\operatorname{Supp}\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}$ (cf. Proposition 2.7).
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}_{1})=\operatorname{Supp}\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}$ (cf. Proposition 2.7).
Case 1. Suppose that  $g:X\rightarrow X_{1}$ is a divisorial contraction.
$g:X\rightarrow X_{1}$ is a divisorial contraction.
We have the following spectral sequence:
 $$\begin{eqnarray}\displaystyle E_{2}^{i,j}:=R^{i}(h_{1})_{\ast }R^{j}g_{\ast }(WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}})\Rightarrow R^{i+j}(h_{1}\circ g)_{\ast }(WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}})=:E^{i+j}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{2}^{i,j}:=R^{i}(h_{1})_{\ast }R^{j}g_{\ast }(WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}})\Rightarrow R^{i+j}(h_{1}\circ g)_{\ast }(WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}})=:E^{i+j}. & & \displaystyle \nonumber\end{eqnarray}$$Hence, it is sufficient to show the following two equations:
 $$\begin{eqnarray}\displaystyle g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}=WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}=WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}} & & \displaystyle\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle R^{i}g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}=0\quad \text{for}~i>0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}=0\quad \text{for}~i>0. & & \displaystyle\end{eqnarray}$$Here, the equation (4.1.1) is equivalent to the equation
 $$\begin{eqnarray}\displaystyle g(\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}))=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}))=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}) & & \displaystyle\end{eqnarray}$$as sets.
Case 1-1. Suppose that the contracted divisor  $E$ is an irreducible component of
$E$ is an irreducible component of  $\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$.
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$.
In this case, the equation (4.1.2) follows from [Reference Berthelot, Bloch and EsnaultBBE07, Theorem 2.4], since  $g$ is an isomorphism outside
$g$ is an isomorphism outside  $\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$. By (ii),
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$. By (ii),  $g(E)$ is a non-klt centre of
$g(E)$ is a non-klt centre of  $(X_{1},\unicode[STIX]{x1D6FA}_{1})$. Thanks to (iii), it holds that
$(X_{1},\unicode[STIX]{x1D6FA}_{1})$. Thanks to (iii), it holds that  $g(E)\subset \operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1})$, which implies the required equation (4.1.3).
$g(E)\subset \operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1})$, which implies the required equation (4.1.3).
Case 1-2. Suppose that the contracted divisor  $E$ is not contained in
$E$ is not contained in  $\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$.
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$.
The equation (4.1.3) is trivial in this case. We have the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$In order to prove (4.1.2), it is sufficient to show that:
∙
 $0\rightarrow g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\rightarrow g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0$ is exact; and
$0\rightarrow g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\rightarrow g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0$ is exact; and∙
 $R^{i}g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\simeq R^{i}g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}$ holds for
$R^{i}g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\simeq R^{i}g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}$ holds for  $i>0$.
$i>0$.
Since
 $$\begin{eqnarray}\displaystyle R^{i}g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{X_{1},\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0)\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{X_{1},\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0)\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$ holds by the  $W{\mathcal{O}}$-rationality of the klt threefolds
$W{\mathcal{O}}$-rationality of the klt threefolds  $X$ and
$X$ and  $X_{1}$ (Theorem 3.1(i)), it is sufficient to show that
$X_{1}$ (Theorem 3.1(i)), it is sufficient to show that
 $$\begin{eqnarray}\displaystyle R^{i}g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0).\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0).\end{array}\right. & & \displaystyle\end{eqnarray}$$This follows from the Mayer–Vietoris exact sequence (Lemma 2.18)
 $$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{S_{1}\cup S_{2},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{S_{1},\mathbb{Q}}\oplus W{\mathcal{O}}_{S_{2},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{S_{1}\cap S_{2},\mathbb{Q}}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{S_{1}\cup S_{2},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{S_{1},\mathbb{Q}}\oplus W{\mathcal{O}}_{S_{2},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{S_{1}\cap S_{2},\mathbb{Q}}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ for each union  $S_{i}$ of strata of
$S_{i}$ of strata of  $\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$ and Claim 4.2 below. To summarise, in order to prove (4.1.2), it suffices to show Claim 4.2.
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$ and Claim 4.2 below. To summarise, in order to prove (4.1.2), it suffices to show Claim 4.2.
Claim 4.2. If  $S$ is a stratum of
$S$ is a stratum of  $\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$, then
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})$, then  $g$ induces
$g$ induces
 $$\begin{eqnarray}\displaystyle R^{i}g_{\ast }W{\mathcal{O}}_{S,\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{g(S),\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0).\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}g_{\ast }W{\mathcal{O}}_{S,\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{g(S),\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0).\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$Proof of Claim 4.2.
Note that  $S$ is normal, since
$S$ is normal, since  $(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt and
$(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt and  $p>5$ (cf. [Reference Hacon and XuHX15, Proposition 4.1]). We define an effective
$p>5$ (cf. [Reference Hacon and XuHX15, Proposition 4.1]). We define an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6EC}_{S}$ by adjunction:
$\unicode[STIX]{x1D6EC}_{S}$ by adjunction:  $K_{S}+\unicode[STIX]{x1D6EC}_{S}=(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})|_{S}$. Then
$K_{S}+\unicode[STIX]{x1D6EC}_{S}=(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})|_{S}$. Then  $-(K_{S}+\unicode[STIX]{x1D6EC}_{S})$ is
$-(K_{S}+\unicode[STIX]{x1D6EC}_{S})$ is  $(g|_{S})$-ample and
$(g|_{S})$-ample and  $(S,\unicode[STIX]{x1D6EC}_{S})$ is dlt. Hence,
$(S,\unicode[STIX]{x1D6EC}_{S})$ is dlt. Hence,  $R^{i}g_{\ast }W{\mathcal{O}}_{S,\mathbb{Q}}=0$ holds for
$R^{i}g_{\ast }W{\mathcal{O}}_{S,\mathbb{Q}}=0$ holds for  $i>0$ by [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 3.3].
$i>0$ by [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 3.3].
In order to prove the required equation  $g_{\ast }W{\mathcal{O}}_{S,\mathbb{Q}}=W{\mathcal{O}}_{g(S),\mathbb{Q}}$, it is sufficient to prove that
$g_{\ast }W{\mathcal{O}}_{S,\mathbb{Q}}=W{\mathcal{O}}_{g(S),\mathbb{Q}}$, it is sufficient to prove that  $g:S\rightarrow g(S)$ has connected fibres (Lemma 2.17). When
$g:S\rightarrow g(S)$ has connected fibres (Lemma 2.17). When  $\dim S=2$, then this follows because
$\dim S=2$, then this follows because  $g:S\rightarrow g(S)$ is a projective birational morphism of normal varieties. When
$g:S\rightarrow g(S)$ is a projective birational morphism of normal varieties. When  $\dim S\leqslant 1$, we can apply [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10] (cf. Remark 4.4).◻
$\dim S\leqslant 1$, we can apply [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10] (cf. Remark 4.4).◻
Case 2. Suppose that  $g:X\rightarrow Z^{\prime }$ is a
$g:X\rightarrow Z^{\prime }$ is a  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-flipping contraction over
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-flipping contraction over  $Z$ and let
$Z$ and let  $g_{1}:X_{1}\rightarrow Z^{\prime }$ be its flip.
$g_{1}:X_{1}\rightarrow Z^{\prime }$ be its flip.
- (4.3.1)
 $g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\simeq (g_{1})_{\ast }WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}}$ holds; and
$g_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}}\simeq (g_{1})_{\ast }WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}}$ holds; and- (4.3.2)
 $R^{i}g_{\ast }WI_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}=0$ and
$R^{i}g_{\ast }WI_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}=0$ and  $R^{i}(g_{1})_{\ast }WI_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}=0$ hold for any
$R^{i}(g_{1})_{\ast }WI_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}=0$ hold for any  $i>0$.
$i>0$.
Proof of Claim 4.3.
First, (4.3.1) follows from the set-theoretical equation  $g(\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}))=g_{1}(\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}))$, which is trivial.
$g(\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}))=g_{1}(\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}))$, which is trivial.
Let us prove (4.3.2). We may assume that  $i=1$, since both
$i=1$, since both  $g$ and
$g$ and  $g_{1}$ have at most one-dimensional fibres [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.20]. Consider the exact sequences
$g_{1}$ have at most one-dimensional fibres [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.20]. Consider the exact sequences
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}} & \rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}} & \rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}} & \rightarrow W{\mathcal{O}}_{X_{1},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}} & \rightarrow W{\mathcal{O}}_{X_{1},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$ We have that  $R^{1}g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}=0$ and
$R^{1}g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}=0$ and  $R^{1}(g_{1})_{\ast }W{\mathcal{O}}_{X_{1},\mathbb{Q}}=0$, since all of
$R^{1}(g_{1})_{\ast }W{\mathcal{O}}_{X_{1},\mathbb{Q}}=0$, since all of  $X$,
$X$,  $X_{1}$ and
$X_{1}$ and  $Z^{\prime }$ have
$Z^{\prime }$ have  $W{\mathcal{O}}$-rational singularities (Theorem 3.1(i)). Hence, it is sufficient to show the surjectivity of
$W{\mathcal{O}}$-rational singularities (Theorem 3.1(i)). Hence, it is sufficient to show the surjectivity of
 $$\begin{eqnarray}\displaystyle g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle (g_{1})_{\ast }W{\mathcal{O}}_{X_{1},\mathbb{Q}}\rightarrow (g_{1})_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (g_{1})_{\ast }W{\mathcal{O}}_{X_{1},\mathbb{Q}}\rightarrow (g_{1})_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$which are equivalent to
 $$\begin{eqnarray}\displaystyle g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}=W{\mathcal{O}}_{g(\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})),\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1}),\mathbb{Q}}=W{\mathcal{O}}_{g(\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})),\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle (g_{1})_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}=W{\mathcal{O}}_{g_{1}(\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1})),\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (g_{1})_{\ast }W{\mathcal{O}}_{\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1}),\mathbb{Q}}=W{\mathcal{O}}_{g_{1}(\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1})),\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$respectively. Therefore, by Lemma 2.17, it is enough to prove the following:
(i)
 $g^{\prime }:\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})\rightarrow Z^{\prime }$ has connected fibres;
$g^{\prime }:\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})\rightarrow Z^{\prime }$ has connected fibres;(ii)
 $g_{1}^{\prime }:\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1})\rightarrow Z^{\prime }$ has connected fibres.
$g_{1}^{\prime }:\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1})\rightarrow Z^{\prime }$ has connected fibres.
Both (i) and (ii) follow from (1) and Theorem 2.15. This completes the proof of Claim 4.3. ◻
For the induced morphism  $\unicode[STIX]{x1D703}:Z^{\prime }\rightarrow Z$, we obtain isomorphisms
$\unicode[STIX]{x1D703}:Z^{\prime }\rightarrow Z$, we obtain isomorphisms
 $$\begin{eqnarray}\displaystyle Rh_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}} & \simeq & \displaystyle R\unicode[STIX]{x1D703}_{\ast }Rg_{\ast }(WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}})\nonumber\\ \displaystyle & \simeq & \displaystyle R\unicode[STIX]{x1D703}_{\ast }R(g_{1})_{\ast }(WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}})\simeq R(h_{1})_{\ast }(WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rh_{\ast }WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}} & \simeq & \displaystyle R\unicode[STIX]{x1D703}_{\ast }Rg_{\ast }(WI_{\unicode[STIX]{x1D6FA}^{{\geqslant}1},\mathbb{Q}})\nonumber\\ \displaystyle & \simeq & \displaystyle R\unicode[STIX]{x1D703}_{\ast }R(g_{1})_{\ast }(WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}})\simeq R(h_{1})_{\ast }(WI_{\unicode[STIX]{x1D6FA}_{1}^{{\geqslant}1},\mathbb{Q}}),\nonumber\end{eqnarray}$$where the second isomorphism follows from Claim 4.3. This completes the proof of Proposition 4.1. ◻
Remark 4.4. In the proof above, we use [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10], which is a special case of the two-dimensional version of Theorem 1.1. In the proof of [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10], they use [Reference TanakaTan16, Proposition 2.2], whose proof depends on a classification result on surfaces. Here, for the reader’s convenience, we give a sketch of an alternative proof. When  $U$ in [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10] has positive dimension, the assertion follows from the Nadel vanishing theorem for two-dimensional relative cases [Reference TanakaTan15, Theorem 2.10]. Hence, the remaining case is when
$U$ in [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10] has positive dimension, the assertion follows from the Nadel vanishing theorem for two-dimensional relative cases [Reference TanakaTan15, Theorem 2.10]. Hence, the remaining case is when  $(S,\unicode[STIX]{x1D6E5}_{S})$ is a two-dimensional dlt pair over an algebraically closed field such that
$(S,\unicode[STIX]{x1D6E5}_{S})$ is a two-dimensional dlt pair over an algebraically closed field such that  $-(K_{S}+\unicode[STIX]{x1D6E5}_{S})$ is ample, and it is sufficient to show that
$-(K_{S}+\unicode[STIX]{x1D6E5}_{S})$ is ample, and it is sufficient to show that  $\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner$ is connected. In this case, we may apply the idea of this paper (cf. (B) of § 1.1), and the problem can be reduced to the study on Mori fibre spaces (cf. § 4.2).
$\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner$ is connected. In this case, we may apply the idea of this paper (cf. (B) of § 1.1), and the problem can be reduced to the study on Mori fibre spaces (cf. § 4.2).
4.2 Vanishing for Mori fibre spaces
In this subsection, we prove Lemma 4.7, which is a special case of Theorem 4.10. We start with the following auxiliary result.
Lemma 4.5. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>0$. Let
$p>0$. Let  $(S,\unicode[STIX]{x1D6E5}_{S})$ be a two-dimensional dlt pair over
$(S,\unicode[STIX]{x1D6E5}_{S})$ be a two-dimensional dlt pair over  $k$ and let
$k$ and let  $f:S\rightarrow Z$ be a projective
$f:S\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$. Assume that
$Z$. Assume that  $-(K_{S}+\unicode[STIX]{x1D6E5}_{S})$ is
$-(K_{S}+\unicode[STIX]{x1D6E5}_{S})$ is  $f$-ample. Let
$f$-ample. Let  $h:\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner \rightarrow Z$ be the induced morphism. Then the following holds:
$h:\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner \rightarrow Z$ be the induced morphism. Then the following holds:
(i)
 $R^{i}h_{\ast }{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner }=0$ for
$R^{i}h_{\ast }{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner }=0$ for  $i>0$;
$i>0$;(ii)
 $R^{i}h_{\ast }(W{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ,\mathbb{Q}})=0$ for
$R^{i}h_{\ast }(W{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ,\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Proof. Let us prove (i). Taking the Stein factorisation of  $f$, we may assume that
$f$, we may assume that  $f_{\ast }{\mathcal{O}}_{S}={\mathcal{O}}_{Z}$. Furthermore, the problem is reduced to the case when
$f_{\ast }{\mathcal{O}}_{S}={\mathcal{O}}_{Z}$. Furthermore, the problem is reduced to the case when  $k$ is algebraically closed. Thanks to [Reference TanakaTan15, Theorems 2.12 and 3.5], it holds that
$k$ is algebraically closed. Thanks to [Reference TanakaTan15, Theorems 2.12 and 3.5], it holds that  $R^{i}f_{\ast }{\mathcal{O}}_{S}=0$ for
$R^{i}f_{\ast }{\mathcal{O}}_{S}=0$ for  $i>0$. If
$i>0$. If  $\dim Z\geqslant 1$, then we have a surjection:
$\dim Z\geqslant 1$, then we have a surjection:
 $$\begin{eqnarray}\displaystyle 0=R^{1}f_{\ast }{\mathcal{O}}_{S}\rightarrow R^{1}h_{\ast }{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner }, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=R^{1}f_{\ast }{\mathcal{O}}_{S}\rightarrow R^{1}h_{\ast }{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner }, & & \displaystyle \nonumber\end{eqnarray}$$ which implies that  $R^{i}h_{\ast }{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner }=0$ for
$R^{i}h_{\ast }{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner }=0$ for  $i>0$. Thus, we may assume that
$i>0$. Thus, we may assume that  $\dim Z=0$, i.e.
$\dim Z=0$, i.e.  $Z=\operatorname{Spec}\,k$. Then we have the exact sequence
$Z=\operatorname{Spec}\,k$. Then we have the exact sequence
 $$\begin{eqnarray}\displaystyle 0=H^{1}(S,{\mathcal{O}}_{S})\rightarrow H^{1}(\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ,{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner })\rightarrow H^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner )). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=H^{1}(S,{\mathcal{O}}_{S})\rightarrow H^{1}(\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ,{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner })\rightarrow H^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner )). & & \displaystyle \nonumber\end{eqnarray}$$ Hence, it suffices to prove that  $H^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=0$.
$H^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=0$.
It follows from Serre duality that
 $$\begin{eqnarray}\displaystyle h^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=h^{0}(S,{\mathcal{O}}_{S}(K_{S}+\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner )). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=h^{0}(S,{\mathcal{O}}_{S}(K_{S}+\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner )). & & \displaystyle \nonumber\end{eqnarray}$$ For an ample Cartier divisor  $A$, we have that
$A$, we have that
 $$\begin{eqnarray}\displaystyle (K_{S}+\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner )\cdot A=((K_{S}+\unicode[STIX]{x1D6E5}_{S})-\{\unicode[STIX]{x1D6E5}_{S}\})\cdot A<0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{S}+\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner )\cdot A=((K_{S}+\unicode[STIX]{x1D6E5}_{S})-\{\unicode[STIX]{x1D6E5}_{S}\})\cdot A<0, & & \displaystyle \nonumber\end{eqnarray}$$ which in turn implies that  $H^{0}(S,{\mathcal{O}}_{S}(K_{S}+\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=0$. Hence, it holds that
$H^{0}(S,{\mathcal{O}}_{S}(K_{S}+\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=0$. Hence, it holds that  $H^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=0$, as desired. This completes the proof of (i).
$H^{2}(S,{\mathcal{O}}_{S}(-\llcorner \unicode[STIX]{x1D6E5}_{S}\lrcorner ))=0$, as desired. This completes the proof of (i).
The assertion (ii) follows from (i) and [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.19]. ◻
Lemma 4.6. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6EF})$ be a three-dimensional
$(X,\unicode[STIX]{x1D6EF})$ be a three-dimensional  $\mathbb{Q}$-factorial dlt pair over
$\mathbb{Q}$-factorial dlt pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a projective surjective
$f:X\rightarrow Z$ be a projective surjective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$ such that:
$Z$ such that:
(i)
 $\dim X>\dim Z$;
$\dim X>\dim Z$;(ii)
 $f$ has connected fibres;
$f$ has connected fibres;(iii)
 $-(K_{X}+\unicode[STIX]{x1D6EF})$ is
$-(K_{X}+\unicode[STIX]{x1D6EF})$ is  $f$-ample; and
$f$-ample; and(iv) there exists an irreducible component
 $D_{0}$ of
$D_{0}$ of  $\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ such that
$\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ such that  $D_{0}$ is
$D_{0}$ is  $f$-ample.
$f$-ample.
Then
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }W{\mathcal{O}}_{\operatorname{Supp}\lfloor \unicode[STIX]{x1D6EF}\rfloor ,\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{Z,\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0)\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }W{\mathcal{O}}_{\operatorname{Supp}\lfloor \unicode[STIX]{x1D6EF}\rfloor ,\mathbb{Q}}\simeq \left\{\begin{array}{@{}ll@{}}W{\mathcal{O}}_{Z,\mathbb{Q}}\quad & (i=0),\\ 0\quad & (i>0)\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$holds.
Proof. Replacing  $Z$ by
$Z$ by  $Z^{\prime }$ for the Stein factorisation
$Z^{\prime }$ for the Stein factorisation  $X\rightarrow Z^{\prime }\rightarrow Z$ of
$X\rightarrow Z^{\prime }\rightarrow Z$ of  $f$, we may assume that
$f$, we may assume that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$. Let
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$. Let  $g:D_{0}\rightarrow Z$ be the induced morphism. Let
$g:D_{0}\rightarrow Z$ be the induced morphism. Let  $\llcorner \unicode[STIX]{x1D6EF}\lrcorner =\sum _{i=0}^{m}D_{i}$ be the irreducible decomposition.
$\llcorner \unicode[STIX]{x1D6EF}\lrcorner =\sum _{i=0}^{m}D_{i}$ be the irreducible decomposition.
Step 1. The isomorphism  $Rg_{\ast }W{\mathcal{O}}_{D_{0},\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}$ holds. In particular, Lemma 4.6 holds if
$Rg_{\ast }W{\mathcal{O}}_{D_{0},\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}$ holds. In particular, Lemma 4.6 holds if  $m=0$.
$m=0$.
Proof of Step 1.
We define an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6EF}_{D_{0}}$ by adjunction:
$\unicode[STIX]{x1D6EF}_{D_{0}}$ by adjunction:  $(K_{X}+\unicode[STIX]{x1D6EF})|_{D_{0}}=K_{D_{0}}+\unicode[STIX]{x1D6EF}_{D_{0}}$. It holds that
$(K_{X}+\unicode[STIX]{x1D6EF})|_{D_{0}}=K_{D_{0}}+\unicode[STIX]{x1D6EF}_{D_{0}}$. It holds that  $(D_{0},\unicode[STIX]{x1D6EF}_{D_{0}})$ is dlt and
$(D_{0},\unicode[STIX]{x1D6EF}_{D_{0}})$ is dlt and  $-(K_{D_{0}}+\unicode[STIX]{x1D6EF}_{D_{0}})$ is
$-(K_{D_{0}}+\unicode[STIX]{x1D6EF}_{D_{0}})$ is  $g$-ample. Hence, it follows from [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 3.3] that
$g$-ample. Hence, it follows from [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 3.3] that  $R^{i}g_{\ast }W{\mathcal{O}}_{D_{0},\mathbb{Q}}=0$ for
$R^{i}g_{\ast }W{\mathcal{O}}_{D_{0},\mathbb{Q}}=0$ for  $i>0$.
$i>0$.
In order to prove that  $g_{\ast }W{\mathcal{O}}_{D_{0},\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}$, it suffices to show that
$g_{\ast }W{\mathcal{O}}_{D_{0},\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}$, it suffices to show that  $g:D_{0}\rightarrow Z$ has connected fibres (Lemma 2.17). Since
$g:D_{0}\rightarrow Z$ has connected fibres (Lemma 2.17). Since  $Z$ is normal, it is enough to prove that
$Z$ is normal, it is enough to prove that  $D_{0}|_{F}$ is geometrically connected for the generic fibre
$D_{0}|_{F}$ is geometrically connected for the generic fibre  $F:=X\times _{Z}\operatorname{Spec}\,K(Z)$ of
$F:=X\times _{Z}\operatorname{Spec}\,K(Z)$ of  $f$. If
$f$. If  $\dim F\geqslant 2$, then the restriction
$\dim F\geqslant 2$, then the restriction  $D_{0}|_{F}$ is geometrically connected because
$D_{0}|_{F}$ is geometrically connected because  $D_{0}|_{F}$ is an ample
$D_{0}|_{F}$ is an ample  $\mathbb{Q}$-Cartier
$\mathbb{Q}$-Cartier  $\mathbb{Z}$-divisor on
$\mathbb{Z}$-divisor on  $F$. Thus, we may assume that
$F$. Thus, we may assume that  $\dim F=1$. Since
$\dim F=1$. Since  $-(K_{X}+\unicode[STIX]{x1D6EF})$ is
$-(K_{X}+\unicode[STIX]{x1D6EF})$ is  $f$-ample, the geometric generic fibre
$f$-ample, the geometric generic fibre  $\overline{F}:=F\times _{K(Z)}\overline{K(Z)}$ is
$\overline{F}:=F\times _{K(Z)}\overline{K(Z)}$ is  $\mathbb{P}_{\overline{K(Z)}}^{1}$. Moreover, it holds that
$\mathbb{P}_{\overline{K(Z)}}^{1}$. Moreover, it holds that
 $$\begin{eqnarray}\displaystyle 0>\deg (K_{X}+\unicode[STIX]{x1D6EF})|_{\overline{F}}\geqslant \deg (K_{\overline{F}}+D_{0}|_{\overline{F}})=-2+\deg (D_{0}|_{\overline{F}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0>\deg (K_{X}+\unicode[STIX]{x1D6EF})|_{\overline{F}}\geqslant \deg (K_{\overline{F}}+D_{0}|_{\overline{F}})=-2+\deg (D_{0}|_{\overline{F}}). & & \displaystyle \nonumber\end{eqnarray}$$ This implies that  $g$ has connected fibres. This completes the proof of Step 1.◻
$g$ has connected fibres. This completes the proof of Step 1.◻
Step 2. For any  $i\in \{1,\ldots ,m\}$, it holds that:
$i\in \{1,\ldots ,m\}$, it holds that:
(a)
 $\dim f(D_{i})<\dim D_{i}$; and
$\dim f(D_{i})<\dim D_{i}$; and(b)
 $f(D_{i})=f(D_{i}\,\cap \,D_{0})$.
$f(D_{i})=f(D_{i}\,\cap \,D_{0})$.
Proof of Step 2.
Let us prove (a). If  $\dim Z\leqslant 1$, then there is nothing to show. Thus, we may assume that
$\dim Z\leqslant 1$, then there is nothing to show. Thus, we may assume that  $\dim Z=2$. Assuming that there is
$\dim Z=2$. Assuming that there is  $i\in \{1,\ldots ,m\}$ such that
$i\in \{1,\ldots ,m\}$ such that  $f(D_{i})=Z$, let us derive a contradiction. Since a general fibre
$f(D_{i})=Z$, let us derive a contradiction. Since a general fibre  $F$ of
$F$ of  $f$ is
$f$ is  $\mathbb{P}^{1}$, it holds that
$\mathbb{P}^{1}$, it holds that
 $$\begin{eqnarray}\displaystyle (K_{X}+\unicode[STIX]{x1D6EF})\cdot F\geqslant (K_{X}+D_{0}+D_{i})\cdot F\geqslant 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{X}+\unicode[STIX]{x1D6EF})\cdot F\geqslant (K_{X}+D_{0}+D_{i})\cdot F\geqslant 0. & & \displaystyle \nonumber\end{eqnarray}$$ This contradicts the fact that  $-(K_{X}+\unicode[STIX]{x1D6EF})$ is
$-(K_{X}+\unicode[STIX]{x1D6EF})$ is  $f$-ample. Therefore,
$f$-ample. Therefore,  $D_{i}$ does not dominate
$D_{i}$ does not dominate  $Z$ for any
$Z$ for any  $i\in \{1,\ldots ,m\}$, which implies (a).
$i\in \{1,\ldots ,m\}$, which implies (a).
Let us prove (b). Fix an arbitrary closed point  $x\in f(D_{i})$. Since
$x\in f(D_{i})$. Since  $\dim f(D_{i})<\dim D_{i}$, there exists a curve
$\dim f(D_{i})<\dim D_{i}$, there exists a curve  $C$ on
$C$ on  $X$ contained in
$X$ contained in  $D_{i}\,\cap \,f^{-1}(x)$. Since
$D_{i}\,\cap \,f^{-1}(x)$. Since  $D_{0}$ is ample over
$D_{0}$ is ample over  $Z$, the contracted curve
$Z$, the contracted curve  $C$ intersects
$C$ intersects  $D_{0}$. This implies that
$D_{0}$. This implies that  $x\in f(D_{i}\,\cap \,D_{0})$. Thus, we get
$x\in f(D_{i}\,\cap \,D_{0})$. Thus, we get  $f(D_{i})=f(D_{i}\,\cap \,D_{0})$. Hence, (b) holds. This completes the proof of Step 2.◻
$f(D_{i})=f(D_{i}\,\cap \,D_{0})$. Hence, (b) holds. This completes the proof of Step 2.◻
Step 3. For any  $i\in \{1,\ldots ,m\}$, it holds that the induced homomorphism
$i\in \{1,\ldots ,m\}$, it holds that the induced homomorphism
 $$\begin{eqnarray}\displaystyle R^{q}f_{\ast }W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow R^{q}f_{\ast }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{q}f_{\ast }W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow R^{q}f_{\ast }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$ is an isomorphism for any  $q\geqslant 0$, where
$q\geqslant 0$, where  $E:=\bigcup _{j\in \{0,\ldots ,m\}\setminus \{i\}}D_{j}$.
$E:=\bigcup _{j\in \{0,\ldots ,m\}\setminus \{i\}}D_{j}$.
Proof of Step 3.
Set  $C:=f(D_{i})$ and let
$C:=f(D_{i})$ and let  $D_{i}\xrightarrow[{}]{f^{\prime }}C^{\prime }\xrightarrow[{}]{s}C$ be the Stein factorisation of
$D_{i}\xrightarrow[{}]{f^{\prime }}C^{\prime }\xrightarrow[{}]{s}C$ be the Stein factorisation of  $D_{i}\rightarrow C$. Let
$D_{i}\rightarrow C$. Let  $\unicode[STIX]{x1D6EF}_{D_{i}}$ be the effective
$\unicode[STIX]{x1D6EF}_{D_{i}}$ be the effective  $\mathbb{R}$-divisor on
$\mathbb{R}$-divisor on  $D_{i}$ defined by adjunction:
$D_{i}$ defined by adjunction:  $(K_{X}+\unicode[STIX]{x1D6EF})|_{D_{i}}=K_{D_{i}}+\unicode[STIX]{x1D6EF}_{D_{i}}$. Then the following properties hold:
$(K_{X}+\unicode[STIX]{x1D6EF})|_{D_{i}}=K_{D_{i}}+\unicode[STIX]{x1D6EF}_{D_{i}}$. Then the following properties hold:
(c)
 $(D_{i},\unicode[STIX]{x1D6EF}_{D_{i}})$ is dlt and
$(D_{i},\unicode[STIX]{x1D6EF}_{D_{i}})$ is dlt and  $\operatorname{Supp}(\lfloor \unicode[STIX]{x1D6EF}_{D_{i}}\rfloor )=D_{i}\,\cap \,E$;
$\operatorname{Supp}(\lfloor \unicode[STIX]{x1D6EF}_{D_{i}}\rfloor )=D_{i}\,\cap \,E$;(d)
 $-(K_{D_{i}}+\unicode[STIX]{x1D6EF}_{D_{i}})$ is
$-(K_{D_{i}}+\unicode[STIX]{x1D6EF}_{D_{i}})$ is  $f^{\prime }$-ample.
$f^{\prime }$-ample.
We have the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\llcorner \unicode[STIX]{x1D6EF}_{D_{i}}\lrcorner ,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\llcorner \unicode[STIX]{x1D6EF}_{D_{i}}\lrcorner ,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$By [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 3.3] and Lemma 4.5, it holds that
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i},\mathbb{Q}}=0\quad \text{and}\quad R^{i}f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i},\mathbb{Q}}=0\quad \text{and}\quad R^{i}f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}=0 & & \displaystyle \nonumber\end{eqnarray}$$ for  $i>0$, respectively. Hence, it suffices to prove that
$i>0$, respectively. Hence, it suffices to prove that  $f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}$ is an isomorphism. By Step 2(b), it is enough to prove that the induced morphism
$f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow f_{\ast }^{\prime }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}$ is an isomorphism. By Step 2(b), it is enough to prove that the induced morphism  $D_{i}\,\cap \,E\rightarrow C^{\prime }$ has connected fibres (Lemma 2.17), which follows from [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10]. This completes the proof of Step 3.◻
$D_{i}\,\cap \,E\rightarrow C^{\prime }$ has connected fibres (Lemma 2.17), which follows from [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 3.10]. This completes the proof of Step 3.◻
Step 4. The assertion of Lemma 4.6 holds.
Proof of Step 4.
We prove the assertion by induction on  $m$. By Step 1, there is nothing to show if
$m$. By Step 1, there is nothing to show if  $m=0$. Thus, assume that
$m=0$. Thus, assume that  $m>0$ and that the assertion of Lemma 4.6 holds if the number of the irreducible components of
$m>0$ and that the assertion of Lemma 4.6 holds if the number of the irreducible components of  $\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ is less than
$\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ is less than  $m$. Fix
$m$. Fix  $i\in \{1,\ldots ,m\}$. Since
$i\in \{1,\ldots ,m\}$. Since  $(X,\unicode[STIX]{x1D6EF}^{\prime }:=\unicode[STIX]{x1D6EF}-\unicode[STIX]{x1D716}D_{i})$ satisfies the same assumption as in Lemma 4.6 for sufficiently small
$(X,\unicode[STIX]{x1D6EF}^{\prime }:=\unicode[STIX]{x1D6EF}-\unicode[STIX]{x1D716}D_{i})$ satisfies the same assumption as in Lemma 4.6 for sufficiently small  $\unicode[STIX]{x1D716}>0$, it follows from the induction hypothesis that
$\unicode[STIX]{x1D716}>0$, it follows from the induction hypothesis that
 $$\begin{eqnarray}\displaystyle Rf_{\ast }W{\mathcal{O}}_{E,\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }W{\mathcal{O}}_{E,\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}, & & \displaystyle \nonumber\end{eqnarray}$$ where  $E:=\bigcup _{j\in \{0,\ldots ,m\}\setminus \{i\}}D_{j}$. By the Mayer–Vietoris exact sequence (Lemma 2.18)
$E:=\bigcup _{j\in \{0,\ldots ,m\}\setminus \{i\}}D_{j}$. By the Mayer–Vietoris exact sequence (Lemma 2.18)
 $$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{D_{i}\cup E,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i},\mathbb{Q}}\oplus W{\mathcal{O}}_{E,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow W{\mathcal{O}}_{D_{i}\cup E,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i},\mathbb{Q}}\oplus W{\mathcal{O}}_{E,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$it is sufficient to show that the induced homomorphism
 $$\begin{eqnarray}\displaystyle R^{q}f_{\ast }W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow R^{q}f_{\ast }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{q}f_{\ast }W{\mathcal{O}}_{D_{i},\mathbb{Q}}\rightarrow R^{q}f_{\ast }W{\mathcal{O}}_{D_{i}\cap E,\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$ is an isomorphism for any  $q\geqslant 0$. This is nothing but the assertion of Step 3. This completes the proof of Step 4.◻
$q\geqslant 0$. This is nothing but the assertion of Step 3. This completes the proof of Step 4.◻
Lemma 4.7. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6EF})$ be a three-dimensional
$(X,\unicode[STIX]{x1D6EF})$ be a three-dimensional  $\mathbb{Q}$-factorial dlt pair over
$\mathbb{Q}$-factorial dlt pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a
$f:X\rightarrow Z$ be a  $(K_{X}+\unicode[STIX]{x1D6EF})$-Mori fibre space to a quasi-projective
$(K_{X}+\unicode[STIX]{x1D6EF})$-Mori fibre space to a quasi-projective  $k$-variety
$k$-variety  $Z$. Suppose that
$Z$. Suppose that  $f(\operatorname{Supp}\lfloor \unicode[STIX]{x1D6EF}\rfloor )=Z$. Then
$f(\operatorname{Supp}\lfloor \unicode[STIX]{x1D6EF}\rfloor )=Z$. Then
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }WI_{\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }WI_{\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}=0 & & \displaystyle \nonumber\end{eqnarray}$$ for any  $i\geqslant 0$.
$i\geqslant 0$.
Proof. It follows from Theorem 3.11 that
 $$\begin{eqnarray}\displaystyle Rf_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}. & & \displaystyle \nonumber\end{eqnarray}$$ By  $f(\operatorname{Supp}\lfloor \unicode[STIX]{x1D6EF}\rfloor )=Z$, there exists an irreducible component
$f(\operatorname{Supp}\lfloor \unicode[STIX]{x1D6EF}\rfloor )=Z$, there exists an irreducible component  $D_{0}$ of
$D_{0}$ of  $\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ such that
$\llcorner \unicode[STIX]{x1D6EF}\lrcorner$ such that  $f(D_{0})=Z$. Since
$f(D_{0})=Z$. Since  $\unicode[STIX]{x1D70C}(X/Z)=1$, we have that
$\unicode[STIX]{x1D70C}(X/Z)=1$, we have that  $D_{0}$ is
$D_{0}$ is  $f$-ample. In particular, we may apply Lemma 4.6 and obtain the isomorphism
$f$-ample. In particular, we may apply Lemma 4.6 and obtain the isomorphism
 $$\begin{eqnarray}\displaystyle Rf_{\ast }W{\mathcal{O}}_{\operatorname{Supp}\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }W{\mathcal{O}}_{\operatorname{Supp}\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}\simeq W{\mathcal{O}}_{Z,\mathbb{Q}}. & & \displaystyle \nonumber\end{eqnarray}$$Therefore, by the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Supp}\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$the induced homomorphism
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow R^{i}f_{\ast }W{\mathcal{O}}_{\operatorname{Supp}\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow R^{i}f_{\ast }W{\mathcal{O}}_{\operatorname{Supp}\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}} & & \displaystyle \nonumber\end{eqnarray}$$ is an isomorphism for any  $i\geqslant 0$. Therefore,
$i\geqslant 0$. Therefore,  $R^{i}f_{\ast }WI_{\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}=0$ for any
$R^{i}f_{\ast }WI_{\llcorner \unicode[STIX]{x1D6EF}\lrcorner ,\mathbb{Q}}=0$ for any  $i\geqslant 0$.◻
$i\geqslant 0$.◻
4.3 Proof of the main theorem and related results
In this subsection, we prove the main theorem of this paper (Theorem 4.10) and a generalisation of it (Theorem 4.11). As a consequence, we obtain the Kollár–Shokurov connectedness theorem (Theorem 4.12).
Lemma 4.8. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional quasi-projective log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional quasi-projective log pair over  $k$. Let
$k$. Let  $f:Y\rightarrow X$ be a projective birational morphism that satisfies the properties (i)–(iii) of Proposition 2.10. Set
$f:Y\rightarrow X$ be a projective birational morphism that satisfies the properties (i)–(iii) of Proposition 2.10. Set  $\unicode[STIX]{x1D6E5}_{Y}$ to be the effective
$\unicode[STIX]{x1D6E5}_{Y}$ to be the effective  $\mathbb{R}$-divisor defined by
$\mathbb{R}$-divisor defined by  $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$. Then we have the following:
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$. Then we have the following:
(a)
 $f_{\ast }WI_{\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}}=WI_{\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{X}),\mathbb{Q}}$ holds;
$f_{\ast }WI_{\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}}=WI_{\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{X}),\mathbb{Q}}$ holds;(b)
 $R^{i}f_{\ast }WI_{\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}}=0$ holds for
$R^{i}f_{\ast }WI_{\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}}=0$ holds for  $i>0$.
$i>0$.
Proof. The condition (a) follows from the equation  $f(\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}))=\text{Nklt}(X,\unicode[STIX]{x1D6E5})$ (Lemma2.6).
$f(\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}))=\text{Nklt}(X,\unicode[STIX]{x1D6E5})$ (Lemma2.6).
Let us prove (b). By the  $W{\mathcal{O}}$-rationality of klt threefolds (Theorem 3.1(i)), the vanishing in (b) holds outside
$W{\mathcal{O}}$-rationality of klt threefolds (Theorem 3.1(i)), the vanishing in (b) holds outside  $\text{Nklt}(X,\unicode[STIX]{x1D6E5})$. The set of the non-
$\text{Nklt}(X,\unicode[STIX]{x1D6E5})$. The set of the non- $\mathbb{Q}$-factorial points on a three-dimensional klt pair is a zero-dimensional closed subset [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.15(4)]. Thus, after removing finitely many closed points of
$\mathbb{Q}$-factorial points on a three-dimensional klt pair is a zero-dimensional closed subset [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.15(4)]. Thus, after removing finitely many closed points of  $X\setminus \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$, we may assume that all the non-
$X\setminus \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$, we may assume that all the non- $\mathbb{Q}$-factorial points of
$\mathbb{Q}$-factorial points of  $X$ are contained in
$X$ are contained in  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$. Hence, it follows that
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$. Hence, it follows that  $\operatorname{Ex}(f)\subset f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$. Then we get
$\operatorname{Ex}(f)\subset f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$. Then we get
 $$\begin{eqnarray}\displaystyle \operatorname{Ex}(f)\subset f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Ex}(f)\subset f^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}), & & \displaystyle \nonumber\end{eqnarray}$$ where the equality holds by Proposition 2.10(iii). Since  $f$ is an isomorphism outside
$f$ is an isomorphism outside  $\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})$, it follows from [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.23] that
$\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y})$, it follows from [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.23] that  $R^{i}f_{\ast }WI_{\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}}=0$ holds for
$R^{i}f_{\ast }WI_{\text{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}}=0$ holds for  $i>0$. This completes the proof of (b).◻
$i>0$. This completes the proof of (b).◻
Proposition 4.9. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6FA})$ be a three-dimensional
$(X,\unicode[STIX]{x1D6FA})$ be a three-dimensional  $\mathbb{Q}$-factorial log pair over
$\mathbb{Q}$-factorial log pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a projective
$f:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$. Assume that:
$Z$. Assume that:
(i)
 $(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt;
$(X,\unicode[STIX]{x1D6FA}^{\wedge 1})$ is dlt;(ii)
 $K_{X}+\unicode[STIX]{x1D6FA}{\sim}_{f,\mathbb{R}}0$;
$K_{X}+\unicode[STIX]{x1D6FA}{\sim}_{f,\mathbb{R}}0$;(iii)
 $\unicode[STIX]{x1D6FA}$ is
$\unicode[STIX]{x1D6FA}$ is  $f$-big; and
$f$-big; and(iv)
 $\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{>}1}=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}$.
$\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{>}1}=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}$.
Then  $R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Proof. Taking the Stein factorisation of  $f$, we may assume that
$f$, we may assume that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$. We have that
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$. We have that
 $$\begin{eqnarray}\displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{>}1}=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}=\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{>}1}=\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1}=\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}), & & \displaystyle\end{eqnarray}$$where the second equality holds by (iv) and the third one follows from Proposition 2.7.
Step 1. The assertion of Proposition 4.9 holds if there is a  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-Mori fibre space
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-Mori fibre space  $g:X\rightarrow Z^{\prime }$ over
$g:X\rightarrow Z^{\prime }$ over  $Z$.
$Z$.
Proof of Step 1.
We have the induced morphisms
 $$\begin{eqnarray}\displaystyle f:X\xrightarrow[{}]{g}Z^{\prime }\xrightarrow[{}]{h}Z. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f:X\xrightarrow[{}]{g}Z^{\prime }\xrightarrow[{}]{h}Z. & & \displaystyle \nonumber\end{eqnarray}$$ Since  $\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1}$ is
$\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1}$ is  $g$-ample, it follows from (4.9.1) that
$g$-ample, it follows from (4.9.1) that  $g(\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1})=Z^{\prime }$. Therefore, Lemma 4.7 implies that
$g(\operatorname{Supp}\unicode[STIX]{x1D6FA}^{{\geqslant}1})=Z^{\prime }$. Therefore, Lemma 4.7 implies that  $Rg_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0$. Hence, we have that
$Rg_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0$. Hence, we have that
 $$\begin{eqnarray}\displaystyle Rf_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})\simeq Rh_{\ast }Rg_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})\simeq Rh_{\ast }Rg_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0. & & \displaystyle \nonumber\end{eqnarray}$$This completes the proof of Step 1. ◻
Step 2. In order to prove the assertion of Proposition 4.9, it is sufficient to prove the assertion under the following additional assumptions:
(i)
 $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$ is
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$ is  $f$-nef;
$f$-nef;(ii)
 $(X,\unicode[STIX]{x1D6FA})$ is not klt, i.e.
$(X,\unicode[STIX]{x1D6FA})$ is not klt, i.e.  $\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})\neq \emptyset$;
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}^{{\geqslant}1})\neq \emptyset$;(iii) the set-theoretic equation
 $\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=f^{-1}(Z_{1})$ holds for some closed subset
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=f^{-1}(Z_{1})$ holds for some closed subset  $Z_{1}$ of
$Z_{1}$ of  $Z$;
$Z$;(iv) if we set
 $Z_{0}:=Z\setminus Z_{1}$ and
$Z_{0}:=Z\setminus Z_{1}$ and  $X_{0}:=f^{-1}(Z_{0})$, then
$X_{0}:=f^{-1}(Z_{0})$, then  $X_{0}$ is of Fano type over
$X_{0}$ is of Fano type over  $Z_{0}$; and
$Z_{0}$; and(v)
 $\dim Z=1$.
$\dim Z=1$.
Proof of Step 2.
By Theorem 2.9, there exists a  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-MMP over
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-MMP over  $Z$ that terminates:
$Z$ that terminates:
 $$\begin{eqnarray}\displaystyle X=:X_{0}{\dashrightarrow}X_{1}{\dashrightarrow}\cdots {\dashrightarrow}X_{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X=:X_{0}{\dashrightarrow}X_{1}{\dashrightarrow}\cdots {\dashrightarrow}X_{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$ Let  $f_{i}:X_{i}\rightarrow Z$ be the induced morphism and let
$f_{i}:X_{i}\rightarrow Z$ be the induced morphism and let  $\unicode[STIX]{x1D6FA}_{i}$ be the push-forward of
$\unicode[STIX]{x1D6FA}_{i}$ be the push-forward of  $\unicode[STIX]{x1D6FA}$ on
$\unicode[STIX]{x1D6FA}$ on  $X_{i}$. Then
$X_{i}$. Then  $(X_{\ell },\unicode[STIX]{x1D6FA}_{\ell })$ still satisfies the conditions (i)–(iv) in Proposition 4.9. By Proposition 4.1, replacing
$(X_{\ell },\unicode[STIX]{x1D6FA}_{\ell })$ still satisfies the conditions (i)–(iv) in Proposition 4.9. By Proposition 4.1, replacing  $(X,\unicode[STIX]{x1D6FA})$ by
$(X,\unicode[STIX]{x1D6FA})$ by  $(X_{\ell },\unicode[STIX]{x1D6FA}_{\ell })$, we may assume that
$(X_{\ell },\unicode[STIX]{x1D6FA}_{\ell })$, we may assume that  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$ is
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$ is  $f$-nef or that there is a
$f$-nef or that there is a  $(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-Mori fibre space
$(K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1})$-Mori fibre space  $g:X\rightarrow Z^{\prime }$ over
$g:X\rightarrow Z^{\prime }$ over  $Z$. In the latter case, the assertion of Proposition 4.9 follows from Step 1. Thus, we may assume that (i) holds. If
$Z$. In the latter case, the assertion of Proposition 4.9 follows from Step 1. Thus, we may assume that (i) holds. If  $(X,\unicode[STIX]{x1D6FA})$ is klt, then (ii) and (iii) imply that
$(X,\unicode[STIX]{x1D6FA})$ is klt, then (ii) and (iii) imply that  $X$ is of Fano type over
$X$ is of Fano type over  $Z$. In this case, the assertion of Proposition 4.9 follows from Theorem 3.11. Thus, we may assume (ii).
$Z$. In this case, the assertion of Proposition 4.9 follows from Theorem 3.11. Thus, we may assume (ii).
Since  $K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1}{\sim}_{f,\mathbb{R}}-(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$, it holds that
$K_{X}+\unicode[STIX]{x1D6FA}^{\wedge 1}{\sim}_{f,\mathbb{R}}-(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$, it holds that  $-(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$ is
$-(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$ is  $f$-nef. Since
$f$-nef. Since  $\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1}$ is a non-zero effective divisor by (iv) and (ii), we have that
$\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1}$ is a non-zero effective divisor by (iv) and (ii), we have that  $\dim Z\geqslant 1$. If
$\dim Z\geqslant 1$. If  $z\in Z$ is a closed point such that
$z\in Z$ is a closed point such that  $f^{-1}(z)\,\cap \,\operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})\neq \emptyset$, then it follows that
$f^{-1}(z)\,\cap \,\operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})\neq \emptyset$, then it follows that  $f^{-1}(z)\subset \operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$ because
$f^{-1}(z)\subset \operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$ because  $-(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$ is
$-(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})$ is  $f$-nef. Thus, there exists a closed subset
$f$-nef. Thus, there exists a closed subset  $Z_{1}$ of
$Z_{1}$ of  $Z$ such that
$Z$ such that  $Z_{1}\subsetneq Z$ and
$Z_{1}\subsetneq Z$ and
 $$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=\operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})=f^{-1}(Z_{1}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})=\operatorname{Supp}(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D6FA}^{\wedge 1})=f^{-1}(Z_{1}), & & \displaystyle \nonumber\end{eqnarray}$$where the first equality follows from (4.9.1). Thus, (iii) holds. It is clear that (iii) implies (iv).
Therefore, assuming that  $\dim Z\neq 1$, it is enough to show the assertion of Proposition 4.9. Since
$\dim Z\neq 1$, it is enough to show the assertion of Proposition 4.9. Since  $\dim Z\geqslant 1$, we have
$\dim Z\geqslant 1$, we have  $\dim Z\geqslant 2$. Then there are finitely many closed points
$\dim Z\geqslant 2$. Then there are finitely many closed points  $z_{1},\ldots ,z_{n}$ of
$z_{1},\ldots ,z_{n}$ of  $Z_{0}$ such that
$Z_{0}$ such that  $R^{i}f_{\ast }{\mathcal{O}}_{X}|_{Z_{0}\setminus \{z_{1},\ldots ,z_{n}\}}=0$ for
$R^{i}f_{\ast }{\mathcal{O}}_{X}|_{Z_{0}\setminus \{z_{1},\ldots ,z_{n}\}}=0$ for  $i>0$. Indeed, if
$i>0$. Indeed, if  $\operatorname{Supp}(R^{i}f_{\ast }{\mathcal{O}}_{X})\,\cap \,Z_{0}$ contains a curve
$\operatorname{Supp}(R^{i}f_{\ast }{\mathcal{O}}_{X})\,\cap \,Z_{0}$ contains a curve  $C$, then it contradicts the vanishing obtained by [Reference TanakaTan18b, Theorem 3.3] for the morphism
$C$, then it contradicts the vanishing obtained by [Reference TanakaTan18b, Theorem 3.3] for the morphism  $X\times _{Z}\operatorname{Spec}{\mathcal{O}}_{Z,\unicode[STIX]{x1D709}_{C}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{Z,\unicode[STIX]{x1D709}_{C}}$, where
$X\times _{Z}\operatorname{Spec}{\mathcal{O}}_{Z,\unicode[STIX]{x1D709}_{C}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{Z,\unicode[STIX]{x1D709}_{C}}$, where  $\unicode[STIX]{x1D709}_{C}$ denotes the generic point of
$\unicode[STIX]{x1D709}_{C}$ denotes the generic point of  $C$. By (iii), [Reference Chatzistamatiou and RüllingCR12, Proposition 4.6.1] and
$C$. By (iii), [Reference Chatzistamatiou and RüllingCR12, Proposition 4.6.1] and  $R^{i}f_{\ast }{\mathcal{O}}_{X}|_{Z_{0}\setminus \{z_{1},\ldots ,z_{n}\}}=0$, it holds that
$R^{i}f_{\ast }{\mathcal{O}}_{X}|_{Z_{0}\setminus \{z_{1},\ldots ,z_{n}\}}=0$, it holds that
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z\setminus \{z_{1},\ldots ,z_{n}\}}=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z\setminus \{z_{1},\ldots ,z_{n}\}}=0 & & \displaystyle \nonumber\end{eqnarray}$$ for any  $i>0$. Since
$i>0$. Since  $X_{0}$ is of Fano type over
$X_{0}$ is of Fano type over  $Z_{0}$, it follows from Theorem 3.11 that
$Z_{0}$, it follows from Theorem 3.11 that
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z_{0}}=R^{i}(f|_{X_{0}})_{\ast }(W{\mathcal{O}}_{X_{0},\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z_{0}}=R^{i}(f|_{X_{0}})_{\ast }(W{\mathcal{O}}_{X_{0},\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ holds for any  $i>0$. Since
$i>0$. Since  $Z=Z_{0}\cup (Z\setminus \{z_{1},\ldots ,z_{n}\})$, we obtain
$Z=Z_{0}\cup (Z\setminus \{z_{1},\ldots ,z_{n}\})$, we obtain
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ for any  $i>0$. Thus, the assertion of Proposition 4.9 holds. This completes the proof of Step 2.◻
$i>0$. Thus, the assertion of Proposition 4.9 holds. This completes the proof of Step 2.◻
Step 3. Assume (i)–(v) in Step 2. There exists a commutative diagram of projective morphisms of normal varieties:

such that:
(vi)
 $f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}={\mathcal{O}}_{Z^{\prime }}$;
$f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}={\mathcal{O}}_{Z^{\prime }}$;(vii)
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ and  $\unicode[STIX]{x1D6FE}$ are finite universal homeomorphisms;
$\unicode[STIX]{x1D6FE}$ are finite universal homeomorphisms;(viii)
 $g$ is a log resolution of
$g$ is a log resolution of  $(X,\unicode[STIX]{x1D6FA})$ and
$(X,\unicode[STIX]{x1D6FA})$ and  $g^{\prime }$ is birational; and
$g^{\prime }$ is birational; and(ix) there are finitely many closed points
 $z_{1},\ldots ,z_{n}$ of
$z_{1},\ldots ,z_{n}$ of  $Z_{0}$ such that for
$Z_{0}$ such that for $$\begin{eqnarray}\displaystyle R^{i}h_{\ast }^{\prime }{\mathcal{O}}_{Y^{\prime }}|_{\unicode[STIX]{x1D6FE}^{-1}(Z_{0}\setminus \{z_{1},\ldots ,z_{n}\})}=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}h_{\ast }^{\prime }{\mathcal{O}}_{Y^{\prime }}|_{\unicode[STIX]{x1D6FE}^{-1}(Z_{0}\setminus \{z_{1},\ldots ,z_{n}\})}=0 & & \displaystyle \nonumber\end{eqnarray}$$ $i>0$, where
$i>0$, where  $h^{\prime }:=f^{\prime }\circ g^{\prime }$.
$h^{\prime }:=f^{\prime }\circ g^{\prime }$.
We set  $h:=f\circ g$ for later use.
$h:=f\circ g$ for later use.
Proof of Step 3.
Set  ${\mathcal{X}}:=X_{K(Z)}$. There exist a finite purely inseparable extension
${\mathcal{X}}:=X_{K(Z)}$. There exist a finite purely inseparable extension  $K(Z)\subset L$ and a projective birational
$K(Z)\subset L$ and a projective birational  $L$-morphism
$L$-morphism  $\mathfrak{g}_{1}^{\prime }:{\mathcal{Y}}_{1}^{\prime }\rightarrow {\mathcal{X}}^{\prime }$ of projective normal surfaces over
$\mathfrak{g}_{1}^{\prime }:{\mathcal{Y}}_{1}^{\prime }\rightarrow {\mathcal{X}}^{\prime }$ of projective normal surfaces over  $L$ such that there is a finite universal homeomorphism
$L$ such that there is a finite universal homeomorphism  $\mathfrak{a}:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{X}}$,
$\mathfrak{a}:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{X}}$,  ${\mathcal{X}}^{\prime }\times _{L}\overline{L}$ is isomorphic to the normalisation of
${\mathcal{X}}^{\prime }\times _{L}\overline{L}$ is isomorphic to the normalisation of  $({\mathcal{X}}\times _{K(Z)}\overline{K(Z)})_{\operatorname{red}}$ and
$({\mathcal{X}}\times _{K(Z)}\overline{K(Z)})_{\operatorname{red}}$ and  $\mathfrak{g}_{1}^{\prime }\times _{L}\overline{L}:{\mathcal{Y}}_{1}^{\prime }\times _{L}\overline{L}\rightarrow {\mathcal{X}}^{\prime }\times _{L}\overline{L}$ is a resolution of singularities of
$\mathfrak{g}_{1}^{\prime }\times _{L}\overline{L}:{\mathcal{Y}}_{1}^{\prime }\times _{L}\overline{L}\rightarrow {\mathcal{X}}^{\prime }\times _{L}\overline{L}$ is a resolution of singularities of  ${\mathcal{X}}^{\prime }\times _{L}\overline{L}$ (cf. Lemma 3.3). In particular,
${\mathcal{X}}^{\prime }\times _{L}\overline{L}$ (cf. Lemma 3.3). In particular,  ${\mathcal{Y}}_{1}^{\prime }$ is smooth over
${\mathcal{Y}}_{1}^{\prime }$ is smooth over  $L$. There exists a normal projective surface
$L$. There exists a normal projective surface  ${\mathcal{Y}}_{1}$ over
${\mathcal{Y}}_{1}$ over  $K(Z)$ which completes the following commutative diagram:
$K(Z)$ which completes the following commutative diagram:

where  $\mathfrak{g}_{1}$ is a projective birational morphism and
$\mathfrak{g}_{1}$ is a projective birational morphism and  $\mathfrak{b}_{1}$ is a finite universal homeomorphism. Indeed, we have
$\mathfrak{b}_{1}$ is a finite universal homeomorphism. Indeed, we have  $K({\mathcal{Y}}_{1}^{\prime })^{p^{e}}=K({\mathcal{X}}^{\prime })^{p^{e}}\subset K({\mathcal{X}})$ for sufficiently large
$K({\mathcal{Y}}_{1}^{\prime })^{p^{e}}=K({\mathcal{X}}^{\prime })^{p^{e}}\subset K({\mathcal{X}})$ for sufficiently large  $e\in \mathbb{Z}_{{>}0}$ and hence we can find such
$e\in \mathbb{Z}_{{>}0}$ and hence we can find such  ${\mathcal{Y}}_{1}$ by taking the normalisation of
${\mathcal{Y}}_{1}$ by taking the normalisation of  ${\mathcal{Y}}_{1}^{\prime \prime }$ in
${\mathcal{Y}}_{1}^{\prime \prime }$ in  $K({\mathcal{X}})$, where
$K({\mathcal{X}})$, where  ${\mathcal{Y}}_{1}^{\prime }\rightarrow {\mathcal{Y}}_{1}^{\prime }=:{\mathcal{Y}}_{1}^{\prime \prime }$ denotes the
${\mathcal{Y}}_{1}^{\prime }\rightarrow {\mathcal{Y}}_{1}^{\prime }=:{\mathcal{Y}}_{1}^{\prime \prime }$ denotes the  $e$th iterated absolute Frobenius morphism. Since
$e$th iterated absolute Frobenius morphism. Since  $({\mathcal{X}}\times _{K(Z)}\overline{K(Z)})_{\operatorname{red}}$ is a rational surface (Proposition 2.26),
$({\mathcal{X}}\times _{K(Z)}\overline{K(Z)})_{\operatorname{red}}$ is a rational surface (Proposition 2.26),  ${\mathcal{Y}}_{1}^{\prime }\times _{L}\overline{L}$ is a smooth rational surface. Therefore, we obtain
${\mathcal{Y}}_{1}^{\prime }\times _{L}\overline{L}$ is a smooth rational surface. Therefore, we obtain  $H^{i}({\mathcal{Y}}_{1}^{\prime },{\mathcal{O}}_{{\mathcal{Y}}_{1}^{\prime }})=0$ for
$H^{i}({\mathcal{Y}}_{1}^{\prime },{\mathcal{O}}_{{\mathcal{Y}}_{1}^{\prime }})=0$ for  $i>0$.
$i>0$.
Then there exists a commutative diagram of projective morphisms of normal varieties:

such that the horizontal arrows are finite universal homeomorphisms and the base change of (
4.9.4) by  $(-)\times _{Z}\operatorname{Spec}K(Z)$ is (4.9.3). Let
$(-)\times _{Z}\operatorname{Spec}K(Z)$ is (4.9.3). Let  $g:Y\rightarrow X$ be a log resolution of
$g:Y\rightarrow X$ be a log resolution of  $(X,\unicode[STIX]{x1D6FA})$ which factors through
$(X,\unicode[STIX]{x1D6FA})$ which factors through  $g_{1}:Y_{1}\rightarrow X$:
$g_{1}:Y_{1}\rightarrow X$:
 $$\begin{eqnarray}\displaystyle g:Y\rightarrow Y_{1}\xrightarrow[{}]{g_{1}}X. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g:Y\rightarrow Y_{1}\xrightarrow[{}]{g_{1}}X. & & \displaystyle \nonumber\end{eqnarray}$$ Set  $Y^{\prime }$ to be the normalisation of
$Y^{\prime }$ to be the normalisation of  $Y$ in
$Y$ in  $K(Y_{1}^{\prime })$. Automatically, we obtain a commutative diagram of the induced morphisms:
$K(Y_{1}^{\prime })$. Automatically, we obtain a commutative diagram of the induced morphisms:

Combining (
4.9.4) and (
4.9.5), we obtain a commutative diagram (4.9.2). By the construction, the properties (vi)–(viii) hold. It suffices to show (ix). For  ${\mathcal{Y}}^{\prime }:=Y^{\prime }\times _{Z}\operatorname{Spec}\,K(Z)$,
${\mathcal{Y}}^{\prime }:=Y^{\prime }\times _{Z}\operatorname{Spec}\,K(Z)$,  $\mathfrak{g}_{2}^{\prime }:{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}_{1}^{\prime }$ is a birational morphism of projective normal surfaces over
$\mathfrak{g}_{2}^{\prime }:{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}_{1}^{\prime }$ is a birational morphism of projective normal surfaces over  $\operatorname{Spec}\,K(Z)$. As
$\operatorname{Spec}\,K(Z)$. As  ${\mathcal{Y}}_{1}^{\prime }$ is smooth,
${\mathcal{Y}}_{1}^{\prime }$ is smooth,  ${\mathcal{Y}}^{\prime }$ has at worst rational singularities by [Reference LipmanLip69, Proposition 1.2(2)] or the same argument as in Lemma 3.7. Since
${\mathcal{Y}}^{\prime }$ has at worst rational singularities by [Reference LipmanLip69, Proposition 1.2(2)] or the same argument as in Lemma 3.7. Since  $H^{i}({\mathcal{Y}}_{1}^{\prime },{\mathcal{O}}_{{\mathcal{Y}}_{1}^{\prime }})=0$ for
$H^{i}({\mathcal{Y}}_{1}^{\prime },{\mathcal{O}}_{{\mathcal{Y}}_{1}^{\prime }})=0$ for  $i>0$, we have
$i>0$, we have  $H^{i}({\mathcal{Y}}^{\prime },{\mathcal{O}}_{{\mathcal{Y}}^{\prime }})=0$ for
$H^{i}({\mathcal{Y}}^{\prime },{\mathcal{O}}_{{\mathcal{Y}}^{\prime }})=0$ for  $i>0$. Thus, (ix) holds. This completes the proof of Step 3.◻
$i>0$. Thus, (ix) holds. This completes the proof of Step 3.◻
Step 4. Assume (i)–(v) in Step 2. We use the same notation as in Step 3. Then there exists an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $D$ on
$D$ on  $Y$ such that:
$Y$ such that:
(x)
 $(Y,D)$ is dlt;
$(Y,D)$ is dlt;(xi) the set-theoretic equation
 $\operatorname{Nklt}(Y,D)=h^{-1}(Z_{1})$ holds; and
$\operatorname{Nklt}(Y,D)=h^{-1}(Z_{1})$ holds; and(xii)
 $Rg_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})\simeq WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}}$.
$Rg_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})\simeq WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}}$.
Proof of Step 4.
Let  $E$ be the sum of the
$E$ be the sum of the  $g$-exceptional prime divisors
$g$-exceptional prime divisors  $F$ such that
$F$ such that  $F\subset h^{-1}(Z_{1})$. Let
$F\subset h^{-1}(Z_{1})$. Let  $E^{\prime }$ be the sum of the
$E^{\prime }$ be the sum of the  $g$-exceptional prime divisors
$g$-exceptional prime divisors  $F^{\prime }$ such that
$F^{\prime }$ such that  $F^{\prime }\not \subset h^{-1}(Z_{1})$. Set
$F^{\prime }\not \subset h^{-1}(Z_{1})$. Set
 $$\begin{eqnarray}\displaystyle D:=g_{\ast }^{-1}\unicode[STIX]{x1D6FA}^{\wedge 1}+E+(1-\unicode[STIX]{x1D716})E^{\prime } & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D:=g_{\ast }^{-1}\unicode[STIX]{x1D6FA}^{\wedge 1}+E+(1-\unicode[STIX]{x1D716})E^{\prime } & & \displaystyle \nonumber\end{eqnarray}$$ for a sufficiently small positive real number  $\unicode[STIX]{x1D716}$. It is clear that (x) and (xi) hold.
$\unicode[STIX]{x1D716}$. It is clear that (x) and (xi) hold.
Let us prove that (xii) holds. We fix a closed point  $x$ of
$x$ of  $X$. Since the problem is local on
$X$. Since the problem is local on  $X$, it is enough to find an open neighbourhood
$X$, it is enough to find an open neighbourhood  $\widetilde{X}$ of
$\widetilde{X}$ of  $x\in X$ such that
$x\in X$ such that  $Rg_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})|_{\widetilde{X}}\simeq WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}}|_{\widetilde{X}}$.
$Rg_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})|_{\widetilde{X}}\simeq WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}}|_{\widetilde{X}}$.
By Theorem 2.9, there is a  $(K_{Y}+D)$-MMP over
$(K_{Y}+D)$-MMP over  $X$ that terminates:
$X$ that terminates:
 $$\begin{eqnarray}\displaystyle Y=Y_{0}\overset{\unicode[STIX]{x1D711}_{0}}{{\dashrightarrow}}Y_{1}\overset{\unicode[STIX]{x1D711}_{0}}{{\dashrightarrow}}\cdots \overset{\unicode[STIX]{x1D711}_{\ell -1}}{{\dashrightarrow}}Y_{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y=Y_{0}\overset{\unicode[STIX]{x1D711}_{0}}{{\dashrightarrow}}Y_{1}\overset{\unicode[STIX]{x1D711}_{0}}{{\dashrightarrow}}\cdots \overset{\unicode[STIX]{x1D711}_{\ell -1}}{{\dashrightarrow}}Y_{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$ Let  $g_{j}:Y_{j}\rightarrow X$ be the induced morphism and let
$g_{j}:Y_{j}\rightarrow X$ be the induced morphism and let  $D_{j}$ be the push-forward of
$D_{j}$ be the push-forward of  $D$ on
$D$ on  $Y_{j}$. By the construction of
$Y_{j}$. By the construction of  $D$ and the
$D$ and the  $\mathbb{Q}$-factoriality of
$\mathbb{Q}$-factoriality of  $X$,
$X$,
 $$\begin{eqnarray}\displaystyle g_{j}^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}))=\operatorname{Nklt}(Y_{j},D_{j}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{j}^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}))=\operatorname{Nklt}(Y_{j},D_{j}) & & \displaystyle\end{eqnarray}$$ holds for any  $j\in \{0,\ldots ,\ell \}$. In particular, it holds that
$j\in \{0,\ldots ,\ell \}$. In particular, it holds that  $g_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})=WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}}$. Thus, it is enough to prove that
$g_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})=WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}}$. Thus, it is enough to prove that
 $$\begin{eqnarray}\displaystyle R^{i}(g_{j})_{\ast }(WI_{\operatorname{Nklt}(Y_{j},\unicode[STIX]{x1D6FA}_{Y_{j}}),\mathbb{Q}})=0 & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}(g_{j})_{\ast }(WI_{\operatorname{Nklt}(Y_{j},\unicode[STIX]{x1D6FA}_{Y_{j}}),\mathbb{Q}})=0 & & \displaystyle\end{eqnarray}$$ for any  $i>0$ and
$i>0$ and  $j\in \{0,\ldots ,\ell \}$. We prove this by descending induction on
$j\in \{0,\ldots ,\ell \}$. We prove this by descending induction on  $j$.
$j$.
We first prove (4.9.7) for  $j=\ell$. We have
$j=\ell$. We have
 $$\begin{eqnarray}\displaystyle K_{Y}+D{\sim}_{X,\mathbb{R}}g_{\ast }^{-1}\unicode[STIX]{x1D6FA}^{\wedge 1}+E+(1-\unicode[STIX]{x1D716})E^{\prime }-\unicode[STIX]{x1D6FA}_{Y}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{Y}+D{\sim}_{X,\mathbb{R}}g_{\ast }^{-1}\unicode[STIX]{x1D6FA}^{\wedge 1}+E+(1-\unicode[STIX]{x1D716})E^{\prime }-\unicode[STIX]{x1D6FA}_{Y}, & & \displaystyle \nonumber\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FA}_{Y}$ is defined by
$\unicode[STIX]{x1D6FA}_{Y}$ is defined by  $K_{Y}+\unicode[STIX]{x1D6FA}_{Y}=g^{\ast }(K_{X}+\unicode[STIX]{x1D6FA})$. Since
$K_{Y}+\unicode[STIX]{x1D6FA}_{Y}=g^{\ast }(K_{X}+\unicode[STIX]{x1D6FA})$. Since  $\unicode[STIX]{x1D716}$ is sufficiently small, it follows from the negativity lemma that any
$\unicode[STIX]{x1D716}$ is sufficiently small, it follows from the negativity lemma that any  $g$-exceptional prime divisor
$g$-exceptional prime divisor  $G$ with
$G$ with  $a_{G}(X,\unicode[STIX]{x1D6FA})>0$ is contracted on
$a_{G}(X,\unicode[STIX]{x1D6FA})>0$ is contracted on  $Y_{\ell }$. Since
$Y_{\ell }$. Since  $X$ is
$X$ is  $\mathbb{Q}$-factorial,
$\mathbb{Q}$-factorial,  $Y_{\ell }\rightarrow X$ is isomorphic over
$Y_{\ell }\rightarrow X$ is isomorphic over  $X\setminus \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$. Therefore, we obtain
$X\setminus \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$. Therefore, we obtain
 $$\begin{eqnarray}\displaystyle \operatorname{Ex}(g_{\ell })\subset g_{\ell }^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}))=\operatorname{Nklt}(Y_{\ell },D_{\ell }). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Ex}(g_{\ell })\subset g_{\ell }^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}))=\operatorname{Nklt}(Y_{\ell },D_{\ell }). & & \displaystyle \nonumber\end{eqnarray}$$ Then [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.23] implies that the equation (4.9.7) holds when  $j=\ell$.
$j=\ell$.
Suppose that  $0\leqslant j<\ell$. Then
$0\leqslant j<\ell$. Then  $\unicode[STIX]{x1D711}_{j}:Y_{j}{\dashrightarrow}Y_{j+1}$ is either a divisorial contraction or a flip. We first treat the case when
$\unicode[STIX]{x1D711}_{j}:Y_{j}{\dashrightarrow}Y_{j+1}$ is either a divisorial contraction or a flip. We first treat the case when  $\unicode[STIX]{x1D711}_{j}$ is a divisorial contraction. In order to prove the equation (4.9.7) by induction, it is sufficient to show that
$\unicode[STIX]{x1D711}_{j}$ is a divisorial contraction. In order to prove the equation (4.9.7) by induction, it is sufficient to show that
 $$\begin{eqnarray}\displaystyle R^{i}(\unicode[STIX]{x1D711}_{j})_{\ast }(WI_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}})=0 & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}(\unicode[STIX]{x1D711}_{j})_{\ast }(WI_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}})=0 & & \displaystyle\end{eqnarray}$$ for  $i>0$. Let
$i>0$. Let  $G=\text{Ex}(\unicode[STIX]{x1D711}_{j})$ be the contracted divisor. Suppose that
$G=\text{Ex}(\unicode[STIX]{x1D711}_{j})$ be the contracted divisor. Suppose that  $\dim \unicode[STIX]{x1D711}_{j}(G)=0$. If
$\dim \unicode[STIX]{x1D711}_{j}(G)=0$. If  $G\subset \operatorname{Nklt}(Y_{j},D_{j})$, then the equation (4.9.8) follows from [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.23]. If
$G\subset \operatorname{Nklt}(Y_{j},D_{j})$, then the equation (4.9.8) follows from [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.23]. If  $G\not \subset \operatorname{Nklt}(Y_{j},D_{j})$, then
$G\not \subset \operatorname{Nklt}(Y_{j},D_{j})$, then  $G\,\cap \,\operatorname{Nklt}(Y_{j},D_{j})=\emptyset$ holds by (4.9.6). Therefore, since
$G\,\cap \,\operatorname{Nklt}(Y_{j},D_{j})=\emptyset$ holds by (4.9.6). Therefore, since  $g_{j}$ is an isomorphism outside
$g_{j}$ is an isomorphism outside  $G$, it is sufficient to check the equation (4.9.8) outside
$G$, it is sufficient to check the equation (4.9.8) outside  $\operatorname{Nklt}(Y_{j},D_{j})$ and this follows from Theorem 3.11. Suppose that
$\operatorname{Nklt}(Y_{j},D_{j})$ and this follows from Theorem 3.11. Suppose that  $\dim \unicode[STIX]{x1D711}_{j}(G)=1$. In this case, the relative dimension of
$\dim \unicode[STIX]{x1D711}_{j}(G)=1$. In this case, the relative dimension of  $\unicode[STIX]{x1D711}$ is one and therefore it is sufficient to show the equation (4.9.8) only for
$\unicode[STIX]{x1D711}$ is one and therefore it is sufficient to show the equation (4.9.8) only for  $i=1$ (cf. [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.20]). This follows from the exact sequence
$i=1$ (cf. [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.20]). This follows from the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}}\rightarrow W{\mathcal{O}}_{Y_{j},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}}\rightarrow W{\mathcal{O}}_{Y_{j},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$ the fact that  $R^{1}(\unicode[STIX]{x1D711}_{j})_{\ast }W{\mathcal{O}}_{Y_{j},\mathbb{Q}}=0$ by Theorem 3.11 and the surjectivity of
$R^{1}(\unicode[STIX]{x1D711}_{j})_{\ast }W{\mathcal{O}}_{Y_{j},\mathbb{Q}}=0$ by Theorem 3.11 and the surjectivity of  $(\unicode[STIX]{x1D711}_{j})_{\ast }W{\mathcal{O}}_{Y_{j},\mathbb{Q}}\rightarrow (\unicode[STIX]{x1D711}_{j})_{\ast }W{\mathcal{O}}_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}}$ by Theorem 2.15.
$(\unicode[STIX]{x1D711}_{j})_{\ast }W{\mathcal{O}}_{Y_{j},\mathbb{Q}}\rightarrow (\unicode[STIX]{x1D711}_{j})_{\ast }W{\mathcal{O}}_{\operatorname{Nklt}(Y_{j},D_{j}),\mathbb{Q}}$ by Theorem 2.15.
Next we assume that  $\unicode[STIX]{x1D711}_{j}:Y_{j}{\dashrightarrow}Y_{j+1}$ is a flip. Let
$\unicode[STIX]{x1D711}_{j}:Y_{j}{\dashrightarrow}Y_{j+1}$ is a flip. Let  $\unicode[STIX]{x1D713}:Y_{j}\rightarrow V$ be the corresponding flipping contraction and let
$\unicode[STIX]{x1D713}:Y_{j}\rightarrow V$ be the corresponding flipping contraction and let  $\unicode[STIX]{x1D713}^{+}:Y_{j+1}\rightarrow V$ be the induced morphism. In order to prove the equation (4.9.7) by induction, it is sufficient to show that
$\unicode[STIX]{x1D713}^{+}:Y_{j+1}\rightarrow V$ be the induced morphism. In order to prove the equation (4.9.7) by induction, it is sufficient to show that
 $$\begin{eqnarray}\displaystyle R^{i}\unicode[STIX]{x1D713}_{\ast }(WI_{\operatorname{Nklt}(Y_{j},\unicode[STIX]{x1D6FA}_{Y_{j}}),\mathbb{Q}})=R^{i}\unicode[STIX]{x1D713}_{\ast }^{+}(WI_{\operatorname{ Nklt}(Y_{j+1},\unicode[STIX]{x1D6FA}_{Y_{j+1}}),\mathbb{Q}}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}\unicode[STIX]{x1D713}_{\ast }(WI_{\operatorname{Nklt}(Y_{j},\unicode[STIX]{x1D6FA}_{Y_{j}}),\mathbb{Q}})=R^{i}\unicode[STIX]{x1D713}_{\ast }^{+}(WI_{\operatorname{ Nklt}(Y_{j+1},\unicode[STIX]{x1D6FA}_{Y_{j+1}}),\mathbb{Q}}) & & \displaystyle\end{eqnarray}$$ for any  $i\geqslant 0$. When
$i\geqslant 0$. When  $i=0$, the equation (4.9.9) can be confirmed by the set-theoretic equation
$i=0$, the equation (4.9.9) can be confirmed by the set-theoretic equation  $\unicode[STIX]{x1D713}(\operatorname{Nklt}(Y_{j},\unicode[STIX]{x1D6FA}_{Y_{j}}))=\unicode[STIX]{x1D713}^{+}(\operatorname{Nklt}(Y_{j+1},\unicode[STIX]{x1D6FA}_{Y_{j+1}}))$ and this follows from the equation (4.9.6). In what follows, we prove that both sides in the equation (4.9.9) are zero for
$\unicode[STIX]{x1D713}(\operatorname{Nklt}(Y_{j},\unicode[STIX]{x1D6FA}_{Y_{j}}))=\unicode[STIX]{x1D713}^{+}(\operatorname{Nklt}(Y_{j+1},\unicode[STIX]{x1D6FA}_{Y_{j+1}}))$ and this follows from the equation (4.9.6). In what follows, we prove that both sides in the equation (4.9.9) are zero for  $i\geqslant 1$. Since we work around a fixed closed point
$i\geqslant 1$. Since we work around a fixed closed point  $x\in X$, after replacing
$x\in X$, after replacing  $X$ by an open neighbourhood of
$X$ by an open neighbourhood of  $x\in X$, we may assume that
$x\in X$, we may assume that  $g_{j}(\operatorname{Ex}(\unicode[STIX]{x1D713}))=\{x\}$. There are the following two cases:
$g_{j}(\operatorname{Ex}(\unicode[STIX]{x1D713}))=\{x\}$. There are the following two cases:  $x\in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$ and
$x\in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$ and  $x\not \in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$. In the case when
$x\not \in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$. In the case when  $x\in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$, it follows from (4.9.6) that
$x\in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$, it follows from (4.9.6) that  $\operatorname{Ex}(\unicode[STIX]{x1D713})\subset \operatorname{Nklt}(Y_{j},D_{j})$ and
$\operatorname{Ex}(\unicode[STIX]{x1D713})\subset \operatorname{Nklt}(Y_{j},D_{j})$ and  $\operatorname{Ex}(\unicode[STIX]{x1D713}^{+})\subset \operatorname{Nklt}(Y_{j+1},D_{j+1})$. Then both sides in the equation (4.9.9) are zero for
$\operatorname{Ex}(\unicode[STIX]{x1D713}^{+})\subset \operatorname{Nklt}(Y_{j+1},D_{j+1})$. Then both sides in the equation (4.9.9) are zero for  $i\geqslant 1$ by [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.23]. In the case when
$i\geqslant 1$ by [Reference Gongyo, Nakamura and TanakaGNT19, Proposition 2.23]. In the case when  $x\not \in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$, we may assume that
$x\not \in \operatorname{Nklt}(X,\unicode[STIX]{x1D6FA})$, we may assume that  $(X,\unicode[STIX]{x1D6FA})$ is klt and hence so is each
$(X,\unicode[STIX]{x1D6FA})$ is klt and hence so is each  $(Y_{j},D_{j})$. Then both sides in the equation (4.9.9) are zero for
$(Y_{j},D_{j})$. Then both sides in the equation (4.9.9) are zero for  $i\geqslant 1$ by Theorem 3.11. This completes the proof of Step 4.◻
$i\geqslant 1$ by Theorem 3.11. This completes the proof of Step 4.◻
Proof. We use the same notation as in Step 3 and Step 4. By (vii), (ix), (xi) and [Reference Chatzistamatiou and RüllingCR12, Proposition 4.6.1], it holds that
 $$\begin{eqnarray}\displaystyle R^{i}h_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})|_{Z\setminus \{z_{1},\ldots ,z_{n}\}}=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}h_{\ast }(WI_{\operatorname{Nklt}(Y,D),\mathbb{Q}})|_{Z\setminus \{z_{1},\ldots ,z_{n}\}}=0 & & \displaystyle \nonumber\end{eqnarray}$$ for any  $i>0$. Then (xii) implies that
$i>0$. Then (xii) implies that
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z\setminus \{z_{1},\ldots ,z_{n}\}}=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z\setminus \{z_{1},\ldots ,z_{n}\}}=0 & & \displaystyle \nonumber\end{eqnarray}$$ for any  $i>0$. Since
$i>0$. Since  $X_{0}$ is of Fano type over
$X_{0}$ is of Fano type over  $Z_{0}$, it follows from Theorem 3.11 that
$Z_{0}$, it follows from Theorem 3.11 that
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z_{0}}=R^{i}(f|_{X_{0}})_{\ast }(W{\mathcal{O}}_{X_{0},\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})|_{Z_{0}}=R^{i}(f|_{X_{0}})_{\ast }(W{\mathcal{O}}_{X_{0},\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ holds for any  $i>0$. Since
$i>0$. Since  $Z=Z_{0}\cup (Z\setminus \{z_{1},\ldots ,z_{n}\})$, we obtain
$Z=Z_{0}\cup (Z\setminus \{z_{1},\ldots ,z_{n}\})$, we obtain
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6FA}),\mathbb{Q}})=0. & & \displaystyle \nonumber\end{eqnarray}$$This completes the proof of Step 5. ◻
Theorem 4.10. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a projective
$f:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$. Assume that
$Z$. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Then
$f$-big. Then  $R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=0$ for  $i>0$.
$i>0$.
Proof. We divide the proof into two steps.
Step 1. The assertion of Theorem 4.10 holds if  $X$ is
$X$ is  $\mathbb{Q}$-factorial and
$\mathbb{Q}$-factorial and  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-ample.
$f$-ample.
Proof of Step 1.
Let  $g:Y\rightarrow X$ be a projective birational morphism satisfying the properties (i)–(iii) in Proposition 2.10. Let
$g:Y\rightarrow X$ be a projective birational morphism satisfying the properties (i)–(iii) in Proposition 2.10. Let  $\unicode[STIX]{x1D6E5}_{Y}$ be the
$\unicode[STIX]{x1D6E5}_{Y}$ be the  $\mathbb{R}$-divisor on
$\mathbb{R}$-divisor on  $Y$ defined by
$Y$ defined by  $g^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})=K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$. Then
$g^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})=K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$. Then  $(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1})$ is dlt. It follows from Lemma 4.8 that
$(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1})$ is dlt. It follows from Lemma 4.8 that
 $$\begin{eqnarray}\displaystyle Rg_{\ast }(WI_{\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}})\simeq WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rg_{\ast }(WI_{\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}})\simeq WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}. & & \displaystyle \nonumber\end{eqnarray}$$Therefore, it holds that
 $$\begin{eqnarray}\displaystyle Rh_{\ast }(WI_{\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}})\simeq Rf_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rh_{\ast }(WI_{\operatorname{Nklt}(Y,\unicode[STIX]{x1D6E5}_{Y}),\mathbb{Q}})\simeq Rf_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}), & & \displaystyle\end{eqnarray}$$ where  $h:Y\xrightarrow[{}]{g}X\xrightarrow[{}]{f}Z$ is the composition. Thanks to (4.10.1) and Proposition 4.9, it suffices to find an effective
$h:Y\xrightarrow[{}]{g}X\xrightarrow[{}]{f}Z$ is the composition. Thanks to (4.10.1) and Proposition 4.9, it suffices to find an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6FA}_{Y}$ on
$\unicode[STIX]{x1D6FA}_{Y}$ on  $Y$ such that:
$Y$ such that:
(i)
 $(Y,\unicode[STIX]{x1D6FA}_{Y}^{\wedge 1})$ is dlt;
$(Y,\unicode[STIX]{x1D6FA}_{Y}^{\wedge 1})$ is dlt;(ii)
 $K_{Y}+\unicode[STIX]{x1D6FA}_{Y}{\sim}_{h,\mathbb{R}}0$;
$K_{Y}+\unicode[STIX]{x1D6FA}_{Y}{\sim}_{h,\mathbb{R}}0$;(iii)
 $\unicode[STIX]{x1D6FA}_{Y}$ is
$\unicode[STIX]{x1D6FA}_{Y}$ is  $h$-big; and
$h$-big; and(iv)
 $\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{>}1})=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1})=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$.
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{>}1})=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1})=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$.
Since  $X$ is
$X$ is  $\mathbb{Q}$-factorial, there exists an effective
$\mathbb{Q}$-factorial, there exists an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $F$ on
$F$ on  $Y$ such that
$Y$ such that  $-F$ is
$-F$ is  $g$-ample and
$g$-ample and  $\operatorname{Supp}F=\operatorname{Ex}(g)$. Since
$\operatorname{Supp}F=\operatorname{Ex}(g)$. Since  $-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})$ is the pullback of an
$-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})$ is the pullback of an  $f$-ample
$f$-ample  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $-(K_{X}+\unicode[STIX]{x1D6E5})$ on
$-(K_{X}+\unicode[STIX]{x1D6E5})$ on  $X$, it follows that
$X$, it follows that  $-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})-\unicode[STIX]{x1D716}F$ is
$-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})-\unicode[STIX]{x1D716}F$ is  $h$-ample for any sufficiently small
$h$-ample for any sufficiently small  $\unicode[STIX]{x1D716}>0$.
$\unicode[STIX]{x1D716}>0$.
Note that  $\operatorname{Supp}F\subset \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$. Thus, we can find an effective
$\operatorname{Supp}F\subset \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$. Thus, we can find an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $B$ on
$B$ on  $Y$ such that
$Y$ such that  $B\geqslant \unicode[STIX]{x1D716}F$,
$B\geqslant \unicode[STIX]{x1D716}F$,  $-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})-B$ is
$-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})-B$ is  $h$-ample and
$h$-ample and  $\operatorname{Supp}B=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$. Lemma 2.8 enables us to find an effective
$\operatorname{Supp}B=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$. Lemma 2.8 enables us to find an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $A$ on
$A$ on  $Y$ such that
$Y$ such that  $A{\sim}_{h,\mathbb{R}}-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})-B$ and
$A{\sim}_{h,\mathbb{R}}-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})-B$ and  $(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt. In particular,
$(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt. In particular,  $(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+A)$ is dlt.
$(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+A)$ is dlt.
Set  $\unicode[STIX]{x1D6FA}_{Y}:=\unicode[STIX]{x1D6E5}_{Y}+A+B$. Then both (ii) and (iii) hold automatically. We obtain
$\unicode[STIX]{x1D6FA}_{Y}:=\unicode[STIX]{x1D6E5}_{Y}+A+B$. Then both (ii) and (iii) hold automatically. We obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{Y}^{\wedge 1}=(\unicode[STIX]{x1D6E5}_{Y}+A+B)^{\wedge 1}=(\unicode[STIX]{x1D6E5}_{Y}+A)^{\wedge 1}=\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+A, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{Y}^{\wedge 1}=(\unicode[STIX]{x1D6E5}_{Y}+A+B)^{\wedge 1}=(\unicode[STIX]{x1D6E5}_{Y}+A)^{\wedge 1}=\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+A, & & \displaystyle\end{eqnarray}$$ where the second equality follows from  $\operatorname{Supp}B=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$ and the third one holds by the fact that
$\operatorname{Supp}B=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$ and the third one holds by the fact that  $(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt. Thus, (i) holds.
$(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt. Thus, (i) holds.
Let us prove (iv). It is clear that  $\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{>}1})\subset \operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1})$. The inverse inclusion follows from
$\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{>}1})\subset \operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1})$. The inverse inclusion follows from
 $$\begin{eqnarray}\displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1}) & = & \displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+A+B)^{{\geqslant}1}=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+B)^{{\geqslant}1}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+B)^{{>}1}\subset \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+A+B)^{{>}1}=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{>}1}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1}) & = & \displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+A+B)^{{\geqslant}1}=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+B)^{{\geqslant}1}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+B)^{{>}1}\subset \operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}+A+B)^{{>}1}=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{{>}1}),\nonumber\end{eqnarray}$$ where the second equality follows from the fact that  $(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt and the third one holds by
$(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt and the third one holds by  $\operatorname{Supp}B=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$. Then we obtain the remaining equality as follows:
$\operatorname{Supp}B=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1})$. Then we obtain the remaining equality as follows:
 $$\begin{eqnarray}\displaystyle \operatorname{Supp}\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1}=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{\wedge 1})^{=1}=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+A)^{=1}=\operatorname{Supp}\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Supp}\unicode[STIX]{x1D6FA}_{Y}^{{\geqslant}1}=\operatorname{Supp}(\unicode[STIX]{x1D6FA}_{Y}^{\wedge 1})^{=1}=\operatorname{Supp}(\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+A)^{=1}=\operatorname{Supp}\unicode[STIX]{x1D6E5}_{Y}^{{\geqslant}1}, & & \displaystyle \nonumber\end{eqnarray}$$ where the second equality follows from (4.10.2) and the third one holds by the fact that  $(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt. Thus, (iv) holds. This completes the proof of Step 1.◻
$(Y,\unicode[STIX]{x1D6E5}_{Y}^{\wedge 1}+2A)$ is dlt. Thus, (iv) holds. This completes the proof of Step 1.◻
Step 2. The assertion of Theorem 4.10 holds without any additional assumptions.
Proof of Step 2.
Lemma 4.8 enables us to replace  $(X,\unicode[STIX]{x1D6E5})$ by the log pair
$(X,\unicode[STIX]{x1D6E5})$ by the log pair  $(Y,\unicode[STIX]{x1D6E5}_{Y})$ appearing in Proposition 2.10 (cf. (4.10.1)). Hence, we may assume that
$(Y,\unicode[STIX]{x1D6E5}_{Y})$ appearing in Proposition 2.10 (cf. (4.10.1)). Hence, we may assume that  $X$ is
$X$ is  $\mathbb{Q}$-factorial.
$\mathbb{Q}$-factorial.
Since  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big, there exists an effective
$f$-big, there exists an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $E$ such that
$E$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})-\unicode[STIX]{x1D716}E$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})-\unicode[STIX]{x1D716}E$ is  $f$-ample for any real number
$f$-ample for any real number  $\unicode[STIX]{x1D716}$ satisfying
$\unicode[STIX]{x1D716}$ satisfying  $0<\unicode[STIX]{x1D716}<1$. The equation
$0<\unicode[STIX]{x1D716}<1$. The equation
 $$\begin{eqnarray}\displaystyle \text{Nklt}(X,\unicode[STIX]{x1D6E5})=\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D716}E) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Nklt}(X,\unicode[STIX]{x1D6E5})=\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D716}E) & & \displaystyle \nonumber\end{eqnarray}$$ holds for sufficiently small  $\unicode[STIX]{x1D716}>0$. Therefore, replacing
$\unicode[STIX]{x1D716}>0$. Therefore, replacing  $\unicode[STIX]{x1D6E5}$ by
$\unicode[STIX]{x1D6E5}$ by  $\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D716}E$, we may assume that
$\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D716}E$, we may assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-ample. Hence, Step 2 follows from Step 1.◻
$f$-ample. Hence, Step 2 follows from Step 1.◻
Theorem 4.11. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a projective
$f:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$. Let
$Z$. Let  $Z^{\prime }$ be a closed subscheme of
$Z^{\prime }$ be a closed subscheme of  $Z$, set
$Z$, set  $X^{\prime }:=X\times _{Z}Z^{\prime }$ and let
$X^{\prime }:=X\times _{Z}Z^{\prime }$ and let  $f^{\prime }:X^{\prime }\rightarrow Z^{\prime }$ be the induced morphism. Assume that
$f^{\prime }:X^{\prime }\rightarrow Z^{\prime }$ be the induced morphism. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Then the following hold:
$f$-big. Then the following hold:
(i)
 $R^{i}f_{\ast }(WI_{X^{\prime }\cup \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=0$ for
$R^{i}f_{\ast }(WI_{X^{\prime }\cup \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=0$ for  $i>0$;
$i>0$;(ii)
 $R^{i}f_{\ast }^{\prime }(WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}})=0$ for
$R^{i}f_{\ast }^{\prime }(WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}})=0$ for  $i>0$, where
$i>0$, where  $j:X^{\prime }\rightarrow X$ denotes the induced closed immersion.
$j:X^{\prime }\rightarrow X$ denotes the induced closed immersion.
Proof. Taking the Stein factorisation of  $f$, we may assume that
$f$, we may assume that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$.
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$.
Let us prove (i). Since the problem is local on  $Z$, the problem is reduced to the case when
$Z$, the problem is reduced to the case when  $Z$ is affine. Hence, we can write
$Z$ is affine. Hence, we can write
 $$\begin{eqnarray}\displaystyle Z=\operatorname{Spec}A,\quad Z^{\prime }=\operatorname{Spec}(A/I),\quad I=(a_{1},\ldots ,a_{r}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z=\operatorname{Spec}A,\quad Z^{\prime }=\operatorname{Spec}(A/I),\quad I=(a_{1},\ldots ,a_{r}) & & \displaystyle \nonumber\end{eqnarray}$$ for some  $a_{1},\ldots ,a_{r}\in A$. We show the assertion (i) by induction on
$a_{1},\ldots ,a_{r}\in A$. We show the assertion (i) by induction on  $r$.
$r$.
We now treat the case when  $r=1$. If
$r=1$. If  $Z^{\prime }=Z$, then there is nothing to show. If
$Z^{\prime }=Z$, then there is nothing to show. If  $Z^{\prime }=\emptyset$, then the assertion follows from Theorem 4.10. Thus, we may assume that
$Z^{\prime }=\emptyset$, then the assertion follows from Theorem 4.10. Thus, we may assume that  $X^{\prime }$ is a non-zero effective Cartier divisor on
$X^{\prime }$ is a non-zero effective Cartier divisor on  $X$. Since
$X$. Since  $-(K_{X}+\unicode[STIX]{x1D6E5}+X^{\prime })$ is
$-(K_{X}+\unicode[STIX]{x1D6E5}+X^{\prime })$ is  $f$-nef and
$f$-nef and  $f$-big, Theorem 4.10 implies that
$f$-big, Theorem 4.10 implies that
 $$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{X^{\prime }\cup \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}+X^{\prime }),\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{i}f_{\ast }(WI_{X^{\prime }\cup \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}})=R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}+X^{\prime }),\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ for  $i>0$. Thus, the assertion (i) holds if
$i>0$. Thus, the assertion (i) holds if  $r=1$.
$r=1$.
Assume that  $r\geqslant 2$ and that the assertion (i) holds for the case when
$r\geqslant 2$ and that the assertion (i) holds for the case when  $I$ is generated by fewer than
$I$ is generated by fewer than  $r$ elements. We set
$r$ elements. We set
 $$\begin{eqnarray}\displaystyle & \displaystyle Z^{\prime \prime }:=\operatorname{Spec}(A/(f_{1},\ldots ,f_{r-1})),\quad Z_{r}:=\operatorname{Spec}(A/(f_{r})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle X^{\prime \prime }:=X\times _{Z}Z^{\prime \prime },\quad X_{r}:=X\times _{Z}Z_{r}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Z^{\prime \prime }:=\operatorname{Spec}(A/(f_{1},\ldots ,f_{r-1})),\quad Z_{r}:=\operatorname{Spec}(A/(f_{r})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle X^{\prime \prime }:=X\times _{Z}Z^{\prime \prime },\quad X_{r}:=X\times _{Z}Z_{r}. & \displaystyle \nonumber\end{eqnarray}$$ For  $N:=\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$, we have the exact sequence (Lemma 2.18)
$N:=\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$, we have the exact sequence (Lemma 2.18)
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{(X^{\prime \prime }\cup N)\cup (X_{r}\cup N),\mathbb{Q}}\rightarrow WI_{X^{\prime \prime }\cup N,\mathbb{Q}}\oplus WI_{X_{r}\cup N,\mathbb{Q}}\rightarrow WI_{X^{\prime }\cup N,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{(X^{\prime \prime }\cup N)\cup (X_{r}\cup N),\mathbb{Q}}\rightarrow WI_{X^{\prime \prime }\cup N,\mathbb{Q}}\oplus WI_{X_{r}\cup N,\mathbb{Q}}\rightarrow WI_{X^{\prime }\cup N,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$Then the assertion (i) follows by induction.
Let us prove (ii). Thanks to the exact sequence (Lemma 2.18)
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cup X^{\prime },\mathbb{Q}}\rightarrow WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}\oplus WI_{X^{\prime },\mathbb{Q}}\rightarrow WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cup X^{\prime },\mathbb{Q}}\rightarrow WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}\oplus WI_{X^{\prime },\mathbb{Q}}\rightarrow WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$(i) implies that the natural map
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{i}:R^{i}f_{\ast }(WI_{X^{\prime },\mathbb{Q}})\rightarrow R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{i}:R^{i}f_{\ast }(WI_{X^{\prime },\mathbb{Q}})\rightarrow R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$ is bijective for  $i>0$. Thanks to the following commutative diagram with exact horizontal sequence
$i>0$. Thanks to the following commutative diagram with exact horizontal sequence

the snake lemma induces the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{X^{\prime },\mathbb{Q}}\xrightarrow[{}]{\unicode[STIX]{x1D711}}WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}}\rightarrow j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{X^{\prime },\mathbb{Q}}\xrightarrow[{}]{\unicode[STIX]{x1D711}}WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}}\rightarrow j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$ Since the map  $\unicode[STIX]{x1D711}^{i}:R^{i}f_{\ast }(WI_{X^{\prime },\mathbb{Q}})\rightarrow R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}})$ induced by
$\unicode[STIX]{x1D711}^{i}:R^{i}f_{\ast }(WI_{X^{\prime },\mathbb{Q}})\rightarrow R^{i}f_{\ast }(WI_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\cap X^{\prime },\mathbb{Q}})$ induced by  $\unicode[STIX]{x1D711}$ is bijective for
$\unicode[STIX]{x1D711}$ is bijective for  $i>0$, we get
$i>0$, we get
 $$\begin{eqnarray}\displaystyle Rf_{\ast }(j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}})\simeq f_{\ast }j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }(j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}})\simeq f_{\ast }j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}. & & \displaystyle\end{eqnarray}$$ If  $i$ denotes the induced closed immersion
$i$ denotes the induced closed immersion  $Z^{\prime }\rightarrow Z$, then it holds that
$Z^{\prime }\rightarrow Z$, then it holds that
 $$\begin{eqnarray}\displaystyle f_{\ast }j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}} & \simeq & \displaystyle Rf_{\ast }(j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}})\nonumber\\ \displaystyle & \simeq & \displaystyle Rf_{\ast }Rj_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\nonumber\\ \displaystyle & \simeq & \displaystyle Ri_{\ast }Rf_{\ast }^{\prime }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\nonumber\\ \displaystyle & \simeq & \displaystyle i_{\ast }Rf_{\ast }^{\prime }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{\ast }j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}} & \simeq & \displaystyle Rf_{\ast }(j_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}})\nonumber\\ \displaystyle & \simeq & \displaystyle Rf_{\ast }Rj_{\ast }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\nonumber\\ \displaystyle & \simeq & \displaystyle Ri_{\ast }Rf_{\ast }^{\prime }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\nonumber\\ \displaystyle & \simeq & \displaystyle i_{\ast }Rf_{\ast }^{\prime }WI_{j^{-1}(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}},\nonumber\end{eqnarray}$$ where the first isomorphism follows from (4.11.1) and the second and last ones hold because  $j_{\ast }$ and
$j_{\ast }$ and  $i_{\ast }$ are exact functors. This completes the proof of (ii).◻
$i_{\ast }$ are exact functors. This completes the proof of (ii).◻
Theorem 4.12. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over  $k$ and let
$k$ and let  $f:X\rightarrow Z$ be a projective
$f:X\rightarrow Z$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Z$ such that
$Z$ such that  $f$ has connected fibres. Assume that
$f$ has connected fibres. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Then the induced morphism
$f$-big. Then the induced morphism  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow Z$ has connected fibres.
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow Z$ has connected fibres.
Proof. Thanks to Theorem 4.10, the homomorphism
 $$\begin{eqnarray}\displaystyle W{\mathcal{O}}_{Z,\mathbb{Q}}=f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow f_{\ast }(W{\mathcal{O}}_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W{\mathcal{O}}_{Z,\mathbb{Q}}=f_{\ast }W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow f_{\ast }(W{\mathcal{O}}_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$ is surjective. Since this homomorphism factors through  $W{\mathcal{O}}_{f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}$, also the induced homomorphism
$W{\mathcal{O}}_{f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}$, also the induced homomorphism
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}:W{\mathcal{O}}_{f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\rightarrow f_{\ast }(W{\mathcal{O}}_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}:W{\mathcal{O}}_{f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})),\mathbb{Q}}\rightarrow f_{\ast }(W{\mathcal{O}}_{\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}),\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$ is surjective. Since this is automatically injective,  $\unicode[STIX]{x1D703}$ is bijective. Therefore, the morphism
$\unicode[STIX]{x1D703}$ is bijective. Therefore, the morphism  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ has connected fibres (cf. Lemma 2.17), as desired.◻
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\rightarrow f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))$ has connected fibres (cf. Lemma 2.17), as desired.◻
5 Application to rational points on varieties over finite fields
As an application of our vanishing theorem of Nadel type (Theorems 4.10 and 4.11), we deduce some consequences for rational points on varieties over finite fields (Theorems 5.1 and 5.3).
Theorem 5.1. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over a finite field
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional log pair over a finite field  $k$ of characteristic
$k$ of characteristic  $p>5$. Let
$p>5$. Let  $f:X\rightarrow Y$ be a projective
$f:X\rightarrow Y$ be a projective  $k$-morphism to a quasi-projective
$k$-morphism to a quasi-projective  $k$-scheme
$k$-scheme  $Y$ such that
$Y$ such that  $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. Assume that
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Y}$. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Then the congruence
$f$-big. Then the congruence
 $$\begin{eqnarray}\displaystyle \#X(k)-\#V(k)\equiv \#Y(k)-\#f(V)(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#X(k)-\#V(k)\equiv \#Y(k)-\#f(V)(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$ holds, where  $V:=\text{Nklt}(X,\unicode[STIX]{x1D6E5})$.
$V:=\text{Nklt}(X,\unicode[STIX]{x1D6E5})$.
Proof. If  $Y(k)=\emptyset$, then there is nothing to show. Thus, the problem is reduced to the case when
$Y(k)=\emptyset$, then there is nothing to show. Thus, the problem is reduced to the case when  $Y(k)\neq \emptyset$. Fix a
$Y(k)\neq \emptyset$. Fix a  $k$-rational point
$k$-rational point  $y\in Y$. Since the problem is local on
$y\in Y$. Since the problem is local on  $Y$, we may assume that
$Y$, we may assume that  $Y(k)=\{y\}$. If
$Y(k)=\{y\}$. If  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\,\cap \,f^{-1}(y)=\emptyset$, then the assertion follows from [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.4]. Hence, we may assume that
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\,\cap \,f^{-1}(y)=\emptyset$, then the assertion follows from [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.4]. Hence, we may assume that  $y\in f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=f(V)$, i.e.
$y\in f(\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}))=f(V)$, i.e.  $V_{y}\neq \emptyset$. In particular, it holds that
$V_{y}\neq \emptyset$. In particular, it holds that
 $$\begin{eqnarray}\displaystyle Y(k)=f(V)(k)=\{y\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y(k)=f(V)(k)=\{y\}. & & \displaystyle \nonumber\end{eqnarray}$$Since
 $$\begin{eqnarray}\displaystyle X(k)=X_{y}(k),\quad V(k)=V_{y}(k), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X(k)=X_{y}(k),\quad V(k)=V_{y}(k), & & \displaystyle \nonumber\end{eqnarray}$$it suffices to prove that
 $$\begin{eqnarray}\displaystyle \#X_{y}(k)\equiv \#V_{y}(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#X_{y}(k)\equiv \#V_{y}(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k. & & \displaystyle \nonumber\end{eqnarray}$$Consider the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{V_{y},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X_{y},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{V_{y},\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{V_{y},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X_{y},\mathbb{Q}}\rightarrow W{\mathcal{O}}_{V_{y},\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$Thanks to Theorem 4.11(ii), it holds that
 $$\begin{eqnarray}\displaystyle H^{i}(X_{y},WI_{V_{y},\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{i}(X_{y},WI_{V_{y},\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ for  $i>0$. Furthermore, we get
$i>0$. Furthermore, we get  $H^{0}(X_{y},WI_{V_{y},\mathbb{Q}})=0$ by
$H^{0}(X_{y},WI_{V_{y},\mathbb{Q}})=0$ by  $V_{y}\neq \emptyset$ and the fact that
$V_{y}\neq \emptyset$ and the fact that  $X_{y}$ is connected. Hence, the natural map
$X_{y}$ is connected. Hence, the natural map
 $$\begin{eqnarray}\displaystyle H^{i}(X_{y},W{\mathcal{O}}_{X_{y},\mathbb{Q}})\rightarrow H^{i}(V_{y},W{\mathcal{O}}_{V_{y},\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{i}(X_{y},W{\mathcal{O}}_{X_{y},\mathbb{Q}})\rightarrow H^{i}(V_{y},W{\mathcal{O}}_{V_{y},\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$ is bijective for  $i\geqslant 0$. Therefore, the assertion holds by [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 6.9(i)].◻
$i\geqslant 0$. Therefore, the assertion holds by [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 6.9(i)].◻
Corollary 5.2. Let  $(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional geometrically connected projective log pair over a finite field
$(X,\unicode[STIX]{x1D6E5})$ be a three-dimensional geometrically connected projective log pair over a finite field  $k$ of characteristic
$k$ of characteristic  $p>5$. Assume that
$p>5$. Assume that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big and that
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big and that  $(X,\unicode[STIX]{x1D6E5})$ is not klt. Then the congruence
$(X,\unicode[STIX]{x1D6E5})$ is not klt. Then the congruence
 $$\begin{eqnarray}\displaystyle \#X(k)\equiv \#V(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#X(k)\equiv \#V(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$ holds, where  $V:=\text{Nklt}(X,\unicode[STIX]{x1D6E5})$.
$V:=\text{Nklt}(X,\unicode[STIX]{x1D6E5})$.
Proof. Applying Theorem 5.1 for  $Y:=\operatorname{Spec}k$, the assertion holds.◻
$Y:=\operatorname{Spec}k$, the assertion holds.◻
Theorem 5.3. Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$. Let
$p>5$. Let  $X$ be a projective normal variety over
$X$ be a projective normal variety over  $k$ with
$k$ with  $\dim X\leqslant 3$. Let
$\dim X\leqslant 3$. Let  $D$ be a non-zero effective
$D$ be a non-zero effective  $\mathbb{Q}$-Cartier
$\mathbb{Q}$-Cartier  $\mathbb{Z}$-divisor on
$\mathbb{Z}$-divisor on  $X$. Assume that there exists an effective
$X$. Assume that there exists an effective  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $\unicode[STIX]{x1D6E5}$ such that:
$\unicode[STIX]{x1D6E5}$ such that:
(a)
 $(X,\unicode[STIX]{x1D6E5})$ is klt;
$(X,\unicode[STIX]{x1D6E5})$ is klt;(b)
 $-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big; and
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is nef and big; and(c)
 $-(K_{X}+\unicode[STIX]{x1D6E5}+D)$ is nef and big.
$-(K_{X}+\unicode[STIX]{x1D6E5}+D)$ is nef and big.
Then the following hold.
(i) The equation
holds for $$\begin{eqnarray}\displaystyle H^{i}(D,W{\mathcal{O}}_{D,\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{i}(D,W{\mathcal{O}}_{D,\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ $i>0$ and the induced map is bijective.
$i>0$ and the induced map is bijective. $$\begin{eqnarray}\displaystyle H^{0}(X,W{\mathcal{O}}_{X,\mathbb{Q}})\rightarrow H^{0}(D,W{\mathcal{O}}_{D,\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{0}(X,W{\mathcal{O}}_{X,\mathbb{Q}})\rightarrow H^{0}(D,W{\mathcal{O}}_{D,\mathbb{Q}}) & & \displaystyle \nonumber\end{eqnarray}$$(ii) If
 $k$ is a finite field and
$k$ is a finite field and  $X$ is geometrically connected over
$X$ is geometrically connected over  $k$, then the congruence holds.
$k$, then the congruence holds. $$\begin{eqnarray}\displaystyle \#D(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#D(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k & & \displaystyle \nonumber\end{eqnarray}$$
Proof. Let us prove (i). We have the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow WI_{D,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow WI_{D,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{X,\mathbb{Q}}\rightarrow W{\mathcal{O}}_{D,\mathbb{Q}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$It follows from (a), (b) and Theorem 3.1(ii) that the equation
 $$\begin{eqnarray}\displaystyle H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{i}(X,W{\mathcal{O}}_{X,\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ holds for  $i>0$. Note that
$i>0$. Note that  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}+D)=\operatorname{Supp}D$. Hence, by (c) and Theorem 4.10, we get
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}+D)=\operatorname{Supp}D$. Hence, by (c) and Theorem 4.10, we get
 $$\begin{eqnarray}\displaystyle H^{i}(X,WI_{D,\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{i}(X,WI_{D,\mathbb{Q}})=0 & & \displaystyle \nonumber\end{eqnarray}$$ for  $i>0$. Since
$i>0$. Since  $D\neq 0$, we obtain
$D\neq 0$, we obtain  $H^{0}(X,WI_{D,\mathbb{Q}})=0$. This completes the proof of (i).
$H^{0}(X,WI_{D,\mathbb{Q}})=0$. This completes the proof of (i).
Let us show (ii). Thanks to (i), we may apply [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 6.9(i)] and obtain the congruence  $\#X(k)\equiv \#D(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k$. On the other hand, we have another congruence
$\#X(k)\equiv \#D(k)\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k$. On the other hand, we have another congruence  $\#X(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k$, which is guaranteed by [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.4]. To summarise, we get
$\#X(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k$, which is guaranteed by [Reference Gongyo, Nakamura and TanakaGNT19, Theorem 5.4]. To summarise, we get  $\#D(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k$, as desired.◻
$\#D(k)\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}\#k$, as desired.◻
Remark 5.4. As applications of a vanishing theorem of Nadel type (Theorem 4.10), we obtain two results: the Kollár–Shokurov connectedness theorem (Theorem 4.12) and the existence of rational points (Theorem 5.1). For certain special cases, these two consequences are also related as follows.
Let  $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic  $p>5$ and let
$p>5$ and let  $(X,\unicode[STIX]{x1D6E5})$ be a projective log pair over
$(X,\unicode[STIX]{x1D6E5})$ be a projective log pair over  $k$ with
$k$ with  $\dim X\leqslant 3$ such that
$\dim X\leqslant 3$ such that  $-(K_{X}+\unicode[STIX]{x1D6E5})$ is
$-(K_{X}+\unicode[STIX]{x1D6E5})$ is  $f$-nef and
$f$-nef and  $f$-big. Assume that
$f$-big. Assume that  $X$ is geometrically connected over
$X$ is geometrically connected over  $k$,
$k$,  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\neq \emptyset$ and
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})\neq \emptyset$ and  $\dim \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})=0$. Then
$\dim \operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})=0$. Then  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ is geometrically connected over
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ is geometrically connected over  $k$ by the Kollár–Shokurov connectedness theorem (Theorem 4.12), which implies that
$k$ by the Kollár–Shokurov connectedness theorem (Theorem 4.12), which implies that  $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ consists of a single
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5})$ consists of a single  $k$-rational point.
$k$-rational point.
Acknowledgements
We would like to thank Professors Hélène Esnault, Yoshinori Gongyo, Shunsuke Takagi and Chenyang Xu for many useful discussions. The authors also thank the referees for reading the manuscript carefully, suggesting several improvements and pointing out mistakes. The first author is partially supported by JSPS KAKENHI Grant Number 18K13384. The second author is partially supported by EPSRC and JSPS KAKENHI Grant Number 18K13386.