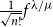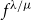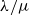1. Introduction
In enumerative and algebraic combinatorics, Young tableaux are fundamental objects that have been studied for over a century with a remarkable variety of both results and applications to other fields. The asymptotic study of the number of standard Young tableaux is an interesting area in its own right, motivated by both probabilistic combinatorics (longest increasing subsequences) and representation theory. This paper is a surprising new advance in this direction, representing a progress which until recently could not be obtained by existing tools.
1.1. Main results
Let us begin by telling the story behind this paper. Denote by
![]() $f^{\lambda/\mu}=\operatorname{SYT}(\lambda/\mu)$
the number of standard Young tableaux of skew shape
$f^{\lambda/\mu}=\operatorname{SYT}(\lambda/\mu)$
the number of standard Young tableaux of skew shape
![]() $\lambda/\mu$
. There is Feit’s determinant formula for
$\lambda/\mu$
. There is Feit’s determinant formula for
![]() $f^{\lambda/\mu}$
, which can also be derived from the Jacobi–Trudy identity for skew shapes. In some cases, there are multiplicative formulas for
$f^{\lambda/\mu}$
, which can also be derived from the Jacobi–Trudy identity for skew shapes. In some cases, there are multiplicative formulas for
![]() $f^{\lambda/\mu}$
, e.g. the hook-length formula (HLF) when
$f^{\lambda/\mu}$
, e.g. the hook-length formula (HLF) when
![]() $\mu=\varnothing$
, see also [Reference Morales, Pak and PanovaMPP3]. However, in general, it is difficult to use Feit’s formula to obtain even the first order of asymptotics, since there is no easy way to diagonalize the corresponding matrices.
$\mu=\varnothing$
, see also [Reference Morales, Pak and PanovaMPP3]. However, in general, it is difficult to use Feit’s formula to obtain even the first order of asymptotics, since there is no easy way to diagonalize the corresponding matrices.
It is easy to show (see e.g. [Reference PakPak2]), that when
![]() $|\lambda/\mu|=N$
and
$|\lambda/\mu|=N$
and
![]() $\lambda_1,\ell(\lambda) \hskip.03cm \le \hskip.03cm s \sqrt{N}$
, we have:
$\lambda_1,\ell(\lambda) \hskip.03cm \le \hskip.03cm s \sqrt{N}$
, we have:
where
![]() $c_1,c_2>0$
are universal constants which depend only on s. Improving upon these estimates is of interest in both combinatorics and applications (cf. [Reference Morales, Pak and PanovaMPP3, Reference Morales, Pak and PanovaMPP4]).
$c_1,c_2>0$
are universal constants which depend only on s. Improving upon these estimates is of interest in both combinatorics and applications (cf. [Reference Morales, Pak and PanovaMPP3, Reference Morales, Pak and PanovaMPP4]).
In [Reference Morales, Pak and PanovaMPP4], much sharper bounds on
![]() $c_1,c_2$
were given, when the diagrams
$c_1,c_2$
were given, when the diagrams
![]() $\lambda$
and
$\lambda$
and
![]() $\mu$
have a limit shape
$\mu$
have a limit shape
![]() $\psi/\phi$
under
$\psi/\phi$
under
![]() $1/\sqrt{N}$
scaling in both directions (see below). Based on observations in special cases, we conjectured that there is always a limit
$1/\sqrt{N}$
scaling in both directions (see below). Based on observations in special cases, we conjectured that there is always a limit
in this setting. The main result of this paper is a proof of this conjecture.
Theorem 1.1 Let
![]() $\bigl\{\lambda^{(N)}\bigr\}$
and
$\bigl\{\lambda^{(N)}\bigr\}$
and
![]() $\bigl\{\mu^{(N)}\bigr\}$
be two partition sequences with strongly stable (limit) shapes
$\bigl\{\mu^{(N)}\bigr\}$
be two partition sequences with strongly stable (limit) shapes
![]() $\psi$
and
$\psi$
and
![]() $\phi$
, respectively (see
$\phi$
, respectively (see
![]() $\S$
2.4 for precise definitions). Let
$\S$
2.4 for precise definitions). Let
![]() $\nu^{(N)} := \lambda^{(N)}/\mu^{(N)}$
, such that
$\nu^{(N)} := \lambda^{(N)}/\mu^{(N)}$
, such that
![]() $|\nu^{(N)}| = N + o(N/\log N)$
. Then
$|\nu^{(N)}| = N + o(N/\log N)$
. Then
for some fixed constant
![]() $c(\psi/\phi)$
.
$c(\psi/\phi)$
.
The constant
![]() $c(\psi/\phi)$
is given in Corollary 4.7. The proof of the theorem is even more interesting perhaps than one would expect. In [Reference NaruseNar], Naruse developed a novel approach to counting
$c(\psi/\phi)$
is given in Corollary 4.7. The proof of the theorem is even more interesting perhaps than one would expect. In [Reference NaruseNar], Naruse developed a novel approach to counting
![]() $f^{\lambda/\mu}$
, via what is now known as the Naruse hook-length formula (NHLF):
$f^{\lambda/\mu}$
, via what is now known as the Naruse hook-length formula (NHLF):
where
![]() $\mathcal{E}(\lambda/\mu)\subseteq \binom{[\lambda]}{|\mu|}$
is a collection of certain subsets of the Young diagram
$\mathcal{E}(\lambda/\mu)\subseteq \binom{[\lambda]}{|\mu|}$
is a collection of certain subsets of the Young diagram
![]() $[\lambda]$
called excited diagram (see e.g. [Reference Morales, Pak and PanovaMPP3, Sec. 2.6]), and
$[\lambda]$
called excited diagram (see e.g. [Reference Morales, Pak and PanovaMPP3, Sec. 2.6]), and
![]() $\textsf{h}_{\lambda}(u)$
is the hook-length at
$\textsf{h}_{\lambda}(u)$
is the hook-length at
![]() $u \in \lambda$
. The (usual) hook-length formula is a special case
$u \in \lambda$
. The (usual) hook-length formula is a special case
![]() $\mu=\varnothing$
. Let us mention that
$\mu=\varnothing$
. Let us mention that
![]() $\mathcal{E}(\lambda/\mu)$
can be viewed as the set of certain particle configurations, giving it additional structure [Reference Morales, Pak and PanovaMPP3].
$\mathcal{E}(\lambda/\mu)$
can be viewed as the set of certain particle configurations, giving it additional structure [Reference Morales, Pak and PanovaMPP3].
Although
![]() $\mathcal{E}(\lambda/\mu)$
can have exponential size, the NHLF can be useful in getting the asymptotic bounds [Reference Morales, Pak and PanovaMPP4]. It has been reproved and studied further in [Reference Morales, Pak and PanovaMPP1, Reference Morales, Pak and PanovaMPP2], including the q-analogues and generalisations to trees and shifted shapes. See
$\mathcal{E}(\lambda/\mu)$
can have exponential size, the NHLF can be useful in getting the asymptotic bounds [Reference Morales, Pak and PanovaMPP4]. It has been reproved and studied further in [Reference Morales, Pak and PanovaMPP1, Reference Morales, Pak and PanovaMPP2], including the q-analogues and generalisations to trees and shifted shapes. See
![]() $\S$
2.3 for the precise statements.
$\S$
2.3 for the precise statements.
The next logical step was made in [Reference Morales, Pak and PanovaMPP3], where a bijection between
![]() $\mathcal{E}(\lambda/\mu)$
and lozenge tilings of a certain region was constructed. Thus, the number of standard Young tableaux
$\mathcal{E}(\lambda/\mu)$
and lozenge tilings of a certain region was constructed. Thus, the number of standard Young tableaux
![]() $f^{\lambda/\mu}$
can be viewed as a statistical sum of weighted lozenge tilings. In a special case of thick hooks, this connection is especially interesting, as the corresponding weighted lozenge tilings were previously studied in [Reference Borodin, Gorin and RainsBGR] (see the example below).
$f^{\lambda/\mu}$
can be viewed as a statistical sum of weighted lozenge tilings. In a special case of thick hooks, this connection is especially interesting, as the corresponding weighted lozenge tilings were previously studied in [Reference Borodin, Gorin and RainsBGR] (see the example below).
Now, there is a large literature on random lozenge tilings of the hexagon and its relatives in connection with the arctic circle phenomenon, see [Reference Cohn, Elkies and ProppCEP, Reference Cohn, Kenyon and ProppCKP, Reference KenyonKen]. In this paper, we adapt the variational principle approach in these papers to obtain the arctic circle behavior for the weighted tilings as well. Putting all these pieces together implies Theorem 1.1.
Let us emphasise that the approach in this paper can be used to obtain certain probabilistic information on random SYTs of large shapes, e.g. in [MPP3,
![]() $\S$
8] we show how to compute asymptotics of various path probabilities. However, in the absence of a direct bijective proof of NHLF, our approach cannot be easily adapted to obtain limit shapes of SYTs as Sun has done recently [Reference SunSun] using the beads model, and Gordenko [Reference GordenkoGor] using a modified totally asymmetric simple exclusion process (TASEP); see also
$\S$
8] we show how to compute asymptotics of various path probabilities. However, in the absence of a direct bijective proof of NHLF, our approach cannot be easily adapted to obtain limit shapes of SYTs as Sun has done recently [Reference SunSun] using the beads model, and Gordenko [Reference GordenkoGor] using a modified totally asymmetric simple exclusion process (TASEP); see also
![]() $\S$
6.5.
$\S$
6.5.
1.2. Thick hooks
Let
![]() $\lambda = (a+c)^{b+c}$
,
$\lambda = (a+c)^{b+c}$
,
![]() $\mu = a^b$
,
$\mu = a^b$
,
![]() $N=|\lambda/\mu|=c\hskip.03cm (a+b+c)$
, where
$N=|\lambda/\mu|=c\hskip.03cm (a+b+c)$
, where
![]() $a,b,c\ge 0$
. This shape is called the thick hook in [Reference Morales, Pak and PanovaMPP4]. The HLF applied to the 180 degree rotation of
$a,b,c\ge 0$
. This shape is called the thick hook in [Reference Morales, Pak and PanovaMPP4]. The HLF applied to the 180 degree rotation of
![]() $\lambda/\mu$
gives:
$\lambda/\mu$
gives:
Here the superfactorial
![]() $\Phi(n)\hskip.03cm =\hskip.03cm 1!\cdot 2! \hskip.03cm \cdots \hskip.03cm (n-1)!$
is the integer value of the Barnes G-function, see e.g. [Reference Askey, Roy and OlverAsR].
$\Phi(n)\hskip.03cm =\hskip.03cm 1!\cdot 2! \hskip.03cm \cdots \hskip.03cm (n-1)!$
is the integer value of the Barnes G-function, see e.g. [Reference Askey, Roy and OlverAsR].
On the other hand,
![]() $\mathcal{E}(\lambda/\mu)$
in this case in bijection with the set of lozenge tilings of the hexagon
$\mathcal{E}(\lambda/\mu)$
in this case in bijection with the set of lozenge tilings of the hexagon
![]() $\operatorname{\mathbb H}(a,b,c) = \langle\hskip.03cm a\times b \times c \times a \times b \times c\hskip.03cm\rangle$
, and the weight is simply a product of a linear function on horizontal lozenges (see below). The number of lozenge tilings in this case is famously counted by the MacMahon box formula for the number
$\operatorname{\mathbb H}(a,b,c) = \langle\hskip.03cm a\times b \times c \times a \times b \times c\hskip.03cm\rangle$
, and the weight is simply a product of a linear function on horizontal lozenges (see below). The number of lozenge tilings in this case is famously counted by the MacMahon box formula for the number
![]() ${\textsf{P}}(a,b,c)$
of solid partitions which fit into a
${\textsf{P}}(a,b,c)$
of solid partitions which fit into a
![]() $[a\times b \times c]$
box:
$[a\times b \times c]$
box:
see e.g. [Reference StanleySta2,
![]() $\S$
7.21]. It was noticed by Rains (see [Reference Morales, Pak and PanovaMPP3,
$\S$
7.21]. It was noticed by Rains (see [Reference Morales, Pak and PanovaMPP3,
![]() $\S$
9.5]), that in this example our weights are special cases of multiparameter weights studied in [Reference Borodin, Gorin and RainsBGR] in connection with closed formulas for q-Racah polynomials, cf.
$\S$
9.5]), that in this example our weights are special cases of multiparameter weights studied in [Reference Borodin, Gorin and RainsBGR] in connection with closed formulas for q-Racah polynomials, cf.
![]() $\S$
6.2.
$\S$
6.2.
Now, Theorem 1.1 in this case does not give anything new, of course, as existence of the limit when
![]() $c\to \infty$
,
$c\to \infty$
,
![]() $a/c \to \alpha$
and
$a/c \to \alpha$
and
![]() $b/c\to \beta$
, follows from either the Vershik–Kerov–Logan–Shepp hook integral of the strongly stable shapes [Reference Morales, Pak and PanovaMPP4,
$b/c\to \beta$
, follows from either the Vershik–Kerov–Logan–Shepp hook integral of the strongly stable shapes [Reference Morales, Pak and PanovaMPP4,
![]() $\S$
6.2] (see also [Reference RomikRom]), or from the asymptotics of the superfactorial:
$\S$
6.2] (see also [Reference RomikRom]), or from the asymptotics of the superfactorial:
This gives the exact value
![]() $c(\psi/\phi)$
as an elementary function of
$c(\psi/\phi)$
as an elementary function of
![]() $(\alpha,\beta)$
.
$(\alpha,\beta)$
.
1.3. Thick ribbons
Let
![]() $\nu_k:=(2k-1,2k-2,\ldots,2,1)/(k-1,k-2,\ldots,2,1)$
. This skew shape is a strongly stable shape. The main theorem implies that there is a limit
$\nu_k:=(2k-1,2k-2,\ldots,2,1)/(k-1,k-2,\ldots,2,1)$
. This skew shape is a strongly stable shape. The main theorem implies that there is a limit
where
![]() $N=|\nu_k| = k(3k-1)/2$
. This proves a conjecture in [Reference Morales, Pak and PanovaMPP4,
$N=|\nu_k| = k(3k-1)/2$
. This proves a conjecture in [Reference Morales, Pak and PanovaMPP4,
![]() $\S$
13.7]. The best known upper and lower bounds for C calculated in [Reference PakPak2] are
$\S$
13.7]. The best known upper and lower bounds for C calculated in [Reference PakPak2] are
but the exact value of C has no known closed formula. This paper describes C as solution of a certain very involved variational problem (see Corollary 4.7 and
![]() $\S$
6.5).
$\S$
6.5).
1.4. Structure of the paper
We start with Section 2 which reviews the notation and known results on tilings, standard Young tableaux and limit shapes. In Section 3, we state our main technical result (Theorem 3.3) on the variational principle for weighted lozenge tilings, whose proof is postponed until Section 5. In the technical Section 4, we deduce Theorem 1.1 from the variational principle. We conclude with final remarks and open problems in Section 6.
2. Background and notation
2.1. Tilings and height functions
Let R be a connected region in the triangular lattice. One can view a lozenge tiling of R as a stepped surface in
![]() $\mathbb{R}^3$
where the first two coordinates are the coordinates of the points in the lattice and the third coordinates is the height function
$\mathbb{R}^3$
where the first two coordinates are the coordinates of the points in the lattice and the third coordinates is the height function
![]() $h(\cdot)$
of a lozenge tiling defined in the following way:
$h(\cdot)$
of a lozenge tiling defined in the following way:
-
• For every edge (x, y) in R,
 $h(y)-h(x)= 1$
if (x, y) is a vertical edge and
$h(y)-h(x)= 1$
if (x, y) is a vertical edge and
 $h(y)-h(x)= 0$
otherwise.
$h(y)-h(x)= 0$
otherwise.
In fact, there is a one to one correspondence between tilings of a given region and functions which verify this property defined up to a constant. Using this bijection, we will denote by
![]() $\textsf{t}_h$
the tiling associated to a given height function h and we will do most of the subsequent reasoning using height functions rather than tilings. The position (x, y) of a horizontal lozenge in
$\textsf{t}_h$
the tiling associated to a given height function h and we will do most of the subsequent reasoning using height functions rather than tilings. The position (x, y) of a horizontal lozenge in
![]() $\textsf{t}_h$
is the coordinates of its upper corner in the triangular lattice.
$\textsf{t}_h$
is the coordinates of its upper corner in the triangular lattice.
We extend the definition of height functions to any region of the lattice as follows: for general sets S, we say that a function
![]() $h:S \to \mathbb{Z}$
is a height function if its restriction on each simply connected component of S is a height function.
$h:S \to \mathbb{Z}$
is a height function if its restriction on each simply connected component of S is a height function.
Let R be a lozenge tileable region. We say that the three-dimensional curve obtained by traveling along
![]() $\partial R$
and recording the height of each point is an admissible stepped curve (ASC). See Figure 1.
$\partial R$
and recording the height of each point is an admissible stepped curve (ASC). See Figure 1.

Figure 1. A region R of the triangular lattice. A lozenge tiling of that region and the associated admissible stepped curve (ASC).
Lemma 2.1 Let R be a connected region in the triangular grid and let g be a height function on a subset S of R, such that for all
![]() $x=(x_1,x_2),y = (y_1,y_2) \in S$
:
$x=(x_1,x_2),y = (y_1,y_2) \in S$
:
Then g can be extended into a height function on the whole region R.
The lemma is a variation on [Reference Pak, Sheffer and TassyPST, Thm. 4.1] (see also [Reference ThurstonThu]). It can be viewed as a Lipschitz extendability property on height functions (cf. [Reference Chandgotia, Pak and TassyCPT]). We include a quick proof for completeness.
Proof. Note that
![]() $h_x(y)=g(x) + \min \{ y_1-x_1,y_2-x_2\}$
is the height function of the maximal tiling centered at x and with height g(x) at x (see Figure 2). Define
$h_x(y)=g(x) + \min \{ y_1-x_1,y_2-x_2\}$
is the height function of the maximal tiling centered at x and with height g(x) at x (see Figure 2). Define
![]() $h(y):= \min_{x\in S} \hskip.03cm h_x(y)$
. Since the minimum of two height functions is still a height function, we conclude that h is itself a height function. Moreover, the inequality (2.1) implies that for all pairs
$h(y):= \min_{x\in S} \hskip.03cm h_x(y)$
. Since the minimum of two height functions is still a height function, we conclude that h is itself a height function. Moreover, the inequality (2.1) implies that for all pairs
![]() $x,y \in S: g(y) \leq h_x(y)$
. We conclude that
$x,y \in S: g(y) \leq h_x(y)$
. We conclude that
![]() $h(y)=g(y)$
, which implies the result.
$h(y)=g(y)$
, which implies the result.

Figure 2. Left: height function of the maximal tiling centered at x with height g(x). Right: the local move on lozenges.
Second, we need the following standard proposition which will be useful later in this article.
Proposition 2.2 (see [Reference ThurstonThu]). Every two lozenge tilings of a simply connected region R have equal number of lozenges of each type.
In other words, the number of lozenges of each type depends only on R and not on the tiling. This follows, e.g. since every two tilings of R are connected by local moves which do not change the number of lozenges of each type (see Figure 2).
2.2. Skew shapes and tableaux
Let
![]() $\lambda = (\lambda_1,\ldots,\lambda_r)$
and
$\lambda = (\lambda_1,\ldots,\lambda_r)$
and
![]() $\mu=(\mu_1,\ldots,\mu_s)$
denote integer partitions of length
$\mu=(\mu_1,\ldots,\mu_s)$
denote integer partitions of length
![]() $\ell(\lambda)=r$
and
$\ell(\lambda)=r$
and
![]() $\ell(\mu)=s$
. The size of the partition is denoted by
$\ell(\mu)=s$
. The size of the partition is denoted by
![]() $|\lambda|$
. We denote by
$|\lambda|$
. We denote by
![]() $\lambda'$
the conjugate partition, and by
$\lambda'$
the conjugate partition, and by
![]() $[\lambda]$
the corresponding Young diagram (in English notation). The hook length
$[\lambda]$
the corresponding Young diagram (in English notation). The hook length
![]() $\textsf{h}_{\lambda}(x,y)$
of a cell
$\textsf{h}_{\lambda}(x,y)$
of a cell
![]() $(x,y)\in\lambda$
is defined as
$(x,y)\in\lambda$
is defined as
![]() $\textsf{h}_{\lambda}(x,y):=\lambda_x-x+\lambda'_y-y+1$
. It counts the number of cells directly to the right and directly below (x, y) in
$\textsf{h}_{\lambda}(x,y):=\lambda_x-x+\lambda'_y-y+1$
. It counts the number of cells directly to the right and directly below (x, y) in
![]() $[\lambda]$
. The content of a cell
$[\lambda]$
. The content of a cell
![]() $(x,y) \in \lambda$
is
$(x,y) \in \lambda$
is
![]() $c(x,y)=y-x$
.
$c(x,y)=y-x$
.
A skew shape
![]() $\lambda/\mu$
is defined as the difference of two shapes. Let
$\lambda/\mu$
is defined as the difference of two shapes. Let
![]() $N = |\lambda/\mu|$
. We always assume that the skew shape is connected. Let
$N = |\lambda/\mu|$
. We always assume that the skew shape is connected. Let
![]() $N = |\lambda/\mu|$
,
$N = |\lambda/\mu|$
,
![]() $a=\mu_1$
,
$a=\mu_1$
,
![]() $b=\ell(\mu)$
and
$b=\ell(\mu)$
and
![]() $d_a,d_{a-1},\ldots,d_{-b}$
be the length of the diagonals in
$d_a,d_{a-1},\ldots,d_{-b}$
be the length of the diagonals in
![]() $[\lambda/\mu]$
with contents
$[\lambda/\mu]$
with contents
![]() $x-y=a,a-1,\ldots,-b$
, respectively. Note that the
$x-y=a,a-1,\ldots,-b$
, respectively. Note that the
![]() $d_{\mu_1-1},d_{\mu_2-2},\ldots,d_{\mu_b-b}$
are the diagonal lengths of the last cell
$d_{\mu_1-1},d_{\mu_2-2},\ldots,d_{\mu_b-b}$
are the diagonal lengths of the last cell
![]() $(k,\mu_k)$
of a row of
$(k,\mu_k)$
of a row of
![]() $\mu$
.
$\mu$
.
A standard Young tableau (SYT) of shape
![]() $\lambda/\mu$
is a bijective function
$\lambda/\mu$
is a bijective function
![]() $T: [\lambda/\mu] \to \{1,\dots,N\}$
, increasing in rows and columns. The number of such tableaux is denoted by
$T: [\lambda/\mu] \to \{1,\dots,N\}$
, increasing in rows and columns. The number of such tableaux is denoted by
![]() $f^{\lambda/\mu}$
. This counts the number of linear extensions of the poset defined on
$f^{\lambda/\mu}$
. This counts the number of linear extensions of the poset defined on
![]() $[\lambda/\mu]$
, with cells increasing downward and to the right.
$[\lambda/\mu]$
, with cells increasing downward and to the right.
2.3. Naruse’s hook-length formula
As mentioned in the introduction, the Naruse hook-length formula (1.1) gives a positive formula for
![]() $f^{\lambda/\mu}$
. It was restated in [Reference Morales, Pak and PanovaMPP3, §7] in terms of lozenge tilings as follows.
$f^{\lambda/\mu}$
. It was restated in [Reference Morales, Pak and PanovaMPP3, §7] in terms of lozenge tilings as follows.
Let
![]() $\lambda/\mu$
be a skew shape with N cells and
$\lambda/\mu$
be a skew shape with N cells and
![]() $a=\mu_1,b=\ell(\mu)$
. Let
$a=\mu_1,b=\ell(\mu)$
. Let
![]() $\gamma^*_{\lambda/\mu}$
be the ASC in
$\gamma^*_{\lambda/\mu}$
be the ASC in
![]() $\mathbb{R}^3$
bounded below by the polygonal chain with points (0,a,0),(0,0,0),(b,0,0) and with upper side given by the polygonal chain with points
$\mathbb{R}^3$
bounded below by the polygonal chain with points (0,a,0),(0,0,0),(b,0,0) and with upper side given by the polygonal chain with points
![]() $(k,\mu_k,d)$
where
$(k,\mu_k,d)$
where
![]() $d=\max(d_{\mu_1-1},\ldots,d_{\mu_b-b})$
Footnote 1
. Let
$d=\max(d_{\mu_1-1},\ldots,d_{\mu_b-b})$
Footnote 1
. Let
![]() $H^*_{\lambda/\mu}$
be the set of height functions h that extend
$H^*_{\lambda/\mu}$
be the set of height functions h that extend
![]() $\gamma^*_{\lambda/\mu}$
with the additional restriction that on each vertical diagonal
$\gamma^*_{\lambda/\mu}$
with the additional restriction that on each vertical diagonal
![]() $x-y=k$
there are no horizontal lozenges of
$x-y=k$
there are no horizontal lozenges of
![]() $\textsf{t}_h$
with position (x, y) with
$\textsf{t}_h$
with position (x, y) with
![]() $y>\lambda_x$
.
$y>\lambda_x$
.
For our purposes, it will be more convenient to modify the upper side of the ASC instead of imposing the above restriction on the horizontal lozenges. In order to do this, let
![]() $\gamma_{\lambda/\mu}$
be the ASC in
$\gamma_{\lambda/\mu}$
be the ASC in
![]() $\mathbb{R}^3$
bounded below by the polygonal chain with points (0,a,0),(0,0,0),(b,0,0) and with upper side given by the polygonal chain with points
$\mathbb{R}^3$
bounded below by the polygonal chain with points (0,a,0),(0,0,0),(b,0,0) and with upper side given by the polygonal chain with points
![]() $(x_i,y_i,d_i)$
for
$(x_i,y_i,d_i)$
for
![]() $i=a,a-1,\ldots,b$
, where
$i=a,a-1,\ldots,b$
, where
![]() $(x_i,y_i)$
is the last cell of
$(x_i,y_i)$
is the last cell of
![]() $[\mu]$
in the diagonal with content i (see Figure 3). Let
$[\mu]$
in the diagonal with content i (see Figure 3). Let
![]() $H_{\lambda/\mu}$
be the set of height functions h that extend
$H_{\lambda/\mu}$
be the set of height functions h that extend
![]() $\gamma_{\lambda/\mu}$
.
$\gamma_{\lambda/\mu}$
.

Figure 3. Skew shape
![]() $\lambda/\mu$
, the ASC
$\lambda/\mu$
, the ASC
![]() $\gamma^*_{\lambda/\mu}$
(in blue), and the ASC
$\gamma^*_{\lambda/\mu}$
(in blue), and the ASC
![]() $\gamma_{\lambda/\mu}$
(in red).
$\gamma_{\lambda/\mu}$
(in red).
For both height functions in
![]() $H^*_{\lambda/\mu}$
and
$H^*_{\lambda/\mu}$
and
![]() $H_{\lambda/\mu}$
, the weight of a horizontal lozenge of
$H_{\lambda/\mu}$
, the weight of a horizontal lozenge of
![]() $\textsf{t}_h$
with position (x, y) is the hook length
$\textsf{t}_h$
with position (x, y) is the hook length
![]() $\textsf{h}_{\lambda}(x,y)$
. The weight of a tiling
$\textsf{h}_{\lambda}(x,y)$
. The weight of a tiling
![]() $\textsf{t}_h$
is the product of the weights of its horizontal lozenges and we denote it by
$\textsf{t}_h$
is the product of the weights of its horizontal lozenges and we denote it by
![]() $\mathrm{hooks}_{\lambda}(\textsf{t}_h)$
,
$\mathrm{hooks}_{\lambda}(\textsf{t}_h)$
,
Proposition 2.3 There is a weight preserving bijection between the height functions in
![]() $H_{\lambda/\mu}$
and
$H_{\lambda/\mu}$
and
![]() $H^*_{\lambda/\mu}$
.
$H^*_{\lambda/\mu}$
.
Proof. The ASC
![]() $\gamma_{\lambda/\mu}$
and
$\gamma_{\lambda/\mu}$
and
![]() $\gamma^*_{\lambda/\mu}$
are bounded below by the same polygonal chain with points (0,a,0),(0,0,0),(b,0,0). The restriction on the horizontal lozenges of
$\gamma^*_{\lambda/\mu}$
are bounded below by the same polygonal chain with points (0,a,0),(0,0,0),(b,0,0). The restriction on the horizontal lozenges of
![]() $\textsf{t}_h$
for height functions h in
$\textsf{t}_h$
for height functions h in
![]() $H^*_{\lambda/\mu}$
is the same as the restriction imposed by the upper side of the polygonal chain bounding the ASC
$H^*_{\lambda/\mu}$
is the same as the restriction imposed by the upper side of the polygonal chain bounding the ASC
![]() $\gamma_{\lambda/\mu}$
. Therefore, there is a correspondence on the height functions that extend each of the ASCs. Moreover, if h in
$\gamma_{\lambda/\mu}$
. Therefore, there is a correspondence on the height functions that extend each of the ASCs. Moreover, if h in
![]() $H_{\lambda/\mu}$
corresponds to
$H_{\lambda/\mu}$
corresponds to
![]() $h^{\prime}$
in
$h^{\prime}$
in
![]() $H^*_{\lambda/\mu}$
, the horizontal lozenges in
$H^*_{\lambda/\mu}$
, the horizontal lozenges in
![]() $\textsf{t}_h$
and
$\textsf{t}_h$
and
![]() $\textsf{t}_{h'}$
have the same respective positions (x, y) and therefore
$\textsf{t}_{h'}$
have the same respective positions (x, y) and therefore
![]() $\mathrm{hooks}_{\lambda}(\textsf{t}_h)=\mathrm{hooks}_{\lambda}(\textsf{t}_{h'})$
, as desired.
$\mathrm{hooks}_{\lambda}(\textsf{t}_h)=\mathrm{hooks}_{\lambda}(\textsf{t}_{h'})$
, as desired.
Remark 2.4 Alternatively, from the proof of [Reference Morales, Pak and PanovaMPP3, Thm. 7.2] there is a correspondence from lozenge tilings for height functions in
![]() $H^*_{\lambda/\mu}$
(in
$H^*_{\lambda/\mu}$
(in
![]() $H_{\lambda/\mu}$
) to excited diagrams in
$H_{\lambda/\mu}$
) to excited diagrams in
![]() $\mathcal{E}(\lambda/\mu)$
(see e.g. [Reference Morales, Pak and PanovaMPP3, Sec. 2.6] for a definition of these diagrams). The map is as follows,
$\mathcal{E}(\lambda/\mu)$
(see e.g. [Reference Morales, Pak and PanovaMPP3, Sec. 2.6] for a definition of these diagrams). The map is as follows,
![]() $\textsf{t}_h$
corresponds to a reverse plane partition of shape
$\textsf{t}_h$
corresponds to a reverse plane partition of shape
![]() $\mu\,{:}\,$
$\mu\,{:}\,$
![]() $\textsf{t}_h \mapsto \pi$
where
$\textsf{t}_h \mapsto \pi$
where
![]() $\pi(i,j)$
is the height of the horizontal lozenge at position (i, j). Next, such plane partitions
$\pi(i,j)$
is the height of the horizontal lozenge at position (i, j). Next, such plane partitions
![]() $\pi$
correspond to excited diagrams D in
$\pi$
correspond to excited diagrams D in
![]() $\mathcal{E}(\lambda/\mu)$
:
$\mathcal{E}(\lambda/\mu)$
:
![]() $\pi \mapsto D$
where
$\pi \mapsto D$
where
![]() $r_{i,j}:=\pi_{i,j}-i$
is the row number of the final position of cell (i, j) of
$r_{i,j}:=\pi_{i,j}-i$
is the row number of the final position of cell (i, j) of
![]() $\mu$
after it has been moved under the excited moves from
$\mu$
after it has been moved under the excited moves from
![]() $[\mu]$
to D (see Figure 4). The condition that
$[\mu]$
to D (see Figure 4). The condition that
![]() $D\subset [\lambda]$
is equivalent to the restriction on horizontal lozenges imposed by either the height restriction on such lozenges for h in
$D\subset [\lambda]$
is equivalent to the restriction on horizontal lozenges imposed by either the height restriction on such lozenges for h in
![]() $H^*_{\lambda/\mu}$
or by the polygonal chain with points
$H^*_{\lambda/\mu}$
or by the polygonal chain with points
![]() $(x_i,y_i,d_i)$
where
$(x_i,y_i,d_i)$
where
![]() $d_i$
are the lengths of diagonals of
$d_i$
are the lengths of diagonals of
![]() $\lambda/\mu$
in the definition of
$\lambda/\mu$
in the definition of
![]() $H_{\lambda/\mu}$
.
$H_{\lambda/\mu}$
.

Figure 4. A lozenge tiling
![]() $\textsf{t}_h$
for a height function h in
$\textsf{t}_h$
for a height function h in
![]() $H_{\lambda/\mu}$
and its corresponding reverse plane partition
$H_{\lambda/\mu}$
and its corresponding reverse plane partition
![]() $\pi$
and excited diagram D. Excited diagrams appear in Naruse’s formula.
$\pi$
and excited diagram D. Excited diagrams appear in Naruse’s formula.
Theorem 2.5
(Naruse [Reference NaruseNar]; lozenge tiling versions [MPP3,
![]() $\S$
7]).
$\S$
7]).
 \begin{align} f^{\lambda/\mu} &= \frac{N!}{\prod_{(x,y) \in \lambda} \textsf{h}_{\lambda}(x,y)} \sum_{h \in H^*_{\lambda/\mu}} \mathrm{hooks}_{\lambda}(\textsf{t}_h)\end{align}
\begin{align} f^{\lambda/\mu} &= \frac{N!}{\prod_{(x,y) \in \lambda} \textsf{h}_{\lambda}(x,y)} \sum_{h \in H^*_{\lambda/\mu}} \mathrm{hooks}_{\lambda}(\textsf{t}_h)\end{align}
 \begin{align} &= \frac{N!}{\prod_{(x,y) \in \lambda} \textsf{h}_{\lambda}(x,y)} \sum_{h \in H_{\lambda/\mu}} \mathrm{hooks}_{\lambda}(\textsf{t}_h). \end{align}
\begin{align} &= \frac{N!}{\prod_{(x,y) \in \lambda} \textsf{h}_{\lambda}(x,y)} \sum_{h \in H_{\lambda/\mu}} \mathrm{hooks}_{\lambda}(\textsf{t}_h). \end{align}
Proof. The first lozenge tiling reformulation is implicit in [Reference Morales, Pak and PanovaMPP3, §7.1]. The second formulation follows from the first one by using Proposition 2.3.
Example 2.6 The skew shape
![]() $332/21$
has five height functions that extend
$332/21$
has five height functions that extend
![]() $\gamma_{2,1,1}$
:
$\gamma_{2,1,1}$
:
Formula (2.3) yields in this case
2.4. Stable shapes
Let
![]() $\psi:[0,a] \to [0,b]$
be a nonincreasing left continuous function. Assume a sequence of partitions
$\psi:[0,a] \to [0,b]$
be a nonincreasing left continuous function. Assume a sequence of partitions
![]() $\{\lambda^{(N)}\}$
satisfies the following property
$\{\lambda^{(N)}\}$
satisfies the following property
where
![]() $[\lambda]$
denotes the function giving the boundary of the Young diagram of
$[\lambda]$
denotes the function giving the boundary of the Young diagram of
![]() $\lambda$
. In this setting, we say that
$\lambda$
. In this setting, we say that
![]() $\{\lambda^{(N)}\}$
has a strongly stable shape
$\{\lambda^{(N)}\}$
has a strongly stable shape
![]() $\psi$
and denote it by
$\psi$
and denote it by
![]() $\lambda^{(N)} \to \psi$
. Note that
$\lambda^{(N)} \to \psi$
. Note that
![]() $\ell(\lambda^{(N)})$
,
$\ell(\lambda^{(N)})$
,
![]() $\ell(\lambda^{(N)'}) = O(\sqrt{N})$
. Such shapes are also called balanced (see e.g. [Reference Féray and ŚniadyFeS]).
$\ell(\lambda^{(N)'}) = O(\sqrt{N})$
. Such shapes are also called balanced (see e.g. [Reference Féray and ŚniadyFeS]).
Let
![]() $\psi,\phi: [0,a] \to [0,b]$
be nonincreasing left continuous functions, and suppose that
$\psi,\phi: [0,a] \to [0,b]$
be nonincreasing left continuous functions, and suppose that
![]() $area(\psi/\phi)=1$
. Let
$area(\psi/\phi)=1$
. Let
![]() $\{ v_N = \lambda^{(N)}/\mu^{(N)}\}$
be a sequence of skew shapes with the strongly stable shape
$\{ v_N = \lambda^{(N)}/\mu^{(N)}\}$
be a sequence of skew shapes with the strongly stable shape
![]() $\psi/\phi$
, i.e.
$\psi/\phi$
, i.e.
![]() $\lambda^{(N)} \to \psi$
,
$\lambda^{(N)} \to \psi$
,
![]() $\mu^{(N)} \to \phi$
and in addition they satisfy the condition
$\mu^{(N)} \to \phi$
and in addition they satisfy the condition
Denote by
![]() $\mathcal C(\psi), \mathcal C(\psi/\phi) \subset \mathbb R_+^2$
the region below the curve
$\mathcal C(\psi), \mathcal C(\psi/\phi) \subset \mathbb R_+^2$
the region below the curve
![]() $\psi$
and between the curves
$\psi$
and between the curves
![]() $\psi$
and
$\psi$
and
![]() $\phi$
, respectively. One can view
$\phi$
, respectively. One can view
![]() $\mathcal C(\psi/\phi)$
as the stable shape of the skew diagrams.
$\mathcal C(\psi/\phi)$
as the stable shape of the skew diagrams.
Finally, define the hook function
![]() $\hbar\,{:}\,\mathcal{C}(\psi) \to \mathbb{R}_+$
to be the limit of the scaled function of the hooks:
$\hbar\,{:}\,\mathcal{C}(\psi) \to \mathbb{R}_+$
to be the limit of the scaled function of the hooks:
where
![]() $\psi^{-1}:[0,b] \to [0,a]$
is the inverse of the function
$\psi^{-1}:[0,b] \to [0,a]$
is the inverse of the function
![]() $\psi$
, which is the continuous analogue of the conjugate partition, i.e.
$\psi$
, which is the continuous analogue of the conjugate partition, i.e.
![]() $\lambda^{'(N)} \to \psi^{-1}$
.
$\lambda^{'(N)} \to \psi^{-1}$
.
3. Variational principle for weighted lozenge tilings
Lozenge tilings is a dimer model and the existence of a variational principle which governs the limiting behavior of dimers under the uniform measure is a well known result (see [Reference Cohn, Kenyon and ProppCKP]). Our goal in this section will be to extend it to the case where we add weights to each tilings that depend on the position and the type of the lozenge tiles.
3.1. Weighted tilings and smooth weights
Let
![]() $D\subset \mathbb{R}^2$
be a connected domain in the plane, and let
$D\subset \mathbb{R}^2$
be a connected domain in the plane, and let
![]() $\{w^{(i)}\,{:}\,D \to \mathbb{R} \}_{i \leq 3}$
be three real valued functions corresponding to the weight of each type of lozenge. For a region
$\{w^{(i)}\,{:}\,D \to \mathbb{R} \}_{i \leq 3}$
be three real valued functions corresponding to the weight of each type of lozenge. For a region
![]() $R \subset D$
, define the weight of a height function h on R associated to the weight functions
$R \subset D$
, define the weight of a height function h on R associated to the weight functions
![]() $w=(w^{(1)},w^{(2)},w^{(3)})$
as
$w=(w^{(1)},w^{(2)},w^{(3)})$
as
where
![]() $(x_\lozenge,y_\lozenge)$
are the coordinates of the center of the tile
$(x_\lozenge,y_\lozenge)$
are the coordinates of the center of the tile
![]() $\lozenge$
and
$\lozenge$
and
![]() $i_\lozenge \in \{1,2,3\}$
is the type of the lozenge tile:
$i_\lozenge \in \{1,2,3\}$
is the type of the lozenge tile:
Given a weight function w, the partition function associated to an ASC
![]() $\gamma$
is defined as
$\gamma$
is defined as
where
![]() $H_{\gamma}$
is the set of height functions which extend
$H_{\gamma}$
is the set of height functions which extend
![]() $\gamma$
. Let
$\gamma$
. Let
![]() $N_{\gamma}$
be the size of
$N_{\gamma}$
be the size of
![]() $H_{\gamma}$
and let
$H_{\gamma}$
and let
![]() $\mathcal{L}^{(i)}(\gamma)$
be the (common) number of type i lozenges in each height function that extends
$\mathcal{L}^{(i)}(\gamma)$
be the (common) number of type i lozenges in each height function that extends
![]() $\gamma$
.
$\gamma$
.
Definition 3.1 Let D be a domain in
![]() $\mathbb{R}^2$
. A sequence of weight functions
$\mathbb{R}^2$
. A sequence of weight functions
![]() $\{w_n\}_{n \in \mathbb{N}}$
converges to a piecewise smooth function
$\{w_n\}_{n \in \mathbb{N}}$
converges to a piecewise smooth function
![]() $\rho\,{:}\, D \to \mathbb{R}^3$
if it has the following property:
$\rho\,{:}\, D \to \mathbb{R}^3$
if it has the following property:
3.2. The variational principle
Our goal in this section is to establish a variational principle for weighted tilings. We recall the unweighted version of the variational principle from [Reference KenyonKen, Thm. 9]. Let
![]() $\mathrm{Lip}_{[0,1]}$
be the set of 1-Lipschitz functions
$\mathrm{Lip}_{[0,1]}$
be the set of 1-Lipschitz functions
![]() $f\,{:}\,\mathbb{R}^2 \to \mathbb{R}$
that satisfy
$f\,{:}\,\mathbb{R}^2 \to \mathbb{R}$
that satisfy
everywhere except on a set of Lebesgue measure 0. Let
where
![]() $\Lambda(\cdot)$
is the Lobachevsky function, see e.g. [Reference Thurston and MilnorTM].
$\Lambda(\cdot)$
is the Lobachevsky function, see e.g. [Reference Thurston and MilnorTM].
Theorem 3.2
([Reference KenyonKen]). Let
![]() $\{ \gamma_n\}_{n\in \mathbb{N}}$
be a sequence of ASC. Suppose that
$\{ \gamma_n\}_{n\in \mathbb{N}}$
be a sequence of ASC. Suppose that
![]() $\frac{1}{n}\gamma_n$
converges to a closed curve
$\frac{1}{n}\gamma_n$
converges to a closed curve
![]() $\gamma$
in
$\gamma$
in
![]() $\mathbb{R}^3$
in the
$\mathbb{R}^3$
in the
![]() $\ell_{\infty}$
norm as
$\ell_{\infty}$
norm as
![]() $n \to \infty$
. Then:
$n \to \infty$
. Then:
where
![]() $g_{\max}: U \to R$
is the only extension of
$g_{\max}: U \to R$
is the only extension of
![]() $\gamma$
in
$\gamma$
in
![]() $\mathrm{Lip}_{[0,1]}$
that maximizes the following integral:
$\mathrm{Lip}_{[0,1]}$
that maximizes the following integral:
and U is the region enclosed by the projection of
![]() $\gamma$
. Moreover, for all
$\gamma$
. Moreover, for all
![]() $\epsilon > 0$
the height function of a random tiling chosen from the weighted measure associated to
$\epsilon > 0$
the height function of a random tiling chosen from the weighted measure associated to
![]() $w_n$
on height functions with boundary
$w_n$
on height functions with boundary
![]() $\gamma_n$
, stays within
$\gamma_n$
, stays within
![]() $\epsilon$
of
$\epsilon$
of
![]() $g_{\max}$
with probability
$g_{\max}$
with probability
![]() $\to 1$
as
$\to 1$
as
![]() $n\to\infty$
.
$n\to\infty$
.
The proof of this result is sketched in [Reference KenyonKen] and is the analogue of an earlier result for dominoes [Reference Cohn, Kenyon and ProppCKP]. The argument in the latter paper extends to our setting of lozenges.
We are now ready to state the variational principle for the weighted case. The proof is postponed to Section 5.
Theorem 3.3
(Weighted variational principle). Let
![]() $\{\gamma_n \}_{n\in \mathbb{N}}$
be a sequence of ASC, and let
$\{\gamma_n \}_{n\in \mathbb{N}}$
be a sequence of ASC, and let
![]() $\{w_n\}_{n \in \mathbb{N}}$
be a sequence of weight functions converging to a function
$\{w_n\}_{n \in \mathbb{N}}$
be a sequence of weight functions converging to a function
![]() $\rho$
. Suppose that
$\rho$
. Suppose that
![]() $\frac{1}{n}\gamma_n$
converges to a closed curved
$\frac{1}{n}\gamma_n$
converges to a closed curved
![]() $\gamma$
in
$\gamma$
in
![]() $\mathbb{R}^3$
in the
$\mathbb{R}^3$
in the
![]() $\ell_{\infty}$
norm as
$\ell_{\infty}$
norm as
![]() $n\to \infty$
. Then we have:
$n\to \infty$
. Then we have:
Here
![]() $f_{\max}: U \to \mathbb{R}$
is the only extension of
$f_{\max}: U \to \mathbb{R}$
is the only extension of
![]() $\gamma$
in
$\gamma$
in
![]() $\mathrm{Lip}_{[0,1]}$
which maximises the following integral:
$\mathrm{Lip}_{[0,1]}$
which maximises the following integral:
where U is the region enclosed by the projection of
![]() $\gamma$
, and
$\gamma$
, and
Moreover, for all
![]() $\epsilon > 0$
, the height function of a random tiling chosen from the weighted measure associated to
$\epsilon > 0$
, the height function of a random tiling chosen from the weighted measure associated to
![]() $w_n$
on height functions with boundary
$w_n$
on height functions with boundary
![]() $\gamma_n$
, stays within
$\gamma_n$
, stays within
![]() $\epsilon$
of
$\epsilon$
of
![]() $\,f_{\max}$
with probability tending to 1 as
$\,f_{\max}$
with probability tending to 1 as
![]() $n\to \infty$
.
$n\to \infty$
.
4. From lozenge tilings to standard Young tableaux
In this section, we apply the weighted variational principle to prove the main result on asymptotics of the number of skew SYT of skew shapes with strongly stable shapes.
Recall that
![]() $\{ \nu_N = \lambda^{(N)}/\mu^{(N)}\}$
is a sequence of skew shapes with the strongly stable shape
$\{ \nu_N = \lambda^{(N)}/\mu^{(N)}\}$
is a sequence of skew shapes with the strongly stable shape
![]() $\psi/\phi$
as defined in Section 2.4. We denote by U the region enclosed by
$\psi/\phi$
as defined in Section 2.4. We denote by U the region enclosed by
![]() $\phi$
in the first quandrant of
$\phi$
in the first quandrant of
![]() $\mathbb{R}^2$
.
$\mathbb{R}^2$
.
4.1. The weight function of hook lengths
In order to apply the weighted variational principle, we need weight functions that converge in the sense of Definition 3.1. In order to obtain a partition function that matches Naruse’s formula (2.3), the natural choice of weight function on U is the following
Denote by
![]() $\mathrm{wt}_N(h)$
the corresponding weight on height functions. Then
$\mathrm{wt}_N(h)$
the corresponding weight on height functions. Then
However for this choice of weight function,
![]() $\log h_{\lambda^{(N)}}(x,y)$
can be very small for points (x, y) near the border of the shape
$\log h_{\lambda^{(N)}}(x,y)$
can be very small for points (x, y) near the border of the shape
![]() $\lambda^{(N)}$
; see Figure 5:Left. In this regime, Property (*) might not hold. To fix this, we change the weight function to cap these small values as follows. For
$\lambda^{(N)}$
; see Figure 5:Left. In this regime, Property (*) might not hold. To fix this, we change the weight function to cap these small values as follows. For
![]() $\epsilon >0$
and (x, y) in
$\epsilon >0$
and (x, y) in
![]() $\mathcal{C}(\psi/\phi)$
, let
$\mathcal{C}(\psi/\phi)$
, let
Denote by
![]() $\mathrm{wt}_N^{\epsilon}(h)$
the corresponding weights on a height function h. Similarly, denote by
$\mathrm{wt}_N^{\epsilon}(h)$
the corresponding weights on a height function h. Similarly, denote by
![]() $Z_N$
and
$Z_N$
and
![]() $Z_N^{\epsilon}$
the corresponding partition functions associated to weights
$Z_N^{\epsilon}$
the corresponding partition functions associated to weights
![]() $w_N$
and
$w_N$
and
![]() $w^{\epsilon}_N$
, respectively.
$w^{\epsilon}_N$
, respectively.

Figure 5. Left: For points (x, y) near the top border (schematically indicated in grey) of the region the values of
![]() $\log h_{\lambda}(x,y)$
are small and can affect convergence of the weight function. Right: The hook measured in
$\log h_{\lambda}(x,y)$
are small and can affect convergence of the weight function. Right: The hook measured in
![]() $h_{\lambda^{(N)}}(x,y)$
.
$h_{\lambda^{(N)}}(x,y)$
.
4.2. From lozenge tilings to counting tableaux
We first show in Lemma 4.2 that the weighted variational principle, Theorem 3.3, applies to
![]() $Z_N^{\epsilon}$
. We then apply the variational principle in this case to obtain
$Z_N^{\epsilon}$
. We then apply the variational principle in this case to obtain
for some constant
![]() $c(\epsilon)$
depending on
$c(\epsilon)$
depending on
![]() $\epsilon$
and the shapes
$\epsilon$
and the shapes
![]() $\psi$
and
$\psi$
and
![]() $\phi$
. We then show that the constant
$\phi$
. We then show that the constant
![]() $c(\epsilon)$
converges to a constant c as
$c(\epsilon)$
converges to a constant c as
![]() $\epsilon \to 0$
(Lemma 4.3). In Corollary 4.4, we show that
$\epsilon \to 0$
(Lemma 4.3). In Corollary 4.4, we show that
![]() $\log Z_N^{\epsilon}$
converges to c as
$\log Z_N^{\epsilon}$
converges to c as
![]() $\epsilon \to 0$
. Finally, we conclude that
$\epsilon \to 0$
. Finally, we conclude that
by showing that
![]() $\log Z_N^{\epsilon}$
must also converge to
$\log Z_N^{\epsilon}$
must also converge to
![]() $\lim_{N\to \infty} \hskip.06cm \frac{1}{N} \hskip.06cm \log Z_N$
as
$\lim_{N\to \infty} \hskip.06cm \frac{1}{N} \hskip.06cm \log Z_N$
as
![]() $\epsilon \to 0$
(Theorem 4.5). In Section 4.3, we use this last result to prove Theorem 1.1. An explicit formulation of the constant c is given in Corollary 4.7
$\epsilon \to 0$
(Theorem 4.5). In Section 4.3, we use this last result to prove Theorem 1.1. An explicit formulation of the constant c is given in Corollary 4.7
We need some extra definitions. For the nonincreasing left continuous function
![]() $\phi:[0,a] \to [0,b]$
define
$\phi:[0,a] \to [0,b]$
define
![]() $\tilde{\phi}:[-b,a]\to \mathbb{R}$
by:
$\tilde{\phi}:[-b,a]\to \mathbb{R}$
by:
and define
![]() $\tilde{\psi}$
in an similar way. In other words,
$\tilde{\psi}$
in an similar way. In other words,
![]() $\tilde{\phi}$
and
$\tilde{\phi}$
and
![]() $\tilde{\psi}$
are continuous analogues of the Russian representations of partitions. Next, we define the continuous limit of the ASCs associated to the sets of polygonal regions
$\tilde{\psi}$
are continuous analogues of the Russian representations of partitions. Next, we define the continuous limit of the ASCs associated to the sets of polygonal regions
![]() $H_{\lambda^{(N)}/\mu^{(N)}}$
.
$H_{\lambda^{(N)}/\mu^{(N)}}$
.
Definition 4.1 Let
![]() $\gamma$
in
$\gamma$
in
![]() $\mathbb{R}^3$
be the continuous closed curve that is formed by: the line segment from
$\mathbb{R}^3$
be the continuous closed curve that is formed by: the line segment from
![]() $\{a,0,\tilde{\psi}(a)-\tilde{\phi}(a)\}$
to
$\{a,0,\tilde{\psi}(a)-\tilde{\phi}(a)\}$
to
![]() $\{a,0,0\}$
, the line segment from
$\{a,0,0\}$
, the line segment from
![]() $\{a,0,0\}$
to the origin, the line segment from the origin to
$\{a,0,0\}$
to the origin, the line segment from the origin to
![]() $\{0,b,0\}$
, the line segment from
$\{0,b,0\}$
, the line segment from
![]() $\{0,b,0\}$
to
$\{0,b,0\}$
to
![]() $\{0,b,\tilde{\psi}(-b)-\tilde{\phi}(-b)\}$
and the curve
$\{0,b,\tilde{\psi}(-b)-\tilde{\phi}(-b)\}$
and the curve
![]() $\{\phi(x),x,\tilde{\psi}(x-\phi(x))-\tilde{\phi}(x-\phi(x))\}$
for x in [0,a].
$\{\phi(x),x,\tilde{\psi}(x-\phi(x))-\tilde{\phi}(x-\phi(x))\}$
for x in [0,a].
Let
![]() $\mathrm{Lip}_{[0,1]}(\gamma)$
be the subset of
$\mathrm{Lip}_{[0,1]}(\gamma)$
be the subset of
![]() $\mathrm{Lip}_{[0,1]}$
of functions which extend
$\mathrm{Lip}_{[0,1]}$
of functions which extend
![]() $\gamma$
.
$\gamma$
.
Lemma 4.2 We have:
where
![]() $\Psi_{\epsilon}(\cdot)$
is the integral defined in (3.4) for the limiting weight function
$\Psi_{\epsilon}(\cdot)$
is the integral defined in (3.4) for the limiting weight function
Proof. First, we show that the weight function
![]() $w^{\epsilon}_N(x,y)$
converges to
$w^{\epsilon}_N(x,y)$
converges to
![]() $\rho_{\epsilon}(x,y)$
, in the sense of Definition 3.1 verifying property (*). By convergence of the sequence of shapes, for N large enough, either both
$\rho_{\epsilon}(x,y)$
, in the sense of Definition 3.1 verifying property (*). By convergence of the sequence of shapes, for N large enough, either both
![]() $\textsf{h}_{\lambda^{(N)}}(x,y)/\sqrt{N}$
and
$\textsf{h}_{\lambda^{(N)}}(x,y)/\sqrt{N}$
and
![]() $\hbar(x,y)$
defined in (2.5) are smaller than or equal
$\hbar(x,y)$
defined in (2.5) are smaller than or equal
![]() $\epsilon$
or both are greater or equal to
$\epsilon$
or both are greater or equal to
![]() $\epsilon$
. In the first case, we have
$\epsilon$
. In the first case, we have
![]() $w^{\epsilon}_N(x,y) = \rho_{\epsilon}(x,y)=(0,0,\log\epsilon)$
, and property (*) vacuously holds.
$w^{\epsilon}_N(x,y) = \rho_{\epsilon}(x,y)=(0,0,\log\epsilon)$
, and property (*) vacuously holds.
In the second case, we have that for all
![]() $(x,y)\in D$
:
$(x,y)\in D$
:
 \begin{align*}\left| w^{\epsilon}_N(x\sqrt{N},y\sqrt{N}) - \rho_{\epsilon}(x,y)\right| \, & = \, \left| \log \frac{1}{\sqrt{N}} \hskip.06cm \textsf{h}_{\lambda^{(N)}}\bigl(\lfloor x\sqrt{N}\rfloor, \lfloor y\sqrt{N}\rfloor\bigr) - \log \hbar(x,y) \right| \\[3pt] &\leq \, k_{\epsilon} \hskip.06cm \left| \frac{1}{\sqrt{N}} \hskip.06cm \textsf{h}_{\lambda^{(N)}}\bigl(\lfloor x\sqrt{N}\rfloor, \lfloor y \sqrt{N}\rfloor \bigr) - \hbar(x,y) \right|,\end{align*}
\begin{align*}\left| w^{\epsilon}_N(x\sqrt{N},y\sqrt{N}) - \rho_{\epsilon}(x,y)\right| \, & = \, \left| \log \frac{1}{\sqrt{N}} \hskip.06cm \textsf{h}_{\lambda^{(N)}}\bigl(\lfloor x\sqrt{N}\rfloor, \lfloor y\sqrt{N}\rfloor\bigr) - \log \hbar(x,y) \right| \\[3pt] &\leq \, k_{\epsilon} \hskip.06cm \left| \frac{1}{\sqrt{N}} \hskip.06cm \textsf{h}_{\lambda^{(N)}}\bigl(\lfloor x\sqrt{N}\rfloor, \lfloor y \sqrt{N}\rfloor \bigr) - \hbar(x,y) \right|,\end{align*}
where the inequality follows because the logarithm function is k-Lipschitz on
![]() $[\epsilon, \infty)$
, for some constant
$[\epsilon, \infty)$
, for some constant
![]() $k_{\epsilon}$
. From the definition of hook lengths (see Figure 5:Right), we also have:
$k_{\epsilon}$
. From the definition of hook lengths (see Figure 5:Right), we also have:
Thus, by convergence of the sequence of shapes, we have
 \begin{align*}&\lim_{N\to \infty} \hskip.06cm \left| w^{\epsilon}_N(\sqrt{N}x,\sqrt{N}y) - \rho_{\epsilon}(x,y)\right|\\[3pt] &\quad \leq \lim_{N\to \infty} k_{\epsilon} \cdot \left( \bigl\|\lambda^{(N)}/\sqrt{N} - \psi \bigr\|_{\infty} + \bigl\|\lambda'^{(N)}/\sqrt{N} - \psi^{-1} \bigr\|_{\infty} \right) \,= \hskip.06cm 0.\end{align*}
\begin{align*}&\lim_{N\to \infty} \hskip.06cm \left| w^{\epsilon}_N(\sqrt{N}x,\sqrt{N}y) - \rho_{\epsilon}(x,y)\right|\\[3pt] &\quad \leq \lim_{N\to \infty} k_{\epsilon} \cdot \left( \bigl\|\lambda^{(N)}/\sqrt{N} - \psi \bigr\|_{\infty} + \bigl\|\lambda'^{(N)}/\sqrt{N} - \psi^{-1} \bigr\|_{\infty} \right) \,= \hskip.06cm 0.\end{align*}
This proves property (*).
By construction of the sequence of polygonal regions
![]() $H_{\lambda^{(N)}/\mu^{(N)}}$
, after rescaling by
$H_{\lambda^{(N)}/\mu^{(N)}}$
, after rescaling by
![]() $\sqrt{N}$
, the corresponding sequence of ASCs
$\sqrt{N}$
, the corresponding sequence of ASCs
![]() $\frac{1}{\sqrt{N}}\gamma_{\lambda^{(N)}/\mu^{(N)}}$
converges to
$\frac{1}{\sqrt{N}}\gamma_{\lambda^{(N)}/\mu^{(N)}}$
converges to
![]() $\gamma$
for the infinite norm. Thus the weighted variational principle, Theorem 3.3, applies giving
$\gamma$
for the infinite norm. Thus the weighted variational principle, Theorem 3.3, applies giving
as desired.
The next lemma explains what happens to
![]() $\sup_{f \in \mathrm{Lip}_{[0,1](\gamma)}}\Psi_{\epsilon}(f)$
as
$\sup_{f \in \mathrm{Lip}_{[0,1](\gamma)}}\Psi_{\epsilon}(f)$
as
![]() $\epsilon\to 0$
.
$\epsilon\to 0$
.
Lemma 4.3 Let
![]() $\Psi(f)$
be the integral defined in (3.4) for
$\Psi(f)$
be the integral defined in (3.4) for
![]() $f \in\mathrm{Lip}_{[0,1]}(\gamma)$
and the weight function
$f \in\mathrm{Lip}_{[0,1]}(\gamma)$
and the weight function
Then
In particular,
Proof. Let
![]() $f \in \mathrm{Lip}_{[0,1]}(\gamma)$
, since the
$f \in \mathrm{Lip}_{[0,1]}(\gamma)$
, since the
![]() $||\cdot||_{\infty}$
-norm of the partial derivatives of f are uniformly bounded by 1 on U (see (3.2)), we obtain directly that:
$||\cdot||_{\infty}$
-norm of the partial derivatives of f are uniformly bounded by 1 on U (see (3.2)), we obtain directly that:
 \begin{equation*}\bigl|\Psi_{\epsilon}(f)-\Psi(f)\bigr| \, = \, \iint_{U} (\rho_{\epsilon}(x_1,x_2)-\rho(x_1,x_2)) \cdot(\partial_{x_1} f,\partial_{x_2}f,1-\partial_{x_1} f-\partial_{x_2} f) \hskip.06cm dx_1 \hskip.03cm dx_2 \le \, \iint_{U} ||\rho_{\epsilon}(x_1,x_2)-\rho(x_1,x_2)||_{\infty}\hskip.06cm dx_1\hskip.03cm dx_2 \,\end{equation*}
\begin{equation*}\bigl|\Psi_{\epsilon}(f)-\Psi(f)\bigr| \, = \, \iint_{U} (\rho_{\epsilon}(x_1,x_2)-\rho(x_1,x_2)) \cdot(\partial_{x_1} f,\partial_{x_2}f,1-\partial_{x_1} f-\partial_{x_2} f) \hskip.06cm dx_1 \hskip.03cm dx_2 \le \, \iint_{U} ||\rho_{\epsilon}(x_1,x_2)-\rho(x_1,x_2)||_{\infty}\hskip.06cm dx_1\hskip.03cm dx_2 \,\end{equation*}
The last integral of the previous inequality can be rewritten as
 \begin{eqnarray*}\iint_{U} ||\rho_{\epsilon}(x_1,x_2)-\rho(x_1,x_2)||_\infty \hskip.03cm dx_1\hskip.03cm dx_2 & = &\iint_{\{\log \hbar(x_1,x_2) \leq \log \epsilon \}} |\log \hbar(x_1,x_2)- \log {\epsilon}| \hskip.03cm dx_1\hskip.03cm dx_2 \\[3pt]& \leq & \iint_{\{\log \hbar(x_1,x_2) \leq \log \epsilon \}} \biggl(|\log \hbar(x_1,x_2)|+ |\log {\epsilon}|\biggr)\hskip.03cm \hskip.03cm dx_1\hskip.03cm dx_2\hskip.03cm.\end{eqnarray*}
\begin{eqnarray*}\iint_{U} ||\rho_{\epsilon}(x_1,x_2)-\rho(x_1,x_2)||_\infty \hskip.03cm dx_1\hskip.03cm dx_2 & = &\iint_{\{\log \hbar(x_1,x_2) \leq \log \epsilon \}} |\log \hbar(x_1,x_2)- \log {\epsilon}| \hskip.03cm dx_1\hskip.03cm dx_2 \\[3pt]& \leq & \iint_{\{\log \hbar(x_1,x_2) \leq \log \epsilon \}} \biggl(|\log \hbar(x_1,x_2)|+ |\log {\epsilon}|\biggr)\hskip.03cm \hskip.03cm dx_1\hskip.03cm dx_2\hskip.03cm.\end{eqnarray*}
The last integral converges to 0 when
![]() $\epsilon$
goes to 0 provided the function
$\epsilon$
goes to 0 provided the function
![]() $\log \hbar$
is integrable on the domain U. To show the integrability of
$\log \hbar$
is integrable on the domain U. To show the integrability of
![]() $\log \hbar$
we use the following bounds on
$\log \hbar$
we use the following bounds on
![]() $\hbar(x,y)$
:
$\hbar(x,y)$
:
where the upper bound follows from the definition of a hook and the bound of
![]() $\psi(x) \in [0,b]$
. The lower bound follows from the fact that
$\psi(x) \in [0,b]$
. The lower bound follows from the fact that
![]() $\hbar(x,y) \geq |\psi(x)-y|$
(see Figure 6) and the inequality
$\hbar(x,y) \geq |\psi(x)-y|$
(see Figure 6) and the inequality
![]() $\phi(x)\leq\psi(x)$
implied by the definition of the stable shape
$\phi(x)\leq\psi(x)$
implied by the definition of the stable shape
![]() $\psi/\phi$
. By taking the log and the absolute value, the bound (4.2) becomes
$\psi/\phi$
. By taking the log and the absolute value, the bound (4.2) becomes
Using standard analysis, one can show that the RHS of (4.3) is integrable on U and thus the function
![]() $\log \hbar$
is also integrable on U, as desired.
$\log \hbar$
is also integrable on U, as desired.

Figure 6. Representation of the rescaled hook function
![]() $\hbar(x,y)$
. The segment of length
$\hbar(x,y)$
. The segment of length
![]() $\phi(x)-y$
(depicted in red) is a lower bound for the hook length
$\phi(x)-y$
(depicted in red) is a lower bound for the hook length
![]() $\hbar(x,y)$
(depicted in gray).
$\hbar(x,y)$
(depicted in gray).

Figure 7. The slope of a periodic tiling.
Next, we write the log of the partition function
![]() $Z_N^{\epsilon}$
in terms of the log of the partition function
$Z_N^{\epsilon}$
in terms of the log of the partition function
![]() $Z_N$
.
$Z_N$
.
As a direct corollary of the previous two lemmas we obtain the following.
Corollary 4.4
Proof. This follows by combining lemmas 4.2 and 4.3.
We can now prove our main tool used to prove the main result on asymptotics of the number of skew SYT.
Theorem 4.5 We have
Proof. By Corollary 4.4 it suffices to show that
Since by definition of
![]() $Z^{\epsilon}_N$
and
$Z^{\epsilon}_N$
and
![]() $Z_N$
(see §4.1) we have that
$Z_N$
(see §4.1) we have that
![]() $Z^{\epsilon}_N \geq Z_N$
and
$Z^{\epsilon}_N \geq Z_N$
and
it is enough to prove that
By the median inequality, we have
Outside of a border strip of
![]() $\mu^{(N)}$
of height
$\mu^{(N)}$
of height
![]() $\lfloor \epsilon \sqrt{N}\rfloor$
the weights will not change. The hooks on the remaining lozenges in the strip are lower bounded by their depth. So the RHS in (4.6) can be bounded as follows:
$\lfloor \epsilon \sqrt{N}\rfloor$
the weights will not change. The hooks on the remaining lozenges in the strip are lower bounded by their depth. So the RHS in (4.6) can be bounded as follows:
 \begin{equation} \max_{h} \frac{ \mathrm{wt}_N^{\epsilon}(h)}{\mathrm{wt}_N(h)} \, \leq \, \frac{ (e^{\log \epsilon})^{\epsilon N}}{ \prod_{k=1}^{\lfloor \epsilon \sqrt{N}\rfloor} (e^{\log \left( k/(\epsilon \sqrt{N})\right) } )^{\epsilon \sqrt{N}}}\, = \,\frac{ (e^{\log \epsilon})^{\epsilon N}}{ \exp\left(\sum_{k=1}^{\lfloor \epsilon \sqrt{N}\rfloor} \epsilon\sqrt{N} \log \left(k/(\epsilon \sqrt{N})\right) \right)}\hskip.06cm.\end{equation}
\begin{equation} \max_{h} \frac{ \mathrm{wt}_N^{\epsilon}(h)}{\mathrm{wt}_N(h)} \, \leq \, \frac{ (e^{\log \epsilon})^{\epsilon N}}{ \prod_{k=1}^{\lfloor \epsilon \sqrt{N}\rfloor} (e^{\log \left( k/(\epsilon \sqrt{N})\right) } )^{\epsilon \sqrt{N}}}\, = \,\frac{ (e^{\log \epsilon})^{\epsilon N}}{ \exp\left(\sum_{k=1}^{\lfloor \epsilon \sqrt{N}\rfloor} \epsilon\sqrt{N} \log \left(k/(\epsilon \sqrt{N})\right) \right)}\hskip.06cm.\end{equation}
We can rewrite the denominator on the RHS above as
 \begin{equation} \exp\left(\sum_{k=1}^{\lfloor \epsilon \sqrt{N}\rfloor} \epsilon \sqrt{N} \log \frac{k}{\epsilon\sqrt{N}}\right) \,=\, \exp\left(\frac{\epsilon^2 N}{\epsilon \sqrt{N}} \sum_{k=1}^{\lfloor \epsilon \sqrt{N} \rfloor} \log \frac{k}{\epsilon \sqrt{N}} \right).\end{equation}
\begin{equation} \exp\left(\sum_{k=1}^{\lfloor \epsilon \sqrt{N}\rfloor} \epsilon \sqrt{N} \log \frac{k}{\epsilon\sqrt{N}}\right) \,=\, \exp\left(\frac{\epsilon^2 N}{\epsilon \sqrt{N}} \sum_{k=1}^{\lfloor \epsilon \sqrt{N} \rfloor} \log \frac{k}{\epsilon \sqrt{N}} \right).\end{equation}
If
![]() $\epsilon$
is fixed and N goes to infinity, the quantity
$\epsilon$
is fixed and N goes to infinity, the quantity
![]() $\frac{1}{\epsilon \sqrt{N}} \sum_{k=1}^{\lfloor \epsilon \sqrt{N} \rfloor} \log \frac{k}{\epsilon \sqrt{N}} $
is a Riemann sum for the function
$\frac{1}{\epsilon \sqrt{N}} \sum_{k=1}^{\lfloor \epsilon \sqrt{N} \rfloor} \log \frac{k}{\epsilon \sqrt{N}} $
is a Riemann sum for the function
![]() $x \to \log x$
on the interval [0,1]. Hence,
$x \to \log x$
on the interval [0,1]. Hence,
 \begin{equation}\frac{1}{\epsilon \sqrt{N}} \hskip.06cm \sum_{k=1}^{\lfloor \epsilon \sqrt{N} \rfloor} \log \frac{k}{\epsilon \sqrt{N}} \, = \, \int^{1}_0 \log x \hskip.03cm dx \hskip.06cm + \hskip.06cm o_{\epsilon}(1)\end{equation}
\begin{equation}\frac{1}{\epsilon \sqrt{N}} \hskip.06cm \sum_{k=1}^{\lfloor \epsilon \sqrt{N} \rfloor} \log \frac{k}{\epsilon \sqrt{N}} \, = \, \int^{1}_0 \log x \hskip.03cm dx \hskip.06cm + \hskip.06cm o_{\epsilon}(1)\end{equation}
where
![]() $o_{\epsilon}(1)$
is a function depending on
$o_{\epsilon}(1)$
is a function depending on
![]() $\epsilon$
which goes to 0 when N goes to
$\epsilon$
which goes to 0 when N goes to
![]() $\infty$
. Thus, using (4.8) and (4.9), (4.7) becomes
$\infty$
. Thus, using (4.8) and (4.9), (4.7) becomes
Combining the previous equation with the bound in (4.6), taking logs, and letting
![]() $N \to \infty$
yields the following upper bound
$N \to \infty$
yields the following upper bound
Since
![]() $\lim_{\epsilon \to 0} \epsilon \left(\log \epsilon -\epsilon\int^{1}_0 \log x \hskip.03cm dx \right)=0$
, by taking the limit when
$\lim_{\epsilon \to 0} \epsilon \left(\log \epsilon -\epsilon\int^{1}_0 \log x \hskip.03cm dx \right)=0$
, by taking the limit when
![]() $\epsilon$
goes to 0 in the previous bound we obtain (4.5) which finishes our proof.
$\epsilon$
goes to 0 in the previous bound we obtain (4.5) which finishes our proof.
4.3. The number of standard Young tableaux
We are now ready to prove Theorem 1.1. We require the following technical result.
Lemma 4.6 We have:
 \begin{equation*}\frac{1}{N} \left[\hskip.06cm \log \biggl(\hskip.06cm \sum_{h \in H_{\lambda^{(N)}/\mu^{(N)}}} \mathrm{hooks}_{\lambda^{(N)}}(\textsf{t}_h)\biggr) \hskip.06cm - \hskip.06cm \frac{\text{\rm area}(\phi)}{2} \hskip.03cm N \log N\right] \, \to \, c,\end{equation*}
\begin{equation*}\frac{1}{N} \left[\hskip.06cm \log \biggl(\hskip.06cm \sum_{h \in H_{\lambda^{(N)}/\mu^{(N)}}} \mathrm{hooks}_{\lambda^{(N)}}(\textsf{t}_h)\biggr) \hskip.06cm - \hskip.06cm \frac{\text{\rm area}(\phi)}{2} \hskip.03cm N \log N\right] \, \to \, c,\end{equation*}
where
![]() $c:=\Psi(f_{\max})$
is a constant which depends only on
$c:=\Psi(f_{\max})$
is a constant which depends only on
![]() $\psi$
and
$\psi$
and
![]() $\phi$
.
$\phi$
.
Proof. Recall that for the weight function
![]() $w_N(x,y)$
and a height function h in
$w_N(x,y)$
and a height function h in
![]() $H_{\lambda^{(N)}/\mu^{(N)}}$
we have that
$H_{\lambda^{(N)}/\mu^{(N)}}$
we have that
 \begin{align}\notag\mathrm{hooks}_{\lambda^{(N)}}(\textsf{t}_h) &= \prod_{\lozenge \in \textsf{t}_h} \textsf{h}_{\lambda^{(N)}}(x_{\lozenge},y_{\lozenge}) = (\sqrt{N})^{|\mu^{(N)}|} \times \prod_{\lozenge \in \textsf{t}_h}e^{w^{i_{\lozenge}}(x_{\lozenge}y_{\lozenge})} \\& =(\sqrt{N})^{|\mu^{(N)}|} \times \mathrm{wt}(h),\end{align}
\begin{align}\notag\mathrm{hooks}_{\lambda^{(N)}}(\textsf{t}_h) &= \prod_{\lozenge \in \textsf{t}_h} \textsf{h}_{\lambda^{(N)}}(x_{\lozenge},y_{\lozenge}) = (\sqrt{N})^{|\mu^{(N)}|} \times \prod_{\lozenge \in \textsf{t}_h}e^{w^{i_{\lozenge}}(x_{\lozenge}y_{\lozenge})} \\& =(\sqrt{N})^{|\mu^{(N)}|} \times \mathrm{wt}(h),\end{align}
where
![]() $\mathrm{wt}(h)$
is a defined in (3.1). Then the log of the partition function of all height functions in
$\mathrm{wt}(h)$
is a defined in (3.1). Then the log of the partition function of all height functions in
![]() $H_{\lambda^{(N)}/\mu^{(N)}}$
equals
$H_{\lambda^{(N)}/\mu^{(N)}}$
equals
where
![]() $Z_N = \sum_{h \in H_{\lambda^{(N)}/\mu^{(N)}}} \mathrm{wt}(h)$
. We treat each of the two summands in the RHS above separately.
$Z_N = \sum_{h \in H_{\lambda^{(N)}/\mu^{(N)}}} \mathrm{wt}(h)$
. We treat each of the two summands in the RHS above separately.
By condition (2.4) on the area of
![]() $\phi$
in the definition of the stable shape we have that
$\phi$
in the definition of the stable shape we have that
Next, by Theorem 4.5 we have
where
![]() $c := \Psi(f_{\max})$
is a constant that only depends on
$c := \Psi(f_{\max})$
is a constant that only depends on
![]() $\psi$
and
$\psi$
and
![]() $\phi$
.
$\phi$
.
Finally, we take the limit as
![]() $N \to \infty$
in (4.12) and use both (4.13) and (4.14) to obtain the desired result.
$N \to \infty$
in (4.12) and use both (4.13) and (4.14) to obtain the desired result.
Proof of Theorem 1.1. We take logs in (2.3) to obtain
 \begin{equation} \log f^{\nu^{(N)}} = \log |\nu^{(N)}|! - \left(\sum_{(x,y) \in \lambda^{(N)}} \log\textsf{h}_{\lambda^{(N)}}(x,y)\right) + \log \left(\sum_{h \in H_{\lambda^{(N)}/\mu^{(N)}}} \mathrm{hooks}_{\lambda}(\textsf{t}_h)\right) \end{equation}
\begin{equation} \log f^{\nu^{(N)}} = \log |\nu^{(N)}|! - \left(\sum_{(x,y) \in \lambda^{(N)}} \log\textsf{h}_{\lambda^{(N)}}(x,y)\right) + \log \left(\sum_{h \in H_{\lambda^{(N)}/\mu^{(N)}}} \mathrm{hooks}_{\lambda}(\textsf{t}_h)\right) \end{equation}
Observe that
![]() $|\nu^{(N)}| = N + O(\sqrt{N})$
as
$|\nu^{(N)}| = N + O(\sqrt{N})$
as
![]() $N\to \infty$
. Then by Stirling’s formula we have
$N\to \infty$
. Then by Stirling’s formula we have
Next, we use the definition and compactness of the stable shape
![]() $\mathcal{C}(\psi)$
$\mathcal{C}(\psi)$
 \begin{equation*}\sum_{(x,y) \in \lambda^{(N)}} \log \textsf{h}_{\lambda^{(N)}}(x,y) \, = \,N\iint_{\mathcal{C}(\psi)} \hskip.06cm \log\bigl(\sqrt{N}\hbar(x,y)\bigr) \hskip.03cm dx\hskip.03cm dy \hskip.06cm + \hskip.06cm o(N),\end{equation*}
\begin{equation*}\sum_{(x,y) \in \lambda^{(N)}} \log \textsf{h}_{\lambda^{(N)}}(x,y) \, = \,N\iint_{\mathcal{C}(\psi)} \hskip.06cm \log\bigl(\sqrt{N}\hbar(x,y)\bigr) \hskip.03cm dx\hskip.03cm dy \hskip.06cm + \hskip.06cm o(N),\end{equation*}
where the leading N outside the integral comes from a change of variables
![]() $x \to \sqrt{N}x$
,
$x \to \sqrt{N}x$
,
![]() $y\to \sqrt{N}y$
and the
$y\to \sqrt{N}y$
and the
![]() $\sqrt{N}$
inside the integral comes from rewriting
$\sqrt{N}$
inside the integral comes from rewriting
![]() $\textsf{h}_{\lambda^{(N)}}(\cdot ,\cdot)$
in terms of
$\textsf{h}_{\lambda^{(N)}}(\cdot ,\cdot)$
in terms of
![]() $\hbar(x,y)$
defined in (2.5). The error term o(N) comes from approximating the sum with the scaled integral (cf. [MPP4, Thm. 6.3]).
$\hbar(x,y)$
defined in (2.5). The error term o(N) comes from approximating the sum with the scaled integral (cf. [MPP4, Thm. 6.3]).
By linearity of integration with respect to the integrand
![]() $\frac{1}{2}\log N + \log \hbar(x,y),$
we obtain
$\frac{1}{2}\log N + \log \hbar(x,y),$
we obtain
 \begin{equation} \sum_{(x,y) \in \lambda^{(N)}} \log \textsf{h}_{\lambda^{(N)}}(x,y) \, = \, \frac{{\textrm{area}}(\psi)}{2} \hskip.03cm N \hskip.03cm \log N \hskip.06cm + \hskip.06cm k(\psi)N \hskip.06cm + \hskip.06cm o(N), \end{equation}
\begin{equation} \sum_{(x,y) \in \lambda^{(N)}} \log \textsf{h}_{\lambda^{(N)}}(x,y) \, = \, \frac{{\textrm{area}}(\psi)}{2} \hskip.03cm N \hskip.03cm \log N \hskip.06cm + \hskip.06cm k(\psi)N \hskip.06cm + \hskip.06cm o(N), \end{equation}
where
![]() $k(\psi) = \iint_{\mathcal{C}(\psi)} \hbar(x,y) \hskip.06cm dx\hskip.03cm dy$
. Lastly, applying to each term in (4.15) the bounds from (4.16), (4.17) and Lemma 4.6, respectively, we obtain
$k(\psi) = \iint_{\mathcal{C}(\psi)} \hbar(x,y) \hskip.06cm dx\hskip.03cm dy$
. Lastly, applying to each term in (4.15) the bounds from (4.16), (4.17) and Lemma 4.6, respectively, we obtain
where
![]() $c(\psi/\phi):=c+k(\psi)$
is the sum of the constant c from Lemma 4.6 and
$c(\psi/\phi):=c+k(\psi)$
is the sum of the constant c from Lemma 4.6 and
![]() $k(\psi)$
. Finally, since
$k(\psi)$
. Finally, since
![]() ${\textrm{area}}(\psi/\phi)=1$
, the result follows.
${\textrm{area}}(\psi/\phi)=1$
, the result follows.
We end this section by extracting from the proof above the explicit expression for the constant of Theorem 1.1.
Corollary 4.7 The constant
![]() $c(\psi/\phi)$
of Theorem 1.1 is given by
$c(\psi/\phi)$
of Theorem 1.1 is given by
where
 \begin{align*}k(\psi) \hskip.06cm & = \hskip.06cm\iint_{\mathcal{C}(\psi)} \hbar(x,y) \hskip.06cm dx\hskip.03cm dy,\\\Psi(f) \hskip.06cm &= \hskip.06cm \iint_U \Bigl( \sigma(\nabla f)\hskip.06cm + \hskip.06cm (1-\partial_{x} f - \partial_{y} f) \hskip.03cm \log \hbar(x,y) \Bigr) \hskip.03cm dx\hskip.03cm dy,\end{align*}
\begin{align*}k(\psi) \hskip.06cm & = \hskip.06cm\iint_{\mathcal{C}(\psi)} \hbar(x,y) \hskip.06cm dx\hskip.03cm dy,\\\Psi(f) \hskip.06cm &= \hskip.06cm \iint_U \Bigl( \sigma(\nabla f)\hskip.06cm + \hskip.06cm (1-\partial_{x} f - \partial_{y} f) \hskip.03cm \log \hbar(x,y) \Bigr) \hskip.03cm dx\hskip.03cm dy,\end{align*}
for
![]() $\sigma(\cdot)$
defined by (3.3), U is the region enclosed by the projection of
$\sigma(\cdot)$
defined by (3.3), U is the region enclosed by the projection of
![]() $\gamma$
from Definition 4.1, and
$\gamma$
from Definition 4.1, and
![]() $f_{\max}:U\to \mathbb{R}$
is the only function in
$f_{\max}:U\to \mathbb{R}$
is the only function in
![]() $\mathrm{Lip}_{[0,1]}(\gamma)$
which maximizes the integral
$\mathrm{Lip}_{[0,1]}(\gamma)$
which maximizes the integral
![]() $\Psi(f)$
.
$\Psi(f)$
.
5. Proof of the weighted variational principle
Our strategy to prove this theorem consists of three parts. In the first part, we give a lemma (Lemma 5.1) that shows that fundamental domains with similar plane-like boundary conditions have the same number of tilings and that all those tilings contain a similar number of lozenges of each type. Both numbers depend on the slope of the domain. In the second part, we give a lemma (Lemma 5.3) that shows that the weighted contribution of lozenges with similar plane-like boundary conditions is also the same. Finally, in the third part, we use the two previous lemmas to prove the weighted variational principle.
5.1. Tilings of similar plane-like regions (unweighted)
Let (s, t) be a pair of numbers such that
![]() $\{ 0 \leq s,t,1-s-t\leq 1 \}$
, let
$\{ 0 \leq s,t,1-s-t\leq 1 \}$
, let
![]() $\epsilon> 0$
and let
$\epsilon> 0$
and let
![]() $D_m$
be the
$D_m$
be the
![]() $m \times m$
diamond of the hexagonal grid whose left corner is the origin.
$m \times m$
diamond of the hexagonal grid whose left corner is the origin.
Let
![]() $\overline{H}^{\epsilon}_{D_m}(s,t)$
be the set of admissible boundary height functions
$\overline{H}^{\epsilon}_{D_m}(s,t)$
be the set of admissible boundary height functions
![]() $\bar{h}\,{:}\, \partial D_m \rightarrow \mathbb{Z} $
, such that:
$\bar{h}\,{:}\, \partial D_m \rightarrow \mathbb{Z} $
, such that:
-
• the left corner of the diamond has height 0
-
• for all
 $x=(x_1,x_2) \in \partial D_m $
we have
$x=(x_1,x_2) \in \partial D_m $
we have  \begin{equation*}| \bar{h}(x_1,x_2) -( sx_1+tx_2 ) | \leq \epsilon m.\end{equation*}
\begin{equation*}| \bar{h}(x_1,x_2) -( sx_1+tx_2 ) | \leq \epsilon m.\end{equation*}
Lemma 5.1 Let (s,t) be such that
![]() $\{ 0 \leq s,t,1-s-t\leq 1 \}$
, let
$\{ 0 \leq s,t,1-s-t\leq 1 \}$
, let
![]() $\epsilon > 0$
and let
$\epsilon > 0$
and let
![]() $D_m\subset \mathbb{Z}^2$
and
$D_m\subset \mathbb{Z}^2$
and
![]() $\overline{H}^{\epsilon}_{D_m}(s,t)$
be as defined above. Then for each
$\overline{H}^{\epsilon}_{D_m}(s,t)$
be as defined above. Then for each
![]() $\bar{h} \in \overline{H}^{\epsilon}_{D_m}(s,t)$
we have that
$\bar{h} \in \overline{H}^{\epsilon}_{D_m}(s,t)$
we have that
 \begin{equation} \lim_{m \to \infty} \frac{1}{m^2} \log N(\bar{h}) = \lim_{m \to \infty} \frac{1}{m^2} \log \sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h}) = \sigma(s,t)+ O (\epsilon \log(1/\epsilon)),\end{equation}
\begin{equation} \lim_{m \to \infty} \frac{1}{m^2} \log N(\bar{h}) = \lim_{m \to \infty} \frac{1}{m^2} \log \sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h}) = \sigma(s,t)+ O (\epsilon \log(1/\epsilon)),\end{equation}
and
Proof. Let
![]() $\mathcal{P}_m(s,t)$
be the set of tilings of
$\mathcal{P}_m(s,t)$
be the set of tilings of
![]() $D_m$
with periodic boundary conditions with slope (s, t) and
$D_m$
with periodic boundary conditions with slope (s, t) and
![]() ${N}_m(s,t)$
be the number of tilings in
${N}_m(s,t)$
be the number of tilings in
![]() $\mathcal{P}_m(s,t)$
. Note that
$\mathcal{P}_m(s,t)$
. Note that
![]() $\mathcal{P}_m(s,t)$
is also the set of tilings of a torus with slope (s, t). By [Reference KenyonKen, Thm. 8] we have that:
$\mathcal{P}_m(s,t)$
is also the set of tilings of a torus with slope (s, t). By [Reference KenyonKen, Thm. 8] we have that:
and that each of those tilings has exactly
![]() $\{m^2s,m^2t,m^2(1-s-t)\}$
lozenges of each type. Additionally, if we choose a height function uniformly amongst all height functions in
$\{m^2s,m^2t,m^2(1-s-t)\}$
lozenges of each type. Additionally, if we choose a height function uniformly amongst all height functions in
![]() $\mathcal{P}_m(s,t)$
then we have the following concentration results:
$\mathcal{P}_m(s,t)$
then we have the following concentration results:
This can be shown by applying the same martingale argument as in [Reference Cohn, Elkies and ProppCEP, Prop. 22]. Although the argument in this paper is made for simply connected regions, it extends for tilings of a torus with given slopes.
Denote by
![]() $\mathcal{P}^{\epsilon}_m(s,t)$
the set of periodic configurations on a torus of size m whose height function stays within
$\mathcal{P}^{\epsilon}_m(s,t)$
the set of periodic configurations on a torus of size m whose height function stays within
![]() $\epsilon m$
of a linear plane of slope (s, t) that is
$\epsilon m$
of a linear plane of slope (s, t) that is
Let
![]() $N^{\epsilon}_m(s,t)$
be the size of
$N^{\epsilon}_m(s,t)$
be the size of
![]() $\mathcal{P}^{\epsilon}_m(s,t)$
. As a direct consequence of the inequality (5.3), we have
$\mathcal{P}^{\epsilon}_m(s,t)$
. As a direct consequence of the inequality (5.3), we have
Therefore,
We must now distinguish between the case where
![]() $\epsilon\leq \frac{1}{2}(1-\max\{s,t,1-s-t\})$
and the case
$\epsilon\leq \frac{1}{2}(1-\max\{s,t,1-s-t\})$
and the case
![]() $\epsilon >\frac{1}{2}\max\{s,t,1-s-t\}$
.
$\epsilon >\frac{1}{2}\max\{s,t,1-s-t\}$
.
Case 1: Suppose
![]() $ \epsilon \leq \frac{1}{2}(1-\max\{s,t,1-s-t\})$
. Consider
$ \epsilon \leq \frac{1}{2}(1-\max\{s,t,1-s-t\})$
. Consider
![]() $\bar{h} \in \overline{H}^{\epsilon}_{D_{m}}(s,t)$
and
$\bar{h} \in \overline{H}^{\epsilon}_{D_{m}}(s,t)$
and
![]() $h_- \in\mathcal{P}^{\epsilon}_{m(1-3\epsilon)}(s,t)$
. For all
$h_- \in\mathcal{P}^{\epsilon}_{m(1-3\epsilon)}(s,t)$
. For all
![]() $x=(x_1,x_2) \in \partial D_{m(1-3\epsilon)}$
and
$x=(x_1,x_2) \in \partial D_{m(1-3\epsilon)}$
and
![]() $y=(y_1,y_2) \in \partial D_m$
we have
$y=(y_1,y_2) \in \partial D_m$
we have
 \begin{eqnarray*}{\bar{h}(y)-h_-(x) \, \leq }\\[3pt]& \, \leq \, & \biggl[\bar{h}(y)-(sy_1+ty_2)\biggr] \,+\, \biggl[(sy_1 +ty_2)-(sx_1+tx_2)\biggr] \,+\, \biggl[(sx_1+tx_2)-h_-(x)\biggr] \\[3pt] & \, \leq \, & \epsilon \hskip.03cm m \hskip.06cm + \hskip.06cm \max\{s,t,1-s-t\}\cdot \max\{y_1-x_1,y_2-x_2\} \hskip.06cm+ \hskip.06cm\epsilon \hskip.03cm m \\[3pt] & \, \leq \, & {\bigl(}1-\max\{s,t,1-s-t\}{\bigr)}\|x-y\|_1 \hskip.06cm + \hskip.06cm\max\{s,t,1-s-t\}\cdot \max\{y_1-x_1,y_2-x_2\} \\[3pt] & \, \leq \, & \max\{y_1-x_1,y_2-x_2\}. \end{eqnarray*}
\begin{eqnarray*}{\bar{h}(y)-h_-(x) \, \leq }\\[3pt]& \, \leq \, & \biggl[\bar{h}(y)-(sy_1+ty_2)\biggr] \,+\, \biggl[(sy_1 +ty_2)-(sx_1+tx_2)\biggr] \,+\, \biggl[(sx_1+tx_2)-h_-(x)\biggr] \\[3pt] & \, \leq \, & \epsilon \hskip.03cm m \hskip.06cm + \hskip.06cm \max\{s,t,1-s-t\}\cdot \max\{y_1-x_1,y_2-x_2\} \hskip.06cm+ \hskip.06cm\epsilon \hskip.03cm m \\[3pt] & \, \leq \, & {\bigl(}1-\max\{s,t,1-s-t\}{\bigr)}\|x-y\|_1 \hskip.06cm + \hskip.06cm\max\{s,t,1-s-t\}\cdot \max\{y_1-x_1,y_2-x_2\} \\[3pt] & \, \leq \, & \max\{y_1-x_1,y_2-x_2\}. \end{eqnarray*}
where
![]() $\|\cdot\|_1$
denotes the 1-norm.
$\|\cdot\|_1$
denotes the 1-norm.
Using Lemma 2.1, we deduce that there exists a height function h on
![]() $D_m$
such that
$D_m$
such that
![]() $h=\bar{h}$
on
$h=\bar{h}$
on
![]() $\partial{D_m}$
and
$\partial{D_m}$
and
![]() $h=h_-$
on
$h=h_-$
on
![]() $\partial{D_{m(1-3\epsilon)}}$
. As a consequence, we obtain that
$\partial{D_{m(1-3\epsilon)}}$
. As a consequence, we obtain that
![]() $N(\bar{h}) \geq N^{\epsilon}_{m(1-3\epsilon)}(s,t)$
. For the same reasons, for
$N(\bar{h}) \geq N^{\epsilon}_{m(1-3\epsilon)}(s,t)$
. For the same reasons, for
![]() $h_+ \in \mathcal{P}^{\epsilon}_{m(1+3\epsilon)}(s,t)$
, for all
$h_+ \in \mathcal{P}^{\epsilon}_{m(1+3\epsilon)}(s,t)$
, for all
![]() $x \in \partial D_m$
and
$x \in \partial D_m$
and
![]() $z \in \partial D_{m(1+3\epsilon)}$
we have
$z \in \partial D_{m(1+3\epsilon)}$
we have
Thus, every boundary height functions in
![]() $\mathcal{P}^{\epsilon}_{m(1+3\epsilon)}(s,t)$
can be extended to
$\mathcal{P}^{\epsilon}_{m(1+3\epsilon)}(s,t)$
can be extended to
![]() $\bar{h}$
on
$\bar{h}$
on
![]() $\partial D_m$
. This implies:
$\partial D_m$
. This implies:
which can be rewritten as
Since
![]() $1/(m^2(1-3\epsilon)) = 1/m^2+O(\epsilon)$
, we deduce that
$1/(m^2(1-3\epsilon)) = 1/m^2+O(\epsilon)$
, we deduce that
Finally, we can bound the number of boundary conditions in
![]() $H^{\epsilon}_{D_m}(s,t)$
by the number of different types of lozenges to the power of the length of
$H^{\epsilon}_{D_m}(s,t)$
by the number of different types of lozenges to the power of the length of
![]() $\partial D_m$
. Since there are at most
$\partial D_m$
. Since there are at most
![]() $3^{4m}=e^{o(m^2)}$
different boundary height functions in
$3^{4m}=e^{o(m^2)}$
different boundary height functions in
![]() $\overline{H}^{\epsilon}_{D_m}(s,t)$
, then this allows us to deduce (5.1):
$\overline{H}^{\epsilon}_{D_m}(s,t)$
, then this allows us to deduce (5.1):
 \begin{equation*}\lim_{m \to \infty} \frac{1}{m^2} \log \sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h}) = \sigma(s,t)+ O (\epsilon).\end{equation*}
\begin{equation*}\lim_{m \to \infty} \frac{1}{m^2} \log \sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h}) = \sigma(s,t)+ O (\epsilon).\end{equation*}
For the second part of the statement, we notice that when attaching two tilings as described above (see Figure 8), we are adding at most
![]() $\epsilon^2m^2$
tilings of each type. Hence, we obtain that for all
$\epsilon^2m^2$
tilings of each type. Hence, we obtain that for all
![]() $i \in \{1,2,3\}$
:
$i \in \{1,2,3\}$
:
Dividing by
![]() $m^2$
and taking the logarithm, we obtain (5.2).
$m^2$
and taking the logarithm, we obtain (5.2).

Figure 8. Illustration of the proof of Lemma 5.1. The number of tilings with boundary conditions in
![]() $\overline{h} \in \partial D_m$
is at least the number of tilings with periodic boundary conditions in
$\overline{h} \in \partial D_m$
is at least the number of tilings with periodic boundary conditions in
![]() $\partial D_{m(1-3\epsilon)}$
and at most the number of tilings with periodic boundary conditions in
$\partial D_{m(1-3\epsilon)}$
and at most the number of tilings with periodic boundary conditions in
![]() $\partial D_{m(1+3\epsilon)}$
.
$\partial D_{m(1+3\epsilon)}$
.
Case 2: Suppose
![]() $ \epsilon \geq\frac{1}{2}(1-\max\{s,t,1-s-t\})$
. Let
$ \epsilon \geq\frac{1}{2}(1-\max\{s,t,1-s-t\})$
. Let
![]() $\bar{h} \in\overline{H}^{\epsilon}_{D_{m}}(s,t)$
. Without loss of generality we can assume that
$\bar{h} \in\overline{H}^{\epsilon}_{D_{m}}(s,t)$
. Without loss of generality we can assume that
![]() $\max\{s,t,1-s-t\}=1-s-t$
so that
$\max\{s,t,1-s-t\}=1-s-t$
so that
![]() $ \epsilon \geq (s+t)/2$
. The height difference between the top vertex and the bottom vertex of each vertical section of
$ \epsilon \geq (s+t)/2$
. The height difference between the top vertex and the bottom vertex of each vertical section of
![]() $D_m$
is at most
$D_m$
is at most
![]() $4\hskip.03cm \epsilon \hskip.03cm m$
. Hence, each of such vertical sections contains at most
$4\hskip.03cm \epsilon \hskip.03cm m$
. Hence, each of such vertical sections contains at most
![]() $\lfloor 4 \epsilon m \rfloor$
vertical edges. This means that the total number of non-horizontal lozenges in each tiling of a height function that extends
$\lfloor 4 \epsilon m \rfloor$
vertical edges. This means that the total number of non-horizontal lozenges in each tiling of a height function that extends
![]() $ \bar{h}$
is smaller than
$ \bar{h}$
is smaller than
![]() $\lfloor 4\hskip.03cm \epsilon \hskip.03cm m^2\rfloor$
and implies directly (5.2). Notice that we can determine a tiling by specifying what is the position of the non-horizontal lozenges and their types. Hence, the total number of tilings
$\lfloor 4\hskip.03cm \epsilon \hskip.03cm m^2\rfloor$
and implies directly (5.2). Notice that we can determine a tiling by specifying what is the position of the non-horizontal lozenges and their types. Hence, the total number of tilings
![]() $N(\bar{h})$
is bounded by
$N(\bar{h})$
is bounded by
 $\left(\begin{array}{l}{m^2 }\\ {\lfloor 4\epsilon m^2 \rfloor}\end{array}\right)2^{\lfloor 4\hskip.03cm \epsilon \hskip.03cm m^2 \rfloor}$
. By using Stirling’s formula, we obtain
$\left(\begin{array}{l}{m^2 }\\ {\lfloor 4\epsilon m^2 \rfloor}\end{array}\right)2^{\lfloor 4\hskip.03cm \epsilon \hskip.03cm m^2 \rfloor}$
. By using Stirling’s formula, we obtain
 \begin{equation*}N(\bar{h}) \leq \left(\begin{array}{c}{m^2}\\ {\lfloor 4\epsilon m^2 \rfloor}\end{array}\right)2^{\lfloor 4\hskip.03cm \epsilon \hskip.03cm m^2\rfloor}\hskip.06cm = \hskip.06cm e^{m^2O(\epsilon \log(1/\epsilon))}\hskip.03cm.\end{equation*}
\begin{equation*}N(\bar{h}) \leq \left(\begin{array}{c}{m^2}\\ {\lfloor 4\epsilon m^2 \rfloor}\end{array}\right)2^{\lfloor 4\hskip.03cm \epsilon \hskip.03cm m^2\rfloor}\hskip.06cm = \hskip.06cm e^{m^2O(\epsilon \log(1/\epsilon))}\hskip.03cm.\end{equation*}
Therefore, the total number of configurations with boundary
![]() $\bar{h}$
satisfies
$\bar{h}$
satisfies
Since
![]() $\sigma(0,0)=0$
, this implies (5.1) and concludes our proof.
$\sigma(0,0)=0$
, this implies (5.1) and concludes our proof.
Lemma 5.1 holds when we replace lozenges by equilateral triangles. This will be useful for the remainder of the proof as explained in Section 5.2.
Corollary 5.2 Let
![]() $T_m$
be an equilateral triangle of size m and
$T_m$
be an equilateral triangle of size m and
![]() $\overline{H}^{\epsilon}_{T_m}(s,t)$
be as defined above. Then for each
$\overline{H}^{\epsilon}_{T_m}(s,t)$
be as defined above. Then for each
![]() $\bar{h} \in \overline{H}^{\epsilon}_{T_m}(s,t)$
we have that
$\bar{h} \in \overline{H}^{\epsilon}_{T_m}(s,t)$
we have that
 \begin{equation} \lim_{m \to \infty} \frac{4}{\sqrt{3}m^2} \log N(\bar{h}) \, = \, \lim_{m \to \infty} \hskip.06cm \frac{4}{\sqrt{3}m^2} \hskip.06cm \log \left(\sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h})\right) \, = \, \sigma(s,t) \hskip.06cm + \hskip.06cm O\bigl(\epsilon \log(1/\epsilon)\bigr), \end{equation}
\begin{equation} \lim_{m \to \infty} \frac{4}{\sqrt{3}m^2} \log N(\bar{h}) \, = \, \lim_{m \to \infty} \hskip.06cm \frac{4}{\sqrt{3}m^2} \hskip.06cm \log \left(\sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h})\right) \, = \, \sigma(s,t) \hskip.06cm + \hskip.06cm O\bigl(\epsilon \log(1/\epsilon)\bigr), \end{equation}
and
Proof. Let
![]() $T_m$
be a triangle of size m and
$T_m$
be a triangle of size m and
![]() $\bar{h}$
be a boundary height function which stays within
$\bar{h}$
be a boundary height function which stays within
![]() $\epsilon m$
of the plane with slope (s, t). For each
$\epsilon m$
of the plane with slope (s, t). For each
![]() $h \in \bar{h}$
, if we reflect h along one side we obtain a height function of a lozenge
$h \in \bar{h}$
, if we reflect h along one side we obtain a height function of a lozenge
![]() $D_m$
which also stays within
$D_m$
which also stays within
![]() $\epsilon m$
of the plane with slope (s, t). Hence we can bound
$\epsilon m$
of the plane with slope (s, t). Hence we can bound
![]() $N(\bar{h})^2$
by the number of ways to extend a boundary in
$N(\bar{h})^2$
by the number of ways to extend a boundary in
![]() $\overline{H}^{\epsilon}_{D_m}(s,t)$
and we obtain
$\overline{H}^{\epsilon}_{D_m}(s,t)$
and we obtain
 \begin{equation*}\frac{2}{m^2}\log N(\bar{h}) \, = \, \frac{1}{m^2}\log\left(N(\bar{h})^2\right) \, \leq \,\frac{1}{m^2}\hskip.06cm\log \left[\sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h})\right]\hskip.06cm \leq \hskip.06cm \sigma(s,t)\hskip.06cm + \hskip.06cm O\bigl(\epsilon \log(1/\epsilon)\bigr).\end{equation*}
\begin{equation*}\frac{2}{m^2}\log N(\bar{h}) \, = \, \frac{1}{m^2}\log\left(N(\bar{h})^2\right) \, \leq \,\frac{1}{m^2}\hskip.06cm\log \left[\sum_{\bar{h} \in\overline{H}^{\epsilon}_{D_m}(s,t)} N(\bar{h})\right]\hskip.06cm \leq \hskip.06cm \sigma(s,t)\hskip.06cm + \hskip.06cm O\bigl(\epsilon \log(1/\epsilon)\bigr).\end{equation*}
Now consider a triangle
![]() $T_{m^2}$
of size
$T_{m^2}$
of size
![]() $m^2$
,
$m^2$
,
![]() $\bar{h}$
be a boundary height function which stays within
$\bar{h}$
be a boundary height function which stays within
![]() $\epsilon m$
of the plane with slope (s, t). We can fill partially
$\epsilon m$
of the plane with slope (s, t). We can fill partially
![]() $T_{m^2}$
with
$T_{m^2}$
with
![]() $m-o(1)$
lozenges of size m each having the same periodic boundary height function with slope (s, t). Using a similar argument as the one in the previous lemma for attaching configurations, we can attach
$m-o(1)$
lozenges of size m each having the same periodic boundary height function with slope (s, t). Using a similar argument as the one in the previous lemma for attaching configurations, we can attach
![]() $\bar{h}$
to the height function on those lozenges and we obtain
$\bar{h}$
to the height function on those lozenges and we obtain
as desired.
5.2. Tilings of similar plane-like regions (weighted)
For the remainder of this proof we will be working with triangles since later in this proof we will need to approximate surfaces with piecewise-linear functions. Such approximations are done in a standard way using triangles (see for example Lemma 2.2 in [Reference Cohn, Kenyon and ProppCKP]).
Since the weight of each individual lozenge tile depends on its position in the lattice, we now evaluate the weight contribution of a large triangle as a function of its position.
Lemma 5.3 Let
![]() $x=(x_1,x_2) \in \mathbb{R}^2$
and
$x=(x_1,x_2) \in \mathbb{R}^2$
and
![]() $\ell \in \mathbb{R}$
be such that
$\ell \in \mathbb{R}$
be such that
![]() $\rho$
is smooth on
$\rho$
is smooth on
![]() $B(x,\ell)$
. Let
$B(x,\ell)$
. Let
![]() $T(x,\ell n)$
be the triangle of size
$T(x,\ell n)$
be the triangle of size
![]() $ \ell n$
centered at the point
$ \ell n$
centered at the point
![]() $x^n:=(\lfloor n x_1 \rfloor,\lfloor n x_2 \rfloor)$
and let
$x^n:=(\lfloor n x_1 \rfloor,\lfloor n x_2 \rfloor)$
and let
![]() $\bar{h} \in \overline{H}^{\epsilon}_{T(x, \ell n)}(s,t)$
. For a converging sequence of weights
$\bar{h} \in \overline{H}^{\epsilon}_{T(x, \ell n)}(s,t)$
. For a converging sequence of weights
![]() $\{w_{n} \}_{n \in \mathbb{N}}$
we have
$\{w_{n} \}_{n \in \mathbb{N}}$
we have
 \begin{align} \lim_{n\to \infty} \frac{4}{\sqrt{3}(\ell n)^2} \hskip.06cm \log Z(H_{\bar{h}},w_{\ell}) \, & = \, \lim_{n\to \infty}\frac{4}{\sqrt{3}(\ell n)^2}\hskip.06cm \log \left[\sum_{\bar{h} \in \overline{H}^{\epsilon}_{T(x,\ell n)}(s,t)} \hskip.06cm Z\bigl(H_{\bar{h}},w_{\ell}\bigr)\right] \notag \\ &= \, \sigma(s,t)\hskip.06cm + \hskip.06cm L(x_1,x_2,s,t)\hskip.06cm + \hskip.06cm O\bigl(\epsilon \log (1/\epsilon)\bigr)\hskip.06cm + \hskip.06cm O(\ell), \end{align}
\begin{align} \lim_{n\to \infty} \frac{4}{\sqrt{3}(\ell n)^2} \hskip.06cm \log Z(H_{\bar{h}},w_{\ell}) \, & = \, \lim_{n\to \infty}\frac{4}{\sqrt{3}(\ell n)^2}\hskip.06cm \log \left[\sum_{\bar{h} \in \overline{H}^{\epsilon}_{T(x,\ell n)}(s,t)} \hskip.06cm Z\bigl(H_{\bar{h}},w_{\ell}\bigr)\right] \notag \\ &= \, \sigma(s,t)\hskip.06cm + \hskip.06cm L(x_1,x_2,s,t)\hskip.06cm + \hskip.06cm O\bigl(\epsilon \log (1/\epsilon)\bigr)\hskip.06cm + \hskip.06cm O(\ell), \end{align}
where
![]() $Z(H_{\bar{h}},w_{\ell})$
is the total weight of all configurations with boundary
$Z(H_{\bar{h}},w_{\ell})$
is the total weight of all configurations with boundary
![]() $\bar{h}$
.
$\bar{h}$
.
Proof. The sequence of weights
![]() $\{w_{n} \}_{n \in \mathbb{N}}$
is convergent, by Condition (ii) of Definition 3.1. Thus, for all
$\{w_{n} \}_{n \in \mathbb{N}}$
is convergent, by Condition (ii) of Definition 3.1. Thus, for all
![]() $ny \in T(x,\ell n)$
, and for each type of lozenge tile
$ny \in T(x,\ell n)$
, and for each type of lozenge tile
![]() $i \in \{1,2.3\}$
, we have:
$i \in \{1,2.3\}$
, we have:
Here we used the smoothness of
![]() $\rho$
on
$\rho$
on
![]() $B(x,\ell)$
to bound
$B(x,\ell)$
to bound
![]() $|\rho^i(y)-\rho^i(x)| = O(\ell)$
. This means that for all height function
$|\rho^i(y)-\rho^i(x)| = O(\ell)$
. This means that for all height function
![]() $h \in H^{\epsilon}_{T(x,l)}(s,t)$
with boundary
$h \in H^{\epsilon}_{T(x,l)}(s,t)$
with boundary
![]() $\bar{h}$
, we must have
$\bar{h}$
, we must have
 \begin{align*} \mathrm{wt}(h) & = \prod_{\lozenge \in h} e^{w^{i_{\lozenge}}(x_{\lozenge})} = \prod_{\lozenge \in h} e^{(\rho^{i_\lozenge}(x)+O(\ell)+o(1))}\\ & = \, \sum_{j=1}^3 \hskip.06cm \exp\left[\frac{\sqrt{3}(\ell n)^2}{4}\bigl(x_j\hskip.06cm + \hskip.06cm o(1)\hskip.06cm + \hskip.06cm O(\epsilon)\bigr)\right] \cdot\exp\biggl[\rho^{1}(x)\hskip.06cm + \hskip.06cm o(1)\hskip.06cm + \hskip.06cm O(\ell)\biggr] \\ & = \, \exp\left[\frac{\sqrt{3}(\ell n)^2}{4}\biggl(L(x_1,x_2,s,t)\hskip.06cm + \hskip.06cm o(1)\hskip.06cm + \hskip.06cm O(\ell)\hskip.06cm + \hskip.06cm O(\epsilon)\biggr)\right], \end{align*}
\begin{align*} \mathrm{wt}(h) & = \prod_{\lozenge \in h} e^{w^{i_{\lozenge}}(x_{\lozenge})} = \prod_{\lozenge \in h} e^{(\rho^{i_\lozenge}(x)+O(\ell)+o(1))}\\ & = \, \sum_{j=1}^3 \hskip.06cm \exp\left[\frac{\sqrt{3}(\ell n)^2}{4}\bigl(x_j\hskip.06cm + \hskip.06cm o(1)\hskip.06cm + \hskip.06cm O(\epsilon)\bigr)\right] \cdot\exp\biggl[\rho^{1}(x)\hskip.06cm + \hskip.06cm o(1)\hskip.06cm + \hskip.06cm O(\ell)\biggr] \\ & = \, \exp\left[\frac{\sqrt{3}(\ell n)^2}{4}\biggl(L(x_1,x_2,s,t)\hskip.06cm + \hskip.06cm o(1)\hskip.06cm + \hskip.06cm O(\ell)\hskip.06cm + \hskip.06cm O(\epsilon)\biggr)\right], \end{align*}
where
![]() $x_3 = 1-x_1-x_2$
. Then the contribution of all configurations with boundary
$x_3 = 1-x_1-x_2$
. Then the contribution of all configurations with boundary
![]() $\bar{h}$
is given by:
$\bar{h}$
is given by:
 \begin{align*} Z(H_{\bar{h}},w_{n}) & \, = \, \sum_{h \in H^{\epsilon}_{T(x,\ell)}(s,t)} \mathrm{wt}(h) \\ & = \, \exp\left[\frac{\sqrt{3}(\ell \hskip.03cm n)^2}{4}\biggl(L(x_1,x_2,s,t)\hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O(\ell) \hskip.06cm + \hskip.06cm O(\epsilon )\biggr)\right] \hskip.06cm N(\bar{h}). \end{align*}
\begin{align*} Z(H_{\bar{h}},w_{n}) & \, = \, \sum_{h \in H^{\epsilon}_{T(x,\ell)}(s,t)} \mathrm{wt}(h) \\ & = \, \exp\left[\frac{\sqrt{3}(\ell \hskip.03cm n)^2}{4}\biggl(L(x_1,x_2,s,t)\hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O(\ell) \hskip.06cm + \hskip.06cm O(\epsilon )\biggr)\right] \hskip.06cm N(\bar{h}). \end{align*}
Applying Corollary 5.2 to the equation above, we obtain
 \begin{align*} Z(H_{\bar{h}},w_{n}) & \, = \, \exp\left[\frac{\sqrt{3}(\ell \hskip.03cm n)^2}{4}\biggl(L(x_1,x_2,s,t) \hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O(\epsilon)\biggr)\right] \, \times \notag \\&\hskip2.cm \times \, \exp\left[\frac{\sqrt{3}(\ell \hskip.03cm n)^2}{4}\biggl(\sigma(s,t) \hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O\bigl(\epsilon \log (1/\epsilon)\bigr)\biggr)\right] \notag \\ & \, = \, \exp\left[\frac{\sqrt{3}(\ell\hskip.03cm n)^2}{4}\biggl(\sigma(s,t) \hskip.06cm + \hskip.06cm L(x_1,x_2,s,t) \hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O(\ell) \hskip.06cm + \hskip.06cm O\bigl(\epsilon\log(1/\epsilon)\bigr)\biggr)\right]. \end{align*}
\begin{align*} Z(H_{\bar{h}},w_{n}) & \, = \, \exp\left[\frac{\sqrt{3}(\ell \hskip.03cm n)^2}{4}\biggl(L(x_1,x_2,s,t) \hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O(\epsilon)\biggr)\right] \, \times \notag \\&\hskip2.cm \times \, \exp\left[\frac{\sqrt{3}(\ell \hskip.03cm n)^2}{4}\biggl(\sigma(s,t) \hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O\bigl(\epsilon \log (1/\epsilon)\bigr)\biggr)\right] \notag \\ & \, = \, \exp\left[\frac{\sqrt{3}(\ell\hskip.03cm n)^2}{4}\biggl(\sigma(s,t) \hskip.06cm + \hskip.06cm L(x_1,x_2,s,t) \hskip.06cm + \hskip.06cm o(1) \hskip.06cm + \hskip.06cm O(\ell) \hskip.06cm + \hskip.06cm O\bigl(\epsilon\log(1/\epsilon)\bigr)\biggr)\right]. \end{align*}
Then (5.6) follows by taking the logarithm of the equation above. Since the number of boundary height functions for a given triangle is bounded by
![]() $3^{3\ell n}=e^{o(\ell^2 n^2)}$
, we also obtain:
$3^{3\ell n}=e^{o(\ell^2 n^2)}$
, we also obtain:
 \begin{equation*} \lim_{\ell\to \infty}\frac{4}{\sqrt{3}(\ell n)^2} \sum_{\bar{h} \in \overline{H}^{\epsilon}_{T(x,\ell)}(s,t)} Z(H_{\bar{h}},w_{\ell}) \, = \, \sigma(s,t)\hskip.06cm +\hskip.06cm L(x_1,x_2,s,t)\hskip.06cm +\hskip.06cm O\bigl(\epsilon \log (1/\epsilon)\bigr)\hskip.06cm +\hskip.06cm O(\ell).\end{equation*}
\begin{equation*} \lim_{\ell\to \infty}\frac{4}{\sqrt{3}(\ell n)^2} \sum_{\bar{h} \in \overline{H}^{\epsilon}_{T(x,\ell)}(s,t)} Z(H_{\bar{h}},w_{\ell}) \, = \, \sigma(s,t)\hskip.06cm +\hskip.06cm L(x_1,x_2,s,t)\hskip.06cm +\hskip.06cm O\bigl(\epsilon \log (1/\epsilon)\bigr)\hskip.06cm +\hskip.06cm O(\ell).\end{equation*}
This finishes the proof.
5.3. Proof of Theorem 3.3
We now prove the weighted variational principle. At this stage our strategy is exactly the same as Theorem 4.3 in [Reference Cohn, Kenyon and ProppCKP] or Theorem 2.9 in [Reference Menz and TassyMT]. We recall the following two lemmas from [Reference Cohn, Kenyon and ProppCKP] which will be useful in our proof.
Lemma 5.4
([Reference Cohn, Kenyon and ProppCKP] Lemma 2.2). For
![]() $\ell > 0$
, consider a mesh made up of equilateral triangles of side length
$\ell > 0$
, consider a mesh made up of equilateral triangles of side length
![]() $\ell$
(which we call an
$\ell$
(which we call an
![]() $\ell$
-mesh). Let
$\ell$
-mesh). Let
![]() $f \in \mathrm{Lip}_{[0,1]}$
be such that
$f \in \mathrm{Lip}_{[0,1]}$
be such that
![]() $f= \gamma$
on U, and let
$f= \gamma$
on U, and let
![]() $\epsilon > 0$
. If
$\epsilon > 0$
. If
![]() $\ell$
is sufficiently small then on at least
$\ell$
is sufficiently small then on at least
![]() $(1-\epsilon)$
fractions of the triangles in the
$(1-\epsilon)$
fractions of the triangles in the
![]() $\ell$
-mesh that intersect U we have the following two properties:
$\ell$
-mesh that intersect U we have the following two properties:
-
1. The piecewise linear approximation
 $\widetilde{f}$
stays within
$\widetilde{f}$
stays within
 $\ell \epsilon$
of f.
$\ell \epsilon$
of f. -
2. For at least a
 $(1-\epsilon)$
fraction (in measure) of the points x of the triangle, the tilt
$(1-\epsilon)$
fraction (in measure) of the points x of the triangle, the tilt
 $\nabla f(x)$
exists and is within
$\nabla f(x)$
exists and is within
 $\epsilon$
of
$\epsilon$
of
 $\widetilde{f}(x)$
.
$\widetilde{f}(x)$
.
Lemma 5.5
([Reference Cohn, Kenyon and ProppCKP] Lemma 2.3). Suppose that T is an equilateral triangle of length
![]() $\ell$
, and the height function f satisfies
$\ell$
, and the height function f satisfies
![]() $|f_{\delta T} - \widetilde{f}| \leq \epsilon \ell$
on
$|f_{\delta T} - \widetilde{f}| \leq \epsilon \ell$
on
![]() $\delta T$
, where
$\delta T$
, where
![]() $\widetilde{f}$
is the piecewise linear approximation from Lemma 5.4, then
$\widetilde{f}$
is the piecewise linear approximation from Lemma 5.4, then
Remark 5.6 Note that Lemma 2.3 in [Reference Cohn, Kenyon and ProppCKP] is stated for
![]() $\Upsilon(\cdot)$
, however, since the function
$\Upsilon(\cdot)$
, however, since the function
![]() $L(\cdots)$
from the definition of
$L(\cdots)$
from the definition of
![]() $\Psi(\cdot)$
in (3.4) is linear, this lemma still holds for
$\Psi(\cdot)$
in (3.4) is linear, this lemma still holds for
![]() $\Psi(\cdot)$
.
$\Psi(\cdot)$
.
Next, we approximate the partition function of all height functions which stays close to a given function f using
![]() $\Psi$
and show that the error term goes to zero.
$\Psi$
and show that the error term goes to zero.
Lemma 5.7 Let
![]() $f \in \mathrm{Lip}_{[0,1]}$
be such that
$f \in \mathrm{Lip}_{[0,1]}$
be such that
![]() $f= \gamma$
on U and let
$f= \gamma$
on U and let
![]() $\delta > 0$
. If we denote by
$\delta > 0$
. If we denote by
![]() $ Z(H^{\delta}_{f}, w_n)$
the total weight of height functions which stay within
$ Z(H^{\delta}_{f}, w_n)$
the total weight of height functions which stay within
![]() $\delta n$
of f, then:
$\delta n$
of f, then:
Proof. Let
![]() $\epsilon < 1$
and consider a sequence of grids
$\epsilon < 1$
and consider a sequence of grids
![]() $\{G_n\}_{n \in \mathbb{N}}$
which partition the triangular lattice into equilateral triangles of size
$\{G_n\}_{n \in \mathbb{N}}$
which partition the triangular lattice into equilateral triangles of size
![]() $\ell n$
. Denote by
$\ell n$
. Denote by
![]() $\widetilde{G}_n$
the
$\widetilde{G}_n$
the
![]() $\ell$
-mesh obtained by rescaling
$\ell$
-mesh obtained by rescaling
![]() $G_n$
and
$G_n$
and
![]() $\widetilde{f}$
the linear approximation of f on
$\widetilde{f}$
the linear approximation of f on
![]() $\widetilde{G}_n$
. See Figure 9.
$\widetilde{G}_n$
. See Figure 9.

Figure 9. The grid
![]() $\widetilde{G}_n$
of equilateral triangles of size
$\widetilde{G}_n$
of equilateral triangles of size
![]() $\ell$
that partitions U used in the proof of Theorem 3.3.
$\ell$
that partitions U used in the proof of Theorem 3.3.
We start by approximating
![]() $\Psi(f)$
by the terms on the RHS of (5.6) of Lemma 5.3. According to Lemma 5.4, for
$\Psi(f)$
by the terms on the RHS of (5.6) of Lemma 5.3. According to Lemma 5.4, for
![]() $\ell$
small enough we have:
$\ell$
small enough we have:
on all but a portion at most
![]() $\epsilon$
of the triangles in U. Next, we rewrite
$\epsilon$
of the triangles in U. Next, we rewrite
![]() $\Psi(\widetilde{f})$
as
$\Psi(\widetilde{f})$
as
where the error term
![]() $o\bigl({\textrm{area}}(U)\bigr)$
comes from bounding the following integral
$o\bigl({\textrm{area}}(U)\bigr)$
comes from bounding the following integral
using the uniform continuity of
![]() $\rho$
on each component of U where it is smooth.
$\rho$
on each component of U where it is smooth.
Combining (5.8) with Lemma 5.5 we have
 \begin{equation*}\left|\Psi(f)-\sum_{T \in U} \frac{4\ell^2}{\sqrt{3}} \left(\sigma(\nabla \widetilde{f}) \hskip.03cm + \hskip.03cm L(x^{T}_1,x^{T}_2,\widetilde{f}) \right)\right| \hskip.06cm = \hskip.06cm o(1).\end{equation*}
\begin{equation*}\left|\Psi(f)-\sum_{T \in U} \frac{4\ell^2}{\sqrt{3}} \left(\sigma(\nabla \widetilde{f}) \hskip.03cm + \hskip.03cm L(x^{T}_1,x^{T}_2,\widetilde{f}) \right)\right| \hskip.06cm = \hskip.06cm o(1).\end{equation*}
With this approximation, we are now ready to prove (5.7). Choose
![]() $\delta < \ell\epsilon$
and
$\delta < \ell\epsilon$
and
![]() $\{h_n\}$
to be any height function with boundary
$\{h_n\}$
to be any height function with boundary
![]() $\gamma_n$
. Define
$\gamma_n$
. Define
Then
![]() $|g_n/n-f| \leq \delta/2$
and
$|g_n/n-f| \leq \delta/2$
and
![]() $g_n \in H^{\delta}_{f}$
, by construction.
$g_n \in H^{\delta}_{f}$
, by construction.
We can ignore the contribution of triangles that are not fully included in U which is
![]() $O(\delta)=O(\epsilon)$
. The quantity
$O(\delta)=O(\epsilon)$
. The quantity
![]() $\log Z(H_{f}^{\delta}, w_n)$
is bounded from below by the weight of all height functions that agree with
$\log Z(H_{f}^{\delta}, w_n)$
is bounded from below by the weight of all height functions that agree with
![]() $g_n$
on the boundary of all triangles in
$g_n$
on the boundary of all triangles in
![]() $G_n$
completely contained in U after rescaling. This gives
$G_n$
completely contained in U after rescaling. This gives
where the product is taken over all triangle T fully contained in U and such that
Now include the
![]() $O(\epsilon)$
in the bound. Then
$O(\epsilon)$
in the bound. Then
![]() $\log Z(H_{f}^{\delta}, w_n)$
is bounded from above by the total free product of all height functions which stays within
$\log Z(H_{f}^{\delta}, w_n)$
is bounded from above by the total free product of all height functions which stays within
![]() $\delta$
of
$\delta$
of
![]() $\widetilde{f}$
on each one of those triangles. In other words,
$\widetilde{f}$
on each one of those triangles. In other words,
Using Lemma 5.3 to approximate each
![]() $\log Z(H_{\bar{g}_{\partial T}},w_n)$
and
$\log Z(H_{\bar{g}_{\partial T}},w_n)$
and
![]() $\log Z(H^{\delta}_{\widetilde{f}_{\partial T}},w_n) $
in the above inequalities, we obtain
$\log Z(H^{\delta}_{\widetilde{f}_{\partial T}},w_n) $
in the above inequalities, we obtain
 \begin{align*} &\frac{1}{n^2} \log Z(H^{\delta}_{f}, w_n) \, = \\& \qquad = \, \frac{1}{n^2} \sum_{T \in U}\left[\frac{\sqrt{3}}{4}\ell^2n^{2} \left(\sigma(\widetilde{f}) + L(x^{T}_1,x^{T}_2,\widetilde{f})+ o( 1)+O(\ell) +O(\epsilon \log 1 / \epsilon)\right)\right]+o(1) \\& \qquad = \, \sum_{T \in U} \left[\frac{\sqrt{3}}{4}\ell^2\left( \sigma(\widetilde{f}) +L(x^{T}_1,x^{T}_2,\widetilde{f}) + o( 1)+O(\ell) \hskip.03cm +\hskip.03cm O(\epsilon \log 1 / \epsilon)\right)\right]+o(1)\\& \qquad = \, \Psi(\widetilde{f})+O(\ell) \hskip.06cm + \hskip.06cm O(\epsilon \log 1 / \epsilon) \hskip.06cm + \hskip.06cm o(1).\end{align*}
\begin{align*} &\frac{1}{n^2} \log Z(H^{\delta}_{f}, w_n) \, = \\& \qquad = \, \frac{1}{n^2} \sum_{T \in U}\left[\frac{\sqrt{3}}{4}\ell^2n^{2} \left(\sigma(\widetilde{f}) + L(x^{T}_1,x^{T}_2,\widetilde{f})+ o( 1)+O(\ell) +O(\epsilon \log 1 / \epsilon)\right)\right]+o(1) \\& \qquad = \, \sum_{T \in U} \left[\frac{\sqrt{3}}{4}\ell^2\left( \sigma(\widetilde{f}) +L(x^{T}_1,x^{T}_2,\widetilde{f}) + o( 1)+O(\ell) \hskip.03cm +\hskip.03cm O(\epsilon \log 1 / \epsilon)\right)\right]+o(1)\\& \qquad = \, \Psi(\widetilde{f})+O(\ell) \hskip.06cm + \hskip.06cm O(\epsilon \log 1 / \epsilon) \hskip.06cm + \hskip.06cm o(1).\end{align*}
Since both
![]() $\ell$
and
$\ell$
and
![]() $\epsilon$
can be chosen as small as needed when
$\epsilon$
can be chosen as small as needed when
![]() $\delta\to 0$
, we have
$\delta\to 0$
, we have
as desired.
The function
![]() $\sigma$
is strictly convex and L is linear, thus the function
$\sigma$
is strictly convex and L is linear, thus the function
![]() $\sigma + L$
is itself strictly convex. This implies that there exist a unique function
$\sigma + L$
is itself strictly convex. This implies that there exist a unique function
![]() $f_{\max}$
in
$f_{\max}$
in
![]() $\mathrm{Lip}_{[0,1]}$
that maximize
$\mathrm{Lip}_{[0,1]}$
that maximize
![]() $\Psi$
. By the previous lemma, we obtain
$\Psi$
. By the previous lemma, we obtain
Moreover, the set
![]() $\mathrm{Lip}_{[0,1]}(U,\gamma)$
of functions
$\mathrm{Lip}_{[0,1]}(U,\gamma)$
of functions
![]() $f \in \mathrm{Lip}_{[0,1]}$
such that
$f \in \mathrm{Lip}_{[0,1]}$
such that
![]() $f= \gamma$
on U is compact for the
$f= \gamma$
on U is compact for the
![]() $\ell_{\infty}$
norm. Hence, for every fixed
$\ell_{\infty}$
norm. Hence, for every fixed
![]() $\alpha > 0$
, there exist a finite covering
$\alpha > 0$
, there exist a finite covering
![]() $\bigcup_{i=1}^{k_{\alpha}}B_{\ell_{\infty}}(f_i,\delta_{i})$
of
$\bigcup_{i=1}^{k_{\alpha}}B_{\ell_{\infty}}(f_i,\delta_{i})$
of
![]() $\mathrm{Lip}_{[0,1]}(U,\gamma)$
such that for all
$\mathrm{Lip}_{[0,1]}(U,\gamma)$
such that for all
![]() $i \leq k_{\alpha}$
:
$i \leq k_{\alpha}$
:
If we denote by
![]() $C(\delta, \alpha)$
the number of balls in this covering, this implies that for all
$C(\delta, \alpha)$
the number of balls in this covering, this implies that for all
![]() $\delta, \alpha > 0$
:
$\delta, \alpha > 0$
:
Letting
![]() $\delta$
and
$\delta$
and
![]() $\alpha$
go to 0 gives the desired result. This finishes the proof of Theorem 3.3.
$\alpha$
go to 0 gives the desired result. This finishes the proof of Theorem 3.3.
6. Final remarks and open problems
6.1 The Okounkov–Olshanski formula
There are other positive formulas for
![]() $f^{\lambda/\mu}$
using the Littlewood–Richardson coefficients and the Okounkov–Olshanski formula, see [Reference Morales, Pak and PanovaMPP1,
$f^{\lambda/\mu}$
using the Littlewood–Richardson coefficients and the Okounkov–Olshanski formula, see [Reference Morales, Pak and PanovaMPP1,
![]() $\S$
9] and [Reference Morales and ZhuMZ] for the discussion and references. It would be interesting to see if the variational principle applies in either case.
$\S$
9] and [Reference Morales and ZhuMZ] for the discussion and references. It would be interesting to see if the variational principle applies in either case.
6.2 The case of thick hooks
In case of the thick hooks (see
![]() $\S$
1.2), the variational principle result (Theorem 3.3) is already interesting and is now well understood. It corresponds to a degenerate case of more general weights introduced in [Reference Borodin, Gorin and RainsBGR] and further studied in [Reference BeteaBet, Reference Dimitrov and KnizelDK] (see also [Reference Borodin, Gorin and RainsMPP3]), where both the frozen region and the probability density are computed.
$\S$
1.2), the variational principle result (Theorem 3.3) is already interesting and is now well understood. It corresponds to a degenerate case of more general weights introduced in [Reference Borodin, Gorin and RainsBGR] and further studied in [Reference BeteaBet, Reference Dimitrov and KnizelDK] (see also [Reference Borodin, Gorin and RainsMPP3]), where both the frozen region and the probability density are computed.
It is worth comparing frozen regions in the uniform and weighed cases, see Figure 10. The uniform frozen region is famously a circle, while the weighted frozen region is an algebraic curve with only mirror symmetry. Let us mention that explicit product formulas for q-Racah polynomials allow a direct sampling from these weighted tilings in this case, see [Reference BeteaBet,
![]() $\S$
7.5] and [Reference Borodin, Gorin and RainsBGR,
$\S$
7.5] and [Reference Borodin, Gorin and RainsBGR,
![]() $\S$
9]. This approach does not generalize to other skew shapes.
$\S$
9]. This approach does not generalize to other skew shapes.

Figure 10. Uniform and weighted random lozenge tilings of the hexagon
![]() $\operatorname{\mathbb H}(50,50,50)$
from [Reference Morales, Pak and PanovaMPP3, Fig. 2].
$\operatorname{\mathbb H}(50,50,50)$
from [Reference Morales, Pak and PanovaMPP3, Fig. 2].
6.3 Frozen regions for weighted lozenge tilings
It would be interesting to compute the frozen region explicitly for the weighted lozenge tilings in some important special cases, such as thick ribbons described in
![]() $\S$
1.3. From the variational principle, we cannot even tell if these regions are bounded by algebraic curves.
$\S$
1.3. From the variational principle, we cannot even tell if these regions are bounded by algebraic curves.
6.4 Other families of skew shapes
Beside stable limits shapes, there are other asymptotic regimes when the problem of computing
![]() $f^{\lambda/\mu}$
is of interest, see [Reference Dousse and FérayDF, Reference Morales, Pak and PanovaMPP4, Reference StanleySta1]. Except for the case when
$f^{\lambda/\mu}$
is of interest, see [Reference Dousse and FérayDF, Reference Morales, Pak and PanovaMPP4, Reference StanleySta1]. Except for the case when
![]() $|\mu|=O(1)$
, obtaining better bounds is an interesting and difficult challenge.
$|\mu|=O(1)$
, obtaining better bounds is an interesting and difficult challenge.
6.5 Limit curves for skew standard tableaux
In an important recent development, Sun showed the existence of limit curves for random standard Young tableaux with stable limit shape [Reference SunSun], also by modifying the variational principle and using the beads model to encode standard tableaux. Soon after Gordenko [Reference GordenkoGor] wrote an explicit conjectural description of this limit shape using a modified TASEP on dimer configurations. This suggests that in principle one can hope to evaluate the constant C of the for thick ribbons (see
![]() $\S$
1.3).
$\S$
1.3).
6.6 Bijective proofs
It would be interesting to see if the strategy sketched in [Reference PakPak1, 3.5] can be used to conclude that there is no natural bijective proof of the Naruse hook-length formula (1.1). Let us mention that [Reference KonvalinkaKon] gives a bijective proof of a recurrence involved in the proof of the NHLF. Unfortunately, there seem to be no way to use this bijection for uniform sampling of random standard Young tableaux of skew shape.
Acknowledgements
The authors would like to thank Nishant Chandgotia, Jehanne Dousse, Valentin Féray, Anna Gordenko, Vadim Gorin, Rick Kenyon, Victor Kleptsyn, Georg Menz, Jay Pantone, Leo Petrov, István Prause, Dan Romik, Richard Stanley and Damir Yeliussizov for helpful discussions. We are especially thankful to Greta Panova for the ongoing extended collaboration in the area; notably, the idea of this paper is stemming from the lozenge tiling results in [Reference Morales, Pak and PanovaMPP3]. We also thank the anonymous referee for helpful comments and suggestions. The first two authors were partially supported by the NSF.