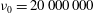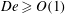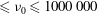1 Introduction
The interaction of an immersed particle with a solid surface has been extensively researched due to its practical relevance in many industrial and natural processes including filtration, agglomeration, adhesion, wet granular flow, spray coating, drying, polishing, pollen capture on wet leaves, erosion and sedimentation. The first studies in this rich topic investigated the interaction of dry objects resulting in the classical Hertz contact theory (Love Reference Love1927; Landau & Lifshitz Reference Landau and Lifshitz1959), which assumed the collisions to be perfectly elastic with no energy losses. Thus, the particles were predicted to rebound with no change in their kinetic energy. In reality however, energy loses are inevitable owing to interparticle adhesive forces (Dahneke Reference Dahneke1972; Löffler Reference Löffler1980), plastic deformation in the solids (Johnson Reference Johnson1985) and energy radiated away by vibrations (Zener Reference Zener1941).
In the case of a spherical particle colliding with a wetted surface, energy losses by viscous dissipation within the liquid also have to be taken into account. The liquid in the diminishing gap between the sphere and wall squeezes to create a lubrication force (Brenner Reference Brenner1961), expressed as
![]() $F_{l}=6{\rm\pi}{\it\mu}R_{0}^{2}{\dot{h}}/h$
, where
$F_{l}=6{\rm\pi}{\it\mu}R_{0}^{2}{\dot{h}}/h$
, where
![]() $R_{0}$
is the radius of the sphere,
$R_{0}$
is the radius of the sphere,
![]() ${\it\mu}$
is the liquid’s dynamic viscosity,
${\it\mu}$
is the liquid’s dynamic viscosity,
![]() $h$
is the separation distance and
$h$
is the separation distance and
![]() ${\dot{h}}=\text{d}h/\text{d}t$
is the speed of the approaching sphere. When the impact velocity of the sphere is above a critical value, this force can be large enough to deform the sphere around the axis of symmetry and store a portion of its kinetic energy as elastic strain energy. The conversion of this stored energy back to kinetic energy allows the sphere to rebound, even without wall contact, if a sufficiently high hydrodynamic pressure is built up during sphere approach. This is called the elastohydrodynamic model (Davis, Serayssol & Hinch Reference Davis, Serayssol and Hinch1986) which integrates both Hertz theory and lubrication theory. It reveals that the tendency of an impacting particle to bounce back from a wetted surface is largely dependent on two parameters, namely the Stokes number,
${\dot{h}}=\text{d}h/\text{d}t$
is the speed of the approaching sphere. When the impact velocity of the sphere is above a critical value, this force can be large enough to deform the sphere around the axis of symmetry and store a portion of its kinetic energy as elastic strain energy. The conversion of this stored energy back to kinetic energy allows the sphere to rebound, even without wall contact, if a sufficiently high hydrodynamic pressure is built up during sphere approach. This is called the elastohydrodynamic model (Davis, Serayssol & Hinch Reference Davis, Serayssol and Hinch1986) which integrates both Hertz theory and lubrication theory. It reveals that the tendency of an impacting particle to bounce back from a wetted surface is largely dependent on two parameters, namely the Stokes number,
![]() $St$
, and the elasticity parameter,
$St$
, and the elasticity parameter,
![]() ${\it\epsilon}$
, given as:
${\it\epsilon}$
, given as:
The elastohydrodynamic theory has since been put to use in several other studies; Serayssol & Davis (Reference Serayssol and Davis1986) incorporated interparticle force potentials, Davis (Reference Davis1987) included the effects of surface roughness, Barnocky & Davis (Reference Barnocky and Davis1989) accounted for the changes in fluid density and viscosity with pressure and Barnocky & Davis (Reference Barnocky and Davis1988a
) replaced no-slip boundary conditions at the surfaces by Maxwell slip boundary conditions when the separation gap reduces to a few nanometers for high inertial impacts. Experimental verification of the elastohydrodynamic model was provided by Barnocky & Davis (Reference Barnocky and Davis1988b
), Lundberg & Shen (Reference Lundberg and Shen1992) and Gondret et al. (Reference Gondret, Hallouin, Lance and Petit1999). Davis, Rager & Good (Reference Davis, Rager and Good2002) performed experiments to investigate the non-zero rebound velocity cases, which were shown to occur only above a critical Stokes number value,
![]() $St_{c}$
. The separation distance
$St_{c}$
. The separation distance
![]() $h$
at which the lubrication force becomes large enough to deform the sphere was approximated as being comparable to an elasticity length scale,
$h$
at which the lubrication force becomes large enough to deform the sphere was approximated as being comparable to an elasticity length scale,
![]() $x_{r}=(3{\rm\pi}{\it\theta}{\it\mu}R_{0}^{3/2}V_{0}/\sqrt{2})^{2/5}$
. This was recently verified in a time-resolved experimental investigation by Marston, Yong & Thoroddsen (Reference Marston, Yong and Thoroddsen2010). As most of the collisions in real situations are not normal but oblique, Kantak & Davis (Reference Kantak and Davis2004) conducted experiments for oblique impacts to find that the previous results for head-on collisions can be applied, considering only the normal component in the oblique impact cases. A comprehensive model for oblique impacts was presented in further work by Kantak & Davis (Reference Kantak and Davis2006). Donahue et al. (Reference Donahue, Hrenya, Davis, Nakagawa, Zelinskaya and Joseph2010) investigated three-particle collisions using a Stokes’ cradle, comparing their results to the theory of a series of two-particle collisions. Their proposed theory incorporated the effect of glass transition whereby the silicone oils behave like a solid at a high enough pressure called the glass-transition pressure.
$x_{r}=(3{\rm\pi}{\it\theta}{\it\mu}R_{0}^{3/2}V_{0}/\sqrt{2})^{2/5}$
. This was recently verified in a time-resolved experimental investigation by Marston, Yong & Thoroddsen (Reference Marston, Yong and Thoroddsen2010). As most of the collisions in real situations are not normal but oblique, Kantak & Davis (Reference Kantak and Davis2004) conducted experiments for oblique impacts to find that the previous results for head-on collisions can be applied, considering only the normal component in the oblique impact cases. A comprehensive model for oblique impacts was presented in further work by Kantak & Davis (Reference Kantak and Davis2006). Donahue et al. (Reference Donahue, Hrenya, Davis, Nakagawa, Zelinskaya and Joseph2010) investigated three-particle collisions using a Stokes’ cradle, comparing their results to the theory of a series of two-particle collisions. Their proposed theory incorporated the effect of glass transition whereby the silicone oils behave like a solid at a high enough pressure called the glass-transition pressure.
Some studies have also investigated particle–wall collisions in non-Newtonian fluids having both elastic and shear-thinning properties. The relevant parameters here are the Stokes and Deborah numbers, the latter being defined by
![]() $De={\it\lambda}V_{0}/R_{0}$
, which is the ratio of the characteristic relaxation time of the fluid
$De={\it\lambda}V_{0}/R_{0}$
, which is the ratio of the characteristic relaxation time of the fluid
![]() ${\it\lambda}$
to the characteristic time scale of the experiment
${\it\lambda}$
to the characteristic time scale of the experiment
![]() $R_{0}/V_{0}$
. The Stokes number has either been based on the apparent viscosity
$R_{0}/V_{0}$
. The Stokes number has either been based on the apparent viscosity
![]() ${\it\mu}_{app}$
of the liquid, obtained from an estimation of the shear rate
${\it\mu}_{app}$
of the liquid, obtained from an estimation of the shear rate
![]() $\dot{{\it\gamma}}$
, or its low-shear viscosity
$\dot{{\it\gamma}}$
, or its low-shear viscosity
![]() ${\it\mu}_{0}$
for simplicity purposes.
${\it\mu}_{0}$
for simplicity purposes.
One of the first studies in this area was performed by Stocchino & Guala (Reference Stocchino and Guala2005), who investigated particle–wall collisions in a shear-thinning fluid (aqueous carboxymethyl cellulose, CMC). For a fixed Stokes number, the coefficient of restitution,
![]() $e=v_{r}/v_{i}$
(ratio of the rebound to the impact velocity), was found to be higher than that obtained for Newtonian fluids, which was reasoned to be due to the viscoelastic nature of the CMC solution. Ardekani, Rangel & Joseph (Reference Ardekani, Rangel and Joseph2007) examined the forces and normal stresses on a spherical particle moving towards a wall in a second-order fluid. It was found that the fluid contributed with an attractive force towards the wall, irrespective of the direction of motion of the particle. Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) conducted impacts in viscoelastic liquids to study the effect of the Stokes and Deborah numbers on the coefficient of restitution. The rate at which the value of
$e=v_{r}/v_{i}$
(ratio of the rebound to the impact velocity), was found to be higher than that obtained for Newtonian fluids, which was reasoned to be due to the viscoelastic nature of the CMC solution. Ardekani, Rangel & Joseph (Reference Ardekani, Rangel and Joseph2007) examined the forces and normal stresses on a spherical particle moving towards a wall in a second-order fluid. It was found that the fluid contributed with an attractive force towards the wall, irrespective of the direction of motion of the particle. Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) conducted impacts in viscoelastic liquids to study the effect of the Stokes and Deborah numbers on the coefficient of restitution. The rate at which the value of
![]() $e$
increased with the Stokes number was found to become smaller for higher Deborah numbers, corresponding to liquids with higher viscoelastic and shear-thinning properties. For a given Stokes number, higher rebounds were noted for larger
$e$
increased with the Stokes number was found to become smaller for higher Deborah numbers, corresponding to liquids with higher viscoelastic and shear-thinning properties. For a given Stokes number, higher rebounds were noted for larger
![]() $De$
values.
$De$
values.
While many studies have investigated the motion and deformation of spheres for wetted impacts, only a few have focused on the resulting behaviour and dynamics of the fluid during this process. The sudden deceleration of the sphere upon impact, followed by expansion of the gap between the solid surfaces during rebound, causes depressurization around the axis of symmetry of the sphere, inducing cavitation (Brennen Reference Brennen1995). A series of images portraying this event is shown in figure 1. Chen & Israelachvili (Reference Chen and Israelachvili1991) and Kuhl et al. (Reference Kuhl, Ruths, Chen and Israelachvili1994) conducted experimental studies to show that cavitation can only occur when a fluid is subjected to a threshold value of tensile stress.
An extensive review of the criterion for cavitation was presented by Joseph (Reference Joseph1998), who predicted that for a liquid at atmospheric pressure which cannot tolerate tension, cavitation will occur once tensile stresses in the liquid exceeds one atmosphere. A model for shear-stress-induced cavitation was also proposed. This predicted that the liquid squeezing in the diminishing gap between the approaching sphere and the wall could be ripped open in tension in the direction of the principal stresses. The first experimental evidence for shear-induced cavitation was provided earlier by Blair & Winer (Reference Blair and Winer1992), who utilized a custom-built rotary viscometer (Blair & Winer Reference Blair and Winer1987) to investigate the yielding shear stresses of high molecular weight polymers at variable absolute pressures. The polymers tested were noted to yield at shear stresses slightly higher than the absolute pressure for the lowest pressures investigated, which suggested the maximum principal stress criterion to be applicable at low pressures.
Experimental visualization of shear-induced cavitation was claimed recently by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012), who performed particle–wall collisions in Newtonian fluids (
![]() ${\it\mu}=1{-}1200$
mPa s) for spheres dropped from heights ranging 1–200 mm. However, since the qualitative results provided therein suffered from a relatively low spatial and temporal resolution, further investigation was conducted by Mansoor et al. (Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014) using a synchronized dual-view (side and bottom) high-speed imaging system for similar experimental parameters. The results clarified that the annular bubble structure misinterpreted by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) as cavitation was in reality created by the entrapment of bubbles (Marston, Vakarelski & Thoroddsen Reference Marston, Vakarelski and Thoroddsen2011a
) on the sphere surface as it entered into the viscous film, which subsequently squeezed radially outwards from the sphere centre as it approached the wall. Cavitation was only observed once the sphere made wall contact and started to rebound (e.g. figure 1), agreeing with the conventional theory which predicts cavitation during depressurization. Hence, although the occurrence of shear-stress-induced cavitation was thereby confirmed to be highly unrealistic in the parameter space of these collisions employing Newtonian fluids, no further studies have been conducted so far to investigate this phenomenon in highly viscous and non-Newtonian liquids with high viscoelastic properties.
${\it\mu}=1{-}1200$
mPa s) for spheres dropped from heights ranging 1–200 mm. However, since the qualitative results provided therein suffered from a relatively low spatial and temporal resolution, further investigation was conducted by Mansoor et al. (Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014) using a synchronized dual-view (side and bottom) high-speed imaging system for similar experimental parameters. The results clarified that the annular bubble structure misinterpreted by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) as cavitation was in reality created by the entrapment of bubbles (Marston, Vakarelski & Thoroddsen Reference Marston, Vakarelski and Thoroddsen2011a
) on the sphere surface as it entered into the viscous film, which subsequently squeezed radially outwards from the sphere centre as it approached the wall. Cavitation was only observed once the sphere made wall contact and started to rebound (e.g. figure 1), agreeing with the conventional theory which predicts cavitation during depressurization. Hence, although the occurrence of shear-stress-induced cavitation was thereby confirmed to be highly unrealistic in the parameter space of these collisions employing Newtonian fluids, no further studies have been conducted so far to investigate this phenomenon in highly viscous and non-Newtonian liquids with high viscoelastic properties.

Figure 1. Sequence of images showing cavity formation during the impact of a tungsten carbide sphere onto a glass plate covered with a 37 mm deep layer of water. The sphere was released with its bottom just touching the surface of the water (
![]() $h_{r}=37$
mm).
$h_{r}=37$
mm).
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() ${\it\mu}_{0}=9.1\times 10^{-4}$
Pa s;
${\it\mu}_{0}=9.1\times 10^{-4}$
Pa s;
![]() $h$
represents the distance between the bottom tip of the sphere and the glass plate. The frame at which the sphere makes first contact with the glass base is taken as a reference point (
$h$
represents the distance between the bottom tip of the sphere and the glass plate. The frame at which the sphere makes first contact with the glass base is taken as a reference point (
![]() $t_{0}=0~{\rm\mu}\text{s}$
and
$t_{0}=0~{\rm\mu}\text{s}$
and
![]() $h_{0}=0~{\rm\mu}\text{m}$
, marked with the asterisk * symbol) and can be seen to coincide with the onset of cavitation. The arrows pointing downwards and upwards indicate the sphere’s approach towards and rebound away from the wall, respectively.
$h_{0}=0~{\rm\mu}\text{m}$
, marked with the asterisk * symbol) and can be seen to coincide with the onset of cavitation. The arrows pointing downwards and upwards indicate the sphere’s approach towards and rebound away from the wall, respectively.
More relevant to the work presented in this paper, Guala & Stocchino (Reference Guala and Stocchino2007) used particle image velocimetry to investigate large-scale flow structures formed during fully immersed particle–wall collisions in Newtonian (water, aqueous glycerol) and in non-Newtonian (1 % aqueous CMC, shear thinning, weakly viscoelastic,
![]() $De\ll 1$
) liquids. A similar velocity field and vortical structure evolution was obtained in both the glycerol and CMC solutions, which showed that the shear-thinning effect of the non-Newtonian CMC fluid was dominant over its viscoelastic nature for low Deborah numbers. Dabiri, Sirignano & Joseph (Reference Dabiri, Sirignano and Joseph2010) performed numerical simulations to study the deformation of a cavitation bubble in simple shear and extensional flows. The deformation of the bubble during growth was shown to result in high pressure regions at its sides upon collapse. This produced re-entrant jets that impinged the bubble internally to cause bubble break-up in some instances. Uddin, Marston & Thoroddsen (Reference Uddin, Marston and Thoroddsen2012) investigated the squeeze flow during the impact of a sphere onto a thin film of viscous non-Newtonian (Carreau) fluid. High-speed imaging and particle tracking were used to visualize the flow in the film and provide measurements for the corresponding velocity fields. Marston et al. (Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
) presented a detailed analysis of the complex cavitation structures formed during the rebound stages of impacts onto a thin (1.5 mm deep) film of Newtonian (glycerol, syrup) and non-Newtonian (silicone oil, low-shear
$De\ll 1$
) liquids. A similar velocity field and vortical structure evolution was obtained in both the glycerol and CMC solutions, which showed that the shear-thinning effect of the non-Newtonian CMC fluid was dominant over its viscoelastic nature for low Deborah numbers. Dabiri, Sirignano & Joseph (Reference Dabiri, Sirignano and Joseph2010) performed numerical simulations to study the deformation of a cavitation bubble in simple shear and extensional flows. The deformation of the bubble during growth was shown to result in high pressure regions at its sides upon collapse. This produced re-entrant jets that impinged the bubble internally to cause bubble break-up in some instances. Uddin, Marston & Thoroddsen (Reference Uddin, Marston and Thoroddsen2012) investigated the squeeze flow during the impact of a sphere onto a thin film of viscous non-Newtonian (Carreau) fluid. High-speed imaging and particle tracking were used to visualize the flow in the film and provide measurements for the corresponding velocity fields. Marston et al. (Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
) presented a detailed analysis of the complex cavitation structures formed during the rebound stages of impacts onto a thin (1.5 mm deep) film of Newtonian (glycerol, syrup) and non-Newtonian (silicone oil, low-shear
![]() $\dot{{\it\gamma}}<100~\text{s}^{-1}$
kinematic viscosity of
$\dot{{\it\gamma}}<100~\text{s}^{-1}$
kinematic viscosity of
![]() ${\it\nu}_{0}=12\,500{-}1000\,000$
cSt) liquid. The cavitation bubbles in both kinds of fluids were observed to form in discrete rings, growing radially outwards from the centre of impact. However, the bubbles were more discrete and increased in size in Newtonian liquids, while those in the shear-thinning non-Newtonian fluids, appeared to be connected in a foam-like structure and decrease in size with increasing distance from the centre. Cavitation structures in non-Newtonian liquids with high viscoelastic properties were not investigated.
${\it\nu}_{0}=12\,500{-}1000\,000$
cSt) liquid. The cavitation bubbles in both kinds of fluids were observed to form in discrete rings, growing radially outwards from the centre of impact. However, the bubbles were more discrete and increased in size in Newtonian liquids, while those in the shear-thinning non-Newtonian fluids, appeared to be connected in a foam-like structure and decrease in size with increasing distance from the centre. Cavitation structures in non-Newtonian liquids with high viscoelastic properties were not investigated.
The present work extends the analysis of aforementioned studies by investigating cavitation structures formed during wetted particle–wall collisions in extremely high viscosity (
![]() ${\it\nu}_{0}\leqslant 20$
million cSt) non-Newtonian liquids. These liquids are highly shear thinning and also possess viscoelastic properties. The latter promotes sphere rebound without prior contact with the solid wall, which leads to significantly different cavitation structures compared to those observed in contact cases by Marston et al. (Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
). These structures are found to originate specifically from bubbles entrapped on the sphere surface during its entry into the thin film (Marston et al.
Reference Marston, Vakarelski and Thoroddsen2011a
; Mansoor et al.
Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014). In addition, given the lack of any conclusive experimental evidence supporting or disproving the possibility of shear-stress-induced cavitation in such liquids, we use a synchronized dual-view (side and bottom) high-speed imaging system to determine the first point of cavity inception in time, as the sphere approaches and rebounds from a solid wall during a collision.
${\it\nu}_{0}\leqslant 20$
million cSt) non-Newtonian liquids. These liquids are highly shear thinning and also possess viscoelastic properties. The latter promotes sphere rebound without prior contact with the solid wall, which leads to significantly different cavitation structures compared to those observed in contact cases by Marston et al. (Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
). These structures are found to originate specifically from bubbles entrapped on the sphere surface during its entry into the thin film (Marston et al.
Reference Marston, Vakarelski and Thoroddsen2011a
; Mansoor et al.
Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014). In addition, given the lack of any conclusive experimental evidence supporting or disproving the possibility of shear-stress-induced cavitation in such liquids, we use a synchronized dual-view (side and bottom) high-speed imaging system to determine the first point of cavity inception in time, as the sphere approaches and rebounds from a solid wall during a collision.

Figure 2. (a) Schematic of the experimental set-up used. (b) Close-up view of the impact region showing the gap distance at the sphere tip,
![]() $h$
, the sphere radius,
$h$
, the sphere radius,
![]() $R_{0}$
, the radial distance from the axis of symmetry,
$R_{0}$
, the radial distance from the axis of symmetry,
![]() $r$
, the oil film thickness,
$r$
, the oil film thickness,
![]() ${\it\delta}$
, the gap height across the sphere curvature,
${\it\delta}$
, the gap height across the sphere curvature,
![]() $H(r)=h+R_{0}-\sqrt{R_{0}^{2}-r^{2}}$
and the wetted radius of the sphere,
$H(r)=h+R_{0}-\sqrt{R_{0}^{2}-r^{2}}$
and the wetted radius of the sphere,
![]() $B=\sqrt{({\it\delta}-h)(2R_{0}-({\it\delta}-h))}$
.
$B=\sqrt{({\it\delta}-h)(2R_{0}-({\it\delta}-h))}$
.
2 Experimental set-up, fluid rheology and parameter space
Figure 2(a) shows a schematic of the experimental set-up used in this study. A tungsten carbide sphere (Fritsch GmbH, Germany,
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() ${\it\rho}_{s}=14\,890~\text{kg}~\text{m}^{-3}$
,
${\it\rho}_{s}=14\,890~\text{kg}~\text{m}^{-3}$
,
![]() $E=550$
GPa) was attached to an electromagnet, which was placed directly above the centre of a thick-bottomed glass container having inner measurements of
$E=550$
GPa) was attached to an electromagnet, which was placed directly above the centre of a thick-bottomed glass container having inner measurements of
![]() $100\times 100\times 20$
mm. The matte finishing of Tungsten carbide helped to eliminate any reflections from the sphere surface during experiments. To avoid impact-induced oscillations in the glass container, it was firmly fixed to a 10 kg U-shaped solid stainless steel frame, which was in turn screwed to a 1000 kg optical table. A
$100\times 100\times 20$
mm. The matte finishing of Tungsten carbide helped to eliminate any reflections from the sphere surface during experiments. To avoid impact-induced oscillations in the glass container, it was firmly fixed to a 10 kg U-shaped solid stainless steel frame, which was in turn screwed to a 1000 kg optical table. A
![]() $45^{\circ }$
angled mirror was placed below the glass container at the base of the U-shaped frame to make observations from underneath the sphere. Two high-speed cameras, a Phantom v1610 and a Photron SA-5, were each equipped with a long working distance microscope and synchronized to record images at 33 018 f.p.s. from the side and bottom with effective pixel resolutions of 7 and
$45^{\circ }$
angled mirror was placed below the glass container at the base of the U-shaped frame to make observations from underneath the sphere. Two high-speed cameras, a Phantom v1610 and a Photron SA-5, were each equipped with a long working distance microscope and synchronized to record images at 33 018 f.p.s. from the side and bottom with effective pixel resolutions of 7 and
![]() $5~{\rm\mu}\text{m}~\text{pixel}^{-1}$
, respectively. Gap distances could hence be measured with an accuracy of up to
$5~{\rm\mu}\text{m}~\text{pixel}^{-1}$
, respectively. Gap distances could hence be measured with an accuracy of up to
![]() $7~{\rm\mu}\text{m}$
and time to
$7~{\rm\mu}\text{m}$
and time to
![]() $\pm$
1 frame, translating to a maximum velocity error of
$\pm$
1 frame, translating to a maximum velocity error of
![]() $\pm 0.2~\text{m}~\text{s}^{-1}$
. Lighting was provided by two 350 W Sumita metal halide lights, which were equipped with fibre optic light guides. Regular temperature measurements showed these to induce minimal heating in the liquid films. All ultra-viscous non-Newtonian films were prepared at least one week (left covered) before the experiments were performed to ensure that a uniform thickness
$\pm 0.2~\text{m}~\text{s}^{-1}$
. Lighting was provided by two 350 W Sumita metal halide lights, which were equipped with fibre optic light guides. Regular temperature measurements showed these to induce minimal heating in the liquid films. All ultra-viscous non-Newtonian films were prepared at least one week (left covered) before the experiments were performed to ensure that a uniform thickness
![]() ${\it\delta}$
was achieved. The experimental environment was maintained at a temperature of
${\it\delta}$
was achieved. The experimental environment was maintained at a temperature of
![]() $22\,^{\circ }\text{C}$
and a relative humidity of 55 %.
$22\,^{\circ }\text{C}$
and a relative humidity of 55 %.
When the electromagnet was switched off, the sphere fell freely to impact the liquid surface with a velocity of
![]() $V_{0}\approx \sqrt{2g(h_{r}-{\it\delta})}$
, where
$V_{0}\approx \sqrt{2g(h_{r}-{\it\delta})}$
, where
![]() $h_{r}$
is the release height (measured from the bottom tip of the sphere to the base of the glass wall). A close-up view of the impact region is shown in figure 2(b). Upon detecting motion in the side view, the Phantom v1610 employed the IBAT (Image based auto-trigger) function to trigger the recording automatically on both cameras. The resulting set of video clips was saved on a PC for post-processing. After each trial the glass container was replaced with a new one containing a fresh, uniform and level film of the same thickness.
$h_{r}$
is the release height (measured from the bottom tip of the sphere to the base of the glass wall). A close-up view of the impact region is shown in figure 2(b). Upon detecting motion in the side view, the Phantom v1610 employed the IBAT (Image based auto-trigger) function to trigger the recording automatically on both cameras. The resulting set of video clips was saved on a PC for post-processing. After each trial the glass container was replaced with a new one containing a fresh, uniform and level film of the same thickness.

Figure 3. Rheological properties of the silicone oils used having low-shear kinematic viscosities of
![]() ${\it\nu}_{0}=1000$
cSt, 10 000 cSt, 100 000 cSt, 1000 000 cSt and 20 000 000 cSt measured from tests performed on a research rheometer (ARES-G2, TA Instruments). Fits to the data (dashed lines) are formed using the Carreau model with parameters listed in table 1.
${\it\nu}_{0}=1000$
cSt, 10 000 cSt, 100 000 cSt, 1000 000 cSt and 20 000 000 cSt measured from tests performed on a research rheometer (ARES-G2, TA Instruments). Fits to the data (dashed lines) are formed using the Carreau model with parameters listed in table 1.
Table 1. Physical properties of the silicone oils (dimethylpolysiloxane, Clearco Products Co. Inc, USA) used in the experiments. The parameters
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() $n$
are obtained by fitting the Carreau model to the apparent viscosity versus shear data shown in figure 3.
$n$
are obtained by fitting the Carreau model to the apparent viscosity versus shear data shown in figure 3.
![]() $G^{\prime }$
and
$G^{\prime }$
and
![]() $G^{\prime \prime }$
correspond to the storage (elastic) and loss (viscous) moduli, respectively, obtained from the linear viscoelastic region in oscillation strain sweeps.
$G^{\prime \prime }$
correspond to the storage (elastic) and loss (viscous) moduli, respectively, obtained from the linear viscoelastic region in oscillation strain sweeps.

2.1 Liquid rheology
The liquids used in this study were (dimethylpolysiloxane) silicone oils (Clearco Products Co. Inc, USA) with low-shear kinematic viscosities of
![]() ${\it\nu}_{0}=100$
, 1000, 10 000, 1000 000 and 20 000 000 cSt (at
${\it\nu}_{0}=100$
, 1000, 10 000, 1000 000 and 20 000 000 cSt (at
![]() $25\,^{\circ }\text{C}$
). The shear-thinning nature of these liquids for
$25\,^{\circ }\text{C}$
). The shear-thinning nature of these liquids for
![]() ${\it\nu}_{0}\geqslant 1000$
cSt can be seen in figure 3 from the apparent viscosity
${\it\nu}_{0}\geqslant 1000$
cSt can be seen in figure 3 from the apparent viscosity
![]() ${\it\mu}_{app}$
versus shear rate
${\it\mu}_{app}$
versus shear rate
![]() $\dot{{\it\gamma}}$
data, obtained from tests conducted on a research rheometer (ARES-G2, TA Instruments). Fits to the rheological properties of these fluids have been formed using the Carreau model,
$\dot{{\it\gamma}}$
data, obtained from tests conducted on a research rheometer (ARES-G2, TA Instruments). Fits to the rheological properties of these fluids have been formed using the Carreau model,
where
![]() ${\it\mu}_{\infty }=0$
and values for the relaxation time
${\it\mu}_{\infty }=0$
and values for the relaxation time
![]() ${\it\lambda}$
and power index
${\it\lambda}$
and power index
![]() $n$
are given in Table 1. Liquids with
$n$
are given in Table 1. Liquids with
![]() ${\it\nu}_{0}\geqslant 1000\,000$
cSt are found to be associated with relatively large relaxation times and
${\it\nu}_{0}\geqslant 1000\,000$
cSt are found to be associated with relatively large relaxation times and
![]() $G^{\prime \prime }/G^{\prime }$
ratios approaching closer to unity, which indicates their high viscoelastic nature.
$G^{\prime \prime }/G^{\prime }$
ratios approaching closer to unity, which indicates their high viscoelastic nature.
2.2 Parameter space
In accordance with previous studies (Ardekani et al.
Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009; Marston et al.
Reference Marston, Vakarelski and Thoroddsen2011a
; Uddin et al.
Reference Uddin, Marston and Thoroddsen2012), the main dimensionless numbers used in this work are the impact Stokes number,
![]() $St_{0}=2{\it\rho}_{s}R_{0}V_{0}/9{\it\mu}_{0}$
, Deborah number,
$St_{0}=2{\it\rho}_{s}R_{0}V_{0}/9{\it\mu}_{0}$
, Deborah number,
![]() $De={\it\lambda}V_{0}/R_{0}$
and the capillary number,
$De={\it\lambda}V_{0}/R_{0}$
and the capillary number,
![]() $Ca={\it\mu}_{0}V_{0}/{\it\sigma}$
. Since a single-valued viscosity
$Ca={\it\mu}_{0}V_{0}/{\it\sigma}$
. Since a single-valued viscosity
![]() ${\it\mu}_{0}$
is assumed, the impact Stokes number and capillary number do not account for non-Newtonian effects. The film thickness was kept in the range of
${\it\mu}_{0}$
is assumed, the impact Stokes number and capillary number do not account for non-Newtonian effects. The film thickness was kept in the range of
![]() ${\it\delta}=4{-}6$
mm. Experiments for the relatively low viscosity liquids (100 and 1000 cSt silicone oils), however, were conducted for
${\it\delta}=4{-}6$
mm. Experiments for the relatively low viscosity liquids (100 and 1000 cSt silicone oils), however, were conducted for
![]() ${\it\delta}=37$
mm to result in fully immersed impacts. The release height was varied between
${\it\delta}=37$
mm to result in fully immersed impacts. The release height was varied between
![]() $h_{r}=4.2{-}170$
cm, giving impact velocities of
$h_{r}=4.2{-}170$
cm, giving impact velocities of
![]() $0.31\leqslant V_{0}\leqslant 5.77~\text{m}~\text{s}^{-1}$
based on the film thicknesses used. These correspond to Stokes numbers ranging
$0.31\leqslant V_{0}\leqslant 5.77~\text{m}~\text{s}^{-1}$
based on the film thicknesses used. These correspond to Stokes numbers ranging
![]() $8.18\times 10^{-3}\leqslant St_{0}\leqslant 305.3$
, Deborah numbers ranging
$8.18\times 10^{-3}\leqslant St_{0}\leqslant 305.3$
, Deborah numbers ranging
![]() $0\leqslant De\leqslant 401$
and capillary numbers of
$0\leqslant De\leqslant 401$
and capillary numbers of
![]() $1.44\leqslant Ca\leqslant 5.23\times 10^{6}$
depending on
$1.44\leqslant Ca\leqslant 5.23\times 10^{6}$
depending on
![]() ${\it\mu}_{0}$
and
${\it\mu}_{0}$
and
![]() ${\it\lambda}$
, respectively.
${\it\lambda}$
, respectively.

Figure 4. Series of images (top to bottom and left to right) showing cavitation during the impact from
![]() $h_{r}=67$
mm onto a glass plate covered with a 37 mm deep pool of
$h_{r}=67$
mm onto a glass plate covered with a 37 mm deep pool of
![]() ${\it\nu}_{0}=100$
cSt silicone oil.
${\it\nu}_{0}=100$
cSt silicone oil.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=0.77~\text{m}~\text{s}^{-1}$
,
$V_{0}=0.77~\text{m}~\text{s}^{-1}$
,
![]() $St_{0}=264$
,
$St_{0}=264$
,
![]() $Ca=3.54$
. The insets present an enlarged image of the primary bubble entrapment (indicated by black arrows). The secondary bubbles are denoted with grey arrows in the first side-view image. A close-up of the bottom view at
$Ca=3.54$
. The insets present an enlarged image of the primary bubble entrapment (indicated by black arrows). The secondary bubbles are denoted with grey arrows in the first side-view image. A close-up of the bottom view at
![]() $t=125~{\rm\mu}\text{s}$
labelled with various cavitation structure features has also been provided. (See caption of figure 1 for description of
$t=125~{\rm\mu}\text{s}$
labelled with various cavitation structure features has also been provided. (See caption of figure 1 for description of
![]() $t_{0}$
,
$t_{0}$
,
![]() $h_{0}$
, *,
$h_{0}$
, *,
![]() $\uparrow$
,
$\uparrow$
,
![]() $\downarrow$
and
$\downarrow$
and
![]() $h$
for this and all figures presented hereafter.)
$h$
for this and all figures presented hereafter.)
3 Results and discussion
3.1 Qualitative results
Figure 4 shows the impact of a sphere onto a glass wall covered with a 37 mm deep pool of
![]() ${\it\nu}_{0}=100$
cSt silicone oil (see caption for details). Since the sphere is released from above the surface of the liquid (
${\it\nu}_{0}=100$
cSt silicone oil (see caption for details). Since the sphere is released from above the surface of the liquid (
![]() $h_{r}=67$
mm), we observe a main or ‘primary’ bubble entrapped on the sphere surface due to the lubrication pressure of the air (Marston et al.
Reference Marston, Vakarelski and Thoroddsen2011a
). This is clearly seen at the bottom tip of the sphere in the first image (see black arrow). Other smaller (secondary) bubbles are also observed (see grey arrows), caused by the dynamic wetting of the sphere with the viscous liquid, as the main (outer) contact line moves up around the sphere.
$h_{r}=67$
mm), we observe a main or ‘primary’ bubble entrapped on the sphere surface due to the lubrication pressure of the air (Marston et al.
Reference Marston, Vakarelski and Thoroddsen2011a
). This is clearly seen at the bottom tip of the sphere in the first image (see black arrow). Other smaller (secondary) bubbles are also observed (see grey arrows), caused by the dynamic wetting of the sphere with the viscous liquid, as the main (outer) contact line moves up around the sphere.
As the sphere approaches the wall, these bubbles squeeze radially outwards and act as flow tracers. However, as soon as the sphere makes contact with the wall (taken as the reference point,
![]() $t_{0}=0~{\rm\mu}\text{s}$
and
$t_{0}=0~{\rm\mu}\text{s}$
and
![]() $h_{0}=0~{\rm\mu}\text{m}$
) and undergoes rapid deceleration, the liquid near the sphere surface depressurizes, causing the entrapped bubbles to expand and form more small bubbles around the region of contact. This region was shown by Marston et al. (Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
) to be approximately equal to the Hertzian contact area, being the area on the tip of the sphere that flattens elastically during the collision period (
$h_{0}=0~{\rm\mu}\text{m}$
) and undergoes rapid deceleration, the liquid near the sphere surface depressurizes, causing the entrapped bubbles to expand and form more small bubbles around the region of contact. This region was shown by Marston et al. (Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
) to be approximately equal to the Hertzian contact area, being the area on the tip of the sphere that flattens elastically during the collision period (
![]() $t=0{-}31~{\rm\mu}\text{s}$
). As the bubbles expand rapidly, the radial expanse of the cavitation increases reaching a maximum
$t=0{-}31~{\rm\mu}\text{s}$
). As the bubbles expand rapidly, the radial expanse of the cavitation increases reaching a maximum
![]() $r_{max}\approx 6.6$
mm at
$r_{max}\approx 6.6$
mm at
![]() $t=63~{\rm\mu}\text{s}$
. By this time the sphere has reversed its direction of motion and the cavitation structure then starts to contract radially inwards. While bubbles on the outer edge collapse, those closer to the centre expand to form a distinct inner ring. Bubbles different from the rest of the structure having elongated interfaces are also observed immediately around the region of contact. At
$t=63~{\rm\mu}\text{s}$
. By this time the sphere has reversed its direction of motion and the cavitation structure then starts to contract radially inwards. While bubbles on the outer edge collapse, those closer to the centre expand to form a distinct inner ring. Bubbles different from the rest of the structure having elongated interfaces are also observed immediately around the region of contact. At
![]() $t=219~{\rm\mu}\text{s}$
, bubbles collapsing at the outer extent reach the inner bubble ring, preventing it from further expansion. The inner ring then shrinks as the sphere moves further away and the entire structure disappears at
$t=219~{\rm\mu}\text{s}$
, bubbles collapsing at the outer extent reach the inner bubble ring, preventing it from further expansion. The inner ring then shrinks as the sphere moves further away and the entire structure disappears at
![]() $t=594~{\rm\mu}\text{s}$
. These observations are in agreement with those of Mansoor et al. (Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014) and show cavitation to occur by depressurization in the liquid when the sphere makes contact and rebounds away from the wall, as predicted by the conventional theory. Though the primary bubble entrapped by the lubrication pressure of the air can be observed as a large expanded bubble during the collision, bubbles expanding from the air entrainment by the dynamic wetting of the sphere (secondary bubbles) are difficult to distinguish from cavitation bubbles surrounding the region of contact.
$t=594~{\rm\mu}\text{s}$
. These observations are in agreement with those of Mansoor et al. (Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014) and show cavitation to occur by depressurization in the liquid when the sphere makes contact and rebounds away from the wall, as predicted by the conventional theory. Though the primary bubble entrapped by the lubrication pressure of the air can be observed as a large expanded bubble during the collision, bubbles expanding from the air entrainment by the dynamic wetting of the sphere (secondary bubbles) are difficult to distinguish from cavitation bubbles surrounding the region of contact.

Figure 5. Bottom-view images of impacts onto a 37 mm deep pool of
![]() ${\it\nu}_{0}=1000$
cSt silicone oil from release heights of
${\it\nu}_{0}=1000$
cSt silicone oil from release heights of
![]() $h_{r}=47$
, 77 and 147 mm.
$h_{r}=47$
, 77 and 147 mm.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=0.44~\text{m}~\text{s}^{-1}$
,
$V_{0}=0.44~\text{m}~\text{s}^{-1}$
,
![]() $0.89~\text{m}~\text{s}^{-1}$
,
$0.89~\text{m}~\text{s}^{-1}$
,
![]() $1.47~\text{m}~\text{s}^{-1}$
corresponding to
$1.47~\text{m}~\text{s}^{-1}$
corresponding to
![]() $St_{0}=15.0$
, 30.4, 50.1,
$St_{0}=15.0$
, 30.4, 50.1,
![]() $De=4.44\times 10^{-3}$
,
$De=4.44\times 10^{-3}$
,
![]() $8.99\times 10^{-3}$
,
$8.99\times 10^{-3}$
,
![]() $1.50\times 10^{-2}$
and
$1.50\times 10^{-2}$
and
![]() $Ca=20.1$
, 40.7, 67.3, in (a), (b) and (c) respectively. Notice the decrease in size but increase in number of the secondary bubbles as the release height is increased (see insets for magnified views). The bubble entrapped by the lubrication pressure of air in each case has been marked by a white arrow.
$Ca=20.1$
, 40.7, 67.3, in (a), (b) and (c) respectively. Notice the decrease in size but increase in number of the secondary bubbles as the release height is increased (see insets for magnified views). The bubble entrapped by the lubrication pressure of air in each case has been marked by a white arrow.
This is not true for collisions occurring in more viscous liquids, whereby bubbles expanding from secondary bubbles and those opening from within the liquid to form cavitation bubbles can be observed to form in distinct regions at the sphere’s surface. Figure 5 shows the impact of a sphere onto a glass wall covered with 37 mm deep pool of
![]() ${\it\nu}_{0}=1000$
cSt silicone oil, for three different release heights
${\it\nu}_{0}=1000$
cSt silicone oil, for three different release heights
![]() $h_{r}=47$
, 77 and 147 mm. It can be observed that the air bubbles entrained by the dynamic wetting of the sphere become smaller in size and larger in number as the speed of impact onto the liquid surface increases (see insets). This phenomenon can be explained by the mechanism with which air entrainment occurs in liquid coating procedures (e.g. slot die coating), where a thin liquid film is applied onto a moving substrate. Air entrainment results from a series of processes which initiate when the dynamic contact line is unable to move quicker than a threshold speed perpendicular to itself (i.e. when the dynamic contact angle between the film and the substrate approaches
$h_{r}=47$
, 77 and 147 mm. It can be observed that the air bubbles entrained by the dynamic wetting of the sphere become smaller in size and larger in number as the speed of impact onto the liquid surface increases (see insets). This phenomenon can be explained by the mechanism with which air entrainment occurs in liquid coating procedures (e.g. slot die coating), where a thin liquid film is applied onto a moving substrate. Air entrainment results from a series of processes which initiate when the dynamic contact line is unable to move quicker than a threshold speed perpendicular to itself (i.e. when the dynamic contact angle between the film and the substrate approaches
![]() $180^{\circ }$
), producing sawtooth structures or air pockets (Blake & Ruschak Reference Blake and Ruschak1979). At this point, viscous forces pulling the liquid in the direction of substrate motion become dominant over surface tension forces acting in the opposite direction (Bhamidipati, Didari & Harris Reference Bhamidipati, Didari and Harris2012), which results in an interfacial instability, causing the film liquid to entrain the air pocket from all sides (Severtson & Aidun Reference Severtson and Aidun1996). When the substrate velocity (scaling with
$180^{\circ }$
), producing sawtooth structures or air pockets (Blake & Ruschak Reference Blake and Ruschak1979). At this point, viscous forces pulling the liquid in the direction of substrate motion become dominant over surface tension forces acting in the opposite direction (Bhamidipati, Didari & Harris Reference Bhamidipati, Didari and Harris2012), which results in an interfacial instability, causing the film liquid to entrain the air pocket from all sides (Severtson & Aidun Reference Severtson and Aidun1996). When the substrate velocity (scaling with
![]() $V_{0}$
in our case) is increased, the viscous stresses also increase, enabling them to propagate upstream more quickly and causing the sawteeth to extend over a smaller area before pinch-off occurs (Bhamidipati et al.
Reference Bhamidipati, Didari and Harris2012). This mechanism, which is dictated by the capillary number, results in the entrainment of smaller air bubbles as also noted in figure 5 (see figure caption).
$V_{0}$
in our case) is increased, the viscous stresses also increase, enabling them to propagate upstream more quickly and causing the sawteeth to extend over a smaller area before pinch-off occurs (Bhamidipati et al.
Reference Bhamidipati, Didari and Harris2012). This mechanism, which is dictated by the capillary number, results in the entrainment of smaller air bubbles as also noted in figure 5 (see figure caption).
For all three release heights, the primary (white arrows) and secondary bubbles squeeze radially outwards as the sphere approaches towards the glass wall to create an annular bubble structure, which has previously been misinterpreted as shear-induced cavitation by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012). While the deceleration of the sphere upon contact for
![]() $h_{r}=47$
mm is not enough for the liquid to open from these bubbles, an annular pattern of small bubbles connected in a foam-like structure is clearly seen for
$h_{r}=47$
mm is not enough for the liquid to open from these bubbles, an annular pattern of small bubbles connected in a foam-like structure is clearly seen for
![]() $h_{r}=147$
mm. In contrast, a distinct pattern of elongated cavity bubbles (Marston et al.
Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
) is observed immediately around the Hertzian contact area for all three release heights. While bubbles expanding from pressure reduction in the annular structure comprise of a mixture of air and vapour, those surrounding the contact region are mainly vapour filled. Also, since the liquid films are exposed to the atmosphere, the possibility of dissolved air cannot be neglected, which can result in optically similar cavity bubbles near the contact region and in the annular structure during the decompression stage.
$h_{r}=147$
mm. In contrast, a distinct pattern of elongated cavity bubbles (Marston et al.
Reference Marston, Yong, Ng, Tan and Thoroddsen2011b
) is observed immediately around the Hertzian contact area for all three release heights. While bubbles expanding from pressure reduction in the annular structure comprise of a mixture of air and vapour, those surrounding the contact region are mainly vapour filled. Also, since the liquid films are exposed to the atmosphere, the possibility of dissolved air cannot be neglected, which can result in optically similar cavity bubbles near the contact region and in the annular structure during the decompression stage.
Figure 6 shows the sphere impact from
![]() $h_{r}=25$
cm onto a glass plate covered with a 5 mm thick layer of
$h_{r}=25$
cm onto a glass plate covered with a 5 mm thick layer of
![]() ${\it\nu}_{0}=10\,000$
cSt silicone oil. The primary bubble, which initially spreads into an air sheet following the entry of the sphere into the liquid, is observed to deform into a ring of several smaller bubbles as the sphere approaches closer towards the wall (
${\it\nu}_{0}=10\,000$
cSt silicone oil. The primary bubble, which initially spreads into an air sheet following the entry of the sphere into the liquid, is observed to deform into a ring of several smaller bubbles as the sphere approaches closer towards the wall (
![]() $h=809~{\rm\mu}\text{m}$
). These bubbles squeeze radially outwards in the final moments before contact, which is followed by a series of cavity formation events similar in nature to those observed from underneath the sphere in the 1000 cSt silicone oil film (figure 5). Since the secondary bubbles entrained are even smaller in size and larger in number, due to further increase in viscous forces experienced by the liquid, the annular cavitation structure formed is much more densely packed and noted to occur for a brief time period (
$h=809~{\rm\mu}\text{m}$
). These bubbles squeeze radially outwards in the final moments before contact, which is followed by a series of cavity formation events similar in nature to those observed from underneath the sphere in the 1000 cSt silicone oil film (figure 5). Since the secondary bubbles entrained are even smaller in size and larger in number, due to further increase in viscous forces experienced by the liquid, the annular cavitation structure formed is much more densely packed and noted to occur for a brief time period (
![]() $t=0{-}30~{\rm\mu}\text{s}$
). Meanwhile, the cavity pattern formed immediately around the contact area is composed of a distinct ring of fine bubbles (see inset for magnified view). The cavitation bubbles and the film liquid peel off from the sphere’s surface as it rebounds away from the wall to form a single larger cavity, which extends into a noticeably large hourglass shape (
$t=0{-}30~{\rm\mu}\text{s}$
). Meanwhile, the cavity pattern formed immediately around the contact area is composed of a distinct ring of fine bubbles (see inset for magnified view). The cavitation bubbles and the film liquid peel off from the sphere’s surface as it rebounds away from the wall to form a single larger cavity, which extends into a noticeably large hourglass shape (
![]() $t=30~{\rm\mu}\text{s}$
–1.79 ms). Such an occurrence is not noted for impacts in lower viscosity liquids discussed in the preceding figures.
$t=30~{\rm\mu}\text{s}$
–1.79 ms). Such an occurrence is not noted for impacts in lower viscosity liquids discussed in the preceding figures.

Figure 6. Images of an impact from
![]() $h_{r}=25$
cm onto a glass wall covered with a 5 mm thick layer of
$h_{r}=25$
cm onto a glass wall covered with a 5 mm thick layer of
![]() ${\it\nu}_{0}=10\,000$
cSt silicone oil.
${\it\nu}_{0}=10\,000$
cSt silicone oil.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=2.19~\text{m}~\text{s}^{-1}$
,
$V_{0}=2.19~\text{m}~\text{s}^{-1}$
,
![]() $St_{0}=7.43$
,
$St_{0}=7.43$
,
![]() $De=0.17$
,
$De=0.17$
,
![]() $Ca=993$
. The primary bubble entrapped on the sphere’s surface deforms by viscous shear flow as the sphere approaches the base wall (see insets for magnified views). The cavity is noted to peel off from the sphere’s surface while extending vertically to assume an hourglass shape.
$Ca=993$
. The primary bubble entrapped on the sphere’s surface deforms by viscous shear flow as the sphere approaches the base wall (see insets for magnified views). The cavity is noted to peel off from the sphere’s surface while extending vertically to assume an hourglass shape.
Impacts from (a)
![]() $h_{r}=40$
cm and (b)
$h_{r}=40$
cm and (b)
![]() $h_{r}=60$
cm onto a glass plate covered with a 5 mm thick layer
$h_{r}=60$
cm onto a glass plate covered with a 5 mm thick layer
![]() ${\it\nu}_{0}=100\,000$
cSt silicone oil are shown in figure 7. In both cases the primary bubble entrapped on the sphere’s surface is squeezed radially outwards until it escapes into the atmosphere. The process however is so intense and instant that the bubble fragments at the sphere–bubble interface, leaving behind a cluster of much smaller bubbles in a circular patch at the point of close approach. We call these ‘remnant bubbles’ and indicate them by black arrows.
${\it\nu}_{0}=100\,000$
cSt silicone oil are shown in figure 7. In both cases the primary bubble entrapped on the sphere’s surface is squeezed radially outwards until it escapes into the atmosphere. The process however is so intense and instant that the bubble fragments at the sphere–bubble interface, leaving behind a cluster of much smaller bubbles in a circular patch at the point of close approach. We call these ‘remnant bubbles’ and indicate them by black arrows.

Figure 7. Images of impacts from (a)
![]() $h_{r}=40$
cm and (b)
$h_{r}=40$
cm and (b)
![]() $h_{r}=60$
cm onto a 5 mm thick layer of
$h_{r}=60$
cm onto a 5 mm thick layer of
![]() ${\it\nu}_{0}=100\,000$
cSt silicone oil.
${\it\nu}_{0}=100\,000$
cSt silicone oil.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=$
(a)
$V_{0}=$
(a)
![]() $2.78~\text{m}~\text{s}^{-1}$
, (b)
$2.78~\text{m}~\text{s}^{-1}$
, (b)
![]() $3.42~\text{m}~\text{s}^{-1}$
corresponding to
$3.42~\text{m}~\text{s}^{-1}$
corresponding to
![]() $St_{0}=0.94$
, 1.16,
$St_{0}=0.94$
, 1.16,
![]() $De=1.59$
, 1.95 and
$De=1.59$
, 1.95 and
![]() $Ca=12.6\times 10^{3}$
,
$Ca=12.6\times 10^{3}$
,
![]() $15.5\times 10^{3}$
, respectively. The black arrows indicate remnant bubbles composed in a circular patch at the point of close approach. The sphere rebounds without making contact for
$15.5\times 10^{3}$
, respectively. The black arrows indicate remnant bubbles composed in a circular patch at the point of close approach. The sphere rebounds without making contact for
![]() $h_{r}=40$
cm where the onset of cavitation is observed
$h_{r}=40$
cm where the onset of cavitation is observed
![]() $181~{\rm\mu}\text{s}$
after time
$181~{\rm\mu}\text{s}$
after time
![]() $t_{m}$
(reference point at which the sphere reaches its minimum gap distance
$t_{m}$
(reference point at which the sphere reaches its minimum gap distance
![]() $h_{m}$
, marked with the square symbol ▫ for this and all other figures presented hereafter). See also supplementary movie 1 available at http://dx.doi.org/10.1017/jfm.2016.229.
$h_{m}$
, marked with the square symbol ▫ for this and all other figures presented hereafter). See also supplementary movie 1 available at http://dx.doi.org/10.1017/jfm.2016.229.
The inertia of the sphere is insufficient to fully penetrate the film and contact the base for
![]() $h_{r}=40$
cm (i.e.
$h_{r}=40$
cm (i.e.
![]() $St_{0}<St_{0}^{c}$
in § 3.2), as a significant portion of the kinetic energy is lost due to viscous dissipation, while the remaining is stored as elastic energy in the liquid film. The sphere is not expected to deform elastically in this manner since the deformation length scale, identified by Davis et al. (Reference Davis, Serayssol and Hinch1986) as
$St_{0}<St_{0}^{c}$
in § 3.2), as a significant portion of the kinetic energy is lost due to viscous dissipation, while the remaining is stored as elastic energy in the liquid film. The sphere is not expected to deform elastically in this manner since the deformation length scale, identified by Davis et al. (Reference Davis, Serayssol and Hinch1986) as
![]() $x_{1}=(4{\it\theta}{\it\mu}V_{0}R_{0}^{3/2})^{2/5}$
, is calculated as being small (
$x_{1}=(4{\it\theta}{\it\mu}V_{0}R_{0}^{3/2})^{2/5}$
, is calculated as being small (
![]() $x_{1}\approx 10~{\rm\mu}\text{m}$
) relative to the minimum separation distance
$x_{1}\approx 10~{\rm\mu}\text{m}$
) relative to the minimum separation distance
![]() $h_{m}$
reached, even when the shear-thinning effects are neglected for
$h_{m}$
reached, even when the shear-thinning effects are neglected for
![]() $h\leqslant x_{0}$
. As the sphere reaches
$h\leqslant x_{0}$
. As the sphere reaches
![]() $h_{m}$
at time
$h_{m}$
at time
![]() $t_{m}$
(taken as the reference point for non-contact cases), the remnant bubbles compress from the pressure in the squeeze flow, making them nearly invisible in the process. After this point the elastic energy stored in the film starts converting back to the kinetic energy of the sphere, enabling it to rebound. The liquid however does not cavitate immediately during the depressurization stage but at
$t_{m}$
(taken as the reference point for non-contact cases), the remnant bubbles compress from the pressure in the squeeze flow, making them nearly invisible in the process. After this point the elastic energy stored in the film starts converting back to the kinetic energy of the sphere, enabling it to rebound. The liquid however does not cavitate immediately during the depressurization stage but at
![]() $t=121~{\rm\mu}\text{s}$
after reaching
$t=121~{\rm\mu}\text{s}$
after reaching
![]() $h_{m}$
. To our knowledge, this is the first experimental evidence of cavitation by depressurization for a new class of non-contact cases during the impact of a sphere onto a wall covered with a film of viscoelastic liquid. Cavitation is first observed to originate from the same patch of remnant bubbles to form a dense foam-like circular structure, which then extends to a pattern composed of discrete bubbles. These bubbles generally increase in size as we move radially outwards from the point of closest approach. The circular foam-like structure is formed in the same region as the position of remnant bubbles observed when the sphere enters and descends (
$h_{m}$
. To our knowledge, this is the first experimental evidence of cavitation by depressurization for a new class of non-contact cases during the impact of a sphere onto a wall covered with a film of viscoelastic liquid. Cavitation is first observed to originate from the same patch of remnant bubbles to form a dense foam-like circular structure, which then extends to a pattern composed of discrete bubbles. These bubbles generally increase in size as we move radially outwards from the point of closest approach. The circular foam-like structure is formed in the same region as the position of remnant bubbles observed when the sphere enters and descends (
![]() $t=-909~{\rm\mu}\text{s}$
) into the film, which confirms them to exist in a compressed form and not to squeeze radially outwards at
$t=-909~{\rm\mu}\text{s}$
) into the film, which confirms them to exist in a compressed form and not to squeeze radially outwards at
![]() $h_{m}$
. The cavity reaches its maximum radial extent at
$h_{m}$
. The cavity reaches its maximum radial extent at
![]() $t=1.67$
ms. As the sphere rebounds away from the wall, its motion is slowed down by gravity and viscous lubrication forces until it comes to a halt at
$t=1.67$
ms. As the sphere rebounds away from the wall, its motion is slowed down by gravity and viscous lubrication forces until it comes to a halt at
![]() $t=3.15$
ms. By this time the liquid has started to flow back into the cavitated region, which causes the cavity to shrink, and with further passage of time (
$t=3.15$
ms. By this time the liquid has started to flow back into the cavitated region, which causes the cavity to shrink, and with further passage of time (
![]() $t=10.75$
ms) the sphere gradually moves back towards the wall.
$t=10.75$
ms) the sphere gradually moves back towards the wall.
For
![]() $h_{r}=60$
cm, the sphere has enough kinetic energy to impact the glass wall after penetrating into the liquid film. The remnant bubbles in a circular patch (observed e.g. at
$h_{r}=60$
cm, the sphere has enough kinetic energy to impact the glass wall after penetrating into the liquid film. The remnant bubbles in a circular patch (observed e.g. at
![]() $t=-394~{\rm\mu}\text{s}$
) are again difficult to perceive in their compressed state (
$t=-394~{\rm\mu}\text{s}$
) are again difficult to perceive in their compressed state (
![]() $t=-91~{\rm\mu}\text{s}$
), but then get squeezed out from the diminishing gap to create a dark circular area as physical contact is made (
$t=-91~{\rm\mu}\text{s}$
), but then get squeezed out from the diminishing gap to create a dark circular area as physical contact is made (
![]() $t_{0}=0~{\rm\mu}\text{s}$
, see panel 3 in the final column of figure 7). The dark spot, which corresponds to the Hertzian contact area, contrasts with the reflection of light from secondary bubbles in the surrounding region formed by air entrainment. These secondary bubbles are also present in the case of
$t_{0}=0~{\rm\mu}\text{s}$
, see panel 3 in the final column of figure 7). The dark spot, which corresponds to the Hertzian contact area, contrasts with the reflection of light from secondary bubbles in the surrounding region formed by air entrainment. These secondary bubbles are also present in the case of
![]() $h_{r}=40$
cm but are not as easily noticeable. Similar to contact cases in the less viscous liquid films shown in the preceding figures, cavitation for
$h_{r}=40$
cm but are not as easily noticeable. Similar to contact cases in the less viscous liquid films shown in the preceding figures, cavitation for
![]() $h_{r}=60$
cm is observed as soon as the sphere impacts and starts to rebound away from the wall. In comparison to figure 6 however, the cavitation bubbles coalesce to form a single cavity structure, which extends into an hourglass shape (
$h_{r}=60$
cm is observed as soon as the sphere impacts and starts to rebound away from the wall. In comparison to figure 6 however, the cavitation bubbles coalesce to form a single cavity structure, which extends into an hourglass shape (
![]() $t=3.03$
ms). The bubbles expand radially in the process to form elongated interfaces (see bottom views), which are more prominently observed at the periphery of the structure. The annular cavitation structure, which is known to originate from the secondary bubbles, is not observed upon impact.
$t=3.03$
ms). The bubbles expand radially in the process to form elongated interfaces (see bottom views), which are more prominently observed at the periphery of the structure. The annular cavitation structure, which is known to originate from the secondary bubbles, is not observed upon impact.
To understand the change in cavitation structures as the wetted collision changes from a non-contact to a contact case, we show a series of images in figure 8 taken from underneath the sphere for release heights ranging 36–70 cm (
![]() $V_{0}=2.64{-}3.69~\text{m}~\text{s}^{-1}$
). The images are taken when the cavitation structure reaches its maximum radial extent, from the moment the sphere either reaches its minimum gap distance (
$V_{0}=2.64{-}3.69~\text{m}~\text{s}^{-1}$
). The images are taken when the cavitation structure reaches its maximum radial extent, from the moment the sphere either reaches its minimum gap distance (
![]() $t_{m}$
) or makes contact with the wall (
$t_{m}$
) or makes contact with the wall (
![]() $t_{0}$
). This time interval
$t_{0}$
). This time interval
![]() $t$
is generally noted to decrease as
$t$
is generally noted to decrease as
![]() $h_{r}$
is increased (see figure for details). As seen from the images, the fine foam-like structure in a circular region, which originates from the remnant bubbles at the point of closest approach, is consistent among all three non-contact cases (
$h_{r}$
is increased (see figure for details). As seen from the images, the fine foam-like structure in a circular region, which originates from the remnant bubbles at the point of closest approach, is consistent among all three non-contact cases (
![]() $h_{r}=36$
, 38 and 40 cm). The differences develop in the surrounding bubbles, which enlarge in size and become increasingly discrete entities (
$h_{r}=36$
, 38 and 40 cm). The differences develop in the surrounding bubbles, which enlarge in size and become increasingly discrete entities (
![]() $h_{r}=40$
cm) from being connected by small bubbles in a foam-like network (
$h_{r}=40$
cm) from being connected by small bubbles in a foam-like network (
![]() $h_{r}=36$
cm). The discrete bubbles begin experiencing radial expansion and coalescence to form a single cavity bubble for contact cases starting with
$h_{r}=36$
cm). The discrete bubbles begin experiencing radial expansion and coalescence to form a single cavity bubble for contact cases starting with
![]() $h_{r}=50$
cm. More energetic impacts occurring for
$h_{r}=50$
cm. More energetic impacts occurring for
![]() $h_{r}\geqslant 60$
cm intensify this phenomenon to result in the formation of elongated interfaces in the bottom views; these are generally prominent at the periphery of the structure, and are also found immediately around the Hertz contact area for
$h_{r}\geqslant 60$
cm intensify this phenomenon to result in the formation of elongated interfaces in the bottom views; these are generally prominent at the periphery of the structure, and are also found immediately around the Hertz contact area for
![]() $h_{r}=70$
cm. This area corresponds to the white region at the point of closest approach, which can be noticed to increase with the impact velocity. It is noteworthy to mention that while impacts here are categorized into non-contact and contact cases based on the visual appearance of a separation gap between the sphere and base wall before rebound, the impacting surfaces in the latter case can still be separated by an extremely thin liquid layer, as dictated by the elastohydrodynamic theory. A true contact in such cases may occur if the sphere has sufficient initial inertia to reduce the separation gap to a few nanometers (Serayssol & Davis Reference Serayssol and Davis1986), where additional effects such as surface roughness and interparticle surface forces become important.
$h_{r}=70$
cm. This area corresponds to the white region at the point of closest approach, which can be noticed to increase with the impact velocity. It is noteworthy to mention that while impacts here are categorized into non-contact and contact cases based on the visual appearance of a separation gap between the sphere and base wall before rebound, the impacting surfaces in the latter case can still be separated by an extremely thin liquid layer, as dictated by the elastohydrodynamic theory. A true contact in such cases may occur if the sphere has sufficient initial inertia to reduce the separation gap to a few nanometers (Serayssol & Davis Reference Serayssol and Davis1986), where additional effects such as surface roughness and interparticle surface forces become important.

Figure 8. Comparison of cavitation structures observed underneath impacts from various release heights onto a 5 mm thick layer of
![]() ${\it\nu}_{0}=100\,000$
cSt silicone oil.
${\it\nu}_{0}=100\,000$
cSt silicone oil.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=2.64~\text{m}~\text{s}^{-1}$
,
$V_{0}=2.64~\text{m}~\text{s}^{-1}$
,
![]() $2.71~\text{m}~\text{s}^{-1}$
,
$2.71~\text{m}~\text{s}^{-1}$
,
![]() $2.78~\text{m}~\text{s}^{-1}$
,
$2.78~\text{m}~\text{s}^{-1}$
,
![]() $3.12~\text{m}~\text{s}^{-1}$
,
$3.12~\text{m}~\text{s}^{-1}$
,
![]() $3.42~\text{m}~\text{s}^{-1}$
,
$3.42~\text{m}~\text{s}^{-1}$
,
![]() $3.69~\text{m}~\text{s}^{-1}$
corresponding to
$3.69~\text{m}~\text{s}^{-1}$
corresponding to
![]() $St_{0}=0.89$
, 0.92, 0.94, 1.06, 1.16, 1.25 and
$St_{0}=0.89$
, 0.92, 0.94, 1.06, 1.16, 1.25 and
![]() $De=1.51$
, 1.55, 1.59, 1.78, 1.95, 2.11, respectively. The images are taken when the cavity reaches its maximum radial distance during the rebound stage of the sphere. The Hertzian contact area can be observed as a white circular region at the centre of the structure for
$De=1.51$
, 1.55, 1.59, 1.78, 1.95, 2.11, respectively. The images are taken when the cavity reaches its maximum radial distance during the rebound stage of the sphere. The Hertzian contact area can be observed as a white circular region at the centre of the structure for
![]() $h_{r}=50$
, 60 and 70 cm.
$h_{r}=50$
, 60 and 70 cm.

Figure 9. Images of impacts onto a 5.5 mm thick layer of
![]() ${\it\nu}_{0}=1000\,000$
cSt silicone oil from (a)
${\it\nu}_{0}=1000\,000$
cSt silicone oil from (a)
![]() $h_{r}=90$
cm and (b)
$h_{r}=90$
cm and (b)
![]() $h_{r}=120$
cm.
$h_{r}=120$
cm.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=$
(a)
$V_{0}=$
(a)
![]() $4.19~\text{m}~\text{s}^{-1}$
, (b)
$4.19~\text{m}~\text{s}^{-1}$
, (b)
![]() $4.84~\text{m}~\text{s}^{-1}$
giving
$4.84~\text{m}~\text{s}^{-1}$
giving
![]() $St_{0}=0.14$
, 0.16 and
$St_{0}=0.14$
, 0.16 and
![]() $De=32.9$
, 38.0, respectively. The remnant bubbles are observed to expand, coalesce and form a single large cavity bubble in the rebound stage of the non-contact case.
$De=32.9$
, 38.0, respectively. The remnant bubbles are observed to expand, coalesce and form a single large cavity bubble in the rebound stage of the non-contact case.
Investigating cavitation structures in the ultra-viscous liquid regime, figure 9 shows the impact of a sphere onto a 5.5 mm thick layer of
![]() ${\it\nu}_{0}=1000\,000$
cSt silicone oil for (a)
${\it\nu}_{0}=1000\,000$
cSt silicone oil for (a)
![]() $h_{r}=90$
cm (non-contact case) and (b) 120 cm (contact case). A circular patch of remnant bubbles at the point of closest approach is again observed in the bottom view (
$h_{r}=90$
cm (non-contact case) and (b) 120 cm (contact case). A circular patch of remnant bubbles at the point of closest approach is again observed in the bottom view (
![]() $t=-545~{\rm\mu}\text{s}$
) for the non-contact case (figure 9
a), which fades as the sphere reaches its minimum separation gap distance
$t=-545~{\rm\mu}\text{s}$
) for the non-contact case (figure 9
a), which fades as the sphere reaches its minimum separation gap distance
![]() $h_{m}$
. Cavitation is noticed to initiate at
$h_{m}$
. Cavitation is noticed to initiate at
![]() $t=273~{\rm\mu}\text{s}$
in the form of small bubbles, which originate from the region of remnant bubbles observed earlier. The bubbles expand and coalesce as the sphere rebounds further away from the wall to form a single cavity bubble. Similar to the contact case shown in figure 7, a single cavity bubble having an hourglass shape is also formed on contact for
$t=273~{\rm\mu}\text{s}$
in the form of small bubbles, which originate from the region of remnant bubbles observed earlier. The bubbles expand and coalesce as the sphere rebounds further away from the wall to form a single cavity bubble. Similar to the contact case shown in figure 7, a single cavity bubble having an hourglass shape is also formed on contact for
![]() $h_{r}=120$
cm in figure 9(b). The cavity surface, however, has a much smoother texture, which comprises of a few streak lines extending along the length of the cavity bubble, but many at the interface where the cavity attaches to the sphere (from above) and the wall (from below). The cavity reaches its maximum radial extent at
$h_{r}=120$
cm in figure 9(b). The cavity surface, however, has a much smoother texture, which comprises of a few streak lines extending along the length of the cavity bubble, but many at the interface where the cavity attaches to the sphere (from above) and the wall (from below). The cavity reaches its maximum radial extent at
![]() $t=1.51$
ms and then starts shrinking as the sphere is brought to a halt by viscous forces and gravity, at a maximum rebound height of
$t=1.51$
ms and then starts shrinking as the sphere is brought to a halt by viscous forces and gravity, at a maximum rebound height of
![]() $h=3.45$
mm at
$h=3.45$
mm at
![]() $t=4.30$
ms. A portion of the rebound kinetic energy is again stored as elastic energy in the film, which pulls the sphere back towards the wall (
$t=4.30$
ms. A portion of the rebound kinetic energy is again stored as elastic energy in the film, which pulls the sphere back towards the wall (
![]() $t=8.96$
ms). The process repeats resulting in a series of sphere oscillations which come to a complete halt at
$t=8.96$
ms). The process repeats resulting in a series of sphere oscillations which come to a complete halt at
![]() $t=45.97$
ms. The cavity bubble shrinks to a structure composed of thin filaments, which break up one by one till the sphere is completely detached from the wall at
$t=45.97$
ms. The cavity bubble shrinks to a structure composed of thin filaments, which break up one by one till the sphere is completely detached from the wall at
![]() $t=148.94$
ms.
$t=148.94$
ms.

Figure 10. Bottom-view images of impacts from various drop heights onto a 5.5 mm thick layer of
![]() ${\it\nu}_{0}=1000\,000$
cSt silicone oil.
${\it\nu}_{0}=1000\,000$
cSt silicone oil.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=4.07~\text{m}~\text{s}^{-1}$
,
$V_{0}=4.07~\text{m}~\text{s}^{-1}$
,
![]() $4.30~\text{m}~\text{s}^{-1}$
,
$4.30~\text{m}~\text{s}^{-1}$
,
![]() $4.53~\text{m}~\text{s}^{-1}$
,
$4.53~\text{m}~\text{s}^{-1}$
,
![]() $4.63~\text{m}~\text{s}^{-1}$
,
$4.63~\text{m}~\text{s}^{-1}$
,
![]() $4.84~\text{m}~\text{s}^{-1}$
, corresponding to
$4.84~\text{m}~\text{s}^{-1}$
, corresponding to
![]() $St_{0}=0.138$
, 0.145, 0.153, 0.157, 0.164 and
$St_{0}=0.138$
, 0.145, 0.153, 0.157, 0.164 and
![]() $De=31.9$
, 33.7, 35.5, 36.3, 38.0, respectively. For each release height the pictures show the maximum radial distance reached by the cavity during sphere rebound. Notice the reduction in the maximum radial cavity distance in the contact case of
$De=31.9$
, 33.7, 35.5, 36.3, 38.0, respectively. For each release height the pictures show the maximum radial distance reached by the cavity during sphere rebound. Notice the reduction in the maximum radial cavity distance in the contact case of
![]() $h_{r}=120$
cm.
$h_{r}=120$
cm.
Figure 10 shows a series of cavities at their maximum radial extent as the release height onto the liquid film is systematically increased. As also noticed in figure 8, the time interval
![]() $t$
between reaching
$t$
between reaching
![]() $t_{m}$
(for non-contact cases) or
$t_{m}$
(for non-contact cases) or
![]() $t_{0}$
(for contact cases) and this state is found to decrease as
$t_{0}$
(for contact cases) and this state is found to decrease as
![]() $h_{r}$
is increased (see figure for details). Cavitation in the non-contact cases is observed to originate from remnant bubbles, which expand and coalesce during the rebound stage to form a single cavity bubble. Since the minimum gap distance decreases with increase in release height, the remnant bubbles at the point of close approach have an increasingly lesser room to expand longitudinally. This forms a region appearing grainy at the centre of the cavity structure, which increases in size till
$h_{r}$
is increased (see figure for details). Cavitation in the non-contact cases is observed to originate from remnant bubbles, which expand and coalesce during the rebound stage to form a single cavity bubble. Since the minimum gap distance decreases with increase in release height, the remnant bubbles at the point of close approach have an increasingly lesser room to expand longitudinally. This forms a region appearing grainy at the centre of the cavity structure, which increases in size till
![]() $h_{r}=105$
cm. For
$h_{r}=105$
cm. For
![]() $h_{r}=110$
cm, the
$h_{r}=110$
cm, the
![]() $h_{m}$
reached is small enough to squeeze the remnant bubbles radially outwards from the point of closest approach. Qualitatively, the maximum radial cavity extent is observed to decrease as the collision changes from a non-contact to a contact case at
$h_{m}$
reached is small enough to squeeze the remnant bubbles radially outwards from the point of closest approach. Qualitatively, the maximum radial cavity extent is observed to decrease as the collision changes from a non-contact to a contact case at
![]() $h_{r}=120$
cm. This is simply because the cavity attaches to the glass wall in the latter, which resists its radial expansion as the sphere rebounds away. This trend is not observed for contact cases shown in figure 8 as the cavities formed therein are only attached around the Hertzian contact area (see figure 7
b).
$h_{r}=120$
cm. This is simply because the cavity attaches to the glass wall in the latter, which resists its radial expansion as the sphere rebounds away. This trend is not observed for contact cases shown in figure 8 as the cavities formed therein are only attached around the Hertzian contact area (see figure 7
b).

Figure 11. Images of an impact from
![]() $h_{r}=150$
cm onto a 5 mm thick layer of
$h_{r}=150$
cm onto a 5 mm thick layer of
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil.
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=5.42~\text{m}~\text{s}^{-1}$
,
$V_{0}=5.42~\text{m}~\text{s}^{-1}$
,
![]() $St_{0}=9.16\times 10^{-3}$
,
$St_{0}=9.16\times 10^{-3}$
,
![]() $De=376$
. The grey arrow indicates the escape direction of the primary bubble entrapment into the atmosphere for reference purposes. Notice that the deposition of remnant bubbles on the sphere’s surface is not uniform.
$De=376$
. The grey arrow indicates the escape direction of the primary bubble entrapment into the atmosphere for reference purposes. Notice that the deposition of remnant bubbles on the sphere’s surface is not uniform.

Figure 12. Side-view images of impacts onto a 5 mm thick layer of
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil from
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil from
![]() $h_{r}=155$
, 160 and 170 cm.
$h_{r}=155$
, 160 and 170 cm.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=5.51~\text{m}~\text{s}^{-1}$
,
$V_{0}=5.51~\text{m}~\text{s}^{-1}$
,
![]() $5.59~\text{m}~\text{s}^{-1}$
,
$5.59~\text{m}~\text{s}^{-1}$
,
![]() $5.77~\text{m}~\text{s}^{-1}$
corresponding to
$5.77~\text{m}~\text{s}^{-1}$
corresponding to
![]() $St_{0}=9.31\times 10^{-3}$
,
$St_{0}=9.31\times 10^{-3}$
,
![]() $9.45\times 10^{-3}$
,
$9.45\times 10^{-3}$
,
![]() $9.75\times 10^{-3}$
and
$9.75\times 10^{-3}$
and
![]() $De=383$
, 388, 401, respectively. The onset of shear-induced cavitation and cavitation by depressurization is marked by symbols Ⓢ and Ⓓ, respectively. See also supplementary movie 2.
$De=383$
, 388, 401, respectively. The onset of shear-induced cavitation and cavitation by depressurization is marked by symbols Ⓢ and Ⓓ, respectively. See also supplementary movie 2.
Investigating cavitation structures in the most viscous liquid used in this study, figure 11 shows the impact onto a glass wall covered with a 5 mm thick layer of
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil. The release height is
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil. The release height is
![]() $h_{r}=150$
cm for which the sphere rebounds without making contact with the base wall. Though the close approach region is again observed to contain remnant bubbles (
$h_{r}=150$
cm for which the sphere rebounds without making contact with the base wall. Though the close approach region is again observed to contain remnant bubbles (
![]() $t=-424~{\rm\mu}\text{s}$
), their deposition is not uniform (as compared to those shown in figures 7 and 9) but rather concentrated in the direction of the primary bubble’s escape into the atmosphere (see grey arrow). A fact proved later in the rebound stage when the bubbles start to expand (
$t=-424~{\rm\mu}\text{s}$
), their deposition is not uniform (as compared to those shown in figures 7 and 9) but rather concentrated in the direction of the primary bubble’s escape into the atmosphere (see grey arrow). A fact proved later in the rebound stage when the bubbles start to expand (
![]() $t=242~{\rm\mu}\text{s}$
) and coalesce in the process to form a single cavity bubble, which is noticed to grow faster (
$t=242~{\rm\mu}\text{s}$
) and coalesce in the process to form a single cavity bubble, which is noticed to grow faster (
![]() $t=363~{\rm\mu}\text{s}$
) in the region where the majority of the remnant bubbles are situated. With the passage of more time (
$t=363~{\rm\mu}\text{s}$
) in the region where the majority of the remnant bubbles are situated. With the passage of more time (
![]() $t=666~{\rm\mu}\text{s}$
) the cavity enlarges further to develop an inverted conical structure.
$t=666~{\rm\mu}\text{s}$
) the cavity enlarges further to develop an inverted conical structure.
Cavitation structures formed for increased release heights of
![]() $h_{r}=155$
, 160 and 170 cm are shown in figure 12 (see caption for details). In contrast to all the preceding figures where cavitation is only observed upon contact or during the rebound stage for non-contact cases, here we observe the liquid to cavitate when the sphere has reached a sufficiently small separation distance while approaching towards the glass wall i.e. during pressurization (marked with symbol Ⓢ). This phenomenon known as shear-stress-induced cavitation was first predicted on theoretical grounds by Joseph (Reference Joseph1998). The model presented was considered by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) in proposing a new formal requirement for the onset of cavitation (see § 4, (4.1)). This stated that a liquid squeezing radially outwards in the diminishing gap between the sphere and the wall could rip open in tension if the applied shear stress overcomes the pressure in the film, reducing it below the liquid vapour pressure.
$h_{r}=155$
, 160 and 170 cm are shown in figure 12 (see caption for details). In contrast to all the preceding figures where cavitation is only observed upon contact or during the rebound stage for non-contact cases, here we observe the liquid to cavitate when the sphere has reached a sufficiently small separation distance while approaching towards the glass wall i.e. during pressurization (marked with symbol Ⓢ). This phenomenon known as shear-stress-induced cavitation was first predicted on theoretical grounds by Joseph (Reference Joseph1998). The model presented was considered by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) in proposing a new formal requirement for the onset of cavitation (see § 4, (4.1)). This stated that a liquid squeezing radially outwards in the diminishing gap between the sphere and the wall could rip open in tension if the applied shear stress overcomes the pressure in the film, reducing it below the liquid vapour pressure.
We find shear-induced cavities formed in figure 12 not to be characterized by well-defined edges but rather a hazy interface, which makes observing them in the bottom views (not shown) difficult. The cavities grow while the sphere continues its approach towards the wall to either reach a minimum gap distance (for
![]() $h_{r}=155$
cm) or make wall contact (for
$h_{r}=155$
cm) or make wall contact (for
![]() $h_{r}=160$
and 170 cm). Before shear-induced cavitation initiates however, remnant bubbles deposited on the sphere’s surface begin squeezing radially outwards from the point of closest approach. These are subsequently caught up and get trapped at the expanding interface of the cavity bubble formed by depressurization (marked with symbol Ⓓ), when the sphere rebounds away from the wall.
$h_{r}=160$
and 170 cm). Before shear-induced cavitation initiates however, remnant bubbles deposited on the sphere’s surface begin squeezing radially outwards from the point of closest approach. These are subsequently caught up and get trapped at the expanding interface of the cavity bubble formed by depressurization (marked with symbol Ⓓ), when the sphere rebounds away from the wall.

Figure 13. Close-up views from the side and bottom of selected cavitation events shown in figure 12 for
![]() $h_{r}=155$
and 160 cm. The remnant bubbles that squeeze radially out during the sphere’s close approach towards the base wall and get caught up in the cavity walls can be seen as small pecks.
$h_{r}=155$
and 160 cm. The remnant bubbles that squeeze radially out during the sphere’s close approach towards the base wall and get caught up in the cavity walls can be seen as small pecks.
In contrast to perfect hourglass shaped cavity bubbles observed for impacts in less viscous liquids, figure 12 and close-ups in figure 13 collectively show strikingly different cavitation structures. The radial expansion and longitudinal extension of structures along their length occurs in a disproportionate manner. Considering the case of
![]() $h_{r}=155$
cm for example (figure 12), the cavity bubble elongates more extensively in the central region during its early stages of formation by depressurization (
$h_{r}=155$
cm for example (figure 12), the cavity bubble elongates more extensively in the central region during its early stages of formation by depressurization (
![]() $151{-}666~{\rm\mu}\text{s}$
) to experience necking. As the cavity stretches further with time (
$151{-}666~{\rm\mu}\text{s}$
) to experience necking. As the cavity stretches further with time (
![]() $666{-}909~{\rm\mu}\text{s}$
), it starts to peel off from the sphere’s surface creating a grainy texture at the top of the cavity wall (see figure 13). The neck shrinks further meanwhile and the cavity region underneath also experiences a strong resistance to radial expansion due to the ongoing longitudinal extension. As soon as the depressurization in the cavity bubble overcomes the effect of radial shrinkage resulting from its longitudinal elongation, the structure starts expanding radially outwards, reaching its maximum radial extent at
$666{-}909~{\rm\mu}\text{s}$
), it starts to peel off from the sphere’s surface creating a grainy texture at the top of the cavity wall (see figure 13). The neck shrinks further meanwhile and the cavity region underneath also experiences a strong resistance to radial expansion due to the ongoing longitudinal extension. As soon as the depressurization in the cavity bubble overcomes the effect of radial shrinkage resulting from its longitudinal elongation, the structure starts expanding radially outwards, reaching its maximum radial extent at
![]() $t=1.97$
ms. Close-up images of this process are shown in figure 13. Remnant bubbles that are squeezed radially outwards from the point of closest approach but subsequently caught and carried up along the cavity wall, can also be observed as spots or shorts streaks due to elongation. Because the cavity–sphere interface peels off steadily, the longitudinal extension is noted to localize beneath the necking region. The concentration of remnant bubbles in this cavity wall region therefore reduces, which becomes apparent with the increasingly reflective area formed. Interestingly, even though the sphere makes no contact with the wall for
$t=1.97$
ms. Close-up images of this process are shown in figure 13. Remnant bubbles that are squeezed radially outwards from the point of closest approach but subsequently caught and carried up along the cavity wall, can also be observed as spots or shorts streaks due to elongation. Because the cavity–sphere interface peels off steadily, the longitudinal extension is noted to localize beneath the necking region. The concentration of remnant bubbles in this cavity wall region therefore reduces, which becomes apparent with the increasingly reflective area formed. Interestingly, even though the sphere makes no contact with the wall for
![]() $h_{r}=155$
cm, the cavity formed is still observed to be attached to it by means of small bubbles, which rip open from the wall under depressurization. These bubbles are also noticed to form around the base of the cavity bubble for contact cases as shown for
$h_{r}=155$
cm, the cavity formed is still observed to be attached to it by means of small bubbles, which rip open from the wall under depressurization. These bubbles are also noticed to form around the base of the cavity bubble for contact cases as shown for
![]() $h_{r}=160$
cm.
$h_{r}=160$
cm.
After reaching its maximum radial extent (
![]() $t=1.97$
ms), the cavity starts to shrink radially inwards again due to the ongoing elongation as the sphere rebounds further away. The rebound kinetic energy is enough to overcome viscous forces, allowing the sphere to escape the fluid film. When the peeling cavity–sphere interface rises to the height at which it is about to break open into the atmosphere (
$t=1.97$
ms), the cavity starts to shrink radially inwards again due to the ongoing elongation as the sphere rebounds further away. The rebound kinetic energy is enough to overcome viscous forces, allowing the sphere to escape the fluid film. When the peeling cavity–sphere interface rises to the height at which it is about to break open into the atmosphere (
![]() $t=2.63$
ms) in the process, the cavity reaches its maximum elongation (marked by symbol
$t=2.63$
ms) in the process, the cavity reaches its maximum elongation (marked by symbol
![]() $\unicode[STIX]{x2460}$
). As soon as the seal breaks (
$\unicode[STIX]{x2460}$
). As soon as the seal breaks (
![]() $t=2.82$
ms) allowing air to enter inside, the partially detached cavity shrinks further radially inwards and starts to contract back towards the wall (marked by symbol
$t=2.82$
ms) allowing air to enter inside, the partially detached cavity shrinks further radially inwards and starts to contract back towards the wall (marked by symbol
![]() $\unicode[STIX]{x2461}$
). After the sphere has detached completely and escaped the liquid film, the longitudinal contraction of the cavity becomes rapid (
$\unicode[STIX]{x2461}$
). After the sphere has detached completely and escaped the liquid film, the longitudinal contraction of the cavity becomes rapid (
![]() $t=3.03$
ms). Since the process of peeling does not occur proportionately along the cavity–sphere interface, the grainy textured cavity wall formed is asymmetric, which detaches and retracts earlier from one side to give the structure a noticeable tilt (marked by symbol
$t=3.03$
ms). Since the process of peeling does not occur proportionately along the cavity–sphere interface, the grainy textured cavity wall formed is asymmetric, which detaches and retracts earlier from one side to give the structure a noticeable tilt (marked by symbol
![]() $\unicode[STIX]{x2462}$
). The cavity contracts to a minimum length (marked by symbol
$\unicode[STIX]{x2462}$
). The cavity contracts to a minimum length (marked by symbol
![]() $\unicode[STIX]{x2463}$
) at
$\unicode[STIX]{x2463}$
) at
![]() $t=3.21$
ms where a portion of its kinetic energy is stored as elastic energy in the film. The release of this energy enables the cavity to elongate again (
$t=3.21$
ms where a portion of its kinetic energy is stored as elastic energy in the film. The release of this energy enables the cavity to elongate again (
![]() $t=3.48$
ms, marked by symbol
$t=3.48$
ms, marked by symbol
![]() $\unicode[STIX]{x2464}$
), hence completing a cycle of vertical oscillation, which repeats with decreasing amplitudes until all the energy is dissipated internally by viscous forces. The ultra-viscous liquid flows back slowly into the cavitated space amidst these events thus collapsing the cavitation bubble. This becomes evident with the passage of further time, for example, at
$\unicode[STIX]{x2464}$
), hence completing a cycle of vertical oscillation, which repeats with decreasing amplitudes until all the energy is dissipated internally by viscous forces. The ultra-viscous liquid flows back slowly into the cavitated space amidst these events thus collapsing the cavitation bubble. This becomes evident with the passage of further time, for example, at
![]() $t=59.63$
ms (marked by symbol
$t=59.63$
ms (marked by symbol
![]() $\unicode[STIX]{x2465}$
).
$\unicode[STIX]{x2465}$
).
For the higher release height of
![]() $h_{r}=170$
cm, in which case the sphere impacts the wall, the radial extent of the cavity formed in the initial stages of depressurization (
$h_{r}=170$
cm, in which case the sphere impacts the wall, the radial extent of the cavity formed in the initial stages of depressurization (
![]() $t=30{-}91~{\rm\mu}\text{s}$
) is comparatively much larger (see figure 12). However, the effect of elongation during (
$t=30{-}91~{\rm\mu}\text{s}$
) is comparatively much larger (see figure 12). However, the effect of elongation during (
![]() $t=91{-}515~{\rm\mu}\text{s}$
) is so dominant that the cavity not only develops a smaller neck but also shrinks noticeably radially inwards. This causes the contact angle of the cavity–wall interface to increase significantly, which promotes the formation of an additional necking region near the wall as the cavity extends further (
$t=91{-}515~{\rm\mu}\text{s}$
) is so dominant that the cavity not only develops a smaller neck but also shrinks noticeably radially inwards. This causes the contact angle of the cavity–wall interface to increase significantly, which promotes the formation of an additional necking region near the wall as the cavity extends further (
![]() $t=848~{\rm\mu}\text{s}$
). The cavity then expands as the effect of depressurization becomes prominent, reaching its maximum radial extent at
$t=848~{\rm\mu}\text{s}$
). The cavity then expands as the effect of depressurization becomes prominent, reaching its maximum radial extent at
![]() $t=1.70$
ms, which is succeeded by the sequence of development stages marked
$t=1.70$
ms, which is succeeded by the sequence of development stages marked
![]() $\unicode[STIX]{x2460}$
–
$\unicode[STIX]{x2460}$
–
![]() $\unicode[STIX]{x2465}$
explained in the preceding passage.
$\unicode[STIX]{x2465}$
explained in the preceding passage.

Figure 14. Close-up images from the side and bottom of shear-induced cavitation and cavitation by depressurization (onsets marked by Ⓢ and Ⓓ, respectively) for an impact onto a
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil film from
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil film from
![]() $h_{r}=165$
cm.
$h_{r}=165$
cm.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() ${\it\delta}=5$
mm,
${\it\delta}=5$
mm,
![]() $V_{0}=5.68~\text{m}~\text{s}^{-1}$
,
$V_{0}=5.68~\text{m}~\text{s}^{-1}$
,
![]() $St_{0}=9.6\times 10^{-3}$
,
$St_{0}=9.6\times 10^{-3}$
,
![]() $De=395$
. Areas indicated by white and grey dashed lines are further magnified. An additional bottom-view sketches the areas of shear-induced cavitation (solid white line) and cavitation by depressurization (dashed black line) and the site of impact (black region).
$De=395$
. Areas indicated by white and grey dashed lines are further magnified. An additional bottom-view sketches the areas of shear-induced cavitation (solid white line) and cavitation by depressurization (dashed black line) and the site of impact (black region).

Figure 15. Summary of qualitative results in a three-dimensional (
![]() $St_{0}$
,
$St_{0}$
,
![]() $Ca$
,
$Ca$
,
![]() $De$
) plot, showing phase diagrams in the
$De$
) plot, showing phase diagrams in the
![]() $St{-}Ca$
and
$St{-}Ca$
and
![]() $St{-}De$
planes. Phases in the horizontal
$St{-}De$
planes. Phases in the horizontal
![]() $St{-}Ca$
plane are identified as: (i) annular cavitation structure with a distinct pattern of elongated bubbles around Hertzian contact area, (ii) dense annular cavitation structure with a ring of fine bubbles around contact region and (iii) formation of remnant bubbles from primary bubble fragmentation at film entry. The dashed line serves as a phase boundary between contact (blue) and non-contact cases (yellow) in the
$St{-}Ca$
plane are identified as: (i) annular cavitation structure with a distinct pattern of elongated bubbles around Hertzian contact area, (ii) dense annular cavitation structure with a ring of fine bubbles around contact region and (iii) formation of remnant bubbles from primary bubble fragmentation at film entry. The dashed line serves as a phase boundary between contact (blue) and non-contact cases (yellow) in the
![]() $St{-}De$
plane. The letters here correspond to cavity features: (a) dense foam-like circular structure surrounded by a pattern of discrete bubbles; (b) single large cavity bubble, which assumes an inverted conical structure in (c); (d) hourglass-shaped single large cavity bubble, characterized by a smooth texture in (e). The region in red indicates shear-induced cavitation.
$St{-}De$
plane. The letters here correspond to cavity features: (a) dense foam-like circular structure surrounded by a pattern of discrete bubbles; (b) single large cavity bubble, which assumes an inverted conical structure in (c); (d) hourglass-shaped single large cavity bubble, characterized by a smooth texture in (e). The region in red indicates shear-induced cavitation.
![]() ${\it\delta}=5$
mm and 37 mm for
${\it\delta}=5$
mm and 37 mm for
![]() ${\it\nu}_{0}\geqslant 10\,000$
cSt and
${\it\nu}_{0}\geqslant 10\,000$
cSt and
![]() ${\it\nu}_{0}\leqslant 1000$
cSt, respectively.
${\it\nu}_{0}\leqslant 1000$
cSt, respectively.
Investigating shear-induced cavitation structures in further detail, figure 14 shows close-up images taken from the side and bottom for the impact of a sphere from
![]() $h_{r}=165$
cm onto a 5 mm thick layer of
$h_{r}=165$
cm onto a 5 mm thick layer of
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil film. From the images shown, shear-induced cavitation is observed to originate from the sphere’s bottom tip (
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil film. From the images shown, shear-induced cavitation is observed to originate from the sphere’s bottom tip (
![]() $t=-91~{\rm\mu}\text{s}$
) upon reaching
$t=-91~{\rm\mu}\text{s}$
) upon reaching
![]() $h=102~{\rm\mu}\text{m}$
, while advancing towards the wall. As mentioned earlier, the cavity is observed to have a hazy interface from the side views, which makes it difficult to see in the images taken from underneath. Therefore, an additional close-up view taken from the bottom, outlining the region of impact, shear-induced cavitation and cavitation by depressurization (see caption for details), has also been provided. The bottom views reveal the cavity to have an irregular shape, which grows radially until the sphere makes contact with the wall (
$h=102~{\rm\mu}\text{m}$
, while advancing towards the wall. As mentioned earlier, the cavity is observed to have a hazy interface from the side views, which makes it difficult to see in the images taken from underneath. Therefore, an additional close-up view taken from the bottom, outlining the region of impact, shear-induced cavitation and cavitation by depressurization (see caption for details), has also been provided. The bottom views reveal the cavity to have an irregular shape, which grows radially until the sphere makes contact with the wall (
![]() $t_{0}=0~{\rm\mu}\text{s}$
). Cavitation by depressurization initiates as soon as the sphere reverses its direction of motion (
$t_{0}=0~{\rm\mu}\text{s}$
). Cavitation by depressurization initiates as soon as the sphere reverses its direction of motion (
![]() $t=30~{\rm\mu}\text{s}$
) to form a circular structure, which overlaps a large portion of the volume cavitated earlier by shear stress. The rebound also implies an absence of positive shear stress in the film, causing the shear-induced cavitation structure to shrink radially inwards. This resists the expansion of the cavity structure forming by depressurization to create an evident lag (
$t=30~{\rm\mu}\text{s}$
) to form a circular structure, which overlaps a large portion of the volume cavitated earlier by shear stress. The rebound also implies an absence of positive shear stress in the film, causing the shear-induced cavitation structure to shrink radially inwards. This resists the expansion of the cavity structure forming by depressurization to create an evident lag (
![]() $t=30{-}61~{\rm\mu}\text{s}$
) at the interface where the two cavities meet. No further resistance upon the complete collapse of the shear-induced cavity at
$t=30{-}61~{\rm\mu}\text{s}$
) at the interface where the two cavities meet. No further resistance upon the complete collapse of the shear-induced cavity at
![]() $t=91~{\rm\mu}\text{s}$
allows the lag to be overcome and the structure to become perfectly circular. We also note the cavity walls in the corresponding side views to become relatively well defined at this point. As the sphere rebounds further away, the effect of elongation becomes prominent (
$t=91~{\rm\mu}\text{s}$
allows the lag to be overcome and the structure to become perfectly circular. We also note the cavity walls in the corresponding side views to become relatively well defined at this point. As the sphere rebounds further away, the effect of elongation becomes prominent (
![]() $t=151~{\rm\mu}\text{s}$
), causing the cavity to shrink radially inwards and onset the formation of a necking region.
$t=151~{\rm\mu}\text{s}$
), causing the cavity to shrink radially inwards and onset the formation of a necking region.
We summarize our qualitative results in figure 15 by producing a three-dimensional space (
![]() $St_{0}$
,
$St_{0}$
,
![]() $Ca$
,
$Ca$
,
![]() $De$
) plot and categorizing the principal observations into
$De$
) plot and categorizing the principal observations into
![]() $St{-}Ca$
and
$St{-}Ca$
and
![]() $St{-}De$
phase diagrams on the horizontal and vertical planes, respectively. Phases in the
$St{-}De$
phase diagrams on the horizontal and vertical planes, respectively. Phases in the
![]() $St{-}Ca$
plane are marked (i)–(iii) and distinct features in the
$St{-}Ca$
plane are marked (i)–(iii) and distinct features in the
![]() $St{-}De$
plane are lettered a–e, (see caption for details).
$St{-}De$
plane are lettered a–e, (see caption for details).

Figure 16. (a–d) Cavity diameter
![]() $D_{cavity}$
versus time
$D_{cavity}$
versus time
![]() $t$
from impact onto the glass wall (
$t$
from impact onto the glass wall (
![]() $t_{0}=0~{\rm\mu}\text{s}$
for contact cases) or from reaching the minimum separation distance (
$t_{0}=0~{\rm\mu}\text{s}$
for contact cases) or from reaching the minimum separation distance (
![]() $t_{m}=0~{\rm\mu}\text{s}$
for non-contact cases) in different silicone oil viscosities and increasing impact velocities
$t_{m}=0~{\rm\mu}\text{s}$
for non-contact cases) in different silicone oil viscosities and increasing impact velocities
![]() $V_{0}$
(see legend). (e) Time to cavity initiation
$V_{0}$
(see legend). (e) Time to cavity initiation
![]() $t_{c}$
and (f) maximum cavity diameter
$t_{c}$
and (f) maximum cavity diameter
![]() $D_{max}$
versus impact velocity onto liquid films, corresponding to plots in (a–d). (a)
$D_{max}$
versus impact velocity onto liquid films, corresponding to plots in (a–d). (a)
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() ${\it\delta}=5$
mm,
${\it\delta}=5$
mm,
![]() ${\it\nu}_{0}=10\,000$
cSt (
${\it\nu}_{0}=10\,000$
cSt (
![]() $St_{0}=4.65{-}7.43$
,
$St_{0}=4.65{-}7.43$
,
![]() $De=0.11{-}0.17$
), (b)
$De=0.11{-}0.17$
), (b)
![]() ${\it\nu}_{0}=100\,000$
cSt (
${\it\nu}_{0}=100\,000$
cSt (
![]() $St_{0}=0.66{-}1.25$
,
$St_{0}=0.66{-}1.25$
,
![]() $De=1.12{-}2.11$
), (c)
$De=1.12{-}2.11$
), (c)
![]() ${\it\nu}_{0}=1000\,000$
cSt (
${\it\nu}_{0}=1000\,000$
cSt (
![]() $St_{0}=0.10{-}0.16$
,
$St_{0}=0.10{-}0.16$
,
![]() $De=24.5{-}36.3$
), (d)
$De=24.5{-}36.3$
), (d)
![]() ${\it\nu}_{0}=20\,000\,000$
cSt (
${\it\nu}_{0}=20\,000\,000$
cSt (
![]() $St_{0}=8.18\times 10^{-3}$
–
$St_{0}=8.18\times 10^{-3}$
–
![]() $9.75\times 10^{-3}$
,
$9.75\times 10^{-3}$
,
![]() $De=336{-}401$
). The fits in (b) plot
$De=336{-}401$
). The fits in (b) plot
![]() $V_{0}={\it\alpha}t_{c}+{\it\beta}$
(in SI units for
$V_{0}={\it\alpha}t_{c}+{\it\beta}$
(in SI units for
![]() $t_{c}\geqslant 0$
m), where
$t_{c}\geqslant 0$
m), where
![]() ${\it\alpha}=-5397,-2450,-1559$
and
${\it\alpha}=-5397,-2450,-1559$
and
![]() ${\it\beta}=3.42$
, 4.54, 5.75 for
${\it\beta}=3.42$
, 4.54, 5.75 for
![]() ${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.
${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.
3.2 Quantitative results
In figure 16(a–d) we plot data for the cavity diameter,
![]() $D_{cavity}$
as a function of time
$D_{cavity}$
as a function of time
![]() $t$
for impacts onto different viscosity silicone oil films with increasing impact velocities (see caption for details). Contrary to contact cases where the cavity is noted to form as soon as, or immediately after, the sphere touches the glass wall, a noticeable time period from when
$t$
for impacts onto different viscosity silicone oil films with increasing impact velocities (see caption for details). Contrary to contact cases where the cavity is noted to form as soon as, or immediately after, the sphere touches the glass wall, a noticeable time period from when
![]() $h_{m}$
is reached is required in non-contact cases for cavity initiation during rebound. Plotting the time period taken for cavity initiation
$h_{m}$
is reached is required in non-contact cases for cavity initiation during rebound. Plotting the time period taken for cavity initiation
![]() $t_{c}$
versus the impact speed
$t_{c}$
versus the impact speed
![]() $V_{0}$
for all trials in figure 16(a–d), we produce figure 16(e,f). Interestingly,
$V_{0}$
for all trials in figure 16(a–d), we produce figure 16(e,f). Interestingly,
![]() $t_{c}$
values are found to decrease linearly with increase in impact speed for all non-contact cases until reaching minimum values in the range of
$t_{c}$
values are found to decrease linearly with increase in impact speed for all non-contact cases until reaching minimum values in the range of
![]() $0{-}30~{\rm\mu}\text{s}$
, for cases where the sphere impacts the glass wall. Reasonable linear empirical fits to the data have been found using
$0{-}30~{\rm\mu}\text{s}$
, for cases where the sphere impacts the glass wall. Reasonable linear empirical fits to the data have been found using
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
as prefactors (see caption of figure 16
e,f).
${\it\beta}$
as prefactors (see caption of figure 16
e,f).
Following cavity initiation,
![]() $D_{cavity}$
values in figure 16(a–d) are generally noted to increase and reach a maximum value
$D_{cavity}$
values in figure 16(a–d) are generally noted to increase and reach a maximum value
![]() $D_{max}$
, followed by a gradual reduction with time due to the incoming fluid. An exception to this trend occurs for
$D_{max}$
, followed by a gradual reduction with time due to the incoming fluid. An exception to this trend occurs for
![]() $V_{0}=5.77~\text{m}~\text{s}^{-1}$
(
$V_{0}=5.77~\text{m}~\text{s}^{-1}$
(
![]() $h_{r}=170$
cm) in the 20 million cSt silicone oil film, where the cavity formed upon impact shrinks instantly and expands again (as explained in the preceding section). Figure 16(f) plots
$h_{r}=170$
cm) in the 20 million cSt silicone oil film, where the cavity formed upon impact shrinks instantly and expands again (as explained in the preceding section). Figure 16(f) plots
![]() $D_{max}$
versus
$D_{max}$
versus
![]() $V_{0}$
values for instances in figure 16(a–d) where the cavity diameter reaches a maximum value in the time frame of the videos recorded. Since
$V_{0}$
values for instances in figure 16(a–d) where the cavity diameter reaches a maximum value in the time frame of the videos recorded. Since
![]() $D_{max}$
values also depend noticeably on the degree of cavity attachment to the glass wall (e.g. as shown in figure 10), we classify each type for both sphere contact and non-contact cases into distinct categories (see legend). For contact cases the cavity either attaches only around the Hertzian contact area (e.g. figure 7
b) marked as partial cavity attachment or entirely at its base (e.g. figure 9
b) referring to a complete cavity attachment. The cavity does not attach to the wall in non-contact sphere cases with the exception of the impact at
$D_{max}$
values also depend noticeably on the degree of cavity attachment to the glass wall (e.g. as shown in figure 10), we classify each type for both sphere contact and non-contact cases into distinct categories (see legend). For contact cases the cavity either attaches only around the Hertzian contact area (e.g. figure 7
b) marked as partial cavity attachment or entirely at its base (e.g. figure 9
b) referring to a complete cavity attachment. The cavity does not attach to the wall in non-contact sphere cases with the exception of the impact at
![]() $V_{0}=5.51~\text{m}~\text{s}^{-1}$
in the 20 million cSt film (as shown in figure 13,
$V_{0}=5.51~\text{m}~\text{s}^{-1}$
in the 20 million cSt film (as shown in figure 13,
![]() $h_{r}=155$
cm).
$h_{r}=155$
cm).
The increasing viscosity of films up to 20 million cSt adds resistance to cavity expansion under depressurization in the form of fluid friction, requiring higher impact velocities to obtain a given
![]() $D_{max}$
value. While
$D_{max}$
value. While
![]() $D_{max}$
increases with
$D_{max}$
increases with
![]() $V_{0}$
for
$V_{0}$
for
![]() ${\it\nu}_{0}=10\,000$
cSt, the values become steady as soon as contact cases start occurring for
${\it\nu}_{0}=10\,000$
cSt, the values become steady as soon as contact cases start occurring for
![]() ${\it\nu}_{0}=100\,000$
cSt. When
${\it\nu}_{0}=100\,000$
cSt. When
![]() ${\it\nu}_{0}=1000\,000$
cSt, a decline in
${\it\nu}_{0}=1000\,000$
cSt, a decline in
![]() $D_{max}$
is noted for the contact case due to the added resistance to radial expansion offered by a complete cavity–wall attachment.
$D_{max}$
is noted for the contact case due to the added resistance to radial expansion offered by a complete cavity–wall attachment.

Figure 17. (a–d) Separation height
![]() $h$
plotted as a function of time
$h$
plotted as a function of time
![]() $t$
for realizations in figure 16(a–d).
$t$
for realizations in figure 16(a–d).
![]() $t=0~{\rm\mu}\text{s}$
is taken as a reference point corresponding to the moment of impact with the glass wall (for contact cases) or reaching the minimum separation distance (for non-contact cases). The inset provides a magnified view in one of the plots. (e) Minimum separation height
$t=0~{\rm\mu}\text{s}$
is taken as a reference point corresponding to the moment of impact with the glass wall (for contact cases) or reaching the minimum separation distance (for non-contact cases). The inset provides a magnified view in one of the plots. (e) Minimum separation height
![]() $h_{m}$
plotted against the impact velocity
$h_{m}$
plotted against the impact velocity
![]() $V_{0}$
from results in (a–d). Notice the linear decay in
$V_{0}$
from results in (a–d). Notice the linear decay in
![]() $h_{m}$
as
$h_{m}$
as
![]() $V_{0}$
increases for all non-contact cases. The fits plot
$V_{0}$
increases for all non-contact cases. The fits plot
![]() $V_{0}={\it\alpha}h_{m}+{\it\beta}$
(in SI units for
$V_{0}={\it\alpha}h_{m}+{\it\beta}$
(in SI units for
![]() $h_{m}\geqslant 0$
m) where
$h_{m}\geqslant 0$
m) where
![]() ${\it\alpha}=-1027,-1203,-1767$
and
${\it\alpha}=-1027,-1203,-1767$
and
![]() ${\it\beta}=2.83$
, 4.49, 5.66 for
${\it\beta}=2.83$
, 4.49, 5.66 for
![]() ${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.
${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.
Figure 17(a–d) shows plots of the separation height
![]() $h$
between the sphere’s bottom tip and the glass wall versus time
$h$
between the sphere’s bottom tip and the glass wall versus time
![]() $t$
(see caption for details) for realizations in figure 16(a–d). The sphere is noted to reach a minimum position (set at
$t$
(see caption for details) for realizations in figure 16(a–d). The sphere is noted to reach a minimum position (set at
![]() $t=0~{\rm\mu}\text{s}$
) in non-contact cases before rebounding away from the wall. This refers to the minimum separation height
$t=0~{\rm\mu}\text{s}$
) in non-contact cases before rebounding away from the wall. This refers to the minimum separation height
![]() $h_{m}$
, which has been plotted for increasing impact velocities and film viscosities in figure 17(e). The data shows
$h_{m}$
, which has been plotted for increasing impact velocities and film viscosities in figure 17(e). The data shows
![]() $h_{m}$
values to decrease linearly with increase in impact velocity until becoming zero for contact cases. Larger film viscosities require higher impact velocities to achieve a given
$h_{m}$
values to decrease linearly with increase in impact velocity until becoming zero for contact cases. Larger film viscosities require higher impact velocities to achieve a given
![]() $h_{m}$
value due to the increase in energy dissipation by internal fluid friction.
$h_{m}$
value due to the increase in energy dissipation by internal fluid friction.

Figure 18. The (a) normalized minimum separation distance
![]() $h_{m}/{\it\delta}$
and (b) normalized cavity initiation time
$h_{m}/{\it\delta}$
and (b) normalized cavity initiation time
![]() $t_{c}V_{0}/{\it\delta}$
plotted against the impact Stokes number
$t_{c}V_{0}/{\it\delta}$
plotted against the impact Stokes number
![]() $St_{0}=2{\it\rho}_{s}R_{0}V_{0}/9{\it\mu}_{0}$
corresponding to results in figures 16(e,f) and 17(e), respectively. The fits plot (a)
$St_{0}=2{\it\rho}_{s}R_{0}V_{0}/9{\it\mu}_{0}$
corresponding to results in figures 16(e,f) and 17(e), respectively. The fits plot (a)
![]() $h_{m}/{\it\delta}={\it\alpha}ln(St_{0})+{\it\beta}$
where
$h_{m}/{\it\delta}={\it\alpha}ln(St_{0})+{\it\beta}$
where
![]() ${\it\alpha}=-0.46,-0.62,-0.58$
and
${\it\alpha}=-0.46,-0.62,-0.58$
and
![]() ${\it\beta}=-1.60\times 10^{-2},-1.16,-2.70$
and (b)
${\it\beta}=-1.60\times 10^{-2},-1.16,-2.70$
and (b)
![]() $t_{c}V_{0}/{\it\delta}={\it\eta}ln(St_{0})+{\it\zeta}$
where
$t_{c}V_{0}/{\it\delta}={\it\eta}ln(St_{0})+{\it\zeta}$
where
![]() ${\it\eta}=-0.18,-0.91,-3.44$
and
${\it\eta}=-0.18,-0.91,-3.44$
and
![]() ${\it\zeta}=0.04,-1.65,-15.96$
for
${\it\zeta}=0.04,-1.65,-15.96$
for
![]() ${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.
${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.
Non-dimensionalizing the results in figures 16(e) and 17(e), figure 18 plots the (a) normalized minimum seperation distance
![]() $h_{m}/{\it\delta}$
and (b) normalized cavity initiation time
$h_{m}/{\it\delta}$
and (b) normalized cavity initiation time
![]() $t_{c}V_{0}/{\it\delta}$
against the impact Stokes number
$t_{c}V_{0}/{\it\delta}$
against the impact Stokes number
![]() $St_{0}=2{\it\rho}_{s}R_{0}V_{0}/9{\it\mu}_{0}$
, respectively. The results show
$St_{0}=2{\it\rho}_{s}R_{0}V_{0}/9{\it\mu}_{0}$
, respectively. The results show
![]() $h_{m}/{\it\delta}$
and
$h_{m}/{\it\delta}$
and
![]() $t_{c}V_{0}/{\it\delta}$
values to decrease as the impact Stokes number is increased for a given film viscosity. Also,
$t_{c}V_{0}/{\it\delta}$
values to decrease as the impact Stokes number is increased for a given film viscosity. Also,
![]() $St_{0}$
values at which the first contact case occurs decline as the viscosities are increased for a steady film thickness of
$St_{0}$
values at which the first contact case occurs decline as the viscosities are increased for a steady film thickness of
![]() ${\it\delta}=5$
mm. From the empirical fits to the data plotted (see caption for details), the critical impact Stokes number
${\it\delta}=5$
mm. From the empirical fits to the data plotted (see caption for details), the critical impact Stokes number
![]() $St_{0}^{c}$
for contact cases to begin occurring is calculated to be 0.97, 0.15 and
$St_{0}^{c}$
for contact cases to begin occurring is calculated to be 0.97, 0.15 and
![]() $9.5\times 10^{-3}$
for
$9.5\times 10^{-3}$
for
![]() ${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.
${\it\nu}_{0}=100\,000$
, 1 million and 20 million cSt, respectively.

Figure 19. Shear rate
![]() ${\it\gamma}_{rz}$
versus separation distance
${\it\gamma}_{rz}$
versus separation distance
![]() $h$
at the line of closest approach (a,c,e,g) and rebound (b,d,f,h) corresponding to plots in figure 17(a–d).
$h$
at the line of closest approach (a,c,e,g) and rebound (b,d,f,h) corresponding to plots in figure 17(a–d).
Performing a regression analysis of the data shown in figure 17(a–d) and differentiating the
![]() $h$
profiles with respect to
$h$
profiles with respect to
![]() $t$
, we calculate the sphere tip velocity
$t$
, we calculate the sphere tip velocity
![]() $V_{z}$
as a function of time. Using the lubrication length scale in accordance with Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009), the average radial velocity from the continuity equation can be expressed as
$V_{z}$
as a function of time. Using the lubrication length scale in accordance with Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009), the average radial velocity from the continuity equation can be expressed as
![]() $V_{r}\approx V_{z}\sqrt{R_{0}h}/h$
. We then obtain estimates of the apparent horizontal shear rate
$V_{r}\approx V_{z}\sqrt{R_{0}h}/h$
. We then obtain estimates of the apparent horizontal shear rate
![]() $\dot{{\it\gamma}}={\it\gamma}_{rz}=V_{r}/h\approx V_{z}\sqrt{R_{0}h}/h^{2}$
as the sphere approaches towards and rebounds away from the wall with time. Plots of
$\dot{{\it\gamma}}={\it\gamma}_{rz}=V_{r}/h\approx V_{z}\sqrt{R_{0}h}/h^{2}$
as the sphere approaches towards and rebounds away from the wall with time. Plots of
![]() ${\it\gamma}_{rz}$
versus
${\it\gamma}_{rz}$
versus
![]() $h$
in this manner are presented in figure 19 (see caption for details) for all realizations in figure 17(a–d).
$h$
in this manner are presented in figure 19 (see caption for details) for all realizations in figure 17(a–d).
Shear rates during the approach stage (figure 19
a,c,e,g) for contact cases are noted to increase with a decrease in
![]() $h$
, reaching maximum values in the range of
$h$
, reaching maximum values in the range of
![]() $6.5\times 10^{5}~\text{s}^{-1}\lesssim {\it\gamma}_{rz}\lesssim 2.7\times 10^{7}~\text{s}^{-1}$
for
$6.5\times 10^{5}~\text{s}^{-1}\lesssim {\it\gamma}_{rz}\lesssim 2.7\times 10^{7}~\text{s}^{-1}$
for
![]() $h\leqslant 35~{\rm\mu}\text{m}$
. In the non-contact cases,
$h\leqslant 35~{\rm\mu}\text{m}$
. In the non-contact cases,
![]() ${\it\gamma}_{rz}$
increases until suddenly coming to a decline as the sphere comes to a halt upon reaching
${\it\gamma}_{rz}$
increases until suddenly coming to a decline as the sphere comes to a halt upon reaching
![]() $h_{m}$
. Maximum values here were found to reach as high as
$h_{m}$
. Maximum values here were found to reach as high as
![]() $10^{5}~\text{s}^{-1}$
at close approach in some instances. In the rebound stage (figure 19
b,d,f,h), the direction of fluid flow reverses as indicated by the negative
$10^{5}~\text{s}^{-1}$
at close approach in some instances. In the rebound stage (figure 19
b,d,f,h), the direction of fluid flow reverses as indicated by the negative
![]() ${\it\gamma}_{rz}$
values. Shear rates in contact cases decline as the separation distance increases while in non-contact cases, an immediate increase to reach a maximum is noticed before the values start to decline as the sphere rebounds further away.
${\it\gamma}_{rz}$
values. Shear rates in contact cases decline as the separation distance increases while in non-contact cases, an immediate increase to reach a maximum is noticed before the values start to decline as the sphere rebounds further away.
3.3 Velocity field measured by particle image velocimetry analysis
Results for the apparent horizontal shear rate
![]() ${\it\gamma}_{rz}$
in the preceding section are based on average values of the radial velocity
${\it\gamma}_{rz}$
in the preceding section are based on average values of the radial velocity
![]() $V_{r}$
derived from
$V_{r}$
derived from
![]() $V_{z}$
. In order to obtain more reliable results directly from the velocity fields, we conducted further experiments employing particle image velocimetry (PIV) techniques.
$V_{z}$
. In order to obtain more reliable results directly from the velocity fields, we conducted further experiments employing particle image velocimetry (PIV) techniques.
For this purpose the ultra-viscous liquids were seeded with
![]() $10~{\rm\mu}\text{m}$
diameter hollow glass beads (Potters Industries Inc.) and mixed thoroughly to ensure a uniform composition was achieved before being left for a week to set into evenly levelled films. The use of high magnification (
$10~{\rm\mu}\text{m}$
diameter hollow glass beads (Potters Industries Inc.) and mixed thoroughly to ensure a uniform composition was achieved before being left for a week to set into evenly levelled films. The use of high magnification (
![]() $4\times$
) ensured a narrow depth-of-field, which coupled with the high capture rate (33 018 f.p.s.) rendered a pseudo-high-speed micro-PIV, where the plane of interest was directly in alignment with the focus of the bottom tip of the sphere. Consecutive images from the recorded videos were then analysed using using a sequential frame cross-correlation in MATLAB and DaVis 7.2 software (LaVision GmbH).
$4\times$
) ensured a narrow depth-of-field, which coupled with the high capture rate (33 018 f.p.s.) rendered a pseudo-high-speed micro-PIV, where the plane of interest was directly in alignment with the focus of the bottom tip of the sphere. Consecutive images from the recorded videos were then analysed using using a sequential frame cross-correlation in MATLAB and DaVis 7.2 software (LaVision GmbH).

Figure 20. Particle image velocimetry measurements for a non-contact impact from
![]() $h_{r}=65$
cm onto a
$h_{r}=65$
cm onto a
![]() ${\it\delta}=4$
mm thick layer of
${\it\delta}=4$
mm thick layer of
![]() ${\it\nu}_{0}=1000\,000$
cSt silicone oil.
${\it\nu}_{0}=1000\,000$
cSt silicone oil.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=3.56~\text{m}~\text{s}^{-1}$
,
$V_{0}=3.56~\text{m}~\text{s}^{-1}$
,
![]() $St_{0}=0.12$
,
$St_{0}=0.12$
,
![]() $De=27.9$
. The left half of the sphere displays the velocity vectors (see scale bar) while the right half maps the radial component of velocity
$De=27.9$
. The left half of the sphere displays the velocity vectors (see scale bar) while the right half maps the radial component of velocity
![]() $V_{r}$
(see colour bar). Plots of
$V_{r}$
(see colour bar). Plots of
![]() $V_{r}$
versus height
$V_{r}$
versus height
![]() $Z$
(mm) from the base wall at a radial distance of
$Z$
(mm) from the base wall at a radial distance of
![]() $r=3$
mm (vertical dashed line) have also been shown. The horizontal dashed line corresponds to
$r=3$
mm (vertical dashed line) have also been shown. The horizontal dashed line corresponds to
![]() $H(r,t)=h(t)+R_{0}-\sqrt{R_{0}^{2}-r^{2}}$
at
$H(r,t)=h(t)+R_{0}-\sqrt{R_{0}^{2}-r^{2}}$
at
![]() $r=3$
mm. See also supplementary movie 3.
$r=3$
mm. See also supplementary movie 3.
Figure 20 shows results for the PIV analysis of a tungsten carbide sphere (
![]() $R_{0}=20$
mm) impacting onto a 4 mm thick film of
$R_{0}=20$
mm) impacting onto a 4 mm thick film of
![]() ${\it\nu}_{0}=1000\,000$
cSt silicone oil when released from a height
${\it\nu}_{0}=1000\,000$
cSt silicone oil when released from a height
![]() $h_{r}=65$
cm. The presence of PIV particles in the film here provides additional points for the liquid to cavitate from during depressurization in comparison to films without beads used in figure 9. These appear as a few number of small bubbles that originate at the surface of the sphere and the base wall, in the vicinity of the significantly larger single cavity bubble (see also supplementary movie 3), and are noted to have a negligible effect on the surrounding flow field. The velocity fields where the vectors represent the absolute velocity,
$h_{r}=65$
cm. The presence of PIV particles in the film here provides additional points for the liquid to cavitate from during depressurization in comparison to films without beads used in figure 9. These appear as a few number of small bubbles that originate at the surface of the sphere and the base wall, in the vicinity of the significantly larger single cavity bubble (see also supplementary movie 3), and are noted to have a negligible effect on the surrounding flow field. The velocity fields where the vectors represent the absolute velocity,
![]() $|v|$
are superimposed on the left half of the raw images in order that the sphere, cavity and wall edges can be observed. Colour maps of the radial velocity component,
$|v|$
are superimposed on the left half of the raw images in order that the sphere, cavity and wall edges can be observed. Colour maps of the radial velocity component,
![]() $V_{r}$
are superimposed on the right half where positive values correspond to flow away from the sphere’s centre and negative values towards it. Plots of
$V_{r}$
are superimposed on the right half where positive values correspond to flow away from the sphere’s centre and negative values towards it. Plots of
![]() $V_{r}$
versus height
$V_{r}$
versus height
![]() $Z$
(mm) above the wall at
$Z$
(mm) above the wall at
![]() $r=3$
mm (see caption) have also been included to portray the changes incurred by the radial velocity component at a given a radial distance.
$r=3$
mm (see caption) have also been included to portray the changes incurred by the radial velocity component at a given a radial distance.
The velocity fields obtained in the squeeze flow regime during the approach stage are noted to be in agreement with Engmann, Servais & Burbidge (Reference Engmann, Servais and Burbidge2005) and Uddin et al. (Reference Uddin, Marston and Thoroddsen2012). At
![]() $t=-787~{\rm\mu}\text{s}$
for example, the radial velocity component is observed to be prominent in a central band, the vertical position of which increases with radial distance. An approximately parabolic profile for
$t=-787~{\rm\mu}\text{s}$
for example, the radial velocity component is observed to be prominent in a central band, the vertical position of which increases with radial distance. An approximately parabolic profile for
![]() $V_{r}$
at
$V_{r}$
at
![]() $r=3$
mm further implies
$r=3$
mm further implies
![]() $V_{r,max}$
to occur at
$V_{r,max}$
to occur at
![]() $z\sim h(r,t)/2$
, as also predicted by Uddin et al. (Reference Uddin, Marston and Thoroddsen2012). The band is noted to draw towards the axis of symmetry as the sphere approaches closer to the wall (
$z\sim h(r,t)/2$
, as also predicted by Uddin et al. (Reference Uddin, Marston and Thoroddsen2012). The band is noted to draw towards the axis of symmetry as the sphere approaches closer to the wall (
![]() $t=-212~{\rm\mu}\text{s}$
). Moments before the sphere comes to a halt (
$t=-212~{\rm\mu}\text{s}$
). Moments before the sphere comes to a halt (
![]() $t=-60~{\rm\mu}\text{s}$
) and reaches its minimum gap distance,
$t=-60~{\rm\mu}\text{s}$
) and reaches its minimum gap distance,
![]() $V_{r}$
diminishes rapidly as noticed by the almost vertical line, indicating a nearly zero radial flow
$V_{r}$
diminishes rapidly as noticed by the almost vertical line, indicating a nearly zero radial flow
![]() $V_{r}\approx 0$
across the gap. This flow direction reverses (
$V_{r}\approx 0$
across the gap. This flow direction reverses (
![]() $t=242~{\rm\mu}\text{s}$
) once the sphere starts to rebound, forming a completely inverted parabolic
$t=242~{\rm\mu}\text{s}$
) once the sphere starts to rebound, forming a completely inverted parabolic
![]() $V_{r}$
profile in the negative half. The expanding cavity bubble (
$V_{r}$
profile in the negative half. The expanding cavity bubble (
![]() $t=454~{\rm\mu}\text{s}$
), observed briefly after the onset of cavitation, opposes the radial influx of film liquid into the extending sphere–wall gap, as indicated by the velocity vectors near the cavity surface. The opposition weakens (see colour maps) as the rate of radial cavity expansion decreases with time (
$t=454~{\rm\mu}\text{s}$
), observed briefly after the onset of cavitation, opposes the radial influx of film liquid into the extending sphere–wall gap, as indicated by the velocity vectors near the cavity surface. The opposition weakens (see colour maps) as the rate of radial cavity expansion decreases with time (
![]() $t=454~{\rm\mu}\text{s}$
–1.64 ms) until eventually becoming zero when the cavity starts to shrink radially inwards (
$t=454~{\rm\mu}\text{s}$
–1.64 ms) until eventually becoming zero when the cavity starts to shrink radially inwards (
![]() $t=2.30$
ms). Further away from the cavity interface at
$t=2.30$
ms). Further away from the cavity interface at
![]() $r=3$
mm, the fluid inflow is noted to decrease incessantly (
$r=3$
mm, the fluid inflow is noted to decrease incessantly (
![]() $t=454~{\rm\mu}\text{s}$
–2.30 ms) as the sphere moves away from the wall.
$t=454~{\rm\mu}\text{s}$
–2.30 ms) as the sphere moves away from the wall.

Figure 21. (a,b) Shear rate
![]() ${\it\gamma}_{rz}$
versus separation distance
${\it\gamma}_{rz}$
versus separation distance
![]() $h$
, (c,d) apparent viscosity
$h$
, (c,d) apparent viscosity
![]() ${\it\mu}_{app}$
versus
${\it\mu}_{app}$
versus
![]() $h$
and (e,f) apparent Stokes number
$h$
and (e,f) apparent Stokes number
![]() $St_{app}=2{\it\rho}_{s}R_{0}V_{z}/9{\it\mu}_{app}$
versus normalized gap height
$St_{app}=2{\it\rho}_{s}R_{0}V_{z}/9{\it\mu}_{app}$
versus normalized gap height
![]() $h/{\it\delta}$
profiles obtained from direct measurements of the velocity fields at
$h/{\it\delta}$
profiles obtained from direct measurements of the velocity fields at
![]() $r=2$
and 3 mm (see legend), by the PIV analysis of the realization in figure 20 (
$r=2$
and 3 mm (see legend), by the PIV analysis of the realization in figure 20 (
![]() $V_{0}=3.56~\text{m}~\text{s}^{-1}$
,
$V_{0}=3.56~\text{m}~\text{s}^{-1}$
,
![]() ${\it\mu}_{0}=978$
Pa s,
${\it\mu}_{0}=978$
Pa s,
![]() $St_{0}=0.12$
,
$St_{0}=0.12$
,
![]() $De=27.9$
). Estimated shear rate values derived from
$De=27.9$
). Estimated shear rate values derived from
![]() $V_{z}$
using
$V_{z}$
using
![]() ${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/h^{2}$
(Ardekani et al.
Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) and the empirical scaling
${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/h^{2}$
(Ardekani et al.
Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) and the empirical scaling
![]() ${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/3h^{2}$
, have also been inscribed in (a) for comparison purposes. (a,c,e) and (b,d,f) correspond to the approach and rebound stages, respectively.
${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/3h^{2}$
, have also been inscribed in (a) for comparison purposes. (a,c,e) and (b,d,f) correspond to the approach and rebound stages, respectively.
Given the experimental configuration in this study, the horizontal shear is
![]() ${\it\gamma}_{rz}\equiv \partial V_{r}/\partial z$
. In accordance with Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) and Uddin et al. (Reference Uddin, Marston and Thoroddsen2012) this shear rate at a given radial distance can be calculated as
${\it\gamma}_{rz}\equiv \partial V_{r}/\partial z$
. In accordance with Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) and Uddin et al. (Reference Uddin, Marston and Thoroddsen2012) this shear rate at a given radial distance can be calculated as
![]() ${\it\gamma}_{rz}\approx V_{r,max}/H(r,t)$
where:
${\it\gamma}_{rz}\approx V_{r,max}/H(r,t)$
where:
is the separation gap distance across the curvature of the sphere in time.
From the PIV analysis of the realization in figure 20, figure 21(a,b) shows plots of
![]() ${\it\gamma}_{rz}$
at
${\it\gamma}_{rz}$
at
![]() $r=2$
and 3 mm versus the separation distance
$r=2$
and 3 mm versus the separation distance
![]() $h$
at sphere tip. Results derived from
$h$
at sphere tip. Results derived from
![]() $V_{z}$
values where
$V_{z}$
values where
![]() ${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/h^{2}$
(Ardekani et al.
Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) are also added for comparison purposes. While these derived shear rate values are found to be higher by approximately 0.5–1 orders of magnitude than those obtained directly from the velocity fields during both the approach and rebound stages, they capture the trend noted in the PIV results with reasonable accuracy. The shear profiles produced in a similar manner in figure 19, based on the scaling from Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009), can hence be deemed in accordance with actual values only at a qualitative level. Performing fits to the PIV results to form an empirical scaling, an acceptable agreement can be obtained for
${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/h^{2}$
(Ardekani et al.
Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) are also added for comparison purposes. While these derived shear rate values are found to be higher by approximately 0.5–1 orders of magnitude than those obtained directly from the velocity fields during both the approach and rebound stages, they capture the trend noted in the PIV results with reasonable accuracy. The shear profiles produced in a similar manner in figure 19, based on the scaling from Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009), can hence be deemed in accordance with actual values only at a qualitative level. Performing fits to the PIV results to form an empirical scaling, an acceptable agreement can be obtained for
![]() ${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/3h^{2}$
. From the PIV measurements of the non-contact case in figure 20, we note the shear rates in the approach stage to rise from
${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/3h^{2}$
. From the PIV measurements of the non-contact case in figure 20, we note the shear rates in the approach stage to rise from
![]() ${\it\gamma}_{rz}\sim 800~\text{s}^{-1}$
at
${\it\gamma}_{rz}\sim 800~\text{s}^{-1}$
at
![]() $h\approx 2.6$
mm to
$h\approx 2.6$
mm to
![]() ${\it\gamma}_{rz}\sim 3000~\text{s}^{-1}$
at
${\it\gamma}_{rz}\sim 3000~\text{s}^{-1}$
at
![]() $h\sim 0.60$
mm, before declining steeply as the sphere slows down to reach its minimum gap distance. For the reversed flow direction in the rebound stage, shear rate values increase rapidly to reach an average maximum of
$h\sim 0.60$
mm, before declining steeply as the sphere slows down to reach its minimum gap distance. For the reversed flow direction in the rebound stage, shear rate values increase rapidly to reach an average maximum of
![]() ${\it\gamma}_{rz}\sim -2500~\text{s}^{-1}$
at
${\it\gamma}_{rz}\sim -2500~\text{s}^{-1}$
at
![]() $h\sim 0.40$
mm, followed by a continuous decline to
$h\sim 0.40$
mm, followed by a continuous decline to
![]() ${\it\gamma}_{rz}\sim -80$
and
${\it\gamma}_{rz}\sim -80$
and
![]() $-125~\text{s}^{-1}$
at
$-125~\text{s}^{-1}$
at
![]() $r=2$
and 3 mm respectively, when the sphere reaches
$r=2$
and 3 mm respectively, when the sphere reaches
![]() $h\sim 2.1$
mm.
$h\sim 2.1$
mm.
Given the shear-thinning nature of the fluid used, these shear rates can correspond to apparent viscosities that are significantly different from the zero shear viscosity value,
![]() ${\it\mu}_{0}$
. This effect is depicted in figure 21(c,d) where the Carreau model and parameters from Table 1 are used to plot the apparent viscosity,
${\it\mu}_{0}$
. This effect is depicted in figure 21(c,d) where the Carreau model and parameters from Table 1 are used to plot the apparent viscosity,
![]() ${\it\mu}_{app}$
(from shear values at a given radial distance), at
${\it\mu}_{app}$
(from shear values at a given radial distance), at
![]() $r=1$
and 2 mm as a function of gap height
$r=1$
and 2 mm as a function of gap height
![]() $h$
. We note the local viscosity in the approach stage to decline at a similar rate at both radial positions to reach a minimum of
$h$
. We note the local viscosity in the approach stage to decline at a similar rate at both radial positions to reach a minimum of
![]() ${\it\mu}_{app}\sim 28$
Pa s (
${\it\mu}_{app}\sim 28$
Pa s (
![]() ${\it\gamma}_{rz}\sim 3000~\text{s}^{-1}$
at
${\it\gamma}_{rz}\sim 3000~\text{s}^{-1}$
at
![]() $h\sim 0.60$
mm,
$h\sim 0.60$
mm,
![]() ${\it\mu}_{app}/{\it\mu}_{0}\sim 0.03$
), followed by a steep increase as the shear rates decrease. A minimum of
${\it\mu}_{app}/{\it\mu}_{0}\sim 0.03$
), followed by a steep increase as the shear rates decrease. A minimum of
![]() ${\it\mu}_{app}\sim 32$
Pa s is noted, corresponding to the maximum shear rate in the rebound stage at
${\it\mu}_{app}\sim 32$
Pa s is noted, corresponding to the maximum shear rate in the rebound stage at
![]() $h\sim 0.40$
mm. With further increase in gap height, the local viscosity increases at a distinctly higher rate at
$h\sim 0.40$
mm. With further increase in gap height, the local viscosity increases at a distinctly higher rate at
![]() $r=2$
mm than 3 mm, reaching
$r=2$
mm than 3 mm, reaching
![]() ${\it\mu}_{app}\sim 300$
and 220 Pa s respectively, when
${\it\mu}_{app}\sim 300$
and 220 Pa s respectively, when
![]() $h\sim 2.1$
mm.
$h\sim 2.1$
mm.

Figure 22. PIV measurements for the contact case of a sphere dropped onto a 4 mm thick layer of
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil from
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil from
![]() $h_{r}=140$
cm.
$h_{r}=140$
cm.
![]() $R_{0}=10$
mm,
$R_{0}=10$
mm,
![]() $V_{0}=5.23~\text{m}~\text{s}^{-1}$
,
$V_{0}=5.23~\text{m}~\text{s}^{-1}$
,
![]() $St_{0}=8.84\times 10^{-3}$
,
$St_{0}=8.84\times 10^{-3}$
,
![]() $De=363$
. Similar to figure 19, the left and right half of the sphere display the velocity vectors (see scale bar) and colour maps of the radial velocity component
$De=363$
. Similar to figure 19, the left and right half of the sphere display the velocity vectors (see scale bar) and colour maps of the radial velocity component
![]() $V_{r}$
, respectively. Plots on the right side show the variation in
$V_{r}$
, respectively. Plots on the right side show the variation in
![]() $V_{r}$
versus distance
$V_{r}$
versus distance
![]() $Z$
(mm) from the base wall at
$Z$
(mm) from the base wall at
![]() $r=2$
mm (see vertical dashed line). The horizontal dashed line marks the distance to the sphere edge from the base wall at
$r=2$
mm (see vertical dashed line). The horizontal dashed line marks the distance to the sphere edge from the base wall at
![]() $r=2$
mm, using (3.1). See also supplementary movie 4.
$r=2$
mm, using (3.1). See also supplementary movie 4.

Figure 23. (a,b) Shear rate
![]() ${\it\gamma}_{rz}$
versus the separation distance
${\it\gamma}_{rz}$
versus the separation distance
![]() $h$
, (c,d)
$h$
, (c,d)
![]() ${\it\mu}_{app}$
versus
${\it\mu}_{app}$
versus
![]() $h$
and (e,f)
$h$
and (e,f)
![]() $St_{app}$
versus normalized gap height
$St_{app}$
versus normalized gap height
![]() $h/{\it\delta}$
obtained from the PIV measurements at
$h/{\it\delta}$
obtained from the PIV measurements at
![]() $r=1$
and 2 mm of the realization in figure 22 (
$r=1$
and 2 mm of the realization in figure 22 (
![]() $V_{0}=5.23~\text{m}~\text{s}^{-1}$
,
$V_{0}=5.23~\text{m}~\text{s}^{-1}$
,
![]() ${\it\mu}_{0}=19\,580$
Pa s,
${\it\mu}_{0}=19\,580$
Pa s,
![]() $St_{0}=8.84\times 10^{-3}$
,
$St_{0}=8.84\times 10^{-3}$
,
![]() $De=363$
). Shear rate results derived from
$De=363$
). Shear rate results derived from
![]() $V_{z}$
using the empirical scaling
$V_{z}$
using the empirical scaling
![]() ${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/3h^{2}$
and that provided by Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) have also been included in (a). The approach and rebound stages have been assigned the (a,c,e) and (b,d,f), respectively.
${\it\gamma}_{rz}\approx V_{z}\sqrt{R_{0}h}/3h^{2}$
and that provided by Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009) have also been included in (a). The approach and rebound stages have been assigned the (a,c,e) and (b,d,f), respectively.
Since the apparent viscosity varies substantially, a modified Stokes number,
![]() $St_{app}=2{\it\rho}_{s}R_{0}V_{z}/9{\it\mu}_{app}$
, based on
$St_{app}=2{\it\rho}_{s}R_{0}V_{z}/9{\it\mu}_{app}$
, based on
![]() ${\it\mu}_{app}$
is more pertinent to the flow configuration, as also suggested by Uddin et al. (Reference Uddin, Marston and Thoroddsen2012). From the plots of modified Stokes number versus normalized gap height produced accordingly in figure 21(e,f), we note
${\it\mu}_{app}$
is more pertinent to the flow configuration, as also suggested by Uddin et al. (Reference Uddin, Marston and Thoroddsen2012). From the plots of modified Stokes number versus normalized gap height produced accordingly in figure 21(e,f), we note
![]() $St_{app}$
(i.e. the instantaneous ratio of sphere inertia to viscous forces) to increase during approach, despite the decline in sphere velocity and reach a maximum of
$St_{app}$
(i.e. the instantaneous ratio of sphere inertia to viscous forces) to increase during approach, despite the decline in sphere velocity and reach a maximum of
![]() $St_{app}\sim 2.4$
. The effect of decreasing
$St_{app}\sim 2.4$
. The effect of decreasing
![]() $V_{z}$
, however, becomes prominent for
$V_{z}$
, however, becomes prominent for
![]() $h/{\it\delta}\lesssim 0.23$
and 0.38 at
$h/{\it\delta}\lesssim 0.23$
and 0.38 at
![]() $r=2$
and 3 mm, leading to the onset of
$r=2$
and 3 mm, leading to the onset of
![]() $St_{app}$
decline. A maximum of only
$St_{app}$
decline. A maximum of only
![]() $St_{app}\sim 0.7$
is noted in the rebound stage, which reduces to become almost negligible as the sphere slows down, while
$St_{app}\sim 0.7$
is noted in the rebound stage, which reduces to become almost negligible as the sphere slows down, while
![]() ${\it\mu}_{app}$
rises with further increase in gap distance.
${\it\mu}_{app}$
rises with further increase in gap distance.
In addition to the PIV analysis of the non-contact case in figure 20, figure 22 shows velocity vectors,
![]() $V_{r}$
colour maps and plots against length
$V_{r}$
colour maps and plots against length
![]() $Z$
(mm) at
$Z$
(mm) at
![]() $r=2$
mm for the contact case of a sphere impacting a
$r=2$
mm for the contact case of a sphere impacting a
![]() ${\it\delta}=4$
mm thick layer of
${\it\delta}=4$
mm thick layer of
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil from
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil from
![]() $h_{r}=140$
cm. The glass beads here do not have any discernible effect on the inception or structure of the cavity in comparison to observations made in non-seeded films. As expected, the radial velocity profiles are noted to be approximately parabolic, which invert due to flow reversal in the rebound stages (see arrows). The cavity bubble formed by depressurization following the onset of cavitation shrinks radially inwards and experiences necking (
$h_{r}=140$
cm. The glass beads here do not have any discernible effect on the inception or structure of the cavity in comparison to observations made in non-seeded films. As expected, the radial velocity profiles are noted to be approximately parabolic, which invert due to flow reversal in the rebound stages (see arrows). The cavity bubble formed by depressurization following the onset of cavitation shrinks radially inwards and experiences necking (
![]() $t=333$
, 515 and
$t=333$
, 515 and
![]() $666~{\rm\mu}\text{s}$
, see explanation in § 3.1), resulting in the influx of nearby fluid. Radial expansion begins to occur when the effect of depressurization becomes dominant, which is observed from the velocity vectors and the corresponding
$666~{\rm\mu}\text{s}$
, see explanation in § 3.1), resulting in the influx of nearby fluid. Radial expansion begins to occur when the effect of depressurization becomes dominant, which is observed from the velocity vectors and the corresponding
![]() $V_{r}$
colour map (
$V_{r}$
colour map (
![]() $t=969~{\rm\mu}\text{s}$
) to initiate in the cavity section beneath the necking region.
$t=969~{\rm\mu}\text{s}$
) to initiate in the cavity section beneath the necking region.
Similar in format to figure 21, figure 23 plots (a,b)
![]() ${\it\gamma}_{rz}$
versus
${\it\gamma}_{rz}$
versus
![]() $h$
, (c,d)
$h$
, (c,d)
![]() ${\it\mu}_{app}$
versus
${\it\mu}_{app}$
versus
![]() $h$
and (e,f)
$h$
and (e,f)
![]() $St_{app}$
versus
$St_{app}$
versus
![]() $h/{\it\delta}$
at
$h/{\it\delta}$
at
![]() $r=1$
and 2 mm, from the PIV analysis of the realization in figure 21. Shear values derived from
$r=1$
and 2 mm, from the PIV analysis of the realization in figure 21. Shear values derived from
![]() $V_{z}$
in (a), based on the approximation from Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009), are again only in qualitative agreement with those obtained by particle tracking measurements while being approximately
$V_{z}$
in (a), based on the approximation from Ardekani et al. (Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009), are again only in qualitative agreement with those obtained by particle tracking measurements while being approximately
![]() $O(0.5{-}1)$
higher in magnitude. Results from the empirical scaling (obtained in figure 21
a,b) are however in accordance with the PIV measurements, indicating
$O(0.5{-}1)$
higher in magnitude. Results from the empirical scaling (obtained in figure 21
a,b) are however in accordance with the PIV measurements, indicating
![]() $V_{r}\approx V_{z}\sqrt{R_{0}h}/3h$
to be the pertinent scaling for the average radial velocity in this study. The PIV measurements show shear values to increase incessantly in the approach stage to reach maximums of
$V_{r}\approx V_{z}\sqrt{R_{0}h}/3h$
to be the pertinent scaling for the average radial velocity in this study. The PIV measurements show shear values to increase incessantly in the approach stage to reach maximums of
![]() ${\it\gamma}_{rz}\sim 65\,000~\text{s}^{-1}$
and
${\it\gamma}_{rz}\sim 65\,000~\text{s}^{-1}$
and
![]() $30\,000~\text{s}^{-1}$
at
$30\,000~\text{s}^{-1}$
at
![]() $h\sim 0.05$
mm for
$h\sim 0.05$
mm for
![]() $r=1$
and 2 mm, corresponding to apparent viscosities of
$r=1$
and 2 mm, corresponding to apparent viscosities of
![]() ${\it\mu}_{app}\sim 8$
Pa s and 15 Pa s, respectively. Declining shear rates are noted throughout the rebound stage which translate to apparent viscosities increasing at a higher rate for the smaller radial distance of
${\it\mu}_{app}\sim 8$
Pa s and 15 Pa s, respectively. Declining shear rates are noted throughout the rebound stage which translate to apparent viscosities increasing at a higher rate for the smaller radial distance of
![]() $r=1$
mm, as also noticed in figure 21(c,d). Maximum values here are found to be
$r=1$
mm, as also noticed in figure 21(c,d). Maximum values here are found to be
![]() ${\it\mu}_{app}\sim 550$
Pa s and 250 Pa s at
${\it\mu}_{app}\sim 550$
Pa s and 250 Pa s at
![]() $h=2.16$
mm, for
$h=2.16$
mm, for
![]() $r=1$
and 2 mm.
$r=1$
and 2 mm.
In contrast to figure 21(e,f), the modified Stokes number for the contact case in figure 23(e,f) increases uninterruptedly during sphere approach at
![]() $r=1$
mm, to reach
$r=1$
mm, to reach
![]() $St_{app}\sim 5.8$
at
$St_{app}\sim 5.8$
at
![]() $h/{\it\delta}\sim 0.012$
. Values at
$h/{\it\delta}\sim 0.012$
. Values at
![]() $r=2$
mm meanwhile plateau at
$r=2$
mm meanwhile plateau at
![]() $St_{app}\sim 3.3$
, signifying a higher dominance of viscous effects further away for
$St_{app}\sim 3.3$
, signifying a higher dominance of viscous effects further away for
![]() $h/{\it\delta}\lesssim 0.1$
. A similar occurrence is observed in the rebound stage for
$h/{\it\delta}\lesssim 0.1$
. A similar occurrence is observed in the rebound stage for
![]() $h/{\it\delta}\lesssim 0.05$
, where maxima of
$h/{\it\delta}\lesssim 0.05$
, where maxima of
![]() $St_{app}\sim 2.5$
and 1.7 at
$St_{app}\sim 2.5$
and 1.7 at
![]() $r=1$
and 2 mm decline with increase in normalized gap height. Lower values of
$r=1$
and 2 mm decline with increase in normalized gap height. Lower values of
![]() $St_{app}$
for the rebound compared to approach stages in this and figure 21(e,f) are expected due to energy losses by viscous dissipation in the fluid film.
$St_{app}$
for the rebound compared to approach stages in this and figure 21(e,f) are expected due to energy losses by viscous dissipation in the fluid film.
4 Theoretical considerations
For small separation gap distances (
![]() $h\lesssim 100~{\rm\mu}\text{m}$
), the number of seeding particles available to the PIV interrogation window for tracking purposes are insufficient to produce reasonably accurate velocity field measurements. Since these gap heights correspond to the regime whereby cavitation is noted to occur during sphere approach (e.g. in figures 12 and 14 for
$h\lesssim 100~{\rm\mu}\text{m}$
), the number of seeding particles available to the PIV interrogation window for tracking purposes are insufficient to produce reasonably accurate velocity field measurements. Since these gap heights correspond to the regime whereby cavitation is noted to occur during sphere approach (e.g. in figures 12 and 14 for
![]() ${\it\nu}_{0}=20$
million cSt silicone oil films), it is important to analyse the squeeze flow for these parameters in further detail.
${\it\nu}_{0}=20$
million cSt silicone oil films), it is important to analyse the squeeze flow for these parameters in further detail.
For this purpose, we solve a theoretical model for the motion of sphere towards a solid wall covered with a thin layer of Carreau fluid (see figure 2
b), which has been shown (Uddin et al.
Reference Uddin, Marston and Thoroddsen2012) to be in good agreement with results from experiments similar in nature to those found here. We then examine if the criterion for cavitation, based on the concept of vapour pressure
![]() $p_{v}$
by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012), holds true inline with the shear-induced cavity observations made in this study. This is given as:
$p_{v}$
by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012), holds true inline with the shear-induced cavity observations made in this study. This is given as:
where
![]() $S_{11}$
is the largest component of shear stress (in the principal coordinate system) and
$S_{11}$
is the largest component of shear stress (in the principal coordinate system) and
![]() $P$
is the pressure.
$P$
is the pressure.
We formulate the equations in a cylindrical coordinate system describing an axially symmetric incompressible squeeze flow. To simulate the most favourable conditions for shear-induced cavitation and also for simplicity purposes, we assume the liquid to be devoid of any elastic effects. Under these circumstances and in conjunction with the lubrication approximation, where the inertial effects of the fluid can be neglected, the continuity and momentum equations can be expressed as:
where
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() $n$
are described earlier. When
$n$
are described earlier. When
![]() $\dot{{\it\gamma}}\equiv \partial u_{r}/\partial z\gg 1$
, i.e. for large shear rates which occur when the sphere approaches close to the base wall,
$\dot{{\it\gamma}}\equiv \partial u_{r}/\partial z\gg 1$
, i.e. for large shear rates which occur when the sphere approaches close to the base wall,
![]() ${\it\mu}_{app}$
can be represented by a power-law model (Lian et al.
Reference Lian, Xu, Huang and Adams2001) given as:
${\it\mu}_{app}$
can be represented by a power-law model (Lian et al.
Reference Lian, Xu, Huang and Adams2001) given as:
Using this, the momentum equation can be written as:
We then apply the no-slip boundary condition on the sphere surface and the base wall as:
where
![]() $H(r)=h+R_{0}-\sqrt{R_{0}^{2}-r^{2}}$
and
$H(r)=h+R_{0}-\sqrt{R_{0}^{2}-r^{2}}$
and
![]() $V$
is the velocity of approach of the sphere. The boundary conditions for pressure under the lubrication approximation are given by:
$V$
is the velocity of approach of the sphere. The boundary conditions for pressure under the lubrication approximation are given by:
Solving (4.2) and (4.8) together with the boundary conditions (4.9)–(4.12), the pressure distribution inside the squeeze film is given by:
and the radial velocity component is expressed by:

Figure 24. Contour plots of the (a) radial velocity
![]() $u_{r}$
, (b) absolute tangential shear stress
$u_{r}$
, (b) absolute tangential shear stress
![]() $|S_{11}|$
, (c) pressure
$|S_{11}|$
, (c) pressure
![]() $P$
and (d) the quantity
$P$
and (d) the quantity
![]() $P-|S_{11}|$
when the sphere from figure 14 reaches
$P-|S_{11}|$
when the sphere from figure 14 reaches
![]() $h=53~{\rm\mu}\text{m}$
while approaching the base wall at a velocity of
$h=53~{\rm\mu}\text{m}$
while approaching the base wall at a velocity of
![]() $V=1.62~\text{m}~\text{s}^{-1}$
. The insets provide a magnified view of the close approach region.
$V=1.62~\text{m}~\text{s}^{-1}$
. The insets provide a magnified view of the close approach region.
We then use the model for a case where cavitation is observed when a sphere is travelling through a fluid film towards a solid wall (i.e. the pressurization stage) e.g. in figure 14 at
![]() $t=-61~{\rm\mu}\text{s}$
when
$t=-61~{\rm\mu}\text{s}$
when
![]() $h=53~{\rm\mu}\text{m}$
. The corresponding distribution of the radial velocity
$h=53~{\rm\mu}\text{m}$
. The corresponding distribution of the radial velocity
![]() $u_{r}$
, absolute tangential shear stress
$u_{r}$
, absolute tangential shear stress
![]() $|S_{11}|$
, pressure
$|S_{11}|$
, pressure
![]() $P$
and the quantity
$P$
and the quantity
![]() $P-|S_{11}|$
is shown in figure 24(a–d), respectively.
$P-|S_{11}|$
is shown in figure 24(a–d), respectively.
From the results obtained,
![]() $P-|S_{11}|$
values are never noted to fall below the vapour pressure of
$P-|S_{11}|$
values are never noted to fall below the vapour pressure of
![]() $p_{v}=133$
Pa for a
$p_{v}=133$
Pa for a
![]() ${\it\nu}_{0}=20\,000\,000$
cSt silicone oil film, except in regions far from the sphere centre (
${\it\nu}_{0}=20\,000\,000$
cSt silicone oil film, except in regions far from the sphere centre (
![]() $r\geqslant 7.2$
mm i.e. near the edges), where the lubrication approximation is no longer valid. Also, since the model here does not account for the liquid’s elasticity, which acts to oppose the formation of shear-induced cavitation, it becomes more apparent that the criterion for cavitation framed in terms of the vapour pressure by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) does not concur with our experimental observations. Interestingly though, for this and all other cases where we observe cavitation to onset during the pressurization stage, the maximum tangential shear stress is noted to reach a threshold value of
$r\geqslant 7.2$
mm i.e. near the edges), where the lubrication approximation is no longer valid. Also, since the model here does not account for the liquid’s elasticity, which acts to oppose the formation of shear-induced cavitation, it becomes more apparent that the criterion for cavitation framed in terms of the vapour pressure by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) does not concur with our experimental observations. Interestingly though, for this and all other cases where we observe cavitation to onset during the pressurization stage, the maximum tangential shear stress is noted to reach a threshold value of
![]() $S_{11}\approx 1\times 10^{6}$
Pa. These findings raise questions as to how effectively pressurization opposes shear-induced cavitation and what criterion should be considered to model it.
$S_{11}\approx 1\times 10^{6}$
Pa. These findings raise questions as to how effectively pressurization opposes shear-induced cavitation and what criterion should be considered to model it.
The vast literature on cavitation, which recognizes liquids to open up only in tension, frames the cavitation threshold either in terms of the vapour pressure
![]() $p_{v}$
or the tensile strength
$p_{v}$
or the tensile strength
![]() ${\it\sigma}_{l}$
of the liquids. A few studies (e.g. Knapp, Daily & Hammit Reference Knapp, Daily and Hammit1970; Plesset Reference Plesset1969), which have compared the two concepts in this context, reason
${\it\sigma}_{l}$
of the liquids. A few studies (e.g. Knapp, Daily & Hammit Reference Knapp, Daily and Hammit1970; Plesset Reference Plesset1969), which have compared the two concepts in this context, reason
![]() ${\it\sigma}_{l}$
to be more pertinent in determining the break-up of liquids. Knapp et al. (Reference Knapp, Daily and Hammit1970) say that:
${\it\sigma}_{l}$
to be more pertinent in determining the break-up of liquids. Knapp et al. (Reference Knapp, Daily and Hammit1970) say that:
We define the vapour pressure as the equilibrium pressure, at a specified temperature, of the liquid’s vapour which is in contact with an existing free surface. If a cavity is to be created in a homogeneous liquid, the liquid must be ruptured, and the stress required to do this is not measured by the vapour pressure but is the tensile strength of the liquid at that temperature. The question naturally arises then as to the magnitudes of tensile strengths and the relation these have to experimental findings about inception.
Joseph (Reference Joseph1998) reported that the state of stress described by the principal stresses at each point in the moving liquid should be considered in determining the criteria for cavitation. The breaking threshold should be defined in terms of the tensile strength along the principal axes of stress, and the liquid would open up in the direction of maximum tension in principal coordinates. Also, since the stresses cannot be averaged in the case of a moving fluid, the pressure has no intrinsic significance. In the words of Joseph (Reference Joseph1998):
Cavitation criteria for liquids in motion must be based on the stress and not on the pressure. The liquid cannot average its stresses or recognize the non-unique quantity called pressure in non-Newtonian fluids.
Considering the stress
![]() $T$
in the flow conditions of our study, we have:
$T$
in the flow conditions of our study, we have:
 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}ccc@{}}T_{11} & T_{12} & 0\\ T_{21} & T_{22} & 0\\ 0 & 0 & T_{33}\end{array}\right] & = & \displaystyle \left[\begin{array}{@{}ccc@{}}-{\it\sigma}_{11}^{p}-{\it\sigma}_{11}^{e} & 0 & 0\\ 0 & -{\it\sigma}_{22}^{p}-{\it\sigma}_{22}^{e} & 0\\ 0 & 0 & -{\it\sigma}_{33}^{p}+{\it\sigma}_{33}^{e}\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\hat{{\it\mu}}\left[\begin{array}{@{}ccc@{}}0 & \left(\displaystyle \frac{\partial u_{r}}{\partial z}\right)^{n} & 0\\ \left(\displaystyle \frac{\partial u_{r}}{\partial z}\right)^{n} & 0 & 0\\ 0 & 0 & 0\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}ccc@{}}T_{11} & T_{12} & 0\\ T_{21} & T_{22} & 0\\ 0 & 0 & T_{33}\end{array}\right] & = & \displaystyle \left[\begin{array}{@{}ccc@{}}-{\it\sigma}_{11}^{p}-{\it\sigma}_{11}^{e} & 0 & 0\\ 0 & -{\it\sigma}_{22}^{p}-{\it\sigma}_{22}^{e} & 0\\ 0 & 0 & -{\it\sigma}_{33}^{p}+{\it\sigma}_{33}^{e}\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\hat{{\it\mu}}\left[\begin{array}{@{}ccc@{}}0 & \left(\displaystyle \frac{\partial u_{r}}{\partial z}\right)^{n} & 0\\ \left(\displaystyle \frac{\partial u_{r}}{\partial z}\right)^{n} & 0 & 0\\ 0 & 0 & 0\end{array}\right],\end{eqnarray}$$
where
![]() ${\it\sigma}_{11}^{p},{\it\sigma}_{22}^{p},{\it\sigma}_{33}^{p}$
and
${\it\sigma}_{11}^{p},{\it\sigma}_{22}^{p},{\it\sigma}_{33}^{p}$
and
![]() ${\it\sigma}_{11}^{e},{\it\sigma}_{22}^{e},{\it\sigma}_{33}^{e}$
are the orthogonal normal stresses resulting from pressure and the elastic strain developed inside the liquid, respectively. Since the separation gap distances for which shear-induced cavitation observations occur are very small (
${\it\sigma}_{11}^{e},{\it\sigma}_{22}^{e},{\it\sigma}_{33}^{e}$
are the orthogonal normal stresses resulting from pressure and the elastic strain developed inside the liquid, respectively. Since the separation gap distances for which shear-induced cavitation observations occur are very small (
![]() $h\lesssim 100~{\rm\mu}\text{m}$
), the orthogonal normal stresses resulting from pressure are significantly higher than those arising from the liquid’s elasticity. Under these circumstances, where the elastic stresses can be omitted, we diagonalize the system in principal coordinates to get:
$h\lesssim 100~{\rm\mu}\text{m}$
), the orthogonal normal stresses resulting from pressure are significantly higher than those arising from the liquid’s elasticity. Under these circumstances, where the elastic stresses can be omitted, we diagonalize the system in principal coordinates to get:
 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}ccc@{}}T_{11} & 0 & 0\\ 0 & T_{22} & 0\\ 0 & 0 & T_{33}\end{array}\right]=-\left[\begin{array}{@{}ccc@{}}{\it\sigma}_{11}^{p} & 0 & 0\\ 0 & {\it\sigma}_{22}^{p} & 0\\ 0 & 0 & {\it\sigma}_{33}^{p}\end{array}\right]+\hat{{\it\mu}}\left(\frac{\partial u_{r}}{\partial z}\right)^{n}\left[\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 0\end{array}\right] & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}ccc@{}}T_{11} & 0 & 0\\ 0 & T_{22} & 0\\ 0 & 0 & T_{33}\end{array}\right]=-\left[\begin{array}{@{}ccc@{}}{\it\sigma}_{11}^{p} & 0 & 0\\ 0 & {\it\sigma}_{22}^{p} & 0\\ 0 & 0 & {\it\sigma}_{33}^{p}\end{array}\right]+\hat{{\it\mu}}\left(\frac{\partial u_{r}}{\partial z}\right)^{n}\left[\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 0\end{array}\right] & & \displaystyle\end{eqnarray}$$
and since
applies in the case of a moving fluid (Joseph Reference Joseph1998), pressure is not the fundamental quantity to be compared with the tangential shear stress
![]() $S_{11}$
in (4.1). Instead the individual normal stress component
$S_{11}$
in (4.1). Instead the individual normal stress component
![]() ${\it\sigma}_{11}^{p}$
, which occurs as a consequence of pressure and directly opposes the effect of
${\it\sigma}_{11}^{p}$
, which occurs as a consequence of pressure and directly opposes the effect of
![]() $S_{11}$
(as per (4.16)), should be evaluated at each point in the moving liquid to determine if:
$S_{11}$
(as per (4.16)), should be evaluated at each point in the moving liquid to determine if:
holds true for the liquid to rip open in tension. Since the break-up in essence occurs from the liquid being subjected to a sufficiently large tension, the cavitation threshold here is expressed in terms of the liquid’s tensile strength (Knapp et al. Reference Knapp, Daily and Hammit1970).
Although formulating an expression for
![]() ${\it\sigma}_{11}^{p}$
is beyond the scope of this work, the fact that we find cavitation during sphere approach in our experiments to be dictated primarily by a threshold value of
${\it\sigma}_{11}^{p}$
is beyond the scope of this work, the fact that we find cavitation during sphere approach in our experiments to be dictated primarily by a threshold value of
![]() $S_{11}$
indicates
$S_{11}$
indicates
![]() ${\it\sigma}_{11}^{p}$
to be relatively insignificant. Considering (4.18), we predict this threshold (
${\it\sigma}_{11}^{p}$
to be relatively insignificant. Considering (4.18), we predict this threshold (
![]() $1\times 10^{6}$
Pa) to be approximately equal to the tensile strength of a
$1\times 10^{6}$
Pa) to be approximately equal to the tensile strength of a
![]() ${\it\nu}_{0}=20$
million cSt silicone oil. However, given the absence of any data in the archival literature on
${\it\nu}_{0}=20$
million cSt silicone oil. However, given the absence of any data in the archival literature on
![]() ${\it\sigma}_{l}$
for such a liquid, reaching a conclusion on this subject matter at this point is not possible. Further studies in the future investigating the breaking strength of ultra-viscous silicone oils are therefore recommended. It is also noteworthy to mention that, since the time scale of the impacts performed is short, the delay incurred by the microstructure of viscoelastic liquids in reacting to the flow and also in undergoing deformation, can become relatively important. The Carreau model not being effective instantaneously can hence introduce discrepancies between the actual and calculated shear-stress values. These postulated errors, however, may have been compensated to an extent by the higher shear rates from assuming the liquids as being inelastic in this study. The thixotropic properties of the ultra-viscous liquids used here are still important in this regard and can be a potential topic for investigation by future studies.
${\it\sigma}_{l}$
for such a liquid, reaching a conclusion on this subject matter at this point is not possible. Further studies in the future investigating the breaking strength of ultra-viscous silicone oils are therefore recommended. It is also noteworthy to mention that, since the time scale of the impacts performed is short, the delay incurred by the microstructure of viscoelastic liquids in reacting to the flow and also in undergoing deformation, can become relatively important. The Carreau model not being effective instantaneously can hence introduce discrepancies between the actual and calculated shear-stress values. These postulated errors, however, may have been compensated to an extent by the higher shear rates from assuming the liquids as being inelastic in this study. The thixotropic properties of the ultra-viscous liquids used here are still important in this regard and can be a potential topic for investigation by future studies.
5 Summary and conclusions
We have presented an experimental investigation of the onset of cavitation and its structures during the collision of a sphere with a solid surface covered with a layer of ultra-viscous non-Newtonian liquid (kinematic viscosities
![]() ${\it\nu}_{0}\leqslant 20\,000\,000$
cSt). A synchronized dual-view high-speed imaging system was used to make simultaneous observations from the side and bottom. It has been shown that both the primary bubble entrapped by the lubrication pressure of air and secondary bubbles from air entrainment by the dynamic wetting of the sphere with viscous liquids can play a significant role in the formation of cavitation structures. The secondary bubbles formed as the main (outer) contact line moves up around the sphere are noted to become smaller in size and larger in number as viscous forces become increasingly dominant relative to surface tension effects, in essence being characterized by the capillary number,
${\it\nu}_{0}\leqslant 20\,000\,000$
cSt). A synchronized dual-view high-speed imaging system was used to make simultaneous observations from the side and bottom. It has been shown that both the primary bubble entrapped by the lubrication pressure of air and secondary bubbles from air entrainment by the dynamic wetting of the sphere with viscous liquids can play a significant role in the formation of cavitation structures. The secondary bubbles formed as the main (outer) contact line moves up around the sphere are noted to become smaller in size and larger in number as viscous forces become increasingly dominant relative to surface tension effects, in essence being characterized by the capillary number,
![]() $Ca={\it\mu}_{0}V_{0}/{\it\sigma}$
.
$Ca={\it\mu}_{0}V_{0}/{\it\sigma}$
.
For impacts conducted on relatively low viscosity silicone oils (
![]() ${\it\nu}_{0}=100$
cSt, 1000 cSt,
${\it\nu}_{0}=100$
cSt, 1000 cSt,
![]() $St_{0}=O(10{-}10^{2})$
,
$St_{0}=O(10{-}10^{2})$
,
![]() $Ca=O(1{-}10)$
), the entrapped bubbles act as flow tracers as the sphere approaches towards the wall to create an annular bubble structure similar to the observations of Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) and Mansoor et al. (Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014). As soon as the sphere makes contact and starts to rebound away from the base wall, causing depressurization in the liquid film, the entrapped bubbles expand to form an annular cavitation structure while a distinct pattern of elongated cavity bubbles is also observed immediately around the region of sphere contact.
$Ca=O(1{-}10)$
), the entrapped bubbles act as flow tracers as the sphere approaches towards the wall to create an annular bubble structure similar to the observations of Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) and Mansoor et al. (Reference Mansoor, Uddin, Marston, Vakarelski and Thoroddsen2014). As soon as the sphere makes contact and starts to rebound away from the base wall, causing depressurization in the liquid film, the entrapped bubbles expand to form an annular cavitation structure while a distinct pattern of elongated cavity bubbles is also observed immediately around the region of sphere contact.
In the event of using a higher film viscosity of
![]() ${\it\nu}_{0}=10\,000$
cSt (
${\it\nu}_{0}=10\,000$
cSt (
![]() $St=O(1)$
,
$St=O(1)$
,
![]() $Ca=O(10^{2}{-}10^{3})$
), the primary bubble, which initially spreads into an air sheet as the sphere enters into the liquid film (Marston et al.
Reference Marston, Vakarelski and Thoroddsen2011a
), is deformed into a ring of several smaller bubbles as the flow approaches the squeeze flow configuration. Since the size of the air entrained bubbles reduces further causing the effect of surface tension to be more influential, the annular cavitation structure forms momentarily upon sphere contact and is noted to be very densely packed. The cavity pattern formed immediately around the contact region is observed to consist of an annulus of fine bubbles. Unlike impacts in less viscous liquids, the cavity bubbles and the film liquid peel off from the sphere’s surface to form a single larger cavity, which extends vertically to assume an hourglass shape as the sphere rebounds further away from the wall.
$Ca=O(10^{2}{-}10^{3})$
), the primary bubble, which initially spreads into an air sheet as the sphere enters into the liquid film (Marston et al.
Reference Marston, Vakarelski and Thoroddsen2011a
), is deformed into a ring of several smaller bubbles as the flow approaches the squeeze flow configuration. Since the size of the air entrained bubbles reduces further causing the effect of surface tension to be more influential, the annular cavitation structure forms momentarily upon sphere contact and is noted to be very densely packed. The cavity pattern formed immediately around the contact region is observed to consist of an annulus of fine bubbles. Unlike impacts in less viscous liquids, the cavity bubbles and the film liquid peel off from the sphere’s surface to form a single larger cavity, which extends vertically to assume an hourglass shape as the sphere rebounds further away from the wall.
For impacts onto
![]() ${\it\nu}_{0}\geqslant 100\,000$
cSt films (
${\it\nu}_{0}\geqslant 100\,000$
cSt films (
![]() $St\leqslant O(1)$
,
$St\leqslant O(1)$
,
![]() $Ca\geqslant O(10^{4})$
), the primary bubble entrapped at the sphere’s bottom tip is instantly squeezed out into the atmosphere. The intensity of the process fragments the bubble at the sphere–bubble interface, leaving behind a cluster of small remnant bubbles at the point of close approach.
$Ca\geqslant O(10^{4})$
), the primary bubble entrapped at the sphere’s bottom tip is instantly squeezed out into the atmosphere. The intensity of the process fragments the bubble at the sphere–bubble interface, leaving behind a cluster of small remnant bubbles at the point of close approach.
When
![]() $St_{0}<St_{0}^{c}$
(critical impact Stokes number for contact), films with high viscoelasticity characterized by
$St_{0}<St_{0}^{c}$
(critical impact Stokes number for contact), films with high viscoelasticity characterized by
![]() $De\geqslant O(1)$
, are found to enable sphere rebound without prior contact with the base wall, resulting in cavitation by depressurization for a new class of non-contact cases. The cavity here is noted to originate from the remnant bubbles during sphere rebound. While a dense foam-like circular structure extending into a pattern consisting of discrete bubbles, which generally increase in size away from the point of close approach, is observed in
$De\geqslant O(1)$
, are found to enable sphere rebound without prior contact with the base wall, resulting in cavitation by depressurization for a new class of non-contact cases. The cavity here is noted to originate from the remnant bubbles during sphere rebound. While a dense foam-like circular structure extending into a pattern consisting of discrete bubbles, which generally increase in size away from the point of close approach, is observed in
![]() ${\it\nu}_{0}=100\,000$
cSt films, the remnant bubbles expand and coalesce to form a single large cavity bubble in
${\it\nu}_{0}=100\,000$
cSt films, the remnant bubbles expand and coalesce to form a single large cavity bubble in
![]() ${\it\nu}_{0}\geqslant 1000\,000$
cSt films. Cavity initiation is observed to occur after a notable time delay
${\it\nu}_{0}\geqslant 1000\,000$
cSt films. Cavity initiation is observed to occur after a notable time delay
![]() $t_{c}$
from when the sphere reaches its minimum gap distance
$t_{c}$
from when the sphere reaches its minimum gap distance
![]() $h_{m}$
, both of which are noted to decrease linearly with increase in impact speed.
$h_{m}$
, both of which are noted to decrease linearly with increase in impact speed.
For contact cases (
![]() $St_{0}>St_{0}^{c}$
), the annular cavitation structure is no longer observed upon impact with the base wall. The cavitation bubbles formed by depressurization coalesce to produce a single large cavity, which extends into an hourglass shape with sphere rebound, and is characterized by an increasingly smooth texture up till impacts onto
$St_{0}>St_{0}^{c}$
), the annular cavitation structure is no longer observed upon impact with the base wall. The cavitation bubbles formed by depressurization coalesce to produce a single large cavity, which extends into an hourglass shape with sphere rebound, and is characterized by an increasingly smooth texture up till impacts onto
![]() ${\it\nu}_{0}=1000\,000$
cSt films. The maximum cavity diameter is noted to reduce as the collision changes from a non-contact to contact case in
${\it\nu}_{0}=1000\,000$
cSt films. The maximum cavity diameter is noted to reduce as the collision changes from a non-contact to contact case in
![]() ${\it\nu}_{0}=1000\,000$
cSt films. This results from the added resistance against radial expansion arising from a complete cavity attachment in contrast to a partial cavity attachment to the base wall in
${\it\nu}_{0}=1000\,000$
cSt films. This results from the added resistance against radial expansion arising from a complete cavity attachment in contrast to a partial cavity attachment to the base wall in
![]() ${\it\nu}_{0}=100\,000$
cSt films, whereby the cavities attach only around the Hertzian contact area.
${\it\nu}_{0}=100\,000$
cSt films, whereby the cavities attach only around the Hertzian contact area.
Remarkably different cavitation structures are noted to form in
![]() ${\it\nu}_{0}=20\,000\,000$
cSt films, where the cavities experience an ongoing competition between radial expansion and shrinkage, resulting from depressurization and localized elongation along the cavity length, respectively. Necking is therefore observed even in the initial stages of cavity formation during sphere rebound. As the cavities are stretched in the process, they peel off from the sphere’s surface to form a grainy wall texture. The remnant bubbles, which are initially squeezed radially outwards during sphere approach, are caught and carried up by these cavity walls, appearing as spots or short streaks from elongation.
${\it\nu}_{0}=20\,000\,000$
cSt films, where the cavities experience an ongoing competition between radial expansion and shrinkage, resulting from depressurization and localized elongation along the cavity length, respectively. Necking is therefore observed even in the initial stages of cavity formation during sphere rebound. As the cavities are stretched in the process, they peel off from the sphere’s surface to form a grainy wall texture. The remnant bubbles, which are initially squeezed radially outwards during sphere approach, are caught and carried up by these cavity walls, appearing as spots or short streaks from elongation.
Velocity field measurements inside the fluid film are obtained by performing pseudo-micro high-speed PIV. Horizontal shear rates calculated from these are noted to increase during sphere approach to values as high as
![]() ${\it\gamma}_{rz}=O(10^{3}~\text{s}^{-1})$
and
${\it\gamma}_{rz}=O(10^{3}~\text{s}^{-1})$
and
![]() $O(10^{4}~\text{s}^{-1})$
at
$O(10^{4}~\text{s}^{-1})$
at
![]() $r/R_{0}=0.2$
, for the non-contact (
$r/R_{0}=0.2$
, for the non-contact (
![]() $St_{0}=0.12$
,
$St_{0}=0.12$
,
![]() $De=27.9$
) and contact cases (
$De=27.9$
) and contact cases (
![]() $St_{0}=8.84\times 10^{-3}$
,
$St_{0}=8.84\times 10^{-3}$
,
![]() $De=363.5$
) analysed, respectively. These corresponded to significantly large viscosity reductions of
$De=363.5$
) analysed, respectively. These corresponded to significantly large viscosity reductions of
![]() ${\it\mu}_{app}/{\it\mu}_{0}=0.03$
and
${\it\mu}_{app}/{\it\mu}_{0}=0.03$
and
![]() $7.7\times 10^{-4}$
, suggesting the use of a modified Stokes number
$7.7\times 10^{-4}$
, suggesting the use of a modified Stokes number
![]() $St_{app}$
(being the instantaneous ratio of sphere inertia to viscous forces) to be a more relevant parameter for the shear-thinning flow. Although the sphere velocity
$St_{app}$
(being the instantaneous ratio of sphere inertia to viscous forces) to be a more relevant parameter for the shear-thinning flow. Although the sphere velocity
![]() $V_{z}$
declines as the sphere approaches the base wall,
$V_{z}$
declines as the sphere approaches the base wall,
![]() $St_{app}$
is noted to increase for
$St_{app}$
is noted to increase for
![]() $h/{\it\delta}\geqslant 0.23$
and 0.012 at
$h/{\it\delta}\geqslant 0.23$
and 0.012 at
![]() $r/R_{0}=0.2$
and 0.1, in the non-contact and contact case, respectively. Hence, despite the ultra-viscous nature of the liquids used, the inertial effects of the sphere remain dominant for a significant portion of the penetration into the film.
$r/R_{0}=0.2$
and 0.1, in the non-contact and contact case, respectively. Hence, despite the ultra-viscous nature of the liquids used, the inertial effects of the sphere remain dominant for a significant portion of the penetration into the film.
In contradiction to the conventional theory predicting cavitation to occur during depressurization, the inception of cavitation in
![]() ${\it\nu}_{0}=20\,000\,000$
cSt films (
${\it\nu}_{0}=20\,000\,000$
cSt films (
![]() $St=O(10^{-3})$
,
$St=O(10^{-3})$
,
![]() $De=O(10^{2})$
) is observed when the sphere reaches a sufficiently small separation distance (
$De=O(10^{2})$
) is observed when the sphere reaches a sufficiently small separation distance (
![]() $h\lesssim 100~{\rm\mu}\text{m}$
) while approaching towards the base wall (i.e. in the pressurization stage). The cavity formed is characterized by a hazy interface rather than a well-defined edge and of having an irregular shape, which grows radially until the sphere makes contact with the base wall.
$h\lesssim 100~{\rm\mu}\text{m}$
) while approaching towards the base wall (i.e. in the pressurization stage). The cavity formed is characterized by a hazy interface rather than a well-defined edge and of having an irregular shape, which grows radially until the sphere makes contact with the base wall.
This phenomenon described as shear-stress-induced cavitation (Joseph Reference Joseph1998) can result from the liquid breaking open in tension, in the direction defined by principal stresses. The cavitation criterion (equation (4.1)) attributed to this concept by Seddon et al. (Reference Seddon, Kok, Linnartz and Lohse2012) suggests the liquid break-up to occur when the largest element of the shear-stress tensor dominates over pressure to reduce it below the liquid vapour pressure. However, results from a theoretical model for the motion of a rigid sphere through a thin film of Carreau fluid towards a solid wall in our study do not agree with this requirement, in the parameter space for shear-induced cavity observations made in our experiments.
The disagreement is explained as follows: firstly, pressure itself is not recognized by a fluid in motion since the fluid cannot average its stresses (Joseph Reference Joseph1998). Only the normal stress component resulting from pressure, which directly opposes the maximum shear-stress component in principal coordinates, needs to be considered. Secondly, since rupturing the liquid essentially requires it being subjected to a sufficiently large tension, the breaking threshold should be considered in terms of the tensile strength
![]() ${\it\sigma}_{l}$
rather then the vapour pressure
${\it\sigma}_{l}$
rather then the vapour pressure
![]() $p_{v}$
of the liquid (Knapp et al.
Reference Knapp, Daily and Hammit1970).
$p_{v}$
of the liquid (Knapp et al.
Reference Knapp, Daily and Hammit1970).
Though a modified cavitation criterion (equation (4.18)) is proposed in consideration of these arguments, the archival literature lacks data on the tensile strength of ultra-viscous silicone oils needed for validation purposes. Investigations on the measurement of
![]() ${\it\sigma}_{l}$
for such liquids and on the evaluation of normal stress components, arising from pressure in squeeze films, can be prospective research topics for future studies in this context. Also, since the remnant bubbles formed on the sphere surface can act as weak points for the liquid to open up in shear during the approach stage, it would be interesting to study submerged spheres being forced towards the base wall, to investigate the possibility of shear-induced cavitation from the bulk liquid. Similar observations of shear-induced cavitation during pressurization may seem highly unlikely but are still plausible in the less viscous Newtonian liquids, if subjected to extremely high shear rates (e.g. a minimum of
${\it\sigma}_{l}$
for such liquids and on the evaluation of normal stress components, arising from pressure in squeeze films, can be prospective research topics for future studies in this context. Also, since the remnant bubbles formed on the sphere surface can act as weak points for the liquid to open up in shear during the approach stage, it would be interesting to study submerged spheres being forced towards the base wall, to investigate the possibility of shear-induced cavitation from the bulk liquid. Similar observations of shear-induced cavitation during pressurization may seem highly unlikely but are still plausible in the less viscous Newtonian liquids, if subjected to extremely high shear rates (e.g. a minimum of
![]() ${\it\gamma}_{rz}\approx 10^{7}~\text{s}^{-1}$
is required for the
${\it\gamma}_{rz}\approx 10^{7}~\text{s}^{-1}$
is required for the
![]() ${\it\nu}_{0}=100$
cSt silicone oil in figure 4 at
${\it\nu}_{0}=100$
cSt silicone oil in figure 4 at
![]() $h=26~{\rm\mu}\text{m}$
). Such experiments will similarly be far from realistic conditions but ought to be attempted in the future. Extensions of the theoretical flow model presented here to incorporate viscoelastic in addition to non-Newtonian effects of the ultra-viscous liquids is the subject of ongoing work.
$h=26~{\rm\mu}\text{m}$
). Such experiments will similarly be far from realistic conditions but ought to be attempted in the future. Extensions of the theoretical flow model presented here to incorporate viscoelastic in addition to non-Newtonian effects of the ultra-viscous liquids is the subject of ongoing work.
Acknowledgement
We gratefully acknowledge support from the KAUST Office of Competitive Research Funds.
Supplementary movies
Supplementary movies are available at http://dx.doi.org/10.1017/jfm.2016.229.