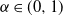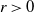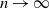1. Introduction
Kingman in [Reference Kingman18] suggested a way of constructing random distributions on the unit simplex by ranking the jumps of a subordinator up to a specified (possibly random) time, then normalising them by the value of the subordinator at that time. Taking the subordinator to be a driftless gamma subordinator generates his well known Poisson–Dirichlet distribution
![]() $\textrm{PD}(\theta)$
, which was later shown to be intimately connected with the famous Ewens sampling formula in genetics [Reference Ewens6]. Another of Kingman’s distributions, denoted by
$\textrm{PD}(\theta)$
, which was later shown to be intimately connected with the famous Ewens sampling formula in genetics [Reference Ewens6]. Another of Kingman’s distributions, denoted by
![]() $\textrm{PD}_\alpha$
, arises when a driftless
$\textrm{PD}_\alpha$
, arises when a driftless
![]() $\alpha$
-stable subordinator with parameter
$\alpha$
-stable subordinator with parameter
![]() $\alpha\in(0,1)$
is used instead of the gamma subordinator. These distributions and the methodologies associated with them have subsequently had an enormous impact in many areas of application, ranging from the excursion theory of stochastic processes to the theory of random partitions, random graphs and networks, probabilistic number theory, machine learning, Bayesian statistics, and a variety of others.
$\alpha\in(0,1)$
is used instead of the gamma subordinator. These distributions and the methodologies associated with them have subsequently had an enormous impact in many areas of application, ranging from the excursion theory of stochastic processes to the theory of random partitions, random graphs and networks, probabilistic number theory, machine learning, Bayesian statistics, and a variety of others.
Ipsen and Maller [Reference Ipsen and Maller12] generalised Kingman’s
![]() $\textrm{PD}_\alpha$
class in another direction, namely, to the two-parameter
$\textrm{PD}_\alpha$
class in another direction, namely, to the two-parameter
![]() $\textrm{PD}_\alpha^{(r)}$
class, defined for
$\textrm{PD}_\alpha^{(r)}$
class, defined for
![]() $\alpha\in(0,1)$
, and
$\alpha\in(0,1)$
, and
![]() $r>0$
. Like
$r>0$
. Like
![]() $\textrm{PD}_\alpha$
, the class
$\textrm{PD}_\alpha$
, the class
![]() $\textrm{PD}_\alpha^{(r)}$
is based on an
$\textrm{PD}_\alpha^{(r)}$
is based on an
![]() $\alpha$
-stable subordinator, but the extra parameter r arises from a connection with the negative binomial point process introduced by Gregoire [Reference Gregoire9] (whereas
$\alpha$
-stable subordinator, but the extra parameter r arises from a connection with the negative binomial point process introduced by Gregoire [Reference Gregoire9] (whereas
![]() $\textrm{PD}_\alpha$
is associated with a Poisson point process). Ipsen, Maller and Shemehsavar [Reference Ipsen, Maller and Shemehsavar14] developed connections between various Poisson–Dirichlet models by letting
$\textrm{PD}_\alpha$
is associated with a Poisson point process). Ipsen, Maller and Shemehsavar [Reference Ipsen, Maller and Shemehsavar14] developed connections between various Poisson–Dirichlet models by letting
![]() $r\to\infty$
and
$r\to\infty$
and
![]() $\alpha\downarrow 0$
in
$\alpha\downarrow 0$
in
![]() $\textrm{PD}_\alpha^{(r)}$
, while Ipsen, Shemehsavar and Maller [Reference Ipsen, Shemehsavar and Maller16] fitted
$\textrm{PD}_\alpha^{(r)}$
, while Ipsen, Shemehsavar and Maller [Reference Ipsen, Shemehsavar and Maller16] fitted
![]() $\textrm{PD}_\alpha^{(r)}$
to gene and species sampling data, demonstrating the utility of allowing the extra parameter r in a data analysis.
$\textrm{PD}_\alpha^{(r)}$
to gene and species sampling data, demonstrating the utility of allowing the extra parameter r in a data analysis.
An aspect of particular interest in practice is the distribution of
![]() $K_n(\alpha,r)$
, the number of distinct species observed in a sample of size n from the
$K_n(\alpha,r)$
, the number of distinct species observed in a sample of size n from the
![]() $\textrm{PD}_\alpha^{(r)}$
distribution. Herein we derive the asymptotic distribution (as
$\textrm{PD}_\alpha^{(r)}$
distribution. Herein we derive the asymptotic distribution (as
![]() $n\to\infty$
) of
$n\to\infty$
) of
![]() $K_n(\alpha,r)$
for fixed
$K_n(\alpha,r)$
for fixed
![]() $\alpha$
and r, and discuss how it depends on the parameters
$\alpha$
and r, and discuss how it depends on the parameters
![]() $\alpha$
and r.
$\alpha$
and r.
The relevance of the Dickman function [Reference Dickman5] and the corresponding distribution to the theory of the Poisson–Dirichlet distribution has been observed before (see, e.g., Arratia, Barbour and Tavaré [Reference Arratia, Barbour and Tavaré1] (pp. xi, 14, 76), Watterson [Reference Watterson28] (Equation (27) and the material above it), and Watterson and Guess [Reference Watterson and Guess29] (Equation (3.2.4)), but in our development a generalised version of it plays a particularly significant role. More details are in Section 5.
2. Asymptotic distribution of the number of species
In a sample of size n from
![]() $\textrm{PD}_\alpha^{(r)}$
, the blocks count vector is
$\textrm{PD}_\alpha^{(r)}$
, the blocks count vector is
where
![]() $M_j(\alpha,r)$
counts the number of allele types or species having j representatives in the sample. The number of distinct species observed in the sample is
$M_j(\alpha,r)$
counts the number of allele types or species having j representatives in the sample. The number of distinct species observed in the sample is
![]() $K_n(\alpha,r) \,{:}\,{\raise-1.5pt{=}}\, M_1(\alpha,r)+\cdots+M_n(\alpha,r)$
. In the Poisson–Dirichlet model
$K_n(\alpha,r) \,{:}\,{\raise-1.5pt{=}}\, M_1(\alpha,r)+\cdots+M_n(\alpha,r)$
. In the Poisson–Dirichlet model
![]() $\textrm{PD}(\theta)$
, the probability of any particular realisation of the blocks count vector is given by the Ewens sampling formula in [Reference Ewens6].
$\textrm{PD}(\theta)$
, the probability of any particular realisation of the blocks count vector is given by the Ewens sampling formula in [Reference Ewens6].
For the
![]() $\textrm{PD}_\alpha^{(r)}$
model, a formula is obtained in [Reference Ipsen, Maller and Shemehsavar14] for the distribution of the (n+1)-vector
$\textrm{PD}_\alpha^{(r)}$
model, a formula is obtained in [Reference Ipsen, Maller and Shemehsavar14] for the distribution of the (n+1)-vector
![]() $({\textbf M}_n(\alpha,r),K_n(\alpha,r))$
, where
$({\textbf M}_n(\alpha,r),K_n(\alpha,r))$
, where
![]() ${\textbf M}_n(\alpha,r)$
takes values among all n-vectors of nonnegative integers
${\textbf M}_n(\alpha,r)$
takes values among all n-vectors of nonnegative integers
![]() ${\textbf m}= (m_1,\ldots,m_n)$
satisfying
${\textbf m}= (m_1,\ldots,m_n)$
satisfying
![]() $$\sum\nolimits_{j = 1}^n {j{m_j}} = n$$
, while
$$\sum\nolimits_{j = 1}^n {j{m_j}} = n$$
, while
![]() $K_n(\alpha,r)$
takes values
$K_n(\alpha,r)$
takes values
![]() $k=\sum_{j=1}^{n} m_j\in\mathbb{N}_n \,{:} \,{\raise-1.5pt{=}}\, \{1,2,\ldots,n\}$
. Equation (5.11) of [Reference Ipsen, Maller and Shemehsavar14] gives the formula
$k=\sum_{j=1}^{n} m_j\in\mathbb{N}_n \,{:} \,{\raise-1.5pt{=}}\, \{1,2,\ldots,n\}$
. Equation (5.11) of [Reference Ipsen, Maller and Shemehsavar14] gives the formula
 \begin{equation}\mathbb{P}({\textbf M}_n(\alpha,r)={\textbf m},\qquad K_n(\alpha,r)=k)= n\int_{0}^{\infty}\frac{ r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}}\prod_{j=1}^n \frac{1}{m_j!} \big(F_j(\lambda)\big)^{m_j}\, \text{d} \lambda,\end{equation}
\begin{equation}\mathbb{P}({\textbf M}_n(\alpha,r)={\textbf m},\qquad K_n(\alpha,r)=k)= n\int_{0}^{\infty}\frac{ r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}}\prod_{j=1}^n \frac{1}{m_j!} \big(F_j(\lambda)\big)^{m_j}\, \text{d} \lambda,\end{equation}
where
![]() $r^{(k)}=r(r+1)\cdots (r+k-1)$
,
$r^{(k)}=r(r+1)\cdots (r+k-1)$
,
and
Both
![]() ${\textbf M}_n(\alpha,r)$
and
${\textbf M}_n(\alpha,r)$
and
![]() $K_n(\alpha,r)$
depend on the two parameters
$K_n(\alpha,r)$
depend on the two parameters
![]() $\alpha\in(0,1)$
and
$\alpha\in(0,1)$
and
![]() $r>0$
. These are kept fixed in the large-sample analysis (as
$r>0$
. These are kept fixed in the large-sample analysis (as
![]() $n\to\infty$
) which follows. Equation (2.1) can be compared with an analogous formula, Equation (4.14) on page 81 of [Reference Pitman23], which is based on a Poisson rather than negative binomial construction.
$n\to\infty$
) which follows. Equation (2.1) can be compared with an analogous formula, Equation (4.14) on page 81 of [Reference Pitman23], which is based on a Poisson rather than negative binomial construction.
Defining
 \begin{equation}A_{nk} \,{:}\,{\raise-1.5pt{=}}\, \Bigg\{{\textbf m}= (m_1,\ldots,m_n)\,:\, m_j\ge 0, \, \sum_{j=1}^njm_j=n,\, \sum_{j=1}^nm_j=k\Bigg\} \end{equation}
\begin{equation}A_{nk} \,{:}\,{\raise-1.5pt{=}}\, \Bigg\{{\textbf m}= (m_1,\ldots,m_n)\,:\, m_j\ge 0, \, \sum_{j=1}^njm_j=n,\, \sum_{j=1}^nm_j=k\Bigg\} \end{equation}
for
![]() $k\in \mathbb{N}_n$
,
$k\in \mathbb{N}_n$
,
![]() $n\in\mathbb{N}$
, and summing over the
$n\in\mathbb{N}$
, and summing over the
![]() $m_j$
, we can reduce (2.1) to the following formula for the distribution of
$m_j$
, we can reduce (2.1) to the following formula for the distribution of
![]() $K_n(\alpha,r)$
in a sample of size n from
$K_n(\alpha,r)$
in a sample of size n from
![]() $\textrm{PD}_\alpha^{(r)}$
:
$\textrm{PD}_\alpha^{(r)}$
:
 \begin{align}&\mathbb{P}(K_n(\alpha,r)=k)=n\int_{0}^{\infty}\frac{ r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}}\sum_{{\textbf m}\in A_{nk}}\prod_{j=1}^n \frac{1}{m_j!} \big(F_j(\lambda)\big)^{m_j}\, \text{d} \lambda,\qquad k\in\mathbb{N}_n.\end{align}
\begin{align}&\mathbb{P}(K_n(\alpha,r)=k)=n\int_{0}^{\infty}\frac{ r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}}\sum_{{\textbf m}\in A_{nk}}\prod_{j=1}^n \frac{1}{m_j!} \big(F_j(\lambda)\big)^{m_j}\, \text{d} \lambda,\qquad k\in\mathbb{N}_n.\end{align}
Our aim herein is to derive the limiting large-sample distribution of
![]() $K_n(\alpha,r)$
in the
$K_n(\alpha,r)$
in the
![]() $\textrm{PD}_\alpha^{(r)}$
model, working from (2.5).
$\textrm{PD}_\alpha^{(r)}$
model, working from (2.5).
To state the result, we need to introduce for each
![]() $\lambda>0$
a subordinator
$\lambda>0$
a subordinator
![]() $${({Y_t}(\lambda ))_{t > 0}}$$
having Laplace transform
$${({Y_t}(\lambda ))_{t > 0}}$$
having Laplace transform
 \begin{equation}\mathbb{E} e^{-\tau Y_t(\lambda)} =\exp\Bigg(- t\int_0^1 \big( 1-e^{-\tau y}\big) \Pi_\lambda(\text{d} y)\Bigg), \qquad t>0,\ \tau>0,\end{equation}
\begin{equation}\mathbb{E} e^{-\tau Y_t(\lambda)} =\exp\Bigg(- t\int_0^1 \big( 1-e^{-\tau y}\big) \Pi_\lambda(\text{d} y)\Bigg), \qquad t>0,\ \tau>0,\end{equation}
with Lévy measure
Theorem 2.1. Each
![]() $Y_t(\lambda)$
,
$Y_t(\lambda)$
,
![]() $t>0$
,
$t>0$
,
![]() $\lambda>0$
, has a continuous bounded density which we denote by
$\lambda>0$
, has a continuous bounded density which we denote by
![]() $f_{Y_t(\lambda)}(y)$
,
$f_{Y_t(\lambda)}(y)$
,
![]() $y>0$
. The asymptotic distribution of
$y>0$
. The asymptotic distribution of
![]() $n^{-\alpha}K_n(\alpha,r)$
as
$n^{-\alpha}K_n(\alpha,r)$
as
![]() $n\to\infty$
can be written in terms of it as
$n\to\infty$
can be written in terms of it as
 \begin{align}\lim_{n\to\infty} \mathbb{P}\Bigg(0<\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg)= &\frac{1}{\Gamma(r)\Gamma^r(1-\alpha)} \nonumber\\
& \times \int_{x=0}^y \int_{\lambda>0}x^{r-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x(\lambda^{-\alpha}\vee 1)}{\Gamma(1-\alpha)}\right) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x,\qquad y>0.\end{align}
\begin{align}\lim_{n\to\infty} \mathbb{P}\Bigg(0<\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg)= &\frac{1}{\Gamma(r)\Gamma^r(1-\alpha)} \nonumber\\
& \times \int_{x=0}^y \int_{\lambda>0}x^{r-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x(\lambda^{-\alpha}\vee 1)}{\Gamma(1-\alpha)}\right) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x,\qquad y>0.\end{align}
Formula (2.8) looks rather forbidding, but as we will see in Section 6, it can be simplified and written in a form amenable to numerical computation.
The proof of Theorem 2.1 proceeds by a number of steps as set out next.
2.1. Outline of the proof of Theorem 2.1
Deriving (2.8) from (2.5) requires an extensive analysis whose basic ingredients are as follows:
-
The formula (2.5) appears far from transparent but in fact possesses a lot of structure. (It’s not even clear that (2.5) defines a proper probability mass function, i.e., sums to 1 over
 $k\in\mathbb{N}_n$
. That this is so is demonstrated in [Reference Ipsen, Maller and Shemehsavar14].) A first step is to notice a Poissonian component in (2.5) and observe that the term summed over
$k\in\mathbb{N}_n$
. That this is so is demonstrated in [Reference Ipsen, Maller and Shemehsavar14].) A first step is to notice a Poissonian component in (2.5) and observe that the term summed over
 ${\textbf m}\in A_{nk}$
can be interpreted as giving rise to a joint Poisson probability (see (3.1) below). Conditioning on one of the Poisson components then produces a multinomial probability ((3.2) below) and a marginal Poisson probability.
${\textbf m}\in A_{nk}$
can be interpreted as giving rise to a joint Poisson probability (see (3.1) below). Conditioning on one of the Poisson components then produces a multinomial probability ((3.2) below) and a marginal Poisson probability. -
• The unpromising-looking first factor under the integral sign in (2.5) combines with the marginal Poisson to produce a negative binomial probability, modulo a correction factor ((3.7) below).
-
• A useful trick, used also in [Reference Watterson27], is to write the multinomial probability as a probability involving a sum of independent and identically distributed (i.i.d.) random variables
 $${({X_{in}}(\lambda ))_{i \ge 1}}$$
((3.9) below), resulting in the representation (3.26) for the distribution of
$${({X_{in}}(\lambda ))_{i \ge 1}}$$
((3.9) below), resulting in the representation (3.26) for the distribution of
 $K_n(\alpha,r)$
as a product of this probability, the negative binomial probability, and the correction factor, all functions of
$K_n(\alpha,r)$
as a product of this probability, the negative binomial probability, and the correction factor, all functions of
 $\lambda>0$
, and integrated over
$\lambda>0$
, and integrated over
 $\lambda>0$
.
$\lambda>0$
. -
• The next step is to rescale
 $K_n(\alpha,r)$
and find the limits of the probabilities under the integral sign in (3.26). None of the representations from (2.5)–(3.26) give much clue as to an appropriate scaling for
$K_n(\alpha,r)$
and find the limits of the probabilities under the integral sign in (3.26). None of the representations from (2.5)–(3.26) give much clue as to an appropriate scaling for
 $K_n(\alpha,r)$
, but we recall that for the corresponding quantity (the number of species observed) in Kingman’s
$K_n(\alpha,r)$
, but we recall that for the corresponding quantity (the number of species observed) in Kingman’s
 $\textrm{PD}_\alpha$
model, the correct scaling is by
$\textrm{PD}_\alpha$
model, the correct scaling is by
 $n^\alpha$
, and this results in a limiting Mittag-Leffler distribution for that quantity; see [Reference Pitman23, Theorem 3.8, p. 68]. So we are tempted to try this scaling for
$n^\alpha$
, and this results in a limiting Mittag-Leffler distribution for that quantity; see [Reference Pitman23, Theorem 3.8, p. 68]. So we are tempted to try this scaling for
 $K_n(\alpha,r)$
here. Less obvious however is that to make this work, it’s necessary to change variable from
$K_n(\alpha,r)$
here. Less obvious however is that to make this work, it’s necessary to change variable from
 $\lambda$
to
$\lambda$
to
 $\lambda n$
in the integral in (3.26), thereby giving the integral in (3.27).
$\lambda n$
in the integral in (3.26), thereby giving the integral in (3.27). -
• Following these manipulations, we need to find the limits as
 $n\to\infty$
of the functions in the integrand in (3.27). This is done in Proposition 3.2. The limit of the correction factor is easily obtained in the form of an exponential, and the negative binomial probability can be handled using Stirling’s formula (the limit in fact is a gamma distribution). For the probability involving the i.i.d. random variables
$n\to\infty$
of the functions in the integrand in (3.27). This is done in Proposition 3.2. The limit of the correction factor is easily obtained in the form of an exponential, and the negative binomial probability can be handled using Stirling’s formula (the limit in fact is a gamma distribution). For the probability involving the i.i.d. random variables
 $(X_{in}(\lambda))$
we apply a classical limit theorem for sums of a triangular array (the distribution of the
$(X_{in}(\lambda))$
we apply a classical limit theorem for sums of a triangular array (the distribution of the
 $X_{in}$
depends on n) and then require a local version of this for i.i.d. discrete lattice random variables, which we derive directly.
$X_{in}$
depends on n) and then require a local version of this for i.i.d. discrete lattice random variables, which we derive directly. -
• Having found the limits of the functions in the integrand in (3.27), we formally take the limit as
 $n\to\infty$
under the integral sign, obtaining the right-hand side of (2.8). But rather than try to justify this interchange of limit and integral, the approach we adopt is to show that the limiting function is in fact a probability density function, i.e., integrates to 1. This suffices to give convergence in distribution in (2.8). Our route to showing it goes by way of developing a kind of generalised Dickman distribution which is of interest in itself. This is done in Section 5 and is used to complete the proof of Theorem 2.1.
$n\to\infty$
under the integral sign, obtaining the right-hand side of (2.8). But rather than try to justify this interchange of limit and integral, the approach we adopt is to show that the limiting function is in fact a probability density function, i.e., integrates to 1. This suffices to give convergence in distribution in (2.8). Our route to showing it goes by way of developing a kind of generalised Dickman distribution which is of interest in itself. This is done in Section 5 and is used to complete the proof of Theorem 2.1. -
• Finally we derive expressions for the moments of the distribution in (2.8), and some computation-friendly formulae for it, and give some concluding comments, in Section 6. Some tables of moments and plots of distributions are in an appendix.
3. Ingredients for the proof of Theorem 2.1
To initiate the programme outlined in the previous section, write the right-hand side of (2.5) as
 \begin{align}n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}}\sum_{{\textbf m}\in A_{nk}} P\big(N_j(\lambda)=m_j,\, j\in\mathbb{N}_n\big) \exp\Bigg(\sum_{j=1}^nF_j(\lambda)\Bigg)\, \text{d} \lambda,\end{align}
\begin{align}n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}}\sum_{{\textbf m}\in A_{nk}} P\big(N_j(\lambda)=m_j,\, j\in\mathbb{N}_n\big) \exp\Bigg(\sum_{j=1}^nF_j(\lambda)\Bigg)\, \text{d} \lambda,\end{align}
where, for each
![]() $\lambda>0$
, the
$\lambda>0$
, the
![]() $N_j(\lambda)$
are independent Poisson(
$N_j(\lambda)$
are independent Poisson(
![]() $F_j(\lambda))$
random variables,
$F_j(\lambda))$
random variables,
![]() $j\in\mathbb{N}_n$
. In
$j\in\mathbb{N}_n$
. In
![]() $A_{nk}$
we add over integers
$A_{nk}$
we add over integers
![]() $m_j\ge 0$
such that
$m_j\ge 0$
such that
![]() $\sum_{j=1}^njm_j=n$
and
$\sum_{j=1}^njm_j=n$
and
![]() $\sum_{j=1}^nm_j=k$
. For brevity, write
$\sum_{j=1}^nm_j=k$
. For brevity, write
![]() $e_n(\lambda) \,{:}\,{\raise-1.5pt{=}}\, \exp\big(\!\sum_{j=1}^nF_j(\lambda)\big)$
. Then from (3.1) we have
$e_n(\lambda) \,{:}\,{\raise-1.5pt{=}}\, \exp\big(\!\sum_{j=1}^nF_j(\lambda)\big)$
. Then from (3.1) we have
 \begin{align}\mathbb{P}(K_n(\alpha,r)=k) & = n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\sum_{j=1}^njN_j(\lambda)=n,\, \sum_{j=1}^nN_j(\lambda)=k\Bigg) e_n(\lambda)\, \text{d} \lambda\nonumber \\
& =n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg)\mathbb{P}\Bigg(\sum_{j=1}^nN_j(\lambda)=k\Bigg) e_n(\lambda)\, \text{d} \lambda.\end{align}
\begin{align}\mathbb{P}(K_n(\alpha,r)=k) & = n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\sum_{j=1}^njN_j(\lambda)=n,\, \sum_{j=1}^nN_j(\lambda)=k\Bigg) e_n(\lambda)\, \text{d} \lambda\nonumber \\
& =n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg)\mathbb{P}\Bigg(\sum_{j=1}^nN_j(\lambda)=k\Bigg) e_n(\lambda)\, \text{d} \lambda.\end{align}
Here, for each
![]() $\lambda>0$
,
$\lambda>0$
,
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
![]() $k\in\mathbb{N}_n$
,
$k\in\mathbb{N}_n$
,
![]() ${\textbf M}_{nk}(\lambda) \,{:}\,{\raise-1.5pt{=}}\, (M_{nkj}(\lambda))_{j\in\mathbb{N}_n}$
is a multinomial
${\textbf M}_{nk}(\lambda) \,{:}\,{\raise-1.5pt{=}}\, (M_{nkj}(\lambda))_{j\in\mathbb{N}_n}$
is a multinomial
![]() $$(k,{{\textbf p}_n}(\lambda ))$$
vector with
$$(k,{{\textbf p}_n}(\lambda ))$$
vector with
which results from conditioning on the sum
![]() $ \sum_{j=1}^nN_j(\lambda)$
of Poisson random variables in (3.2). Specifically, the distribution of
$ \sum_{j=1}^nN_j(\lambda)$
of Poisson random variables in (3.2). Specifically, the distribution of
![]() ${\textbf M}_{nk}(\lambda)$
is given by
${\textbf M}_{nk}(\lambda)$
is given by
for
![]() $m_j\ge 0$
,
$m_j\ge 0$
,
![]() $j\in\mathbb{N}_n$
, with
$j\in\mathbb{N}_n$
, with
![]() $\sum_{j=1}^nm_j=k$
. We can rewrite (3.2) as
$\sum_{j=1}^nm_j=k$
. We can rewrite (3.2) as
 \begin{align} \mathbb{P}(K_n(\alpha,r)=k)= n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg) \mathbb{P}\Bigg(\text{Poiss}\Bigg(\sum_{j=1}^nF_j(\lambda)\Bigg) =k\Bigg) e_n(\lambda)\, \text{d} \lambda.\end{align}
\begin{align} \mathbb{P}(K_n(\alpha,r)=k)= n \int_{0}^{\infty}\frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg) \mathbb{P}\Bigg(\text{Poiss}\Bigg(\sum_{j=1}^nF_j(\lambda)\Bigg) =k\Bigg) e_n(\lambda)\, \text{d} \lambda.\end{align}
In this expression, by (2.3),
 \begin{align*}\sum_{j=1}^nF_j(\lambda)= \alpha \int_0^\lambda\sum_{j=1}^n \frac{z^j}{j!}z^{-\alpha-1}e^{- z} \text{d} z = \lambda^{-\alpha}(\Psi_n(\lambda)-1),\end{align*}
\begin{align*}\sum_{j=1}^nF_j(\lambda)= \alpha \int_0^\lambda\sum_{j=1}^n \frac{z^j}{j!}z^{-\alpha-1}e^{- z} \text{d} z = \lambda^{-\alpha}(\Psi_n(\lambda)-1),\end{align*}
where we define
Also define the ratio
In (3.4), recall
![]() $e_n(\lambda) \,{:}\,{\raise-1.5pt{=}}\, \exp\big(\!\sum_{j=1}^nF_j(\lambda)\big)$
, and consider the component
$e_n(\lambda) \,{:}\,{\raise-1.5pt{=}}\, \exp\big(\!\sum_{j=1}^nF_j(\lambda)\big)$
, and consider the component
 \begin{align*} & \frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\text{Poiss}\Bigg(\sum_{j=1}^nF_j(\lambda)\Bigg) =k\Bigg) e_n(\lambda)\\
&= \frac{\Gamma(r+k)}{\Gamma(r)} \frac{\lambda^{-1}}{\Psi(\lambda)^{r+k}} \frac{\left( \lambda^{\alpha}\sum_{j=1}^nF_j(\lambda)\right)^k}{k!} \exp\Bigg(-\sum_{j=1}^nF_j(\lambda)\Bigg)\times e_n(\lambda)\\
&= \frac{\Gamma(r+k)}{\Gamma(r)\,k!} \frac{\lambda^{-1}}{\Psi(\lambda)^{r+k}}\left(\Psi_n(\lambda)-1\right)^k\\
&= \frac{\Gamma(r+k)}{\Gamma(r)\,k!} \frac{\lambda^{-1}}{\Psi(\lambda)^{r}}\left(\frac{\Psi(\lambda)-1}{\Psi(\lambda)}\right)^k\left(\frac{\Psi_n(\lambda)-1}{\Psi(\lambda)-1}\right)^k\\
&=\ell_n(\lambda)^k \lambda^{-1}\mathbb{P}\Bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda)}\bigg) =k\Bigg).\end{align*}
\begin{align*} & \frac{r^{(k)}\lambda^{\alpha k-1}}{\Psi(\lambda)^{r+k}} \mathbb{P}\Bigg(\text{Poiss}\Bigg(\sum_{j=1}^nF_j(\lambda)\Bigg) =k\Bigg) e_n(\lambda)\\
&= \frac{\Gamma(r+k)}{\Gamma(r)} \frac{\lambda^{-1}}{\Psi(\lambda)^{r+k}} \frac{\left( \lambda^{\alpha}\sum_{j=1}^nF_j(\lambda)\right)^k}{k!} \exp\Bigg(-\sum_{j=1}^nF_j(\lambda)\Bigg)\times e_n(\lambda)\\
&= \frac{\Gamma(r+k)}{\Gamma(r)\,k!} \frac{\lambda^{-1}}{\Psi(\lambda)^{r+k}}\left(\Psi_n(\lambda)-1\right)^k\\
&= \frac{\Gamma(r+k)}{\Gamma(r)\,k!} \frac{\lambda^{-1}}{\Psi(\lambda)^{r}}\left(\frac{\Psi(\lambda)-1}{\Psi(\lambda)}\right)^k\left(\frac{\Psi_n(\lambda)-1}{\Psi(\lambda)-1}\right)^k\\
&=\ell_n(\lambda)^k \lambda^{-1}\mathbb{P}\Bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda)}\bigg) =k\Bigg).\end{align*}
Here
![]() $ \text{Negbin}\big(r, 1/\Psi(\lambda)\big)$
is a negative binomial random variable with parameter
$ \text{Negbin}\big(r, 1/\Psi(\lambda)\big)$
is a negative binomial random variable with parameter
![]() $r>0$
and success probability
$r>0$
and success probability
![]() $1/\Psi(\lambda)$
. So (3.4) can be written as
$1/\Psi(\lambda)$
. So (3.4) can be written as
 \begin{align}\mathbb{P}(K_n(\alpha,r)=k)=n \int_{0}^{\infty}\ell_n(\lambda)^k \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda)}\Bigg) =k\Bigg) \, \frac{\text{d} \lambda}{\lambda}.\nonumber\\
\end{align}
\begin{align}\mathbb{P}(K_n(\alpha,r)=k)=n \int_{0}^{\infty}\ell_n(\lambda)^k \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda)}\Bigg) =k\Bigg) \, \frac{\text{d} \lambda}{\lambda}.\nonumber\\
\end{align}
The multinomial vector
![]() ${\textbf M}_{nk}(\lambda)=(M_{nkj}(\lambda))_{j\in\mathbb{N}_n}$
has moment generating function
${\textbf M}_{nk}(\lambda)=(M_{nkj}(\lambda))_{j\in\mathbb{N}_n}$
has moment generating function
 \begin{equation*}\mathbb{E}\Bigg(\prod_{j=1}^n \exp\big(\theta_j M_{nkj}(\lambda)\big)\Bigg)=\Bigg(\sum_{j=1}^n e^{\theta_j}p_{nj}(\lambda)\Bigg)^k,\end{equation*}
\begin{equation*}\mathbb{E}\Bigg(\prod_{j=1}^n \exp\big(\theta_j M_{nkj}(\lambda)\big)\Bigg)=\Bigg(\sum_{j=1}^n e^{\theta_j}p_{nj}(\lambda)\Bigg)^k,\end{equation*}
where
![]() $\theta_j>0$
,
$\theta_j>0$
,
![]() $j\in\mathbb{N}_n$
. Set
$j\in\mathbb{N}_n$
. Set
![]() $\theta_j=\theta \times j$
,
$\theta_j=\theta \times j$
,
![]() $\theta>0$
, in this to get
$\theta>0$
, in this to get
 \begin{equation*}\mathbb{E}\exp\Bigg(\theta \sum_{j=1}^n j M_{nkj}(\lambda)\big)\Bigg)=\Bigg(\sum_{j=1}^n e^{\theta \times j}p_{nj}(\lambda)\Bigg)^k \,\,{\raise-1.5pt{=}}{:}\, \mathbb{E} \exp\Bigg(\theta\sum_{i=1}^k X_{in}(\lambda)\Bigg),\end{equation*}
\begin{equation*}\mathbb{E}\exp\Bigg(\theta \sum_{j=1}^n j M_{nkj}(\lambda)\big)\Bigg)=\Bigg(\sum_{j=1}^n e^{\theta \times j}p_{nj}(\lambda)\Bigg)^k \,\,{\raise-1.5pt{=}}{:}\, \mathbb{E} \exp\Bigg(\theta\sum_{i=1}^k X_{in}(\lambda)\Bigg),\end{equation*}
where
![]() $${({X_{in}}(\lambda ))_{1 \le i \le k}}$$
are i.i.d. with
$${({X_{in}}(\lambda ))_{1 \le i \le k}}$$
are i.i.d. with
So we see that
 \begin{equation} \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg) =\mathbb{P}\Bigg(\sum_{i=1}^k X_{in}(\lambda)=n\Bigg). \end{equation}
\begin{equation} \mathbb{P}\Bigg(\sum_{j=1}^njM_{nkj}(\lambda)=n\Bigg) =\mathbb{P}\Bigg(\sum_{i=1}^k X_{in}(\lambda)=n\Bigg). \end{equation}
We need information on the limiting behaviour of the
![]() $X_{in}(\lambda)$
.
$X_{in}(\lambda)$
.
Proposition 3.1. For each
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $h>0$
, we have the following:
$h>0$
, we have the following:
-
(a)
(3.10) \begin{equation}\lim_{n\to\infty}n^\alpha \mathbb{P}(X_{1n}(\lambda n)\ge hn)=\begin{cases}0, &\lambda<h<1\ \text{or}\ h>1,\\
\displaystyle{\frac{h^{-\alpha} - \lambda^{-\alpha}}{\Gamma(1-\alpha)}}, & h<\lambda<1,\\
\displaystyle{\frac{h^{-\alpha} -1}{\Gamma(1-\alpha)}},&h<1<\lambda;\end{cases}\end{equation}
\begin{equation}\lim_{n\to\infty}n^\alpha \mathbb{P}(X_{1n}(\lambda n)\ge hn)=\begin{cases}0, &\lambda<h<1\ \text{or}\ h>1,\\
\displaystyle{\frac{h^{-\alpha} - \lambda^{-\alpha}}{\Gamma(1-\alpha)}}, & h<\lambda<1,\\
\displaystyle{\frac{h^{-\alpha} -1}{\Gamma(1-\alpha)}},&h<1<\lambda;\end{cases}\end{equation}
-
(b)
(3.11) \begin{equation}\lim_{n\to\infty} n^{\alpha-1}\mathbb{E}\big(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\big)=\frac{\alpha}{\Gamma(2-\alpha)}\big(\lambda^{1-\alpha}\wedge(h^{1-\alpha}\wedge1)\big);\end{equation}
\begin{equation}\lim_{n\to\infty} n^{\alpha-1}\mathbb{E}\big(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\big)=\frac{\alpha}{\Gamma(2-\alpha)}\big(\lambda^{1-\alpha}\wedge(h^{1-\alpha}\wedge1)\big);\end{equation}
-
(c)
(3.12) \begin{equation}\lim_{n\to\infty} n^{\alpha-2}\mathbb{E}\big( (X_{1n}^2(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\big)=\frac{\alpha}{(2-\alpha)\Gamma(1-\alpha)} \big(\lambda^{1-\alpha}\wedge(h^{1-\alpha}\wedge1)\big). \quad \end{equation}
\begin{equation}\lim_{n\to\infty} n^{\alpha-2}\mathbb{E}\big( (X_{1n}^2(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\big)=\frac{\alpha}{(2-\alpha)\Gamma(1-\alpha)} \big(\lambda^{1-\alpha}\wedge(h^{1-\alpha}\wedge1)\big). \quad \end{equation}
Proof of Proposition 3.1: Throughout, keep
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $h>0$
. For Part (a) we can compute, according to (3.8), for
$h>0$
. For Part (a) we can compute, according to (3.8), for
![]() $0<h\le 1$
,
$0<h\le 1$
,
(the left-hand side of (3.13) is 0 for
![]() $h>1$
). In the denominator of (3.13), by (2.3),
$h>1$
). In the denominator of (3.13), by (2.3),
as
![]() $n\to\infty$
. For the numerator of (3.13), consider
$n\to\infty$
. For the numerator of (3.13), consider
 \begin{eqnarray} n^{\alpha}\sum_{j=\lfloor h n\rfloor}^n F_j(\lambda n)\ &=&\ \alpha n^{\alpha} \int_0^{\lambda n}\sum_{j=\lfloor h n\rfloor}^n \frac{z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\sum_{j=\lfloor h n\rfloor}^n \frac{(nz)^{j}}{j!}e^{-nz} z^{-\alpha-1}\text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\mathbb{P}\big(\lfloor h n\rfloor\le \text{Poiss} (nz)\le n\big) z^{-\alpha-1} \text{d} z. \end{eqnarray}
\begin{eqnarray} n^{\alpha}\sum_{j=\lfloor h n\rfloor}^n F_j(\lambda n)\ &=&\ \alpha n^{\alpha} \int_0^{\lambda n}\sum_{j=\lfloor h n\rfloor}^n \frac{z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\sum_{j=\lfloor h n\rfloor}^n \frac{(nz)^{j}}{j!}e^{-nz} z^{-\alpha-1}\text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\mathbb{P}\big(\lfloor h n\rfloor\le \text{Poiss} (nz)\le n\big) z^{-\alpha-1} \text{d} z. \end{eqnarray}
When
![]() $0<\delta<h$
, by Chebyshev’s inequality,
$0<\delta<h$
, by Chebyshev’s inequality,
 \begin{align*} & \alpha \int_0^{\delta} \mathbb{P}(\text{Poiss} (nz)>hn) z^{-\alpha-1}\text{d} z\\
&\quad = \alpha \int_0^{\delta} \mathbb{P}(\text{Poiss} (nz)-nz>n(h-z)) z^{-\alpha-1}\text{d} z \\
&\quad \le \alpha\int_0^{\delta} \frac{(nz) z^{-\alpha-1}\text{d} z}{(n(h-z))^2}\le \frac{\delta^{1-\alpha}}{n(h-\delta)^2} \ \to 0,\ \text{as}\ n\to \infty.\end{align*}
\begin{align*} & \alpha \int_0^{\delta} \mathbb{P}(\text{Poiss} (nz)>hn) z^{-\alpha-1}\text{d} z\\
&\quad = \alpha \int_0^{\delta} \mathbb{P}(\text{Poiss} (nz)-nz>n(h-z)) z^{-\alpha-1}\text{d} z \\
&\quad \le \alpha\int_0^{\delta} \frac{(nz) z^{-\alpha-1}\text{d} z}{(n(h-z))^2}\le \frac{\delta^{1-\alpha}}{n(h-\delta)^2} \ \to 0,\ \text{as}\ n\to \infty.\end{align*}
For each
![]() $z>0$
, Poiss
$z>0$
, Poiss
![]() $$(nz)/nz \mathop \to \limits^P 1$$
as
$$(nz)/nz \mathop \to \limits^P 1$$
as
![]() $n\to\infty$
by the weak law of large numbers. Thus by dominated convergence
$n\to\infty$
by the weak law of large numbers. Thus by dominated convergence
 \begin{equation*}\alpha \int_\delta^{\lambda}\mathbb{P}\Bigg( \frac{\lfloor h n\rfloor}{nz}\le \frac{ \text{Poiss} (nz)}{nz}\le \frac{ n}{nz}\Bigg) z^{-\alpha-1} \text{d} z\to\alpha \int_\delta^\lambda {\textbf 1}_{\{h<z<1\}} z^{-\alpha-1}\text{d} z. \end{equation*}
\begin{equation*}\alpha \int_\delta^{\lambda}\mathbb{P}\Bigg( \frac{\lfloor h n\rfloor}{nz}\le \frac{ \text{Poiss} (nz)}{nz}\le \frac{ n}{nz}\Bigg) z^{-\alpha-1} \text{d} z\to\alpha \int_\delta^\lambda {\textbf 1}_{\{h<z<1\}} z^{-\alpha-1}\text{d} z. \end{equation*}
Letting
![]() $\delta\downarrow 0$
we obtain the right-hand side of (3.10).
$\delta\downarrow 0$
we obtain the right-hand side of (3.10).
For Part (b) we calculate, from (3.3) and (3.8), that
 \begin{equation} n^{\alpha-1}\mathbb{E}(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}) = n^{\alpha-1}\sum_{j=1}^ {\lfloor h n\rfloor}j p_{nj}(\lambda n) = \frac{ n^{\alpha-1}\sum_{j=1}^ {\lfloor h n\rfloor}j F_j(\lambda n)} {\sum_{j=1}^n F_j(\lambda n)}.\end{equation}
\begin{equation} n^{\alpha-1}\mathbb{E}(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}) = n^{\alpha-1}\sum_{j=1}^ {\lfloor h n\rfloor}j p_{nj}(\lambda n) = \frac{ n^{\alpha-1}\sum_{j=1}^ {\lfloor h n\rfloor}j F_j(\lambda n)} {\sum_{j=1}^n F_j(\lambda n)}.\end{equation}
The denominator in (3.16) tends to
![]() $\Gamma(1-\alpha)$
, by (3.14). In the numerator, by (2.3),
$\Gamma(1-\alpha)$
, by (3.14). In the numerator, by (2.3),
 \begin{eqnarray} n^{\alpha-1}\sum_{j=1}^{\lfloor h n\rfloor} jF_j(\lambda n)\ &=&\ \alpha n^{\alpha-1}\int_0^{\lambda n}\sum_{j=1}^{\lfloor h n\rfloor} \frac{z^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{- z} \text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\sum_{j=1}^{\lfloor h n\rfloor} \frac{(nz)^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{-nz} \text{d} z \nonumber\\
&=&\ \alpha \int_0^{\lambda}\mathbb{P}( \text{Poiss} (nz)\le {\lfloor h n\rfloor} -1) z^{-\alpha} \text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\mathbb{P}\Bigg( \frac{\text{Poiss} (nz)}{nz}\le \frac{ {\lfloor h n\rfloor} -1}{nz}\Bigg) z^{-\alpha} \text{d} z.\end{eqnarray}
\begin{eqnarray} n^{\alpha-1}\sum_{j=1}^{\lfloor h n\rfloor} jF_j(\lambda n)\ &=&\ \alpha n^{\alpha-1}\int_0^{\lambda n}\sum_{j=1}^{\lfloor h n\rfloor} \frac{z^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{- z} \text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\sum_{j=1}^{\lfloor h n\rfloor} \frac{(nz)^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{-nz} \text{d} z \nonumber\\
&=&\ \alpha \int_0^{\lambda}\mathbb{P}( \text{Poiss} (nz)\le {\lfloor h n\rfloor} -1) z^{-\alpha} \text{d} z\nonumber \\
&=&\ \alpha \int_0^{\lambda}\mathbb{P}\Bigg( \frac{\text{Poiss} (nz)}{nz}\le \frac{ {\lfloor h n\rfloor} -1}{nz}\Bigg) z^{-\alpha} \text{d} z.\end{eqnarray}
In this, consider values of
![]() $h\le 1$
and
$h\le 1$
and
![]() $h>1$
separately. For
$h>1$
separately. For
![]() $h>1$
the sum on the left-hand side of (3.17) should be replaced by the sum over
$h>1$
the sum on the left-hand side of (3.17) should be replaced by the sum over
![]() $1\le j\le n$
and h in (3.17) by 1. Then, again using the fact that Poiss
$1\le j\le n$
and h in (3.17) by 1. Then, again using the fact that Poiss
![]() $$(nz)/nz \mathop \to \limits^P 1$$
for each
$$(nz)/nz \mathop \to \limits^P 1$$
for each
![]() $z>0$
, along with dominated convergence, we get
$z>0$
, along with dominated convergence, we get
For
![]() $0\le h\le 1$
, similarly,
$0\le h\le 1$
, similarly,
Dividing by
![]() $\Gamma(1-\alpha)$
(from (3.14)) gives the right-hand side of (3.11).
$\Gamma(1-\alpha)$
(from (3.14)) gives the right-hand side of (3.11).
For Part (c), keep
![]() $0<h<1$
at first. Then by (3.3) and (3.8),
$0<h<1$
at first. Then by (3.3) and (3.8),
 \begin{eqnarray}n^{\alpha-2}\mathbb{E}\big(X_{1n}^2(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\big)\ & = & \ n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 p_{nj}(\lambda n)\\
&& =\ \frac{ n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 F_j(\lambda n)} {\sum_{j=1}^n F_j(\lambda n)} \sim \frac{ n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 F_j(\lambda n)} {\Gamma(1-\alpha)},\ \text{as}\ n\to\infty\nonumber\end{eqnarray}
\begin{eqnarray}n^{\alpha-2}\mathbb{E}\big(X_{1n}^2(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\big)\ & = & \ n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 p_{nj}(\lambda n)\\
&& =\ \frac{ n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 F_j(\lambda n)} {\sum_{j=1}^n F_j(\lambda n)} \sim \frac{ n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 F_j(\lambda n)} {\Gamma(1-\alpha)},\ \text{as}\ n\to\infty\nonumber\end{eqnarray}
(using (3.14)). In the numerator of the last expression,
 \begin{eqnarray*} n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 F_j(\lambda n) & = &\ \alpha n^{\alpha-2}\int_0^{\lambda n}\sum_{j=1}^{\lfloor h n\rfloor} \frac{j^2 z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z\nonumber \\
&=&\ \alpha n^{-2} \int_0^{\lambda}\sum_{j=1}^{\lfloor h n\rfloor} \frac{j^2 (nz)^{j}}{j!}z^{-\alpha-1}e^{-nz} \text{d} z\nonumber \\
&=&\ \alpha n^{-2} \int_0^{\lambda}\sum_{j=1}^{\lfloor h n\rfloor} \frac{j(nz)^{j}}{(\kern1.2pt j-1)!}z^{-\alpha-1}e^{-nz} \text{d} z\quad (\text{keep}\ n>2)\nonumber \\
&=&\ \alpha n^{-2} \int_0^{\lambda} \Bigg(\sum_{j=2}^{\lfloor h n\rfloor} \frac{j(nz)^{j}}{(\kern1.2pt j-1)!}+nz\Bigg) z^{-\alpha-1}e^{-nz} \text{d} z \nonumber\\
&=&\ \alpha n^{-2} \int_0^{\lambda} \Bigg(\sum_{j=2}^{\lfloor h n\rfloor} \frac{(nz)^{j-2}}{(\kern1.2pt j-2)!}(nz)^2+\sum_{j=2}^{\lfloor h n\rfloor} \frac{(nz)^{j}}{(\kern1.2pt j-1)!}+nz\Bigg) z^{-\alpha-1}e^{-nz} \text{d} z.\end{eqnarray*}
\begin{eqnarray*} n^{\alpha-2}\sum_{j=1}^{\lfloor h n\rfloor} j^2 F_j(\lambda n) & = &\ \alpha n^{\alpha-2}\int_0^{\lambda n}\sum_{j=1}^{\lfloor h n\rfloor} \frac{j^2 z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z\nonumber \\
&=&\ \alpha n^{-2} \int_0^{\lambda}\sum_{j=1}^{\lfloor h n\rfloor} \frac{j^2 (nz)^{j}}{j!}z^{-\alpha-1}e^{-nz} \text{d} z\nonumber \\
&=&\ \alpha n^{-2} \int_0^{\lambda}\sum_{j=1}^{\lfloor h n\rfloor} \frac{j(nz)^{j}}{(\kern1.2pt j-1)!}z^{-\alpha-1}e^{-nz} \text{d} z\quad (\text{keep}\ n>2)\nonumber \\
&=&\ \alpha n^{-2} \int_0^{\lambda} \Bigg(\sum_{j=2}^{\lfloor h n\rfloor} \frac{j(nz)^{j}}{(\kern1.2pt j-1)!}+nz\Bigg) z^{-\alpha-1}e^{-nz} \text{d} z \nonumber\\
&=&\ \alpha n^{-2} \int_0^{\lambda} \Bigg(\sum_{j=2}^{\lfloor h n\rfloor} \frac{(nz)^{j-2}}{(\kern1.2pt j-2)!}(nz)^2+\sum_{j=2}^{\lfloor h n\rfloor} \frac{(nz)^{j}}{(\kern1.2pt j-1)!}+nz\Bigg) z^{-\alpha-1}e^{-nz} \text{d} z.\end{eqnarray*}
Here again we see Poisson distributions and can write the last expression as
 \begin{eqnarray*}&&\alpha \int_0^{\lambda}\mathbb{P}(\text{Poiss} (nz)\le {\lfloor h n\rfloor}-2) z^{1-\alpha}\text{d} z\\
&& \hskip 3cm+\alpha n^{-2}\int_0^\lambda\sum_{j=1}^{\lfloor h n\rfloor} \frac{(nz)^{j-1}} {(\kern1.2pt j-1)!} (nz) z^{-\alpha-1}e^{-nz}\text{d} z\\
&&=\alpha\int_0^\lambda {\textbf 1}_{\{z<h\}} z^{1-\alpha} \text{d} z +o(1)+\alpha n^{-1} \int_0^{\lambda}\mathbb{P}(\text{Poiss} (nz)\le {\lfloor h n\rfloor}-1) z^{-\alpha}\text{dz}.\end{eqnarray*}
\begin{eqnarray*}&&\alpha \int_0^{\lambda}\mathbb{P}(\text{Poiss} (nz)\le {\lfloor h n\rfloor}-2) z^{1-\alpha}\text{d} z\\
&& \hskip 3cm+\alpha n^{-2}\int_0^\lambda\sum_{j=1}^{\lfloor h n\rfloor} \frac{(nz)^{j-1}} {(\kern1.2pt j-1)!} (nz) z^{-\alpha-1}e^{-nz}\text{d} z\\
&&=\alpha\int_0^\lambda {\textbf 1}_{\{z<h\}} z^{1-\alpha} \text{d} z +o(1)+\alpha n^{-1} \int_0^{\lambda}\mathbb{P}(\text{Poiss} (nz)\le {\lfloor h n\rfloor}-1) z^{-\alpha}\text{dz}.\end{eqnarray*}
As
![]() $n\to\infty$
, this tends to
$n\to\infty$
, this tends to
Dividing this by
![]() $\Gamma(1-\alpha)$
(from (3.14)) gives the right-hand side of (3.12) when
$\Gamma(1-\alpha)$
(from (3.14)) gives the right-hand side of (3.12) when
![]() $0<h<1$
. For
$0<h<1$
. For
![]() $h>1$
, similar analysis gives a limit of
$h>1$
, similar analysis gives a limit of
![]() $\alpha/(2-\alpha) (\lambda^{2-\alpha}\wedge 1)$
. Combining these gives the right-hand side of (3.12) and completes the proof of Proposition 3.1.
$\alpha/(2-\alpha) (\lambda^{2-\alpha}\wedge 1)$
. Combining these gives the right-hand side of (3.12) and completes the proof of Proposition 3.1.
We next list some properties of the subordinator
![]() $${({Y_t}(\lambda ))_{t > 0}}$$
whose Laplace transform is in (2.6) with the canonical measure in (2.7). From that measure we can calculate, for
$${({Y_t}(\lambda ))_{t > 0}}$$
whose Laplace transform is in (2.6) with the canonical measure in (2.7). From that measure we can calculate, for
![]() $z>0$
,
$z>0$
,
 \begin{align}\liminf_{z\downarrow 0}\frac{1}{z^{2-\alpha} }\int_{-z}^z y^2 \Pi_\lambda(\text{d} y)& = \frac{ \alpha } {1-\alpha}\liminf_{z\downarrow 0}\frac{1}{z^{2-\alpha} }\int_0^{1\vee z} y^{1-\alpha} \text{d} y\nonumber \\
&= \frac{ \alpha } {(1-\alpha)(2-\alpha)}>0, \end{align}
\begin{align}\liminf_{z\downarrow 0}\frac{1}{z^{2-\alpha} }\int_{-z}^z y^2 \Pi_\lambda(\text{d} y)& = \frac{ \alpha } {1-\alpha}\liminf_{z\downarrow 0}\frac{1}{z^{2-\alpha} }\int_0^{1\vee z} y^{1-\alpha} \text{d} y\nonumber \\
&= \frac{ \alpha } {(1-\alpha)(2-\alpha)}>0, \end{align}
so by a result of Orey (see [Reference Sato26, p. 190]), each
![]() $Y_t(\lambda)$
has a
$Y_t(\lambda)$
has a
![]() $C^\infty$
density all of whose derivatives tend to 0 at
$C^\infty$
density all of whose derivatives tend to 0 at
![]() $\infty$
. Write
$\infty$
. Write
 \begin{equation}\mathbb{E} e^{\text{i}\theta Y_t(\lambda)} =\exp\Bigg(t\int_0^1 \big( e^{\text{i}\theta y}-1\big)\frac{k_\lambda(y)}{y} \text{d} y\Bigg), \qquad \theta\in \Bbb{R},\end{equation}
\begin{equation}\mathbb{E} e^{\text{i}\theta Y_t(\lambda)} =\exp\Bigg(t\int_0^1 \big( e^{\text{i}\theta y}-1\big)\frac{k_\lambda(y)}{y} \text{d} y\Bigg), \qquad \theta\in \Bbb{R},\end{equation}
where
is left-continuous and decreasing on
![]() $$(0,\infty )$$
. So by [Reference Sato26, Theorem 28.4, p. 191],
$$(0,\infty )$$
. So by [Reference Sato26, Theorem 28.4, p. 191],
![]() $${({Y_t}(\lambda ))_{t > 0}}$$
is a self-decomposable Lévy process for each
$${({Y_t}(\lambda ))_{t > 0}}$$
is a self-decomposable Lévy process for each
![]() $\lambda>0$
, and by a similar argument as in [Reference Sato26, Lemma 28.5, p. 191], we can deduce that
$\lambda>0$
, and by a similar argument as in [Reference Sato26, Lemma 28.5, p. 191], we can deduce that
Now proceeding with the main proof, from (3.7) and (3.9) we get
 \begin{eqnarray}&&\mathbb{P}(K_n(\alpha,r)=k) = n \int_{0}^{\infty}\ell_n(\lambda)^k\mathbb{P}\Bigg(\sum_{i=1}^k X_{in}(\lambda)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda)}\Bigg) =k\Bigg) \, \frac{\text{d} \lambda}{\lambda}.\nonumber\\
\end{eqnarray}
\begin{eqnarray}&&\mathbb{P}(K_n(\alpha,r)=k) = n \int_{0}^{\infty}\ell_n(\lambda)^k\mathbb{P}\Bigg(\sum_{i=1}^k X_{in}(\lambda)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda)}\Bigg) =k\Bigg) \, \frac{\text{d} \lambda}{\lambda}.\nonumber\\
\end{eqnarray}
Change variable from
![]() $\lambda$
to
$\lambda$
to
![]() $\lambda n$
to write this as
$\lambda n$
to write this as
 \begin{align} \mathbb{P}(K_n=k) & = n \int_{0}^{\infty}\ell_n(\lambda n)^k\mathbb{P}\Bigg(\sum_{i=1}^k X_{in}(\lambda n)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda n)}\Bigg) =k\Bigg) \, \frac{\text{d} \lambda}{\lambda}\nonumber\\
& \,\,{\raise-1.5pt{=}}{:}\, f_n(k).\end{align}
\begin{align} \mathbb{P}(K_n=k) & = n \int_{0}^{\infty}\ell_n(\lambda n)^k\mathbb{P}\Bigg(\sum_{i=1}^k X_{in}(\lambda n)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda n)}\Bigg) =k\Bigg) \, \frac{\text{d} \lambda}{\lambda}\nonumber\\
& \,\,{\raise-1.5pt{=}}{:}\, f_n(k).\end{align}
Then for
![]() $0<a<b$
,
$0<a<b$
,
 \begin{align*}\mathbb{P}( an^\alpha <K_n(\alpha,r)\le bn^\alpha) & = \sum_{ an^\alpha <x \le bn^\alpha} \mathbb{P}(K_n =\lfloor x\rfloor)\nonumber\\
& = \int_{\lceil an^\alpha \rceil }^{\lfloor bn^\alpha \rfloor}f_n(\lfloor x\rfloor)\text{d} x=n^\alpha \int_{a_n}^{b_n} f_n( \lfloor xn^\alpha\rfloor )\text{d} x,\end{align*}
\begin{align*}\mathbb{P}( an^\alpha <K_n(\alpha,r)\le bn^\alpha) & = \sum_{ an^\alpha <x \le bn^\alpha} \mathbb{P}(K_n =\lfloor x\rfloor)\nonumber\\
& = \int_{\lceil an^\alpha \rceil }^{\lfloor bn^\alpha \rfloor}f_n(\lfloor x\rfloor)\text{d} x=n^\alpha \int_{a_n}^{b_n} f_n( \lfloor xn^\alpha\rfloor )\text{d} x,\end{align*}
where
![]() $a_n \,{:}\,{\raise-1.5pt{=}}\, \lceil an^\alpha \rceil/n^\alpha$
and
$a_n \,{:}\,{\raise-1.5pt{=}}\, \lceil an^\alpha \rceil/n^\alpha$
and
![]() $ b_n \,{:}\,{\raise-1.5pt{=}}\, \lfloor bn^\alpha\rfloor/n^\alpha$
. Thus we can write
$ b_n \,{:}\,{\raise-1.5pt{=}}\, \lfloor bn^\alpha\rfloor/n^\alpha$
. Thus we can write
 \begin{align}\mathbb{P}( an^\alpha <K_n(\alpha,r)\le bn^\alpha) =\, & n^{\alpha+1} \int_{a_n}^{b_n}\text{dx}\int_{\lambda>0}(\ell_n(\lambda n))^{\lfloor xn^\alpha\rfloor} \nonumber \\
&\times \mathbb{P}\Bigg(\sum_{i=1}^{ \lfloor xn^\alpha\rfloor}X_{in}(\lambda n)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda n)}\Bigg) =\lfloor xn^\alpha\rfloor\Bigg) \, \frac{\text{d} \lambda}{\lambda}. \end{align}
\begin{align}\mathbb{P}( an^\alpha <K_n(\alpha,r)\le bn^\alpha) =\, & n^{\alpha+1} \int_{a_n}^{b_n}\text{dx}\int_{\lambda>0}(\ell_n(\lambda n))^{\lfloor xn^\alpha\rfloor} \nonumber \\
&\times \mathbb{P}\Bigg(\sum_{i=1}^{ \lfloor xn^\alpha\rfloor}X_{in}(\lambda n)=n\Bigg)\mathbb{P}\Bigg( \text{Negbin}\Bigg(r, \frac{1}{\Psi(\lambda n)}\Bigg) =\lfloor xn^\alpha\rfloor\Bigg) \, \frac{\text{d} \lambda}{\lambda}. \end{align}
We have
![]() $a_n\to a$
,
$a_n\to a$
,
![]() $b_n\to b$
, and we need to find the limits of the
$b_n\to b$
, and we need to find the limits of the
![]() $\ell_n$
term and the probabilities in (3.28).
$\ell_n$
term and the probabilities in (3.28).
Proposition 3.2. Holding
![]() $x>0$
and
$x>0$
and
![]() $\lambda>0$
fixed, we have
$\lambda>0$
fixed, we have
-
(a)
(3.29) \begin{equation}\lim_{n\to\infty} n\mathbb{P}\Bigg(\sum_{i=1}^{\lfloor xn^\alpha\rfloor} X_{in}(\lambda n)=n\Bigg)= f_{Y_x(\lambda)}(1);\end{equation}
\begin{equation}\lim_{n\to\infty} n\mathbb{P}\Bigg(\sum_{i=1}^{\lfloor xn^\alpha\rfloor} X_{in}(\lambda n)=n\Bigg)= f_{Y_x(\lambda)}(1);\end{equation}
-
(b)
(3.30) \begin{equation}\lim_{n\to\infty} n^\alpha\mathbb{P}\bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda n)}\bigg) =\lfloor xn^\alpha\rfloor\bigg)= \frac{x^{r-1}\lambda^{-\alpha r}}{\Gamma(r)\Gamma^r(1-\alpha)}\exp\bigg(-\frac{x\lambda^{-\alpha}}{\Gamma(1-\alpha)}\bigg);\end{equation}
\begin{equation}\lim_{n\to\infty} n^\alpha\mathbb{P}\bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda n)}\bigg) =\lfloor xn^\alpha\rfloor\bigg)= \frac{x^{r-1}\lambda^{-\alpha r}}{\Gamma(r)\Gamma^r(1-\alpha)}\exp\bigg(-\frac{x\lambda^{-\alpha}}{\Gamma(1-\alpha)}\bigg);\end{equation}
-
(c)
(3.31) \begin{equation}\lim_{n\to\infty}(\ell_n(\lambda n))^{\lfloor xn^\alpha\rfloor}=\exp\bigg(-\frac{x(1-\lambda^{-\alpha}){\textbf 1}_{\{\lambda>1\}}}{\Gamma(1-\alpha)}\bigg).\end{equation}
\begin{equation}\lim_{n\to\infty}(\ell_n(\lambda n))^{\lfloor xn^\alpha\rfloor}=\exp\bigg(-\frac{x(1-\lambda^{-\alpha}){\textbf 1}_{\{\lambda>1\}}}{\Gamma(1-\alpha)}\bigg).\end{equation}
Consequently,
-
(d)
(3.32) \begin{align} \lim_{n\to\infty} n^\alpha(\ell_n(\lambda n))^{\lfloor xn^\alpha\rfloor}\mathbb{P}\bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda n)}\bigg) & = \lfloor xn^\alpha\rfloor\bigg)\nonumber\\
& = \frac{x^{r-1}\lambda^{-\alpha r}}{\Gamma(r)\Gamma^r(1-\alpha)}\exp\bigg(-\frac{x(\lambda^{-\alpha}\vee 1)}{\Gamma(1-\alpha)}\bigg).\end{align}
\begin{align} \lim_{n\to\infty} n^\alpha(\ell_n(\lambda n))^{\lfloor xn^\alpha\rfloor}\mathbb{P}\bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda n)}\bigg) & = \lfloor xn^\alpha\rfloor\bigg)\nonumber\\
& = \frac{x^{r-1}\lambda^{-\alpha r}}{\Gamma(r)\Gamma^r(1-\alpha)}\exp\bigg(-\frac{x(\lambda^{-\alpha}\vee 1)}{\Gamma(1-\alpha)}\bigg).\end{align}
Proof of Proposition 3.2: We keep
![]() $x>0$
and
$x>0$
and
![]() $\lambda>0$
fixed throughout this proof.
$\lambda>0$
fixed throughout this proof.
(a) We begin by finding the limiting distribution of the sum
 \begin{equation*}n^{-1} \sum_{i=1}^{\lfloor xn^\alpha\rfloor} X_{in}(\lambda n)\end{equation*}
\begin{equation*}n^{-1} \sum_{i=1}^{\lfloor xn^\alpha\rfloor} X_{in}(\lambda n)\end{equation*}
as
![]() $n\to\infty$
, using a classical limit theorem for sums of a triangular array. Thus, we verify Conditions (i), (ii), and (iii) of [Reference Kallenberg17, Corollary 15.16, p. 297]. It suffices to set
$n\to\infty$
, using a classical limit theorem for sums of a triangular array. Thus, we verify Conditions (i), (ii), and (iii) of [Reference Kallenberg17, Corollary 15.16, p. 297]. It suffices to set
![]() $x=1$
for this. Those conditions can be read from (3.10)–(3.12) of Proposition 3.1 as follows.
$x=1$
for this. Those conditions can be read from (3.10)–(3.12) of Proposition 3.1 as follows.
First, recalling the definition of
![]() $\Pi_\lambda$
in (2.7), we note that (3.10) implies
$\Pi_\lambda$
in (2.7), we note that (3.10) implies
which is Condition (i) of [Reference Kallenberg17, Corollary 15.16].
For Condition (ii), we can deduce from (3.11) and using the definition of
![]() $\Pi_\lambda$
in (2.7) that
$\Pi_\lambda$
in (2.7) that
 \begin{equation}\lim_{n\to\infty} n^{\alpha}\mathbb{E}\Bigg(\frac{X_{1n}(\lambda n)}{n} {\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\Bigg)= \int_{0<y\le h}y\Pi_\lambda(\text{d} y)=b- \int_{h<y\le 1}y\Pi_\lambda(\text{d} y),\end{equation}
\begin{equation}\lim_{n\to\infty} n^{\alpha}\mathbb{E}\Bigg(\frac{X_{1n}(\lambda n)}{n} {\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\Bigg)= \int_{0<y\le h}y\Pi_\lambda(\text{d} y)=b- \int_{h<y\le 1}y\Pi_\lambda(\text{d} y),\end{equation}
where
![]() $b= \int_{0<y\le 1}y\Pi_\lambda(\text{d} y)$
. The right-hand side of (3.34) is in the form required by Condition (ii) of [Reference Kallenberg17].
$b= \int_{0<y\le 1}y\Pi_\lambda(\text{d} y)$
. The right-hand side of (3.34) is in the form required by Condition (ii) of [Reference Kallenberg17].
For Condition (iii) of [Reference Kallenberg17, Corollary 15.16] we require
 \begin{equation}\lim_{n\to\infty} n^{\alpha}\mathbb{E}\Bigg(\frac{X_{1n}^2(\lambda n)}{n^2} {\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\Bigg)=a+ \int_{0<y\le h}y^2\Pi_\lambda(\text{d} y)\end{equation}
\begin{equation}\lim_{n\to\infty} n^{\alpha}\mathbb{E}\Bigg(\frac{X_{1n}^2(\lambda n)}{n^2} {\textbf 1}_{\{X_{1n}(\lambda n)<hn\}}\Bigg)=a+ \int_{0<y\le h}y^2\Pi_\lambda(\text{d} y)\end{equation}
for a finite constant a and all
![]() $h>0$
. That this holds, in fact with
$h>0$
. That this holds, in fact with
![]() $a=0$
, can be deduced from (3.12).
$a=0$
, can be deduced from (3.12).
With these three conditions satisfied, [Reference Kallenberg17, Corollary 15.16] then gives that the normed sum
 \begin{equation*} n^{-1} \sum_{i=1}^{\lfloor n^\alpha\rfloor} X_{in}(\lambda n) \end{equation*}
\begin{equation*} n^{-1} \sum_{i=1}^{\lfloor n^\alpha\rfloor} X_{in}(\lambda n) \end{equation*}
converges in distribution to the infinitely divisible distribution
![]() $id(a,b,\Pi_\lambda)$
, in Kallenberg’s notation. This distribution has characteristic exponent (see [Reference Kallenberg17, Corollary 15.8, p. 291]) given by
$id(a,b,\Pi_\lambda)$
, in Kallenberg’s notation. This distribution has characteristic exponent (see [Reference Kallenberg17, Corollary 15.8, p. 291]) given by
 \begin{eqnarray} &&\text{i}\theta b -\tfrac{1}{2} \theta^2 a +\int_{\Bbb{R}\setminus\{0\}} (e^{ \text{i}\theta y} -1 - \text{i}\theta y{\textbf 1}_{\{0<y<1}) \Pi_\lambda(\text{d} y)\nonumber\\
&&\quad = \text{i}\theta\Bigg(b -\int_{0<y<1} y\Pi_\lambda(\text{d} y)\Bigg) +\int_{\Bbb{R}\setminus\{0\}} \big(e^{ \text{i}\theta y} -1 \big) \Pi_\lambda(\text{d} y) \end{eqnarray}
\begin{eqnarray} &&\text{i}\theta b -\tfrac{1}{2} \theta^2 a +\int_{\Bbb{R}\setminus\{0\}} (e^{ \text{i}\theta y} -1 - \text{i}\theta y{\textbf 1}_{\{0<y<1}) \Pi_\lambda(\text{d} y)\nonumber\\
&&\quad = \text{i}\theta\Bigg(b -\int_{0<y<1} y\Pi_\lambda(\text{d} y)\Bigg) +\int_{\Bbb{R}\setminus\{0\}} \big(e^{ \text{i}\theta y} -1 \big) \Pi_\lambda(\text{d} y) \end{eqnarray}
(since
![]() $a=0$
). Here
$a=0$
). Here
![]() $b=\int_{0<y<1} y\Pi_\lambda(\text{d} y)$
, so the first term on the right-hand side of (3.36) equals 0. The limit distribution thus has characteristic exponent
$b=\int_{0<y<1} y\Pi_\lambda(\text{d} y)$
, so the first term on the right-hand side of (3.36) equals 0. The limit distribution thus has characteristic exponent
![]() $\int_{\Bbb{R}\setminus\{0\}} (e^{ \text{i}\theta y} -1 ) \Pi_\lambda(\text{d} y)$
, and hence is the distribution of
$\int_{\Bbb{R}\setminus\{0\}} (e^{ \text{i}\theta y} -1 ) \Pi_\lambda(\text{d} y)$
, and hence is the distribution of
![]() $ Y_1(\lambda)$
having Laplace transform (2.6) for
$ Y_1(\lambda)$
having Laplace transform (2.6) for
![]() $t=1$
.
$t=1$
.
Continuing with the proof of Part (a), we have that the characteristic function of the normed sum
![]() $n^{-1} \sum_{i=1}^{\lfloor n^\alpha\rfloor} X_{in}(\lambda n)$
also converges, so we can write
$n^{-1} \sum_{i=1}^{\lfloor n^\alpha\rfloor} X_{in}(\lambda n)$
also converges, so we can write
 \begin{equation} \lim_{n\to\infty} \phi_{\lambda n}^{ \lfloor n^\alpha\rfloor}(\theta/n)=\lim_{n\to\infty} \mathbb{E}\exp\Bigg(\frac{ \text{i}\theta}{n} \sum_{i=1}^{\lfloor n^\alpha\rfloor} X_{in}(\lambda n)\Bigg)= \mathbb{E} e^{ \text{i}\theta Y_1(\lambda)}. \end{equation}
\begin{equation} \lim_{n\to\infty} \phi_{\lambda n}^{ \lfloor n^\alpha\rfloor}(\theta/n)=\lim_{n\to\infty} \mathbb{E}\exp\Bigg(\frac{ \text{i}\theta}{n} \sum_{i=1}^{\lfloor n^\alpha\rfloor} X_{in}(\lambda n)\Bigg)= \mathbb{E} e^{ \text{i}\theta Y_1(\lambda)}. \end{equation}
For (3.29) we need a local version of this convergence, given as Lemma 3.1.
Lemma 3.1. For each
![]() $x>0$
and
$x>0$
and
![]() $\lambda>0$
, (3.29) holds.
$\lambda>0$
, (3.29) holds.
We defer the proof of Lemma 3.1 to Appendix A. Assuming it, we have completed the proof of Part (a) of Proposition 3.2.
(b) For (3.30) write
and use Stirling’s approximation to get
Also, recalling (2.2),
 \begin{eqnarray}n^{-\alpha}\Psi(\lambda n)&=& n^{-\alpha} \Bigg(1+\alpha (\lambda n)^\alpha \int_0^{\lambda n} z^{-\alpha-1}(1-e^{- z}) \text{d} z\Bigg)\nonumber\\
&\to& \alpha \lambda^\alpha \int_0^\infty z^{-\alpha-1}(1-e^{- z}) \text{d} z = \lambda^{\alpha} \Gamma(1-\alpha), \quad \text{as}\ n\to\infty.\end{eqnarray}
\begin{eqnarray}n^{-\alpha}\Psi(\lambda n)&=& n^{-\alpha} \Bigg(1+\alpha (\lambda n)^\alpha \int_0^{\lambda n} z^{-\alpha-1}(1-e^{- z}) \text{d} z\Bigg)\nonumber\\
&\to& \alpha \lambda^\alpha \int_0^\infty z^{-\alpha-1}(1-e^{- z}) \text{d} z = \lambda^{\alpha} \Gamma(1-\alpha), \quad \text{as}\ n\to\infty.\end{eqnarray}
So from (3.38)
 \begin{align*}&\mathbb{P}\bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda n)}\bigg) =\lfloor xn^\alpha\rfloor \bigg)\\
&\quad \sim \frac{(xn^\alpha)^{r-1}}{\Gamma(r)} \frac{1}{(n^ \alpha \lambda^\alpha \Gamma(1-\alpha))^r}\left( 1- \frac{1}{\Psi(\lambda n)}\right)^{\lfloor xn^\alpha\rfloor }\\
&\quad \sim \frac{n^{-\alpha}x^{r-1}\lambda^{-\alpha r}}{\Gamma(r)\Gamma^r(1-\alpha)}\exp\left(-\frac{x\lambda^{-\alpha}}{\Gamma(1-\alpha)}\right),\end{align*}
\begin{align*}&\mathbb{P}\bigg( \text{Negbin}\bigg(r, \frac{1}{\Psi(\lambda n)}\bigg) =\lfloor xn^\alpha\rfloor \bigg)\\
&\quad \sim \frac{(xn^\alpha)^{r-1}}{\Gamma(r)} \frac{1}{(n^ \alpha \lambda^\alpha \Gamma(1-\alpha))^r}\left( 1- \frac{1}{\Psi(\lambda n)}\right)^{\lfloor xn^\alpha\rfloor }\\
&\quad \sim \frac{n^{-\alpha}x^{r-1}\lambda^{-\alpha r}}{\Gamma(r)\Gamma^r(1-\alpha)}\exp\left(-\frac{x\lambda^{-\alpha}}{\Gamma(1-\alpha)}\right),\end{align*}
Here we used (3.39) and
 \begin{align*}\lim_{n\to\infty}\left( 1- \frac{1}{\Psi(\lambda n)}\right)^{ \lfloor xn^\alpha\rfloor} & = \lim_{n\to\infty}\left( 1- \frac{x}{(xn^\alpha)n^{-\alpha}\Psi(\lambda n)}\right)^{ \lfloor xn^\alpha\rfloor}\\
& = \exp\left(-\frac{x\lambda^{-\alpha}}{\Gamma(1-\alpha)}\right).\end{align*}
\begin{align*}\lim_{n\to\infty}\left( 1- \frac{1}{\Psi(\lambda n)}\right)^{ \lfloor xn^\alpha\rfloor} & = \lim_{n\to\infty}\left( 1- \frac{x}{(xn^\alpha)n^{-\alpha}\Psi(\lambda n)}\right)^{ \lfloor xn^\alpha\rfloor}\\
& = \exp\left(-\frac{x\lambda^{-\alpha}}{\Gamma(1-\alpha)}\right).\end{align*}
Thus we have proved (3.30).
(c) From (3.6) we can write
 \begin{align}\ell_n(\lambda n)& = \frac{ \int_0^{\lambda n} \sum_{j=1}^n (z^j/j!) z^{-\alpha-1}e^{-z}\text{d} z}{\int_0^{\lambda n}z^{-\alpha-1}(1-e^{-z})\text{d} z}\nonumber\\
& = 1- \frac{ \int_0^{\lambda n} \sum_{j=n+1}^\infty (z^j/j!) z^{-\alpha-1}e^{-z}\text{d} z}{\int_0^{\lambda n}z^{-\alpha-1}(1-e^{-z})\text{d} z}.\end{align}
\begin{align}\ell_n(\lambda n)& = \frac{ \int_0^{\lambda n} \sum_{j=1}^n (z^j/j!) z^{-\alpha-1}e^{-z}\text{d} z}{\int_0^{\lambda n}z^{-\alpha-1}(1-e^{-z})\text{d} z}\nonumber\\
& = 1- \frac{ \int_0^{\lambda n} \sum_{j=n+1}^\infty (z^j/j!) z^{-\alpha-1}e^{-z}\text{d} z}{\int_0^{\lambda n}z^{-\alpha-1}(1-e^{-z})\text{d} z}.\end{align}
The numerator here is
When
![]() $0<\lambda<1$
, the right-hand side is, by Chebyshev’s inequality,
$0<\lambda<1$
, the right-hand side is, by Chebyshev’s inequality,
 \begin{eqnarray*} && n^{-\alpha} \int_0^{\lambda }\mathbb{P}(\text{Poiss} (nz)-nz>n(1-z)) z^{-\alpha-1}\text{dz} \\
&\le & \ n^{-\alpha} \int_0^{1 } \frac{(nz)z^{-\alpha-1}}{(n(1-z))^2} \text{d} z = o(n^{-\alpha}),\ \text{as}\ n\to \infty,\end{eqnarray*}
\begin{eqnarray*} && n^{-\alpha} \int_0^{\lambda }\mathbb{P}(\text{Poiss} (nz)-nz>n(1-z)) z^{-\alpha-1}\text{dz} \\
&\le & \ n^{-\alpha} \int_0^{1 } \frac{(nz)z^{-\alpha-1}}{(n(1-z))^2} \text{d} z = o(n^{-\alpha}),\ \text{as}\ n\to \infty,\end{eqnarray*}
so the right-hand side of (3.41) is asymptotic to
 \begin{equation*} n^{-\alpha} {\textbf 1}_{\{\lambda>1\}} \int_1^{\lambda }\mathbb{P}\Bigg(\frac{ \text{Poiss} (nz)} {nz} >\frac{1}{z}\Bigg) z^{-\alpha-1}\text{d} z \sim n^{-\alpha} {\textbf 1}_{\{\lambda>1\}} \frac{1-\lambda^{-\alpha}} {\alpha}.\end{equation*}
\begin{equation*} n^{-\alpha} {\textbf 1}_{\{\lambda>1\}} \int_1^{\lambda }\mathbb{P}\Bigg(\frac{ \text{Poiss} (nz)} {nz} >\frac{1}{z}\Bigg) z^{-\alpha-1}\text{d} z \sim n^{-\alpha} {\textbf 1}_{\{\lambda>1\}} \frac{1-\lambda^{-\alpha}} {\alpha}.\end{equation*}
Since the denominator in (3.40) tends to
![]() $\Gamma(1-\alpha)/\alpha$
, we have
$\Gamma(1-\alpha)/\alpha$
, we have
and the right-hand side here tends to the right-hand side of (3.31).
Finally, to prove (3.32) simply multiply (3.30) and (3.31) together.
Now to continue with the proof of Theorem 2.1, return to (3.28) and, formally, take the limits in (3.29) and (3.32) through the integral in (3.28) to get the expression on the right-hand side of (2.8).
Justifying this interchange directly by dominated convergence seems difficult, so we take an indirect approach. The idea is to show that the right-hand side of (2.8) is in fact a probability density function, i.e., integrates to 1. This will complete the proof of the theorem by the following argument.
Take
![]() $a=0$
and
$a=0$
and
![]() $b=y>0$
in (3.27), and write, for
$b=y>0$
in (3.27), and write, for
![]() $y>0$
,
$y>0$
,
 \begin{equation*} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg)=\int_0^y \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \in \text{d} x\Bigg)= \int_{x=0}^y \int_{\lambda>0} f_n(x,\lambda)\text{d} x,\end{equation*}
\begin{equation*} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg)=\int_0^y \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \in \text{d} x\Bigg)= \int_{x=0}^y \int_{\lambda>0} f_n(x,\lambda)\text{d} x,\end{equation*}
where
![]() $ f_n(x,\lambda)$
is the integrand in (2.8). Then by Fatou’s lemma
$ f_n(x,\lambda)$
is the integrand in (2.8). Then by Fatou’s lemma
 \begin{eqnarray*} \liminf_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg) & =& \ \liminf_{n\to\infty}\int_{x=0} ^y \int_{\lambda>0} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \nonumber \\
&\ge &\ \int_ {x=0} ^y \int_{\lambda>0} \liminf_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda=\int_{x=0}^y \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda,\end{eqnarray*}
\begin{eqnarray*} \liminf_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg) & =& \ \liminf_{n\to\infty}\int_{x=0} ^y \int_{\lambda>0} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \nonumber \\
&\ge &\ \int_ {x=0} ^y \int_{\lambda>0} \liminf_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda=\int_{x=0}^y \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda,\end{eqnarray*}
where the limit
![]() $ \lim_{n\to\infty} f_n(x,\lambda)$
exists as the product of the limits (3.29) and (3.32) in Proposition 3.2. Similarly
$ \lim_{n\to\infty} f_n(x,\lambda)$
exists as the product of the limits (3.29) and (3.32) in Proposition 3.2. Similarly
 \begin{eqnarray*}\liminf_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} >y\Bigg) & =& \ \liminf_{n\to\infty}\int_{x=y} ^\infty \int_{\lambda>0} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \nonumber \\
&\ge &\ \int_{x=y}^\infty \int_{\lambda>0} \liminf_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda=\int_{x=y}^\infty \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda .\end{eqnarray*}
\begin{eqnarray*}\liminf_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} >y\Bigg) & =& \ \liminf_{n\to\infty}\int_{x=y} ^\infty \int_{\lambda>0} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \nonumber \\
&\ge &\ \int_{x=y}^\infty \int_{\lambda>0} \liminf_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda=\int_{x=y}^\infty \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda .\end{eqnarray*}
Suppose we know
Then
 \begin{align*} \limsup_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg) & = 1- \liminf_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} >y\Bigg)\\
&= 1- \liminf_{n\to\infty}\int_{x=y}^\infty \int_{\lambda>0} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \\
&\le 1-\int_{x=y}^\infty \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \\
& = \int_{x=0}^y \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda,\end{align*}
\begin{align*} \limsup_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg) & = 1- \liminf_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} >y\Bigg)\\
&= 1- \liminf_{n\to\infty}\int_{x=y}^\infty \int_{\lambda>0} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \\
&\le 1-\int_{x=y}^\infty \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda \\
& = \int_{x=0}^y \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda,\end{align*}
and from these we deduce
 \begin{eqnarray*} \lim_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg)=\int_0^y \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda.\end{eqnarray*}
\begin{eqnarray*} \lim_{n\to\infty} \mathbb{P}\Bigg(\frac{K_n(\alpha,r)}{n^\alpha} \le y\Bigg)=\int_0^y \int_{\lambda>0} \lim_{n\to\infty} f_n(x,\lambda)\text{d} x \, \text{d} \lambda.\end{eqnarray*}
Since
![]() $ \lim_{n\to\infty} f_n(x,\lambda)$
is the integrand in (2.8), this completes the proof of (2.8) subject to proving (3.42). This is done in the next two sections.
$ \lim_{n\to\infty} f_n(x,\lambda)$
is the integrand in (2.8), this completes the proof of (2.8) subject to proving (3.42). This is done in the next two sections.
4. The negative binomial point process and its sum
We need some concepts concerning a negative binomial point process which are set out in [Reference Ipsen, Maller and Shemehsavar14]. We refer to that paper for further background and details. The dependence of the various quantities on the parameters
![]() $\alpha$
and r is not always made explicit in that paper. Here we need to make it explicit for clarity.
$\alpha$
and r is not always made explicit in that paper. Here we need to make it explicit for clarity.
Let
![]() $\mathbb{B}^{(r)}$
be a negative binomial point process with measure
$\mathbb{B}^{(r)}$
be a negative binomial point process with measure
![]() $\alpha x^{-\alpha-1} \text{d} x {\textbf 1}_{\{0<x\le 1\}}$
, for
$\alpha x^{-\alpha-1} \text{d} x {\textbf 1}_{\{0<x\le 1\}}$
, for
![]() $r>0$
,
$r>0$
,
![]() $\alpha\in(0,1)$
, in the sense of Gregoire [Reference Gregoire9], and define
$\alpha\in(0,1)$
, in the sense of Gregoire [Reference Gregoire9], and define
![]() ${}^{(\alpha,r)}T$
to be the sum of the points in
${}^{(\alpha,r)}T$
to be the sum of the points in
![]() $\mathbb{B}^{(r)}$
. The variable
$\mathbb{B}^{(r)}$
. The variable
![]() ${}^{( \alpha, r)}T$
has a density
${}^{( \alpha, r)}T$
has a density
and a Laplace transform
 \begin{equation}\mathbb{E}\big(e^{ -\tau\times {}^{( \alpha, r)}T}\big) =\int_0^\infty e^{-\tau t} g_{ \alpha, r}(t) \text{d} t =\Bigg(1 + \alpha \int_{0}^{1} (1- e^{ -\tau x})x^{-\alpha-1} \text{d} x \Bigg)^{-r},\end{equation}
\begin{equation}\mathbb{E}\big(e^{ -\tau\times {}^{( \alpha, r)}T}\big) =\int_0^\infty e^{-\tau t} g_{ \alpha, r}(t) \text{d} t =\Bigg(1 + \alpha \int_{0}^{1} (1- e^{ -\tau x})x^{-\alpha-1} \text{d} x \Bigg)^{-r},\end{equation}
for
![]() $ \tau>0$
,
$ \tau>0$
,
![]() $r\in\mathbb{N}$
. This implies the convolution formula
$r\in\mathbb{N}$
. This implies the convolution formula
(independent copies on the left-hand side). Let
![]() $G_{\alpha,r}(t) =\int_0^t g_{\alpha,r}(y)\text{d} y$
,
$G_{\alpha,r}(t) =\int_0^t g_{\alpha,r}(y)\text{d} y$
,
![]() $t\ge 0$
, be the cumulative distribution function of
$t\ge 0$
, be the cumulative distribution function of
![]() $ {}^{(\alpha, r)}T$
. The next lemma connects these ideas with the result of Theorem 2.1.
$ {}^{(\alpha, r)}T$
. The next lemma connects these ideas with the result of Theorem 2.1.
Lemma 4.1. The integral on the right-hand side of (2.8), taken with
![]() $y=\infty$
, equals
$y=\infty$
, equals
Proof of Lemma 4.1: Split the
![]() $\lambda$
-integral on the right-hand side of (2.8) into two components: one component over
$\lambda$
-integral on the right-hand side of (2.8) into two components: one component over
![]() $\lambda\in(0,1]$
and the other over
$\lambda\in(0,1]$
and the other over
![]() $\lambda>1$
. For the integral over
$\lambda>1$
. For the integral over
![]() $\lambda\in (1,\infty)$
we compute (with
$\lambda\in (1,\infty)$
we compute (with
![]() $y=\infty$
in (2.8))
$y=\infty$
in (2.8))
 \begin{eqnarray}&& \frac{1}{\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty \int_{\lambda=1}^\infty x^{r-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x}{\Gamma(1-\alpha)}\right) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x \nonumber \\
&&\quad = \frac{1}{\alpha r\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty x^{r-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x}{\Gamma(1-\alpha)}\right) \text{d} x.\end{eqnarray}
\begin{eqnarray}&& \frac{1}{\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty \int_{\lambda=1}^\infty x^{r-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x}{\Gamma(1-\alpha)}\right) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x \nonumber \\
&&\quad = \frac{1}{\alpha r\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty x^{r-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x}{\Gamma(1-\alpha)}\right) \text{d} x.\end{eqnarray}
By (2.6) and (2.7), each
![]() $Y_x(\lambda)$
has characteristic function
$Y_x(\lambda)$
has characteristic function
 \begin{equation}\mathbb{E} e^{\text{i}\theta Y_x(\lambda)} =\exp\Bigg(\frac{x}{\Gamma(1-\alpha)}\int_0^{\lambda\wedge 1} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y)\Bigg), \qquad \theta\in \Bbb{R}.\end{equation}
\begin{equation}\mathbb{E} e^{\text{i}\theta Y_x(\lambda)} =\exp\Bigg(\frac{x}{\Gamma(1-\alpha)}\int_0^{\lambda\wedge 1} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y)\Bigg), \qquad \theta\in \Bbb{R}.\end{equation}
Taking
![]() $\lambda>1$
in (4.6), the right-hand side of (4.5) is, by Fourier inversion,
$\lambda>1$
in (4.6), the right-hand side of (4.5) is, by Fourier inversion,
 \begin{eqnarray}&& \frac{1}{\alpha r\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty x^{r-1} \exp\left(-\frac{x}{\Gamma(1-\alpha)}\right) \nonumber \\
&&\quad \times \frac{1}{2\pi}\int_{\theta=-\infty}^\infty e^{-\text{i}\theta}\exp\Bigg(\frac{x}{\Gamma(1-\alpha)}\int_0^{1} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Bigg) \text{d} x\, \text{d} \theta\nonumber\\
&&\quad = \frac{1}{2\pi\alpha r}\int_{\theta=-\infty}^\infty\frac{ e^{-\text{i}\theta} \text{d} \theta}{\Bigg(1-\int_0^{1} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Bigg)^r}\nonumber\\
&&\quad = \frac{1}{\alpha r}g_{\alpha,r}(1).\end{eqnarray}
\begin{eqnarray}&& \frac{1}{\alpha r\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty x^{r-1} \exp\left(-\frac{x}{\Gamma(1-\alpha)}\right) \nonumber \\
&&\quad \times \frac{1}{2\pi}\int_{\theta=-\infty}^\infty e^{-\text{i}\theta}\exp\Bigg(\frac{x}{\Gamma(1-\alpha)}\int_0^{1} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Bigg) \text{d} x\, \text{d} \theta\nonumber\\
&&\quad = \frac{1}{2\pi\alpha r}\int_{\theta=-\infty}^\infty\frac{ e^{-\text{i}\theta} \text{d} \theta}{\Bigg(1-\int_0^{1} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Bigg)^r}\nonumber\\
&&\quad = \frac{1}{\alpha r}g_{\alpha,r}(1).\end{eqnarray}
The last line follows from setting
![]() $\tau=-\text{i} \theta$
in (4.2) and observing that we have the Fourier inverse of
$\tau=-\text{i} \theta$
in (4.2) and observing that we have the Fourier inverse of
![]() $g_{\alpha,r}$
at 1. For the integral over
$g_{\alpha,r}$
at 1. For the integral over
![]() $\lambda\in(0,1] $
we compute
$\lambda\in(0,1] $
we compute
 \begin{eqnarray}&& \frac{1}{2\pi\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty \int_{\lambda=0}^1 \int_{\theta=-\infty}^\infty e^{-\text{i}\theta}x^{r-1}\exp\left(-\frac{x \lambda^{-\alpha }}{\Gamma(1-\alpha)}\right) \nonumber\\
&&\times \exp\Bigg(\frac{x}{\Gamma(1-\alpha)}\int_0^{\lambda} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Bigg) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x \text{d} \theta \nonumber\\
&&= \int_{\lambda=0}^1\frac{1}{2\pi}\int_{\theta=-\infty}^\infty\frac{ e^{-\text{i}\theta }\lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} \theta}{\Big(\lambda^{-\alpha} -\lambda^{-\alpha } \int_0^1 \big( e^{\text{i}\theta y\lambda}-1\big) \alpha y^{-\alpha-1}\text{d} y\Big)^r}\nonumber\\
&&= \int_{\lambda=0}^1 \frac{1}{2\pi}\int_{\theta=-\infty}^\infty\frac{ e^{-\text{i}\theta/\lambda }\lambda^{-2}\text{d} \lambda\, \text{d} \theta}{\Big(1 -\int_0^1 \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Big)^r}\nonumber\\
&&= \int_{\lambda=0}^1 \lambda^{-2} g_{\alpha,r}(1/\lambda) \text{d} \lambda\nonumber\\
&&= \int_{\lambda=1}^\infty g_{\alpha,r}(\lambda) \text{d} \lambda=1- \int_{\lambda=0}^1 g_{\alpha,r}(\lambda) \text{d} \lambda=1- G_{\alpha,r}(1).\end{eqnarray}
\begin{eqnarray}&& \frac{1}{2\pi\Gamma(r)\Gamma^r(1-\alpha)}\int_{x=0}^\infty \int_{\lambda=0}^1 \int_{\theta=-\infty}^\infty e^{-\text{i}\theta}x^{r-1}\exp\left(-\frac{x \lambda^{-\alpha }}{\Gamma(1-\alpha)}\right) \nonumber\\
&&\times \exp\Bigg(\frac{x}{\Gamma(1-\alpha)}\int_0^{\lambda} \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Bigg) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x \text{d} \theta \nonumber\\
&&= \int_{\lambda=0}^1\frac{1}{2\pi}\int_{\theta=-\infty}^\infty\frac{ e^{-\text{i}\theta }\lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} \theta}{\Big(\lambda^{-\alpha} -\lambda^{-\alpha } \int_0^1 \big( e^{\text{i}\theta y\lambda}-1\big) \alpha y^{-\alpha-1}\text{d} y\Big)^r}\nonumber\\
&&= \int_{\lambda=0}^1 \frac{1}{2\pi}\int_{\theta=-\infty}^\infty\frac{ e^{-\text{i}\theta/\lambda }\lambda^{-2}\text{d} \lambda\, \text{d} \theta}{\Big(1 -\int_0^1 \big( e^{\text{i}\theta y}-1\big) \alpha y^{-\alpha-1}\text{d} y\Big)^r}\nonumber\\
&&= \int_{\lambda=0}^1 \lambda^{-2} g_{\alpha,r}(1/\lambda) \text{d} \lambda\nonumber\\
&&= \int_{\lambda=1}^\infty g_{\alpha,r}(\lambda) \text{d} \lambda=1- \int_{\lambda=0}^1 g_{\alpha,r}(\lambda) \text{d} \lambda=1- G_{\alpha,r}(1).\end{eqnarray}
Adding (4.7) and (4.8) gives (4.4).
Thus to achieve our aim of showing that the right-hand side of (2.8) defines a proper distribution, we have to show that the expression in (4.4) equals 1. We do this by developing a connection with the theory of Dickman functions.
5. Generalised Dickman functions
The generalised Dickman function, when normalised, occurs naturally as the density of the infinitely divisible random variable
![]() $Y_a$
having Laplace transform
$Y_a$
having Laplace transform
 \begin{equation}\mathbb{E} (e^{-\tau Y_a} )=\exp\Bigg(-a\int_0^1 \big( 1-e^{-\tau y}\big) \text{d} y/y\Bigg), \qquad \tau>0, \ a>0.\end{equation}
\begin{equation}\mathbb{E} (e^{-\tau Y_a} )=\exp\Bigg(-a\int_0^1 \big( 1-e^{-\tau y}\big) \text{d} y/y\Bigg), \qquad \tau>0, \ a>0.\end{equation}
(There should be no confusion with the
![]() $Y_t(\lambda)$
defined in (2.6).) The descriptor ‘generalised’ was added by [Reference Pinsky22]; it signifies the inclusion of the parameter
$Y_t(\lambda)$
defined in (2.6).) The descriptor ‘generalised’ was added by [Reference Pinsky22]; it signifies the inclusion of the parameter
![]() $a>0$
in (5.1), where
$a>0$
in (5.1), where
![]() $a=1$
defines the Dickman distribution as usually understood. The process
$a=1$
defines the Dickman distribution as usually understood. The process
![]() $${({Y_t})_{t > 0}}$$
is described as the Dickman subordinator in [Reference Caravenna, Sun and Zygouras3].
$${({Y_t})_{t > 0}}$$
is described as the Dickman subordinator in [Reference Caravenna, Sun and Zygouras3].
Properties of the Dickman function (also known as the Dickman–de Bruijn function; see [Reference Moree20] for a review) and of its associated distribution have been teased out over the years since its original formulation in [Reference Dickman5] in a number-theoretic context. The papers [Reference Penrose and Wade21] and [Reference Pinsky22] provide convenient summaries, for our purposes, of these properties, and of the generalised version. In particular, they give the formula for the density
![]() $f_{Y_a}(y)$
of
$f_{Y_a}(y)$
of
![]() $Y_a$
as
$Y_a$
as
![]() $f_{Y_a}(y)= e^{-a\gamma} \rho_a(y)/ \Gamma(a)$
,
$f_{Y_a}(y)= e^{-a\gamma} \rho_a(y)/ \Gamma(a)$
,
![]() $y>0$
, where
$y>0$
, where
![]() $\gamma=0.577...$
is Euler’s constant,
$\gamma=0.577...$
is Euler’s constant,
and
![]() $\rho_a(y)$
satisfies a certain differential-delay equation for
$\rho_a(y)$
satisfies a certain differential-delay equation for
![]() $y>1$
. There is also the representation
$y>1$
. There is also the representation
(see [Reference Pinsky22, Propositian 5.1, p. 14]) where the Uniform [0, 1] random variable U and the
![]() $Y_a$
on the right-hand side are independent. Notably, with
$Y_a$
on the right-hand side are independent. Notably, with
![]() $ F_{Y_a}(y) \,{:}\,{\raise-1.5pt{=}}\, \mathbb{P}(Y_a\le y)$
, we see from (5.2) that
$ F_{Y_a}(y) \,{:}\,{\raise-1.5pt{=}}\, \mathbb{P}(Y_a\le y)$
, we see from (5.2) that
which can be compared with (4.4).
Suppose we were to let
![]() $r\to\infty$
and
$r\to\infty$
and
![]() $\alpha=\alpha_r\downarrow 0$
in such a way that
$\alpha=\alpha_r\downarrow 0$
in such a way that
![]() $\alpha_rr\to a\in(0,\infty)$
, and it were the case that
$\alpha_rr\to a\in(0,\infty)$
, and it were the case that
That this is plausible is indicated by inspection of (4.2) and (5.1). Then from (5.4) and (5.5) we would have
suggesting perhaps that the identity
is true for each
![]() $\alpha\in(0,1)$
and
$\alpha\in(0,1)$
and
![]() $r>0$
, not just in the limit. This would prove that the expression in (4.4) equals 1.
$r>0$
, not just in the limit. This would prove that the expression in (4.4) equals 1.
These heuristics could possibly be made to give a rigorous proof of (5.7), but we do not go down that route; rather, we deal directly with
![]() $g_{\alpha,r}(x)$
and show that (5.7) holds by generalising the Dickman relationship, in the next subsection.
$g_{\alpha,r}(x)$
and show that (5.7) holds by generalising the Dickman relationship, in the next subsection.
5.1. The function
 $\textbf{\textit{g}}_{\boldsymbol{\alpha}, \textbf{\textit{r}}}$
as an
$\textbf{\textit{g}}_{\boldsymbol{\alpha}, \textbf{\textit{r}}}$
as an
 ${\boldsymbol{(\alpha,} \textbf{\textit{r}}\textbf{)}}$
-generalised Dickman distribution
${\boldsymbol{(\alpha,} \textbf{\textit{r}}\textbf{)}}$
-generalised Dickman distribution
We proceed by giving an analogue of (5.3) for the negative binomial sums
![]() $^{(\alpha,r)}T$
, then show that this implies (5.7).
$^{(\alpha,r)}T$
, then show that this implies (5.7).
Proposition 5.1.
-
(i) For each
 $\alpha\in(0,1)$
and
$\alpha\in(0,1)$
and
 $r>0$
we have
(5.8)where the Uniform [0, 1] random variable U and the
$r>0$
we have
(5.8)where the Uniform [0, 1] random variable U and the $$^{(\alpha ,r)}T\mathop = \limits^{\rm{D}} {U^{{1 \over {\alpha r}}}}{(^{(\alpha ,r + 1)}}T + 1),$$
$$^{(\alpha ,r)}T\mathop = \limits^{\rm{D}} {U^{{1 \over {\alpha r}}}}{(^{(\alpha ,r + 1)}}T + 1),$$
 $^{(\alpha,r+1)}T $
on the right-hand side are independent.
$^{(\alpha,r+1)}T $
on the right-hand side are independent.
-
(ii) Consequently, (5.7) is true for each
 $\alpha\in(0,1)$
and
$\alpha\in(0,1)$
and
 $r>0$
.
$r>0$
.
Proof of Proposition 5.1: First we prove Part (i). Throughout this proof we write
![]() $a= \alpha r$
for the combination
$a= \alpha r$
for the combination
![]() $ \alpha r$
, which will occur frequently. With this in mind, we begin by noting that
$ \alpha r$
, which will occur frequently. With this in mind, we begin by noting that
 \begin{eqnarray*} &&\frac{\text{d} }{\text{d\ u}} \Bigg( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Bigg)^{-r} \\
&&\quad =-\tau u^{1/a-1}\int_0^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y\times \frac{1}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r+1}},\end{eqnarray*}
\begin{eqnarray*} &&\frac{\text{d} }{\text{d\ u}} \Bigg( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Bigg)^{-r} \\
&&\quad =-\tau u^{1/a-1}\int_0^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y\times \frac{1}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r+1}},\end{eqnarray*}
for
![]() $0<u<1$
. So, integrating by parts,
$0<u<1$
. So, integrating by parts,
 \begin{eqnarray}&&\int_{u=0}^1\frac{\tau u^{1/a}}{u}\int_{y=0}^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y\times \frac{ u\, \text{d} u}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r+1}} \nonumber \\
&&\quad =-\frac{1}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau y}\big) y^{-\alpha-1}\text{d} y\Big)^r} + \int_{u=0}^1\frac{\text{d} u}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r}}.\nonumber\\
\end{eqnarray}
\begin{eqnarray}&&\int_{u=0}^1\frac{\tau u^{1/a}}{u}\int_{y=0}^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y\times \frac{ u\, \text{d} u}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r+1}} \nonumber \\
&&\quad =-\frac{1}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau y}\big) y^{-\alpha-1}\text{d} y\Big)^r} + \int_{u=0}^1\frac{\text{d} u}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r}}.\nonumber\\
\end{eqnarray}
The first term on the right-hand side of (5.9) is
![]() $-\mathbb{E}(e^{-\tau \times ^{(\alpha,r)}T})$
(recall (4.2)). Rearranging (5.9) gives
$-\mathbb{E}(e^{-\tau \times ^{(\alpha,r)}T})$
(recall (4.2)). Rearranging (5.9) gives
 \begin{align}\mathbb{E}(e^{-\tau \times ^{(\alpha,r)}T})= & \int_0^1 \frac{1}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r}}\nonumber \\
& \times \left(1-\frac{\tau u^{1/a}}{{ 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y} }\int_0^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y\right)\text{d} u.\nonumber\\
\end{align}
\begin{align}\mathbb{E}(e^{-\tau \times ^{(\alpha,r)}T})= & \int_0^1 \frac{1}{ \Big( 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a}y}\big) y^{-\alpha-1}\text{d} y\Big)^{r}}\nonumber \\
& \times \left(1-\frac{\tau u^{1/a}}{{ 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y} }\int_0^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y\right)\text{d} u.\nonumber\\
\end{align}
The second term on the right-hand side, in parentheses, equals
 \begin{equation*}\frac{1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y-\tau u^{1/a}\int_0^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y }{{ 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y} },\end{equation*}
\begin{equation*}\frac{1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y-\tau u^{1/a}\int_0^1 e^{-\tau u^{1/a}y} y^{-\alpha}\text{d} y }{{ 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y} },\end{equation*}
and after an integration by parts in the numerator this equals
 \begin{equation*}\frac{ e^{-\tau u^{1/a} } }{{ 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y} }=e^{-\tau u^{1/a} } \times \mathbb{E}\big(e^{-\tau u^{1/a}\times ^{(\alpha,1)}T}\big).\end{equation*}
\begin{equation*}\frac{ e^{-\tau u^{1/a} } }{{ 1+\alpha \int_0^1\big(1- e^{-\tau u^{1/a} y}\big) y^{-\alpha-1}\text{d} y} }=e^{-\tau u^{1/a} } \times \mathbb{E}\big(e^{-\tau u^{1/a}\times ^{(\alpha,1)}T}\big).\end{equation*}
Substituting back in (5.10) gives
 \begin{align}\mathbb{E}\big(e^{-\tau \times ^{(\alpha,r)}T}\big) & = \int_0^1 e^{-\tau u^{1/a}} \times \mathbb{E}\big(e^{-\tau u^{1/a} \times ^{(\alpha,1)}T}\big)\times \mathbb{E}\big(e^{-\tau u^{1/a}\times ^{(\alpha,r)}T}\big)\text{d} u\nonumber \\
& = \int_0^1 \mathbb{E}\big(e^{-\tau u^{1/a}(^{(\alpha,r+1)}T+1)}\big)\text{d} u,\end{align}
\begin{align}\mathbb{E}\big(e^{-\tau \times ^{(\alpha,r)}T}\big) & = \int_0^1 e^{-\tau u^{1/a}} \times \mathbb{E}\big(e^{-\tau u^{1/a} \times ^{(\alpha,1)}T}\big)\times \mathbb{E}\big(e^{-\tau u^{1/a}\times ^{(\alpha,r)}T}\big)\text{d} u\nonumber \\
& = \int_0^1 \mathbb{E}\big(e^{-\tau u^{1/a}(^{(\alpha,r+1)}T+1)}\big)\text{d} u,\end{align}
where the last equality follows from (4.3). So, recalling that
![]() $a\equiv \alpha r$
, we arrive at (5.8).
$a\equiv \alpha r$
, we arrive at (5.8).
We now prove Part (ii). From (5.8) we can write, for
![]() $t>0$
,
$t>0$
,
 \begin{align} G_{\alpha,r}(t) & = \mathbb{P}\big( ^{(\alpha,r)}T \le t\big)=\mathbb{P}\big( U^{\frac{1}{ \alpha r} } \big( ^{(\alpha,r+1)}T +1\big)\le t\big)\nonumber\\
& = \int_0^1 \mathbb{P}\big( ^{(\alpha,r+1)}T \le t u^{-1/a}-1\big) \text{d} u \nonumber\\
& = \int_0^1 G_{\alpha,r+1}\big(t u^{-1/a}-1\big) \text{d} u\nonumber\\
& = at^a \int_{t-1}^\infty G_{\alpha,r+1}(v) (1+v )^{-1-a} \text{d} v.\end{align}
\begin{align} G_{\alpha,r}(t) & = \mathbb{P}\big( ^{(\alpha,r)}T \le t\big)=\mathbb{P}\big( U^{\frac{1}{ \alpha r} } \big( ^{(\alpha,r+1)}T +1\big)\le t\big)\nonumber\\
& = \int_0^1 \mathbb{P}\big( ^{(\alpha,r+1)}T \le t u^{-1/a}-1\big) \text{d} u \nonumber\\
& = \int_0^1 G_{\alpha,r+1}\big(t u^{-1/a}-1\big) \text{d} u\nonumber\\
& = at^a \int_{t-1}^\infty G_{\alpha,r+1}(v) (1+v )^{-1-a} \text{d} v.\end{align}
Now since
![]() $ G_{\alpha,r+1}(v) =0$
for
$ G_{\alpha,r+1}(v) =0$
for
![]() $v<0$
, we have for
$v<0$
, we have for
![]() $0<t\le 1$
$0<t\le 1$
It follows that
![]() $ G_{\alpha,r}(t) = a t^a c_{\alpha,r+1} $
for
$ G_{\alpha,r}(t) = a t^a c_{\alpha,r+1} $
for
![]() $0<t\le 1$
; hence
$0<t\le 1$
; hence
for
![]() $0<t\le 1$
. So, recalling that
$0<t\le 1$
. So, recalling that
![]() $a\equiv \alpha r$
, we have proved (5.7).
$a\equiv \alpha r$
, we have proved (5.7).
With (5.7), we have completed the proof of Theorem 2.1.
Remark 5.1. In (5.8), letting
![]() $r\to\infty$
and
$r\to\infty$
and
![]() $\alpha\downarrow 0$
so that
$\alpha\downarrow 0$
so that
![]() $r\alpha\to a\in(0,\infty)$
, we recover (5.3), and taking the same limit in (4.2) we recover (5.1). In this sense the negative binomial sums
$r\alpha\to a\in(0,\infty)$
, we recover (5.3), and taking the same limit in (4.2) we recover (5.1). In this sense the negative binomial sums
![]() $^{(\alpha,r)}T$
can be thought of as a two-parameter generalisation of the Dickman random variable
$^{(\alpha,r)}T$
can be thought of as a two-parameter generalisation of the Dickman random variable
![]() $Y_a$
. (This is distinct from a two-parameter generalisation of the Dickman function due to [Reference Handa11], and from the two-parameter generalisation of the Poisson–Dirichlet distribution in [Reference Pitman and Yor24]. Another generalisation having application in polymer modelling occurs in [Reference Caravenna, Sun and Zygouras3] as a multivariate Dickman–Gaussian combination.)
$Y_a$
. (This is distinct from a two-parameter generalisation of the Dickman function due to [Reference Handa11], and from the two-parameter generalisation of the Poisson–Dirichlet distribution in [Reference Pitman and Yor24]. Another generalisation having application in polymer modelling occurs in [Reference Caravenna, Sun and Zygouras3] as a multivariate Dickman–Gaussian combination.)
Differentiating (5.12) we obtain, for
![]() $t>1$
, the density in the form
$t>1$
, the density in the form
and differentiating this further gives
This can be compared with the corresponding differential-delay equation for the Dickman function (see [Reference Pinsky22, Equation (5.10)]). See Section 6 of [Reference Pinsky22] for further interesting discussion.
6. Properties of the limiting distribution
Let
![]() $K=K(\alpha,r)$
be the limiting random variable of
$K=K(\alpha,r)$
be the limiting random variable of
![]() $n^{-\alpha}K_n(\alpha,r)$
as
$n^{-\alpha}K_n(\alpha,r)$
as
![]() $n\to\infty$
, whose distribution is given by the right-hand side of (2.8), and let
$n\to\infty$
, whose distribution is given by the right-hand side of (2.8), and let
![]() $f_{Y_t(\lambda)}(y)$
,
$f_{Y_t(\lambda)}(y)$
,
![]() $y>0$
, be the density of the subordinator
$y>0$
, be the density of the subordinator
![]() $${({Y_t}(\lambda ))_{t > 0}}$$
whose Laplace transform is in (2.6). In this section we derive some properties of this distribution, first getting it in a form more amenable to numerical computation, then, in Subsection 6.2, deriving formulae for the moments of the distribution.
$${({Y_t}(\lambda ))_{t > 0}}$$
whose Laplace transform is in (2.6). In this section we derive some properties of this distribution, first getting it in a form more amenable to numerical computation, then, in Subsection 6.2, deriving formulae for the moments of the distribution.
6.1. The limiting distribution as a gamma mixture and subordinated truncated stable process
As before, consider the
![]() $\lambda$
-integral on the right-hand side of (2.8) in two components: one over
$\lambda$
-integral on the right-hand side of (2.8) in two components: one over
![]() $\lambda\in(0,1]$
and the other over
$\lambda\in(0,1]$
and the other over
![]() $\lambda>1$
. From (2.6), when
$\lambda>1$
. From (2.6), when
![]() $0<\lambda\le 1$
,
$0<\lambda\le 1$
,
![]() $x>0$
,
$x>0$
,
![]() $\theta\in\Bbb{R}$
,
$\theta\in\Bbb{R}$
,
 \begin{align}\mathbb{E}\big( e^{\text{i}\theta Y_x(\lambda)} \big) & = \exp\Bigg(x\int_0^\lambda \big( e^{\text{i}\theta y}-1 \big) \alpha y^{-\alpha-1}\text{d} y/\Gamma(1-\alpha)\Bigg)\nonumber\\
& = \exp\Bigg(x\lambda^{-\alpha} \int_0^1\big( e^{\text{i}\theta\lambda y}-1 \big) \alpha y^{-\alpha-1}\text{d} y/\Gamma(1-\alpha)\Bigg)\nonumber\\
& = \mathbb{E}\big( e^{\text{i}\theta\lambda Y_{x\lambda^{-\alpha}}(1)} \big),\end{align}
\begin{align}\mathbb{E}\big( e^{\text{i}\theta Y_x(\lambda)} \big) & = \exp\Bigg(x\int_0^\lambda \big( e^{\text{i}\theta y}-1 \big) \alpha y^{-\alpha-1}\text{d} y/\Gamma(1-\alpha)\Bigg)\nonumber\\
& = \exp\Bigg(x\lambda^{-\alpha} \int_0^1\big( e^{\text{i}\theta\lambda y}-1 \big) \alpha y^{-\alpha-1}\text{d} y/\Gamma(1-\alpha)\Bigg)\nonumber\\
& = \mathbb{E}\big( e^{\text{i}\theta\lambda Y_{x\lambda^{-\alpha}}(1)} \big),\end{align}
so by the inversion formula for absolutely continuous distributions [Reference Sato26, p. 9],
 \begin{align}f_{Y_x(\lambda)}(1) & = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i}\theta}\mathbb{E}\big( e^{\text{i}\theta Y_x(\lambda)} \big)\text{d} \theta\nonumber\\
& = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i}\theta}\mathbb{E}\big( e^{\text{i}\theta\lambda Y_{x\lambda^{-\alpha}}(1)} \big)\text{d} \theta\nonumber\\
& = \frac{1}{2\pi\lambda} \int_{-\infty}^\infty e^{-\text{i}\theta/\lambda}\mathbb{E}\big( e^{\text{i}\theta Y_{x\lambda^{-\alpha}}(1)} \big)\text{d} \theta\nonumber\\
& = \lambda^{-1} f_{Y_{x\lambda^{-\alpha}}(1)}(\lambda^{-1}).\end{align}
\begin{align}f_{Y_x(\lambda)}(1) & = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i}\theta}\mathbb{E}\big( e^{\text{i}\theta Y_x(\lambda)} \big)\text{d} \theta\nonumber\\
& = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i}\theta}\mathbb{E}\big( e^{\text{i}\theta\lambda Y_{x\lambda^{-\alpha}}(1)} \big)\text{d} \theta\nonumber\\
& = \frac{1}{2\pi\lambda} \int_{-\infty}^\infty e^{-\text{i}\theta/\lambda}\mathbb{E}\big( e^{\text{i}\theta Y_{x\lambda^{-\alpha}}(1)} \big)\text{d} \theta\nonumber\\
& = \lambda^{-1} f_{Y_{x\lambda^{-\alpha}}(1)}(\lambda^{-1}).\end{align}
Substituting in (2.8) and changing variable from
![]() $x/\Gamma(1-\alpha)$
to x, we obtain
$x/\Gamma(1-\alpha)$
to x, we obtain
where now
![]() $\big(\widetilde Y_{t}\big)_{t>0}= \big(Y_{t\Gamma(1-\alpha)}(1)\big)_{t>0}$
is a subordinator with Laplace transform
$\big(\widetilde Y_{t}\big)_{t>0}= \big(Y_{t\Gamma(1-\alpha)}(1)\big)_{t>0}$
is a subordinator with Laplace transform
 \begin{equation}\mathbb{E}\big( e^{-\tau \widetilde Y_{t}} \big)=\exp\Bigg(-t \int_0^1\big( 1-e^{-\tau y} \big) \alpha y^{-\alpha-1}\text{d} y\Bigg), \qquad \tau>0, \ t\ge 0,\end{equation}
\begin{equation}\mathbb{E}\big( e^{-\tau \widetilde Y_{t}} \big)=\exp\Bigg(-t \int_0^1\big( 1-e^{-\tau y} \big) \alpha y^{-\alpha-1}\text{d} y\Bigg), \qquad \tau>0, \ t\ge 0,\end{equation}
not depending on
![]() $\lambda$
. To avoid carrying the factor
$\lambda$
. To avoid carrying the factor
![]() $\Gamma(1-\alpha)$
along, we replace
$\Gamma(1-\alpha)$
along, we replace
![]() $y/\Gamma(1-\alpha)$
by y in (6.3), so that we are now dealing with the cumulative distribution function of
$y/\Gamma(1-\alpha)$
by y in (6.3), so that we are now dealing with the cumulative distribution function of
![]() $K(\alpha,r)\Gamma(1-\alpha)$
. After a change of variable from
$K(\alpha,r)\Gamma(1-\alpha)$
. After a change of variable from
![]() $x\lambda^{-\alpha}$
to x, the expression in (6.3), with this replacement, equals
$x\lambda^{-\alpha}$
to x, the expression in (6.3), with this replacement, equals
 \begin{eqnarray}&& \frac{1}{\Gamma(r)}\int_{\lambda=0}^1\int_{x=0}^{y\lambda^{-\alpha}} x^{r-1} f_{\widetilde Y_{x}}(\lambda^{-1})e^{-x} \lambda^{-2}\text{d} \lambda\, \text{d} x \nonumber\\
&&= \frac{1}{\Gamma(r)} \left[\int_{x=0}^y \int_{\lambda=0}^1+ \int_{x=y}^\infty \int_{\lambda=0}^{(y/x)^{1/\alpha}} \right] x^{r-1} f_{\widetilde Y_{x}}(\lambda^{-1})e^{-x} \lambda^{-2}\text{d} \lambda\, \text{d} x,\end{eqnarray}
\begin{eqnarray}&& \frac{1}{\Gamma(r)}\int_{\lambda=0}^1\int_{x=0}^{y\lambda^{-\alpha}} x^{r-1} f_{\widetilde Y_{x}}(\lambda^{-1})e^{-x} \lambda^{-2}\text{d} \lambda\, \text{d} x \nonumber\\
&&= \frac{1}{\Gamma(r)} \left[\int_{x=0}^y \int_{\lambda=0}^1+ \int_{x=y}^\infty \int_{\lambda=0}^{(y/x)^{1/\alpha}} \right] x^{r-1} f_{\widetilde Y_{x}}(\lambda^{-1})e^{-x} \lambda^{-2}\text{d} \lambda\, \text{d} x,\end{eqnarray}
after an interchange of integration order. Let
![]() $\Gamma_r$
be a Gamma(r) random variable with density
$\Gamma_r$
be a Gamma(r) random variable with density
Changing variable from
![]() $\lambda^{-1}$
to
$\lambda^{-1}$
to
![]() $\lambda$
, we can write the right-hand side of (6.5) as
$\lambda$
, we can write the right-hand side of (6.5) as
 \begin{align} & \left[\int_{x=0}^y \int_{\lambda=1}^\infty+ \int_{x=y}^\infty \int_{\lambda=(x/y)^{1/\alpha}}^\infty \right] f_{\widetilde Y_{x}}(\lambda)f_{\Gamma_r}(x) \text{d} \lambda\, \text{d} x\nonumber\\
& =\int_{x=0}^y (1-F_{\widetilde Y_{x}}(1)) f_{\Gamma_r}(x) \text{d} x+ \int_{x=y}^\infty (1-F_{\widetilde Y_{x}} ((x/y)^{1/\alpha}) f_{\Gamma_r}(x) \text{d} x,\end{align}
\begin{align} & \left[\int_{x=0}^y \int_{\lambda=1}^\infty+ \int_{x=y}^\infty \int_{\lambda=(x/y)^{1/\alpha}}^\infty \right] f_{\widetilde Y_{x}}(\lambda)f_{\Gamma_r}(x) \text{d} \lambda\, \text{d} x\nonumber\\
& =\int_{x=0}^y (1-F_{\widetilde Y_{x}}(1)) f_{\Gamma_r}(x) \text{d} x+ \int_{x=y}^\infty (1-F_{\widetilde Y_{x}} ((x/y)^{1/\alpha}) f_{\Gamma_r}(x) \text{d} x,\end{align}
where
![]() $F_{\widetilde Y_{x}}$
is the cumulative distribution function of
$F_{\widetilde Y_{x}}$
is the cumulative distribution function of
![]() $\widetilde Y_x$
. This is for the component over
$\widetilde Y_x$
. This is for the component over
![]() $0<\lambda\le 1$
.
$0<\lambda\le 1$
.
For the integral over
![]() $\lambda\in (1,\infty)$
in (2.8) (with y replaced by
$\lambda\in (1,\infty)$
in (2.8) (with y replaced by
![]() $y/\Gamma(1-\alpha)$
), we compute
$y/\Gamma(1-\alpha)$
), we compute
 \begin{eqnarray}&& \frac{1}{\Gamma(r)} \int_{x=0}^y \int_{\lambda=1}^\infty x^{r-1} f_{\widetilde Y_{x}}(1)e^{-x} \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x\nonumber \\
&&= \frac{1}{\alpha r\Gamma(r)} \int_{x=0}^y x^{r-1} f_{\widetilde Y_{x}}(1)e^{-x}\text{d} x= \frac{1}{\alpha r} \int_{x=0}^y f_{\widetilde Y_{x}}(1) f_{\Gamma_r}(x) \text{d} x.\end{eqnarray}
\begin{eqnarray}&& \frac{1}{\Gamma(r)} \int_{x=0}^y \int_{\lambda=1}^\infty x^{r-1} f_{\widetilde Y_{x}}(1)e^{-x} \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x\nonumber \\
&&= \frac{1}{\alpha r\Gamma(r)} \int_{x=0}^y x^{r-1} f_{\widetilde Y_{x}}(1)e^{-x}\text{d} x= \frac{1}{\alpha r} \int_{x=0}^y f_{\widetilde Y_{x}}(1) f_{\Gamma_r}(x) \text{d} x.\end{eqnarray}
Adding (6.6) and (6.7) gives an expression for the cumulative distribution function of
![]() $K(\alpha,r)\Gamma(1-\alpha)$
as a kind of gamma mixture:
$K(\alpha,r)\Gamma(1-\alpha)$
as a kind of gamma mixture:
 \begin{align} \mathbb{P}(K(\alpha,r)\Gamma(1-\alpha)\le y) & = \int_{x=0}^y \left(1-F_{\widetilde Y_{x}}(1) + \frac{1}{\alpha r} f_{\widetilde Y_{x}}(1)\right) f_{\Gamma_r}(x) \text{d} x\nonumber\\
& + \int_{x=y}^\infty \big(1-F_{\widetilde Y_{x}}\big(\frac{x}{y}\big)^{1/\alpha}\big) f_{\Gamma_r}(x) \text{d} x.\ \ \ \quad \end{align}
\begin{align} \mathbb{P}(K(\alpha,r)\Gamma(1-\alpha)\le y) & = \int_{x=0}^y \left(1-F_{\widetilde Y_{x}}(1) + \frac{1}{\alpha r} f_{\widetilde Y_{x}}(1)\right) f_{\Gamma_r}(x) \text{d} x\nonumber\\
& + \int_{x=y}^\infty \big(1-F_{\widetilde Y_{x}}\big(\frac{x}{y}\big)^{1/\alpha}\big) f_{\Gamma_r}(x) \text{d} x.\ \ \ \quad \end{align}
This can also be written in terms of the subordinated variable
![]() $\widetilde Y_{\Gamma_r}$
, where now
$\widetilde Y_{\Gamma_r}$
, where now
![]() $${({\tilde Y_t})_{t > 0}}$$
and
$${({\tilde Y_t})_{t > 0}}$$
and
![]() $\Gamma_r$
are taken to be independent. The standardised process
$\Gamma_r$
are taken to be independent. The standardised process
![]() $${({\tilde Y_t})_{t > 0}}$$
has the Laplace transform in (6.4). which is that of a truncated stable process. Notice that the effects of the parameters
$${({\tilde Y_t})_{t > 0}}$$
has the Laplace transform in (6.4). which is that of a truncated stable process. Notice that the effects of the parameters
![]() $\alpha$
and r are well separated in (6.8), which is helpful for numerical computation purposes. Equation (6.8) and the subordinated representation
$\alpha$
and r are well separated in (6.8), which is helpful for numerical computation purposes. Equation (6.8) and the subordinated representation
![]() $\widetilde Y_{\Gamma_r}$
are also useful for simulating versions of the distribution.
$\widetilde Y_{\Gamma_r}$
are also useful for simulating versions of the distribution.
Some further reductions are helpful for numerical computations. The Gil-Pelaez [Reference Gil-Pelaez8] inversion formula gives for the cumulative distribution function of the subordinator
![]() $$({\tilde Y_t})$$
the expression
$$({\tilde Y_t})$$
the expression
 \begin{align} F_{\widetilde Y_t}(x) & = \frac{1}{2}- \frac{1}{\pi} \int_0^\infty {\mathcal{I}}\Big[e^{-\text{i}\theta x }\mathbb{E}\Big(e^{-\text{i}\theta \widetilde Y_t}\Big)\Big]\frac{\text{d} \theta}{\theta}\nonumber \\
&= \frac{1}{2} +\frac{1}{\pi} \int_0^\infty\sin \Bigg(\theta x - t\theta^\alpha \int_0^\theta\alpha z^{-\alpha-1}\sin z \text{d} z\Bigg)e^{-t \theta^\alpha \int_0^\theta (1-\cos z) \alpha z^{-\alpha-1} \text{d} z}\frac{\text{d} \theta}{\theta}.\end{align}
\begin{align} F_{\widetilde Y_t}(x) & = \frac{1}{2}- \frac{1}{\pi} \int_0^\infty {\mathcal{I}}\Big[e^{-\text{i}\theta x }\mathbb{E}\Big(e^{-\text{i}\theta \widetilde Y_t}\Big)\Big]\frac{\text{d} \theta}{\theta}\nonumber \\
&= \frac{1}{2} +\frac{1}{\pi} \int_0^\infty\sin \Bigg(\theta x - t\theta^\alpha \int_0^\theta\alpha z^{-\alpha-1}\sin z \text{d} z\Bigg)e^{-t \theta^\alpha \int_0^\theta (1-\cos z) \alpha z^{-\alpha-1} \text{d} z}\frac{\text{d} \theta}{\theta}.\end{align}
6.2. Moments of the limiting distribution
An advantage of the limiting random variable
![]() $K(\alpha,r)$
in (6.8) is that it has finite moments of all orders, whereas the Mittag-Leffler distribution of order
$K(\alpha,r)$
in (6.8) is that it has finite moments of all orders, whereas the Mittag-Leffler distribution of order
![]() $\alpha$
(the analogous limiting distribution for
$\alpha$
(the analogous limiting distribution for
![]() $\textrm{PD}_\alpha$
) has finite moments only of order less than
$\textrm{PD}_\alpha$
) has finite moments only of order less than
![]() $\alpha$
.
$\alpha$
.
Proposition 6.1.
-
(a) For
 $q>0$
(6.10)where
$q>0$
(6.10)where \begin{equation}\mathbb{E}(K^q(\alpha,r))=\frac{\Gamma(r+q) \Gamma^q(1-\alpha)}{\Gamma(r)}\mathbb{E}\big(\big( ^{(\alpha,r+q)}T \big)^{-\alpha q}\big),\end{equation}
\begin{equation}\mathbb{E}(K^q(\alpha,r))=\frac{\Gamma(r+q) \Gamma^q(1-\alpha)}{\Gamma(r)}\mathbb{E}\big(\big( ^{(\alpha,r+q)}T \big)^{-\alpha q}\big),\end{equation}
-
(b)
(6.11) \begin{equation}\mathbb{E}\big(\big( ^{(\alpha,r+q)}T \big)^{-\alpha q}\big)=\frac{1}{\Gamma(\alpha q)}\int_0^\infty \frac{ \lambda^{\alpha q-1} \text{d} \lambda}{\big(1 + \alpha \int_{0}^{1} (1- e^{ -\lambda x})x^{-\alpha-1} \text{d} x \big)^{r+q}}.\end{equation}
\begin{equation}\mathbb{E}\big(\big( ^{(\alpha,r+q)}T \big)^{-\alpha q}\big)=\frac{1}{\Gamma(\alpha q)}\int_0^\infty \frac{ \lambda^{\alpha q-1} \text{d} \lambda}{\big(1 + \alpha \int_{0}^{1} (1- e^{ -\lambda x})x^{-\alpha-1} \text{d} x \big)^{r+q}}.\end{equation}
Proof of Proposition 6.1: (a) This is a modification of the proof of Lemma 4.1. From (2.8) we can compute
 \begin{align}\mathbb{E}(K^q(\alpha,r)) = & \frac{1}{\Gamma(r)\Gamma^r(1-\alpha)}\times\nonumber \\
& \times \int_{x=0}^\infty \int_{\lambda>0} x^{r+q-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x(\lambda^{-\alpha}\vee 1)}{\Gamma(1-\alpha)}\right) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x.\end{align}
\begin{align}\mathbb{E}(K^q(\alpha,r)) = & \frac{1}{\Gamma(r)\Gamma^r(1-\alpha)}\times\nonumber \\
& \times \int_{x=0}^\infty \int_{\lambda>0} x^{r+q-1}f_{Y_x(\lambda)}(1)\exp\left(-\frac{x(\lambda^{-\alpha}\vee 1)}{\Gamma(1-\alpha)}\right) \lambda^{-\alpha r-1}\text{d} \lambda\, \text{d} x.\end{align}
Then, following a similar path as in the proof of Lemma 4.1, we split the
![]() $\lambda$
-integral in (6.12) into two components: one over
$\lambda$
-integral in (6.12) into two components: one over
![]() $\lambda\in(0,1]$
and the other over
$\lambda\in(0,1]$
and the other over
![]() $\lambda>1$
. For the component over
$\lambda>1$
. For the component over
![]() $\lambda>1$
, the
$\lambda>1$
, the
![]() $\lambda$
-integral gives
$\lambda$
-integral gives
![]() $1/\alpha r$
, as before. The x-integral for this component can again be computed in terms of gamma functions. The result is
$1/\alpha r$
, as before. The x-integral for this component can again be computed in terms of gamma functions. The result is
where (5.13) was used in the last equality.
For the component over
![]() $\lambda\in(0,1]$
, using similar computations as in the proof of Lemma 4.1, we arrive at the expression
$\lambda\in(0,1]$
, using similar computations as in the proof of Lemma 4.1, we arrive at the expression
We can write this as
in which the second component is, by (5.13),
 \begin{align*} & \frac{\Gamma(r+q) \Gamma^q(1-\alpha)}{ \Gamma(r)}\int_0^1 \lambda^{-\alpha q} \times (\alpha r)^2\times c_{\alpha,r+q+1} \times \lambda^{\alpha (r+q)-1} \text{d} \lambda\\
& \quad = \frac{\Gamma(r+q) \Gamma^q(1-\alpha)}{ \Gamma(r)} \times (\alpha r)^2 \times c_{\alpha,r+q+1}\times \frac{1}{\alpha r}.\end{align*}
\begin{align*} & \frac{\Gamma(r+q) \Gamma^q(1-\alpha)}{ \Gamma(r)}\int_0^1 \lambda^{-\alpha q} \times (\alpha r)^2\times c_{\alpha,r+q+1} \times \lambda^{\alpha (r+q)-1} \text{d} \lambda\\
& \quad = \frac{\Gamma(r+q) \Gamma^q(1-\alpha)}{ \Gamma(r)} \times (\alpha r)^2 \times c_{\alpha,r+q+1}\times \frac{1}{\alpha r}.\end{align*}
This equals the right-hand side of (6.13), so we have cancellation in (6.14), thereby proving (6.10).
For (6.11), we use (4.2) and the identity
This completes the proof of Proposition 6.1.
Tables 1 and 2 in Appendix B show the mean and variance of
![]() $K(\alpha,r)$
calculated from (6.10) for some values of
$K(\alpha,r)$
calculated from (6.10) for some values of
![]() $\alpha, r$
using the R package [25]. Some graphs of the density corresponding to (6.9) are also in Appendix B.
$\alpha, r$
using the R package [25]. Some graphs of the density corresponding to (6.9) are also in Appendix B.
6.3. Concluding comments and some related literature
-
(i) Zhou, Favaro and Walker in [Reference Zhou, Favaro and Walker30] consider a different generalised negative binomial process model constructed from a gamma mixture of Poisson processes. Their emphasis is on fitting it to an observed ‘frequency of frequencies’ sample (i.e., the observed
 ${\textbf M}_n$
, in our notation).
${\textbf M}_n$
, in our notation). -
(ii) The (generalised) Dickman function occurs in the calculation and simulation of perpetuities [Reference Fill and Huber7], and thereby with sorting routines in computer science [Reference Diaconis4], [Reference Mahmoud, Modarres and Smythe19]. See also [Reference Arratia, Barbour and Tavaré1, Chapter 4] and [Reference Arratia and Baxendale2] for relationships with size-biased random variables. In a recent paper [Reference Ipsen, Maller and Shemehsavar15] we considered size-biased sampling from the Dickman subordinator.
Appendix A. Proof of Lemma 3.1
Proof of Lemma 3.1: The inversion formula for the characteristic function of a discrete random variable [Reference Gnedenko and Kolmogorov10, p. 233] gives
 \begin{align}n\mathbb{P}\Bigg(\sum_{i=1}^{ \lfloor xn^\alpha\rfloor} X_{1n}(\lambda n)=n \Bigg) & = \frac{n}{2\pi} \int_{-\pi}^\pi e^{-\text{i} n\theta} \phi_{\lambda n}^{ \lfloor xn^\alpha\rfloor}(\theta) \text{d} \theta \nonumber\\
&= \frac{1}{2\pi} \int_{-n\pi}^{n\pi} e^{-\text{i} \theta} \phi_{\lambda n}^{ \lfloor xn^\alpha\rfloor}(\theta/n) \text{d} \theta.\end{align}
\begin{align}n\mathbb{P}\Bigg(\sum_{i=1}^{ \lfloor xn^\alpha\rfloor} X_{1n}(\lambda n)=n \Bigg) & = \frac{n}{2\pi} \int_{-\pi}^\pi e^{-\text{i} n\theta} \phi_{\lambda n}^{ \lfloor xn^\alpha\rfloor}(\theta) \text{d} \theta \nonumber\\
&= \frac{1}{2\pi} \int_{-n\pi}^{n\pi} e^{-\text{i} \theta} \phi_{\lambda n}^{ \lfloor xn^\alpha\rfloor}(\theta/n) \text{d} \theta.\end{align}
Formally taking the limit under the integral and using (3.37), we can write
 \begin{align}\lim_{n\to\infty} n\mathbb{P}\Bigg(\sum_{i=1}^{ \lfloor xn^\alpha\rfloor} X_{1n}(\lambda n)=n \Bigg) & = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i} \theta}\big( \mathbb{E} e^{ \text{i}\theta Y_1(\lambda)}\big)^x \text{d} \theta\nonumber\\
& = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i} \theta}\mathbb{E} e^{ \text{i}\theta Y_x(\lambda)} \text{d} \theta.\end{align}
\begin{align}\lim_{n\to\infty} n\mathbb{P}\Bigg(\sum_{i=1}^{ \lfloor xn^\alpha\rfloor} X_{1n}(\lambda n)=n \Bigg) & = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i} \theta}\big( \mathbb{E} e^{ \text{i}\theta Y_1(\lambda)}\big)^x \text{d} \theta\nonumber\\
& = \frac{1}{2\pi} \int_{-\infty}^\infty e^{-\text{i} \theta}\mathbb{E} e^{ \text{i}\theta Y_x(\lambda)} \text{d} \theta.\end{align}
The last integral is absolutely convergent for each
![]() $x>0$
and
$x>0$
and
![]() $\lambda>0$
, which can be checked as follows. By (4.6)
$\lambda>0$
, which can be checked as follows. By (4.6)
 \begin{equation*}\big|\mathbb{E} e^{\text{i}\theta Y_x(\lambda)}\big| =\exp\Bigg(-\frac{x}{\Gamma(1-\alpha)}\int_0^{\lambda\wedge 1} \big(1-\cos \theta y \big) \alpha y^{-\alpha-1}\text{d} y)\Bigg).\end{equation*}
\begin{equation*}\big|\mathbb{E} e^{\text{i}\theta Y_x(\lambda)}\big| =\exp\Bigg(-\frac{x}{\Gamma(1-\alpha)}\int_0^{\lambda\wedge 1} \big(1-\cos \theta y \big) \alpha y^{-\alpha-1}\text{d} y)\Bigg).\end{equation*}
For a given
![]() $\lambda>0$
choose
$\lambda>0$
choose
![]() $|\theta|> 1/(\lambda\wedge 1)=1/\lambda\vee 1$
. Then since
$|\theta|> 1/(\lambda\wedge 1)=1/\lambda\vee 1$
. Then since
![]() $1-\cos y\ge y^2/4$
for
$1-\cos y\ge y^2/4$
for
![]() $|y|\le 1$
, we get
$|y|\le 1$
, we get
When
![]() $|\theta|\le 1/\lambda\vee 1$
, we have
$|\theta|\le 1/\lambda\vee 1$
, we have
![]() $\big|\mathbb{E} e^{ \text{i}\theta Y_x(\lambda)}\big| \le 1$
. Hence for some
$\big|\mathbb{E} e^{ \text{i}\theta Y_x(\lambda)}\big| \le 1$
. Hence for some
![]() $c_\alpha>0$
,
$c_\alpha>0$
,
thus establishing the absolute convergence in (A.2). It follows that the right-hand side of (A.2) is the inverse to the characteristic function of a random variable
![]() $ Y_x(\lambda)$
with a continuous bounded density and thus equals the right-hand side of (3.29).
$ Y_x(\lambda)$
with a continuous bounded density and thus equals the right-hand side of (3.29).
To justify the limiting procedure which produces (A.2) we need a bound on the characteristic function in (A.1). For this, split the integral into three components,
where
![]() $A>0$
and
$A>0$
and
![]() $0<\varepsilon<1/4$
will be chosen large and small, respectively, later. The first component is, by (3.37),
$0<\varepsilon<1/4$
will be chosen large and small, respectively, later. The first component is, by (3.37),
and by dominated convergence it has limit
This is arbitrarily close to the integral on the right-hand side of (A.2) once A is large enough, depending on x and
![]() $\lambda$
.
$\lambda$
.
To deal with
![]() $I_2$
, we use an inequality of the form
$I_2$
, we use an inequality of the form
We see that we need a lower bound for
![]() $1-|\phi_{\lambda n}^{ \lfloor n^\alpha\rfloor}(\theta/n)|^2$
. Let
$1-|\phi_{\lambda n}^{ \lfloor n^\alpha\rfloor}(\theta/n)|^2$
. Let
![]() $ X_{1n}^s(\lambda)$
denote a symmetrised version of
$ X_{1n}^s(\lambda)$
denote a symmetrised version of
![]() $ X_{1n}(\lambda)$
, obtained by subtracting an independent copy, and having probability mass function
$ X_{1n}(\lambda)$
, obtained by subtracting an independent copy, and having probability mass function
![]() $p_{nj}^s(\lambda)$
,
$p_{nj}^s(\lambda)$
,
![]() $-n\le j\le n$
. Then, for
$-n\le j\le n$
. Then, for
![]() $\theta\ne 0$
,
$\theta\ne 0$
,
 \begin{align}1-|\phi_{\lambda n}^{ \lfloor n^\alpha\rfloor}(\theta/n)|^2 & = \mathbb{E}\big(1- \cos(\theta X_{1n}^s(\lambda n)/n) \big)\nonumber\\
& = \sum_{j=-n}^n (1- \cos(\theta j/n) p_{nj}^s(\lambda n)\ge\frac{\theta^2}{4n^2} \sum_{|\theta j/n|\le 1} j^2p_{nj}^s(\lambda n)\nonumber\\
& = \frac{\theta^2}{4n^2}\mathbb{E}\big((X_{1n}^s(\lambda n))^2 {\textbf 1}_{\{|X_{1n}^s|(\lambda n)<n/|\theta| \}}\big).\end{align}
\begin{align}1-|\phi_{\lambda n}^{ \lfloor n^\alpha\rfloor}(\theta/n)|^2 & = \mathbb{E}\big(1- \cos(\theta X_{1n}^s(\lambda n)/n) \big)\nonumber\\
& = \sum_{j=-n}^n (1- \cos(\theta j/n) p_{nj}^s(\lambda n)\ge\frac{\theta^2}{4n^2} \sum_{|\theta j/n|\le 1} j^2p_{nj}^s(\lambda n)\nonumber\\
& = \frac{\theta^2}{4n^2}\mathbb{E}\big((X_{1n}^s(\lambda n))^2 {\textbf 1}_{\{|X_{1n}^s|(\lambda n)<n/|\theta| \}}\big).\end{align}
To replace
![]() $X_{1n}^s$
by
$X_{1n}^s$
by
![]() $X_{1n}$
in this we use the inequality
$X_{1n}$
in this we use the inequality
 \begin{eqnarray}&&\mathbb{E}\big((X_{1n}^s(\lambda n))^2 {\textbf 1}_{\{|X_{1n}^s|(\lambda n)<n/|\theta| \}}\nonumber\\
&&\quad \ge 2\mathbb{E}\big((X_{1n}(\lambda n))^2 {\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big)\mathbb{P}(X_{1n}(\lambda n)<n/|\theta|)\nonumber\\
&&\qquad -2\mathbb{E}^2\big(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big).\end{eqnarray}
\begin{eqnarray}&&\mathbb{E}\big((X_{1n}^s(\lambda n))^2 {\textbf 1}_{\{|X_{1n}^s|(\lambda n)<n/|\theta| \}}\nonumber\\
&&\quad \ge 2\mathbb{E}\big((X_{1n}(\lambda n))^2 {\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big)\mathbb{P}(X_{1n}(\lambda n)<n/|\theta|)\nonumber\\
&&\qquad -2\mathbb{E}^2\big(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big).\end{eqnarray}
This follows from a general inequality proved as follows:
 \begin{eqnarray*}&& \int_{|X-X'|\le a} (X-X')^2 \text{d} P\ge \int_{X\le a, X'\le a} (X^2-2XX'+(X')^2) \text{d} P \\
&&\quad =2 \mathbb{E} (X^2 {\textbf 1}_{\{X<a \}}) \mathbb{P}(X<a)-2\mathbb{E}^2 (X{\textbf 1}_{\{X<a \}}),\end{eqnarray*}
\begin{eqnarray*}&& \int_{|X-X'|\le a} (X-X')^2 \text{d} P\ge \int_{X\le a, X'\le a} (X^2-2XX'+(X')^2) \text{d} P \\
&&\quad =2 \mathbb{E} (X^2 {\textbf 1}_{\{X<a \}}) \mathbb{P}(X<a)-2\mathbb{E}^2 (X{\textbf 1}_{\{X<a \}}),\end{eqnarray*}
where X and X
′ are any two nonnegative i.i.d. random variables. (Here
![]() $a>0$
, and in the inequality we used that
$a>0$
, and in the inequality we used that
![]() $0<X\le a$
and
$0<X\le a$
and
![]() $0<X'\le a$
, implying
$0<X'\le a$
, implying
![]() $X-X'\le a$
and
$X-X'\le a$
and
![]() $X-X'\ge -a$
, so that
$X-X'\ge -a$
, so that
![]() $|X-X'|\le a$
.) Applying this to
$|X-X'|\le a$
.) Applying this to
![]() $X_{1n}^s(\lambda n)$
and
$X_{1n}^s(\lambda n)$
and
![]() $X_{1n}(\lambda n)$
with
$X_{1n}(\lambda n)$
with
![]() $a=n/|\theta|$
we get (A.5). Referring to (A.4) and (A.5), we need a lower bound for
$a=n/|\theta|$
we get (A.5). Referring to (A.4) and (A.5), we need a lower bound for
 \begin{align}\frac{\theta^2}{n^2}\mathbb{E}\big((X_{1n}(\lambda n))^2 {\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big) & = \frac{\theta^2}{n^2} \sum_{j=1}^{\lfloor n/|\theta|\rfloor} j^2p_{nj}(\lambda n)\nonumber\\
&\quad \ge \frac{\alpha \theta^2}{n^2\Gamma(1-\alpha)} \int_0^{\lambda n}\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{j^2 z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z \nonumber\\
&\quad \ge \frac{\alpha \theta^2}{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\sum_{j=2}^{\lfloor n/|\theta|\rfloor} \frac{(nz)^{j-2}}{(j-2)!}z^{1-\alpha}e^{-nz} \text{d} z.\end{align}
\begin{align}\frac{\theta^2}{n^2}\mathbb{E}\big((X_{1n}(\lambda n))^2 {\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big) & = \frac{\theta^2}{n^2} \sum_{j=1}^{\lfloor n/|\theta|\rfloor} j^2p_{nj}(\lambda n)\nonumber\\
&\quad \ge \frac{\alpha \theta^2}{n^2\Gamma(1-\alpha)} \int_0^{\lambda n}\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{j^2 z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z \nonumber\\
&\quad \ge \frac{\alpha \theta^2}{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\sum_{j=2}^{\lfloor n/|\theta|\rfloor} \frac{(nz)^{j-2}}{(j-2)!}z^{1-\alpha}e^{-nz} \text{d} z.\end{align}
The first inequality in (A.6) follows because the denominator of
![]() $p_{nj}(\lambda n)$
, by (3.13) and (3.14), is less than
$p_{nj}(\lambda n)$
, by (3.13) and (3.14), is less than
![]() $\Gamma(1-\alpha)$
, and the second inequality follows just because
$\Gamma(1-\alpha)$
, and the second inequality follows just because
![]() $j^2\ge j(\kern1.2pt j-1)$
. The right-hand side of (A.6) equals
$j^2\ge j(\kern1.2pt j-1)$
. The right-hand side of (A.6) equals
 \begin{equation}\frac{\alpha \theta^2}{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\Bigg(1-\mathbb{P}\Bigg(\text{Poiss} (nz)\ge \frac{n}{|\theta|} -2\Bigg) \Bigg) z^{1-\alpha} \text{d} z,\end{equation}
\begin{equation}\frac{\alpha \theta^2}{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\Bigg(1-\mathbb{P}\Bigg(\text{Poiss} (nz)\ge \frac{n}{|\theta|} -2\Bigg) \Bigg) z^{1-\alpha} \text{d} z,\end{equation}
in which, by Markov’s inequality, and because
![]() $|\theta|\le \varepsilon n$
in
$|\theta|\le \varepsilon n$
in
![]() $I_2$
,
$I_2$
,
Now choose
![]() $A>1/\lambda$
for the given
$A>1/\lambda$
for the given
![]() $\lambda>0$
. Then since
$\lambda>0$
. Then since
![]() $A<|\theta|\le \varepsilon n$
in
$A<|\theta|\le \varepsilon n$
in
![]() $I_2$
, we have
$I_2$
, we have
![]() $1/|\theta|<\lambda$
. It follows that the integral in (A.7) is no smaller than
$1/|\theta|<\lambda$
. It follows that the integral in (A.7) is no smaller than
 \begin{eqnarray*} &&\frac{\alpha \theta^2}{n^\alpha\Gamma(1-\alpha) } \int_0^{1/2|\theta|}\Bigg(1- \frac{z|\theta|}{1-2\varepsilon}\Bigg) z^{1-\alpha} \text{d} z\\
&&\quad \ge\frac{1-4\varepsilon}{2(1-2\varepsilon)} \times \frac{\alpha |\theta|^\alpha}{(2-\alpha)2^{2-\alpha}n^\alpha\Gamma(1-\alpha)} \,=\!:\, \frac{C_1(\varepsilon, \alpha)|\theta|^\alpha}{n^\alpha}.\end{eqnarray*}
\begin{eqnarray*} &&\frac{\alpha \theta^2}{n^\alpha\Gamma(1-\alpha) } \int_0^{1/2|\theta|}\Bigg(1- \frac{z|\theta|}{1-2\varepsilon}\Bigg) z^{1-\alpha} \text{d} z\\
&&\quad \ge\frac{1-4\varepsilon}{2(1-2\varepsilon)} \times \frac{\alpha |\theta|^\alpha}{(2-\alpha)2^{2-\alpha}n^\alpha\Gamma(1-\alpha)} \,=\!:\, \frac{C_1(\varepsilon, \alpha)|\theta|^\alpha}{n^\alpha}.\end{eqnarray*}
Returning to (A.5), we also need a lower bound for the probability term. By (3.13) and (3.14),
 \begin{align}\mathbb{P}(X_{1n}(\lambda n)<n/|\theta|)&\ge \frac{\alpha}{\Gamma(1-\alpha)} \int_0^{\lambda n}\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{ z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z\nonumber \\
& = \frac{\alpha }{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{(nz)^{j}}{j!}e^{-nz} z^{-\alpha-1}\text{d} z \nonumber\\
& = \frac{\alpha}{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\mathbb{P}\bigg( 1\le \text{Poiss} (nz) \le \frac{n}{|\theta|}\bigg) z^{-\alpha-1} \text{d} z.\end{align}
\begin{align}\mathbb{P}(X_{1n}(\lambda n)<n/|\theta|)&\ge \frac{\alpha}{\Gamma(1-\alpha)} \int_0^{\lambda n}\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{ z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z\nonumber \\
& = \frac{\alpha }{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{(nz)^{j}}{j!}e^{-nz} z^{-\alpha-1}\text{d} z \nonumber\\
& = \frac{\alpha}{n^\alpha\Gamma(1-\alpha)} \int_0^{\lambda }\mathbb{P}\bigg( 1\le \text{Poiss} (nz) \le \frac{n}{|\theta|}\bigg) z^{-\alpha-1} \text{d} z.\end{align}
Again since
![]() $A>1/\lambda$
and
$A>1/\lambda$
and
![]() $A<|\theta|\le \varepsilon n$
in
$A<|\theta|\le \varepsilon n$
in
![]() $I_2$
, we have
$I_2$
, we have
![]() $1/|\theta|<\lambda$
, so the last expression is no smaller than
$1/|\theta|<\lambda$
, so the last expression is no smaller than
The probability in the integrand is, by Markov’s inequality,
so we obtain
 \begin{equation}\mathbb{P}\bigg(X_{1n}(\lambda n)<\frac{n}{|\theta|}\bigg)\ge\frac{ n^\alpha- (2|\theta|)^\alpha}{10 n^\alpha\Gamma(1-\alpha)}=\frac{1}{10\Gamma(1-\alpha)}\Bigg( 1-\frac{(2|\theta|)^\alpha}{n^\alpha}\Bigg).\end{equation}
\begin{equation}\mathbb{P}\bigg(X_{1n}(\lambda n)<\frac{n}{|\theta|}\bigg)\ge\frac{ n^\alpha- (2|\theta|)^\alpha}{10 n^\alpha\Gamma(1-\alpha)}=\frac{1}{10\Gamma(1-\alpha)}\Bigg( 1-\frac{(2|\theta|)^\alpha}{n^\alpha}\Bigg).\end{equation}
Since
![]() $|\theta|<\varepsilon n$
, the term in brackets is no smaller than
$|\theta|<\varepsilon n$
, the term in brackets is no smaller than
![]() $$(1 - {(2\varepsilon )^\alpha }) > 0$$
for a small enough choice of
$$(1 - {(2\varepsilon )^\alpha }) > 0$$
for a small enough choice of
![]() $\varepsilon$
. So for the first term on the right-hand side of (A.5) we have the lower bound
$\varepsilon$
. So for the first term on the right-hand side of (A.5) we have the lower bound
where
![]() $C_2( \varepsilon,\alpha) \,{:}\,{\raise-1.5pt{=}}\, 2C_1( 1- (2\varepsilon)^\alpha)/ 10\Gamma(1-\alpha)$
.
$C_2( \varepsilon,\alpha) \,{:}\,{\raise-1.5pt{=}}\, 2C_1( 1- (2\varepsilon)^\alpha)/ 10\Gamma(1-\alpha)$
.
For the
![]() $\mathbb{E}^2$
term on the right-hand side of (A.5), use the formula
$\mathbb{E}^2$
term on the right-hand side of (A.5), use the formula
 \begin{equation}\mathbb{E}(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta|\}}) = \sum_{j=1}^ {\lfloor n/|\theta| \rfloor}j p_{nj}(\lambda n) = \frac{ \sum_{j=1}^ {\lfloor n/|\theta| \rfloor}j F_j(\lambda n)} {\sum_{j=1}^n F_j(\lambda n)}\end{equation}
\begin{equation}\mathbb{E}(X_{1n}(\lambda n){\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta|\}}) = \sum_{j=1}^ {\lfloor n/|\theta| \rfloor}j p_{nj}(\lambda n) = \frac{ \sum_{j=1}^ {\lfloor n/|\theta| \rfloor}j F_j(\lambda n)} {\sum_{j=1}^n F_j(\lambda n)}\end{equation}
(cf. (3.16)), and for the denominator, use the lower bound
 \begin{eqnarray}\sum_{j=1}^ n F_j(\lambda n) &=&\alpha \int_0^{\lambda n}\sum_{j=1}^n \frac{z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z \nonumber\\
&\ge &\alpha \int_0^{1/\varepsilon}\sum_{j=1}^n \frac{z^{j}}{j!} z^{-\alpha-1} e^{-z}\text{d} z \nonumber\\
&\to&\ \alpha \int_0^{1/\varepsilon} z^{-\alpha-1} (1-e^{-z}) \text{d} z\ (\text{as}\ n\to \infty) \nonumber\\
&\ge &\tfrac{1}{2}\Gamma(1-\alpha) \end{eqnarray}
\begin{eqnarray}\sum_{j=1}^ n F_j(\lambda n) &=&\alpha \int_0^{\lambda n}\sum_{j=1}^n \frac{z^{j}}{j!}z^{-\alpha-1}e^{- z} \text{d} z \nonumber\\
&\ge &\alpha \int_0^{1/\varepsilon}\sum_{j=1}^n \frac{z^{j}}{j!} z^{-\alpha-1} e^{-z}\text{d} z \nonumber\\
&\to&\ \alpha \int_0^{1/\varepsilon} z^{-\alpha-1} (1-e^{-z}) \text{d} z\ (\text{as}\ n\to \infty) \nonumber\\
&\ge &\tfrac{1}{2}\Gamma(1-\alpha) \end{eqnarray}
(for
![]() $\varepsilon$
small enough). Thus the lower bound
$\varepsilon$
small enough). Thus the lower bound
![]() $\sum_{j=1}^ n F_j(\lambda n)\ge \Gamma(1-\alpha)/2$
holds for
$\sum_{j=1}^ n F_j(\lambda n)\ge \Gamma(1-\alpha)/2$
holds for
![]() $\lambda>1/|\theta|$
,
$\lambda>1/|\theta|$
,
![]() $|\theta|\le \varepsilon n$
, n greater than or equal to some
$|\theta|\le \varepsilon n$
, n greater than or equal to some
![]() $n_0(\varepsilon, \alpha)$
, and
$n_0(\varepsilon, \alpha)$
, and
![]() $\varepsilon$
less than or equal to some
$\varepsilon$
less than or equal to some
![]() $\varepsilon_0(\alpha)>0$
. To deal with the numerator in the
$\varepsilon_0(\alpha)>0$
. To deal with the numerator in the
![]() $\mathbb{E}^2$
term, write, as in (3.17),
$\mathbb{E}^2$
term, write, as in (3.17),
 \begin{align} n^{\alpha-1}\sum_{j=1}^{\lfloor n/|\theta| \rfloor} jF_j(\lambda n) & = \alpha n^{\alpha-1}\int_0^{\lambda n}\sum_{j=1}^{\lfloor n/|\theta| \rfloor} \frac{z^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{- z} \text{d} z \nonumber\\
& = \alpha \int_0^{\lambda}\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{(nz)^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{-nz} \text{d} z \nonumber\\
&\quad\le \alpha \int_0^{\lambda}\mathbb{P}\big( \text{Poiss} (nz)\le n/|\theta|\big) z^{-\alpha} \text{d} z.\end{align}
\begin{align} n^{\alpha-1}\sum_{j=1}^{\lfloor n/|\theta| \rfloor} jF_j(\lambda n) & = \alpha n^{\alpha-1}\int_0^{\lambda n}\sum_{j=1}^{\lfloor n/|\theta| \rfloor} \frac{z^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{- z} \text{d} z \nonumber\\
& = \alpha \int_0^{\lambda}\sum_{j=1}^{\lfloor n/|\theta|\rfloor} \frac{(nz)^{j-1}}{(\kern1.2pt j-1)!}z^{-\alpha}e^{-nz} \text{d} z \nonumber\\
&\quad\le \alpha \int_0^{\lambda}\mathbb{P}\big( \text{Poiss} (nz)\le n/|\theta|\big) z^{-\alpha} \text{d} z.\end{align}
This time we keep
![]() $|\theta|>2/\lambda$
and upper-bound the right-hand side of (A.14) by
$|\theta|>2/\lambda$
and upper-bound the right-hand side of (A.14) by
 \begin{eqnarray*}&&\alpha \left(\int_0^{2/|\theta| } + \int_{2/|\theta|}^{\lambda} \right)\mathbb{P}\big( \text{Poiss} (nz)\le n/|\theta|\big) z^{-\alpha} \text{d} z\\
&&\quad \le \alpha \int_0^{2/|\theta| } z^{-\alpha} \text{d} z+ \int_{2/|\theta|}^{\lambda}\mathbb{P}\big( \text{Poiss} (nz)\le n/|\theta|\big) z^{-\alpha} \text{d} z.\end{eqnarray*}
\begin{eqnarray*}&&\alpha \left(\int_0^{2/|\theta| } + \int_{2/|\theta|}^{\lambda} \right)\mathbb{P}\big( \text{Poiss} (nz)\le n/|\theta|\big) z^{-\alpha} \text{d} z\\
&&\quad \le \alpha \int_0^{2/|\theta| } z^{-\alpha} \text{d} z+ \int_{2/|\theta|}^{\lambda}\mathbb{P}\big( \text{Poiss} (nz)\le n/|\theta|\big) z^{-\alpha} \text{d} z.\end{eqnarray*}
Here the first integral equals
The second integral can be bounded using Chebyshev’s inequality as
 \begin{eqnarray*}&&\alpha \int_{2/|\theta|}^{\lambda}\mathbb{P}\big( \text{Poiss} (nz)-nz\le -n/(z-1/|\theta|)\big) z^{-\alpha} \text{d} z\\
&&\quad \le\alpha \int_{2/|\theta|}^{\lambda}\frac{nz^{1-\alpha}}{n^2(z-1/|\theta|)^2} \text{d} z\\
&&\quad \le \frac{\alpha|\theta|^\alpha}{n} \int_{2}^\infty\frac{y^{1-\alpha}}{(y-1)^2} \text{d} y\le \varepsilon C_4(\alpha) |\theta|^{\alpha-1}\le C_4(\alpha) |\theta|^{\alpha-1},\end{eqnarray*}
\begin{eqnarray*}&&\alpha \int_{2/|\theta|}^{\lambda}\mathbb{P}\big( \text{Poiss} (nz)-nz\le -n/(z-1/|\theta|)\big) z^{-\alpha} \text{d} z\\
&&\quad \le\alpha \int_{2/|\theta|}^{\lambda}\frac{nz^{1-\alpha}}{n^2(z-1/|\theta|)^2} \text{d} z\\
&&\quad \le \frac{\alpha|\theta|^\alpha}{n} \int_{2}^\infty\frac{y^{1-\alpha}}{(y-1)^2} \text{d} y\le \varepsilon C_4(\alpha) |\theta|^{\alpha-1}\le C_4(\alpha) |\theta|^{\alpha-1},\end{eqnarray*}
using
![]() $|\theta|\le \varepsilon n$
,
$|\theta|\le \varepsilon n$
,
![]() $n\ge|\theta|/\varepsilon$
, and
$n\ge|\theta|/\varepsilon$
, and
![]() $\varepsilon\le 1$
in the last inequality. Combining this with the first integral, we now have a bound for the left-hand side of (A.14) of the form
$\varepsilon\le 1$
in the last inequality. Combining this with the first integral, we now have a bound for the left-hand side of (A.14) of the form
![]() $ C_5(\alpha) |\theta|^{\alpha-1}$
, where
$ C_5(\alpha) |\theta|^{\alpha-1}$
, where
![]() $ C_5(\alpha) = C_3(\alpha) + C_4(\alpha) $
. This leads to the bound
$ C_5(\alpha) = C_3(\alpha) + C_4(\alpha) $
. This leads to the bound
 \begin{align*}\frac{\theta^2}{n^2}\mathbb{E}^2\big(X_{1n}(\lambda n) {\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big)& \le \frac{4\theta^2}{n^2\Gamma(1-\alpha)}\big( C_5(\alpha) n^{1-\alpha} |\theta|^{\alpha-1}\big)^2 \\
& = \frac{C_6(\alpha)}{n^{2\alpha}} |\theta|^{2\alpha} \le\frac{\varepsilon^{\alpha} C_6(\alpha)}{n^{\alpha}} |\theta|^{\alpha}\end{align*}
\begin{align*}\frac{\theta^2}{n^2}\mathbb{E}^2\big(X_{1n}(\lambda n) {\textbf 1}_{\{X_{1n}(\lambda n)<n/|\theta| \}}\big)& \le \frac{4\theta^2}{n^2\Gamma(1-\alpha)}\big( C_5(\alpha) n^{1-\alpha} |\theta|^{\alpha-1}\big)^2 \\
& = \frac{C_6(\alpha)}{n^{2\alpha}} |\theta|^{2\alpha} \le\frac{\varepsilon^{\alpha} C_6(\alpha)}{n^{\alpha}} |\theta|^{\alpha}\end{align*}
for the
![]() $\mathbb{E}^2$
term on the right-hand side of (A.5). This is smaller than the first term on the right-hand side of (A.5), which is bounded below in (A.11), giving a lower bound for the left-hand side of (A.4) as
$\mathbb{E}^2$
term on the right-hand side of (A.5). This is smaller than the first term on the right-hand side of (A.5), which is bounded below in (A.11), giving a lower bound for the left-hand side of (A.4) as
![]() $C_7(\varepsilon, \alpha) |\theta|^\alpha/n^\alpha$
, where
$C_7(\varepsilon, \alpha) |\theta|^\alpha/n^\alpha$
, where
![]() $C_7(\varepsilon, \alpha)=2(C_2(\varepsilon, \alpha)-\varepsilon C_6(\varepsilon, \alpha))$
. Going back to (A.4), we now have a lower bound for
$C_7(\varepsilon, \alpha)=2(C_2(\varepsilon, \alpha)-\varepsilon C_6(\varepsilon, \alpha))$
. Going back to (A.4), we now have a lower bound for
of the form
![]() $C_7(\varepsilon, \alpha) |\theta|^\alpha/n^\alpha $
. Then from (A.3),
$C_7(\varepsilon, \alpha) |\theta|^\alpha/n^\alpha $
. Then from (A.3),
is integrable on
![]() $(0,\infty)$
and provides the required upper bound for
$(0,\infty)$
and provides the required upper bound for
![]() $I_2$
.
$I_2$
.
Finally, to deal with
![]() $I_3$
, we use the fact that
$I_3$
, we use the fact that
![]() $X_{1n}(\lambda n)$
is a lattice variable with span 1 (it takes values
$X_{1n}(\lambda n)$
is a lattice variable with span 1 (it takes values
![]() $j=1,2,\dots,n$
with probabilities
$j=1,2,\dots,n$
with probabilities
![]() $p_{nj}(\lambda)>0$
,
$p_{nj}(\lambda)>0$
,
![]() $\sum_{j=1}^n p_{nj}(\lambda)=1$
.) Thus by Corollary 2 to Theorem 5 in Section 14 of [Reference Gnedenko and Kolmogorov10], for all
$\sum_{j=1}^n p_{nj}(\lambda)=1$
.) Thus by Corollary 2 to Theorem 5 in Section 14 of [Reference Gnedenko and Kolmogorov10], for all
![]() $\varepsilon>0$
there is a
$\varepsilon>0$
there is a
![]() $c=c(\varepsilon,\lambda)$
such that for
$c=c(\varepsilon,\lambda)$
such that for
![]() $\varepsilon<|\theta|<2\pi-\varepsilon$
we have
$\varepsilon<|\theta|<2\pi-\varepsilon$
we have
![]() $|\phi_{\lambda n}(\theta)|<e^{-c}$
. Thus
$|\phi_{\lambda n}(\theta)|<e^{-c}$
. Thus
for
![]() $\varepsilon n<|\theta|<n\pi$
, and so
$\varepsilon n<|\theta|<n\pi$
, and so
This completes the proof of Lemma 3.1.
Appendix B. Mean and variance of
 $K(\alpha,{\textbf{\textit{r}}})$
, and density of
$K(\alpha,{\textbf{\textit{r}}})$
, and density of
 $\widetilde{\textbf{\textit{Y}}}_{\textbf{\textit{t}}}$
$\widetilde{\textbf{\textit{Y}}}_{\textbf{\textit{t}}}$
Tables 1 and 2 show the mean and variance of
![]() $K(\alpha,r)$
for various values of
$K(\alpha,r)$
for various values of
![]() $\alpha$
and r calculated from (6.10) using the R package [25].
$\alpha$
and r calculated from (6.10) using the R package [25].
Table 1. Expected value of
![]() $K(\alpha,r)$
.
$K(\alpha,r)$
.


Figure 1: Densities of the subordinator
![]() $\widetilde Y_t$
for values of
$\widetilde Y_t$
for values of
![]() $\alpha=0.3,0.5,0.7,0.9$
and values of t being (left to right) 1 (blue), 2 (red), 5 (green), and 7 (black). The horizontal axis shows values of x; the vertical axis shows values of
$\alpha=0.3,0.5,0.7,0.9$
and values of t being (left to right) 1 (blue), 2 (red), 5 (green), and 7 (black). The horizontal axis shows values of x; the vertical axis shows values of
![]() $f_{\widetilde Y_t}(x)$
.
$f_{\widetilde Y_t}(x)$
.
![]() $\widetilde Y_t$
tends to 0 in probability as
$\widetilde Y_t$
tends to 0 in probability as
![]() $t\downarrow 0$
, for large t, and tends to normality with mean and variance proportional to t as
$t\downarrow 0$
, for large t, and tends to normality with mean and variance proportional to t as
![]() $t\to\infty$
.
$t\to\infty$
.
The tables show that the expected value of
![]() $K(\alpha,r)$
increases with r for each
$K(\alpha,r)$
increases with r for each
![]() $\alpha\in(0,1)$
, while the variance of
$\alpha\in(0,1)$
, while the variance of
![]() $K(\alpha,r)$
increases with r for
$K(\alpha,r)$
increases with r for
![]() $\alpha\le 1/2 $
but, curiously, decreases with r for
$\alpha\le 1/2 $
but, curiously, decreases with r for
![]() $\alpha>1/2 $
, eventually tending to 0 as
$\alpha>1/2 $
, eventually tending to 0 as
![]() $\alpha\uparrow 1$
or
$\alpha\uparrow 1$
or
![]() $r\to\infty$
.
$r\to\infty$
.
Figure 1 shows plots of the density of the subordinator
![]() $\widetilde Y_t$
having Laplace transform (6.4) for various values of
$\widetilde Y_t$
having Laplace transform (6.4) for various values of
![]() $\alpha$
and t. The functions were calculated in the package R by evaluating the cumulative distribution function in (6.9), then using R’s numerical differentiation routine.
$\alpha$
and t. The functions were calculated in the package R by evaluating the cumulative distribution function in (6.9), then using R’s numerical differentiation routine.
Table 2. Variance of
![]() $K(\alpha,r)$
.
$K(\alpha,r)$
.