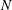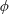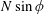1 Introduction
The aptly named ‘St. Andrew’s Cross’ experiment performed by Mowbray & Rarity (Reference Mowbray and Rarity1967) is one of the most celebrated studies of internal gravity waves, although, as acknowledged by these authors, it was Görtler (Reference Görtler1943) who was the first to realize the phenomenon. For this experiment, a cylinder aligned horizontally with a plane of constant gravitational potential is oscillated vertically with small amplitude in a density stratification of constant buoyancy frequency. Since gravity provides a preferred direction, internal wave propagation in this setting is anisotropic, with energy being transported along rather than perpendicular to wave crests. As a result, the wave disturbance generated by the oscillating cylinder, instead of circular wave crests, features four wave beams that emanate from the cylinder, forming a cross pattern whose opening is determined by the dispersion relation. The realization of the St. Andrew’s Cross in the laboratory was a striking validation of the rather unusual fundamental properties of internal wave motion predicted by Lamb (Reference Lamb1932), Lighthill (Reference Lighthill1965) and Yih (Reference Yih1965), inspiring a rich body of subsequent research in the field.
A succinct anthology of this vast research activity includes experimental investigations of the wave beams generated by an oscillating cylinder using particle tracking (Gordon & Stevenson Reference Gordon and Stevenson1972; Thomas & Stevenson Reference Thomas and Stevenson1972) and interferometry (Peters Reference Peters1985; Merzkirch & Peters Reference Merzkirch and Peters1992), and theoretical investigations by Appleby & Crighton (Reference Appleby and Crighton1986) and Makarov, Neklyudov & Chashechkin (Reference Makarov, Neklyudov and Chashechkin1990). Hurley (Reference Hurley1997) and Hurley & Keady (Reference Hurley and Keady1997) considered cylinders of elliptical cross-section, incorporating viscosity in a theoretical model in order to resolve the issue that the inviscid response predicts infinite displacements of fluid particles; various aspects of this model were subsequently confirmed in laboratory experiments (Sutherland et al. Reference Sutherland, Dalziel, Hughes and Linden1999, Reference Sutherland, Hughes, Dalziel and Linden2000; Ermanyuk Reference Ermanyuk2000; Ermanyuk & Gavrilov Reference Ermanyuk and Gavrilov2002; Sutherland & Linden Reference Sutherland and Linden2002). Pursuing variations on a theme, there have been numerous studies that deviate from the original configuration of Mowbray & Rarity (Reference Mowbray and Rarity1967), including: horizontal cylinders of square cross-section (Dalziel Reference Dalziel, Lawrence, Pieters and Yonemitsu2000), transient behaviour of wave beams upon initiation of excitation (Voisin Reference Voisin2003; Ermanyuk & Gavrilov Reference Ermanyuk and Gavrilov2005), excitation by circular and rectilinear, rather than vertical, oscillations (Gavrilov & Ermanyuk Reference Gavrilov and Ermanyuk1997; Ermanyuk & Gavrilov Reference Ermanyuk and Gavrilov2008), and the response to large-amplitude oscillations (Ermanyuk & Gavrilov Reference Ermanyuk and Gavrilov2008).
The other canonical, and related, configuration that has also been substantially investigated is the wave field generated by a vertically oscillating sphere, in which case rather than the St. Andrew’s Cross a conical wave field arises (Voisin Reference Voisin1991; Flynn, Onu & Sutherland Reference Flynn, Onu and Sutherland2003; Peacock & Weidman Reference Peacock and Weidman2005; Voisin, Ermanyuk & Flor Reference Voisin, Ermanyuk and Flor2011; Ghaemsaidi & Peacock Reference Ghaemsaidi and Peacock2013). Furthermore, there are studies of subsequent nonlinear interactions of internal wave beams due to reflections at boundaries and beam collisions (Peacock & Tabaei Reference Peacock and Tabaei2005; Tabaei, Akylas & Lamb Reference Tabaei, Akylas and Lamb2005; Jiang & Marcus Reference Jiang and Marcus2009; Rodenborn et al. Reference Rodenborn, Kiefer, Zhang and Swinney2011; Akylas & Karimi Reference Akylas and Karimi2012; Smith & Crockett Reference Smith and Crockett2014).
One reason the St. Andrew’s Cross configuration has such broad appeal is that it provides insight into many scenarios that are relevant to the ocean and atmosphere. For example, internal wave beams have been observed to originate from ocean ridges (Cole et al. Reference Cole, Rudnick, Hodges and Martin2009) and continental shelves (Lien & Gregg Reference Lien and Gregg2001; Holbrook & Fer Reference Holbrook and Fer2005), giving rise to solitary wave phenomena when they impinge upon the ocean pycnocline (Pingree & New Reference Pingree and New1989; Akylas et al. Reference Akylas, Grimshaw, Clarke and Tabaei2007; Grisouard, Staquet & Gerkema Reference Grisouard, Staquet and Gerkema2011). Indeed, for the continental shelf case, the solution of Hurley (Reference Hurley1997) for an oscillating cylinder has been shown to reasonably model the resulting wave-beam structure (Gostiaux & Dauxois Reference Gostiaux and Dauxois2007). In regards to atmospheric phenomena, Fovell, Durran & Holton (Reference Fovell, Durran and Holton1992) and Alexander, Holton & Durran (Reference Alexander, Holton and Durran1995) explored the generation of internal wave beams by two-dimensional squall lines, and proposed a mechanism analogous to mechanical forcing by an oscillating cylinder; this ‘mechanical oscillator effect’ was further supported by simulations of actual storms (Piani et al. Reference Piani, Durran, Alexander and Holton2000; Lane, Reeder & Clark Reference Lane, Reeder and Clark2001). Moreover, evidence of thunderstorm-generated wave-beam structures was found in satellite observations of the upper stratosphere (Dewan et al. Reference Dewan, Picard, O’Neil, Gardiner and Gibson1998).
Here, we step away from the canonical St. Andrew’s Cross to consider a more generic setting that has not been previously explored, and in so-doing we find results that are profoundly different and potentially of broad interest. Specifically, we study internal wave generation by a vertically oscillating cylinder that is tilted with respect to the horizontal. This forcing arrangement exploits further the inherent anisotropy of internal wave motion and leads to a variant of the classical St. Andrew’s Cross that has features with no counterpart in the corresponding horizontal cylinder problem. For example, for a given tilt of the cylinder there is a cutoff frequency below which there is no longer a radiated wave field. Furthermore, three-dimensional effects due to the finite length of the cylinder, which are minor in the horizontal configuration, here become a significant factor and eventually dominate the wave field as the cutoff frequency is approached. These results follow from elementary linear wave theory and are also confirmed by supporting laboratory experiments.
The response when the tilted cylinder oscillates at a frequency close to cutoff is of special interest. Exactly at cutoff, the group-velocity component perpendicular to the cylinder direction vanishes, so energy cannot be radiated easily away from the source, suggesting a possible resonance phenomenon. From prior experience with cutoff frequencies in simpler problems (Aranha, Yue & Mei Reference Aranha, Yue and Mei1982; Akylas Reference Akylas1984), nonlinear and viscous effects are likely to play an important part in the response near cutoff. This scenario is examined by adapting a recently developed theory for three-dimensional modulated wave beams (Kataoka & Akylas Reference Kataoka and Akylas2015), to consider the near-resonant wave field due to a tilted line source of large but finite length. According to this model, the combination of three-dimensional, nonlinear and viscous effects near cutoff triggers transfer of energy, through the action of Reynolds stresses, to a circulating horizontal mean flow, analogous to that observed accompanying a three-dimensional propagating beam (Bordes et al. Reference Bordes, Venaille, Joubaud, Odier and Dauxois2012). Furthermore, we present experimental evidence of such an induced mean flow near cutoff.
The theoretical models and supporting experiments discussed below point to certain unique features of internal waves generated by line forcing tilted to the horizontal. These results are likely to have implications for geophysical flow modelling, as real-world wave sources need not be horizontal, and the ‘oblique’ St. Andrew’s Cross due to a tilted oscillating cylinder could serve as a paradigm for improving understanding of internal wave-beam generation and propagation in geophysical systems.
2 Wave-beam geometry
We first discuss the geometry of the steady-state internal wave pattern induced by time-harmonic line forcing, modelling an oscillating long thin cylinder, in an unbounded, non-rotating, uniformly stratified Boussinesq fluid. Here, the forcing is taken to be infinitely long; the effects of finite length of the wave source will be examined in § 3. Our analysis makes use of the well-known dispersion relation of internal gravity waves,
where
![]() $\unicode[STIX]{x1D714}$
is the dimensionless wave frequency (scaled with the constant background buoyancy frequency
$\unicode[STIX]{x1D714}$
is the dimensionless wave frequency (scaled with the constant background buoyancy frequency
![]() $N$
) and
$N$
) and
![]() $\unicode[STIX]{x1D703}$
is the inclination angle of the wavevector to the vertical
$\unicode[STIX]{x1D703}$
is the inclination angle of the wavevector to the vertical
![]() $(y)$
axis pointing upwards. As illustrated in figure 1(a), the wave source stretches along the
$(y)$
axis pointing upwards. As illustrated in figure 1(a), the wave source stretches along the
![]() $\unicode[STIX]{x1D709}$
-direction in the
$\unicode[STIX]{x1D709}$
-direction in the
![]() $xy$
-plane and is tilted to the horizontal (
$xy$
-plane and is tilted to the horizontal (
![]() $x$
) axis by an angle
$x$
) axis by an angle
![]() $0<\unicode[STIX]{x1D719}<\unicode[STIX]{x03C0}/2$
, with
$0<\unicode[STIX]{x1D719}<\unicode[STIX]{x03C0}/2$
, with
![]() $z$
being the transverse horizontal direction. Similar to the classical St. Andrew’s Cross due to horizontal forcing (
$z$
being the transverse horizontal direction. Similar to the classical St. Andrew’s Cross due to horizontal forcing (
![]() $\unicode[STIX]{x1D719}=0$
), the dispersion relation (2.1) being independent of the wavevector magnitude is key to the kinematic argument used below for deducing the wave pattern due to a tilted line source.
$\unicode[STIX]{x1D719}=0$
), the dispersion relation (2.1) being independent of the wavevector magnitude is key to the kinematic argument used below for deducing the wave pattern due to a tilted line source.

Figure 1. Geometry of wave beams induced by infinitely long line forcing tilted to the horizontal by
![]() $\unicode[STIX]{x1D719}$
and oscillating with frequency
$\unicode[STIX]{x1D719}$
and oscillating with frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: (a) three-dimensional view; four beams propagate along the directions
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: (a) three-dimensional view; four beams propagate along the directions
![]() $\pm \hat{\boldsymbol{e}}^{\pm }$
in (2.3) and form an oblique cross whose opening is measured by
$\pm \hat{\boldsymbol{e}}^{\pm }$
in (2.3) and form an oblique cross whose opening is measured by
![]() $\unicode[STIX]{x1D713}=\cos ^{-1}(\cot \unicode[STIX]{x1D703}\tan \unicode[STIX]{x1D719})$
; (b) intersection of the planes of constant phase
$\unicode[STIX]{x1D713}=\cos ^{-1}(\cot \unicode[STIX]{x1D703}\tan \unicode[STIX]{x1D719})$
; (b) intersection of the planes of constant phase
![]() $\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}=0$
for the four
$\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}=0$
for the four
![]() $\boldsymbol{k}$
-directions (2.2) with the
$\boldsymbol{k}$
-directions (2.2) with the
![]() $yz$
-plane; seen in this plane, the four cross arms are inclined to the horizontal by
$yz$
-plane; seen in this plane, the four cross arms are inclined to the horizontal by
![]() $\unicode[STIX]{x1D712}=\tan ^{-1}\sqrt{\tan ^{2}\unicode[STIX]{x1D703}-\tan ^{2}\unicode[STIX]{x1D719}}$
, forming a symmetric cross pattern.
$\unicode[STIX]{x1D712}=\tan ^{-1}\sqrt{\tan ^{2}\unicode[STIX]{x1D703}-\tan ^{2}\unicode[STIX]{x1D719}}$
, forming a symmetric cross pattern.
From elementary linear wave theory, the steady-state response to a time-harmonic source comprises plane waves at the driving frequency; thus, according to (2.1), for given
![]() $0<\unicode[STIX]{x1D714}<1$
, all participating wavevectors
$0<\unicode[STIX]{x1D714}<1$
, all participating wavevectors
![]() $\boldsymbol{k}=(k_{x},k_{y},k_{z})$
have fixed inclination to the vertical. In addition, for infinitely long, uniform line forcing, the response does not vary in
$\boldsymbol{k}=(k_{x},k_{y},k_{z})$
have fixed inclination to the vertical. In addition, for infinitely long, uniform line forcing, the response does not vary in
![]() $\unicode[STIX]{x1D709}$
, so
$\unicode[STIX]{x1D709}$
, so
![]() $\boldsymbol{k}$
must be perpendicular to the source direction. These requirements constrain
$\boldsymbol{k}$
must be perpendicular to the source direction. These requirements constrain
![]() $\boldsymbol{k}$
to point in four specific directions:
$\boldsymbol{k}$
to point in four specific directions:
for given
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
(
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
(
![]() $0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2$
). Also, (2.2) reveals that steady-state disturbances radiate in the far field only if
$0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2$
). Also, (2.2) reveals that steady-state disturbances radiate in the far field only if
![]() $0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x1D703}$
. Under this condition, upon varying the wavevector magnitude
$0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x1D703}$
. Under this condition, upon varying the wavevector magnitude
![]() $k$
in (2.2), superposition of plane waves yields four wave beams. The location of these beams relative to the source is determined by the group velocity
$k$
in (2.2), superposition of plane waves yields four wave beams. The location of these beams relative to the source is determined by the group velocity
![]() $\boldsymbol{c}_{g}=\unicode[STIX]{x1D6FB}_{\boldsymbol{k}}\unicode[STIX]{x1D714}$
, which is at right angles to
$\boldsymbol{c}_{g}=\unicode[STIX]{x1D6FB}_{\boldsymbol{k}}\unicode[STIX]{x1D714}$
, which is at right angles to
![]() $\boldsymbol{k}$
and must point away from the source, in keeping with the radiation condition. Specifically, as shown in figure 1(a), two beams are found above the line source and propagate towards
$\boldsymbol{k}$
and must point away from the source, in keeping with the radiation condition. Specifically, as shown in figure 1(a), two beams are found above the line source and propagate towards
![]() $y\rightarrow \infty$
along the corresponding group-velocity directions
$y\rightarrow \infty$
along the corresponding group-velocity directions
where
the other two beams are located below the line source and propagate towards
![]() $y\rightarrow -\infty$
in the opposite directions.
$y\rightarrow -\infty$
in the opposite directions.
Overall, the generated wave pattern is in the form of a cross that leans in the direction of the forcing. This ‘oblique’ cross undergoes dramatic transformation as the source tilt angle
![]() $\unicode[STIX]{x1D719}$
is varied in the range
$\unicode[STIX]{x1D719}$
is varied in the range
![]() $0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x1D703}$
. As indicated in figure 1(a), a measure of the cross opening is the angle
$0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x1D703}$
. As indicated in figure 1(a), a measure of the cross opening is the angle
![]() $\unicode[STIX]{x1D713}$
in (2.4), which decreases monotonically with
$\unicode[STIX]{x1D713}$
in (2.4), which decreases monotonically with
![]() $\unicode[STIX]{x1D719}$
, from
$\unicode[STIX]{x1D719}$
, from
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x03C0}/2$
for
$\unicode[STIX]{x1D713}=\unicode[STIX]{x03C0}/2$
for
![]() $\unicode[STIX]{x1D719}=0$
to
$\unicode[STIX]{x1D719}=0$
to
![]() $\unicode[STIX]{x1D713}=0$
for
$\unicode[STIX]{x1D713}=0$
for
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}$
. As a result, the classical St. Andrew’s Cross for horizontal forcing
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}$
. As a result, the classical St. Andrew’s Cross for horizontal forcing
![]() $(\unicode[STIX]{x1D719}=0)$
gradually closes as
$(\unicode[STIX]{x1D719}=0)$
gradually closes as
![]() $\unicode[STIX]{x1D719}$
is increased, and ultimately degenerates to a single standing beam along the forcing (
$\unicode[STIX]{x1D719}$
is increased, and ultimately degenerates to a single standing beam along the forcing (
![]() $\unicode[STIX]{x1D709}$
) direction in the limit
$\unicode[STIX]{x1D709}$
) direction in the limit
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
.
A convenient way to visualize this transformation is by considering the intersection of the oblique-cross wave pattern – specifically, the planes of constant phase
![]() $\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}=0$
(figure 1
a) for the four
$\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}=0$
(figure 1
a) for the four
![]() $\boldsymbol{k}$
-directions (2.2) – with the (vertical)
$\boldsymbol{k}$
-directions (2.2) – with the (vertical)
![]() $yz$
-plane. Seen in this plane, the four cross arms are inclined at
$yz$
-plane. Seen in this plane, the four cross arms are inclined at
to the (horizontal)
![]() $z$
-axis, as can be deduced from (2.2), and form a symmetric configuration centred at the origin (figure 1
b). The angle
$z$
-axis, as can be deduced from (2.2), and form a symmetric configuration centred at the origin (figure 1
b). The angle
![]() $\unicode[STIX]{x1D712}$
attains the maximum
$\unicode[STIX]{x1D712}$
attains the maximum
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D703}$
for the classical St. Andrew’s Cross (
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D703}$
for the classical St. Andrew’s Cross (
![]() $\unicode[STIX]{x1D719}=0$
) which lies in the
$\unicode[STIX]{x1D719}=0$
) which lies in the
![]() $yz$
-plane (
$yz$
-plane (
![]() $k_{x}=0$
). As
$k_{x}=0$
). As
![]() $\unicode[STIX]{x1D719}$
is increased and the cross leans towards the forcing,
$\unicode[STIX]{x1D719}$
is increased and the cross leans towards the forcing,
![]() $\unicode[STIX]{x1D712}$
monotonically decreases and eventually
$\unicode[STIX]{x1D712}$
monotonically decreases and eventually
![]() $\unicode[STIX]{x1D712}\rightarrow 0$
as
$\unicode[STIX]{x1D712}\rightarrow 0$
as
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
; in this limit,
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
; in this limit,
![]() $\boldsymbol{k}=\pm k(-\!\sin \unicode[STIX]{x1D719},\cos \unicode[STIX]{x1D719},0)$
according to (2.2), corresponding to a beam standing along
$\boldsymbol{k}=\pm k(-\!\sin \unicode[STIX]{x1D719},\cos \unicode[STIX]{x1D719},0)$
according to (2.2), corresponding to a beam standing along
![]() $\unicode[STIX]{x1D709}$
and uniform in
$\unicode[STIX]{x1D709}$
and uniform in
![]() $z$
.
$z$
.
For fixed source tilt angle
![]() $\unicode[STIX]{x1D719}$
, the limiting configuration of a single standing beam arises when the driving frequency
$\unicode[STIX]{x1D719}$
, the limiting configuration of a single standing beam arises when the driving frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
approaches the critical value
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
approaches the critical value
Thus, the condition
![]() $\unicode[STIX]{x1D703}\geqslant \unicode[STIX]{x1D719}$
for the appearance of a far-field response translates into
$\unicode[STIX]{x1D703}\geqslant \unicode[STIX]{x1D719}$
for the appearance of a far-field response translates into
![]() $\unicode[STIX]{x1D714}\geqslant \unicode[STIX]{x1D714}_{c}$
, and
$\unicode[STIX]{x1D714}\geqslant \unicode[STIX]{x1D714}_{c}$
, and
![]() $\unicode[STIX]{x1D714}_{c}$
may be regarded as a cutoff frequency which marks the borderline between a radiating wave field and a locally confined response in the vicinity of the source. It should be noted that when
$\unicode[STIX]{x1D714}_{c}$
may be regarded as a cutoff frequency which marks the borderline between a radiating wave field and a locally confined response in the vicinity of the source. It should be noted that when
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}$
(
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}$
(
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
) the beam propagation directions
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
) the beam propagation directions
![]() $\hat{\boldsymbol{e}}^{\pm }$
in (2.3), which are along the corresponding group velocity, coincide with the forcing (
$\hat{\boldsymbol{e}}^{\pm }$
in (2.3), which are along the corresponding group velocity, coincide with the forcing (
![]() $\unicode[STIX]{x1D709}$
) direction (figure 1
a). This suggests a resonance phenomenon, as energy cannot be transported away from the forcing and the inviscid steady-state response is expected to be unbounded at the cutoff frequency
$\unicode[STIX]{x1D709}$
) direction (figure 1
a). This suggests a resonance phenomenon, as energy cannot be transported away from the forcing and the inviscid steady-state response is expected to be unbounded at the cutoff frequency
![]() $\unicode[STIX]{x1D714}_{c}$
. An analogous situation was encountered in a study of oblique collisions of internal wave beams (Akylas & Karimi Reference Akylas and Karimi2012). The transient response near the cutoff condition
$\unicode[STIX]{x1D714}_{c}$
. An analogous situation was encountered in a study of oblique collisions of internal wave beams (Akylas & Karimi Reference Akylas and Karimi2012). The transient response near the cutoff condition
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
is discussed in § 4.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
is discussed in § 4.
3 End effects
We now turn to the effects of finite length of the line source. These end effects become progressively more significant with increasing source tilt angle
![]() $\unicode[STIX]{x1D719}$
, and understanding their role is crucial in interpreting the experimental observations in § 6.
$\unicode[STIX]{x1D719}$
, and understanding their role is crucial in interpreting the experimental observations in § 6.
As in the case of infinitely long forcing, the steady-state response to a time-harmonic line source of finite length
![]() $L$
is again made of plane waves with wavevectors inclined to the vertical by a fixed angle
$L$
is again made of plane waves with wavevectors inclined to the vertical by a fixed angle
![]() $\unicode[STIX]{x1D703}$
, determined by the driving frequency
$\unicode[STIX]{x1D703}$
, determined by the driving frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
. Thus, treating the forcing ends as point sources, the plane waves emitted there propagate along vertical cones of angle
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
. Thus, treating the forcing ends as point sources, the plane waves emitted there propagate along vertical cones of angle
![]() $\unicode[STIX]{x1D703}$
from the horizontal, and contaminate the four wave beams that emanate from the interior of the forcing. Specifically, for tilted forcing as sketched in figure 2(a), the dominant end effects are expected to come from the upper cone due to the left end and the lower cone due to the right end, as these cones are closest to the main body of the forcing, where the wave beams are generated.
$\unicode[STIX]{x1D703}$
from the horizontal, and contaminate the four wave beams that emanate from the interior of the forcing. Specifically, for tilted forcing as sketched in figure 2(a), the dominant end effects are expected to come from the upper cone due to the left end and the lower cone due to the right end, as these cones are closest to the main body of the forcing, where the wave beams are generated.

Figure 2. Kinematics of internal waves generated by line forcing of finite length
![]() $L$
, tilted at an angle
$L$
, tilted at an angle
![]() $\unicode[STIX]{x1D719}$
to the horizontal and oscillating with angular frequency
$\unicode[STIX]{x1D719}$
to the horizontal and oscillating with angular frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: (a) the dominant end effects arise due to plane waves that propagate along the two vertical cones shown; (b) intersection of the wave pattern with the
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: (a) the dominant end effects arise due to plane waves that propagate along the two vertical cones shown; (b) intersection of the wave pattern with the
![]() $yz$
-plane across the middle of the forcing (
$yz$
-plane across the middle of the forcing (
![]() $x=0$
). Here the dashed lines represent the end effects due to the two cones shown in (a), and the solid lines depict the four beams shown in figure 1(b), which emanate from the main body of the forcing.
$x=0$
). Here the dashed lines represent the end effects due to the two cones shown in (a), and the solid lines depict the four beams shown in figure 1(b), which emanate from the main body of the forcing.
To illustrate our approach, we now discuss how end effects modify the wave-beam pattern in the vertical
![]() $yz$
-plane across the middle of the forcing (
$yz$
-plane across the middle of the forcing (
![]() $x=0$
). As argued above, the combined response (see figure 2
b) consists of the four beams (solid lines) found earlier (figure 1
b) and the two hyperbolae (dashed lines)
$x=0$
). As argued above, the combined response (see figure 2
b) consists of the four beams (solid lines) found earlier (figure 1
b) and the two hyperbolae (dashed lines)
![]() $\{y\pm (L/2)\sin \unicode[STIX]{x1D719}\}^{2}-z^{2}\tan ^{2}\unicode[STIX]{x1D703}=(L/2)^{2}\cos ^{2}\unicode[STIX]{x1D719}\tan ^{2}\unicode[STIX]{x1D703}$
formed by the intersection of the
$\{y\pm (L/2)\sin \unicode[STIX]{x1D719}\}^{2}-z^{2}\tan ^{2}\unicode[STIX]{x1D703}=(L/2)^{2}\cos ^{2}\unicode[STIX]{x1D719}\tan ^{2}\unicode[STIX]{x1D703}$
formed by the intersection of the
![]() $yz$
-plane with the end cones shown in figure 2(a). From geometric considerations, it turns out that the four beam directions become tangent to these hyperbolae at the points
$yz$
-plane with the end cones shown in figure 2(a). From geometric considerations, it turns out that the four beam directions become tangent to these hyperbolae at the points
Hence, the wave beams remain distinct from the disturbances emanating from the ends, within a rectangle centred at the origin and of width
and height
![]() $D\tan \unicode[STIX]{x1D712}$
(figure 2
b).
$D\tan \unicode[STIX]{x1D712}$
(figure 2
b).
It should be noted that
![]() $D\rightarrow \infty$
when
$D\rightarrow \infty$
when
![]() $\unicode[STIX]{x1D719}\rightarrow 0$
(horizontal forcing); in this instance, the wave beams coincide with the asymptotes of the two hyperbolae so the classical St. Andrew’s Cross is hardly affected by the ends. As the tilt angle
$\unicode[STIX]{x1D719}\rightarrow 0$
(horizontal forcing); in this instance, the wave beams coincide with the asymptotes of the two hyperbolae so the classical St. Andrew’s Cross is hardly affected by the ends. As the tilt angle
![]() $\unicode[STIX]{x1D719}$
is increased and
$\unicode[STIX]{x1D719}$
is increased and
![]() $D$
is reduced according to (3.2), however, end effects are felt progressively more seriously. Finally,
$D$
is reduced according to (3.2), however, end effects are felt progressively more seriously. Finally,
![]() $D\rightarrow 0$
as the cutoff condition is approached (
$D\rightarrow 0$
as the cutoff condition is approached (
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
); in this limit, the forcing is tangent to the end cones in figure 2(a) so end disturbances totally interfere with the beams from the main body of the forcing. These kinematic results are confirmed by more detailed computations as well as laboratory experiments in § 6.
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
); in this limit, the forcing is tangent to the end cones in figure 2(a) so end disturbances totally interfere with the beams from the main body of the forcing. These kinematic results are confirmed by more detailed computations as well as laboratory experiments in § 6.
4 Response near cutoff
The preceding, purely kinematic analysis has brought out the cutoff frequency
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}$
in (2.6), at which the group velocity of the kinematically allowed steady-state beams becomes parallel to the forcing direction. This condition arises only for tilted line forcing (
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}$
in (2.6), at which the group velocity of the kinematically allowed steady-state beams becomes parallel to the forcing direction. This condition arises only for tilted line forcing (
![]() $\unicode[STIX]{x1D719}>0$
) and suggests the possibility of a resonance as energy keeps accumulating near the forcing. Based on prior experience with cutoff frequencies in simpler settings (Aranha et al.
Reference Aranha, Yue and Mei1982; Akylas Reference Akylas1984), it is expected that transient, nonlinear and viscous effects come into play when the driving frequency is close to
$\unicode[STIX]{x1D719}>0$
) and suggests the possibility of a resonance as energy keeps accumulating near the forcing. Based on prior experience with cutoff frequencies in simpler settings (Aranha et al.
Reference Aranha, Yue and Mei1982; Akylas Reference Akylas1984), it is expected that transient, nonlinear and viscous effects come into play when the driving frequency is close to
![]() $\unicode[STIX]{x1D714}_{c}$
. Here, we present an asymptotic model which takes into account these effects near cutoff in the problem at hand.
$\unicode[STIX]{x1D714}_{c}$
. Here, we present an asymptotic model which takes into account these effects near cutoff in the problem at hand.
The transient response to tilted, infinitely long, uniform line forcing at the cutoff frequency, ignoring viscous and nonlinear effects, was discussed in Akylas & Karimi (Reference Akylas and Karimi2012) by solving an appropriate initial-value problem. Owing to the slow transport of energy away from the source, the generated long-time disturbance takes the form of a spatially modulated wave beam with continuously growing amplitude in time, like
![]() $t^{1/2}$
. Specifically, this modulated beam is uniform in the along-beam direction which coincides with the forcing (
$t^{1/2}$
. Specifically, this modulated beam is uniform in the along-beam direction which coincides with the forcing (
![]() $\unicode[STIX]{x1D709}$
) direction (see figure 1
a); however, the beam profile is not only a function of the cross-beam coordinate
$\unicode[STIX]{x1D709}$
) direction (see figure 1
a); however, the beam profile is not only a function of the cross-beam coordinate
![]() $\unicode[STIX]{x1D702}$
, but also evolves in a self-similar fashion via the similarity variable
$\unicode[STIX]{x1D702}$
, but also evolves in a self-similar fashion via the similarity variable
![]() $z/t^{1/2}$
, which accounts for the presence of slow modulations in the transverse (
$z/t^{1/2}$
, which accounts for the presence of slow modulations in the transverse (
![]() $z$
) direction. The unbounded beam-amplitude growth (like
$z$
) direction. The unbounded beam-amplitude growth (like
![]() $t^{1/2}$
) due to the vanishing group velocity normal to the source, and the self-similar spreading of the disturbance (like
$t^{1/2}$
) due to the vanishing group velocity normal to the source, and the self-similar spreading of the disturbance (like
![]() $z/t^{1/2}$
) due to dispersion, are characteristic of the linear forced response at a cutoff frequency (Akylas Reference Akylas1984).
$z/t^{1/2}$
) due to dispersion, are characteristic of the linear forced response at a cutoff frequency (Akylas Reference Akylas1984).
In subsequent work, Kataoka & Akylas (Reference Kataoka and Akylas2015) analysed the propagation of weakly nonlinear modulated wave beams, including also the effects of weak viscous dissipation. This study pointed out the significance of three-dimensional beam variations, which enable resonant transfer of energy, via nonlinear interactions, to a strong horizontal mean flow. Moreover, Kataoka & Akylas (Reference Kataoka and Akylas2015) derived a system of two coupled evolution equations for this resonant beam–mean-flow interaction.
As the transient forced response near the cutoff frequency
![]() $\unicode[STIX]{x1D714}_{c}$
takes the form of a modulated beam, we shall adapt the theoretical model of Kataoka & Akylas (Reference Kataoka and Akylas2015) to the tilted-line-forcing geometry of interest here. The modifications required for this purpose turn out to be minor, and only the final results of the analysis will be highlighted below. Readers interested in more details are referred to Kataoka & Akylas (Reference Kataoka and Akylas2015), and to ease such reference we shall use the same non-dimensional variables and notation as in the earlier study.
$\unicode[STIX]{x1D714}_{c}$
takes the form of a modulated beam, we shall adapt the theoretical model of Kataoka & Akylas (Reference Kataoka and Akylas2015) to the tilted-line-forcing geometry of interest here. The modifications required for this purpose turn out to be minor, and only the final results of the analysis will be highlighted below. Readers interested in more details are referred to Kataoka & Akylas (Reference Kataoka and Akylas2015), and to ease such reference we shall use the same non-dimensional variables and notation as in the earlier study.
We first look at the modulation scales relevant to the present setting. The similarity variable
![]() $z/t^{1/2}$
revealed by the transient linear response at cutoff (Akylas & Karimi Reference Akylas and Karimi2012) suggests that the appropriate transverse coordinate and ‘slow’ evolution time are
$z/t^{1/2}$
revealed by the transient linear response at cutoff (Akylas & Karimi Reference Akylas and Karimi2012) suggests that the appropriate transverse coordinate and ‘slow’ evolution time are
where
![]() $0<\unicode[STIX]{x1D700}\ll 1$
is related to the forcing amplitude below (see (4.4)). Moreover, in order to balance transverse with longitudinal dispersion, the along-beam coordinate is scaled as
$0<\unicode[STIX]{x1D700}\ll 1$
is related to the forcing amplitude below (see (4.4)). Moreover, in order to balance transverse with longitudinal dispersion, the along-beam coordinate is scaled as
The modulation variables (4.1) and (4.2) are identical to those in Kataoka & Akylas (Reference Kataoka and Akylas2015); here, however, the orientation of the external forcing is different, and
![]() $\unicode[STIX]{x1D700}$
is related to the forcing amplitude parameter
$\unicode[STIX]{x1D700}$
is related to the forcing amplitude parameter
![]() $\unicode[STIX]{x1D6FC}$
in a distinct way from the earlier work. Specifically, rather than being along the transverse horizontal (
$\unicode[STIX]{x1D6FC}$
in a distinct way from the earlier work. Specifically, rather than being along the transverse horizontal (
![]() $z$
) direction, the source
$z$
) direction, the source
![]() $F$
(an externally applied line force along
$F$
(an externally applied line force along
![]() $\unicode[STIX]{x1D709}$
) now stretches along the
$\unicode[STIX]{x1D709}$
) now stretches along the
![]() $\unicode[STIX]{x1D709}$
-direction, which is tilted to the horizontal by the angle
$\unicode[STIX]{x1D709}$
-direction, which is tilted to the horizontal by the angle
![]() $\unicode[STIX]{x1D719}$
(figure 1
a):
$\unicode[STIX]{x1D719}$
(figure 1
a):
The forcing profile
![]() $\hat{F}=O(1)$
is locally confined in
$\hat{F}=O(1)$
is locally confined in
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $z$
, as is appropriate for a line source; moreover,
$z$
, as is appropriate for a line source; moreover,
![]() $\hat{F}$
depends on
$\hat{F}$
depends on
![]() $X=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D709}$
, to allow for slow along-source dependence, in view of the key role of three-dimensional variations noted earlier.
$X=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D709}$
, to allow for slow along-source dependence, in view of the key role of three-dimensional variations noted earlier.
Now, for tilt angle
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}$
, as is the case at cutoff, the linear, inviscid response to uniform line forcing (i.e.
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}$
, as is the case at cutoff, the linear, inviscid response to uniform line forcing (i.e.
![]() $\hat{F}(\unicode[STIX]{x1D702},z)$
in (4.3)) is known to be resonant and grows like
$\hat{F}(\unicode[STIX]{x1D702},z)$
in (4.3)) is known to be resonant and grows like
![]() $t^{1/2}$
(Akylas & Karimi Reference Akylas and Karimi2012). As a result, by the time
$t^{1/2}$
(Akylas & Karimi Reference Akylas and Karimi2012). As a result, by the time
![]() $t\sim 1/\unicode[STIX]{x1D700}^{2}$
when
$t\sim 1/\unicode[STIX]{x1D700}^{2}$
when
![]() $T=O(1)$
, the response amplitude is
$T=O(1)$
, the response amplitude is
![]() $O(\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D700})$
. However, from Kataoka & Akylas (Reference Kataoka and Akylas2015), in order for nonlinear effects to be comparable to dispersion effects due to the modulation scales (4.1) and (4.2), the beam amplitude has to be
$O(\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D700})$
. However, from Kataoka & Akylas (Reference Kataoka and Akylas2015), in order for nonlinear effects to be comparable to dispersion effects due to the modulation scales (4.1) and (4.2), the beam amplitude has to be
![]() $O(\unicode[STIX]{x1D700}^{1/2})$
. Hence, the appropriate scaling of the forcing amplitude parameter
$O(\unicode[STIX]{x1D700}^{1/2})$
. Hence, the appropriate scaling of the forcing amplitude parameter
![]() $\unicode[STIX]{x1D6FC}$
relative to
$\unicode[STIX]{x1D6FC}$
relative to
![]() $\unicode[STIX]{x1D700}$
is
$\unicode[STIX]{x1D700}$
is
compared with
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D700}^{1/2}$
found in Kataoka & Akylas (Reference Kataoka and Akylas2015), (4.4) makes sense near resonance:
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D700}^{1/2}$
found in Kataoka & Akylas (Reference Kataoka and Akylas2015), (4.4) makes sense near resonance:
![]() $O(\unicode[STIX]{x1D700}^{3/2})$
forcing results in a larger-amplitude,
$O(\unicode[STIX]{x1D700}^{3/2})$
forcing results in a larger-amplitude,
![]() $O(\unicode[STIX]{x1D700}^{1/2})$
, wave-beam response.
$O(\unicode[STIX]{x1D700}^{1/2})$
, wave-beam response.
The final modification to the Kataoka & Akylas (Reference Kataoka and Akylas2015) model is to allow for possible detuning of the resonance condition
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}$
(
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{c}$
(
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
). Specifically, consistent with the slow time
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
). Specifically, consistent with the slow time
![]() $T=\unicode[STIX]{x1D700}^{2}t$
, we put
$T=\unicode[STIX]{x1D700}^{2}t$
, we put
where
![]() $\unicode[STIX]{x1D6FE}=O(1)$
is a detuning parameter. In view of (4.1), (4.4) and (4.5), the forcing (4.3), as it is locally confined in
$\unicode[STIX]{x1D6FE}=O(1)$
is a detuning parameter. In view of (4.1), (4.4) and (4.5), the forcing (4.3), as it is locally confined in
![]() $z$
, can be approximated by
$z$
, can be approximated by
where
![]() $\unicode[STIX]{x1D6FF}(Z)$
denotes the delta function and
$\unicode[STIX]{x1D6FF}(Z)$
denotes the delta function and
![]() $f=O(1)$
.
$f=O(1)$
.
Using (4.6) as forcing, and taking into account (4.5), the perturbation procedure detailed in Kataoka & Akylas (Reference Kataoka and Akylas2015) leads to the following coupled evolution equations for the wave-beam response and induced mean flow near cutoff:
 $$\begin{eqnarray}\displaystyle & & \displaystyle U_{T}-\text{i}\unicode[STIX]{x1D6FE}U+\overline{V}_{\infty }U_{\unicode[STIX]{x1D702}}+\text{i}\cos \unicode[STIX]{x1D719}\left(\int ^{\unicode[STIX]{x1D702}}U_{X}\,\text{d}\unicode[STIX]{x1D702}^{\prime }+\frac{\cot \unicode[STIX]{x1D719}}{\text{2}}\int ^{\unicode[STIX]{x1D702}}\int ^{\unicode[STIX]{x1D702}^{\prime }}U_{ZZ}\,\text{d}\unicode[STIX]{x1D702}^{\prime \prime }\,\text{d}\unicode[STIX]{x1D702}^{\prime }\right)-\frac{\unicode[STIX]{x1D6FD}}{2}U_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad =f(X,\unicode[STIX]{x1D702})\unicode[STIX]{x1D6FF}(Z),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle U_{T}-\text{i}\unicode[STIX]{x1D6FE}U+\overline{V}_{\infty }U_{\unicode[STIX]{x1D702}}+\text{i}\cos \unicode[STIX]{x1D719}\left(\int ^{\unicode[STIX]{x1D702}}U_{X}\,\text{d}\unicode[STIX]{x1D702}^{\prime }+\frac{\cot \unicode[STIX]{x1D719}}{\text{2}}\int ^{\unicode[STIX]{x1D702}}\int ^{\unicode[STIX]{x1D702}^{\prime }}U_{ZZ}\,\text{d}\unicode[STIX]{x1D702}^{\prime \prime }\,\text{d}\unicode[STIX]{x1D702}^{\prime }\right)-\frac{\unicode[STIX]{x1D6FD}}{2}U_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad =f(X,\unicode[STIX]{x1D702})\unicode[STIX]{x1D6FF}(Z),\end{eqnarray}$$
Here,
![]() $U(X,\unicode[STIX]{x1D702},Z,T)$
is the complex amplitude of the beam flow velocity in the along-beam (
$U(X,\unicode[STIX]{x1D702},Z,T)$
is the complex amplitude of the beam flow velocity in the along-beam (
![]() $X$
) direction, and
$X$
) direction, and
![]() $\overline{V}_{\infty }(X,Z,T)$
is the induced-mean-flow component in the cross-beam (
$\overline{V}_{\infty }(X,Z,T)$
is the induced-mean-flow component in the cross-beam (
![]() $\unicode[STIX]{x1D702}$
) direction. Furthermore,
$\unicode[STIX]{x1D702}$
) direction. Furthermore,
![]() ${\mathcal{H}}$
stands for the Hilbert transform with respect to
${\mathcal{H}}$
stands for the Hilbert transform with respect to
![]() $Z$
and the parameter
$Z$
and the parameter
![]() $\unicode[STIX]{x1D6FD}=O(1)$
controls the effects of viscous dissipation,
$\unicode[STIX]{x1D6FD}=O(1)$
controls the effects of viscous dissipation,
![]() $\unicode[STIX]{x1D708}$
being an inverse Reynolds number.
$\unicode[STIX]{x1D708}$
being an inverse Reynolds number.
Compared with the Kataoka & Akylas (Reference Kataoka and Akylas2015) model, equation (4.7) includes an additional term, which accounts for the resonance detuning (4.5), and the variables
![]() $X$
,
$X$
,
![]() $Z$
in the forcing term of (4.7) are interchanged. The latter difference derives from the fact that the line source here is tilted and coincides with the along-beam (
$Z$
in the forcing term of (4.7) are interchanged. The latter difference derives from the fact that the line source here is tilted and coincides with the along-beam (
![]() $X$
), rather than the transverse horizontal (
$X$
), rather than the transverse horizontal (
![]() $Z$
), direction. It should be noted that, in the present setting, it cannot be immediately concluded that the induced mean flow vanishes (i.e.
$Z$
), direction. It should be noted that, in the present setting, it cannot be immediately concluded that the induced mean flow vanishes (i.e.
![]() $\overline{V}_{\infty }=0$
) when the forcing is infinitely long and uniform (i.e.
$\overline{V}_{\infty }=0$
) when the forcing is infinitely long and uniform (i.e.
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}X=0$
), with the response being independent of
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}X=0$
), with the response being independent of
![]() $X$
; this is in contrast to the case of horizontal line forcing, where the absence of transverse (
$X$
; this is in contrast to the case of horizontal line forcing, where the absence of transverse (
![]() $Z$
) variations trivially implies
$Z$
) variations trivially implies
![]() $\overline{V}_{\infty }=0$
according to the mean-flow equation (4.8).
$\overline{V}_{\infty }=0$
according to the mean-flow equation (4.8).
Nevertheless, under some conditions, it is still true that
![]() $\overline{V}_{\infty }=0$
when the forcing
$\overline{V}_{\infty }=0$
when the forcing
![]() $f(X,\unicode[STIX]{x1D702})=f(\unicode[STIX]{x1D702})$
in (4.7). Specifically, upon introducing the Fourier transform in
$f(X,\unicode[STIX]{x1D702})=f(\unicode[STIX]{x1D702})$
in (4.7). Specifically, upon introducing the Fourier transform in
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
equations (4.7) and (4.8) become
From this form of the evolution equations, it is clear that if
![]() $|\widetilde{f}(l)|$
is even in
$|\widetilde{f}(l)|$
is even in
![]() $l$
(as is the case when
$l$
(as is the case when
![]() $f(\unicode[STIX]{x1D702})$
is real, for instance), so is
$f(\unicode[STIX]{x1D702})$
is real, for instance), so is
![]() $|\widetilde{U}(l,Z,T)|$
; under this assumption, the right-hand side of (4.12) then vanishes and so does
$|\widetilde{U}(l,Z,T)|$
; under this assumption, the right-hand side of (4.12) then vanishes and so does
![]() $\overline{V}_{\infty }$
.
$\overline{V}_{\infty }$
.
Finally, it is worth noting that for infinitely long uniform line forcing
![]() $f(\unicode[STIX]{x1D702})$
such that
$f(\unicode[STIX]{x1D702})$
such that
![]() $\overline{V}_{\infty }=0$
, the transient inviscid (
$\overline{V}_{\infty }=0$
, the transient inviscid (
![]() $\unicode[STIX]{x1D6FD}=0$
) response exactly at cutoff (
$\unicode[STIX]{x1D6FD}=0$
) response exactly at cutoff (
![]() $\unicode[STIX]{x1D6FE}=0$
) obtains the similarity form
$\unicode[STIX]{x1D6FE}=0$
) obtains the similarity form
![]() $U\propto T^{1/2}G(\unicode[STIX]{x1D702},Z/T^{1/2})$
, consistent with Akylas & Karimi (Reference Akylas and Karimi2012). Moreover, for concentrated line forcing,
$U\propto T^{1/2}G(\unicode[STIX]{x1D702},Z/T^{1/2})$
, consistent with Akylas & Karimi (Reference Akylas and Karimi2012). Moreover, for concentrated line forcing,
![]() $f=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D702})$
, under conditions of steady state and exact resonance (
$f=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D702})$
, under conditions of steady state and exact resonance (
![]() $\unicode[STIX]{x1D6FE}=0$
), (4.7) reduces to
$\unicode[STIX]{x1D6FE}=0$
), (4.7) reduces to
This equation accepts a similarity solution in the form
![]() $U\propto Z^{-1/2}G(\unicode[STIX]{x1D702}/Z^{1/2})$
, which happens to be identical to the one derived by Gordon & Stevenson (Reference Gordon and Stevenson1972) for the profile of a vertically propagating viscous beam due to a horizontal line source oscillating at the background buoyancy frequency (
$U\propto Z^{-1/2}G(\unicode[STIX]{x1D702}/Z^{1/2})$
, which happens to be identical to the one derived by Gordon & Stevenson (Reference Gordon and Stevenson1972) for the profile of a vertically propagating viscous beam due to a horizontal line source oscillating at the background buoyancy frequency (
![]() $\unicode[STIX]{x1D714}=1$
).
$\unicode[STIX]{x1D714}=1$
).
5 Experimental set-up
Laboratory experiments were performed to investigate the geometry of the wave-beam response due to a tilted oscillating cylinder as well as the nature of the induced mean flows near cutoff. Here, we provide some details of the experimental arrangements, before presenting results in § 6.
The experiments were performed in a glass wave tank 5.46 m long, 0.55 m wide and 0.6 m deep; figure 3 presents schematics of the experimental configurations. A partition ran nearly the length of the tank, dividing it into 0.44 m and 0.06 m sections, with experiments being conducted in the wider section. A linear density stratification, by virtue of vertically varying salinity, was set up via the double-bucket method (Fortuin Reference Fortuin1960; Oster Reference Oster1965). The final stratification was measured using a calibrated Precision Measurements Engineering (PME) conductivity and temperature (CT) probe. A typical buoyancy frequency for an experiment was
![]() $N=0.901\pm 0.09~\text{s}^{-1}$
.
$N=0.901\pm 0.09~\text{s}^{-1}$
.

Figure 3. Schematics of experimental arrangements for measuring: (a) beam angle
![]() $\unicode[STIX]{x1D712}$
; (b) induced mean flows. The
$\unicode[STIX]{x1D712}$
; (b) induced mean flows. The
![]() $xyz$
-coordinate system is the same as in figure 2(a), with the oscillating tilted cylinder (length
$xyz$
-coordinate system is the same as in figure 2(a), with the oscillating tilted cylinder (length
![]() $L$
and diameter
$L$
and diameter
![]() $d$
) lying in the (vertical)
$d$
) lying in the (vertical)
![]() $xy$
-plane through
$xy$
-plane through
![]() $z=0$
. Experimental data for (a) was obtained in
$z=0$
. Experimental data for (a) was obtained in
![]() $yz$
-planes close to the lower end of the cylinder, and for (b) in the
$yz$
-planes close to the lower end of the cylinder, and for (b) in the
![]() $xy$
-plane containing the cylinder. The bright area under the cylinder in figure (b) indicates the domain of integration used for computing
$xy$
-plane containing the cylinder. The bright area under the cylinder in figure (b) indicates the domain of integration used for computing
![]() $S^{\prime }$
, the approximate form of the overall mean-flow strength
$S^{\prime }$
, the approximate form of the overall mean-flow strength
![]() $S$
in (6.2) and (6.3). In the theoretical model, the ‘inner’ region of the induced mean flow immediately below the cylinder is taken to be one cylinder radius wide (
$S$
in (6.2) and (6.3). In the theoretical model, the ‘inner’ region of the induced mean flow immediately below the cylinder is taken to be one cylinder radius wide (
![]() $=1.25~\text{cm}$
).
$=1.25~\text{cm}$
).
For studies of the wave-beam geometry, we used as forcing three
![]() $25.0\pm 0.1~\text{mm}$
diameter acrylic cylinders of different lengths and tilt angles. The tilt angles were
$25.0\pm 0.1~\text{mm}$
diameter acrylic cylinders of different lengths and tilt angles. The tilt angles were
![]() $\unicode[STIX]{x1D719}=0^{\circ },27^{\circ }$
and
$\unicode[STIX]{x1D719}=0^{\circ },27^{\circ }$
and
![]() $44^{\circ }$
, with an accuracy of
$44^{\circ }$
, with an accuracy of
![]() $\pm 1^{\circ }$
. The ends of the cylinders were all cut vertical (see figure 3
a) so that each of the three cylinders had the same horizontal projected length of 25 cm, and therefore different actual lengths. A vertical thin metal rod was attached to the mid-point of each cylinder so that the cylinder could be oscillated vertically via a National Instruments/Axis New England based motion control system operating a lead screw traverse. The peak-to-peak amplitude of vertical oscillation was
$\pm 1^{\circ }$
. The ends of the cylinders were all cut vertical (see figure 3
a) so that each of the three cylinders had the same horizontal projected length of 25 cm, and therefore different actual lengths. A vertical thin metal rod was attached to the mid-point of each cylinder so that the cylinder could be oscillated vertically via a National Instruments/Axis New England based motion control system operating a lead screw traverse. The peak-to-peak amplitude of vertical oscillation was
![]() $6.00\pm 0.1~\text{mm}$
.
$6.00\pm 0.1~\text{mm}$
.
The experimental studies of mean-flow generation near cutoff (
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}$
) involved cylinders tilted at
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D703}$
) involved cylinders tilted at
![]() $\unicode[STIX]{x1D719}=45^{\circ }$
and
$\unicode[STIX]{x1D719}=45^{\circ }$
and
![]() $60^{\circ }$
, positioned mid-width of the tank (see figure 3
b). Each cylinder had a diameter
$60^{\circ }$
, positioned mid-width of the tank (see figure 3
b). Each cylinder had a diameter
![]() $d=25.0\pm 0.1~\text{mm}$
and length
$d=25.0\pm 0.1~\text{mm}$
and length
![]() $L=28.8\pm 0.1~\text{cm}$
. Experiments were performed at forcing frequencies
$L=28.8\pm 0.1~\text{cm}$
. Experiments were performed at forcing frequencies
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
in the range of
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
in the range of
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}\pm 20^{\circ }$
, and with driving peak-to-peak amplitudes between 5 and 16 mm.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}\pm 20^{\circ }$
, and with driving peak-to-peak amplitudes between 5 and 16 mm.
Wave-field visualization was performed using a previously validated LaVision stereo-scopic particle image velocimetry (PIV) system (Ghaemsaidi & Peacock Reference Ghaemsaidi and Peacock2013) for the cross experiments, and a traditional PIV configuration for the induced-mean-flow experiments, with the latter taking advantage of symmetry in the
![]() $z$
direction. The density stratification was seeded with Sphericel hollow glass oxide particles of diameter
$z$
direction. The density stratification was seeded with Sphericel hollow glass oxide particles of diameter
![]() $8{-}12~\unicode[STIX]{x03BC}\text{m}$
and densities ranging from 100 to
$8{-}12~\unicode[STIX]{x03BC}\text{m}$
and densities ranging from 100 to
![]() $1050~\text{kg}~\text{m}^{-3}$
. Images were collected using a pair of Imager Pro X 4M CCD cameras with a resolution of
$1050~\text{kg}~\text{m}^{-3}$
. Images were collected using a pair of Imager Pro X 4M CCD cameras with a resolution of
![]() $2042\times 2042~\text{pixels}$
. The cameras had a relative angle of around
$2042\times 2042~\text{pixels}$
. The cameras had a relative angle of around
![]() $45^{\circ }$
and the experimental field of view varied between
$45^{\circ }$
and the experimental field of view varied between
![]() ${\sim}0.3\times 0.3~\text{m}^{2}$
and
${\sim}0.3\times 0.3~\text{m}^{2}$
and
![]() ${\sim}0.4\times 0.4~\text{m}^{2}$
for different experiments. Images were collected at 16 frames per period of oscillation for each experiment, and were processed using the LaVision DaVis PIV software in order to obtain three-dimensional velocity fields in the plane of the laser sheet. For the analysis described in this paper, however, only the in-plane velocity components have been used.
${\sim}0.4\times 0.4~\text{m}^{2}$
for different experiments. Images were collected at 16 frames per period of oscillation for each experiment, and were processed using the LaVision DaVis PIV software in order to obtain three-dimensional velocity fields in the plane of the laser sheet. For the analysis described in this paper, however, only the in-plane velocity components have been used.
6 Experimental results and comparison with theory
6.1 Cross geometry
Our experimental study of the oblique-cross geometry focused on measuring the angle
![]() $\unicode[STIX]{x1D712}$
that the four cross arms make to the horizontal in the
$\unicode[STIX]{x1D712}$
that the four cross arms make to the horizontal in the
![]() $yz$
-plane (figure 1
b). As discussed in § 3, the response to tilted line forcing is always affected by the finite length of the source, and these end effects are amplified as the cutoff condition
$yz$
-plane (figure 1
b). As discussed in § 3, the response to tilted line forcing is always affected by the finite length of the source, and these end effects are amplified as the cutoff condition
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
is approached. Specifically, in the
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
is approached. Specifically, in the
![]() $yz$
-plane across the middle of the forcing (figure 2
b), where the wave pattern is symmetric in
$yz$
-plane across the middle of the forcing (figure 2
b), where the wave pattern is symmetric in
![]() $y$
, the four wave beams due to the main body of the forcing remain intact within a rectangular region of width
$y$
, the four wave beams due to the main body of the forcing remain intact within a rectangular region of width
![]() $D$
given by (3.2), which shrinks to zero as
$D$
given by (3.2), which shrinks to zero as
![]() $\unicode[STIX]{x1D703}\rightarrow \unicode[STIX]{x1D719}$
. As a result, it becomes increasingly difficult to measure the angle
$\unicode[STIX]{x1D703}\rightarrow \unicode[STIX]{x1D719}$
. As a result, it becomes increasingly difficult to measure the angle
![]() $\unicode[STIX]{x1D712}$
when the driving frequency
$\unicode[STIX]{x1D712}$
when the driving frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
of the cylinder approaches
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
of the cylinder approaches
![]() $\unicode[STIX]{x1D714}_{c}=\sin \unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D714}_{c}=\sin \unicode[STIX]{x1D719}$
.
To tackle this issue, experimental data for
![]() $\unicode[STIX]{x1D712}$
was obtained in
$\unicode[STIX]{x1D712}$
was obtained in
![]() $yz$
-planes closest to the cameras so as to observe the wave field near the lower end (
$yz$
-planes closest to the cameras so as to observe the wave field near the lower end (
![]() $y=-(L/2)\sin \unicode[STIX]{x1D719}$
) of the cylinder (see figure 3
a). In this set-up, as sketched in figure 4, the wave pattern is no longer symmetric as the wave beams emanating from the interior of the forcing appear only below the cylinder (
$y=-(L/2)\sin \unicode[STIX]{x1D719}$
) of the cylinder (see figure 3
a). In this set-up, as sketched in figure 4, the wave pattern is no longer symmetric as the wave beams emanating from the interior of the forcing appear only below the cylinder (
![]() $y<-(L/2)\sin \unicode[STIX]{x1D719}$
), in keeping with the beam propagation directions
$y<-(L/2)\sin \unicode[STIX]{x1D719}$
), in keeping with the beam propagation directions
![]() $-\hat{\boldsymbol{e}}^{\pm }$
relative to the forcing (see figure 1
a). Moreover, the disturbance above the cylinder (
$-\hat{\boldsymbol{e}}^{\pm }$
relative to the forcing (see figure 1
a). Moreover, the disturbance above the cylinder (
![]() $y>-(L/2)\sin \unicode[STIX]{x1D719}$
) is entirely an end effect, from the intersection of the
$y>-(L/2)\sin \unicode[STIX]{x1D719}$
) is entirely an end effect, from the intersection of the
![]() $yz$
-plane with the end cone at the lower end of the cylinder (figure 2
a), and turns out to be rather weak. As demonstrated below, this wave-field geometry makes it possible to accurately measure the beam angle
$yz$
-plane with the end cone at the lower end of the cylinder (figure 2
a), and turns out to be rather weak. As demonstrated below, this wave-field geometry makes it possible to accurately measure the beam angle
![]() $\unicode[STIX]{x1D712}$
even quite close to cutoff, by focusing on the wedge formed by the two beams just below the lower end of the cylinder.
$\unicode[STIX]{x1D712}$
even quite close to cutoff, by focusing on the wedge formed by the two beams just below the lower end of the cylinder.

Figure 4. Kinematics of internal waves generated by line forcing of finite length, tilted at an angle
![]() $\unicode[STIX]{x1D719}$
to the horizontal and oscillating with frequency
$\unicode[STIX]{x1D719}$
to the horizontal and oscillating with frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
. The sketch shows the intersection of the wave pattern with the (vertical)
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
. The sketch shows the intersection of the wave pattern with the (vertical)
![]() $yz$
-plane across the lower end of the forcing (
$yz$
-plane across the lower end of the forcing (
![]() $y=-(L/2)\sin \unicode[STIX]{x1D719}$
). Using the same
$y=-(L/2)\sin \unicode[STIX]{x1D719}$
). Using the same
![]() $xyz$
-coordinate system presented in figure 2, the solid lines represent the two beams emanating from the main body of the forcing and the dashed lines represent disturbances due to the finite source length, or the end effects. Specifically, the dashed line represents the disturbance coming from the upper end and the dotted line that from the lower end.
$xyz$
-coordinate system presented in figure 2, the solid lines represent the two beams emanating from the main body of the forcing and the dashed lines represent disturbances due to the finite source length, or the end effects. Specifically, the dashed line represents the disturbance coming from the upper end and the dotted line that from the lower end.
Before presenting experimental results, we verify that the above kinematic approach to end effects is also supported by more detailed computations based on the steady linear version of the evolution equation (4.7) near cutoff. Specifically, as right-hand side of this equation we chose
to roughly mimic the forcing due to the oscillating cylinder (of diameter
![]() $d=2.5~\text{cm}$
and length
$d=2.5~\text{cm}$
and length
![]() $L=34.8~\text{cm}$
) used in the experiments for tilt angle
$L=34.8~\text{cm}$
) used in the experiments for tilt angle
![]() $\unicode[STIX]{x1D719}=44^{\circ }$
. Taking
$\unicode[STIX]{x1D719}=44^{\circ }$
. Taking
![]() $d$
as characteristic length, we set
$d$
as characteristic length, we set
![]() $\unicode[STIX]{x1D700}=\sqrt{d/L}$
; thus, the length of the source (6.1) in terms of
$\unicode[STIX]{x1D700}=\sqrt{d/L}$
; thus, the length of the source (6.1) in terms of
![]() $X=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D709}$
is normalized to 1, and the values of
$X=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D709}$
is normalized to 1, and the values of
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FD}$
are determined from (4.5) and (4.9), respectively. (The inverse Reynolds number
$\unicode[STIX]{x1D6FD}$
are determined from (4.5) and (4.9), respectively. (The inverse Reynolds number
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\ast }/Nd^{2}$
, where
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\ast }/Nd^{2}$
, where
![]() $\unicode[STIX]{x1D708}_{\ast }=1~\text{mm}^{2}~\text{s}^{-1}$
is the kinematic viscosity.)
$\unicode[STIX]{x1D708}_{\ast }=1~\text{mm}^{2}~\text{s}^{-1}$
is the kinematic viscosity.)

Figure 5. Computed steady-state wave fields showing the magnitude of flow velocity in the
![]() $yz$
-plane across the mid-point (a,b) and the lower end (c,d) of a cylinder of length
$yz$
-plane across the mid-point (a,b) and the lower end (c,d) of a cylinder of length
![]() $L=34.8~\text{cm}$
tilted at
$L=34.8~\text{cm}$
tilted at
![]() $\unicode[STIX]{x1D719}=44^{\circ }$
to the horizontal and oscillating with (dimensionless) frequency
$\unicode[STIX]{x1D719}=44^{\circ }$
to the horizontal and oscillating with (dimensionless) frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: (a,c)
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: (a,c)
![]() $\unicode[STIX]{x1D703}=44^{\circ }$
(
$\unicode[STIX]{x1D703}=44^{\circ }$
(
![]() $\unicode[STIX]{x1D712}=0^{\circ }$
); (b,d)
$\unicode[STIX]{x1D712}=0^{\circ }$
); (b,d)
![]() $\unicode[STIX]{x1D703}=50^{\circ }$
(
$\unicode[STIX]{x1D703}=50^{\circ }$
(
![]() $\unicode[STIX]{x1D712}=35^{\circ }$
). The angle
$\unicode[STIX]{x1D712}=35^{\circ }$
). The angle
![]() $\unicode[STIX]{x1D712}$
in (d) is defined in (2.5) and is also marked in figures 2(b) and 4. These results were obtained from the steady linear version of equation (4.7) with (6.1) as forcing.
$\unicode[STIX]{x1D712}$
in (d) is defined in (2.5) and is also marked in figures 2(b) and 4. These results were obtained from the steady linear version of equation (4.7) with (6.1) as forcing.
Figure 5 compares the computed steady-state wave pattern in the
![]() $yz$
-plane across the mid-point with that in the
$yz$
-plane across the mid-point with that in the
![]() $yz$
-plane at the lower end of a cylinder tilted at
$yz$
-plane at the lower end of a cylinder tilted at
![]() $\unicode[STIX]{x1D719}=44^{\circ }$
, for two driving frequencies corresponding to
$\unicode[STIX]{x1D719}=44^{\circ }$
, for two driving frequencies corresponding to
![]() $\unicode[STIX]{x1D703}=44^{\circ }$
and
$\unicode[STIX]{x1D703}=44^{\circ }$
and
![]() $\unicode[STIX]{x1D703}=50^{\circ }$
. Exactly at cutoff (figure 5
a,c), end effects dominate the horizontal (
$\unicode[STIX]{x1D703}=50^{\circ }$
. Exactly at cutoff (figure 5
a,c), end effects dominate the horizontal (
![]() $\unicode[STIX]{x1D712}=0^{\circ }$
) wave beams from the interior of the forcing, which collapse to a point, in keeping with
$\unicode[STIX]{x1D712}=0^{\circ }$
) wave beams from the interior of the forcing, which collapse to a point, in keeping with
![]() $D\rightarrow 0$
as
$D\rightarrow 0$
as
![]() $\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
in (3.2). Moreover, as expected from the kinematic analysis (figures 2 and 4), the end disturbances are of hyperbolic shape, both at the mid-point (figure 5
a) and the lower end (figure 5
c) of the cylinder; in the latter location, it is also possible to discern above the cylinder two, rather weak, straight rays at the angle
$\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D703}$
in (3.2). Moreover, as expected from the kinematic analysis (figures 2 and 4), the end disturbances are of hyperbolic shape, both at the mid-point (figure 5
a) and the lower end (figure 5
c) of the cylinder; in the latter location, it is also possible to discern above the cylinder two, rather weak, straight rays at the angle
![]() $\unicode[STIX]{x1D703}=44^{\circ }$
to the horizontal, as suggested by the sketch in figure 4. By contrast, above cutoff (
$\unicode[STIX]{x1D703}=44^{\circ }$
to the horizontal, as suggested by the sketch in figure 4. By contrast, above cutoff (
![]() $\unicode[STIX]{x1D703}=50^{\circ }$
, figure 5
b,d), the straight wave beams emanating from the main body of the cylinder, at the angle
$\unicode[STIX]{x1D703}=50^{\circ }$
, figure 5
b,d), the straight wave beams emanating from the main body of the cylinder, at the angle
![]() $\unicode[STIX]{x1D712}=35^{\circ }$
to the horizontal, remain intact close to the cylinder, while end disturbances of hyperbolic shape prevail away from the cylinder. According to the kinematic estimate (3.2), the width of the rectangular region where the wave beams are free of end effects is
$\unicode[STIX]{x1D712}=35^{\circ }$
to the horizontal, remain intact close to the cylinder, while end disturbances of hyperbolic shape prevail away from the cylinder. According to the kinematic estimate (3.2), the width of the rectangular region where the wave beams are free of end effects is
![]() $18~\text{cm}$
at the mid-point (figure 2
b) and
$18~\text{cm}$
at the mid-point (figure 2
b) and
![]() $36~\text{cm}$
at the lower end (figure 4) of the cylinder. These predictions are in reasonable agreement with the wave patterns in figure 5(b,d); moreover, the geometry of the computed wave field at the lower end of the forcing (figure 5
d) is consistent with the kinematic results sketched in figure 4.
$36~\text{cm}$
at the lower end (figure 4) of the cylinder. These predictions are in reasonable agreement with the wave patterns in figure 5(b,d); moreover, the geometry of the computed wave field at the lower end of the forcing (figure 5
d) is consistent with the kinematic results sketched in figure 4.

Figure 6. (a) Phase field plot across central plane of cylinder for
![]() $\unicode[STIX]{x1D719}=44^{\circ }$
and
$\unicode[STIX]{x1D719}=44^{\circ }$
and
![]() $\unicode[STIX]{x1D703}=49.5^{\circ }$
; this is a composite of an image showing measured data for
$\unicode[STIX]{x1D703}=49.5^{\circ }$
; this is a composite of an image showing measured data for
![]() $z<0$
and its mirror image about the
$z<0$
and its mirror image about the
![]() $y$
-axis. (b) Phase field plot across end plane of cylinder for
$y$
-axis. (b) Phase field plot across end plane of cylinder for
![]() $\unicode[STIX]{x1D719}=44^{\circ }$
and
$\unicode[STIX]{x1D719}=44^{\circ }$
and
![]() $\unicode[STIX]{x1D703}=49.5^{\circ }$
(
$\unicode[STIX]{x1D703}=49.5^{\circ }$
(
![]() $\unicode[STIX]{x1D712}_{theory}=33.6^{\circ }$
and
$\unicode[STIX]{x1D712}_{theory}=33.6^{\circ }$
and
![]() $\unicode[STIX]{x1D712}_{measured}=35.2\pm 1.1^{\circ }$
). (c) Phase field plot across end plane of cylinder for
$\unicode[STIX]{x1D712}_{measured}=35.2\pm 1.1^{\circ }$
). (c) Phase field plot across end plane of cylinder for
![]() $\unicode[STIX]{x1D719}=27^{\circ }$
and
$\unicode[STIX]{x1D719}=27^{\circ }$
and
![]() $\unicode[STIX]{x1D703}=28.3^{\circ }$
(
$\unicode[STIX]{x1D703}=28.3^{\circ }$
(
![]() $\unicode[STIX]{x1D712}_{theory}=10.1^{\circ }$
and
$\unicode[STIX]{x1D712}_{theory}=10.1^{\circ }$
and
![]() $\unicode[STIX]{x1D712}_{measured}=15.8\pm 0.5^{\circ }$
).(d) Velocity amplitude plot (with superposed arrows) corresponding to phase results in (b); for comparison, see model results in figure 5(d). In each image, the black ellipse marks the location and area of the cylinder.
$\unicode[STIX]{x1D712}_{measured}=15.8\pm 0.5^{\circ }$
).(d) Velocity amplitude plot (with superposed arrows) corresponding to phase results in (b); for comparison, see model results in figure 5(d). In each image, the black ellipse marks the location and area of the cylinder.
Turning now to the experimental observations, figure 6 shows snapshots of wave fields for
![]() $\unicode[STIX]{x1D719}=44^{\circ }$
and
$\unicode[STIX]{x1D719}=44^{\circ }$
and
![]() $\unicode[STIX]{x1D703}=49.5^{\circ }$
obtained in the
$\unicode[STIX]{x1D703}=49.5^{\circ }$
obtained in the
![]() $yz$
-planes across the mid-point and the lower end of the cylinder, corresponding to the theoretical results in figure 5(b,d); the quantity plotted is the phase field of the vertical velocity component, which was chosen to maximize the clarity of the wave-field structure. Consistent with the theoretical predictions in figure 5(b,d), in the central plane of the cylinder (figure 6
a) the wave field is dominated by end disturbances at the angle
$yz$
-planes across the mid-point and the lower end of the cylinder, corresponding to the theoretical results in figure 5(b,d); the quantity plotted is the phase field of the vertical velocity component, which was chosen to maximize the clarity of the wave-field structure. Consistent with the theoretical predictions in figure 5(b,d), in the central plane of the cylinder (figure 6
a) the wave field is dominated by end disturbances at the angle
![]() $\unicode[STIX]{x1D703}$
whereas in the end plane of the cylinder (figure 6
b) the desired beam angle
$\unicode[STIX]{x1D703}$
whereas in the end plane of the cylinder (figure 6
b) the desired beam angle
![]() $\unicode[STIX]{x1D712}$
can be readily determined in the lower half of the field of view. The velocity amplitude plot (figure 6
d) also shows good qualitative agreement with the model results (figure 5
d), except for the response in the immediate vicinity of the cylinder. This discrepancy is not surprising, as the time-harmonic force (4.6) and (6.1) assumed in the model is different from the oscillating cylinder used as excitation in the experiments.
$\unicode[STIX]{x1D712}$
can be readily determined in the lower half of the field of view. The velocity amplitude plot (figure 6
d) also shows good qualitative agreement with the model results (figure 5
d), except for the response in the immediate vicinity of the cylinder. This discrepancy is not surprising, as the time-harmonic force (4.6) and (6.1) assumed in the model is different from the oscillating cylinder used as excitation in the experiments.
Experiments were run across a wide range of driving frequencies
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
for the three tilt angles
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
for the three tilt angles
![]() $\unicode[STIX]{x1D719}=0^{\circ }$
,
$\unicode[STIX]{x1D719}=0^{\circ }$
,
![]() $27^{\circ }$
and
$27^{\circ }$
and
![]() $44^{\circ }$
, and the apparent beam angle
$44^{\circ }$
, and the apparent beam angle
![]() $\unicode[STIX]{x1D712}$
was determined as follows. For any given
$\unicode[STIX]{x1D712}$
was determined as follows. For any given
![]() $(y,z)$
coordinate, the velocity became a periodic function of time once the wave field reached a harmonic state. Via Fourier analysis, we verified that the fundamental frequency was dominant and higher harmonics were negligible. The velocity at a
$(y,z)$
coordinate, the velocity became a periodic function of time once the wave field reached a harmonic state. Via Fourier analysis, we verified that the fundamental frequency was dominant and higher harmonics were negligible. The velocity at a
![]() $(y,z)$
location therefore takes the form
$(y,z)$
location therefore takes the form
![]() $A(y,z)\sin (\unicode[STIX]{x1D714}Nt+\unicode[STIX]{x1D6FC}(y,z))$
and using a sinusoidal fit we determined the amplitude
$A(y,z)\sin (\unicode[STIX]{x1D714}Nt+\unicode[STIX]{x1D6FC}(y,z))$
and using a sinusoidal fit we determined the amplitude
![]() $A(y,z)$
and phase
$A(y,z)$
and phase
![]() $\unicode[STIX]{x1D6FC}(y,z)$
fields from the experimental data. The phase fields very clearly displayed the wave-beam orientation and were used as the basis for measuring propagation angles. As indicated in figures 6(b) and 6(c), a pair of roughly
$\unicode[STIX]{x1D6FC}(y,z)$
fields from the experimental data. The phase fields very clearly displayed the wave-beam orientation and were used as the basis for measuring propagation angles. As indicated in figures 6(b) and 6(c), a pair of roughly
![]() $500\times 250~\text{pixel}$
windows (which corresponds to around
$500\times 250~\text{pixel}$
windows (which corresponds to around
![]() $60\times 30$
PIV data points) located in the lower beams in the vicinity of the cylinder were selected. Matlab’s contour function was used to extract several lines of constant phase within these windows. Linear regression was then used to determine the angle of a best fit line through several such contours of constant phase, from which the average angle
$60\times 30$
PIV data points) located in the lower beams in the vicinity of the cylinder were selected. Matlab’s contour function was used to extract several lines of constant phase within these windows. Linear regression was then used to determine the angle of a best fit line through several such contours of constant phase, from which the average angle
![]() $\unicode[STIX]{x1D712}$
was determined; the corresponding experimental precision for each data point was typically 1 or 2 degrees, with a little more variability for smaller values of
$\unicode[STIX]{x1D712}$
was determined; the corresponding experimental precision for each data point was typically 1 or 2 degrees, with a little more variability for smaller values of
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.

Figure 7. Experimental data for the beam angle
![]() $\unicode[STIX]{x1D712}$
as a function of
$\unicode[STIX]{x1D712}$
as a function of
![]() $\unicode[STIX]{x1D703}$
set by the driving frequency
$\unicode[STIX]{x1D703}$
set by the driving frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
, for tilt angle
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
, for tilt angle
![]() $\unicode[STIX]{x1D719}=0^{\circ }$
(○),
$\unicode[STIX]{x1D719}=0^{\circ }$
(○),
![]() $\unicode[STIX]{x1D719}=27^{\circ }$
(▵) and
$\unicode[STIX]{x1D719}=27^{\circ }$
(▵) and
![]() $\unicode[STIX]{x1D719}=44^{\circ }$
(▫); the corresponding theoretical curves, obtained by (2.5), are included as solid, dashed and dotted lines, respectively. The error bars are the standard deviation of the mean.
$\unicode[STIX]{x1D719}=44^{\circ }$
(▫); the corresponding theoretical curves, obtained by (2.5), are included as solid, dashed and dotted lines, respectively. The error bars are the standard deviation of the mean.
The resulting data for
![]() $\unicode[STIX]{x1D712}$
as a function of
$\unicode[STIX]{x1D712}$
as a function of
![]() $\unicode[STIX]{x1D703}=\sin ^{-1}\unicode[STIX]{x1D714}$
is presented in figure 7, in which the error bars presented represent the standard deviation of the mean. There is generally excellent agreement between experiment and the theoretical predictions obtained from (2.5). Most notably, for fixed driving frequency
$\unicode[STIX]{x1D703}=\sin ^{-1}\unicode[STIX]{x1D714}$
is presented in figure 7, in which the error bars presented represent the standard deviation of the mean. There is generally excellent agreement between experiment and the theoretical predictions obtained from (2.5). Most notably, for fixed driving frequency
![]() $\unicode[STIX]{x1D714}$
, the beam projected angle
$\unicode[STIX]{x1D714}$
, the beam projected angle
![]() $\unicode[STIX]{x1D712}$
is reduced as the cylinder tilt angle
$\unicode[STIX]{x1D712}$
is reduced as the cylinder tilt angle
![]() $\unicode[STIX]{x1D719}$
increases, and for non-zero
$\unicode[STIX]{x1D719}$
increases, and for non-zero
![]() $\unicode[STIX]{x1D719}$
there is a lower cutoff driving frequency corresponding to
$\unicode[STIX]{x1D719}$
there is a lower cutoff driving frequency corresponding to
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
at which
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
at which
![]() $\unicode[STIX]{x1D712}$
goes to zero; as expected, no radiated wave beams were observed below cutoff (
$\unicode[STIX]{x1D712}$
goes to zero; as expected, no radiated wave beams were observed below cutoff (
![]() $\unicode[STIX]{x1D703}<\unicode[STIX]{x1D719}$
). As noted earlier, the wave beams emanating from the cylinder interior are masked by end disturbances when the cutoff condition is approached; only as a result of studying the form of the wave field in the end plane of the cylinder, having been guided by the theoretical predictions in figures 4 and 5, were we able to make reliable measurements of
$\unicode[STIX]{x1D703}<\unicode[STIX]{x1D719}$
). As noted earlier, the wave beams emanating from the cylinder interior are masked by end disturbances when the cutoff condition is approached; only as a result of studying the form of the wave field in the end plane of the cylinder, having been guided by the theoretical predictions in figures 4 and 5, were we able to make reliable measurements of
![]() $\unicode[STIX]{x1D712}$
approaching the critical condition
$\unicode[STIX]{x1D712}$
approaching the critical condition
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
. Away from the critical condition the phase plots were very well defined, but as
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}$
. Away from the critical condition the phase plots were very well defined, but as
![]() $\unicode[STIX]{x1D703}$
approached
$\unicode[STIX]{x1D703}$
approached
![]() $\unicode[STIX]{x1D719}$
they became somewhat less so (e.g., compare figures 6
b and 6
c), likely due to the induced mean flow discussed in § 6.2 below. Moreover, according to (2.5),
$\unicode[STIX]{x1D719}$
they became somewhat less so (e.g., compare figures 6
b and 6
c), likely due to the induced mean flow discussed in § 6.2 below. Moreover, according to (2.5),
![]() $\text{d}\unicode[STIX]{x1D712}/\text{d}\unicode[STIX]{x1D703}\rightarrow \infty$
as
$\text{d}\unicode[STIX]{x1D712}/\text{d}\unicode[STIX]{x1D703}\rightarrow \infty$
as
![]() $\unicode[STIX]{x1D703}\rightarrow \unicode[STIX]{x1D719}$
, which makes
$\unicode[STIX]{x1D703}\rightarrow \unicode[STIX]{x1D719}$
, which makes
![]() $\unicode[STIX]{x1D712}$
sensitive to changes of
$\unicode[STIX]{x1D712}$
sensitive to changes of
![]() $\unicode[STIX]{x1D703}$
near the critical condition. For these reasons, no data are plotted in figure 7 for
$\unicode[STIX]{x1D703}$
near the critical condition. For these reasons, no data are plotted in figure 7 for
![]() $\unicode[STIX]{x1D712}$
below a certain threshold, and this inaccessible range of beam angles widens as the tilt angle
$\unicode[STIX]{x1D712}$
below a certain threshold, and this inaccessible range of beam angles widens as the tilt angle
![]() $\unicode[STIX]{x1D719}$
is increased. (In the case of a horizontal cylinder, no such difficulty arises even though figure 7 only shows measured values of
$\unicode[STIX]{x1D719}$
is increased. (In the case of a horizontal cylinder, no such difficulty arises even though figure 7 only shows measured values of
![]() $\unicode[STIX]{x1D712}$
above about
$\unicode[STIX]{x1D712}$
above about
![]() $25^{\circ }$
.)
$25^{\circ }$
.)
6.2 Induced mean flow near cutoff
We also sought experimental evidence of resonance and associated nonlinear effects when the cylinder driving frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
approaches the cutoff frequency
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
approaches the cutoff frequency
![]() $\unicode[STIX]{x1D714}_{c}=\sin \unicode[STIX]{x1D719}$
, as suggested by the asymptotic model (4.7) and (4.8). From the kinematic analyses in §§ 2 and 3, the wave-beam response near cutoff is contained within the vicinity of the source. However, our theoretical model, which uses the time-harmonic force (4.6) as excitation, is not expected to accurately predict the near-field response due to an oscillating cylinder. Given this limitation, we pursued a qualitative comparison in regard to the generation of horizontal mean flow – the most prominent nonlinear feature of the resonant response near cutoff according to theory.
$\unicode[STIX]{x1D714}_{c}=\sin \unicode[STIX]{x1D719}$
, as suggested by the asymptotic model (4.7) and (4.8). From the kinematic analyses in §§ 2 and 3, the wave-beam response near cutoff is contained within the vicinity of the source. However, our theoretical model, which uses the time-harmonic force (4.6) as excitation, is not expected to accurately predict the near-field response due to an oscillating cylinder. Given this limitation, we pursued a qualitative comparison in regard to the generation of horizontal mean flow – the most prominent nonlinear feature of the resonant response near cutoff according to theory.
Returning to the experimental configuration in figure 3(b), as an overall measure of mean-flow strength, we take
here,
where
![]() $\overline{u}$
denotes the
$\overline{u}$
denotes the
![]() $x$
-component of the induced mean flow. It should be noted that, by Green’s theorem,
$x$
-component of the induced mean flow. It should be noted that, by Green’s theorem,
![]() $\unicode[STIX]{x1D6E9}(y,t)$
is the integrated mean vertical vorticity over the horizontal half-plane
$\unicode[STIX]{x1D6E9}(y,t)$
is the integrated mean vertical vorticity over the horizontal half-plane
![]() $-\infty <x<\infty$
,
$-\infty <x<\infty$
,
![]() $z>0$
(or
$z>0$
(or
![]() $z<0$
) at height
$z<0$
) at height
![]() $y$
.
$y$
.
In the experiment, velocity-field data was from the portion of the
![]() $xy$
-plane that lay beneath the cylinder, as illustrated in figure 3(b), since data could not be obtained in the shadow of the laser above the cylinder. Accordingly, integration of
$xy$
-plane that lay beneath the cylinder, as illustrated in figure 3(b), since data could not be obtained in the shadow of the laser above the cylinder. Accordingly, integration of
![]() $\unicode[STIX]{x1D6E9}$
and
$\unicode[STIX]{x1D6E9}$
and
![]() $\overline{u}$
in (6.2) and (6.3) was carried out over the finite region under the cylinder in figure 3(b); we refer to this approximation to
$\overline{u}$
in (6.2) and (6.3) was carried out over the finite region under the cylinder in figure 3(b); we refer to this approximation to
![]() $S$
as
$S$
as
![]() $S^{\prime }$
.
$S^{\prime }$
.
The same integration region was also used in computing
![]() $S^{\prime }$
theoretically. To this end, the model equations (4.7) and (4.8), with (6.1) as forcing, were solved numerically following the procedure described in Kataoka & Akylas (Reference Kataoka and Akylas2015). The cross mean flow
$S^{\prime }$
theoretically. To this end, the model equations (4.7) and (4.8), with (6.1) as forcing, were solved numerically following the procedure described in Kataoka & Akylas (Reference Kataoka and Akylas2015). The cross mean flow
![]() $\overline{V}_{\infty }$
obtained from the model was then used to estimate
$\overline{V}_{\infty }$
obtained from the model was then used to estimate
![]() $\overline{u}$
, the desired horizontal mean-flow component along
$\overline{u}$
, the desired horizontal mean-flow component along
![]() $x$
. According to the asymptotic analysis of Kataoka & Akylas (Reference Kataoka and Akylas2015), the induced mean flow extends far away from the cylinder (
$x$
. According to the asymptotic analysis of Kataoka & Akylas (Reference Kataoka and Akylas2015), the induced mean flow extends far away from the cylinder (
![]() $|\unicode[STIX]{x1D702}|\gg 1$
) and the contribution to
$|\unicode[STIX]{x1D702}|\gg 1$
) and the contribution to
![]() $S^{\prime }$
from
$S^{\prime }$
from
![]() $\overline{u}$
in the vicinity of the cylinder (‘inner’ region) would be sub-dominant compared with the far-field (‘outer’-region) contribution. However, as the assumed separation of scales is not strictly satisfied in the experiment (
$\overline{u}$
in the vicinity of the cylinder (‘inner’ region) would be sub-dominant compared with the far-field (‘outer’-region) contribution. However, as the assumed separation of scales is not strictly satisfied in the experiment (
![]() $\unicode[STIX]{x1D700}=\sqrt{d/L}=0.29$
), we also included the near-field contribution, taking the width of the inner region to be one cylinder radius (
$\unicode[STIX]{x1D700}=\sqrt{d/L}=0.29$
), we also included the near-field contribution, taking the width of the inner region to be one cylinder radius (
![]() $d/2=1.25~\text{cm}$
) as indicated in figure 3(b).
$d/2=1.25~\text{cm}$
) as indicated in figure 3(b).

Figure 8. Overall mean-flow strength
![]() $S^{\prime }$
versus oscillation cycles of cylinder tilted at
$S^{\prime }$
versus oscillation cycles of cylinder tilted at
![]() $\unicode[STIX]{x1D719}=45^{\circ }$
to the horizontal and oscillating at frequency
$\unicode[STIX]{x1D719}=45^{\circ }$
to the horizontal and oscillating at frequency
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: experimental results for
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
: experimental results for
![]() $\unicode[STIX]{x1D703}=40^{\circ }$
(○),
$\unicode[STIX]{x1D703}=40^{\circ }$
(○),
![]() $\unicode[STIX]{x1D703}=45^{\circ }$
(▵),
$\unicode[STIX]{x1D703}=45^{\circ }$
(▵),
![]() $\unicode[STIX]{x1D703}=50^{\circ }$
(▫),
$\unicode[STIX]{x1D703}=50^{\circ }$
(▫),
![]() $\unicode[STIX]{x1D703}=60^{\circ }$
(
$\unicode[STIX]{x1D703}=60^{\circ }$
(
![]() $\times$
); theoretical results for
$\times$
); theoretical results for
![]() $\unicode[STIX]{x1D703}=40^{\circ }$
(●),
$\unicode[STIX]{x1D703}=40^{\circ }$
(●),
![]() $\unicode[STIX]{x1D703}=45^{\circ }$
(▴),
$\unicode[STIX]{x1D703}=45^{\circ }$
(▴),
![]() $\unicode[STIX]{x1D703}=50^{\circ }$
(▪),
$\unicode[STIX]{x1D703}=50^{\circ }$
(▪),
![]() $\unicode[STIX]{x1D703}=60^{\circ }$
(+). In the experiment, the cylinder (length
$\unicode[STIX]{x1D703}=60^{\circ }$
(+). In the experiment, the cylinder (length
![]() $L=28.8~\text{cm}$
and diameter
$L=28.8~\text{cm}$
and diameter
![]() $d=2.5~\text{cm}$
) is oscillated with peak-to-peak amplitude 16 mm. In the theoretical model, equations (4.7) and (4.8) are solved with (6.1) as forcing and the delta function approximated by
$d=2.5~\text{cm}$
) is oscillated with peak-to-peak amplitude 16 mm. In the theoretical model, equations (4.7) and (4.8) are solved with (6.1) as forcing and the delta function approximated by
![]() $\unicode[STIX]{x1D6FF}(Z)\simeq (2/\sqrt{\unicode[STIX]{x03C0}})\exp \{-(2Z)^{2}\}$
.
$\unicode[STIX]{x1D6FF}(Z)\simeq (2/\sqrt{\unicode[STIX]{x03C0}})\exp \{-(2Z)^{2}\}$
.
Figure 8 displays time histories of the overall induced-mean-flow strength
![]() $S^{\prime }$
, as computed from experimental data and numerical results, generated by a cylinder tilted at
$S^{\prime }$
, as computed from experimental data and numerical results, generated by a cylinder tilted at
![]() $\unicode[STIX]{x1D719}=45^{\circ }$
and oscillating at various driving frequencies
$\unicode[STIX]{x1D719}=45^{\circ }$
and oscillating at various driving frequencies
![]() $\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
near the cutoff
$\unicode[STIX]{x1D714}=\sin \unicode[STIX]{x1D703}$
near the cutoff
![]() $\unicode[STIX]{x1D714}_{c}=\sin \unicode[STIX]{x1D719}$
. Even though there is only rough quantitative agreement, the experimental and theoretical results are generally in the same ball park and also exhibit similar qualitative trends, namely:
$\unicode[STIX]{x1D714}_{c}=\sin \unicode[STIX]{x1D719}$
. Even though there is only rough quantitative agreement, the experimental and theoretical results are generally in the same ball park and also exhibit similar qualitative trends, namely:
![]() $S^{\prime }$
grows rapidly at early times and then begins to plateau as the beam response reaches a quasisteady state. Most notably, however,
$S^{\prime }$
grows rapidly at early times and then begins to plateau as the beam response reaches a quasisteady state. Most notably, however,
![]() $S^{\prime }$
reaches significantly higher levels for driving frequencies slightly above cutoff (
$S^{\prime }$
reaches significantly higher levels for driving frequencies slightly above cutoff (
![]() $\unicode[STIX]{x1D703}\approx 50^{\circ }$
), suggesting that the induced mean flow is particularly strong in this narrow frequency range. This is an indication of resonant behaviour according to our asymptotic model, where the mean flow is driven by Reynolds stresses brought about by three-dimensional nonlinear interactions of the wave-beam response as described on the right-hand side of (4.8). It should be pointed out, however, that the time-harmonic line forcing used in this model does not account for the viscous boundary layer around the oscillating cylinder and related phenomena that could affect the mean flow observed experimentally. A definitive discussion of the beam response and induced mean flow near cutoff, including quantitative comparison with experiment, would require computing the actual flow field in the vicinity of the oscillating cylinder.
$\unicode[STIX]{x1D703}\approx 50^{\circ }$
), suggesting that the induced mean flow is particularly strong in this narrow frequency range. This is an indication of resonant behaviour according to our asymptotic model, where the mean flow is driven by Reynolds stresses brought about by three-dimensional nonlinear interactions of the wave-beam response as described on the right-hand side of (4.8). It should be pointed out, however, that the time-harmonic line forcing used in this model does not account for the viscous boundary layer around the oscillating cylinder and related phenomena that could affect the mean flow observed experimentally. A definitive discussion of the beam response and induced mean flow near cutoff, including quantitative comparison with experiment, would require computing the actual flow field in the vicinity of the oscillating cylinder.
7 Concluding remarks
We have discussed the generation of internal gravity waves by a time-harmonic line source that is tilted with respect to the horizontal in a stratified Boussinesq fluid of constant buoyancy frequency. In the laboratory, this flow configuration can be realized by oscillating a cylinder tilted to the horizontal in a stratified fluid. In this regard, the present study shares much in common with the classical experiment by Mowbray & Rarity (Reference Mowbray and Rarity1967) for a horizontal cylinder, which first drew attention to internal wave beams and the now familiar St. Andrew’s Cross wave pattern. However, our analysis and supporting laboratory experiments have pointed out that the response to tilted forcing is profoundly different from the corresponding horizontal source problem in two main respects: (i) radiation of wave beams, forming an ‘oblique’ St. Andrew’s Cross, is limited due to a lower cutoff frequency set by the source tilt angle to the horizontal; and (ii) the response is essentially three-dimensional, as end effects eventually come into play when the cutoff frequency is approached, however long a line source may be. These unique aspects of radiated wave beams from a tilted source may have far-reaching implications for geophysical flow modelling. For instance, these findings would be relevant to modelling gravity wave generation in the atmosphere due to squall lines that need not be horizontal. Moreover, the oblique St. Andrew’s Cross may prove useful in understanding the geometry of three-dimensional ocean internal waves induced by tidal flow over a ridge with large-scale height variations along the ridge.
The present paper has focused on the kinematics of the steady-state radiated wave field. We have also made a preliminary study, based on an asymptotic model using a time-harmonic line force as excitation, of the transient response near the cutoff frequency. On kinematic grounds, the wave-beam response near cutoff is contained within the vicinity of the forcing, suggesting a resonance phenomenon due to energy accumulation there. According to our model, the combination of nonlinear, viscous and three-dimensional effects near this resonance results in transfer of energy to a horizontal mean flow. The generation of such an induced mean flow is also qualitatively supported by our experimental findings. A complete investigation of the response near cutoff, including quantitative comparison with experiment, would require computing the detailed flow field close to the source and is left to future studies.
Acknowledgements
We wish to thank Mr. Spencer Wilson for assisting in carrying out the laboratory experiments. This work was supported in part by the US National Science Foundation under grant DMS-1512925.