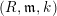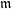1 Introduction
In this paper we consider the problem of determining when two rings have similar singularities. As a motivating example let ![]() $R=k[[x_{1},\ldots ,x_{n}]]$ be the power series ring in
$R=k[[x_{1},\ldots ,x_{n}]]$ be the power series ring in ![]() $n$ variables over a field
$n$ variables over a field ![]() $k$ and
$k$ and ![]() $f\in R$. If we add a term of sufficiently high order to
$f\in R$. If we add a term of sufficiently high order to ![]() $f$, will the new singularity be similar to that of
$f$, will the new singularity be similar to that of ![]() $f$?
$f$?
The origin of the above question can be traced at least as far back as 1956. Samuel [Reference SamuelSam56] proved if the Jacobian ideal ![]() $J(f)$ of
$J(f)$ of ![]() $f$ is
$f$ is ![]() $\mathfrak{m}$-primary and if
$\mathfrak{m}$-primary and if ![]() $f-g\in (x_{1},\ldots ,x_{n})J(f)^{2}$, then there is an automorphism
$f-g\in (x_{1},\ldots ,x_{n})J(f)^{2}$, then there is an automorphism ![]() $\unicode[STIX]{x1D711}:R\rightarrow R$ such that
$\unicode[STIX]{x1D711}:R\rightarrow R$ such that ![]() $\unicode[STIX]{x1D711}(f)=g$. In particular, Samuel’s result asserts that if
$\unicode[STIX]{x1D711}(f)=g$. In particular, Samuel’s result asserts that if ![]() $f$ has an isolated singularity and
$f$ has an isolated singularity and ![]() $g$ is sufficiently close to
$g$ is sufficiently close to ![]() $f$, then the rings
$f$, then the rings ![]() $R/(f)$ and
$R/(f)$ and ![]() $R/(g)$ are isomorphic. Samuel’s result was furthered by Hironaka [Reference HironakaHir65]: if
$R/(g)$ are isomorphic. Samuel’s result was furthered by Hironaka [Reference HironakaHir65]: if ![]() $R/I$ is a reduced and equidimensional isolated singularity, then there is an integer
$R/I$ is a reduced and equidimensional isolated singularity, then there is an integer ![]() $e>0$ such that for any ideal
$e>0$ such that for any ideal ![]() $J$ that also defines a reduced and equidimensional singularity of same dimension and if
$J$ that also defines a reduced and equidimensional singularity of same dimension and if ![]() $I\equiv J\hspace{0.6em}{\rm mod}\hspace{0.2em}(x_{1},\ldots ,x_{n})^{e}$ then
$I\equiv J\hspace{0.6em}{\rm mod}\hspace{0.2em}(x_{1},\ldots ,x_{n})^{e}$ then ![]() $R/I\cong R/J$.
$R/I\cong R/J$.
More recently, Cutkosky and Srinivasan have extended Samuel’s result to include all complete intersection prime ideals and Hironaka’s theorem to all reduced equidimensional ideals. See [Reference Cutkosky and SrinivasanCS93] for precise statements.
However, when ![]() $f\in k[[x_{1},\ldots ,x_{n}]]$ does not have an isolated singularity, the results of Samuel, Hironaka, and Cutkosky and Srinivasan do not allow us to relate the singularities of
$f\in k[[x_{1},\ldots ,x_{n}]]$ does not have an isolated singularity, the results of Samuel, Hironaka, and Cutkosky and Srinivasan do not allow us to relate the singularities of ![]() $R/(f)$ with the singularities of
$R/(f)$ with the singularities of ![]() $R/(g)$. To compare the singularity of
$R/(g)$. To compare the singularity of ![]() $R/(f)$ with the singularity of
$R/(f)$ with the singularity of ![]() $R/(g)$ we first require a formal notion of “closeness” of singularities. For example, one could require the Hilbert–Samuel functions of
$R/(g)$ we first require a formal notion of “closeness” of singularities. For example, one could require the Hilbert–Samuel functions of ![]() $R/(f)$ and
$R/(f)$ and ![]() $R/(g)$ to coincide. Srinivas and Trivedi [Reference Srinivas and TrivediST96] have shown if
$R/(g)$ to coincide. Srinivas and Trivedi [Reference Srinivas and TrivediST96] have shown if ![]() $I=(f_{1},\ldots ,f_{h})$ is a complete intersectionFootnote 1, or more generally if
$I=(f_{1},\ldots ,f_{h})$ is a complete intersectionFootnote 1, or more generally if ![]() $I$ is a parameter ideal in a generalized Cohen–Macaulay ring, then the associated graded rings of
$I$ is a parameter ideal in a generalized Cohen–Macaulay ring, then the associated graded rings of ![]() $I$ and an ideal
$I$ and an ideal ![]() $J=(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{h}+\unicode[STIX]{x1D716}_{h})$ will be isomorphic, provided
$J=(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{h}+\unicode[STIX]{x1D716}_{h})$ will be isomorphic, provided ![]() $\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{h}$ are in a sufficiently large power of the maximal ideal.
$\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{h}$ are in a sufficiently large power of the maximal ideal.
We now turn our attention to numerical invariants in positive characteristic. In particular, we introduce and explore the behavior of F-pure threshold, Hilbert–Kunz multiplicity, and F-signature with respect to ![]() $\mathfrak{m}$-adic topologies. In what follows, let
$\mathfrak{m}$-adic topologies. In what follows, let ![]() $(R,\mathfrak{m})$ be a local ring of prime characteristic
$(R,\mathfrak{m})$ be a local ring of prime characteristic ![]() $p$. Let
$p$. Let ![]() $F:R\rightarrow R$ denote the Frobenius endomorphism. Given ideal
$F:R\rightarrow R$ denote the Frobenius endomorphism. Given ideal ![]() $I\subseteq R$ and
$I\subseteq R$ and ![]() $e\in \mathbb{N}$ let
$e\in \mathbb{N}$ let ![]() $I^{[p^{e}]}=(i^{p^{e}}\mid i\in I)$ be the expansion of
$I^{[p^{e}]}=(i^{p^{e}}\mid i\in I)$ be the expansion of ![]() $I$ along
$I$ along ![]() $F^{e}$. We shall always assume
$F^{e}$. We shall always assume ![]() $R$ is F-finite, meaning that
$R$ is F-finite, meaning that ![]() $F$ is a finite map.
$F$ is a finite map.
The study of F-pure thresholds was initiated by Takagi and Watanabe [Reference Takagi and WatanabeTW04]. If ![]() $(R,\mathfrak{m},k)$ is regular then the F-pure threshold of an element
$(R,\mathfrak{m},k)$ is regular then the F-pure threshold of an element ![]() $f\in R$ can be defined as the limit
$f\in R$ can be defined as the limit ![]() $\operatorname{fpt}(f)=\lim _{e\rightarrow \infty }(\unicode[STIX]{x1D708}_{e}(f)/p^{e})$ where
$\operatorname{fpt}(f)=\lim _{e\rightarrow \infty }(\unicode[STIX]{x1D708}_{e}(f)/p^{e})$ where ![]() $\unicode[STIX]{x1D708}_{e}(f)=\max \{t\in \mathbb{N}\mid f^{t}\not \in \mathfrak{m}^{[p^{e}]}\}$. Two elementary observations concerning F-pure thresholds are that if
$\unicode[STIX]{x1D708}_{e}(f)=\max \{t\in \mathbb{N}\mid f^{t}\not \in \mathfrak{m}^{[p^{e}]}\}$. Two elementary observations concerning F-pure thresholds are that if ![]() $f,g\in R$ then
$f,g\in R$ then ![]() $\operatorname{fpt}(f+g)\leqslant \operatorname{fpt}(f)+\operatorname{fpt}(g)$ and that if
$\operatorname{fpt}(f+g)\leqslant \operatorname{fpt}(f)+\operatorname{fpt}(g)$ and that if ![]() $f\in \mathfrak{m}^{[p^{e_{0}}]}$ then
$f\in \mathfrak{m}^{[p^{e_{0}}]}$ then ![]() $\operatorname{fpt}(f)\leqslant 1/p^{e_{0}}$. From these observations it follows that the F-pure threshold function is continuous as a function from
$\operatorname{fpt}(f)\leqslant 1/p^{e_{0}}$. From these observations it follows that the F-pure threshold function is continuous as a function from ![]() $R\rightarrow \mathbb{R}$: specifically, if
$R\rightarrow \mathbb{R}$: specifically, if ![]() $f\in R$ and
$f\in R$ and ![]() $\unicode[STIX]{x1D6FF}>0$ then there exists
$\unicode[STIX]{x1D6FF}>0$ then there exists ![]() $N\in \mathbb{N}$ such that for all
$N\in \mathbb{N}$ such that for all ![]() $g\in R$ such that
$g\in R$ such that ![]() $f-g\in \mathfrak{m}^{N}$,
$f-g\in \mathfrak{m}^{N}$, ![]() $|\operatorname{fpt}(f)-\operatorname{fpt}(g)|<\unicode[STIX]{x1D6FF}$. Continuity of the F-pure threshold function motivates studying continuity properties of Hilbert–Kunz multiplicity and F-signature and sheds light onto the problem of relating the singularities of
$|\operatorname{fpt}(f)-\operatorname{fpt}(g)|<\unicode[STIX]{x1D6FF}$. Continuity of the F-pure threshold function motivates studying continuity properties of Hilbert–Kunz multiplicity and F-signature and sheds light onto the problem of relating the singularities of ![]() $R/(f)$ with
$R/(f)$ with ![]() $R/(g)$ when
$R/(g)$ when ![]() $f$ and
$f$ and ![]() $g$ are suitably close.
$g$ are suitably close.
In 1983, Monsky, building on the earlier work of Kunz [Reference KunzKun69, Reference KunzKun76], defined a new invariant, the Hilbert–Kunz multiplicity of ![]() $R$, as the limit
$R$, as the limit
Monsky [Reference MonskyMon83] showed that this limit always exists. Values of ![]() $\text{e}_{\text{HK}}(R)$ dictate the severity of the singularities of
$\text{e}_{\text{HK}}(R)$ dictate the severity of the singularities of ![]() $R$. Most notable is that under mild hypotheses
$R$. Most notable is that under mild hypotheses ![]() $\text{e}_{\text{HK}}(R)\geqslant 1$ with equality if and only if
$\text{e}_{\text{HK}}(R)\geqslant 1$ with equality if and only if ![]() $R$ is regular [Reference Watanabe and YoshidaWY00]. It has also been shown in [Reference Blickle and EnescuBE04, Reference Aberbach and EnescuAE08] that small enough values of
$R$ is regular [Reference Watanabe and YoshidaWY00]. It has also been shown in [Reference Blickle and EnescuBE04, Reference Aberbach and EnescuAE08] that small enough values of ![]() $\text{e}_{\text{HK}}(R)$ imply
$\text{e}_{\text{HK}}(R)$ imply ![]() $R$ is Gorenstein and strongly F-regular. To be able to relate the singularities of
$R$ is Gorenstein and strongly F-regular. To be able to relate the singularities of ![]() $R/(f)$ and
$R/(f)$ and ![]() $R/(g)$ when
$R/(g)$ when ![]() $f$ and
$f$ and ![]() $g$ are suitably close it is natural to investigate the following question, which was originally asked to the second author by Luis Núñez-Betancourt:
$g$ are suitably close it is natural to investigate the following question, which was originally asked to the second author by Luis Núñez-Betancourt:
Question 1.1. Let ![]() $(R,\mathfrak{m},k)$ be a regular local ring of prime characteristic. Is the Hilbert–Kunz multiplicity function defined by
$(R,\mathfrak{m},k)$ be a regular local ring of prime characteristic. Is the Hilbert–Kunz multiplicity function defined by ![]() $f\mapsto \text{e}_{\text{HK}}(R/(f))$ a continuous function in the
$f\mapsto \text{e}_{\text{HK}}(R/(f))$ a continuous function in the ![]() $\mathfrak{m}$-adic topology? Namely, if
$\mathfrak{m}$-adic topology? Namely, if ![]() $f\in R$ is an element and we are given
$f\in R$ is an element and we are given ![]() $\unicode[STIX]{x1D6FF}>0$, can we find an integer
$\unicode[STIX]{x1D6FF}>0$, can we find an integer ![]() $N$ such that for all
$N$ such that for all ![]() $g\in R$ such that
$g\in R$ such that ![]() $f-g\in \mathfrak{m}^{N}$,
$f-g\in \mathfrak{m}^{N}$,
We now turn our attention to F-signature. Given finitely generated ![]() $R$-module
$R$-module ![]() $M$ we let
$M$ we let ![]() $\operatorname{frk}(M)$ denote the largest rank of a free
$\operatorname{frk}(M)$ denote the largest rank of a free ![]() $R$-module
$R$-module ![]() $F$ for which there is a surjection
$F$ for which there is a surjection ![]() $M\rightarrow F$. The F-signature of
$M\rightarrow F$. The F-signature of ![]() $(R,\mathfrak{m},k)$ was defined by Huneke and Leuschke [Reference Huneke and LeuschkeHL02], conceptualizing the earlier work [Reference Smith and Van den BerghSVdB97] of Smith and Van den Bergh, as the limit
$(R,\mathfrak{m},k)$ was defined by Huneke and Leuschke [Reference Huneke and LeuschkeHL02], conceptualizing the earlier work [Reference Smith and Van den BerghSVdB97] of Smith and Van den Bergh, as the limit
The number ![]() $\operatorname{frk}(R^{1/p^{e}})$ will be denoted by
$\operatorname{frk}(R^{1/p^{e}})$ will be denoted by ![]() $a_{e}(R)$ and referred to as the
$a_{e}(R)$ and referred to as the ![]() $e$th Frobenius splitting number of
$e$th Frobenius splitting number of ![]() $R$. Tucker [Reference TuckerTuc12] showed existence of the above limit for all local ringsFootnote 2. F-signature is a measurement of singularities: in particular,
$R$. Tucker [Reference TuckerTuc12] showed existence of the above limit for all local ringsFootnote 2. F-signature is a measurement of singularities: in particular, ![]() $s(R)\leqslant 1$ with equality if and only if
$s(R)\leqslant 1$ with equality if and only if ![]() $R$ is regular by [Reference Huneke and LeuschkeHL02] and
$R$ is regular by [Reference Huneke and LeuschkeHL02] and ![]() $s(R)>0$ if and only if
$s(R)>0$ if and only if ![]() $R$ is strongly F-regular by [Reference Aberbach and LeuschkeAL03]. As with Hilbert–Kunz multiplicity, it is natural to relate the singularities of
$R$ is strongly F-regular by [Reference Aberbach and LeuschkeAL03]. As with Hilbert–Kunz multiplicity, it is natural to relate the singularities of ![]() $R/(f)$ with
$R/(f)$ with ![]() $R/(g)$ by investigating continuity properties of F-signature with respect to the
$R/(g)$ by investigating continuity properties of F-signature with respect to the ![]() $\mathfrak{m}$-adic topology.
$\mathfrak{m}$-adic topology.
Question 1.2. Let ![]() $(R,\mathfrak{m},k)$ be a regular local ring of prime characteristic. Is the F-signature function defined by
$(R,\mathfrak{m},k)$ be a regular local ring of prime characteristic. Is the F-signature function defined by ![]() $f\mapsto s(R/(f))$ a continuous function with respect to the
$f\mapsto s(R/(f))$ a continuous function with respect to the ![]() $\mathfrak{m}$-adic topology? Namely, if
$\mathfrak{m}$-adic topology? Namely, if ![]() $f\in R$ is an element and we are given
$f\in R$ is an element and we are given ![]() $\unicode[STIX]{x1D6FF}>0$, can we find an integer
$\unicode[STIX]{x1D6FF}>0$, can we find an integer ![]() $N$ such that for all
$N$ such that for all ![]() $g\in R$ such that
$g\in R$ such that ![]() $f-g\in \mathfrak{m}^{N}$
$f-g\in \mathfrak{m}^{N}$
We are able to answer Questions 1.1 and 1.2, provided that ![]() $f$ has no multiple factors, that is,
$f$ has no multiple factors, that is, ![]() $R/(f)$ is reduced. Our main contribution is the following theorem:
$R/(f)$ is reduced. Our main contribution is the following theorem:
Theorem 1.3. Let ![]() $(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay F-finite ring of prime characteristic
$(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay F-finite ring of prime characteristic ![]() $p>0$. If
$p>0$. If ![]() $(f_{1},\ldots ,f_{c})$ is a parameter ideal such that
$(f_{1},\ldots ,f_{c})$ is a parameter ideal such that ![]() $R/(f_{1},\ldots ,f_{c})$ is reduced then for any
$R/(f_{1},\ldots ,f_{c})$ is reduced then for any ![]() $\unicode[STIX]{x1D6FF}>0$ there exists an integer
$\unicode[STIX]{x1D6FF}>0$ there exists an integer ![]() $N>0$ such that for any
$N>0$ such that for any ![]() $\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{c}\in \mathfrak{m}^{N}\!$:
$\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{c}\in \mathfrak{m}^{N}\!$:
(1) (Corollary 3.7)
 $|\text{e}_{\text{HK}}(R/(f_{1},\ldots ,f_{c}))-\text{e}_{\text{HK}}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))|<\unicode[STIX]{x1D6FF}$; and
$|\text{e}_{\text{HK}}(R/(f_{1},\ldots ,f_{c}))-\text{e}_{\text{HK}}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))|<\unicode[STIX]{x1D6FF}$; and(2) (Theorem 3.12)
 $|\text{s}(R/(f_{1},\ldots ,f_{c}))-\text{s}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))|<\unicode[STIX]{x1D6FF}$.
$|\text{s}(R/(f_{1},\ldots ,f_{c}))-\text{s}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))|<\unicode[STIX]{x1D6FF}$.
We show that Hilbert–Kunz multiplicity and F-signature functions are the uniform limit of functions which are locally constant with respect to the ![]() $\mathfrak{m}$-adic topology. Naively, one might also expect the Hilbert–Kunz multiplicity and F-signature functions are locally constant with respect to the
$\mathfrak{m}$-adic topology. Naively, one might also expect the Hilbert–Kunz multiplicity and F-signature functions are locally constant with respect to the ![]() $\mathfrak{m}$-adic topology:
$\mathfrak{m}$-adic topology: ![]() $\text{e}_{\text{HK}}(R/(f))=\text{e}_{\text{HK}}(R/(g))$ and
$\text{e}_{\text{HK}}(R/(f))=\text{e}_{\text{HK}}(R/(g))$ and ![]() $s(R/(f))=s(R/(g))$ can be forced by making
$s(R/(f))=s(R/(g))$ can be forced by making ![]() $f-g$ is sufficiently small. We point that this cannot hold for Hilbert–Kunz multiplicity in Example 4.1 and for F-signature in Example 4.2.
$f-g$ is sufficiently small. We point that this cannot hold for Hilbert–Kunz multiplicity in Example 4.1 and for F-signature in Example 4.2.
Similar to a number of recent developments in the study of invariants in prime characteristic rings, the proof of Theorem 1.3 comes by showing uniform convergence of continuous functions. We get our uniform convergence result by using the methods of Polstra and Tucker [Reference Polstra and TuckerPT18], where it was shown that suitable Noether normalizations provide a kind of “canonical” convergence estimate. The essential reason is that when ![]() $R$ is a module-finite generically separable extension of a regular local ring
$R$ is a module-finite generically separable extension of a regular local ring ![]() $A$, then
$A$, then ![]() $R[A^{1/p}]\cong R^{\oplus p^{d}}$. The “canonicity” in our construction comes from discriminants, and we show that the discriminant of
$R[A^{1/p}]\cong R^{\oplus p^{d}}$. The “canonicity” in our construction comes from discriminants, and we show that the discriminant of ![]() $R/(f)$ does not “change” much when
$R/(f)$ does not “change” much when ![]() $f$ changes slightly (Lemma 3.3). This allows us to show that one can control the convergence rate of Hilbert–Kunz function uniformly, independent of a small perturbation (Theorem 3.5).
$f$ changes slightly (Lemma 3.3). This allows us to show that one can control the convergence rate of Hilbert–Kunz function uniformly, independent of a small perturbation (Theorem 3.5).
2 Preliminary results
Definition 2.1. Let ![]() $A$ be a ring and
$A$ be a ring and ![]() $R$ a finite
$R$ a finite ![]() $A$-algebra which is free as an
$A$-algebra which is free as an ![]() $A$-module. Let
$A$-module. Let ![]() $e_{1},\ldots ,e_{n}$ be a basis of
$e_{1},\ldots ,e_{n}$ be a basis of ![]() $R$ as an
$R$ as an ![]() $A$-module. The discriminant of
$A$-module. The discriminant of ![]() $R$ is
$R$ is
 $$\begin{eqnarray}\text{D}_{A}(R)=\det \left(\begin{array}{@{}cccc@{}}\operatorname{Tr}(e_{1}^{2}) & \operatorname{Tr}(e_{1}e_{2}) & \cdots \, & \operatorname{Tr}(e_{1}e_{n})\\ \operatorname{Tr}(e_{2}e_{1}) & \operatorname{Tr}(e_{2}^{2}) & \cdots \, & \operatorname{Tr}(e_{2}e_{n})\\ \vdots & \vdots & \cdots \, & \vdots \\ \operatorname{Tr}(e_{n}e_{1}) & \operatorname{Tr}(e_{n}e_{2}) & \cdots \, & \operatorname{Tr}(e_{n}^{2})\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\text{D}_{A}(R)=\det \left(\begin{array}{@{}cccc@{}}\operatorname{Tr}(e_{1}^{2}) & \operatorname{Tr}(e_{1}e_{2}) & \cdots \, & \operatorname{Tr}(e_{1}e_{n})\\ \operatorname{Tr}(e_{2}e_{1}) & \operatorname{Tr}(e_{2}^{2}) & \cdots \, & \operatorname{Tr}(e_{2}e_{n})\\ \vdots & \vdots & \cdots \, & \vdots \\ \operatorname{Tr}(e_{n}e_{1}) & \operatorname{Tr}(e_{n}e_{2}) & \cdots \, & \operatorname{Tr}(e_{n}^{2})\end{array}\right),\end{eqnarray}$$ where ![]() $\operatorname{Tr}(r)$ denotes the trace of the multiplication map
$\operatorname{Tr}(r)$ denotes the trace of the multiplication map ![]() $\times r$ on
$\times r$ on ![]() $R$. Up to multiplication by a unit of
$R$. Up to multiplication by a unit of ![]() $A$, the discriminant is independent of the choice of basis.
$A$, the discriminant is independent of the choice of basis.
If ![]() $A$ is a regular local ring and
$A$ is a regular local ring and ![]() $R$ is a finite Cohen–Macaulay extension of
$R$ is a finite Cohen–Macaulay extension of ![]() $A$, then
$A$, then ![]() $R$ is necessarily a free
$R$ is necessarily a free ![]() $A$-module by the Auslander–Buchsbaum formula, and thus the discriminant of
$A$-module by the Auslander–Buchsbaum formula, and thus the discriminant of ![]() $R$ over
$R$ over ![]() $A$ is well defined. We begin by recording some well-known and useful facts concerning discriminants.
$A$ is well defined. We begin by recording some well-known and useful facts concerning discriminants.
Proposition 2.2. Let ![]() $A$ be a ring and
$A$ be a ring and ![]() $R$ a finitely generated
$R$ a finitely generated ![]() $A$-algebra which is free as an
$A$-algebra which is free as an ![]() $A$-module.
$A$-module.
(1) If
 $A$ is a normal domain, then
$A$ is a normal domain, then  $D_{A}(R)\in A$.
$D_{A}(R)\in A$.(2) If
 $I$ is an ideal of
$I$ is an ideal of  $A$ then the image of
$A$ then the image of  $D_{A}(R)$ in
$D_{A}(R)$ in  $R/IR$ is
$R/IR$ is  $D_{A/I}(R/IR)$.
$D_{A/I}(R/IR)$.(3) If
 $A$ is a domain then the ring
$A$ is a domain then the ring  $R$ is generically separable over
$R$ is generically separable over  $A$ if and only if
$A$ if and only if  $D_{A}(R)\not =0$.
$D_{A}(R)\not =0$.
Proof. We refer the reader to [Reference HochsterHoca, p. 200] for a proof of (1). For (2), if ![]() $e_{1},\ldots ,e_{n}\in R$ form a basis of
$e_{1},\ldots ,e_{n}\in R$ form a basis of ![]() $R$ as an
$R$ as an ![]() $A$-module then the images of
$A$-module then the images of ![]() $e_{1},\ldots ,e_{n}$ form a basis of
$e_{1},\ldots ,e_{n}$ form a basis of ![]() $R/IR$ as an
$R/IR$ as an ![]() $A/IA$-module. Moreover, if
$A/IA$-module. Moreover, if ![]() $x\in R$ and
$x\in R$ and ![]() $\overline{x}$ denotes the image of
$\overline{x}$ denotes the image of ![]() $x$ in
$x$ in ![]() $R/IR$, then
$R/IR$, then ![]() $\operatorname{Tr}(\overline{x})=\overline{\operatorname{Tr}(x)}$. Hence the image of
$\operatorname{Tr}(\overline{x})=\overline{\operatorname{Tr}(x)}$. Hence the image of ![]() $\text{D}_{A}(R)$ in
$\text{D}_{A}(R)$ in ![]() $R/IR$ is indeed
$R/IR$ is indeed ![]() $\text{D}_{A/I}(R/IR)$.
$\text{D}_{A/I}(R/IR)$.
For (3), as a first step, let ![]() $L$ be the fraction field of
$L$ be the fraction field of ![]() $A$. We observe that
$A$. We observe that ![]() $\text{D}_{A}(R)=\text{D}_{L}(R\otimes _{A}L)$, since the decomposition of an element
$\text{D}_{A}(R)=\text{D}_{L}(R\otimes _{A}L)$, since the decomposition of an element ![]() $a=\sum a_{i}e_{i}$ over
$a=\sum a_{i}e_{i}$ over ![]() $A$ can be considered as a decomposition of
$A$ can be considered as a decomposition of ![]() $a\otimes 1=\sum a_{i}e_{i}\otimes 1$ of an element
$a\otimes 1=\sum a_{i}e_{i}\otimes 1$ of an element ![]() $a\otimes 1$ over
$a\otimes 1$ over ![]() $L$ and
$L$ and ![]() $e_{i}\otimes 1$ still form a basis of
$e_{i}\otimes 1$ still form a basis of ![]() $R\otimes _{A}L$ over
$R\otimes _{A}L$ over ![]() $L$. Thus we can replace
$L$. Thus we can replace ![]() $R$ by
$R$ by ![]() $R\otimes _{A}L$ and assume
$R\otimes _{A}L$ and assume ![]() $A=L$ is a field. It is well known that
$A=L$ is a field. It is well known that ![]() $\text{D}_{L}(R)\neq 0$ if
$\text{D}_{L}(R)\neq 0$ if ![]() $R$ is a finite separable field extension of
$R$ is a finite separable field extension of ![]() $L$. By linearity this can be extended to the product and show one direction.
$L$. By linearity this can be extended to the product and show one direction.
For the other direction, we first show that ![]() $R$ is reduced. Since the nilradical is an ideal, it is a vector space over
$R$ is reduced. Since the nilradical is an ideal, it is a vector space over ![]() $L$, so we may extend a basis of it to a basis of
$L$, so we may extend a basis of it to a basis of ![]() $R$ over
$R$ over ![]() $L$. If
$L$. If ![]() $x$ is a nilpotent element, then
$x$ is a nilpotent element, then ![]() $\operatorname{Tr}(xe)=0$ for any element
$\operatorname{Tr}(xe)=0$ for any element ![]() $e\in R$, because the trace of a nilpotent matrix is nilpotent. This shows that
$e\in R$, because the trace of a nilpotent matrix is nilpotent. This shows that ![]() $\operatorname{Tr}$ gives a degenerate bilinear form and
$\operatorname{Tr}$ gives a degenerate bilinear form and ![]() $\text{D}_{L}(R)=0$. Since
$\text{D}_{L}(R)=0$. Since ![]() $R$ is reduced and finite over
$R$ is reduced and finite over ![]() $L$, it is a direct sum of fields. Again, by linearity we can see that each of these fields must be separable over
$L$, it is a direct sum of fields. Again, by linearity we can see that each of these fields must be separable over ![]() $L$.◻
$L$.◻
Let ![]() $(R,\mathfrak{m},k)$ be a complete local ring of positive characteristic
$(R,\mathfrak{m},k)$ be a complete local ring of positive characteristic ![]() $p>0$ with the residue field
$p>0$ with the residue field ![]() $k$. Cohen’s structure theorem shows that there is an injection
$k$. Cohen’s structure theorem shows that there is an injection ![]() $\unicode[STIX]{x1D719}:k\rightarrow R$ such that the induced map to
$\unicode[STIX]{x1D719}:k\rightarrow R$ such that the induced map to ![]() $R/\mathfrak{m}$ is an isomorphism. We call
$R/\mathfrak{m}$ is an isomorphism. We call ![]() $\unicode[STIX]{x1D719}(k)$ a coefficient field. Moreover, Cohen’s structure theorem asserts that for any system of parameters
$\unicode[STIX]{x1D719}(k)$ a coefficient field. Moreover, Cohen’s structure theorem asserts that for any system of parameters ![]() $x_{1},\ldots ,x_{d}$ the
$x_{1},\ldots ,x_{d}$ the ![]() $k$-subalgebra of
$k$-subalgebra of ![]() $R$ generated by the system of parameters,
$R$ generated by the system of parameters, ![]() $k[x_{1},\ldots ,x_{n}]$, is isomorphic to a polynomial ring. Since
$k[x_{1},\ldots ,x_{n}]$, is isomorphic to a polynomial ring. Since ![]() $R$ is complete, it therefore contains the completion
$R$ is complete, it therefore contains the completion ![]() $A=k[[x_{1},\ldots ,x_{d}]]$ and, since
$A=k[[x_{1},\ldots ,x_{d}]]$ and, since ![]() $x_{1},\ldots ,x_{d}$ form a system of parameters,
$x_{1},\ldots ,x_{d}$ form a system of parameters, ![]() $R$ is module-finite over
$R$ is module-finite over ![]() $A$. Of course, there is a lot of freedom in choosing a system of parameters; the Cohen–Gabber structure theorem [Reference Gabber and OrgogozoGO08, Théorème 7.1]Footnote 3 asserts that
$A$. Of course, there is a lot of freedom in choosing a system of parameters; the Cohen–Gabber structure theorem [Reference Gabber and OrgogozoGO08, Théorème 7.1]Footnote 3 asserts that ![]() $x_{1},\ldots ,x_{d}$ can be chosen so that
$x_{1},\ldots ,x_{d}$ can be chosen so that ![]() $R$ is generically separable over
$R$ is generically separable over ![]() $k[[x_{1},\ldots ,x_{d}]]$.
$k[[x_{1},\ldots ,x_{d}]]$.
Theorem 2.3. Let ![]() $(R,\mathfrak{m},k)$ be a reduced complete local ring of equidimension
$(R,\mathfrak{m},k)$ be a reduced complete local ring of equidimension ![]() $d$ and of prime characteristic
$d$ and of prime characteristic ![]() $p$. There exist a system of parameters
$p$. There exist a system of parameters ![]() $x_{1},\ldots ,x_{d}$ of
$x_{1},\ldots ,x_{d}$ of ![]() $R$ and coefficient field
$R$ and coefficient field ![]() $k\subseteq R$ such that
$k\subseteq R$ such that ![]() $R$ is finite and generically separable over the power series ring
$R$ is finite and generically separable over the power series ring ![]() $k[[x_{1},\ldots ,x_{d}]]$.
$k[[x_{1},\ldots ,x_{d}]]$.
It is useful to keep in mind that generic separability is equivalent to generic étaleness.
3 Main theorem and its applications
We say that a sequence ![]() $f_{1},\ldots ,f_{c}\in \mathfrak{m}$ is a parameter sequence if
$f_{1},\ldots ,f_{c}\in \mathfrak{m}$ is a parameter sequence if ![]() $\dim R/(f_{1},\ldots ,f_{i+1})<\dim R/(f_{1},\ldots ,f_{i})$ for all
$\dim R/(f_{1},\ldots ,f_{i+1})<\dim R/(f_{1},\ldots ,f_{i})$ for all ![]() $i$. We use
$i$. We use ![]() $\text{}\underline{f}$ to denote a sequence of elements
$\text{}\underline{f}$ to denote a sequence of elements ![]() $f_{1},\ldots ,f_{c}$. If
$f_{1},\ldots ,f_{c}$. If ![]() $I$ is an ideal, we say
$I$ is an ideal, we say ![]() $\text{}\underline{f}\in (I)^{\oplus c}$ if each element is in
$\text{}\underline{f}\in (I)^{\oplus c}$ if each element is in ![]() $I$. We add sequences componentwise, so
$I$. We add sequences componentwise, so ![]() $\text{}\underline{f}+\text{}\underline{g}$ is the sequence
$\text{}\underline{f}+\text{}\underline{g}$ is the sequence ![]() $f_{1}+g_{1},\ldots ,f_{c}+g_{c}$. We will use
$f_{1}+g_{1},\ldots ,f_{c}+g_{c}$. We will use ![]() $\unicode[STIX]{x1D706}(M)$ to denote the length of a module, and
$\unicode[STIX]{x1D706}(M)$ to denote the length of a module, and ![]() $\unicode[STIX]{x1D707}(M)$ to denote the minimal number of generators.
$\unicode[STIX]{x1D707}(M)$ to denote the minimal number of generators.
We borrow the following property observed in [Reference Srinivas and TrivediST96, Lemma 1].
Lemma 3.1. Let ![]() $(R,\mathfrak{m},k)$ be a local ring and
$(R,\mathfrak{m},k)$ be a local ring and ![]() $\text{}\underline{f}\in (\mathfrak{m})^{\oplus c}$ be a parameter sequence. Then for any ideal
$\text{}\underline{f}\in (\mathfrak{m})^{\oplus c}$ be a parameter sequence. Then for any ideal ![]() $I$ such that
$I$ such that ![]() $\unicode[STIX]{x1D706}(R/(I,\text{}\underline{f}))$ is finite, there exists
$\unicode[STIX]{x1D706}(R/(I,\text{}\underline{f}))$ is finite, there exists ![]() $N>0$ such that for all
$N>0$ such that for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
In particular, ![]() $\unicode[STIX]{x1D706}(R/(I,\text{}\underline{f}))=\unicode[STIX]{x1D706}(R/(I,\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ for all
$\unicode[STIX]{x1D706}(R/(I,\text{}\underline{f}))=\unicode[STIX]{x1D706}(R/(I,\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$.
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$.
Proof. Take ![]() $N$ such that
$N$ such that ![]() $\mathfrak{m}^{N}\subseteq (I,\text{}\underline{f})$. Then
$\mathfrak{m}^{N}\subseteq (I,\text{}\underline{f})$. Then ![]() $(I,\text{}\underline{f})=(I,\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ for all
$(I,\text{}\underline{f})=(I,\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$.◻
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$.◻
As observed in [Reference Srinivas and TrivediST96, Lemma 2], a small enough perturbation of a system of parameters remains a system of parameters.
Corollary 3.2. Let ![]() $(R,\mathfrak{m},k)$ be a local ring. Suppose
$(R,\mathfrak{m},k)$ be a local ring. Suppose ![]() $\text{}\underline{f}\in (\mathfrak{m})^{\oplus c}$ is a part of a system of parameters. Then there exists
$\text{}\underline{f}\in (\mathfrak{m})^{\oplus c}$ is a part of a system of parameters. Then there exists ![]() $N\in \mathbb{N}$ such that for each
$N\in \mathbb{N}$ such that for each ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$, ![]() $\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}$ is a part of a system of parameters.
$\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}$ is a part of a system of parameters.
Proof. Let ![]() $d$ be the dimension of the ring. We may complete
$d$ be the dimension of the ring. We may complete ![]() $\text{}\underline{f}$ to a full system of parameters
$\text{}\underline{f}$ to a full system of parameters ![]() $\text{}\underline{f},y_{1},\ldots ,y_{d-c}$. Setting
$\text{}\underline{f},y_{1},\ldots ,y_{d-c}$. Setting ![]() $I=(y_{1},\ldots ,y_{d-c})$ in the previous lemma we obtain
$I=(y_{1},\ldots ,y_{d-c})$ in the previous lemma we obtain ![]() $N$ such that for any
$N$ such that for any ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
In particular ![]() $f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c},y_{1},\ldots ,y_{d-c}$ are
$f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c},y_{1},\ldots ,y_{d-c}$ are ![]() $d$ elements that generate an
$d$ elements that generate an ![]() $\mathfrak{m}$-primary ideal, so they form a system of parameters.◻
$\mathfrak{m}$-primary ideal, so they form a system of parameters.◻
Lemma 3.3. Let ![]() $(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay local ring with coefficient field
$(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay local ring with coefficient field ![]() $k\subseteq R$ and let
$k\subseteq R$ and let ![]() $f_{1},\ldots ,f_{c},x_{1},\ldots ,x_{d-c}$ be a system of parameters for
$f_{1},\ldots ,f_{c},x_{1},\ldots ,x_{d-c}$ be a system of parameters for ![]() $R$. Let
$R$. Let ![]() $A=k[[T_{1},\ldots ,T_{d-c}]]$ be the power series ring in
$A=k[[T_{1},\ldots ,T_{d-c}]]$ be the power series ring in ![]() $d-c$ variables over the field
$d-c$ variables over the field ![]() $k$. There exists
$k$. There exists ![]() $C\geqslant 0$ such that for all
$C\geqslant 0$ such that for all ![]() $n\geqslant 1$ and all
$n\geqslant 1$ and all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{Cn})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{Cn})^{\oplus c}$,
is a system of parameters and
where ![]() $R/(\text{}\underline{f})$ and
$R/(\text{}\underline{f})$ and ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ are
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ are ![]() $A$-algebras by mapping
$A$-algebras by mapping ![]() $T_{i}\mapsto x_{i}$ and identifying the coefficient field of
$T_{i}\mapsto x_{i}$ and identifying the coefficient field of ![]() $A$ with the induced coefficient fields of
$A$ with the induced coefficient fields of ![]() $R/(\text{}\underline{f})$ and
$R/(\text{}\underline{f})$ and ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$.
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$.
Proof. We can choose ![]() $C$ as in Lemma 3.1, so for all
$C$ as in Lemma 3.1, so for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{C})^{\oplus c}$ we have
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{C})^{\oplus c}$ we have ![]() $(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},x_{1},\ldots ,x_{d-c})=(\text{}\underline{f},x_{1},\ldots ,x_{d-c})$ and thus
$(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},x_{1},\ldots ,x_{d-c})=(\text{}\underline{f},x_{1},\ldots ,x_{d-c})$ and thus ![]() $\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},x_{1},\ldots ,x_{d-c}$ is a system of parameters. Hence
$\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},x_{1},\ldots ,x_{d-c}$ is a system of parameters. Hence ![]() $R/(\text{}\underline{f})$ and
$R/(\text{}\underline{f})$ and ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ are free
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ are free ![]() $A$-modules of the same rank
$A$-modules of the same rank ![]() $\unicode[STIX]{x1D706}_{A}(R/(\text{}\underline{f},x_{1},\ldots ,x_{d-c}))$. Moreover, if
$\unicode[STIX]{x1D706}_{A}(R/(\text{}\underline{f},x_{1},\ldots ,x_{d-c}))$. Moreover, if ![]() $r_{1},\ldots ,r_{n}\in R$ are chosen so that their images in
$r_{1},\ldots ,r_{n}\in R$ are chosen so that their images in ![]() $R/(\text{}\underline{f})$ serve as a basis for
$R/(\text{}\underline{f})$ serve as a basis for ![]() $R/(\text{}\underline{f})$ as an
$R/(\text{}\underline{f})$ as an ![]() $A$-module, then for each
$A$-module, then for each ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{C})^{\oplus c}$, because the images of
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{C})^{\oplus c}$, because the images of ![]() $r_{1},\ldots ,r_{n}$ form a basis of
$r_{1},\ldots ,r_{n}$ form a basis of ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}_{A})=R/(\text{}\underline{f},x_{1},\ldots ,x_{d-c})$, the images of
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}_{A})=R/(\text{}\underline{f},x_{1},\ldots ,x_{d-c})$, the images of ![]() $r_{1},\ldots ,r_{n}$ in
$r_{1},\ldots ,r_{n}$ in ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ are a basis of
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ are a basis of ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ too.
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ too.
Observe that for each ![]() $n\geqslant 1$,
$n\geqslant 1$, ![]() $\mathfrak{m}^{Cn}\subseteq (x_{1},\ldots ,x_{d-c})^{n}+(\text{}\underline{f})$. Thus for each
$\mathfrak{m}^{Cn}\subseteq (x_{1},\ldots ,x_{d-c})^{n}+(\text{}\underline{f})$. Thus for each ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{Cn})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{Cn})^{\oplus c}$, ![]() $R/(\text{}\underline{f},\mathfrak{m}_{A}^{n})=R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}_{A}^{n})$ as
$R/(\text{}\underline{f},\mathfrak{m}_{A}^{n})=R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}_{A}^{n})$ as ![]() $A/\mathfrak{m}_{A}^{n}$-algebras. Then by part (2) of Lemma 2.2
$A/\mathfrak{m}_{A}^{n}$-algebras. Then by part (2) of Lemma 2.2
 $$\begin{eqnarray}\displaystyle \text{D}_{A}(R/(\text{}\underline{f}))\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}R/(\text{}\underline{f}) & = & \displaystyle \text{D}_{A/\mathfrak{m}_{A}^{n}}(R/(\text{}\underline{f},\mathfrak{m}_{A}^{n}))\nonumber\\ \displaystyle & = & \displaystyle \text{D}_{A/\mathfrak{m}_{A}^{n}}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}_{A}^{n}))\nonumber\\ \displaystyle & = & \displaystyle \text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{D}_{A}(R/(\text{}\underline{f}))\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}R/(\text{}\underline{f}) & = & \displaystyle \text{D}_{A/\mathfrak{m}_{A}^{n}}(R/(\text{}\underline{f},\mathfrak{m}_{A}^{n}))\nonumber\\ \displaystyle & = & \displaystyle \text{D}_{A/\mathfrak{m}_{A}^{n}}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}_{A}^{n}))\nonumber\\ \displaystyle & = & \displaystyle \text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}),\nonumber\end{eqnarray}$$ where the middle equality holds since we have a common basis ![]() $r_{1},\ldots ,r_{n}\in R$ for
$r_{1},\ldots ,r_{n}\in R$ for ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ and
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ and ![]() $R/(\text{}\underline{f})$ as
$R/(\text{}\underline{f})$ as ![]() $A$-modules.◻
$A$-modules.◻
Suppose ![]() $(R,\mathfrak{m},k)$ satisfies the hypotheses of Lemma 3.3. The following corollary shows that if
$(R,\mathfrak{m},k)$ satisfies the hypotheses of Lemma 3.3. The following corollary shows that if ![]() $f\in \mathfrak{m}$ is a parameter element and
$f\in \mathfrak{m}$ is a parameter element and ![]() $R/(f)$ is generically separable over a regular ring
$R/(f)$ is generically separable over a regular ring ![]() $A$, then
$A$, then ![]() $R/(g)$ is generically separable over the same regular local ring
$R/(g)$ is generically separable over the same regular local ring ![]() $A$, provided
$A$, provided ![]() $g$ is a small enough perturbation of
$g$ is a small enough perturbation of ![]() $f$.
$f$.
Corollary 3.4. Let ![]() $(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay local ring with coefficient field
$(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay local ring with coefficient field ![]() $k\subseteq R$. Let
$k\subseteq R$. Let ![]() $f_{1},\ldots ,f_{c},x_{1},\ldots ,x_{d-c}$ be a system of parameters for
$f_{1},\ldots ,f_{c},x_{1},\ldots ,x_{d-c}$ be a system of parameters for ![]() $R$. Let
$R$. Let ![]() $A=k[[T_{1},\ldots ,T_{d-c}]]$ be the power series ring in
$A=k[[T_{1},\ldots ,T_{d-c}]]$ be the power series ring in ![]() $d{-}c$ variables over the field
$d{-}c$ variables over the field ![]() $k$ and consider
$k$ and consider ![]() $R/(\text{}\underline{f})$ is an
$R/(\text{}\underline{f})$ is an ![]() $A$-algebra by mapping
$A$-algebra by mapping ![]() $T_{i}\mapsto x_{i}$ and identifying the coefficient field of
$T_{i}\mapsto x_{i}$ and identifying the coefficient field of ![]() $A$ with the induced coefficient field of
$A$ with the induced coefficient field of ![]() $R/(\text{}\underline{f})$. Suppose that
$R/(\text{}\underline{f})$. Suppose that ![]() $A\subseteq R/(\text{}\underline{f})$ is generically separable. Then there exists
$A\subseteq R/(\text{}\underline{f})$ is generically separable. Then there exists ![]() $N\geqslant 1$ such that for any
$N\geqslant 1$ such that for any ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$, ![]() $A\subseteq R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ is generically separable as an
$A\subseteq R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ is generically separable as an ![]() $A$-algebra given by mapping
$A$-algebra given by mapping ![]() $T_{i}\mapsto x_{i}$ and identifying the coefficient field of
$T_{i}\mapsto x_{i}$ and identifying the coefficient field of ![]() $A$ with the induced coefficient field of
$A$ with the induced coefficient field of ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$.
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$.
Proof. The assumption ![]() $R/(\text{}\underline{f})$ is generically separable over
$R/(\text{}\underline{f})$ is generically separable over ![]() $A$ is equivalent to
$A$ is equivalent to ![]() $\text{D}_{A}(R/(\text{}\underline{f}))\not =0$ by Part (1) of Lemma 2.2. Let
$\text{D}_{A}(R/(\text{}\underline{f}))\not =0$ by Part (1) of Lemma 2.2. Let ![]() $C\geqslant 0$ as given by Lemma 3.3. By Krull’s intersection theorem we can choose
$C\geqslant 0$ as given by Lemma 3.3. By Krull’s intersection theorem we can choose ![]() $n\geqslant 1$ so that
$n\geqslant 1$ so that ![]() $\text{D}_{A}(R/(\text{}\underline{f}))\not \equiv 0\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}$. Then for any
$\text{D}_{A}(R/(\text{}\underline{f}))\not \equiv 0\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}$. Then for any ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{Cn})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{Cn})^{\oplus c}$, ![]() $\text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\equiv \text{D}_{A}(R/(\text{}\underline{f}))\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}\not =0$, so
$\text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\equiv \text{D}_{A}(R/(\text{}\underline{f}))\hspace{0.6em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{A}^{n}\not =0$, so ![]() $\text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\not =0$.◻
$\text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\not =0$.◻
3.1 Continuity of Hilbert–Kunz multiplicity
It is time to set up the uniform convergence machinery. We closely follow [Reference Polstra and TuckerPT18, Lemma 2.3, Theorem 3.2]. Let ![]() $(R,\mathfrak{m},k)$ be an F-finite local ring and
$(R,\mathfrak{m},k)$ be an F-finite local ring and ![]() $I$ be an
$I$ be an ![]() $\mathfrak{m}$-primary ideal. Then
$\mathfrak{m}$-primary ideal. Then ![]() $F_{\ast }^{e}R\otimes _{R}R/I\cong F_{\ast }^{e}R/I^{[p^{e}]}$ and we may compute
$F_{\ast }^{e}R\otimes _{R}R/I\cong F_{\ast }^{e}R/I^{[p^{e}]}$ and we may compute
Theorem 3.5. Let ![]() $(R,\mathfrak{m},k)$ be an F-finite Cohen–Macaulay local ring of prime characteristic
$(R,\mathfrak{m},k)$ be an F-finite Cohen–Macaulay local ring of prime characteristic ![]() $p$ and of dimension
$p$ and of dimension ![]() $d+c$. If
$d+c$. If ![]() $\text{}\underline{f}=f_{1},\ldots ,f_{c}$ is a parameter sequence such that
$\text{}\underline{f}=f_{1},\ldots ,f_{c}$ is a parameter sequence such that ![]() $\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced, then there exists a constant
$\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced, then there exists a constant ![]() $C\geqslant 0$ and an integer
$C\geqslant 0$ and an integer ![]() $N\geqslant 1$ such that for any
$N\geqslant 1$ such that for any ![]() $e\geqslant 1$ and
$e\geqslant 1$ and ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
Proof. Without loss of generality, we may assume ![]() $R$ is complete. Because
$R$ is complete. Because ![]() $R$ is Cohen–Macaulay,
$R$ is Cohen–Macaulay, ![]() $R/(\text{}\underline{f})$ is equidimensional and reduced. By Theorem 2.3 there exists a coefficient field
$R/(\text{}\underline{f})$ is equidimensional and reduced. By Theorem 2.3 there exists a coefficient field ![]() $k\subseteq R/(\text{}\underline{f})$ and parameters
$k\subseteq R/(\text{}\underline{f})$ and parameters ![]() $x_{1},\ldots ,x_{d}\in R$ such that
$x_{1},\ldots ,x_{d}\in R$ such that ![]() $x_{1},\ldots ,x_{d}$ is a system of parameters for
$x_{1},\ldots ,x_{d}$ is a system of parameters for ![]() $R/(\text{}\underline{f})$ and
$R/(\text{}\underline{f})$ and ![]() $R/(\text{}\underline{f})$ is module-finite and generically separable over the regular local ring
$R/(\text{}\underline{f})$ is module-finite and generically separable over the regular local ring ![]() $A:=k[[x_{1},\ldots ,x_{d}]]$.
$A:=k[[x_{1},\ldots ,x_{d}]]$.
We observe that the coefficient field can be lifted from ![]() $R/(\text{}\underline{f})$ to
$R/(\text{}\underline{f})$ to ![]() $R$. Essentially, the proof of [Reference MatsumuraMat86, Theorem 28.3] shows that a coefficient field is determined by the lifts of a
$R$. Essentially, the proof of [Reference MatsumuraMat86, Theorem 28.3] shows that a coefficient field is determined by the lifts of a ![]() $p$-basis of
$p$-basis of ![]() $k$ (see also [Reference HochsterHocb, Theorem, p. 12]). Thus we may just lift the
$k$ (see also [Reference HochsterHocb, Theorem, p. 12]). Thus we may just lift the ![]() $p$-basis to
$p$-basis to ![]() $R$.
$R$.
By Lemma 6.5 of [Reference Hochster and HunekeHH90] (the proof still holds if we replace ![]() $R^{\infty }$ by
$R^{\infty }$ by ![]() $R^{1/p}$), we have an exact sequence
$R^{1/p}$), we have an exact sequence
where ![]() $0\neq c=\text{D}_{A}(R/(\text{}\underline{f}))$ annihilates
$0\neq c=\text{D}_{A}(R/(\text{}\underline{f}))$ annihilates ![]() $M$.
$M$.
By Lemma 3.3 and Corollary 3.4, we can find ![]() $N$ such that
$N$ such that ![]() $A\subseteq R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ is still generically separable. Therefore we have an exact sequence
$A\subseteq R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ is still generically separable. Therefore we have an exact sequence
where ![]() $c_{\text{}\underline{\unicode[STIX]{x1D716}}}=\text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ annihilates
$c_{\text{}\underline{\unicode[STIX]{x1D716}}}=\text{D}_{A}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ annihilates ![]() $M_{\text{}\underline{\unicode[STIX]{x1D716}}}$ and
$M_{\text{}\underline{\unicode[STIX]{x1D716}}}$ and ![]() $c_{\text{}\underline{\unicode[STIX]{x1D716}}}-c\in \mathfrak{m}_{A}^{N}$.
$c_{\text{}\underline{\unicode[STIX]{x1D716}}}-c\in \mathfrak{m}_{A}^{N}$.
By [Reference KunzKun69] ![]() $A^{1/p}$ is a free
$A^{1/p}$ is a free ![]() $A$-module of rank
$A$-module of rank ![]() $[k:k^{p}]p^{d}$, so tensoring the above sequence with
$[k:k^{p}]p^{d}$, so tensoring the above sequence with ![]() $\mathfrak{m}^{[p^{e}]}$ we get that
$\mathfrak{m}^{[p^{e}]}$ we get that
 $$\begin{eqnarray}\displaystyle & & \displaystyle [k:k^{p}]\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+1}]}))\nonumber\\ \displaystyle & & \displaystyle \quad -\,[k:k^{p}]p^{d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))\leqslant \unicode[STIX]{x1D706}(M_{\text{}\underline{\unicode[STIX]{x1D716}}}/\mathfrak{m}^{[p^{e}]}M_{\text{}\underline{\unicode[STIX]{x1D716}}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle [k:k^{p}]\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+1}]}))\nonumber\\ \displaystyle & & \displaystyle \quad -\,[k:k^{p}]p^{d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))\leqslant \unicode[STIX]{x1D706}(M_{\text{}\underline{\unicode[STIX]{x1D716}}}/\mathfrak{m}^{[p^{e}]}M_{\text{}\underline{\unicode[STIX]{x1D716}}}).\nonumber\end{eqnarray}$$ Since ![]() $M_{\text{}\underline{\unicode[STIX]{x1D716}}}$ is a
$M_{\text{}\underline{\unicode[STIX]{x1D716}}}$ is a ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}})$-module and a quotient of
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}})$-module and a quotient of ![]() $(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))^{1/p}$,
$(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))^{1/p}$,
Furthermore, it easily follows from the inclusion ![]() $(x_{1},\ldots ,x_{d})\subseteq \mathfrak{m}$ that
$(x_{1},\ldots ,x_{d})\subseteq \mathfrak{m}$ that
thus
where the last inequality follows by filtration.
Now, we can complete ![]() $0\neq c$ to a system of parameters
$0\neq c$ to a system of parameters ![]() $c,t_{1},\ldots ,t_{d-1}$ in
$c,t_{1},\ldots ,t_{d-1}$ in ![]() $A$ and, after increasing
$A$ and, after increasing ![]() $N$ if necessary, by Lemma 3.3 we can assume that
$N$ if necessary, by Lemma 3.3 we can assume that ![]() $c_{\text{}\underline{\unicode[STIX]{x1D716}}},t_{1},\ldots ,t_{d-1}$ is still a system of parameters and that
$c_{\text{}\underline{\unicode[STIX]{x1D716}}},t_{1},\ldots ,t_{d-1}$ is still a system of parameters and that ![]() $(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},t_{1},\ldots ,t_{d-1})=(\text{}\underline{f},c,t_{1},\ldots ,t_{d-1})$. Therefore
$(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},t_{1},\ldots ,t_{d-1})=(\text{}\underline{f},c,t_{1},\ldots ,t_{d-1})$. Therefore
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},\mathfrak{m}^{[p^{e}]})) & {\leqslant} & \displaystyle \unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},t_{1}^{p^{e}},\ldots ,t_{d-1}^{p^{e}}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle p^{e(d-1)}\unicode[STIX]{x1D706}(R/(\text{}\underline{f},c,t_{1},\ldots ,t_{d-1})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},\mathfrak{m}^{[p^{e}]})) & {\leqslant} & \displaystyle \unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},t_{1}^{p^{e}},\ldots ,t_{d-1}^{p^{e}}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle p^{e(d-1)}\unicode[STIX]{x1D706}(R/(\text{}\underline{f},c,t_{1},\ldots ,t_{d-1})).\nonumber\end{eqnarray}$$Let
and observe that we found one of the two required inequalities:
For the other inequality, we can repeat the proof for the exact sequence
where the map is multiplication by ![]() $c=\text{D}_{A}(R/(\text{}\underline{f}))$. Again the cokernel is annihilated by
$c=\text{D}_{A}(R/(\text{}\underline{f}))$. Again the cokernel is annihilated by ![]() $c$, because
$c$, because ![]() $R/(\text{}\underline{f})[A^{1/p}]\subseteq (R/(\text{}\underline{f}))^{1/p}$. Moreover, we get for each
$R/(\text{}\underline{f})[A^{1/p}]\subseteq (R/(\text{}\underline{f}))^{1/p}$. Moreover, we get for each ![]() $\text{}\underline{\unicode[STIX]{x1D716}}$ a short exact sequence
$\text{}\underline{\unicode[STIX]{x1D716}}$ a short exact sequence
Most of the proof carries through as above, except that now we estimate
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}(L_{\text{}\underline{\unicode[STIX]{x1D716}}}/\mathfrak{m}^{[p^{e}]}L_{\text{}\underline{\unicode[STIX]{x1D716}}}) & {\leqslant} & \displaystyle \unicode[STIX]{x1D707}(R/(\text{}\underline{f})[A^{1/p}])\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},\mathfrak{m}^{[p^{e}]}))\nonumber\\ \displaystyle & = & \displaystyle [k:k^{p}]p^{d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},\mathfrak{m}^{[p^{e}]}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}(L_{\text{}\underline{\unicode[STIX]{x1D716}}}/\mathfrak{m}^{[p^{e}]}L_{\text{}\underline{\unicode[STIX]{x1D716}}}) & {\leqslant} & \displaystyle \unicode[STIX]{x1D707}(R/(\text{}\underline{f})[A^{1/p}])\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},\mathfrak{m}^{[p^{e}]}))\nonumber\\ \displaystyle & = & \displaystyle [k:k^{p}]p^{d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},c_{\text{}\underline{\unicode[STIX]{x1D716}}},\mathfrak{m}^{[p^{e}]}))\nonumber\end{eqnarray}$$and from there obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle p^{d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))-\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+1}]}))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (p^{d}[k:k^{p}]\unicode[STIX]{x1D706}(R/(\text{}\underline{f},c,t_{1},\ldots ,t_{d-1})))p^{e(d-1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle p^{d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))-\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+1}]}))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (p^{d}[k:k^{p}]\unicode[STIX]{x1D706}(R/(\text{}\underline{f},c,t_{1},\ldots ,t_{d-1})))p^{e(d-1)}.\nonumber\end{eqnarray}$$Following the treatment in [Reference TuckerTuc12], we obtain the following corollary:
Corollary 3.6. Let ![]() $(R,\mathfrak{m},k)$ be an F-finite Cohen–Macaulay local ring of prime characteristic
$(R,\mathfrak{m},k)$ be an F-finite Cohen–Macaulay local ring of prime characteristic ![]() $p$ and of dimension
$p$ and of dimension ![]() $d+c$. If
$d+c$. If ![]() $\text{}\underline{f}$ is a parameter sequence of length
$\text{}\underline{f}$ is a parameter sequence of length ![]() $c$ and such that
$c$ and such that ![]() $\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced, then there exist a constant
$\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced, then there exist a constant ![]() $C\geqslant 0$ and an integer
$C\geqslant 0$ and an integer ![]() $N\geqslant 1$ such that for any
$N\geqslant 1$ such that for any ![]() $e\geqslant 1$ and
$e\geqslant 1$ and ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
Proof. Using induction on ![]() $q^{\prime }$ as in the proof of [Reference TuckerTuc12, Proposition 3.4] we may obtain from Theorem 3.5 that
$q^{\prime }$ as in the proof of [Reference TuckerTuc12, Proposition 3.4] we may obtain from Theorem 3.5 that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+e^{\prime }}]}))-p^{e^{\prime }d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant Cp^{(e+e^{\prime }-1)(d-1)}(1+p+\cdots +p^{e^{\prime }-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+e^{\prime }}]}))-p^{e^{\prime }d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant Cp^{(e+e^{\prime }-1)(d-1)}(1+p+\cdots +p^{e^{\prime }-1}).\nonumber\end{eqnarray}$$ Thus, dividing by ![]() $p^{(e+e^{\prime })d}$ we get that
$p^{(e+e^{\prime })d}$ we get that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |p^{-(e+e^{\prime })d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+e^{\prime }}]}))-p^{-ed}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{(1+p+\cdots +p^{e^{\prime }-1})}{p^{d-1}p^{e+e^{\prime }}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |p^{-(e+e^{\prime })d}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e+e^{\prime }}]}))-p^{-ed}\unicode[STIX]{x1D706}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},\mathfrak{m}^{[p^{e}]}))|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{(1+p+\cdots +p^{e^{\prime }-1})}{p^{d-1}p^{e+e^{\prime }}}.\nonumber\end{eqnarray}$$Note that
so the claim follows after letting ![]() $e^{\prime }\rightarrow \infty$.◻
$e^{\prime }\rightarrow \infty$.◻
Continuity of Hilbert–Kunz multiplicity follows from Corollary 3.6.
Corollary 3.7. Let ![]() $(R,\mathfrak{m},k)$ be a Cohen–Macaulay F-finite local ring of prime characteristic
$(R,\mathfrak{m},k)$ be a Cohen–Macaulay F-finite local ring of prime characteristic ![]() $p$ and dimension
$p$ and dimension ![]() $d+c$. If
$d+c$. If ![]() $\text{}\underline{f}$ is a parameter sequence of length
$\text{}\underline{f}$ is a parameter sequence of length ![]() $c$ and such that
$c$ and such that ![]() $\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced, then for any
$\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced, then for any ![]() $\unicode[STIX]{x1D6FF}>0$ there exists an integer
$\unicode[STIX]{x1D6FF}>0$ there exists an integer ![]() $N>0$ such that for any
$N>0$ such that for any ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
Proof. By Lemma 3.1, for any given ![]() $e$ there exists
$e$ there exists ![]() $N$ such that
$N$ such that
for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$. By Corollary 3.6, we may further assume that for some constant
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$. By Corollary 3.6, we may further assume that for some constant ![]() $C>0$
$C>0$
Thus
and the claim follows. ◻
3.2 Continuity of F-signature
To establish continuity of F-signature we will need an effective way of comparing the ![]() $e$th Frobenius splitting numbers of rings which are the homomorphic image of a common ring. We begin by recalling an effective method which allows us to measure Frobenius splitting numbers in rings which are approximately Gorenstein [Reference HochsterHoc77].
$e$th Frobenius splitting numbers of rings which are the homomorphic image of a common ring. We begin by recalling an effective method which allows us to measure Frobenius splitting numbers in rings which are approximately Gorenstein [Reference HochsterHoc77].
Lemma 3.8. Let ![]() $(R,\mathfrak{m},k)$ be an F-finite approximately Gorenstein ring, that is there exists a descending chain of irreducible
$(R,\mathfrak{m},k)$ be an F-finite approximately Gorenstein ring, that is there exists a descending chain of irreducible ![]() $\mathfrak{m}$-primary ideals
$\mathfrak{m}$-primary ideals ![]() $\{I_{t}\}$ cofinal with
$\{I_{t}\}$ cofinal with ![]() $\{\mathfrak{m}^{t}\}$. Let
$\{\mathfrak{m}^{t}\}$. Let ![]() $u_{t}$ generate the socle modulo
$u_{t}$ generate the socle modulo ![]() $I_{t}$.
$I_{t}$.
(1) Then for each
 $e$ there exists
$e$ there exists  $t_{e}$ such that
$t_{e}$ such that  $a_{e}(R)=[k:k^{p^{e}}]\unicode[STIX]{x1D706}(R/(I_{t}^{[p^{e}]}:_{R}u_{t}^{p^{e}}))$ for all
$a_{e}(R)=[k:k^{p^{e}}]\unicode[STIX]{x1D706}(R/(I_{t}^{[p^{e}]}:_{R}u_{t}^{p^{e}}))$ for all  $t\geqslant t_{e}$.
$t\geqslant t_{e}$.(2) If
 $R$ is Cohen–Macaulay and
$R$ is Cohen–Macaulay and  $J\subseteq R$ is an ideal of
$J\subseteq R$ is an ideal of  $R$ isomorphic to the canonical module of
$R$ isomorphic to the canonical module of  $R$ and
$R$ and  $x_{1}\in J$ is not a zero divisor, then
$x_{1}\in J$ is not a zero divisor, then  $I_{t}$ can be taken to be
$I_{t}$ can be taken to be  $(x_{1}^{t-1}J,x_{2}^{t},\ldots ,x_{d}^{t})$ where
$(x_{1}^{t-1}J,x_{2}^{t},\ldots ,x_{d}^{t})$ where  $x_{2},\ldots ,x_{d}$ is a system of parameters for
$x_{2},\ldots ,x_{d}$ is a system of parameters for  $R/J$. Moreover,
$R/J$. Moreover,  $u$ generates the socle mod
$u$ generates the socle mod  $(J,x_{2},\ldots ,x_{d})$ then
$(J,x_{2},\ldots ,x_{d})$ then  $u_{t}:=(x_{1}\cdots x_{d})^{t-1}$ generates the socle mod
$u_{t}:=(x_{1}\cdots x_{d})^{t-1}$ generates the socle mod  $I_{t}$.
$I_{t}$.(3) Under the assumptions and notation of
 $(2)$, there exists
$(2)$, there exists  $t_{e}$ such that for all
$t_{e}$ such that for all $$\begin{eqnarray}a_{e}(R)=[k:k^{p^{e}}]\unicode[STIX]{x1D706}(R/(J,x_{2}^{t},\ldots ,x_{d}^{t})^{[p^{e}]}:_{R}(x_{2}\cdots x_{d})^{tp^{e}})\end{eqnarray}$$
$$\begin{eqnarray}a_{e}(R)=[k:k^{p^{e}}]\unicode[STIX]{x1D706}(R/(J,x_{2}^{t},\ldots ,x_{d}^{t})^{[p^{e}]}:_{R}(x_{2}\cdots x_{d})^{tp^{e}})\end{eqnarray}$$ $t\geqslant t_{e}$.
$t\geqslant t_{e}$.
We refer the reader to [Reference Polstra and TuckerPT18, Lemma 6.2] and the proof of [Reference Polstra and TuckerPT18, Corollary 6.6] for details.
Lemma 3.9. Let ![]() $(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay domain of dimension at least
$(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay domain of dimension at least ![]() $c+1$, not necessarily of prime characteristic. Let
$c+1$, not necessarily of prime characteristic. Let ![]() $\text{}\underline{f}$ be a regular sequence of length
$\text{}\underline{f}$ be a regular sequence of length ![]() $c$ and such that
$c$ and such that ![]() $R/(\text{}\underline{f})$ is generically Gorenstein. Then there exists a canonical ideal
$R/(\text{}\underline{f})$ is generically Gorenstein. Then there exists a canonical ideal ![]() $J\subseteq R$ such that the ideal
$J\subseteq R$ such that the ideal ![]() $J+(\text{}\underline{f})$ of
$J+(\text{}\underline{f})$ of ![]() $R/(\text{}\underline{f})$ is the canonical module of
$R/(\text{}\underline{f})$ is the canonical module of ![]() $R/(\text{}\underline{f})$. Moreover, there exists
$R/(\text{}\underline{f})$. Moreover, there exists ![]() $N\in \mathbb{N}$ such that for all
$N\in \mathbb{N}$ such that for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$, the ideal
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$, the ideal ![]() $(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J)/(f)$ of
$(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J)/(f)$ of ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ is the canonical module of
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ is the canonical module of ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$.
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$.
Proof. Recall that ![]() $R$ has a canonical ideal
$R$ has a canonical ideal ![]() $\unicode[STIX]{x1D714}$ if and only if it is generically Gorenstein [Reference Bruns and HerzogBH93, Proposition 3.3.18]. We also recall that
$\unicode[STIX]{x1D714}$ if and only if it is generically Gorenstein [Reference Bruns and HerzogBH93, Proposition 3.3.18]. We also recall that ![]() $R$ is generically Gorenstein if and only if
$R$ is generically Gorenstein if and only if ![]() $R_{P_{i}}$ is Gorenstein for any minimal prime
$R_{P_{i}}$ is Gorenstein for any minimal prime ![]() $P_{i}$ of
$P_{i}$ of ![]() $R$.
$R$.
Let ![]() $S=R\setminus \cup P_{i}$ where
$S=R\setminus \cup P_{i}$ where ![]() $P_{i}$ are the minimal primes of
$P_{i}$ are the minimal primes of ![]() $(\text{}\underline{f})$. Then
$(\text{}\underline{f})$. Then ![]() $S^{-1}\unicode[STIX]{x1D714}\subseteq S^{-1}R$ is a canonical module of
$S^{-1}\unicode[STIX]{x1D714}\subseteq S^{-1}R$ is a canonical module of ![]() $S^{-1}R$ and, since
$S^{-1}R$ and, since ![]() $S^{-1}R$ is Gorenstein,
$S^{-1}R$ is Gorenstein, ![]() $S^{-1}\unicode[STIX]{x1D714}=(u)$ is a principal ideal, and we may assume that
$S^{-1}\unicode[STIX]{x1D714}=(u)$ is a principal ideal, and we may assume that ![]() $u\in \unicode[STIX]{x1D714}$. This means that there exists
$u\in \unicode[STIX]{x1D714}$. This means that there exists ![]() $s\in S$ such that for some ideal
$s\in S$ such that for some ideal ![]() $J$ in
$J$ in ![]() $R$,
$R$,
Since ![]() $R$ is a domain,
$R$ is a domain, ![]() $\unicode[STIX]{x1D714}\cong J$. Furthermore, we claim that
$\unicode[STIX]{x1D714}\cong J$. Furthermore, we claim that ![]() $J\not \subseteq \cup P_{i}$. Namely, if
$J\not \subseteq \cup P_{i}$. Namely, if ![]() $J\subseteq P_{i}$ for some
$J\subseteq P_{i}$ for some ![]() $i$, then
$i$, then ![]() $s\unicode[STIX]{x1D714}=uJ\subseteq uP_{i}\subseteq \unicode[STIX]{x1D714}P_{i}$. But then localizing at
$s\unicode[STIX]{x1D714}=uJ\subseteq uP_{i}\subseteq \unicode[STIX]{x1D714}P_{i}$. But then localizing at ![]() $P_{i}$ we obtain that
$P_{i}$ we obtain that ![]() $\unicode[STIX]{x1D714}R_{P_{i}}\subseteq P_{i}\unicode[STIX]{x1D714}R_{P_{i}}$, which contradicts Nakayama’s lemma.
$\unicode[STIX]{x1D714}R_{P_{i}}\subseteq P_{i}\unicode[STIX]{x1D714}R_{P_{i}}$, which contradicts Nakayama’s lemma.
We verify that ![]() $J$ satisfies the assertions of the theorem. Since
$J$ satisfies the assertions of the theorem. Since ![]() $J$ is not contained in any minimal prime of
$J$ is not contained in any minimal prime of ![]() $(\text{}\underline{f})$,
$(\text{}\underline{f})$, ![]() $\operatorname{ht}(J,\text{}\underline{f})\geqslant c+1$. Moreover,
$\operatorname{ht}(J,\text{}\underline{f})\geqslant c+1$. Moreover, ![]() $J$ has height
$J$ has height ![]() $1$ and
$1$ and ![]() $R$ is Cohen–Macaulay, so
$R$ is Cohen–Macaulay, so ![]() $\operatorname{ht}(\text{}\underline{f},J)R/J\geqslant c$ and
$\operatorname{ht}(\text{}\underline{f},J)R/J\geqslant c$ and ![]() $\text{}\underline{f}$ must be a parameter sequence in
$\text{}\underline{f}$ must be a parameter sequence in ![]() $R/J$. Since
$R/J$. Since ![]() $R/J$ is Gorenstein [Reference Bruns and HerzogBH93, Proposition 3.3.18], the images of
$R/J$ is Gorenstein [Reference Bruns and HerzogBH93, Proposition 3.3.18], the images of ![]() $\text{}\underline{f}$ form a regular sequence. Hence
$\text{}\underline{f}$ form a regular sequence. Hence
is a canonical module of ![]() $R/(\text{}\underline{f})$. By Corollary 3.2 we can choose a neighborhood
$R/(\text{}\underline{f})$. By Corollary 3.2 we can choose a neighborhood ![]() $\mathfrak{m}^{N}$ such that the images of
$\mathfrak{m}^{N}$ such that the images of ![]() $\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}$ are still a part of a system of parameters in the Gorenstein ring
$\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}$ are still a part of a system of parameters in the Gorenstein ring ![]() $R/J$ for all
$R/J$ for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$ and the statement follows.◻
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$ and the statement follows.◻
Corollary 3.10. Let ![]() $(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay F-finite domain of prime characteristic
$(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay F-finite domain of prime characteristic ![]() $p$. Let
$p$. Let ![]() $\text{}\underline{f}$ be a regular sequence of length
$\text{}\underline{f}$ be a regular sequence of length ![]() $c$ such that
$c$ such that ![]() $R/(\text{}\underline{f})$ is generically Gorenstein. Then for any integer
$R/(\text{}\underline{f})$ is generically Gorenstein. Then for any integer ![]() $e$ there exists an integer
$e$ there exists an integer ![]() $N$ such that
$N$ such that ![]() $a_{e}(R/(\text{}\underline{f}))=a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ for any
$a_{e}(R/(\text{}\underline{f}))=a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ for any ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$.
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$.
In particular, if ![]() $R$ is also normal, then the functions
$R$ is also normal, then the functions ![]() $a_{e}:R\rightarrow \mathbb{R}$,
$a_{e}:R\rightarrow \mathbb{R}$, ![]() $f\mapsto a_{e}(R/f)$, are locally constant at parameter elements with respect to the
$f\mapsto a_{e}(R/f)$, are locally constant at parameter elements with respect to the ![]() $\mathfrak{m}$-adic topology.
$\mathfrak{m}$-adic topology.
Proof. If ![]() $\dim (R)=c$, then
$\dim (R)=c$, then ![]() $R/(f)$ is Artinian and, thus, has a splitting if and only if it is a field. If we take
$R/(f)$ is Artinian and, thus, has a splitting if and only if it is a field. If we take ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{2})^{\oplus c}$, then
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{2})^{\oplus c}$, then ![]() $(\text{}\underline{f})=\mathfrak{m}$ if and only if
$(\text{}\underline{f})=\mathfrak{m}$ if and only if ![]() $(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})=\mathfrak{m}$. So the Frobenius splitting numbers of
$(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})=\mathfrak{m}$. So the Frobenius splitting numbers of ![]() $R/(\text{}\underline{f})$ and
$R/(\text{}\underline{f})$ and ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ will be the same, either
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ will be the same, either ![]() $0$ or
$0$ or ![]() $[k:k^{p^{e}}]$, the latter of which occurs if and only if
$[k:k^{p^{e}}]$, the latter of which occurs if and only if ![]() $(\text{}\underline{f})=\mathfrak{m}$.
$(\text{}\underline{f})=\mathfrak{m}$.
Suppose ![]() $\dim (R)=d+c>c$ and choose
$\dim (R)=d+c>c$ and choose ![]() $J$ and
$J$ and ![]() $N$ as in Lemma 3.9. If
$N$ as in Lemma 3.9. If ![]() $J=R$ replace
$J=R$ replace ![]() $J$ by a principal ideal
$J$ by a principal ideal ![]() $(g)$ such that
$(g)$ such that ![]() $\text{}\underline{f},g$ is a regular sequence. Let
$\text{}\underline{f},g$ is a regular sequence. Let ![]() $x_{2},\ldots ,x_{d}$ be a system of parameters for
$x_{2},\ldots ,x_{d}$ be a system of parameters for ![]() $R/(\text{}\underline{f},J)$. If necessary, increase
$R/(\text{}\underline{f},J)$. If necessary, increase ![]() $N$ so that
$N$ so that ![]() $\mathfrak{m}^{N}\subseteq \mathfrak{m}^{[p^{e}]}$ and
$\mathfrak{m}^{N}\subseteq \mathfrak{m}^{[p^{e}]}$ and ![]() $\mathfrak{m}^{N}\subseteq (\text{}\underline{f},J,x_{2},\ldots ,x_{d})$. In particular, we have for each
$\mathfrak{m}^{N}\subseteq (\text{}\underline{f},J,x_{2},\ldots ,x_{d})$. In particular, we have for each ![]() $\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}$ that
$\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}$ that ![]() $x_{2},\ldots ,x_{d}$ is a system of parameters for
$x_{2},\ldots ,x_{d}$ is a system of parameters for ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J)$.
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J)$.
For each ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$, ![]() $(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J)/(\text{}\underline{f})$ is the canonical module of
$(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J)/(\text{}\underline{f})$ is the canonical module of ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ by Lemma 3.9; hence
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})$ by Lemma 3.9; hence
is an irreducible ![]() $\mathfrak{m}$-primary ideal [Reference Bruns and HerzogBH93, Proposition 3.3.18]. Let
$\mathfrak{m}$-primary ideal [Reference Bruns and HerzogBH93, Proposition 3.3.18]. Let ![]() $u\in R$ generate the socle mod
$u\in R$ generate the socle mod ![]() $(\text{}\underline{f},J,x_{2},\ldots ,x_{d})=(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J,x_{2},\ldots ,x_{d})$. For each
$(\text{}\underline{f},J,x_{2},\ldots ,x_{d})=(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},J,x_{2},\ldots ,x_{d})$. For each ![]() $t\in \mathbb{N}$ let
$t\in \mathbb{N}$ let ![]() $I_{t}=(J,x_{2}^{t},\ldots ,x_{d}^{t})$ and
$I_{t}=(J,x_{2}^{t},\ldots ,x_{d}^{t})$ and ![]() $u_{t}=(x_{2}\cdots x_{d})^{t-1}u$. By Lemma 3.8 there is for each
$u_{t}=(x_{2}\cdots x_{d})^{t-1}u$. By Lemma 3.8 there is for each ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$ a
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$ a ![]() $t_{\text{}\underline{\unicode[STIX]{x1D716}}}$ such that
$t_{\text{}\underline{\unicode[STIX]{x1D716}}}$ such that
 $$\begin{eqnarray}a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))=[k:k^{p^{e}}]\unicode[STIX]{x1D706}\left(\frac{R}{(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},(I_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{[p^{e}]}:_{R}u_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{p^{e}}))}\right)\end{eqnarray}$$
$$\begin{eqnarray}a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))=[k:k^{p^{e}}]\unicode[STIX]{x1D706}\left(\frac{R}{(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},(I_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{[p^{e}]}:_{R}u_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{p^{e}}))}\right)\end{eqnarray}$$and
 $$\begin{eqnarray}a_{e}(R/(\text{}\underline{f}))=[k:k^{p^{e}}]\unicode[STIX]{x1D706}\left(\frac{R}{(\text{}\underline{f},(I_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{[p^{e}]}:_{R}u_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{p^{e}}))}\right).\end{eqnarray}$$
$$\begin{eqnarray}a_{e}(R/(\text{}\underline{f}))=[k:k^{p^{e}}]\unicode[STIX]{x1D706}\left(\frac{R}{(\text{}\underline{f},(I_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{[p^{e}]}:_{R}u_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{p^{e}}))}\right).\end{eqnarray}$$ Moreover, we have ![]() $\mathfrak{m}^{[p^{e}]}\subseteq (\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},(I_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{[p^{e}]}:_{R}u_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{p^{e}}))$. Since
$\mathfrak{m}^{[p^{e}]}\subseteq (\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}},(I_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{[p^{e}]}:_{R}u_{t_{\text{}\underline{\unicode[STIX]{x1D716}}}}^{p^{e}}))$. Since ![]() $N$ was chosen so that
$N$ was chosen so that ![]() $\mathfrak{m}^{N}\subseteq \mathfrak{m}^{[p^{e}]}$, we have
$\mathfrak{m}^{N}\subseteq \mathfrak{m}^{[p^{e}]}$, we have
Therefore for each ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$, ![]() $a_{e}(R/(\text{}\underline{f}))=a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$.◻
$a_{e}(R/(\text{}\underline{f}))=a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$.◻
We need less assumptions for an inequality.
Lemma 3.11. Let ![]() $(R,\mathfrak{m},k)$ be a complete F-finite ring of positive characteristic
$(R,\mathfrak{m},k)$ be a complete F-finite ring of positive characteristic ![]() $p>0$. Then for any parameter sequence
$p>0$. Then for any parameter sequence ![]() $\text{}\underline{f}$ of length
$\text{}\underline{f}$ of length ![]() $c$ and a fixed positive integer
$c$ and a fixed positive integer ![]() $e$ there exists integer
$e$ there exists integer ![]() $N$ such that for all
$N$ such that for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
Proof. Since ![]() $R$ is complete, we can represent it as a quotient of a regular local ring
$R$ is complete, we can represent it as a quotient of a regular local ring ![]() $(S,\mathfrak{m})$,
$(S,\mathfrak{m})$, ![]() $R=S/I$. Then by [Reference Enescu and YaoEY11, Proposition 3.1]
$R=S/I$. Then by [Reference Enescu and YaoEY11, Proposition 3.1]
Let ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$ for an arbitrary
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$ for an arbitrary ![]() $N$. Then
$N$. Then
Since ![]() $\unicode[STIX]{x1D716}_{i}$ are in
$\unicode[STIX]{x1D716}_{i}$ are in ![]() $\mathfrak{m}^{N}$,
$\mathfrak{m}^{N}$,
By Krull’s intersection theorem
so by Chevalley’s lemma we could have chosen ![]() $N$ so that
$N$ so that
In which case ![]() $a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\leqslant a_{e}(R/(\text{}\underline{f}))$.◻
$a_{e}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))\leqslant a_{e}(R/(\text{}\underline{f}))$.◻
Theorem 3.12. Let ![]() $(R,\mathfrak{m},k)$ be a Cohen–Macaulay F-finite ring of prime characteristic
$(R,\mathfrak{m},k)$ be a Cohen–Macaulay F-finite ring of prime characteristic ![]() $p$ and dimension
$p$ and dimension ![]() $d+c$. If
$d+c$. If ![]() $\text{}\underline{f}$ is a parameter sequence of length
$\text{}\underline{f}$ is a parameter sequence of length ![]() $c$ such that
$c$ such that ![]() $\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced then for any
$\hat{R}/(\text{}\underline{f})\hat{R}$ is reduced then for any ![]() $\unicode[STIX]{x1D6FF}>0$ there exists an integer
$\unicode[STIX]{x1D6FF}>0$ there exists an integer ![]() $N>0$ such that for any
$N>0$ such that for any ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
Proof. We may assume ![]() $R$ is complete. By Theorem 2.3 we may choose parameters
$R$ is complete. By Theorem 2.3 we may choose parameters ![]() $x_{1},\ldots ,x_{d}\in R$ such that
$x_{1},\ldots ,x_{d}\in R$ such that ![]() $x_{1},\ldots ,x_{d}$ is a system of parameters for
$x_{1},\ldots ,x_{d}$ is a system of parameters for ![]() $R/(\text{}\underline{f})$ and
$R/(\text{}\underline{f})$ and ![]() $R/(\text{}\underline{f})$ is module-finite and generically separable over the regular local ring
$R/(\text{}\underline{f})$ is module-finite and generically separable over the regular local ring ![]() $A:=k[[x_{1},\ldots ,x_{d}]]$. In which case we have a short exact sequence
$A:=k[[x_{1},\ldots ,x_{d}]]$. In which case we have a short exact sequence
and ![]() $0\neq c=\text{D}_{A}(R/(\text{}\underline{f}))$ annihilates
$0\neq c=\text{D}_{A}(R/(\text{}\underline{f}))$ annihilates ![]() $M$.
$M$.
Let ![]() $M$ and
$M$ and ![]() $M_{\text{}\underline{\unicode[STIX]{x1D716}}}$ be as in the proof of Theorem 3.5. In which case, there are isomorphisms
$M_{\text{}\underline{\unicode[STIX]{x1D716}}}$ be as in the proof of Theorem 3.5. In which case, there are isomorphisms ![]() $R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})[A^{1/p}]\cong \oplus ^{p^{d}[k:k^{p}]}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ and short exact sequences
$R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}})[A^{1/p}]\cong \oplus ^{p^{d}[k:k^{p}]}(R/(\text{}\underline{f}+\text{}\underline{\unicode[STIX]{x1D716}}))$ and short exact sequences
Apply the exact functor ![]() $(-)^{1/p^{e}}$ to the above to get the exact sequence
$(-)^{1/p^{e}}$ to the above to get the exact sequence
By [Reference Polstra and TuckerPT18, Lemma 2.1]
or, equivalently,
Techniques used in the proof of Theorem 3.5 give the existence of a constant ![]() $C$ such that for all
$C$ such that for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
Let ![]() $L$ and
$L$ and ![]() $L_{\text{}\underline{\unicode[STIX]{x1D716}}}$ be as in the proof of Theorem 3.5. Similarly, we can also bound
$L_{\text{}\underline{\unicode[STIX]{x1D716}}}$ be as in the proof of Theorem 3.5. Similarly, we can also bound
and can once again obtain constant ![]() $C$ independent of
$C$ independent of ![]() $\text{}\underline{\unicode[STIX]{x1D716}}$ so that
$\text{}\underline{\unicode[STIX]{x1D716}}$ so that
Since ![]() $\operatorname{rank}R^{1/p^{e}}=p^{ed}[k:k^{p^{e}}]$ [Reference KunzKun76, Proposition 2.3], as explained in Corollary 3.7, this gives us a uniform convergence statement: there exist
$\operatorname{rank}R^{1/p^{e}}=p^{ed}[k:k^{p^{e}}]$ [Reference KunzKun76, Proposition 2.3], as explained in Corollary 3.7, this gives us a uniform convergence statement: there exist ![]() $D,N>0$ such that for all
$D,N>0$ such that for all ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$
Now, if ![]() $\text{s}(R/(\text{}\underline{f}))=0$, for any given
$\text{s}(R/(\text{}\underline{f}))=0$, for any given ![]() $\unicode[STIX]{x1D6FF}>0$ we can find
$\unicode[STIX]{x1D6FF}>0$ we can find ![]() $e$ such that
$e$ such that ![]() $a_{e}(R/(\text{}\underline{f}))<\unicode[STIX]{x1D6FF}/2$ and
$a_{e}(R/(\text{}\underline{f}))<\unicode[STIX]{x1D6FF}/2$ and ![]() $D/p^{e}<\unicode[STIX]{x1D6FF}/2$. By Lemma 3.11, we can find
$D/p^{e}<\unicode[STIX]{x1D6FF}/2$. By Lemma 3.11, we can find ![]() $N$ such that for any
$N$ such that for any ![]() $\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$,
$\text{}\underline{\unicode[STIX]{x1D716}}\in (\mathfrak{m}^{N})^{\oplus c}$,
Thus, in this case the claim follows from the bound
If ![]() $\text{s}(R/(\text{}\underline{f}))>0$, then
$\text{s}(R/(\text{}\underline{f}))>0$, then ![]() $R/(\text{}\underline{f})$ is strongly
$R/(\text{}\underline{f})$ is strongly ![]() $F$-regular and, in particular, is a domain [Reference Aberbach and LeuschkeAL03, main result]. Thus
$F$-regular and, in particular, is a domain [Reference Aberbach and LeuschkeAL03, main result]. Thus ![]() $(\text{}\underline{f})$ is a prime ideal, so
$(\text{}\underline{f})$ is a prime ideal, so ![]() $R/(\text{}\underline{f})$ is then generically Gorenstein. The statement now follows by employing Corollary 3.10 and using the methods of the proof of Corollary 3.7.◻
$R/(\text{}\underline{f})$ is then generically Gorenstein. The statement now follows by employing Corollary 3.10 and using the methods of the proof of Corollary 3.7.◻
4 Examples and questions
In this section we want to present examples relevant to the results in Section 3. The first example shows that we cannot expect Hilbert–Kunz multiplicity to be locally constant at reduced parameter elements.
Example 4.1. Consider an element ![]() $f=xy$ in
$f=xy$ in ![]() $R=k[[x,y,t]]$. An easy computation shows that
$R=k[[x,y,t]]$. An easy computation shows that ![]() $\text{e}_{\text{HK}}(R/(xy))=2$, while we will show that
$\text{e}_{\text{HK}}(R/(xy))=2$, while we will show that ![]() $\text{e}_{\text{HK}}(R/(xy+t^{n}))=2-2/n$ for
$\text{e}_{\text{HK}}(R/(xy+t^{n}))=2-2/n$ for ![]() $n\geqslant 2$. Thus:
$n\geqslant 2$. Thus:
(1) there is no neighborhood of
 $xy$ such that
$xy$ such that  $\text{e}_{\text{HK}}$ is constant;
$\text{e}_{\text{HK}}$ is constant;(2) of course,
 $\text{e}(R/(xy+t^{n}))=2=\text{e}(R/(xy))$ for all
$\text{e}(R/(xy+t^{n}))=2=\text{e}(R/(xy))$ for all  $n\geqslant 2$;
$n\geqslant 2$;(3) moreover, we have
 $\operatorname{Gr}_{(x,y,t)}(R/(xy+t^{n}))=k[x,y,t]/(xy)=\operatorname{Gr}_{(x,y,t)}(R/(xy))$ for all
$\operatorname{Gr}_{(x,y,t)}(R/(xy+t^{n}))=k[x,y,t]/(xy)=\operatorname{Gr}_{(x,y,t)}(R/(xy))$ for all  $n\geqslant 3$.
$n\geqslant 3$.
In order to compute the Hilbert–Kunz multiplicity we will compute the length of
by counting monomials. It is easy to see that a basis is given by monomials of the form ![]() $x^{a}t^{n},y^{a}t^{b}$ where
$x^{a}t^{n},y^{a}t^{b}$ where ![]() $a<p^{e}-\lfloor b/n\rfloor$ and
$a<p^{e}-\lfloor b/n\rfloor$ and ![]() $b<p^{e}$. Thus when
$b<p^{e}$. Thus when ![]() $e\rightarrow \infty$ the number of such monomials is
$e\rightarrow \infty$ the number of such monomials is
Example 4.2. Essentially the same example works for F-signature. Clearly, ![]() $k[[x,y,t]]/(x^{2}+y^{2})$ is not normal, so the F-signature is 0. On the other hand,
$k[[x,y,t]]/(x^{2}+y^{2})$ is not normal, so the F-signature is 0. On the other hand, ![]() $k[[x,y,t]]/(x^{2}+y^{2}+t^{n})$ is the
$k[[x,y,t]]/(x^{2}+y^{2}+t^{n})$ is the ![]() $A_{n-1}$ singularity, its F-signature is known to be
$A_{n-1}$ singularity, its F-signature is known to be ![]() $1/n$ [Reference Huneke and LeuschkeHL02, Example 18].
$1/n$ [Reference Huneke and LeuschkeHL02, Example 18].
By comparison, it is not that hard to see that Hilbert–Samuel multiplicity is locally constant at parameter elements in regular local ring. In fact, Srinivas and Trivedi [Reference Srinivas and TrivediST96, Corollary 5] showed that the entire Hilbert function is locally constant.
4.1 Cohen–Macaulayness
The Cohen–Macaulay assumption of our main results may not be completely necessary. For a possible extension, one could recall that Srinivas and Trivedi [Reference Srinivas and TrivediST96, Corollary 5] show continuity of the Hilbert–Samuel multiplicity if ![]() $R$ is generalized Cohen–Macaulay, that is,
$R$ is generalized Cohen–Macaulay, that is, ![]() $\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{i}(R))<\infty$ for all
$\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{i}(R))<\infty$ for all ![]() $i<\dim R$.
$i<\dim R$.
We also want to give two examples that show that one cannot relax Cohen–Macaulayness too much. The first example comes from [Reference Srinivas and TrivediST96, Example 1].
Example 4.3. Let ![]() $R$ be the localization at
$R$ be the localization at ![]() $\mathfrak{m}=(x,y,z)$ of
$\mathfrak{m}=(x,y,z)$ of ![]() $k[x,y,z]/(xy,xz)$. Note that
$k[x,y,z]/(xy,xz)$. Note that ![]() $R$ is not equidimensional. Because
$R$ is not equidimensional. Because ![]() $\dim R/(y)=1$, the two multiplicities coincide and we easily see that
$\dim R/(y)=1$, the two multiplicities coincide and we easily see that
On the other hand, ![]() $R/(y+x^{N})=k[x,z]_{\mathfrak{m}}/(x^{N+1},xz)$ has the only minimal prime
$R/(y+x^{N})=k[x,z]_{\mathfrak{m}}/(x^{N+1},xz)$ has the only minimal prime ![]() $(x)$ for all
$(x)$ for all ![]() $N$. Hence, by the associativity formula,
$N$. Hence, by the associativity formula,
Proposition 4.4. Let ![]() $R$ be the subring
$R$ be the subring ![]() $k[[x^{3},x^{2}y,y^{3},y^{2}z,z^{3},z^{2}x]]\subseteq k[[x,y]]$. Observe that
$k[[x^{3},x^{2}y,y^{3},y^{2}z,z^{3},z^{2}x]]\subseteq k[[x,y]]$. Observe that ![]() $x^{3},y^{3},z^{3}$ form a system of parameters and consider a family of ideals
$x^{3},y^{3},z^{3}$ form a system of parameters and consider a family of ideals ![]() $J_{k}=(x^{3},y^{3}+z^{3k})$. Then:
$J_{k}=(x^{3},y^{3}+z^{3k})$. Then:
(1)
 $\text{e}_{\text{HK}}(R/(x^{3},y^{3}))=\text{e}(R/(x^{3},y^{3}))=11$;
$\text{e}_{\text{HK}}(R/(x^{3},y^{3}))=\text{e}(R/(x^{3},y^{3}))=11$;(2)
 $\text{e}_{\text{HK}}(R/J_{k})=\text{e}(R/J_{k})\neq 11$ for all
$\text{e}_{\text{HK}}(R/J_{k})=\text{e}(R/J_{k})\neq 11$ for all  $k\neq 1\hspace{0.6em}({\rm mod}\hspace{0.2em}3)$.
$k\neq 1\hspace{0.6em}({\rm mod}\hspace{0.2em}3)$.
Proof. First, we observe that ![]() $\dim R/(x^{3},y^{3})=\dim R/J_{k}=1$, so multiplicity equals to Hilbert–Kunz multiplicity.
$\dim R/(x^{3},y^{3})=\dim R/J_{k}=1$, so multiplicity equals to Hilbert–Kunz multiplicity.
We compute ![]() $\text{e}(R/(x^{3},y^{3}))$ by using the associativity formula. Observe that
$\text{e}(R/(x^{3},y^{3}))$ by using the associativity formula. Observe that
is prime. Thus the associativity formula gives that ![]() $\text{e}_{\text{HK}}(R/(x^{3},y^{3}))=\text{e}_{\text{HK}}(R/P)\unicode[STIX]{x1D706}(R_{P}/(x^{3},y^{3}))$.
$\text{e}_{\text{HK}}(R/(x^{3},y^{3}))=\text{e}_{\text{HK}}(R/P)\unicode[STIX]{x1D706}(R_{P}/(x^{3},y^{3}))$.
The quotient ![]() $R/P\cong k[z^{3}]$ is regular, so
$R/P\cong k[z^{3}]$ is regular, so ![]() $\text{e}_{\text{HK}}(R/P)=1$. Now,
$\text{e}_{\text{HK}}(R/P)=1$. Now,
and it is easy to compute the basis of this ring over ![]() $k(z^{3})$:
$k(z^{3})$:
Therefore, ![]() $\text{e}(R/(x^{3},y^{3}))=11$.
$\text{e}(R/(x^{3},y^{3}))=11$.
The computation for ![]() $J_{k}$ is similar but a bit more complicated. First of all, if
$J_{k}$ is similar but a bit more complicated. First of all, if ![]() $k\neq 1\hspace{0.6em}({\rm mod}\hspace{0.2em}3)$ (so
$k\neq 1\hspace{0.6em}({\rm mod}\hspace{0.2em}3)$ (so ![]() $2k+1$ is not divisible by 3), then
$2k+1$ is not divisible by 3), then
is prime as can be seen by taking the presentation
In this case, ![]() $\text{e}(R/Q)=3$, so
$\text{e}(R/Q)=3$, so ![]() $\text{e}(R/J_{k})$ is divisible by 3 and we already know that it cannot be equal to 11.◻
$\text{e}(R/J_{k})$ is divisible by 3 and we already know that it cannot be equal to 11.◻
Thus even Hilbert–Samuel multiplicity does not behave well in this example. Observe that ![]() $xy^{2}=x^{3}y^{3}/x^{2}y$ and
$xy^{2}=x^{3}y^{3}/x^{2}y$ and ![]() $xyz=y^{3}z^{2}x/y^{2}z$, so the normalization of
$xyz=y^{3}z^{2}x/y^{2}z$, so the normalization of ![]() $R$ is the Veronese subring
$R$ is the Veronese subring
Because ![]() $xy^{2}\cdot y^{3n}\notin R$ for all
$xy^{2}\cdot y^{3n}\notin R$ for all ![]() $n$, the quotient
$n$, the quotient ![]() $S/R$ does not have finite length. On the other hand,
$S/R$ does not have finite length. On the other hand, ![]() $x^{3}y^{3}V\subseteq R$, so
$x^{3}y^{3}V\subseteq R$, so ![]() $\dim S/R$ must equal to 1.
$\dim S/R$ must equal to 1.
Therefore since ![]() $\operatorname{depth}V=2$, from the exact sequence of local cohomology we have
$\operatorname{depth}V=2$, from the exact sequence of local cohomology we have
Therefore, ![]() $\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(R))<\infty$, but
$\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{1}(R))<\infty$, but ![]() $\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{2}(R))=\infty$. This example shows that the assumptions of Srinivas and Trivedi are close to being necessary.
$\unicode[STIX]{x1D706}(\text{H}_{\mathfrak{m}}^{2}(R))=\infty$. This example shows that the assumptions of Srinivas and Trivedi are close to being necessary.
4.2 Questions
The techniques used to prove the main theorems of the paper, which are summarized in Theorem 1.3, rely on the assumption that the parameter sequence ![]() $f_{1},\ldots ,f_{h}$ forms a reduced ideal.
$f_{1},\ldots ,f_{h}$ forms a reduced ideal.
Question 4.5. Let ![]() $(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay F-finite ring of prime characteristic
$(R,\mathfrak{m},k)$ be a complete Cohen–Macaulay F-finite ring of prime characteristic ![]() $p$. If
$p$. If ![]() $(f_{1},\ldots ,f_{c})$ is a parameter ideal, but
$(f_{1},\ldots ,f_{c})$ is a parameter ideal, but ![]() $R/(f_{1},\ldots ,f_{c})$ is not reduced, then given
$R/(f_{1},\ldots ,f_{c})$ is not reduced, then given ![]() $\unicode[STIX]{x1D6FF}>0$ does there exit an integer
$\unicode[STIX]{x1D6FF}>0$ does there exit an integer ![]() $N>0$ such that for any
$N>0$ such that for any ![]() $\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{h}\in \mathfrak{m}^{N}$:
$\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{h}\in \mathfrak{m}^{N}$:
(1)
 $|\text{e}_{\text{HK}}(R/(f_{1},\ldots ,f_{c}))-\text{e}_{\text{HK}}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))|<\unicode[STIX]{x1D6FF}$; and
$|\text{e}_{\text{HK}}(R/(f_{1},\ldots ,f_{c}))-\text{e}_{\text{HK}}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))|<\unicode[STIX]{x1D6FF}$; and(2)
 $\text{s}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))<\unicode[STIX]{x1D6FF}$? Note that
$\text{s}(R/(f_{1}+\unicode[STIX]{x1D716}_{1},\ldots ,f_{c}+\unicode[STIX]{x1D716}_{c}))<\unicode[STIX]{x1D6FF}$? Note that  $\text{s}(R/(f_{1},\ldots ,f_{c}))=0$ since
$\text{s}(R/(f_{1},\ldots ,f_{c}))=0$ since  $R/(f_{1},\ldots ,f_{c})$ is not reduced.
$R/(f_{1},\ldots ,f_{c})$ is not reduced.
Originally, the second author hoped to approach Question 1.1, by passing to the associated graded ring. Namely, Srinivas and Trivedi [Reference Srinivas and TrivediST96, Theorem 3] show ![]() $\operatorname{Gr}_{\mathfrak{m}}(R/(f))$ is a locally constant function of
$\operatorname{Gr}_{\mathfrak{m}}(R/(f))$ is a locally constant function of ![]() $f$ in
$f$ in ![]() $\mathfrak{m}$-adic topology, which immediately implies that Hilbert–Samuel multiplicity is locally constant.
$\mathfrak{m}$-adic topology, which immediately implies that Hilbert–Samuel multiplicity is locally constant.
However the Hilbert–Kunz multiplicities of a local ring and its associated graded ring need not be equal ([Reference Watanabe and YoshidaWY00, p. 302] and also Example 4.1). Moreover, Hilbert–Kunz multiplicity is not an invariant of the associated graded ring, that is, as we see in Example 4.1, it may happen that ![]() $\text{e}_{\text{HK}}(R)\neq \text{e}_{\text{HK}}(S)$ even though
$\text{e}_{\text{HK}}(R)\neq \text{e}_{\text{HK}}(S)$ even though ![]() $\operatorname{Gr}_{\mathfrak{m}_{R}}(R)\cong \operatorname{Gr}_{\mathfrak{m}_{S}}(S)$. Investigation of the following question could yield an explanation.
$\operatorname{Gr}_{\mathfrak{m}_{R}}(R)\cong \operatorname{Gr}_{\mathfrak{m}_{S}}(S)$. Investigation of the following question could yield an explanation.
Question 4.6. Does the convergence rate of the Hilbert–Kunz multiplicity come from the associated graded ring? Namely, is there a constant ![]() $C$ that depends only on the associated graded ring of
$C$ that depends only on the associated graded ring of ![]() $S$ (not
$S$ (not ![]() $S$!) such that
$S$!) such that
for all ![]() $e$?
$e$?
This question can be stated even more explicitly: consider the family of ideals in ![]() $\operatorname{Gr}_{\mathfrak{m}}(R)$
$\operatorname{Gr}_{\mathfrak{m}}(R)$
By the definition, ![]() $\unicode[STIX]{x1D706}(R/\mathfrak{m}^{[p^{e}]})=\unicode[STIX]{x1D706}(\operatorname{Gr}_{\mathfrak{m}}(R)/J_{e})$. Because
$\unicode[STIX]{x1D706}(R/\mathfrak{m}^{[p^{e}]})=\unicode[STIX]{x1D706}(\operatorname{Gr}_{\mathfrak{m}}(R)/J_{e})$. Because ![]() $J_{e}^{[p]}\subseteq J_{e+1}$, we can show the existence of
$J_{e}^{[p]}\subseteq J_{e+1}$, we can show the existence of ![]() $\text{e}_{\text{HK}}(R)$ directly in
$\text{e}_{\text{HK}}(R)$ directly in ![]() $\operatorname{Gr}_{\mathfrak{m}}(R)$ [Reference Polstra and TuckerPT18, Theorem 4.3]. However, in order to get the convergence rate, the current techniques [Reference Polstra and TuckerPT18, Corollary 4.5] require us to find a
$\operatorname{Gr}_{\mathfrak{m}}(R)$ [Reference Polstra and TuckerPT18, Theorem 4.3]. However, in order to get the convergence rate, the current techniques [Reference Polstra and TuckerPT18, Corollary 4.5] require us to find a ![]() $p^{-1}$-linear map
$p^{-1}$-linear map ![]() $\unicode[STIX]{x1D713}$ on
$\unicode[STIX]{x1D713}$ on ![]() $\operatorname{Gr}_{\mathfrak{m}}(R)$ such that
$\operatorname{Gr}_{\mathfrak{m}}(R)$ such that ![]() $\unicode[STIX]{x1D713}(J_{e+1})\subseteq J_{e}$ for all
$\unicode[STIX]{x1D713}(J_{e+1})\subseteq J_{e}$ for all ![]() $e$.
$e$.
Because for a fixed ![]() $e$ the individual Hilbert–Kunz function
$e$ the individual Hilbert–Kunz function ![]() $R/(f,\mathfrak{m}^{[p^{e}]})$ is clearly continuous (Lemma 3.1), we can employ the uniform convergence machinery to show that a positive answer to Question 4.6 gives a positive answer to Question 1.1. However, we currently do not see how to approach Question 4.6, so we had to search for other methods.
$R/(f,\mathfrak{m}^{[p^{e}]})$ is clearly continuous (Lemma 3.1), we can employ the uniform convergence machinery to show that a positive answer to Question 4.6 gives a positive answer to Question 1.1. However, we currently do not see how to approach Question 4.6, so we had to search for other methods.
We also want to offer two questions motivated by intuitive understanding of singularities: we expect that singularity will not get worse after a sufficiently small perturbation.
Question 4.7. Let ![]() $(R,\mathfrak{m},k)$ be a local ring of prime characteristic
$(R,\mathfrak{m},k)$ be a local ring of prime characteristic ![]() $p$. Is there
$p$. Is there ![]() $N$ such that for all
$N$ such that for all ![]() $\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}~\text{e}_{\text{HK}}(R/(f))\geqslant \text{e}_{\text{HK}}(R/(f+\unicode[STIX]{x1D716}))$?
$\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}~\text{e}_{\text{HK}}(R/(f))\geqslant \text{e}_{\text{HK}}(R/(f+\unicode[STIX]{x1D716}))$?
Question 4.8. Let ![]() $(R,\mathfrak{m},k)$ be a local ring of prime characteristic
$(R,\mathfrak{m},k)$ be a local ring of prime characteristic ![]() $p$. Is there
$p$. Is there ![]() $N$ such that for all
$N$ such that for all ![]() $\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}~\text{s}(R/(f))\leqslant \text{s}(R/(f+\unicode[STIX]{x1D716}))$?
$\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}~\text{s}(R/(f))\leqslant \text{s}(R/(f+\unicode[STIX]{x1D716}))$?
We remark that Srinivas and Trivedi [Reference Srinivas and TrivediST96, Corollary 2] showed that the analogue of Question 4.7 holds for Hilbert–Samuel multiplicity. They prove that if ![]() $(R,\mathfrak{m},k)$ is local then one can always find a small neighborhood
$(R,\mathfrak{m},k)$ is local then one can always find a small neighborhood ![]() $\mathfrak{m}^{N}$ such that
$\mathfrak{m}^{N}$ such that ![]() $\text{e}(R/(f))\geqslant \text{e}(R/(f+\unicode[STIX]{x1D716}))$ for all
$\text{e}(R/(f))\geqslant \text{e}(R/(f+\unicode[STIX]{x1D716}))$ for all ![]() $\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}$.
$\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}$.
4.3 Comments on F-pure thresholds
A conjecture related to the results of this paper is the Ascending Chain Condition conjecture for F-pure thresholds, very recently resolved by Sato [Reference SatoSat17, Reference SatoSat18], which states that if ![]() $(R,\mathfrak{m},k)$ is a regular local ring and
$(R,\mathfrak{m},k)$ is a regular local ring and ![]() $f_{1},f_{2},f_{3},\ldots$ are elements of
$f_{1},f_{2},f_{3},\ldots$ are elements of ![]() $R$ such that
$R$ such that
then ![]() $\operatorname{fpt}(f_{n})=\operatorname{fpt}(f_{n+1})$ for all
$\operatorname{fpt}(f_{n})=\operatorname{fpt}(f_{n+1})$ for all ![]() $n\gg 0$. The conjecture is motivated by Shokurov’s ACC conjecture for log canonical thresholds [Reference ShokurovSho92], which was also resolved in the smooth case [Reference de Fernex, Ein and MustaţădFEM10, Reference Hacon, McKernan and XuHMX14]. As the F-pure threshold function is continuous with respect to the
$n\gg 0$. The conjecture is motivated by Shokurov’s ACC conjecture for log canonical thresholds [Reference ShokurovSho92], which was also resolved in the smooth case [Reference de Fernex, Ein and MustaţădFEM10, Reference Hacon, McKernan and XuHMX14]. As the F-pure threshold function is continuous with respect to the ![]() $\mathfrak{m}$-adic topology, it follows that if the ACC conjecture holds then for each
$\mathfrak{m}$-adic topology, it follows that if the ACC conjecture holds then for each ![]() $f\in R$ there exists
$f\in R$ there exists ![]() $N\in \mathbb{N}$ such that for each
$N\in \mathbb{N}$ such that for each ![]() $\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}$,
$\unicode[STIX]{x1D716}\in \mathfrak{m}^{N}$, ![]() $\operatorname{fpt}(f+\unicode[STIX]{x1D716})\geqslant \operatorname{fpt}(f)$. Hernández, Núñez-Betancourt, and Witt [Reference Hernández, Núñez-Betancourt and WittHNnW17] recently investigated this particular implication of the ACC conjecture. Their techniques establish that if the Jacobian ideal of an element
$\operatorname{fpt}(f+\unicode[STIX]{x1D716})\geqslant \operatorname{fpt}(f)$. Hernández, Núñez-Betancourt, and Witt [Reference Hernández, Núñez-Betancourt and WittHNnW17] recently investigated this particular implication of the ACC conjecture. Their techniques establish that if the Jacobian ideal of an element ![]() $f\in R$ is
$f\in R$ is ![]() $\mathfrak{m}$-primary, then
$\mathfrak{m}$-primary, then ![]() $\operatorname{fpt}(f)=\operatorname{fpt}(g)$ for all
$\operatorname{fpt}(f)=\operatorname{fpt}(g)$ for all ![]() $g$ sufficiently close to
$g$ sufficiently close to ![]() $f$. Their result is also recovered by Samuel’s theorem from [Reference SamuelSam56] mentioned in the introduction.
$f$. Their result is also recovered by Samuel’s theorem from [Reference SamuelSam56] mentioned in the introduction.
A natural analogue to the ACC conjecture for Hilbert–Kunz multiplicity would be a descending chain condition. That is given a sequence of elements ![]() $f_{1},f_{2},f_{3},\ldots$ in a regular local ring
$f_{1},f_{2},f_{3},\ldots$ in a regular local ring ![]() $(R,\mathfrak{m},k)$ such that
$(R,\mathfrak{m},k)$ such that ![]() $\text{e}_{\text{HK}}(R/(f_{1}))\geqslant \text{e}_{\text{HK}}(R/(f_{2}))\geqslant \text{e}_{\text{HK}}(R/(f_{3}))\geqslant \cdots \,$ is it necessarily the case that
$\text{e}_{\text{HK}}(R/(f_{1}))\geqslant \text{e}_{\text{HK}}(R/(f_{2}))\geqslant \text{e}_{\text{HK}}(R/(f_{3}))\geqslant \cdots \,$ is it necessarily the case that ![]() $\text{e}_{\text{HK}}(R/(f_{n}))=\text{e}_{\text{HK}}(R/(f_{n+1}))$ for all
$\text{e}_{\text{HK}}(R/(f_{n}))=\text{e}_{\text{HK}}(R/(f_{n+1}))$ for all ![]() $n\gg 0$? Work of Monsky [Reference MonskyMon98] shows the natural analogue of the ACC conjecture for Hilbert–Kunz multiplicity does not hold.
$n\gg 0$? Work of Monsky [Reference MonskyMon98] shows the natural analogue of the ACC conjecture for Hilbert–Kunz multiplicity does not hold.
Example 4.9. In [Reference MonskyMon98] Monsky computed the Hilbert–Kunz multiplicity of a family of hypersurfaces of the form ![]() $R_{\unicode[STIX]{x1D6FC}}=k[[x,y,z]]/(z^{4}+xyz^{2}+(x^{3}+y^{3})z+\unicode[STIX]{x1D6FC}x^{2}y^{2})$ where
$R_{\unicode[STIX]{x1D6FC}}=k[[x,y,z]]/(z^{4}+xyz^{2}+(x^{3}+y^{3})z+\unicode[STIX]{x1D6FC}x^{2}y^{2})$ where ![]() $\unicode[STIX]{x1D6FC}\in k$, an algebraically closed field of characteristic 2. His computations show that there is a sequence
$\unicode[STIX]{x1D6FC}\in k$, an algebraically closed field of characteristic 2. His computations show that there is a sequence ![]() $\unicode[STIX]{x1D6FC}_{n}$ such that
$\unicode[STIX]{x1D6FC}_{n}$ such that ![]() $\text{e}_{\text{HK}}(R_{\unicode[STIX]{x1D6FC}_{n}})=3+4^{-n}$, which gives an infinite decreasing sequence.
$\text{e}_{\text{HK}}(R_{\unicode[STIX]{x1D6FC}_{n}})=3+4^{-n}$, which gives an infinite decreasing sequence.
We suspect there is a family of hyperplanes, similar to that of Example 4.9, whose F-signatures form an infinite increasing sequence.
Acknowledgments
We want to thank Ian Aberbach, Bhargav Bhatt, Dale Cutkosky, and Mel Hochster for the discussion of this work. In particular, Bhargav Bhatt has helped shape Lemma 3.3 and Proposition 4.4 was suggested by Mel Hochster. This project started while the first author was visiting University of Michigan, we thank Mel Hochster and University of Michigan for making that trip possible.
We are grateful to Linquan Ma for pointing an inaccuracy in an earlier draft of this paper.