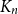1. Introduction
Increasing trees or increasingly labelled trees are rooted labelled trees. The nodes of a tree T of size
![]() $|T| = n$
are labelled with distinct integers from a label set
$|T| = n$
are labelled with distinct integers from a label set
![]() $\mathcal{M}$
of size
$\mathcal{M}$
of size
![]() $|\mathcal{M}|=n$
. Here, the size
$|\mathcal{M}|=n$
. Here, the size
![]() $|T|$
of a tree denotes the number of vertices of T (and thus coincides with the number of labels). One chooses as label set the first n positive integers, i.e.,
$|T|$
of a tree denotes the number of vertices of T (and thus coincides with the number of labels). One chooses as label set the first n positive integers, i.e.,
![]() $\mathcal{M} = [n] \,:\!=\, \{1, 2, \dots, n\}$
, in such a way that the label of any node in the tree is smaller than the labels of its children. As a consequence, the labels of each path from the root to an arbitrary node in the tree are forming an increasing sequence, which explains the name of such a labelling. Various increasing tree models turned out to be appropriate in order to describe the growth behaviour of quantities in a number of applications and occurred in the probabilistic literature. E.g., they are used to describe the spread of epidemics, to model pyramid schemes, and as a simplified growth model of the world wide web. See Mahmoud and Smythe [Reference Mahmoud and Smythe19] for a survey collecting results about recursive trees, a subfamily of increasing trees, prior 1995. For recent results about increasing trees we refer to the books of Drmota [Reference Drmota5], Flajolet and Sedgewick [Reference Flajolet and Segdewick6] and references therein.
$\mathcal{M} = [n] \,:\!=\, \{1, 2, \dots, n\}$
, in such a way that the label of any node in the tree is smaller than the labels of its children. As a consequence, the labels of each path from the root to an arbitrary node in the tree are forming an increasing sequence, which explains the name of such a labelling. Various increasing tree models turned out to be appropriate in order to describe the growth behaviour of quantities in a number of applications and occurred in the probabilistic literature. E.g., they are used to describe the spread of epidemics, to model pyramid schemes, and as a simplified growth model of the world wide web. See Mahmoud and Smythe [Reference Mahmoud and Smythe19] for a survey collecting results about recursive trees, a subfamily of increasing trees, prior 1995. For recent results about increasing trees we refer to the books of Drmota [Reference Drmota5], Flajolet and Sedgewick [Reference Flajolet and Segdewick6] and references therein.
In above definition of increasing trees each node in the tree gets exactly one label. Here in this work we discuss an extension of increasing trees to bucket increasing trees. These are multilabelled increasing tree families. All the nodes v in the tree T are buckets with a maximal capacity of b labels. Here and throughout this work the integer
![]() $b\in{\mathbb{N}}$
denotes the maximal capacity or bucket size. The integer
$b\in{\mathbb{N}}$
denotes the maximal capacity or bucket size. The integer
![]() $c=c(v)$
denotes the current capacity or load of a node
$c=c(v)$
denotes the current capacity or load of a node
![]() $v\in T$
, with
$v\in T$
, with
![]() $1 \le c \le b$
. We always call a node v with capacity
$1 \le c \le b$
. We always call a node v with capacity
![]() $c(v) = b$
saturated and otherwise unsaturated. We impose the additional restriction that all internal nodes (i.e., non-leaves) in the tree must be saturated. In contrast, the leaves might be either saturated or unsaturated. The size of a tree
$c(v) = b$
saturated and otherwise unsaturated. We impose the additional restriction that all internal nodes (i.e., non-leaves) in the tree must be saturated. In contrast, the leaves might be either saturated or unsaturated. The size of a tree
![]() $|T|$
is here and throughout this work measured by the sum of all node capacities c(v):
$|T|$
is here and throughout this work measured by the sum of all node capacities c(v):
![]() $|T| = \sum_{v\in T} c(v)$
; equivalently, it is given by the number of labels in the tree T. We note in passing that tree families where all leaves have to be saturated have been considered and discussed recently in [Reference Kuba and Panholzer14, Reference Kuba and Panholzer15] in connection with so-called hook-length formulas. Moreover, closely related combinatorial objects named increasing diamonds have been studied in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4], as discussed later.
$|T| = \sum_{v\in T} c(v)$
; equivalently, it is given by the number of labels in the tree T. We note in passing that tree families where all leaves have to be saturated have been considered and discussed recently in [Reference Kuba and Panholzer14, Reference Kuba and Panholzer15] in connection with so-called hook-length formulas. Moreover, closely related combinatorial objects named increasing diamonds have been studied in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4], as discussed later.
A specific family of bucket increasing trees called bucket recursive trees has been introduced by Mahmoud and Smythe [Reference Mahmoud and Smythe18]. The probabilistic description of random bucket recursive trees is given by a stochastic growth rule: a tree grows by progressive attraction of increasing integer labels. Such growth rules are part of a general (preferential) attachment rule with fertility and ageing, see Berger et al. [Reference Berger, Borgs, Chayes, D’Souza and Kleinberg1, Reference Berger, Borgs, Chayes, D’Souza and Kleinberg2]. A general combinatorial model for bucket recursive trees has been introduced in [Reference Kuba and Panholzer13]. Note that also different models of bucket recursive trees appeared, see for example [Reference Kazemi9], where the capacities of internal nodes might also vary. Technically, this work and related articles are published in a journal, though they do not seem to be written to professional standards.Footnote 1
The aims of this paper are the following: first, we discuss the general combinatorial framework for bucket increasing trees and the corresponding random tree model. We introduce and analyse two new families of bucket increasing trees. For the two new families of (b,d)-ary increasing trees and
![]() $(b,\alpha)$
-plane-oriented recursive trees we present both, a stochastic growth rule and a combinatorial description. Then, we prove that both descriptions are equivalent. As a byproduct of our study we complement previous results [Reference Kuba and Panholzer13, Reference Mahmoud and Smythe18] for bucket recursive trees. Furthermore we present a clustering map for ordinary increasing trees, which maps them to bucket increasing trees. In the special case of bucket size
$(b,\alpha)$
-plane-oriented recursive trees we present both, a stochastic growth rule and a combinatorial description. Then, we prove that both descriptions are equivalent. As a byproduct of our study we complement previous results [Reference Kuba and Panholzer13, Reference Mahmoud and Smythe18] for bucket recursive trees. Furthermore we present a clustering map for ordinary increasing trees, which maps them to bucket increasing trees. In the special case of bucket size
![]() $b=2$
we state a bijection between bucket increasing trees and so-called increasing diamonds studied in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4], providing an explanation for phenomena observed in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4]; see Corollary 19 for the precise statement.
$b=2$
we state a bijection between bucket increasing trees and so-called increasing diamonds studied in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4], providing an explanation for phenomena observed in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4]; see Corollary 19 for the precise statement.
We obtain the combinatorial description using a generalisation of a class of weighted tree families, so called simple families of increasing trees, to a class of bucket trees, which we call families of bucket increasing trees. All considered tree families will then be special instances of a bucket increasing tree family. As in the previous analysis of bucket recursive trees the gain of the combinatorial description provided here is that the natural combinatorial decomposition of a bucket increasing tree into a root bucket and its subtrees will lead to a recursive description of several important tree parameters in random bucket recursive trees. This combinatorial decomposition can be translated into certain differential equations for suitably defined generating functions. On the other hand the stochastic growth rules will allow us to present decompositions of random variables of interest.
The combination of both methods – a combinatorial approach leading to exact expressions and the stochastic growth rule leading to decompositions – turns out to be a particularly useful tool for a variety of parameters. First we study the random variables (r.v. for short)
![]() $K_{n}$
counting the size of the bucket containing label n. Explicit results for the probability mass function of
$K_{n}$
counting the size of the bucket containing label n. Explicit results for the probability mass function of
![]() $K_n$
are obtained by the combinatorial approach. The explicit expression for
$K_n$
are obtained by the combinatorial approach. The explicit expression for
![]() ${\mathbb{P}}\{K_n=m\}$
readily leads to a discrete limit law for
${\mathbb{P}}\{K_n=m\}$
readily leads to a discrete limit law for
![]() $K_n$
as n tends to infinity. Then, we relate
$K_n$
as n tends to infinity. Then, we relate
![]() $K_n$
to the random variables
$K_n$
to the random variables
![]() $N_{n,k}$
, counting the number of buckets of capacity k,
$N_{n,k}$
, counting the number of buckets of capacity k,
![]() $1\le k\le b$
.
$1\le k\le b$
.
Next, we turn to the analysis of the r.v.
![]() $Y_{n,j}$
, counting the number of descendants of label j. The results for
$Y_{n,j}$
, counting the number of descendants of label j. The results for
![]() $K_n$
and its limit law are used to obtain the exact distribution of
$K_n$
and its limit law are used to obtain the exact distribution of
![]() $Y_{n,j}$
, as well as several limit laws depending on the growth of
$Y_{n,j}$
, as well as several limit laws depending on the growth of
![]() $j=j(n)$
as n tends to infinity. Moreover, we study the random variable
$j=j(n)$
as n tends to infinity. Moreover, we study the random variable
![]() $X_{n,j}$
counting the out-degree of the bucket containing label j in a size n bucket tree. The analysis of
$X_{n,j}$
counting the out-degree of the bucket containing label j in a size n bucket tree. The analysis of
![]() $X_{n,j}$
is based on a stopping time closely related to
$X_{n,j}$
is based on a stopping time closely related to
![]() $Y_{n,j}$
. We also provide decompositions of the random variables
$Y_{n,j}$
. We also provide decompositions of the random variables
![]() $X_{n,j}$
and
$X_{n,j}$
and
![]() $Y_{n,j}$
in terms of
$Y_{n,j}$
in terms of
![]() $K_n$
for fixed n.
$K_n$
for fixed n.
1.1. Notation
We denote with
![]() $X \stackrel{(d)}{=} Y$
the equality in distribution of two random variables X and Y. We write
$X \stackrel{(d)}{=} Y$
the equality in distribution of two random variables X and Y. We write
![]() $X_{n} \xrightarrow{(d)} X$
for the weak convergence (i.e., convergence in distribution) of a sequence of random variables
$X_{n} \xrightarrow{(d)} X$
for the weak convergence (i.e., convergence in distribution) of a sequence of random variables
![]() $X_{n}$
to a r.v. X. Let
$X_{n}$
to a r.v. X. Let
![]() $H_{n} \,:\!=\, \sum_{k=1}^{n} \frac{1}{k}$
denote the harmonic numbers and
$H_{n} \,:\!=\, \sum_{k=1}^{n} \frac{1}{k}$
denote the harmonic numbers and
![]() $H_{n+\alpha}-H_{\alpha} \,:\!=\, \sum_{k=1}^{n} \frac{1}{k+\alpha}$
the continuation of the harmonic numbers for a complex
$H_{n+\alpha}-H_{\alpha} \,:\!=\, \sum_{k=1}^{n} \frac{1}{k+\alpha}$
the continuation of the harmonic numbers for a complex
![]() $\alpha \in \mathbb{C}\setminus\{-1, -2, -3, \dots\}$
. Here and throughout this work we use the notation
$\alpha \in \mathbb{C}\setminus\{-1, -2, -3, \dots\}$
. Here and throughout this work we use the notation
![]() ${x^{\underline{s}}}\,:\!=\,x(x-1)\dots(x-(s-1))$
for the falling factorials, and
${x^{\underline{s}}}\,:\!=\,x(x-1)\dots(x-(s-1))$
for the falling factorials, and
![]() ${x^{\overline{s}}}\,:\!=\,x(x+1)\dots(x+s-1)$
for the rising factorials,
${x^{\overline{s}}}\,:\!=\,x(x+1)\dots(x+s-1)$
for the rising factorials,
![]() $s\in{\mathbb{N}}_0$
.Footnote 2 Throughout this work we will use the abbreviation (b,d)-ary ITs for (b,d)-ary bucket increasing trees and
$s\in{\mathbb{N}}_0$
.Footnote 2 Throughout this work we will use the abbreviation (b,d)-ary ITs for (b,d)-ary bucket increasing trees and
![]() ${(\mathrm{b},\alpha)}$
-PORTs for bucket
${(\mathrm{b},\alpha)}$
-PORTs for bucket
![]() $(b,\alpha)$
-plane-oriented increasing trees.
$(b,\alpha)$
-plane-oriented increasing trees.
2. Description of bucket increasing trees
2.1. Tree evolution processes
In [Reference Mahmoud and Smythe18] a stochastic growth rule for bucket recursive trees has been given, generalising the rule for ordinary random recursive trees (which are the special instance
![]() $b=1$
): a bucket tree grows by progressive attraction of increasing integer labels: when inserting element
$b=1$
): a bucket tree grows by progressive attraction of increasing integer labels: when inserting element
![]() $n+1$
into an existing bucket recursive tree containing n elements (i.e., containing the labels
$n+1$
into an existing bucket recursive tree containing n elements (i.e., containing the labels
![]() $\{1, 2, \dots, n\}$
) all n existing elements in the tree compete to attract the element
$\{1, 2, \dots, n\}$
) all n existing elements in the tree compete to attract the element
![]() $n+1$
, where all existing elements have equal chance to recruit the new element. If the element winning this competition is contained in a node with less than b elements (an unsaturated bucket or node), element
$n+1$
, where all existing elements have equal chance to recruit the new element. If the element winning this competition is contained in a node with less than b elements (an unsaturated bucket or node), element
![]() $n+1$
is added to this node, otherwise if the winning element is contained in a node with already b elements (a saturated bucket or node), element
$n+1$
is added to this node, otherwise if the winning element is contained in a node with already b elements (a saturated bucket or node), element
![]() $n+1$
is attached to this node as a new bucket containing only the element
$n+1$
is attached to this node as a new bucket containing only the element
![]() $n+1$
. Starting with a single bucket as root node containing only element 1 leads after
$n+1$
. Starting with a single bucket as root node containing only element 1 leads after
![]() $n-1$
insertion steps, where the labels
$n-1$
insertion steps, where the labels
![]() $2, 3, \dots, n$
are successively inserted according to this growth rule, to a so called random bucket recursive tree with n elements and maximal bucket size b. Of course, the above growth rule for inserting the element
$2, 3, \dots, n$
are successively inserted according to this growth rule, to a so called random bucket recursive tree with n elements and maximal bucket size b. Of course, the above growth rule for inserting the element
![]() $n+1$
could also be formulated by saying that, for an existing bucket recursive tree T with n elements, the probability that a certain node
$n+1$
could also be formulated by saying that, for an existing bucket recursive tree T with n elements, the probability that a certain node
![]() $v \in T$
attracts the new element
$v \in T$
attracts the new element
![]() $n+1$
is proportional to the number of elements contained in v, let us say k with
$n+1$
is proportional to the number of elements contained in v, let us say k with
![]() $1 \le k \le b$
, and is thus given by
$1 \le k \le b$
, and is thus given by
![]() $\frac{k}{n}$
. Summarising this procedure we obtain the following definition.
$\frac{k}{n}$
. Summarising this procedure we obtain the following definition.
Definition 1 (Bucket recursive trees). We start with a single bucket as root node containing only label 1. Given a tree T of size
![]() $n\ge 1$
. Let
$n\ge 1$
. Let
![]() $p(v)={\mathbb{P}}(n+1 <_t v \mid c(v)\}$
denote the probability that node
$p(v)={\mathbb{P}}(n+1 <_t v \mid c(v)\}$
denote the probability that node
![]() $v\in {T}$
attracts label
$v\in {T}$
attracts label
![]() $n+1$
conditioned on its capacity c(v). The family of random bucket recursive trees is generated according to the probabilities
$n+1$
conditioned on its capacity c(v). The family of random bucket recursive trees is generated according to the probabilities
with capacity
![]() $1\le c(v)\le b$
, thus independent of the out-degree
$1\le c(v)\le b$
, thus independent of the out-degree
![]() $\text{deg}^{+}(v)\ge 0$
of node v.
$\text{deg}^{+}(v)\ge 0$
of node v.
Note that here and throughout this work the capacities
![]() $c(v)=c_n(v)$
and the out-degree
$c(v)=c_n(v)$
and the out-degree
![]() $\text{deg}^{+}(v)=\text{deg}^{+}_n(v)$
of a node v in a tree T are always dependent on the size
$\text{deg}^{+}(v)=\text{deg}^{+}_n(v)$
of a node v in a tree T are always dependent on the size
![]() $|T|=n$
.
$|T|=n$
.
In the following we present two new stochastic growth rules. They generate families of random bucket increasing trees with bucket size
![]() $b\ge 1$
. Concerning the created trees, they are by definition unordered. For both rules there is an additional dependence on the out-degree
$b\ge 1$
. Concerning the created trees, they are by definition unordered. For both rules there is an additional dependence on the out-degree
![]() $\text{deg}^{+}(v)$
of the nodes.
$\text{deg}^{+}(v)$
of the nodes.
Definition 2 ((b,d)-ary increasing). We start, case
![]() $n=1$
, with a single bucket as root node containing only label 1. Given a tree T of size
$n=1$
, with a single bucket as root node containing only label 1. Given a tree T of size
![]() $n\ge 1$
. Let p(v) denote the probability that node
$n\ge 1$
. Let p(v) denote the probability that node
![]() $v\in T$
attracts label
$v\in T$
attracts label
![]() $n+1$
in a bucket increasing tree of size
$n+1$
in a bucket increasing tree of size
![]() $n\in{\mathbb{N}}$
.
$n\in{\mathbb{N}}$
.
The family of random (b,d)-ary increasing trees, with
![]() $d\in\mathbb{Q}$
such that
$d\in\mathbb{Q}$
such that
![]() $(d-1)b\in\mathbb{N}$
, is generated according to the probabilities
$(d-1)b\in\mathbb{N}$
, is generated according to the probabilities
with
![]() $1\le c(v)\le b$
and
$1\le c(v)\le b$
and
![]() $\text{deg}^{+}(v)\ge 0$
.
$\text{deg}^{+}(v)\ge 0$
.
Definition 3 (
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees). We start, case
$(\mathrm{b},\alpha)$
-plane oriented recursive trees). We start, case
![]() $n=1$
, with a single bucket as root node containing only label 1. Given a tree T of size
$n=1$
, with a single bucket as root node containing only label 1. Given a tree T of size
![]() $n\ge 1$
. The family of random (b,
$n\ge 1$
. The family of random (b,
![]() $\alpha$
)-plane oriented recursive trees, with
$\alpha$
)-plane oriented recursive trees, with
![]() $\alpha>0$
, is generated according to the probabilities p(v) that node
$\alpha>0$
, is generated according to the probabilities p(v) that node
![]() $v\in T$
attracts label
$v\in T$
attracts label
![]() $n+1$
:
$n+1$
:
with
![]() $1\le c(v)\le b$
and
$1\le c(v)\le b$
and
![]() $\text{deg}^{+}(v)\ge 0$
.
$\text{deg}^{+}(v)\ge 0$
.
Remark 4. Panholzer and Prodinger [Reference Panholzer and Prodinger21] characterised increasing tree families, which can be constructed by a simple stochastic growth rule. They obtained a unifying description based on two parameter, leading to three different families of trees. The two growth processes for (b,d)-ary increasing trees and
![]() $(\mathrm{b},\alpha)$
-PORTs together with the process for random bucket recursive trees stated before, generalise the processes of [Reference Panholzer and Prodinger21], namely, they correspond to the special case of bucket size
$(\mathrm{b},\alpha)$
-PORTs together with the process for random bucket recursive trees stated before, generalise the processes of [Reference Panholzer and Prodinger21], namely, they correspond to the special case of bucket size
![]() $b=1$
. For general
$b=1$
. For general
![]() $b\in {\mathbb{N}}$
, we can show [Reference Kuba and Panholzer10] that the three processes introduced before are the only ones, which can be constructed by a simple stochastic growth rule.
$b\in {\mathbb{N}}$
, we can show [Reference Kuba and Panholzer10] that the three processes introduced before are the only ones, which can be constructed by a simple stochastic growth rule.
Remark 5 (Linear bucket increasing trees). Plane-oriented recursive trees (PORTs, i.e., (1,1)-PORTs) and their generalisation also appeared in the literature under different names: Pittel [Reference Pittel22] calls such tree families linear increasing trees, also unifying recursive trees and d-ary increasing trees into a single family. Closely related tree families are so-called scale-free trees, which can also be generated by a preferential attachment rule.
In the spirit of Pittel, we can define linear bucket increasing trees as follows. Given a tree T of size
![]() $n\ge 1$
, a label
$n\ge 1$
, a label
![]() $n+1$
is attracted by a node
$n+1$
is attracted by a node
![]() $v\in T$
that is chosen with probability proportional to
$v\in T$
that is chosen with probability proportional to
with
![]() $1\le c(v)\le b$
and
$1\le c(v)\le b$
and
![]() $\text{deg}^{+}(v)\ge 0$
. Here
$\text{deg}^{+}(v)\ge 0$
. Here
![]() $\alpha,\beta,m\in{\mathbb{R}}$
denote real parameters such that the sum is non-negative. For
$\alpha,\beta,m\in{\mathbb{R}}$
denote real parameters such that the sum is non-negative. For
![]() $b=1$
we have
$b=1$
we have
![]() $c(v)=1$
and we reobtain Pittel’s linear increasing trees.
$c(v)=1$
and we reobtain Pittel’s linear increasing trees.
2.2 Combinatorial description of bucket increasing tree families
Our basic objects are rooted ordered trees
![]() $T\in\mathcal{B}$
. Here, the order of the subtrees of a node is of relevance. The nodes of the trees are buckets with an integer capacity c, with
$T\in\mathcal{B}$
. Here, the order of the subtrees of a node is of relevance. The nodes of the trees are buckets with an integer capacity c, with
![]() $1 \le c \le b$
for a given maximal integer bucket size
$1 \le c \le b$
for a given maximal integer bucket size
![]() $b \ge 1$
. We assume that all internal nodes (i.e., non-leaves) in the tree must be saturated, while the leaves might be either saturated or unsaturated. Here
$b \ge 1$
. We assume that all internal nodes (i.e., non-leaves) in the tree must be saturated, while the leaves might be either saturated or unsaturated. Here
![]() $\mathcal{B}$
denotes the family of all bucket ordered trees with maximal bucket size b. A tree T defined in this way is called a bucket ordered tree with maximal bucket size b. As already mentioned we define for bucket ordered trees the size
$\mathcal{B}$
denotes the family of all bucket ordered trees with maximal bucket size b. A tree T defined in this way is called a bucket ordered tree with maximal bucket size b. As already mentioned we define for bucket ordered trees the size
![]() $|T|$
of a tree T via
$|T|$
of a tree T via
![]() $|T| = \sum_{v} c(v)$
, where c(v) ranges over all vertices of T. An increasing labelling
$|T| = \sum_{v} c(v)$
, where c(v) ranges over all vertices of T. An increasing labelling
![]() $\ell(T)$
of a bucket ordered tree T is then a labelling of T, where the labels
$\ell(T)$
of a bucket ordered tree T is then a labelling of T, where the labels
![]() $\{1, 2,\dots, |T|\}$
are distributed amongst the nodes of T, such that the following conditions are satisfied: (i) every node v contains exactly c(v) labels, (ii) the labels within a node are arranged in increasing order, (iii) each sequence of labels along any path starting at the root is increasing. A bucket ordered increasing tree
$\{1, 2,\dots, |T|\}$
are distributed amongst the nodes of T, such that the following conditions are satisfied: (i) every node v contains exactly c(v) labels, (ii) the labels within a node are arranged in increasing order, (iii) each sequence of labels along any path starting at the root is increasing. A bucket ordered increasing tree
![]() $\tilde{T}$
is given by a pair
$\tilde{T}$
is given by a pair
![]() $\tilde{T}=(T,\ell(T))$
.
$\tilde{T}=(T,\ell(T))$
.
Then a class
![]() $\mathcal{T}$
of a family of bucket increasing trees with maximal bucket size b can be defined in the following way. A sequence of non-negative numbers
$\mathcal{T}$
of a family of bucket increasing trees with maximal bucket size b can be defined in the following way. A sequence of non-negative numbers
![]() $(\varphi_{k})_{k \ge 0}$
with
$(\varphi_{k})_{k \ge 0}$
with
![]() $\varphi_{0} > 0$
and a sequence of non-negative numbers
$\varphi_{0} > 0$
and a sequence of non-negative numbers
![]() $\psi_{1}, \psi_{2}, \dots, \psi_{b-1}$
is used to define the weight w(T) of any bucket ordered tree T by
$\psi_{1}, \psi_{2}, \dots, \psi_{b-1}$
is used to define the weight w(T) of any bucket ordered tree T by
![]() $w(T) \,:\!=\, \prod_{v} w(v)$
, where v ranges over all vertices of T. The weight w(v) of a node v is given as follows, where
$w(T) \,:\!=\, \prod_{v} w(v)$
, where v ranges over all vertices of T. The weight w(v) of a node v is given as follows, where
![]() $\text{deg}^{+}(v)$
denotes the out-degree (i.e., the number of children) of node v:
$\text{deg}^{+}(v)$
denotes the out-degree (i.e., the number of children) of node v:
 \begin{equation*} w(v) = \begin{cases} \varphi_{\text{deg}^{+}(v)}, & \quad \text{if} \enspace c(v)=b, \\ \psi_{c(v)}, & \quad \text{if} \enspace c(v) < b. \end{cases}\end{equation*}
\begin{equation*} w(v) = \begin{cases} \varphi_{\text{deg}^{+}(v)}, & \quad \text{if} \enspace c(v)=b, \\ \psi_{c(v)}, & \quad \text{if} \enspace c(v) < b. \end{cases}\end{equation*}
Thus, for saturated nodes the weight depends on the out-degree
![]() $\text{deg}^{+}(v)$
and is described by the sequence
$\text{deg}^{+}(v)$
and is described by the sequence
![]() $\varphi_{k}$
, whereas for unsaturated nodes the weight depends on the capacity c(v) and is described by the sequence
$\varphi_{k}$
, whereas for unsaturated nodes the weight depends on the capacity c(v) and is described by the sequence
![]() $\psi_{k}$
.
$\psi_{k}$
.
Furthermore,
![]() $\mathcal{L}(T)$
denotes the set of different increasing labellings
$\mathcal{L}(T)$
denotes the set of different increasing labellings
![]() $\ell(T)$
of the tree T with distinct integers
$\ell(T)$
of the tree T with distinct integers
![]() $\{1, 2, \dots, |T|\}$
, where
$\{1, 2, \dots, |T|\}$
, where
![]() $L(T) \,:\!=\, \big|\mathcal{L}(T)\big|$
denotes its cardinality. The family
$L(T) \,:\!=\, \big|\mathcal{L}(T)\big|$
denotes its cardinality. The family
![]() $\mathcal{T}$
consists of all trees
$\mathcal{T}$
consists of all trees
![]() $\tilde{T}=(T,\ell(T))$
, with their weights w(T) and the set of increasing labellings
$\tilde{T}=(T,\ell(T))$
, with their weights w(T) and the set of increasing labellings
![]() $\mathcal{L}(T)$
and we define
$\mathcal{L}(T)$
and we define
![]() $w(\tilde{T})\,:\!=\,w(T)$
. Concerning bucket ordered increasing trees, note that the left-to-right order of the subtrees of the nodes is relevant. E.g., the trees
$w(\tilde{T})\,:\!=\,w(T)$
. Concerning bucket ordered increasing trees, note that the left-to-right order of the subtrees of the nodes is relevant. E.g., the trees ![]() and
and ![]() are forming two different trees.
are forming two different trees.
For a given degree-weight sequence
![]() $(\varphi_{k})_{k \ge 0}$
with a degree-weight generating function
$(\varphi_{k})_{k \ge 0}$
with a degree-weight generating function
![]() $\varphi(t) \,:\!=\, \sum_{k \ge 0} \varphi_{k} t^{k}$
and a bucket-weight sequence
$\varphi(t) \,:\!=\, \sum_{k \ge 0} \varphi_{k} t^{k}$
and a bucket-weight sequence
![]() $\psi_{1}, \dots, \psi_{b-1}$
, we define now the total weights
$\psi_{1}, \dots, \psi_{b-1}$
, we define now the total weights
![]() $T_n$
by
$T_n$
by
It is advantageous for such enumeration problems to describe a family of increasing trees
![]() $\mathcal{T}$
by the following formal recursive equation:
$\mathcal{T}$
by the following formal recursive equation:

where ![]() denotes a bucket of capacity k labelled by
denotes a bucket of capacity k labelled by
![]() $1, 2, \dots, k$
,
$1, 2, \dots, k$
,
![]() $\times$
the cartesian product,
$\times$
the cartesian product,
![]() $\ast$
the partition product for labelled objects, and
$\ast$
the partition product for labelled objects, and
![]() $\varphi(\mathcal{T})$
the substituted structure. On the other hand, we can use standard notation [Reference Flajolet and Segdewick6]. Let
$\varphi(\mathcal{T})$
the substituted structure. On the other hand, we can use standard notation [Reference Flajolet and Segdewick6]. Let
![]() $\mathcal{Z}$
denote the atomic class (i.e., a single (uni)labelled node),
$\mathcal{Z}$
denote the atomic class (i.e., a single (uni)labelled node),
![]() $\mathcal{A}^{\Box} \ast \mathcal{B}$
the boxed product (i.e., the smallest label is constrained to lie in the
$\mathcal{A}^{\Box} \ast \mathcal{B}$
the boxed product (i.e., the smallest label is constrained to lie in the
![]() $\mathcal{A}$
component) of the combinatorial classes
$\mathcal{A}$
component) of the combinatorial classes
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
. Then,
$\mathcal{B}$
. Then,
 \begin{align*} \mathcal{T} & = \psi_1\cdot \mathcal{Z}^{\Box} + \psi_2\cdot \left(\mathcal{Z}^{\Box}\right)^2+ \dots+ \psi_{b-1}\cdot \left(\mathcal{Z}^{\Box}\right)^{b-1} + \left(\mathcal{Z}^{\Box}\right)^{b}\ast \varphi(\mathcal{T})\\ & = \sum_{k=1}^{b-1}\psi_{k}\cdot \left(\mathcal{Z}^{\Box}\right)^{k} + \left(\mathcal{Z}^{\Box}\right)^{b}\ast \varphi(\mathcal{T}).\end{align*}
\begin{align*} \mathcal{T} & = \psi_1\cdot \mathcal{Z}^{\Box} + \psi_2\cdot \left(\mathcal{Z}^{\Box}\right)^2+ \dots+ \psi_{b-1}\cdot \left(\mathcal{Z}^{\Box}\right)^{b-1} + \left(\mathcal{Z}^{\Box}\right)^{b}\ast \varphi(\mathcal{T})\\ & = \sum_{k=1}^{b-1}\psi_{k}\cdot \left(\mathcal{Z}^{\Box}\right)^{k} + \left(\mathcal{Z}^{\Box}\right)^{b}\ast \varphi(\mathcal{T}).\end{align*}
Here the meaning of
![]() $(\mathcal{Z}^{\Box})^{k} \ast \mathcal{B}$
is
$(\mathcal{Z}^{\Box})^{k} \ast \mathcal{B}$
is
![]() $\mathcal{Z}^{\Box} \ast \big(\mathcal{Z}^{\Box} \ast \big(\cdots \ast \big(\mathcal{Z}^{\Box} \ast \mathcal{B}\big)\big)\big)$
, with k occurrences of
$\mathcal{Z}^{\Box} \ast \big(\mathcal{Z}^{\Box} \ast \big(\cdots \ast \big(\mathcal{Z}^{\Box} \ast \mathcal{B}\big)\big)\big)$
, with k occurrences of
![]() $\mathcal{Z}^{\Box}$
.
$\mathcal{Z}^{\Box}$
.
Using above formal description, one can show that the exponential generating function
![]() $T(z) \,:\!=\, \sum_{n \ge 1} T_{n} \frac{z^{n}}{n!}$
of the total weights
$T(z) \,:\!=\, \sum_{n \ge 1} T_{n} \frac{z^{n}}{n!}$
of the total weights
![]() $T_{n}$
is characterised by the following result of [Reference Kuba and Panholzer13].
$T_{n}$
is characterised by the following result of [Reference Kuba and Panholzer13].
Proposition 6. The exponential generating function T(z) of bucket increasing trees with degree-weight generating function
![]() $\varphi(t)$
satisfies an ordinary differential equation of order b:
$\varphi(t)$
satisfies an ordinary differential equation of order b:
with initial conditions
Example 7 (Bucket size one – ordinary increasing trees). In the case of bucket size
![]() $b=1$
we obtain ordinary increasing trees. We have a simple description using the boxed product:
$b=1$
we obtain ordinary increasing trees. We have a simple description using the boxed product:
The exponential generating function T(z) of bucket increasing trees with degree-weight generating function
![]() $\varphi(t)$
is implicitly defined by
$\varphi(t)$
is implicitly defined by
Prominent varieties include recursive trees, binary increasing and plane-oriented recursive trees; for an overview see, e.g., [Reference Drmota5, Reference Flajolet and Segdewick6].
Example 8 (Bucket size two – bilabelled trees). Trees with bucket size
![]() $b=2$
, degree-weight generating function
$b=2$
, degree-weight generating function
![]() $\varphi(t)$
and weight
$\varphi(t)$
and weight
![]() $\psi=\psi_1\ge 0$
correspond to so-called bilabelled trees. The family
$\psi=\psi_1\ge 0$
correspond to so-called bilabelled trees. The family
![]() $\widehat{\mathcal{T}}$
can be described by the following symbolic equation:
$\widehat{\mathcal{T}}$
can be described by the following symbolic equation:
The differential equation
![]() $T''(z)=\varphi(T(z))$
can be readily translated to a first-order equation. Namely, multiplication with
$T''(z)=\varphi(T(z))$
can be readily translated to a first-order equation. Namely, multiplication with
![]() $T^{\prime}(z)$
and integration leads to the first-order differential equation
$T^{\prime}(z)$
and integration leads to the first-order differential equation
with
![]() $\Phi(x)=\int_{0}^{x} \varphi(t)dt$
. Hence,
$\Phi(x)=\int_{0}^{x} \varphi(t)dt$
. Hence,
![]() $T=T(z)$
is implicitly given via
$T=T(z)$
is implicitly given via
The special choice
![]() $\psi=0$
leads to so-called strict bilabelled increasing tree families. Here, due to the choice
$\psi=0$
leads to so-called strict bilabelled increasing tree families. Here, due to the choice
![]() $\psi=0$
, all nodes have to be saturated. Such tree families naturally give rise to hook-length formulas; see [Reference Kuba and Panholzer15] for many examples.
$\psi=0$
, all nodes have to be saturated. Such tree families naturally give rise to hook-length formulas; see [Reference Kuba and Panholzer15] for many examples.
Example 9 (Strict b labelled tree families). Families of strictly b-labelled trees have been recently studied due to their connection to hook-length formulas [Reference Kuba and Panholzer14, Reference Kuba and Panholzer15]. Here
![]() $\psi_1=\dots=\psi_{b-1}=0$
, thus only saturated nodes are allowed.
$\psi_1=\dots=\psi_{b-1}=0$
, thus only saturated nodes are allowed.
3. Combinatorial models of the tree evolution processes
3.1 Random tree models
For each class
![]() $\mathcal{T}$
of bucket increasing trees associated to a given degree-weight sequence
$\mathcal{T}$
of bucket increasing trees associated to a given degree-weight sequence
![]() $(\varphi_{k})_{k \ge 0}$
and bucket-weight sequence
$(\varphi_{k})_{k \ge 0}$
and bucket-weight sequence
![]() $\psi_{1}, \dots, \psi_{b-1}$
we define in a natural way probability models for random (ordered) bucket increasing trees
$\psi_{1}, \dots, \psi_{b-1}$
we define in a natural way probability models for random (ordered) bucket increasing trees
![]() $\mathcal{T}_n$
of size n. We assume that each increasingly labelled bucket ordered increasing tree
$\mathcal{T}_n$
of size n. We assume that each increasingly labelled bucket ordered increasing tree
![]() $\tilde{T} = \big(T,\ell(T)\big)\in\mathcal{T}_n$
of size n is chosen with a probability proportional to its weight
$\tilde{T} = \big(T,\ell(T)\big)\in\mathcal{T}_n$
of size n is chosen with a probability proportional to its weight
![]() $w(\tilde{T})$
.
$w(\tilde{T})$
.
Definition 10 (Random bucket ordered increasing trees). A probability measure on ordered bucket increasing trees
![]() $\tilde{T}\in\mathcal{T}_n$
of size n is defined by
$\tilde{T}\in\mathcal{T}_n$
of size n is defined by
 \begin{equation*} {\mathbb{P}}{^{[\mathcal{T}]}}\big(\big\{\tilde{T}\big\}\big) = \frac{w\left(\tilde{T}\right)}{T_{n}} =\frac{\displaystyle{\left(\prod_{v\in \tilde{T}\colon c(v)<b} \psi_{c(v)} \right) \cdot \left(\prod_{v\in \tilde{T}\colon c(v)=b}\varphi_{\text{deg}^{+}(v)}\right)}}{T_{n}}.\end{equation*}
\begin{equation*} {\mathbb{P}}{^{[\mathcal{T}]}}\big(\big\{\tilde{T}\big\}\big) = \frac{w\left(\tilde{T}\right)}{T_{n}} =\frac{\displaystyle{\left(\prod_{v\in \tilde{T}\colon c(v)<b} \psi_{c(v)} \right) \cdot \left(\prod_{v\in \tilde{T}\colon c(v)=b}\varphi_{\text{deg}^{+}(v)}\right)}}{T_{n}}.\end{equation*}
We speak then about random ordered bucket increasing trees of size n of the family
![]() $\mathcal{T}$
under the random tree model.
$\mathcal{T}$
under the random tree model.
From a combinatorial point of view it is often convenient to work with ordered trees. However, the trees generated by the tree evolution processes are by definition unordered. Thus, we turn our attention to unordered trees. Our basic objects are unordered bucket trees
![]() $T{^{[U]}}$
together with an increasing labelling
$T{^{[U]}}$
together with an increasing labelling
![]() $\ell\big(T{^{[U]}}\big)$
. In order to obtain a measure on unordered bucket increasing trees
$\ell\big(T{^{[U]}}\big)$
. In order to obtain a measure on unordered bucket increasing trees
![]() $\mathcal{T}{^{[U]}}$
we proceed in a standard way embedding unordered trees into ordered trees. Each unordered bucket increasing tree
$\mathcal{T}{^{[U]}}$
we proceed in a standard way embedding unordered trees into ordered trees. Each unordered bucket increasing tree
![]() $\tilde{T}{^{[U]}} =\big(T{^{[U]}},\ell\big(T{^{[U]}}\big)\big)$
corresponds to
$\tilde{T}{^{[U]}} =\big(T{^{[U]}},\ell\big(T{^{[U]}}\big)\big)$
corresponds to
different ordered bucket increasing trees. We obtain a canonical ordered representative
![]() $\tilde{T}\in\mathcal{T}$
of the unordered tree
$\tilde{T}\in\mathcal{T}$
of the unordered tree
![]() $\tilde{T}{^{[U]}}=\big(T{^{[U]}},\ell\big(T{^{[U]}}\big)\big)$
by ordering the subtrees of each node
$\tilde{T}{^{[U]}}=\big(T{^{[U]}},\ell\big(T{^{[U]}}\big)\big)$
by ordering the subtrees of each node
![]() $v\in\tilde{T}{^{[U]}}$
in an increasing left-to-right way according to the smallest labels contained in the respective subtrees taking into account the labelling
$v\in\tilde{T}{^{[U]}}$
in an increasing left-to-right way according to the smallest labels contained in the respective subtrees taking into account the labelling
![]() $\ell\big(T{^{[U]}}\big)$
. Let
$\ell\big(T{^{[U]}}\big)$
. Let
![]() $f\colon \mathcal{T}{^{[U]}}\to \mathcal{T}$
denote this injective ordering map.
$f\colon \mathcal{T}{^{[U]}}\to \mathcal{T}$
denote this injective ordering map.
Definition 11 (Random unordered bucket increasing trees). A probability measure
![]() ${\mathbb{P}}{^{[\mathcal{T}]}}$
on unordered bucket increasing trees
${\mathbb{P}}{^{[\mathcal{T}]}}$
on unordered bucket increasing trees
![]() $\tilde{T}{^{[U]}}\in\mathcal{T}{^{[U]}}_{n}$
of size n is defined by
$\tilde{T}{^{[U]}}\in\mathcal{T}{^{[U]}}_{n}$
of size n is defined by
 \begin{equation*} {\mathbb{P}}{^{[\mathcal{T}]}}\big\{\tilde{T}{^{[U]}}\big\} = \frac{(w\circ f)\left(\tilde{T}{^{[U]}}\right) \cdot \prod_{v\in T{^{[U]}}}\text{deg}^{+}(v)! }{T_{n}}.\end{equation*}
\begin{equation*} {\mathbb{P}}{^{[\mathcal{T}]}}\big\{\tilde{T}{^{[U]}}\big\} = \frac{(w\circ f)\left(\tilde{T}{^{[U]}}\right) \cdot \prod_{v\in T{^{[U]}}}\text{deg}^{+}(v)! }{T_{n}}.\end{equation*}
We speak then about random unordered bucket increasing trees of size n of the family
![]() $\mathcal{T}{^{[U]}}$
under the random tree model.
$\mathcal{T}{^{[U]}}$
under the random tree model.
Possibly different models of randomness are introduced when generating an unordered tree of size n according to one of the three tree evolution processes described before. Given an integer
![]() $j\ge 2$
and any tree
$j\ge 2$
and any tree
![]() $\tilde{T}{^{[U]}}=\big(T{^{[U]}},\ell\big(T{^{[U]}}\big)\big)$
, we denote by
$\tilde{T}{^{[U]}}=\big(T{^{[U]}},\ell\big(T{^{[U]}}\big)\big)$
, we denote by
![]() $\text{attr}(j)$
the node in
$\text{attr}(j)$
the node in
![]() $\tilde{T}{^{[U]}}$
that attracted label j, and by
$\tilde{T}{^{[U]}}$
that attracted label j, and by
![]() $\tilde{T}_{< j}{^{[U]}}$
the tree obtained from
$\tilde{T}_{< j}{^{[U]}}$
the tree obtained from
![]() $\tilde{T}{^{[U]}}$
when restricting to labels less than j. Then we define
$\tilde{T}{^{[U]}}$
when restricting to labels less than j. Then we define
![]() $\pi^{(j)}$
as the map
$\pi^{(j)}$
as the map
![]() $\pi^{(j)}\colon \tilde{T}{^{[U]}} \to [0,1]$
that gives the probability that label j will be attracted by node
$\pi^{(j)}\colon \tilde{T}{^{[U]}} \to [0,1]$
that gives the probability that label j will be attracted by node
![]() $\text{attr}(j)$
in
$\text{attr}(j)$
in
![]() $\tilde{T}_{< j}{^{[U]}}$
:
$\tilde{T}_{< j}{^{[U]}}$
:
 \[\pi^{(j)}(\tilde{T}{^{[U]}})=\begin{cases}{\mathbb{P}}\big\{j<_t \text{attr}(j) \: \big| \: \tilde{T}_{< j} {^{[U]}}\big\},\qquad |\tilde{T}{^{[U]}}|\ge j,\\[6pt]0, \qquad |\tilde{T}{^{[U]}}|<j,\end{cases}\]
\[\pi^{(j)}(\tilde{T}{^{[U]}})=\begin{cases}{\mathbb{P}}\big\{j<_t \text{attr}(j) \: \big| \: \tilde{T}_{< j} {^{[U]}}\big\},\qquad |\tilde{T}{^{[U]}}|\ge j,\\[6pt]0, \qquad |\tilde{T}{^{[U]}}|<j,\end{cases}\]
with
![]() ${\mathbb{P}}\big\{j<_t \text{attr}(j) \: \big| \: \tilde{T}_{< j}{^{[U]}}\big\}$
being determined by the tree evolution processes.
${\mathbb{P}}\big\{j<_t \text{attr}(j) \: \big| \: \tilde{T}_{< j}{^{[U]}}\big\}$
being determined by the tree evolution processes.
The point-wise product
![]() ${\mathbb{P}}^{[e]}=\prod_{j=2}^{n}\pi^{(j)}$
is then a probability measure on unordered bucket increasing trees
${\mathbb{P}}^{[e]}=\prod_{j=2}^{n}\pi^{(j)}$
is then a probability measure on unordered bucket increasing trees
![]() $\mathcal{T}_{n}{^{[U]}}$
of size n. In the following we denote with a superscript the source of randomness on
$\mathcal{T}_{n}{^{[U]}}$
of size n. In the following we denote with a superscript the source of randomness on
![]() $\mathcal{T}_n$
:
$\mathcal{T}_n$
:
![]() ${\mathbb{P}}{^{[\mathcal{T}]}}$
for the random tree model and
${\mathbb{P}}{^{[\mathcal{T}]}}$
for the random tree model and
![]() ${\mathbb{P}}{^{[e]}}$
for the tree evolution process. It holds
${\mathbb{P}}{^{[e]}}$
for the tree evolution process. It holds
 \[{\mathbb{P}}{^{[e]}}\left\{\tilde{T}{^{[U]}}\right\}=\prod_{j=2}^{n}\pi^{(j)}\left(\tilde{T}{^{[U]}}\right).\]
\[{\mathbb{P}}{^{[e]}}\left\{\tilde{T}{^{[U]}}\right\}=\prod_{j=2}^{n}\pi^{(j)}\left(\tilde{T}{^{[U]}}\right).\]
Let
![]() $\text{deg}^{+}_{< j}(v)$
be the out-degree of node v when restricting to labels less than j. Then, a probability measure on ordered trees is obtained via
$\text{deg}^{+}_{< j}(v)$
be the out-degree of node v when restricting to labels less than j. Then, a probability measure on ordered trees is obtained via
 \[{\mathbb{P}}{^{[e]}}\{\tilde{T}\}=\prod_{j=2}^{n}\frac{\pi^{(j)}\left(\tilde{T}{^{[U]}}\right)}{\text{deg}^{+}_{< j}(\text{attr}(j))}.\]
\[{\mathbb{P}}{^{[e]}}\{\tilde{T}\}=\prod_{j=2}^{n}\frac{\pi^{(j)}\left(\tilde{T}{^{[U]}}\right)}{\text{deg}^{+}_{< j}(\text{attr}(j))}.\]
3.2 Combinatorial models
It was already proven in [Reference Kuba and Panholzer13] that bucket recursive trees generated according to the growth process as stated in Subsection 2.1 can be considered as a certain bucket increasing tree family. In the following we extend this result, where, for the sake of completeness, we also collect the findings of [Reference Kuba and Panholzer13] for bucket recursive trees.
Theorem 12 (Combinatorial models for families generated by a stochastic growth rule). The tree evolution processes that generate families of random unordered bucket recursive trees, (b,d)-ary increasing trees and
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees, with bucket size
$(\mathrm{b},\alpha)$
-plane oriented recursive trees, with bucket size
![]() $b\ge 1$
, can be realised combinatorially by suitably chosen sequences of degree-weights
$b\ge 1$
, can be realised combinatorially by suitably chosen sequences of degree-weights
![]() $(\varphi_{k})_{k\ge 0}$
and bucket weights
$(\varphi_{k})_{k\ge 0}$
and bucket weights
![]() $\psi_{1}, \dots, \psi_{b-1}$
. Given an arbitrary ordered bucket increasing tree
$\psi_{1}, \dots, \psi_{b-1}$
. Given an arbitrary ordered bucket increasing tree
![]() $T\in\mathcal{T}$
of size
$T\in\mathcal{T}$
of size
![]() $|T| = n$
, then it holds that under the random tree model the probability that a new element
$|T| = n$
, then it holds that under the random tree model the probability that a new element
![]() $n + 1$
is attracted by a node
$n + 1$
is attracted by a node
![]() $v \in T$
with capacity
$v \in T$
with capacity
![]() $c(v) = k$
is given by
$c(v) = k$
is given by
![]() $p(v)={\mathbb{P}}\{n+1<_t v\mid c(v)=k\}$
as defined in Definitions 1-3 for the corresponding tree evolution process.
$p(v)={\mathbb{P}}\{n+1<_t v\mid c(v)=k\}$
as defined in Definitions 1-3 for the corresponding tree evolution process.
Consequently, both models of randomness for (un)ordered trees coincide:
![]() ${\mathbb{P}}{^{[e]}}={\mathbb{P}}{^{[\mathcal{T}]}}$
.
${\mathbb{P}}{^{[e]}}={\mathbb{P}}{^{[\mathcal{T}]}}$
.
-
1. Bucket recursive trees: a combinatorial model can be obtained from the sequences
such that \begin{equation*} \varphi_{k} = \frac{(b-1)! b^{k}}{k!}, \quad \text{for} \enspace k \ge 0, \qquad \psi_{k} = (k-1)!, \quad \text{for} \enspace 1 \le k \le b-1,\end{equation*}
\begin{equation*} \varphi_{k} = \frac{(b-1)! b^{k}}{k!}, \quad \text{for} \enspace k \ge 0, \qquad \psi_{k} = (k-1)!, \quad \text{for} \enspace 1 \le k \le b-1,\end{equation*}
 $\varphi(t)=\sum_{k\ge 0}\varphi_k t^k=(b-1)! \cdot \exp(b t)$
. For this model of bucket recursive trees the exponential generating function T(z) and the total weights
$\varphi(t)=\sum_{k\ge 0}\varphi_k t^k=(b-1)! \cdot \exp(b t)$
. For this model of bucket recursive trees the exponential generating function T(z) and the total weights
 $T_n$
are given by
$T_n$
are given by  \begin{equation*}T(z)=\log\left(\frac{1}{1-z}\right),\quad T_n=(n-1)!.\end{equation*}
\begin{equation*}T(z)=\log\left(\frac{1}{1-z}\right),\quad T_n=(n-1)!.\end{equation*}
-
2. (b,d)-ary increasing trees: a combinatorial model can be obtained from the sequences
such that \begin{equation*}\begin{split} \varphi_{k} &= (b-1)!(d-1)^{b-1}\binom{b-1+\frac{1}{d-1}}{b-1}\binom{b(d-1)+1}{k}, \quad \text{for} \enspace k \ge 0,\\ \psi_{k} &= (k-1)!(d-1)^{k-1}\binom{k-1+\frac{1}{d-1}}{k-1}, \quad \text{for} \enspace 1 \le k \le b-1,\end{split}\end{equation*}
\begin{equation*}\begin{split} \varphi_{k} &= (b-1)!(d-1)^{b-1}\binom{b-1+\frac{1}{d-1}}{b-1}\binom{b(d-1)+1}{k}, \quad \text{for} \enspace k \ge 0,\\ \psi_{k} &= (k-1)!(d-1)^{k-1}\binom{k-1+\frac{1}{d-1}}{k-1}, \quad \text{for} \enspace 1 \le k \le b-1,\end{split}\end{equation*}
 $\varphi(t)= (b-1)!(d-1)^{b-1}\binom{b-1+\frac{1}{d-1}}{b-1}(1+t)^{b(d-1)+1}$
. For this model of (b,d)-ary increasing trees the exponential generating function T(z) and the total weights
$\varphi(t)= (b-1)!(d-1)^{b-1}\binom{b-1+\frac{1}{d-1}}{b-1}(1+t)^{b(d-1)+1}$
. For this model of (b,d)-ary increasing trees the exponential generating function T(z) and the total weights
 $T_n=[z^n]T(z)$
are given by
$T_n=[z^n]T(z)$
are given by \begin{equation*} T(z)=\frac{1}{(1-(d-1)z)^{\frac1{d-1}}}-1,\quad T_n=(n-1)!(d-1)^{n-1}\binom{n-1+\frac{1}{d-1}}{n-1}.\end{equation*}
\begin{equation*} T(z)=\frac{1}{(1-(d-1)z)^{\frac1{d-1}}}-1,\quad T_n=(n-1)!(d-1)^{n-1}\binom{n-1+\frac{1}{d-1}}{n-1}.\end{equation*}
-
3.
 $(\mathrm{b},\alpha)$
-plane oriented recursive trees: a combinatorial model can be obtained from the sequences such that
$(\mathrm{b},\alpha)$
-plane oriented recursive trees: a combinatorial model can be obtained from the sequences such that \begin{equation*}\begin{split} \varphi_{k} &=(b-1)!(\alpha+1)^{b-1}\binom{b-1-\frac{1}{\alpha+1}}{b-1}\binom{(\alpha+1)b-2+k}{k}, \quad \text{for} \enspace k \ge 0,\\ \psi_{k} &= (k-1)!(\alpha+1)^{k-1}\binom{k-1-\frac{1}{\alpha+1}}{k-1}, \quad \text{for} \enspace 1 \le k \le b-1,\end{split}\end{equation*}
\begin{equation*}\begin{split} \varphi_{k} &=(b-1)!(\alpha+1)^{b-1}\binom{b-1-\frac{1}{\alpha+1}}{b-1}\binom{(\alpha+1)b-2+k}{k}, \quad \text{for} \enspace k \ge 0,\\ \psi_{k} &= (k-1)!(\alpha+1)^{k-1}\binom{k-1-\frac{1}{\alpha+1}}{k-1}, \quad \text{for} \enspace 1 \le k \le b-1,\end{split}\end{equation*}
 $\varphi(t)=\frac{(b-1)!(\alpha+1)^{b-1}\binom{b-1-\frac{1}{\alpha+1}}{b-1}}{(1-t)^{(\alpha+1)b-1}}$
. For this model of
$\varphi(t)=\frac{(b-1)!(\alpha+1)^{b-1}\binom{b-1-\frac{1}{\alpha+1}}{b-1}}{(1-t)^{(\alpha+1)b-1}}$
. For this model of
 $(\mathrm{b},\alpha)$
-plane oriented recursive trees the exponential generating function T(z) and the total weights
$(\mathrm{b},\alpha)$
-plane oriented recursive trees the exponential generating function T(z) and the total weights
 $T_n=[z^n]T(z)$
are given by
$T_n=[z^n]T(z)$
are given by  \begin{equation*}T(z)=1-(1-(\alpha+1)z)^{\frac1{\alpha+1}},\quad T_n=(n-1)!(\alpha+1)^{n-1}\binom{n-1-\frac{1}{\alpha+1}}{n-1}.\end{equation*}
\begin{equation*}T(z)=1-(1-(\alpha+1)z)^{\frac1{\alpha+1}},\quad T_n=(n-1)!(\alpha+1)^{n-1}\binom{n-1-\frac{1}{\alpha+1}}{n-1}.\end{equation*}
Proof. To prove that these choices of sequences
![]() $(\varphi_k)_{k\in{\mathbb{N}}}$
and
$(\varphi_k)_{k\in{\mathbb{N}}}$
and
![]() $(\psi_k)_{1\le k\le b-1}$
are actually models for bucket increasing trees generated according to the stochastic growth rules defined in Subsection 2.1, we have to show that the combinatorial families
$(\psi_k)_{1\le k\le b-1}$
are actually models for bucket increasing trees generated according to the stochastic growth rules defined in Subsection 2.1, we have to show that the combinatorial families
![]() $\mathcal{T}$
of bucket increasing trees have the same stochastic growth rules as the counterparts created probabilistically. Given an arbitrary bucket increasing tree
$\mathcal{T}$
of bucket increasing trees have the same stochastic growth rules as the counterparts created probabilistically. Given an arbitrary bucket increasing tree
![]() $T \in \mathcal{T}$
of size
$T \in \mathcal{T}$
of size
![]() $|T|=n$
, then the probability that a new element
$|T|=n$
, then the probability that a new element
![]() $n+1$
is attracted by a node
$n+1$
is attracted by a node
![]() $v \in T$
with capacity
$v \in T$
with capacity
![]() $c(v)=k$
has to coincide with the corresponding probability stated in Definitions 1–3.
$c(v)=k$
has to coincide with the corresponding probability stated in Definitions 1–3.
We use now the notation
![]() $T \to T'$
to denote that
$T \to T'$
to denote that
![]() $ T^{\prime}$
is obtained from T with
$ T^{\prime}$
is obtained from T with
![]() $|T|=n$
by incorporating element
$|T|=n$
by incorporating element
![]() $n+1$
, i.e., either by attaching element
$n+1$
, i.e., either by attaching element
![]() $n+1$
to a saturated node
$n+1$
to a saturated node
![]() $v \in T$
at one of the
$v \in T$
at one of the
![]() $\text{deg}^{+}(v)+1$
possible positions (recall that bucket increasing trees are per definition ordered trees and thus the order of the subtrees is of relevance) by creating a new bucket of capacity 1 containing element
$\text{deg}^{+}(v)+1$
possible positions (recall that bucket increasing trees are per definition ordered trees and thus the order of the subtrees is of relevance) by creating a new bucket of capacity 1 containing element
![]() $n+1$
or by adding element
$n+1$
or by adding element
![]() $n+1$
to an unsaturated node
$n+1$
to an unsaturated node
![]() $v \in T$
by increasing the capacity of v by 1. If we want to express that node
$v \in T$
by increasing the capacity of v by 1. If we want to express that node
![]() $v \in T$
has attracted the element
$v \in T$
has attracted the element
![]() $n+1$
leading from T to
$n+1$
leading from T to
![]() $ T^{\prime}$
we use the notation
$ T^{\prime}$
we use the notation
![]() $T \xrightarrow{v} T'$
. If there exists a stochastic growth rule for a bucket increasing tree family
$T \xrightarrow{v} T'$
. If there exists a stochastic growth rule for a bucket increasing tree family
![]() $\mathcal{T}$
, then it must hold that for a given tree
$\mathcal{T}$
, then it must hold that for a given tree
![]() $T \in \mathcal{T}$
of size
$T \in \mathcal{T}$
of size
![]() $|T|=n$
and a given node
$|T|=n$
and a given node
![]() $v \in T$
the probability
$v \in T$
the probability
![]() $p_{T}(v)$
, which gives the probability that element
$p_{T}(v)$
, which gives the probability that element
![]() $n+1$
is attracted by node
$n+1$
is attracted by node
![]() $v \in T$
, is given as follows:
$v \in T$
, is given as follows:
 \begin{equation} p_{T}(v) = \frac{\sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} w(T')}{\sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} w(\tilde{T})} = \frac{\sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} \frac{w\left(T'\right)}{w(T)}}{\sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)}}.\end{equation}
\begin{equation} p_{T}(v) = \frac{\sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} w(T')}{\sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} w(\tilde{T})} = \frac{\sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} \frac{w\left(T'\right)}{w(T)}}{\sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)}}.\end{equation}
The remaining task is to simplify the expression above into the form stated in Definitions 1–3. For a certain tree
![]() $\tilde{T}$
with
$\tilde{T}$
with
![]() $T \xrightarrow{u} \tilde{T}$
and
$T \xrightarrow{u} \tilde{T}$
and
![]() $u \in T$
the quotient of the weight of the trees
$u \in T$
the quotient of the weight of the trees
![]() $\tilde{T}$
and T is due to the definition of bucket increasing trees given as follows, where we define for simplicity
$\tilde{T}$
and T is due to the definition of bucket increasing trees given as follows, where we define for simplicity
![]() $\psi_{b} \,:\!=\, \varphi_{0}$
:
$\psi_{b} \,:\!=\, \varphi_{0}$
:
 \begin{equation*} \frac{w(\tilde{T})}{w(T)} = \begin{cases} \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}}, & \quad \text{for} \enspace c(u)=b \quad \text{and} \quad \text{deg}^{+}(u)=k, \\[5pt] \frac{\psi_{k+1}}{\psi_{k}}, & \quad \text{for} \enspace c(u)=k < b. \end{cases}\end{equation*}
\begin{equation*} \frac{w(\tilde{T})}{w(T)} = \begin{cases} \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}}, & \quad \text{for} \enspace c(u)=b \quad \text{and} \quad \text{deg}^{+}(u)=k, \\[5pt] \frac{\psi_{k+1}}{\psi_{k}}, & \quad \text{for} \enspace c(u)=k < b. \end{cases}\end{equation*}
For a given tree
![]() $T \in \mathcal{T}$
we define by
$T \in \mathcal{T}$
we define by
![]() $m_{k} \,:\!=\, |\{u \in T : c(u)=k<b\}|$
the number of unsaturated nodes of T with capacity
$m_{k} \,:\!=\, |\{u \in T : c(u)=k<b\}|$
the number of unsaturated nodes of T with capacity
![]() $k<b$
and by
$k<b$
and by
![]() $n_{k} \,:\!=\, |\{u \in T : c(u)=b \enspace \text{and} \enspace \text{deg}^{+}(u)=k\}|$
the number of saturated nodes of T with out-degree
$n_{k} \,:\!=\, |\{u \in T : c(u)=b \enspace \text{and} \enspace \text{deg}^{+}(u)=k\}|$
the number of saturated nodes of T with out-degree
![]() $k \ge 0$
. It holds then
$k \ge 0$
. It holds then
 \begin{equation} n = \sum_{u \in T} c(u) = \sum_{k=1}^{b-1} k m_{k} + b \sum_{k \ge 0} n_{k}\end{equation}
\begin{equation} n = \sum_{u \in T} c(u) = \sum_{k=1}^{b-1} k m_{k} + b \sum_{k \ge 0} n_{k}\end{equation}
and (where we use that there are
![]() $k+1$
possibilities of attaching a new node to a saturated node
$k+1$
possibilities of attaching a new node to a saturated node
![]() $u \in T$
with out-degree
$u \in T$
with out-degree
![]() $\text{deg}^{+}(u)=k$
):
$\text{deg}^{+}(u)=k$
):
 \begin{equation*} \sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)} = \sum_{k=1}^{b-1} m_{k} \frac{\psi_{k+1}}{\psi_{k}} + \sum_{k \ge 0} n_{k} (k+1) \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}}.\end{equation*}
\begin{equation*} \sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)} = \sum_{k=1}^{b-1} m_{k} \frac{\psi_{k+1}}{\psi_{k}} + \sum_{k \ge 0} n_{k} (k+1) \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}}.\end{equation*}
Moreover, we also have the relation
 \begin{equation} 1 = \sum_{k=1}^{b-1} m_{k} - \sum_{k \ge 0} (k-1)n_{k},\end{equation}
\begin{equation} 1 = \sum_{k=1}^{b-1} m_{k} - \sum_{k \ge 0} (k-1)n_{k},\end{equation}
which follows as the difference between the node-sum and edge-sum equation for the tree T:
 \begin{equation*}\text{$\#$ nodes} = \sum_{k=1}^{b-1} m_{k} + \sum_{k \ge 0} n_{k}, \qquad \text{$\#$ edges} = \text{$\#$ nodes} - 1 = \sum_{k \ge 0} k n_{k}.\end{equation*}
\begin{equation*}\text{$\#$ nodes} = \sum_{k=1}^{b-1} m_{k} + \sum_{k \ge 0} n_{k}, \qquad \text{$\#$ edges} = \text{$\#$ nodes} - 1 = \sum_{k \ge 0} k n_{k}.\end{equation*}
First we turn our attention to the family of (b,d)-ary increasing trees and the weights as given in Theorem 12. We have
 \begin{equation*} \sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} \frac{w(T')}{w(T)} = \begin{cases} (k+1) \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}} = b(d-1)+1-k, & \quad \text{for} \enspace c(v)=b \quad \text{and} \quad \text{deg}^+(v)=k, \\[12pt] \frac{\psi_{k+1}}{\psi_{k}} = k(d-1)+1, & \quad \text{for} \enspace c(v)=k < b, \end{cases}\end{equation*}
\begin{equation*} \sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} \frac{w(T')}{w(T)} = \begin{cases} (k+1) \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}} = b(d-1)+1-k, & \quad \text{for} \enspace c(v)=b \quad \text{and} \quad \text{deg}^+(v)=k, \\[12pt] \frac{\psi_{k+1}}{\psi_{k}} = k(d-1)+1, & \quad \text{for} \enspace c(v)=k < b, \end{cases}\end{equation*}
and consequently
 \begin{equation*}\begin{split} \sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)} &= \sum_{k=1}^{b-1} (k(d-1)+1) m_{k} + \sum_{k \ge 0} n_{k} (b(d-1)+1-k)\\ &= (d-1)\left(\sum_{k=1}^{b-1} k m_{k} + b \sum_{k \ge 0} n_{k}\right) + \sum_{k=1}^{b-1} m_{k} - \sum_{k \ge 0} (k-1)n_{k} =(d-1)n+1,\end{split}\end{equation*}
\begin{equation*}\begin{split} \sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)} &= \sum_{k=1}^{b-1} (k(d-1)+1) m_{k} + \sum_{k \ge 0} n_{k} (b(d-1)+1-k)\\ &= (d-1)\left(\sum_{k=1}^{b-1} k m_{k} + b \sum_{k \ge 0} n_{k}\right) + \sum_{k=1}^{b-1} m_{k} - \sum_{k \ge 0} (k-1)n_{k} =(d-1)n+1,\end{split}\end{equation*}
due to equations (7) and (8). Thus, with this choice of weight sequences
![]() $(\varphi_k)_k$
and
$(\varphi_k)_k$
and
![]() $(\psi_k)_k$
, the probability
$(\psi_k)_k$
, the probability
![]() $p_{T}(v)$
that in a bucket increasing tree T of size
$p_{T}(v)$
that in a bucket increasing tree T of size
![]() $|T|=n$
the node v with capacity
$|T|=n$
the node v with capacity
![]() $c(v)=k$
attracts element
$c(v)=k$
attracts element
![]() $n+1$
coincides with the corresponding probability of the stochastic growth rule for (b,d)-ary increasing trees given in Definition 2.
$n+1$
coincides with the corresponding probability of the stochastic growth rule for (b,d)-ary increasing trees given in Definition 2.
We obtain then from equation (2) that the exponential generating function
![]() $T(z)\,:\!=\,\sum_{n\ge 1}T_n\frac{z^{n}}{n!}$
of the total-weight
$T(z)\,:\!=\,\sum_{n\ge 1}T_n\frac{z^{n}}{n!}$
of the total-weight
![]() $T_{n}$
of bucket increasing trees of size n satisfies the differential equation
$T_{n}$
of bucket increasing trees of size n satisfies the differential equation
with initial conditions
![]() $T(0)=0$
and
$T(0)=0$
and
![]() $\left.\frac{d^k}{dz^k}T(z)\right|_{z=0}\!=(k-1)!(d-1)^{k-1}\binom{k-1+\frac{1}{d-1}}{k-1}$
, for
$\left.\frac{d^k}{dz^k}T(z)\right|_{z=0}\!=(k-1)!(d-1)^{k-1}\binom{k-1+\frac{1}{d-1}}{k-1}$
, for
![]() $1\le k \le b-1$
. The solution of this equation is given by
$1\le k \le b-1$
. The solution of this equation is given by
 \begin{equation} T(z)=\frac{1}{(1-(d-1)z)^{\frac1{d-1}}}-1=\sum_{n\ge 1}(n-1)!(d-1)^{n-1}\binom{n-1+\frac{1}{d-1}}{n-1} \frac{z^{n}}{n!},\end{equation}
\begin{equation} T(z)=\frac{1}{(1-(d-1)z)^{\frac1{d-1}}}-1=\sum_{n\ge 1}(n-1)!(d-1)^{n-1}\binom{n-1+\frac{1}{d-1}}{n-1} \frac{z^{n}}{n!},\end{equation}
as can be checked easily Hence the total weight of all size n (b,d)-ary increasing trees is given by
![]() $T_n=(n-1)!(d-1)^{n-1}\binom{n-1+\frac{1}{d-1}}{n-1}$
as stated in Theorem 12.
$T_n=(n-1)!(d-1)^{n-1}\binom{n-1+\frac{1}{d-1}}{n-1}$
as stated in Theorem 12.
For
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees and weights as given in Theorem 12 we obtain
$(\mathrm{b},\alpha)$
-plane oriented recursive trees and weights as given in Theorem 12 we obtain
 \begin{equation*} \sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} \frac{w(T')}{w(T)} = \begin{cases} (k+1) \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}} = (\alpha+1)b-1+k, & \quad \text{for} \enspace c(v)=b \quad \text{and} \quad \text{deg}^+(v)=k, \\ \frac{\psi_{k+1}}{\psi_{k}} = k(\alpha+1)-1, & \quad \text{for} \enspace c(v)=k < b, \end{cases}\end{equation*}
\begin{equation*} \sum_{T' \in \mathcal{T} : T \xrightarrow{v} T'} \frac{w(T')}{w(T)} = \begin{cases} (k+1) \psi_{1} \frac{\varphi_{k+1}}{\varphi_{k}} = (\alpha+1)b-1+k, & \quad \text{for} \enspace c(v)=b \quad \text{and} \quad \text{deg}^+(v)=k, \\ \frac{\psi_{k+1}}{\psi_{k}} = k(\alpha+1)-1, & \quad \text{for} \enspace c(v)=k < b, \end{cases}\end{equation*}
and consequently
 \begin{equation*}\begin{split} \sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)} &= \sum_{k=1}^{b-1} (k(\alpha+1)-1) m_{k} + \sum_{k \ge 0} n_{k} ((\alpha+1)b-1+k)\\ &= (\alpha+1)\left(\sum_{k=1}^{b-1} k m_{k} + b \sum_{k \ge 0} n_{k}\right) - \left(\sum_{k=1}^{b-1} m_{k} - \sum_{k \ge 0} (k-1)n_{k}\right) =(\alpha+1)n-1,\end{split}\end{equation*}
\begin{equation*}\begin{split} \sum_{\tilde{T} \in \mathcal{T} : T \to \tilde{T}} \frac{w(\tilde{T})}{w(T)} &= \sum_{k=1}^{b-1} (k(\alpha+1)-1) m_{k} + \sum_{k \ge 0} n_{k} ((\alpha+1)b-1+k)\\ &= (\alpha+1)\left(\sum_{k=1}^{b-1} k m_{k} + b \sum_{k \ge 0} n_{k}\right) - \left(\sum_{k=1}^{b-1} m_{k} - \sum_{k \ge 0} (k-1)n_{k}\right) =(\alpha+1)n-1,\end{split}\end{equation*}
due to equations (7) and (8). Again, with this choice of weight sequences
![]() $(\varphi_k)_k$
and
$(\varphi_k)_k$
and
![]() $(\psi_k)_k$
, it follows that the probability
$(\psi_k)_k$
, it follows that the probability
![]() $p_{T}(v)$
that in a bucket increasing tree T of size
$p_{T}(v)$
that in a bucket increasing tree T of size
![]() $|T|=n$
the node v with capacity
$|T|=n$
the node v with capacity
![]() $c(v)=k$
attracts element
$c(v)=k$
attracts element
![]() $n+1$
coincides with the corresponding probability in the stochastic growth rule for
$n+1$
coincides with the corresponding probability in the stochastic growth rule for
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees given in Definition 3.
$(\mathrm{b},\alpha)$
-plane oriented recursive trees given in Definition 3.
We obtain then from equation (2) that the exponential generating function
![]() $T(z)\,:\!=\,\sum_{n\ge 1}T_n\frac{z^{n}}{n!}$
of the total-weight
$T(z)\,:\!=\,\sum_{n\ge 1}T_n\frac{z^{n}}{n!}$
of the total-weight
![]() $T_{n}$
of
$T_{n}$
of
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees of size n satisfies the differential equation
$(\mathrm{b},\alpha)$
-plane oriented recursive trees of size n satisfies the differential equation
with initial conditions
![]() $T(0)=0$
and
$T(0)=0$
and
![]() $\left.\frac{d^k}{dz^k}T(z)\right|_{z=0}\!\!=(k-1)!(\alpha+1)^{k-1}\binom{k-1-\frac{1}{\alpha+1}}{k-1}$
, for
$\left.\frac{d^k}{dz^k}T(z)\right|_{z=0}\!\!=(k-1)!(\alpha+1)^{k-1}\binom{k-1-\frac{1}{\alpha+1}}{k-1}$
, for
![]() $1\le k \le b-1$
. Again it can be checked easily that the solution of this equation is given by
$1\le k \le b-1$
. Again it can be checked easily that the solution of this equation is given by
 \begin{equation} T(z)=(1-(\alpha+1)z)^{\frac1{\alpha+1}}-1=\sum_{n\ge 1}(n-1)!(\alpha+1)^{n-1}\binom{n-1-\frac{1}{\alpha+1}}{n-1} \frac{z^{n}}{n!}.\end{equation}
\begin{equation} T(z)=(1-(\alpha+1)z)^{\frac1{\alpha+1}}-1=\sum_{n\ge 1}(n-1)!(\alpha+1)^{n-1}\binom{n-1-\frac{1}{\alpha+1}}{n-1} \frac{z^{n}}{n!}.\end{equation}
Hence the total weight of all size n
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees is given by
$(\mathrm{b},\alpha)$
-plane oriented recursive trees is given by
![]() $T_n=(n-1)!(\alpha+1)^{n-1}\binom{n-1-\frac{1}{\alpha+1}}{n-1}$
, which finishes the proof of Theorem 12
$T_n=(n-1)!(\alpha+1)^{n-1}\binom{n-1-\frac{1}{\alpha+1}}{n-1}$
, which finishes the proof of Theorem 12
In Tables 1–2 we summarise the combinatorial properties as well as the growth processes of the bucket increasing tree families considered in this work.
Table 1 Summary: bucket increasing tree families and their growth processes

Table 2 Summary: bucket increasing tree families and their combinatorial properties

4. Clustering process and weight sequences
Up to this point, no indication has been given how to find the weight sequences in Theorem 12. Similarly, we did not give any motivation behind the definition of the growth processes. Here, as Algorithm 1 we will present a clustering map for ordinary increasing trees, case
![]() $b=1$
. It leads directly to the stated weight sequences and serves as a motivation behind the definition of the growth processes and weight sequences.
$b=1$
. It leads directly to the stated weight sequences and serves as a motivation behind the definition of the growth processes and weight sequences.

Let
![]() $\mathcal{T}^{[b]}$
denote the family of ordered bucket increasing trees with maximal bucket size b, such that
$\mathcal{T}^{[b]}$
denote the family of ordered bucket increasing trees with maximal bucket size b, such that
![]() $\mathcal{T}^{[1]}$
denotes the family of ordinary ordered increasing trees. Algorithm 1, which defines a map
$\mathcal{T}^{[1]}$
denotes the family of ordinary ordered increasing trees. Algorithm 1, which defines a map
![]() $\mathcal{C}\colon \mathcal{T}^{[1]}\to\mathcal{T}^{[b]}$
, is given as follows; furthermore it is illustrated in Figure 1.
$\mathcal{C}\colon \mathcal{T}^{[1]}\to\mathcal{T}^{[b]}$
, is given as follows; furthermore it is illustrated in Figure 1.

Figure 1. A plane-oriented recursive tree T of size eleven, the clustered tree with
![]() $b=2$
and the corresponding bilabelled increasing ordered tree
$b=2$
and the corresponding bilabelled increasing ordered tree
![]() $\tilde{T}=\mathcal{C}(T)$
.
$\tilde{T}=\mathcal{C}(T)$
.
Proposition 13. The map
![]() $\mathcal{C}\colon \mathcal{T}^{[1]}\to\mathcal{T}^{[b]}$
defined in Algorithm 1 is not injective, but surjective.
$\mathcal{C}\colon \mathcal{T}^{[1]}\to\mathcal{T}^{[b]}$
defined in Algorithm 1 is not injective, but surjective.
Remark 14. Note that for arbitrary increasing tree families the map
![]() $\mathcal{C}$
does neither take into account the weight sequence
$\mathcal{C}$
does neither take into account the weight sequence
![]() $(\phi_k)_{k\ge 0}$
of
$(\phi_k)_{k\ge 0}$
of
![]() $\mathcal{T}^{[1]}$
, nor it determines
$\mathcal{T}^{[1]}$
, nor it determines
![]() $(\varphi_k)_{k\ge 0}$
and
$(\varphi_k)_{k\ge 0}$
and
![]() $(\psi_k)_{1\le k\le b-1}$
of
$(\psi_k)_{1\le k\le b-1}$
of
![]() $\mathcal{T}^{[b]}$
. We will see later, see Examples 16 and 17, that the map can be modified to obtain bijections between ordinary increasing trees and specific families of bucket increasing trees.
$\mathcal{T}^{[b]}$
. We will see later, see Examples 16 and 17, that the map can be modified to obtain bijections between ordinary increasing trees and specific families of bucket increasing trees.
Proof. Apparently, all trees
![]() $T\in\mathcal{T}^{[1]}$
of size k,
$T\in\mathcal{T}^{[1]}$
of size k,
![]() $1\le k\le b$
, are mapped to a tree
$1\le k\le b$
, are mapped to a tree
![]() $\mathcal{C}(T)$
consisting only of a single bucket v of capacity
$\mathcal{C}(T)$
consisting only of a single bucket v of capacity
![]() $c(v)=k$
, thus the map is not injective, except for degenerate choices of the weight sequence. However, the map
$c(v)=k$
, thus the map is not injective, except for degenerate choices of the weight sequence. However, the map
![]() $\mathcal{C}$
is surjective: every size n bucket increasing tree can be created by clustering an ordinary increasing tree. Given a bucket increasing tree
$\mathcal{C}$
is surjective: every size n bucket increasing tree can be created by clustering an ordinary increasing tree. Given a bucket increasing tree
![]() $\tilde{T}\in\mathcal{T}^{[b]}$
, we can replace all buckets by corresponding increasing chains, holding the corresponding labels. This gives an ordinary ordered increasing tree
$\tilde{T}\in\mathcal{T}^{[b]}$
, we can replace all buckets by corresponding increasing chains, holding the corresponding labels. This gives an ordinary ordered increasing tree
![]() $T\in\mathcal{T}^{[1]}$
with
$T\in\mathcal{T}^{[1]}$
with
![]() $\mathcal{C}(T)=\tilde{T}$
.
$\mathcal{C}(T)=\tilde{T}$
.
Given a family of ordinary increasing trees
![]() $\mathcal{T}^{[1]}$
with weights
$\mathcal{T}^{[1]}$
with weights
![]() $(\phi_k)_{k\ge 0}$
, we are interest in the resulting clustered tree families and its properties. Since we can freely choose the weight sequences
$(\phi_k)_{k\ge 0}$
, we are interest in the resulting clustered tree families and its properties. Since we can freely choose the weight sequences
![]() $(\varphi_k)_{k\ge 0}$
and
$(\varphi_k)_{k\ge 0}$
and
![]() $(\psi_k)_{1\le k\le b-1}$
of the associated bucket increasing families, we choose them in a weight preserving way, depending on the given weights
$(\psi_k)_{1\le k\le b-1}$
of the associated bucket increasing families, we choose them in a weight preserving way, depending on the given weights
![]() $(\phi_k)_{k\ge 0}$
.
$(\phi_k)_{k\ge 0}$
.
Definition 15 (Weight preserving bucket trees). Given a family of ordinary increasing trees
![]() $\mathcal{T}^{[1]}$
with weights
$\mathcal{T}^{[1]}$
with weights
![]() $(\phi_k)_{k\ge 0}$
. We call a family
$(\phi_k)_{k\ge 0}$
. We call a family
![]() $\mathcal{T}^{[b]}$
of bucket increasing trees with weights
$\mathcal{T}^{[b]}$
of bucket increasing trees with weights
![]() $(\varphi_k)_{k\ge 0}$
and
$(\varphi_k)_{k\ge 0}$
and
![]() $(\psi_k)_{1\le k\le b-1}$
weight preserving, if it holds, for all
$(\psi_k)_{1\le k\le b-1}$
weight preserving, if it holds, for all
![]() $\tilde{T}\in\mathcal{T}_n$
,
$\tilde{T}\in\mathcal{T}_n$
,
Given
![]() $(\phi_k)_{k\ge 0}$
, the total weights
$(\phi_k)_{k\ge 0}$
, the total weights
![]() $T_n$
of the bucket increasing trees, with weight preserving
$T_n$
of the bucket increasing trees, with weight preserving
![]() $(\varphi_k)_{k\ge 0}$
and
$(\varphi_k)_{k\ge 0}$
and
![]() $(\psi_k)_{1\le k\le b-1}$
, equals the weight
$(\psi_k)_{1\le k\le b-1}$
, equals the weight
![]() $T_n$
of their ordinary increasing trees counterpart:
$T_n$
of their ordinary increasing trees counterpart:
Moreover, we directly obtain from (13)
where
![]() $T_k$
denotes the total weight of size k trees of the ordinary increasing tree family.
$T_k$
denotes the total weight of size k trees of the ordinary increasing tree family.
Next, we consider star-shaped trees
![]() $\tilde{T}$
of size
$\tilde{T}$
of size
![]() $b+k$
and root degree k. We get
$b+k$
and root degree k. We get
On the other hand, we can describe all trees
![]() $T\in \mathcal{T}^{[1]}$
satisfying
$T\in \mathcal{T}^{[1]}$
satisfying
![]() $\mathcal{C}(T)=\tilde{T}$
. Namely, all such trees can be created by taking an arbitrary tree of size b and attaching k new nodes labelled
$\mathcal{C}(T)=\tilde{T}$
. Namely, all such trees can be created by taking an arbitrary tree of size b and attaching k new nodes labelled
![]() $k+1,\dots,k+b$
to any of the existing b nodes. We denote by
$k+1,\dots,k+b$
to any of the existing b nodes. We denote by
![]() $v_1,\dots,v_b$
the nodes labelled
$v_1,\dots,v_b$
the nodes labelled
![]() $1,\dots, b$
in T, by
$1,\dots, b$
in T, by
![]() $\text{deg}^{+}_{\le b}(v_{m})$
the out-degree of node
$\text{deg}^{+}_{\le b}(v_{m})$
the out-degree of node
![]() $v_{m}$
when restricting to labels
$v_{m}$
when restricting to labels
![]() $\le b$
, and by
$\le b$
, and by
![]() $j_{m}$
the number of nodes with labels
$j_{m}$
the number of nodes with labels
![]() $> b$
attached to
$> b$
attached to
![]() $v_{m}$
. This gives
$v_{m}$
. This gives
 \[\sum_{T\in \mathcal{T}^{[1]}\colon \mathcal{C}(T)=\tilde{T}}w(T)=\phi_0^k\sum_{T\in \mathcal{T}^{[1]}\colon |T|=b}w(T)\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}\frac{\phi_{\text{deg}^{+}_{\le b}(v_m)+j_m}}{\phi_{\text{deg}^{+}_{\le b}(v_m)}}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m}{j_m}.\]
\[\sum_{T\in \mathcal{T}^{[1]}\colon \mathcal{C}(T)=\tilde{T}}w(T)=\phi_0^k\sum_{T\in \mathcal{T}^{[1]}\colon |T|=b}w(T)\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}\frac{\phi_{\text{deg}^{+}_{\le b}(v_m)+j_m}}{\phi_{\text{deg}^{+}_{\le b}(v_m)}}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m}{j_m}.\]
We use
![]() $\psi_1=\phi_0=T_1$
and obtain for
$\psi_1=\phi_0=T_1$
and obtain for
![]() $\varphi_k$
the expression
$\varphi_k$
the expression
 \begin{equation}\varphi_k=\sum_{T\in \mathcal{T}^{[1]}\colon |T|=b}w(T)\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}\frac{\phi_{\text{deg}^{+}_{\le b}(v_m)+j_m}}{\phi_{\text{deg}^{+}_{\le b}(v_m)}}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m}{j_m}.\end{equation}
\begin{equation}\varphi_k=\sum_{T\in \mathcal{T}^{[1]}\colon |T|=b}w(T)\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}\frac{\phi_{\text{deg}^{+}_{\le b}(v_m)+j_m}}{\phi_{\text{deg}^{+}_{\le b}(v_m)}}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m}{j_m}.\end{equation}
As mentioned earlier, it has been shown in [Reference Panholzer and Prodinger21] that only three families of increasing trees can be constructed using a stochastic growth process. These are ordinary recursive trees, generalised plane-oriented recursive trees and d-ary increasing trees, and they are determined by the degree-weight sequences
![]() $\phi_k=\frac1{k!}$
,
$\phi_k=\frac1{k!}$
,
![]() $\phi_k=\binom{k+\alpha-1}{k}$
and
$\phi_k=\binom{k+\alpha-1}{k}$
and
![]() $\phi_k=\binom{d}{k}$
,
$\phi_k=\binom{d}{k}$
,
![]() $k\ge 0$
, respectively. The three weight sequences
$k\ge 0$
, respectively. The three weight sequences
![]() $(\phi_k)_{k\ge 0}$
together with (14) directly lead to the result of Theorem 12. Below we present the calculations for
$(\phi_k)_{k\ge 0}$
together with (14) directly lead to the result of Theorem 12. Below we present the calculations for
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees derived from generalised plane-oriented recursive trees with
$(\mathrm{b},\alpha)$
-plane oriented recursive trees derived from generalised plane-oriented recursive trees with
![]() $\phi_k=\binom{k+\alpha-1}{k}$
. Using
$\phi_k=\binom{k+\alpha-1}{k}$
. Using
 \[\frac{\phi_{\text{deg}^{+}_{\le b}(v_m)+j_m}}{\phi_{\text{deg}^{+}_{\le b}(v_m)}}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m}{j_m}=\binom{\text{deg}^{+}_{\le b}(v_m)+j_m+\alpha-1}{j_{m}}\]
\[\frac{\phi_{\text{deg}^{+}_{\le b}(v_m)+j_m}}{\phi_{\text{deg}^{+}_{\le b}(v_m)}}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m}{j_m}=\binom{\text{deg}^{+}_{\le b}(v_m)+j_m+\alpha-1}{j_{m}}\]
and
 \begin{align*}&\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m+\alpha-1}{j_m}=\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}[t^{j_m}]\frac{1}{(1-t)^{\text{deg}^{+}_{\le b}(v_m)+\alpha}}\\&\quad=[t^{k}]\frac{1}{(1-t)^{b-1+b\alpha}}=\binom{b+b\alpha+k-2}{k},\end{align*}
\begin{align*}&\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}\binom{\text{deg}^{+}_{\le b}(v_m)+j_m+\alpha-1}{j_m}=\sum_{\substack{\sum_{s=1}^{b}j_s=k,\\j_s\ge 0}}\prod_{m=1}^{b}[t^{j_m}]\frac{1}{(1-t)^{\text{deg}^{+}_{\le b}(v_m)+\alpha}}\\&\quad=[t^{k}]\frac{1}{(1-t)^{b-1+b\alpha}}=\binom{b+b\alpha+k-2}{k},\end{align*}
we get indeed the result stated in Theorem 12:
Example 16 (Bijection between PORTs and three-bundled bilabelled bucket ordered increasing trees). Following the terminology of [Reference Janson, Kuba and Panholzer8], we call an ordered (bucket) increasing tree d-bundled, if every node has d positions, with a (possibly empty) sequence of d-bundled trees (with disjoint sets of labels) attached to each position. Equivalently, one may think of each node of the ordered tree as having
![]() $d-1$
separation walls, which can be regarded as a special type of edges or half-edges, that separate the subtrees of each node into d bundles. t is known that d-bundled increasing trees correspond to ordinary ordered increasing trees with degree-weight generating function
$d-1$
separation walls, which can be regarded as a special type of edges or half-edges, that separate the subtrees of each node into d bundles. t is known that d-bundled increasing trees correspond to ordinary ordered increasing trees with degree-weight generating function
![]() $\varphi(t)=1/(1-t)^{d}$
; analogous the family
$\varphi(t)=1/(1-t)^{d}$
; analogous the family
![]() $\mathcal{B}_{d}$
of d-bundled bucket increasing trees corresponds to the family of bucket ordered increasing trees with
$\mathcal{B}_{d}$
of d-bundled bucket increasing trees corresponds to the family of bucket ordered increasing trees with
![]() $\varphi(t) = 1/(1-t)^{d}$
.
$\varphi(t) = 1/(1-t)^{d}$
.
Given an ordinary plane-oriented recursive tree with degree-weight generating function
![]() $\phi(t)=1/(1-t)$
, we modify the clustering map
$\phi(t)=1/(1-t)$
, we modify the clustering map
![]() $\mathcal{C}$
defined in Algorithm 1 to a map
$\mathcal{C}$
defined in Algorithm 1 to a map
![]() $\mathcal{C}^{\ast}$
, such that the corresponding bilabelled bucket ordered increasing tree is three-bundled: when redirecting edges to the buckets, we keep track of their previous ancestor. Given a resulting bucket
$\mathcal{C}^{\ast}$
, such that the corresponding bilabelled bucket ordered increasing tree is three-bundled: when redirecting edges to the buckets, we keep track of their previous ancestor. Given a resulting bucket
![]() $v=(\ell_{\min},\ell_{\max})$
, edges originally incident to the node with smaller label
$v=(\ell_{\min},\ell_{\max})$
, edges originally incident to the node with smaller label
![]() $\ell_{\min}$
that are lying to the left of the node with larger label
$\ell_{\min}$
that are lying to the left of the node with larger label
![]() $\ell_{\max}$
are grouped into the first bundle, whereas edges incident to
$\ell_{\max}$
are grouped into the first bundle, whereas edges incident to
![]() $\ell_{\min}$
lying to the right of
$\ell_{\min}$
lying to the right of
![]() $\ell_{\max}$
are grouped into the third bundle. All edges incident to the node with larger label
$\ell_{\max}$
are grouped into the third bundle. All edges incident to the node with larger label
![]() $\ell_{\max}$
are put into the second bundle, the centre.
$\ell_{\max}$
are put into the second bundle, the centre.
Then, the map
![]() $\mathcal{C}_\ast\colon\mathcal{T}^{[1]}\to\mathcal{B}_3$
, with bucket size
$\mathcal{C}_\ast\colon\mathcal{T}^{[1]}\to\mathcal{B}_3$
, with bucket size
![]() $b=2$
of bucket three-bundled ordered increasing trees, is a bijection. This bijection is illustrated in Figure 2.
$b=2$
of bucket three-bundled ordered increasing trees, is a bijection. This bijection is illustrated in Figure 2.

Figure 2. The plane-oriented recursive tree T of size eleven from Figure 1, the corresponding clustered tree with
![]() $b=2$
, and the corresponding bilabelled 3-bundled increasing ordered tree
$b=2$
, and the corresponding bilabelled 3-bundled increasing ordered tree
![]() $\tilde{T}=\mathcal{C}^{\ast}(T)$
.
$\tilde{T}=\mathcal{C}^{\ast}(T)$
.
Example 17 (Bijection between recursive trees and two-bundled bilabelled bucket recursive trees). We introduce two-bundled bucket recursive trees
![]() $\mathcal{BR}_2$
with bucket size two. Each saturated node has an half-edge that separates its subtrees into two bundles. The tree family corresponds to the degree-weight generating function
$\mathcal{BR}_2$
with bucket size two. Each saturated node has an half-edge that separates its subtrees into two bundles. The tree family corresponds to the degree-weight generating function
![]() $\varphi(t)=\exp(2t)$
and
$\varphi(t)=\exp(2t)$
and
![]() $\psi_1=1$
. Then, we modify the clustering map
$\psi_1=1$
. Then, we modify the clustering map
![]() $\mathcal{C}$
again to a map
$\mathcal{C}$
again to a map
![]() $\hat{\mathcal{C}}$
, such that the corresponding bilabelled bucket recursive tree is two-bundled: when redirecting edges to the buckets, we keep track of their previous ancestor. Given a resulting bucket
$\hat{\mathcal{C}}$
, such that the corresponding bilabelled bucket recursive tree is two-bundled: when redirecting edges to the buckets, we keep track of their previous ancestor. Given a resulting bucket
![]() $v=(\ell_{\min},\ell_{\max})$
, all edges originally incident to the smaller label
$v=(\ell_{\min},\ell_{\max})$
, all edges originally incident to the smaller label
![]() $\ell_{\min}$
are grouped into the first bundle, whereas all edges incident to the larger label
$\ell_{\min}$
are grouped into the first bundle, whereas all edges incident to the larger label
![]() $\ell_{\max}$
are put into the second bundle.
$\ell_{\max}$
are put into the second bundle.
Then, the map
![]() $\hat{\mathcal{C}}\colon \mathcal{R} \to \mathcal{BR}_2$
from ordinary recursive trees to two-bundled bilabelled bucket recursive trees is a bijection.
$\hat{\mathcal{C}}\colon \mathcal{R} \to \mathcal{BR}_2$
from ordinary recursive trees to two-bundled bilabelled bucket recursive trees is a bijection.
Similar bijections for bucket size
![]() $b=2$
can be obtained also for binary increasing trees and variants.
$b=2$
can be obtained also for binary increasing trees and variants.
5. Increasing diamonds and bucket increasing trees
5.1 Symbolic description and bijections
We consider trees with bucket size
![]() $b=2$
, degree-weight generating function
$b=2$
, degree-weight generating function
![]() $\varphi(t)$
and weight
$\varphi(t)$
and weight
![]() $\psi = \psi_{1} = 1$
. As stated in Example 8 they allow the symbolic description
$\psi = \psi_{1} = 1$
. As stated in Example 8 they allow the symbolic description
The exponential generating function T(z) satisfies the first-order differential equation
with
![]() $\Phi(x)=\int_{0}^{x} \varphi(t)dt$
. Moreover,
$\Phi(x)=\int_{0}^{x} \varphi(t)dt$
. Moreover,
![]() $T=T(z)$
is implicitly given via
$T=T(z)$
is implicitly given via
On the other hand, increasing diamonds as proposed in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4] are defined by the symbolic equation
where the latter boxed product constrains the largest label. They constitute a combinatorial family of labelled, directed acyclic graphs (DAGs) with a source and a sink such that the labels along any path are increasing. The functional operation
![]() $\varphi$
occurring in (17) is here specifying possible degrees respectively their weights, see [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4] for more details. Figure 3 illustrates two examples of increasing diamonds.
$\varphi$
occurring in (17) is here specifying possible degrees respectively their weights, see [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4] for more details. Figure 3 illustrates two examples of increasing diamonds.

Figure 3. Two different increasing diamonds of size nine and fourteen, respectively.
The symbolic description (17) of increasing diamonds leads to exactly the same exponential generating function as for bucket increasing trees with bucket size
![]() $b=2$
described formally via (16). Thus, it is natural to ask for a bijection between these combinatorial objects of a given size, where the size of an increasing diamond is given by the number of its nodes.
$b=2$
described formally via (16). Thus, it is natural to ask for a bijection between these combinatorial objects of a given size, where the size of an increasing diamond is given by the number of its nodes.
Before stating such a bijection we note that it is convenient to think of an increasing diamond
![]() $F\in\mathcal{F}$
as having three types of nodes stemming from the recursive combinatorial construction given in (17), which partitions the set of nodes into small nodes, inner nodes and large nodes, i.e.,
$F\in\mathcal{F}$
as having three types of nodes stemming from the recursive combinatorial construction given in (17), which partitions the set of nodes into small nodes, inner nodes and large nodes, i.e.,
Namely, if F has size one its only vertex is assigned to an inner node. Otherwise, the smallest node and the largest node of F are assigned to the respective node type; furthermore by removing these two nodes of F we obtain a (possibly empty) sequence of increasing diamonds
![]() $F_{1}, \dots, F_{r}$
, and to each of these structures we apply this assignment recursively.
$F_{1}, \dots, F_{r}$
, and to each of these structures we apply this assignment recursively.
Theorem 18. The family of ordered increasing diamonds
![]() $\mathcal{F}_n$
of size n, with degree-weight generating function
$\mathcal{F}_n$
of size n, with degree-weight generating function
![]() $\varphi(t)$
, are in a natural bijection
$\varphi(t)$
, are in a natural bijection
![]() $\mathcal{M}$
with ordered bucket increasing trees
$\mathcal{M}$
with ordered bucket increasing trees
![]() $\mathcal{T}_n$
of size n with the same degree-weight generating function,
$\mathcal{T}_n$
of size n with the same degree-weight generating function,
![]() $\mathcal{F}_n\cong \mathcal{T}_n$
.
$\mathcal{F}_n\cong \mathcal{T}_n$
.
The bijection
![]() $\mathcal{M}$
together with the characterisation given in Theorem 12 provides a characterisation of families
$\mathcal{M}$
together with the characterisation given in Theorem 12 provides a characterisation of families
![]() $\mathcal{F}$
of increasing diamonds with a total weight
$\mathcal{F}$
of increasing diamonds with a total weight
![]() $T_n$
, resembling the weights of ordinary increasing trees and thus leading to simple counting formulas. In particular, this explains the strikingly simple formula observed in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4], which we collect in the next statement.
$T_n$
, resembling the weights of ordinary increasing trees and thus leading to simple counting formulas. In particular, this explains the strikingly simple formula observed in [Reference Bodini, Dien, Fontaine, Genitrini and Hwang4], which we collect in the next statement.
Corollary 19. The number
![]() $T_n$
of increasing diamonds of size n with degree-weight generating function
$T_n$
of increasing diamonds of size n with degree-weight generating function
![]() $\varphi(t)=1/(1-t)^{3}$
equals the number of plane-oriented recursive trees of size n. It is given by the simple formula
$\varphi(t)=1/(1-t)^{3}$
equals the number of plane-oriented recursive trees of size n. It is given by the simple formula
Proof of Corollary 19. By bijection
![]() $\mathcal{M}$
in Theorem 18 increasing diamonds
$\mathcal{M}$
in Theorem 18 increasing diamonds
![]() $\mathcal{F}$
with degree-weight generating function
$\mathcal{F}$
with degree-weight generating function
![]() $\varphi(t)=1/(1-t)^{3}$
are mapped to three-bundled bilabelled bucket ordered increasing trees
$\varphi(t)=1/(1-t)^{3}$
are mapped to three-bundled bilabelled bucket ordered increasing trees
![]() $\mathcal{B}_3$
with the same degree-weight generating function. Furthermore, the refined clustering map
$\mathcal{B}_3$
with the same degree-weight generating function. Furthermore, the refined clustering map
![]() $\mathcal{C}_\ast$
maps the family
$\mathcal{C}_\ast$
maps the family
![]() $\mathcal{B}_3$
bijectively to a family of ordinary increasing trees
$\mathcal{B}_3$
bijectively to a family of ordinary increasing trees
![]() $\mathcal{T}^{[1]}$
, called plane-oriented recursive trees, with degree-weight generating function
$\mathcal{T}^{[1]}$
, called plane-oriented recursive trees, with degree-weight generating function
![]() $\phi(t)=1/(1-t)$
. Symbolically, we have
$\phi(t)=1/(1-t)$
. Symbolically, we have
The number of plane-oriented recursive trees of size n is well known [Reference Bergeron, Flajolet and Salvy3, Reference Drmota5, Reference Flajolet and Segdewick6, Reference Prodinger23, Reference Prodinger24] and obtained from the the classical generating function of the total numbers
![]() $T(z)=1-\sqrt{1-2z}$
, satisfying
$T(z)=1-\sqrt{1-2z}$
, satisfying
Extraction of coefficients gives
Proof. Our bijection
![]() $\mathcal{M} : \mathcal{F}_{n} \to \mathcal{T}_{n}$
uses two steps: first we construct recursively intermediate objects that we call increasing-decreasing bilabelled trees, where each bucket holds the smallest as well as the largest label in its subtree. Thus, when considering a tree
$\mathcal{M} : \mathcal{F}_{n} \to \mathcal{T}_{n}$
uses two steps: first we construct recursively intermediate objects that we call increasing-decreasing bilabelled trees, where each bucket holds the smallest as well as the largest label in its subtree. Thus, when considering a tree
![]() $\hat{T} \in \mathcal{ID}$
of this family and restricting to the smaller or larger labels in each bucket, it is an increasing or decreasing tree, respectively. Then we give a recursive procedure that transforms, by using cyclic permutations of the labels, such trees to bucket increasing trees of the same shape. These recursive procedures are given as Algorithms 3–4; combining them leads to Algorithm 2 and thus the map
$\hat{T} \in \mathcal{ID}$
of this family and restricting to the smaller or larger labels in each bucket, it is an increasing or decreasing tree, respectively. Then we give a recursive procedure that transforms, by using cyclic permutations of the labels, such trees to bucket increasing trees of the same shape. These recursive procedures are given as Algorithms 3–4; combining them leads to Algorithm 2 and thus the map
![]() $\mathcal{M}$
. We further observe that the weight sequence
$\mathcal{M}$
. We further observe that the weight sequence
![]() $(\varphi_k)_{k\ge 0}$
is not involved in the bijection, as the weights are directly preserved: if a certain substructure of an increasing diamonds F decomposes into the node with smallest label, the node with largest label and
$(\varphi_k)_{k\ge 0}$
is not involved in the bijection, as the weights are directly preserved: if a certain substructure of an increasing diamonds F decomposes into the node with smallest label, the node with largest label and
![]() $r \ge 0$
increasing subdiamonds, then the corresponding subtree in the bucket increasing tree
$r \ge 0$
increasing subdiamonds, then the corresponding subtree in the bucket increasing tree
![]() $\tilde{T} = \mathcal{M}(F)$
decomposes into the root bucket and exactly r subtrees. We also note that the reverse map
$\tilde{T} = \mathcal{M}(F)$
decomposes into the root bucket and exactly r subtrees. We also note that the reverse map
![]() $\mathcal{M}^{-1}$
is readily obtained by inverting the recursive procedures in a natural way.
$\mathcal{M}^{-1}$
is readily obtained by inverting the recursive procedures in a natural way.



The bijection
![]() $\mathcal{M}$
is illustrated in Figures 4–5 for the increasing diamonds given in Figure 3.
$\mathcal{M}$
is illustrated in Figures 4–5 for the increasing diamonds given in Figure 3.

Figure 4. The increasing diamond of size nine from Figure 2 with three different label types is mapped to an increasing-decreasing bilabelled tree and then to a bucket increasing tree.

Figure 5. The increasing diamond from Figure 2 of size 14 with three different label types is mapped to an increasing-decreasing bilabelled tree and then to a bucket increasing tree.
The map also gives a correspondence between quantities in increasing diamonds and bucket increasing trees. Let
![]() $I_{n}$
denote the random variable counting the number of inner nodes in a random increasing diamond of size n. Moreover, let
$I_{n}$
denote the random variable counting the number of inner nodes in a random increasing diamond of size n. Moreover, let
![]() $N_n$
denote the number of nodes with capacity one in a random bucket increasing tree of size n. Then we get the following corollary.
$N_n$
denote the number of nodes with capacity one in a random bucket increasing tree of size n. Then we get the following corollary.
Corollary 20. Under the bijection
![]() $\mathcal{M}$
given in Theorem 18 the number of inner nodes in an increasing diamond F coincides with the number of nodes of capacity one in the corresponding bucket increasing tree
$\mathcal{M}$
given in Theorem 18 the number of inner nodes in an increasing diamond F coincides with the number of nodes of capacity one in the corresponding bucket increasing tree
![]() $\mathcal{M}(F)$
. Consequently, the r.v.
$\mathcal{M}(F)$
. Consequently, the r.v.
![]() $I_{n}$
and
$I_{n}$
and
![]() $N_{n}$
are equal in distribution,
$N_{n}$
are equal in distribution,
![]() $I_{n} \stackrel{(d)}{=} N_{n}$
.
$I_{n} \stackrel{(d)}{=} N_{n}$
.
We note that a refined enumeration of increasing diamonds according to the number of inner nodes is possible in a rather direct way. Let
 \[f(z,u)=\sum_{n\ge 1}\sum_{j=1}^{n}\frac{T_{n,j}}{n!}z^n u^j=\sum_{n\ge 1}\frac{T_n\cdot {\mathbb{E}}\left(u^{I_n}\right)}{n!}z^n\]
\[f(z,u)=\sum_{n\ge 1}\sum_{j=1}^{n}\frac{T_{n,j}}{n!}z^n u^j=\sum_{n\ge 1}\frac{T_n\cdot {\mathbb{E}}\left(u^{I_n}\right)}{n!}z^n\]
denote the refined generating function with
![]() $f(z,1)=T(z)$
.
$f(z,1)=T(z)$
.
Then from the symbolic equation (17) and the resulting differential equation for f(z,u) one gets that
![]() $f=f(z,u)$
is characterised implicitly via
$f=f(z,u)$
is characterised implicitly via
Many interesting concrete generating functions and examples can be obtained by specialising
![]() $\varphi(t)$
; the authors are currently investigating into this matter.
$\varphi(t)$
; the authors are currently investigating into this matter.
6. Initial bucket size of a specified element
We consider now the random variable
![]() $K_{n}$
, which denotes the size of the bucket containing element n in a random bucket increasing tree (with maximal bucket size b) of size n. Note that by definition
$K_{n}$
, which denotes the size of the bucket containing element n in a random bucket increasing tree (with maximal bucket size b) of size n. Note that by definition
![]() $1\le K_{n} \le b$
. As it will turn out later, the precise analysis of
$1\le K_{n} \le b$
. As it will turn out later, the precise analysis of
![]() $K_n$
is required in order to obtain distributional decompositions for two further r.v. of interest, the number of descendants
$K_n$
is required in order to obtain distributional decompositions for two further r.v. of interest, the number of descendants
![]() $Y_{n,j}$
of label j as well as the out-degree
$Y_{n,j}$
of label j as well as the out-degree
![]() $X_{n,j}$
node j. We derive the probability mass function of
$X_{n,j}$
node j. We derive the probability mass function of
![]() $K_n$
using a generating function approach. Then, we relate the parameter
$K_n$
using a generating function approach. Then, we relate the parameter
![]() $K_n$
to the distribution of node types in bucket increasing trees.
$K_n$
to the distribution of node types in bucket increasing trees.
6.1. The generating functions approach
In order to study
![]() $K_{n}$
for bucket increasing trees we introduce the bivariate generating function
$K_{n}$
for bucket increasing trees we introduce the bivariate generating function
To establish a functional equation for N(z,v) from the formal recursive equation (1) it is now convenient to think of specifically bicoloured bucket increasing trees, where the colouring is as follows: exactly one element, namely the element with largest label, is coloured red, and all elements having a label smaller than the red element are coloured black. Let us first assume that the red element of T is not contained in the root node. Then the red element is located in one of the r subtrees of the root of T; let us assume that it is in the j-th subtree. Let us now consider these r subtrees. After order preserving relabellings, each subtree
![]() $S_{1}, \dots, S_{r}$
is an bucket increasing tree by itself, where one of the r subtrees contains the red element. Note the obvious fact that the size of the bucket of the red element is the same in T and in the respective subtree
$S_{1}, \dots, S_{r}$
is an bucket increasing tree by itself, where one of the r subtrees contains the red element. Note the obvious fact that the size of the bucket of the red element is the same in T and in the respective subtree
![]() $S_{j}$
.
$S_{j}$
.
We introduce now generating functions, with exponential variable z, where z marks the black elements,
![]() $f(z) = \sum_{n \ge 0} f_{n} \frac{z^n}{n! }$
for sequences
$f(z) = \sum_{n \ge 0} f_{n} \frac{z^n}{n! }$
for sequences
![]() $f_{n}$
and
$f_{n}$
and
![]() $f(z,v)=\sum_{n,m \ge 0} f_{n,m} \frac{z^n }{n!}v^m$
for sequences
$f(z,v)=\sum_{n,m \ge 0} f_{n,m} \frac{z^n }{n!}v^m$
for sequences
![]() $f_{n,m}$
, where v counts the initial bucket size of the red element. With this setting, the total weight of all suitably bicoloured bucket increasing trees, where the initial bucket size of the red element is exactly m, is given by
$f_{n,m}$
, where v counts the initial bucket size of the red element. With this setting, the total weight of all suitably bicoloured bucket increasing trees, where the initial bucket size of the red element is exactly m, is given by
![]() ${\mathbb{P}}\{K_{n+1} = m\} T_{n+1}$
, and thus its generating function is given by
${\mathbb{P}}\{K_{n+1} = m\} T_{n+1}$
, and thus its generating function is given by
whereas the total weight of suitably monocoloured ordinary bucket increasing trees is
![]() $T_{n}$
and its generating function is given by
$T_{n}$
and its generating function is given by
The
![]() $r-1$
monocoloured trees and the bicoloured bucket tree lead then to the expression
$r-1$
monocoloured trees and the bicoloured bucket tree lead then to the expression
![]() $T(z)^{r-1} \cdot N(z,v)$
. Since the red element can be in the first, second,
$T(z)^{r-1} \cdot N(z,v)$
. Since the red element can be in the first, second,
![]() $\dots$
, r-th subtree, we additionally get a factor r. Furthermore, the event that the root has out-degree r leads to a factor
$\dots$
, r-th subtree, we additionally get a factor r. Furthermore, the event that the root has out-degree r leads to a factor
![]() $\varphi_r$
. Summing over all
$\varphi_r$
. Summing over all
![]() $r \ge 1$
leads thus to
$r \ge 1$
leads thus to
![]() $\sum_{r\ge 1} r \varphi_r T(z)^{r-1} N(z,v) =\varphi'(T(z)) N(z,v).$
Since the elements labelled by
$\sum_{r\ge 1} r \varphi_r T(z)^{r-1} N(z,v) =\varphi'(T(z)) N(z,v).$
Since the elements labelled by
![]() $1, 2, \dots, b$
contained in the root node are all coloured black (which again means that b elements in a labelled object are fixed), equation (1) leads thus to the following differential equation of order b for N(z,v):
$1, 2, \dots, b$
contained in the root node are all coloured black (which again means that b elements in a labelled object are fixed), equation (1) leads thus to the following differential equation of order b for N(z,v):
The cases, where the red element is contained in the root of the tree do not appear explicitly in the differential equation itself, but will be described by the initial conditions. Since
![]() $\mathbb{P}\{K_{n}=n\}=1$
, for
$\mathbb{P}\{K_{n}=n\}=1$
, for
![]() $1 \le n \le b$
(if element n is contained in the root node then all elements with a label
$1 \le n \le b$
(if element n is contained in the root node then all elements with a label
![]() $\le n$
are also contained in the root node), we obtain the following initial conditions, for
$\le n$
are also contained in the root node), we obtain the following initial conditions, for
![]() $0 \le \ell \le b-1$
:
$0 \le \ell \le b-1$
:
 \begin{align*} \left.\frac{\partial^{\ell}}{\partial z^{\ell}} N(z,v)\right|_{z=0} & = \sum_{m \ge 0} \mathbb{P}\{K_{\ell+1}=m\} T_{\ell+1} v^{m}=T_{\ell+1} v^{\ell+1}, \end{align*}
\begin{align*} \left.\frac{\partial^{\ell}}{\partial z^{\ell}} N(z,v)\right|_{z=0} & = \sum_{m \ge 0} \mathbb{P}\{K_{\ell+1}=m\} T_{\ell+1} v^{m}=T_{\ell+1} v^{\ell+1}, \end{align*}
with
![]() $T_{n} = n! [z^{n}] T(z)$
and T(z) as characterised in Proposition 12 for the particular tree families.
$T_{n} = n! [z^{n}] T(z)$
and T(z) as characterised in Proposition 12 for the particular tree families.
Now we can specify the sequences according to the tree family of interest. Note that for bucket recursive trees the initial bucket size of node n was already (implicitly) characterised in [Reference Kuba and Panholzer13], hence we will skip this case. For (b,d)-ary increasing trees we obtain the following Cauchy-Euler type differential equation together with the initial conditions for the bivariate generating function N(z,v):
For
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees we obtain a very similar Cauchy-Euler type differential equation together with the initial conditions for the bivariate generating function N(z,v):
$(\mathrm{b},\alpha)$
-plane oriented recursive trees we obtain a very similar Cauchy-Euler type differential equation together with the initial conditions for the bivariate generating function N(z,v):
6.2. The distribution of the initial bucket size
In order to obtain the exact distribution of the r.v.
![]() $K_{n}$
we will give the exact solution of the homogeneous differential equations (20), (21), which are of Cauchy-Euler-type. Plugging in the Ansatz
$K_{n}$
we will give the exact solution of the homogeneous differential equations (20), (21), which are of Cauchy-Euler-type. Plugging in the Ansatz
![]() $N(z,v) = \frac{1}{(1-(d-1)z)^{\lambda}}$
for (b,d)-ary increasing trees, and
$N(z,v) = \frac{1}{(1-(d-1)z)^{\lambda}}$
for (b,d)-ary increasing trees, and
![]() $N(z,v) = \frac{1}{(1-(\alpha+1)z)^{\lambda}}$
for
$N(z,v) = \frac{1}{(1-(\alpha+1)z)^{\lambda}}$
for
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees, with unspecified
$(\mathrm{b},\alpha)$
-plane oriented recursive trees, with unspecified
![]() $\lambda$
, into equations (20), (21) leads to the indicial equation
$\lambda$
, into equations (20), (21) leads to the indicial equation
 \begin{equation} \lambda^{\overline{b}} = \begin{cases} \displaystyle{\frac{T_{b+1}}{(d-1)^{b}}},\\[15pt]\displaystyle{\frac{T_{b+1}}{(\alpha+1)^{b}}}, \end{cases} \quad \text{or equivalently} \quad \binom{\lambda+b-1}{b} = \begin{cases} \displaystyle{\binom{b+\frac{1}{d-1}}{b}},\quad\textrm{(b,d)}\text{-ary ITs},\\[15pt]\displaystyle{\binom{b-\frac{1}{\alpha+1}}{b}},\quad (\text{b},\alpha)\text{-PORTs}. \end{cases}\end{equation}
\begin{equation} \lambda^{\overline{b}} = \begin{cases} \displaystyle{\frac{T_{b+1}}{(d-1)^{b}}},\\[15pt]\displaystyle{\frac{T_{b+1}}{(\alpha+1)^{b}}}, \end{cases} \quad \text{or equivalently} \quad \binom{\lambda+b-1}{b} = \begin{cases} \displaystyle{\binom{b+\frac{1}{d-1}}{b}},\quad\textrm{(b,d)}\text{-ary ITs},\\[15pt]\displaystyle{\binom{b-\frac{1}{\alpha+1}}{b}},\quad (\text{b},\alpha)\text{-PORTs}. \end{cases}\end{equation}
Similar equations have been studied in [Reference Mahmoud and Smythe18] for bucket recursive trees. It is convenient to give a unified analysis of the indicial equations for all three models. Let
 \begin{equation}\quad \kappa=\begin{cases} \displaystyle{0}, & \quad \text{bucket recursive trees}, \\[5pt] \displaystyle{\frac{1}{d-1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[14pt] \displaystyle{-\frac{1}{\alpha+1}}, & \quad (\text{b},\alpha)\text{-PORTs}. \end{cases}\end{equation}
\begin{equation}\quad \kappa=\begin{cases} \displaystyle{0}, & \quad \text{bucket recursive trees}, \\[5pt] \displaystyle{\frac{1}{d-1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[14pt] \displaystyle{-\frac{1}{\alpha+1}}, & \quad (\text{b},\alpha)\text{-PORTs}. \end{cases}\end{equation}
Then, the indicial equations can be written in a unified way:
Equations of this or similar kind have been treated in [Reference Kuba and Panholzer13, Reference Kuba and Panholzer17, Reference Mahmoud and Smythe18]. It follows from these considerations that, for
![]() $\kappa$
given in (23), all solutions
$\kappa$
given in (23), all solutions
![]() $\lambda_{1}, \lambda_{2}, \dots, \lambda_{b}$
of (24) are simple, and when arranging them in descending order of real parts it further holds
$\lambda_{1}, \lambda_{2}, \dots, \lambda_{b}$
of (24) are simple, and when arranging them in descending order of real parts it further holds
![]() $1+\frac{1}{d-1}=\lambda_{1} > \Re(\lambda_{2}) \ge \Re(\lambda_{3}) \ge \cdots\ge \Re(\lambda_{b})$
for (b,d)-ary increasing trees and
$1+\frac{1}{d-1}=\lambda_{1} > \Re(\lambda_{2}) \ge \Re(\lambda_{3}) \ge \cdots\ge \Re(\lambda_{b})$
for (b,d)-ary increasing trees and
![]() $1-\frac{1}{\alpha+1}=\lambda_{1} > \Re(\lambda_{2}) \ge \Re(\lambda_{3}) \ge \cdots\ge \Re(\lambda_{b})$
for
$1-\frac{1}{\alpha+1}=\lambda_{1} > \Re(\lambda_{2}) \ge \Re(\lambda_{3}) \ge \cdots\ge \Re(\lambda_{b})$
for
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees. Thus the general solutions of (20), (21) are given by
$(\mathrm{b},\alpha)$
-plane oriented recursive trees. Thus the general solutions of (20), (21) are given by
 \begin{equation} N(z,v) = \begin{cases} \displaystyle{\sum_{i=1}^{b} \frac{\beta_{i}(v)}{(1-(d-1)z)^{\lambda_{i}}}},\quad \text{(b,d)} \text{-ary ITs},\\[15pt]\displaystyle{\sum_{i=1}^{b} \frac{\beta_{i}(v)}{(1-(\alpha+1)z)^{\lambda_{i}}}},\quad(\text{b},\alpha)\text{-PORTs}, \end{cases}\end{equation}
\begin{equation} N(z,v) = \begin{cases} \displaystyle{\sum_{i=1}^{b} \frac{\beta_{i}(v)}{(1-(d-1)z)^{\lambda_{i}}}},\quad \text{(b,d)} \text{-ary ITs},\\[15pt]\displaystyle{\sum_{i=1}^{b} \frac{\beta_{i}(v)}{(1-(\alpha+1)z)^{\lambda_{i}}}},\quad(\text{b},\alpha)\text{-PORTs}, \end{cases}\end{equation}
with certain functions
![]() $\beta_{i}(u,v)$
, which are specified by the initial conditions as given in (20), (21). When these initial conditions are plugged into (25) this leads to the following system of linear equations for the unknown functions
$\beta_{i}(u,v)$
, which are specified by the initial conditions as given in (20), (21). When these initial conditions are plugged into (25) this leads to the following system of linear equations for the unknown functions
![]() $\beta_{i}(v)$
,
$\beta_{i}(v)$
,
![]() $1 \le i \le b$
:
$1 \le i \le b$
:
 \begin{equation*} \sum_{i=1}^{b} \lambda_{i}^{\overline{\ell}} \beta_{i}(v)= \begin{cases} \displaystyle{v^{\ell+1}l!\binom{\ell+\frac{1}{d-1}}{\ell}},\quad\text{(b,d)}\text{-ary ITs},\\[15pt]\displaystyle{v^{\ell+1}l!\binom{\ell-\frac{1}{\alpha+1}}{\ell}},\quad(\text{b},\alpha)\text{-PORTs}. \end{cases}\end{equation*}
\begin{equation*} \sum_{i=1}^{b} \lambda_{i}^{\overline{\ell}} \beta_{i}(v)= \begin{cases} \displaystyle{v^{\ell+1}l!\binom{\ell+\frac{1}{d-1}}{\ell}},\quad\text{(b,d)}\text{-ary ITs},\\[15pt]\displaystyle{v^{\ell+1}l!\binom{\ell-\frac{1}{\alpha+1}}{\ell}},\quad(\text{b},\alpha)\text{-PORTs}. \end{cases}\end{equation*}
Using the abbreviations
 \begin{equation} s_{\ell} \,:\!=\, s_{\ell}(v) \,:\!=\, \begin{cases} \displaystyle{v^{\ell+1}\binom{\ell+\frac{1}{d-1}}{\ell}},\quad\text{(b,d)}\text{-ary ITs},\\[15pt]\displaystyle{v^{\ell+1}\binom{\ell-\frac{1}{\alpha+1}}{\ell}},\quad(\text{b},\alpha)\text{-PORTs}, \end{cases}\end{equation}
\begin{equation} s_{\ell} \,:\!=\, s_{\ell}(v) \,:\!=\, \begin{cases} \displaystyle{v^{\ell+1}\binom{\ell+\frac{1}{d-1}}{\ell}},\quad\text{(b,d)}\text{-ary ITs},\\[15pt]\displaystyle{v^{\ell+1}\binom{\ell-\frac{1}{\alpha+1}}{\ell}},\quad(\text{b},\alpha)\text{-PORTs}, \end{cases}\end{equation}
we obtain the following system of linear equations for the unknown
![]() $\beta_{i}=\beta_i(v)$
,
$\beta_{i}=\beta_i(v)$
,
![]() $1 \le i \le b$
:
$1 \le i \le b$
:
 \begin{equation} \sum_{i=1}^{b} \binom{\lambda_{i}+\ell-1}{\ell} \beta_{i} = s_{\ell}, \quad \text{for} \enspace 0 \le \ell \le b-1.\end{equation}
\begin{equation} \sum_{i=1}^{b} \binom{\lambda_{i}+\ell-1}{\ell} \beta_{i} = s_{\ell}, \quad \text{for} \enspace 0 \le \ell \le b-1.\end{equation}
To obtain the solution of (27) we can use results and respective computations given in [Reference Kuba and Panholzer13, equations (22) and (30)], slightly adapted to
![]() $\kappa$
occurring in the indicial equation (24) of the tree families considered.
$\kappa$
occurring in the indicial equation (24) of the tree families considered.
Lemma 21 ([Reference Kuba and Panholzer13]). For given numbers
![]() $\lambda_i$
, with
$\lambda_i$
, with
![]() $1\le i\le b$
, specified as the solutions of equation (24), and numbers
$1\le i\le b$
, specified as the solutions of equation (24), and numbers
![]() $s_{\ell}$
,
$s_{\ell}$
,
![]() $0\le \ell\le b-1$
, the system of linear equations with unknowns
$0\le \ell\le b-1$
, the system of linear equations with unknowns
![]() $\beta_i$
,
$\beta_i$
,
 \begin{equation*}\sum_{i=1}^{b} \binom{\lambda_{i}+\ell-1}{\ell-1}\beta_{i}=s_{\ell},\quad 0\le \ell\le b-1,\end{equation*}
\begin{equation*}\sum_{i=1}^{b} \binom{\lambda_{i}+\ell-1}{\ell-1}\beta_{i}=s_{\ell},\quad 0\le \ell\le b-1,\end{equation*}
has the exact solution
 \begin{equation*}\beta_i=\begin{cases}\displaystyle{\sum_{r=0}^{b-1}s_r \frac{\binom{\lambda_i+b-1}{b-r-1}}{\binom{b}{r}(b-r)\binom{b+\frac{1}{d-1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad 1\le i\le b,\quad\text{(b,d)}\text{-ary ITs},\\[22pt]\displaystyle{\sum_{r=0}^{b-1}s_r \frac{\binom{\lambda_i+b-1}{b-r-1}}{\binom{b}{r}(b-r)\binom{b-\frac{1}{\alpha+1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad 1\le i\le b,\quad(\text{b},\alpha)\text{-PORTs}.\end{cases}\end{equation*}
\begin{equation*}\beta_i=\begin{cases}\displaystyle{\sum_{r=0}^{b-1}s_r \frac{\binom{\lambda_i+b-1}{b-r-1}}{\binom{b}{r}(b-r)\binom{b+\frac{1}{d-1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad 1\le i\le b,\quad\text{(b,d)}\text{-ary ITs},\\[22pt]\displaystyle{\sum_{r=0}^{b-1}s_r \frac{\binom{\lambda_i+b-1}{b-r-1}}{\binom{b}{r}(b-r)\binom{b-\frac{1}{\alpha+1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad 1\le i\le b,\quad(\text{b},\alpha)\text{-PORTs}.\end{cases}\end{equation*}
An application of Lemma 21 immediately gives the values
![]() $\beta_i(v)$
with respect to the initial conditions (26). Thus extracting coefficients yields
$\beta_i(v)$
with respect to the initial conditions (26). Thus extracting coefficients yields
 \begin{equation*}[z^{n-1}v^m]N(z,v)={\mathbb{P}}\{K_{n}=m\}\frac{T_{n}}{(n-1)!}=\begin{cases} \displaystyle{\sum_{i=1}^{b}\binom{\lambda_i+n-2}{n-1}(d-1)^{n-1}[v^m]\beta_i(v)},\quad\text{(b,d)}\text{-ary ITs},\\[15pt] \displaystyle{\sum_{i=1}^{b}\binom{\lambda_i+n-2}{n-1}(\alpha+1)^{n-1}[v^m]\beta_i(v)},\quad(\text{b},\alpha)\text{-PORTs}, \end{cases}\end{equation*}
\begin{equation*}[z^{n-1}v^m]N(z,v)={\mathbb{P}}\{K_{n}=m\}\frac{T_{n}}{(n-1)!}=\begin{cases} \displaystyle{\sum_{i=1}^{b}\binom{\lambda_i+n-2}{n-1}(d-1)^{n-1}[v^m]\beta_i(v)},\quad\text{(b,d)}\text{-ary ITs},\\[15pt] \displaystyle{\sum_{i=1}^{b}\binom{\lambda_i+n-2}{n-1}(\alpha+1)^{n-1}[v^m]\beta_i(v)},\quad(\text{b},\alpha)\text{-PORTs}, \end{cases}\end{equation*}
and by specifying
![]() $T_{n}$
as given in Theorem 12 and
$T_{n}$
as given in Theorem 12 and
![]() $s_{\ell}(v)$
as given in (26) we obtain the exact distribution of
$s_{\ell}(v)$
as given in (26) we obtain the exact distribution of
![]() $K_{n}$
stated in the following theorem.
$K_{n}$
stated in the following theorem.
Theorem 22. The probability mass function of the random variable
![]() $K_n$
counting the initial bucket size of node n in a random bucket tree of size n is given by the following closed formula.
$K_n$
counting the initial bucket size of node n in a random bucket tree of size n is given by the following closed formula.
 \begin{equation*}{\mathbb{P}}\{K_n=m\}=\begin{cases}\displaystyle{\sum_{i=1}^{b}\frac{\binom{\lambda_i+n-2}{n-1}\binom{\lambda_i+b-1}{b-m}\binom{m-1+\frac{1}{d-1}}{m-1}}{\binom{n-1+\frac{1}{d-1}}{n-1}\binom{b}{m-1}(b-m+1)\binom{b+\frac{1}{d-1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad\text{for }\text{(b,d)}\text{-ary ITs},\\[25pt]\displaystyle{\sum_{i=1}^{b}\frac{\binom{\lambda_i+n-2}{n-1}\binom{\lambda_i+b-1}{b-m}\binom{m-1-\frac{1}{\alpha+1}}{m-1}}{\binom{n-1-\frac{1}{\alpha+1}}{n-1}\binom{b}{m-1}(b-m+1)\binom{b-\frac{1}{\alpha+1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad\text{for }(\text{b},\alpha)\text{-PORTs},\end{cases}\end{equation*}
\begin{equation*}{\mathbb{P}}\{K_n=m\}=\begin{cases}\displaystyle{\sum_{i=1}^{b}\frac{\binom{\lambda_i+n-2}{n-1}\binom{\lambda_i+b-1}{b-m}\binom{m-1+\frac{1}{d-1}}{m-1}}{\binom{n-1+\frac{1}{d-1}}{n-1}\binom{b}{m-1}(b-m+1)\binom{b+\frac{1}{d-1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad\text{for }\text{(b,d)}\text{-ary ITs},\\[25pt]\displaystyle{\sum_{i=1}^{b}\frac{\binom{\lambda_i+n-2}{n-1}\binom{\lambda_i+b-1}{b-m}\binom{m-1-\frac{1}{\alpha+1}}{m-1}}{\binom{n-1-\frac{1}{\alpha+1}}{n-1}\binom{b}{m-1}(b-m+1)\binom{b-\frac{1}{\alpha+1}}{b}\left(H_{\lambda_i+b-1}-H_{\lambda_i-1}\right)}},\quad\text{for }(\text{b},\alpha)\text{-PORTs},\end{cases}\end{equation*}
for
![]() $1\le m\le b$
.
$1\le m\le b$
.
For n tending to infinity the random variable
![]() $K_n$
converges in distribution to a limit K, whose discrete distribution is given as follows.
$K_n$
converges in distribution to a limit K, whose discrete distribution is given as follows.
 \begin{equation*}{\mathbb{P}}\{K=m\}=\begin{cases}\displaystyle{\frac{\binom{b+\frac{1}{d-1}}{b-m}\binom{m-1+\frac{1}{d-1}}{m-1}}{\binom{b}{m-1}(b-m+1)\binom{b+\frac{1}{d-1}}{b}\left(H_{b+\frac{1}{d-1}}-H_{\frac{1}{d-1}}\right)}},\quad {(b,d)}{-ary ITs},\\[25pt]\displaystyle{\frac{\binom{b-\frac{1}{\alpha-1}}{b-m}\binom{m-1-\frac{1}{\alpha+1}}{m-1}}{\binom{b}{m-1}(b-m+1)\binom{b-\frac{1}{\alpha+1}}{b}\left(H_{b-\frac{1}{\alpha+1}}-H_{-\frac{1}{\alpha+1}}\right)}},\quad({b},\alpha){-PORTs},\end{cases}\end{equation*}
\begin{equation*}{\mathbb{P}}\{K=m\}=\begin{cases}\displaystyle{\frac{\binom{b+\frac{1}{d-1}}{b-m}\binom{m-1+\frac{1}{d-1}}{m-1}}{\binom{b}{m-1}(b-m+1)\binom{b+\frac{1}{d-1}}{b}\left(H_{b+\frac{1}{d-1}}-H_{\frac{1}{d-1}}\right)}},\quad {(b,d)}{-ary ITs},\\[25pt]\displaystyle{\frac{\binom{b-\frac{1}{\alpha-1}}{b-m}\binom{m-1-\frac{1}{\alpha+1}}{m-1}}{\binom{b}{m-1}(b-m+1)\binom{b-\frac{1}{\alpha+1}}{b}\left(H_{b-\frac{1}{\alpha+1}}-H_{-\frac{1}{\alpha+1}}\right)}},\quad({b},\alpha){-PORTs},\end{cases}\end{equation*}
for
![]() $1\le m \le b$
.
$1\le m \le b$
.
Remark 23. The corresponding results for bucket recursive trees were already derived in [Reference Kuba and Panholzer13] (although not stated explicitly):
 \begin{equation*} \mathbb{P}\{K_{n}=m\} = \sum_{i=1}^{b} \frac{\binom{\lambda_{i}+b-1}{b-m} \binom{\lambda_{i}+n-2}{n-1}} {\binom{b}{m-1} (b-m+1) \left(H_{\lambda_{i}+b-1} - H_{\lambda_{i}-1}\right)},\end{equation*}
\begin{equation*} \mathbb{P}\{K_{n}=m\} = \sum_{i=1}^{b} \frac{\binom{\lambda_{i}+b-1}{b-m} \binom{\lambda_{i}+n-2}{n-1}} {\binom{b}{m-1} (b-m+1) \left(H_{\lambda_{i}+b-1} - H_{\lambda_{i}-1}\right)},\end{equation*}
for
![]() $1\le m\le b$
. Furthermore, for bucket recursive trees the random variable
$1\le m\le b$
. Furthermore, for bucket recursive trees the random variable
![]() $K_n$
converges, for
$K_n$
converges, for
![]() $n \to \infty$
, in distribution to a Zipf-distributed limit K:
$n \to \infty$
, in distribution to a Zipf-distributed limit K:
Proof. It remains to show the stated limiting distribution results. We apply Stirling’s formula for the Gamma-function
and get
 \[ \binom{n-1+\frac{1}{d-1}}{n-1}=\frac{\Gamma\left(n+\frac{1}{d-1}\right)}{\Gamma\left(1+\frac{1}{d-1}\right)\Gamma(n)}=\frac{n^{\frac{1}{d-1}}}{\Gamma\left(1+\frac{1}{d-1}\right)}\left(1+\mathcal{O}\left(n^{-1}\right)\right),\]
\[ \binom{n-1+\frac{1}{d-1}}{n-1}=\frac{\Gamma\left(n+\frac{1}{d-1}\right)}{\Gamma\left(1+\frac{1}{d-1}\right)\Gamma(n)}=\frac{n^{\frac{1}{d-1}}}{\Gamma\left(1+\frac{1}{d-1}\right)}\left(1+\mathcal{O}\left(n^{-1}\right)\right),\]
as well as
 \[ \binom{n-1-\frac{1}{\alpha+1}}{n-1}=\frac{\Gamma\left(n-\frac{1}{\alpha+1}\right)}{\Gamma\left(1-\frac{1}{\alpha+1}\right)\Gamma(n)}=\frac{n^{-\frac{1}{\alpha+1}}}{\Gamma\left(1-\frac{1}{\alpha+1}\right)}\left(1+\mathcal{O}(n^{-1})\right).\]
\[ \binom{n-1-\frac{1}{\alpha+1}}{n-1}=\frac{\Gamma\left(n-\frac{1}{\alpha+1}\right)}{\Gamma\left(1-\frac{1}{\alpha+1}\right)\Gamma(n)}=\frac{n^{-\frac{1}{\alpha+1}}}{\Gamma\left(1-\frac{1}{\alpha+1}\right)}\left(1+\mathcal{O}(n^{-1})\right).\]
Concerning the roots of the indicial equations recall from remarks stated past equation (24) that
 \[\lambda_1=\begin{cases}1+\frac{1}{d-1},\quad\text{(b,d)}\text{-ary ITs},\\[9pt]1-\frac{1}{\alpha+1},\quad(\text{b},\alpha)\text{-PORTs}.\end{cases}\]
\[\lambda_1=\begin{cases}1+\frac{1}{d-1},\quad\text{(b,d)}\text{-ary ITs},\\[9pt]1-\frac{1}{\alpha+1},\quad(\text{b},\alpha)\text{-PORTs}.\end{cases}\]
For (b,d)-ary increasing trees we obtain the following asymptotic expansions:
 \begin{align*} \binom{n-2+\lambda_{i}}{n-1} & = \frac{n^{\lambda_{i}-1}}{\Gamma(\lambda_{i})} \left(1+\mathcal{O}(n^{-1})\right) = \begin{cases} \frac{n^{\frac{1}{d-1}}}{\Gamma\left(1+\frac{1}{d-1}\right)}\left(1+\mathcal{O}(n^{-1})\right), & \quad i=1, \\[18pt] \mathcal{O}\left(n^{\Re \lambda_{i}-1}\right), & \quad 2 \le i \le b. \end{cases}\end{align*}
\begin{align*} \binom{n-2+\lambda_{i}}{n-1} & = \frac{n^{\lambda_{i}-1}}{\Gamma(\lambda_{i})} \left(1+\mathcal{O}(n^{-1})\right) = \begin{cases} \frac{n^{\frac{1}{d-1}}}{\Gamma\left(1+\frac{1}{d-1}\right)}\left(1+\mathcal{O}(n^{-1})\right), & \quad i=1, \\[18pt] \mathcal{O}\left(n^{\Re \lambda_{i}-1}\right), & \quad 2 \le i \le b. \end{cases}\end{align*}
For
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees we have the corresponding results
$(\mathrm{b},\alpha)$
-plane oriented recursive trees we have the corresponding results
 \begin{align*} \binom{n-2+\lambda_{i}}{n-1} = \begin{cases} \frac{n^{-\frac{1}{\alpha+1}}}{\Gamma\left(1-\frac{1}{\alpha+1}\right)}\left(1+\mathcal{O}(n^{-1})\right), & \quad i=1, \\[18pt] \mathcal{O}\left(n^{\Re \lambda_{i}-1}\right), & \quad 2 \le i \le b. \end{cases}\end{align*}
\begin{align*} \binom{n-2+\lambda_{i}}{n-1} = \begin{cases} \frac{n^{-\frac{1}{\alpha+1}}}{\Gamma\left(1-\frac{1}{\alpha+1}\right)}\left(1+\mathcal{O}(n^{-1})\right), & \quad i=1, \\[18pt] \mathcal{O}\left(n^{\Re \lambda_{i}-1}\right), & \quad 2 \le i \le b. \end{cases}\end{align*}
Thus, for
![]() $n\to\infty$
, the dominant contribution in the asymptotic expansions of
$n\to\infty$
, the dominant contribution in the asymptotic expansions of
![]() ${\mathbb{P}}\{K_n=m\}$
and the finite sum stems from the index
${\mathbb{P}}\{K_n=m\}$
and the finite sum stems from the index
![]() $i=1$
and
$i=1$
and
![]() $\lambda_1$
, leading to the stated result.
$\lambda_1$
, leading to the stated result.
6.3 Relation to node types in bucket increasing trees
Let
![]() $N_{n,j}$
denote the random variable counting the number of nodes with capacity
$N_{n,j}$
denote the random variable counting the number of nodes with capacity
![]() $c(v)=j$
,
$c(v)=j$
,
![]() $1\le j \le b$
. Furthermore, let
$1\le j \le b$
. Furthermore, let
![]() ${\textbf{N}}_n$
denote the random vector
${\textbf{N}}_n$
denote the random vector
![]() $(N_{n,1},\dots,N_{n,b})$
. Mahmoud and Smythe [Reference Mahmoud and Smythe18] considered bucket recursive trees. They proved a multivariate central limit theorem for
$(N_{n,1},\dots,N_{n,b})$
. Mahmoud and Smythe [Reference Mahmoud and Smythe18] considered bucket recursive trees. They proved a multivariate central limit theorem for
![]() ${\textbf{N}}_n$
for trees with bucket size
${\textbf{N}}_n$
for trees with bucket size
![]() $b \le 26$
. For trees with
$b \le 26$
. For trees with
![]() $b > 26$
a phase change in the limiting distribution of
$b > 26$
a phase change in the limiting distribution of
![]() ${\textbf{N}}_n$
was detected and the central limit theorem does not hold anymore. In the following we are going to analyse the limiting distribution of the random vector
${\textbf{N}}_n$
was detected and the central limit theorem does not hold anymore. In the following we are going to analyse the limiting distribution of the random vector
![]() ${\textbf{N}}_n$
for (b,d)-ary increasing trees and
${\textbf{N}}_n$
for (b,d)-ary increasing trees and
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees. We also summarise the main results for bucket recursive trees. There is a close connection between the random variables
$(\mathrm{b},\alpha)$
-plane oriented recursive trees. We also summarise the main results for bucket recursive trees. There is a close connection between the random variables
![]() $K_n$
and
$K_n$
and
![]() ${\textbf{N}}_n$
. The distribution of the initial bucket size
${\textbf{N}}_n$
. The distribution of the initial bucket size
![]() $K_{n+1}$
depends on the different node types present at time n,
$K_{n+1}$
depends on the different node types present at time n,
![]() $n\ge 1$
. Let
$n\ge 1$
. Let
![]() $v_{k}=v_{n,m,k}$
denote the buckets of capacity m contributing to
$v_{k}=v_{n,m,k}$
denote the buckets of capacity m contributing to
![]() $N_{n,m}$
, with
$N_{n,m}$
, with
![]() $1\le m\le b$
and
$1\le m\le b$
and
![]() $1\le k\le N_{n,j}$
. Then, by definition of the growth processes
$1\le k\le N_{n,j}$
. Then, by definition of the growth processes
 \[{\mathbb{P}}\left\{K_{n+1}=1 \mid {\textbf{N}}_n\right\}=\sum_{k=1}^{N_{n,b}}{\mathbb{P}}\left\{n+1<_t v_{n,b,k}\right\}\]
\[{\mathbb{P}}\left\{K_{n+1}=1 \mid {\textbf{N}}_n\right\}=\sum_{k=1}^{N_{n,b}}{\mathbb{P}}\left\{n+1<_t v_{n,b,k}\right\}\]
and, for
![]() $2\le m\le b$
,
$2\le m\le b$
,
 \[{\mathbb{P}}\left\{K_{n+1}=m \mid {\textbf{N}}_n\right\}=\sum_{k=1}^{N_{n,m-1}}{\mathbb{P}}\left\{n+1<_t v_{n,m-1,k}\right\}.\]
\[{\mathbb{P}}\left\{K_{n+1}=m \mid {\textbf{N}}_n\right\}=\sum_{k=1}^{N_{n,m-1}}{\mathbb{P}}\left\{n+1<_t v_{n,m-1,k}\right\}.\]
Of course, for each k, the probabilities
![]() ${\mathbb{P}}\{n+1<_t v_{n,b,k}\}$
coincide and are given according to Definitions 1–3:
${\mathbb{P}}\{n+1<_t v_{n,b,k}\}$
coincide and are given according to Definitions 1–3:
 \[{\mathbb{P}}\{n+1<_t v_{n,m,k}\}=\begin{cases}\dfrac{m}{n}, & \text{bucket recursive trees},\\[12pt]\dfrac{(d-1)m+1-\text{deg}^{+}(v)}{(d-1)n+1}, & \text{(b,d)}\text{-ary ITs},\\[12pt]\dfrac{\text{deg}^{+}(v)+(\alpha+1)m-1}{(\alpha+1)n-1}, & (\text{b},\alpha)\text{-PORTs}.\\\end{cases}\]
\[{\mathbb{P}}\{n+1<_t v_{n,m,k}\}=\begin{cases}\dfrac{m}{n}, & \text{bucket recursive trees},\\[12pt]\dfrac{(d-1)m+1-\text{deg}^{+}(v)}{(d-1)n+1}, & \text{(b,d)}\text{-ary ITs},\\[12pt]\dfrac{\text{deg}^{+}(v)+(\alpha+1)m-1}{(\alpha+1)n-1}, & (\text{b},\alpha)\text{-PORTs}.\\\end{cases}\]
Note that for
![]() $1\le m\le b-1$
the individual nodes
$1\le m\le b-1$
the individual nodes
![]() $v_{k}=v_{n,m,k}$
are unsaturated, such that
$v_{k}=v_{n,m,k}$
are unsaturated, such that
![]() $\text{deg}^+(v_{n,m,k})=0$
. Consequently, summation leads to the following result.
$\text{deg}^+(v_{n,m,k})=0$
. Consequently, summation leads to the following result.
Proposition 24. The random variable
![]() $K_n$
counting the initial size of the bucket containing label n is related to the number of nodes
$K_n$
counting the initial size of the bucket containing label n is related to the number of nodes
![]() ${\textbf{N}}_n=(N_{n,1},\dots,N_{n,b})$
with respective capacities as follows. For
${\textbf{N}}_n=(N_{n,1},\dots,N_{n,b})$
with respective capacities as follows. For
![]() $2\le m\le b$
it holds
$2\le m\le b$
it holds
 \[{\mathbb{P}}\{K_{n+1}=m\}={\mathbb{E}}(N_{n,m-1})\cdot\begin{cases}\dfrac{m-1}{n}, & \text{bucket recursive trees},\\[15pt]\dfrac{(d-1)(m-1)+1}{(d-1)n+1}, & \text{(b,d)}\text{-ary ITs},\\[15pt]\dfrac{(\alpha+1)(m-1)-1}{(\alpha+1)n-1}, & (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
\[{\mathbb{P}}\{K_{n+1}=m\}={\mathbb{E}}(N_{n,m-1})\cdot\begin{cases}\dfrac{m-1}{n}, & \text{bucket recursive trees},\\[15pt]\dfrac{(d-1)(m-1)+1}{(d-1)n+1}, & \text{(b,d)}\text{-ary ITs},\\[15pt]\dfrac{(\alpha+1)(m-1)-1}{(\alpha+1)n-1}, & (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
and
 \[{\mathbb{P}}\{K_{n+1}=1\}=\begin{cases}{\mathbb{E}}\left(N_{n,b}\right)\cdot \dfrac{b}{n}, & \text{bucket recursive trees},\\[15pt]{\mathbb{E}}(N_{n,b})\cdot \dfrac{(d-1)b+1}{(d-1)n+1}+\dfrac{1-\sum_{j=1}^b{\mathbb{E}}(N_{n,j})}{(d-1)b+1}, & \text{(b,d)}\text{-ary ITs},\\[15pt]{\mathbb{E}}(N_{n,b})\cdot \dfrac{(\alpha+1)b-1}{(\alpha+1)n-1}+\dfrac{-1+\sum_{j=1}^b{\mathbb{E}}\left(N_{n,j}\right)}{(\alpha+1)n-1}, & (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
\[{\mathbb{P}}\{K_{n+1}=1\}=\begin{cases}{\mathbb{E}}\left(N_{n,b}\right)\cdot \dfrac{b}{n}, & \text{bucket recursive trees},\\[15pt]{\mathbb{E}}(N_{n,b})\cdot \dfrac{(d-1)b+1}{(d-1)n+1}+\dfrac{1-\sum_{j=1}^b{\mathbb{E}}(N_{n,j})}{(d-1)b+1}, & \text{(b,d)}\text{-ary ITs},\\[15pt]{\mathbb{E}}(N_{n,b})\cdot \dfrac{(\alpha+1)b-1}{(\alpha+1)n-1}+\dfrac{-1+\sum_{j=1}^b{\mathbb{E}}\left(N_{n,j}\right)}{(\alpha+1)n-1}, & (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
In the following we consider generalised Pólya-Eggenberger urn models (see, e.g., [Reference Janson7]) with b different types of balls. For bucket recursive trees Mahmoud and Smythe [Reference Mahmoud and Smythe18] studied the following urn model.
Urn 25 (Bucket recursive trees) Consider a balanced urn with balls of b colours and let
![]() $Q_{n,m}$
denote the number of balls of type m,
$Q_{n,m}$
denote the number of balls of type m,
![]() $1\le m\le b$
, in the urn after n draws.
$1\le m\le b$
, in the urn after n draws.
![]() $(Q_{n,1},\dots,Q_{n,b})$
denotes the corresponding random vector at time n. At each time step, draw one ball at random from the urn, observe its colour, and add balls according to the ball replacement matrix
$(Q_{n,1},\dots,Q_{n,b})$
denotes the corresponding random vector at time n. At each time step, draw one ball at random from the urn, observe its colour, and add balls according to the ball replacement matrix
 \[M=\left(\begin{matrix}-1 & \quad 2 & \quad 0 & \quad \dots & \quad 0\\[3pt]0 & \quad -2 & \quad 3 & \quad \dots & \quad 0\\[3pt]\vdots & & \quad \ddots & & \quad \vdots\\[3pt]0 & \quad \dots & \quad 0& \quad -(b-1) & \quad b \\[3pt]1 & \quad 0 & \quad 0 & \quad \dots &\quad 0 \\\end{matrix}\right)\]
\[M=\left(\begin{matrix}-1 & \quad 2 & \quad 0 & \quad \dots & \quad 0\\[3pt]0 & \quad -2 & \quad 3 & \quad \dots & \quad 0\\[3pt]\vdots & & \quad \ddots & & \quad \vdots\\[3pt]0 & \quad \dots & \quad 0& \quad -(b-1) & \quad b \\[3pt]1 & \quad 0 & \quad 0 & \quad \dots &\quad 0 \\\end{matrix}\right)\]
and initial composition a single ball of type one. Then, the random variables
![]() $Q_{n,m}$
are related to the node types via
$Q_{n,m}$
are related to the node types via
The characteristic polynomial of M is given
For
![]() $b\le 26$
and
$b\le 26$
and
![]() $b > 26$
, respectively, there occurs a phase change: the limit law changes from normal to non-normal, which is due to the structure of the characteristic polynomial and the general results revealed in [Reference Janson7]. We assume that the eigenvalues
$b > 26$
, respectively, there occurs a phase change: the limit law changes from normal to non-normal, which is due to the structure of the characteristic polynomial and the general results revealed in [Reference Janson7]. We assume that the eigenvalues
![]() $\lambda_1,\dots,\lambda_b$
are indexed according to their real parts
$\lambda_1,\dots,\lambda_b$
are indexed according to their real parts
If the real part of
![]() $\lambda_2$
exceeds
$\lambda_2$
exceeds
![]() $\frac12$
then the limit law changes. In the following we denote the random vector of ball types as
$\frac12$
then the limit law changes. In the following we denote the random vector of ball types as
![]() ${\textbf{Q}}_{n}=(Q_{n,1},\dots,Q_{n,b})$
.
${\textbf{Q}}_{n}=(Q_{n,1},\dots,Q_{n,b})$
.
Theorem 26 (Mahmoud and Smythe [Reference Mahmoud and Smythe18]). For
![]() $b\le 26$
the limit law of
$b\le 26$
the limit law of
![]() $\frac{1}{\sqrt{n}}\big({\textbf{Q}}_n-{\mathbb{E}}({\textbf{Q}}_n)\big)$
is asymptotically normal. For
$\frac{1}{\sqrt{n}}\big({\textbf{Q}}_n-{\mathbb{E}}({\textbf{Q}}_n)\big)$
is asymptotically normal. For
![]() $b>26$
there is no normal limit law (under the same normalisation).
$b>26$
there is no normal limit law (under the same normalisation).
Here we introduce two new urn models.
Urn 27 (
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees) Consider the urn with ball replacement matrix
$(\mathrm{b},\alpha)$
-plane oriented recursive trees) Consider the urn with ball replacement matrix
 \[M=\left(\begin{matrix}-\alpha & \quad 2\alpha +1 & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad -(2\alpha +1) & \quad 3\alpha +2 & \quad \dots & \quad 0\\[4pt]\vdots & \quad & \quad \ddots & \quad & \quad \vdots\\[4pt]0 & \quad \dots & \quad 0& \quad -((b-1)\alpha +b-2) & \quad b\alpha +b-1 \\[4pt]\alpha & \quad 0 & \quad 0 & \quad \dots & \quad 1 \\[4pt]\end{matrix}\right)\]
\[M=\left(\begin{matrix}-\alpha & \quad 2\alpha +1 & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad -(2\alpha +1) & \quad 3\alpha +2 & \quad \dots & \quad 0\\[4pt]\vdots & \quad & \quad \ddots & \quad & \quad \vdots\\[4pt]0 & \quad \dots & \quad 0& \quad -((b-1)\alpha +b-2) & \quad b\alpha +b-1 \\[4pt]\alpha & \quad 0 & \quad 0 & \quad \dots & \quad 1 \\[4pt]\end{matrix}\right)\]
and initial composition
![]() $\alpha$
balls of type one. Then, the random variables
$\alpha$
balls of type one. Then, the random variables
![]() $Q_{n,m}$
are related to the node types by
$Q_{n,m}$
are related to the node types by
The characteristic polynomial of M is given
 \begin{equation}\chi_M(\lambda)=\det(M-\lambda I)=(-1)^{b}(\alpha+1)^{b}\left({{\left(\frac{\lambda-1}{\alpha+1}\right)}^{\overline{b}}}-{\left(\frac{\alpha}{\alpha+1}\right)}^{\overline{b}}\right).\end{equation}
\begin{equation}\chi_M(\lambda)=\det(M-\lambda I)=(-1)^{b}(\alpha+1)^{b}\left({{\left(\frac{\lambda-1}{\alpha+1}\right)}^{\overline{b}}}-{\left(\frac{\alpha}{\alpha+1}\right)}^{\overline{b}}\right).\end{equation}
Urn 28 ((b,d)-ary increasing trees) Consider the urn with ball replacement matrix
 \[M=\left(\begin{matrix}-d & \quad 2d-1 & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad -(2d-1) & \quad 3d-2 & \quad \dots & \quad 0\\[4pt]\vdots & \quad & \quad \ddots & \quad & \quad \vdots\\[4pt]0 & \quad \dots & \quad 0& \quad -((b-1)d -(b-2)) & \quad bd-(b-1) \\[4pt]d & \quad 0 & \quad 0 & \quad \dots & \quad -1 \\[4pt]\end{matrix}\right)\]
\[M=\left(\begin{matrix}-d & \quad 2d-1 & \quad 0 & \quad \dots & \quad 0\\[4pt]0 & \quad -(2d-1) & \quad 3d-2 & \quad \dots & \quad 0\\[4pt]\vdots & \quad & \quad \ddots & \quad & \quad \vdots\\[4pt]0 & \quad \dots & \quad 0& \quad -((b-1)d -(b-2)) & \quad bd-(b-1) \\[4pt]d & \quad 0 & \quad 0 & \quad \dots & \quad -1 \\[4pt]\end{matrix}\right)\]
and initial composition d balls of type one. Then, the random variables
![]() $Q_{n,m}$
are related to the node types by
$Q_{n,m}$
are related to the node types by
The characteristic polynomial of M is given
 \begin{equation}\chi_M(\lambda)=\det(M-\lambda I)=(-1)^b(d-1)^b\left({\left(\frac{\lambda+1}{d-1}\right)}^{\overline{b}}-{\left(\frac{d}{d-1}\right)}^{\overline{b}}\right).\end{equation}
\begin{equation}\chi_M(\lambda)=\det(M-\lambda I)=(-1)^b(d-1)^b\left({\left(\frac{\lambda+1}{d-1}\right)}^{\overline{b}}-{\left(\frac{d}{d-1}\right)}^{\overline{b}}\right).\end{equation}
As indicated by the connection between
![]() $K_n$
and
$K_n$
and
![]() ${\textbf{N}}_n$
, there is also a close connection between the characteristic polynomials (28), (29), (30) and the indicial equation (24):
${\textbf{N}}_n$
, there is also a close connection between the characteristic polynomials (28), (29), (30) and the indicial equation (24):
In particular, there is an affine transformation between these two polynomials. We note in passing that the general theorems of Janson [Reference Janson7] and Müller [Reference Müller20] allow to describe a phase change in the limit laws for
![]() $\textbf{N}_n$
similar to the results of Mahmoud and Smythe [Reference Mahmoud and Smythe18].
$\textbf{N}_n$
similar to the results of Mahmoud and Smythe [Reference Mahmoud and Smythe18].
7. Applications
In the following we present a few applications of the results obtained in Section 6. The stochastic growth rule discussed in Subsection 2.1 and the analysis of the initial bucket size
![]() $K_n$
can be used to analyse several parameters. We consider in the following the random variable
$K_n$
can be used to analyse several parameters. We consider in the following the random variable
![]() $Y_{n,j}$
, which counts the number of descendants of element j, i.e., the total number of elements with a label greater or equal j contained in the subtree rooted with the bucket containing element j, in a random bucket increasing tree (with maximal bucket size b) of size n. For this random variable we provide the exact distribution, as well as a decomposition of the random variable of interest in terms of the initial bucket size
$Y_{n,j}$
, which counts the number of descendants of element j, i.e., the total number of elements with a label greater or equal j contained in the subtree rooted with the bucket containing element j, in a random bucket increasing tree (with maximal bucket size b) of size n. For this random variable we provide the exact distribution, as well as a decomposition of the random variable of interest in terms of the initial bucket size
![]() $K_n$
. Then we apply our results to the root degree as well as the out-degree
$K_n$
. Then we apply our results to the root degree as well as the out-degree
![]() $X_{n,j}$
of the node containing element j. There we also present a decomposition of the random variable of interest, complementing earlier results.
$X_{n,j}$
of the node containing element j. There we also present a decomposition of the random variable of interest, complementing earlier results.
7.1 Descendants in bucket increasing trees
In order to avoid degeneracy we assume that
![]() $j\ge b+1$
(for
$j\ge b+1$
(for
![]() $1\le j\le b$
it holds
$1\le j\le b$
it holds
![]() $Y_{n,j}=n+1-j$
). Explicit results for the probability mass functions and the moments of both r.v.
$Y_{n,j}=n+1-j$
). Explicit results for the probability mass functions and the moments of both r.v.
![]() $Y_{n,j}$
and
$Y_{n,j}$
and
![]() $X_{n,j}$
can be obtained in principle by purely combinatorial means and a generating functions approach similar to the parameter initial bucket size treated above. However, here we take a different point of view utilising the previous results for the initial bucket size to provide concise decompositions of the random variables based on results already known in the literature. Such decompositions readily lead to limit laws and seem to be more difficult to obtain by using a purely analytic combinatorial approach.
$X_{n,j}$
can be obtained in principle by purely combinatorial means and a generating functions approach similar to the parameter initial bucket size treated above. However, here we take a different point of view utilising the previous results for the initial bucket size to provide concise decompositions of the random variables based on results already known in the literature. Such decompositions readily lead to limit laws and seem to be more difficult to obtain by using a purely analytic combinatorial approach.
In order to obtain to analyse
![]() $Y_{n,j}$
, we introduce a refinement of this r.v.: let
$Y_{n,j}$
, we introduce a refinement of this r.v.: let
![]() $Y_{n,\ell,j}=Y_{n,j}\mid K_j=\ell$
denote
$Y_{n,\ell,j}=Y_{n,j}\mid K_j=\ell$
denote
![]() $Y_{n,j}$
conditioned on the event
$Y_{n,j}$
conditioned on the event
![]() $K_j=\ell$
. According to the stochastic growth processes defined in Subsection 2.1 we obtain the recurrence relation
$K_j=\ell$
. According to the stochastic growth processes defined in Subsection 2.1 we obtain the recurrence relation
for
![]() $m\ge 1$
and the initial value
$m\ge 1$
and the initial value
![]() $Y_{j,\ell,j}=1$
. The parameters
$Y_{j,\ell,j}=1$
. The parameters
![]() $c_1,c_2$
occurring in this description of the law of
$c_1,c_2$
occurring in this description of the law of
![]() $Y_{n,\ell,j}$
are determined by the fraction
$Y_{n,\ell,j}$
are determined by the fraction
![]() $\frac{c_2}{c_1}=\kappa$
as given in (23). Alternatively,
$\frac{c_2}{c_1}=\kappa$
as given in (23). Alternatively,
![]() $Y_{n,\ell,j}$
can be described as follows.
$Y_{n,\ell,j}$
can be described as follows.
Proposition 29. The r.v.
![]() $Y_{n,\ell,j}$
can be described by a sum of dependent random variables
$Y_{n,\ell,j}$
can be described by a sum of dependent random variables
![]() $A_{i,\ell,j}$
,
$A_{i,\ell,j}$
,
![]() $i\ge j$
, all taking values in
$i\ge j$
, all taking values in
![]() $\{0,1\}$
, and initial value
$\{0,1\}$
, and initial value
![]() $A_{j,\ell,j}=1$
, where
$A_{j,\ell,j}=1$
, where
![]() $A_{i,\ell,j}$
denotes the indicator variable of the event that label i is a descendant of label j conditioned on the event
$A_{i,\ell,j}$
denotes the indicator variable of the event that label i is a descendant of label j conditioned on the event
![]() $K_{j}=\ell$
, and we get
$K_{j}=\ell$
, and we get
 \begin{equation}Y_{n,\ell,j}= \sum_{i=j}^{n}A_{i,\ell,j},\quad {\mathbb{P}}\{A_{i+1,\ell,j}=1 \mid Y_{i,\ell,j}\}= \frac{c_1\left(\ell-1+Y_{i,\ell,j}\right)+c_2}{c_1 i+c_2}.\end{equation}
\begin{equation}Y_{n,\ell,j}= \sum_{i=j}^{n}A_{i,\ell,j},\quad {\mathbb{P}}\{A_{i+1,\ell,j}=1 \mid Y_{i,\ell,j}\}= \frac{c_1\left(\ell-1+Y_{i,\ell,j}\right)+c_2}{c_1 i+c_2}.\end{equation}
Proof. It suffices to show that the probabilities
![]() ${\mathbb{P}}\{A_{i+1,\ell,j}=1 \mid Y_{i,\ell,j}\}$
are indeed given as stated above. Given
${\mathbb{P}}\{A_{i+1,\ell,j}=1 \mid Y_{i,\ell,j}\}$
are indeed given as stated above. Given
![]() $K_j$
assume that node v containing label j has
$K_j$
assume that node v containing label j has
![]() $m\ge 1$
descendants at time
$m\ge 1$
descendants at time
![]() $i\ge j$
. If
$i\ge j$
. If
![]() $m< b+1-K_j$
then node v has out-degree zero and capacity
$m< b+1-K_j$
then node v has out-degree zero and capacity
![]() $c(v)=K_j+m-1$
. It attracts a new label
$c(v)=K_j+m-1$
. It attracts a new label
![]() $i+1$
with probability
$i+1$
with probability
![]() $p(v)=p_{i+1}(v)$
determined directly by the stochastic growth rules:
$p(v)=p_{i+1}(v)$
determined directly by the stochastic growth rules:
 \[p(v)=\begin{cases} \displaystyle{\frac{K_j+m-1}{i}}, & \quad \text{bucket recursive trees}, \\[10pt] \displaystyle{\frac{(d-1)(K_j+m-1)+1}{(d-1)i+1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[15pt] \displaystyle{\frac{(\alpha+1)(K_j+m-1)-1}{(\alpha+1)i-1}}, & \quad (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
\[p(v)=\begin{cases} \displaystyle{\frac{K_j+m-1}{i}}, & \quad \text{bucket recursive trees}, \\[10pt] \displaystyle{\frac{(d-1)(K_j+m-1)+1}{(d-1)i+1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[15pt] \displaystyle{\frac{(\alpha+1)(K_j+m-1)-1}{(\alpha+1)i-1}}, & \quad (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
Otherwise, assume that the number of descendants is given by
![]() $m\ge b+1-K_j$
. Thus, node v is saturated and the remaining
$m\ge b+1-K_j$
. Thus, node v is saturated and the remaining
![]() $m-(b+1-K_j)$
labels are distributed amongst the r non-root nodes
$m-(b+1-K_j)$
labels are distributed amongst the r non-root nodes
![]() $u_1,\dots,u_r$
in the subtree rooted at v. The probability
$u_1,\dots,u_r$
in the subtree rooted at v. The probability
![]() ${\mathbb{P}}\{i+1 <_d j\}$
that label
${\mathbb{P}}\{i+1 <_d j\}$
that label
![]() $i+1$
is a descendant of label j is given by
$i+1$
is a descendant of label j is given by
where
![]() ${\mathbb{P}}\{i+1 <_c x\}$
denotes the probability that label
${\mathbb{P}}\{i+1 <_c x\}$
denotes the probability that label
![]() $i+1$
is contained in the node x. We note that
$i+1$
is contained in the node x. We note that
For bucket recursive trees we obtain
For (b,d)-ary increasing trees we have
 \begin{align*}{\mathbb{P}}\{i+1 <_d j\} &= \frac{(d-1)c(v)+1-\text{deg}^{+}(v)}{(d-1)i+1} + \sum_{k=1}^{r}\frac{(d-1)c(u_k)+1-\text{deg}^{+}(u_k)}{(d-1)i+1}\\[5pt]&= \frac{(d-1)b+r+1 + (d-1)(m-(b+1-K_j))-r}{(d-1)i+1}=\frac{(d-1)(K_j+m-1)+1}{(d-1)i+1}.\end{align*}
\begin{align*}{\mathbb{P}}\{i+1 <_d j\} &= \frac{(d-1)c(v)+1-\text{deg}^{+}(v)}{(d-1)i+1} + \sum_{k=1}^{r}\frac{(d-1)c(u_k)+1-\text{deg}^{+}(u_k)}{(d-1)i+1}\\[5pt]&= \frac{(d-1)b+r+1 + (d-1)(m-(b+1-K_j))-r}{(d-1)i+1}=\frac{(d-1)(K_j+m-1)+1}{(d-1)i+1}.\end{align*}
Finally, for
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees we get
$(\mathrm{b},\alpha)$
-plane oriented recursive trees we get
 \begin{align*}{\mathbb{P}}\left\{i+1 <_d j\right\} &= \frac{\text{deg}^{+}(v)+(\alpha+1)c(v)-1}{(\alpha+1)i-1} + \sum_{k=1}^{r}\frac{\text{deg}^{+}(u_k)+(\alpha+1)c(u_k)-1}{(\alpha+1)i-1}\\[8pt]&= \frac{r+(\alpha+1)(b+m-(b+1-K_j))-r-1}{(\alpha+1)i-1}=\frac{(\alpha+1)(K_j+m-1)-1}{(\alpha+1)i-1}.\end{align*}
\begin{align*}{\mathbb{P}}\left\{i+1 <_d j\right\} &= \frac{\text{deg}^{+}(v)+(\alpha+1)c(v)-1}{(\alpha+1)i-1} + \sum_{k=1}^{r}\frac{\text{deg}^{+}(u_k)+(\alpha+1)c(u_k)-1}{(\alpha+1)i-1}\\[8pt]&= \frac{r+(\alpha+1)(b+m-(b+1-K_j))-r-1}{(\alpha+1)i-1}=\frac{(\alpha+1)(K_j+m-1)-1}{(\alpha+1)i-1}.\end{align*}
Summarising we obtain the probabilities
 \begin{equation*} {\mathbb{P}}\left\{i+1 <_d j \mid Y_{i,\ell,j}=m\right\} = \begin{cases} \displaystyle{\frac{\ell-1+m}{i}}, & \quad \text{bucket recursive trees}, \\[10pt] \displaystyle{\frac{(d-1)(\ell-1+m)+1}{(d-1)i+1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[17pt] \displaystyle{\frac{(\alpha+1)(\ell-1+m)-1}{(\alpha+1)i-1}}, & \quad (\text{b},\alpha)\text{-PORTs},\end{cases}\end{equation*}
\begin{equation*} {\mathbb{P}}\left\{i+1 <_d j \mid Y_{i,\ell,j}=m\right\} = \begin{cases} \displaystyle{\frac{\ell-1+m}{i}}, & \quad \text{bucket recursive trees}, \\[10pt] \displaystyle{\frac{(d-1)(\ell-1+m)+1}{(d-1)i+1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[17pt] \displaystyle{\frac{(\alpha+1)(\ell-1+m)-1}{(\alpha+1)i-1}}, & \quad (\text{b},\alpha)\text{-PORTs},\end{cases}\end{equation*}
thus leading to the decomposition stated in (31).
We remark in passing that, alternatively,
![]() $Y_{n,\ell,j}$
can also be described via a generalised Pólya urn model; see [Reference Kuba and Panholzer16].
$Y_{n,\ell,j}$
can also be described via a generalised Pólya urn model; see [Reference Kuba and Panholzer16].
It is a key observation that the distribution of
![]() $Y_{n,\ell,j}$
is identical to the distribution of a r.v.
$Y_{n,\ell,j}$
is identical to the distribution of a r.v.
![]() $D_{n,\ell,j}$
, counting so-called generalised descendants
$D_{n,\ell,j}$
, counting so-called generalised descendants
![]() $D_{n,\ell,j}$
in ordinary families of increasing trees, which has been introduced and studied in [Reference Kuba and Panholzer12]. Namely, the r.v.
$D_{n,\ell,j}$
in ordinary families of increasing trees, which has been introduced and studied in [Reference Kuba and Panholzer12]. Namely, the r.v.
![]() $D_{n,\ell,j}$
also admits a description as a sum of dependent r.v. equivalent to (31), see [12, equations (7)–(8)], thus
$D_{n,\ell,j}$
also admits a description as a sum of dependent r.v. equivalent to (31), see [12, equations (7)–(8)], thus
![]() $Y_{n,\ell,j} \stackrel{(d)}{=} D_{n,\ell,j}$
. Unconditioning immediately leads to the following result.
$Y_{n,\ell,j} \stackrel{(d)}{=} D_{n,\ell,j}$
. Unconditioning immediately leads to the following result.
Proposition 30 (Decomposition of the number of descendants). The random variable
![]() $Y_{n,j}$
counting the number of descendants of label j in a bucket increasing tree of size n for the families bucket recursive trees, (b,d)-ary increasing trees, and
$Y_{n,j}$
counting the number of descendants of label j in a bucket increasing tree of size n for the families bucket recursive trees, (b,d)-ary increasing trees, and
![]() $(\mathrm{b},\alpha)$
-plane oriented recursive trees is related to the random variable
$(\mathrm{b},\alpha)$
-plane oriented recursive trees is related to the random variable
![]() $D_{n,\ell,j}$
, counting generalised descendants with parameter
$D_{n,\ell,j}$
, counting generalised descendants with parameter
![]() $\ell$
for the corresponding ordinary increasing tree families as studied in [Reference Kuba and Panholzer12], where the parameter
$\ell$
for the corresponding ordinary increasing tree families as studied in [Reference Kuba and Panholzer12], where the parameter
![]() $\ell$
is given by the random variable
$\ell$
is given by the random variable
![]() $K_j$
measuring the initial bucket size of label j:
$K_j$
measuring the initial bucket size of label j:
The probability mass function of
![]() $D_{n,\ell,j}$
as well as limit laws have been obtained in [Reference Kuba and Panholzer12] using lattice path counting arguments. Using them this easily leads to the following limiting distribution result of
$D_{n,\ell,j}$
as well as limit laws have been obtained in [Reference Kuba and Panholzer12] using lattice path counting arguments. Using them this easily leads to the following limiting distribution result of
![]() $Y_{n,j}$
, also slightly refining the results of [Reference Kuba and Panholzer13] for bucket recursive trees. We thus omit the details.
$Y_{n,j}$
, also slightly refining the results of [Reference Kuba and Panholzer13] for bucket recursive trees. We thus omit the details.
Corollary 31 (Limit laws for the number of descendants). For
![]() $n \to \infty$
and
$n \to \infty$
and
![]() $j=j(n)$
, the random variable
$j=j(n)$
, the random variable
![]() $Y_{n,j}$
has the following limit laws, depending on the random initial bucket size
$Y_{n,j}$
has the following limit laws, depending on the random initial bucket size
![]() $K_j$
or its limit K.
$K_j$
or its limit K.
-
1. The region for j fixed. The normalised random variable
 $Y_{n,j}$
is asymptotically Beta-distributed,
$Y_{n,j}$
is asymptotically Beta-distributed,
 $Y_{n,j}/n {\xrightarrow{(d)}} \beta\big(K_j+\frac{c_{2}}{c_{1}},j-K_j\big)$
.
$Y_{n,j}/n {\xrightarrow{(d)}} \beta\big(K_j+\frac{c_{2}}{c_{1}},j-K_j\big)$
. -
2. The region for small j:
 $j \to \infty$
such that
$j \to \infty$
such that
 $j = o(n)$
. The normalised random variable
$j = o(n)$
. The normalised random variable
 $j Y_{n,j}/n$
is asymptotically Gamma-distributed,
$j Y_{n,j}/n$
is asymptotically Gamma-distributed,
 $j Y_{n,j}/n {\xrightarrow{(d)}} \gamma\big(K+\frac{c_{2}}{c_{1}},1\big)$
.
$j Y_{n,j}/n {\xrightarrow{(d)}} \gamma\big(K+\frac{c_{2}}{c_{1}},1\big)$
. -
3. The central region for j:
 $j \to \infty$
such that
$j \to \infty$
such that
 $j \sim \rho n$
, with
$j \sim \rho n$
, with
 $0 < \rho < 1$
. The shifted random variable
$0 < \rho < 1$
. The shifted random variable
 $Y_{n,j}-1$
is asymptotically negative binomial-distributed,
$Y_{n,j}-1$
is asymptotically negative binomial-distributed,
 $Y_{n,j}-1{\xrightarrow{(d)}} \text{NegBin}\big(K+\frac{c_{2}}{c_{1}},\rho\big)$
.
$Y_{n,j}-1{\xrightarrow{(d)}} \text{NegBin}\big(K+\frac{c_{2}}{c_{1}},\rho\big)$
. -
4. The region for large j:
 $j \to \infty$
such that
$j \to \infty$
such that
 $k \,:\!=\, n-j = o(n)$
. The random variable
$k \,:\!=\, n-j = o(n)$
. The random variable
 $Y_{n,j}$
has asymptotically all its mass concentrated at 1,
$Y_{n,j}$
has asymptotically all its mass concentrated at 1,
 $ {\mathbb{P}}\{Y_{n,j}=1\}=1+\mathcal{O}\big(\frac{k}{n}\big)$
.
$ {\mathbb{P}}\{Y_{n,j}=1\}=1+\mathcal{O}\big(\frac{k}{n}\big)$
.
Remark 32. We mention the possibility to improve the distributional convergence of
![]() $Y_{n,j}$
in several ways. First, one can prove moment convergence. Second, local limit theorems can be deduced using the explicit expressions for the probability mass functions of
$Y_{n,j}$
in several ways. First, one can prove moment convergence. Second, local limit theorems can be deduced using the explicit expressions for the probability mass functions of
![]() $K_j$
and
$K_j$
and
![]() $D_{n,\ell,j}$
. Third, for fixed j one can measure the difference between
$D_{n,\ell,j}$
. Third, for fixed j one can measure the difference between
![]() $Y_{n,j}/n$
and the limiting beta random variable in terms of a so-called martingale tail sum using discrete martingales.
$Y_{n,j}/n$
and the limiting beta random variable in terms of a so-called martingale tail sum using discrete martingales.
7.2 Node degrees in bucket increasing trees
Let
![]() $X_{n,j}$
denote the random variable counting the out-degree of the bucket containing label j in a size n random bucket increasing tree. By definition, we can decompose
$X_{n,j}$
denote the random variable counting the out-degree of the bucket containing label j in a size n random bucket increasing tree. By definition, we can decompose
![]() $X_{n,j}$
into a sequence of dependent indicator variables
$X_{n,j}$
into a sequence of dependent indicator variables
 \[X_{n,j}=\sum_{\ell=j+1}^{n}{\mathbb{I}}\{\ell <_a j\},\]
\[X_{n,j}=\sum_{\ell=j+1}^{n}{\mathbb{I}}\{\ell <_a j\},\]
where
![]() $\{\ell <_a j\}$
denotes the event that label
$\{\ell <_a j\}$
denotes the event that label
![]() $\ell$
is attached as a new node to the node containing label j. Similar to the case
$\ell$
is attached as a new node to the node containing label j. Similar to the case
![]() $b=1$
, see for example [Reference Kuba and Panholzer11], the random variable
$b=1$
, see for example [Reference Kuba and Panholzer11], the random variable
![]() $X_{n,j}$
does not obey a uniform behaviour, but it is similar to the r.v. number of descendants considered before. Basically, we will observe that for
$X_{n,j}$
does not obey a uniform behaviour, but it is similar to the r.v. number of descendants considered before. Basically, we will observe that for
![]() $b>1$
the random variable
$b>1$
the random variable
![]() $X_{n,j}$
behaves similar to the case
$X_{n,j}$
behaves similar to the case
![]() $b=1$
once the bucket containing the label j is fully saturated. Compared to the two “stages” of
$b=1$
once the bucket containing the label j is fully saturated. Compared to the two “stages” of
![]() $Y_{n,j}$
, insertion of label j into a node of size
$Y_{n,j}$
, insertion of label j into a node of size
![]() $K_j$
and then attraction of new labels, we have three stages: first, label j is inserted into a node v of size
$K_j$
and then attraction of new labels, we have three stages: first, label j is inserted into a node v of size
![]() $K_j$
; second, node v attracts new labels until it is fully saturated; then, until time n the node v attracts new labels and its out-degree increases. In order to state the precise decompositions of
$K_j$
; second, node v attracts new labels until it is fully saturated; then, until time n the node v attracts new labels and its out-degree increases. In order to state the precise decompositions of
![]() $X_{n,j}$
we utilise our previous results for
$X_{n,j}$
we utilise our previous results for
![]() $K_j$
and
$K_j$
and
![]() $Y_{n,j}$
. We also collect known results about additional random variables.
$Y_{n,j}$
. We also collect known results about additional random variables.
We introduce first the stopping time
![]() $\tau_{n,j}\,:\!=\,\min_{j\le\ell\le n}\{Y_{\ell,j}=b+1-K_j\}$
until the node containing label j is saturated. Let
$\tau_{n,j}\,:\!=\,\min_{j\le\ell\le n}\{Y_{\ell,j}=b+1-K_j\}$
until the node containing label j is saturated. Let
![]() $\nabla$
denote the backward difference operator, i.e.,
$\nabla$
denote the backward difference operator, i.e.,
![]() $\nabla x_{k} \,:\!=\, x_{k} - x_{k-1}$
. The random variable
$\nabla x_{k} \,:\!=\, x_{k} - x_{k-1}$
. The random variable
![]() $\tau_{n,j}$
can be expressed in terms of indicator variables as follows:
$\tau_{n,j}$
can be expressed in terms of indicator variables as follows:
 \[\tau_{n,j}=\sum_{k=j}^{n}{\mathbb{I}}\left\{Y_{k,j}= b+1-K_j,\,\nabla Y_{k,j}=1\right\}\cdot k + {\mathbb{I}}\left\{Y_{n,j}< b+1-K_j\right\} \cdot n,\]
\[\tau_{n,j}=\sum_{k=j}^{n}{\mathbb{I}}\left\{Y_{k,j}= b+1-K_j,\,\nabla Y_{k,j}=1\right\}\cdot k + {\mathbb{I}}\left\{Y_{n,j}< b+1-K_j\right\} \cdot n,\]
where
![]() $Y_{j-1,j}=0$
. Let
$Y_{j-1,j}=0$
. Let
![]() ${\mathbb{P}}\{m<_t v \mid c(v)=b-1\}$
denote the conditional probability that node v, containing label j, attracts label m conditioned on the event
${\mathbb{P}}\{m<_t v \mid c(v)=b-1\}$
denote the conditional probability that node v, containing label j, attracts label m conditioned on the event
![]() $c(v)=b-1$
, as determined by the stochastic growth processes of the three tree families considered:
$c(v)=b-1$
, as determined by the stochastic growth processes of the three tree families considered:
 \[{\mathbb{P}}\{m<_t v\mid c(v)=b-1\}=\begin{cases} \displaystyle{\frac{b-1}{m-1}}, & \quad \text{bucket recursive trees}, \\[16pt] \displaystyle{\frac{(d-1)(b-1)+1}{(d-1)(m-1)+1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[16pt] \displaystyle{\frac{(\alpha+1)(b-1)-1}{(\alpha+1)(m-1)-1}}, & \quad (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
\[{\mathbb{P}}\{m<_t v\mid c(v)=b-1\}=\begin{cases} \displaystyle{\frac{b-1}{m-1}}, & \quad \text{bucket recursive trees}, \\[16pt] \displaystyle{\frac{(d-1)(b-1)+1}{(d-1)(m-1)+1}}, & \quad \text{(b,d)}\text{-ary ITs}, \\[16pt] \displaystyle{\frac{(\alpha+1)(b-1)-1}{(\alpha+1)(m-1)-1}}, & \quad (\text{b},\alpha)\text{-PORTs}.\end{cases}\]
The probability mass function
![]() ${\mathbb{P}}\{\tau_{n,j}=m\}$
is readily obtained in terms of the probability mass functions of
${\mathbb{P}}\{\tau_{n,j}=m\}$
is readily obtained in terms of the probability mass functions of
![]() $K_j$
,
$K_j$
,
![]() $Y_{n,j}$
and thus
$Y_{n,j}$
and thus
![]() $Y_{n,\ell,j}$
, where the constants
$Y_{n,\ell,j}$
, where the constants
![]() $c_1,c_2$
are determined by (23) via
$c_1,c_2$
are determined by (23) via
![]() $c_{2}/c_{1} = \kappa$
.
$c_{2}/c_{1} = \kappa$
.
Lemma 33 (Distribution of the saturation time). For
![]() $1\le j \le b$
the random variable
$1\le j \le b$
the random variable
![]() $\tau_{n,j}$
is deterministic:
$\tau_{n,j}$
is deterministic:
![]() $\tau_{n,j}=b$
.
$\tau_{n,j}=b$
.
For
![]() $j\ge b+1$
the probability mass function
$j\ge b+1$
the probability mass function
![]() ${\mathbb{P}}\{\tau_{n,j}=m\}$
is given as follows:
${\mathbb{P}}\{\tau_{n,j}=m\}$
is given as follows:
For
![]() $m=j$
we have
$m=j$
we have
for
![]() $j+1\le m<n$
we get
$j+1\le m<n$
we get
 \[{\mathbb{P}}\{\tau_{n,j}=m\}=\sum_{\ell=1}^{b-1}{\mathbb{P}}\{K_j=\ell\}\cdot{\mathbb{P}}\{Y_{m-1,\ell,j}=b-\ell\}\cdot {\mathbb{P}}\{m<_t v \mid c(v)=b-1\},\]
\[{\mathbb{P}}\{\tau_{n,j}=m\}=\sum_{\ell=1}^{b-1}{\mathbb{P}}\{K_j=\ell\}\cdot{\mathbb{P}}\{Y_{m-1,\ell,j}=b-\ell\}\cdot {\mathbb{P}}\{m<_t v \mid c(v)=b-1\},\]
whereas for
![]() $m=n$
we obtain
$m=n$
we obtain
 \[{\mathbb{P}}\{\tau_{n,j}=n\}=\sum_{\ell=1}^{b-1}{\mathbb{P}}\{K_j=\ell\}\cdot \big( {\mathbb{P}}\{Y_{n,\ell,j}< b+1-\ell\}+{\mathbb{P}}\{Y_{n-1,\ell,j}=b-\ell\}\cdot {\mathbb{P}}\{n<_t v\mid c(v)=b-1\}\big).\]
\[{\mathbb{P}}\{\tau_{n,j}=n\}=\sum_{\ell=1}^{b-1}{\mathbb{P}}\{K_j=\ell\}\cdot \big( {\mathbb{P}}\{Y_{n,\ell,j}< b+1-\ell\}+{\mathbb{P}}\{Y_{n-1,\ell,j}=b-\ell\}\cdot {\mathbb{P}}\{n<_t v\mid c(v)=b-1\}\big).\]
Remark 34. In the case
![]() $j=b+1$
the expressions above simplify due to the fact that
$j=b+1$
the expressions above simplify due to the fact that
![]() $K_{b+1}=1$
, which is evident from the stochastic growth rules.
$K_{b+1}=1$
, which is evident from the stochastic growth rules.
Proof. For
![]() $1\le j\le b$
there is only one bucket present. It is saturated after the insertion of label b. Assume that
$1\le j\le b$
there is only one bucket present. It is saturated after the insertion of label b. Assume that
![]() $j\ge b+1$
. The probability
$j\ge b+1$
. The probability
![]() ${\mathbb{P}}\{\tau_{n,j}=j\}$
is given by
${\mathbb{P}}\{\tau_{n,j}=j\}$
is given by
For
![]() $j<m<n$
we obtain the probability of the event
$j<m<n$
we obtain the probability of the event
![]() $\{Y_{k,j}= b+1-K_j,\,\nabla Y_{k,j}=1\}$
by conditioning on the initial bucket size
$\{Y_{k,j}= b+1-K_j,\,\nabla Y_{k,j}=1\}$
by conditioning on the initial bucket size
![]() $K_j$
. Finally, for
$K_j$
. Finally, for
![]() $j=n$
we also take into account the probability of the event
$j=n$
we also take into account the probability of the event
![]() $\{Y_{n,j}<b+1-K_j\}$
.
$\{Y_{n,j}<b+1-K_j\}$
.
Let
![]() $\text{Be}(p)$
denote a Bernoulli-distributed random variable:
$\text{Be}(p)$
denote a Bernoulli-distributed random variable:
Furthermore, let
![]() $W_N(w_0,b_0)$
denote the number of white balls at time N in a triangular urn model with balls of two colours and initial values
$W_N(w_0,b_0)$
denote the number of white balls at time N in a triangular urn model with balls of two colours and initial values
![]() $w_0>0$
and
$w_0>0$
and
![]() $b_0>0$
, whose balanced replacement matrix given by
$b_0>0$
, whose balanced replacement matrix given by
![]() $\left(\begin{smallmatrix}1& \quad \alpha\\[3pt] 0& \quad 1+\alpha\\\end{smallmatrix}\right)$
.
$\left(\begin{smallmatrix}1& \quad \alpha\\[3pt] 0& \quad 1+\alpha\\\end{smallmatrix}\right)$
.
We obtain the following result.
Theorem 35. The random variable
![]() $X_{n,j}$
counting the out-degree of label j in a random bucket increasing tree of size n, with
$X_{n,j}$
counting the out-degree of label j in a random bucket increasing tree of size n, with
![]() $1\le j\le n$
, satisfies the following.
$1\le j\le n$
, satisfies the following.
-
For bucket recursive trees,
 $X_{n,j}$
is distributed as a random sum of mutually independent indicator variables:
$X_{n,j}$
is distributed as a random sum of mutually independent indicator variables:  \[X_{n,j}{\stackrel{(d)}=}\sum_{\ell=\tau_{n,j}+1}^{n}{\mathbb{I}}(\ell<_c j),\qquad\text{with} \enspace {\mathbb{I}}\left(\ell<_c j\right)=\text{Be}\left(\textstyle{\frac{b}{\ell}}\right).\]
\[X_{n,j}{\stackrel{(d)}=}\sum_{\ell=\tau_{n,j}+1}^{n}{\mathbb{I}}(\ell<_c j),\qquad\text{with} \enspace {\mathbb{I}}\left(\ell<_c j\right)=\text{Be}\left(\textstyle{\frac{b}{\ell}}\right).\]
-
For
 $(\mathrm{b},\alpha)$
-plane oriented recursive trees,
$(\mathrm{b},\alpha)$
-plane oriented recursive trees,
 $X_{n,j}$
is distributed as the number of white balls in the balanced triangular urn model described above: In both cases, the stopping time
$X_{n,j}$
is distributed as the number of white balls in the balanced triangular urn model described above: In both cases, the stopping time \[X_{n,j}{\stackrel{(d)}=} W_{n-\tau_{n,j}}(w_0,b_0),\quad w_0=b(\alpha+1)-1,\, b_0=(\alpha+1)(\tau_{n,j}-b).\]
\[X_{n,j}{\stackrel{(d)}=} W_{n-\tau_{n,j}}(w_0,b_0),\quad w_0=b(\alpha+1)-1,\, b_0=(\alpha+1)(\tau_{n,j}-b).\]
 $\tau_{n,j}\,:\!=\,\min_{j\le\ell\le n}\{Y_{\ell,j}=b+1-K_j\}$
depends on
$\tau_{n,j}\,:\!=\,\min_{j\le\ell\le n}\{Y_{\ell,j}=b+1-K_j\}$
depends on
 $K_j$
as well as on
$K_j$
as well as on
 $Y_{n,j}$
.
$Y_{n,j}$
.
Remark 36. A similar result holds for (b,d)-ary increasing trees; however, the random variable
![]() $X_{n,j}$
is by definition bounded, thus we leave the result to the interested reader. We further note that the probability mass functions of
$X_{n,j}$
is by definition bounded, thus we leave the result to the interested reader. We further note that the probability mass functions of
![]() $X_{n,j}$
can alternatively be obtained by a generating functions approach, but without revealing the structural decompositions (compare with the corresponding results of [Reference Kuba and Panholzer13] for bucket recursive trees).
$X_{n,j}$
can alternatively be obtained by a generating functions approach, but without revealing the structural decompositions (compare with the corresponding results of [Reference Kuba and Panholzer13] for bucket recursive trees).
8. Conclusion
In this work we introduced two new families of bucket increasing trees, which can be generated by a stochastic growth process.
We introduced a clustering process
![]() $\mathcal{C}$
for ordinary increasing trees that generate bucket increasing trees. Moreover, by modifying the map
$\mathcal{C}$
for ordinary increasing trees that generate bucket increasing trees. Moreover, by modifying the map
![]() $\mathcal{C}$
we obtain bijections between certain ordinary increasing tree families and families of bilabelled bucket increasing trees. Additionally, we obtained a bijection between increasing diamonds and bilabelled bucket increasing trees.
$\mathcal{C}$
we obtain bijections between certain ordinary increasing tree families and families of bilabelled bucket increasing trees. Additionally, we obtained a bijection between increasing diamonds and bilabelled bucket increasing trees.
We analysed structural properties of bucket increasing trees, in particular, the tree parameter
![]() $K_n$
, counting the initial bucket size of the node containing label n in a random tree of size n. Using the combinatorial description as well as the tree evolution process, a study of further quantities in bucket increasing tree families is possible, e.g., we want to mention node distances. Moreover, there exist relations of bucket increasing trees to further combinatorial structures as, e.g., certain models of series-parallel networks, see [Reference Kuba and Panholzer17].
$K_n$
, counting the initial bucket size of the node containing label n in a random tree of size n. Using the combinatorial description as well as the tree evolution process, a study of further quantities in bucket increasing tree families is possible, e.g., we want to mention node distances. Moreover, there exist relations of bucket increasing trees to further combinatorial structures as, e.g., certain models of series-parallel networks, see [Reference Kuba and Panholzer17].
Acknowledgements
The authors warmly thank Henning Sulzbach for his feedback and the anonymous referees for their insightful comments, improving the presentation of this work.