Let 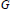 $G$ be an affine Kac-Moody group,
$G$ be an affine Kac-Moody group, 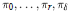 ${{\pi }_{0}},...,{{\pi }_{r}},{{\pi }_{\delta }}$ its fundamental irreducible representations and
${{\pi }_{0}},...,{{\pi }_{r}},{{\pi }_{\delta }}$ its fundamental irreducible representations and 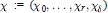 ${{\chi }_{0}},...,{{\chi }_{r}},{{\chi }_{\delta }}$ their characters. We determine the set of all group elements
${{\chi }_{0}},...,{{\chi }_{r}},{{\chi }_{\delta }}$ their characters. We determine the set of all group elements  $x$ such that all
$x$ such that all 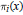 ${{\pi }_{i}}(x)$ act as trace class operators, i.e., such that
${{\pi }_{i}}(x)$ act as trace class operators, i.e., such that 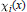 ${{\chi }_{i}}(x)$ exists, then prove that the
${{\chi }_{i}}(x)$ exists, then prove that the  ${{\chi }_{i}}$ are class functions. Thus, (
${{\chi }_{i}}$ are class functions. Thus, (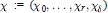 $\chi \,:=\,({{\chi }_{0}},...,{{\chi }_{r}},\,{{\chi }_{\delta }})$)factors to an adjoint quotient
$\chi \,:=\,({{\chi }_{0}},...,{{\chi }_{r}},\,{{\chi }_{\delta }})$)factors to an adjoint quotient 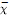 $\bar{\chi }$ for
$\bar{\chi }$ for 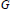 $G$. In a second part, following Steinberg, we define a cross-section
$G$. In a second part, following Steinberg, we define a cross-section  $C$ for the potential regular classes in
$C$ for the potential regular classes in 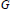 $G$. We prove that the restriction
$G$. We prove that the restriction 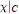 $\chi \text{ }\!\!|\!\!\text{ }c$ behaves well algebraically. Moreover, we obtain an action of
$\chi \text{ }\!\!|\!\!\text{ }c$ behaves well algebraically. Moreover, we obtain an action of 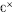 ${{\mathbb{C}}^{\times }}$ on
${{\mathbb{C}}^{\times }}$ on  $C$, which leads to a functional identity for
$C$, which leads to a functional identity for 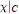 $\text{ }\chi |\text{ c}$ which shows that
$\text{ }\chi |\text{ c}$ which shows that 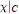 $\text{ }\chi |\text{ c}$ is quasi-homogeneous.
$\text{ }\chi |\text{ c}$ is quasi-homogeneous.