Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-09T22:54:25.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Tempered Representations and the Theta Correspondence

Published online by Cambridge University Press:  20 November 2018

Brooks Roberts
Brooks Roberts*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 3G3 email:brooks@math.toronto.edu
*
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $V$ be an even dimensional nondegenerate symmetric bilinear space over a nonarchimedean local field $F$ of characteristic zero, and let $n$ be a nonnegative integer. Suppose that 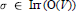$\sigma \,\in \,\text{Irr(O(}V\text{))}$ and 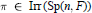$\pi \,\in \,\text{Irr}\,\text{(Sp(}n,\,F\text{))}$ correspond under the theta correspondence. Assuming that $\sigma $ is tempered, we investigate the problem of determining the Langlands quotient data for $\text{ }\!\!\pi\!\!\text{ }$.

Keywords

11F2722E50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 5 , 01 October 1998 , pp. 1105 - 1118
Copyright
Copyright © Canadian Mathematical Society 1998

Footnotes

This research was supported by NSERC research grant OGP0183677.

References

[Car] Cartier, P., Representations of p-adic groups: a survey. Proc. Sympos. Pure Math. 33, Part 1, 111–155. American Mathematical Society, Providence, RI, 1979.Google Scholar
[C] Casselman, W., Introduction to the theory of admissible representations of p-adic reductive groups. Preprint.Google Scholar
[G] Garrett, P., Intergral representations of Eisenstein series and L-functions. In: Number Theory, Trace Formulas and Discrete Groups, Academic Press, 1989. 241–264.Google Scholar
[K1] Kudla, S.S., On the local theta-correspondence. Invent. Math. 83(1986), 229–255.Google Scholar
[K2] Kudla, S.S., The local Langlands correspondence: the non-archimedean case. Proc. Sympos. Pure Math. 55, Part 2, 365–391. American Mathematical Society, Providence, RI, 1994.Google Scholar
[K-R1] Kudla, S.S. and Rallis, S., Ramified degenerate principal series representations for. Sp(n). Israel J.Math. 78(1992), 209–256.Google Scholar
[K-R2] Kudla, S.S., A regularized Siegel-Weil formula: The first term identity. Ann. of Math. 140(1994), 1–80.Google Scholar
[MVW] Moeglin, C., Vignéras, M.-F. and Waldspurger, J.-L., Correspondances de Howe sur un corps p-adique. Lecture Notes in Math. 1291, Springer-Verlag, 1987.Google Scholar
[Rod] Rodier, F., Représentations de Gl(n, k) où k est un corps p-adique (Sém. Bourbaki, 1981.82). Astérisque 92-93(1982), 201–218.Google Scholar
[T] Tadić, M., Representations of p-adic symplectic groups. Compositio Math. 90(1994), 123–181.Google Scholar
[W] Waldspurger, J.-L., Demonstration d’une conjecture de duality de Howe dans le case p-adique, p. 6= 2. IsraelMath. Conf. Proc. 2(1990), 267–324.Google Scholar