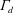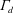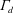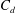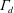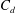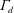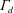1 Introduction
The fluid mechanics of displacement ventilation in a room with vents at floor and ceiling levels was examined theoretically by Linden, Lane-Serff & Smeed (Reference Linden, Lane-Serff and Smeed1990). Their model (known as the ‘emptying–filling box’ model) considered a turbulent plume driven by a point source of buoyancy and a stable stratification with an upper layer of buoyant fluid underneath the ceiling. This buoyant layer is fed by the entraining plume and drives a flow through the upper vent due to the hydrostatic pressure difference. In both transients and at steady state, the emptying–filling box model allows the thickness and the mean temperature (or density) of the buoyant layer to be estimated, as well as the flow rate of buoyant fluid through the upper vent. In this model, the filling mechanism is similar to that which had been considered by Baines & Turner (Reference Baines and Turner1969) in their ‘filling box’ model, and the draining flow (emptying process) is estimated using Bernoulli’s theorem.
In the Boussinesq limit, one of the major results obtained by Linden et al. (Reference Linden, Lane-Serff and Smeed1990) is that, at steady state, the buoyant layer thickness is a function of a non-dimensional geometrical parameter only, which is defined from the vent areas, the height of the room and the discharge coefficient
$C_{d}$
. In most engineering applications, this discharge coefficient is taken as a constant approximately 0.6–0.7. However, in two conference papers, Hunt & Holford (Reference Hunt and Holford2000) and Holford & Hunt (Reference Holford, Hunt and Dally2001) quantified experimentally the dependence of
$C_{d}$
on density contrast for a horizontal vent involved in a process of emptying or simultaneous filling and emptying of a box. Their experimental results (discussed further in § 4.1) showed that
$C_{d}$
can rapidly decrease with increasing density contrast between the buoyant and ambient fluids. Such a finding suggests that assuming a constant value of
$C_{d}$
could lead to an overestimate of flow rates in natural ventilation problems for which density (or temperature) differences may be significant.
Contrary to what the titles of their papers may suggest, Holford and Hunt’s corrections for
$C_{d}$
were not based explicitly on the density contrast but on the value of a dimensionless discharge (plume) parameter
$\unicode[STIX]{x1D6E4}_{d}$
which quantifies the ratio between buoyancy and momentum in the plume-like flow that develops outside the box from the vent. We can therefore imagine that the behaviour of the external plume (above the vent) is not simply an indicator since it can control the state within the box by modifying the vent discharge coefficient value. The main objective of this paper is to address this issue.
The discharge plume parameter
$\unicode[STIX]{x1D6E4}_{d}$
depends not only on the density contrast, but also on the outflow velocity and the size of the vent. Thus, for an emptying–filling box problem, the value of
$\unicode[STIX]{x1D6E4}_{d}$
could in theory be estimated from the output data of the model proposed by Linden et al. (Reference Linden, Lane-Serff and Smeed1990). Since this model was originally developed using the Boussinesq approximation, we first reformulate in § 2 the general non-Boussinesq case. The expression of the discharge plume parameter
$\unicode[STIX]{x1D6E4}_{d}$
is then obtained explicitly in § 3. In § 4, the dependence of the discharge coefficient
$C_{d}$
on
$\unicode[STIX]{x1D6E4}_{d}$
is discussed on the basis of Holford and Hunt’s experiments and a simple theoretical model is proposed. Implications of a modified
$C_{d}$
(via
$\unicode[STIX]{x1D6E4}_{d}$
) for both steady state and transients of an emptying–filling box are then examined and discussed in § 5.
2 The non-Boussinesq ‘emptying–filling box’ model
2.1 Configuration and hypothesis
As shown in figure 1, we consider the simultaneous filling and emptying of a cuboid box of height
$H$
and (constant) horizontal surface area
$S$
. The box has an upper opening of area
$A$
located at the ceiling and a large lower opening at the floor. Note that this lower opening is large enough that the pressure at floor level is the same as that outside the box. For this reason, only the upper opening is referred to as a vent in what follows. For simplicity, we assume that this vent is a circular opening of diameter
$D$
. A (non-Boussinesq) point source of buoyancy flux
$B$
is set at the floor (
$z=0$
). An internal turbulent plume then rises, impinges with the ceiling and flows along it to form a thin layer in the upper part of the box at the initial time
$t=0$
. Hydrostatic pressure difference then allows the light (or hot) fluid to escape through the vent. The interface between the buoyant fluid layer and ambient air descends over time until steady state is reached. Both during the transients and at steady state, a situation of ideal displacement flow is assumed which supposes: a negligible ‘overturning’ of the initial buoyant layer after colliding with the lateral walls (Kaye & Hunt Reference Kaye and Hunt2007) and a lower opening (for the incoming ambient air) large enough to overcome bidirectional flows at the vent or an inlet jet strongly mixing the interface (Coffey & Hunt Reference Coffey and Hunt2010; Hunt & Coffey Reference Hunt and Coffey2010). For the sake of simplicity, heat transfers (Faure & Le Roux Reference Faure and Le Roux2012; Lane-Serff & Sandbach Reference Lane-Serff and Sandbach2012) and external wind effects (Hunt & Linden Reference Hunt and Linden2001; Li & Delsante Reference Li and Delsante2001; Coomaraswamy & Caulfield Reference Coomaraswamy and Caulfield2011) are ignored.
Figure 1. Schematic of the studied configuration.
2.2 The internal plume model
Following the turbulent plume theory proposed by Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956), we model the internal buoyant release using the self-similar solutions of a non-Boussinesq axisymmetric plume in which the classical Morton’s entrainment coefficient is multiplied by the square root of the plume local density to account for the non-Boussinesq effects (Ricou & Spalding Reference Ricou and Spalding1961; Rooney & Linden Reference Rooney and Linden1996; Woods Reference Woods1997). Note that these solutions are similar to those used for fire plumes (Heskestad Reference Heskestad1984). Using a ‘top-hat’ formalism, the plume characteristics (mean vertical velocity
$u_{p}$
, radius
$b_{p}$
and mean density deficit
$\unicode[STIX]{x1D702}_{p}$
) are then expressed as functions of the vertical coordinate
$z$
, thus
$$\begin{eqnarray}\displaystyle & \displaystyle u_{p}(z)=a^{1/3}B^{1/3}z^{-1/3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle b_{p}(z)=\frac{6\unicode[STIX]{x1D6FC}}{5}z\left[\frac{\unicode[STIX]{x1D70C}_{0}}{\unicode[STIX]{x1D70C}_{p}(z)}\right]^{1/2}=\frac{6\unicode[STIX]{x1D6FC}}{5}z\sqrt{1+\unicode[STIX]{x1D702}_{p}(z)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{p}(z)=\frac{\unicode[STIX]{x1D70C}_{0}-\unicode[STIX]{x1D70C}_{p}(z)}{\unicode[STIX]{x1D70C}_{p}(z)}=\frac{4}{3g}a^{2/3}B^{2/3}z^{-5/3}, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}_{p}$
is the plume mean density (at location
$z$
),
$\unicode[STIX]{x1D70C}_{0}$
is the ambient density,
$g$
is the gravitational acceleration,
$\unicode[STIX]{x1D6FC}$
is the entrainment coefficient (generally taken to be approximately
$0.1$
) and
$a$
is a constant equal to
$25/48\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FC}^{2}$
. The buoyancy flux
$B$
is an invariant which can be expressed from the plume characteristics as:
$$\begin{eqnarray}B=\frac{\unicode[STIX]{x1D702}_{p}g\unicode[STIX]{x03C0}u_{p}b_{p}^{2}}{1+\unicode[STIX]{x1D702}_{p}}.\end{eqnarray}$$
For a buoyant fluid released from a finite area source, these solutions can be vertically shifted using a virtual origin correction at location
$z_{v}$
,
$z$
may be replaced by
$z-z_{v}$
in relations (2.1)–(2.3), and
$z$
may therefore be considered as the height above this virtual origin. The determination of
$z_{v}$
has been extensively studied in the past. Convenient analytical solutions may be found in Candelier & Vauquelin (Reference Candelier and Vauquelin2012) for a wide range of non-Boussinesq round plumes.
2.3 Emptying–filling box conservation equations
Conservation equations are written for the buoyant layer of thickness
$h$
and density
$\unicode[STIX]{x1D70C}$
shown in figure 1. This layer is fed by the internal plume (at height
$z=H-h$
) and the buoyant fluid escapes at the mean velocity
$w$
through the vent of area
$A$
located on the ceiling of the box. These equations are, for the mass flux and the buoyancy flux, respectively:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D70C}Sh}{\text{d}t}=\left.\unicode[STIX]{x1D70C}_{p}\unicode[STIX]{x03C0}b_{p}^{2}u_{p}\right|_{z=H-h}-\unicode[STIX]{x1D70C}wA, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\left[g\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}_{0}}Sh\right]=B-g\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}_{0}}wA, & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}-\unicode[STIX]{x1D70C}$
. Note that by combining these two relations, we naturally obtain the volume flux conservation equation for the buoyant layer.
The outflow velocity
$w$
can be estimated by applying Bernoulli’s theorem between a point located at the interface and a point located at the vent. Denoting
$C_{d}$
the vent discharge coefficient, this may be expressed as
$$\begin{eqnarray}\frac{1}{2}\unicode[STIX]{x1D70C}\left(\frac{w}{C_{d}}\right)^{2}=\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gh.\end{eqnarray}$$
We first replace
$b_{p}$
,
$u_{p}$
and
$\unicode[STIX]{x1D702}_{p}$
from (2.1), (2.2) and (2.3) as functions of
$z$
in equation (2.5) and we then introduce the dimensionless variables
$\unicode[STIX]{x1D701}=z/H$
,
$\unicode[STIX]{x1D702}=\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D714}=w/\sqrt{gH}$
. Following some algebraic manipulations, equations (2.5), (2.6) and (2.7) can then be rewritten as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D714}-\unicode[STIX]{x1D705}\unicode[STIX]{x1D6E9}^{1/2}(\unicode[STIX]{x1D701}^{5/3}+\unicode[STIX]{x1D6E9}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D702}}{\text{d}\unicode[STIX]{x1D70F}}=\frac{1+\unicode[STIX]{x1D702}}{1-\unicode[STIX]{x1D701}}\unicode[STIX]{x1D705}\unicode[STIX]{x1D6E9}^{1/2}(\unicode[STIX]{x1D6E9}-\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}^{5/3}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D714}=C_{d}\sqrt{2\unicode[STIX]{x1D702}(1-\unicode[STIX]{x1D701})}, & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x1D6EC}=A/H^{2}$
a geometrical parameter,
$\unicode[STIX]{x1D70F}=g^{1/2}H^{3/2}t/S$
the dimensionless time,
$\unicode[STIX]{x1D705}$
a constant equal to
$18\sqrt{3}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x03C0}/25$
and
$\unicode[STIX]{x1D6E9}=4a^{2/3}B^{2/3}/3gH^{5/3}$
. Note that the dimensionless parameter
$\unicode[STIX]{x1D6E9}$
corresponds to the value of
$\unicode[STIX]{x1D702}_{p}$
for
$z=H$
(or
$\unicode[STIX]{x1D701}=1$
), namely the value of the density deficit in the initial layer that is formed at the ceiling at
$t=0$
. This parameter also characterizes the strength of the buoyant source relative to the box height.
At steady state, the time derivative terms vanish. Combining (2.8), (2.9) and (2.10) yields:
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D701}_{ss}^{5/3}(\unicode[STIX]{x1D701}_{ss}^{5/3}+\unicode[STIX]{x1D6E9})^{2}}{1-\unicode[STIX]{x1D701}_{ss}}=2\frac{\unicode[STIX]{x1D6EC}^{2}C_{d}^{2}}{\unicode[STIX]{x1D705}^{2}},\end{eqnarray}$$
with
$\unicode[STIX]{x1D701}_{ss}$
the dimensionless interface height at steady state. Note that under the Boussinesq approximation (
$\unicode[STIX]{x1D6E9}\approx 0$
) it may be found that
$\unicode[STIX]{x1D701}_{ss}$
only depends on the geometrical parameter
$\unicode[STIX]{x1D6EC}$
, as highlighted by Linden et al. (Reference Linden, Lane-Serff and Smeed1990). Subsequently, the density difference
$\unicode[STIX]{x1D702}_{ss}$
and the dimensionless outflow velocity
$\unicode[STIX]{x1D714}_{ss}$
at steady state can be expressed as a function of
$\unicode[STIX]{x1D701}_{ss}$
:
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{ss}=\frac{\unicode[STIX]{x1D6E9}}{\unicode[STIX]{x1D701}_{ss}^{5/3}}\quad \text{and}\quad \unicode[STIX]{x1D714}_{ss}=\frac{\unicode[STIX]{x1D705}\unicode[STIX]{x1D6E9}^{1/2}}{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D701}_{ss}^{5/3}+\unicode[STIX]{x1D6E9}).\end{eqnarray}$$
3 The discharge plume parameter
$\unicode[STIX]{x1D6E4}_{d}$
A vertical turbulent plume which results from the upward discharge of a light fluid in a heavier ambient fluid of density
$\unicode[STIX]{x1D70C}_{0}$
may be characterized by a non-dimensional function
$\unicode[STIX]{x1D6E4}(z)$
called the ‘plume function’. The vertical coordinate,
$z$
, is measured positively upwards with the source of the plume at
$z=0$
. By recasting the conservation equations of Morton et al. (Reference Morton, Taylor and Turner1956), this function was introduced by Hunt & Kaye (Reference Hunt and Kaye2005) from a combination of the fluxes (volume, buoyancy and momentum) and later extended in the general non-Boussinesq case by Michaux & Vauquelin (Reference Michaux and Vauquelin2008) from the local plume variables (density
$\unicode[STIX]{x1D70C}_{p}$
, radius
$b_{p}$
and velocity
$u_{p}$
). The plume function quantifies locally the ratio between buoyancy and momentum and can be seen as a normalized form of a Richardson number. Using ‘top-hat’ profiles, it is expressed as
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}(z)=\frac{5}{8\unicode[STIX]{x1D6FC}}\frac{\unicode[STIX]{x1D702}_{p}gb_{p}}{u_{p}^{2}\sqrt{1+\unicode[STIX]{x1D702}_{p}}}.\end{eqnarray}$$
For a pure (or ideal) plume,
$\unicode[STIX]{x1D6E4}(0)=1$
by definition, and the plume function turns out to be invariant with
$z$
. For a non-pure plume,
$\unicode[STIX]{x1D6E4}(z)$
monotonically evolves from its value at the source
$\unicode[STIX]{x1D6E4}(0)$
to unity at large heights. The value of the plume function at
$z=0$
, which is called the ‘plume parameter’, was identified and discussed a long time ago by Morton (Reference Morton1959). In Morton & Middleton (Reference Morton and Middleton1973) a classification was proposed to distinguish the forced plumes (
$\unicode[STIX]{x1D6E4}(0)<1$
) initially dominated by momentum from the lazy plumes (
$\unicode[STIX]{x1D6E4}(0)>1$
) initially dominated by buoyancy.
In an emptying–filling box problem, the flow at the upper vent is characterized by its vertical velocity
$w$
, its density deficit
$\unicode[STIX]{x1D702}$
and its equivalent radius which can be expressed as
$\sqrt{A/\unicode[STIX]{x03C0}}$
with
$A$
the vent area. From relation (3.1), the plume parameter
$\unicode[STIX]{x1D6E4}_{d}$
of the plume-like flow that arises from the vent then reads
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{d}=\frac{5}{8\unicode[STIX]{x1D6FC}}\frac{\unicode[STIX]{x1D702}g\sqrt{A/\unicode[STIX]{x03C0}}}{w^{2}\sqrt{1+\unicode[STIX]{x1D702}}}=\frac{5}{16\unicode[STIX]{x1D6FC}}\frac{1}{C_{d}^{2}}\frac{\sqrt{\unicode[STIX]{x1D6EC}/\unicode[STIX]{x03C0}}}{(1-\unicode[STIX]{x1D701})\sqrt{1+\unicode[STIX]{x1D702}}},\end{eqnarray}$$
and is now called the ‘discharge plume parameter’. Note that this plume-like flow arising from the vent will be simply referred as ‘the plume’ in the following. It corresponds to the external plume of the problem and should not be confused with the internal plume within the box.
Since
$\unicode[STIX]{x1D701}$
decreases (from
$1$
to smaller values) during transients of an emptying–filling box, relation (3.2) indicates that
$\unicode[STIX]{x1D6E4}_{d}$
must be infinite at the beginning. Since
$\unicode[STIX]{x1D702}$
increases (from
$\unicode[STIX]{x1D6E9}$
to higher values),
$\unicode[STIX]{x1D6E4}_{d}$
always decreases over time (
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{d}/\unicode[STIX]{x2202}\unicode[STIX]{x1D701}>0$
and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{d}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}<0$
) except if the variables
$\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D702}$
overshoot their final location (see Kaye & Hunt Reference Kaye and Hunt2004 and Vauquelin Reference Vauquelin2015). In such a case the time derivative of
$\unicode[STIX]{x1D6E4}_{d}$
,
$$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D6E4}_{d}}{\text{d}\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6E4}_{d}\left[\frac{1}{1-\unicode[STIX]{x1D701}}\frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}\unicode[STIX]{x1D70F}}-\frac{1}{2}\frac{1}{1+\unicode[STIX]{x1D702}}\frac{\text{d}\unicode[STIX]{x1D702}}{\text{d}\unicode[STIX]{x1D70F}}\right],\end{eqnarray}$$
indicates that
$\unicode[STIX]{x1D6E4}_{d}$
can overshoot and reach a minimal value if
$\text{d}\unicode[STIX]{x1D701}/\text{d}\unicode[STIX]{x1D70F}$
and
$\text{d}\unicode[STIX]{x1D702}/\text{d}\unicode[STIX]{x1D70F}$
are both positive, that is to say between the layer overshoot (
$\text{d}\unicode[STIX]{x1D701}/\text{d}\unicode[STIX]{x1D70F}=0$
) and the so-called thermal overshoot (
$\text{d}\unicode[STIX]{x1D702}/\text{d}\unicode[STIX]{x1D70F}=0$
). This behaviour is illustrated in figure 2 from a numerical integration of conservation equations (2.8), (2.9) and (2.10) for a particular case where
$\unicode[STIX]{x1D6EC}=0.02$
and
$\unicode[STIX]{x1D6E9}=0.5$
.
Figure 2. Evolution and overshoot occurrence of
$\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D6E4}_{d}$
as a function of the dimensionless time
$\unicode[STIX]{x1D70F}$
. Calculations were made for
$\unicode[STIX]{x1D6EC}=0.02$
and
$\unicode[STIX]{x1D6E9}=0.5$
.
At steady state, by using relations (2.11) and (2.12) in (3.2), we find that:
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{d}=\left(\frac{3}{8}\right)^{5/4}C_{d}^{-5/2}\left(\frac{\unicode[STIX]{x1D701}_{ss}}{1-\unicode[STIX]{x1D701}_{ss}}\right)^{5/4}\quad \Longrightarrow \quad \unicode[STIX]{x1D701}_{ss}=\frac{1}{1+\displaystyle \frac{3}{8C_{d}^{2}\unicode[STIX]{x1D6E4}_{d}^{4/5}}}.\end{eqnarray}$$
This result is of considerable practical value since it demonstrates that the thickness of the buoyant layer (or the smoke free height for fire safety issues) is a function of the plume discharge parameter alone and is independent of the source buoyancy flux and of the geometry. Hence, it is possible to estimate the interface location at steady state from the ‘laziness’ of the plume at the vent alone. In particular, if we consider the classical value
$C_{d}\approx 0.6$
we find that the plume at the vent will be lazy (
$\unicode[STIX]{x1D6E4}_{d}>1$
) as long as
$z_{ss}/H=\unicode[STIX]{x1D701}_{ss}\gtrsim 0.49$
, and then forced (
$\unicode[STIX]{x1D6E4}_{d}<1$
) at lower locations of the interface. Furthermore, for lazy plumes, a contraction (also called a neck) can occur as soon as the plume parameter exceeds
$1.5$
or
$2.5$
, depending on the density contrast (Fanneløp & Webber Reference Fanneløp and Webber2003; Michaux & Vauquelin Reference Michaux and Vauquelin2008), that is to say in the range
$0.53\lesssim \unicode[STIX]{x1D701}_{ss}\lesssim 0.67$
according to relation (3.4). These results are summarized in figure 3 in which a classification of the plume rising through the vent is given as a function of the interface location at steady state. We should note, of course, that the numerical values indicated in figure 3 are related to the assumptions used: ‘top-hat’ profiles and constant entrainment coefficient
$\unicode[STIX]{x1D6FC}$
.
Figure 3. Classification of the plume at the vent as a function of the interface location at steady state (for
$C_{d}=0.6$
).
4 How
$C_{d}$
depends on
$\unicode[STIX]{x1D6E4}_{d}$
4.1 Holford and Hunt’s experimental results
Holford and Hunt’s experiments investigated a displacement mode of ventilation. A layer of salt solution drained out through an opening in the base of a container immersed in a larger water-filled tank (note that there is a switch in directions between salt and heat). Their first paper (Hunt & Holford Reference Hunt and Holford2000) reported only a few experiments, carried out for a restricted range of
$\unicode[STIX]{x1D6E4}_{d}$
lying between
$0$
and
$40$
in steady state experiments that involved simultaneous filling and emptying of the immersed container. A quadratic fit:
$$\begin{eqnarray}C_{d}=0.71-1.910^{-4}\unicode[STIX]{x1D6E4}_{d}^{2}\quad \text{for }0\leqslant \unicode[STIX]{x1D6E4}_{d}\leqslant 40,\end{eqnarray}$$
was proposed. The authors justified this fit with the observation that it is consistent with
$\text{d}C_{d}/\text{d}\unicode[STIX]{x1D6E4}_{d}=0$
at
$\unicode[STIX]{x1D6E4}_{d}=0$
. Although the data were somewhat dispersed, these early experiments clearly indicate a rapid decrease of the discharge coefficient
$C_{d}$
when the plume discharge parameter
$\unicode[STIX]{x1D6E4}_{d}$
rises above
$10$
. Their second paper (Holford & Hunt Reference Holford, Hunt and Dally2001) reported additional data obtained from transient draining experiments. The discharge coefficient
$C_{d}$
was deduced from a comparison between the experimental volume flow rate and that given by an ideal model. A best fit was derived in two regions, for a wider range of
$\unicode[STIX]{x1D6E4}_{d}$
:
$$\begin{eqnarray}C_{d}=\left\{\begin{array}{@{}ll@{}}0.63 & \text{if }0<\unicode[STIX]{x1D6E4}_{d}<4.9,\\ 1.11\unicode[STIX]{x1D6E4}_{d}^{-0.356} & \text{if }4.9<\unicode[STIX]{x1D6E4}_{d}<500.\\ \end{array}\right.\end{eqnarray}$$
It can be seen that a correction on the discharge coefficient is then required for a discharge plume parameter that exceeds the critical value
$\unicode[STIX]{x1D6E4}_{d}^{crit}=4.9$
, and thus for a lazy plume exhibiting a neck (i.e. a contraction relatively close to the source). In their analyses, the authors considered that this buoyancy-induced contraction reduces the fraction of the opening area occupied by the discharge, giving rise to reduced values of
$C_{d}$
.
4.2 A proposal for a simple model
Following the idea of an opening area reduction due to a plume contraction introduced by Holford & Hunt (Reference Holford, Hunt and Dally2001), we can consider that if an unmodified discharge coefficient
$C_{d}^{\star }$
(
${\sim}0.6$
) can be applied to the reduced area
$A_{neck}$
, then the discharge coefficient has to be modified considering the effective area
$A$
of the vent. This would mean that
$C_{d}^{\star }A_{neck}=C_{d}A$
, i.e.
$C_{d}/C_{d}^{\star }=(b_{neck}/b)^{2}$
where
$b_{neck}$
is the plume radius at the neck and
$b$
is the radius (or the equivalent radius) of the vent.
For non-Boussinesq lazy plumes, Michaux & Vauquelin (Reference Michaux and Vauquelin2008) showed that the plume radius
$b_{p}(z)$
and the plume density deficit
$\unicode[STIX]{x1D702}_{p}(z)$
can be expressed from the plume function
$\unicode[STIX]{x1D6E4}(z)$
and the known initial values at
$z=0$
(indicated with the subscript
$i$
) as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{b_{p}(z)}{b_{i}}=\left[\frac{1+\unicode[STIX]{x1D702}(z)}{1+\unicode[STIX]{x1D702}_{i}}\right]^{1/2}\left[\frac{\unicode[STIX]{x1D6E4}(z)}{\unicode[STIX]{x1D6E4}_{i}}\right]^{1/2}\left[\frac{\unicode[STIX]{x1D6E4}_{i}-1}{\unicode[STIX]{x1D6E4}(z)-1}\right]^{3/10}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D702}_{p}(z)}{\unicode[STIX]{x1D702}_{i}}=\left[\frac{\unicode[STIX]{x1D6E4}_{i}}{\unicode[STIX]{x1D6E4}(z)}\right]^{1/2}\left[\frac{\unicode[STIX]{x1D6E4}(z)-1}{\unicode[STIX]{x1D6E4}_{i}-1}\right]^{1/2}. & \displaystyle\end{eqnarray}$$
Thus, for a contracting lazy plume, by considering
$z$
at the neck location and the (initial) values of the plume variables at the vent (radius
$b$
, density deficit
$\unicode[STIX]{x1D702}$
and plume parameter
$\unicode[STIX]{x1D6E4}_{d}$
), relations (4.3) and (4.4) lead to
$$\begin{eqnarray}\left(\frac{b_{neck}}{b}\right)^{2}=\frac{1+\unicode[STIX]{x1D702}\displaystyle \left(\frac{\unicode[STIX]{x1D6E4}_{d}}{\unicode[STIX]{x1D6E4}_{neck}}\right)^{1/2}\left(\frac{\unicode[STIX]{x1D6E4}_{neck}-1}{\unicode[STIX]{x1D6E4}_{d}-1}\right)^{1/2}}{1+\unicode[STIX]{x1D702}}\frac{\unicode[STIX]{x1D6E4}_{neck}}{\unicode[STIX]{x1D6E4}_{d}}\left(\frac{\unicode[STIX]{x1D6E4}_{d}-1}{\unicode[STIX]{x1D6E4}_{neck}-1}\right)^{3/5}.\end{eqnarray}$$
For non-Boussinesq plumes, the value of
$\unicode[STIX]{x1D6E4}_{neck}$
is the real root of a third-order polynomial form whose coefficients depend on the value of
$\unicode[STIX]{x1D702}$
(see Michaux & Vauquelin Reference Michaux and Vauquelin2008). This introduces an additional parameter, so we will simply consider the two asymptotic cases corresponding to low and to high density contrasts in the following.
For low density contrasts (
$\unicode[STIX]{x1D702}\ll 1$
, i.e. in the Boussinesq approximation) the value of the plume function at the neck location is exactly
$5/2$
(Fanneløp & Webber Reference Fanneløp and Webber2003) and the previous relation then becomes:
$$\begin{eqnarray}\frac{C_{d}}{C_{d}^{\star }}=\frac{5}{2^{2/5}3^{3/5}}\frac{(\unicode[STIX]{x1D6E4}_{d}-1)^{3/5}}{\unicode[STIX]{x1D6E4}_{d}}\simeq 1.96\frac{(\unicode[STIX]{x1D6E4}_{d}-1)^{3/5}}{\unicode[STIX]{x1D6E4}_{d}}\quad \text{for }\unicode[STIX]{x1D6E4}_{d}>\unicode[STIX]{x1D6E4}_{d}^{crit}=5/2.\end{eqnarray}$$
For large density contrasts (
$\unicode[STIX]{x1D702}\rightarrow \infty$
) the value of the plume function decreases towards
$5/4$
(Michaux & Vauquelin Reference Michaux and Vauquelin2008) yielding:
$$\begin{eqnarray}\frac{C_{d}}{C_{d}^{\star }}=\frac{\sqrt{5}}{2^{4/5}}\frac{(\unicode[STIX]{x1D6E4}_{d}-1)^{1/10}}{\unicode[STIX]{x1D6E4}_{d}^{1/2}}\simeq 1.28\frac{(\unicode[STIX]{x1D6E4}_{d}-1)^{1/10}}{\unicode[STIX]{x1D6E4}_{d}^{1/2}}\quad \text{for }\unicode[STIX]{x1D6E4}_{d}>\unicode[STIX]{x1D6E4}_{d}^{crit}=5/4.\end{eqnarray}$$
In both cases, when
$\unicode[STIX]{x1D6E4}_{d}\gg 1$
, we find that
$C_{d}\propto \unicode[STIX]{x1D6E4}_{d}^{-2/5}$
is qualitatively consistent with the correlation (4.2) derived by Holford & Hunt (Reference Holford, Hunt and Dally2001) from their draining experiments.
The fits (4.1) and (4.2) proposed in Hunt & Holford (Reference Hunt and Holford2000) and Holford & Hunt (Reference Holford, Hunt and Dally2001) are plotted with the theoretical wrap-around relations (4.6) and (4.7) illustrated in figure 4. The first fit given by the relation (4.1) does not seem to fully reflect physical reality probably because it was derived from a very limited number of data points. The second fit given by relation (4.2) and the theoretical relation (4.6) for low density contrasts are more likely to agree. However, whatever the hypothesis with respect to the density contrast, the main difference between the theoretical relations in (4.6) and (4.7) and Holford and Hunt’s second correlation is due to our choice of
$\unicode[STIX]{x1D6E4}_{d}^{crit}$
(theoretically
$5/2$
for low density contrasts and
$5/4$
for large density contrast instead of the experimental value
$4.9$
). This difference is not really surprising since our theoretical model based on the necking effect only is a somewhat simplified view of the physics of such a discharge flow. Furthermore, the present plume theory considers ‘top-hat’ profiles and a constant entrainment coefficient, which is probably, in the near field of a lazy plume, a source of additional uncertainties, as recently discussed by van Reeuwijk & Craske (Reference van Reeuwijk and Craske2015) and Carlotti & Hunt (Reference Carlotti and Hunt2017).
Nevertheless, in spite of the simplicity of our approach, by rescaling the theoretical relations (4.6) and (4.7) using the suitable (experimental) critical value
$\unicode[STIX]{x1D6E4}_{d}^{crit}=4.9$
, the coefficients in these relations become
$2.16$
and
$1.89$
(instead of
$1.96$
and
$1.28$
), respectively, in good agreement with (4.2) as shown in figure 5.
Figure 4. Decrease of the discharge coefficient (divided by the constant unmodified discharge coefficient
$C_{d}^{\star }$
) as a function of the discharge plume parameter
$\unicode[STIX]{x1D6E4}_{d}$
. Here, (a) is the best fit from Hunt & Holford (Reference Hunt and Holford2000), (b) is the best fit from Holford & Hunt (Reference Holford, Hunt and Dally2001), (c) is the relation (4.6) for low density contrasts and (d) is the relation (4.7) for high density contrasts.
Figure 5. Decrease of the discharge coefficient (divided by the constant unmodified discharge coefficient
$C_{d}^{\star }$
) as a function of the discharge plume parameter
$\unicode[STIX]{x1D6E4}_{d}$
. Here, the bold line is the best fit from Holford & Hunt (Reference Holford, Hunt and Dally2001), (c) is the relation (4.6) and (d) is the relation (4.7) both corrected to agree with the experimental critical value
$\unicode[STIX]{x1D6E4}_{d}^{crit}=4.9$
.
Figure 6. Time evolution of the dimensionless interface height
$\unicode[STIX]{x1D701}$
for
$\unicode[STIX]{x1D6EC}=0.1$
and three different values of
$\unicode[STIX]{x1D6E9}$
:
$0.5$
(a);
$1$
(b);
$1.5$
(c). The solid line represents a constant discharge coefficient
$C_{d}=0.6$
, and the dashed line the modified discharge coefficient given in relation (5.1).
5 The modified emptying–filling box model
In this section, the emptying–filling box equations are solved for a variable discharge coefficient
$C_{d}=f(\unicode[STIX]{x1D6E4}_{d})$
. In particular, comparisons are made with results obtained for an unmodified discharge coefficient
$C_{d}^{\star }=0.6$
. For these comparisons we have chosen to use the theoretical relation (4.6), modified to be in accordance with the critical value
$\unicode[STIX]{x1D6E4}_{d}^{crit}=4.9$
found experimentally by Holford & Hunt (Reference Holford, Hunt and Dally2001):
$$\begin{eqnarray}C_{d}=\left\{\begin{array}{@{}ll@{}}0.6 & \displaystyle \text{if }\unicode[STIX]{x1D6E4}_{d}<4.9,\\ \displaystyle 1.3\frac{(\unicode[STIX]{x1D6E4}_{d}-1)^{3/5}}{\unicode[STIX]{x1D6E4}_{d}} & \text{if }\unicode[STIX]{x1D6E4}_{d}>4.9.\\ \end{array}\right.\end{eqnarray}$$
Note that according to relation (3.4), the critical value
$\unicode[STIX]{x1D6E4}_{d}^{crit}=4.9$
corresponds to a dimensionless layer height
$\unicode[STIX]{x1D701}_{ss}^{crit}\approx 0.77$
which indicates that consideration of a variable
$C_{d}$
will have an impact on steady state predictions only for relatively thin upper layers (lower than
$\backsim 23\,\%$
of the box height).
Figure 6 presents the results of a numerical integration of conservation equations (2.8), (2.9) and (2.10) with and without correction of the discharge coefficient, for a geometrical parameter
$\unicode[STIX]{x1D6EC}=0.1$
and three values of the dimensionless parameter
$\unicode[STIX]{x1D6E9}$
(
$0.5$
,
$1$
and
$1.5$
). Curves (a) for
$\unicode[STIX]{x1D6E9}=0.5$
reveal faster filling, a slight overshoot and a deeper layer of buoyant fluid at steady state when considering the modified discharge coefficient. By doubling the value of
$\unicode[STIX]{x1D6E9}$
(that is, by multiplying the buoyancy flux by
$2^{3/2}$
), it can be seen from curves (b) that
$\unicode[STIX]{x1D701}$
drops below the critical value (
$\unicode[STIX]{x1D701}^{crit}=0.77$
) during transients and the steady state is then unaffected by the correction of the discharge coefficient. Filling is still faster with the modified model. Curves (c) for
$\unicode[STIX]{x1D6E9}=1.5$
no longer allow us to distinguish between the two models since
$\unicode[STIX]{x1D701}$
rapidly drops below
$\unicode[STIX]{x1D701}^{crit}$
during transients.
6 Conclusion
In the simultaneous filling (by an internal plume issuing from a point source of buoyancy) and emptying of a box, the characteristics of the plume-like flow that develops outside the box from an upper vent allows a ‘plume parameter’ to be constructed: the ‘discharge plume parameter’ which we denote
$\unicode[STIX]{x1D6E4}_{d}$
. This non-dimensional parameter quantifies the ratio between buoyancy and momentum in the flow at the vent and it can be expressed analytically from the output data of the emptying–filling box model assuming a displacement ventilation mode. In the transient phase of an emptying–filling box, the discharge plume parameter decreases from an infinite value (at
$t=0$
) to a finite value at steady state which allows the height of the interface (between air and buoyant fluid) to be estimated whatever the source buoyancy flux. In particular, the plume above the vent is buoyancy dominated at the beginning and can become momentum dominated as soon as the box is (approximately) half-filled. Previous experiments have shown that the discharge coefficient
$C_{d}$
of a draining process may fall dramatically below its classical value (
$C_{d}\sim 0.6{-}0.7$
) for large values of the discharge plume parameter. By including the relation that links
$C_{d}$
to
$\unicode[STIX]{x1D6E4}_{d}$
in the emptying–filling box model, we show that transients and steady state are broadly unchanged provided the buoyant layer depth is greater than approximately one-quarter of the box height. For thinner buoyant layers however, estimations made with an unmodified
$C_{d}$
significantly underestimate the buoyant layer depth in both transients and steady state of an emptying–filling box.
