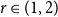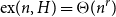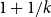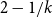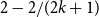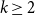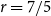1. Introduction
Given a family
$\mathcal{H}$
of graphs, a graph G is called
$\mathcal{H}$
-free if it contains no member of
$\mathcal{H}$
as a subgraph. The Turán number
$ex(n,\mathcal{H})$
of
$\mathcal{H}$
is the maximum number of edges in an n-vertex
$\mathcal{H}$
-free graph. When
$\mathcal{H}$
consists of a single graph H, we write ex(n,H) for
$ex(n,\{H\})$
. The study of Turán numbers plays a central role in extremal graph theory. The celebrated Erdős–Simonovits–Stone theorem [Reference Erdős and Simonovits12,Reference Erdős and Stone14] states that if
$\chi(\mathcal{H})$
denotes the minimum chromatic number of a graph in
$\mathcal{H}$
, then
\[\mathrm{ex}(n,\mathcal{ H})=\left(1-\frac{1}{\chi(\mathcal{H})-1}\right)\binom{n}{2}+o(n^2).\]
Thus, the function is asymptotically determined if
$\chi(\mathcal{H})\geq 3$
. If
$\chi(\mathcal{H})=2$
, that is, if
$\mathcal{H}$
contains a bipartite graph, then this only gives
$\mathrm{ex}(n,\mathcal{H})=o(n^2)$
. The numbers
$\mathrm{ex}(n,\mathcal{H})$
when
$\chi(\mathcal{H})=2$
are commonly referred in literature as degenerate Turán numbers and are known even asymptotically only for few families. More generally, Erdős and Simonovits conjectured that if
$\mathcal{H}$
is a finite family with
$\chi(\mathcal{H})=2$
then there is a rational
$r\in [1,2)$
and a constant
$c>0$
such that
$\lim_{n\to \infty}\mathrm{ex}(n,\mathcal{H})/n^r=c$
(see Conjecture 1.6 of [Reference Füredi and Simonovits20]). This conjecture is still wide open. Another conjecture which may be viewed as the inverse extremal problem of the previous one is that for every rational
$r\in [1,2)$
there exists a finite family
$\mathcal{H}$
of graphs such that
$\mathrm{ex}(n,\mathcal{H})=\Theta(n^r)$
. (See Conjecture 2.37 of [Reference Füredi and Simonovits20].) In recent breakthrough work by Bukh and Conlon [Reference Bukh and Conlon4], this second conjecture has been verified, using a random algebraic method that is built on the earlier work coming from [Reference Blagojević, Bukh and Karasev2,Reference Bukh3,Reference Conlon7].
However, the following analogous problem on the Turán number of a single bipartite graph, raised by Erdős and Simonovits [Reference Erdős10], is still wide open.
Question 1.1
(([Reference Erdős10])). Is it true that for every rational number r in [1,2) there exists a single bipartite graph
$H_r$
such that
$\mathrm{ex}(n,H_r)=\Theta(n^r)$
?
We will refer to a rational r for which Question 1.1 has an affirmative answer as a Turán exponent for a single graph. The only known Turán exponents for single graphs from the literature are rational numbers of the forms
$1, 1+\frac{1}{s}$
and
$2-\frac{1}{s}$
for all integers
$s\geq 2$
. For any tree T of at least two edges, it is clear that
$\mathrm{ex}(n,T)=\Theta(n)$
. It is known that
$\mathrm{ex}(n,K_{s,t})=\Theta(n^{2-1/s})$
when
$t>(s-1)!$
(by [Reference Alon, Rónyai and Szabó1, Reference Kollár, Rónyai and Szabó29, Reference KövÁri, Sós and Turán30]). Let
$\theta_{k,p}$
denote the graph obtained by taking the union of p internally disjoint paths of length k between a pair of vertices. Faudree and Simonovits [Reference Faudree and Simonovits15] showed that
$\mathrm{ex}(n,\theta_{k,p})=O(n^{1+1/k})$
for all
$p\geq 2$
(also see [Reference Bukh and Tait5] for recent improvement on the bound) while Conlon [Reference Conlon7] showed that for every
$k\geq 2$
there exists
$p_0$
such that for all
$p\geq p_0$
we have
$\mathrm{ex}(n,\theta_{k,p})=\Omega(n^{1+1/k})$
. Hence, for each k and sufficiently large p, we have
$\mathrm{ex}(n,\theta_{k,p})=\Theta(n^{1+1/k})$
. For a more thorough discussion about degenerate Turán numbers, the reader is referred to the recent survey by Füredi and Simonovits [Reference Füredi and Simonovits20]. Our main theorem is as follows, which in particular establishes a new family of Turán exponents.
Theorem 1.2. For any rational number
$r=2-\frac{2}{2s+1}$
, where
$s\geq 2$
is an integer, or
$r=\frac75$
, there exists a graph H such that
$\mathrm{ex}(n,H)=\Theta(n^r)$
.
In establishing the first part of our main theorem, we establish a stronger result concerning the Turán numbers of cube-like graphs, which also answers a question of Pinchasi and Sharir [Reference Pinchasi and Sharir32]. This result may be of independent interest. To establish the second part of our main result, we develop an asymmetric Turán bound on
$\theta_{k,p}$
which may be viewed as a common generalisation of results of Faudree and Simonovits [Reference Faudree and Simonovits15] as well as of Naor and Verstraëte[Reference Naor and Verstraëte31]. To describe our results, we need some more detailed background, which we discuss over several subsections.
1.1. The theorem of Bukh and Conlon and a conjecture
Bukh and Conlon [Reference Bukh and Conlon4] proved the existence of a finite family with a given Turán exponent by considering bipartite graphs constructed in the following way. Given a tree T together with an independent set
$R\subseteq V(T)$
, we call (T,R) a rooted tree and R the root set. Given any
$S\subseteq V(T)\setminus R$
, let e(S) denote the number of edges of T with at least one endpoint in S. Let
$\rho_S=e(S)/|S|$
. Let
$\rho_T=\rho(V(T)\setminus R)$
. We say that the rooted tree (T,R) is balanced if
$\rho_S\geq \rho_T$
for all
$S\subseteq V(T)\setminus R$
. Given a rooted tree (T,R) and a positive integer p, let
$\mathcal{T}^p_R$
denote the family of graphs consisting of all possible union of p distinct labelled copies of T, each of which agree on the root set R. We call
$\mathcal{T}^p_R$
the pth power family of (T,R). The key result of Bukh and Conlon [Reference Bukh and Conlon4] is the following:
Theorem 1.3
([Reference Bukh and Conlon4]). For any balanced rooted tree (T, R), there exists a
$p_0$
such that for all
$p\geq p_0$
,
\[\mathrm{ex}(n,\mathcal{T}^p_R)=\Omega(n^{2-1/\rho_T}).\]
A straightforward counting argument shows that
$\mathrm{ex}(n,\mathcal{T}^p_R)=O(n^{2-1/\rho_T})$
and thus implies that
$\mathrm{ex}(n,\mathcal{T}^p_R)=\Theta(n^{2-1/\rho_T})$
for sufficiently large p. Bukh and Conlon [Reference Bukh and Conlon4] also showed that for each rational r in (1,2), there exists a balanced rooted tree (T,R) with
$\rho_T=\frac{1}{2-r}$
, thereby establishing the existence of a family
$\mathcal{H}_r$
with
$\mathrm{ex}(n,\mathcal{H}_r)=\Theta(n^r)$
for each rational
$r\in (1,2)$
.
Let (T, R) be a balanced rooted tree. Let
$T^p_R$
denote the unique member of
$\mathcal{T}^p_R$
in which the p labelled copies of T are pairwise vertex disjoint outside R. We call
$T^p_R$
the pth power of (T, R). By Theorem 1.3,
\[\mathrm{ex}(n,T^p_R)\geq \mathrm{ex}(n,\mathcal{T}^p_R)= \Omega(n^{2-1/\rho_T}).\]
Bukh and Conlon [Reference Bukh and Conlon4] made the following conjecture.
Conjecture 1.4 ([4]). If (T, R) is a balanced rooted tree, then
\[\mathrm{ex}(n, T^p_R) =O(n^{2-1/\rho_T}).\]
Note that if Conjecture 1.4 is true then together with Theorem 1.3 it would answer Question 1.1 in a very strong sense.
Let
$D_s$
be the tree obtained by taking two disjoint stars with s leaves and joining the two central vertices by an edge, and R the set of all the leaves in
$D_s$
. It is easy to check that
$(D_s,R)$
is balanced with
$\rho_{D_s}=\frac{2s+1}{2}$
. For brevity, from now on we will drop the subscript R, and denote the tth power of
$(D_s,R)$
by
$D_s^t$
.
We will show that (in Corollary 1.7)
$\mathrm{ex}(n, D_s^t)=O(n^{2-\frac{2}{2s+1}})$
for all
$t\geq s\geq 2$
and thereby making a first step towards Conjecture 1.4. To obtain our upper bound on
$\mathrm{ex}(n, D_s^t)$
, we consider a supergraph
$H_{s,t}$
of
$ D_s^t$
defined to be the graph obtained from two vertex disjoint copies of
$K_{s,t}$
by adding a matching that joins the two images of every vertex in
$K_{s,t}$
. In particular, we note that
$H_{2,2}=Q_8$
, the 3-dimensional cube.
1.2. The cube and its generalisation
The well-known cube theorem of Erdős and Simonovits [Reference Erdős and Simonovits13] states that
$\mathrm{ex}(n,Q_8)=O(n^{8/5})$
. Pinchasi and Sharir [Reference Pinchasi and Sharir32] gave a new proof of this and extended it to bipartite setting. More recently, Füredi [Reference Füredi19] showed that
$\mathrm{ex}(n,Q_8)\leq n^{8/5}+(2n)^{3/2}$
, giving yet another proof of the cube theorem.
Pinchasi and Sharir found it to be more convenient to view
$Q_8$
as
$H_{2,2}$
and, more generally, view
$H_{s,t}$
as being obtained as follows. Let
$t\geq s\geq 2$
be positive integers. Let M be an s-matching
$a_1b_1,a_2b_2,\ldots, a_sb_s$
, and N a t-matching
$c_1d_1,c_2d_2, \ldots, c_t d_t$
, where M and N are vertex disjoint. Then
$H_{s,t}$
is obtained from
$M\cup N$
by adding edges
$a_id_j$
and
$b_ic_j$
over all
$i\in [s]$
and
$j\in [t]$
. Motivated by the method of their proof of the cube theorem, Pinchasi and Sharir [Reference Pinchasi and Sharir32] posed the following question:
Question 1.5
[Reference Pinchasi and Sharir32]. Is it true that for all
$t\geq s\geq 2$
,
\[\mathrm{ex}(n,H_{s,t})=O(n^{2-2/(2s+1)})?\]
They were able to show that
$\mathrm{ex}(n,\{H_{s,t}, K_{s+1,s+1}\})=O(n^{2-2/(2s+1)})$
. Also in [Reference Jiang and Newman24] it was shown that
$\mathrm{ex}(n,H_{s,s})=O(n^{2-2/(2s+1)})$
. In this paper, we answer Pinchasi and Sharir
$^{\prime}$
s question affirmatively as follows.
Theorem 1.6. For any
$t\geq s\geq 2$
,
$\mathrm{ex}(n,H_{s,t})=O\left(n^{2-2/(2s+1)}\right)$
.
Note that
$ D_s^t\subseteq H_{s,t}$
. Hence, Theorems 1.3 and 1.6 together yield the following.
Corollary 1.7. There exists a function
$\ell$
such that for all
$s\geq 2$
and
$t\geq \ell(s)$
,
\[\mathrm{ex}(n,H_{s,t})=\Theta(n^{2-2/(2s+1)}) \quad \mbox{and} \quad\mathrm{ex}(n, D_s^t) = \Theta(n^{2-2/(2s+1)}).\]
1.3. Theta graphs and power of a 3-comb
We call a 3-comb, denoted by
$T_3$
, the tree obtained from a 3-vertex path
$P=abc$
by adding three new vertices a
$^{\prime}$
,b
$^{\prime}$
,c
$^{\prime}$
and three new edges aa
$^{\prime}$
, bb
$^{\prime}$
, cc
$^{\prime}$
. Let R be the set of all the leaves of
$T_3$
. For each
$p\geq 2$
, recall that
$(T_3)^p_R$
is the p-th power of
$(T_3,R)$
. For convenience, we will drop the subscript R and abbreviate
$(T_3)^p_R$
as
$T_3^p$
.
It is easy to see that
$(T_3,R)$
is balanced with density
$5/3$
. Hence, by Theorem 1.3, there exists
$p_0$
such that for all
$p\geq p_0$
,
$\mathrm{ex}(n,T_3^p)=\Omega(n^{7/5})$
.
We prove a matching upper bound as follows.
Theorem 1.8. For all
$p\geq 2$
, it holds that
$\mathrm{ex}(n,T_3^p)=O(n^{7/5})$
.
Corollary 1.9. There exists a positive integer
$p_0$
such that for all
$p\geq p_0$
,
$\mathrm{ex}(n,T_3^p)=\Theta(n^{7/5}).$
A key step in the proof of Theorem 1.8 is to study Turán numbers of theta graphs in the bipartite setting. Given a family
$\mathcal{H}$
of graphs and positive integers m, n, the asymmetric bipartite Turán number
$ex(m,n,\mathcal{H})$
of
$\mathcal{H}$
denotes the maximum number of edges in an m by n bipartite graph that does not contain any member of
$\mathcal{H}$
as a subgraph. If
$\mathcal{H}$
has just one member H, we write ex(m,n,H) for
$ex(m,n,\{H\})$
. The function
$ex(m,n, C_{2k})$
had been studied in the context of number theoretic and geometric problems. Naor and Verstraëte [Reference Naor and Verstraëte31] proved that for
$m\le n$
and
$k\ge 2$
,
\begin{equation*}ex(m,n,C_{2k})\le \left\{\begin{array}{ll} (2k-3)\cdot [(mn)^{\frac{k+1}{2k}}+m+n] & \text{if } k \text{ is odd}, \\ (2k-3)\cdot [m^{\frac{k+2}{2k}}n^{\frac{1}{2}}+m+n] & \text{if } k \text{ is even}. \end{array}\right.\end{equation*}
Recall that Faudree and Simonovits [Reference Faudree and Simonovits15] showed that
$\mathrm{ex}(n,\theta_{k,p})=O(n^{1+1/k})$
. Since
$\theta_{k,2}=C_{2k}$
, the following theorem can be viewed as a common generalisation of the results in [Reference Faudree and Simonovits15, Reference Naor and Verstraëte31].
Theorem 1.10. Let
$m,n, k,p\geq 2$
be integers, where
$m\leq n$
. There exists a positive constant
$c=c(k,p)$
such that
\begin{equation*}ex(m,n,\theta_{k,p})\le \left\{\begin{array}{ll} c\cdot [(mn)^{\frac{k+1}{2k}}+m+n] & \text{if } k \text{ is odd}, \\ c\cdot [m^{\frac{k+2}{2k}}n^{\frac{1}{2}}+m+n] & \text{if } k \text{ is even}. \end{array}\right.\end{equation*}
Furthermore, it suffices to take
$c=16kp^k$
.
The rest of the paper is organised as follows. In Section 2, we state some preliminary results. In Section 3, we prove Theorem 1.6. In Section 4, we prove Theorem 1.10. In Section 5, we prove Theorem 1.8.
2. Preliminaries
In this section, we present some of the auxiliary lemmas which are used in the proofs of main results. The first three are folklore, and the proofs of the other two can be found in [Reference Jiang and Newman24].
Lemma 2.1. Every graph G has a bipartite subgraph G
$^{\prime}$
with
$e(G')\geq \frac12 e(G)$
. Also, every graph H with average degree d has a subgraph H
$^{\prime}$
with
$\delta(H')\geq \frac{1}{2} d$
.
Lemma 2.2. Let G be a bipartite graph with a bipartition (A,B). Let
$d_A=e(G)/|A|$
and
$d_B=e(G)/|B|$
. There exists a subgraph G
$^{\prime}$
of G with
$e(G')\geq \frac12 e(G)$
such that each vertex in
$V(G')\cap A$
has degree at least
$\frac14 d_A$
in G
$^{\prime}$
and each vertex in
$V(G')\cap B$
has degree at least
$\frac14 d_B$
in G
$^{\prime}$
.
Lemma 2.3. Let k be a positive integer and T be a rooted tree with k edges. If G is a graph with minimum degree at least k and v is any vertex in G, then G contains a copy of T rooted at v.
Lemma 2.4
([Reference Jiang and Newman24], Lemma 5.3). Let t be a positive integer and G be an n-vertex bipartite graph with at least 4t n edges. Then the number of t-matchings in G is at least
$\frac{e(G)^t}{2^tt!}$
.
Lemma 2.5
([Reference Jiang and Newman24], Lemma 5.5). Let t be a positive integer and G be an n-vertex bipartite graph with a bipartition (A,B). Suppose G has at least
$4\sqrt{2t} n^{3/2}$
edges. Then the number of
$H_{1,t}$
$^{\prime}$
s in G is at least
\[\frac{1}{2^{5t+2} t!}\cdot \frac{e(G)^{3t+1}}{|A|^{2t}|B|^{2t}}.\]
We also need the following regularisation theorem of Erdős and Simonovits which is an important tool for Turán-type problems of sparse graphs. Recently, the first and third authors have developed a version of this result for linear hypergraphs [Reference Jiang and Yepremyan27]. For a positive real
$\lambda$
, G is called
$\lambda$
-almost-regular if
$\Delta(G)\leq \lambda\cdot \delta(G)$
.
Theorem 2.6
([Reference Erdős and Simonovits13]). Let
$\alpha$
be any real in (0,1),
$\lambda=20\cdot 2^{(1/\alpha)^2}$
, and n be a sufficiently large integer depending only on
$\alpha$
. Suppose G is an n-vertex graph with
$e(G)\geq n^{1+\alpha}$
. Then G has a
$\lambda$
-almost-regular subgraph on m vertices, where
$m>n^{\alpha\frac{1-\alpha}{1+\alpha}}$
such that
$e(G')>\frac{2}{5} m^{1+\alpha}$
.
3. Turán numbers of generalized cubes
In this section, we prove Theorem 1.6. Our proof is partly based on the ideas of Pinchasi and Sharir [Reference Pinchasi and Sharir32]. The key new idea is Lemma 3.1. To state the lemma, we need some notation.
In a graph G, for any
$S\subseteq V(G)$
, the common neighbourhood of S in G is defined by
$N_G(S)=\bigcap_{v\in S} N_G(v),$
and the common degree of S in G is
$d_G(S)=|N_G(S)|$
. When G is clear from the context, we will drop the subscripts. For a matching M in the bipartite graph G with bipartition (A,B), we define
$A_M=V(M)\cap A,\;B_M= V(M)\cap B$
. We call the subgraph induced by the vertex sets
$ N(B_M)\setminus V(M) $
and
$N(A_M)\setminus V(M)$
the neighbourhood graph of M and with some abuse of notation, for brevity, we denote it by N(M).
Let M and L be two matchings in G. We write
$M\sim L$
if L is a subgraph in N(M). For a non-negative integer t, we say that an ordered pair (M,L) of matchings is t-correlated if
$M \sim L$
and there exists a vertex v in V(M) such that
$d_{N(L)}(v)\geq t$
.
Lemma 3.1. Let G be an
$H_{s,t}$
-free bipartite graph and M be an
$(s-1)$
-matching in G. Then the number of s-matchings L in N(M) such that (M,L) is 2t-correlated is at most
$(s-1)(t-1)\cdot e(N(M))^{s-1}v(N(M))$
.
Proof. Let M be given. Suppose
$M=\{a_1b_1,\dots, a_{s-1}b_{s-1}\}$
, where
$\forall i\in [s-1],a_i\in A$
and
$b_i\in B$
. The lemma immediately follows from the following claim.
Claim 3.2. Let
$x\in A_M$
. Let L
$^{\prime}$
be an
$(s-1)$
-matching in N(M). Let
$y\in (V(N(M))\cap B)\setminus V(L')$
. Then the number of s-matchings L in N(M) that contain L
$^{\prime}$
and y and satisfy
$d_{N(L)}(x)\geq 2t$
is at most
$t-1$
.
Proof of Claim 3.2. Suppose otherwise that for some
$(s-1)$
-matching
$L'=\{c_1d_1,\dots, c_{s-1}d_{s-1}\}$
in N(M), where
$c_i\in A$
and
$d_i\in B$
for
$\forall i\in [s-1]$
, there exist t distinct s-matchings
$L_1,\dots, L_t$
in N(M) containing L
$^{\prime}$
and y that satisfy
$d_{N(L_i)}(x)\geq 2t$
. Let
$u_1, u_2,\dots, u_t$
be distinct vertices such that
$L_i=L'\cup \{u_i y\}$
. For each
$i\in [t]$
, since
$d_{N(L_i)}(x)\geq 2t$
, we have
$|N_{N(L_i)}(x)\setminus B_M|\geq t$
. We can therefore find t distinct vertices
$v_1,\dots, v_t$
such that for each
$i\in [t]$
$v_i\in N_{N(L_i)}(x)\setminus B_M$
.
Let
$B^*=\{b_1,\dots, b_{s-1}, y\}, U^*=\{u_1, \dots, u_t\},C^*=\{x, c_1,\dots, c_{s-1}\}$
, and
$V^*=\{v_1,\dots, v_t\}$
. It is easy to see that
$G_1\,:\!=\,G[B^*\cup U^*]$
,
$G_2\,:\!=\,G[C^*\cup V^*]$
are both copies of
$K_{s,t}$
. Let
$M_1\,:\!=\,\{u_1v_1,\dots, u_tv_t\}$
,
$M_2=\{b_1c_1,\dots,b_{s-1}c_{s-1}, xy\}$
. One can easily check that
$G_1\cup G_2\cup M_1\cup M_2$
is a copy of
$H_{s,t}$
in G, contradicting G being
$H_{s,t}$
-free.
This completes the proof of Lemma 3.1.
Proof of Theorem 1.6. Our choice of constant C here will be explicit. Let
$\alpha=\frac{2s-1}{2s+1}$
. As
$s\geq 2$
, we have
$\frac{3}{5}\leq \alpha<1$
. Let
$\lambda$
be the constant derived from Theorem 2.6 applied for
$\alpha$
. By Theorem 2.6, it suffices to show that there is a constant
$C=C(s,t)>0$
such that the following holds for sufficiently large n: if G is a
$\lambda$
-almost-regular graph with n vertices and
$m\geq Cn^{1+\alpha}$
edges, then G contains a copy of
$H_{s,t}$
. By Proposition 2.1, we may further assume that G is bipartite with a bipartition (A,B). Let
$\mathcal{M}$
be the collection of all
$(s-1)$
-matchings in G. Denote
\begin{align*}\mathcal{M}_1&=\{M: M \in \mathcal{M}, e(N(M))\leq 2^{s+1} s! (s-1)(t-1) v(N(M))\},\\\mathcal{M}_2&=\mathcal{M}\setminus \mathcal{M}_1,\\\mathcal{M}_2^{2t,s}&=\{(M,L): M\in \mathcal{M}_2, L\in \mathcal{L}, L \mbox{ is an} s-\mbox{matching}, M\sim L, (M,L) \mbox { is not} 2 t-\mbox{correlated} \}.\end{align*}
We suppose that G is
$H_{s,t}$
-free and derive a contradiction on the number of edges of the graph G. For doing so, we will use upper and lower bounds on the size of the set
$\mathcal{M}_2^{2t,s}$
.
Claim 3.3.
$\sum_{M\in \mathcal{M}_2} e(N(M))= \Omega(\frac{m^{3s-2}}{n^{4s-4}})$
.
Proof of Claim 3.3. Let us call a tree obtained from
$K_{1,p}$
by subdividing each edge once a p-spider of height 2. Note that
$\sum_{M\in \mathcal{M}} v(N(M))$
counts the number of
$(s-1)$
-spiders of height 2 in G. Since G is
$\lambda$
-almost-regular,
$\Delta\,:\!=\,\Delta(G)\leq \lambda\cdot \delta(G)\leq \lambda\cdot 2m/n$
. Thus,
\[\sum_{M\in \mathcal{M}} v(N(M))\leq n \Delta^{2s-2}= O\left(\frac{m^{2s-2}}{n^{2s-3}}\right).\]
By the definition of
$\mathcal{M}_1$
, we have
$\sum_{M\in \mathcal{M}_1} e(N(M))= O\left(\sum_{M\in \mathcal{M}_1} v(N(M))\right)= O\left(\frac{m^{2s-2}}{n^{2s-3}}\right).$
On the other hand,
$\sum_{M\in \mathcal{M}} e(N(M))$
counts the number of
$H_{1,s-1}$
$^{\prime}$
s in G. So by Lemma 2.5, we have
$\sum_{M\in \mathcal{M}} e(N(M)) = \Omega\left( \frac{m^{3s-2}}{n^{4s-4}}\right).$
Since
$m\geq Cn^{4s/(2s+1)}$
and n is sufficiently large, we have
$\frac{m^{3s-2}}{n^{4s-4}}\gg \frac{m^{2s-2}}{n^{2s-3}}$
; thus, the claim follows.
Now consider a matching
$M\in \mathcal{M}_2$
. By Lemma 2.4, the number of s-matchings L in N(M) is at least
$(1/2^s s!)e(N(M))^s$
. By Lemma 3.1 and the definition of
$\mathcal{M}_2$
, the number of s-matchings L in N(M) such that (M,L) is 2t-correlated is at most
\[(s-1)(t-1) e(N(M))^{s-1} v(N(M)) \leq \frac{ e(N(M))^s}{2^{s+1} s!}.\]
Hence, the number of s-matchings L in N(M) such that (M,L) is not 2t-correlated is at least
$(1/2) (1/2^s s!)e(N(M))^s$
.
By Claim 3.3, the convexity of the function
$f(x)=x^s$
and the fact that
$|\mathcal{M}_2|\leq m^{s-1}$
,
\[|\mathcal{M}_2^{2t,s}|\geq (1/2^{s+1} s!)\sum_{M\in \mathcal{M}_2} e(N(M))^s= \Omega\left(\frac{(\sum_{M\in \mathcal{M}_2} e(N(M)))^s}{|\mathcal{M}_2|^{s-1}}\right)=\Omega\left(\frac{m^{2s^2-1}}{n^{4s^2-4s}}\right).\]
Claim 3.4.
$|\mathcal{M}_2^{2t,s}| \leq \binom{t-1}{s-1}(2t-1)^{s-1}m^s$
.
Proof of Claim 3.4. Let L be an s-matching in G. Since G is
$H_{s,t}$
-free, N(L) has matching number at most
$t-1$
. Since N(L) is bipartite, by the König–Egerváry theorem it has a vertex cover Q of size at most
$t-1$
. Let
$Q^+$
denote the set of vertices in Q that have degree at least 2t in N(L) and
$Q^-=Q\setminus Q^+$
. If M is an
$(s-1)$
-matching in G that satisfies
$M\sim L$
and that (M,L) is not 2t-correlated, then M is contained in N(L) and could not contain any vertex in
$Q^+$
. Since
$Q=Q^+\cup Q^-$
is a vertex cover in N(L), each edge of M must contain a vertex in
$Q^-$
. Thus,
\[|\mathcal{M}_2^{2t,s}| \leq \binom{|Q^-|}{s-1} (2t-1)^{s-1} m^s\leq \binom{t-1}{s-1}(2t-1)^{s-1}m^s.\]
Combining the lower and upper bounds on
$|\mathcal{M}_2^{2t,s}|$
, we get that
$\frac{m^{2s^2-1}}{n^{4s^2-4s}}=O(m^s)$
, which implies that
$m= O(n^{4s/(2s+1)})$
, where the constant factor in
$O(\cdot)$
only depends on s and t. This contradicts that
$m\geq Cn^{4s/(2s+1)}$
, assuming C is chosen to be sufficiently large.
4. Asymmetric bipartite Turán numbers of Theta graphs
In this section, we establish an upper bound (i.e., Theorem 1.10) of the asymmetric bipartite Turán numbers of theta graphs
$\theta_{k,p}$
. This in its turn will be crucial in the proof of Theorem 1.8. Our proof, in a conspectus, employs the standard breadth-first search (BFS) tree approach. The major challenge is to show that the distance levels of the BFS tree should grow in magnitude rapidly. This will be essentially unravelled by the following lemma, where we adopt a modification of the so-called ‘blowup method
$^{\prime}$
by Faudree and Simonovits [Reference Faudree and Simonovits15].
Lemma 4.1. Let k,p,t be integers, where
$k,p\geq 2$
and
$0\leq t\leq k-1$
. Let T be a tree of height t rooted at a vertex x. Let A be the set of vertices at distance t from x in T. Let B be set of vertices disjoint from V(T). Let G be a bipartite graph with a bipartition (A,B). If
$T\cup G$
is
$\theta_{k,p}$
-free, then
$e(G)\leq 2p^t k |A\cup B|.$
Proof. We use induction on t. For the basis case
$t=0$
(i.e.,
$A=\{x\}$
), the claim holds trivially. For the induction step, let
$t\geq 1$
. Let
$x_1,\dots, x_q$
denote the children of x in T. For each
$i\in [q]$
, let
$T_i$
denote the subtree of
$T-x$
that contains
$x_i$
and let
$S_i=V(T_i)\cap A$
. Then
$S_1,\dots, S_q$
partition A. For each
$u\in A$
, let
$P_u$
denote the unique path from u to x in T. We define subsets
$B^+$
and
$B^-$
of B as follows. Let
\[B^+\,:\!=\,\{ y\in B| \forall I\subseteq [q], |I|=p-1, |N_G(y)\setminus \bigcup_{i\in I} S_i|>pk\} \mbox {and} B^-\,:\!=\,B\setminus B^+.\]
Claim 4.2.
$e(G[A\cup B^+])\leq pk \cdot |A\cup B^+|$
.
Proof. Suppose for contradiction that
$e(G[A\cup B^+])> pk \cdot |A\cup B^+|$
. Then by Lemma 2.1,
$G[A\cup B^+]$
contains a subgraph H with minimum degree more than pk. If
$k-t-1$
is odd, then let v be a vertex in
$V(H)\cap A$
; and if
$k-t-1$
is even, then let v be a vertex in
$V(H)\cap B^+$
. If
$t<k-1$
, then let S denote a spider with p legs of length
$k-t-1$
rooted at v. If
$t=k-1$
, then let
$S=\{v\}$
. By Lemma 2.3, H contains S as a subgraph. First suppose
$k<t-1$
. Let
$v_1,\dots, v_p$
denote the leaves of S. By our choice of v, we have
$v_1,\dots, v_p\in V(H)\cap B^+$
. By definition of
$B^+$
, we can find
$w_1,\dots, w_p$
outside V(S) such that they all lie in different
$S_i$
$^{\prime}$
s and
$v_1w_1, v_2w_2,\dots, v_pw_p\in E(G)$
. Since
$w_1,\dots, w_p$
all lie in different
$S_i$
$^{\prime}$
s, the paths
$P_{w_1},\dots, P_{w_p}$
pairwise intersect only at vertex x; therefore,
$S\cup \{v_1w_1,\dots, v_pw_p\}\cup \bigcup_{i=1}^p P_{w_i}$
forms a copy of
$\theta_{k,p}$
in G, a contradiction. Next, suppose
$t=k-1$
. Then
$S=\{v\}$
. Since
$v\in B^+$
, we can find
$w_1,\dots, w_p$
outside V(S) such that they all lie in different
$S_i$
$^{\prime}$
s and
$vw_1, vw_2,\dots, vw_p\in E(G)$
. Since
$w_1,\dots, w_p$
all lie in different
$S_i$
$^{\prime}$
s, the paths
$P_{w_1},\dots, P_{w_p}$
pairwise intersect only at vertex x. Now,
$\{w_1,\dots, vw_p\}\cup \bigcup_{i=1}^p P_{w_i}$
forms a copy of
$\theta_{k,p}$
in G, a contradiction. Hence, we must have
$e(G[A\cup B^+])\leq pk\cdot |A\cup B^+|$
.
Claim 4.3.
$e(G[A\cup B^-])\leq (2p^tk-pk)|A|+2p^tk|B^-|$
.
Proof. First, suppose
$t=1$
. So
$S_i=\{x_i\}$
for each i. By the definition of
$B^-$
, for each
$y\in B^-$
,
$|N_G(y)|\leq (pk-1)+p-1\leq pk+p$
. So
$e(G[A\cup B^-])\leq (pk+p)|B^-|\leq 2p^tk|B^-|$
. Hence, the claim holds. Next, suppose
$t\geq 2$
. For each
$y\in B^-$
by definition there exists some
$I\subseteq [q]$
with
$|I|=p-1$
such that
\[|N_G(y)\cap \cup_{i\in I}{S_i}| \geq d_G(y)-pk,\]
thus, there exists some
$i(y)\in [q]$
such that
$|N_G(y)\cap S_{i(y)}|\geq \frac{1}{p-1}(d_G(y) -pk)$
. (Note that the statement still holds even if
$d_G(y)-pk<0$
.) We define a subgraph H of G obtained from
$G[A\cup B^-]$
by only taking the edges from every
$y\in B^-$
to
$N_G(y)\cap S_{i(y)}$
. By the definition of H, we see that
$e(H)\geq \frac{1}{p-1}(e(G[A\cup B^-])-pk|B^-|)$
. Now, for each
$j\in [q]$
let
$B_j=\{y\in B^-: i(y)=j\}$
. Then in fact H is the vertex-disjoint union of
$H[S_1\cup B_1], H[S_2\cup B_2],\dots, H[S_q\cup B_q]$
. By the induction hypothesis, for each
$j\in [q]$
,
$e(H[S_j,B_j])\leq 2p^{t-1}k |S_j\cup B_j|$
. Hence,
\begin{align*}e(H)&=\sum_{j=1}^q e(H[S_j, B_j])\\&\leq 2p^{t-1}k \sum_{j=1}^q |S_j\cup B_j|\leq 2p^{t-1}k (|A|+|B^-|),\end{align*}
implying that (using
$t\geq 2$
)
\begin{align*}e(G[A\cup B^-])&\leq (p-1)\cdot e(H) +pk|B^-|\\&\leq 2p^{t-1}(p-1)k (|A|+|B^-|) +pk|B^-|\\&\leq (2p^tk-pk)|A|+2p^tk|B^-|,\end{align*}
as desired.
Combining the two claims proved above, we get that
\begin{align*}e(G) &=e(G[A,B^+])+e(G[A,B^-])\\&\leq pk\cdot (|A|+|B^+|)+ (2p^tk-pk)|A|+2p^tk|B^-|\\&\leq 2p^tk (|A|+|B|),\end{align*}
as desired.
Proof of Theorem 1.10. Let G be a
$\theta_{k,p}$
-free bipartite graph with a bipartition (A,B) where
$|A|=m$
and
$|B|=n$
. Let
$c=16kp^k$
. If k is odd, then we assume
$e(G)> c\cdot (mn)^{\frac{1}{2}+\frac{1}{2k}}+c\cdot (m+n)$
, otherwise assume
$e(G)> c\cdot m^{\frac{1}{2}+\frac{1}{k}} n^{\frac{1}{2}} +c\cdot (m+n)$
. Denote
$d_A=e(G)/|A|$
and
$d_B=e(G)/|B|$
. Note that both
$d_A, d_B\geq 16kp^k$
.
By Lemma 2.2, G contains a subgraph G
$^{\prime}$
with
$e(G')\geq \frac{1}{2} e(G)$
such that each vertex in
$V(G')\cap A$
has degree at least
$\frac14d_A$
in G
$^{\prime}$
and that each vertex in
$V(G')\cap B$
has degree at least
$\frac14 d_B$
in G
$^{\prime}$
. Fix a vertex
$x\in V(G')\cap A$
. For each integer
$i\geq 0$
, let
$L_i$
denote the set of vertices at distance i from x in G
$^{\prime}$
, and let
$d_i=d_A$
if i is odd and
$d_i=d_B$
if i is even. So we see that every vertex in
$L_{i-1}$
has degree at least
$\frac14d_i$
in G
$^{\prime}$
. Using Lemma 4.1, we show that the growth ratio of two consecutive levels must be large in the following sense.
Claim 4.4. For each
$i\in [k]$
, we have
$|L_i|/|L_{i-1}|\geq \frac{d_{i}} {16kp^i}$
. In particular,
$|L_i|\geq |L_{i-1}|$
holds.
Proof. It suffices to prove the first statement, which we do by induction on i. If
$i=1$
, then we have
$\frac{|L_1|}{|L_0|}\geq \frac{1}{4} d_A\geq \frac{d_1}{16kp}$
.
For the inductive step, consider
$i\geq 2$
. Let
$T_{i-1}$
be a BFS tree in G
$^{\prime}$
rooted at x of height
$i-1$
, so the vertex set of this tree is
$\cup_{j<i}{L_j}$
. Applying Lemma 4.1 to
$T_{i-1}$
and
$G'[L_{i-1}\cup L_i]$
, we get
\[e(G'[L_{i-1}, L_i])\leq 2k p^{i-1} (|L_{i-1}|+|L_i|).\]
Similarly, one can get that
\[e(G'[L_{i-2}\cup L_{i-1}|)\leq 2k p^{i-2}(|L_{i-2}|+|L_{i-1}|)\leq 4k p^{i-2}|L_{i-1}|,\]
where the last step holds because
$|L_{i-2}|\leq |L_{i-1}|$
by the induction hypothesis. Combining these two, we get that
\[e(G'[L_{i-2}\cup L_{i-1}\cup L_i])=e(G'[L_{i-2}\cup L_{i-1}|)+e(G'[L_{i-1}, L_i])\leq 2kp^i\cdot (|L_{i-1}|+|L_i|).\]
On the other hand, each vertex in
$L_{i-1}$
has degree at least
$\frac14 d_i$
in G
$^{\prime}$
, and all edges of G
$^{\prime}$
incident to
$L_{i-1}$
lie in
$L_{i-2}$
or
$L_i$
. Hence, we have
\[\frac14 d_i\cdot |L_{i-1}| \leq e(G'[L_{i-2}\cup L_{i-1}\cup L_i])\leq 2kp^i\cdot (|L_{i-1}|+|L_i|).\]
Thus, we get
$|L_i|\geq \left(\frac{d_i}{8kp^i} -1\right)\cdot|L_{i-1}|\geq \frac{d_i}{16kp^i}\cdot|L_{i-1}|,$
proving the claim.
Thus, we have
$|L_k|\geq \alpha\cdot \prod_{i=1}^k d_i,$
where
$\alpha=\prod_{i=1}^k \frac{1}{16kp^i}$
. Recall that
$c=16k p^k$
and so
$\alpha c^k>1$
. Suppose first that k is odd, say
$k=2s+1$
. Then it follows that
$L_k\subseteq B$
and
\[|L_k|\geq \alpha \cdot d_A^{s+1}d_B^s =\alpha\cdot \frac{e(G)^k}{m^{s+1}n^s}. \]
By the assumption, we have
$e(G)>c\cdot (mn)^{\frac{1}{2}+\frac{1}{2k}}$
, which shows that
$|L_{k}|\geq \alpha c^k n>n.$
This is a contradiction, since
$L_{k}\subseteq B$
and
$|B|=n$
. Now consider that k is even, say
$k=2s$
. Then we have
\[|L_{k}|\geq \alpha \cdot d_A^s d_B^s =\alpha\cdot \frac{e(G)^{k}}{m^s n^s}. \]
In this case,
$e(G)> c\cdot m^{\frac{1}{2}+\frac{1}{k}}n^{\frac{1}{2}}$
. This gives that
$|L_{k}|\geq \alpha c^k\cdot \left(m^{\frac{1}{2}+\frac{1}{k}}n^{\frac{1}{2}}\right)^k/m^sn^s=\alpha c^k\cdot m>m,$
again a contradiction, since
$L_{k}\subseteq A$
and
$|A|=m$
. This completes the proof of Theorem 1.10.
As a special case of Theorem 1.10, we derive the following corollary on the asymmetric bipartite Turán number of
$\theta_{3,p}$
which will play an important role in the proof of Theorem 1.8.
Corollary 4.5. Let
$m,n,p\geq 2$
be integers. Then
\[ex(m,n, \theta_{3,p})\leq 48p^3\cdot \left((mn)^{2/3}+m+n\right).\]
5. The Turán exponent of 7/5
Here we prove the existence of the Turán exponent of
$7/5$
. This is achieved by the combination of Theorem 1.8, which states that
$\mathrm{ex}(n,T_3^p)=O(n^{7/5})$
for all
$p\geq 2$
, and a matching lower bound on this function for sufficiently large p from [Reference Bukh and Conlon4].
By considering a graph that contains
$T_3^p$
as its subgraph, in fact we will prove a slightly stronger result than Theorem 1.8. We start with a definition introduced by Faudree and Simonovits [Reference Faudree and Simonovits15]. Let H be a bipartite graph with an ordered pair (A,B) of partite sets and
$t\geq 2$
be an integer. Define
$L_t(H)$
to be the graph obtained from H by adding a new vertex u and joining u to all vertices of A by internally disjoint paths of length
$t-1$
such that the vertices of these paths are disjoint from V(H).
Observe that the theta graph
$\theta_{3,p}$
is symmetric between its two partite sets. So
$L_3(\theta_{3,p})$
is uniquely defined. It is easy to see that
$T_3^p\subseteq L_3(\theta_{3,p})$
. We prove the following strengthening of Theorem 1.8.
Theorem 5.1. For each
$p\geq 2$
, there exists a positive constant
$c_p$
such that
\[\mathrm{ex}(n, L_3(\theta_{3,p}))\leq c_p n^{7/5}.\]
Proof. We will show that it suffices to choose
$c_p=2(192)^{3/2} p^6$
. Suppose for a contradiction that there exists an n-vertex
$L_3(\theta_{3,p})$
-free graph G with
$e(G)> c_p n^{7/5}$
. By Proposition 2.1, G contains a bipartite subgraph
$G_1$
with
\begin{equation}d\,:\!=\,\delta(G_1)\geq d(G)/4\geq (c_p/2)\cdot n^{2/5}>(192)^{3/2}p^6\cdot n^{2/5}.\end{equation}
Let x be a vertex of minimum degree in
$G_1$
. For each
$i\geq 0$
, let
$L_i$
denote the set of vertices at distance i from x in
$G_1$
. Then
$|L_1|=|\delta(G_1)|= d$
. Let
$L_2^+$
denote the set of vertices v in
$L_2$
such that
$|N_{G_1}(v)\cap L_1|\geq 2p+2$
, and
$L_2^-=L_2\setminus L_2^+$
.
Claim 5.2.
$G_1[L_1\cup L_2^+]$
is
$\theta_{3,p}$
-free.
Proof. Suppose for contradiction that
$G_1[L_1\cup L_2^+]$
contains a copy F of
$\theta_{3,p}$
. Let A,B denote the two partite sets of F where
$A\subseteq L_1$
and
$B\subseteq L_2^+$
. Then
$|A|=|B|=p+1$
. Suppose
$B=\{b_1,\dots, b_{p+1}\}$
. Since each vertex in
$L_2^+$
has at least
$2p+2$
neighbours in
$L_1$
, we can find distinct vertices
$c_1,\dots, c_{p+1}$
in
$L_1\setminus A$
such that
$b_1c_1,\dots, b_{p+1}c_{p+1}\in E(G_1)$
. Now F together with the paths
$b_1c_1x, \dots, b_{p+1}c_{p+1} x$
forms a copy of
$L_3(\theta_{3,p})$
in G, a contradiction.
Claim 5.3.
$|L_2|\geq d^2/[(192)^{3/2}p^{9/2}]$
.
Proof. By Claim 5.2 and Corollary 4.5, we have
\[ e(G_1[L_1\cup L_2^+])\leq 48 p^3\cdot \left(|L_1|^{2/3}|L_2^+|^{2/3}+|L_1|+|L_2^+|\right); \]
and by the definition of
$L_2^-$
,
$e(G_1[L_1\cup L_2^-])\leq (2p+2)\cdot |L_2^-|.$
Adding these inequalities up, we have
\begin{equation}e(G_1[L_1,L_2])=e(G_1[L_1\cup L_2^+])+e(G_1[L_1\cup L_2^-])\leq 48 p^3\cdot \left(|L_1|^{2/3}|L_2|^{2/3}+|L_1|+|L_2|\right).\end{equation}
Since every vertex in
$L_1$
has at least
$d-1\geq 3d/4$
neighbours in
$L_2$
, it follows that
\begin{equation*} (3d/4)|L_1|\leq e(G_1[L_1,L_2])\leq 48 p^3\cdot \left(|L_1|^{2/3}|L_2|^{2/3}+|L_1|+|L_2|\right).\end{equation*}
Since
$d\geq (192)^{3/2} p^6$
, we see
$48p^3|L_1|\leq (d/4)|L_1|$
. Thus, it follows that either
$48 p^3|L_1|^{2/3}|L_2|^{2/3}\geq (d/4)|L_1|$
or
$48 p^3 |L_2|\geq (d/4)|L_1|$
. Using
$|L_1|=d$
, we get that
\[|L_2|\geq \min\left\{\frac{d^2}{(192)^{3/2}p^{9/2}}, \frac{d^2}{192 p^3}\right\}=\frac{d^2}{(192)^{3/2}p^{9/2}},\]
as desired.
Next we consider the subgraph H of
$G_1$
induced on
$L_2\cup L_3$
, i.e.,
$H=G_1[L_2\cup L_3].$
Our goal in the rest of the proof is to reach a contradiction by showing that H cannot contain
$\theta_{3,s}$
for large s, which in turn shows that
$|L_3|$
must be of order
$\Omega(d^{5/2})$
and thus exceed the total number of vertices in G.
Let T be a BFS tree rooted at x with vertex set
$\{x\}\cup L_1\cup L_2$
. Let
$x_1,\dots, x_m$
be the children of x in T. For each
$i\in [m]$
, let
$S_i$
be the set of children of
$x_i$
in T. Then
$S_1,\dots, S_m$
partition
$L_2$
. Since each vertex in
$L_2$
has degree at least d in
$G_1$
, we have
$e(G_1[L_1\cup L_2])+e(G_1[L_2\cup L_3])\geq d|L_2|.$
Since
$d\geq (192)^{3/2} p^6$
,
$|L_1|=d$
, and
$|L_2|\geq \frac{d^2}{(192)^{3/2} p^{9/2}}$
by Claim 5.3, it is easy to check that
$48p^3 |L_1|^{2/3}|L_2^+|^{2/3}\leq d|L_2|/4.$
By (2), we have
$e(G_1[L_1\cup L_2])\leq d|L_2|/4+48p^3(|L_1|+|L_2|)\leq d|L_2|/2.$
Hence,
\begin{equation}e(H)=e(G_1[L_2\cup L_3])\geq d|L_2|/2.\end{equation}
Given a vertex
$u\in L_3$
and some
$S_i$
, we say the pair
$(u,S_i)$
is rich, if u has at least
$2p+1$
neighbours of H in
$S_i$
. Let
$E_H(u,S_i)$
denote the set of all edges in H between u and
$S_i$
. We now partition H into two (spanning) subgraphs
$H_1,H_2$
such that
\[E(H_1)=\bigcup E_H(u,S_i) \quad \mbox{ and }\quad E(H_2)=E(H)\setminus E(H_1),\]
where the union in
$E(H_1)$
is over all rich pairs
$(u,S_i)$
. Note that by this definition, any
$u\in L_3$
has at most 2p neighbours of
$H_2$
in any
$S_i$
, i.e.,
$|E_{H_2}(u,S_i)|\leq 2p$
. Let
$H_3$
be a subgraph of
$H_2$
obtained by including exactly one edge in
$E_{H_2}(u,S_i)$
over all pairs
$(u,S_i)$
with
$|E_{H_2}(u,S_i)|\geq 1$
. By the above discussion, it follows that
\begin{equation}e(H_3)\geq e(H_2)/(2p),\end{equation}
and for any
$u\in L_3$
, all its neighbours in
$H_3$
belong to distinct
$S_i$
$^{\prime}$
s.
Claim 5.4.
$H_1$
is
$\theta_{3,p^2}$
-free.
Proof. Suppose for contradiction that
$H_1$
contains a copy F of
$\theta_{3,p^2}$
. Suppose F consists of
$p^2$
internally disjoint paths of length three between u and v where
$u\in L_3$
and
$v\in L_2$
. Let these paths be
$ua_1b_1v, ua_2b_2v,\dots, ua_{p^2}b_{p^2}v$
, where
$a_1,\dots, a_{p^2}\in L_2$
and
$b_1,\dots, b_{p^2}\in L_3$
.
We consider two cases. First, suppose that there exists some
$S_i$
which contains p different
$a_j$
$^{\prime}$
s. Without loss of generality, suppose that
$S_1$
contains
$a_1,\dots a_p$
. For each
$j\in [p]$
, since
$b_ja_j\in E(H_1)$
, by definition
$(b_j,S_1)$
is a rich pair, that is, there are at least
$2p+1$
edges of H from
$b_j$
to
$S_1$
. Similarly as
$ua_1\in E(H_1)$
, there are at least
$2p+1$
edges of H from u to
$S_1$
. Hence, we can find distinct vertices
$u', a_1',\dots, a_p'\in S_1\setminus \{a_1,\dots, a_p\}$
such that
$uu', a_1'b_1, \dots, a'_pb_p\in E(H)$
. Now
$F\cup \{uu', a'_1b_1,\dots, a'_pb_p\}\cup \{x_1u', x_1a_1',\dots, x_1a_p'\}$
forms a copy of
$L_3(\theta_{3,p})$
in G, a contradiction.
Next, suppose that each
$S_i$
contains at most
$p-1$
different
$a_j$
$^{\prime}$
s. Then among
$a_1,\dots, a_{p^2}$
we can find
$p+1$
of them, say
$a_1,\dots, a_{p+1}$
that all lie in different
$S_i$
$^{\prime}$
s. Furthermore, we may assume that
$a_1,\dots, a_p$
are outside the
$S_i$
$^{\prime}$
s that contains v. Now F together with the paths in T from x to
$a_1,\dots, a_p,v$
forms a copy of
$L_3(\theta_{3,p})$
in G, a contradiction. Hence,
$H_1$
must be
$\theta_{3,p^2}$
-free.
Claim 5.5.
$H_3$
is
$\theta_{3,p}$
-free.
Proof. Suppose for contradiction that
$H_3$
contains a copy F of
$\theta_{3,p}$
. Suppose F consists of p internally disjoint paths of length three between u and v, where
$u\in L_3$
and
$v\in L_2$
. Suppose these paths are
$ua_1b_1v,\dots, ua_pb_pv$
, where
$a_1,\dots, a_p\in L_2$
and
$b_1,\dots, b_p\in L_3$
. By the definition of
$H_3$
, since
$ua_1,\dots, ua_p\in E(H_3)$
,
$a_1,\dots, a_p$
must all lie in different
$S_i$
$^{\prime}$
s. Also, for each
$j\in [p]$
since
$b_ja_j, b_jv\in E(H_3)$
,
$a_j$
and v must lie in different
$S_i$
. So
$a_1,\dots, a_p$
and v all lie in different
$S_i$
$^{\prime}$
s. Now, F together with the paths in T from x to
$a_1,\dots, a_p,v$
respectively forms a copy of
$L_3(\theta_{3,p})$
in G, a contradiction.
Now, we consider two cases.
Case 1.
$e(H_1)\geq e(H)/2$
. In this case, by (3), we have
$e(H_1)\geq d|L_2|/4$
. On the other hand, by Claim 5.4, we see that
$H_1$
is
$\theta_{3,p^2}$
-free, so by Corollary 4.5, we have
\begin{equation}d|L_2|/4\leq e(H_1)\leq 48p^6\cdot\left(|L_2|^{2/3} |L_3|^{2/3}+|L_2|+|L_3|\right).\end{equation}
Since
$d\geq (192)^{3/2} p^6$
, one can check that
$48p^6|L_2|\leq d|L_2|/12$
. Hence, we have either
\begin{equation*}48p^6 |L_2|^{2/3} |L_3|^{2/3}\geq d|L_2|/12 \quad \mbox{ or }\quad 48p^6|L_3|\geq d|L_2|/12.\end{equation*}
Using this and Claim 5.3, we get that
\[|L_3|\geq \min\left\{\frac{d^{3/2}|L_2|^{1/2}}{24^3p^9}, \frac{d|L_2|}{24^2p^6}\right\}=\frac{d^{3/2}|L_2|^{1/2}}{24^3p^9}\geq \frac{d^{5/2}}{24^3 (192)^{3/4}p^{45/4}}\]
Since
$d\geq (192)^{3/2} p^6 \cdot n^{2/5}$
, this yields
$|L_3|>n$
, a contradiction.
Case 2.
$e(H_2)\geq e(H)/2$
. Then by (3) and (4), we have
$e(H_3)\geq e(H)/4p\geq d|L_2|/8p$
. By Claim 5.5,
$H_3$
is
$\theta_{3,p}$
-free. Thus, by Corollary 4.5 we get
\[d|L_2|/8p\leq e(H_3)\leq 48 p^3\cdot \left(|L_2|^{2/3} |L_3|^{2/3}+|L_2|+|L_3|\right).\]
Since
$p\geq 2$
, the above inequality would also imply (5). So we can apply the same analysis as in Case 1 to get a contradiction.
This completes the proof of Theorem 5.1 (and thus of Theorem 1.8).
6. Additional comments
Since the original submission of our manuscript, many new developments on Question 1.1 have been obtained. See [Reference Conlon, Janzer and Lee8,Reference Janzer21,Reference Jiang, Jiang and Ma23,Reference Jiang and Qiu26,Reference Kang, Kim and Liu28], for instance.
