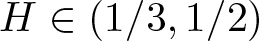1. Introduction
The topic of this article is to studying the slow-fast rough differential equation (abbreviated by RDE) in time interval ![]() $[0,T]$ under the controlled rough path (RP) framework as follows:
$[0,T]$ under the controlled rough path (RP) framework as follows:
 \begin{equation}
\left\{
\begin{array}{l}
X^{\varepsilon, \delta}_t =X_0+\int_{0}^{t} f_{1}(X^{\varepsilon, \delta}_s, Y^{\varepsilon, \delta}_s)ds + \int_{0}^{t}\sqrt \varepsilon \sigma_{1}( X^{\varepsilon, \delta}_s)dB^H_{s},\\
Y^{\varepsilon, \delta}_t =Y_0+\frac{1}{\delta} \int_{0}^{t}f_{2}( X^{\varepsilon, \delta}_s, Y^{\varepsilon, \delta}_s)ds + \frac{1}{{\sqrt \delta}}\int_{0}^{t}\sigma_2( X^{\varepsilon, \delta}_s, Y^{\varepsilon, \delta}_s)dW_{s}.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{l}
X^{\varepsilon, \delta}_t =X_0+\int_{0}^{t} f_{1}(X^{\varepsilon, \delta}_s, Y^{\varepsilon, \delta}_s)ds + \int_{0}^{t}\sqrt \varepsilon \sigma_{1}( X^{\varepsilon, \delta}_s)dB^H_{s},\\
Y^{\varepsilon, \delta}_t =Y_0+\frac{1}{\delta} \int_{0}^{t}f_{2}( X^{\varepsilon, \delta}_s, Y^{\varepsilon, \delta}_s)ds + \frac{1}{{\sqrt \delta}}\int_{0}^{t}\sigma_2( X^{\varepsilon, \delta}_s, Y^{\varepsilon, \delta}_s)dW_{s}.
\end{array}
\right.
\end{equation} Here, the RP ![]() $(B^H,W)$ is lifted from the mixed fractional Brownian motion (FBM)
$(B^H,W)$ is lifted from the mixed fractional Brownian motion (FBM) ![]() $(b^H,w)$ with Hurst parameter
$(b^H,w)$ with Hurst parameter  $H\in (\frac{1}{3},\frac{1}{2})$, and
$H\in (\frac{1}{3},\frac{1}{2})$, and ![]() $(B^H,W)$ is α-Hölder RP with
$(B^H,W)$ is α-Hölder RP with ![]() $1/3 \lt \alpha \lt H$. Two small parameters ɛ and δ satisfy the condition that
$1/3 \lt \alpha \lt H$. Two small parameters ɛ and δ satisfy the condition that ![]() $0 \lt \delta=o(\varepsilon) \lt \varepsilon\leqslant 1$.
$0 \lt \delta=o(\varepsilon) \lt \varepsilon\leqslant 1$. ![]() ${X^{\varepsilon,\delta}}$ is the slow component and
${X^{\varepsilon,\delta}}$ is the slow component and ![]() ${Y^{\varepsilon,\delta}}$ is the fast component with the (arbitrary but deterministic) initial data
${Y^{\varepsilon,\delta}}$ is the fast component with the (arbitrary but deterministic) initial data  $(X^{\varepsilon, \delta}_0, Y^{\varepsilon, \delta}_0)=(X_0, Y_0)\in \mathbb{R}^{{m}}\times \mathbb{R}^{{n}}$. The coefficients
$(X^{\varepsilon, \delta}_0, Y^{\varepsilon, \delta}_0)=(X_0, Y_0)\in \mathbb{R}^{{m}}\times \mathbb{R}^{{n}}$. The coefficients ![]() $f_{1}:\mathbb{R}^{{m}}\times \mathbb{R}^{{n}}\to\mathbb{R}^{{m}}$,
$f_{1}:\mathbb{R}^{{m}}\times \mathbb{R}^{{n}}\to\mathbb{R}^{{m}}$, ![]() $f_2:\mathbb{R}^{{m}}\times \mathbb{R}^{{n}}\to\mathbb{R}^{{n}}$,
$f_2:\mathbb{R}^{{m}}\times \mathbb{R}^{{n}}\to\mathbb{R}^{{n}}$, ![]() $\sigma_{1}: \mathbb{R}^{{m}}\to \mathbb{R}^{{m}\times{d}}$ and
$\sigma_{1}: \mathbb{R}^{{m}}\to \mathbb{R}^{{m}\times{d}}$ and ![]() $\sigma_{2}: \mathbb{R}^{{m}}\times \mathbb{R}^{{n}}\to \mathbb{R}^{{n}\times{e}} $ are non-linear regular enough functions, which assumed to satisfy some suitable conditions in §3. Such a slow-fast model has been applied in many real-world fields, for example, typical examples could be found in climate-weather (see [Reference Kiefer25]), biological field, and so on [Reference Krupa, Popović and Kopell27]. The dynamical behaviour for slow-fast model is an active research area, see for instance, the monographs [Reference Pavliotis and Stuart35] and references [Reference Bourguin, Gailus and Spiliopoulos4, Reference Hairer and Li20, Reference Röckner, Xie and Yang38] therein for a comprehensive overview.
$\sigma_{2}: \mathbb{R}^{{m}}\times \mathbb{R}^{{n}}\to \mathbb{R}^{{n}\times{e}} $ are non-linear regular enough functions, which assumed to satisfy some suitable conditions in §3. Such a slow-fast model has been applied in many real-world fields, for example, typical examples could be found in climate-weather (see [Reference Kiefer25]), biological field, and so on [Reference Krupa, Popović and Kopell27]. The dynamical behaviour for slow-fast model is an active research area, see for instance, the monographs [Reference Pavliotis and Stuart35] and references [Reference Bourguin, Gailus and Spiliopoulos4, Reference Hairer and Li20, Reference Röckner, Xie and Yang38] therein for a comprehensive overview.
As a generalization of the standard Wiener process ![]() $(H=1/2)$, the FBM is self-similar and possesses long-range dependence, which has become widely popular for applications [Reference Biagini, Hu, Oksendal and Zhang2, Reference Decreusefond and Ustnel10, Reference Rascanu39]. Its Hurst parameter H could depict the roughness of the sample paths, with a lower value leading to a rougher motion [Reference Mishura and Mishura34]. Especially, the case of
$(H=1/2)$, the FBM is self-similar and possesses long-range dependence, which has become widely popular for applications [Reference Biagini, Hu, Oksendal and Zhang2, Reference Decreusefond and Ustnel10, Reference Rascanu39]. Its Hurst parameter H could depict the roughness of the sample paths, with a lower value leading to a rougher motion [Reference Mishura and Mishura34]. Especially, the case of ![]() $H \lt 1/2$ seems rather troublesome to be handled with the conventional stochastic techniques. To get over the hump that is caused by rougher sample paths for
$H \lt 1/2$ seems rather troublesome to be handled with the conventional stochastic techniques. To get over the hump that is caused by rougher sample paths for ![]() $H \lt 1/2$, our model is within the RP setting. The so-called RP theory does not require martingale theory, Markovian property, or filtration theory. This also determines the de-randomization when being applied in the stochastic situation, so it can provide a new prescription to FBM problems. The RP theory was originally proposed by Terry Lyons in 1998 [Reference Lyons31, Reference Lyons and Qian32] and has sparked tremendous interest from the fields of probability [Reference Inahama21, Reference Inahama22] and applied mathematics [Reference Friz and Victoir19, Reference Liu and Tindel30] after 2010. Briefly, the main idea of RP theory states that it not only considers the path itself but also considers the iterated integral of the path, so that the continuity of the solution mapping could be ensured. This continuity property of the solution mapping is the core of RP theory. Until now, there have been three formalisms to RP theory [Reference Friz and Hairer16, Reference Friz and Victoir19, Reference Lyons and Qian32] and we adopt that one of them, which is so-called controlled RP theory [Reference Friz and Hairer16]. By resorting to the controlled RP framework, the slow-fast RDE (1.1) under suitable conditions admits a unique (pathwise) solution
$H \lt 1/2$, our model is within the RP setting. The so-called RP theory does not require martingale theory, Markovian property, or filtration theory. This also determines the de-randomization when being applied in the stochastic situation, so it can provide a new prescription to FBM problems. The RP theory was originally proposed by Terry Lyons in 1998 [Reference Lyons31, Reference Lyons and Qian32] and has sparked tremendous interest from the fields of probability [Reference Inahama21, Reference Inahama22] and applied mathematics [Reference Friz and Victoir19, Reference Liu and Tindel30] after 2010. Briefly, the main idea of RP theory states that it not only considers the path itself but also considers the iterated integral of the path, so that the continuity of the solution mapping could be ensured. This continuity property of the solution mapping is the core of RP theory. Until now, there have been three formalisms to RP theory [Reference Friz and Hairer16, Reference Friz and Victoir19, Reference Lyons and Qian32] and we adopt that one of them, which is so-called controlled RP theory [Reference Friz and Hairer16]. By resorting to the controlled RP framework, the slow-fast RDE (1.1) under suitable conditions admits a unique (pathwise) solution ![]() $(X^{\varepsilon, \delta},Y^{\varepsilon,\delta})\in \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m}) \times \mathcal{C}\left([0,T], \mathbb{R}^n\right)$ with
$(X^{\varepsilon, \delta},Y^{\varepsilon,\delta})\in \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m}) \times \mathcal{C}\left([0,T], \mathbb{R}^n\right)$ with ![]() $1/3 \lt \beta \lt \alpha \lt H$, which will be precisely stated in §3. Here,
$1/3 \lt \beta \lt \alpha \lt H$, which will be precisely stated in §3. Here, ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ and
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ and ![]() $\mathcal{C}\left([0,T], \mathbb{R}^n\right)$ are the β-Hölder continuous path space and the continuous path space, respectively.
$\mathcal{C}\left([0,T], \mathbb{R}^n\right)$ are the β-Hölder continuous path space and the continuous path space, respectively.
In accordance with the averaging principle, as δ → 0, ![]() $X^{\varepsilon, \delta}$ is well approximated by an effective dynamics
$X^{\varepsilon, \delta}$ is well approximated by an effective dynamics ![]() $\bar X$ which is defined as following,
$\bar X$ which is defined as following,
 \begin{equation}
\left\{\begin{array}{l}
d \bar{X}_t=\bar{f}_1\left(\bar{X}_t\right) d t \\
\bar{X}_0=X_0 \in \mathbb{R}^m,
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{l}
d \bar{X}_t=\bar{f}_1\left(\bar{X}_t\right) d t \\
\bar{X}_0=X_0 \in \mathbb{R}^m,
\end{array}\right.
\end{equation} with  $\bar{f}_1(x)=\int_{\mathbb{R}^{n}}f_{1}(x, {y})\mu^{x}(d{y})$ for
$\bar{f}_1(x)=\int_{\mathbb{R}^{n}}f_{1}(x, {y})\mu^{x}(d{y})$ for ![]() $x\in\mathbb{R}^m$. Here, µ x is a unique invariant probability measure of the fast component with the ‘frozen’-x. The precise proof is a small extension of [Reference Inahama23, theorem 2.1].
$x\in\mathbb{R}^m$. Here, µ x is a unique invariant probability measure of the fast component with the ‘frozen’-x. The precise proof is a small extension of [Reference Inahama23, theorem 2.1].
However, the small parameter δ cannot be zero and when it is small enough, the trajectory of the slow component would stay in a small neighbourhood of ![]() $\bar X$. The large deviation principle (LDP) could describe the extent to which the slow component deviates from the average component exponentially, which is more accurate. As a result, the main objective of this work is to prove a LDP for the slow component
$\bar X$. The large deviation principle (LDP) could describe the extent to which the slow component deviates from the average component exponentially, which is more accurate. As a result, the main objective of this work is to prove a LDP for the slow component ![]() $X^{\varepsilon,\delta}$ of the above RDE (1.1). The family
$X^{\varepsilon,\delta}$ of the above RDE (1.1). The family ![]() ${X^{\varepsilon,\delta} }$ is called to satisfy a LDP on
${X^{\varepsilon,\delta} }$ is called to satisfy a LDP on ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ (
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ (![]() $1/3 \lt \beta \lt \alpha \lt H$) with a good rate function
$1/3 \lt \beta \lt \alpha \lt H$) with a good rate function ![]() $I: \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})\rightarrow [0, \infty]$ if the following two conditions hold:
$I: \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})\rightarrow [0, \infty]$ if the following two conditions hold:
• For each closed subset F of
 $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$,
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$,
 \begin{equation*}\limsup _{\varepsilon \rightarrow 0} \varepsilon \log \mathbb{P}\big(X^{\varepsilon,\delta}\in F\big) \leqslant-\inf _{x \in F} I(x).\end{equation*}
\begin{equation*}\limsup _{\varepsilon \rightarrow 0} \varepsilon \log \mathbb{P}\big(X^{\varepsilon,\delta}\in F\big) \leqslant-\inf _{x \in F} I(x).\end{equation*}• For each open subset G of
 $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$,
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$,
 \begin{equation*}\liminf _{\varepsilon \rightarrow 0} \varepsilon \log \mathbb{P}\big(X^{\varepsilon,\delta}\in G\big) \geqslant-\inf _{x \in G} I(x).\end{equation*}
\begin{equation*}\liminf _{\varepsilon \rightarrow 0} \varepsilon \log \mathbb{P}\big(X^{\varepsilon,\delta}\in G\big) \geqslant-\inf _{x \in G} I(x).\end{equation*}
This will be stated in our main result (theorem 3.7) and the definition of I will also be given there.
The LDP for stochastic dynamical systems was pioneered by Freidlin and Wentzell [Reference Wentzell and Freidlin42], which has inspired much of the subsequent substantial development [Reference Cerrai and Röckner8, Reference Dupuis and Spiliopoulos13, Reference Peszat37, Reference Sritharan and Sundar40]. Up to date, there have been several different approaches to studying LDP for the stochastic slow-fast system, such as the weak convergence method [Reference Budhiraja, Dupuis and Maroulas6, Reference Dupuis and Ellis12, Reference Sun, Wang, Xu and Yang41], the PDE theory [Reference Bardi, Cesaroni and Scotti1], non-linear semigroups, and viscosity solution theory [Reference Feng, Fouque and Kumar14, Reference Feng and Kurtz15]. It is remarkable that the weak convergence method, which was founded on the variational representation for the non-negative functional of BM [Reference Boué and Dupuis3], has been extensively utilized in the LDP of the slow-fast systems with BM. As well as this, the weak convergence method is powerful for solving LDP problems in FBM situations [Reference Budhiraja and Song7, Reference Inahama, Xu and Yang24] with ![]() $H \gt 1/2$.
$H \gt 1/2$.
Nevertheless, it is a priori not clear if the LDP for slow-fast RDE (1.1) holds and the aforementioned methods are not sufficient to answer this question. For the single-time scale RDE, the RP theory is proven efficient in the LDP problems by using the exponentially good approximations of Gaussian processes [Reference Friz and Victoir18, Reference Ledoux, Qian and Zhang28, Reference Millet and Sanz-Solé33]. However, due to hinging on the fast equation, this exponentially good approximation method is invalidated in our slow-fast case. In response to this challenge, new approach has to be developed. Our work is to adopt the variational framework to solve the LDP for the slow-fast RDE. The technical core of the proof is the continuity of the solution mapping and the weak convergence method, which is based on the variational representation of mixed FBM. Here, we remark some differences between our work and [Reference Inahama23, Reference Inahama, Xu and Yang24]. (1) Different from the LDP for slow-fast system under FBM (![]() $H\in (1/2,1)$) [Reference Inahama, Xu and Yang24], this work is under controlled RP framework, which causes more difficulties. Before applying the variational representation, we firstly need to prove that the translation of mixed FBM in the direction of Cameron–Martin components can be lifted to RP. (2) Even though the Khasminskii’s averaging principle is proved efficient under controlled RP framework [Reference Inahama23], due to the extra RP term related to the control, it is more difficult to apply this technique in the weak convergence approach. To deal with this problem, we used the continuity of the solution mapping, continuous mapping theorem, and the invariant measure of the fast equation with frozen slow component.
$H\in (1/2,1)$) [Reference Inahama, Xu and Yang24], this work is under controlled RP framework, which causes more difficulties. Before applying the variational representation, we firstly need to prove that the translation of mixed FBM in the direction of Cameron–Martin components can be lifted to RP. (2) Even though the Khasminskii’s averaging principle is proved efficient under controlled RP framework [Reference Inahama23], due to the extra RP term related to the control, it is more difficult to apply this technique in the weak convergence approach. To deal with this problem, we used the continuity of the solution mapping, continuous mapping theorem, and the invariant measure of the fast equation with frozen slow component.
Before stating outline of our proof, two important results are needed. The first one is that for each ![]() $0 \lt \delta, \varepsilon\leqslant 1$,
$0 \lt \delta, \varepsilon\leqslant 1$, ![]() $Y^{\varepsilon,\delta}$ coincides with the Itô SDE almost surely and it possesses a unique invariant probability measure with frozen slow component [Reference Inahama23, proposition 4.7]. The second result is that the translation of mixed FBM in the direction of Cameron–Martin components can be lifted to RP, which will be proved in §2. Then, we give the outline of our proof. Firstly, based on the variational representation formula for a standard BM [Reference Budhiraja and Dupuis5], the variational representation formula for mixed RP is given. Then, the LDP problem could be transformed into weak convergence of the controlled slow RDE. It is a key ingredient in the weak convergence to average out the controlled fast component. Then, we show that the controlled fast component could be replaced by the fast component without controlled term in the limit by the condition that
$Y^{\varepsilon,\delta}$ coincides with the Itô SDE almost surely and it possesses a unique invariant probability measure with frozen slow component [Reference Inahama23, proposition 4.7]. The second result is that the translation of mixed FBM in the direction of Cameron–Martin components can be lifted to RP, which will be proved in §2. Then, we give the outline of our proof. Firstly, based on the variational representation formula for a standard BM [Reference Budhiraja and Dupuis5], the variational representation formula for mixed RP is given. Then, the LDP problem could be transformed into weak convergence of the controlled slow RDE. It is a key ingredient in the weak convergence to average out the controlled fast component. Then, we show that the controlled fast component could be replaced by the fast component without controlled term in the limit by the condition that ![]() $\delta=o(\varepsilon)$. Finally, we derive the weak convergence of the controlled slow component by exploiting the exponential ergodicity of the auxiliary fast component without control, continuity of the solution mapping, the continuous mapping theorem, and so on.
$\delta=o(\varepsilon)$. Finally, we derive the weak convergence of the controlled slow component by exploiting the exponential ergodicity of the auxiliary fast component without control, continuity of the solution mapping, the continuous mapping theorem, and so on.
We now give the outline of this article. In §2, we introduce some notation and preliminaries. In §3, we give assumptions and the statement of our main result. Section 4 is devoted to a-priori estimates. In §5, the proof of our main result is achieved. Throughout this article, c, C, c 1, C 1, ![]() $\ldots$ denote certain positive constants that may vary from line to line.
$\ldots$ denote certain positive constants that may vary from line to line. ![]() $\mathbb{N}=\{1,2, \ldots\}$ and time horizon T > 0.
$\mathbb{N}=\{1,2, \ldots\}$ and time horizon T > 0.
2. Notations and preliminaries
2.1. Notations
Firstly, we introduce the notations which will be used throughout the article. Let ![]() $[a,b]\subset[0,T]$ and
$[a,b]\subset[0,T]$ and  $\Delta_{[a,b]}:=\{(s,t)\in \mathbb{R}^2|a\leqslant s\leqslant t\leqslant b\}$. We write
$\Delta_{[a,b]}:=\{(s,t)\in \mathbb{R}^2|a\leqslant s\leqslant t\leqslant b\}$. We write ![]() $\Delta_{T}$ simply when
$\Delta_{T}$ simply when ![]() $[a,b]=[0,T]$. Denote
$[a,b]=[0,T]$. Denote ![]() $\nabla$ be the standard gradient on a Euclidean space. Throughout this section,
$\nabla$ be the standard gradient on a Euclidean space. Throughout this section, ![]() $\mathcal{V}$ and
$\mathcal{V}$ and ![]() $\mathcal{W}$ are Euclidean spaces.
$\mathcal{W}$ are Euclidean spaces.
• (Continuous space) Denote
 $\mathcal{C}([a,b],\mathcal{V})$ by the space of continuous functions
$\mathcal{C}([a,b],\mathcal{V})$ by the space of continuous functions  $\varphi:[a,b]\to \mathcal{V}$ with the norm
$\varphi:[a,b]\to \mathcal{V}$ with the norm  $\|\varphi\|_{\infty}=\sup _{t \in[a, b]}|\varphi_t| \lt \infty$, which is a Banach space. The set of continuous functions starts from 0 is denoted by
$\|\varphi\|_{\infty}=\sup _{t \in[a, b]}|\varphi_t| \lt \infty$, which is a Banach space. The set of continuous functions starts from 0 is denoted by  $\mathcal{C}_0([a,b],\mathcal{V})$.
$\mathcal{C}_0([a,b],\mathcal{V})$.• (Hölder continuous space and variation space) For
 $\eta \in(0,1]$, denote
$\eta \in(0,1]$, denote  $\mathcal{C}^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$ by the space of η-Hölder continuous functions
$\mathcal{C}^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$ by the space of η-Hölder continuous functions  $\varphi:[a,b]\to \mathcal{V}$, equipped with the semi-norm
$\varphi:[a,b]\to \mathcal{V}$, equipped with the semi-norm
 \begin{equation*}
\|\varphi\|_{\eta-\operatorname{hld},[a,b]}:=\sup _{a \leqslant s \lt t \leqslant b} \frac{|\varphi_t-\varphi_s|}{(t-s)^\eta} \lt \infty.
\end{equation*}
\begin{equation*}
\|\varphi\|_{\eta-\operatorname{hld},[a,b]}:=\sup _{a \leqslant s \lt t \leqslant b} \frac{|\varphi_t-\varphi_s|}{(t-s)^\eta} \lt \infty.
\end{equation*}The Banach norm in
 $\mathcal{C}^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$ is
$\mathcal{C}^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$ is  $ |\varphi_a|_{\mathcal{V}}+\|\varphi\|_{\eta-\operatorname{hld},[a,b]}$.
$ |\varphi_a|_{\mathcal{V}}+\|\varphi\|_{\eta-\operatorname{hld},[a,b]}$.For
 $1\leqslant p \lt \infty $, denote
$1\leqslant p \lt \infty $, denote  $\mathcal{C}^{p-\operatorname{var}}\left([a,b],\mathcal{V}\right)=\left\{\varphi \in \mathcal{C}\left([a,b],\mathcal{V}\right):\|\varphi\|_{p \text {-var }} \lt \infty\right\}$ where
$\mathcal{C}^{p-\operatorname{var}}\left([a,b],\mathcal{V}\right)=\left\{\varphi \in \mathcal{C}\left([a,b],\mathcal{V}\right):\|\varphi\|_{p \text {-var }} \lt \infty\right\}$ where  $\|\varphi\|_{p \text {-var }}$ is the usual p-variation semi-norm. The set of η-Hölder continuous functions starts from 0 is denoted by
$\|\varphi\|_{p \text {-var }}$ is the usual p-variation semi-norm. The set of η-Hölder continuous functions starts from 0 is denoted by  $\mathcal{C}_0^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$. The space
$\mathcal{C}_0^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$. The space  $\mathcal{C}_0^{p \text{-var}}([a,b],\mathcal{V})$ is defined in a similar way.
$\mathcal{C}_0^{p \text{-var}}([a,b],\mathcal{V})$ is defined in a similar way.For a continuous map
 $\psi:\Delta_{[a,b]}\to \mathcal{V}$, we set
$\psi:\Delta_{[a,b]}\to \mathcal{V}$, we set
 \begin{equation*}
\|\psi\|_{\eta-\operatorname{hld},[a,b]}:=\sup _{a \leqslant s \lt t \leqslant b} \frac{|\psi_t-\psi_s|}{(t-s)^\eta}.
\end{equation*}
\begin{equation*}
\|\psi\|_{\eta-\operatorname{hld},[a,b]}:=\sup _{a \leqslant s \lt t \leqslant b} \frac{|\psi_t-\psi_s|}{(t-s)^\eta}.
\end{equation*}We denote the set of above such ψ of
 $\|\psi\|_{\eta-\operatorname{hld},[a,b]} \lt \infty$ by
$\|\psi\|_{\eta-\operatorname{hld},[a,b]} \lt \infty$ by  $\mathcal{C}_2^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$. It is a Banach space equipped with the norm
$\mathcal{C}_2^{\eta-\operatorname{hld}}([a,b],\mathcal{V})$. It is a Banach space equipped with the norm  $\|\psi\|_{\eta-\operatorname{hld},[a,b]}$. For simplicity, set
$\|\psi\|_{\eta-\operatorname{hld},[a,b]}$. For simplicity, set  $\|\psi\|_{\beta-\operatorname{hld}}:=\|\psi\|_{\beta-\operatorname{hld},[0,T]}$.
$\|\psi\|_{\beta-\operatorname{hld}}:=\|\psi\|_{\beta-\operatorname{hld},[0,T]}$.• (H α space)
 $H^\alpha = H^\alpha ([0,T], \mathcal{V})$ is the space that for all
$H^\alpha = H^\alpha ([0,T], \mathcal{V})$ is the space that for all  $\phi\in \mathcal{C}^{\alpha-\operatorname{hld}}([0,T], \mathcal{V})$, equipped with the norm
$\phi\in \mathcal{C}^{\alpha-\operatorname{hld}}([0,T], \mathcal{V})$, equipped with the norm
 \begin{equation*}
\lim_{\delta\to0+}\sup_{\substack{|t-s|\leqslant \delta\\0 \leqslant s \lt t \leqslant T}} \frac{|\phi_t-\phi_s|}{(t-s)^\beta}=0.
\end{equation*}
\begin{equation*}
\lim_{\delta\to0+}\sup_{\substack{|t-s|\leqslant \delta\\0 \leqslant s \lt t \leqslant T}} \frac{|\phi_t-\phi_s|}{(t-s)^\beta}=0.
\end{equation*}The space H α is a separable Banach space. Moreover,
 $H^\alpha=\overline{\bigcup_{\kappa \gt 0}\mathcal{C}^{(\alpha+\kappa)-\operatorname{hld}}}$ with the closure being taken in the norm
$H^\alpha=\overline{\bigcup_{\kappa \gt 0}\mathcal{C}^{(\alpha+\kappa)-\operatorname{hld}}}$ with the closure being taken in the norm  $\|\cdot\|_{\alpha-\operatorname{hld}}$ and H α is continuously embedded in
$\|\cdot\|_{\alpha-\operatorname{hld}}$ and H α is continuously embedded in  $\mathcal{C}^{\alpha-\operatorname{hld}}([0,T], \mathcal{V})$ [Reference Ciesielski9].
$\mathcal{C}^{\alpha-\operatorname{hld}}([0,T], \mathcal{V})$ [Reference Ciesielski9].• (Sobolev space) For
 $\phi:[a,b] \rightarrow \mathcal{V}$ and
$\phi:[a,b] \rightarrow \mathcal{V}$ and  $\delta \in(0,1) $ and
$\delta \in(0,1) $ and  $p \in(1, \infty)$, we define the Sobolev space
$p \in(1, \infty)$, we define the Sobolev space  $W^{\delta, p}\left([a,b],\mathcal{V}\right)$ equipped with the following norm:
(2.1)
$W^{\delta, p}\left([a,b],\mathcal{V}\right)$ equipped with the following norm:
(2.1) \begin{equation}
\|\phi\|_{W^{\delta, p}}=\|\phi\|_{L^p}+\left(\iint_{[a,b]^2} \frac{\left|\phi_t-\phi_s\right|^p}{|t-s|^{1+\delta p}} d s d t\right)^{1 / p} \lt \infty.
\end{equation}
\begin{equation}
\|\phi\|_{W^{\delta, p}}=\|\phi\|_{L^p}+\left(\iint_{[a,b]^2} \frac{\left|\phi_t-\phi_s\right|^p}{|t-s|^{1+\delta p}} d s d t\right)^{1 / p} \lt \infty.
\end{equation}Moreover, when
 $\eta'=\delta-1/p \gt 0$, we have the continuous imbedding that
$\eta'=\delta-1/p \gt 0$, we have the continuous imbedding that  $W^{\delta, p}([a,b],\mathcal{V}) \subset \mathcal{C}^{\eta'-\operatorname{hld}}([a,b],\mathcal{V})$ [Reference Friz and Victoir17, theorem 2].
$W^{\delta, p}([a,b],\mathcal{V}) \subset \mathcal{C}^{\eta'-\operatorname{hld}}([a,b],\mathcal{V})$ [Reference Friz and Victoir17, theorem 2].• (Ck norm and
 $C^k_b$ norm) Let
$C^k_b$ norm) Let  $U\subset \mathcal{V}$ be an open set. For
$U\subset \mathcal{V}$ be an open set. For  $k\in \mathbb{N}$, denote
$k\in \mathbb{N}$, denote  $C^k(U,\mathcal{W})$ by the set of Ck-functions from U to
$C^k(U,\mathcal{W})$ by the set of Ck-functions from U to  $\mathcal{W}$.
$\mathcal{W}$.  $C_b^k(U,\mathcal{W})$ stands the set of Ck-bounded functions whose derivatives up to order
$C_b^k(U,\mathcal{W})$ stands the set of Ck-bounded functions whose derivatives up to order  $k-$ are also bounded. The space
$k-$ are also bounded. The space  $C_b^k(U,\mathcal{W})$ is a Banach space equipped with the norm
$C_b^k(U,\mathcal{W})$ is a Banach space equipped with the norm  $\|\varphi\|_{C_b^k}:=\sum_{i=0}^{k}\|\nabla^i\varphi\|_\infty \lt \infty$.
$\|\varphi\|_{C_b^k}:=\sum_{i=0}^{k}\|\nabla^i\varphi\|_\infty \lt \infty$.•
 $L(\mathcal{W},\mathcal{V})$ denotes the set of bounded linear maps from
$L(\mathcal{W},\mathcal{V})$ denotes the set of bounded linear maps from  $\mathcal{W}$ to
$\mathcal{W}$ to  $\mathcal{V}$. We set
$\mathcal{V}$. We set  $L(\mathcal{V}, L(\mathcal{V}, \mathcal{W})) \cong L^{(2)}(\mathcal{V} \times \mathcal{V}, \mathcal{W}) \cong L(\mathcal{V} \otimes \mathcal{V}, \mathcal{W})$ where
$L(\mathcal{V}, L(\mathcal{V}, \mathcal{W})) \cong L^{(2)}(\mathcal{V} \times \mathcal{V}, \mathcal{W}) \cong L(\mathcal{V} \otimes \mathcal{V}, \mathcal{W})$ where  $L^{(2)}(\mathcal{V} \times \mathcal{V}, \mathcal{W})$ is the vector space of bounded bilinear maps from
$L^{(2)}(\mathcal{V} \times \mathcal{V}, \mathcal{W})$ is the vector space of bounded bilinear maps from  $\mathcal{V} \times \mathcal{V}$ to
$\mathcal{V} \times \mathcal{V}$ to  $\mathcal{W}$.
$\mathcal{W}$.• (Young integral) If
 $p,q\ge 1$ with
$p,q\ge 1$ with  $\frac{1}{p}+\frac{1}{q} \gt 1$,
$\frac{1}{p}+\frac{1}{q} \gt 1$,  $k\in \mathcal{C}^{q-\operatorname{var}}\left([a,b],\mathcal{L}(\mathcal{W}, \mathcal{V})\right)$ and
$k\in \mathcal{C}^{q-\operatorname{var}}\left([a,b],\mathcal{L}(\mathcal{W}, \mathcal{V})\right)$ and  $l\in \mathcal{C}^{p-\operatorname{var}}\left([a,b],\mathcal{W}\right)$, then given the partition
$l\in \mathcal{C}^{p-\operatorname{var}}\left([a,b],\mathcal{W}\right)$, then given the partition  $\mathcal{P}:=\{t_i\}_{i=0}^{N}$ with
$\mathcal{P}:=\{t_i\}_{i=0}^{N}$ with  $t_0=a, t_N=b$ and the mesh
$t_0=a, t_N=b$ and the mesh  $|\mathcal{P}|:=\max_{i=1,\cdots,N} |t_i-t_{i-1}|$, the Young integral
$|\mathcal{P}|:=\max_{i=1,\cdots,N} |t_i-t_{i-1}|$, the Young integral
 \begin{equation*}
\int_{a}^{b} k_udl_u:=\lim_{|\mathcal{P}| \rightarrow 0} \sum_{i=1}^{N}k_{t_{i-1}}(l_{t_i}-l_{t_i-1})
\end{equation*}
\begin{equation*}
\int_{a}^{b} k_udl_u:=\lim_{|\mathcal{P}| \rightarrow 0} \sum_{i=1}^{N}k_{t_{i-1}}(l_{t_i}-l_{t_i-1})
\end{equation*}is well-defined.
2.2. Mixed fractional Brownian motion
This subsection features a brief overview of the mixed FBM of Hurst parameter H, and only focuses on the case that ![]() $H\in(1/3,1/2)$.
$H\in(1/3,1/2)$.
Consider the ![]() $\mathbb{R}^{d}$-valued continuous stochastic process
$\mathbb{R}^{d}$-valued continuous stochastic process  $(b^H_t)_{t\in[0,T]}$ starting from 0 as following:
$(b^H_t)_{t\in[0,T]}$ starting from 0 as following:
 \begin{equation*}b^H_t=(b_t^{H,1},b_t^{H,2},\ldots,b_t^{H,d}).\end{equation*}
\begin{equation*}b^H_t=(b_t^{H,1},b_t^{H,2},\ldots,b_t^{H,d}).\end{equation*} The above  $(b^H_t)_{t\in[0,T]}$ is said to be an FBM if it is a centred Gaussian process, satisfying that
$(b^H_t)_{t\in[0,T]}$ is said to be an FBM if it is a centred Gaussian process, satisfying that
 \begin{equation*}\mathbb{E}\big[b_{t}^{H} b_{s}^{H}\big]=\frac{1}{2}\left[t^{2 H}+s^{2 H}-|t-s|^{2 H}\right]\times I_{d}, \quad(0\leqslant s\leqslant t \leqslant T),\end{equation*}
\begin{equation*}\mathbb{E}\big[b_{t}^{H} b_{s}^{H}\big]=\frac{1}{2}\left[t^{2 H}+s^{2 H}-|t-s|^{2 H}\right]\times I_{d}, \quad(0\leqslant s\leqslant t \leqslant T),\end{equation*} where Id stands the identity matrix in ![]() $\mathbb{R}^{d\times d}$. Then, it is easy to see that
$\mathbb{R}^{d\times d}$. Then, it is easy to see that
 \begin{equation*}\mathbb{E}\big[(b_{t}^{H}-b_{s}^{H})^{2}\big]=|t-s|^{2 H} \times I_{d},\quad (0\leqslant s\leqslant t \leqslant T).\end{equation*}
\begin{equation*}\mathbb{E}\big[(b_{t}^{H}-b_{s}^{H})^{2}\big]=|t-s|^{2 H} \times I_{d},\quad (0\leqslant s\leqslant t \leqslant T).\end{equation*} From the Kolmogorov’s continuity criterion, the trajectories of bH are of H ʹ-Hölder continuous (![]() $H'\in(0,H)$) and
$H'\in(0,H)$) and ![]() $\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$-variation almost surely. The reproducing kernel Hilbert space of the FBM bH is denoted by
$\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$-variation almost surely. The reproducing kernel Hilbert space of the FBM bH is denoted by ![]() $\mathcal{H}^{H,d}$. Each element
$\mathcal{H}^{H,d}$. Each element ![]() $g\in \mathcal{H}^{H,d}$ is H ʹ-Hölder continuous and of finite
$g\in \mathcal{H}^{H,d}$ is H ʹ-Hölder continuous and of finite ![]() $(H+1/2)^{-1} \lt q \lt 2$-variation, moreover,
$(H+1/2)^{-1} \lt q \lt 2$-variation, moreover, ![]() ${\mathcal{H}^{H,d}} \hookrightarrow W^{\delta, 2} $ (compact embedding) [Reference Inahama21, proposition 3.4].
${\mathcal{H}^{H,d}} \hookrightarrow W^{\delta, 2} $ (compact embedding) [Reference Inahama21, proposition 3.4].
Then, we consider the ![]() $\mathbb{R}^{e}$-valued standard BM
$\mathbb{R}^{e}$-valued standard BM ![]() $(w_t)_{t\in[0,T]}$,
$(w_t)_{t\in[0,T]}$,
The reproducing kernel Hilbert space for ![]() $(w_t)_{t\in[0,T]}$, denoted by
$(w_t)_{t\in[0,T]}$, denoted by  $\mathcal{H}^{\frac{1}{2},e}$, which is defined as follows,
$\mathcal{H}^{\frac{1}{2},e}$, which is defined as follows,
 \begin{align*}\mathcal{H}^{\frac{1}{2},e}&:=\big\{k \in \mathcal{C}_0([0,T],\mathbb{R}^{e})\mid k _{t}=\int_{0}^{t} k _{s}^{\prime} d s \,\text {for } t\in[0,T] \text {with }\| k \|_{\mathcal{H}^{\frac{1}{2},e}}^{2}\\ &:=\int_{0}^{T}| k _{t}^{\prime}|_{\mathbb{R}^{e}}^{2} d t \lt \infty\big\}.\end{align*}
\begin{align*}\mathcal{H}^{\frac{1}{2},e}&:=\big\{k \in \mathcal{C}_0([0,T],\mathbb{R}^{e})\mid k _{t}=\int_{0}^{t} k _{s}^{\prime} d s \,\text {for } t\in[0,T] \text {with }\| k \|_{\mathcal{H}^{\frac{1}{2},e}}^{2}\\ &:=\int_{0}^{T}| k _{t}^{\prime}|_{\mathbb{R}^{e}}^{2} d t \lt \infty\big\}.\end{align*} In the following, we denote the ![]() $\mathbb{R}^{d+e}$-valued mixed FBM by
$\mathbb{R}^{d+e}$-valued mixed FBM by ![]() $(b_t^H, w_t)_{0\leqslant t\leqslant T}$. It is not too difficult to see that
$(b_t^H, w_t)_{0\leqslant t\leqslant T}$. It is not too difficult to see that ![]() $(b^H, w)$ has H ʹ-Hölder continuous (
$(b^H, w)$ has H ʹ-Hölder continuous (![]() $H'\in(0,H)$) and
$H'\in(0,H)$) and ![]() $\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$-variation trajectories almost surely. Let
$\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$-variation trajectories almost surely. Let  $\mathcal{H}:={{\mathcal{H}^{H,d}}\oplus{\mathcal{H}^{\frac{1}{2},e}}}$ be the Cameron–Martin subspace related to
$\mathcal{H}:={{\mathcal{H}^{H,d}}\oplus{\mathcal{H}^{\frac{1}{2},e}}}$ be the Cameron–Martin subspace related to ![]() $(b_t^H, w_t)_{0\leqslant t\leqslant T}$. Then,
$(b_t^H, w_t)_{0\leqslant t\leqslant T}$. Then, ![]() $(\phi, \psi)\in \mathcal{H}$ is of finite q-variation with
$(\phi, \psi)\in \mathcal{H}$ is of finite q-variation with ![]() $(H+1/2)^{-1} \lt q \lt 2$.
$(H+1/2)^{-1} \lt q \lt 2$.
For ![]() $N\in\mathbb{N}$, we define
$N\in\mathbb{N}$, we define
 \begin{equation*}
S_N=\left\{(\phi,\psi) \in \mathcal{H}:
\frac{1}{2}\|(\phi,\psi)\|_{\mathcal{H}}^2 := \frac{1}{2}
(\|\phi\|_{\mathcal{H}^{H,d}}^{2} +\|\psi \|_{\mathcal{H}^{\frac{1}{2},e}}^{2})
\leqslant N\right\}.
\end{equation*}
\begin{equation*}
S_N=\left\{(\phi,\psi) \in \mathcal{H}:
\frac{1}{2}\|(\phi,\psi)\|_{\mathcal{H}}^2 := \frac{1}{2}
(\|\phi\|_{\mathcal{H}^{H,d}}^{2} +\|\psi \|_{\mathcal{H}^{\frac{1}{2},e}}^{2})
\leqslant N\right\}.
\end{equation*} The ball SN is a compact Polish space under the weak topology of ![]() $\mathcal{H}$.
$\mathcal{H}$.
The complete probability space ![]() $(\Omega, \mathcal{F}, \mathbb{P})$ supports bH and w exists independently, where
$(\Omega, \mathcal{F}, \mathbb{P})$ supports bH and w exists independently, where ![]() $\Omega=\mathcal{C}_0\left([0,T], \mathbb{R}^{d+e}\right)$,
$\Omega=\mathcal{C}_0\left([0,T], \mathbb{R}^{d+e}\right)$, ![]() $\mathbb{P}$ is the unique probability measure on Ω and
$\mathbb{P}$ is the unique probability measure on Ω and ![]() $\mathcal{F}=\mathcal{B}\left(\mathcal{C}_0\left([0,T], \mathbb{R}^{d+e}\right)\right)$ is the
$\mathcal{F}=\mathcal{B}\left(\mathcal{C}_0\left([0,T], \mathbb{R}^{d+e}\right)\right)$ is the ![]() $\mathbb{P}$-completion of the Borel σ-field. Then, we consider the canonical filtration given by
$\mathbb{P}$-completion of the Borel σ-field. Then, we consider the canonical filtration given by ![]() $\left\{\mathcal{F}_t^H: t \in[0,T]\right\}$, where
$\left\{\mathcal{F}_t^H: t \in[0,T]\right\}$, where ![]() $\mathcal{F}_t^H=\sigma\left\{(b_s^H,w_s): 0 \leqslant s \leqslant t\right\} \vee \mathcal{N}$ and
$\mathcal{F}_t^H=\sigma\left\{(b_s^H,w_s): 0 \leqslant s \leqslant t\right\} \vee \mathcal{N}$ and ![]() $\mathcal{N}$ is the set of the
$\mathcal{N}$ is the set of the ![]() $\mathbb{P}$-negligible events.
$\mathbb{P}$-negligible events.
We denote the set of all ![]() $\mathbb{R}^{d+e}$-valued processes
$\mathbb{R}^{d+e}$-valued processes ![]() $(\phi_t,\psi_t)_{t \in [0,T]}$ on
$(\phi_t,\psi_t)_{t \in [0,T]}$ on ![]() $(\Omega, {\mathcal{F}}, {\mathbb{P}})$ by
$(\Omega, {\mathcal{F}}, {\mathbb{P}})$ by ![]() ${\mathcal{A}}_b^N$ for
${\mathcal{A}}_b^N$ for ![]() $N\in \mathbb{N}$ and let
$N\in \mathbb{N}$ and let ![]() ${\mathcal{A}}_b =\cup_{N\in \mathbb{N}} {\mathcal{A}}_b^N$. Since each
${\mathcal{A}}_b =\cup_{N\in \mathbb{N}} {\mathcal{A}}_b^N$. Since each ![]() $(\phi,\psi)\in {\mathcal{A}}_b^N$ is a random variable taking values in the compact ball
$(\phi,\psi)\in {\mathcal{A}}_b^N$ is a random variable taking values in the compact ball ![]() ${S}_N$, the family
${S}_N$, the family ![]() $\{\mathbb{P}\circ (\phi,\psi)^{-1} : (\phi,\psi) \in {\mathcal{A}}_b^N\}$ of probability measures is tight automatically. Due to Girsanov’s formula, for every
$\{\mathbb{P}\circ (\phi,\psi)^{-1} : (\phi,\psi) \in {\mathcal{A}}_b^N\}$ of probability measures is tight automatically. Due to Girsanov’s formula, for every ![]() $(\phi,\psi) \in {\mathcal{A}}_b$, the law of
$(\phi,\psi) \in {\mathcal{A}}_b$, the law of ![]() $(b^H +\phi,w+\psi)$ is mutually absolutely continuous to that of
$(b^H +\phi,w+\psi)$ is mutually absolutely continuous to that of ![]() $(b^H,w)$. In the following, we recall the variational representation formula for the mixed FBM, whose precise proof refers to [Reference Inahama, Xu and Yang24, proposition 2.3].
$(b^H,w)$. In the following, we recall the variational representation formula for the mixed FBM, whose precise proof refers to [Reference Inahama, Xu and Yang24, proposition 2.3].
Proposition 2.1.
Let ![]() $\alpha\in (0,H)$. For a bounded Borel measurable function
$\alpha\in (0,H)$. For a bounded Borel measurable function ![]() $\Phi:\Omega\to \mathbb{R}$,
$\Phi:\Omega\to \mathbb{R}$,
 \begin{equation}
-\log \mathbb{E}[\exp (-\Phi(b^H, w))]=\inf _{(\phi, \psi) \in \mathcal{A}_b} \mathbb{E}[\Phi(b^H+\phi, w+\psi)+\frac{1}{2}\|(\phi, \psi)\|_{\mathcal{H}}^2].
\end{equation}
\begin{equation}
-\log \mathbb{E}[\exp (-\Phi(b^H, w))]=\inf _{(\phi, \psi) \in \mathcal{A}_b} \mathbb{E}[\Phi(b^H+\phi, w+\psi)+\frac{1}{2}\|(\phi, \psi)\|_{\mathcal{H}}^2].
\end{equation}2.3. Rough path
In this subsection, we introduce RP and some explanations which will be utilized in our main proof. In the all following sections, we assume ![]() $\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$ and
$\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$ and ![]() $(H+1/2)^{-1} \lt q \lt 2$ such that
$(H+1/2)^{-1} \lt q \lt 2$ such that ![]() $1/p+1/q \gt 1$, where
$1/p+1/q \gt 1$, where ![]() $\lfloor \cdot \rfloor$ stands for the integer part. For example, we take
$\lfloor \cdot \rfloor$ stands for the integer part. For example, we take ![]() $1 / p=H-2\kappa$ and
$1 / p=H-2\kappa$ and ![]() $1 / q=H+1 / 2-\kappa$ with small parameter
$1 / q=H+1 / 2-\kappa$ with small parameter ![]() $0 \lt \kappa \lt H/2$.
$0 \lt \kappa \lt H/2$.
Now, we give the definition of the RP.
Definition 2.2 ([Reference Friz and Hairer16], Section 2)
A continuous map
 \begin{equation*}
\Xi=\big(1, \Xi^{1}, \Xi^{2}\big): \Delta \rightarrow T^{2}(\mathcal{V})=\mathbb{R} \oplus \mathcal{V} \oplus \mathcal{V}^{\otimes 2} ,
\end{equation*}
\begin{equation*}
\Xi=\big(1, \Xi^{1}, \Xi^{2}\big): \Delta \rightarrow T^{2}(\mathcal{V})=\mathbb{R} \oplus \mathcal{V} \oplus \mathcal{V}^{\otimes 2} ,
\end{equation*} is said to be a ![]() $\mathcal{V}$-valued RP of roughness 2 if it satisfies the following conditions,
$\mathcal{V}$-valued RP of roughness 2 if it satisfies the following conditions,
(Condition A): For any ![]() $s \leqslant u \leqslant t$,
$s \leqslant u \leqslant t$, ![]() $\Xi_{s, t}=\Xi_{s, u} \otimes \Xi_{u, t}$ where ⊗ stands for the tensor product.
$\Xi_{s, t}=\Xi_{s, u} \otimes \Xi_{u, t}$ where ⊗ stands for the tensor product.
(Condition B): ![]() $\|\Xi^{1}\|_{\alpha \mathrm{-hld}} \lt \infty$ and
$\|\Xi^{1}\|_{\alpha \mathrm{-hld}} \lt \infty$ and ![]() $\|\Xi^{2}\|_{2\alpha \mathrm{-hld}} \lt \infty$.
$\|\Xi^{2}\|_{2\alpha \mathrm{-hld}} \lt \infty$.
Obviously, the 0-th element 1 is omitted and we denote the RP by ![]() $\Xi=\left(\Xi^{1}, \Xi^{2}\right)$. The (Condition A) is also called Chen’s identity. Below, we set
$\Xi=\left(\Xi^{1}, \Xi^{2}\right)$. The (Condition A) is also called Chen’s identity. Below, we set  $\left\vert\!\left\vert\!\left\vert{\Xi}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}:=\|\Xi^{1}\|_{\alpha \mathrm{-hld}}+\|\Xi^{2}\|^{1/2}_{2\alpha \mathrm{-hld}}$. The set of all
$\left\vert\!\left\vert\!\left\vert{\Xi}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}:=\|\Xi^{1}\|_{\alpha \mathrm{-hld}}+\|\Xi^{2}\|^{1/2}_{2\alpha \mathrm{-hld}}$. The set of all ![]() $\mathcal{V}$-valued RPs with
$\mathcal{V}$-valued RPs with ![]() $1/3 \lt \alpha \lt 1/2$ is denoted by
$1/3 \lt \alpha \lt 1/2$ is denoted by ![]() $\Omega_{\alpha}(\mathcal{V})$. Equipped with the α-Hölder distance, it is a complete space. It is easy to verify that
$\Omega_{\alpha}(\mathcal{V})$. Equipped with the α-Hölder distance, it is a complete space. It is easy to verify that ![]() $\Omega_\alpha(\mathcal{V}) \subset \Omega_\beta(\mathcal{V})$ for
$\Omega_\alpha(\mathcal{V}) \subset \Omega_\beta(\mathcal{V})$ for  $\frac{1}{3} \lt \beta \leqslant \alpha \leqslant \frac{1}{2}$. For two different RPs
$\frac{1}{3} \lt \beta \leqslant \alpha \leqslant \frac{1}{2}$. For two different RPs ![]() $\Xi=(\Xi^1,\Xi^2)\in \Omega_\alpha(\mathcal{V})$ and
$\Xi=(\Xi^1,\Xi^2)\in \Omega_\alpha(\mathcal{V})$ and ![]() $\tilde{\Xi}=(\tilde{\Xi}^1,\tilde{\Xi}^2)\in \Omega_\alpha(\mathcal{V})$, we denote the distance between them by
$\tilde{\Xi}=(\tilde{\Xi}^1,\tilde{\Xi}^2)\in \Omega_\alpha(\mathcal{V})$, we denote the distance between them by ![]() $\rho_\alpha(\star, \cdot)$ which is defined as following:
$\rho_\alpha(\star, \cdot)$ which is defined as following:
Next, we introduce the control function, which will be used in proposition 2.6.
Definition 2.3 ([Reference Lyons and Qian32], Page 16)
Let ![]() $[0,T]$ be a finite interval and let
$[0,T]$ be a finite interval and let ![]() $\Delta_T$ denote the simplex
$\Delta_T$ denote the simplex ![]() $\{(s,t):0\leqslant s\leqslant t\leqslant T\}$. A control function ω is a non-negative continuous function on
$\{(s,t):0\leqslant s\leqslant t\leqslant T\}$. A control function ω is a non-negative continuous function on ![]() $\Delta_T$ which is super-additive, namely
$\Delta_T$ which is super-additive, namely
for all ![]() $0\leqslant s\leqslant t\leqslant u\leqslant T$ and for which
$0\leqslant s\leqslant t\leqslant u\leqslant T$ and for which ![]() $\omega(t,t)=0$ for all
$\omega(t,t)=0$ for all ![]() $t\in [0,T]$.
$t\in [0,T]$.
Next, we give some explanations for RP which will be used in this work. Firstly, we show that the mixed FBM can be lifted to RP, whose precise proof is a minor modification of [Reference Yang, Xu and Pei43, proposition 2.2] by subtracting a term  $\frac{1}{2}I_e(t-s)$ where Ie stands the identity matrix in
$\frac{1}{2}I_e(t-s)$ where Ie stands the identity matrix in ![]() $\mathbb{R}^{e\times e}$.
$\mathbb{R}^{e\times e}$.
Remark 2.4.
Let ![]() $(b^H,w)^\mathrm{T}\in \mathbb{R}^{d+e}$ with
$(b^H,w)^\mathrm{T}\in \mathbb{R}^{d+e}$ with ![]() $H\in(1/3,1/2)$ be the mixed FBM and
$H\in(1/3,1/2)$ be the mixed FBM and ![]() $\alpha\in (0,H)$. Then
$\alpha\in (0,H)$. Then ![]() $(b^H,w)$ can be lifted to RP
$(b^H,w)$ can be lifted to RP ![]() $(B^H,W)=((B^H,W)^1,(B^H,W)^2)\in \Omega_{\alpha}(\mathbb{R}^{d+e})$ with
$(B^H,W)=((B^H,W)^1,(B^H,W)^2)\in \Omega_{\alpha}(\mathbb{R}^{d+e})$ with
 \begin{equation}
(B^H,W)^1_{s t}=\left(b^H_{s t}, w_{s t}\right)^{\mathrm{T}}, \quad (B^H,W)^2_{s t}=\left(\begin{array}{ll}
B_{s t}^{H,2} & I[b_H, w]_{s t} \\
I[w, b_H]_{s t} & W_{s t}^{2}
\end{array}\right).
\end{equation}
\begin{equation}
(B^H,W)^1_{s t}=\left(b^H_{s t}, w_{s t}\right)^{\mathrm{T}}, \quad (B^H,W)^2_{s t}=\left(\begin{array}{ll}
B_{s t}^{H,2} & I[b_H, w]_{s t} \\
I[w, b_H]_{s t} & W_{s t}^{2}
\end{array}\right).
\end{equation} Here, ![]() $(B^{H, 1}, B^{H,2})\in \Omega_{\alpha}(\mathbb{R}^{d})$ is a canonical geometric RPs associated with FBM and
$(B^{H, 1}, B^{H,2})\in \Omega_{\alpha}(\mathbb{R}^{d})$ is a canonical geometric RPs associated with FBM and ![]() $(W^{1}, W^{2})\in \Omega_{\alpha}(\mathbb{R}^{d})$ is a Itô-type Brownian RP. Moreover,
$(W^{1}, W^{2})\in \Omega_{\alpha}(\mathbb{R}^{d})$ is a Itô-type Brownian RP. Moreover,
 \begin{equation}
I[b^H, w]_{s t} \triangleq \int_{s}^{t} b^H_{s r} \otimes \mathrm{d}^{\mathrm{I}} w_{r},
\end{equation}
\begin{equation}
I[b^H, w]_{s t} \triangleq \int_{s}^{t} b^H_{s r} \otimes \mathrm{d}^{\mathrm{I}} w_{r},
\end{equation} \begin{equation}
I[w,b^H]_{s t} \triangleq w_{s t} \otimes b^H_{s t}-\int_{s}^{t} \mathrm{~d}^{\mathrm{I}} w_{r} \otimes b^H_{s r},
\end{equation}
\begin{equation}
I[w,b^H]_{s t} \triangleq w_{s t} \otimes b^H_{s t}-\int_{s}^{t} \mathrm{~d}^{\mathrm{I}} w_{r} \otimes b^H_{s r},
\end{equation} where ![]() $\int \cdots \mathrm{d}^{\mathrm{I}} w$ stands for the Itô integral.
$\int \cdots \mathrm{d}^{\mathrm{I}} w$ stands for the Itô integral.
Moreover, according to the [Reference Inahama23, lemma 4.6], for ![]() $\alpha' \lt \alpha$,
$\alpha' \lt \alpha$,  $\mathbb{E}\left[\|\Lambda\|_{\alpha'}^q\right] \lt \infty$ holds for every
$\mathbb{E}\left[\|\Lambda\|_{\alpha'}^q\right] \lt \infty$ holds for every ![]() $q \in[1, \infty)$. Then, we turn to the observation that
$q \in[1, \infty)$. Then, we turn to the observation that ![]() $u\in \mathcal{H}^{H,d}$ can be lifted to RP.
$u\in \mathcal{H}^{H,d}$ can be lifted to RP.
Remark 2.5.
Let ![]() $H\in (1/3,1/2)$ and
$H\in (1/3,1/2)$ and ![]() $\alpha\in (0,H)$. The elements
$\alpha\in (0,H)$. The elements ![]() $u\in \mathcal{H}^{H,d}$ can be lifted to RP
$u\in \mathcal{H}^{H,d}$ can be lifted to RP ![]() $U=(U^1,U^2)\in \Omega_{\alpha}(\mathbb{R}^d)$ with
$U=(U^1,U^2)\in \Omega_{\alpha}(\mathbb{R}^d)$ with
 \begin{equation}
U^1_{s,t}=u_{s,t},\quad U^2_{s,t}=\int_{s}^{t}u_{s,r}du_r
\end{equation}
\begin{equation}
U^1_{s,t}=u_{s,t},\quad U^2_{s,t}=\int_{s}^{t}u_{s,r}du_r
\end{equation} where U 2 is well-defined in the variation setting. Moreover, ![]() $U=(U^1,U^2)$ is a locally Lipschitz continuous mapping from
$U=(U^1,U^2)$ is a locally Lipschitz continuous mapping from ![]() $\mathcal{H}^{H,d}$ to
$\mathcal{H}^{H,d}$ to ![]() $\Omega_\alpha(\mathbb{R}^d)$.
$\Omega_\alpha(\mathbb{R}^d)$.
Proof. Recall that ![]() $u\in \mathcal{H}^{H,d}$ is of finite
$u\in \mathcal{H}^{H,d}$ is of finite ![]() $(H+1/2)^{-1} \lt q \lt 2$-variation and
$(H+1/2)^{-1} \lt q \lt 2$-variation and  $\frac{2}{q} \gt 1$. Then, U 2 is well-defined as a Young integral. Then, by applying the fact that
$\frac{2}{q} \gt 1$. Then, U 2 is well-defined as a Young integral. Then, by applying the fact that ![]() $u\in \mathcal{H}^{H,d}$ is α-Hölder continuous, the proof is completed.
$u\in \mathcal{H}^{H,d}$ is α-Hölder continuous, the proof is completed.
Similarly, we can show that the elements  $v\in \mathcal{H}^{\frac{1}{2},e}$ can be lifted to RP
$v\in \mathcal{H}^{\frac{1}{2},e}$ can be lifted to RP ![]() $V=(V^1,V^2)\in \Omega_{\alpha}(\mathbb{R}^e)$ with
$V=(V^1,V^2)\in \Omega_{\alpha}(\mathbb{R}^e)$ with
 \begin{equation*}
V^1_{s,t}=v_{s,t},\quad V^2_{s,t}=\int_{s}^{t}v_{s,r}dv_r
\end{equation*}
\begin{equation*}
V^1_{s,t}=v_{s,t},\quad V^2_{s,t}=\int_{s}^{t}v_{s,r}dv_r
\end{equation*}where V 2 is well-defined since v is differentiable.
Next, we will show that the translation of mixed FBM in the direction ![]() $h:=(u,v)\in \mathcal{H}$ can be lifted to RP.
$h:=(u,v)\in \mathcal{H}$ can be lifted to RP.
Remark 2.6.
Let ![]() $(b^H+u,w+v)$ be the translation of
$(b^H+u,w+v)$ be the translation of ![]() $(b^H,w)^\mathrm{T}\in \mathbb{R}^{d+e}$ with
$(b^H,w)^\mathrm{T}\in \mathbb{R}^{d+e}$ with ![]() $H\in(1/3,1/2)$ in the direction
$H\in(1/3,1/2)$ in the direction ![]() $h:=(u,v)\in \mathcal{H}$ and
$h:=(u,v)\in \mathcal{H}$ and ![]() $\alpha\in (0,H)$. Then,
$\alpha\in (0,H)$. Then, ![]() $(b^H+u,w+v)$ can be lifted to RP
$(b^H+u,w+v)$ can be lifted to RP ![]() $T^h(B^H,W)=(T^{h,1}(B^H,W),T^{h,2}(B^H,W))\in \Omega_{\alpha}(\mathbb{R}^{d+e})$, which is defined as following:
$T^h(B^H,W)=(T^{h,1}(B^H,W),T^{h,2}(B^H,W))\in \Omega_{\alpha}(\mathbb{R}^{d+e})$, which is defined as following:
 \begin{align}
\begin{array}{l}
T_{s,t}^{h,1}(B^H,W)=(b^H+u,w+v)_{s,t}, \\
T_{s, t}^{h,2}(B^H,W)\\
={\!\left(\!\!\begin{array}{ll}
B^{H,2}+I[b^H,u]+I[u,b^H]+ U^2& I[b_H, w]\,{+}\,I[b_H, v]\,{+}\,I[u, w]\,{+}\,I[u, v] \\
I[w, b_H]\,{+}\,I[w, u]\,{+}\, I[v, b_H]\,{+}\, I[v, u] & W^2+I[w,v]+I[v,w]+V^2
\end{array}\!\!\right)\!}_{s, t}\\
=B^H,W^2_{s t}+
\left(\begin{array}{ll}
I[b^H,u]+I[u,b^H]+ U^2& I[b_H, v]+I[u, w]+I[u, v] \\
I[w, u]+ I[v, b_H]+ I[v, u] & I[w,v]+I[v,w]+V^2
\end{array}\right)_{s, t}.
\end{array}\nonumber\\
\end{align}
\begin{align}
\begin{array}{l}
T_{s,t}^{h,1}(B^H,W)=(b^H+u,w+v)_{s,t}, \\
T_{s, t}^{h,2}(B^H,W)\\
={\!\left(\!\!\begin{array}{ll}
B^{H,2}+I[b^H,u]+I[u,b^H]+ U^2& I[b_H, w]\,{+}\,I[b_H, v]\,{+}\,I[u, w]\,{+}\,I[u, v] \\
I[w, b_H]\,{+}\,I[w, u]\,{+}\, I[v, b_H]\,{+}\, I[v, u] & W^2+I[w,v]+I[v,w]+V^2
\end{array}\!\!\right)\!}_{s, t}\\
=B^H,W^2_{s t}+
\left(\begin{array}{ll}
I[b^H,u]+I[u,b^H]+ U^2& I[b_H, v]+I[u, w]+I[u, v] \\
I[w, u]+ I[v, b_H]+ I[v, u] & I[w,v]+I[v,w]+V^2
\end{array}\right)_{s, t}.
\end{array}\nonumber\\
\end{align}Here, the second term in (2.7) is well-defined in the variation setting.
Proof. It is obvious that ![]() $T^{h,1}(B^H,W)$ is a translation of mixed FBM in the direction
$T^{h,1}(B^H,W)$ is a translation of mixed FBM in the direction ![]() $h:=(u,v)\in \mathcal{H}$ and it is α-Hölder continuous. So we mainly prove that the second level path
$h:=(u,v)\in \mathcal{H}$ and it is α-Hölder continuous. So we mainly prove that the second level path ![]() $T^{h,2}(B^H,W)$ is also well-defined. From remarks 2.4 and 2.5, we have shown that
$T^{h,2}(B^H,W)$ is also well-defined. From remarks 2.4 and 2.5, we have shown that ![]() $(B^H,W)^2$, U 2 and V 2 are well-defined. Hence, we are in the position to estimate the remaining terms.
$(B^H,W)^2$, U 2 and V 2 are well-defined. Hence, we are in the position to estimate the remaining terms.
Firstly, we will prove that ![]() $I[b^H,u]$ is well-defined as a Young integral. Recall that the trajectories of bH are of p-variation almost surely for
$I[b^H,u]$ is well-defined as a Young integral. Recall that the trajectories of bH are of p-variation almost surely for ![]() $\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$ and
$\lfloor 1 / H \rfloor \lt {p} \lt \lfloor 1 / H \rfloor+1$ and ![]() $u\in \mathcal{H}^{H,d}$ is of finite
$u\in \mathcal{H}^{H,d}$ is of finite ![]() $(H+1/2)^{-1} \lt q \lt 2$-variation. Since
$(H+1/2)^{-1} \lt q \lt 2$-variation. Since  $\frac{1}{p}+\frac{1}{q} \gt 1$,
$\frac{1}{p}+\frac{1}{q} \gt 1$,  $\int_{s}^{t}b^H_{s,r}du_r$ is well-defined in the Young integral. Then, we will show that it is 2α-Hölder continuous. According to [Reference Friz and Victoir17, theorem 2] and definition 2.3, we have that bH can be dominated by the function
$\int_{s}^{t}b^H_{s,r}du_r$ is well-defined in the Young integral. Then, we will show that it is 2α-Hölder continuous. According to [Reference Friz and Victoir17, theorem 2] and definition 2.3, we have that bH can be dominated by the function  $\omega_1 (s,t):=\|b^H\|^{1/(H-\kappa)}_{(H-\kappa) \mathrm{-hld}}{(t-s)}$ for any small
$\omega_1 (s,t):=\|b^H\|^{1/(H-\kappa)}_{(H-\kappa) \mathrm{-hld}}{(t-s)}$ for any small ![]() $0 \lt \kappa \lt H$. Similarly, the elements u is dominated by the control function
$0 \lt \kappa \lt H$. Similarly, the elements u is dominated by the control function  $\omega_2 (s,t):=\|u\|^{q}_{W^{\delta,2}}{(t-s)}^{\alpha q}$ for
$\omega_2 (s,t):=\|u\|^{q}_{W^{\delta,2}}{(t-s)}^{\alpha q}$ for ![]() $(H+1/2)^{-1} \lt q \lt 2$ in the sense of [Reference Lyons and Qian32, p. 16]. The control function has following super-additivity properties: for
$(H+1/2)^{-1} \lt q \lt 2$ in the sense of [Reference Lyons and Qian32, p. 16]. The control function has following super-additivity properties: for ![]() $i=1,2$,
$i=1,2$,
Let ![]() $J_{s,t}=b^H_s(u_t-u_s)$. Then, for
$J_{s,t}=b^H_s(u_t-u_s)$. Then, for ![]() $s\leqslant r\leqslant t$, we have
$s\leqslant r\leqslant t$, we have
 \begin{equation*}
\begin{array}{rcl}
J_{s,r}+J_{r,t}-J_{s,t}&=&b^H_s(u_r-u_s)+b^H_r(u_t-u_r)-b^H_s(u_t-u_s)\\
&=&(b^H_t-b^H_s)(u_t-u_s).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{rcl}
J_{s,r}+J_{r,t}-J_{s,t}&=&b^H_s(u_r-u_s)+b^H_r(u_t-u_r)-b^H_s(u_t-u_s)\\
&=&(b^H_t-b^H_s)(u_t-u_s).
\end{array}
\end{equation*} After that, we take a partition ![]() $\mathcal{P}=\{s=t_0\leqslant t_1 \leqslant ...\leqslant t_N=t\}$ and denote
$\mathcal{P}=\{s=t_0\leqslant t_1 \leqslant ...\leqslant t_N=t\}$ and denote
 \begin{equation*}
J_{s,t}(\mathcal{P})=\sum_{i=1}^{N}J_{t_{i-1},t_i},\quad J_{s,t}(\{s,t\})=J_{s,t}.
\end{equation*}
\begin{equation*}
J_{s,t}(\mathcal{P})=\sum_{i=1}^{N}J_{t_{i-1},t_i},\quad J_{s,t}(\{s,t\})=J_{s,t}.
\end{equation*}By taking direct computation and using (2.8), we obtain
 \begin{equation*}\begin{array}{rcl}
|J_{s,t}(\mathcal{P})-J_{s,t}(\mathcal{P} \backslash \{t_i\})|&\leqslant&|J_{t_{i-1},t_i}+J_{t_{i},t_{i+1}}-J_{t_{i-1},t_{i+1}}|\\
&\leqslant&|(b^H_{t_{i}}-b^H_{t_{i-1}})(u_{t_{i+1}}-u_{t_{i}})|\\
&\leqslant& C \{\omega^{^{1/p}}_1 (t_{i-1},t_{i+1})\omega^{^{1/q}}_2 (t_{i-1},t_{i+1})\}\\
&\leqslant& {\big(\frac{2}{N}\big)}^{1/p+1/q} \omega^{1/p}_1 (s,t)\omega^{1/q}_2 (s,t).
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
|J_{s,t}(\mathcal{P})-J_{s,t}(\mathcal{P} \backslash \{t_i\})|&\leqslant&|J_{t_{i-1},t_i}+J_{t_{i},t_{i+1}}-J_{t_{i-1},t_{i+1}}|\\
&\leqslant&|(b^H_{t_{i}}-b^H_{t_{i-1}})(u_{t_{i+1}}-u_{t_{i}})|\\
&\leqslant& C \{\omega^{^{1/p}}_1 (t_{i-1},t_{i+1})\omega^{^{1/q}}_2 (t_{i-1},t_{i+1})\}\\
&\leqslant& {\big(\frac{2}{N}\big)}^{1/p+1/q} \omega^{1/p}_1 (s,t)\omega^{1/q}_2 (s,t).
\end{array}
\end{equation*}Then, by iterating the above procedure again, we have
 \begin{equation*}\begin{array}{rcl}
|J_{s,t}(\mathcal{P})-J_{s,t}|&\leqslant& \sum\limits_{k=2}^{N} {\big(\frac{2}{k-1}\big)}^{1/p+1/q} \omega^{1/p}_1 (s,t)\omega^{1/q}_2 (s,t)\\
&\leqslant& 2^{1/p+1/q}\zeta({1/p+1/q})\omega^{1/p}_1 (s,t)\omega^{1/q}_2 (s,t)\\
&\leqslant& 2^{1/p+1/q}\zeta({1/p+1/q})\|b^H\|^{1/p(H-\kappa)}_{(H-\kappa) \mathrm{-hld}} \|u\|_{W^{\delta,2}}{(t-s)}^{\alpha+1/p }\\
&\leqslant& C 2^{1/p+1/q}\zeta({1/p+1/q}){(t-s)}^{\alpha+1/p },
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
|J_{s,t}(\mathcal{P})-J_{s,t}|&\leqslant& \sum\limits_{k=2}^{N} {\big(\frac{2}{k-1}\big)}^{1/p+1/q} \omega^{1/p}_1 (s,t)\omega^{1/q}_2 (s,t)\\
&\leqslant& 2^{1/p+1/q}\zeta({1/p+1/q})\omega^{1/p}_1 (s,t)\omega^{1/q}_2 (s,t)\\
&\leqslant& 2^{1/p+1/q}\zeta({1/p+1/q})\|b^H\|^{1/p(H-\kappa)}_{(H-\kappa) \mathrm{-hld}} \|u\|_{W^{\delta,2}}{(t-s)}^{\alpha+1/p }\\
&\leqslant& C 2^{1/p+1/q}\zeta({1/p+1/q}){(t-s)}^{\alpha+1/p },
\end{array}
\end{equation*} where ζ is the Zeta function. Since ![]() $\alpha+1/p \gt 2\alpha$, we verify that the second level path
$\alpha+1/p \gt 2\alpha$, we verify that the second level path  $\int_{s}^{t}b^H_{s,r}du_r$ is 2α-Hölder continuous.
$\int_{s}^{t}b^H_{s,r}du_r$ is 2α-Hölder continuous.
Next, by taking similar estimations as above, we can obtain that the other remaining terms are also well-defined in the Young sense and of 2α-Hölder continuous.
Moreover, we could verify that ![]() $T^h(B^H,W)=(T^{h,1}(B^H,W),T^{h,2}(B^H,W))$ satisfies (Condition A) in definition 2.2 by some direct computations. Then we have
$T^h(B^H,W)=(T^{h,1}(B^H,W),T^{h,2}(B^H,W))$ satisfies (Condition A) in definition 2.2 by some direct computations. Then we have ![]() $T^h(B^H,W)=(T^{h,1}(B^H,W),T^{h,2}(B^H,W))\in \Omega_{\alpha}({\mathbb{R}^{d+e}})$. The proof is completed.
$T^h(B^H,W)=(T^{h,1}(B^H,W),T^{h,2}(B^H,W))\in \Omega_{\alpha}({\mathbb{R}^{d+e}})$. The proof is completed.
Next, we introduce the controlled RP. Firstly, we recall the definition of controlled RP with respect to the reference RP ![]() $\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$. It says that
$\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$. It says that ![]() $(Y, Y^{\dagger}, Y^{\sharp})$ is a
$(Y, Y^{\dagger}, Y^{\sharp})$ is a ![]() $\mathcal{W}$-valued controlled RP with respect to
$\mathcal{W}$-valued controlled RP with respect to ![]() $\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$ if it satisfies the following conditions:
$\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$ if it satisfies the following conditions:
 \begin{equation*}
Y_t-Y_s=Y_s^{\dagger} \Xi_{s, t}^1+R^{Y}_{s, t}, \quad(s, t) \in \triangle_{[a, b]}
\end{equation*}
\begin{equation*}
Y_t-Y_s=Y_s^{\dagger} \Xi_{s, t}^1+R^{Y}_{s, t}, \quad(s, t) \in \triangle_{[a, b]}
\end{equation*}and
 \begin{equation*}
\left(Y, Y^{\dagger}, R^{Y}\right) \in \mathcal{C}^{\alpha-\operatorname{hld}}([a, b], \mathcal{W}) \times \mathcal{C}^{\alpha-\operatorname{hld}}([a, b], L(\mathcal{V}, \mathcal{W})) \times \mathcal{C}_2^{2\alpha-\operatorname{hld}}([a, b], \mathcal{W}).
\end{equation*}
\begin{equation*}
\left(Y, Y^{\dagger}, R^{Y}\right) \in \mathcal{C}^{\alpha-\operatorname{hld}}([a, b], \mathcal{W}) \times \mathcal{C}^{\alpha-\operatorname{hld}}([a, b], L(\mathcal{V}, \mathcal{W})) \times \mathcal{C}_2^{2\alpha-\operatorname{hld}}([a, b], \mathcal{W}).
\end{equation*} Let ![]() $\mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ stand for the set of all above controlled RPs. Denote the semi-norm of controlled RP
$\mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ stand for the set of all above controlled RPs. Denote the semi-norm of controlled RP ![]() $(Y, Y^{\dagger}, R^{Y})\in \mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ by
$(Y, Y^{\dagger}, R^{Y})\in \mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ by
 \begin{equation*}\|\left(Y, Y^{\dagger}, R^{Y}\right)\|_{\mathcal{Q}_{\Xi}^\alpha,[a, b]}=\|Y^{\dagger}\|_{{\alpha-\operatorname{hld}},[a, b]}+\|R^{Y}\|_{{2\alpha-\operatorname{hld}},[a, b]}.\end{equation*}
\begin{equation*}\|\left(Y, Y^{\dagger}, R^{Y}\right)\|_{\mathcal{Q}_{\Xi}^\alpha,[a, b]}=\|Y^{\dagger}\|_{{\alpha-\operatorname{hld}},[a, b]}+\|R^{Y}\|_{{2\alpha-\operatorname{hld}},[a, b]}.\end{equation*} The controlled RP space ![]() $\mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ is a Banach space equipped with the norm
$\mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ is a Banach space equipped with the norm  $|Y_a|_{\mathcal{W}}+|Y_a^{\dagger}|_{L(\mathcal{V}, \mathcal{W})}+\|(Y, Y^{\dagger}, R^{Y})\|_{\mathcal{Q}_{\Xi}^\alpha,[a, b]}$. In the following,
$|Y_a|_{\mathcal{W}}+|Y_a^{\dagger}|_{L(\mathcal{V}, \mathcal{W})}+\|(Y, Y^{\dagger}, R^{Y})\|_{\mathcal{Q}_{\Xi}^\alpha,[a, b]}$. In the following, ![]() $(Y, Y^{\dagger}, R^{Y})$ is replaced by
$(Y, Y^{\dagger}, R^{Y})$ is replaced by ![]() $(Y, Y^{\dagger})$ for simplicity.
$(Y, Y^{\dagger})$ for simplicity.
For two different controlled RPs ![]() $(Y, Y^{\dagger})\in \mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ and
$(Y, Y^{\dagger})\in \mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$ and  $(\tilde{Y}, \tilde{Y}^{\dagger})\in \mathcal{Q}_{\tilde \Xi}^\alpha([a, b], \mathcal{W})$, we set their distance as follows,
$(\tilde{Y}, \tilde{Y}^{\dagger})\in \mathcal{Q}_{\tilde \Xi}^\alpha([a, b], \mathcal{W})$, we set their distance as follows,
 \begin{equation*}d_{\Xi, \tilde{\Xi}, 2 \alpha}\big(Y, Y^{\dagger} ; \tilde{Y}, \tilde{Y}^{\dagger}\big) \stackrel{\text {def }}{=}\big\|Y^{\dagger}-\tilde{Y}^{\dagger}\big\|_{\alpha-\operatorname{hld}}+\big\|R^Y-R^{\tilde{Y}}\big\|_{{2\alpha-\operatorname{hld}}}.\end{equation*}
\begin{equation*}d_{\Xi, \tilde{\Xi}, 2 \alpha}\big(Y, Y^{\dagger} ; \tilde{Y}, \tilde{Y}^{\dagger}\big) \stackrel{\text {def }}{=}\big\|Y^{\dagger}-\tilde{Y}^{\dagger}\big\|_{\alpha-\operatorname{hld}}+\big\|R^Y-R^{\tilde{Y}}\big\|_{{2\alpha-\operatorname{hld}}}.\end{equation*}In the following, we show that the integration of controlled RP against RP is again a controlled RP, whose precise proof refers to [Reference Inahama23, proposition 3.2].
Remark 2.7.
Let ![]() $1/3 \lt \alpha \lt 1/2$ and
$1/3 \lt \alpha \lt 1/2$ and ![]() $[a,b]\subset[0,T]$. For a RP
$[a,b]\subset[0,T]$. For a RP ![]() $\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$ and controlled RP
$\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$ and controlled RP ![]() $(Y, Y^{\dagger}) \in \mathcal{Q}_{\Xi}^\alpha([a, b], L(\mathcal{V}, \mathcal{W}))$, we have
$(Y, Y^{\dagger}) \in \mathcal{Q}_{\Xi}^\alpha([a, b], L(\mathcal{V}, \mathcal{W}))$, we have  $\left(\int_a^{\cdot} Y_u d {\Xi}_u, Y\right) \in \mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$.
$\left(\int_a^{\cdot} Y_u d {\Xi}_u, Y\right) \in \mathcal{Q}_{\Xi}^\alpha([a, b], \mathcal{W})$.
We now turn to the stability estimate of the solution map to the RDE with a drift term.
Proposition 2.8.
Let ![]() $\xi\in \mathcal{W}$ and
$\xi\in \mathcal{W}$ and ![]() $\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$ with
$\Xi=\left(\Xi^{1}, \Xi^{2}\right)\in \Omega_{\alpha}(\mathcal{V})$ with ![]() $1/3 \lt \alpha \lt 1/2$. Assume
$1/3 \lt \alpha \lt 1/2$. Assume  $(\Psi; \sigma(\Psi))\in \mathcal{Q}_{\Xi}^\beta([0, T], \mathcal{W})$ with
$(\Psi; \sigma(\Psi))\in \mathcal{Q}_{\Xi}^\beta([0, T], \mathcal{W})$ with ![]() $1/3 \lt \beta \lt \alpha \lt 1/2$ be the (unique) solution to the following RDE
$1/3 \lt \beta \lt \alpha \lt 1/2$ be the (unique) solution to the following RDE
Here, f is globally bounded and Lipschitz continuous function and ![]() $\sigma\in C_b^3$. Similarly, let
$\sigma\in C_b^3$. Similarly, let  $(\tilde{\Psi}; \sigma(\tilde\Psi)) \in \mathcal{Q}_{\tilde \Xi}^\beta([0, T], \mathcal{W})$ with initial value
$(\tilde{\Psi}; \sigma(\tilde\Psi)) \in \mathcal{Q}_{\tilde \Xi}^\beta([0, T], \mathcal{W})$ with initial value ![]() $(\tilde \xi, \sigma(\tilde\xi))$. Assume
$(\tilde \xi, \sigma(\tilde\xi))$. Assume
 \begin{equation*}\left\vert\!\left\vert\!\left\vert{\Xi}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}},\left\vert\!\left\vert\!\left\vert{\tilde\Xi}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}\leqslant M \lt \infty.\end{equation*}
\begin{equation*}\left\vert\!\left\vert\!\left\vert{\Xi}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}},\left\vert\!\left\vert\!\left\vert{\tilde\Xi}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}\leqslant M \lt \infty.\end{equation*}Then, we have the (local) Lipschitz estimates as following:
 \begin{equation}
d_{\Xi, \tilde{\Xi}, 2 \beta}(\Psi, \sigma(\Psi) ; \tilde{\Psi}, \sigma(\tilde{\Psi})) \leqslant C_M\left(|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})\right).
\end{equation}
\begin{equation}
d_{\Xi, \tilde{\Xi}, 2 \beta}(\Psi, \sigma(\Psi) ; \tilde{\Psi}, \sigma(\tilde{\Psi})) \leqslant C_M\left(|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})\right).
\end{equation}and
 \begin{equation}
\|\Psi-\tilde{\Psi}\|_{\beta-\operatorname{hld}} \leqslant C_M\left(|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})\right).
\end{equation}
\begin{equation}
\|\Psi-\tilde{\Psi}\|_{\beta-\operatorname{hld}} \leqslant C_M\left(|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})\right).
\end{equation} Here,  $C_M=C(M,\alpha,\beta,L_f,\|\sigma\|_{C_b^3}) \gt 0$.
$C_M=C(M,\alpha,\beta,L_f,\|\sigma\|_{C_b^3}) \gt 0$.
Proof. This proposition is a minor modification of [Reference Friz and Hairer16, theorem 8.5] with the drift term, and its proof is in Appendix A.
3. Assumptions and statement of our main result
In this section, we give necessary assumptions and the statement of our main LDP result. In the all following sections, we set ![]() $1/3 \lt \beta \lt \alpha \lt H \lt 1/2$.
$1/3 \lt \beta \lt \alpha \lt H \lt 1/2$.
We write ![]() $Z^{\varepsilon,\delta}=(X^{\varepsilon,\delta},Y^{\varepsilon,\delta})$. Then, the precise definition of slow-fast RDE (1.1) can be rewritten as following:
$Z^{\varepsilon,\delta}=(X^{\varepsilon,\delta},Y^{\varepsilon,\delta})$. Then, the precise definition of slow-fast RDE (1.1) can be rewritten as following:
 \begin{equation}
\begin{array}{rcl}
Z_t^{\varepsilon,\delta}&=&Z_0+\int_0^t F_{\varepsilon,\delta}\big(Z_s^{\varepsilon,\delta}\big) d s+\int_0^t \Sigma_{\varepsilon,\delta}\big(Z_s^{\varepsilon,\delta}\big) d(\varepsilon(B^H,W)_s),\\
\big(Z^{\varepsilon,\delta}\big)_t^{\dagger}&=&\Sigma_{\varepsilon,\delta}\big(Z_t^{\varepsilon,\delta}\big),
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
Z_t^{\varepsilon,\delta}&=&Z_0+\int_0^t F_{\varepsilon,\delta}\big(Z_s^{\varepsilon,\delta}\big) d s+\int_0^t \Sigma_{\varepsilon,\delta}\big(Z_s^{\varepsilon,\delta}\big) d(\varepsilon(B^H,W)_s),\\
\big(Z^{\varepsilon,\delta}\big)_t^{\dagger}&=&\Sigma_{\varepsilon,\delta}\big(Z_t^{\varepsilon,\delta}\big),
\end{array}
\end{equation} with ![]() $t \in[0, T]$ and the initial value
$t \in[0, T]$ and the initial value ![]() $Z_0=(X_0,Y_0)$ and
$Z_0=(X_0,Y_0)$ and
 \begin{equation*}
F_{\varepsilon,\delta}(x, y)=\left(\begin{array}{c}
f_1(x, y) \\
\delta^{-1} f_2(x, y)
\end{array}\right), \quad \Sigma_{\varepsilon,\delta}(x, y)=\left(\begin{array}{cc}
\sigma_1(x) & O \\
O & (\varepsilon\delta)^{-1 / 2} \sigma_2(x, y)
\end{array}\right) .
\end{equation*}
\begin{equation*}
F_{\varepsilon,\delta}(x, y)=\left(\begin{array}{c}
f_1(x, y) \\
\delta^{-1} f_2(x, y)
\end{array}\right), \quad \Sigma_{\varepsilon,\delta}(x, y)=\left(\begin{array}{cc}
\sigma_1(x) & O \\
O & (\varepsilon\delta)^{-1 / 2} \sigma_2(x, y)
\end{array}\right) .
\end{equation*} Here, ![]() $\varepsilon(B^H,W)=(\sqrt{\varepsilon}(B^H,W)^1,\varepsilon(B^H,W)^2)\in \Omega_{\alpha}(\mathbb{R}^{d+e})$ is the dilation of
$\varepsilon(B^H,W)=(\sqrt{\varepsilon}(B^H,W)^1,\varepsilon(B^H,W)^2)\in \Omega_{\alpha}(\mathbb{R}^{d+e})$ is the dilation of ![]() $(B^H,W)=((B^H,W)^1,(B^H,W)^2)\in \Omega_{\alpha}(\mathbb{R}^{d+e})$, which is defined in (2.3). Then,
$(B^H,W)=((B^H,W)^1,(B^H,W)^2)\in \Omega_{\alpha}(\mathbb{R}^{d+e})$, which is defined in (2.3). Then,  $(Z^{\varepsilon,\delta},(Z^{\varepsilon,\delta})^{\dagger})\in \mathcal{Q}_{\varepsilon(B^H,W)}^\beta([a, b], \mathbb{R}^{m+n})$ with
$(Z^{\varepsilon,\delta},(Z^{\varepsilon,\delta})^{\dagger})\in \mathcal{Q}_{\varepsilon(B^H,W)}^\beta([a, b], \mathbb{R}^{m+n})$ with ![]() $1/3 \lt \beta \lt \alpha \lt H$ is a controlled RP, where the Gubinelli derivative
$1/3 \lt \beta \lt \alpha \lt H$ is a controlled RP, where the Gubinelli derivative  $\big(Z^{\varepsilon,\delta}\big)^{\dagger}$ is defined as following:
$\big(Z^{\varepsilon,\delta}\big)^{\dagger}$ is defined as following:
 \begin{equation*}
{(Z^{\varepsilon,\delta})}^\dagger:= \Sigma_{\varepsilon,\delta}(x, y)=\left(\begin{array}{cc}
\sigma_1(x) & O \\
O & (\varepsilon\delta)^{-1 / 2} \sigma_2(x, y)
\end{array}\right) .
\end{equation*}
\begin{equation*}
{(Z^{\varepsilon,\delta})}^\dagger:= \Sigma_{\varepsilon,\delta}(x, y)=\left(\begin{array}{cc}
\sigma_1(x) & O \\
O & (\varepsilon\delta)^{-1 / 2} \sigma_2(x, y)
\end{array}\right) .
\end{equation*}To ensure the existence and uniqueness of solutions to the RDE (3.1), we impose the following conditions.
A1.
 $\sigma_{1}\in \mathcal{C}_b^3$.
$\sigma_{1}\in \mathcal{C}_b^3$.A2. There exists a constant L > 0 such that for any
 $ (x_1,y_1) $,
$ (x_1,y_1) $,  $ (x_2,y_2)\in \mathbb{R}^{m} \times\mathbb{R}^{n}$,
$ (x_2,y_2)\in \mathbb{R}^{m} \times\mathbb{R}^{n}$,
 \begin{equation*}
\left|f_1\left( x_1, y_1\right)-f_1\left( x_2, y_2\right)\right| + \left|f_2\left(x_1, y_1\right)-f_2\left(x_2, y_2\right)\right| \leqslant L\left(\left|x_1-x_2\right|+\left|y_1-y_2\right|\right),
\end{equation*}
\begin{equation*}
\left|f_1\left( x_1, y_1\right)-f_1\left( x_2, y_2\right)\right| + \left|f_2\left(x_1, y_1\right)-f_2\left(x_2, y_2\right)\right| \leqslant L\left(\left|x_1-x_2\right|+\left|y_1-y_2\right|\right),
\end{equation*}and
 \begin{equation*}|f_1\left( x_1, y_1\right)|\leqslant L\end{equation*}
\begin{equation*}|f_1\left( x_1, y_1\right)|\leqslant L\end{equation*}hold.
A3. Assume σ 2 is of
 $ \mathcal{C}^3$. We further assume that there exists a constant L > 0 such that for any
$ \mathcal{C}^3$. We further assume that there exists a constant L > 0 such that for any  $ (x_1,y_1) $,
$ (x_1,y_1) $,  $ (x_2,y_2)\in \mathbb{R}^{m} \times\mathbb{R}^{n}$,
$ (x_2,y_2)\in \mathbb{R}^{m} \times\mathbb{R}^{n}$,
 \begin{equation*}
\left|\sigma_2\left(x_1, y_1\right)-\sigma_2\left(x_2, y_2\right)\right| \leqslant L\left(\left|x_1-x_2\right|+\left|y_1-y_2\right|\right),
\end{equation*}
\begin{equation*}
\left|\sigma_2\left(x_1, y_1\right)-\sigma_2\left(x_2, y_2\right)\right| \leqslant L\left(\left|x_1-x_2\right|+\left|y_1-y_2\right|\right),
\end{equation*}and that, for any
 $x_1\in \mathbb{R}^m$,
$x_1\in \mathbb{R}^m$,
 \begin{equation*}
\sup_{y_1\in\mathbb{R}^{n}}\left|\sigma_2\left(x_1, y_1\right)\right| \leqslant L\left(1+\left|x_1\right|\right)
\end{equation*}
\begin{equation*}
\sup_{y_1\in\mathbb{R}^{n}}\left|\sigma_2\left(x_1, y_1\right)\right| \leqslant L\left(1+\left|x_1\right|\right)
\end{equation*}hold.
Under above (A1)–(A3), one can deduce from [Reference Inahama23, remark 3.4] that the RDE (3.1) has a unique local solution. Define  $\tau_N^{\varepsilon}=\inf \{t \geqslant 0| | Z_t^{\varepsilon,\delta} \mid \geqslant N\}$ for each
$\tau_N^{\varepsilon}=\inf \{t \geqslant 0| | Z_t^{\varepsilon,\delta} \mid \geqslant N\}$ for each ![]() $N\in \mathbb{N}$ and
$N\in \mathbb{N}$ and ![]() $\tau_{\infty}^{\varepsilon}=\lim _{N \rightarrow \infty} \tau_N^{\varepsilon}$.
$\tau_{\infty}^{\varepsilon}=\lim _{N \rightarrow \infty} \tau_N^{\varepsilon}$.
Proposition 3.1.
Suppose assumptions (A1)–(A3). For each ![]() $0 \lt \delta, \varepsilon\leqslant 1$,
$0 \lt \delta, \varepsilon\leqslant 1$, ![]() $Y^{\varepsilon,\delta}$ satisfies the Itô SDE as following:
$Y^{\varepsilon,\delta}$ satisfies the Itô SDE as following:
 \begin{equation}
Y_t^{\varepsilon,\delta}=Y_0+\frac{1}{\delta} \int_0^{t} f_2\left(X_s^{\varepsilon,\delta}, Y_s^{\varepsilon,\delta}\right) d s+\frac{1}{\sqrt{\delta}} \int_0^{t} \sigma_2\left(X_s^{\varepsilon,\delta}, Y_s^{\varepsilon,\delta}\right) d^{\mathrm{I}} w_s
\end{equation}
\begin{equation}
Y_t^{\varepsilon,\delta}=Y_0+\frac{1}{\delta} \int_0^{t} f_2\left(X_s^{\varepsilon,\delta}, Y_s^{\varepsilon,\delta}\right) d s+\frac{1}{\sqrt{\delta}} \int_0^{t} \sigma_2\left(X_s^{\varepsilon,\delta}, Y_s^{\varepsilon,\delta}\right) d^{\mathrm{I}} w_s
\end{equation} where ![]() $t\in[0,\tau_{\infty}^{\varepsilon})$.
$t\in[0,\tau_{\infty}^{\varepsilon})$.
Proof. For the proof, we refer to [Reference Inahama23, proposition 4.7].
To prove that there exists a global solution to the RDE (3.1), we assume the following conditions.
A4. Assume that there exist positive constants C > 0 and
 $\beta_i \gt 0 \,(i=1,2)$ such that for any
$\beta_i \gt 0 \,(i=1,2)$ such that for any  $ (x,y_1),(x,y_2)\in \mathbb{R}^{m} \times\mathbb{R}^{n}$
(3.3)
$ (x,y_1),(x,y_2)\in \mathbb{R}^{m} \times\mathbb{R}^{n}$
(3.3) \begin{align}
2\left\langle y_1\,{-}\,y_2, f_2(x, y_1)\,{-}\,f_2(x, y_2)\right\rangle\,{+}\,\left|\sigma_2(x, y_1)\,{-}\,\sigma_2(x, y_2)\right|^2
\leqslant-\beta_1\left|y_1-y_2\right|^2 \nonumber\\ \end{align}
\begin{align}
2\left\langle y_1\,{-}\,y_2, f_2(x, y_1)\,{-}\,f_2(x, y_2)\right\rangle\,{+}\,\left|\sigma_2(x, y_1)\,{-}\,\sigma_2(x, y_2)\right|^2
\leqslant-\beta_1\left|y_1-y_2\right|^2 \nonumber\\ \end{align}and
(3.4) \begin{equation}
2\left\langle y_1, f_2\left(x, y_1\right)\right\rangle+\left|\sigma_2\left(x, y_1\right)\right|^2 \leqslant-\beta_2\left|y_1\right|^2+C|x|^2+C
\end{equation}
\begin{equation}
2\left\langle y_1, f_2\left(x, y_1\right)\right\rangle+\left|\sigma_2\left(x, y_1\right)\right|^2 \leqslant-\beta_2\left|y_1\right|^2+C|x|^2+C
\end{equation}hold.
Meanwhile, it is equivalent between the statement that there exists a global solution  $\{Z_t^{\varepsilon,\delta}\}_{t\in [0,T]}$ to the RDE (1.1) and the statement
$\{Z_t^{\varepsilon,\delta}\}_{t\in [0,T]}$ to the RDE (1.1) and the statement ![]() $\tau_{\infty}^{\varepsilon} \gt T$.
$\tau_{\infty}^{\varepsilon} \gt T$.
Proposition 3.2.
Suppose assumptions (A1)–(A4). The probability that ![]() $\tau_{\infty}^{\varepsilon} \gt T$ is zero, moreover,
$\tau_{\infty}^{\varepsilon} \gt T$ is zero, moreover,
 \begin{equation*}\begin{array}{rcl}
\sup\limits_{0 \lt \varepsilon,\delta \leqslant 1} \mathbb{E}[\|X^{\varepsilon,\delta}\|_{\beta-\operatorname{hld}}^p]& \lt &\infty, \quad 1 \leqslant p \lt \infty,\\
\sup\limits_{0 \lt \delta,\varepsilon \leqslant 1} \sup\limits_{0 \leqslant t \leqslant T} \mathbb{E}[|Y_t^{\varepsilon,\delta}|^2]& \lt &\infty.
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
\sup\limits_{0 \lt \varepsilon,\delta \leqslant 1} \mathbb{E}[\|X^{\varepsilon,\delta}\|_{\beta-\operatorname{hld}}^p]& \lt &\infty, \quad 1 \leqslant p \lt \infty,\\
\sup\limits_{0 \lt \delta,\varepsilon \leqslant 1} \sup\limits_{0 \leqslant t \leqslant T} \mathbb{E}[|Y_t^{\varepsilon,\delta}|^2]& \lt &\infty.
\end{array}
\end{equation*}Proof. For the proof, we refer to [Reference Inahama23, proposition 4.7].
Therefore, there exists a unique solution ![]() $Z^{\varepsilon, \delta}$ globally to the RDE (3.1). Then,
$Z^{\varepsilon, \delta}$ globally to the RDE (3.1). Then, ![]() $Y^{\varepsilon,\delta}$ satisfies the Itô SDE (3.2) for all
$Y^{\varepsilon,\delta}$ satisfies the Itô SDE (3.2) for all ![]() $t\in[0,T]$.
$t\in[0,T]$.
Furthermore, we have that  $\left(X^{\varepsilon,\delta}, \sigma_1\left({X}^{\varepsilon,\delta}\right)\right)\in \mathcal{Q}_{\varepsilon B^H}^\beta\left([0, T], \mathbb{R}^m\right)$ is a unique global solution of the RDE driven by
$\left(X^{\varepsilon,\delta}, \sigma_1\left({X}^{\varepsilon,\delta}\right)\right)\in \mathcal{Q}_{\varepsilon B^H}^\beta\left([0, T], \mathbb{R}^m\right)$ is a unique global solution of the RDE driven by ![]() $\varepsilon B^H=(\sqrt{\varepsilon}B^{H,1},\varepsilon B^{H,2})$ as following:
$\varepsilon B^H=(\sqrt{\varepsilon}B^{H,1},\varepsilon B^{H,2})$ as following:
 \begin{equation}
\begin{array}{rcl}
X_t^{\varepsilon,\delta}&=&X_0+\int_0^t f_1\big(X_s^{\varepsilon,\delta}, Y_s^{\varepsilon,\delta}\big) d s+\int_0^t \varepsilon\sigma_1\big(X_s^{\varepsilon,\delta}\big) dB^H_s,\\
\big(X^{\varepsilon,\delta}\big)_t^{\dagger}&=&\sigma_1\big(X_t^{\varepsilon,\delta}\big),
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
X_t^{\varepsilon,\delta}&=&X_0+\int_0^t f_1\big(X_s^{\varepsilon,\delta}, Y_s^{\varepsilon,\delta}\big) d s+\int_0^t \varepsilon\sigma_1\big(X_s^{\varepsilon,\delta}\big) dB^H_s,\\
\big(X^{\varepsilon,\delta}\big)_t^{\dagger}&=&\sigma_1\big(X_t^{\varepsilon,\delta}\big),
\end{array}
\end{equation} with ![]() $t \in[0, T]$. Then there exists a measurable map
$t \in[0, T]$. Then there exists a measurable map
 \begin{equation*}
\mathcal{G}^{(\varepsilon, \delta)}: \mathcal{C}_0\left([0,T], \mathbb{R}^d\right) \rightarrow \mathcal{C}^{\beta-\operatorname{hld}}\left([0,T], \mathbb{R}^m\right)
\end{equation*}
\begin{equation*}
\mathcal{G}^{(\varepsilon, \delta)}: \mathcal{C}_0\left([0,T], \mathbb{R}^d\right) \rightarrow \mathcal{C}^{\beta-\operatorname{hld}}\left([0,T], \mathbb{R}^m\right)
\end{equation*} such that ![]() $X^{\varepsilon,\delta}:=\mathcal{G}^{\varepsilon,\delta}(\sqrt \varepsilon b^H, \sqrt \varepsilon w)$.
$X^{\varepsilon,\delta}:=\mathcal{G}^{\varepsilon,\delta}(\sqrt \varepsilon b^H, \sqrt \varepsilon w)$.
Remark 3.3.
Here, we give a remark on assumption (A4). Condition (3.3) is called strict monotonicity condition, which is to guarantee the exponential ergodicity (see conclusion (b) in remark 3.5). Condition (3.4) is also called strict coercivity condition, which is to ensure the existence of invariant measure for Eq. (3.6) with frozen X. The uniqueness of invariant probability measures for (3.6) is shown at conclusion (a) in remark 3.5.
Consider the following Itô SDE with frozen X
 \begin{equation}
d{Y}^{X,Y_0}_t = f_{2}({X}, {Y}^{X,Y_0}_t) dt +\sigma_2( {X}, {Y}^{X,Y_0}_t)dw_{t}
\end{equation}
\begin{equation}
d{Y}^{X,Y_0}_t = f_{2}({X}, {Y}^{X,Y_0}_t) dt +\sigma_2( {X}, {Y}^{X,Y_0}_t)dw_{t}
\end{equation} with initial value  $Y^{X,Y_0}_0=Y_0\in\mathbb{R}^n$. Let
$Y^{X,Y_0}_0=Y_0\in\mathbb{R}^n$. Let  $\{P^X_t\}_{t\in[0,T]}$ be the transition semigroup of
$\{P^X_t\}_{t\in[0,T]}$ be the transition semigroup of  $\{Y^{X,Y_0}_t\}_{t\in[0,T]}$, i.e. for any bounded measurable function
$\{Y^{X,Y_0}_t\}_{t\in[0,T]}$, i.e. for any bounded measurable function ![]() $\varphi:\mathbb{R}^m\to \mathbb{R}$:
$\varphi:\mathbb{R}^m\to \mathbb{R}$:
 \begin{equation*}
P_s^X \varphi(y):=\mathbb{E}[\varphi(Y_s^{X, Y_0})], \quad Y_0 \in \mathbb{R}^{n}, s \geqslant 0.
\end{equation*}
\begin{equation*}
P_s^X \varphi(y):=\mathbb{E}[\varphi(Y_s^{X, Y_0})], \quad Y_0 \in \mathbb{R}^{n}, s \geqslant 0.
\end{equation*} The following remark 3.4 and Krylov–Bogoliubov argument yield the existence of an invariant probability measure for  $\{P^X_t\}_{t\in[0,T]}$ for every X.
$\{P^X_t\}_{t\in[0,T]}$ for every X.
Remark 3.4.
Under assumption (A4), for any given ![]() $X\in \mathbb{R}^m$,
$X\in \mathbb{R}^m$, ![]() $Y_0\in \mathbb{R}^n$ and
$Y_0\in \mathbb{R}^n$ and ![]() $t\in[0,T]$, it is easily to see
$t\in[0,T]$, it is easily to see
 \begin{equation*}
\mathbb{E}[|Y_t^{X, Y_0}|^2] \leqslant e^{-\beta_2 t}|Y_0|^2+C(1+|X|^2).
\end{equation*}
\begin{equation*}
\mathbb{E}[|Y_t^{X, Y_0}|^2] \leqslant e^{-\beta_2 t}|Y_0|^2+C(1+|X|^2).
\end{equation*} Moreover, for any ![]() $y_1,y_2\in \mathbb{R}^n$, we have
$y_1,y_2\in \mathbb{R}^n$, we have
 \begin{equation*}
\mathbb{E}[|Y_t^{X, y_1}-Y_t^{X, y_2}|^2] \leqslant e^{-\beta_2 t}|y_1-y_2|^2.
\end{equation*}
\begin{equation*}
\mathbb{E}[|Y_t^{X, y_1}-Y_t^{X, y_2}|^2] \leqslant e^{-\beta_2 t}|y_1-y_2|^2.
\end{equation*}Proof. For the proof, we refer to [Reference Liu, Röckner and Sun29, lemmas 3.6 and 3.7] for example.
Remark 3.5.
Suppose that (A2)–(A4) hold. For any given ![]() $X\in\mathbb{R}^m$ and initial value
$X\in\mathbb{R}^m$ and initial value ![]() $Y_0\in \mathbb{R}^n$, the semigroup
$Y_0\in \mathbb{R}^n$, the semigroup  $\{P^X_t\}_{t\in[0,T]}$ has a unique invariant probability measure µ X. Furthermore, the following estimates hold:
$\{P^X_t\}_{t\in[0,T]}$ has a unique invariant probability measure µ X. Furthermore, the following estimates hold:
(a) There exists a constant C > 0 such that
 \begin{equation*}\int_{\mathbb{R}^{n}}|y|^2 \mu^X(d y) \leqslant C\left(1+|X|^2\right).\end{equation*}
\begin{equation*}\int_{\mathbb{R}^{n}}|y|^2 \mu^X(d y) \leqslant C\left(1+|X|^2\right).\end{equation*}Here, C is independent of X.
(b) There exists C > 0 such that for any Lipschitz function ![]() $\varphi:\mathbb{R}^n \to \mathbb{R}$:
$\varphi:\mathbb{R}^n \to \mathbb{R}$:
 \begin{equation*}
\big|P_s^X \varphi(y)-\int_{\mathbb{R}^{n}} \varphi(z) \mu^X(d z)\big| \leqslant C(1+|X|+|Y_0|) e^{-\beta_1 s}|\varphi|_{\text {Lip }}, \quad s \geq 0,
\end{equation*}
\begin{equation*}
\big|P_s^X \varphi(y)-\int_{\mathbb{R}^{n}} \varphi(z) \mu^X(d z)\big| \leqslant C(1+|X|+|Y_0|) e^{-\beta_1 s}|\varphi|_{\text {Lip }}, \quad s \geq 0,
\end{equation*} where ![]() $|\varphi|_{\text {Lip }}$ is the Lipschitz coefficient of φ and
$|\varphi|_{\text {Lip }}$ is the Lipschitz coefficient of φ and ![]() $\beta_1 \gt 0$ is in assumption (A4).
$\beta_1 \gt 0$ is in assumption (A4).
Proof. The proof is a special case of [Reference Liu, Röckner and Sun29, proposition 3.8].
Next, we define the skeleton equation in the rough sense as follows
where ![]() $\tilde{X}_0=X_0$,
$\tilde{X}_0=X_0$, ![]() $U=(U^1,U^2)\in \Omega_{\alpha}(\mathbb{R}^d)$, and
$U=(U^1,U^2)\in \Omega_{\alpha}(\mathbb{R}^d)$, and  $\bar{f}_1(x)=\int_{\mathbb{R}^{n}}f_{1}(x, {y})\mu^{x}(d{y})$ for
$\bar{f}_1(x)=\int_{\mathbb{R}^{n}}f_{1}(x, {y})\mu^{x}(d{y})$ for ![]() $x\in\mathbb{R}^m$. Then, we will show that
$x\in\mathbb{R}^m$. Then, we will show that ![]() $\bar{f}_1$ is Lipschitz continuous and bounded. Firstly, by assumption (A2) and remark 3.5, we have that for all for any
$\bar{f}_1$ is Lipschitz continuous and bounded. Firstly, by assumption (A2) and remark 3.5, we have that for all for any ![]() $ (x_1, x_2)\in \mathbb{R}^{m} $ and initial value
$ (x_1, x_2)\in \mathbb{R}^{m} $ and initial value ![]() $Y_0\in \mathbb{R}^{n} $,
$Y_0\in \mathbb{R}^{n} $,
 \begin{equation}
\begin{array}{rcl}
\left|\bar{f}_1\left(x_1\right)-\bar{f}_1\left(x_2\right)\right| &\leqslant &|\int_{\mathbb{R}^n} f_1(x_1, y) \mu^{x_1}(d y)-\mathbb{E}[f_1(x_1, Y_t^{x_1,Y_0})]| \\
&&+\big|\int_{\mathbb{R}^n} f_1(x_2, y) \mu^{x_1}(d y)-\mathbb{E}[f_1(x_2, Y_t^{x_2,Y_0})]\big| \\
&&+\big|\mathbb{E}[f_1(x_1, Y_t^{x_1,Y_0})]-\mathbb{E}[f_1(x_2, Y_t^{x_2,Y_0})]\big| \\
&\leqslant & C e^{-\beta_1 s}(1+|x_1|+|x_2|+|Y_0|)+L|x_1-x_2|.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\left|\bar{f}_1\left(x_1\right)-\bar{f}_1\left(x_2\right)\right| &\leqslant &|\int_{\mathbb{R}^n} f_1(x_1, y) \mu^{x_1}(d y)-\mathbb{E}[f_1(x_1, Y_t^{x_1,Y_0})]| \\
&&+\big|\int_{\mathbb{R}^n} f_1(x_2, y) \mu^{x_1}(d y)-\mathbb{E}[f_1(x_2, Y_t^{x_2,Y_0})]\big| \\
&&+\big|\mathbb{E}[f_1(x_1, Y_t^{x_1,Y_0})]-\mathbb{E}[f_1(x_2, Y_t^{x_2,Y_0})]\big| \\
&\leqslant & C e^{-\beta_1 s}(1+|x_1|+|x_2|+|Y_0|)+L|x_1-x_2|.
\end{array}
\end{equation} Let ![]() $s\to \infty$, we see that
$s\to \infty$, we see that ![]() $\bar f_1$ is Lipschitz continuous. Since f 1 is globally bounded which is assumed in (A2),
$\bar f_1$ is Lipschitz continuous. Since f 1 is globally bounded which is assumed in (A2), ![]() $\bar f_1$ is also globally bounded. Then, it is not too difficult to see that there exists a unique global solution
$\bar f_1$ is also globally bounded. Then, it is not too difficult to see that there exists a unique global solution  $(\tilde{X},\tilde{X}^{\dagger})\in \mathcal{Q}_{U}^\beta([0, T], \mathbb{R}^m)$ to the RDE (3.7). Moreover, we have for
$(\tilde{X},\tilde{X}^{\dagger})\in \mathcal{Q}_{U}^\beta([0, T], \mathbb{R}^m)$ to the RDE (3.7). Moreover, we have for ![]() $0 \lt \beta \lt \alpha \lt H$ that
$0 \lt \beta \lt \alpha \lt H$ that
 \begin{equation*}\|\tilde{X}\|_{\beta-\operatorname{hld}}\leqslant c,\end{equation*}
\begin{equation*}\|\tilde{X}\|_{\beta-\operatorname{hld}}\leqslant c,\end{equation*}with the constant c > 0 independent of U. Therefore, we also define a map
such that its solution ![]() $\tilde{X}=\mathcal{G}^{0}(u, v)$.
$\tilde{X}=\mathcal{G}^{0}(u, v)$.
Remark 3.6.
The above RDE (3.7) coincides with the Young ordinary differential equation (ODE) as following:
with ![]() $\tilde{X}_t=X_0$ and
$\tilde{X}_t=X_0$ and  $\bar{f}_1(x)=\int_{\mathbb{R}^{n}}f_{1}(x, {y})\mu^{x}(d{y})$ for
$\bar{f}_1(x)=\int_{\mathbb{R}^{n}}f_{1}(x, {y})\mu^{x}(d{y})$ for ![]() $x\in\mathbb{R}^m$. For
$x\in\mathbb{R}^m$. For ![]() $(H+1/2)^{-1} \lt q \lt 2$, we have
$(H+1/2)^{-1} \lt q \lt 2$, we have ![]() $\|(u,v)\|_{q-\operatorname{var}} \lt \infty$. According to Young’s integral theory, it is easy to verify that there exists a unique solution
$\|(u,v)\|_{q-\operatorname{var}} \lt \infty$. According to Young’s integral theory, it is easy to verify that there exists a unique solution  $\tilde {X} \in \mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^d\right)$ to (3.9) in the Young sense for
$\tilde {X} \in \mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^d\right)$ to (3.9) in the Young sense for ![]() $(u, v) \in S_{N}$. Moreover, we have
$(u, v) \in S_{N}$. Moreover, we have
 \begin{equation*}\|\tilde{X}\|_{p-\operatorname{var}}\leqslant c,\end{equation*}
\begin{equation*}\|\tilde{X}\|_{p-\operatorname{var}}\leqslant c,\end{equation*}where the constant c > 0 is independent of (u, v).
Now, we give the statement of our main theorem.
Theorem 3.7.
Let ![]() $H\in(1/3,1/2)$ and
$H\in(1/3,1/2)$ and ![]() $0 \lt \alpha \lt H$. Fix
$0 \lt \alpha \lt H$. Fix ![]() $1/3 \lt \beta \lt \alpha$. Assume (A1)–(A4) and
$1/3 \lt \beta \lt \alpha$. Assume (A1)–(A4) and ![]() $\delta=o(\varepsilon)$. Let ɛ → 0, the slow component
$\delta=o(\varepsilon)$. Let ɛ → 0, the slow component ![]() $X^{\varepsilon,\delta}$ of system (1.1) satisfies an LDP on
$X^{\varepsilon,\delta}$ of system (1.1) satisfies an LDP on ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ with a good rate function
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ with a good rate function ![]() $I: \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^m)\rightarrow [0, \infty)$
$I: \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^m)\rightarrow [0, \infty)$
 \begin{equation*}\begin{array}{rcl}
I(\xi) &=& \inf\Big\{\frac{1}{2}\|u\|^2_{\mathcal{H}^{H,d}} : {u\in \mathcal{H}^{H,d}\quad\text{such that} \quad\xi =\mathcal{G}^{0}(u, 0)}\Big\} \\
&=& \inf\Big\{\frac{1}{2}\|(u,v)\|^2_{\mathcal{H}} : {( u,v)\in \mathcal{H}\quad\text{such that} \quad\xi =\mathcal{G}^{0}(u, v)}\Big\},
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
I(\xi) &=& \inf\Big\{\frac{1}{2}\|u\|^2_{\mathcal{H}^{H,d}} : {u\in \mathcal{H}^{H,d}\quad\text{such that} \quad\xi =\mathcal{G}^{0}(u, 0)}\Big\} \\
&=& \inf\Big\{\frac{1}{2}\|(u,v)\|^2_{\mathcal{H}} : {( u,v)\in \mathcal{H}\quad\text{such that} \quad\xi =\mathcal{G}^{0}(u, v)}\Big\},
\end{array}
\end{equation*} where ![]() $\xi\in \mathcal{C}^{\beta-\operatorname{hld}}\left([0,T], \mathbb{R}^m\right)$.
$\xi\in \mathcal{C}^{\beta-\operatorname{hld}}\left([0,T], \mathbb{R}^m\right)$.
Remark 3.8.
The space ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T], \mathbb{R}^{k})$ is not separable so the variational formula cannot be applied directly. But H β is separable, the variational formula can be used well. For any given β satisfying that
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T], \mathbb{R}^{k})$ is not separable so the variational formula cannot be applied directly. But H β is separable, the variational formula can be used well. For any given β satisfying that ![]() $1/3 \lt \beta \lt \alpha \lt H$, we could find a slight large exponent
$1/3 \lt \beta \lt \alpha \lt H$, we could find a slight large exponent ![]() $\beta+\kappa$ such that
$\beta+\kappa$ such that ![]() $\beta \lt \beta+\kappa \lt \alpha$, then our process takes values in
$\beta \lt \beta+\kappa \lt \alpha$, then our process takes values in ![]() $ \mathcal{C}^{(\beta+\kappa)-\operatorname{hld}} ([0,T], \mathbb{R}^{k} )$, directly, it also belongs to the space H β. The variational formula is applied on the space H β and we only need to prove the weak convergence method under the β-Hölder norm. Finally, the same LDP still holds on the space
$ \mathcal{C}^{(\beta+\kappa)-\operatorname{hld}} ([0,T], \mathbb{R}^{k} )$, directly, it also belongs to the space H β. The variational formula is applied on the space H β and we only need to prove the weak convergence method under the β-Hölder norm. Finally, the same LDP still holds on the space ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T], \mathbb{R}^{k})$ with aid of the conventional contraction principle [Reference Dembo and Zeitouni11, theorem 4.2.1].
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T], \mathbb{R}^{k})$ with aid of the conventional contraction principle [Reference Dembo and Zeitouni11, theorem 4.2.1].
4. A-priori estimates
In this section, we fix ![]() $\varepsilon,\delta\in(0,1]$. In the next section, we will let ɛ → 0. To prove theorem 3.7, some estimates should be given.
$\varepsilon,\delta\in(0,1]$. In the next section, we will let ɛ → 0. To prove theorem 3.7, some estimates should be given.
Firstly, let ![]() $(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}_{b}$. In order to apply the variational representation (2.2), we give the following controlled slow-fast RDE associated with the original slow-fast component
$(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}_{b}$. In order to apply the variational representation (2.2), we give the following controlled slow-fast RDE associated with the original slow-fast component ![]() $({X}^{\varepsilon, \delta}, {Y}^{\varepsilon, \delta})$
$({X}^{\varepsilon, \delta}, {Y}^{\varepsilon, \delta})$
 \begin{equation}
\left\{
\begin{array}{ll}
d\tilde {X}^{\varepsilon, \delta}_t =& f_{1}(\tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dt + \sigma_{1}(\tilde {X}^{\varepsilon, \delta}_t)d[T_{t}^u(\varepsilon B^H) ]\\
d\tilde {Y}^{\varepsilon, \delta}_t =& \frac{1}{\delta}f_{2}( \tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dt +\frac{1}{\sqrt{\delta\varepsilon}}\sigma_2(\tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dv^{\varepsilon, \delta}_t\\ & \quad+ \frac{1}{\sqrt{\delta}}\sigma_2(\tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dw_{t}.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
d\tilde {X}^{\varepsilon, \delta}_t =& f_{1}(\tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dt + \sigma_{1}(\tilde {X}^{\varepsilon, \delta}_t)d[T_{t}^u(\varepsilon B^H) ]\\
d\tilde {Y}^{\varepsilon, \delta}_t =& \frac{1}{\delta}f_{2}( \tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dt +\frac{1}{\sqrt{\delta\varepsilon}}\sigma_2(\tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dv^{\varepsilon, \delta}_t\\ & \quad+ \frac{1}{\sqrt{\delta}}\sigma_2(\tilde {X}^{\varepsilon, \delta}_t, \tilde {Y}^{\varepsilon, \delta}_t)dw_{t}.
\end{array}
\right.
\end{equation} Here, ![]() $T^u(B^H):=(T^{u,1}(\varepsilon B^H),T^{u,2}(\varepsilon B^H)$ with
$T^u(B^H):=(T^{u,1}(\varepsilon B^H),T^{u,2}(\varepsilon B^H)$ with
 \begin{equation}
\begin{array}{rcl}
T_{s,t}^{u,1}(\varepsilon B^H)&=&(\sqrt{\varepsilon}b^H+u^{\varepsilon,\delta})_{s,t} \\
T_{s, t}^{u,2}(\varepsilon B^H)&=&\left(\varepsilon B^{H,2}+\sqrt{\varepsilon} I[b^H,u^{\varepsilon,\delta}]+\sqrt{\varepsilon} I[u^{\varepsilon,\delta},b^H]+ U^{\varepsilon,\delta,2}
\right)_{s, t}.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
T_{s,t}^{u,1}(\varepsilon B^H)&=&(\sqrt{\varepsilon}b^H+u^{\varepsilon,\delta})_{s,t} \\
T_{s, t}^{u,2}(\varepsilon B^H)&=&\left(\varepsilon B^{H,2}+\sqrt{\varepsilon} I[b^H,u^{\varepsilon,\delta}]+\sqrt{\varepsilon} I[u^{\varepsilon,\delta},b^H]+ U^{\varepsilon,\delta,2}
\right)_{s, t}.
\end{array}
\end{equation} Here, ![]() $(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}_{b}$ is called a pair of control.
$(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}_{b}$ is called a pair of control.
We divide ![]() $[0,T]$ into subintervals of equal length Δ. For
$[0,T]$ into subintervals of equal length Δ. For ![]() $t\in[0,T]$, we set
$t\in[0,T]$, we set  $t(\Delta)=\left\lfloor\frac{t}{\Delta}\right\rfloor \Delta$, which is the nearest breakpoint preceding t. Then, we construct the auxiliary process as following:
$t(\Delta)=\left\lfloor\frac{t}{\Delta}\right\rfloor \Delta$, which is the nearest breakpoint preceding t. Then, we construct the auxiliary process as following:
 \begin{equation}
d\hat {Y}^{\varepsilon, \delta}_t = \frac{1}{\delta} f_{2}( \tilde {X}^{\varepsilon, \delta}_{t(\Delta)}, \hat {Y}^{\varepsilon, \delta}_t)dt + \frac{1}{{\sqrt \delta }}\sigma_2(\tilde {X}^{\varepsilon, \delta}_{t(\Delta)}, \hat {Y}^{\varepsilon, \delta}_t)dw_{t}
\end{equation}
\begin{equation}
d\hat {Y}^{\varepsilon, \delta}_t = \frac{1}{\delta} f_{2}( \tilde {X}^{\varepsilon, \delta}_{t(\Delta)}, \hat {Y}^{\varepsilon, \delta}_t)dt + \frac{1}{{\sqrt \delta }}\sigma_2(\tilde {X}^{\varepsilon, \delta}_{t(\Delta)}, \hat {Y}^{\varepsilon, \delta}_t)dw_{t}
\end{equation} with  $\hat {Y}^{\varepsilon, \delta}_0=Y_0$.
$\hat {Y}^{\varepsilon, \delta}_0=Y_0$.
Now we are in the position to give necessary estimates.
Lemma 4.1.
Assume (A1)–(A3) and let ![]() $\nu\geqslant 1$ and
$\nu\geqslant 1$ and ![]() $N\in\mathbb{N}$. Then, for all
$N\in\mathbb{N}$. Then, for all ![]() $\varepsilon,\delta\in(0,1]$, we have
$\varepsilon,\delta\in(0,1]$, we have
 \begin{equation}
\mathbb{E}\big[\|\tilde X^{\varepsilon,\delta}\|^\nu_{\beta-\operatorname{hld}}\big] \leqslant C.
\end{equation}
\begin{equation}
\mathbb{E}\big[\|\tilde X^{\varepsilon,\delta}\|^\nu_{\beta-\operatorname{hld}}\big] \leqslant C.
\end{equation}Here, C is a positive constant which depends only on ν and N.
Proof.  $(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in \mathcal{Q}_{T^u(\varepsilon B^H), [0,T]}^\beta$ satisfies the following RDE driven by
$(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in \mathcal{Q}_{T^u(\varepsilon B^H), [0,T]}^\beta$ satisfies the following RDE driven by ![]() $T^u(\varepsilon B^H)$:
$T^u(\varepsilon B^H)$:
 \begin{equation}
\begin{array}{rcl}
\tilde {X}^{\varepsilon, \delta}_t &=&X_0+ \int_{0}^{t}f_{1}(\tilde {X}^{\varepsilon, \delta}_s, \tilde {Y}^{\varepsilon, \delta}_s)ds + \int_{0}^{t}\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_s)d[T_{s}^u(\varepsilon B^H) ],\\ (\tilde {X}^{\varepsilon, \delta}_t)^{\dagger}&=&\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_t).
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\tilde {X}^{\varepsilon, \delta}_t &=&X_0+ \int_{0}^{t}f_{1}(\tilde {X}^{\varepsilon, \delta}_s, \tilde {Y}^{\varepsilon, \delta}_s)ds + \int_{0}^{t}\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_s)d[T_{s}^u(\varepsilon B^H) ],\\ (\tilde {X}^{\varepsilon, \delta}_t)^{\dagger}&=&\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_t).
\end{array}
\end{equation} with  $\tilde {X}^{\varepsilon, \delta}_{0}=X_0,(\tilde {X}_0^{\varepsilon, \delta})^{\dagger}=\sigma_{1}(X_0)$. For every
$\tilde {X}^{\varepsilon, \delta}_{0}=X_0,(\tilde {X}_0^{\varepsilon, \delta})^{\dagger}=\sigma_{1}(X_0)$. For every  $(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in \mathcal{Q}_{T^u(\varepsilon B^H), [0,T]}^\beta$, we observe that the right hand side of (4.5) also belongs to
$(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in \mathcal{Q}_{T^u(\varepsilon B^H), [0,T]}^\beta$, we observe that the right hand side of (4.5) also belongs to  $ \mathcal{Q}_{T^u(\varepsilon B^H), [0,T]}^\beta$. We denote
$ \mathcal{Q}_{T^u(\varepsilon B^H), [0,T]}^\beta$. We denote  $\tilde {X}^{\varepsilon, \delta}_{s,t}=\tilde {X}^{\varepsilon, \delta}_t-\tilde {X}^{\varepsilon, \delta}_s$. Let
$\tilde {X}^{\varepsilon, \delta}_{s,t}=\tilde {X}^{\varepsilon, \delta}_t-\tilde {X}^{\varepsilon, \delta}_s$. Let ![]() $\tau \in[0,T]$ and set
$\tau \in[0,T]$ and set
 \begin{equation*}
B^{X_0}_{0,\tau}=\{(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in \mathcal{Q}^\beta_{{T^u(\varepsilon B^H)},[0, \tau]}|\|(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\|_{\mathcal{Q}^\beta_{{T^u(\varepsilon B^H)},[0, \tau]}}\leqslant 1 \}.
\end{equation*}
\begin{equation*}
B^{X_0}_{0,\tau}=\{(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in \mathcal{Q}^\beta_{{T^u(\varepsilon B^H)},[0, \tau]}|\|(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\|_{\mathcal{Q}^\beta_{{T^u(\varepsilon B^H)},[0, \tau]}}\leqslant 1 \}.
\end{equation*} The above set is like a ball of radius 1 centred at  $t \mapsto (X_0+\sigma_{1}(X_0)T_{0,t}^u(\varepsilon B^H), \sigma_{1}(X_0))$. By assumption (A1) and some direct computation, we have that for all
$t \mapsto (X_0+\sigma_{1}(X_0)T_{0,t}^u(\varepsilon B^H), \sigma_{1}(X_0))$. By assumption (A1) and some direct computation, we have that for all  $(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in B^{X_0}_{0,\tau}$,
$(\tilde {X}^{\varepsilon, \delta},(\tilde {X}^{\varepsilon, \delta})^{\dagger})\in B^{X_0}_{0,\tau}$,
 \begin{equation*}\begin{array}{rcl}
\|(\tilde {X}^{\varepsilon, \delta})^{\dagger}\|_{\sup,[0,\tau]} &\leqslant& |\sigma_1(X_0)|+\sup_{0 \leqslant s\leqslant \tau}|(\tilde {X}^{\varepsilon, \delta})^{\dagger}_s-(\tilde {X}^{\varepsilon, \delta})^{\dagger}_0|\\
&\leqslant&K+ \|(\tilde {X}^{\varepsilon, \delta})^{\dagger}\|_{\beta-\operatorname{hld},[0,\tau]}\tau^{\beta} \\
&\leqslant& K+1.
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
\|(\tilde {X}^{\varepsilon, \delta})^{\dagger}\|_{\sup,[0,\tau]} &\leqslant& |\sigma_1(X_0)|+\sup_{0 \leqslant s\leqslant \tau}|(\tilde {X}^{\varepsilon, \delta})^{\dagger}_s-(\tilde {X}^{\varepsilon, \delta})^{\dagger}_0|\\
&\leqslant&K+ \|(\tilde {X}^{\varepsilon, \delta})^{\dagger}\|_{\beta-\operatorname{hld},[0,\tau]}\tau^{\beta} \\
&\leqslant& K+1.
\end{array}
\end{equation*} Here, the constant  $K:=\|\sigma_1\|_{C_b^3} \vee\|f_1\|_{\infty} \vee L$ where L is defined in (A2).
$K:=\|\sigma_1\|_{C_b^3} \vee\|f_1\|_{\infty} \vee L$ where L is defined in (A2).
By remark 2.6,
 \begin{equation*}\begin{array}{rcl}
|\tilde {X}^{\varepsilon, \delta}_{s,t}|&\leqslant& |(\tilde {X}^{\varepsilon, \delta})^{\dagger}_{s}T_{s,t}^u(\varepsilon B^H)|+|R_{s,t}^{\tilde {X}^{\varepsilon, \delta}}|\\
&\leqslant& (K+1)\|T^{u,1}(\varepsilon B^H)\|_{\alpha-\operatorname{hld}} (t-s)^{\alpha}+\|R^{\tilde {X}^{\varepsilon, \delta}}\|_{2\beta-\operatorname{hld},[0,\tau]} (t-s)^{2\beta}\\
&\leqslant& (K+1)(\|T^{u,1}(\varepsilon B^H)\|_{\alpha-\operatorname{hld}}+1) (t-s)^{\alpha}.
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
|\tilde {X}^{\varepsilon, \delta}_{s,t}|&\leqslant& |(\tilde {X}^{\varepsilon, \delta})^{\dagger}_{s}T_{s,t}^u(\varepsilon B^H)|+|R_{s,t}^{\tilde {X}^{\varepsilon, \delta}}|\\
&\leqslant& (K+1)\|T^{u,1}(\varepsilon B^H)\|_{\alpha-\operatorname{hld}} (t-s)^{\alpha}+\|R^{\tilde {X}^{\varepsilon, \delta}}\|_{2\beta-\operatorname{hld},[0,\tau]} (t-s)^{2\beta}\\
&\leqslant& (K+1)(\|T^{u,1}(\varepsilon B^H)\|_{\alpha-\operatorname{hld}}+1) (t-s)^{\alpha}.
\end{array}
\end{equation*} Set  $\tau \lt \lambda:= \{8C_\beta(K+1)^3(\left\vert\!\left\vert\!\left\vert{T^{u}(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)^3\}^{-1/(\alpha-\beta)}$, then β-Hölder norm of
$\tau \lt \lambda:= \{8C_\beta(K+1)^3(\left\vert\!\left\vert\!\left\vert{T^{u}(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)^3\}^{-1/(\alpha-\beta)}$, then β-Hölder norm of ![]() $\tilde {X}^{\varepsilon, \delta}$ on subinterval
$\tilde {X}^{\varepsilon, \delta}$ on subinterval ![]() $[0,\tau]$ can be dominated by
$[0,\tau]$ can be dominated by  $\{8C_\beta(K+1)^2(\left\vert\!\left\vert\!\left\vert{T^{u}(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)^2\}^{-1}$(For more proof, see [Reference Inahama23, proposition 3.3]). Since
$\{8C_\beta(K+1)^2(\left\vert\!\left\vert\!\left\vert{T^{u}(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)^2\}^{-1}$(For more proof, see [Reference Inahama23, proposition 3.3]). Since  $\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld}}=\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld},[0,T]}$ and there are
$\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld}}=\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld},[0,T]}$ and there are  $\lfloor\frac{T}{\lambda}\rfloor+1$ subintervals on
$\lfloor\frac{T}{\lambda}\rfloor+1$ subintervals on ![]() $[0,T]$, we have
$[0,T]$, we have
 \begin{equation}
\begin{array}{rcl}
\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld}}&\leqslant& \|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld},[0,\lambda]}(\lfloor\frac{T}{\lambda}\rfloor+1)^{1-\beta}\\
&\leqslant& \{8C_\beta(K+1)^2(\left\vert\!\left\vert\!\left\vert{T^{u}(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)^2\}^{-1}(\lfloor\frac{T}{\lambda}\rfloor+1)^{1-\beta}\\
&\leqslant& c_{\alpha,\beta}\{(K+1){(\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)}\}^{\iota}
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld}}&\leqslant& \|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld},[0,\lambda]}(\lfloor\frac{T}{\lambda}\rfloor+1)^{1-\beta}\\
&\leqslant& \{8C_\beta(K+1)^2(\left\vert\!\left\vert\!\left\vert{T^{u}(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)^2\}^{-1}(\lfloor\frac{T}{\lambda}\rfloor+1)^{1-\beta}\\
&\leqslant& c_{\alpha,\beta}\{(K+1){(\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)}\}^{\iota}
\end{array}
\end{equation} for constants ![]() $c_{\alpha,\beta}$ and ι > 0 which only depends on α and β. Then, for all
$c_{\alpha,\beta}$ and ι > 0 which only depends on α and β. Then, for all ![]() $\nu\ge 1$, by taking expectation of ν-moments of (4.6), we have
$\nu\ge 1$, by taking expectation of ν-moments of (4.6), we have
 \begin{equation}
\mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld}}^\nu]\leqslant c_{\alpha,\beta}\{(K+1){(\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)}\}^{\nu\iota}.
\end{equation}
\begin{equation}
\mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|_{\beta-\operatorname{hld}}^\nu]\leqslant c_{\alpha,\beta}\{(K+1){(\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1)}\}^{\nu\iota}.
\end{equation} Due to the property that for every ![]() $1/3 \lt \alpha \lt H$ and all
$1/3 \lt \alpha \lt H$ and all ![]() $\nu\ge 1$,
$\nu\ge 1$,  $\mathbb{E}[\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}^\nu] \lt \infty$, the estimate (4.4) is derived. This proof is completed.
$\mathbb{E}[\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}^\nu] \lt \infty$, the estimate (4.4) is derived. This proof is completed.
Lemma 4.2.
Assume (A1)–(A4) and let ![]() $N\in\mathbb{N}$. Then, for every
$N\in\mathbb{N}$. Then, for every ![]() $(u^{\varepsilon},v^{\varepsilon})\in \mathcal{A}_b^N$,
$(u^{\varepsilon},v^{\varepsilon})\in \mathcal{A}_b^N$,  $\sup_{0\leqslant s\leqslant t}|\tilde Y_s^{\varepsilon,\delta}|$ has moments of all orders.
$\sup_{0\leqslant s\leqslant t}|\tilde Y_s^{\varepsilon,\delta}|$ has moments of all orders.
Proof. For the proof we refer to [Reference Inahama, Xu and Yang24, lemma 4.3].
Lemma 4.3.
Assume (A1)–(A4) and let ![]() $N\in\mathbb{N}$. Then, for every
$N\in\mathbb{N}$. Then, for every ![]() $(u^{\varepsilon},v^{\varepsilon})\in \mathcal{A}_b^N$, we have
$(u^{\varepsilon},v^{\varepsilon})\in \mathcal{A}_b^N$, we have
 \begin{equation}
\int_{0}^{T} \mathbb{E}\big[|\tilde Y_t^{\varepsilon,\delta}|^2\big] dt\leqslant C.
\end{equation}
\begin{equation}
\int_{0}^{T} \mathbb{E}\big[|\tilde Y_t^{\varepsilon,\delta}|^2\big] dt\leqslant C.
\end{equation}Here, C is a positive constant which depends only on N.
Proof. Due to that ![]() $Y^{\varepsilon,\delta}$ satisfies the Itô SDE and by using Itô’s formula, we have
$Y^{\varepsilon,\delta}$ satisfies the Itô SDE and by using Itô’s formula, we have
 \begin{equation}
\begin{array}{rcl}
{|\tilde Y_t^{\varepsilon,\delta} |^2} &=& {| Y_0 |^2} + \frac{2}{\delta }\int_0^t {\langle \tilde Y_s^{\varepsilon,\delta},f_2( \tilde {X}_{s}^{\varepsilon,\delta},\tilde Y_s^{\varepsilon,\delta})\rangle ds} \\
&&+ \frac{2}{\sqrt{\delta} }\int_0^t {\langle \tilde {Y}_{s}^{\varepsilon,\delta},\sigma_{2}( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ) dw_s\rangle} \\
&&+ \frac{2}{{\sqrt {\varepsilon\delta } }}\int_0^t {\langle \tilde {Y}_{s}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ){\frac{dv_s^{\varepsilon,\delta}}{ds} }\rangle ds} \\
&& + \frac{1}{\delta }\int_0^t |{\sigma_{2} }( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} )|^2ds.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
{|\tilde Y_t^{\varepsilon,\delta} |^2} &=& {| Y_0 |^2} + \frac{2}{\delta }\int_0^t {\langle \tilde Y_s^{\varepsilon,\delta},f_2( \tilde {X}_{s}^{\varepsilon,\delta},\tilde Y_s^{\varepsilon,\delta})\rangle ds} \\
&&+ \frac{2}{\sqrt{\delta} }\int_0^t {\langle \tilde {Y}_{s}^{\varepsilon,\delta},\sigma_{2}( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ) dw_s\rangle} \\
&&+ \frac{2}{{\sqrt {\varepsilon\delta } }}\int_0^t {\langle \tilde {Y}_{s}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ){\frac{dv_s^{\varepsilon,\delta}}{ds} }\rangle ds} \\
&& + \frac{1}{\delta }\int_0^t |{\sigma_{2} }( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} )|^2ds.
\end{array}
\end{equation} From lemma 4.2, lemma 4.1, and (A2), we can prove that the third term in right hand side of (4.9) is a true martingale and  $\mathbb{E}[\int_0^t {\langle \tilde {Y}_{s}^{\varepsilon,\delta},\sigma_{2}( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ) dW_s\rangle}]=0$. Taking expectation for (4.9), we have
$\mathbb{E}[\int_0^t {\langle \tilde {Y}_{s}^{\varepsilon,\delta},\sigma_{2}( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ) dW_s\rangle}]=0$. Taking expectation for (4.9), we have
 \begin{equation}
\begin{array}{rcl}
\frac{d\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon} |^2}]}{dt} &=& \frac{2}{\delta }\mathbb{E} \big[{\langle \tilde {Y}_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta} )\rangle } \big]
+ \frac{2}{{\sqrt {\varepsilon \delta} }}\mathbb{E} \big[{\langle \tilde {Y}_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {Y}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_t^{\varepsilon,\delta}}{dt} }\rangle }\big] \\
&&+ \frac{1}{\delta }\mathbb{E} \big[|{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )|^2\big].
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\frac{d\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon} |^2}]}{dt} &=& \frac{2}{\delta }\mathbb{E} \big[{\langle \tilde {Y}_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta} )\rangle } \big]
+ \frac{2}{{\sqrt {\varepsilon \delta} }}\mathbb{E} \big[{\langle \tilde {Y}_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {Y}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_t^{\varepsilon,\delta}}{dt} }\rangle }\big] \\
&&+ \frac{1}{\delta }\mathbb{E} \big[|{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )|^2\big].
\end{array}
\end{equation}By (A4), we arrive at
 \begin{equation}
\begin{array}{ll}
\frac{2}{\delta }&{\langle \tilde {Y}_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta} )\rangle } +\frac{1}{\delta } |{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )|^2\\
&\leqslant- \frac{{\beta_2 }}{\delta }{{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}} + \frac{{C}}{\delta }|\tilde {X}_{t}^{\varepsilon,\delta}|^2+ \frac{{C}}{\delta }.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{ll}
\frac{2}{\delta }&{\langle \tilde {Y}_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta} )\rangle } +\frac{1}{\delta } |{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )|^2\\
&\leqslant- \frac{{\beta_2 }}{\delta }{{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}} + \frac{{C}}{\delta }|\tilde {X}_{t}^{\varepsilon,\delta}|^2+ \frac{{C}}{\delta }.
\end{array}
\end{equation}With aid of (A4) and lemma 4.1, we obtain
 \begin{equation}
\begin{array}{l}
\frac{2}{{\sqrt {\varepsilon\delta } }}{\langle \tilde {Y}_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_t^{\varepsilon,\delta}}{dt} }\rangle }\\
\leqslant \frac{L}{{\sqrt {\varepsilon\delta } }}\big( 1 + | \tilde {X}_{t}^{\varepsilon,\delta} |^2 \big)| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2+ \frac{1}{{\sqrt {\varepsilon\delta } }}| \tilde {Y}_{t}^{\varepsilon,\delta} |^2 \\
\leqslant \frac{L}{{\sqrt {\varepsilon\delta } }}\big( 1 + T^2\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2 \big)| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2+ \frac{1}{{\sqrt {\varepsilon\delta } }}| \tilde {Y}_{t}^{\varepsilon,\delta} |^2.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\frac{2}{{\sqrt {\varepsilon\delta } }}{\langle \tilde {Y}_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_t^{\varepsilon,\delta}}{dt} }\rangle }\\
\leqslant \frac{L}{{\sqrt {\varepsilon\delta } }}\big( 1 + | \tilde {X}_{t}^{\varepsilon,\delta} |^2 \big)| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2+ \frac{1}{{\sqrt {\varepsilon\delta } }}| \tilde {Y}_{t}^{\varepsilon,\delta} |^2 \\
\leqslant \frac{L}{{\sqrt {\varepsilon\delta } }}\big( 1 + T^2\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2 \big)| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2+ \frac{1}{{\sqrt {\varepsilon\delta } }}| \tilde {Y}_{t}^{\varepsilon,\delta} |^2.
\end{array}
\end{equation}Thus, combine (4.10)–(4.12), it deduces that
 \begin{equation*}\begin{array}{rcl}
\frac{d\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}]}{dt} &\leqslant& {\frac{{- \beta_2 }}{2\delta } } \mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}] + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }} \mathbb{E}[{{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}}}]\\
&& + \frac{{{L }}}{\sqrt {\varepsilon\delta } } \mathbb{E}[{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}] +\frac{{C}}{\delta }\mathbb{E}[|\tilde {X}_{t}^{\varepsilon,\delta}|^2]+ \frac{{C}}{\delta }.
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
\frac{d\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}]}{dt} &\leqslant& {\frac{{- \beta_2 }}{2\delta } } \mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}] + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }} \mathbb{E}[{{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}}}]\\
&& + \frac{{{L }}}{\sqrt {\varepsilon\delta } } \mathbb{E}[{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}] +\frac{{C}}{\delta }\mathbb{E}[|\tilde {X}_{t}^{\varepsilon,\delta}|^2]+ \frac{{C}}{\delta }.
\end{array}
\end{equation*}Consider the following ODE:
 \begin{equation*}
\frac{dA_t}{dt}= {\frac{{- \beta_2 }}{2\delta } }A_t + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }} \mathbb{E}[{{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}}}] + \frac{{{L }}}{\sqrt {\varepsilon\delta } } \mathbb{E}[{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}] +\frac{{C}}{\delta }\mathbb{E}[|\tilde {X}_{t}^{\varepsilon,\delta}|^2]+ \frac{{C}}{\delta }
\end{equation*}
\begin{equation*}
\frac{dA_t}{dt}= {\frac{{- \beta_2 }}{2\delta } }A_t + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }} \mathbb{E}[{{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}}}] + \frac{{{L }}}{\sqrt {\varepsilon\delta } } \mathbb{E}[{| {\frac{dv_t^{\varepsilon,\delta}}{dt} } |^2}] +\frac{{C}}{\delta }\mathbb{E}[|\tilde {X}_{t}^{\varepsilon,\delta}|^2]+ \frac{{C}}{\delta }
\end{equation*} with initial value ![]() $A_0=|Y_0|^2$. Then, some directly computation leads that
$A_0=|Y_0|^2$. Then, some directly computation leads that
 \begin{equation*}\begin{array}{rcl}
{A_t}&=& |Y_0|^2 e^{-\frac{\beta_2}{2\delta} t} + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2}}]} ds \\
&&+ \frac{{{L }}}{\sqrt {\varepsilon\delta } }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2]}ds\\
&& +\frac{{C}}{\delta }{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2}]}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds+ \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds.
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
{A_t}&=& |Y_0|^2 e^{-\frac{\beta_2}{2\delta} t} + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2}}]} ds \\
&&+ \frac{{{L }}}{\sqrt {\varepsilon\delta } }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2]}ds\\
&& +\frac{{C}}{\delta }{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2}]}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds+ \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds.
\end{array}
\end{equation*}Furthermore, by applying the comparison theorem for all t, we get
 \begin{equation}
\begin{array}{rcl}
\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}] &\leqslant& |Y_0|^2 e^{-\frac{\beta_2}{2\delta} t} + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2}}]} ds \\
&&+ \frac{{{L }}}{\sqrt {\varepsilon\delta } }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2]}ds\\
&& +\frac{{C}}{\delta }{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2}]}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds+ \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}] &\leqslant& |Y_0|^2 e^{-\frac{\beta_2}{2\delta} t} + \frac{{{L T^2}}}{{\sqrt {\varepsilon\delta } }}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2}}]} ds \\
&&+ \frac{{{L }}}{\sqrt {\varepsilon\delta } }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2]}ds\\
&& +\frac{{C}}{\delta }{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2}]}\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds+ \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds.
\end{array}
\end{equation}Next, by integrating of (4.13) and using the Fubini theorem and lemma 4.1, we can prove that
 \begin{equation*}
\begin{array}{rcl}\int_{0}^{T}\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon} |^2}]dt &\leqslant& |Y_0|^2 \int_{0}^{T} e^{-\frac{\beta_2}{2\delta} t} dt+ \frac{{{LT^2}}}{{\sqrt {\varepsilon \delta} }}\int_{0}^{T}\int_{0}^{t} e^{-\frac{\beta_2}{2\varepsilon} (t-s)}{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2}}]}\\ &&\times dsdt \\
&& + \frac{{{L }}}{\sqrt {\delta \varepsilon } }\int_{0}^{T}\int_{0}^{t} e^{-\frac{\beta_2}{2\varepsilon} (t-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2]}ds + \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\varepsilon} (t-s)}dsdt\\
&\leqslant & |Y_0|^2 e^{-\frac{\beta_2}{2\delta} T} + \frac{{{LT^2 }}}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\big[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2\times| \int_{0}^{T}\int_{s}^{T} e^{-\frac{\beta_2}{2\delta} (t-s)} dt\\ &&\times | {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2ds\big] \\
&&+ \frac{{{L }}}{\sqrt {\varepsilon\delta } }\int_{0}^{T}\int_{s}^{T} e^{-\frac{\beta_2}{2\delta} (t-s)}dt {\mathbb{E}[|{\frac{dv_s^{\varepsilon\delta}}{ds} } |^2]}ds + \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds\\
&\leqslant & |Y_0|^2 e^{-\frac{\beta_2}{2\delta} T} + \frac{2LT^2 \sqrt{\delta}}{\beta_2\sqrt {\varepsilon } }\mathbb{E}\big[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2\times| \int_{0}^{T} e^{-\frac{\beta_2}{2\delta} (T-s)} | {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2\\ &&\times ds\big] \\
&&+ \frac{2 L \sqrt{\delta}}{\beta_2\sqrt {\varepsilon }}\int_{0}^{T} e^{-\frac{\beta_2}{2\delta} (T-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon\delta}}{ds} } |^2]}ds +{C}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2]\\ &&\times \int_{0}^{T} e^{-\frac{\beta_2}{2\delta} (T-s)}ds \\
&& + C.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{rcl}\int_{0}^{T}\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon} |^2}]dt &\leqslant& |Y_0|^2 \int_{0}^{T} e^{-\frac{\beta_2}{2\delta} t} dt+ \frac{{{LT^2}}}{{\sqrt {\varepsilon \delta} }}\int_{0}^{T}\int_{0}^{t} e^{-\frac{\beta_2}{2\varepsilon} (t-s)}{\mathbb{E}[{\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2{| {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2}}]}\\ &&\times dsdt \\
&& + \frac{{{L }}}{\sqrt {\delta \varepsilon } }\int_{0}^{T}\int_{0}^{t} e^{-\frac{\beta_2}{2\varepsilon} (t-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2]}ds + \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\varepsilon} (t-s)}dsdt\\
&\leqslant & |Y_0|^2 e^{-\frac{\beta_2}{2\delta} T} + \frac{{{LT^2 }}}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\big[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2\times| \int_{0}^{T}\int_{s}^{T} e^{-\frac{\beta_2}{2\delta} (t-s)} dt\\ &&\times | {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2ds\big] \\
&&+ \frac{{{L }}}{\sqrt {\varepsilon\delta } }\int_{0}^{T}\int_{s}^{T} e^{-\frac{\beta_2}{2\delta} (t-s)}dt {\mathbb{E}[|{\frac{dv_s^{\varepsilon\delta}}{ds} } |^2]}ds + \frac{{C}}{\delta }\int_{0}^{t} e^{-\frac{\beta_2}{2\delta} (t-s)}ds\\
&\leqslant & |Y_0|^2 e^{-\frac{\beta_2}{2\delta} T} + \frac{2LT^2 \sqrt{\delta}}{\beta_2\sqrt {\varepsilon } }\mathbb{E}\big[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2\times| \int_{0}^{T} e^{-\frac{\beta_2}{2\delta} (T-s)} | {\frac{dv_s^{\varepsilon,\delta}}{ds} } |^2\\ &&\times ds\big] \\
&&+ \frac{2 L \sqrt{\delta}}{\beta_2\sqrt {\varepsilon }}\int_{0}^{T} e^{-\frac{\beta_2}{2\delta} (T-s)} {\mathbb{E}[|{\frac{dv_s^{\varepsilon\delta}}{ds} } |^2]}ds +{C}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2]\\ &&\times \int_{0}^{T} e^{-\frac{\beta_2}{2\delta} (T-s)}ds \\
&& + C.
\end{array}
\end{equation*}
By using the condition that ![]() $0 \lt \delta \lt \varepsilon
\leqslant 1$ and
$0 \lt \delta \lt \varepsilon
\leqslant 1$ and ![]() $(u^{\varepsilon}, v^{\varepsilon})\in {\mathcal{A}}_{b}^N$, we derive
$(u^{\varepsilon}, v^{\varepsilon})\in {\mathcal{A}}_{b}^N$, we derive
 \begin{equation*}
\int_{0}^{T}\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}]dt \leqslant {C}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2]+C.
\end{equation*}
\begin{equation*}
\int_{0}^{T}\mathbb{E}[{| \tilde {Y}_{t}^{\varepsilon,\delta} |^2}]dt \leqslant {C}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2]+C.
\end{equation*}Thus, by exploiting the lemma 4.1, the estimate (4.8) follows at once. The proof is completed.
Lemma 4.4.
Assume (A1)–(A4), for all ![]() $\varepsilon,\delta\in(0,1]$, we have
$\varepsilon,\delta\in(0,1]$, we have  $\sup_{0 \leqslant t \leqslant T}\mathbb{E}[| \hat Y_{t}^{\varepsilon, \delta}|^2] \lt C$ Here, C > 0 is a constant which depends only on
$\sup_{0 \leqslant t \leqslant T}\mathbb{E}[| \hat Y_{t}^{\varepsilon, \delta}|^2] \lt C$ Here, C > 0 is a constant which depends only on ![]() $\alpha,\beta$.
$\alpha,\beta$.
Proof. The proof is similar to lemma 4.3. (In fact, this one is simpler since there is no control term.)
Lemma 4.5.
Assume (A1)–(A4) and let ![]() $N\in\mathbb{N}$, we have
$N\in\mathbb{N}$, we have
 \begin{equation*}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big] \leqslant C(\frac{\sqrt{\delta}}{{\sqrt{\varepsilon}}}+\Delta^{2\beta}).\end{equation*}
\begin{equation*}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big] \leqslant C(\frac{\sqrt{\delta}}{{\sqrt{\varepsilon}}}+\Delta^{2\beta}).\end{equation*} Here, C > 0 is a constant which depends only on ![]() $N,\alpha,\beta$.
$N,\alpha,\beta$.
Proof. By Itô’s formula, we have
 \begin{equation}
\begin{array}{rcl}
\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}] &=& \frac{2}{\delta }\mathbb{E}\bigg[\int_0^t {\langle\tilde Y_{s}^{\varepsilon,\delta}-\hat Y_{s}^{\varepsilon,\delta},f_2( \tilde {X}_{s}^{\varepsilon,\delta},\tilde Y_s^{\varepsilon,\delta})-f_2( \tilde {X}_{s(\Delta)}^{\varepsilon,\delta},\hat Y_s^{\varepsilon,\delta})\rangle ds}\bigg]\\
&&+ \frac{1}{\delta }\mathbb{E}\bigg[\int_0^t |{\sigma_{2} }( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{s(\Delta)}^{\varepsilon,\delta},\hat {Y}_{s}^{\varepsilon,\delta}} )|^2ds\bigg] \\
&&+ \frac{2}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\bigg[\int_0^t {\langle \tilde Y_{s}^{\varepsilon,\delta}-\hat Y_{s}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ){\frac{dv_s^{\varepsilon,\delta}}{ds} }\rangle ds} \bigg].
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}] &=& \frac{2}{\delta }\mathbb{E}\bigg[\int_0^t {\langle\tilde Y_{s}^{\varepsilon,\delta}-\hat Y_{s}^{\varepsilon,\delta},f_2( \tilde {X}_{s}^{\varepsilon,\delta},\tilde Y_s^{\varepsilon,\delta})-f_2( \tilde {X}_{s(\Delta)}^{\varepsilon,\delta},\hat Y_s^{\varepsilon,\delta})\rangle ds}\bigg]\\
&&+ \frac{1}{\delta }\mathbb{E}\bigg[\int_0^t |{\sigma_{2} }( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{s(\Delta)}^{\varepsilon,\delta},\hat {Y}_{s}^{\varepsilon,\delta}} )|^2ds\bigg] \\
&&+ \frac{2}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\bigg[\int_0^t {\langle \tilde Y_{s}^{\varepsilon,\delta}-\hat Y_{s}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{s}^{\varepsilon,\delta},\tilde {Y}_{s}^{\varepsilon,\delta}} ){\frac{dv_s^{\varepsilon,\delta}}{ds} }\rangle ds} \bigg].
\end{array}
\end{equation}By differentiating with respect to t for (4.14), we find that
 \begin{equation}
\begin{array}{l}
\frac{d}{dt}\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}]\\
= \frac{2}{\delta }\mathbb{E}\big[ {\langle\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde Y_t^{\varepsilon,\delta})-f_2( \tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})\rangle }\big]\\
+ \frac{1}{\delta }\mathbb{E}\big[ |{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )|^2\big] \\
+ \frac{2}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\big[ {\langle \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_s^{\varepsilon,\delta}}{dt} }\rangle } \big]\\
= \frac{1}{\delta }\mathbb{E}\big[ {2\langle\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde Y_t^{\varepsilon,\delta})-f_2( \tilde {X}_{t}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})\rangle } +\big|{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )\\ -{{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )\big|}^2\big]\\
+ \frac{2}{\delta }\mathbb{E}\big[ {\langle\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})-f_2( \hat {X}_{t(\Delta)}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})\rangle }\big]\\
+ \frac{2}{\delta }\mathbb{E}\big[ \langle{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} ),{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )\rangle\big] \\
+ \frac{1}{\delta }\mathbb{E}\big[ |{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )|^2\big] \\
+ \frac{2}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\big[ {\langle \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_t^{\varepsilon,\delta}}{dt} }\rangle } \big]\\
=: I_1+I_2+I_3+I_4+I_5.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\frac{d}{dt}\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}]\\
= \frac{2}{\delta }\mathbb{E}\big[ {\langle\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde Y_t^{\varepsilon,\delta})-f_2( \tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})\rangle }\big]\\
+ \frac{1}{\delta }\mathbb{E}\big[ |{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )|^2\big] \\
+ \frac{2}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\big[ {\langle \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_s^{\varepsilon,\delta}}{dt} }\rangle } \big]\\
= \frac{1}{\delta }\mathbb{E}\big[ {2\langle\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\tilde Y_t^{\varepsilon,\delta})-f_2( \tilde {X}_{t}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})\rangle } +\big|{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )\\ -{{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )\big|}^2\big]\\
+ \frac{2}{\delta }\mathbb{E}\big[ {\langle\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},f_2( \tilde {X}_{t}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})-f_2( \hat {X}_{t(\Delta)}^{\varepsilon,\delta},\hat Y_t^{\varepsilon,\delta})\rangle }\big]\\
+ \frac{2}{\delta }\mathbb{E}\big[ \langle{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} ),{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )\rangle\big] \\
+ \frac{1}{\delta }\mathbb{E}\big[ |{\sigma_{2} }( {\tilde {X}_{t}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )-{\sigma_{2} }( {\tilde {X}_{t(\Delta)}^{\varepsilon,\delta},\hat {Y}_{t}^{\varepsilon,\delta}} )|^2\big] \\
+ \frac{2}{{\sqrt {\varepsilon\delta } }}\mathbb{E}\big[ {\langle \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta},\sigma_{2} ( {\tilde {X}_{t}^{\varepsilon,\delta},\tilde {Y}_{t}^{\varepsilon,\delta}} ){\frac{dv_t^{\varepsilon,\delta}}{dt} }\rangle } \big]\\
=: I_1+I_2+I_3+I_4+I_5.
\end{array}
\end{equation}For the first term I 1, by using (A4), we obtain that
 \begin{equation}
I_1 \leqslant -\frac{\beta_1}{\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big].
\end{equation}
\begin{equation}
I_1 \leqslant -\frac{\beta_1}{\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big].
\end{equation}Then, we compute the second term I 2 by using (A2) and lemma 4.1 as follows,
 \begin{equation}
\begin{array}{rcl}
I_2 &\leqslant& \frac{C_1}{\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|\cdot|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|\big]\\
&\leqslant&\frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_2}{\delta}\mathbb{E}\big[|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|^2\big]\\
&\leqslant& \frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_2}{\delta}\Delta^{2\beta}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2]
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
I_2 &\leqslant& \frac{C_1}{\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|\cdot|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|\big]\\
&\leqslant&\frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_2}{\delta}\mathbb{E}\big[|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|^2\big]\\
&\leqslant& \frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_2}{\delta}\Delta^{2\beta}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2]
\end{array}
\end{equation} where ![]() $C_1,C_2 \gt 0$ is independent of
$C_1,C_2 \gt 0$ is independent of ![]() $\varepsilon,\delta$.
$\varepsilon,\delta$.
For the third term I 3 and fourth term I 4, we estimate them as following:
 \begin{equation}
\begin{array}{rcl}
I_3+I_4 &\leqslant& \frac{C}{\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|\cdot|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|+|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|^2\big]\\
&\leqslant& \frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_3}{\delta}\mathbb{E}\big[|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|^2\big]\\
&\leqslant& \frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_3}{\delta}\Delta^{2\beta}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2],
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
I_3+I_4 &\leqslant& \frac{C}{\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|\cdot|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|+|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|^2\big]\\
&\leqslant& \frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_3}{\delta}\mathbb{E}\big[|\tilde X_{t}^{\varepsilon,\delta}-\tilde X_{t(\Delta)}^{\varepsilon,\delta}|^2\big]\\
&\leqslant& \frac{\beta_1}{4\delta}\mathbb{E}\big[|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2\big]+\frac{C_3}{\delta}\Delta^{2\beta}\mathbb{E}[\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^2],
\end{array}
\end{equation} where ![]() $C_3 \gt 0$ is independent of
$C_3 \gt 0$ is independent of ![]() $\varepsilon,\delta$. Here, for the first inequality, we used (A3). For the final inequality, we applied lemma 4.1 and the definition of Hölder norm.
$\varepsilon,\delta$. Here, for the first inequality, we used (A3). For the final inequality, we applied lemma 4.1 and the definition of Hölder norm.
For the fifth term I 5, by applying (A3), we derive
 \begin{equation}
\begin{array}{rcl}
I_5 &\leqslant& \frac{C}{\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}\big|\times \big|1+\tilde X_{t}^{\varepsilon,\delta}\big|\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|\big]\\
&\leqslant& \frac{\beta_1}{4\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}\big|^2\big]+\frac{C_4}{\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|1+\tilde X_{t}^{\varepsilon,\delta}\big|^2\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|^2\big],
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
I_5 &\leqslant& \frac{C}{\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}\big|\times \big|1+\tilde X_{t}^{\varepsilon,\delta}\big|\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|\big]\\
&\leqslant& \frac{\beta_1}{4\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}\big|^2\big]+\frac{C_4}{\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|1+\tilde X_{t}^{\varepsilon,\delta}\big|^2\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|^2\big],
\end{array}
\end{equation} where ![]() $C_4 \gt 0$ is independent of
$C_4 \gt 0$ is independent of ![]() $\varepsilon,\delta$. Then, by combining (4.15)–(4.19), we have
$\varepsilon,\delta$. Then, by combining (4.15)–(4.19), we have
 \begin{align}
\begin{array}{rcl}
\frac{d}{dt}\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}]&\leqslant&-\frac{\beta_1}{4\delta}\mathbb{E}\big[\big|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}\big|^2\big]+\frac{C_4}{\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|1+\tilde X_{t}^{\varepsilon,\delta}\big|^2\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|^2\big]\\ &&+\frac{C_2+C_3}{\delta}\Delta^{2\beta}.
\end{array}\nonumber\\
\end{align}
\begin{align}
\begin{array}{rcl}
\frac{d}{dt}\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}]&\leqslant&-\frac{\beta_1}{4\delta}\mathbb{E}\big[\big|\tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}\big|^2\big]+\frac{C_4}{\sqrt{\varepsilon\delta}}\mathbb{E}\big[\big|1+\tilde X_{t}^{\varepsilon,\delta}\big|^2\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|^2\big]\\ &&+\frac{C_2+C_3}{\delta}\Delta^{2\beta}.
\end{array}\nonumber\\
\end{align}Thanks to the Gronwall inequality [Reference Inahama23, lemma A.1 (2)] and lemma 4.1, we can observe that
 \begin{align}
\begin{array}{rcl}
\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}]&\leqslant&\frac{C_4\sqrt{\delta}}{\sqrt{\varepsilon}}\int_{0}^{t}\mathbb{E}\big[\big|1+\tilde X_{t}^{\varepsilon,\delta}\big|^2\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|^2dt\big]+(C_2+C_3)\Delta^{2\beta}T\\
&\leqslant&\frac{C_5\sqrt{\delta}}{\sqrt{\varepsilon}}\mathbb{E}\big(1+\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^{2\beta} T^{2\beta}\big)+(C_2+C_3)\Delta^{2\beta}T\\
&\leqslant&C(\frac{\sqrt{\delta}}{{\sqrt{\varepsilon}}}+\Delta^{2\beta}).
\end{array}\nonumber\\
\end{align}
\begin{align}
\begin{array}{rcl}
\mathbb{E}[{| \tilde Y_{t}^{\varepsilon,\delta}-\hat Y_{t}^{\varepsilon,\delta}|^2}]&\leqslant&\frac{C_4\sqrt{\delta}}{\sqrt{\varepsilon}}\int_{0}^{t}\mathbb{E}\big[\big|1+\tilde X_{t}^{\varepsilon,\delta}\big|^2\big|{\frac{dv_t^{\varepsilon,\delta}}{dt} }\big|^2dt\big]+(C_2+C_3)\Delta^{2\beta}T\\
&\leqslant&\frac{C_5\sqrt{\delta}}{\sqrt{\varepsilon}}\mathbb{E}\big(1+\| \tilde {X}^{\varepsilon,\delta} \|_{\beta-\operatorname{hld}}^{2\beta} T^{2\beta}\big)+(C_2+C_3)\Delta^{2\beta}T\\
&\leqslant&C(\frac{\sqrt{\delta}}{{\sqrt{\varepsilon}}}+\Delta^{2\beta}).
\end{array}\nonumber\\
\end{align}The proof is completed.
5. Proof of theorem 3.7
In this section, we are ultimately going to prove our main result theorem 3.7. We divide this proof into three steps.
Step 1. The proof is deterministic in this step . Let ![]() $(u^{(j)}, v^{(j)}),(u, v)\in S_N$ such that
$(u^{(j)}, v^{(j)}),(u, v)\in S_N$ such that ![]() $(u^{(j)}, v^{(j)})\rightarrow(u, v)$ as
$(u^{(j)}, v^{(j)})\rightarrow(u, v)$ as ![]() $j\rightarrow\infty$ with the weak topology in
$j\rightarrow\infty$ with the weak topology in ![]() $\mathcal{H}$. In this step, we will prove that
$\mathcal{H}$. In this step, we will prove that
in ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ as
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ as ![]() $j \to \infty$.
$j \to \infty$.
The skeleton equation satisfies the RDE as follows
 \begin{equation}
d\tilde{X}^{(j)}_t = \bar{f}_1(\tilde{X}^{(j)}_t)dt + \sigma_{1}( \tilde{X}^{(j)}_t)dU^{(j)}_t
\end{equation}
\begin{equation}
d\tilde{X}^{(j)}_t = \bar{f}_1(\tilde{X}^{(j)}_t)dt + \sigma_{1}( \tilde{X}^{(j)}_t)dU^{(j)}_t
\end{equation} where  $\tilde{X}^{(j)}_t=X_0$,
$\tilde{X}^{(j)}_t=X_0$, ![]() $U^{(j)}=({(U^{(j)})^1},{(U^{(j)})^2})\in \Omega_{\alpha}(\mathbb{R}^d)$ and
$U^{(j)}=({(U^{(j)})^1},{(U^{(j)})^2})\in \Omega_{\alpha}(\mathbb{R}^d)$ and  $\bar{f}_1(\cdot)=\int_{\mathbb{R}^{n}}f_{1}(\cdot, {\tilde Y})\mu^{\cdot}(d{\tilde Y})$. By the conclusion that
$\bar{f}_1(\cdot)=\int_{\mathbb{R}^{n}}f_{1}(\cdot, {\tilde Y})\mu^{\cdot}(d{\tilde Y})$. By the conclusion that ![]() $\bar{f}_1$ is Lipschitz continuous and bounded and using [Reference Inahama23, proposition 3.3], we obtain that there exists a unique global solution
$\bar{f}_1$ is Lipschitz continuous and bounded and using [Reference Inahama23, proposition 3.3], we obtain that there exists a unique global solution  $(\tilde{X}^{(j)},(\tilde{X}^{(j)})^{\dagger})\in \mathcal{Q}_{U}^\beta([0, T], \mathbb{R}^m)$ to the (5.2). Moreover, we have
$(\tilde{X}^{(j)},(\tilde{X}^{(j)})^{\dagger})\in \mathcal{Q}_{U}^\beta([0, T], \mathbb{R}^m)$ to the (5.2). Moreover, we have
 \begin{equation*}\|\tilde{X}^{(j)}\|_{\beta-\operatorname{hld}}\leqslant c\end{equation*}
\begin{equation*}\|\tilde{X}^{(j)}\|_{\beta-\operatorname{hld}}\leqslant c\end{equation*} holds for ![]() $0 \lt \beta \lt \alpha \lt H$. Here, the constant c > 0 which is independent of U.
$0 \lt \beta \lt \alpha \lt H$. Here, the constant c > 0 which is independent of U.
Due to a compact embedding ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m}) \subset \mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ for any small parameter
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m}) \subset \mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ for any small parameter ![]() $0 \lt \theta \lt \beta$, we have that the family
$0 \lt \theta \lt \beta$, we have that the family  $\{\tilde{X}^{(j)}\}_{j\ge 1}$ is pre-compact in
$\{\tilde{X}^{(j)}\}_{j\ge 1}$ is pre-compact in ![]() $ \mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$. Let
$ \mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$. Let ![]() $\tilde X$ be any limit point. Then, there exists a subsequence of
$\tilde X$ be any limit point. Then, there exists a subsequence of  $\{\tilde{X}^{(j)}\}_{j\ge 1}$ (denoted by the same symbol) weakly converging to
$\{\tilde{X}^{(j)}\}_{j\ge 1}$ (denoted by the same symbol) weakly converging to ![]() $\tilde X$ in
$\tilde X$ in ![]() $ \mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$. In the following, we will prove that the limit point
$ \mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$. In the following, we will prove that the limit point ![]() $\tilde X$ satisfies the RDE as follows,
$\tilde X$ satisfies the RDE as follows,
According to remark 3.6, we emphasize that  $\{\tilde{X}^{(j)}\}_{j\ge 1}$ solves the following ODE:
$\{\tilde{X}^{(j)}\}_{j\ge 1}$ solves the following ODE:
 \begin{equation}
d\tilde{X}^{(j)}_t = \bar{f}_1(\tilde{X}^{(j)}_t)dt + \sigma_{1}( \tilde{X}^{(j)}_t)du^{(j)}_t
\end{equation}
\begin{equation}
d\tilde{X}^{(j)}_t = \bar{f}_1(\tilde{X}^{(j)}_t)dt + \sigma_{1}( \tilde{X}^{(j)}_t)du^{(j)}_t
\end{equation} where ![]() $\|(u^{(j)},v^{(j)})\|_{q-\operatorname{var}} \lt \infty$ with
$\|(u^{(j)},v^{(j)})\|_{q-\operatorname{var}} \lt \infty$ with ![]() $(H+1/2)^{-1} \lt q \lt 2$ for all
$(H+1/2)^{-1} \lt q \lt 2$ for all ![]() $j\ge 1$. Due to the Young integral theory, it is not too difficult to verify that for all
$j\ge 1$. Due to the Young integral theory, it is not too difficult to verify that for all ![]() $(u, v) \in S_{N}$, there exists a unique solution
$(u, v) \in S_{N}$, there exists a unique solution  $\{\tilde{X}^{(j)}\}_{j\ge 1} \in \mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^m\right)$ to (5.4) in the Young sense. In fact,
$\{\tilde{X}^{(j)}\}_{j\ge 1} \in \mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^m\right)$ to (5.4) in the Young sense. In fact,  $\{\tilde{X}^{(j)}\}_{j\ge 1}$ is independent of
$\{\tilde{X}^{(j)}\}_{j\ge 1}$ is independent of ![]() $\{v^{(j)}\}_{j\ge 1}$. Moreover, we have
$\{v^{(j)}\}_{j\ge 1}$. Moreover, we have
 \begin{equation*}\|\tilde{X}^{(j)}\|_{p-\operatorname{var}}\leqslant c,\end{equation*}
\begin{equation*}\|\tilde{X}^{(j)}\|_{p-\operatorname{var}}\leqslant c,\end{equation*} where the constant c > 0 is independent of ![]() $(u^{(j)}, v^{(j)})$. Note that the Young integral
$(u^{(j)}, v^{(j)})$. Note that the Young integral  $u^{(j)}\mapsto\int_{0}^{\cdot}\sigma_{1}(\tilde{X}_s^{(j)})du^{(j)}_s$ is a linear continuous map from
$u^{(j)}\mapsto\int_{0}^{\cdot}\sigma_{1}(\tilde{X}_s^{(j)})du^{(j)}_s$ is a linear continuous map from ![]() $\mathcal{H}^d$ to
$\mathcal{H}^d$ to ![]() $\mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^m\right)$.
$\mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^m\right)$.
Let us show that the limit point ![]() $\tilde{X}$ satisfies the skeleton equation (3.9). By the direct computation, we derive
$\tilde{X}$ satisfies the skeleton equation (3.9). By the direct computation, we derive
 \begin{equation}
\begin{array}{rcl}
\big|\tilde{X}^{(j)}_t-\tilde{X}_t\big|&\leqslant& \bigg|\int_{0}^{t} \big[\bar{f}_1(\tilde{X}^{(j)}_s)-\bar{f}_1(\tilde{X}_s)\big]ds\bigg|+\bigg|\int_{0}^{t} \big[\sigma_{1}( \tilde{X}^{(j)}_s)-\sigma_{1}( \tilde{X}_s)\big]du^{(j)}_s\bigg|\\
&&+\bigg|\int_{0}^{t} \sigma_{1}( \tilde{X}_s)\big[du^{(j)}_s-du_s\big]\bigg|\\
&=:& J_1+J_2+J_3.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\big|\tilde{X}^{(j)}_t-\tilde{X}_t\big|&\leqslant& \bigg|\int_{0}^{t} \big[\bar{f}_1(\tilde{X}^{(j)}_s)-\bar{f}_1(\tilde{X}_s)\big]ds\bigg|+\bigg|\int_{0}^{t} \big[\sigma_{1}( \tilde{X}^{(j)}_s)-\sigma_{1}( \tilde{X}_s)\big]du^{(j)}_s\bigg|\\
&&+\bigg|\int_{0}^{t} \sigma_{1}( \tilde{X}_s)\big[du^{(j)}_s-du_s\big]\bigg|\\
&=:& J_1+J_2+J_3.
\end{array}
\end{equation} For the first term J 1, by using the result that ![]() $\bar{f}_1$ is Lipschitz continuous and bounded, we have
$\bar{f}_1$ is Lipschitz continuous and bounded, we have
 \begin{equation}
J_1\leqslant L\int_{0}^{t} |\tilde{X}^{(j)}_s-\tilde{X}_s|ds\leqslant C\sup_{0\leqslant s\leqslant t}|\tilde{X}^{(j)}_s-\tilde{X}_s|.
\end{equation}
\begin{equation}
J_1\leqslant L\int_{0}^{t} |\tilde{X}^{(j)}_s-\tilde{X}_s|ds\leqslant C\sup_{0\leqslant s\leqslant t}|\tilde{X}^{(j)}_s-\tilde{X}_s|.
\end{equation}After that, by applying (A1), we estimate J 2 as following:
 \begin{equation}
\begin{array}{rcl}
J_2\leqslant C\bigg|\int_{0}^{t} |\tilde{X}^{(j)}_s-\tilde{X}_s|du^{(j)}_s\bigg|&\leqslant& CT\|u^{(j)}\|_{q-\operatorname{var}}\sup_{0 \leqslant t \leqslant T}|\tilde{X}^{(j)}_t-\tilde{X}_t|\\
&\leqslant& C_1\sup_{0 \leqslant t \leqslant T}|\tilde{X}^{(j)}_t-\tilde{X}_t|
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
J_2\leqslant C\bigg|\int_{0}^{t} |\tilde{X}^{(j)}_s-\tilde{X}_s|du^{(j)}_s\bigg|&\leqslant& CT\|u^{(j)}\|_{q-\operatorname{var}}\sup_{0 \leqslant t \leqslant T}|\tilde{X}^{(j)}_t-\tilde{X}_t|\\
&\leqslant& C_1\sup_{0 \leqslant t \leqslant T}|\tilde{X}^{(j)}_t-\tilde{X}_t|
\end{array}
\end{equation} where ![]() $C_1 \gt 0$ only depends on N and q. Since
$C_1 \gt 0$ only depends on N and q. Since  $\{\tilde X^{(j)}\}_{j\ge 1}$ converges to
$\{\tilde X^{(j)}\}_{j\ge 1}$ converges to ![]() $\tilde X$ in the uniform norm, it is an immediate consequence that
$\tilde X$ in the uniform norm, it is an immediate consequence that ![]() $J_1+ J_2\to 0$ as
$J_1+ J_2\to 0$ as ![]() $j \to \infty$.
$j \to \infty$.
Next, it proceeds to estimates J 3. To do this, we set  $B(u^{(j)},\tilde{X}):=\int_{0}^{t} \sigma_{1}( \tilde{X}_s)du^{(j)}_s$, which is a bilinear continuous map from
$B(u^{(j)},\tilde{X}):=\int_{0}^{t} \sigma_{1}( \tilde{X}_s)du^{(j)}_s$, which is a bilinear continuous map from ![]() $\mathcal{H}^{H,d}\times \mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^m\right)$ to
$\mathcal{H}^{H,d}\times \mathcal{C}^{p-\operatorname{var}}\left([0,T],\mathbb{R}^m\right)$ to ![]() $\mathbb{R}$. According to the Riesz representation theorem, there exists a unique element in
$\mathbb{R}$. According to the Riesz representation theorem, there exists a unique element in ![]() $ \mathcal{H}^{H,d}$ (denoted by
$ \mathcal{H}^{H,d}$ (denoted by ![]() $B(\cdot,\tilde{X})$) such that
$B(\cdot,\tilde{X})$) such that  $B(u^{(j)},\tilde{X})=\langle B(\cdot,\tilde{X}),u^{(j)}\rangle_{\mathcal{H}^{H,d}}$ for all
$B(u^{(j)},\tilde{X})=\langle B(\cdot,\tilde{X}),u^{(j)}\rangle_{\mathcal{H}^{H,d}}$ for all ![]() $u^{(j)}\in \mathcal{H}^{H,d}$. Note that
$u^{(j)}\in \mathcal{H}^{H,d}$. Note that ![]() $B(\cdot,\tilde{X})\in (\mathcal{H}^{H,d})^{*}\cong \mathcal{H}^{H,d}$. Then, we have
$B(\cdot,\tilde{X})\in (\mathcal{H}^{H,d})^{*}\cong \mathcal{H}^{H,d}$. Then, we have
 \begin{equation}
\begin{array}{rcl}
J_3&=& |B(u^{(j)},\tilde{X})-B(u,\tilde{X})|\\
&=& |\langle B(\cdot,\tilde{X}),u^{(j)}\rangle_{\mathcal{H}^{H,d}}-\langle B(\cdot,\tilde{X}),u\rangle_{\mathcal{H}^{H,d}}|.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
J_3&=& |B(u^{(j)},\tilde{X})-B(u,\tilde{X})|\\
&=& |\langle B(\cdot,\tilde{X}),u^{(j)}\rangle_{\mathcal{H}^{H,d}}-\langle B(\cdot,\tilde{X}),u\rangle_{\mathcal{H}^{H,d}}|.
\end{array}
\end{equation} Since ![]() $(u^{(j)}, v^{(j)})\rightarrow(u, v)$ as
$(u^{(j)}, v^{(j)})\rightarrow(u, v)$ as ![]() $j\rightarrow\infty$ with the weak topology in
$j\rightarrow\infty$ with the weak topology in ![]() $\mathcal{H}$, we prove that J 3 converges to 0 as
$\mathcal{H}$, we prove that J 3 converges to 0 as ![]() $j\rightarrow\infty$.
$j\rightarrow\infty$.
By combining (5.5)–(5.8) and remark 3.6, it is clear that the limit point ![]() $\tilde X$ satisfies the ODE (3.9). Consequently, we obtain that
$\tilde X$ satisfies the ODE (3.9). Consequently, we obtain that  $\{\tilde X^{(j)}\}_{j\ge 1}$ weakly converges to
$\{\tilde X^{(j)}\}_{j\ge 1}$ weakly converges to ![]() $\tilde X$ in
$\tilde X$ in ![]() $\mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ for any small
$\mathcal{C}^{(\beta-\theta)-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ for any small ![]() $0 \lt \theta \lt \beta$.
$0 \lt \theta \lt \beta$.
Step 2. We carry out probabilistic arguments in this step. Let ![]() $0 \lt N \lt \infty$ and assume
$0 \lt N \lt \infty$ and assume ![]() $0 \lt \delta=o(\varepsilon)\leqslant 1$ and we will take ɛ → 0.
$0 \lt \delta=o(\varepsilon)\leqslant 1$ and we will take ɛ → 0.
Assume ![]() $(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}^{N}_b$ such that
$(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}^{N}_b$ such that ![]() $(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})$ weakly converges to (u, v) as ɛ → 0. In this step, we will prove that
$(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})$ weakly converges to (u, v) as ɛ → 0. In this step, we will prove that ![]() $\tilde {X}^{\varepsilon, \delta}$ weakly converges to
$\tilde {X}^{\varepsilon, \delta}$ weakly converges to ![]() $\tilde {X}$ in
$\tilde {X}$ in ![]() $\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ as
$\mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^{m})$ as ![]() $\varepsilon\rightarrow 0$, that is,
$\varepsilon\rightarrow 0$, that is,
 \begin{equation}
\mathcal{G}^{(\varepsilon,\delta)}(\sqrt \varepsilon b^H+u^{\varepsilon, \delta}, \sqrt \varepsilon w+v^{\varepsilon, \delta})\xrightarrow{\textrm{weakly}}\mathcal{G}^{0}(u , v) \quad \text{as }\varepsilon\rightarrow 0.
\end{equation}
\begin{equation}
\mathcal{G}^{(\varepsilon,\delta)}(\sqrt \varepsilon b^H+u^{\varepsilon, \delta}, \sqrt \varepsilon w+v^{\varepsilon, \delta})\xrightarrow{\textrm{weakly}}\mathcal{G}^{0}(u , v) \quad \text{as }\varepsilon\rightarrow 0.
\end{equation}We rewrite the controlled slow component of RDE (4.1) as following,
Before showing (5.9) hold, we define an auxiliary process ![]() $\hat X^{\varepsilon,\delta}$ satisfying the following RDE:
$\hat X^{\varepsilon,\delta}$ satisfying the following RDE:
 \begin{equation}
d\hat {X}^{\varepsilon,\delta}_t = \bar f_{1}(\tilde {X}^{\varepsilon,\delta}_t)dt +\sigma_{1}(\tilde {X}^{\varepsilon,\delta}_t)d[T_{t}^u(\varepsilon B^H) ]
\end{equation}
\begin{equation}
d\hat {X}^{\varepsilon,\delta}_t = \bar f_{1}(\tilde {X}^{\varepsilon,\delta}_t)dt +\sigma_{1}(\tilde {X}^{\varepsilon,\delta}_t)d[T_{t}^u(\varepsilon B^H) ]
\end{equation} with initial value  $\hat {X}^{\varepsilon,\delta}_0=X_0$. By taking similar manner as in lemma 4.1, we can have
$\hat {X}^{\varepsilon,\delta}_0=X_0$. By taking similar manner as in lemma 4.1, we can have
 \begin{equation}
\mathbb{E}[\|\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}]\leqslant C
\end{equation}
\begin{equation}
\mathbb{E}[\|\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}]\leqslant C
\end{equation} where C > 0 only depends on ![]() $\alpha,\beta$, and N.
$\alpha,\beta$, and N.
Now, we are in the position to give some estimates which will be used in proving (5.9). Firstly, by some direct computation, we can get that
 \begin{align}
\begin{array}{rcl}
&&\tilde {X}^{\varepsilon,\delta}_t-\hat {X}^{\varepsilon,\delta}_t\\
&=&\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_s, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)]dt +\int_{0}^{t}\big[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}\\
&&\times (\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)\big]ds \\
&&+\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})]ds +\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_s)]ds \\
&& +\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon,\delta}_{s})-\bar f_{1}(\hat {X}^{\varepsilon,\delta}_{s})]ds+\int_{0}^{t}[\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_s)-\sigma_{1}(\hat {X}^{\varepsilon,\delta}_s)]d[T_{s}^u(\varepsilon B^H) ]\\
&:=&K_1+K_2+K_3+K_4+K_5+K_6.
\end{array}\nonumber\\
\end{align}
\begin{align}
\begin{array}{rcl}
&&\tilde {X}^{\varepsilon,\delta}_t-\hat {X}^{\varepsilon,\delta}_t\\
&=&\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_s, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)]dt +\int_{0}^{t}\big[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}\\
&&\times (\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)\big]ds \\
&&+\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})]ds +\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_s)]ds \\
&& +\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon,\delta}_{s})-\bar f_{1}(\hat {X}^{\varepsilon,\delta}_{s})]ds+\int_{0}^{t}[\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_s)-\sigma_{1}(\hat {X}^{\varepsilon,\delta}_s)]d[T_{s}^u(\varepsilon B^H) ]\\
&:=&K_1+K_2+K_3+K_4+K_5+K_6.
\end{array}\nonumber\\
\end{align}Firstly, we estimate K 1 with Hölder inequality, (A2), and lemma 4.1,
 \begin{align}
\begin{array}{rcl}
\mathbb{E}[\sup_{0 \leqslant t \leqslant T}|K_1|^2] &=&\mathbb{E}\bigg[\sup_{0 \leqslant t \leqslant T}\big|\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_s, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)]ds\big|^2\bigg]\\
&\leqslant & \lt \int_{0}^{T}\mathbb{E}[|\tilde {X}^{\varepsilon, \delta}_s-\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}|^2]ds\\
&\leqslant & \lt ^2 \mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]\Delta^{2\beta}.
\end{array}\nonumber\\
\end{align}
\begin{align}
\begin{array}{rcl}
\mathbb{E}[\sup_{0 \leqslant t \leqslant T}|K_1|^2] &=&\mathbb{E}\bigg[\sup_{0 \leqslant t \leqslant T}\big|\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_s, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)]ds\big|^2\bigg]\\
&\leqslant & \lt \int_{0}^{T}\mathbb{E}[|\tilde {X}^{\varepsilon, \delta}_s-\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}|^2]ds\\
&\leqslant & \lt ^2 \mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]\Delta^{2\beta}.
\end{array}\nonumber\\
\end{align}For the second term K 2, with aid of the Hölder inequality and lemma 4.5, we get
 \begin{align}
\begin{array}{rcl}
\mathbb{E}[\sup_{0 \leqslant t \leqslant T}|K_2|^2] &=&\mathbb{E}\bigg[\sup_{0 \leqslant t \leqslant T}\big|\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)]ds\big|^2\bigg] \\
&\leqslant&TL \int_{0}^{T}\mathbb{E}\big[\big|\tilde Y_{s}^{\varepsilon,\delta}-\hat Y_{s}^{\varepsilon,\delta}\big|^2\big]ds \leqslant CT^2(\frac{\sqrt{\delta}}{{\sqrt{\varepsilon}}}+\Delta^{2\beta}).
\end{array}\nonumber\\
\end{align}
\begin{align}
\begin{array}{rcl}
\mathbb{E}[\sup_{0 \leqslant t \leqslant T}|K_2|^2] &=&\mathbb{E}\bigg[\sup_{0 \leqslant t \leqslant T}\big|\int_{0}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \tilde {Y}^{\varepsilon, \delta}_s)-f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)]ds\big|^2\bigg] \\
&\leqslant&TL \int_{0}^{T}\mathbb{E}\big[\big|\tilde Y_{s}^{\varepsilon,\delta}-\hat Y_{s}^{\varepsilon,\delta}\big|^2\big]ds \leqslant CT^2(\frac{\sqrt{\delta}}{{\sqrt{\varepsilon}}}+\Delta^{2\beta}).
\end{array}\nonumber\\
\end{align} In the following part, we will estimate K 3. To this end, we set  $M_{s,t}=\int_{s}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{r(\Delta)}, \hat {Y}^{\varepsilon, \delta}_r)-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{r(\Delta)})]dr$. Then, we give some estimates. Set
$M_{s,t}=\int_{s}^{t}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{r(\Delta)}, \hat {Y}^{\varepsilon, \delta}_r)-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{r(\Delta)})]dr$. Then, we give some estimates. Set ![]() $1/2 \lt \eta \lt 1$. When
$1/2 \lt \eta \lt 1$. When ![]() $0 \lt t-s \lt 2\Delta$, it is immediate to see that
$0 \lt t-s \lt 2\Delta$, it is immediate to see that
When ![]() $t-s \gt 2\Delta$, by using the Schwarz inequality, we obtain
$t-s \gt 2\Delta$, by using the Schwarz inequality, we obtain
 \begin{equation}
\begin{array}{rcl}
\frac{\left|M_{s, t}\right|^2}{(t-s)^{2\eta}} & \leqslant&\frac{\big|M_{s,(\lfloor s / \Delta\rfloor+1) \Delta}+\sum_{k=\lfloor s / \Delta\rfloor+1}^{\lfloor t / \Delta\rfloor-1} M_{k \Delta,(k+1) \Delta}+M_{\lfloor t / \Delta\rfloor \Delta, t}\big|^2}{(t-s)^{2\eta}} \\
& \leqslant& C \Delta^{2-2\eta}+\frac{2C(t-s)^{1-2\eta}}{\Delta} \sum_{k=0}^{\lfloor T / \Delta\rfloor-1}\left|M_{k \Delta,(k+1) \Delta}\right|^2.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\frac{\left|M_{s, t}\right|^2}{(t-s)^{2\eta}} & \leqslant&\frac{\big|M_{s,(\lfloor s / \Delta\rfloor+1) \Delta}+\sum_{k=\lfloor s / \Delta\rfloor+1}^{\lfloor t / \Delta\rfloor-1} M_{k \Delta,(k+1) \Delta}+M_{\lfloor t / \Delta\rfloor \Delta, t}\big|^2}{(t-s)^{2\eta}} \\
& \leqslant& C \Delta^{2-2\eta}+\frac{2C(t-s)^{1-2\eta}}{\Delta} \sum_{k=0}^{\lfloor T / \Delta\rfloor-1}\left|M_{k \Delta,(k+1) \Delta}\right|^2.
\end{array}
\end{equation}Then, by (5.15) and (5.16), it deduces that
 \begin{equation}
\begin{array}{rcl}
\mathbb{E}[\|K_3\|_{\beta-\operatorname{hld}}^2]&=&\mathbb{E}\bigg[\bigg\|\int_{0}^{\cdot}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})]ds\bigg\|_{\beta-\operatorname{hld}}^2\bigg]\\
&\leqslant &\frac{CT}{\Delta^{(1+2\eta)}} \max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \mathbb{E}\big[\big|\int_{k \Delta}^{(k+1) \Delta}\big(f_1( \tilde X_{k \Delta}^{\varepsilon, \delta},\hat {Y}^{\varepsilon, \delta}_s)\\ && -\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta})\big) d s\big|^2\big]\\
&&+C\Delta^{2(1-\eta)}.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\mathbb{E}[\|K_3\|_{\beta-\operatorname{hld}}^2]&=&\mathbb{E}\bigg[\bigg\|\int_{0}^{\cdot}[f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}, \hat {Y}^{\varepsilon, \delta}_s)-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})]ds\bigg\|_{\beta-\operatorname{hld}}^2\bigg]\\
&\leqslant &\frac{CT}{\Delta^{(1+2\eta)}} \max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \mathbb{E}\big[\big|\int_{k \Delta}^{(k+1) \Delta}\big(f_1( \tilde X_{k \Delta}^{\varepsilon, \delta},\hat {Y}^{\varepsilon, \delta}_s)\\ && -\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta})\big) d s\big|^2\big]\\
&&+C\Delta^{2(1-\eta)}.
\end{array}
\end{equation}According to some direct but cumbersome computation, we arrive at
 \begin{equation}
\begin{array}{rcl}
&&\max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \mathbb{E}\big[\big|\int_{k \Delta}^{(k+1) \Delta}\big(f_1( \tilde X_{k \Delta}^{\varepsilon, \delta},\hat {Y}^{\varepsilon, \delta}_s)-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta})\big) d s\big|^2\big]\\
&\leqslant & C \delta^2 \max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \int_0^{\frac{\Delta}{\delta}} \int_r^{\frac{\Delta}{\delta}} \mathbb{E}\big[\big\langle f_1( \tilde X_{k \Delta}^{\varepsilon,\delta}, \hat{Y}_{s \varepsilon+k \Delta}^{\varepsilon,\delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon,\delta}),\big.\big.\\
&&\big.\big.f_1( \tilde X_{k \Delta}^{\varepsilon,\delta}, \hat{Y}_{r \varepsilon+k \Delta}^{\varepsilon,\delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon,\delta})\big\rangle\big] d s d r\\
& \leqslant& C \delta^2 \max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \int_0^{\frac{\Delta}{\delta}} \int_r^{\frac{\Delta}{\delta}} e^{-\frac{\beta_1}{2}(s-r)} d s d r \\
& \leqslant &C \delta^2\left(\frac{2}{\beta_1} \frac{\Delta}{\delta}-\frac{4}{\beta_1^2}+e^{\frac{-\beta_1}{2} \frac{\Delta}{\delta}}\right)\\
& \leqslant &C \delta\Delta.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
&&\max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \mathbb{E}\big[\big|\int_{k \Delta}^{(k+1) \Delta}\big(f_1( \tilde X_{k \Delta}^{\varepsilon, \delta},\hat {Y}^{\varepsilon, \delta}_s)-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta})\big) d s\big|^2\big]\\
&\leqslant & C \delta^2 \max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \int_0^{\frac{\Delta}{\delta}} \int_r^{\frac{\Delta}{\delta}} \mathbb{E}\big[\big\langle f_1( \tilde X_{k \Delta}^{\varepsilon,\delta}, \hat{Y}_{s \varepsilon+k \Delta}^{\varepsilon,\delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon,\delta}),\big.\big.\\
&&\big.\big.f_1( \tilde X_{k \Delta}^{\varepsilon,\delta}, \hat{Y}_{r \varepsilon+k \Delta}^{\varepsilon,\delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon,\delta})\big\rangle\big] d s d r\\
& \leqslant& C \delta^2 \max _{0 \leqslant k \leqslant\left\lfloor\frac{T}{\Delta}\right\rfloor-1} \int_0^{\frac{\Delta}{\delta}} \int_r^{\frac{\Delta}{\delta}} e^{-\frac{\beta_1}{2}(s-r)} d s d r \\
& \leqslant &C \delta^2\left(\frac{2}{\beta_1} \frac{\Delta}{\delta}-\frac{4}{\beta_1^2}+e^{\frac{-\beta_1}{2} \frac{\Delta}{\delta}}\right)\\
& \leqslant &C \delta\Delta.
\end{array}
\end{equation} Here, we exploit the exponential ergodicity of ![]() $\hat Y^{\varepsilon,\delta}$, that is
$\hat Y^{\varepsilon,\delta}$, that is
 \begin{equation}
\begin{array}{rcl}
&&\mathbb{E}\big[\big\langle f_1( \tilde X_{k \Delta}^{\varepsilon, \delta}, \hat{Y}_{s \varepsilon+k \Delta}^{\varepsilon, \delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta}),f_1( \tilde X_{k \Delta}^{\varepsilon, \delta}, \hat{Y}_{r \varepsilon+k \Delta}^{\varepsilon, \delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta})\big\rangle\big]\\
&\leqslant& C(1+\mathbb{E}[| \tilde X_{k \Delta}^{\varepsilon, \delta}|^2]+\mathbb{E}[| \hat Y_{k \Delta}^{\varepsilon, \delta}|^2]) e^{-\frac{\beta_1}{2}(s-r)}\\
&\leqslant& C e^{-\frac{\beta_1}{2}(s-r)},
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
&&\mathbb{E}\big[\big\langle f_1( \tilde X_{k \Delta}^{\varepsilon, \delta}, \hat{Y}_{s \varepsilon+k \Delta}^{\varepsilon, \delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta}),f_1( \tilde X_{k \Delta}^{\varepsilon, \delta}, \hat{Y}_{r \varepsilon+k \Delta}^{\varepsilon, \delta})-\bar{f}_1( \tilde X_{k \Delta}^{\varepsilon, \delta})\big\rangle\big]\\
&\leqslant& C(1+\mathbb{E}[| \tilde X_{k \Delta}^{\varepsilon, \delta}|^2]+\mathbb{E}[| \hat Y_{k \Delta}^{\varepsilon, \delta}|^2]) e^{-\frac{\beta_1}{2}(s-r)}\\
&\leqslant& C e^{-\frac{\beta_1}{2}(s-r)},
\end{array}
\end{equation}where β 1 is in (A4). For the first inequality, we refer to [Reference Pei, Inahama and Xu36, Appendix B] for instance. The final inequality comes from lemmas 4.1 and 4.4. So according to the estimates (5.17)–(5.19), we have
 \begin{equation}
\mathbb{E}[\|K_3\|_{\beta-\operatorname{hld}}^2]\leqslant C\Delta^{2(1-\eta)}+\frac{CT\delta}{\Delta^{2\eta}}.
\end{equation}
\begin{equation}
\mathbb{E}[\|K_3\|_{\beta-\operatorname{hld}}^2]\leqslant C\Delta^{2(1-\eta)}+\frac{CT\delta}{\Delta^{2\eta}}.
\end{equation} Next, for the fourth term K 4, by applying that ![]() $\bar{f}_1$ is Lipschitz continuous and bounded, we obtain
$\bar{f}_1$ is Lipschitz continuous and bounded, we obtain
 \begin{equation}
\begin{array}{rcl}
\mathbb{E}[\sup_{0 \leqslant t \leqslant T}|K_4|^2] &=&\mathbb{E}\bigg[\sup_{0 \leqslant t \leqslant T}\bigg|\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_s)]ds\bigg|^2\bigg]\\
&\leqslant & \lt \int_{0}^{T}\mathbb{E}[|\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}-\tilde {X}^{\varepsilon, \delta}_{s}|^2]ds\\
&\leqslant& \lt ^2 \mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]\Delta^{2\beta}.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\mathbb{E}[\sup_{0 \leqslant t \leqslant T}|K_4|^2] &=&\mathbb{E}\bigg[\sup_{0 \leqslant t \leqslant T}\bigg|\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_{s(\Delta)})-\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_s)]ds\bigg|^2\bigg]\\
&\leqslant & \lt \int_{0}^{T}\mathbb{E}[|\tilde {X}^{\varepsilon, \delta}_{s(\Delta)}-\tilde {X}^{\varepsilon, \delta}_{s}|^2]ds\\
&\leqslant& \lt ^2 \mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]\Delta^{2\beta}.
\end{array}
\end{equation}Next, we set
 \begin{equation}
\begin{array}{rcl}
Q_t&:=&(\tilde {X}^{\varepsilon,\delta}_t-\hat {X}^{\varepsilon,\delta}_t)-\bigg\{\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_s)-\bar f_{1}(\hat {X}^{\varepsilon,\delta}_s)]ds\bigg\} \\
&&-\bigg\{\int_{0}^{t}[\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_s)-\sigma_{1}(\hat {X}^{\varepsilon,\delta}_s)]d[T_{s}^u(\varepsilon B^H)]\bigg\}.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
Q_t&:=&(\tilde {X}^{\varepsilon,\delta}_t-\hat {X}^{\varepsilon,\delta}_t)-\bigg\{\int_{0}^{t}[\bar f_{1}(\tilde {X}^{\varepsilon, \delta}_s)-\bar f_{1}(\hat {X}^{\varepsilon,\delta}_s)]ds\bigg\} \\
&&-\bigg\{\int_{0}^{t}[\sigma_{1}(\tilde {X}^{\varepsilon, \delta}_s)-\sigma_{1}(\hat {X}^{\varepsilon,\delta}_s)]d[T_{s}^u(\varepsilon B^H)]\bigg\}.
\end{array}
\end{equation} The estimates (5.13)–(5.22) furnish the following observation that ![]() $Q\in \mathcal{C}^{1-\operatorname{hld}}([0,T],\mathbb{R}^m)$ and
$Q\in \mathcal{C}^{1-\operatorname{hld}}([0,T],\mathbb{R}^m)$ and
 \begin{equation}
\mathbb{E}\left[\|Q\|_{2 \beta}^2\right] \leqslant C\big(\Delta^{2 \beta}+\Delta^{2(1-2 \beta)}+\Delta^{-4 \beta} \delta+\frac{\sqrt{\delta}}{\sqrt{\varepsilon}}\big) .
\end{equation}
\begin{equation}
\mathbb{E}\left[\|Q\|_{2 \beta}^2\right] \leqslant C\big(\Delta^{2 \beta}+\Delta^{2(1-2 \beta)}+\Delta^{-4 \beta} \delta+\frac{\sqrt{\delta}}{\sqrt{\varepsilon}}\big) .
\end{equation}Due to [Reference Inahama23, proposition 3.5], it deduces that there exist positive constants c and ν such that
 \begin{equation}
\begin{array}{rcl}
&&\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|_{\beta-\operatorname{hld}} \\ &\leqslant& c \exp \big[c\left(K^{\prime}+1\right)^\nu\big(\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1\big)^\nu\big]\|Q\|_{2\beta-\operatorname{hld}}.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
&&\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|_{\beta-\operatorname{hld}} \\ &\leqslant& c \exp \big[c\left(K^{\prime}+1\right)^\nu\big(\left\vert\!\left\vert\!\left\vert{T^u(\varepsilon B^H)}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}+1\big)^\nu\big]\|Q\|_{2\beta-\operatorname{hld}}.
\end{array}
\end{equation} Here,  $K^{\prime}=\max \{\|\sigma_1\|_{C_b^3},\|f_1\|_{\infty}, L\}$. Then, we choose some suitable
$K^{\prime}=\max \{\|\sigma_1\|_{C_b^3},\|f_1\|_{\infty}, L\}$. Then, we choose some suitable ![]() $\Delta \gt 0$ such that
$\Delta \gt 0$ such that  $\mathbb{E}[\|Q\|_{2\beta-\operatorname{hld}}^2] \to 0$ as ɛ. For instance, we could choose
$\mathbb{E}[\|Q\|_{2\beta-\operatorname{hld}}^2] \to 0$ as ɛ. For instance, we could choose ![]() $\Delta:=\delta^{1 /(4 \beta)} \log \delta^{-1}$. Therefore, we have that
$\Delta:=\delta^{1 /(4 \beta)} \log \delta^{-1}$. Therefore, we have that  $\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}$ converges to 0 in probability as ɛ → 0.
$\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}$ converges to 0 in probability as ɛ → 0.
On the other hand, with lemma 4.1 and (5.11), it is clear to find that
 \begin{equation}
\mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}] \leqslant c \mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]+\mathbb{E}[\|\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}]\leqslant C.
\end{equation}
\begin{equation}
\mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}] \leqslant c \mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]+\mathbb{E}[\|\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}]\leqslant C.
\end{equation} So it shows that  $\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}$ is uniformly integrable. Then, we have
$\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}$ is uniformly integrable. Then, we have  $\mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}]$ converges to 0 as ɛ → 0.
$\mathbb{E}[\|\tilde {X}^{\varepsilon, \delta}-\hat {X}^{\varepsilon,\delta}\|^2_{\beta-\operatorname{hld}}]$ converges to 0 as ɛ → 0.
Then, we define
 \begin{equation}
d\tilde {X}^{\varepsilon}_t = \bar f_{1}(\tilde {X}^{\varepsilon}_t)dt +\sigma_{1}(\tilde {X}^{\varepsilon}_t)dU^{\varepsilon,\delta}_t
\end{equation}
\begin{equation}
d\tilde {X}^{\varepsilon}_t = \bar f_{1}(\tilde {X}^{\varepsilon}_t)dt +\sigma_{1}(\tilde {X}^{\varepsilon}_t)dU^{\varepsilon,\delta}_t
\end{equation} with initial value ![]() $\tilde {X}^{\varepsilon}_0=X_0$. By taking similar manner as in lemma 4.1, we observe
$\tilde {X}^{\varepsilon}_0=X_0$. By taking similar manner as in lemma 4.1, we observe
 \begin{equation}
\mathbb{E}[\|\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}]\leqslant C
\end{equation}
\begin{equation}
\mathbb{E}[\|\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}]\leqslant C
\end{equation} where C > 0 only depends on ![]() $\alpha,\beta$ and N.
$\alpha,\beta$ and N.
By using proposition 2.8, we have that
 \begin{equation}
\begin{array}{rcl}
\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|_{\beta-\operatorname{hld}} &\leqslant& C_{N,B^H}\rho_\alpha(T^u(\varepsilon B^H), U^{\varepsilon,\delta})\\
&\leqslant&C_{N,B^H}(\|\sqrt{\varepsilon}b^H\|_{\alpha-\operatorname{hld}}+\|\varepsilon I[b^H,u^{\varepsilon,\delta}] \|_{2\alpha-\operatorname{hld}})\\
&&+C_{N,B^H}(\|\varepsilon I[u^{\varepsilon,\delta},b^H] \|_{2\alpha-\operatorname{hld}}+\|\varepsilon B^{H,2}\|_{2\alpha-\operatorname{hld}})\\
&\leqslant&C_{N,B^H}\sqrt{\varepsilon}
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|_{\beta-\operatorname{hld}} &\leqslant& C_{N,B^H}\rho_\alpha(T^u(\varepsilon B^H), U^{\varepsilon,\delta})\\
&\leqslant&C_{N,B^H}(\|\sqrt{\varepsilon}b^H\|_{\alpha-\operatorname{hld}}+\|\varepsilon I[b^H,u^{\varepsilon,\delta}] \|_{2\alpha-\operatorname{hld}})\\
&&+C_{N,B^H}(\|\varepsilon I[u^{\varepsilon,\delta},b^H] \|_{2\alpha-\operatorname{hld}}+\|\varepsilon B^{H,2}\|_{2\alpha-\operatorname{hld}})\\
&\leqslant&C_{N,B^H}\sqrt{\varepsilon}
\end{array}
\end{equation} where  $C_{N,B^H}:=C_{N,\left\vert\!\left\vert\!\left\vert{B^{H}}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}} \gt 0$ is independent of ɛ and δ. On the other hand, it is not too intractable to verify that
$C_{N,B^H}:=C_{N,\left\vert\!\left\vert\!\left\vert{B^{H}}\right\vert\!\right\vert\!\right\vert_{\alpha-\operatorname{hld}}} \gt 0$ is independent of ɛ and δ. On the other hand, it is not too intractable to verify that
 \begin{equation}
\mathbb{E}[\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}] \leqslant 2 \mathbb{E}[\|\hat {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]+2\mathbb{E}[\|\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}]\leqslant C.
\end{equation}
\begin{equation}
\mathbb{E}[\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}] \leqslant 2 \mathbb{E}[\|\hat {X}^{\varepsilon, \delta}\|^2_{\beta-\operatorname{hld}}]+2\mathbb{E}[\|\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}]\leqslant C.
\end{equation} So it implies that  $\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}$ is uniformly integrable. Then, we have
$\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}$ is uniformly integrable. Then, we have  $\mathbb{E}[\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}]$ converges to 0 as ɛ → 0.
$\mathbb{E}[\|\hat {X}^{\varepsilon, \delta}-\tilde {X}^{\varepsilon}\|^2_{\beta-\operatorname{hld}}]$ converges to 0 as ɛ → 0.
In the following, we will show that ![]() $\tilde X^\varepsilon$ converges in distribution to
$\tilde X^\varepsilon$ converges in distribution to ![]() $\tilde X$ as ɛ → 0. By remark 2.5 and condition that
$\tilde X$ as ɛ → 0. By remark 2.5 and condition that ![]() $(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}^{N}_b$, we have that
$(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})\in \mathcal{A}^{N}_b$, we have that ![]() $ U^{\varepsilon,\delta}: \mathcal{H}^{H,d} \mapsto \Omega_\alpha(\mathbb{R}^d)$ is a Lipschitz continuous mapping. Next, by proposition 2.8, we obtain that
$ U^{\varepsilon,\delta}: \mathcal{H}^{H,d} \mapsto \Omega_\alpha(\mathbb{R}^d)$ is a Lipschitz continuous mapping. Next, by proposition 2.8, we obtain that ![]() $\tilde {X}^{\varepsilon}$ is a continuous solution map with respect to RP
$\tilde {X}^{\varepsilon}$ is a continuous solution map with respect to RP ![]() $ U^{\varepsilon,\delta}$. With aid of the condition that
$ U^{\varepsilon,\delta}$. With aid of the condition that ![]() $(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})$ weakly converges to (u, v) as ɛ → 0 and continuous mapping theorem, it deduces that
$(u^{\varepsilon, \delta}, v^{\varepsilon, \delta})$ weakly converges to (u, v) as ɛ → 0 and continuous mapping theorem, it deduces that ![]() $\tilde X^\varepsilon$ converges in distribution to
$\tilde X^\varepsilon$ converges in distribution to ![]() $\tilde X$ as ɛ → 0.
$\tilde X$ as ɛ → 0.
By employing the Portemanteau theorem [Reference Klenke26, theorem 13.16], we have for any bounded Lipschitz functions ![]() $F:\mathcal{C}^{\beta-\operatorname{hld}}\left([0,T], \mathbb{R}^m\right) \to\mathbb{R}$, that
$F:\mathcal{C}^{\beta-\operatorname{hld}}\left([0,T], \mathbb{R}^m\right) \to\mathbb{R}$, that
 \begin{equation*}\begin{array}{rcl}
|\mathbb{E}[F(\tilde X^{\varepsilon,\delta})]-\mathbb{E}[F(\tilde X)]|&\leqslant& |\mathbb{E}[F(\tilde X^{\varepsilon,\delta})]-\mathbb{E}[F(\tilde X^{\varepsilon})]|+|\mathbb{E}[F(\tilde X^{\varepsilon})]-\mathbb{E}[F(\tilde X)]|\\
&\leqslant& \|F\|_\textrm{Lip}\mathbb{E}[\|\tilde X^{\varepsilon,\delta}-\tilde X^{\varepsilon}\|_{\beta\textrm{-hld}}^2]^{\frac{1}{2}}+\big|\mathbb{E}[F(\tilde X^{\varepsilon})]\\ && -\mathbb{E}[F(\tilde X)]\big|\to 0
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
|\mathbb{E}[F(\tilde X^{\varepsilon,\delta})]-\mathbb{E}[F(\tilde X)]|&\leqslant& |\mathbb{E}[F(\tilde X^{\varepsilon,\delta})]-\mathbb{E}[F(\tilde X^{\varepsilon})]|+|\mathbb{E}[F(\tilde X^{\varepsilon})]-\mathbb{E}[F(\tilde X)]|\\
&\leqslant& \|F\|_\textrm{Lip}\mathbb{E}[\|\tilde X^{\varepsilon,\delta}-\tilde X^{\varepsilon}\|_{\beta\textrm{-hld}}^2]^{\frac{1}{2}}+\big|\mathbb{E}[F(\tilde X^{\varepsilon})]\\ && -\mathbb{E}[F(\tilde X)]\big|\to 0
\end{array}
\end{equation*} as ɛ → 0. Here, ![]() $\|F\|_\textrm{Lip}$ is the Lipschitz constant of F. So we have proved (5.9).
$\|F\|_\textrm{Lip}$ is the Lipschitz constant of F. So we have proved (5.9).
Step 3. By Step 1 and Step 2, for every bounded and continuous function ![]() $\Phi: \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^m)\to \mathbb{R}$, we have that the Laplace lower bound
$\Phi: \mathcal{C}^{\beta-\operatorname{hld}}([0,T],\mathbb{R}^m)\to \mathbb{R}$, we have that the Laplace lower bound
 \begin{equation}
\liminf _{\varepsilon \rightarrow 0} -\varepsilon \log \mathbb{E}\big[e^{-\frac{\Phi(X^{\varepsilon,\delta})}{\varepsilon} }\big] \geq\inf _{\psi:=\mathcal{G}^0(u,v) \in \mathcal{C}^{{\beta-\operatorname{hld}}}([0,T],\mathbb{R}^m)}\left[\Phi(\psi)+I(\psi)\right]
\end{equation}
\begin{equation}
\liminf _{\varepsilon \rightarrow 0} -\varepsilon \log \mathbb{E}\big[e^{-\frac{\Phi(X^{\varepsilon,\delta})}{\varepsilon} }\big] \geq\inf _{\psi:=\mathcal{G}^0(u,v) \in \mathcal{C}^{{\beta-\operatorname{hld}}}([0,T],\mathbb{R}^m)}\left[\Phi(\psi)+I(\psi)\right]
\end{equation}and the Laplace upper bound
 \begin{equation}
\limsup _{\varepsilon \rightarrow 0} -\varepsilon\log \mathbb{E}\big[e^{-\frac{\Phi(X^{\varepsilon,\delta})}{\varepsilon} }\big] \leqslant\inf _{\psi:=\mathcal{G}^0(u,v) \in \mathcal{C}^{{\beta-\operatorname{hld}}}([0,T],\mathbb{R}^m)}\left[\Phi(\psi)+I(\psi)\right]
\end{equation}
\begin{equation}
\limsup _{\varepsilon \rightarrow 0} -\varepsilon\log \mathbb{E}\big[e^{-\frac{\Phi(X^{\varepsilon,\delta})}{\varepsilon} }\big] \leqslant\inf _{\psi:=\mathcal{G}^0(u,v) \in \mathcal{C}^{{\beta-\operatorname{hld}}}([0,T],\mathbb{R}^m)}\left[\Phi(\psi)+I(\psi)\right]
\end{equation}hold and the goodness of rate function I. The precise proof for (5.30)–(5.31) refers to [Reference Inahama, Xu and Yang24, theorem 3.1] as an example.
Hence, our LDP result is concluded by the equivalence between the LDP and Laplace principle at once. This proof is completed.![]() $\square$
$\square$
Acknowledgements
This work was partly supported by the Key International (Regional) Cooperative Research Projects of the NSF of China under Grant No. 12120101002.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.
Proof of proposition 2.8
According to the definition of controlled RP, we have
 \begin{eqnarray}
\|\Psi-\tilde{\Psi}\|_{\beta-\operatorname{hld}} \leqslant C(d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)+|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})),
\end{eqnarray}
\begin{eqnarray}
\|\Psi-\tilde{\Psi}\|_{\beta-\operatorname{hld}} \leqslant C(d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)+|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})),
\end{eqnarray}so it only needs to show (2.10) and (2.11) hold.
Let ![]() $0 \lt \tau \lt T$ and we turn to prove (2.10) holds in the time interval
$0 \lt \tau \lt T$ and we turn to prove (2.10) holds in the time interval ![]() $[0,\tau]$ firstly. To this end, we set
$[0,\tau]$ firstly. To this end, we set  $\mathcal{M}_{[0, \tau]}^1,\mathcal{M}_{[0, \tau]}^2:\mathcal{Q}_{\Xi}^\beta([0, \tau], \mathcal{W})\mapsto \mathcal{Q}_{\Xi}^\beta([0, \tau], \mathcal{W})$ by
$\mathcal{M}_{[0, \tau]}^1,\mathcal{M}_{[0, \tau]}^2:\mathcal{Q}_{\Xi}^\beta([0, \tau], \mathcal{W})\mapsto \mathcal{Q}_{\Xi}^\beta([0, \tau], \mathcal{W})$ by
 \begin{equation}
\begin{array}{rcl}
\mathcal{M}_{[0, \tau]}^1\left(\Psi, \Psi^{\dagger}\right)&=&\left(\int_0^{\cdot} \sigma\left(\Psi_s\right) d \Xi_s, \sigma(\Psi)\right),\\
\mathcal{M}_{[0, \tau]}^2\left(\Psi, \Psi^{\dagger}\right)&=&\left(\int_0^{\cdot} f\left(\Psi_s\right) ds, 0\right)
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\mathcal{M}_{[0, \tau]}^1\left(\Psi, \Psi^{\dagger}\right)&=&\left(\int_0^{\cdot} \sigma\left(\Psi_s\right) d \Xi_s, \sigma(\Psi)\right),\\
\mathcal{M}_{[0, \tau]}^2\left(\Psi, \Psi^{\dagger}\right)&=&\left(\int_0^{\cdot} f\left(\Psi_s\right) ds, 0\right)
\end{array}
\end{equation} and  $(Z, Z^{\dagger}):=\mathcal{M}_{[0, \tau]}^{\xi}:=(\xi, 0)+\mathcal{M}_{[0, \tau]}^1+\mathcal{M}_{[0, \tau]}^2$. Moreover, we stress the fact that the fixed point of
$(Z, Z^{\dagger}):=\mathcal{M}_{[0, \tau]}^{\xi}:=(\xi, 0)+\mathcal{M}_{[0, \tau]}^1+\mathcal{M}_{[0, \tau]}^2$. Moreover, we stress the fact that the fixed point of  $\mathcal{M}_{[0, \tau]}^{\xi}$ is the solution to the (2.9) on the time interval
$\mathcal{M}_{[0, \tau]}^{\xi}$ is the solution to the (2.9) on the time interval ![]() $[0,\tau]$ for
$[0,\tau]$ for ![]() $0 \lt \tau\leqslant T$. Due to the fixed point theorem, we arrive at
$0 \lt \tau\leqslant T$. Due to the fixed point theorem, we arrive at
 \begin{equation}
(\Psi, \sigma(\Psi))=\left(\Psi, \Psi^{\dagger}\right)=\left(Z, Z^{\dagger}\right)=(Z, \sigma(\Psi)).
\end{equation}
\begin{equation}
(\Psi, \sigma(\Psi))=\left(\Psi, \Psi^{\dagger}\right)=\left(Z, Z^{\dagger}\right)=(Z, \sigma(\Psi)).
\end{equation} Abbreviate ![]() $\mathcal{I} \Sigma:=Z_{s, t}$ and
$\mathcal{I} \Sigma:=Z_{s, t}$ and  $\Sigma:=f(\Psi_s)(t-s)+\sigma(\Psi_s)\Xi^1_{s,t}+\sigma^\dagger(\Psi_s)\Xi^2_{s,t}$. Moreover,
$\Sigma:=f(\Psi_s)(t-s)+\sigma(\Psi_s)\Xi^1_{s,t}+\sigma^\dagger(\Psi_s)\Xi^2_{s,t}$. Moreover, ![]() $\mathcal{I} \tilde\Sigma$ and
$\mathcal{I} \tilde\Sigma$ and ![]() $\tilde\Sigma$ could be defined in a similar way with respect to
$\tilde\Sigma$ could be defined in a similar way with respect to ![]() $\tilde{\Psi}$. By some direct computation, we have
$\tilde{\Psi}$. By some direct computation, we have
 \begin{equation}
\begin{array}{rcl}
R_{s, t}^Z&=&Z_{s, t}-Z_s^{\dagger} \Xi_{s, t}\\
&=&\int_s^t f (\Psi_r) dr+\int_s^t \sigma (\Psi_r) d\Xi_r-\sigma (\Psi_s) \Xi_{s, t}\\
&=&(\mathcal{I} \Sigma)_{s, t}-\Sigma_{s,t}+\sigma^\dagger(\Psi_s)\Xi^2_{s,t}+f(\Psi_s)(t-s).
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
R_{s, t}^Z&=&Z_{s, t}-Z_s^{\dagger} \Xi_{s, t}\\
&=&\int_s^t f (\Psi_r) dr+\int_s^t \sigma (\Psi_r) d\Xi_r-\sigma (\Psi_s) \Xi_{s, t}\\
&=&(\mathcal{I} \Sigma)_{s, t}-\Sigma_{s,t}+\sigma^\dagger(\Psi_s)\Xi^2_{s,t}+f(\Psi_s)(t-s).
\end{array}
\end{equation} We set ![]() $\mathcal{Q}:=\Sigma-\tilde\Sigma$. After that, we obtain that
$\mathcal{Q}:=\Sigma-\tilde\Sigma$. After that, we obtain that
 \begin{equation}
\begin{array}{rcl}
|R_{s, t}^Z-R_{s, t}^{\tilde{Z}}|&=&\big|(\mathcal{I} \mathcal{Q})_{s, t}-\mathcal{Q}_{s, t}\big|+\big|\sigma^\dagger(\Psi_s) \Xi^2_{s, t}-\sigma^\dagger(\tilde\Psi_s) \tilde{\Xi}^2_{s, t}\big|\\ &&+\big|(f (\Psi_s)-f (\tilde\Psi_s))(t-s)\big|\\
&\leqslant& C\|\delta \mathcal{Q}\|_{3 \alpha}|t-s|^{3 \beta} +\big|\sigma^\dagger(\Psi_s) \Xi^2_{s, t}-\sigma^\dagger(\tilde\Psi_s) \tilde{\Xi}^2_{s, t}\big|\\
&&+L_f\tau^\beta\|\Psi-\tilde\Psi\|_{\beta-\operatorname{hld}}|t-s|+C|\xi-\tilde{\xi}||t-s|
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
|R_{s, t}^Z-R_{s, t}^{\tilde{Z}}|&=&\big|(\mathcal{I} \mathcal{Q})_{s, t}-\mathcal{Q}_{s, t}\big|+\big|\sigma^\dagger(\Psi_s) \Xi^2_{s, t}-\sigma^\dagger(\tilde\Psi_s) \tilde{\Xi}^2_{s, t}\big|\\ &&+\big|(f (\Psi_s)-f (\tilde\Psi_s))(t-s)\big|\\
&\leqslant& C\|\delta \mathcal{Q}\|_{3 \alpha}|t-s|^{3 \beta} +\big|\sigma^\dagger(\Psi_s) \Xi^2_{s, t}-\sigma^\dagger(\tilde\Psi_s) \tilde{\Xi}^2_{s, t}\big|\\
&&+L_f\tau^\beta\|\Psi-\tilde\Psi\|_{\beta-\operatorname{hld}}|t-s|+C|\xi-\tilde{\xi}||t-s|
\end{array}
\end{equation} where Lf is the Lipschitz coefficient of f and  $\delta \mathcal{Q}_{s, u, t}=R_{s, u}^{\sigma(\tilde{\Psi})} \tilde{\Xi}^1_{u, t}-R_{s, u}^{\sigma(\Psi)} \Xi^1_{u, t}+\sigma^\dagger(\tilde{\Psi})_{s, u} \tilde{\Xi}^2_{u, t}-\sigma^\dagger(\Psi)_{s, u} \Xi^2_{u, t}$.
$\delta \mathcal{Q}_{s, u, t}=R_{s, u}^{\sigma(\tilde{\Psi})} \tilde{\Xi}^1_{u, t}-R_{s, u}^{\sigma(\Psi)} \Xi^1_{u, t}+\sigma^\dagger(\tilde{\Psi})_{s, u} \tilde{\Xi}^2_{u, t}-\sigma^\dagger(\Psi)_{s, u} \Xi^2_{u, t}$.
Furthermore, a straightforward estimate furnishes that
 \begin{equation}
\begin{array}{rcl}
|Z_{s,t}^{\dagger}-\tilde Z_{s,t}^{\dagger}|&=&\big|\sigma({Z})_{s, t}-\sigma(\tilde{Z})_{s, t}\big|\\
&=&\big|\sigma({\Psi})_{s, t}-\sigma(\tilde{\Psi})_{s, t}\big|\\
&=&\big|(\sigma^\dagger({\Psi})_{0, s}+\sigma^\dagger({\Psi})_{0})\Xi_{s,t}-(\sigma^\dagger(\tilde{\Psi})_{0, s}+\sigma^\dagger(\tilde{\Psi})_{0})\tilde{\Xi}_{s,t}+R_{s, t}^{\sigma({\Psi})}\\ &&-R_{s, t}^{\sigma(\tilde{\Psi})}\big|\\
&\leqslant&C|t-s|^\beta\big(|\sigma({\Psi})_{0}-\sigma(\tilde{\Psi})_{0}|+|t-s|^{\alpha-\beta}\|\sigma^\dagger({\Psi})-\sigma^\dagger(\tilde{\Psi})\|_{\beta-\operatorname{hld}}\big.\\
&&\big.+\rho_\alpha(\Xi, \tilde{\Xi})+\|R^{\sigma({\Psi})}-R^{\sigma(\tilde{\Psi})}\|_{2\beta-\operatorname{hld}}\big).
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
|Z_{s,t}^{\dagger}-\tilde Z_{s,t}^{\dagger}|&=&\big|\sigma({Z})_{s, t}-\sigma(\tilde{Z})_{s, t}\big|\\
&=&\big|\sigma({\Psi})_{s, t}-\sigma(\tilde{\Psi})_{s, t}\big|\\
&=&\big|(\sigma^\dagger({\Psi})_{0, s}+\sigma^\dagger({\Psi})_{0})\Xi_{s,t}-(\sigma^\dagger(\tilde{\Psi})_{0, s}+\sigma^\dagger(\tilde{\Psi})_{0})\tilde{\Xi}_{s,t}+R_{s, t}^{\sigma({\Psi})}\\ &&-R_{s, t}^{\sigma(\tilde{\Psi})}\big|\\
&\leqslant&C|t-s|^\beta\big(|\sigma({\Psi})_{0}-\sigma(\tilde{\Psi})_{0}|+|t-s|^{\alpha-\beta}\|\sigma^\dagger({\Psi})-\sigma^\dagger(\tilde{\Psi})\|_{\beta-\operatorname{hld}}\big.\\
&&\big.+\rho_\alpha(\Xi, \tilde{\Xi})+\|R^{\sigma({\Psi})}-R^{\sigma(\tilde{\Psi})}\|_{2\beta-\operatorname{hld}}\big).
\end{array}
\end{equation}As a consequence of [Reference Friz and Hairer16, theorem 4.17] and (A.5)–(A.6), we see that
 \begin{equation}
\begin{array}{rcl}
&&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big) \\ & =&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(Z, Z^{\dagger} ; \tilde{Z}, \tilde{Z}^{\dagger}\big) \\
&=&\|Z^{\dagger}-\tilde Z^{\dagger}\|_{\beta-\operatorname{hld}}+\|R^Z-R^{\tilde{Z}}\|_{2\beta-\operatorname{hld}}\\
& \lesssim& \rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+\tau^\beta d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\sigma(\Psi), {\sigma^\dagger(\Psi)}
; \sigma(\tilde\Psi), {\sigma^\dagger(\tilde\Psi)}\big)\\
&&+L_f\tau^{\beta}\|\Psi-\tilde\Psi\|_{\beta-\operatorname{hld}}.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
&&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big) \\ & =&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(Z, Z^{\dagger} ; \tilde{Z}, \tilde{Z}^{\dagger}\big) \\
&=&\|Z^{\dagger}-\tilde Z^{\dagger}\|_{\beta-\operatorname{hld}}+\|R^Z-R^{\tilde{Z}}\|_{2\beta-\operatorname{hld}}\\
& \lesssim& \rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+\tau^\beta d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\sigma(\Psi), {\sigma^\dagger(\Psi)}
; \sigma(\tilde\Psi), {\sigma^\dagger(\tilde\Psi)}\big)\\
&&+L_f\tau^{\beta}\|\Psi-\tilde\Psi\|_{\beta-\operatorname{hld}}.
\end{array}
\end{equation}Next, with aid of the [Reference Friz and Hairer16, theorem 7.6], we observe that
 \begin{equation}
\begin{array}{rcl}
&&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\sigma(\Psi), {\sigma^\dagger(\Psi)}
; \sigma(\tilde\Psi), {\sigma^\dagger(\tilde\Psi)}\big)\\
& \lesssim& \rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+ d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big).
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
&&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\sigma(\Psi), {\sigma^\dagger(\Psi)}
; \sigma(\tilde\Psi), {\sigma^\dagger(\tilde\Psi)}\big)\\
& \lesssim& \rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+ d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big).
\end{array}
\end{equation} Therefore, by combining (A.1) and (A.7)–(A.8), it deduces that there exists a positive constant ![]() $C_M:=C(M,\alpha,\beta,L_f)$ such that
$C_M:=C(M,\alpha,\beta,L_f)$ such that
 \begin{equation}
\begin{array}{rcl}
&&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big) \\
& \leqslant& C_M\big[\rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+\tau^\beta d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)+\tau^{\beta}\|\Psi-\tilde\Psi\|_{\beta-\operatorname{hld}} \big]\\
& \leqslant& C_M\big[\rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+\tau^\beta d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big) \big]
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
&&d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big) \\
& \leqslant& C_M\big[\rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+\tau^\beta d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)+\tau^{\beta}\|\Psi-\tilde\Psi\|_{\beta-\operatorname{hld}} \big]\\
& \leqslant& C_M\big[\rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|+\tau^\beta d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big) \big]
\end{array}
\end{equation} holds. By taking τ > 0 such that ![]() $C_M\tau^\beta \lt 1/2$, we find
$C_M\tau^\beta \lt 1/2$, we find
 \begin{equation}
d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)
\leqslant C_M(\rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|).
\end{equation}
\begin{equation}
d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)
\leqslant C_M(\rho_\alpha(\Xi, \tilde{\Xi})+|\xi-\tilde{\xi}|).
\end{equation}Then, with (A.1), we arrive at
 \begin{equation}
\begin{array}{rcl}
\|\Psi-\tilde{\Psi}\|_{\beta-\operatorname{hld}} &\leqslant&C(d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)+|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi}))\\
&\leqslant& C_M\big(|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})\big).
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rcl}
\|\Psi-\tilde{\Psi}\|_{\beta-\operatorname{hld}} &\leqslant&C(d_{\Xi, \tilde{\Xi}, 2 \beta}\big(\Psi, \Psi^{\dagger} ; \tilde{\Psi}, \tilde{\Psi}^{\dagger}\big)+|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi}))\\
&\leqslant& C_M\big(|\xi-\tilde{\xi}|+\rho_\alpha(\Xi, \tilde{\Xi})\big).
\end{array}
\end{equation} An iteration argument over ![]() $[0,T]$ furnishes that (2.10) and (2.11) hold at the time interval
$[0,T]$ furnishes that (2.10) and (2.11) hold at the time interval ![]() $[0,T]$. This proof is completed.
$[0,T]$. This proof is completed.![]() ${\square}$
${\square}$