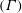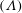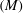1 Introduction
The possibility that solutions of the governing equations for compressible inviscid flows may exhibit jump discontinuities was proposed by Stokes (Reference Stokes1848). Following severe criticism by, among others, Rayleigh, in 1877 the proposal was retracted by Stokes. Arguments in support of shock discontinuities were however provided by Earnshaw (Reference Earnshaw1860) and by Rankine (Reference Rankine1870) and Hugoniot (Reference Hugoniot1887, Reference Hugoniot1889) and form the basis of the present theory of jump discontinuities or shocks. Readers interested in the history of these early developments are referred to the historical reviews of Johnson & Chéret (Reference Johnson and Chéret1998) and Kluwick (Reference Kluwick2018). The main point to be made in this connection has been formulated most clearly in the paper ‘A History of Shock Waves’ by Krehl (Reference Krehl, Ben-Dor, Igra and Lifshitz2001). In summary:
‘The puzzling shock wave, characterised by a stepped wave front, was difficult to accept by early naturalists because it involved the abandonment of the principle ‘Natura non facit saltus’. Surprisingly, however, the problem was tackled neither by experimentalists nor philosophers but rather by mathematical physicists. Jouget wrote: “the shock wave represents a phenomenon of rare peculiarity such that it has been uncovered by the pen of mathematicians, first by Riemann, then by Hugoniot. The experiments followed afterwards”’.
This statement which then applied exclusively to the class of perfect gases now is also known to hold for gases having arbitrary equations of state. This is due to more recent developments starting with the pioneering work by Bethe (Reference Bethe1942). Most importantly he (obviously being unaware of earlier work by Becker (Reference Becker1922)) recognised that shocks may be of expansive rather than compressive type in fluids which exhibit regions of negative isentropic curvature in the pressure, specific volume diagram. In addition he also recognised that this is possible for fluids having large values of specific heat at constant volume (
![]() $c_{v}$
) relative to the universal gas constant (
$c_{v}$
) relative to the universal gas constant (
![]() $R$
), i.e. having complex molecules with a large number of internal degrees of freedom. An estimate based on the van der Waals equation of state indicated that such shocks may form in fluids if
$R$
), i.e. having complex molecules with a large number of internal degrees of freedom. An estimate based on the van der Waals equation of state indicated that such shocks may form in fluids if
![]() $c_{v}/R>17.5$
(a result obtained slightly later also by Zeldovich (Reference Zeldovich1946)). A result which Bethe considered unrealistic. This point of view was contested later by Thompson and coworkers who identified a number of candidates for dense gases which might exhibit negative isentropic curvature in the general neighbourhood of the thermodynamic critical point (see Thompson (Reference Thompson1971) and Thompson & Lambrakis (Reference Thompson and Lambrakis1973)). Measures of isentropic curvature had already been proposed earlier (Duhem Reference Duhem1909) but its non-dimensional version proposed by Thompson (Reference Thompson1971) namely
$c_{v}/R>17.5$
(a result obtained slightly later also by Zeldovich (Reference Zeldovich1946)). A result which Bethe considered unrealistic. This point of view was contested later by Thompson and coworkers who identified a number of candidates for dense gases which might exhibit negative isentropic curvature in the general neighbourhood of the thermodynamic critical point (see Thompson (Reference Thompson1971) and Thompson & Lambrakis (Reference Thompson and Lambrakis1973)). Measures of isentropic curvature had already been proposed earlier (Duhem Reference Duhem1909) but its non-dimensional version proposed by Thompson (Reference Thompson1971) namely
where
![]() $\unicode[STIX]{x1D70C},s$
and
$\unicode[STIX]{x1D70C},s$
and
![]() $c$
are respectively fluid density, entropy and sound speed, is now commonly used. As
$c$
are respectively fluid density, entropy and sound speed, is now commonly used. As
![]() $\unicode[STIX]{x1D6E4}$
plays a predictive role in most areas of compressible flows it is frequently referred to as the fundamental derivative of gas dynamics. When
$\unicode[STIX]{x1D6E4}$
plays a predictive role in most areas of compressible flows it is frequently referred to as the fundamental derivative of gas dynamics. When
![]() $\unicode[STIX]{x1D6E4}$
is small its variation with density
$\unicode[STIX]{x1D6E4}$
is small its variation with density
![]() $\unicode[STIX]{x1D70C}$
becomes important in determining the nature of the flow and this is given by the parameter
$\unicode[STIX]{x1D70C}$
becomes important in determining the nature of the flow and this is given by the parameter
Because of the pioneering research of Bethe, Zel’dovich and Thompson it is now common to identify fluids that exhibit negative
![]() $\unicode[STIX]{x1D6E4}$
regions as BZT-fluids.
$\unicode[STIX]{x1D6E4}$
regions as BZT-fluids.
In passing we mention that theoretical work also suggests a second mechanism which generates states having
![]() $\unicode[STIX]{x1D6E4}<0$
in the two phase region close to the thermodynamic critical point. This second mechanism is associated with the divergence of the isochoric heat capacity as the thermodynamical critical point is approached, see e.g. Kluwick (Reference Kluwick, Ben-Dor, Igra, Elperin and Lifshitz2001) and the more recent study Nannan, Guardone & Colonna (Reference Nannan, Guardone and Colonna2013). In what follows we exclude critical point phenomena and concentrate on effects caused by high molecular complexity in the single phase region.
$\unicode[STIX]{x1D6E4}<0$
in the two phase region close to the thermodynamic critical point. This second mechanism is associated with the divergence of the isochoric heat capacity as the thermodynamical critical point is approached, see e.g. Kluwick (Reference Kluwick, Ben-Dor, Igra, Elperin and Lifshitz2001) and the more recent study Nannan, Guardone & Colonna (Reference Nannan, Guardone and Colonna2013). In what follows we exclude critical point phenomena and concentrate on effects caused by high molecular complexity in the single phase region.
The analysis and results presented in this paper are for fluid flows in the pressure, specific volume (
![]() $V$
) plane close to the
$V$
) plane close to the
![]() $\unicode[STIX]{x1D6E4}=0$
curve. For particular BZT fluids such as PP10 (
$\unicode[STIX]{x1D6E4}=0$
curve. For particular BZT fluids such as PP10 (
![]() $C_{13}F_{22}$
) this curve has been computed based on sophisticated model equations of state. The highlighted gas PP10 has a complex fluorinated molecular structure and has been used as a working fluid in BZT shock tube experiments, (Fergason, Guardone & Argrow Reference Fergason, Guardone and Argrow2003). Qualitative estimates of pressure, specific volume and temperature associated with a negative
$C_{13}F_{22}$
) this curve has been computed based on sophisticated model equations of state. The highlighted gas PP10 has a complex fluorinated molecular structure and has been used as a working fluid in BZT shock tube experiments, (Fergason, Guardone & Argrow Reference Fergason, Guardone and Argrow2003). Qualitative estimates of pressure, specific volume and temperature associated with a negative
![]() $\unicode[STIX]{x1D6E4}$
region have also been obtained for different BZT fluids using various thermodynamic models that includes the Martin–Hou, Soave–Redlich–Kwong and Peng–Robinson model equations of state, see Guardone, Vigevano & Argrow (Reference Guardone, Vigevano and Argrow2004). Strong agreements between computational models are observed and the negative
$\unicode[STIX]{x1D6E4}$
region have also been obtained for different BZT fluids using various thermodynamic models that includes the Martin–Hou, Soave–Redlich–Kwong and Peng–Robinson model equations of state, see Guardone, Vigevano & Argrow (Reference Guardone, Vigevano and Argrow2004). Strong agreements between computational models are observed and the negative
![]() $\unicode[STIX]{x1D6E4}$
region of a BZT fluid is estimated to be within the ranges
$\unicode[STIX]{x1D6E4}$
region of a BZT fluid is estimated to be within the ranges
![]() $0.75<P/P_{c}<1.0$
,
$0.75<P/P_{c}<1.0$
,
![]() $1.4<V/V_{c}<2.5$
and
$1.4<V/V_{c}<2.5$
and
![]() $0.96<T/T_{c}<1.01$
where the subscript
$0.96<T/T_{c}<1.01$
where the subscript
![]() $c$
denotes critical point values. BZT fluid flows in experiments that extend into these ranges, crossing the
$c$
denotes critical point values. BZT fluid flows in experiments that extend into these ranges, crossing the
![]() $\unicode[STIX]{x1D6E4}=0$
curve, are expected to exhibit phenomena similar to those described in this paper.
$\unicode[STIX]{x1D6E4}=0$
curve, are expected to exhibit phenomena similar to those described in this paper.
We should note that by assuming
![]() $\unicode[STIX]{x1D6EC}=O(1)$
we exclude a small region of the
$\unicode[STIX]{x1D6EC}=O(1)$
we exclude a small region of the
![]() $P$
,
$P$
,
![]() $V$
plane lying close to where the
$V$
plane lying close to where the
![]() $\unicode[STIX]{x1D6E4}=0$
curve is tangent to the isentrope. Modelling the flow in this region requires addition terms in the derived model equations similar to those obtained in Kluwick (Reference Kluwick1993) for transonic nozzle flow.
$\unicode[STIX]{x1D6E4}=0$
curve is tangent to the isentrope. Modelling the flow in this region requires addition terms in the derived model equations similar to those obtained in Kluwick (Reference Kluwick1993) for transonic nozzle flow.
Extensive theoretical studies elaborating on the non-classical and often counterintuitive behaviour of BZT fluids, including the possible formation of rarefaction shocks, followed the stimulating work of Thompson (Reference Thompson1971). Early investigations concentrated on unsteady flow phenomena which are not at the core of the present study. Readers interested in this field of research are referred to recent reviews, (Kluwick Reference Kluwick2017, Reference Kluwick2018). The present study focuses on a well-defined specific problem of steady inviscid dense gas flow and, therefore, is not intended to provide a complete account of the rapidly growing literature in general. To put our work in perspective, however, we briefly address important other areas such as unconfined flows, flows past single airfoils as well as nozzle and cascade configurations which have been studied among others by Cramer & Tarkenton (Reference Cramer and Tarkenton1992), Cramer & Fry (Reference Cramer and Fry1993), Kluwick (Reference Kluwick1993), Monaco, Cramer & Watson (Reference Monaco, Cramer and Watson1997), Wang & Rusak (Reference Wang and Rusak1999), Rusak & Wang (Reference Rusak and Wang2000), Cinella & Congedo (Reference Cinella and Congedo2005), Congedo, Corre & Cinella (Reference Congedo, Corre and Cinella2007), Guardone, Zamfirescu & Colonna (Reference Guardone, Zamfirescu and Colonna2010), Gori, Vimercati & Guardone (Reference Gori, Vimercati and Guardone2017), Vimercati, Kluwick & Guardone (Reference Vimercati, Kluwick and Guardone2018).
Unfortunately, efforts to support the theoretical predictions that rarefaction shocks may form in negative
![]() $\unicode[STIX]{x1D6E4}$
fluids by experimental evidence have failed so far. But although fully developed single phase planar rarefaction shocks have not yet been observed in shock tubes, some recent work carried out at the FAST (Flexible Asymmetric Shock Tube) facility of the DTU in Delft points to the existence of ‘embryo’ negative
$\unicode[STIX]{x1D6E4}$
fluids by experimental evidence have failed so far. But although fully developed single phase planar rarefaction shocks have not yet been observed in shock tubes, some recent work carried out at the FAST (Flexible Asymmetric Shock Tube) facility of the DTU in Delft points to the existence of ‘embryo’ negative
![]() $\unicode[STIX]{x1D6E4}$
shocks, (Mathijssen Reference Mathijssen2017). This work, however, also reveals significant challenges for the search of the ‘holy grail’ of rarefaction shocks using shock tubes. Thermodynamic states which can be realised at present have
$\unicode[STIX]{x1D6E4}$
shocks, (Mathijssen Reference Mathijssen2017). This work, however, also reveals significant challenges for the search of the ‘holy grail’ of rarefaction shocks using shock tubes. Thermodynamic states which can be realised at present have
![]() $|\unicode[STIX]{x1D6E4}|\ll 1$
, i.e. isentropes just barely enter the negative
$|\unicode[STIX]{x1D6E4}|\ll 1$
, i.e. isentropes just barely enter the negative
![]() $\unicode[STIX]{x1D6E4}$
region. Rarefaction shocks expected to form thus will be weak and extremely sensitive to disturbances resulting from deviations from one-dimensional flow conditions caused primarily by fast opening devices such as punched diaphragms or valves. In contrast, experimental investigations of shocks under steady flow conditions will not be contaminated by such disturbances and therefore represent a promising alternative – hence the motivation for the present paper where the canonical problem of shock reflection is of primary interest. The associated wave reflection pattern then results from two building blocks – oblique shock fronts and centred wave fans which simplifies both the theoretical analysis and the interpretation of experimental data.
$\unicode[STIX]{x1D6E4}$
region. Rarefaction shocks expected to form thus will be weak and extremely sensitive to disturbances resulting from deviations from one-dimensional flow conditions caused primarily by fast opening devices such as punched diaphragms or valves. In contrast, experimental investigations of shocks under steady flow conditions will not be contaminated by such disturbances and therefore represent a promising alternative – hence the motivation for the present paper where the canonical problem of shock reflection is of primary interest. The associated wave reflection pattern then results from two building blocks – oblique shock fronts and centred wave fans which simplifies both the theoretical analysis and the interpretation of experimental data.
A complete picture of phenomena to be expected in the limit of small disturbances with special emphasis on the transonic flow regime where dense gas effects are most pronounced has recently been given by Kluwick & Cox (Reference Kluwick and Cox2018), while fully nonlinear solutions have been obtained numerically by Vimercati et al. (Reference Vimercati, Kluwick and Guardone2018). Their results are for an oblique shock in an unconfined flow and have to be supplemented with solutions of another canonical problem dealing with the reflection of disturbances from an opposing solid wall to finally provide a realistic picture of phenomena arising in confined geometries of practical importance.
The present study of the reflection problem is based on the assumptions formulated in Kluwick & Cox (Reference Kluwick and Cox2018) which are briefly summarised in § 2. Extensions required to treat shock reflections are also derived in § 2, where it is shown that solutions depend on a set of three non-dimensional parameters which characterise, respectively, the strength of the incoming shock, the Mach number range where transonic effects are of importance and the influence of dense gas behaviour. Based on these parameters different regimes of regular and irregular reflections are identified and analysed in §§ 3 and 4. Finally § 5 summarises the main achievements of the present work and addresses open questions which require further efforts.
2 Formulation
We consider the problem of steady shock wave reflection in a channel as sketched in figure 1. Uniform supersonic flow is incident on a thin wedge located in a channel wall and the shock wave generated is reflected off the opposite facing wall. The channel is of width
![]() $H$
, the wedge has an inclination angle
$H$
, the wedge has an inclination angle
![]() $\unicode[STIX]{x1D703}\approx a\unicode[STIX]{x1D6FF}\ll 1$
and the upstream supersonic uniform flow
$\unicode[STIX]{x1D703}\approx a\unicode[STIX]{x1D6FF}\ll 1$
and the upstream supersonic uniform flow
![]() $\boldsymbol{u}=(u_{\infty },0)$
is aligned with the
$\boldsymbol{u}=(u_{\infty },0)$
is aligned with the
![]() $x$
axis and the channel axis. The wedge geometry introduces a small asymptotic parameter
$x$
axis and the channel axis. The wedge geometry introduces a small asymptotic parameter
![]() $\unicode[STIX]{x1D6FF}>0$
for the problem with the order-one parameter
$\unicode[STIX]{x1D6FF}>0$
for the problem with the order-one parameter
![]() $a$
providing, in the asymptotic model, a measure of the inclination of the wedge. The flow generated by the wedge is described in terms of the velocity
$a$
providing, in the asymptotic model, a measure of the inclination of the wedge. The flow generated by the wedge is described in terms of the velocity
![]() $\boldsymbol{u}=(u,v)$
non-dimensionalised with the free-stream velocity and involves a perturbed velocity with components (
$\boldsymbol{u}=(u,v)$
non-dimensionalised with the free-stream velocity and involves a perturbed velocity with components (
![]() $\tilde{u} ,\tilde{v}$
) given by
$\tilde{u} ,\tilde{v}$
) given by
where we have assumed that
![]() $\unicode[STIX]{x1D6E4}$
given by (1.1) evaluated in the free-stream reference state and denoted by
$\unicode[STIX]{x1D6E4}$
given by (1.1) evaluated in the free-stream reference state and denoted by
![]() $\unicode[STIX]{x1D6E4}_{\infty }$
is
$\unicode[STIX]{x1D6E4}_{\infty }$
is
![]() $O(\unicode[STIX]{x1D6FF}^{1/2})$
. This perturbed flow
$O(\unicode[STIX]{x1D6FF}^{1/2})$
. This perturbed flow
![]() $(\tilde{u} ,\tilde{v})$
can be shown to satisfy the transonic small disturbance equations formulated here for BZT fluids as
$(\tilde{u} ,\tilde{v})$
can be shown to satisfy the transonic small disturbance equations formulated here for BZT fluids as
with the scaled non-dimensional channel coordinates
which account for rapid variations in the
![]() $x$
coordinate compared to
$x$
coordinate compared to
![]() $y$
, consistent with the near normal orientation of incident and reflected shocks.
$y$
, consistent with the near normal orientation of incident and reflected shocks.

Figure 1. Flow geometry for reflection of a plane shock generated by a wedge located at
![]() $x=0,y=0$
with inclination
$x=0,y=0$
with inclination
![]() $a\unicode[STIX]{x1D6FF}>0$
in a channel of width
$a\unicode[STIX]{x1D6FF}>0$
in a channel of width
![]() $H$
.
$H$
.
The order-one similarity parameters
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{2}$
are given by
$K_{2}$
are given by
where
![]() $K_{1}$
is a rescaled transonic similarity parameter with
$K_{1}$
is a rescaled transonic similarity parameter with
![]() $M_{\infty }=u_{\infty }/c_{\infty }$
the Mach number of the unperturbed upstream flow defined using
$M_{\infty }=u_{\infty }/c_{\infty }$
the Mach number of the unperturbed upstream flow defined using
![]() $c_{\infty }$
the upstream unperturbed sound speed. The parameter
$c_{\infty }$
the upstream unperturbed sound speed. The parameter
![]() $K_{2}$
with
$K_{2}$
with
![]() $\unicode[STIX]{x1D6EC}_{\infty }=\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70C}_{\infty },s_{\infty })=O(1)$
measures the relevant importance of cubic and quadratic nonlinearity, see Cramer & Tarkenton (Reference Cramer and Tarkenton1992) for details. The choice of scalings leading to (2.3)–(2.6) ensure that the formulation reduces to the classical case when
$\unicode[STIX]{x1D6EC}_{\infty }=\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70C}_{\infty },s_{\infty })=O(1)$
measures the relevant importance of cubic and quadratic nonlinearity, see Cramer & Tarkenton (Reference Cramer and Tarkenton1992) for details. The choice of scalings leading to (2.3)–(2.6) ensure that the formulation reduces to the classical case when
![]() $\unicode[STIX]{x1D6E4}_{\infty }=O(1)$
see Cole & Cook (Reference Cole and Cook1986). Equations (2.3)–(2.6) were first derived in Cramer & Tarkenton (Reference Cramer and Tarkenton1992) in the context of steady transonic flow over thin airfoils and more recently in Kluwick & Cox (Reference Kluwick and Cox2018) for flow over a wedge.
$\unicode[STIX]{x1D6E4}_{\infty }=O(1)$
see Cole & Cook (Reference Cole and Cook1986). Equations (2.3)–(2.6) were first derived in Cramer & Tarkenton (Reference Cramer and Tarkenton1992) in the context of steady transonic flow over thin airfoils and more recently in Kluwick & Cox (Reference Kluwick and Cox2018) for flow over a wedge.
To the authors’ knowledge evolution equations exhibiting both quadratic and cubic nonlinearity were first studied for the simpler case of unsteady planar waves, e.g. Cramer & Kluwick (Reference Cramer and Kluwick1984). Extensions to more complex geometries are discussed in Kluwick (Reference Kluwick1991) which also includes an example of purely cubic nonlinearity, see also Lee-Bapty & Crighton (Reference Lee-Bapty and Crighton1987).
Just as in the classical case the modified transonic small disturbance equations (2.3), (2.4) arises as a distinguished asymptotic limit for the Euler equations leading to the estimates
and differing from the classical results due to the assumption that
![]() $\unicode[STIX]{x1D6E4}_{\infty }=O(\unicode[STIX]{x1D6FF}^{1/2})$
and
$\unicode[STIX]{x1D6E4}_{\infty }=O(\unicode[STIX]{x1D6FF}^{1/2})$
and
![]() $\unicode[STIX]{x1D6EC}_{\infty }=O(1)$
which ensures that both
$\unicode[STIX]{x1D6EC}_{\infty }=O(1)$
which ensures that both
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{2}$
are
$K_{2}$
are
![]() $O(1)$
. Consistent with the asymptotic scalings in (2.7) we construct solutions of (2.3), (2.4) satisfying the asymptotic boundary conditions
$O(1)$
. Consistent with the asymptotic scalings in (2.7) we construct solutions of (2.3), (2.4) satisfying the asymptotic boundary conditions
The basic building blocks used to construct the flows generated include shock waves and centred simple waves. If we first consider shock waves: denoting the jump in a flow property
![]() $\unicode[STIX]{x1D6FD}$
across a shock as
$\unicode[STIX]{x1D6FD}$
across a shock as
![]() $[\unicode[STIX]{x1D6FD}]=\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FD}_{1}$
, where subscripts
$[\unicode[STIX]{x1D6FD}]=\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FD}_{1}$
, where subscripts
![]() $1$
and
$1$
and
![]() $2$
reference upstream and downstream states, then it is readily established that across a shock we have
$2$
reference upstream and downstream states, then it is readily established that across a shock we have
Details can be found in Kluwick & Cox (Reference Kluwick and Cox2018). It is useful to introduce a scaled Mach number for the flows associated with a shock jump. As shown in Kluwick & Cox (Reference Kluwick and Cox2018) the local Mach number
![]() $M$
satisfies
$M$
satisfies
With supersonic flow upstream, shock jumps described by (2.9) may involve supersonic–supersonic or supersonic–subsonic jump transitions as calculated from (2.10).
The so-called shock polar curve is a plot derived from (2.9) of all possible downstream states (
![]() $\tilde{u} _{2},\tilde{v}_{2}$
) that can be connected to a given fixed upstream state (
$\tilde{u} _{2},\tilde{v}_{2}$
) that can be connected to a given fixed upstream state (
![]() $\tilde{u} _{1},\tilde{v}_{1}$
) by a shock jump. This is illustrated in figure 2(a) for the case
$\tilde{u} _{1},\tilde{v}_{1}$
) by a shock jump. This is illustrated in figure 2(a) for the case
![]() $K_{1}=1,K_{2}=-0.8$
and upstream state
$K_{1}=1,K_{2}=-0.8$
and upstream state
![]() $\tilde{u} _{1}=0,\tilde{v}_{1}=0$
i.e. we plot
$\tilde{u} _{1}=0,\tilde{v}_{1}=0$
i.e. we plot
With decreasing values of the downstream velocity
![]() $\tilde{u} _{2}$
, i.e. increasing shock strength, we see a shock transition
$\tilde{u} _{2}$
, i.e. increasing shock strength, we see a shock transition
![]() $S_{1}$
from a supersonic–supersonic shock to a supersonic–subsonic shock
$S_{1}$
from a supersonic–supersonic shock to a supersonic–subsonic shock
![]() $S_{2}$
.
$S_{2}$
.
If the shock surface is located at
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{s}(\unicode[STIX]{x1D709})$
then integrating (2.3), (2.4) across the shock discontinuity leads to a shock slope given by
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{s}(\unicode[STIX]{x1D709})$
then integrating (2.3), (2.4) across the shock discontinuity leads to a shock slope given by
 $$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D702}_{s}}{\text{d}\unicode[STIX]{x1D709}}=\mp \frac{1}{\displaystyle \sqrt{-\frac{[j]}{[\tilde{u} ]}}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D702}_{s}}{\text{d}\unicode[STIX]{x1D709}}=\mp \frac{1}{\displaystyle \sqrt{-\frac{[j]}{[\tilde{u} ]}}},\end{eqnarray}$$
where we observe the useful geometric construction that the slope of the chord in the
![]() $(\tilde{u} ,\tilde{v})$
hodograph plane, connecting upstream states (
$(\tilde{u} ,\tilde{v})$
hodograph plane, connecting upstream states (
![]() $\tilde{u} _{1},\tilde{v}_{1}$
) to downstream states (
$\tilde{u} _{1},\tilde{v}_{1}$
) to downstream states (
![]() $\tilde{u} _{2},\tilde{v}_{2}$
), given by
$\tilde{u} _{2},\tilde{v}_{2}$
), given by
![]() $[\tilde{v}]/[\tilde{u} ]$
in (2.9) is orthogonal to the shock slope
$[\tilde{v}]/[\tilde{u} ]$
in (2.9) is orthogonal to the shock slope
![]() $\text{d}\unicode[STIX]{x1D702}_{s}/\text{d}\unicode[STIX]{x1D709}$
in the
$\text{d}\unicode[STIX]{x1D702}_{s}/\text{d}\unicode[STIX]{x1D709}$
in the
![]() $(\unicode[STIX]{x1D702},\unicode[STIX]{x1D709})$
plane with appropriately chosen signs. This construction is illustrated in figure 2(a) and the orientation of the shocks
$(\unicode[STIX]{x1D702},\unicode[STIX]{x1D709})$
plane with appropriately chosen signs. This construction is illustrated in figure 2(a) and the orientation of the shocks
![]() $S_{1},S_{2}$
in the physical
$S_{1},S_{2}$
in the physical
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
plane is shown in figures 2(b) and 2(c).
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
plane is shown in figures 2(b) and 2(c).

Figure 2. (a) Shock polar for
![]() $K_{1}=1,K_{2}=-0.8$
with the construction of shocks
$K_{1}=1,K_{2}=-0.8$
with the construction of shocks
![]() $S_{1},S_{2},S_{so},S_{3}$
of increasing strength. The shock
$S_{1},S_{2},S_{so},S_{3}$
of increasing strength. The shock
![]() $S_{so}$
corresponds to downstream sonic conditions
$S_{so}$
corresponds to downstream sonic conditions
![]() $\tilde{u} _{2}=\tilde{u} _{so}$
and the possible shock
$\tilde{u} _{2}=\tilde{u} _{so}$
and the possible shock
![]() $S_{3}$
violates the speed ordering condition. In (b–d) the corresponding shocks in the
$S_{3}$
violates the speed ordering condition. In (b–d) the corresponding shocks in the
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
plane are plotted with the shocks shown in (a) to be orthogonal to the shock chord (Rayleigh line) in the polar plot.
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
plane are plotted with the shocks shown in (a) to be orthogonal to the shock chord (Rayleigh line) in the polar plot.
Not all jump discontinuities described by (2.9) lead to physically acceptable shock solutions. We require in addition the imposing of criteria to eliminate non-physical solutions. A fundamental requirement is that that entropy does not decrease across a shock i.e.
![]() $[s]\geqslant 0$
which leads to the constraint
$[s]\geqslant 0$
which leads to the constraint
![]() $\tilde{u} _{2}\leqslant \tilde{u} _{1}$
, see Kluwick & Cox (Reference Kluwick and Cox2018). Only portions of the solution curve of (2.9) satisfying the entropy jump condition are plotted in figure 2(a). It was shown by Cramer & Kluwick (Reference Cramer and Kluwick1984) in the context of BZT fluids with
$\tilde{u} _{2}\leqslant \tilde{u} _{1}$
, see Kluwick & Cox (Reference Kluwick and Cox2018). Only portions of the solution curve of (2.9) satisfying the entropy jump condition are plotted in figure 2(a). It was shown by Cramer & Kluwick (Reference Cramer and Kluwick1984) in the context of BZT fluids with
![]() $|\unicode[STIX]{x1D6E4}|\ll 1$
and
$|\unicode[STIX]{x1D6E4}|\ll 1$
and
![]() $\unicode[STIX]{x1D6EC}=O(1)$
that the entropy condition is too weak to rule out certain inadmissible supersonic–supersonic shock discontinuities, where inadmissibility is understood in terms of shocks for which no thermoviscous profile can be constructed. It was shown that in addition a wave speed ordering condition must be imposed.
$\unicode[STIX]{x1D6EC}=O(1)$
that the entropy condition is too weak to rule out certain inadmissible supersonic–supersonic shock discontinuities, where inadmissibility is understood in terms of shocks for which no thermoviscous profile can be constructed. It was shown that in addition a wave speed ordering condition must be imposed.
We develop this condition, applicable to supersonic–supersonic shock jumps, by first noting that characteristics of (2.3), (2.4) have slopes in the
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
plane given by
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
plane given by
 $$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D702}}{\text{d}\unicode[STIX]{x1D709}}=\mp \frac{1}{\displaystyle \sqrt{-\frac{\text{d}j}{\text{d}\tilde{u} }}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D702}}{\text{d}\unicode[STIX]{x1D709}}=\mp \frac{1}{\displaystyle \sqrt{-\frac{\text{d}j}{\text{d}\tilde{u} }}},\end{eqnarray}$$
and we then require that the shock slope lies between the characteristic slopes of flow states generating the shock i.e.
Results are stated here for forward orientated waves (i.e.
![]() $\text{d}\unicode[STIX]{x1D702}/\text{d}\unicode[STIX]{x1D709}>0$
) and holding for
$\text{d}\unicode[STIX]{x1D702}/\text{d}\unicode[STIX]{x1D709}>0$
) and holding for
![]() $-\text{d}j/\text{d}\tilde{u} |_{1,2}>0$
which ensures that the characteristics are real and the flow is supersonic ahead and behind the shock. Shocks where one of the equalities in (2.14) holds are termed ‘sonic shocks’, see Kluwick (Reference Kluwick, Ben-Dor, Igra, Elperin and Lifshitz2001). Equation (2.14) is recognised as the Lax entropy condition and when one of the equalities is satisfied the shocks are also referred to as a left or right contact shocks, see Dafermos (Reference Dafermos2005). The possibility of ‘sonic shocks’ (contact shocks) occurring has no classical gas dynamics counterpart – the shock condition given in (2.14) reduces on setting
$-\text{d}j/\text{d}\tilde{u} |_{1,2}>0$
which ensures that the characteristics are real and the flow is supersonic ahead and behind the shock. Shocks where one of the equalities in (2.14) holds are termed ‘sonic shocks’, see Kluwick (Reference Kluwick, Ben-Dor, Igra, Elperin and Lifshitz2001). Equation (2.14) is recognised as the Lax entropy condition and when one of the equalities is satisfied the shocks are also referred to as a left or right contact shocks, see Dafermos (Reference Dafermos2005). The possibility of ‘sonic shocks’ (contact shocks) occurring has no classical gas dynamics counterpart – the shock condition given in (2.14) reduces on setting
![]() $K_{2}=0$
to
$K_{2}=0$
to
which is the well-known classical ideal gas case, with strict inequalities applying, see Cole & Cook (Reference Cole and Cook1986). Also and in contrast to the non-classical gas case this wave speed ordering condition when applied is simply equivalent to the selection rule
![]() $[s]\geqslant 0$
rather than a further constraint.
$[s]\geqslant 0$
rather than a further constraint.
In figure 2(a) the shock labelled
![]() $S_{3}$
represents jumps to downstream states
$S_{3}$
represents jumps to downstream states
![]() $\tilde{u} _{2},\tilde{v}_{2}$
(plotted as a dashed curve) constructed from (2.11) which satisfies
$\tilde{u} _{2},\tilde{v}_{2}$
(plotted as a dashed curve) constructed from (2.11) which satisfies
![]() $[s]>0$
or equivalently
$[s]>0$
or equivalently
![]() $M_{2}<M_{1}$
but violates the speed ordering condition (2.14). There is a limiting shock strength
$M_{2}<M_{1}$
but violates the speed ordering condition (2.14). There is a limiting shock strength
![]() $\tilde{u} _{so}$
where ‘sonic’ conditions hold downstream and represented by shock
$\tilde{u} _{so}$
where ‘sonic’ conditions hold downstream and represented by shock
![]() $S_{so}$
in figures 2(a) and 2(d). The supersonic state
$S_{so}$
in figures 2(a) and 2(d). The supersonic state
![]() $\tilde{u} _{so}$
is determined from the downstream equality in (2.14) i.e. setting
$\tilde{u} _{so}$
is determined from the downstream equality in (2.14) i.e. setting
which leads to
![]() $\tilde{u} _{2}=\tilde{u} _{so}=3/2k_{2}$
. The construction in figure 2 also indicates that when sonic conditions hold the shock chord is tangential to the shock polar curve – a straightforward result to show. Inadmissible shocks then are associated with shock chords that cut the shock polar as seen for
$\tilde{u} _{2}=\tilde{u} _{so}=3/2k_{2}$
. The construction in figure 2 also indicates that when sonic conditions hold the shock chord is tangential to the shock polar curve – a straightforward result to show. Inadmissible shocks then are associated with shock chords that cut the shock polar as seen for
![]() $S_{3}$
.
$S_{3}$
.
The second important class of elementary solutions, aside from shocks, are simple waves – identified as flows associated with only one family of characteristics. Looking for solutions depending on only a single variable
![]() $r(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
i.e.
$r(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
i.e.
![]() $\tilde{u} =\tilde{u} (r),\tilde{v}=\tilde{v}(r)$
we rewrite (2.3), (2.4) as
$\tilde{u} =\tilde{u} (r),\tilde{v}=\tilde{v}(r)$
we rewrite (2.3), (2.4) as
Solutions for
![]() $(r_{\unicode[STIX]{x1D709}},r_{\unicode[STIX]{x1D702}})$
exist then only if
$(r_{\unicode[STIX]{x1D709}},r_{\unicode[STIX]{x1D702}})$
exist then only if
The curve
![]() $\tilde{u} (r),\tilde{v}(r)$
parameterised by the ‘phase’ variable
$\tilde{u} (r),\tilde{v}(r)$
parameterised by the ‘phase’ variable
![]() $r$
has slope
$r$
has slope
which is orthogonal to the straight line of constant phase given by
 $$\begin{eqnarray}\left.\frac{\text{d}\unicode[STIX]{x1D702}}{\text{d}\unicode[STIX]{x1D709}}\right|_{r}=\mp \frac{1}{\displaystyle \sqrt{-\frac{\text{d}j}{\text{d}\tilde{u} }(r)}},\end{eqnarray}$$
$$\begin{eqnarray}\left.\frac{\text{d}\unicode[STIX]{x1D702}}{\text{d}\unicode[STIX]{x1D709}}\right|_{r}=\mp \frac{1}{\displaystyle \sqrt{-\frac{\text{d}j}{\text{d}\tilde{u} }(r)}},\end{eqnarray}$$
which is the characteristic slope (compare with (2.13)). The similarity with (2.9) and (2.12) is clear. A relevant example of a simple wave is a centred wave fan with rays
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D702}}{\unicode[STIX]{x1D709}}=\frac{1}{\displaystyle \sqrt{-\frac{\text{d}j}{\text{d}\tilde{u} }(r)}},\quad r_{a}\leqslant r\leqslant r_{b},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D702}}{\unicode[STIX]{x1D709}}=\frac{1}{\displaystyle \sqrt{-\frac{\text{d}j}{\text{d}\tilde{u} }(r)}},\quad r_{a}\leqslant r\leqslant r_{b},\end{eqnarray}$$
which provides the continuous transition from one uniform flow
![]() $(\tilde{u} (r_{a}),\tilde{v}(r_{a}))$
to another uniform flow
$(\tilde{u} (r_{a}),\tilde{v}(r_{a}))$
to another uniform flow
![]() $(\tilde{u} (r_{b}),\tilde{v}(r_{b}))$
past sharp corners. Details of shock and wave fan constructions can be found in Kluwick & Cox (Reference Kluwick and Cox2018).
$(\tilde{u} (r_{b}),\tilde{v}(r_{b}))$
past sharp corners. Details of shock and wave fan constructions can be found in Kluwick & Cox (Reference Kluwick and Cox2018).
With these basic building blocks we can consider the problem of shock reflection. This problem has been the subject of extensive research in ideal gas dynamics with theoretical results going back to Mach (Reference Mach1878), Neumann (Reference von Neumann and Taub1963a
), Neumann (Reference von Neumann and Taub1963b
) and early experiments in Bleakney & Taub (Reference Bleakney and Taub1949). With the wedge angle measured by the parameter
![]() $a$
we have for small angles the regular reflection pattern of figure 1. As is well known in the classical case
$a$
we have for small angles the regular reflection pattern of figure 1. As is well known in the classical case
![]() $K_{2}=0$
with increasing angle
$K_{2}=0$
with increasing angle
![]() $a$
the shock reflection undergoes so-called irregular reflection off the channel wall. This involves the detachment of both the incident and reflected shock from the surface and the generation of a third and stronger shock which remains attached to the surface. The point at which the three shocks meet is termed the triple point
$a$
the shock reflection undergoes so-called irregular reflection off the channel wall. This involves the detachment of both the incident and reflected shock from the surface and the generation of a third and stronger shock which remains attached to the surface. The point at which the three shocks meet is termed the triple point
![]() $(T)$
. As indicated in figure 3 the flow also includes an expansion fan and a slip line (not drawn as not realisable in the irrotational flow model considered here). The inclusion of the wave fan is significant and helps resolve the so-called von Neumann paradox that three intersecting shocks are seen in experiments but unsupported by theoretical analysis. The inclusion of the wave fan is due to Guderley (Reference Guderley1947), Guderley (Reference Guderley1957) a result that was overlooked for many decades until recent work by Hunter & Brio (Reference Hunter and Brio1997), Hunter & Brio (Reference Hunter and Brio2000), Hunter & Tesdall (Reference Hunter and Tesdall2004) on the unsteady transonic flow equations (the time-dependent form of equations (2.3) and (2.4) with
$(T)$
. As indicated in figure 3 the flow also includes an expansion fan and a slip line (not drawn as not realisable in the irrotational flow model considered here). The inclusion of the wave fan is significant and helps resolve the so-called von Neumann paradox that three intersecting shocks are seen in experiments but unsupported by theoretical analysis. The inclusion of the wave fan is due to Guderley (Reference Guderley1947), Guderley (Reference Guderley1957) a result that was overlooked for many decades until recent work by Hunter & Brio (Reference Hunter and Brio1997), Hunter & Brio (Reference Hunter and Brio2000), Hunter & Tesdall (Reference Hunter and Tesdall2004) on the unsteady transonic flow equations (the time-dependent form of equations (2.3) and (2.4) with
![]() $K_{2}=0$
) and by Vasil’ev (Reference Vasil’ev, Papailiou, Tsahalis, Periaux, Hirsch and Pandolfi1998) and Vasil’ev & Krajko (Reference Vasil’ev and Krajko1999) for the compressible Euler equations. The structure in the neighbourhood of the triple point is complex and revealed in the numerical results of Tesdall & Hunter (Reference Tesdall and Hunter2002) and Tesdall, Sanders & Popivanov (Reference Tesdall, Sanders and Popivanov2015) and the experimental results of Cachucho & Skews (Reference Cachucho and Skews2012). These results are summarised in the sketch of figure 4. Behind the triple point
$K_{2}=0$
) and by Vasil’ev (Reference Vasil’ev, Papailiou, Tsahalis, Periaux, Hirsch and Pandolfi1998) and Vasil’ev & Krajko (Reference Vasil’ev and Krajko1999) for the compressible Euler equations. The structure in the neighbourhood of the triple point is complex and revealed in the numerical results of Tesdall & Hunter (Reference Tesdall and Hunter2002) and Tesdall, Sanders & Popivanov (Reference Tesdall, Sanders and Popivanov2015) and the experimental results of Cachucho & Skews (Reference Cachucho and Skews2012). These results are summarised in the sketch of figure 4. Behind the triple point
![]() $T=T_{1}$
of figure 3 there is a sequence of supersonic patches each patch terminated by a shock leading to multiple triple points
$T=T_{1}$
of figure 3 there is a sequence of supersonic patches each patch terminated by a shock leading to multiple triple points
![]() $T_{2},T_{3}\ldots \,$
.
$T_{2},T_{3}\ldots \,$
.

Figure 3. Flow geometry for irregular reflection of a plane shock generated by a wedge located at
![]() $x=0,y=0$
with inclination
$x=0,y=0$
with inclination
![]() $a\unicode[STIX]{x1D6FF}>0$
in a channel of width
$a\unicode[STIX]{x1D6FF}>0$
in a channel of width
![]() $H$
.
$H$
.

Figure 4. Sketch of the complex reflection structure due to Tesdall & Hunter (Reference Tesdall and Hunter2002). Near the leading triple point
![]() $T_{1}$
there is a cascade of supersonic patches each patch terminated by a shock (in red) leading to multiple triple points
$T_{1}$
there is a cascade of supersonic patches each patch terminated by a shock (in red) leading to multiple triple points
![]() $T_{2},T_{3}\ldots \,$
. Blue lines denote centred wave fans generated at each triple point and dashed curves denote sonic curves bounding the supersonic patches.
$T_{2},T_{3}\ldots \,$
. Blue lines denote centred wave fans generated at each triple point and dashed curves denote sonic curves bounding the supersonic patches.
In this paper we consider shock reflection for non-ideal gases using the modified small disturbance equations (2.3) and (2.4). In a previous paper (Kluwick & Cox Reference Kluwick and Cox2018) the authors consider the flow over a ramp and in this follow-on paper we consider a shock generated by such a flow impinging now on a reflecting surface as encountered in a channel with a wedge.
3 Regular reflection
In Kluwick & Cox (Reference Kluwick and Cox2018) we identified distinctly different flows in the parameter space
![]() $(K_{1}>0,K_{2})$
for the parameter ranges
$(K_{1}>0,K_{2})$
for the parameter ranges
![]() $K_{2}<-1/K_{1}$
,
$K_{2}<-1/K_{1}$
,
![]() $-1/K_{1}<K_{2}<-3/4K_{1}$
,
$-1/K_{1}<K_{2}<-3/4K_{1}$
,
![]() $-3/4K_{1}<K_{2}\leqslant 0$
and
$-3/4K_{1}<K_{2}\leqslant 0$
and
![]() $K_{2}>0$
. For each of these intervals we now consider an incident shock reflection problem with the emphasis on regular reflection. We then show in § 4 that when regular reflection breaks down with increased ramp angle (or equivalently incident shock strength) the pure triple shock structure does not exist. This result extends a well-known result for ideal gases.
$K_{2}>0$
. For each of these intervals we now consider an incident shock reflection problem with the emphasis on regular reflection. We then show in § 4 that when regular reflection breaks down with increased ramp angle (or equivalently incident shock strength) the pure triple shock structure does not exist. This result extends a well-known result for ideal gases.
We note that descriptions of flows in this paper will assume that
![]() $\unicode[STIX]{x1D6E4}_{\infty }$
is positive. This is to simplify the interpretation of the results obtained but is not a requirement for the analysis. As a consequence shocks are compressive and wave fans are expansive. The results are easily reinterpreted for an expanding channel with expansion shocks and compression wave fans associated with
$\unicode[STIX]{x1D6E4}_{\infty }$
is positive. This is to simplify the interpretation of the results obtained but is not a requirement for the analysis. As a consequence shocks are compressive and wave fans are expansive. The results are easily reinterpreted for an expanding channel with expansion shocks and compression wave fans associated with
![]() $\unicode[STIX]{x1D6E4}_{\infty }<0$
.
$\unicode[STIX]{x1D6E4}_{\infty }<0$
.
3.1 Case:
 $K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
$K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
This case is qualitatively similar to the classical case which is included as a special case on setting
![]() $K_{2}=0$
. The wave configuration for regular shock reflection is shown in figure 1 where a steady incident shock wave generated by a wedge reflects from a plane boundary. A reflected shock wave, formed at the point of intersection with the incident shock wave and the channel wall, then returns the flow which is deflected towards the wall by the incident shock to a flow parallel again to the wall.
$K_{2}=0$
. The wave configuration for regular shock reflection is shown in figure 1 where a steady incident shock wave generated by a wedge reflects from a plane boundary. A reflected shock wave, formed at the point of intersection with the incident shock wave and the channel wall, then returns the flow which is deflected towards the wall by the incident shock to a flow parallel again to the wall.

Figure 5. (a) Shock polars (incident polar
![]() $I$
, reflected polar
$I$
, reflected polar
![]() $R$
) for regular reflection of a plane shock generated by a wedge with inclination
$R$
) for regular reflection of a plane shock generated by a wedge with inclination
![]() $a$
for
$a$
for
![]() $K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
$K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
![]() $K_{1}=1,K_{2}=-0.7$
. The incident shock
$K_{1}=1,K_{2}=-0.7$
. The incident shock
![]() $i$
deflects the flow to
$i$
deflects the flow to
![]() $\tilde{u} _{1},\tilde{v}_{1}$
and a weak reflected shock
$\tilde{u} _{1},\tilde{v}_{1}$
and a weak reflected shock
![]() $r$
generates supersonic flow
$r$
generates supersonic flow
![]() $\tilde{u} _{2_{w}},\tilde{v}_{2}=0$
downstream of the shock – flow which is parallel to the channel wall. The incident and reflected shocks are depicted in (b) in the
$\tilde{u} _{2_{w}},\tilde{v}_{2}=0$
downstream of the shock – flow which is parallel to the channel wall. The incident and reflected shocks are depicted in (b) in the
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
plane using the construction indicated in (a). The shock reflection point is labelled as
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
plane using the construction indicated in (a). The shock reflection point is labelled as
![]() $(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.
$(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.
The shock polars describing regular reflection are shown in figure 5(a) and represent the repeated application of (2.9) to the incident and reflected shocks. Without loss of generality we can assume that the upstream perturbed flow for the reflection problem is
![]() $\tilde{u} =0,\tilde{v}=0$
. So the incident shock is described by possible downstream states (
$\tilde{u} =0,\tilde{v}=0$
. So the incident shock is described by possible downstream states (
![]() $\tilde{u} ,\tilde{v}$
) satisfying
$\tilde{u} ,\tilde{v}$
) satisfying
and plotted as curve
![]() $I$
in figure 5(a). A wedge inclination angle of magnitude
$I$
in figure 5(a). A wedge inclination angle of magnitude
![]() $a$
generates, as shown, two possible downstream flows satisfying the wedge boundary condition
$a$
generates, as shown, two possible downstream flows satisfying the wedge boundary condition
![]() $\tilde{v}=a\operatorname{sign}\unicode[STIX]{x1D6E4}_{\infty }$
, see (2.8b
). We will consider a weak incident shock jump to a supersonic state
$\tilde{v}=a\operatorname{sign}\unicode[STIX]{x1D6E4}_{\infty }$
, see (2.8b
). We will consider a weak incident shock jump to a supersonic state
![]() $\tilde{u} _{1},\tilde{v}_{1}=a\operatorname{sign}\unicode[STIX]{x1D6E4}_{\infty }$
located on the incident shock polar
$\tilde{u} _{1},\tilde{v}_{1}=a\operatorname{sign}\unicode[STIX]{x1D6E4}_{\infty }$
located on the incident shock polar
![]() $I$
in figure 5(a).
$I$
in figure 5(a).
The reflected shock then is described by downstream states
![]() $(\tilde{u} _{2},\tilde{v}_{2})$
with states
$(\tilde{u} _{2},\tilde{v}_{2})$
with states
![]() $(\tilde{u} _{1},\tilde{v}_{1})$
upstream. This reflected shock polar derived from (2.9) is given by
$(\tilde{u} _{1},\tilde{v}_{1})$
upstream. This reflected shock polar derived from (2.9) is given by
The reflected shock polar
![]() $R$
intersects the
$R$
intersects the
![]() $\tilde{v}=0$
axis at two values of
$\tilde{v}=0$
axis at two values of
![]() $\tilde{u} _{2}$
both corresponding to possible downstream flow states. We distinguish these two downstream states as in one case generating a weak shock connecting typically to supersonic flow downstream
$\tilde{u} _{2}$
both corresponding to possible downstream flow states. We distinguish these two downstream states as in one case generating a weak shock connecting typically to supersonic flow downstream
![]() $(\tilde{u} _{2_{w}},\tilde{v}_{2}=0)$
and in the other case generating a strong shock connecting always to a subsonic flow downstream
$(\tilde{u} _{2_{w}},\tilde{v}_{2}=0)$
and in the other case generating a strong shock connecting always to a subsonic flow downstream
![]() $(\tilde{u} _{2_{s}},\tilde{v}_{2}=0)$
. Which state is realised in practice depends critically on the boundary conditions downstream and the reader is encouraged to see the discussion in Kluwick & Cox (Reference Kluwick and Cox2018) for more details. It is the weak shock certainly that is commonly observed in experiments and depicted in figure 5. The incident and reflected shocks have slopes given by (2.12) and are plotted in figure 5(b) in the asymptotic coordinate system
$(\tilde{u} _{2_{s}},\tilde{v}_{2}=0)$
. Which state is realised in practice depends critically on the boundary conditions downstream and the reader is encouraged to see the discussion in Kluwick & Cox (Reference Kluwick and Cox2018) for more details. It is the weak shock certainly that is commonly observed in experiments and depicted in figure 5. The incident and reflected shocks have slopes given by (2.12) and are plotted in figure 5(b) in the asymptotic coordinate system
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. We have indicated in figure 5(a) the construction leading to the determination of the shock slopes in figure 5(b) which implements (2.12).
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. We have indicated in figure 5(a) the construction leading to the determination of the shock slopes in figure 5(b) which implements (2.12).

Figure 6. (a) Shock polar for regular reflection of a plane shock generated by a wedge with inclination
![]() $a_{s}$
for
$a_{s}$
for
![]() $K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
$K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
![]() $K_{1}=1,K_{2}=-0.7$
. A weak reflected shock generates sonic flow
$K_{1}=1,K_{2}=-0.7$
. A weak reflected shock generates sonic flow
![]() $\tilde{u} _{2_{w}},\tilde{v}_{2}=0$
which is parallel to the channel wall. The incident (
$\tilde{u} _{2_{w}},\tilde{v}_{2}=0$
which is parallel to the channel wall. The incident (
![]() $i$
) and reflected shock (
$i$
) and reflected shock (
![]() $r$
) are depicted in (b). The shock reflection point is labelled as
$r$
) are depicted in (b). The shock reflection point is labelled as
![]() $(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.
$(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.

Figure 7. (a) Shock polar for regular reflection of a plane shock generated by a wedge with inclination
![]() $a>a_{s}$
for
$a>a_{s}$
for
![]() $K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
$K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
![]() $K_{1}=1,K_{2}=-0.7$
. The incident shock
$K_{1}=1,K_{2}=-0.7$
. The incident shock
![]() $I$
deflects the flow to
$I$
deflects the flow to
![]() $\tilde{u} _{1},\tilde{v}_{1}$
and a weak reflected shock generates subsonic flow
$\tilde{u} _{1},\tilde{v}_{1}$
and a weak reflected shock generates subsonic flow
![]() $\tilde{u} _{2_{w}},\tilde{v}_{2}=0$
which is parallel to the channel wall. The incident and reflected shocks are depicted in (b). The shock reflection point is labelled as
$\tilde{u} _{2_{w}},\tilde{v}_{2}=0$
which is parallel to the channel wall. The incident and reflected shocks are depicted in (b). The shock reflection point is labelled as
![]() $(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.
$(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.
The regular reflection pattern shown in figure 5 holds for small wedge inclination angles. As the wedge angle is increased the weak downstream shock state associated with the reflected shock eventually becomes sonic with
![]() $M=1$
. The value of
$M=1$
. The value of
![]() $a$
at which this occurs is denoted by
$a$
at which this occurs is denoted by
![]() $a_{s}$
. The shock polars for this case are shown in figure 6(a) and the incident and reflected shocks in the (
$a_{s}$
. The shock polars for this case are shown in figure 6(a) and the incident and reflected shocks in the (
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
) plane are shown in figure 6(b). With increasing
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
) plane are shown in figure 6(b). With increasing
![]() $a>a_{s}$
the weak shock now describes a jump to subsonic downstream states as shown in figure 7 and with further increases in wedge angle
$a>a_{s}$
the weak shock now describes a jump to subsonic downstream states as shown in figure 7 and with further increases in wedge angle
![]() $a$
eventually the weak and strong downstream states coalesce. This gives a detachment wedge angle
$a$
eventually the weak and strong downstream states coalesce. This gives a detachment wedge angle
![]() $a=a_{d}$
such that for values of
$a=a_{d}$
such that for values of
![]() $a>a_{d}$
regular reflection becomes impossible. For
$a>a_{d}$
regular reflection becomes impossible. For
![]() $a>a_{d}$
the flow after any reflected shock is still positive towards the wall and the downstream
$a>a_{d}$
the flow after any reflected shock is still positive towards the wall and the downstream
![]() $\tilde{v}=0$
boundary condition cannot be satisfied by any point on the reflected shock polar, see figure 8.
$\tilde{v}=0$
boundary condition cannot be satisfied by any point on the reflected shock polar, see figure 8.

Figure 8. Shock polar for reflection of a plane shock generated by a wedge with inclination
![]() $a>a_{d}$
for
$a>a_{d}$
for
![]() $K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
$K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
![]() $K_{1}=1,K_{2}=-0.7$
. No reflected shock can return the fluid flow to downstream parallel channel flow.
$K_{1}=1,K_{2}=-0.7$
. No reflected shock can return the fluid flow to downstream parallel channel flow.
It is possible in the ideal gas case (
![]() $K_{2}=0$
) to evaluate
$K_{2}=0$
) to evaluate
![]() $a_{s}$
and
$a_{s}$
and
![]() $a_{d}$
explicitly and a straightforward calculation gives
$a_{d}$
explicitly and a straightforward calculation gives
3.2 Case:
 $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
In the previous case the shock reflection problem led to flows similar to the classical case with
![]() $\unicode[STIX]{x1D6EC}_{\infty }=0$
(
$\unicode[STIX]{x1D6EC}_{\infty }=0$
(
![]() $K_{2}=0$
). With decreasing values of
$K_{2}=0$
). With decreasing values of
![]() $K_{2}$
and so larger negative values of
$K_{2}$
and so larger negative values of
![]() $\unicode[STIX]{x1D6EC}_{\infty }$
the shock reflection problem begins to show features that have no counterpart in ideal gas dynamics.
$\unicode[STIX]{x1D6EC}_{\infty }$
the shock reflection problem begins to show features that have no counterpart in ideal gas dynamics.
For small wedge angles the incident and reflected shock polar plots are given in figure 9(a) for
![]() $\tilde{u} _{1}=-0.05$
,
$\tilde{u} _{1}=-0.05$
,
![]() $K_{1}=1$
and
$K_{1}=1$
and
![]() $K_{2}=-0.8$
. The construction is as already described in the previous case in § 3.1. The polar plots terminate now not with normal orientated shocks but with sonic conditions, i.e. shocks of increased strength would result in the shock chord cutting the shock polar – these are excluded. It is clear that the reflected shock polar intersects the
$K_{2}=-0.8$
. The construction is as already described in the previous case in § 3.1. The polar plots terminate now not with normal orientated shocks but with sonic conditions, i.e. shocks of increased strength would result in the shock chord cutting the shock polar – these are excluded. It is clear that the reflected shock polar intersects the
![]() $\tilde{v}=0$
axes now only once to give a unique reflection shock with a supersonic downstream state returning the deflected flow to parallel channel flow. With increasing wedge angle we have a three shock solution shown in figure 10 involving now an additional subsonic downstream flow labelled
$\tilde{v}=0$
axes now only once to give a unique reflection shock with a supersonic downstream state returning the deflected flow to parallel channel flow. With increasing wedge angle we have a three shock solution shown in figure 10 involving now an additional subsonic downstream flow labelled
![]() $\tilde{u} _{3}$
as well as the two-shock solution similar to the classical ideal gas reflections.
$\tilde{u} _{3}$
as well as the two-shock solution similar to the classical ideal gas reflections.

Figure 9. (a) Shock polar for regular reflection of a plane shock generated by a wedge with inclination
![]() $a$
for
$a$
for
![]() $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
![]() $K_{1}=1,K_{2}=-0.8$
. The incident shock generated on the incident shock polar
$K_{1}=1,K_{2}=-0.8$
. The incident shock generated on the incident shock polar
![]() $I$
deflects the flow to
$I$
deflects the flow to
![]() $\tilde{u} _{1},\tilde{v}_{1}$
with
$\tilde{u} _{1},\tilde{v}_{1}$
with
![]() $\tilde{u} _{1}=-0.05$
and a reflected supersonic shock returns the flow parallel to the channel wall. The incident shock
$\tilde{u} _{1}=-0.05$
and a reflected supersonic shock returns the flow parallel to the channel wall. The incident shock
![]() $(i)$
and reflected sonic shock
$(i)$
and reflected sonic shock
![]() $(r)$
are depicted in (b). The shock reflection point is at
$(r)$
are depicted in (b). The shock reflection point is at
![]() $(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.
$(\unicode[STIX]{x1D709}_{s},\unicode[STIX]{x1D702}_{s})$
.

Figure 10. Shock polar for regular reflection of a plane shock generated by a wedge with inclination
![]() $a$
for
$a$
for
![]() $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
![]() $K_{1}=1,K_{2}=-0.8$
. The incident shock generated on the incident shock polar
$K_{1}=1,K_{2}=-0.8$
. The incident shock generated on the incident shock polar
![]() $I$
deflects the flow to
$I$
deflects the flow to
![]() $\tilde{u} _{1},\tilde{v}_{1}$
with
$\tilde{u} _{1},\tilde{v}_{1}$
with
![]() $\tilde{u} _{1}=-0.12175$
. Reflection shocks are possible to three downstream states a weak shock
$\tilde{u} _{1}=-0.12175$
. Reflection shocks are possible to three downstream states a weak shock
![]() $\tilde{u} _{2_{w}}$
and as included in the inset two strong subsonic shock states
$\tilde{u} _{2_{w}}$
and as included in the inset two strong subsonic shock states
![]() $\tilde{u} _{2_{s}}$
and
$\tilde{u} _{2_{s}}$
and
![]() $\tilde{u} _{3}$
.
$\tilde{u} _{3}$
.
As the wedge angle continues to increase the flow scenarios associated with the reflected shock jumps to
![]() $\tilde{u} _{3}$
become more complicated as shown in the reflected shock polar plots of figure 11 which should be compared to the inset in figure 10. The downstream state
$\tilde{u} _{3}$
become more complicated as shown in the reflected shock polar plots of figure 11 which should be compared to the inset in figure 10. The downstream state
![]() $\tilde{u} _{3}$
with increasing angle (i.e. decreasing
$\tilde{u} _{3}$
with increasing angle (i.e. decreasing
![]() $\tilde{u} _{1}$
) eventually becomes supersonic and then with further increases the reflected shock is a downstream sonic shock and shock state
$\tilde{u} _{1}$
) eventually becomes supersonic and then with further increases the reflected shock is a downstream sonic shock and shock state
![]() $\tilde{u} _{3}$
is replaced by a sonic shock to
$\tilde{u} _{3}$
is replaced by a sonic shock to
![]() $\tilde{u} _{so}$
and a centred fan structure returning the flow to parallel channel flow. This latter scenario is shown in figure 12(a) for
$\tilde{u} _{so}$
and a centred fan structure returning the flow to parallel channel flow. This latter scenario is shown in figure 12(a) for
![]() $\tilde{u} _{1}=-0.13185$
with the three possible reflection flows one of which is the compound shock/fan structure. The centred wave fan is constructed from (2.20) (with the appropriate sign) which we integrate from
$\tilde{u} _{1}=-0.13185$
with the three possible reflection flows one of which is the compound shock/fan structure. The centred wave fan is constructed from (2.20) (with the appropriate sign) which we integrate from
![]() $(\tilde{u} _{so},\tilde{v}_{so})$
to
$(\tilde{u} _{so},\tilde{v}_{so})$
to
![]() $(\tilde{u} _{3},0)$
. In figure 12(b) the reflected sonic shock
$(\tilde{u} _{3},0)$
. In figure 12(b) the reflected sonic shock
![]() $r$
and the attached wave fan rays terminating at
$r$
and the attached wave fan rays terminating at
![]() $\tilde{u} _{3}$
are plotted for this latter case where we have used the shock slope condition (2.12) and the characteristic ray equation (2.22).
$\tilde{u} _{3}$
are plotted for this latter case where we have used the shock slope condition (2.12) and the characteristic ray equation (2.22).

Figure 11. Section of reflection polar
![]() $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
![]() $K_{1}=1,K_{2}=-0.8$
. The transition is shown to a compound shock/fan structure as the wedge angle increases (or
$K_{1}=1,K_{2}=-0.8$
. The transition is shown to a compound shock/fan structure as the wedge angle increases (or
![]() $\tilde{u} _{1}$
decreases) leading to the downstream state
$\tilde{u} _{1}$
decreases) leading to the downstream state
![]() $\tilde{u} _{3}$
.
$\tilde{u} _{3}$
.

Figure 12. (a) Shock polar for regular reflection of a plane shock generated by a wedge with inclination
![]() $a$
for
$a$
for
![]() $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
![]() $K_{1}=1,K_{2}=-0.8$
. The incident shock generated on the incident shock polar
$K_{1}=1,K_{2}=-0.8$
. The incident shock generated on the incident shock polar
![]() $I$
deflects the flow to
$I$
deflects the flow to
![]() $\tilde{u} _{1},\tilde{v}_{1}$
with
$\tilde{u} _{1},\tilde{v}_{1}$
with
![]() $\tilde{u} _{1}=-0.13185$
. Reflection shocks are possible to three downstream states a weak shock
$\tilde{u} _{1}=-0.13185$
. Reflection shocks are possible to three downstream states a weak shock
![]() $\tilde{u} _{2_{w}}$
a strong subsonic shock
$\tilde{u} _{2_{w}}$
a strong subsonic shock
![]() $\tilde{u} _{2_{s}}$
and a compound sonic shock
$\tilde{u} _{2_{s}}$
and a compound sonic shock
![]() $\tilde{u} _{so}$
and wave fan to
$\tilde{u} _{so}$
and wave fan to
![]() $\tilde{u} _{3}$
. The sonic shock (
$\tilde{u} _{3}$
. The sonic shock (
![]() $r$
) and rays for the attached fan are shown in (b).
$r$
) and rays for the attached fan are shown in (b).
Shock behaviour described by figure 12 does not persist as the wedge angle continues to increase. The compound downstream shock/wave fan structure requires that the sonic shock involves a jump transition to supersonic flow downstream. A shock bifurcation occurs when the wedge angle increases so that the incident shock involves a jump to
At this point the reflected sonic shock is normal to the channel wall and describes a jump to sonic (
![]() $M=1$
) downstream flow. The shock polar plot for this bifurcating flow is shown in figure 13. For increasing wedge angles so that
$M=1$
) downstream flow. The shock polar plot for this bifurcating flow is shown in figure 13. For increasing wedge angles so that
![]() $\tilde{u} _{1}<(1-2\sqrt{1+K_{1}K_{2}})/K_{2}$
the compound shock/fan flow is now no longer possible and the shock polars describe a classical reflection pattern involving the transition, with increasing wedge angle, from a strong subsonic and weak supersonic reflected shock to two subsonic reflected shocks as shown by the shock polar curves in figure 14 for
$\tilde{u} _{1}<(1-2\sqrt{1+K_{1}K_{2}})/K_{2}$
the compound shock/fan flow is now no longer possible and the shock polars describe a classical reflection pattern involving the transition, with increasing wedge angle, from a strong subsonic and weak supersonic reflected shock to two subsonic reflected shocks as shown by the shock polar curves in figure 14 for
![]() $\tilde{u} _{1}=-0.257$
.
$\tilde{u} _{1}=-0.257$
.
Non-classical behaviour involving a compound sonic shock/wave fan occurs over a narrow range of incident shock strengths (or wedge angles). For the particular flow described with
![]() $K_{1}=1$
and
$K_{1}=1$
and
![]() $K_{2}=-0.8$
the existence of a third solution branch occurs in the interval
$K_{2}=-0.8$
the existence of a third solution branch occurs in the interval

Figure 13. Shock polar for strong reflected shocks for
![]() $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
![]() $K_{1}=1,K_{2}=-0.8$
. A non-classical reflection shock/fan solution is obtained for
$K_{1}=1,K_{2}=-0.8$
. A non-classical reflection shock/fan solution is obtained for
![]() $\tilde{u} _{1}=(1-2\sqrt{1+K_{1}K_{2}})/K_{2}$
involving a normal orientated sonic reflection shock and an attached fan with a transition to
$\tilde{u} _{1}=(1-2\sqrt{1+K_{1}K_{2}})/K_{2}$
involving a normal orientated sonic reflection shock and an attached fan with a transition to
![]() $\tilde{u} _{3}$
downstream.
$\tilde{u} _{3}$
downstream.

Figure 14. Shock polar for
![]() $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
![]() $K_{1}=1$
,
$K_{1}=1$
,
![]() $K_{2}=-0.8$
. Two classical subsonic solutions
$K_{2}=-0.8$
. Two classical subsonic solutions
![]() $\tilde{u} _{2_{w}}$
and
$\tilde{u} _{2_{w}}$
and
![]() $\tilde{u} _{2_{s}}$
are obtained for
$\tilde{u} _{2_{s}}$
are obtained for
![]() $\tilde{u} _{1}=-0.257$
.
$\tilde{u} _{1}=-0.257$
.

Figure 15. Shock polar for regular reflection of a plane shock generated by a wedge with inclination
![]() $a$
for
$a$
for
![]() $K_{1}>0,K_{2}<-1/K_{1}$
. Results are for
$K_{1}>0,K_{2}<-1/K_{1}$
. Results are for
![]() $K_{1}=1,K_{2}=-1.2$
. Small wedge angles lead to a classical regular reflection shock. Larger wedge angles lead to a sonic shock/wave fan configuration. Wedge angles with
$K_{1}=1,K_{2}=-1.2$
. Small wedge angles lead to a classical regular reflection shock. Larger wedge angles lead to a sonic shock/wave fan configuration. Wedge angles with
![]() $a$
greater than
$a$
greater than
![]() $a\operatorname{sign}\unicode[STIX]{x1D6E4}_{\infty }=-(1/K_{2})\sqrt{K_{1}+2/3K_{2}}$
result in a reflected wave fan only.
$a\operatorname{sign}\unicode[STIX]{x1D6E4}_{\infty }=-(1/K_{2})\sqrt{K_{1}+2/3K_{2}}$
result in a reflected wave fan only.
3.3 Case:
 $K_{1}>0,K_{2}<-1/K_{1}$
$K_{1}>0,K_{2}<-1/K_{1}$
In the previous cases the shock reflection problem has multiple solutions. In contrast the shock configuration is unique for
![]() $K_{2}<-1/K_{1}$
. We will consider values of
$K_{2}<-1/K_{1}$
. We will consider values of
![]() $a$
less than
$a$
less than
which is the wedge angle, as shown in figure 15, at which an incident shock becomes sonic and beyond which the incident flow consists of a compound sonic shock/wave fan structure. We have for small wedge angles a classical regular reflection shock configuration as seen in figure 15. With increasing wedge angle the reflected shock consists of a sonic shock/wave fan configuration and as the wedge angle increases further the reflected shock strength decreases until with
![]() $a$
greater than
$a$
greater than
the incident shock generates a reflected wave fan only. The analysis used to plot figure 15 is that already described in §§ 3.1 and 3.2.
3.4 Case:
 $K_{1}>0,K_{2}>0$
$K_{1}>0,K_{2}>0$
From a careful reading of Kluwick & Cox (Reference Kluwick and Cox2018) the only relevant flow is associated with negative downstream
![]() $\tilde{u}$
values. The shock polars are qualitatively similar to the classical case and the reflection problem can be analysed in a similar manner. We do not provide details of this case.
$\tilde{u}$
values. The shock polars are qualitatively similar to the classical case and the reflection problem can be analysed in a similar manner. We do not provide details of this case.

Figure 16. (a) Sketch of the shock geometry in the
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
plane associated with a pure triple point construction. The incident shock
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
plane associated with a pure triple point construction. The incident shock
![]() $(i)$
, reflected shock
$(i)$
, reflected shock
![]() $(r)$
and Mach stem
$(r)$
and Mach stem
![]() $(m)$
intersect at the triple point (
$(m)$
intersect at the triple point (
![]() $T$
). (b) Shock polars for irregular reflection of a plane shock generated by a wedge with inclination
$T$
). (b) Shock polars for irregular reflection of a plane shock generated by a wedge with inclination
![]() $a>a_{d}$
for
$a>a_{d}$
for
![]() $K_{1}>0,3/4K_{1}<K_{2}<0$
. The incident shock
$K_{1}>0,3/4K_{1}<K_{2}<0$
. The incident shock
![]() $i$
deflects the flow to
$i$
deflects the flow to
![]() $\tilde{u} _{2},\tilde{v}_{2}$
and a weak reflected shock (
$\tilde{u} _{2},\tilde{v}_{2}$
and a weak reflected shock (
![]() $r$
) generates supersonic flow
$r$
) generates supersonic flow
![]() $\tilde{u} _{3},\tilde{v}_{3}$
. The pure triple point construction in (a) would require that
$\tilde{u} _{3},\tilde{v}_{3}$
. The pure triple point construction in (a) would require that
![]() $\tilde{u} _{3},\tilde{v}_{3}$
coincides with the point
$\tilde{u} _{3},\tilde{v}_{3}$
coincides with the point
![]() $D$
on the incident shock polar.
$D$
on the incident shock polar.
4 Irregular reflection
It is a well-known result that in planar steady flows a pure triple shock structure does not exist i.e. you cannot have three shocks intersecting with constants states between them. This result is discussed, for example, in Courant & Friedrichs (Reference Courant and Friedrichs1948), Neumann (Reference von Neumann and Taub1963a
), Neumann (Reference von Neumann and Taub1963b
) and Henderson & Menikoff (Reference Henderson and Menikoff1998). More recently in Serre (Reference Serre, Friedlander and Serre2007) a proof is presented that is independent of any assumption on the equation of state of the gas. A corresponding result for the unsteady transonic small disturbance equation can be found in Tabak & Rosales (Reference Tabak and Rosales1994). The result presented here is for steady flow of the modified transonic small disturbance equation and is based on the geometry of the shock polar curves. In figure 16(a) we show the shock geometry associated with a pure triple shock with the reflected shock (
![]() $r$
) and incident shock (
$r$
) and incident shock (
![]() $i$
) both forward facing. Both shocks intersect a third shock – the so-called Mach stem
$i$
) both forward facing. Both shocks intersect a third shock – the so-called Mach stem
![]() $(m)$
at the triple point
$(m)$
at the triple point
![]() $(T)$
. In figure 16(b) we show the plot of the reflected polar when
$(T)$
. In figure 16(b) we show the plot of the reflected polar when
![]() $a>a_{d}$
as illustrated for
$a>a_{d}$
as illustrated for
![]() $K_{2}$
in the parameter range
$K_{2}$
in the parameter range
![]() $-3/4K_{1}<K_{2}<0$
. A shock from state
$-3/4K_{1}<K_{2}<0$
. A shock from state
![]() $(\tilde{u} _{1}=0,\tilde{v}_{1}=0)$
to state
$(\tilde{u} _{1}=0,\tilde{v}_{1}=0)$
to state
![]() $(\tilde{u} _{2},\tilde{v}_{2})$
on the incident shock polar is followed by a second shock from
$(\tilde{u} _{2},\tilde{v}_{2})$
on the incident shock polar is followed by a second shock from
![]() $(\tilde{u} _{2},\tilde{v}_{2})$
to
$(\tilde{u} _{2},\tilde{v}_{2})$
to
![]() $(\tilde{u} _{3},\tilde{v}_{3})$
where
$(\tilde{u} _{3},\tilde{v}_{3})$
where
![]() $(\tilde{u} _{3},\tilde{v}_{3})$
lies on the reflected shock polar. The requirement that a triple shock arrangement is possible would require that the reflected shock polar intersects the incident shock polar at
$(\tilde{u} _{3},\tilde{v}_{3})$
lies on the reflected shock polar. The requirement that a triple shock arrangement is possible would require that the reflected shock polar intersects the incident shock polar at
![]() $(\tilde{u} _{3},\tilde{v}_{3})$
generating a third jump from
$(\tilde{u} _{3},\tilde{v}_{3})$
generating a third jump from
![]() $(0,0)$
to
$(0,0)$
to
![]() $(\tilde{u} _{3},\tilde{v}_{3})$
. This does not occur as seen in figure 16(b) – a result that we can prove holds more generally.
$(\tilde{u} _{3},\tilde{v}_{3})$
. This does not occur as seen in figure 16(b) – a result that we can prove holds more generally.
The incident shock polar for
![]() $(\tilde{u_{1}}=0,\tilde{v_{1}}=0)$
is given by the curve
$(\tilde{u_{1}}=0,\tilde{v_{1}}=0)$
is given by the curve
which gives all flow states (
![]() $\tilde{u} ,\tilde{v}(\tilde{u} )$
) that can be connected to
$\tilde{u} ,\tilde{v}(\tilde{u} )$
) that can be connected to
![]() $(0,0)$
by an incident shock. For a given state
$(0,0)$
by an incident shock. For a given state
![]() $\tilde{v}_{2}=\tilde{v}(\tilde{u} _{2})$
we construct then the reflected shock polar which describes all flows which can be connected to
$\tilde{v}_{2}=\tilde{v}(\tilde{u} _{2})$
we construct then the reflected shock polar which describes all flows which can be connected to
![]() $(\tilde{u_{2}},\tilde{v_{2}})$
by a reflected shock. These are the flow states
$(\tilde{u_{2}},\tilde{v_{2}})$
by a reflected shock. These are the flow states
 $$\begin{eqnarray}\displaystyle & \displaystyle \tilde{v}(\tilde{u} )=-\tilde{u_{2}}\sqrt{K_{1}+\tilde{u_{2}}-\frac{K_{2}}{3}\tilde{u_{2}}^{2}}-(\tilde{u} -\tilde{u_{2}})\sqrt{K_{1}+\tilde{u} +\tilde{u_{2}}-\frac{K_{2}}{3}(\tilde{u} ^{2}+\tilde{u} \tilde{u} _{2}+\tilde{u} _{2}^{2})}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \tilde{u} _{e}\leqslant \tilde{u} <\tilde{u} _{2},\hphantom{\tilde{u_{2}}K_{1}+\tilde{u_{2}}-\frac{K_{2}}{3}\tilde{u_{2}}^{2}-(\tilde{u} -\tilde{u_{2}})\frac{K_{2}}{3}(\tilde{u} ^{2}+\tilde{u} \tilde{u} _{2}+\tilde{u} _{2}^{2})} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{v}(\tilde{u} )=-\tilde{u_{2}}\sqrt{K_{1}+\tilde{u_{2}}-\frac{K_{2}}{3}\tilde{u_{2}}^{2}}-(\tilde{u} -\tilde{u_{2}})\sqrt{K_{1}+\tilde{u} +\tilde{u_{2}}-\frac{K_{2}}{3}(\tilde{u} ^{2}+\tilde{u} \tilde{u} _{2}+\tilde{u} _{2}^{2})}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \tilde{u} _{e}\leqslant \tilde{u} <\tilde{u} _{2},\hphantom{\tilde{u_{2}}K_{1}+\tilde{u_{2}}-\frac{K_{2}}{3}\tilde{u_{2}}^{2}-(\tilde{u} -\tilde{u_{2}})\frac{K_{2}}{3}(\tilde{u} ^{2}+\tilde{u} \tilde{u} _{2}+\tilde{u} _{2}^{2})} & \displaystyle\end{eqnarray}$$
and depicted as the labelled curve
![]() $C_{1}$
in figure 16(b). We have assumed here that the reflected shock is a forward pointing shock. Now we require that the incident shock curve given by (4.1) lies above the reflected shock curve (4.2). It is readily shown that this reduces to the inequality
$C_{1}$
in figure 16(b). We have assumed here that the reflected shock is a forward pointing shock. Now we require that the incident shock curve given by (4.1) lies above the reflected shock curve (4.2). It is readily shown that this reduces to the inequality
which is true providing
This inequality which is trivially true for
![]() $K_{2}=0$
holds in the two cases
$K_{2}=0$
holds in the two cases
![]() $-1/K_{1}<K_{2}<-3/4K_{1}$
and
$-1/K_{1}<K_{2}<-3/4K_{1}$
and
![]() $-3/4K_{1}<K_{2}\leqslant 0$
where we can show that
$-3/4K_{1}<K_{2}\leqslant 0$
where we can show that
For the remaining
![]() $K_{2}>0$
case as we require that that the flow downstream of the incident shock is supersonic this excludes sonic incident shocks. The remaining flows have
$K_{2}>0$
case as we require that that the flow downstream of the incident shock is supersonic this excludes sonic incident shocks. The remaining flows have
![]() $\tilde{u} +\tilde{u} _{2}<0$
and so inequality (4.4) is trivially satisfied.
$\tilde{u} +\tilde{u} _{2}<0$
and so inequality (4.4) is trivially satisfied.
An important consequence of this result is the von Neumann paradox. For ideal gases numerical results and experiments show that for certain parameters the fluid flow appears to be described by three shocks separated by constant states which contradicts the theoretical results. A resolution of this paradox is the scenario given by Tesdall & Hunter (Reference Tesdall and Hunter2002), Tesdall et al. (Reference Tesdall, Sanders and Popivanov2015) where numerical experiments on a fine grid show that there is a supersonic region behind the triple point, which consists of a sequence of supersonic patches, shocks, wave fans and multiple triple points. The numerical results do not indicate whether there are finitely many such triple points or not.
We can provide analysis that suggests a similar construction holds in the dense gas case. Hunter & Brio (Reference Hunter and Brio2000) proposed the shock configuration shown in figure 3 where as well as an incident shock, reflected shock and Mach stem there is a centred simple wave behind the reflected shock. The incident, reflected and Mach shocks are all forward facing and the wave fan is backward facing. Given the upstream state
![]() $(\tilde{u} =0,\tilde{v}=0)$
, the wedge angle
$(\tilde{u} =0,\tilde{v}=0)$
, the wedge angle
![]() $a$
and the flow behind the reflected shock
$a$
and the flow behind the reflected shock
![]() $\tilde{u} _{2}$
this configuration can be uniquely constructed. An argument presented in Guderley (Reference Guderley1957) suggests that the flow behind the reflected shock is sonic. This leads to the shock polar/characteristic construction shown in figure 17 for the case
$\tilde{u} _{2}$
this configuration can be uniquely constructed. An argument presented in Guderley (Reference Guderley1957) suggests that the flow behind the reflected shock is sonic. This leads to the shock polar/characteristic construction shown in figure 17 for the case
![]() $K_{2}>0$
and
$K_{2}>0$
and
![]() $-3/4K_{1}<K_{2}<0$
. The expansion fan is generated by the characteristic curve obtained by integrating
$-3/4K_{1}<K_{2}<0$
. The expansion fan is generated by the characteristic curve obtained by integrating
from the sonic state
![]() $\tilde{u} =\tilde{u} _{3}=(1/K_{2})(1-\sqrt{1+K_{1}K_{2}})$
to
$\tilde{u} =\tilde{u} _{3}=(1/K_{2})(1-\sqrt{1+K_{1}K_{2}})$
to
![]() $\tilde{u} =\tilde{u} _{4}$
where the characteristic curve (4.6) intersects the incident shock polar. While (4.6) can be integrated analytically the point of intersection with the incident shock has to be determined numerically. Figure 17(b) shows the shock and wave fan orientations and the flow deflected through the Mach stem (
$\tilde{u} =\tilde{u} _{4}$
where the characteristic curve (4.6) intersects the incident shock polar. While (4.6) can be integrated analytically the point of intersection with the incident shock has to be determined numerically. Figure 17(b) shows the shock and wave fan orientations and the flow deflected through the Mach stem (
![]() $m$
). The flow downstream of the Mach stem is still not aligned with the channel wall and so cannot describe the full reflection problem which must certainly involve a curved Mach stem eventually orientated to generate a normal shock at the channel wall. The likely solution is that proposed by Tesdall & Hunter (Reference Tesdall and Hunter2002) where the expansion fan reflects off a sonic curve to form a compression wave which in turn generates a shock that incident on the Mach stem generates a new expansion fan. This process can be repeated with a shrinking series of supersonic pockets generated as sketched in figure 4. The recent high resolution results of Tesdall et al. (Reference Tesdall, Sanders and Popivanov2015) confirms this picture for ideal gases.
$m$
). The flow downstream of the Mach stem is still not aligned with the channel wall and so cannot describe the full reflection problem which must certainly involve a curved Mach stem eventually orientated to generate a normal shock at the channel wall. The likely solution is that proposed by Tesdall & Hunter (Reference Tesdall and Hunter2002) where the expansion fan reflects off a sonic curve to form a compression wave which in turn generates a shock that incident on the Mach stem generates a new expansion fan. This process can be repeated with a shrinking series of supersonic pockets generated as sketched in figure 4. The recent high resolution results of Tesdall et al. (Reference Tesdall, Sanders and Popivanov2015) confirms this picture for ideal gases.

Figure 17. (a) Shock polar and characteristic plot for irregular reflection of a plane shock generated by a wedge with inclination
![]() $a$
for
$a$
for
![]() $K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
$K_{1}>0,-3/4K_{1}<K_{2}\leqslant 0$
. Results are for
![]() $K_{1}=1,K_{2}=-0.73$
. The incident shock
$K_{1}=1,K_{2}=-0.73$
. The incident shock
![]() $i$
deflects the flow to
$i$
deflects the flow to
![]() $\tilde{u} _{2},\tilde{v}_{2}$
and a weak reflected shock (
$\tilde{u} _{2},\tilde{v}_{2}$
and a weak reflected shock (
![]() $r$
) generates the sonic flow
$r$
) generates the sonic flow
![]() $\tilde{u} _{3},\tilde{v}_{3}$
downstream. A centred wave fan solution describes a continuous expansion from
$\tilde{u} _{3},\tilde{v}_{3}$
downstream. A centred wave fan solution describes a continuous expansion from
![]() $\tilde{u} _{3},\tilde{v}_{3}$
to
$\tilde{u} _{3},\tilde{v}_{3}$
to
![]() $\tilde{u} _{4},\tilde{v}_{4}$
which intersects the incident shock polar and generates the shock jump across the Mach stem (
$\tilde{u} _{4},\tilde{v}_{4}$
which intersects the incident shock polar and generates the shock jump across the Mach stem (
![]() $m$
). This so-called Guderley reflection is plotted in (b) with a sketch appended (dotted line) of the curved Mach stem that then returns the flow to parallel downstream channel flow.
$m$
). This so-called Guderley reflection is plotted in (b) with a sketch appended (dotted line) of the curved Mach stem that then returns the flow to parallel downstream channel flow.
The scenario of a curved Mach stem orientating the flow to normal channel flow at the boundary has to be modified for the case
![]() $-1/K_{1}<K_{2}<-3/4K_{1}$
. Observations are based on the shock polar diagram of figure 18. As the Mach stem shock originating at
$-1/K_{1}<K_{2}<-3/4K_{1}$
. Observations are based on the shock polar diagram of figure 18. As the Mach stem shock originating at
![]() $\tilde{u} _{4},\tilde{v}_{4}$
increases in strength the flow downstream becomes supersonic and eventually the Mach stem shock turns sonic with downstream flow
$\tilde{u} _{4},\tilde{v}_{4}$
increases in strength the flow downstream becomes supersonic and eventually the Mach stem shock turns sonic with downstream flow
![]() $\tilde{u} _{so}$
. The Mach stem shock remains sonic (and so of fixed orientation) with then decreasing downstream
$\tilde{u} _{so}$
. The Mach stem shock remains sonic (and so of fixed orientation) with then decreasing downstream
![]() $\tilde{v}$
values now associated with a wave fan along the characteristic curve (dash-dot curve) connecting
$\tilde{v}$
values now associated with a wave fan along the characteristic curve (dash-dot curve) connecting
![]() $\tilde{u} _{so}$
to
$\tilde{u} _{so}$
to
![]() $\tilde{u} _{e}$
. This wave fan propagates into a subsonic downstream region and will itself form a supersonic pocket by reflection from a sonic boundary. A possible flow pattern is sketched in figure 19 where we note that as for the triple point the wave fan characteristics reflecting off the sonic curve are expected to intersect constructing a new downstream shock. Current research is underway to confirm this proposed scenario.
$\tilde{u} _{e}$
. This wave fan propagates into a subsonic downstream region and will itself form a supersonic pocket by reflection from a sonic boundary. A possible flow pattern is sketched in figure 19 where we note that as for the triple point the wave fan characteristics reflecting off the sonic curve are expected to intersect constructing a new downstream shock. Current research is underway to confirm this proposed scenario.

Figure 18. Shock polar plot for irregular reflection of a plane shock generated by a wedge with inclination
![]() $a$
for
$a$
for
![]() $K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
$K_{1}>0,-1/K_{1}<K_{2}<-3/4K_{1}$
. Results are for
![]() $K_{1}=1$
,
$K_{1}=1$
,
![]() $K_{2}=-0.8$
. A proposed curved Mach stem is generated from the shock polar connecting the downstream state (
$K_{2}=-0.8$
. A proposed curved Mach stem is generated from the shock polar connecting the downstream state (
![]() $\tilde{u} _{4},\tilde{v}_{4}$
) to
$\tilde{u} _{4},\tilde{v}_{4}$
) to
![]() $\tilde{u} _{so}$
where the Mach stem shock becomes sonic. Flow described by a characteristic (dash-dot) curve returns the flow through a wave fan to normal orientated channel flow on the boundary with
$\tilde{u} _{so}$
where the Mach stem shock becomes sonic. Flow described by a characteristic (dash-dot) curve returns the flow through a wave fan to normal orientated channel flow on the boundary with
![]() $\tilde{u} =\tilde{u} _{e}$
.
$\tilde{u} =\tilde{u} _{e}$
.

Figure 19. Sketch of flow scenario associated with a sonic Mach stem generating a supersonic pocket attached to the reflecting channel wall and terminating in an upstream shock.
5 Conclusions
The analysis of Kluwick & Cox (Reference Kluwick and Cox2018) is extended to treat the problem of weak shock reflection in a channel. Together with the results derived in Kluwick & Cox (Reference Kluwick and Cox2018) the present work yields a complete picture of dense gas transonic flow past a configuration frequently used in wind tunnel experiments which also represents a simple model of the entry region of a gas turbine designed to exploit possible advantages such as increased efficiency resulting from the use of gases with high molecular complexity.
To study non-classical gas dynamic effects associated with such flow media analytically we assume transonic flow
![]() $|M_{\infty }-1|\ll 1$
and
$|M_{\infty }-1|\ll 1$
and
![]() $|\unicode[STIX]{x1D6E4}_{\infty }|\ll 1$
while the quantity
$|\unicode[STIX]{x1D6E4}_{\infty }|\ll 1$
while the quantity
![]() $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70C},s)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70C})|_{s}$
is taken to be of
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70C},s)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70C})|_{s}$
is taken to be of
![]() $O(1)$
. It is then found that solutions of the problem under consideration depend on the elements of the non-dimensional group
$O(1)$
. It is then found that solutions of the problem under consideration depend on the elements of the non-dimensional group
![]() $(a,K_{1},K_{2})$
representing, respectively, the strength of the incident shock generated by a ramp with ramp angle
$(a,K_{1},K_{2})$
representing, respectively, the strength of the incident shock generated by a ramp with ramp angle
![]() $a$
, a generalised transonic similarity parameter and the combined effects of
$a$
, a generalised transonic similarity parameter and the combined effects of
![]() $\unicode[STIX]{x1D6E4}_{\infty }$
and
$\unicode[STIX]{x1D6E4}_{\infty }$
and
![]() $\unicode[STIX]{x1D6EC}_{\infty }$
. As in classical gas dynamics, two essentially different classes of solutions classified as regular and irregular reflections have to be distinguished.
$\unicode[STIX]{x1D6EC}_{\infty }$
. As in classical gas dynamics, two essentially different classes of solutions classified as regular and irregular reflections have to be distinguished.
Flow patterns of the first type are characterised by the property that there exists a reflected shock or a compound shock/wave structure which emanates from the point where the incident shock impinges at the upper channel wall and returns the thereby deflected flow to a flow parallel to the wall again. Consequently, the reflected wave pattern is self-similar and can be constructed by appropriate generalisations of methods introduced in Kluwick & Cox (Reference Kluwick and Cox2018) to study the ramp problem. For upstream supersonic flow
![]() $K_{1}>0$
considered here three ranges of the second similarity parameter
$K_{1}>0$
considered here three ranges of the second similarity parameter
![]() $K_{2}$
corresponding to qualitatively different flow scenarios can be identified. For negative values of
$K_{2}$
corresponding to qualitatively different flow scenarios can be identified. For negative values of
![]() $K_{2}$
larger than
$K_{2}$
larger than
![]() $-3/4K_{1}$
the flow behaviour is similar to the one known from classical gas dynamics, which is included as the special case
$-3/4K_{1}$
the flow behaviour is similar to the one known from classical gas dynamics, which is included as the special case
![]() $K_{2}=0$
. In the two remaining distinguished parameter ranges
$K_{2}=0$
. In the two remaining distinguished parameter ranges
![]() $-1/K_{1}<K_{2}<-3/4K_{1}$
and
$-1/K_{1}<K_{2}<-3/4K_{1}$
and
![]() $K_{2}<-1/K_{1}$
the resulting flow pattern, however, exhibits features which have no counterpart in ideal gas dynamics.
$K_{2}<-1/K_{1}$
the resulting flow pattern, however, exhibits features which have no counterpart in ideal gas dynamics.
Table 1 is intended to provide a more detailed but still compact overview of the phenomena observed for
![]() $K_{2}<0$
.
$K_{2}<0$
.
Table 1. Overview of the phenomena observed for
![]() $K_{2}<0$
.
$K_{2}<0$
.

With increasing ramp angle the point of shock reflection eventually is found to detach from the upper wall if a critical value
![]() $a_{crit}$
is exceeded. In such cases of irregular reflection self-similarity of the associated wave pattern is lost which makes the analytical treatment of the full problem impossible although analytical progress is still possible by seeking local solutions. Experiments for perfect gases suggest the existence of a triple point formed by three colliding shocks: the incident and the reflected shocks and the Mach stem which extends up to the solid wall to satisfy the boundary condition there. Theoretical analysis for perfect as well as arbitrary media, however, predicts that a pure triple shock configuration, i.e. three shocks separated by regions of constant state, is impossible, (Courant & Friedrichs Reference Courant and Friedrichs1948; Neumann Reference von Neumann and Taub1963a
,Reference von Neumann and Taub
b
; Henderson & Menikoff Reference Henderson and Menikoff1998; Serre Reference Serre, Friedlander and Serre2007). The present analysis shows that this result, known as the von Neumann paradox, is consistently captured by the transonic flow approximation for the type of fluids which are of interest here: the reflected shock polar for values
$a_{crit}$
is exceeded. In such cases of irregular reflection self-similarity of the associated wave pattern is lost which makes the analytical treatment of the full problem impossible although analytical progress is still possible by seeking local solutions. Experiments for perfect gases suggest the existence of a triple point formed by three colliding shocks: the incident and the reflected shocks and the Mach stem which extends up to the solid wall to satisfy the boundary condition there. Theoretical analysis for perfect as well as arbitrary media, however, predicts that a pure triple shock configuration, i.e. three shocks separated by regions of constant state, is impossible, (Courant & Friedrichs Reference Courant and Friedrichs1948; Neumann Reference von Neumann and Taub1963a
,Reference von Neumann and Taub
b
; Henderson & Menikoff Reference Henderson and Menikoff1998; Serre Reference Serre, Friedlander and Serre2007). The present analysis shows that this result, known as the von Neumann paradox, is consistently captured by the transonic flow approximation for the type of fluids which are of interest here: the reflected shock polar for values
![]() $a>a_{crit}$
is located completely inside the incident shock polar. Therefore, both polars do not intersect and consequently there is no common state downstream of the Mach stem and the reflected shock. To the authors’ knowledge this graphical interpretation of the von Neumann paradox has been pointed out first by Oswatitsch (Reference Oswatitsch1977) for perfect gases but is non-trivially extended even to cases of dense gases where the incident shock polar in the hodograph plane is no longer closed but terminates if sonic conditions are reached and thus has to be supplemented with characteristic curves which emanate from the point where the shock polar terminates. As for perfect gases one possibility to resolve the von Neumann paradox in the context of transonic flows is that proposed by Guderley as early as 1957 but which did not receive full recognition until recently. Guderley argued that the state behind the reflected shock is sonic and connects with the state downstream of the Mach stem via a weak wave fan. It should be noted that the resulting four wave system formed by the incident shock, the reflected shock, the Mach stem and the intervening wave fan represents an exact solution of the transonic small perturbation equation for both perfect and dense gases. However, it does not satisfy the boundary condition at the upper channel wall and thus, as far as the global flow field is concerned, has to be interpreted as a solution which describes the local flow behaviour close to the origin of the wave fan confined within a small supersonic pocket. Recent numerical solutions, see Tesdall et al. (Reference Tesdall, Sanders and Popivanov2015) and references therein, indicate that this pocket spawns additional local supersonic patches. A possible explanation is based on observations known from conventional aerodynamics, that local supersonic regions in general generate shocks which, in the present context, then provide the agents to perpetuate the mechanism introduced to eliminate the von Neumann paradox in the first place. It is therefore expected that irregular reflections in dense gases will be qualitatively similar to those in perfect gases. A new non-classical feature, however, arises in cases where the shock polar in the hodograph plane is no longer closed but terminates at a sonic point with the normal velocity component
$a>a_{crit}$
is located completely inside the incident shock polar. Therefore, both polars do not intersect and consequently there is no common state downstream of the Mach stem and the reflected shock. To the authors’ knowledge this graphical interpretation of the von Neumann paradox has been pointed out first by Oswatitsch (Reference Oswatitsch1977) for perfect gases but is non-trivially extended even to cases of dense gases where the incident shock polar in the hodograph plane is no longer closed but terminates if sonic conditions are reached and thus has to be supplemented with characteristic curves which emanate from the point where the shock polar terminates. As for perfect gases one possibility to resolve the von Neumann paradox in the context of transonic flows is that proposed by Guderley as early as 1957 but which did not receive full recognition until recently. Guderley argued that the state behind the reflected shock is sonic and connects with the state downstream of the Mach stem via a weak wave fan. It should be noted that the resulting four wave system formed by the incident shock, the reflected shock, the Mach stem and the intervening wave fan represents an exact solution of the transonic small perturbation equation for both perfect and dense gases. However, it does not satisfy the boundary condition at the upper channel wall and thus, as far as the global flow field is concerned, has to be interpreted as a solution which describes the local flow behaviour close to the origin of the wave fan confined within a small supersonic pocket. Recent numerical solutions, see Tesdall et al. (Reference Tesdall, Sanders and Popivanov2015) and references therein, indicate that this pocket spawns additional local supersonic patches. A possible explanation is based on observations known from conventional aerodynamics, that local supersonic regions in general generate shocks which, in the present context, then provide the agents to perpetuate the mechanism introduced to eliminate the von Neumann paradox in the first place. It is therefore expected that irregular reflections in dense gases will be qualitatively similar to those in perfect gases. A new non-classical feature, however, arises in cases where the shock polar in the hodograph plane is no longer closed but terminates at a sonic point with the normal velocity component
![]() $v$
being non-zero. Consequently, the interaction of a single Mach stem shock with the upper wall is not able to satisfy the boundary condition
$v$
being non-zero. Consequently, the interaction of a single Mach stem shock with the upper wall is not able to satisfy the boundary condition
![]() $v=0$
there. Rather the combined action of an oblique Mach stem shock with an attached wave fan is required to return the deflected flow to a flow again parallel to the wall. Numerical work to support this tentative picture is presently been carried out.
$v=0$
there. Rather the combined action of an oblique Mach stem shock with an attached wave fan is required to return the deflected flow to a flow again parallel to the wall. Numerical work to support this tentative picture is presently been carried out.
The present analysis is based on the assumption of inviscid strictly two-dimensional flow. Extensions to represent the dynamics of more ‘realistic’ flows are clearly desirable. Questions concerning the stability of solutions involving shocks have been addressed already in Kluwick & Cox (Reference Kluwick and Cox2018) and will not be repeated here. Following the study by Kluwick & Kornfeld (Reference Kluwick and Kornfeld2014) weakly three-dimensional effects can in principle be incorporated by letting the various flow quantities depend on an additional Cartesian coordinate which varies slowly in the lateral direction. Triple-deck theory is expected to provide the proper framework to account for the effects of laminar boundary layers in the limit of high Reynolds number, (Wrabel & Kluwick Reference Wrabel and Kluwick2005; Kluwick & Meyer Reference Kluwick and Meyer2010, Reference Kluwick and Meyer2011). Here the differences of the flow field caused by compression shocks which drive the flow towards separation and rarefaction shocks which accelerate the flow medium will be of prime interest. First steps in the treatment of fully developed turbulent dense gas in unconfined and channel flows in have been taken by Alferez & Touber (Reference Alferez and Touber2017), Sciacovelli, Cinnella & Gloerfelt (Reference Sciacovelli, Cinnella and Gloerfelt2017). Further progress in the treatment of aerodynamic configurations will require the formulation of a strategy based on the Reynolds averaged equations, see e.g. Walker (Reference Walker and Kluwick1998).