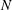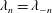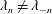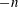1 Introduction
Aircraft noise reduction is an urgent issue nowadays. Among the many sources of noise of an aircraft, jet noise is still a significant contributor. This is especially true when an aircraft is taking off. While the exact role played by jet instabilities in noise generation is still open to some debate for subsonic jets, recent studies (Cavalieri et al. Reference Cavalieri, Jordan, Wolf and Gervais2014; Lyu & Dowling Reference Lyu and Dowling2016; Piantanida et al. Reference Piantanida, Jaunet, Huber, Wolf, Jordan and Cavalieri2016; Lyu, Dowling & Naqavi Reference Lyu, Dowling and Naqavi2017) have shown that installed jet noise is dominated by the scattering of jet instability waves by the trailing edge of aircraft wings or flaps. To suppress or reduce installed jet noise, one can examine the possibility of controlling these instability waves. Since instability waves are closely related to jet mean flows, one such an approach is to modify jet mean flows to become less axisymmetric. The feasibility of this approach, however, hinges on the hope that the instability waves can be somehow suppressed by using a less-axisymmetric jet mean flow. This raises the question of examining the stability characteristics of jets of general non-axisymmetric geometries.
Though jet instability is among the most heavily studied areas in fluid mechanics (Morris Reference Morris2010), the research on the characteristics of the instability waves of non-axisymmetric jets is rather limited. Some of the early attempts include those on elliptic and rectangular jets. These include some analytical (Crighton Reference Crighton1973), numerical (Morris Reference Morris1988; Tam & Thies Reference Tam and Thies1993; Baty & Morris Reference Baty and Morris1995) and some relevant experimental studies focusing on the turbulence, mixing and acoustics of non-axisymmetric jets (Tam & Zaman Reference Tam and Zaman2000; Li et al. Reference Li, Hu, Kobayashi, Saga and Taniguchi2001, Reference Li, Hu, Kobayashi, Saga and Taniguchi2002; Hu et al. Reference Hu, Saga, Kobayashi and Taniguchi2002; Li et al. Reference Li, Hu, Kobayashi, Saga and Taniguchi2002; Zaman, Wang & Georgiadis Reference Zaman, Wang and Georgiadis2003; Miao et al. Reference Miao, Dmitriy, Liu, Qin, Wu, Chu and Wang2015). The analytical work of Crighton (Reference Crighton1973) showed that separable solutions can be obtained for elliptic jets. The instability waves aligned with the major and minor axes exhibit different behaviours. Not surprisingly, the instability waves of rectangular jets share similar characteristics (Tam & Thies Reference Tam and Thies1993). Analytical works normally assumed the mean flow to be of a vortex sheet type to allow mathematical derivations to proceed. For more realistic jet mean flows, numerical methods had to be adopted. For example, Morris (Reference Morris1988) numerically solved the eigenvalue problem in the elliptic cylindrical coordinates for the realistic mean flow in the initial mixing region of a jet. It was found that all modes, no matter whether even or odd about the major axis, have similar spatial growth rates.
Both elliptic and rectangular jets have two symmetric axes (or planes). From the noise reduction point of view, however, it is desirable to promote instability waves of higher-order azimuthal modes. First, this is preferable to suppress isolated jet noise. Because it has been shown that sound sources of lower-order modes are more efficient at low frequencies for subsonic isolated jets owing to the so-called radial compactness (Michalke Reference Michalke1970; Mankbadi & Liu Reference Mankbadi and Liu1984; Cavalieri et al. Reference Cavalieri, Rodríguez, Jordan, Colonius and Gervais2013). Second, this is beneficial to reduce installed jet noise. It is known that high-order instability modes decay faster with radial distance than those of low orders, Hence, when they are scattered into sound by a sharp edge placed nearby, faster decay implies weaker sound generation owing to the scattering of weaker instability waves.
Instability waves of high-order azimuthal modes may be expected to be promoted by jet mean flows with more azimuthal periodic structures, such as lobe jets. One of the simple lobed profiles can be described as
![]() $\unicode[STIX]{x1D70E}=a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D703})$
, where
$\unicode[STIX]{x1D70E}=a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D703})$
, where
![]() $\unicode[STIX]{x1D70E}$
is the radius of the lobed profile,
$\unicode[STIX]{x1D70E}$
is the radius of the lobed profile,
![]() $a$
the mean radius,
$a$
the mean radius,
![]() $N$
the number of lobes and
$N$
the number of lobes and
![]() $\unicode[STIX]{x1D716}$
the penetration ratio quantifying how large the lobes are. The open literature on the stability of lobed jets is, however, very sparse (Morris Reference Morris2010). In a study performed by Kopiev et al. (Reference Kopiev, Ostrikov, Chernyshev and Elliot2004) on supersonic jet noise, a spatial stability analysis was undertaken to examine the effects of weak corrugation on the instability characteristics of a parallel vortex sheet with supersonic flow speed. A leading-order asymptotic correction to the complex wavenumber
$\unicode[STIX]{x1D716}$
the penetration ratio quantifying how large the lobes are. The open literature on the stability of lobed jets is, however, very sparse (Morris Reference Morris2010). In a study performed by Kopiev et al. (Reference Kopiev, Ostrikov, Chernyshev and Elliot2004) on supersonic jet noise, a spatial stability analysis was undertaken to examine the effects of weak corrugation on the instability characteristics of a parallel vortex sheet with supersonic flow speed. A leading-order asymptotic correction to the complex wavenumber
![]() $\unicode[STIX]{x1D6FC}$
for the round jet when
$\unicode[STIX]{x1D6FC}$
for the round jet when
![]() $\unicode[STIX]{x1D716}\rightarrow 0$
was obtained. The results showed that at low
$\unicode[STIX]{x1D716}\rightarrow 0$
was obtained. The results showed that at low
![]() $St$
, where
$St$
, where
![]() $St$
is the Strouhal number based on the jet exit velocity
$St$
is the Strouhal number based on the jet exit velocity
![]() $U$
and
$U$
and
![]() $a$
, a small
$a$
, a small
![]() $\unicode[STIX]{x1D716}$
may lead to a
$\unicode[STIX]{x1D716}$
may lead to a
![]() $O(\unicode[STIX]{x1D716})$
change to the spatial growth rate if the azimuthal mode number
$O(\unicode[STIX]{x1D716})$
change to the spatial growth rate if the azimuthal mode number
![]() $n$
is less than the number of lobes
$n$
is less than the number of lobes
![]() $N$
. More interestingly, it was shown that if the sum of the two positive mode numbers is equal to
$N$
. More interestingly, it was shown that if the sum of the two positive mode numbers is equal to
![]() $N$
, the changes to the values of their
$N$
, the changes to the values of their
![]() $\unicode[STIX]{x1D6FC}$
have opposite tendencies. The asymptotic solution shown in this study, however, relies on numerically solving transcendental equations and is therefore non-trivial to compute. In addition, because the correction is restricted to
$\unicode[STIX]{x1D6FC}$
have opposite tendencies. The asymptotic solution shown in this study, however, relies on numerically solving transcendental equations and is therefore non-trivial to compute. In addition, because the correction is restricted to
![]() $O(\unicode[STIX]{x1D716})$
or
$O(\unicode[STIX]{x1D716})$
or
![]() $O(\unicode[STIX]{x1D716}^{2})$
only when
$O(\unicode[STIX]{x1D716}^{2})$
only when
![]() $\unicode[STIX]{x1D716}\rightarrow 0$
, it remains to be seen to what extent the corrugation can change the stability characteristics at a finite or large
$\unicode[STIX]{x1D716}\rightarrow 0$
, it remains to be seen to what extent the corrugation can change the stability characteristics at a finite or large
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
Of close relevance to the lobed jets are some recent studies on the stability characteristics of chevron jets (Lajús Jr, Cavalieri & Deschamps Reference Lajús, Cavalieri and Deschamps2015; Sinha et al.
Reference Sinha, Gudmundsson, Xia and Colonius2016). This is because the mean flow profiles of chevrons jets are very similar to those of lobed jets. The work of Lajús Jr et al. (Reference Lajús, Cavalieri and Deschamps2015) was based on numerically solving the compressible Rayleigh equation for an azimuthally periodic base flow. This study explored the effects of azimuthal variations of the shear layer thickness and flow radius of the mean flow on the stability characteristics. Two types of base flow were used. The first was fitted based on a Mach
![]() $0.9$
chevron jet and the second on a Mach
$0.9$
chevron jet and the second on a Mach
![]() $0.4$
micro-jet. For the chevron case, the results showed that the variation of shear-layer thickness has opposite effect to that of the radius. The combination of the two, however, results in a larger reduction of the spatial growth rates. It was concluded that chevron is more effective in controlling jet noise. The last section of this paper showed the effects of the number of lobes. The preliminary results showed that the number of lobes is not very important to the mode
$0.4$
micro-jet. For the chevron case, the results showed that the variation of shear-layer thickness has opposite effect to that of the radius. The combination of the two, however, results in a larger reduction of the spatial growth rates. It was concluded that chevron is more effective in controlling jet noise. The last section of this paper showed the effects of the number of lobes. The preliminary results showed that the number of lobes is not very important to the mode
![]() $0$
instability wave, which will be seen to be consistent with the results obtained in this paper.
$0$
instability wave, which will be seen to be consistent with the results obtained in this paper.
In the study of Sinha et al. (Reference Sinha, Gudmundsson, Xia and Colonius2016), a viscous spatial linear stability analysis was performed numerically using the parabolized stability equation (PSE) approach. The solutions to the parallel-flow stability equations were obtained first to initiate the PSE. The linear stability theory (LST) results showed that the serrations reduce the spatial growth rate of the most unstable eigenmodes of the jet, but their phase speeds are similar. For example, the serrations appeared to reduce the spatial growth rate and increase the convection velocity of the mode
![]() $0$
instability wave. These effects are found to be in accord with the findings to be shown in the rest of this paper. The PSE results were compared with the proper orthogonal decomposition (POD) modes of the near-field pressure obtained experimentally. Favourable agreement was achieved. Similar agreement was obtained to the results from a further investigation using a large eddy simulation (LES) database. It was concluded that the coherent hydrodynamic pressure fluctuations of jets from both round and serrated nozzles agree reasonably with the instability modes of turbulent mean flows.
$0$
instability wave. These effects are found to be in accord with the findings to be shown in the rest of this paper. The PSE results were compared with the proper orthogonal decomposition (POD) modes of the near-field pressure obtained experimentally. Favourable agreement was achieved. Similar agreement was obtained to the results from a further investigation using a large eddy simulation (LES) database. It was concluded that the coherent hydrodynamic pressure fluctuations of jets from both round and serrated nozzles agree reasonably with the instability modes of turbulent mean flows.
Given the sparse analytical work on the stability of lobed jets and that the majority of studies on this are numerically based, it is desirable to perform some analytical studies, hoping to unveil more of the physics of lobed jets’ instability waves, such as the effects of varying
![]() $N$
and
$N$
and
![]() $\unicode[STIX]{x1D716}$
on the instability waves of different mode numbers, and provide more insight into understanding the jet physics. In the following section, we present such an analysis within the temporal stability analysis framework, proposing an innovative analytical method of studying how a general non-axisymmetric jet mean flow changes the behaviour of instability waves. More importantly, the method does not involve solving transcendental equations and would work for finite or even large values of
$\unicode[STIX]{x1D716}$
on the instability waves of different mode numbers, and provide more insight into understanding the jet physics. In the following section, we present such an analysis within the temporal stability analysis framework, proposing an innovative analytical method of studying how a general non-axisymmetric jet mean flow changes the behaviour of instability waves. More importantly, the method does not involve solving transcendental equations and would work for finite or even large values of
![]() $\unicode[STIX]{x1D716}$
. The method can also be used to study a wide range of other problems in an efficient and robust manner.
$\unicode[STIX]{x1D716}$
. The method can also be used to study a wide range of other problems in an efficient and robust manner.
2 Temporal stability analysis for non-axisymmetric jets
2.1 The governing equation for non-axisymmetric vortex-sheet flows
Following the routine procedure of stability analysis, we decompose the flow into base and fluctuation parts. Note that the time-average mean flow is often taken as the base flow, and hence in this paper we use the mean flow and base flow interchangeably. We start with the incompressible Navier–Stokes equations since installed jet noise is relevant primarily at low Mach numbers. At this stage, we write equations in a vector form to avoid the introduction of coordinate systems. The momentum equation can be written as
where
![]() $t$
denotes time,
$t$
denotes time,
![]() $\boldsymbol{v}$
denotes the fluid velocity,
$\boldsymbol{v}$
denotes the fluid velocity,
![]() $\unicode[STIX]{x1D70C}$
denotes the flow density,
$\unicode[STIX]{x1D70C}$
denotes the flow density,
![]() $p$
denotes the pressure and
$p$
denotes the pressure and
![]() $\unicode[STIX]{x1D708}$
denotes the dynamic viscosity. We assume that base flow is steady, with flow density, velocity and pressure to be
$\unicode[STIX]{x1D708}$
denotes the dynamic viscosity. We assume that base flow is steady, with flow density, velocity and pressure to be
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $\boldsymbol{U}$
and
$\boldsymbol{U}$
and
![]() $\bar{p}$
, respectively, and that the base flow satisfies
$\bar{p}$
, respectively, and that the base flow satisfies
The total flow field is given by the sum of the base flow and the small perturbation. After substituting the total flow into (2.1) and ignoring second-order quantities, we have the following linearized equation:
where the prime symbols denote the corresponding fluctuation quantities. When the Reynolds number is high, we expect that the viscous term plays a negligible role. Hence the term
![]() $\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}^{\prime }$
can be neglected, i.e.
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}^{\prime }$
can be neglected, i.e.
Equation (2.4), together with the incompressible continuity equation
governs the small-amplitude inviscid perturbations over a steady base flow.
The perturbation field is generally rotational for general shear base flows. Therefore, it cannot be described using a potential function. However, for parallel flows of a vortex-sheet type, the base flows inside and outside the vortex sheet are both irrotational. Hence, the perturbation should also be irrotational. This suggests the existence of a potential function
![]() $\unicode[STIX]{x1D713}$
for the velocity perturbations, i.e.
$\unicode[STIX]{x1D713}$
for the velocity perturbations, i.e.
on either side of the vortex sheet. The function
![]() $\unicode[STIX]{x1D713}$
will be discontinuous across the shear layer. From the (2.5), one can see that the velocity potential satisfies the Laplace equation, i.e.
$\unicode[STIX]{x1D713}$
will be discontinuous across the shear layer. From the (2.5), one can see that the velocity potential satisfies the Laplace equation, i.e.
The pressure perturbation is effectively decoupled from the velocity potential and can be easily obtained from (2.4).
The vortex-sheet simplification was used extensively in stability analysis, in large due to the fact that an analytical dispersion relation can be generally found (Batchelor & Gill Reference Batchelor and Gill1962; Crighton Reference Crighton1973; Kawahara et al. Reference Kawahara, Jiménez, Uhlmann and Pinelli2003). From these dispersion relation, one can gain more insight than numerical simulations can offer. In addition, the vortex-sheet simplification is often permissible, particularly for analysing low-frequency instability waves. Though a realistic jet mean flow spreads slowly and has an increasingly thick mixing layer towards downstream, the vortex-sheet simplification should serve as a good approximation to the realistic flow close to the jet nozzle. Therefore, in this paper we assume the base flow to be parallel and of a vortex-sheet type.
Since the velocity potentials exist for the vortex-sheet problem, we let
![]() $\unicode[STIX]{x1D713}^{+}$
and
$\unicode[STIX]{x1D713}^{+}$
and
![]() $\unicode[STIX]{x1D713}^{-}$
denote the potentials outside and inside of the vortex sheet, respectively, i.e.
$\unicode[STIX]{x1D713}^{-}$
denote the potentials outside and inside of the vortex sheet, respectively, i.e.
where
![]() ${\boldsymbol{v}^{\prime }}^{+}$
and
${\boldsymbol{v}^{\prime }}^{+}$
and
![]() ${\boldsymbol{v}^{\prime }}^{-}$
denote the velocity perturbations outside and inside the vortex sheet, respectively. Considering the parallel-flow assumption, we now introduce the cylindrical coordinates
${\boldsymbol{v}^{\prime }}^{-}$
denote the velocity perturbations outside and inside the vortex sheet, respectively. Considering the parallel-flow assumption, we now introduce the cylindrical coordinates
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $z$
, as shown in figure 1. In this coordinate frame, the velocity potentials
$z$
, as shown in figure 1. In this coordinate frame, the velocity potentials
![]() $\unicode[STIX]{x1D713}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719},z,t)$
satisfy the following Laplace equation:
$\unicode[STIX]{x1D713}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719},z,t)$
satisfy the following Laplace equation:
Note that we have not yet restricted the profiles of the vortex sheet. It therefore can be of arbitrary geometry, such as rectangular, elliptic or lobed. One can therefore let a general function
![]() ${\mathcal{R}}(\unicode[STIX]{x1D719})$
denote the radius of the vortex sheet at polar angle
${\mathcal{R}}(\unicode[STIX]{x1D719})$
denote the radius of the vortex sheet at polar angle
![]() $\unicode[STIX]{x1D719}$
. Consequently, the profile of the vortex sheet can be specified as
$\unicode[STIX]{x1D719}$
. Consequently, the profile of the vortex sheet can be specified as
2.2 The eigenvalue problem
Without losing generality, one may assume
where
![]() $A_{m}$
are complex constants,
$A_{m}$
are complex constants,
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D714}$
are the streamwise wavenumber and frequency, respectively. The functions
$\unicode[STIX]{x1D714}$
are the streamwise wavenumber and frequency, respectively. The functions
![]() $E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are linearly independent of each other and each pair of them at a given
$E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are linearly independent of each other and each pair of them at a given
![]() $m$
satisfies both the governing equations and appropriate boundary conditions. The functions
$m$
satisfies both the governing equations and appropriate boundary conditions. The functions
![]() $E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
$E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
![]() $E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are therefore defined in the two-dimensional regions outside (
$E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are therefore defined in the two-dimensional regions outside (
![]() $\unicode[STIX]{x1D70E}>{\mathcal{R}}(\unicode[STIX]{x1D719})$
) and inside (
$\unicode[STIX]{x1D70E}>{\mathcal{R}}(\unicode[STIX]{x1D719})$
) and inside (
![]() $\unicode[STIX]{x1D70E}\leqslant {\mathcal{R}}(\unicode[STIX]{x1D719})$
) the vortex-sheet profile, respectively, as shown in figure 2.
$\unicode[STIX]{x1D70E}\leqslant {\mathcal{R}}(\unicode[STIX]{x1D719})$
) the vortex-sheet profile, respectively, as shown in figure 2.

Figure 1. The cylindrical coordinate system: the
![]() $z$
axis is parallel to the vortex sheet, the origin is at the centre of the lobed profile and
$z$
axis is parallel to the vortex sheet, the origin is at the centre of the lobed profile and
![]() $\unicode[STIX]{x1D719}$
denotes the anticlockwise angle between the radial axis and the horizontal dashed line.
$\unicode[STIX]{x1D719}$
denotes the anticlockwise angle between the radial axis and the horizontal dashed line.

Figure 2. Schematic illustration of the boundary conditions of the stability problem of a parallel lobed vortex sheet.
We choose to normalize the functions
![]() $E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
such that for any integer
$E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
such that for any integer
![]() $m$
$m$
where
![]() $a$
, as defined in § 1 and shown in figure 2, is the mean radius of the vortex sheet, which is defined by
$a$
, as defined in § 1 and shown in figure 2, is the mean radius of the vortex sheet, which is defined by
We cannot normalize
![]() $E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
according to (2.12), because
$E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
according to (2.12), because
![]() $E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
$E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
![]() $E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are not independent. In fact, either the dynamic or the kinematic boundary condition is sufficient to determine
$E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are not independent. In fact, either the dynamic or the kinematic boundary condition is sufficient to determine
![]() $E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
from a given
$E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
from a given
![]() $E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
. Therefore,
$E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
. Therefore,
![]() $E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
has to be determined such that for the same mode number
$E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
has to be determined such that for the same mode number
![]() $m$
, the functions
$m$
, the functions
![]() $E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
$E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
![]() $E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
satisfy the boundary conditions. One should note that
$E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
satisfy the boundary conditions. One should note that
![]() $E_{m}^{-}(a,\unicode[STIX]{x1D719})$
are not properly defined within some ranges of
$E_{m}^{-}(a,\unicode[STIX]{x1D719})$
are not properly defined within some ranges of
![]() $\unicode[STIX]{x1D719}$
(because
$\unicode[STIX]{x1D719}$
(because
![]() $E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
is defined for
$E_{m}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
is defined for
![]() $\unicode[STIX]{x1D70E}\leqslant {\mathcal{R}}(\unicode[STIX]{x1D719})$
and
$\unicode[STIX]{x1D70E}\leqslant {\mathcal{R}}(\unicode[STIX]{x1D719})$
and
![]() $a>{\mathcal{R}}(\unicode[STIX]{x1D719})$
in some ranges of
$a>{\mathcal{R}}(\unicode[STIX]{x1D719})$
in some ranges of
![]() $\unicode[STIX]{x1D719}$
, see figure 2 for example). However, they can be naturally defined using analytical continuation, which will become clear at a later stage. Hence, the normalization defined by (2.12) is valid.
$\unicode[STIX]{x1D719}$
, see figure 2 for example). However, they can be naturally defined using analytical continuation, which will become clear at a later stage. Hence, the normalization defined by (2.12) is valid.
Substituting
![]() $E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
into (2.9) yields the governing equation
$E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
into (2.9) yields the governing equation
Equation (2.14) is to be solved subject to appropriate boundary conditions. These are a finite value of
![]() $E_{m}^{-}(0,\unicode[STIX]{x1D719})$
, a decay behaviour for
$E_{m}^{-}(0,\unicode[STIX]{x1D719})$
, a decay behaviour for
![]() $E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
as
$E_{m}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
as
![]() $\unicode[STIX]{x1D70E}\rightarrow \infty$
, and the kinematic and dynamic boundary conditions across the vortex sheet (Batchelor & Gill Reference Batchelor and Gill1962; Crighton Reference Crighton1973). Because all the function pairs
$\unicode[STIX]{x1D70E}\rightarrow \infty$
, and the kinematic and dynamic boundary conditions across the vortex sheet (Batchelor & Gill Reference Batchelor and Gill1962; Crighton Reference Crighton1973). Because all the function pairs
![]() $E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
satisfy both (2.14) and their relevant boundary conditions, they are referred to as the eigenfunctions of this system. The functions
$E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
satisfy both (2.14) and their relevant boundary conditions, they are referred to as the eigenfunctions of this system. The functions
![]() $\{E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})\}$
should form a complete set of basis for the Hilbert space determined by (2.14) and appropriate boundary conditions. The aim of the next section is to calculate these eigenfunctions analytically (without discretizing (2.14) and then solving it numerically).
$\{E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})\}$
should form a complete set of basis for the Hilbert space determined by (2.14) and appropriate boundary conditions. The aim of the next section is to calculate these eigenfunctions analytically (without discretizing (2.14) and then solving it numerically).
2.3 The calculation of eigenfunctions
Due to the coupling of
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D719}$
of the boundary conditions,
$\unicode[STIX]{x1D719}$
of the boundary conditions,
![]() $E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are not generally expected to be of a separable form. However, in the case of a cylindrical vortex sheet (round jet), the eigenfunctions
$E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are not generally expected to be of a separable form. However, in the case of a cylindrical vortex sheet (round jet), the eigenfunctions
![]() $E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are known to be separable. Before proceeding to the case of more general vortex sheets, it is instructive to review the characteristics of
$E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are known to be separable. Before proceeding to the case of more general vortex sheets, it is instructive to review the characteristics of
![]() $E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
for a cylindrical vortex sheet.
$E_{m}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
for a cylindrical vortex sheet.
2.3.1 The solution for a cylindrical vortex sheet
For the cylindrical vortex-sheet flow, the solutions were derived by Batchelor & Gill (Reference Batchelor and Gill1962) and we review them to introduce the notation and, more importantly, these solutions form the basis for analysing more complicated geometries in the following section. The potentials
![]() $\unicode[STIX]{x1D713}^{\pm }$
are known to be able to be expanded as
$\unicode[STIX]{x1D713}^{\pm }$
are known to be able to be expanded as
where the functions
![]() $\unicode[STIX]{x1D6F9}_{n}^{\pm }(\unicode[STIX]{x1D70E})$
satisfy the modified Bessel equation
$\unicode[STIX]{x1D6F9}_{n}^{\pm }(\unicode[STIX]{x1D70E})$
satisfy the modified Bessel equation
Considering the boundary condition at the centre of the mean flow and at infinity, one can show that
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D6F9}_{n}^{-}(\unicode[STIX]{x1D70E})=C_{n}^{-}\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}),\\ \displaystyle \unicode[STIX]{x1D6F9}_{n}^{+}(\unicode[STIX]{x1D70E})=C_{n}^{+}\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D6F9}_{n}^{-}(\unicode[STIX]{x1D70E})=C_{n}^{-}\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}),\\ \displaystyle \unicode[STIX]{x1D6F9}_{n}^{+}(\unicode[STIX]{x1D70E})=C_{n}^{+}\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}),\end{array}\right\}\end{eqnarray}$$
where
![]() $C_{n}^{-}$
and
$C_{n}^{-}$
and
![]() $C_{n}^{+}$
are arbitrary complex constants and
$C_{n}^{+}$
are arbitrary complex constants and
![]() $I_{n}$
and
$I_{n}$
and
![]() $K_{n}$
are the modified Bessel functions of the first and second kinds, respectively.
$K_{n}$
are the modified Bessel functions of the first and second kinds, respectively.
Applying the kinematic and dynamic boundary condition on the vortex sheet, one obtains
In this special case, one can verify that the eigenfunctions,
![]() $E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
$E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
![]() $E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
, take the separable form of
$E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
, take the separable form of
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\\ \displaystyle E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\\ \displaystyle E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\end{array}\right\}\end{eqnarray}$$
where
![]() $(1-\unicode[STIX]{x1D6FC}U/\unicode[STIX]{x1D714})$
is obtained from (2.19). Here,
$(1-\unicode[STIX]{x1D6FC}U/\unicode[STIX]{x1D714})$
is obtained from (2.19). Here,
![]() $E_{n}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
take these simple forms because the boundary condition involves no coupling between
$E_{n}^{\pm }(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
take these simple forms because the boundary condition involves no coupling between
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D719}$
(separable), and therefore these separable solutions are just the eigenfunction of the mathematical problem.
$\unicode[STIX]{x1D719}$
(separable), and therefore these separable solutions are just the eigenfunction of the mathematical problem.
2.3.2 The solution for a vortex sheet of arbitrary geometry
For the case of a non-axisymmetric vortex sheet, the perturbations outside and inside the vortex sheet still remain determined by the Laplace equation. However, the boundary condition is now more complicated. If we were to find an orthogonal coordinate system in which the vortex-sheet profile can be represented by one of the constant coordinate axes, we may be able to find a separable solution. For elliptic profiles, such a coordinate system exists and eigenfunctions of separable form can be obtained (Crighton Reference Crighton1973). However, it seems rather unlikely to find such a coordinate system for a general profile.
However, in light of the completeness of the orthogonal function set
![]() $\{\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\}$
, we are still able to write the solutions inside and outside the vortex sheet as
$\{\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\}$
, we are still able to write the solutions inside and outside the vortex sheet as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D713}^{-}=\mathop{\sum }_{-\infty }^{\infty }C_{n}^{-}\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t},\\ \displaystyle \unicode[STIX]{x1D713}^{+}=\mathop{\sum }_{-\infty }^{\infty }C_{n}^{+}\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D713}^{-}=\mathop{\sum }_{-\infty }^{\infty }C_{n}^{-}\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t},\\ \displaystyle \unicode[STIX]{x1D713}^{+}=\mathop{\sum }_{-\infty }^{\infty }C_{n}^{+}\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t},\end{array}\right\}\end{eqnarray}$$
respectively. We must emphasize here that neither the solution
![]() $I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}/I_{n}(\unicode[STIX]{x1D6FC}a)$
nor that
$I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}/I_{n}(\unicode[STIX]{x1D6FC}a)$
nor that
![]() $K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}/K_{n}(\unicode[STIX]{x1D6FC}a)$
is the eigenfunction for this problem, since they do not satisfy the boundary conditions on the vortex sheet (although they satisfy (2.14)). However, since they form a complete set, a suitable combination of these separable solutions which satisfies the boundary conditions will be the eigenfunction that we aim to obtain in this section. There may be multiple such combinations, corresponding to eigenfunctions of different orders. For a more compact presentation of the rest of the derivation, let
$K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}/K_{n}(\unicode[STIX]{x1D6FC}a)$
is the eigenfunction for this problem, since they do not satisfy the boundary conditions on the vortex sheet (although they satisfy (2.14)). However, since they form a complete set, a suitable combination of these separable solutions which satisfies the boundary conditions will be the eigenfunction that we aim to obtain in this section. There may be multiple such combinations, corresponding to eigenfunctions of different orders. For a more compact presentation of the rest of the derivation, let
Hence, equation (2.21) becomes
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D713}^{-}=\mathop{\sum }_{-\infty }^{\infty }\bar{C}_{n}^{-}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t},\\ \displaystyle \unicode[STIX]{x1D713}^{+}=\mathop{\sum }_{-\infty }^{\infty }\bar{C}_{n}^{+}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D713}^{-}=\mathop{\sum }_{-\infty }^{\infty }\bar{C}_{n}^{-}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t},\\ \displaystyle \unicode[STIX]{x1D713}^{+}=\mathop{\sum }_{-\infty }^{\infty }\bar{C}_{n}^{+}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}.\end{array}\right\}\end{eqnarray}$$
Equation (2.24) needs to satisfy both the kinematic and dynamic boundary conditions on the vortex sheet, i.e. when
![]() $\unicode[STIX]{x1D70E}={\mathcal{R}}(\unicode[STIX]{x1D719})$
. The two boundary conditions can be shown to be (see more details in appendix A),
$\unicode[STIX]{x1D70E}={\mathcal{R}}(\unicode[STIX]{x1D719})$
. The two boundary conditions can be shown to be (see more details in appendix A),

Figure 3. (a) The weakly lobed profiles when
![]() $\unicode[STIX]{x1D716}=0.1$
. (b) Strongly lobed profiles when
$\unicode[STIX]{x1D716}=0.1$
. (b) Strongly lobed profiles when
![]() $\unicode[STIX]{x1D716}=0.2$
.
$\unicode[STIX]{x1D716}=0.2$
.
3 Analysis for lobed vortex sheets
In general,
![]() ${\mathcal{R}}$
can be an arbitrary function of
${\mathcal{R}}$
can be an arbitrary function of
![]() $\unicode[STIX]{x1D719}$
. Since we are mostly concerning with the stability of lobed jets, which have a number of identical lobes, it follows that the function
$\unicode[STIX]{x1D719}$
. Since we are mostly concerning with the stability of lobed jets, which have a number of identical lobes, it follows that the function
![]() ${\mathcal{R}}$
is a periodic function of
${\mathcal{R}}$
is a periodic function of
![]() $\unicode[STIX]{x1D719}$
. This suggests that
$\unicode[STIX]{x1D719}$
. This suggests that
![]() ${\mathcal{R}}$
can be readily expanded using Fourier series. As a starting point, we restrict our attention to the simplest case mentioned in § 1, in which case
${\mathcal{R}}$
can be readily expanded using Fourier series. As a starting point, we restrict our attention to the simplest case mentioned in § 1, in which case
![]() ${\mathcal{R}}$
is given by
${\mathcal{R}}$
is given by
For weakly lobed nozzles,
![]() $\unicode[STIX]{x1D716}\ll 1$
, whereas
$\unicode[STIX]{x1D716}\ll 1$
, whereas
![]() $\unicode[STIX]{x1D716}\sim 0.2$
represents a strongly lobed profile. Figure 3(a) shows some relatively weakly lobed profiles when
$\unicode[STIX]{x1D716}\sim 0.2$
represents a strongly lobed profile. Figure 3(a) shows some relatively weakly lobed profiles when
![]() $\unicode[STIX]{x1D716}=0.1$
, while figure 3(b) shows some strongly lobed profiles when
$\unicode[STIX]{x1D716}=0.1$
, while figure 3(b) shows some strongly lobed profiles when
![]() $\unicode[STIX]{x1D716}=0.2$
. In either case, we see that
$\unicode[STIX]{x1D716}=0.2$
. In either case, we see that
![]() $\unicode[STIX]{x1D716}$
is a small quantity, and this suggests that the Taylor expansion of a well-behaved function around
$\unicode[STIX]{x1D716}$
is a small quantity, and this suggests that the Taylor expansion of a well-behaved function around
![]() $\unicode[STIX]{x1D716}=0$
should converge sufficiently quickly. For more general lobed profiles, function
$\unicode[STIX]{x1D716}=0$
should converge sufficiently quickly. For more general lobed profiles, function
![]() $\cos N\unicode[STIX]{x1D719}$
can be replaced by a sum over
$\cos N\unicode[STIX]{x1D719}$
can be replaced by a sum over
![]() $m$
of terms with
$m$
of terms with
![]() $\unicode[STIX]{x1D719}$
dependence
$\unicode[STIX]{x1D719}$
dependence
![]() $\cos mN\unicode[STIX]{x1D719}$
and
$\cos mN\unicode[STIX]{x1D719}$
and
![]() $\sin mN\unicode[STIX]{x1D719}$
. When
$\sin mN\unicode[STIX]{x1D719}$
. When
![]() ${\mathcal{R}}$
is given by (3.1), we see that
${\mathcal{R}}$
is given by (3.1), we see that
and
where
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D70E}}$
and
$\boldsymbol{e}_{\unicode[STIX]{x1D70E}}$
and
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D719}}$
denote the unit vectors in the radial and azimuthal directions, respectively. Substituting (2.24), (3.1) and (3.2) into (2.25a
) and (2.25b
) yields
$\boldsymbol{e}_{\unicode[STIX]{x1D719}}$
denote the unit vectors in the radial and azimuthal directions, respectively. Substituting (2.24), (3.1) and (3.2) into (2.25a
) and (2.25b
) yields
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle \left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\left(\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{+}K_{n}^{\prime }(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right.\\ \displaystyle \qquad +\,\left.\frac{\unicode[STIX]{x1D716}N\sin N\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719})^{2}}\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{+}(\text{i}n)K_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right)\\ \displaystyle \quad =\left(\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{-}I_{n}^{\prime }(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right.\\ \displaystyle \qquad +\,\left.\frac{\unicode[STIX]{x1D716}N\sin N\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719})^{2}}\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{-}(\text{i}n)I_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right),\end{array}\\ \begin{array}{@{}c@{}}\displaystyle \mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{+}K_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}=\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{-}I_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}.\end{array}\end{array}\!\!\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle \left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\left(\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{+}K_{n}^{\prime }(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right.\\ \displaystyle \qquad +\,\left.\frac{\unicode[STIX]{x1D716}N\sin N\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719})^{2}}\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{+}(\text{i}n)K_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right)\\ \displaystyle \quad =\left(\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{-}I_{n}^{\prime }(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right.\\ \displaystyle \qquad +\,\left.\frac{\unicode[STIX]{x1D716}N\sin N\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719})^{2}}\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{-}(\text{i}n)I_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\right),\end{array}\\ \begin{array}{@{}c@{}}\displaystyle \mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{+}K_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}=\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\mathop{\sum }_{n=-\infty }^{\infty }\bar{C}_{n}^{-}I_{n}(\unicode[STIX]{x1D6FC}a(1+\unicode[STIX]{x1D716}\cos N\unicode[STIX]{x1D719}))\text{e}^{\text{i}n\unicode[STIX]{x1D719}}.\end{array}\end{array}\!\!\right\}\end{eqnarray}$$
3.1 Weakly lobed profile
For weakly lobed profile,
![]() $\unicode[STIX]{x1D716}\ll 1$
, therefore we may expand both left- and right-hand sides of (3.4) around
$\unicode[STIX]{x1D716}\ll 1$
, therefore we may expand both left- and right-hand sides of (3.4) around
![]() $\unicode[STIX]{x1D716}=0$
and keep only the first order without causing too much error. In doing so, the first-order equations can be obtained and, after collecting the terms of the same
$\unicode[STIX]{x1D716}=0$
and keep only the first order without causing too much error. In doing so, the first-order equations can be obtained and, after collecting the terms of the same
![]() $\text{e}^{\text{i}n\unicode[STIX]{x1D719}}$
, written as
$\text{e}^{\text{i}n\unicode[STIX]{x1D719}}$
, written as
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle \mathop{\sum }_{n=-\infty }^{\infty }\left[\bar{C}_{n}^{+}K_{n}^{\prime }(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{+}\left(K_{n-N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+K_{n-N}(\unicode[STIX]{x1D6FC}a)\frac{(n-N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right.\\ \displaystyle \qquad \left.+\,C_{n+N}^{+}\left(K_{n+N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}-K_{n+N}(\unicode[STIX]{x1D6FC}a)\frac{(n+N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right]\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\\ \displaystyle \quad =\left(\frac{1}{1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}}\right)\mathop{\sum }_{n=-\infty }^{\infty }\left[\bar{C}_{n}^{-}I_{n}^{\prime }(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{-}\left(I_{n-N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+I_{n-N}(\unicode[STIX]{x1D6FC}a)\frac{(n-N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right.\\ \displaystyle \qquad \left.+\,\bar{C}_{n+N}^{-}\left(I_{n+N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}-I_{n+N}(\unicode[STIX]{x1D6FC}a)\frac{(n+N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right]\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\end{array}\\ \begin{array}{@{}l@{}}\displaystyle \mathop{\sum }_{n=-\infty }^{\infty }\left(\bar{C}_{n}^{+}K_{n}(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{+}K_{n-N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}+\bar{C}_{n+N}^{+}K_{n+N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}\right)\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\\ \displaystyle \quad =\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\mathop{\sum }_{n=-\infty }^{\infty }\!\left(\bar{C}_{n}^{-}I_{n}(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{-}I_{n-N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}+\bar{C}_{n+N}^{-}I_{n+N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}\right)\!\text{e}^{\text{i}n\unicode[STIX]{x1D719}}.\end{array}\end{array}\!\!\!\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle \mathop{\sum }_{n=-\infty }^{\infty }\left[\bar{C}_{n}^{+}K_{n}^{\prime }(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{+}\left(K_{n-N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+K_{n-N}(\unicode[STIX]{x1D6FC}a)\frac{(n-N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right.\\ \displaystyle \qquad \left.+\,C_{n+N}^{+}\left(K_{n+N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}-K_{n+N}(\unicode[STIX]{x1D6FC}a)\frac{(n+N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right]\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\\ \displaystyle \quad =\left(\frac{1}{1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}}\right)\mathop{\sum }_{n=-\infty }^{\infty }\left[\bar{C}_{n}^{-}I_{n}^{\prime }(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{-}\left(I_{n-N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+I_{n-N}(\unicode[STIX]{x1D6FC}a)\frac{(n-N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right.\\ \displaystyle \qquad \left.+\,\bar{C}_{n+N}^{-}\left(I_{n+N}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}-I_{n+N}(\unicode[STIX]{x1D6FC}a)\frac{(n+N)N}{2\unicode[STIX]{x1D6FC}a}\right)\unicode[STIX]{x1D716}\right]\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\end{array}\\ \begin{array}{@{}l@{}}\displaystyle \mathop{\sum }_{n=-\infty }^{\infty }\left(\bar{C}_{n}^{+}K_{n}(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{+}K_{n-N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}+\bar{C}_{n+N}^{+}K_{n+N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}\right)\text{e}^{\text{i}n\unicode[STIX]{x1D719}}\\ \displaystyle \quad =\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\mathop{\sum }_{n=-\infty }^{\infty }\!\left(\bar{C}_{n}^{-}I_{n}(\unicode[STIX]{x1D6FC}a)+\bar{C}_{n-N}^{-}I_{n-N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}+\bar{C}_{n+N}^{-}I_{n+N}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\unicode[STIX]{x1D716}\right)\!\text{e}^{\text{i}n\unicode[STIX]{x1D719}}.\end{array}\end{array}\!\!\!\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The above equations can be written in a more compact matrix form, from which the effects of lobed jets can be seen more clearly. Let
![]() $\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
denote the diagonal matrix
$\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
denote the diagonal matrix
and let
![]() $\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
be
$\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
be
 $$\begin{eqnarray}\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)=\left[\begin{array}{@{}cc@{}}\ldots & \ldots \\ \ldots K_{-N-1}(\unicode[STIX]{x1D6FC}a) & \ldots K_{N-1}(\unicode[STIX]{x1D6FC}a)\ldots \ldots \ldots \\ \ldots \ldots K_{-N}(\unicode[STIX]{x1D6FC}a) & \ldots \ldots K_{N}(\unicode[STIX]{x1D6FC}a)\ldots \ldots \\ \ldots \ldots \ldots K_{-N+1}(\unicode[STIX]{x1D6FC}a) & \ldots \ldots \ldots K_{N+1}(\unicode[STIX]{x1D6FC}a)\ldots \\ \ldots \ldots \ldots \ldots & \ldots \ldots \ldots \ldots \\ \end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)=\left[\begin{array}{@{}cc@{}}\ldots & \ldots \\ \ldots K_{-N-1}(\unicode[STIX]{x1D6FC}a) & \ldots K_{N-1}(\unicode[STIX]{x1D6FC}a)\ldots \ldots \ldots \\ \ldots \ldots K_{-N}(\unicode[STIX]{x1D6FC}a) & \ldots \ldots K_{N}(\unicode[STIX]{x1D6FC}a)\ldots \ldots \\ \ldots \ldots \ldots K_{-N+1}(\unicode[STIX]{x1D6FC}a) & \ldots \ldots \ldots K_{N+1}(\unicode[STIX]{x1D6FC}a)\ldots \\ \ldots \ldots \ldots \ldots & \ldots \ldots \ldots \ldots \\ \end{array}\right],\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)=\left[\begin{array}{@{}cc@{}}\ldots & \ldots \\ \ldots K_{-N-1}(\unicode[STIX]{x1D6FC}a)(-N-1) & \ldots -K_{N-1}(\unicode[STIX]{x1D6FC}a)(N-1)\ldots \ldots \ldots \\ \ldots \ldots K_{-N}(\unicode[STIX]{x1D6FC}a)(-N) & \ldots \ldots -K_{N}(\unicode[STIX]{x1D6FC}a)N\ldots \ldots \\ \ldots \ldots \ldots K_{-N+1}(\unicode[STIX]{x1D6FC}a)(-N+1) & \ldots \ldots \ldots -K_{N+1}(\unicode[STIX]{x1D6FC}a)(N+1)\ldots \\ \ldots \ldots \ldots \ldots & \ldots \ldots \ldots \ldots \\ \end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)=\left[\begin{array}{@{}cc@{}}\ldots & \ldots \\ \ldots K_{-N-1}(\unicode[STIX]{x1D6FC}a)(-N-1) & \ldots -K_{N-1}(\unicode[STIX]{x1D6FC}a)(N-1)\ldots \ldots \ldots \\ \ldots \ldots K_{-N}(\unicode[STIX]{x1D6FC}a)(-N) & \ldots \ldots -K_{N}(\unicode[STIX]{x1D6FC}a)N\ldots \ldots \\ \ldots \ldots \ldots K_{-N+1}(\unicode[STIX]{x1D6FC}a)(-N+1) & \ldots \ldots \ldots -K_{N+1}(\unicode[STIX]{x1D6FC}a)(N+1)\ldots \\ \ldots \ldots \ldots \ldots & \ldots \ldots \ldots \ldots \\ \end{array}\right].\end{eqnarray}$$
Clearly, each element of the matrices
![]() $\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
,
$\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
,
![]() $\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
is a function of
$\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
is a function of
![]() $\unicode[STIX]{x1D6FC}a$
and, consequently, these matrices are essentially function matrices with an argument
$\unicode[STIX]{x1D6FC}a$
and, consequently, these matrices are essentially function matrices with an argument
![]() $\unicode[STIX]{x1D6FC}a$
. We can therefore define the
$\unicode[STIX]{x1D6FC}a$
. We can therefore define the
![]() $n$
th derivative of a matrix to be the matrix formed by the
$n$
th derivative of a matrix to be the matrix formed by the
![]() $n$
th derivative of each element function. For example, the first derivative of
$n$
th derivative of each element function. For example, the first derivative of
![]() $\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
is
$\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)=\left[\begin{array}{@{}cc@{}}\ldots & \ldots \\ \ldots K_{-N-1}^{\prime }(\unicode[STIX]{x1D6FC}a) & \ldots K_{N-1}^{\prime }(\unicode[STIX]{x1D6FC}a)\ldots \ldots \ldots \\ \ldots \ldots K_{-N}^{\prime }(\unicode[STIX]{x1D6FC}a) & \ldots \ldots K_{N}^{\prime }(\unicode[STIX]{x1D6FC}a)\ldots \ldots \\ \ldots \ldots \ldots K_{-N+1}^{\prime }(\unicode[STIX]{x1D6FC}a) & \ldots \ldots \ldots K_{N+1}^{\prime }(\unicode[STIX]{x1D6FC}a)\ldots \\ \ldots \ldots \ldots \ldots & \ldots \ldots \ldots \ldots \\ \end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)=\left[\begin{array}{@{}cc@{}}\ldots & \ldots \\ \ldots K_{-N-1}^{\prime }(\unicode[STIX]{x1D6FC}a) & \ldots K_{N-1}^{\prime }(\unicode[STIX]{x1D6FC}a)\ldots \ldots \ldots \\ \ldots \ldots K_{-N}^{\prime }(\unicode[STIX]{x1D6FC}a) & \ldots \ldots K_{N}^{\prime }(\unicode[STIX]{x1D6FC}a)\ldots \ldots \\ \ldots \ldots \ldots K_{-N+1}^{\prime }(\unicode[STIX]{x1D6FC}a) & \ldots \ldots \ldots K_{N+1}^{\prime }(\unicode[STIX]{x1D6FC}a)\ldots \\ \ldots \ldots \ldots \ldots & \ldots \ldots \ldots \ldots \\ \end{array}\right].\end{eqnarray}$$
If one replaces the modified Bessel function of the second kind
![]() $K_{n}(\unicode[STIX]{x1D6FC}a)$
, in matrices
$K_{n}(\unicode[STIX]{x1D6FC}a)$
, in matrices
![]() $\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
,
$\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
,
![]() $\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D646}_{c}(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
, with function
$\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
, with function
![]() $\unicode[STIX]{x1D644}_{n}(\unicode[STIX]{x1D6FC}a)$
, the matrices
$\unicode[STIX]{x1D644}_{n}(\unicode[STIX]{x1D6FC}a)$
, the matrices
![]() $\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)$
,
$\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)$
,
![]() $\unicode[STIX]{x1D644}_{c}(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D644}_{c}(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)$
can be similarly defined. Upon defining the vector
$\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)$
can be similarly defined. Upon defining the vector
where
![]() $[~\,]^{\text{T}}$
denotes the transpose of matrix
$[~\,]^{\text{T}}$
denotes the transpose of matrix
![]() $[~\,]$
, equation (3.5) can be readily written as
$[~\,]$
, equation (3.5) can be readily written as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle \left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\left[\unicode[STIX]{x1D646}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D646}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)\right]\bar{\boldsymbol{C}}^{+}\\ \displaystyle \quad =\left[\unicode[STIX]{x1D644}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D644}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)\right]\bar{\boldsymbol{C}}^{-},\end{array}\\ \displaystyle \left[\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\right]\bar{\boldsymbol{C}}^{+}=\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\left[\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D644}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\right]\bar{\boldsymbol{C}}^{-}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle \left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\left[\unicode[STIX]{x1D646}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D646}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)\right]\bar{\boldsymbol{C}}^{+}\\ \displaystyle \quad =\left[\unicode[STIX]{x1D644}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D644}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)\right]\bar{\boldsymbol{C}}^{-},\end{array}\\ \displaystyle \left[\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\right]\bar{\boldsymbol{C}}^{+}=\left(1-\frac{\unicode[STIX]{x1D6FC}U}{\unicode[STIX]{x1D714}}\right)\left[\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D644}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}\right]\bar{\boldsymbol{C}}^{-}.\end{array}\right\}\end{eqnarray}$$
Equation (3.11) represents the dispersion relation for the considered lobed jet to the first-order accuracy. It is worth noting that both
![]() $\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)$
are diagonal matrices. Therefore, in the case of
$\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)$
are diagonal matrices. Therefore, in the case of
![]() $\unicode[STIX]{x1D716}=0$
, i.e. the axisymmetric vortex sheet, equation (3.11) represents a set of decoupled dispersion relation equations. Consequently, stability analysis can be performed for each mode individually and the results are identical to those obtained by Batchelor & Gill (Reference Batchelor and Gill1962), as shown above. When
$\unicode[STIX]{x1D716}=0$
, i.e. the axisymmetric vortex sheet, equation (3.11) represents a set of decoupled dispersion relation equations. Consequently, stability analysis can be performed for each mode individually and the results are identical to those obtained by Batchelor & Gill (Reference Batchelor and Gill1962), as shown above. When
![]() $\unicode[STIX]{x1D716}\neq 0$
, the equations governing the dispersion relations are coupled equations, hence the equations must be solved together.
$\unicode[STIX]{x1D716}\neq 0$
, the equations governing the dispersion relations are coupled equations, hence the equations must be solved together.
Before proceeding to solve these equations, it is informative to examine how lobed vortex-sheet profiles affect the characteristic matrices. First, one can see that the coupling only occurs between modes
![]() $n$
,
$n$
,
![]() $n-N$
and
$n-N$
and
![]() $n+N$
. Had we included higher-order terms (
$n+N$
. Had we included higher-order terms (
![]() $\unicode[STIX]{x1D716}^{2},\unicode[STIX]{x1D716}^{3},\ldots$
), the coupling would involve modes
$\unicode[STIX]{x1D716}^{2},\unicode[STIX]{x1D716}^{3},\ldots$
), the coupling would involve modes
![]() $n\pm kN$
(
$n\pm kN$
(
![]() $k=0,\pm 1,\pm 2,\ldots$
). This shows that the lobed profile affects the instability waves by modulating them with its own periodicity. Second, the modulating effects occur in two ways: modifying the radial length scales and changing the normal directions of vortex sheet. The effects of modifying the radial length scales are represented by the
$k=0,\pm 1,\pm 2,\ldots$
). This shows that the lobed profile affects the instability waves by modulating them with its own periodicity. Second, the modulating effects occur in two ways: modifying the radial length scales and changing the normal directions of vortex sheet. The effects of modifying the radial length scales are represented by the
![]() $\unicode[STIX]{x1D646}_{c}^{(i)}(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D646}_{c}^{(i)}(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D644}_{c}^{(i)}(\unicode[STIX]{x1D6FC}a)$
matrices (
$\unicode[STIX]{x1D644}_{c}^{(i)}(\unicode[STIX]{x1D6FC}a)$
matrices (
![]() $i$
here denotes the
$i$
here denotes the
![]() $i$
th derivative). Take the strongly-lobed profile of
$i$
th derivative). Take the strongly-lobed profile of
![]() $N=2$
, as shown in figure 3(b), as an example. At such a large value of
$N=2$
, as shown in figure 3(b), as an example. At such a large value of
![]() $\unicode[STIX]{x1D716}$
, the lobe profile resembles that of an elliptic vortex sheet. Hence, the radial length scales of the major and the minor axes are different. It is known that this causes different behaviour for instability waves orientated with different axes (Crighton Reference Crighton1973). In the dynamic boundary conditions shown in (3.11), the
$\unicode[STIX]{x1D716}$
, the lobe profile resembles that of an elliptic vortex sheet. Hence, the radial length scales of the major and the minor axes are different. It is known that this causes different behaviour for instability waves orientated with different axes (Crighton Reference Crighton1973). In the dynamic boundary conditions shown in (3.11), the
![]() $\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D644}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)$
terms account for the different length scales (to the first-order accuracy) and ensure pressure is continuous across the vortex sheet. The
$\unicode[STIX]{x1D644}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)$
terms account for the different length scales (to the first-order accuracy) and ensure pressure is continuous across the vortex sheet. The
![]() $\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
and
$\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)$
and
![]() $\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)$
matrices, on the other hand, account for changing of the restrictions on the normal perturbation velocities across the vortex sheet. Equation (2.25a
) shows that it is the normal (to the vortex sheet) perturbation velocities that have to satisfy the jump condition. From (3.3) it is evident that the use of lobed nozzles can significantly change the local normal directions of the vortex sheet and, hence, the instability characteristics. In addition, it is clear from (3.3) that the normal direction changes more pronouncedly as
$\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)$
matrices, on the other hand, account for changing of the restrictions on the normal perturbation velocities across the vortex sheet. Equation (2.25a
) shows that it is the normal (to the vortex sheet) perturbation velocities that have to satisfy the jump condition. From (3.3) it is evident that the use of lobed nozzles can significantly change the local normal directions of the vortex sheet and, hence, the instability characteristics. In addition, it is clear from (3.3) that the normal direction changes more pronouncedly as
![]() $N$
increases.
$N$
increases.
To solve (3.11), we write the two matrix equations in a more compact form as
From (3.13b ), we see that
Substituting (3.14) into (3.13a ), we have
Upon multiplying
![]() $\widetilde{\unicode[STIX]{x1D644}}_{k}^{-1}$
on both sides of (3.15) and defining
$\widetilde{\unicode[STIX]{x1D644}}_{k}^{-1}$
on both sides of (3.15) and defining
![]() $\unicode[STIX]{x1D63C}=\widetilde{\unicode[STIX]{x1D644}}_{k}^{\,-1}\widetilde{\unicode[STIX]{x1D646}}_{k}\widetilde{\unicode[STIX]{x1D646}}_{d}^{-1}\widetilde{\unicode[STIX]{x1D644}}_{d}$
, we obtain the following eigenvalue problem
$\unicode[STIX]{x1D63C}=\widetilde{\unicode[STIX]{x1D644}}_{k}^{\,-1}\widetilde{\unicode[STIX]{x1D646}}_{k}\widetilde{\unicode[STIX]{x1D646}}_{d}^{-1}\widetilde{\unicode[STIX]{x1D644}}_{d}$
, we obtain the following eigenvalue problem
where
The matrix
![]() $\unicode[STIX]{x1D63C}$
is of an infinite dimension. To calculate its eigenvalues in practical cases, we may drop all the modes higher than
$\unicode[STIX]{x1D63C}$
is of an infinite dimension. To calculate its eigenvalues in practical cases, we may drop all the modes higher than
![]() $M$
(and less than
$M$
(and less than
![]() $-M$
). Though we expect results to become inaccurate for large modes close to
$-M$
). Though we expect results to become inaccurate for large modes close to
![]() $M$
, it may yield satisfactory results for relatively low-order modes when
$M$
, it may yield satisfactory results for relatively low-order modes when
![]() $M$
is taken to be adequately large. These low-order modes are of our primary interest in this study, since high-order modes vanish sufficiently quickly according to experimental results (Tinney & Jordan Reference Tinney and Jordan2008). In addition, the vortex-sheet assumption would fail for high-order modes anyway. By truncating high-order terms, we obtain a matrix of
$M$
is taken to be adequately large. These low-order modes are of our primary interest in this study, since high-order modes vanish sufficiently quickly according to experimental results (Tinney & Jordan Reference Tinney and Jordan2008). In addition, the vortex-sheet assumption would fail for high-order modes anyway. By truncating high-order terms, we obtain a matrix of
![]() $(2M+1)\times (2M+1)$
, and there are
$(2M+1)\times (2M+1)$
, and there are
![]() $2M+1$
eigenvalues (degenerate eigenvalues are counted more than once) and their corresponding eigenvectors. For each obtained eigenvector
$2M+1$
eigenvalues (degenerate eigenvalues are counted more than once) and their corresponding eigenvectors. For each obtained eigenvector
![]() $\boldsymbol{C}^{-}$
, we can obtain the corresponding
$\boldsymbol{C}^{-}$
, we can obtain the corresponding
![]() $\boldsymbol{C}^{+}$
easily from (3.14). The fact that the non-zero eigenvector
$\boldsymbol{C}^{+}$
easily from (3.14). The fact that the non-zero eigenvector
![]() $\boldsymbol{C}^{-}$
satisfies (3.16) entails that the non-trivial velocity potential
$\boldsymbol{C}^{-}$
satisfies (3.16) entails that the non-trivial velocity potential
![]() $\unicode[STIX]{x1D713}^{-}$
, determined by
$\unicode[STIX]{x1D713}^{-}$
, determined by
![]() $\boldsymbol{C}^{-}$
, and the corresponding
$\boldsymbol{C}^{-}$
, and the corresponding
![]() $\unicode[STIX]{x1D713}^{+}$
, determined by
$\unicode[STIX]{x1D713}^{+}$
, determined by
![]() $\boldsymbol{C}^{+}$
, satisfy both the kinematic and dynamic boundary conditions on the vortex sheet. Therefore, each eigenvector represents an eigenfunction of the lobed problem, i.e.
$\boldsymbol{C}^{+}$
, satisfy both the kinematic and dynamic boundary conditions on the vortex sheet. Therefore, each eigenvector represents an eigenfunction of the lobed problem, i.e.
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\mathop{\sum }_{n=-\infty }^{\infty }C_{n}^{-}\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\\ \displaystyle E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\mathop{\sum }_{n=-\infty }^{\infty }C_{n}^{+}\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\mathop{\sum }_{n=-\infty }^{\infty }C_{n}^{-}\frac{1}{I_{n}(\unicode[STIX]{x1D6FC}a)}I_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}},\\ \displaystyle E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\mathop{\sum }_{n=-\infty }^{\infty }C_{n}^{+}\frac{1}{K_{n}(\unicode[STIX]{x1D6FC}a)}K_{n}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E})\text{e}^{\text{i}n\unicode[STIX]{x1D719}}.\end{array}\right\}\end{eqnarray}$$
One can readily verify that, when
![]() $\boldsymbol{C}^{-}$
is normalized such that
$\boldsymbol{C}^{-}$
is normalized such that
![]() $(\boldsymbol{C}^{-})^{\ast \text{T}}\boldsymbol{C}^{-}=1$
and
$(\boldsymbol{C}^{-})^{\ast \text{T}}\boldsymbol{C}^{-}=1$
and
![]() $\boldsymbol{C}^{+}$
is obtained from the dynamic boundary conditions shown in (3.14), both
$\boldsymbol{C}^{+}$
is obtained from the dynamic boundary conditions shown in (3.14), both
![]() $E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
$E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
![]() $E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are normalized as described in § 2.2.
$E_{n}^{+}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
are normalized as described in § 2.2.
3.2 The mode labelling strategy
When
![]() $\unicode[STIX]{x1D716}=0$
, there is a well-defined mode number for each mode. For example, mode
$\unicode[STIX]{x1D716}=0$
, there is a well-defined mode number for each mode. For example, mode
![]() $n$
can be defined as the eigenvector
$n$
can be defined as the eigenvector
When
![]() $\unicode[STIX]{x1D716}\neq 0$
, however, the eigenvector does not posses this simple property. Instead, the resulting eigenvector has other non-vanishing elements in addition to
$\unicode[STIX]{x1D716}\neq 0$
, however, the eigenvector does not posses this simple property. Instead, the resulting eigenvector has other non-vanishing elements in addition to
![]() $C_{n}^{-}$
. We need to develop an unambiguous strategy to label the eigenmodes.
$C_{n}^{-}$
. We need to develop an unambiguous strategy to label the eigenmodes.
We can show that the eigenvector
![]() $\boldsymbol{C}^{-}$
can be always defined as either symmetric or antisymmetric (with respect to the element of index
$\boldsymbol{C}^{-}$
can be always defined as either symmetric or antisymmetric (with respect to the element of index
![]() $0$
). This is due to the rotationally symmetric property possessed by the matrix
$0$
). This is due to the rotationally symmetric property possessed by the matrix
![]() $\unicode[STIX]{x1D63C}$
, and for brevity we have placed detailed derivation in appendix B.
$\unicode[STIX]{x1D63C}$
, and for brevity we have placed detailed derivation in appendix B.
Based on this property, we define an eigenvector to have a mode number
![]() $n$
if it is symmetric and
$n$
if it is symmetric and
 $$\begin{eqnarray}\Vert \boldsymbol{C}^{-}-\boldsymbol{G}\Vert =\sqrt{\mathop{\sum }_{j=-M}^{M}(|C_{j}^{-}|-G_{j})^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{C}^{-}-\boldsymbol{G}\Vert =\sqrt{\mathop{\sum }_{j=-M}^{M}(|C_{j}^{-}|-G_{j})^{2}}\end{eqnarray}$$
yields a minimum value when
![]() $n$
varies from
$n$
varies from
![]() $-M$
to
$-M$
to
![]() $M$
and
$M$
and
where
![]() $g_{n}$
is the element of the gauge vector
$g_{n}$
is the element of the gauge vector
![]() $\boldsymbol{G}$
. For antisymmetric eigenvectors we label it as
$\boldsymbol{G}$
. For antisymmetric eigenvectors we label it as
![]() $-n$
in a similar manner. For
$-n$
in a similar manner. For
![]() $n=0$
, it is trivial to label its mode number and it can be shown that it is a symmetric vector. By labelling the eigenvectors in this way, equation (3.18) implies that all nonnegative eigenfunctions are even functions of
$n=0$
, it is trivial to label its mode number and it can be shown that it is a symmetric vector. By labelling the eigenvectors in this way, equation (3.18) implies that all nonnegative eigenfunctions are even functions of
![]() $\unicode[STIX]{x1D719}$
and negative ones odd.
$\unicode[STIX]{x1D719}$
and negative ones odd.
In the following analysis, the mode number for the obtained eigenfunction is designated according to the above conventions. Then for each mode
![]() $n$
, we can calculate its corresponding eigenvalue
$n$
, we can calculate its corresponding eigenvalue
![]() $\unicode[STIX]{x1D706}_{n}$
at a given value of
$\unicode[STIX]{x1D706}_{n}$
at a given value of
![]() $\unicode[STIX]{x1D6FC}a$
. The complex frequency
$\unicode[STIX]{x1D6FC}a$
. The complex frequency
![]() $\unicode[STIX]{x1D714}$
can be directly obtained from
$\unicode[STIX]{x1D714}$
can be directly obtained from
![]() $\unicode[STIX]{x1D706}_{n}$
according to (3.17). This complex number determines both the growth rate and the convection velocity of its corresponding instability wave. Therefore, by varying the values of
$\unicode[STIX]{x1D706}_{n}$
according to (3.17). This complex number determines both the growth rate and the convection velocity of its corresponding instability wave. Therefore, by varying the values of
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $N$
, one can easily examine how different lobed geometry changes both the growth rate and convection velocity of instability waves of different mode numbers.
$N$
, one can easily examine how different lobed geometry changes both the growth rate and convection velocity of instability waves of different mode numbers.
3.3 Strongly lobed nozzle
For strongly lobed nozzles, e.g.
![]() $\unicode[STIX]{x1D716}\sim 0.2$
, it is necessary to include high-order terms
$\unicode[STIX]{x1D716}\sim 0.2$
, it is necessary to include high-order terms
![]() $\unicode[STIX]{x1D716}^{n}$
. Luckily this is not a difficult extension, and all the aforementioned procedures used to solve the eigenvalue problem remain the same. It suffices to find the high-order coefficient matrices and add them into (3.11), i.e.
$\unicode[STIX]{x1D716}^{n}$
. Luckily this is not a difficult extension, and all the aforementioned procedures used to solve the eigenvalue problem remain the same. It suffices to find the high-order coefficient matrices and add them into (3.11), i.e.
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D646}_{k}=\unicode[STIX]{x1D646}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D646}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D644}_{k}=\unicode[STIX]{x1D644}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D644}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D646}_{d}=\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D644}_{d}=\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D644}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D646}_{k}=\unicode[STIX]{x1D646}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D646}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D646}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D644}_{k}=\unicode[STIX]{x1D644}^{\prime }(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\left(\unicode[STIX]{x1D644}_{c}^{\prime \prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D644}_{s}(\unicode[STIX]{x1D6FC}a)\frac{N}{2\unicode[STIX]{x1D6FC}a}\right)+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D646}_{d}=\unicode[STIX]{x1D646}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D646}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D644}_{d}=\unicode[STIX]{x1D644}(\unicode[STIX]{x1D6FC}a)+\unicode[STIX]{x1D716}\unicode[STIX]{x1D644}_{c}^{\prime }(\unicode[STIX]{x1D6FC}a)\frac{\unicode[STIX]{x1D6FC}a}{2}+\unicode[STIX]{x1D716}^{2}(\cdots \,)+\cdots \,.\end{array}\right\}\end{eqnarray}$$
It is worth noting that incorporating higher-order terms does not invalidate the matrix
![]() $\unicode[STIX]{x1D63C}$
being rotationally symmetric, hence all the previous conclusions about its eigenvectors still remain valid. Owing to the nature of higher-order modified Bessel functions, expanding them around
$\unicode[STIX]{x1D63C}$
being rotationally symmetric, hence all the previous conclusions about its eigenvectors still remain valid. Owing to the nature of higher-order modified Bessel functions, expanding them around
![]() $\unicode[STIX]{x1D6FC}a$
results in a slow convergence when
$\unicode[STIX]{x1D6FC}a$
results in a slow convergence when
![]() $\unicode[STIX]{x1D716}$
is large. Therefore, the number of high-order terms needed increases quickly as
$\unicode[STIX]{x1D716}$
is large. Therefore, the number of high-order terms needed increases quickly as
![]() $\unicode[STIX]{x1D716}$
increases. It also increases when we increase the value of
$\unicode[STIX]{x1D716}$
increases. It also increases when we increase the value of
![]() $M$
. However, this problem can be overcome by expanding properly scaled modified Bessel functions. Since in this study we only need a relatively small
$M$
. However, this problem can be overcome by expanding properly scaled modified Bessel functions. Since in this study we only need a relatively small
![]() $M$
, and the extension of incorporating more higher-order terms can be promptly automated using computer programming, it is not strictly necessary to expand the scaled modified Bessel functions instead. For example, a MATLAB code has been developed that can automatically incorporate as many orders of terms as needed. Owing to its analytical nature, the computation is very fast. For example, a comprehensive eigenvalue analysis of order
$M$
, and the extension of incorporating more higher-order terms can be promptly automated using computer programming, it is not strictly necessary to expand the scaled modified Bessel functions instead. For example, a MATLAB code has been developed that can automatically incorporate as many orders of terms as needed. Owing to its analytical nature, the computation is very fast. For example, a comprehensive eigenvalue analysis of order
![]() $10$
with
$10$
with
![]() $M=20$
takes less than 50 ms. All the results shown in the following sections are obtained by incorporating higher-order terms to the order of
$M=20$
takes less than 50 ms. All the results shown in the following sections are obtained by incorporating higher-order terms to the order of
![]() $10$
(
$10$
(
![]() $\unicode[STIX]{x1D716}^{10}$
) and with
$\unicode[STIX]{x1D716}^{10}$
) and with
![]() $M=20$
. A convergence analysis, to be shown in § 4.1, shows that this is much more than necessary.
$M=20$
. A convergence analysis, to be shown in § 4.1, shows that this is much more than necessary.
4 Validation and results
As mentioned in the preceding section, both the temporal growth rate and convection velocity of the instability waves can be readily obtained from (3.17). In this section, we present the rich results obtained from this procedure.
4.1 Convergence analysis
We first examine the convergence characteristics of this new method when the order of accuracy
![]() $m$
(
$m$
(
![]() $\unicode[STIX]{x1D716}^{m}$
) and
$\unicode[STIX]{x1D716}^{m}$
) and
![]() $M$
change. To separate the effects of
$M$
change. To separate the effects of
![]() $m$
and
$m$
and
![]() $M$
, we can fix
$M$
, we can fix
![]() $M$
and vary the values of
$M$
and vary the values of
![]() $m$
and then vice versa. For brevity, we choose to present the convection velocity and temporal growth rate of mode
$m$
and then vice versa. For brevity, we choose to present the convection velocity and temporal growth rate of mode
![]() $1$
instability wave and fix the number of lobes
$1$
instability wave and fix the number of lobes
![]() $N=2$
.
$N=2$
.

Figure 4. The convergence of the temporal growth rate and convection velocity for the mode
![]() $1$
instability wave when
$1$
instability wave when
![]() $N=2$
and
$N=2$
and
![]() $\unicode[STIX]{x1D716}=0.1$
: (a) the order of accuracy is fixed at
$\unicode[STIX]{x1D716}=0.1$
: (a) the order of accuracy is fixed at
![]() $\unicode[STIX]{x1D716}^{10}$
while
$\unicode[STIX]{x1D716}^{10}$
while
![]() $M$
varies from
$M$
varies from
![]() $2$
to
$2$
to
![]() $8$
; (b)
$8$
; (b)
![]() $M$
is fixed to be
$M$
is fixed to be
![]() $20$
while the order of accuracy varies from
$20$
while the order of accuracy varies from
![]() $\unicode[STIX]{x1D716}^{2}$
to
$\unicode[STIX]{x1D716}^{2}$
to
![]() $\unicode[STIX]{x1D716}^{7}$
.
$\unicode[STIX]{x1D716}^{7}$
.
We first show the results for a relatively small penetration ratio, i.e.
![]() $\unicode[STIX]{x1D716}=0.1$
. The results are shown in figure 4. For a compact presentation, we define a complex number
$\unicode[STIX]{x1D716}=0.1$
. The results are shown in figure 4. For a compact presentation, we define a complex number
![]() $U_{c}\equiv \unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FC}$
. Therefore, the real part of
$U_{c}\equiv \unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FC}$
. Therefore, the real part of
![]() $U_{c}$
denotes the convection velocity while the imaginary part represents the temporal growth rate. Figure 4 shows the real and imaginary parts of
$U_{c}$
denotes the convection velocity while the imaginary part represents the temporal growth rate. Figure 4 shows the real and imaginary parts of
![]() $U_{c}$
.
$U_{c}$
.
Figure 4(a) shows the results when
![]() $m=10$
and
$m=10$
and
![]() $M$
varies from
$M$
varies from
![]() $2$
to
$2$
to
![]() $8$
. One can see that both the growth rates and convection velocities are hardly distinguishable. This shows that, for a small value of
$8$
. One can see that both the growth rates and convection velocities are hardly distinguishable. This shows that, for a small value of
![]() $\unicode[STIX]{x1D716}\approx 0.1$
,
$\unicode[STIX]{x1D716}\approx 0.1$
,
![]() $M=2$
is essentially sufficient, at least for the mode number
$M=2$
is essentially sufficient, at least for the mode number
![]() $1$
. Of course, we would need a slightly larger value of
$1$
. Of course, we would need a slightly larger value of
![]() $M$
if we were to consider higher-order modes. However, this increase in
$M$
if we were to consider higher-order modes. However, this increase in
![]() $M$
is likely to be on a small scale, because we are only interested in low-order modes as only those are physically relevant in experiments. Figure 4(b) shows the results when
$M$
is likely to be on a small scale, because we are only interested in low-order modes as only those are physically relevant in experiments. Figure 4(b) shows the results when
![]() $M$
is fixed at
$M$
is fixed at
![]() $20$
and
$20$
and
![]() $m$
varies from
$m$
varies from
![]() $2$
to
$2$
to
![]() $7$
. Similar to figure 4(a), the lines are nearly on top of each other. This shows that for
$7$
. Similar to figure 4(a), the lines are nearly on top of each other. This shows that for
![]() $\unicode[STIX]{x1D716}\approx 0.1$
, a second-order accuracy is sufficient for a good convergence.
$\unicode[STIX]{x1D716}\approx 0.1$
, a second-order accuracy is sufficient for a good convergence.
As mentioned in § 3.3, owing to the nature of the modified Bessel functions, the number of high-order
![]() $\unicode[STIX]{x1D716}^{n}$
terms needed increases quickly as
$\unicode[STIX]{x1D716}^{n}$
terms needed increases quickly as
![]() $\unicode[STIX]{x1D716}$
increases. To show that
$\unicode[STIX]{x1D716}$
increases. To show that
![]() $M=20$
and
$M=20$
and
![]() $m=10$
is also sufficient for a large value of
$m=10$
is also sufficient for a large value of
![]() $\unicode[STIX]{x1D716}$
, we present the convergence characteristics of this analysis when
$\unicode[STIX]{x1D716}$
, we present the convergence characteristics of this analysis when
![]() $\unicode[STIX]{x1D716}=0.2$
in figure 5.
$\unicode[STIX]{x1D716}=0.2$
in figure 5.
Figure 5(a) shows the results when
![]() $m=10$
and
$m=10$
and
![]() $M$
varies from
$M$
varies from
![]() $2$
to
$2$
to
![]() $8$
. We can see that there is an observable difference between the convection velocities calculated using
$8$
. We can see that there is an observable difference between the convection velocities calculated using
![]() $M=2$
and
$M=2$
and
![]() $M=4$
. However, there is little change between the results for
$M=4$
. However, there is little change between the results for
![]() $M=4$
and
$M=4$
and
![]() $M=8$
. This shows that for strongly lobed geometry at
$M=8$
. This shows that for strongly lobed geometry at
![]() $\unicode[STIX]{x1D716}\approx 0.2$
,
$\unicode[STIX]{x1D716}\approx 0.2$
,
![]() $M$
must be at least
$M$
must be at least
![]() $4$
. On the other hand, it is interesting to see that the temporal growth rate is much less sensitive to the change in
$4$
. On the other hand, it is interesting to see that the temporal growth rate is much less sensitive to the change in
![]() $M$
than the convection velocity. Figure 5(b) similarly shows the results for a fixed number
$M$
than the convection velocity. Figure 5(b) similarly shows the results for a fixed number
![]() $M=20$
and a varying
$M=20$
and a varying
![]() $m$
. The observation is similar to figure 5(a), and it shows that for
$m$
. The observation is similar to figure 5(a), and it shows that for
![]() $\unicode[STIX]{x1D716}\approx 0.2$
, a high-order accuracy up to
$\unicode[STIX]{x1D716}\approx 0.2$
, a high-order accuracy up to
![]() $\unicode[STIX]{x1D716}^{4}$
or
$\unicode[STIX]{x1D716}^{4}$
or
![]() $\unicode[STIX]{x1D716}^{6}$
is recommended. In summary, the results in this section show that
$\unicode[STIX]{x1D716}^{6}$
is recommended. In summary, the results in this section show that
![]() $M=20$
and
$M=20$
and
![]() $n=10$
can ensure that the obtained eigensolutions are well converged.
$n=10$
can ensure that the obtained eigensolutions are well converged.

Figure 5. The convergence of the temporal growth rate and convection velocity for the mode
![]() $1$
instability wave when
$1$
instability wave when
![]() $N=2$
and
$N=2$
and
![]() $\unicode[STIX]{x1D716}=0.2$
: (a) the order of accuracy is fixed at
$\unicode[STIX]{x1D716}=0.2$
: (a) the order of accuracy is fixed at
![]() $\unicode[STIX]{x1D716}^{10}$
while
$\unicode[STIX]{x1D716}^{10}$
while
![]() $M$
varies from
$M$
varies from
![]() $2$
to
$2$
to
![]() $8$
; (b)
$8$
; (b)
![]() $M$
is fixed to be
$M$
is fixed to be
![]() $20$
while the order of accuracy varies from
$20$
while the order of accuracy varies from
![]() $\unicode[STIX]{x1D716}^{2}$
to
$\unicode[STIX]{x1D716}^{2}$
to
![]() $\unicode[STIX]{x1D716}^{7}$
.
$\unicode[STIX]{x1D716}^{7}$
.
4.2 Validation
Section 4.1 merely shows that
![]() $M=20$
and
$M=20$
and
![]() $n=10$
are sufficient for a good convergence. A converged solution, however, does not always imply a correct one. Consequently, before presenting any results, it is necessary to validate this new analysis framework. Luckily, it is very straightforward to do so. Since the entire analysis is devoted to calculating the eigenfunctions that satisfy both the kinematic and dynamic boundary conditions on the vortex sheet, we can examine the obtained eigenfunctions to ensure that they do indeed satisfy the two boundary conditions. More precisely, we can show that for each pair of eigenfunctions obtained above, we have, on the vortex sheet,
$n=10$
are sufficient for a good convergence. A converged solution, however, does not always imply a correct one. Consequently, before presenting any results, it is necessary to validate this new analysis framework. Luckily, it is very straightforward to do so. Since the entire analysis is devoted to calculating the eigenfunctions that satisfy both the kinematic and dynamic boundary conditions on the vortex sheet, we can examine the obtained eigenfunctions to ensure that they do indeed satisfy the two boundary conditions. More precisely, we can show that for each pair of eigenfunctions obtained above, we have, on the vortex sheet,

Figure 6. The match validation of the dynamic (a,c,e) and kinematic (b,d,f) boundary conditions for the eigenfunctions of modes
![]() $\pm 2$
when the number of lobes
$\pm 2$
when the number of lobes
![]() $N$
are different: (a,b)
$N$
are different: (a,b)
![]() $N=1$
; (c,d)
$N=1$
; (c,d)
![]() $N=2$
; (e,f)
$N=2$
; (e,f)
![]() $N=3$
. The normalized wavenumber is
$N=3$
. The normalized wavenumber is
![]() $\unicode[STIX]{x1D6FC}a=1$
and the lobed profile has a penetration ratio
$\unicode[STIX]{x1D6FC}a=1$
and the lobed profile has a penetration ratio
![]() $\unicode[STIX]{x1D716}=0.1$
.
$\unicode[STIX]{x1D716}=0.1$
.
Figure 6 shows how the boundary conditions are satisfied by the eigenfunctions of modes
![]() $\pm 2$
. These results are obtained with
$\pm 2$
. These results are obtained with
![]() $\unicode[STIX]{x1D6FC}a=1$
and
$\unicode[STIX]{x1D6FC}a=1$
and
![]() $\unicode[STIX]{x1D716}=0.1$
. Figures 6(a) and 6(b) show the matches of the left- and right-hand sides of (4.1b
) and (4.1a
), respectively, when the number of lobes is
$\unicode[STIX]{x1D716}=0.1$
. Figures 6(a) and 6(b) show the matches of the left- and right-hand sides of (4.1b
) and (4.1a
), respectively, when the number of lobes is
![]() $N=1$
. From figure 3(a), one can see that when
$N=1$
. From figure 3(a), one can see that when
![]() $N=1$
, the lobed profile is not very significantly different from the axisymmetric one. The single lobe merely causes a displacement of the profile centre of the circular vortex sheet. Therefore, one expects that the dynamics of instability waves shall remain largely unchanged. Figure 6(a,b) indeed confirms this. Modes
$N=1$
, the lobed profile is not very significantly different from the axisymmetric one. The single lobe merely causes a displacement of the profile centre of the circular vortex sheet. Therefore, one expects that the dynamics of instability waves shall remain largely unchanged. Figure 6(a,b) indeed confirms this. Modes
![]() $2$
and
$2$
and
![]() $-2$
resemble those of an axisymmetric vortex sheet in every aspect. When
$-2$
resemble those of an axisymmetric vortex sheet in every aspect. When
![]() $N$
increases to
$N$
increases to
![]() $2$
, the effects of lobes are more pronounced, as shown in figure 6(c,d). In particular, the symmetric (with respect to
$2$
, the effects of lobes are more pronounced, as shown in figure 6(c,d). In particular, the symmetric (with respect to
![]() $\unicode[STIX]{x1D719}=0$
) eigenfunction shown in figure 6(d) starts to deviate from the normal
$\unicode[STIX]{x1D719}=0$
) eigenfunction shown in figure 6(d) starts to deviate from the normal
![]() $-\text{cos}\,2\unicode[STIX]{x1D719}$
function, with its peak somewhat flattened. The mode
$-\text{cos}\,2\unicode[STIX]{x1D719}$
function, with its peak somewhat flattened. The mode
![]() $-2$
, on the other hand, remains largely similar to
$-2$
, on the other hand, remains largely similar to
![]() $\sin 2\unicode[STIX]{x1D719}$
. When
$\sin 2\unicode[STIX]{x1D719}$
. When
![]() $N$
increases to
$N$
increases to
![]() $3$
, both modes
$3$
, both modes
![]() $2$
and
$2$
and
![]() $-2$
respond to the change of vortex-sheet geometry and change their shapes significantly.
$-2$
respond to the change of vortex-sheet geometry and change their shapes significantly.
It is, however, worth noting that, for
![]() $N=1$
and
$N=1$
and
![]() $N=2$
, the eigenvalues
$N=2$
, the eigenvalues
![]() $\unicode[STIX]{x1D706}_{2}\neq \unicode[STIX]{x1D706}_{-2}$
. Therefore, both
$\unicode[STIX]{x1D706}_{2}\neq \unicode[STIX]{x1D706}_{-2}$
. Therefore, both
![]() $E_{2}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
$E_{2}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
and
![]() $E_{-2}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
have a standing wave pattern with respect to
$E_{-2}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
have a standing wave pattern with respect to
![]() $\unicode[STIX]{x1D719}$
and they cannot be combined to produce a travelling wave. However, for
$\unicode[STIX]{x1D719}$
and they cannot be combined to produce a travelling wave. However, for
![]() $N=3$
we find that
$N=3$
we find that
![]() $\unicode[STIX]{x1D706}_{2}=\unicode[STIX]{x1D706}_{-2}$
. Therefore, a travelling-wave pattern can be obtained. The important observation is that, for all the six figures, exceptionally good matches of the pressure and normal velocity across the layer of vortex sheet are achieved. The excellent agreement seen from figure 6 shows that the analytical framework developed in this section works exceptionally well, at least for the low-order modes such as those we have just shown.
$\unicode[STIX]{x1D706}_{2}=\unicode[STIX]{x1D706}_{-2}$
. Therefore, a travelling-wave pattern can be obtained. The important observation is that, for all the six figures, exceptionally good matches of the pressure and normal velocity across the layer of vortex sheet are achieved. The excellent agreement seen from figure 6 shows that the analytical framework developed in this section works exceptionally well, at least for the low-order modes such as those we have just shown.
4.3 The effects of lobed profiles on the convection velocity and growth rate of instability waves
Having validated the analytical framework, we are now in a position to examine the effects of lobed profiles on the convection velocity and growth rate of instability waves. In the rest of this section, we plot both quantities versus the normalized frequency
![]() $\unicode[STIX]{x1D6FC}a$
, for lobed profiles of different geometry.
$\unicode[STIX]{x1D6FC}a$
, for lobed profiles of different geometry.
We start from showing results for mode
![]() $0$
. These are shown in figure 7. Figure 7(a) shows the convection velocity and growth rate for a single-lobe profile. To facilitate a direct comparison with the results of a cylindrical vortex sheet, both quantities are plotted when
$0$
. These are shown in figure 7. Figure 7(a) shows the convection velocity and growth rate for a single-lobe profile. To facilitate a direct comparison with the results of a cylindrical vortex sheet, both quantities are plotted when
![]() $\unicode[STIX]{x1D716}=0$
first. As can be seen, when the frequency
$\unicode[STIX]{x1D716}=0$
first. As can be seen, when the frequency
![]() $\unicode[STIX]{x1D6FC}a$
increases, the normalized convection velocity (
$\unicode[STIX]{x1D6FC}a$
increases, the normalized convection velocity (
![]() $\text{Re}\,U_{c}/U$
) decreases from unity to around
$\text{Re}\,U_{c}/U$
) decreases from unity to around
![]() $0.5$
, whereas the normalized growth rate (
$0.5$
, whereas the normalized growth rate (
![]() $\text{Im}\,U_{c}/U$
) increases from
$\text{Im}\,U_{c}/U$
) increases from
![]() $0$
to the same limit value. However, it shows that a single lobe does not cause any observable changes to the characteristics of mode
$0$
to the same limit value. However, it shows that a single lobe does not cause any observable changes to the characteristics of mode
![]() $0$
at all frequencies, no matter what value of
$0$
at all frequencies, no matter what value of
![]() $\unicode[STIX]{x1D716}$
is used. The same conclusion can be reached for
$\unicode[STIX]{x1D716}$
is used. The same conclusion can be reached for
![]() $N=2$
, which is shown in figure 7(b). Increasing the number of lobes to
$N=2$
, which is shown in figure 7(b). Increasing the number of lobes to
![]() $3$
, however, starts to cause a slightly larger convection velocity and a marginally lower growth rate. These results are shown in figure 7(c), from which we see that the changes are only observable at high frequencies. However, they become more pronounced when the penetration ratio
$3$
, however, starts to cause a slightly larger convection velocity and a marginally lower growth rate. These results are shown in figure 7(c), from which we see that the changes are only observable at high frequencies. However, they become more pronounced when the penetration ratio
![]() $\unicode[STIX]{x1D716}$
increases. The increase of the convection velocity and the reduction of the temporal growth rate, caused by lobed vortex-sheet profiles, are more evident when the number of lobes is increased to
$\unicode[STIX]{x1D716}$
increases. The increase of the convection velocity and the reduction of the temporal growth rate, caused by lobed vortex-sheet profiles, are more evident when the number of lobes is increased to
![]() $5$
. As shown in figure 7(d), at high frequencies (
$5$
. As shown in figure 7(d), at high frequencies (
![]() $\unicode[STIX]{x1D6FC}a>1.5$
), a large penetration ratio results in an effective rise of the convection velocity and a less effective drop of the growth rate. However, one should note that although these changes are observable, they are not in any way significant.
$\unicode[STIX]{x1D6FC}a>1.5$
), a large penetration ratio results in an effective rise of the convection velocity and a less effective drop of the growth rate. However, one should note that although these changes are observable, they are not in any way significant.

Figure 7. The convection velocity and growth rate of the mode
![]() $0$
jet instability waves for vortex sheets of different lobed geometry: (a)
$0$
jet instability waves for vortex sheets of different lobed geometry: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
.
$N=5$
.
The fact that serrations increase the convection velocity and reduce growth rates of mode
![]() $0$
is in accord with the findings of Lajús Jr et al. (Reference Lajús, Cavalieri and Deschamps2015) and Sinha et al. (Reference Sinha, Gudmundsson, Xia and Colonius2016). However, it should be noted that in the work of Sinha et al. (Reference Sinha, Gudmundsson, Xia and Colonius2016), there also exists a low-frequency band where the spatial convection velocity is slightly reduced. Such a difference might be caused by the difference between temporal and spatial analysis, the difference in jet mean flow profiles or the difference in the shear layer thickness.
$0$
is in accord with the findings of Lajús Jr et al. (Reference Lajús, Cavalieri and Deschamps2015) and Sinha et al. (Reference Sinha, Gudmundsson, Xia and Colonius2016). However, it should be noted that in the work of Sinha et al. (Reference Sinha, Gudmundsson, Xia and Colonius2016), there also exists a low-frequency band where the spatial convection velocity is slightly reduced. Such a difference might be caused by the difference between temporal and spatial analysis, the difference in jet mean flow profiles or the difference in the shear layer thickness.

Figure 8. The convection velocity and growth rate of the mode
![]() $1$
jet instability waves for vortex sheets of different lobed geometry: (a)
$1$
jet instability waves for vortex sheets of different lobed geometry: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
(d)
$N=3$
(d)
![]() $N=5$
.
$N=5$
.
Figure 7 shows that instability waves of mode
![]() $0$
are not very sensitive to either the number of lobes or the penetration ratio. Figure 8, however, shows a different story for mode
$0$
are not very sensitive to either the number of lobes or the penetration ratio. Figure 8, however, shows a different story for mode
![]() $1$
. The eigenfunctions corresponding to mode
$1$
. The eigenfunctions corresponding to mode
![]() $1$
are even functions of
$1$
are even functions of
![]() $\unicode[STIX]{x1D719}$
. Figure 8(a) still indicates that a single lobe does not noticeably change the characteristics of the mode
$\unicode[STIX]{x1D719}$
. Figure 8(a) still indicates that a single lobe does not noticeably change the characteristics of the mode
![]() $1$
instability waves. This is somewhat expected. Because, as we observed before, one single lobe merely causes a displacement of the profile’s geometrical centre. Therefore, the physics should more or less stay the same as that of an axisymmetric vortex sheet. This is consistent with the results shown in figure 8(a). However, figure 8(b) shows that the use of two lobes leads to a pronounced increase of the convection velocity, and a slight decrease of the temporal growth rate. In contrast to those shown in figure 7, the increase of the convection velocity is more marked at low frequencies. Similarly, increasing
$1$
instability waves. This is somewhat expected. Because, as we observed before, one single lobe merely causes a displacement of the profile’s geometrical centre. Therefore, the physics should more or less stay the same as that of an axisymmetric vortex sheet. This is consistent with the results shown in figure 8(a). However, figure 8(b) shows that the use of two lobes leads to a pronounced increase of the convection velocity, and a slight decrease of the temporal growth rate. In contrast to those shown in figure 7, the increase of the convection velocity is more marked at low frequencies. Similarly, increasing
![]() $\unicode[STIX]{x1D716}$
results in a stronger rise of the convection velocity. It is very interesting to note that the rise of the convection velocity is nearly linear with respect to
$\unicode[STIX]{x1D716}$
results in a stronger rise of the convection velocity. It is very interesting to note that the rise of the convection velocity is nearly linear with respect to
![]() $\unicode[STIX]{x1D716}$
. The decrease of the temporal growth rate, however, is most notable in the intermediate frequency range, and the maximum decrease is very small. Figure 8(c) shows the results for
$\unicode[STIX]{x1D716}$
. The decrease of the temporal growth rate, however, is most notable in the intermediate frequency range, and the maximum decrease is very small. Figure 8(c) shows the results for
![]() $N=3$
. Compared with figure 8(b), the effects of lobes on both the convection velocity and the growth rate appear to be more effective. The most pronounced change, however, occurs when
$N=3$
. Compared with figure 8(b), the effects of lobes on both the convection velocity and the growth rate appear to be more effective. The most pronounced change, however, occurs when
![]() $N$
increases to
$N$
increases to
![]() $5$
, as shown in figure 8(d). Again, these results are consistent with the findings of Sinha et al. (Reference Sinha, Gudmundsson, Xia and Colonius2016). The dependence of both the convection velocity and the temporal growth rate on
$5$
, as shown in figure 8(d). Again, these results are consistent with the findings of Sinha et al. (Reference Sinha, Gudmundsson, Xia and Colonius2016). The dependence of both the convection velocity and the temporal growth rate on
![]() $\unicode[STIX]{x1D716}$
appears to linear. However, the relative change of the former is significantly larger than that of the latter.
$\unicode[STIX]{x1D716}$
appears to linear. However, the relative change of the former is significantly larger than that of the latter.

Figure 9. The convection velocity and growth rate of the mode
![]() $-1$
jet instability waves for vortex sheets of different lobed geometry: (a)
$-1$
jet instability waves for vortex sheets of different lobed geometry: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
.
$N=5$
.
Figure 9 presents the results for the mode
![]() $-1$
. The eigenfunctions are odd functions of
$-1$
. The eigenfunctions are odd functions of
![]() $\unicode[STIX]{x1D719}$
. Still, figure 9(a) does not show observable changes when
$\unicode[STIX]{x1D719}$
. Still, figure 9(a) does not show observable changes when
![]() $\unicode[STIX]{x1D716}$
increases. However, zooming in this figure, one can see that the convection velocity is weakly increasing as
$\unicode[STIX]{x1D716}$
increases. However, zooming in this figure, one can see that the convection velocity is weakly increasing as
![]() $\unicode[STIX]{x1D716}$
increases, and this is opposite to that observed in figure 8(a). This different behaviour is because
$\unicode[STIX]{x1D716}$
increases, and this is opposite to that observed in figure 8(a). This different behaviour is because
![]() $\unicode[STIX]{x1D706}_{1}$
is no longer identical to
$\unicode[STIX]{x1D706}_{1}$
is no longer identical to
![]() $\unicode[STIX]{x1D706}_{-1}$
. Therefore, the odd and even eigenfunctions are now independent of each other and they change in opposite ways as
$\unicode[STIX]{x1D706}_{-1}$
. Therefore, the odd and even eigenfunctions are now independent of each other and they change in opposite ways as
![]() $\unicode[STIX]{x1D716}$
increases. If figures 9(a) and 8(a) are too similar to each other to make this trend clear, figure 9(b) makes it much more evident. The number of lobes is now two, and the lobed profile is approximately elliptic. Instead of obtaining higher convection velocities, increasing
$\unicode[STIX]{x1D716}$
increases. If figures 9(a) and 8(a) are too similar to each other to make this trend clear, figure 9(b) makes it much more evident. The number of lobes is now two, and the lobed profile is approximately elliptic. Instead of obtaining higher convection velocities, increasing
![]() $\unicode[STIX]{x1D716}$
from
$\unicode[STIX]{x1D716}$
from
![]() $0$
now results in increasingly smaller convection velocities. The temporal growth rate, on the other hand, starts to drop at low frequencies (
$0$
now results in increasingly smaller convection velocities. The temporal growth rate, on the other hand, starts to drop at low frequencies (
![]() $\unicode[STIX]{x1D6FC}a<0.5$
), but gradually changes to increase at high frequencies, although both are on a small scale. The different eigenvalues of modes
$\unicode[STIX]{x1D6FC}a<0.5$
), but gradually changes to increase at high frequencies, although both are on a small scale. The different eigenvalues of modes
![]() $\pm 1$
, hence distinctive characteristics of instability waves of modes
$\pm 1$
, hence distinctive characteristics of instability waves of modes
![]() $\pm 1$
, are consistent with the analytical results obtained by Crighton (Reference Crighton1973) for elliptic vortex sheets and also agree with the findings in the spatial stability analysis carried out by Kopiev et al. (Reference Kopiev, Ostrikov, Chernyshev and Elliot2004) (because the mode number
$\pm 1$
, are consistent with the analytical results obtained by Crighton (Reference Crighton1973) for elliptic vortex sheets and also agree with the findings in the spatial stability analysis carried out by Kopiev et al. (Reference Kopiev, Ostrikov, Chernyshev and Elliot2004) (because the mode number
![]() $1$
is a half of the number of lobes
$1$
is a half of the number of lobes
![]() $N=2$
). Figure 9(c,d) shows the results for
$N=2$
). Figure 9(c,d) shows the results for
![]() $N=3$
and
$N=3$
and
![]() $N=5$
, respectively. One can easily verify that they are identical to those shown in figure 8(c,d). This is because, for both
$N=5$
, respectively. One can easily verify that they are identical to those shown in figure 8(c,d). This is because, for both
![]() $N=3$
and
$N=3$
and
![]() $N=5$
, the eigenvalues
$N=5$
, the eigenvalues
![]() $\unicode[STIX]{x1D706}_{n}$
remain identical to
$\unicode[STIX]{x1D706}_{n}$
remain identical to
![]() $\unicode[STIX]{x1D706}_{-n}$
. As discussed in § 4.2, this also implies that azimuthally travelling waves can exist, in contrast to the case of
$\unicode[STIX]{x1D706}_{-n}$
. As discussed in § 4.2, this also implies that azimuthally travelling waves can exist, in contrast to the case of
![]() $\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
, where only azimuthally standing waves are allowed.
$\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
, where only azimuthally standing waves are allowed.

Figure 10. The convection velocity and growth rate of the mode
![]() $2$
jet instability waves for vortex sheets of different lobed geometry: (a)
$2$
jet instability waves for vortex sheets of different lobed geometry: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
.
$N=5$
.
Figure 10 shows results for the instability waves of mode
![]() $2$
. Figure 10(a) is for
$2$
. Figure 10(a) is for
![]() $N=1$
. We expect little change caused by one single lobe, and this is demonstrated clearly by the figure. The results for
$N=1$
. We expect little change caused by one single lobe, and this is demonstrated clearly by the figure. The results for
![]() $N=2$
are shown in figure 10(b). The mode
$N=2$
are shown in figure 10(b). The mode
![]() $2$
instability waves have increasingly lower convection velocities when
$2$
instability waves have increasingly lower convection velocities when
![]() $\unicode[STIX]{x1D716}$
increases. However, the changes are very small. The changes of the temporal growth rate are nearly unobservable. However, using three lobes can still effectively reduce the convection velocity while marginally altering the temporal growth rate of the mode
$\unicode[STIX]{x1D716}$
increases. However, the changes are very small. The changes of the temporal growth rate are nearly unobservable. However, using three lobes can still effectively reduce the convection velocity while marginally altering the temporal growth rate of the mode
![]() $2$
instability waves. Like all the results we have reported, the use of five lobes is the most effective way of increasing the convection velocity and decreasing the temporal growth rate. Figure 11 shows the results for the mode
$2$
instability waves. Like all the results we have reported, the use of five lobes is the most effective way of increasing the convection velocity and decreasing the temporal growth rate. Figure 11 shows the results for the mode
![]() $-2$
instability waves. Figure 11(a) exhibits expected behaviour for a lobed profile of
$-2$
instability waves. Figure 11(a) exhibits expected behaviour for a lobed profile of
![]() $N=1$
. Figure 11(b) shows a very slight increase of the convection velocity and no change to the temporal growth rate. We emphasize again that this is due to
$N=1$
. Figure 11(b) shows a very slight increase of the convection velocity and no change to the temporal growth rate. We emphasize again that this is due to
![]() $\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
. Figures 11(c) and 11(d) are identical to figures 10(c) and 10(d) respectively because of identical eigenvalues.
$\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
. Figures 11(c) and 11(d) are identical to figures 10(c) and 10(d) respectively because of identical eigenvalues.

Figure 11. The convection velocity and growth rate of the mode
![]() $-2$
jet instability waves for vortex sheets of different lobed geometry: (a)
$-2$
jet instability waves for vortex sheets of different lobed geometry: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
.
$N=5$
.
In summary, the stability characteristics of base flows of a lobed vortex-sheet type are different from those of axisymmetric ones. The differences consist of changes to both the convection velocity and the temporal growth rate of instability waves. The changes become more pronounced as the number of lobes
![]() $N$
and the penetration ratio
$N$
and the penetration ratio
![]() $\unicode[STIX]{x1D716}$
increase. However, instability waves with different mode numbers are affected differently by the lobed geometry. In particular, little change occurs for mode
$\unicode[STIX]{x1D716}$
increase. However, instability waves with different mode numbers are affected differently by the lobed geometry. In particular, little change occurs for mode
![]() $0$
, no matter how large both
$0$
, no matter how large both
![]() $N$
and
$N$
and
![]() $\unicode[STIX]{x1D716}$
are. On the other hand, an evident alteration of the characteristics of jet instability waves with large mode numbers occurs when
$\unicode[STIX]{x1D716}$
are. On the other hand, an evident alteration of the characteristics of jet instability waves with large mode numbers occurs when
![]() $N>1$
. For
$N>1$
. For
![]() $N=3$
and
$N=3$
and
![]() $N=5$
, azimuthally even and odd instability waves demonstrate the same characteristics. However, for
$N=5$
, azimuthally even and odd instability waves demonstrate the same characteristics. However, for
![]() $N=2$
and
$N=2$
and
![]() $N=1$
, even and odd instability waves of lobed jets exhibit two different types of behaviour, with one having favourable effects on installed jet noise reduction and the other having adverse. Therefore, for the sake of suppressing instability waves, or achieving installed jet noise reduction, it is desired to use a lobed profile of large
$N=1$
, even and odd instability waves of lobed jets exhibit two different types of behaviour, with one having favourable effects on installed jet noise reduction and the other having adverse. Therefore, for the sake of suppressing instability waves, or achieving installed jet noise reduction, it is desired to use a lobed profile of large
![]() $N$
, such as
$N$
, such as
![]() $N=5$
, with a large penetration ratio. Because this results in a larger reduction of the temporal growth rates, and hence may lead to weaker instability waves.
$N=5$
, with a large penetration ratio. Because this results in a larger reduction of the temporal growth rates, and hence may lead to weaker instability waves.
Note that the results discussed above are obtained from a temporal analysis, from which the results of a spatial analysis may be recovered from Gaster’s transformation (Gaster Reference Gaster1962). Gaster’s transformation provides a straightforward way to connect the temporal and spatial stability analyses. One of the key assumptions used in Gaster’s transformation is that both the spatial and temporal growth rates have to be small, and under this assumption Gaster showed that, to the first-order accuracy, the temporal angular frequency,
![]() $\text{Re}(\unicode[STIX]{x1D714})$
, rather than the convection velocity
$\text{Re}(\unicode[STIX]{x1D714})$
, rather than the convection velocity
![]() $\text{Re}(\unicode[STIX]{x1D714})/\unicode[STIX]{x1D6FC}$
, is the same as the spatial angular frequency, and the temporal growth rate is equal to the product of the spatial growth rate and the temporal group velocity. With the temporal results available, we can therefore obtain the spatial growth rate by using Gaster’s transformation, provided the aforementioned assumption is not violated. Care must be taken for the spatial convection velocity as the
$\text{Re}(\unicode[STIX]{x1D714})/\unicode[STIX]{x1D6FC}$
, is the same as the spatial angular frequency, and the temporal growth rate is equal to the product of the spatial growth rate and the temporal group velocity. With the temporal results available, we can therefore obtain the spatial growth rate by using Gaster’s transformation, provided the aforementioned assumption is not violated. Care must be taken for the spatial convection velocity as the
![]() $\text{Re}(\unicode[STIX]{x1D714})$
being identical does not imply the same thing for
$\text{Re}(\unicode[STIX]{x1D714})$
being identical does not imply the same thing for
![]() $\text{Re}(\unicode[STIX]{x1D714})/\text{Re}(\unicode[STIX]{x1D6FC})$
(see the spatial convection velocity of a round vortex sheet given by Michalke (Reference Michalke1970) for example), in which case high-order terms need to be incorporated to improve accuracy.
$\text{Re}(\unicode[STIX]{x1D714})/\text{Re}(\unicode[STIX]{x1D6FC})$
(see the spatial convection velocity of a round vortex sheet given by Michalke (Reference Michalke1970) for example), in which case high-order terms need to be incorporated to improve accuracy.
However, the aim of this study is to investigate the effects of lobes on the growth rates of jet instability waves so as to examine the feasibility of controlling installed jet noise using lobed jets, and these effects are unlikely to be significantly different between the temporal or spatial frameworks. For example, if the lobed geometry slightly reduces the temporal growth rate, we would expect similar behavior for the spatial growth rate. Therefore, in this paper, we focus on the temporal results only. Also note that previous studies mainly focused on chevron jets, and we do not expect their results to be identical to the stability results for the special type of lobed base flow used in this study.
4.4 The change to mode shapes
We have studied the effects of lobed geometries on the convection velocity and temporal growth rate of jet instability waves. In this section, we show their effects on the mode shapes. In the rest of this section, we present the contour plot of the pressure field corresponding to each eigenmode. The pressure is normalized such that it is equal to the right-hand side of (4.1b
) inside the vortex sheet. We choose to shown the pressure fields for modes
![]() $0$
,
$0$
,
![]() $-1$
and
$-1$
and
![]() $2$
, respectively. When doing so, we fix
$2$
, respectively. When doing so, we fix
![]() $\unicode[STIX]{x1D716}=0.15$
but let
$\unicode[STIX]{x1D716}=0.15$
but let
![]() $N$
vary between
$N$
vary between
![]() $1$
,
$1$
,
![]() $2$
,
$2$
,
![]() $3$
and
$3$
and
![]() $5$
, respectively. For each mode at each value of
$5$
, respectively. For each mode at each value of
![]() $N$
, we show the pressure distribution at a low frequency
$N$
, we show the pressure distribution at a low frequency
![]() $\unicode[STIX]{x1D6FC}a\approx 0.25$
and then at a high frequency
$\unicode[STIX]{x1D6FC}a\approx 0.25$
and then at a high frequency
![]() $\unicode[STIX]{x1D6FC}a\approx 2.5$
. These results are shown from figures 12 to 17. In each figure, the lobed profile is represented by a thick solid black line.
$\unicode[STIX]{x1D6FC}a\approx 2.5$
. These results are shown from figures 12 to 17. In each figure, the lobed profile is represented by a thick solid black line.

Figure 12. The shapes of mode 0 for some strongly lobed geometries when
![]() $\unicode[STIX]{x1D716}=0.15$
at a low frequency of
$\unicode[STIX]{x1D716}=0.15$
at a low frequency of
![]() $\unicode[STIX]{x1D6FC}a\approx 0.25$
: (a)
$\unicode[STIX]{x1D6FC}a\approx 0.25$
: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
. The thick black solid lines show the lobed vortex sheets.
$N=5$
. The thick black solid lines show the lobed vortex sheets.

Figure 13. The shapes of mode 0 for some strongly lobed geometries when
![]() $\unicode[STIX]{x1D716}=0.15$
at a high frequency of
$\unicode[STIX]{x1D716}=0.15$
at a high frequency of
![]() $\unicode[STIX]{x1D6FC}a\approx 2.5$
: (a)
$\unicode[STIX]{x1D6FC}a\approx 2.5$
: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
. The thick black solid lines show the lobed vortex sheets.
$N=5$
. The thick black solid lines show the lobed vortex sheets.
Figure 12 shows the pressure distributions for mode
![]() $0$
at
$0$
at
![]() $\unicode[STIX]{x1D6FC}a\approx 0.25$
. Figure 12(a) is for
$\unicode[STIX]{x1D6FC}a\approx 0.25$
. Figure 12(a) is for
![]() $N=1$
. We have mentioned that when
$N=1$
. We have mentioned that when
![]() $N=1$
the lobed profile is more or less the same as a displaced circle and, hence, its stability characteristics should be nearly the same as a round jet. Figure 12(a) proves this by showing a nearly axisymmetric pressure distribution. The pressure inside the vortex sheet is nearly uniform. This is because the frequency is very low and the modified Bessel function of the first kind approaches to a constant value for a small argument. The pressure outside gradually decays to zero as the distance to the centre of the vortex sheet increases. Note how the pressure is matched continuously across the vortex sheet: another indication for a well-converged eigensolution. Figure 12(b) shows the result for
$N=1$
the lobed profile is more or less the same as a displaced circle and, hence, its stability characteristics should be nearly the same as a round jet. Figure 12(a) proves this by showing a nearly axisymmetric pressure distribution. The pressure inside the vortex sheet is nearly uniform. This is because the frequency is very low and the modified Bessel function of the first kind approaches to a constant value for a small argument. The pressure outside gradually decays to zero as the distance to the centre of the vortex sheet increases. Note how the pressure is matched continuously across the vortex sheet: another indication for a well-converged eigensolution. Figure 12(b) shows the result for
![]() $N=2$
. In this case the lobed profile resembles an ellipse. The effect of the geometry change is to stretch the pressure field inside the vortex sheet to have a distribution similar to the shape of the vortex sheet itself. The pressure outside gradually becomes axisymmetric and decays to zero at a large distance. The behaviours for
$N=2$
. In this case the lobed profile resembles an ellipse. The effect of the geometry change is to stretch the pressure field inside the vortex sheet to have a distribution similar to the shape of the vortex sheet itself. The pressure outside gradually becomes axisymmetric and decays to zero at a large distance. The behaviours for
![]() $N=3$
and
$N=3$
and
![]() $5$
, as shown in figure 12(c,d), respectively, are very similar to
$5$
, as shown in figure 12(c,d), respectively, are very similar to
![]() $N=2$
.
$N=2$
.

Figure 14. The shapes of mode
![]() $-$
1 for some strongly lobed geometries when
$-$
1 for some strongly lobed geometries when
![]() $\unicode[STIX]{x1D716}=0.15$
at a low frequency of
$\unicode[STIX]{x1D716}=0.15$
at a low frequency of
![]() $\unicode[STIX]{x1D6FC}a\approx 0.25$
: (a)
$\unicode[STIX]{x1D6FC}a\approx 0.25$
: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
. The thick black solid lines show the lobed vortex sheets.
$N=5$
. The thick black solid lines show the lobed vortex sheets.
Figure 13 shows the pressure fields for mode
![]() $0$
at a high frequency
$0$
at a high frequency
![]() $\unicode[STIX]{x1D6FC}a\approx 2.5$
. A striking difference is the much smaller size of contour regions in each sub-figure. This is due to the fact that the pressure decays more quickly outside the vortex sheet at high frequencies. This is in accord with the fact that installed jet noise is only significant at low frequencies. Figure 13(a) again shows the result for
$\unicode[STIX]{x1D6FC}a\approx 2.5$
. A striking difference is the much smaller size of contour regions in each sub-figure. This is due to the fact that the pressure decays more quickly outside the vortex sheet at high frequencies. This is in accord with the fact that installed jet noise is only significant at low frequencies. Figure 13(a) again shows the result for
![]() $N=1$
. One difference from figure 12(a) is that the pressure variation inside the vortex sheet is clear at this high frequency, which is what we would expect. When
$N=1$
. One difference from figure 12(a) is that the pressure variation inside the vortex sheet is clear at this high frequency, which is what we would expect. When
![]() $N=2$
, the lobed geometry has the same stretching effects as those shown in figure 12(b), but with a more marked pressure variation. The same tendencies can be seen from figure 12(c,d). The relatively insignificant change to the shape of the mode
$N=2$
, the lobed geometry has the same stretching effects as those shown in figure 12(b), but with a more marked pressure variation. The same tendencies can be seen from figure 12(c,d). The relatively insignificant change to the shape of the mode
![]() $0$
instability wave, as shown in figures 12 and 13, is consistent with the fact that both the convection velocity and temporal growth rate remain roughly the same as those for an axisymmetric jet.
$0$
instability wave, as shown in figures 12 and 13, is consistent with the fact that both the convection velocity and temporal growth rate remain roughly the same as those for an axisymmetric jet.

Figure 15. The shapes of mode
![]() $-$
1 for some strongly lobed geometries when
$-$
1 for some strongly lobed geometries when
![]() $\unicode[STIX]{x1D716}=0.15$
at a high frequency of
$\unicode[STIX]{x1D716}=0.15$
at a high frequency of
![]() $\unicode[STIX]{x1D6FC}a\approx 2.5$
: (a)
$\unicode[STIX]{x1D6FC}a\approx 2.5$
: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
. The thick black solid lines show the lobed vortex sheets.
$N=5$
. The thick black solid lines show the lobed vortex sheets.
Figure 14 shows the results for mode
![]() $-1$
at
$-1$
at
![]() $\unicode[STIX]{x1D6FC}a\approx 0.25$
. From § 3.2, we know that for negative mode numbers the pressure distribution is antisymmetric with respect to
$\unicode[STIX]{x1D6FC}a\approx 0.25$
. From § 3.2, we know that for negative mode numbers the pressure distribution is antisymmetric with respect to
![]() $\unicode[STIX]{x1D719}=0$
. This is reflected in figure 14. Figure 14(a) very much resembles to that of an axisymmetric jet. When
$\unicode[STIX]{x1D719}=0$
. This is reflected in figure 14. Figure 14(a) very much resembles to that of an axisymmetric jet. When
![]() $N=2$
, the pressure field still largely resembles that in figure 14(a). A clear change in mode shape occurs when
$N=2$
, the pressure field still largely resembles that in figure 14(a). A clear change in mode shape occurs when
![]() $N=3$
, as shown in figure 14(c). We can see that a three-lobe profile causes the two lobes of the pressure field to tilt towards two lobes of the vortex sheet. This signifies a potentially large change in the convection velocity and temporal growth rate. The mode shape at
$N=3$
, as shown in figure 14(c). We can see that a three-lobe profile causes the two lobes of the pressure field to tilt towards two lobes of the vortex sheet. This signifies a potentially large change in the convection velocity and temporal growth rate. The mode shape at
![]() $N=5$
shows similar characteristics to that at
$N=5$
shows similar characteristics to that at
![]() $N=3$
. Moreover, there are some small and local changes in response to the appearance of local geometry corrugations. We wish to point out, however, that although changes are observed, the mode shapes are still bearing the signature of conventional
$N=3$
. Moreover, there are some small and local changes in response to the appearance of local geometry corrugations. We wish to point out, however, that although changes are observed, the mode shapes are still bearing the signature of conventional
![]() $\sin \unicode[STIX]{x1D719}$
behaviour, suggesting the appropriateness of our earlier mode labelling strategy.
$\sin \unicode[STIX]{x1D719}$
behaviour, suggesting the appropriateness of our earlier mode labelling strategy.
Figure 15 is similar to figure 14 in almost every aspect, apart from the smaller size of the contour regions owing to the quicker decay of the instability waves outside the vortex sheet at high frequencies. We therefore omit a repetitive description. Instead, we try to understand the behaviour of non-identical eigenvalues, as discussed in § 4.3, from the perspective of mode shapes.
We have observed that for
![]() $N=1$
and
$N=1$
and
![]() $N=2$
, the eigenvalue
$N=2$
, the eigenvalue
![]() $\unicode[STIX]{x1D706}_{-1}$
is not degenerate any more, and consequently, only standing modes are allowed, whereas travelling modes (in the azimuthal direction, similar to a behaviour of
$\unicode[STIX]{x1D706}_{-1}$
is not degenerate any more, and consequently, only standing modes are allowed, whereas travelling modes (in the azimuthal direction, similar to a behaviour of
![]() $\text{e}^{\text{i}(m\unicode[STIX]{x1D719}-\unicode[STIX]{x1D714}t)}$
) are allowed for
$\text{e}^{\text{i}(m\unicode[STIX]{x1D719}-\unicode[STIX]{x1D714}t)}$
) are allowed for
![]() $N=3$
and
$N=3$
and
![]() $5$
. To understand the difference we can compare figures 15(b) and 15(c). We conclude that, if an eigenvalue is not degenerate, then each of the symmetric plane of the lobe profile must also be a symmetric (or antisymmetric) plane of the eigenmode. For example, in figure 15(b), the lobed profile has two symmetric planes, namely the horizontal and vertical planes, each of which is also a symmetric or antisymmetric plane of the pressure field. This is consistent with the fact that
$5$
. To understand the difference we can compare figures 15(b) and 15(c). We conclude that, if an eigenvalue is not degenerate, then each of the symmetric plane of the lobe profile must also be a symmetric (or antisymmetric) plane of the eigenmode. For example, in figure 15(b), the lobed profile has two symmetric planes, namely the horizontal and vertical planes, each of which is also a symmetric or antisymmetric plane of the pressure field. This is consistent with the fact that
![]() $\unicode[STIX]{x1D706}_{1}$
is not degenerate. On the other hand, in figure 15(c), the lobed profile has three symmetric planes, but only one of them is the antisymmetric plane of the pressure field. Hence,
$\unicode[STIX]{x1D706}_{1}$
is not degenerate. On the other hand, in figure 15(c), the lobed profile has three symmetric planes, but only one of them is the antisymmetric plane of the pressure field. Hence,
![]() $\unicode[STIX]{x1D706}_{-1}$
must be degenerate. Figure 15(d) is very similar to figure 15(c). For an axisymmetric jet, the vortex sheet profile has infinitely many symmetric planes, however only two of them are the symmetric and antisymmetric planes of mode
$\unicode[STIX]{x1D706}_{-1}$
must be degenerate. Figure 15(d) is very similar to figure 15(c). For an axisymmetric jet, the vortex sheet profile has infinitely many symmetric planes, however only two of them are the symmetric and antisymmetric planes of mode
![]() $-1$
pressure field. Therefore,
$-1$
pressure field. Therefore,
![]() $\unicode[STIX]{x1D706}_{-1}$
is degenerate for a round jet. Note that the vortex sheet profile in figure 15(a) is close to a displaced circle, but is not strictly one. It has a slight eccentricity and, therefore, has a non-degenerate eigenvalue.
$\unicode[STIX]{x1D706}_{-1}$
is degenerate for a round jet. Note that the vortex sheet profile in figure 15(a) is close to a displaced circle, but is not strictly one. It has a slight eccentricity and, therefore, has a non-degenerate eigenvalue.
The connection between the degeneracy and the mode shape can be understood as follows. Take figure 15(c) as an example. We mentioned that only one of three symmetric planes, which are angled by
![]() $120^{\circ }$
from each other, is the antisymmetric plane of the pressure field. Now we can rotate the pressure field by
$120^{\circ }$
from each other, is the antisymmetric plane of the pressure field. Now we can rotate the pressure field by
![]() $120^{\circ }$
, then the resulting pressure field must also be an eigensolution of the stability problem, with the same eigenvalue. Therefore, the corresponding eigenvalue must be degenerate. The combination of the eigenvectors corresponding to the same eigenvalue creates infinitely many eigensolutions, and two of them are those obtained by rotating figure 15(c) by
$120^{\circ }$
, then the resulting pressure field must also be an eigensolution of the stability problem, with the same eigenvalue. Therefore, the corresponding eigenvalue must be degenerate. The combination of the eigenvectors corresponding to the same eigenvalue creates infinitely many eigensolutions, and two of them are those obtained by rotating figure 15(c) by
![]() $120^{\circ }$
and
$120^{\circ }$
and
![]() $240^{\circ }$
, respectively.
$240^{\circ }$
, respectively.

Figure 16. The shapes of mode 2 for some strongly lobed geometries when
![]() $\unicode[STIX]{x1D716}=0.15$
at a low frequency of
$\unicode[STIX]{x1D716}=0.15$
at a low frequency of
![]() $\unicode[STIX]{x1D6FC}a\approx 0.25$
: (a)
$\unicode[STIX]{x1D6FC}a\approx 0.25$
: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
. The thick black solid lines show the lobed vortex sheets.
$N=5$
. The thick black solid lines show the lobed vortex sheets.
We expect that the non-degeneracy is likely to occur when the mode number
![]() $n$
is equal to
$n$
is equal to
![]() $\pm N/2$
,
$\pm N/2$
,
![]() $\pm N$
, etc. This is because, for mode
$\pm N$
, etc. This is because, for mode
![]() $n$
, the pressure field normally has
$n$
, the pressure field normally has
![]() $2|n|$
lobes, and the symmetric and antisymmetric planes of such a mode can be aligned with all the symmetric planes of the vortex sheet profile. Comparing with the figures shown in § 4.3, we find that this is indeed the case. For example, we see
$2|n|$
lobes, and the symmetric and antisymmetric planes of such a mode can be aligned with all the symmetric planes of the vortex sheet profile. Comparing with the figures shown in § 4.3, we find that this is indeed the case. For example, we see
![]() $\unicode[STIX]{x1D706}_{-1}\neq \unicode[STIX]{x1D706}_{1}$
when
$\unicode[STIX]{x1D706}_{-1}\neq \unicode[STIX]{x1D706}_{1}$
when
![]() $N=2$
and
$N=2$
and
![]() $\unicode[STIX]{x1D706}_{-2}\neq \unicode[STIX]{x1D706}_{2}$
when
$\unicode[STIX]{x1D706}_{-2}\neq \unicode[STIX]{x1D706}_{2}$
when
![]() $N=2$
.
$N=2$
.

Figure 17. The shapes of mode 2 for some strongly lobed geometries when
![]() $\unicode[STIX]{x1D716}=0.15$
at a high frequency of
$\unicode[STIX]{x1D716}=0.15$
at a high frequency of
![]() $\unicode[STIX]{x1D6FC}a\approx 2.5$
: (a)
$\unicode[STIX]{x1D6FC}a\approx 2.5$
: (a)
![]() $N=1$
; (b)
$N=1$
; (b)
![]() $N=2$
; (c)
$N=2$
; (c)
![]() $N=3$
; (d)
$N=3$
; (d)
![]() $N=5$
. The thick black solid lines show the lobed vortex sheets.
$N=5$
. The thick black solid lines show the lobed vortex sheets.
Figure 16 shows the distributions of the pressure field for mode
![]() $2$
at the low frequency
$2$
at the low frequency
![]() $\unicode[STIX]{x1D6FC}a\approx 0.25$
. Figure 16(a) shows its similarity to that for an axisymmetric vortex sheet while figure 16(b) for an elliptic vortex sheet. Note how the earlier conclusion about non-degeneracy remains valid in figure 16(b–d). Figure 17 shows qualitatively similar results at a higher frequency so we avoid an unnecessary repetition.
$\unicode[STIX]{x1D6FC}a\approx 0.25$
. Figure 16(a) shows its similarity to that for an axisymmetric vortex sheet while figure 16(b) for an elliptic vortex sheet. Note how the earlier conclusion about non-degeneracy remains valid in figure 16(b–d). Figure 17 shows qualitatively similar results at a higher frequency so we avoid an unnecessary repetition.
5 Conclusion
In the hope of suppressing installed jet noise, an analytical study of the stability characteristics of lobed jets of a vortex sheet type has been performed. It has been shown that the lobed geometry changes both the convection velocity and the temporal growth rate of the instability waves. The effects are more pronounced as the number of lobes
![]() $N$
and the penetration ratio
$N$
and the penetration ratio
![]() $\unicode[STIX]{x1D716}$
increase. However, instability waves of different mode numbers are affected differently by the lobes. For instance, the mode
$\unicode[STIX]{x1D716}$
increase. However, instability waves of different mode numbers are affected differently by the lobes. For instance, the mode
![]() $0$
is particularly insensitive to the geometry changes. Higher modes are more likely to be changed significantly when both
$0$
is particularly insensitive to the geometry changes. Higher modes are more likely to be changed significantly when both
![]() $N$
and
$N$
and
![]() $\unicode[STIX]{x1D716}$
are sufficiently large. An interesting finding is that when
$\unicode[STIX]{x1D716}$
are sufficiently large. An interesting finding is that when
![]() $N=1$
and
$N=1$
and
![]() $N=2$
different behaviour occurs between the even and odd instability waves of certain orders, i.e. the corresponding eigenvalue becomes non-degenerate. We have shown that a necessary condition for a non-degenerate eigenvalue to exist is that each symmetric plane of the lobed vortex sheet must also be a symmetric or antisymmetric plane of the corresponding mode shape. This is likely to occur when the mode number
$N=2$
different behaviour occurs between the even and odd instability waves of certain orders, i.e. the corresponding eigenvalue becomes non-degenerate. We have shown that a necessary condition for a non-degenerate eigenvalue to exist is that each symmetric plane of the lobed vortex sheet must also be a symmetric or antisymmetric plane of the corresponding mode shape. This is likely to occur when the mode number
![]() $n$
is
$n$
is
![]() $\pm N/2$
,
$\pm N/2$
,
![]() $\pm N$
and so on. It is concluded that in order to suppress instability waves for the sake of reducing installed jet noise, a large
$\pm N$
and so on. It is concluded that in order to suppress instability waves for the sake of reducing installed jet noise, a large
![]() $N$
, such as
$N$
, such as
![]() $N=5$
, and a large
$N=5$
, and a large
![]() $\unicode[STIX]{x1D716}$
are desirable.
$\unicode[STIX]{x1D716}$
are desirable.
The insensitiveness of the mode
![]() $0$
instability waves to the lobed geometry implies that using lobed geometry hardly helps in reducing the installed jet noise due to the scattering of the mode
$0$
instability waves to the lobed geometry implies that using lobed geometry hardly helps in reducing the installed jet noise due to the scattering of the mode
![]() $0$
jet instability waves. The reduction of the total installed jet noise would be somewhat limited. If the modes
$0$
jet instability waves. The reduction of the total installed jet noise would be somewhat limited. If the modes
![]() $0$
and
$0$
and
![]() $1$
(including both modes
$1$
(including both modes
![]() $+1$
and
$+1$
and
![]() $-1$
) instability waves are of equal strength, one would expect an observable sound reduction up to
$-1$
) instability waves are of equal strength, one would expect an observable sound reduction up to
![]() $3$
dB (in the ideal case). It is, however, worth noting that the current analysis is based on a parallel vortex sheet assumption. In realistic jets, the jet mean flow is expected to gradually become axisymmetric downstream the jet exit owing to strong jet mixing. To what extent this smoothing of the lobed geometry would affect the jet stability, hence installed jet noise, requires further examination. This constitutes part of our future work.
$3$
dB (in the ideal case). It is, however, worth noting that the current analysis is based on a parallel vortex sheet assumption. In realistic jets, the jet mean flow is expected to gradually become axisymmetric downstream the jet exit owing to strong jet mixing. To what extent this smoothing of the lobed geometry would affect the jet stability, hence installed jet noise, requires further examination. This constitutes part of our future work.
Acknowledgements
The first author (B.L.) wishes to gratefully acknowledge the financial support provided by the Cambridge Commonwealth European and International Trust and the China Scholarship Council.
Appendix A. The kinematic and dynamic boundary conditions
The two equations shown in (2.24), together with the kinematic and dynamic boundary conditions on the vortex sheet, need to be combined to obtain the dispersion relation. The kinematic and dynamic boundary conditions can be obtained as follows. As defined above, the vortex sheet profile is given by
![]() ${\mathcal{F}}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}-{\mathcal{R}}(\unicode[STIX]{x1D719})=0$
. One can assume that the perturbed profile can be described by the function
${\mathcal{F}}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}-{\mathcal{R}}(\unicode[STIX]{x1D719})=0$
. One can assume that the perturbed profile can be described by the function
where
![]() $\unicode[STIX]{x1D702}^{\prime }(\unicode[STIX]{x1D719},z,t)$
denotes a small-amplitude perturbation of the radius of the vortex-sheet profile. The kinematic boundary condition states that, on the perturbed vortex sheet,
$\unicode[STIX]{x1D702}^{\prime }(\unicode[STIX]{x1D719},z,t)$
denotes a small-amplitude perturbation of the radius of the vortex-sheet profile. The kinematic boundary condition states that, on the perturbed vortex sheet,
Substituting the velocity on both sides of the vortex sheet to (A 2) and linearizing around the unperturbed vortex sheet yields
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x2202}z}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}^{-}\boldsymbol{\cdot }\unicode[STIX]{x1D735}{\mathcal{F}}=0,\\ \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}^{+}\boldsymbol{\cdot }\unicode[STIX]{x1D735}{\mathcal{F}}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x2202}z}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}^{-}\boldsymbol{\cdot }\unicode[STIX]{x1D735}{\mathcal{F}}=0,\\ \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}^{+}\boldsymbol{\cdot }\unicode[STIX]{x1D735}{\mathcal{F}}=0.\end{array}\right\}\end{eqnarray}$$
After invoking the harmonic time and
![]() $z$
dependence (
$z$
dependence (
![]() $\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}$
) and eliminating
$\text{e}^{\text{i}\unicode[STIX]{x1D6FC}z}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}$
) and eliminating
![]() $\unicode[STIX]{x1D702}^{\prime }$
, one can show that (A 3) reduces to
$\unicode[STIX]{x1D702}^{\prime }$
, one can show that (A 3) reduces to
where
![]() $\boldsymbol{n}$
denotes the unit vector perpendicular to the vortex-sheet profile, which can be readily shown to be
$\boldsymbol{n}$
denotes the unit vector perpendicular to the vortex-sheet profile, which can be readily shown to be
![]() $\unicode[STIX]{x1D735}{\mathcal{F}}/|\unicode[STIX]{x1D735}{\mathcal{F}}|$
. The dynamic boundary condition requires pressure continuity across the vortex sheet. From the linearized momentum equation, i.e. (2.4), one can readily show that
$\unicode[STIX]{x1D735}{\mathcal{F}}/|\unicode[STIX]{x1D735}{\mathcal{F}}|$
. The dynamic boundary condition requires pressure continuity across the vortex sheet. From the linearized momentum equation, i.e. (2.4), one can readily show that
where
![]() $U_{z}$
can be either
$U_{z}$
can be either
![]() $U$
and
$U$
and
![]() $0$
depending on which side of the vortex sheet is considered. Hence, substituting the velocity potentials on both sides of the vortex sheet yields that on the unperturbed vortex sheet (after linearizing around the unperturbed vortex sheet)
$0$
depending on which side of the vortex sheet is considered. Hence, substituting the velocity potentials on both sides of the vortex sheet yields that on the unperturbed vortex sheet (after linearizing around the unperturbed vortex sheet)
Appendix B. The properties on rotationally symmetric matrices
Since the eigenvector
![]() $\boldsymbol{C}^{-}$
of the matrix
$\boldsymbol{C}^{-}$
of the matrix
![]() $\unicode[STIX]{x1D63C}$
fully determines the eigenfunction
$\unicode[STIX]{x1D63C}$
fully determines the eigenfunction
![]() $E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
, it is important to examine the properties of
$E_{n}^{-}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D719})$
, it is important to examine the properties of
![]() $\unicode[STIX]{x1D63C}$
and its eigenvectors. In order to do this, we need to define the rotation of any vector
$\unicode[STIX]{x1D63C}$
and its eigenvectors. In order to do this, we need to define the rotation of any vector
![]() $\boldsymbol{C}$
as
$\boldsymbol{C}$
as
![]() $\boldsymbol{C}^{R}$
, such that
$\boldsymbol{C}^{R}$
, such that
where
![]() $(\boldsymbol{C}^{R})_{n}$
denotes the
$(\boldsymbol{C}^{R})_{n}$
denotes the
![]() $n$
th the element of the rotation vector
$n$
th the element of the rotation vector
![]() $\boldsymbol{C}^{R}$
and
$\boldsymbol{C}^{R}$
and
![]() $C_{n}$
is the
$C_{n}$
is the
![]() $n$
th element of
$n$
th element of
![]() $\boldsymbol{C}$
. Note here the index of the vector
$\boldsymbol{C}$
. Note here the index of the vector
![]() $\boldsymbol{C}$
ranges from
$\boldsymbol{C}$
ranges from
![]() $-M$
to
$-M$
to
![]() $M$
. Similarly, we can define the rotation of any matrix
$M$
. Similarly, we can define the rotation of any matrix
![]() $\unicode[STIX]{x1D63D}$
as
$\unicode[STIX]{x1D63D}$
as
where
![]() $(\unicode[STIX]{x1D63D}^{R})_{ij}$
denotes the element of
$(\unicode[STIX]{x1D63D}^{R})_{ij}$
denotes the element of
![]() $\unicode[STIX]{x1D63D}^{R}$
at the
$\unicode[STIX]{x1D63D}^{R}$
at the
![]() $i$
th row and the
$i$
th row and the
![]() $j$
th column, and
$j$
th column, and
![]() $B_{ij}$
are the indexed elements of matrix
$B_{ij}$
are the indexed elements of matrix
![]() $\unicode[STIX]{x1D63D}$
. If a vector
$\unicode[STIX]{x1D63D}$
. If a vector
![]() $\boldsymbol{C}$
is equal to its rotation, we define it as symmetric. If, on the other hand,
$\boldsymbol{C}$
is equal to its rotation, we define it as symmetric. If, on the other hand,
![]() $\boldsymbol{C}=-\boldsymbol{C}^{R}$
, we define it as antisymmetric. Similarly, if a matrix
$\boldsymbol{C}=-\boldsymbol{C}^{R}$
, we define it as antisymmetric. Similarly, if a matrix
![]() $\unicode[STIX]{x1D63D}$
is equal to its rotation, we define it as rotationally symmetric. Anti-rotational symmetry follows a self-explanatory definition. One can now show that
$\unicode[STIX]{x1D63D}$
is equal to its rotation, we define it as rotationally symmetric. Anti-rotational symmetry follows a self-explanatory definition. One can now show that
![]() $(\unicode[STIX]{x1D63D}\boldsymbol{C})^{R}=\unicode[STIX]{x1D63D}^{R}\boldsymbol{C}^{R}$
, because
$(\unicode[STIX]{x1D63D}\boldsymbol{C})^{R}=\unicode[STIX]{x1D63D}^{R}\boldsymbol{C}^{R}$
, because
where
![]() $i$
can be any number between
$i$
can be any number between
![]() $-M$
to
$-M$
to
![]() $M$
. Replacing the vector
$M$
. Replacing the vector
![]() $\boldsymbol{C}$
in the above equations with a matrix
$\boldsymbol{C}$
in the above equations with a matrix
![]() $\unicode[STIX]{x1D63D}_{2}$
does not invalidate the formula, i.e.
$\unicode[STIX]{x1D63D}_{2}$
does not invalidate the formula, i.e.
![]() $(\unicode[STIX]{x1D63D}\unicode[STIX]{x1D63D}_{2})^{R}=\unicode[STIX]{x1D63D}^{R}\unicode[STIX]{x1D63D}_{2}^{R}$
also holds. Therefore, if both
$(\unicode[STIX]{x1D63D}\unicode[STIX]{x1D63D}_{2})^{R}=\unicode[STIX]{x1D63D}^{R}\unicode[STIX]{x1D63D}_{2}^{R}$
also holds. Therefore, if both
![]() $\unicode[STIX]{x1D63D}$
and
$\unicode[STIX]{x1D63D}$
and
![]() $\unicode[STIX]{x1D63D}_{2}$
are rationally symmetric matrices, then the product of them is also rotationally symmetric. This is because
$\unicode[STIX]{x1D63D}_{2}$
are rationally symmetric matrices, then the product of them is also rotationally symmetric. This is because
We now prove that the inverse of a rotationally symmetric matrix, if exists, is also rotationally symmetric. First, because it is assumed that the inverse of the rotationally symmetric
![]() $\unicode[STIX]{x1D63D}$
exists, we denote its column vectors by
$\unicode[STIX]{x1D63D}$
exists, we denote its column vectors by
![]() $\boldsymbol{D}_{i}$
(
$\boldsymbol{D}_{i}$
(
![]() $i=-M\cdots M$
), i.e.
$i=-M\cdots M$
), i.e.
Then according to the definition of the inverse matrix, one has
where
![]() $\boldsymbol{I}_{i}$
is the
$\boldsymbol{I}_{i}$
is the
![]() $i$
th column of the identity matrix. Now for any positive number
$i$
th column of the identity matrix. Now for any positive number
![]() $i$
, one has
$i$
, one has
If taking the rotation of both sides of (B 7), one obtains
where use is made of the fact that
![]() $\boldsymbol{I}_{i}^{R}=\boldsymbol{I}_{-i}$
and
$\boldsymbol{I}_{i}^{R}=\boldsymbol{I}_{-i}$
and
![]() $\unicode[STIX]{x1D63D}$
is equal to its own rotation. Comparing (B 8) with the
$\unicode[STIX]{x1D63D}$
is equal to its own rotation. Comparing (B 8) with the
![]() $-i$
column of (B 6), we have
$-i$
column of (B 6), we have
![]() $\boldsymbol{D}_{i}^{R}=\boldsymbol{D}_{-i}$
. This is because
$\boldsymbol{D}_{i}^{R}=\boldsymbol{D}_{-i}$
. This is because
![]() $\unicode[STIX]{x1D63D}$
is invertible, its has a full rank and the solution of (B 8) is unique. We have now proved that
$\unicode[STIX]{x1D63D}$
is invertible, its has a full rank and the solution of (B 8) is unique. We have now proved that
![]() $\unicode[STIX]{x1D63D}^{-1}$
is indeed a rationally symmetric matrix.
$\unicode[STIX]{x1D63D}^{-1}$
is indeed a rationally symmetric matrix.
Examining the definitions of all the relevant
![]() $\unicode[STIX]{x1D644}$
and
$\unicode[STIX]{x1D644}$
and
![]() $\unicode[STIX]{x1D646}$
matrices, it is trivial to show that they are all rotationally symmetric. Based on the two conclusions discussed above, because the matrix
$\unicode[STIX]{x1D646}$
matrices, it is trivial to show that they are all rotationally symmetric. Based on the two conclusions discussed above, because the matrix
![]() $\unicode[STIX]{x1D63C}$
can be written as
$\unicode[STIX]{x1D63C}$
can be written as
it can be easily shown that
![]() $\unicode[STIX]{x1D63C}$
is rotationally symmetric. One important property that follows is that if a vector
$\unicode[STIX]{x1D63C}$
is rotationally symmetric. One important property that follows is that if a vector
![]() $\boldsymbol{C}^{-}$
is one of the eigenvectors of
$\boldsymbol{C}^{-}$
is one of the eigenvectors of
![]() $\unicode[STIX]{x1D63C}$
, so is
$\unicode[STIX]{x1D63C}$
, so is
![]() $\boldsymbol{C}^{-R}$
. This follows naturally after taking the rotation of both sides of the eigenvalue equation
$\boldsymbol{C}^{-R}$
. This follows naturally after taking the rotation of both sides of the eigenvalue equation
![]() $\unicode[STIX]{x1D63C}\boldsymbol{C}^{-}=\unicode[STIX]{x1D706}\boldsymbol{C}^{-}$
. One consequence of this property is that if an eigenvalue
$\unicode[STIX]{x1D63C}\boldsymbol{C}^{-}=\unicode[STIX]{x1D706}\boldsymbol{C}^{-}$
. One consequence of this property is that if an eigenvalue
![]() $\unicode[STIX]{x1D706}_{n}$
of matrix
$\unicode[STIX]{x1D706}_{n}$
of matrix
![]() $\unicode[STIX]{x1D63C}$
has no multiplicity, its eigenvector
$\unicode[STIX]{x1D63C}$
has no multiplicity, its eigenvector
![]() $\boldsymbol{C}^{-}$
must be either symmetric or antisymmetric. The second important property is that, for each multiple-folded eigenvalue
$\boldsymbol{C}^{-}$
must be either symmetric or antisymmetric. The second important property is that, for each multiple-folded eigenvalue
![]() $\unicode[STIX]{x1D706}_{n}$
, we can always construct both a symmetric (e.g.
$\unicode[STIX]{x1D706}_{n}$
, we can always construct both a symmetric (e.g.
![]() $\boldsymbol{C}^{-}+\boldsymbol{C}^{-R}$
) and an antisymmetric (e.g.
$\boldsymbol{C}^{-}+\boldsymbol{C}^{-R}$
) and an antisymmetric (e.g.
![]() $\boldsymbol{C}^{-}-\boldsymbol{C}^{-R}$
) eigenvector. These properties are essential when we try to assign an order to each obtained eigenvector in appendix C.
$\boldsymbol{C}^{-}-\boldsymbol{C}^{-R}$
) eigenvector. These properties are essential when we try to assign an order to each obtained eigenvector in appendix C.
Appendix C. The mode labelling strategy
It is not difficult to show that, when
![]() $\unicode[STIX]{x1D716}=0$
,
$\unicode[STIX]{x1D716}=0$
,
![]() $\unicode[STIX]{x1D63C}$
is diagonal and its eigenvalues (diagonal elements) are
$\unicode[STIX]{x1D63C}$
is diagonal and its eigenvalues (diagonal elements) are
and their corresponding normalized eigenvectors are
where
![]() $1$
appears at the position of
$1$
appears at the position of
![]() $C_{n}^{-}$
. The well-known results for the cylindrical vortex-sheet flow are recovered. When
$C_{n}^{-}$
. The well-known results for the cylindrical vortex-sheet flow are recovered. When
![]() $\unicode[STIX]{x1D716}$
increases gradually, we expect that the eigenvector gradually changes to
$\unicode[STIX]{x1D716}$
increases gradually, we expect that the eigenvector gradually changes to
where
![]() $a_{n}$
are complex numbers and
$a_{n}$
are complex numbers and
![]() $|a_{n}|\ll 1$
. We may use this dominant-component property of
$|a_{n}|\ll 1$
. We may use this dominant-component property of
![]() $\boldsymbol{C}^{-}$
to label the order of the eigenfunctions. That is, the eigenfunction determined by the eigenvector
$\boldsymbol{C}^{-}$
to label the order of the eigenfunctions. That is, the eigenfunction determined by the eigenvector
has an mode number
![]() $n$
, if
$n$
, if
 $$\begin{eqnarray}\Vert \boldsymbol{C}^{-}-\boldsymbol{G}\Vert =\sqrt{\mathop{\sum }_{j=-M}^{M}(|C_{j}^{-}|-G_{j})^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{C}^{-}-\boldsymbol{G}\Vert =\sqrt{\mathop{\sum }_{j=-M}^{M}(|C_{j}^{-}|-G_{j})^{2}}\end{eqnarray}$$
yields a minimum value when
where
![]() $g_{n}$
is the element of the vector
$g_{n}$
is the element of the vector
![]() $\boldsymbol{G}$
.
$\boldsymbol{G}$
.
This strategy, however, hinges on the assumption that there is only one dominant component in the eigenvector
![]() $\boldsymbol{C}^{-}$
. However, this is not always possible. For example, when
$\boldsymbol{C}^{-}$
. However, this is not always possible. For example, when
![]() $\unicode[STIX]{x1D716}\neq 0$
,
$\unicode[STIX]{x1D716}\neq 0$
,
![]() $\unicode[STIX]{x1D706}_{n}$
and
$\unicode[STIX]{x1D706}_{n}$
and
![]() $\unicode[STIX]{x1D706}_{-n}$
do not necessarily have to be same any more. As we discussed above, the eigenvector must be either symmetric or antisymmetric. Since both symmetric and antisymmetric eigenvectors have two dominant components at
$\unicode[STIX]{x1D706}_{-n}$
do not necessarily have to be same any more. As we discussed above, the eigenvector must be either symmetric or antisymmetric. Since both symmetric and antisymmetric eigenvectors have two dominant components at
![]() $n$
and
$n$
and
![]() $-n$
respectively (
$-n$
respectively (
![]() $\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
, therefore one cannot perform a linear combination of the two corresponding eigenvectors), it is hard to determine whether this mode should be called mode
$\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
, therefore one cannot perform a linear combination of the two corresponding eigenvectors), it is hard to determine whether this mode should be called mode
![]() $n$
or
$n$
or
![]() $-n$
.
$-n$
.
To overcome this problem, we force each eigenvector to be either symmetric or antisymmetric. This is always possible, because, as we proved earlier, the eigenvector
![]() $\boldsymbol{C}^{-}$
must be either symmetric or antisymmetric if
$\boldsymbol{C}^{-}$
must be either symmetric or antisymmetric if
![]() $\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
. And if
$\unicode[STIX]{x1D706}_{n}\neq \unicode[STIX]{x1D706}_{-n}$
. And if
![]() $\unicode[STIX]{x1D706}_{n}=\unicode[STIX]{x1D706}_{-n}(n>0)$
, we can always make use the second property of the eigenvectors and redefine one of the two corresponding eigenvectors to be symmetric and the other antisymmetric. In doing so, no matter whether
$\unicode[STIX]{x1D706}_{n}=\unicode[STIX]{x1D706}_{-n}(n>0)$
, we can always make use the second property of the eigenvectors and redefine one of the two corresponding eigenvectors to be symmetric and the other antisymmetric. In doing so, no matter whether
![]() $\unicode[STIX]{x1D706}_{n}$
and
$\unicode[STIX]{x1D706}_{n}$
and
![]() $\unicode[STIX]{x1D706}_{-n}$
are equal or not, each eigenvector would have two dominant components. Now for the symmetric eignvectors if
$\unicode[STIX]{x1D706}_{-n}$
are equal or not, each eigenvector would have two dominant components. Now for the symmetric eignvectors if
![]() $||\boldsymbol{C}^{-}-\boldsymbol{G}||$
obtains its minimum when
$||\boldsymbol{C}^{-}-\boldsymbol{G}||$
obtains its minimum when
we label the eigenvector as mode
![]() $n$
. For antisymmetric eigenvectors we label it as
$n$
. For antisymmetric eigenvectors we label it as
![]() $-n$
in a similar manner. For
$-n$
in a similar manner. For
![]() $n=0$
, it is trivial to label its mode number, and because we require
$n=0$
, it is trivial to label its mode number, and because we require
![]() $C_{0}^{-}\neq 0$
, it can be shown that the eigenvector must be symmetric. By labelling the eigenvectors in this way, from (3.18), this means that all nonnegative eigenfunctions are even functions of
$C_{0}^{-}\neq 0$
, it can be shown that the eigenvector must be symmetric. By labelling the eigenvectors in this way, from (3.18), this means that all nonnegative eigenfunctions are even functions of
![]() $\unicode[STIX]{x1D719}$
and negative ones odd.
$\unicode[STIX]{x1D719}$
and negative ones odd.