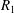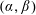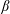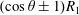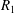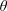1 Introduction
The linear stability theory provides a necessary condition (
![]() $Re\leqslant Re_{L}$
) for a base flow to be conditionally stable, and the energy stability theory (energy method) provides a sufficient condition (
$Re\leqslant Re_{L}$
) for a base flow to be conditionally stable, and the energy stability theory (energy method) provides a sufficient condition (
![]() $Re\leqslant Re_{E}$
) for a base flow to be globally stable, where
$Re\leqslant Re_{E}$
) for a base flow to be globally stable, where
![]() $Re_{L}$
and
$Re_{L}$
and
![]() $Re_{E}$
are the critical Reynolds numbers for the linear stability and energy stability, respectively. In the linear stability analysis of parallel flows, Squire’s theorem implies that the least stable normal modes are two-dimensional waves with spanwise wavenumber
$Re_{E}$
are the critical Reynolds numbers for the linear stability and energy stability, respectively. In the linear stability analysis of parallel flows, Squire’s theorem implies that the least stable normal modes are two-dimensional waves with spanwise wavenumber
![]() $\unicode[STIX]{x1D6FD}=0$
(Squire Reference Squire1933; Knowles & Gebhart Reference Knowles and Gebhart1968). In the energy stability theory, however, there is no analogue to Squire’s theorem. Actually, the least stable mode for the energy stability of the plane Poiseuille flow is a streamwise vortex with streamwise wavenumber
$\unicode[STIX]{x1D6FD}=0$
(Squire Reference Squire1933; Knowles & Gebhart Reference Knowles and Gebhart1968). In the energy stability theory, however, there is no analogue to Squire’s theorem. Actually, the least stable mode for the energy stability of the plane Poiseuille flow is a streamwise vortex with streamwise wavenumber
![]() $\unicode[STIX]{x1D6FC}=0$
(Busse Reference Busse1969; Joseph & Carmi Reference Joseph and Carmi1969).
$\unicode[STIX]{x1D6FC}=0$
(Busse Reference Busse1969; Joseph & Carmi Reference Joseph and Carmi1969).
Two proofs that the least stable mode for the energy stability of the plane Couette flow is a streamwise vortex were given by Joseph (Reference Joseph1966) and Busse (Reference Busse1972). However, Joseph’s proof was uncompleted because it failed to exclude the possibility that the least stable mode might be a two-dimensional wave (Busse Reference Busse1972); Busse’s proof required three particular eigenvalues to be calculated first. Consequently, there is no direct proof (without the need for calculating any particular eigenvalue) that the streamwise vortices are the least stable modes for the energy stability, even in the simplest case of the plane Couette flow.
The critical Reynolds number for the energy stability
![]() $Re_{E}$
is usually calculated in two steps. The first (minimum) positive eigenvalues
$Re_{E}$
is usually calculated in two steps. The first (minimum) positive eigenvalues
![]() $R_{1}$
of an eigenvalue equation are calculated for all wavenumber pairs
$R_{1}$
of an eigenvalue equation are calculated for all wavenumber pairs
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, where
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are the streamwise and spanwise wavenumbers, and then the critical Reynolds number
$\unicode[STIX]{x1D6FD}$
are the streamwise and spanwise wavenumbers, and then the critical Reynolds number
![]() $Re_{E}$
is the minimum
$Re_{E}$
is the minimum
![]() $R_{1}$
in the wavenumber plane.
$R_{1}$
in the wavenumber plane.
In this paper, we explore the variations of the positive eigenvalues in the wavenumber plane, and propose a conjecture on the first positive eigenvalue for a variety of parallel shear flows. This conjecture implies that the least stable modes for the energy stability are streamwise vortices for these base flows. We derive the eigenvalue equation for the energy stability in § 2, and prove two theorems on the monotonicity of the positive eigenvalues in the wavenumber plane in § 3. After the numerical results of the energy stability are introduced in § 4, we propose the conjecture in § 5. Section 6 concludes this work. We consider a special case in appendix A to show the gap in Joseph’s proof that the least stable mode for the energy stability of the plane Couette flow is a streamwise vortex. Appendix B introduces the gradient descent algorithm used in search for the counter-examples to the conjecture.
2 Eigenvalue equation for the energy stability of plane parallel flows
When the fluctuation in the temperature of the fluid is small, the motion of the fluid between parallel plates is governed by the Boussinesq equation (Straughan Reference Straughan1992, p. 56),
where
![]() $x^{\ast }$
,
$x^{\ast }$
,
![]() $y^{\ast }$
and
$y^{\ast }$
and
![]() $z^{\ast }$
are the coordinates in the streamwise, wall-normal and spanwise directions, respectively;
$z^{\ast }$
are the coordinates in the streamwise, wall-normal and spanwise directions, respectively;
![]() $t^{\ast }$
is the time;
$t^{\ast }$
is the time;
![]() $\boldsymbol{U}^{\ast }=(U^{\ast },V^{\ast },W^{\ast })$
,
$\boldsymbol{U}^{\ast }=(U^{\ast },V^{\ast },W^{\ast })$
,
![]() $T^{\ast }$
and
$T^{\ast }$
and
![]() $P^{\ast }$
are the velocity, temperature and pressure of the fluid, respectively;
$P^{\ast }$
are the velocity, temperature and pressure of the fluid, respectively;
![]() $\unicode[STIX]{x1D70C}_{r}$
is the reference density of the fluid at the reference temperature
$\unicode[STIX]{x1D70C}_{r}$
is the reference density of the fluid at the reference temperature
![]() $T_{r}^{\ast }$
;
$T_{r}^{\ast }$
;
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $c_{p}$
are the kinematic viscosity, coefficient of thermal expansion, thermal diffusivity and specific heat capacity at constant pressure of the fluid, respectively;
$c_{p}$
are the kinematic viscosity, coefficient of thermal expansion, thermal diffusivity and specific heat capacity at constant pressure of the fluid, respectively;
![]() $\boldsymbol{g}=-g\boldsymbol{e}_{y}$
is the gravitational acceleration;
$\boldsymbol{g}=-g\boldsymbol{e}_{y}$
is the gravitational acceleration;
![]() $\boldsymbol{e}_{x}$
and
$\boldsymbol{e}_{x}$
and
![]() $\boldsymbol{e}_{y}$
are the unit vectors in the streamwise and wall-normal directions. Both the streamwise component of the body force
$\boldsymbol{e}_{y}$
are the unit vectors in the streamwise and wall-normal directions. Both the streamwise component of the body force
![]() $F_{x}^{\ast }$
and the volumetric heat source
$F_{x}^{\ast }$
and the volumetric heat source
![]() $Q^{\ast }$
are functions of only the wall-normal coordinate
$Q^{\ast }$
are functions of only the wall-normal coordinate
![]() $y^{\ast }$
. The distance between the parallel plates is
$y^{\ast }$
. The distance between the parallel plates is
![]() $2h^{\ast }$
;
$2h^{\ast }$
;
![]() $U_{w,\pm h^{\ast }}^{\ast }$
and
$U_{w,\pm h^{\ast }}^{\ast }$
and
![]() $T_{w,\pm h^{\ast }}^{\ast }$
are the streamwise velocities and the temperatures of the walls at
$T_{w,\pm h^{\ast }}^{\ast }$
are the streamwise velocities and the temperatures of the walls at
![]() $y^{\ast }=\pm h^{\ast }$
.
$y^{\ast }=\pm h^{\ast }$
.
The region is assumed to be periodic in the streamwise and spanwise directions. The velocity of the fluid satisfies the slip boundary condition at the walls, and
![]() $l^{\ast }$
is the slip length. The temperature of the fluid satisfies the convective boundary condition at the walls, and
$l^{\ast }$
is the slip length. The temperature of the fluid satisfies the convective boundary condition at the walls, and
![]() $l_{T}^{\ast }$
is the ratio between the thermal conductivity of the fluid and the convective heat transfer coefficient of the flow. The no-slip boundary condition and the fixed temperature boundary condition correspond to
$l_{T}^{\ast }$
is the ratio between the thermal conductivity of the fluid and the convective heat transfer coefficient of the flow. The no-slip boundary condition and the fixed temperature boundary condition correspond to
![]() $l^{\ast }=0$
and
$l^{\ast }=0$
and
![]() $l_{T}^{\ast }=0$
, respectively.
$l_{T}^{\ast }=0$
, respectively.
Introducing non-dimensional quantities,
where
![]() $U_{c}^{\ast }$
and
$U_{c}^{\ast }$
and
![]() $\unicode[STIX]{x0394}T_{c}^{\ast }$
are the characteristic velocity and temperature difference in the fluid, we have the non-dimensional governing equation,
$\unicode[STIX]{x0394}T_{c}^{\ast }$
are the characteristic velocity and temperature difference in the fluid, we have the non-dimensional governing equation,
where the Reynolds number, the Prandtl number and the Grashof number are defined as
Here we assume
![]() $l\geqslant 0$
and
$l\geqslant 0$
and
![]() $l_{T}\geqslant 0$
. When
$l_{T}\geqslant 0$
. When
![]() $l_{T}>0$
, the Nusselt number can be defined as
$l_{T}>0$
, the Nusselt number can be defined as
![]() $l_{T}^{-1}$
.
$l_{T}^{-1}$
.
The base flow
![]() $(\boldsymbol{U}_{0},T_{0},P_{0})$
is a parallel flow (with
$(\boldsymbol{U}_{0},T_{0},P_{0})$
is a parallel flow (with
![]() $V_{0}=W_{0}=0$
and only depending on the wall-normal coordinate
$V_{0}=W_{0}=0$
and only depending on the wall-normal coordinate
![]() $y$
), and satisfies
$y$
), and satisfies
The governing equation of the disturbance
![]() $(\boldsymbol{u},T^{\prime },p)=(\boldsymbol{U},T,P)-(\boldsymbol{U}_{0},T_{0},P_{0})$
is
$(\boldsymbol{u},T^{\prime },p)=(\boldsymbol{U},T,P)-(\boldsymbol{U}_{0},T_{0},P_{0})$
is
Define the energy of the disturbance as
where
![]() $\unicode[STIX]{x1D706}>0$
is a coupling parameter (Joseph Reference Joseph1966), and
$\unicode[STIX]{x1D706}>0$
is a coupling parameter (Joseph Reference Joseph1966), and
![]() $\text{d}V=\text{d}x\,\text{d}y\,\text{d}z$
. The region is
$\text{d}V=\text{d}x\,\text{d}y\,\text{d}z$
. The region is
![]() $\unicode[STIX]{x1D6FA}=(0,L_{x})\times (-1,1)\times (0,L_{z})$
, where
$\unicode[STIX]{x1D6FA}=(0,L_{x})\times (-1,1)\times (0,L_{z})$
, where
![]() $L_{x}$
and
$L_{x}$
and
![]() $L_{z}$
are the wavelengths of the disturbance in the streamwise and spanwise directions, respectively. From (2.18)–(2.21), we have
$L_{z}$
are the wavelengths of the disturbance in the streamwise and spanwise directions, respectively. From (2.18)–(2.21), we have
where
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert ^{2} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\left(\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\right)\text{d}V+l\int _{0}^{L_{z}}\int _{0}^{L_{x}}\left[\left(\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=1}\right)^{2}+\left(\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=-1}\right)^{2}\right]\text{d}x\,\text{d}z\nonumber\\ \displaystyle & & \displaystyle +\,l\int _{0}^{L_{z}}\int _{0}^{L_{x}}\left[\left(\left.\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}y}\right|_{y=1}\right)^{2}+\left(\left.\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}y}\right|_{y=-1}\right)^{2}\right]\text{d}x\,\text{d}z,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert ^{2} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\left(\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\right)\text{d}V+l\int _{0}^{L_{z}}\int _{0}^{L_{x}}\left[\left(\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=1}\right)^{2}+\left(\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=-1}\right)^{2}\right]\text{d}x\,\text{d}z\nonumber\\ \displaystyle & & \displaystyle +\,l\int _{0}^{L_{z}}\int _{0}^{L_{x}}\left[\left(\left.\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}y}\right|_{y=1}\right)^{2}+\left(\left.\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}y}\right|_{y=-1}\right)^{2}\right]\text{d}x\,\text{d}z,\end{eqnarray}$$
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert ^{2}=\int _{\unicode[STIX]{x1D6FA}}\left(\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}x_{j}}\right)\text{d}V+l_{T}\int _{0}^{L_{z}}\int _{0}^{L_{x}}\left[\left(\left.\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}y}\right|_{y=1}\right)^{2}+\left(\left.\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}y}\right|_{y=-1}\right)^{2}\right]\text{d}x\,\text{d}z,\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert ^{2}=\int _{\unicode[STIX]{x1D6FA}}\left(\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}x_{j}}\right)\text{d}V+l_{T}\int _{0}^{L_{z}}\int _{0}^{L_{x}}\left[\left(\left.\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}y}\right|_{y=1}\right)^{2}+\left(\left.\frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}y}\right|_{y=-1}\right)^{2}\right]\text{d}x\,\text{d}z,\end{eqnarray}$$
and the Einstein summation convention is used.
In the energy stability analysis, the critical Reynolds number
![]() $Re_{E}(Pr,\unicode[STIX]{x1D706})$
is defined by
$Re_{E}(Pr,\unicode[STIX]{x1D706})$
is defined by
 $$\begin{eqnarray}\frac{1}{Re_{E}(Pr,\unicode[STIX]{x1D706})}=\max \frac{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\left(-uv{\displaystyle \frac{\text{d}U_{0}}{\text{d}y}}-\unicode[STIX]{x1D706}PrvT^{\prime }{\displaystyle \frac{\text{d}\tilde{T}_{0}}{\text{d}y}}\right)\text{d}V}{\Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert ^{2}+\unicode[STIX]{x1D706}\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert ^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{Re_{E}(Pr,\unicode[STIX]{x1D706})}=\max \frac{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\left(-uv{\displaystyle \frac{\text{d}U_{0}}{\text{d}y}}-\unicode[STIX]{x1D706}PrvT^{\prime }{\displaystyle \frac{\text{d}\tilde{T}_{0}}{\text{d}y}}\right)\text{d}V}{\Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert ^{2}+\unicode[STIX]{x1D706}\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert ^{2}},\end{eqnarray}$$
where the maximum is searched among all divergence-free disturbances satisfying the boundary condition (2.21). Therefore, we have
when
![]() $Re\leqslant Re_{E}(Pr,\unicode[STIX]{x1D706})$
. We also have
$Re\leqslant Re_{E}(Pr,\unicode[STIX]{x1D706})$
. We also have
![]() $E\rightarrow 0$
when
$E\rightarrow 0$
when
![]() $Re<Re_{E}(Pr,\unicode[STIX]{x1D706})$
, because
$Re<Re_{E}(Pr,\unicode[STIX]{x1D706})$
, because
![]() $\Vert \boldsymbol{u}\Vert$
and
$\Vert \boldsymbol{u}\Vert$
and
![]() $\Vert T^{\prime }\Vert$
are controlled by
$\Vert T^{\prime }\Vert$
are controlled by
![]() $\Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert$
and
$\Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert$
and
![]() $\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert$
in the bounded domain according to the Poincaré inequality.
$\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert$
in the bounded domain according to the Poincaré inequality.
The Euler–Lagrange equation corresponding to (2.27) is
where
![]() $R$
and
$R$
and
![]() $q(x,y,z)$
are the Lagrange multipliers.
$q(x,y,z)$
are the Lagrange multipliers.
From (2.25), (2.26) and (2.29)–(2.34), we have
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert ^{2}+\unicode[STIX]{x1D706}\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert ^{2} & = & \displaystyle -\int _{\unicode[STIX]{x1D6FA}}(u\unicode[STIX]{x1D6FB}^{2}u+v\unicode[STIX]{x1D6FB}^{2}v+w\unicode[STIX]{x1D6FB}^{2}w+\unicode[STIX]{x1D706}T^{\prime }\unicode[STIX]{x1D6FB}^{2}T^{\prime })\,\text{d}V\nonumber\\ \displaystyle & = & \displaystyle R\int _{\unicode[STIX]{x1D6FA}}\left(-uv\frac{\text{d}U_{0}}{\text{d}y}-\unicode[STIX]{x1D706}PrvT^{\prime }\frac{\text{d}\tilde{T}_{0}}{\text{d}y}\right)\text{d}V.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D735}\boldsymbol{u}\Vert ^{2}+\unicode[STIX]{x1D706}\Vert \unicode[STIX]{x1D735}T^{\prime }\Vert ^{2} & = & \displaystyle -\int _{\unicode[STIX]{x1D6FA}}(u\unicode[STIX]{x1D6FB}^{2}u+v\unicode[STIX]{x1D6FB}^{2}v+w\unicode[STIX]{x1D6FB}^{2}w+\unicode[STIX]{x1D706}T^{\prime }\unicode[STIX]{x1D6FB}^{2}T^{\prime })\,\text{d}V\nonumber\\ \displaystyle & = & \displaystyle R\int _{\unicode[STIX]{x1D6FA}}\left(-uv\frac{\text{d}U_{0}}{\text{d}y}-\unicode[STIX]{x1D706}PrvT^{\prime }\frac{\text{d}\tilde{T}_{0}}{\text{d}y}\right)\text{d}V.\end{eqnarray}$$
Comparing (2.35) with (2.27), we notice that the critical Reynolds number
![]() $Re_{E}(Pr,\unicode[STIX]{x1D706})$
is just the minimum positive eigenvalue
$Re_{E}(Pr,\unicode[STIX]{x1D706})$
is just the minimum positive eigenvalue
![]() $R$
.
$R$
.
Introducing the normal mode
![]() $(u,v,w,T^{\prime },q)=(\hat{u} ,\hat{v},{\hat{w}},\hat{T},\hat{q})\exp [\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}z)]+\text{c.c.}$
, where
$(u,v,w,T^{\prime },q)=(\hat{u} ,\hat{v},{\hat{w}},\hat{T},\hat{q})\exp [\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}z)]+\text{c.c.}$
, where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are the streamwise and spanwise wavenumbers, and c.c. denotes the complex conjugate, we have
$\unicode[STIX]{x1D6FD}$
are the streamwise and spanwise wavenumbers, and c.c. denotes the complex conjugate, we have
where
![]() $\text{D}\equiv \text{d}/\text{d}y$
,
$\text{D}\equiv \text{d}/\text{d}y$
,
![]() $k=(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})^{1/2}$
and
$k=(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})^{1/2}$
and
![]() $\unicode[STIX]{x1D703}=\arctan (\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC})$
. If we denote the positive eigenvalues of (2.36)–(2.41) as
$\unicode[STIX]{x1D703}=\arctan (\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC})$
. If we denote the positive eigenvalues of (2.36)–(2.41) as
![]() $R_{1}(k,\unicode[STIX]{x1D703},Pr,\unicode[STIX]{x1D706})\leqslant R_{2}(k,\unicode[STIX]{x1D703},Pr,\unicode[STIX]{x1D706})\leqslant \cdots \,$
, then the critical Reynolds number for the energy stability is
$R_{1}(k,\unicode[STIX]{x1D703},Pr,\unicode[STIX]{x1D706})\leqslant R_{2}(k,\unicode[STIX]{x1D703},Pr,\unicode[STIX]{x1D706})\leqslant \cdots \,$
, then the critical Reynolds number for the energy stability is
Note that the
![]() $n$
th positive eigenvalue
$n$
th positive eigenvalue
![]() $R_{n}$
and the corresponding eigenvector may be only piecewise continuously differentiable where
$R_{n}$
and the corresponding eigenvector may be only piecewise continuously differentiable where
![]() $R_{n}=R_{n+1}$
or
$R_{n}=R_{n+1}$
or
![]() $R_{n}=R_{n-1}$
(figure 1). Due to the symmetry of (2.36)–(2.41), only the cases with
$R_{n}=R_{n-1}$
(figure 1). Due to the symmetry of (2.36)–(2.41), only the cases with
![]() $k>0$
and
$k>0$
and
![]() $0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
need to be considered.
$0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
need to be considered.

Figure 1. The fifth and sixth positive eigenvalues for the energy stability of the parallel shear flow with
![]() $\text{D}U_{0}=\sin (8\unicode[STIX]{x03C0}y)$
,
$\text{D}U_{0}=\sin (8\unicode[STIX]{x03C0}y)$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
,
$Pr\,\text{D}\tilde{T}_{0}=0$
,
![]() $l=0$
and
$l=0$
and
![]() $k=1$
.
$k=1$
.
The critical Reynolds number for the energy stability
![]() $Re_{E}$
depends on the definition of the energy of the disturbance (2.22), and is therefore a function of the Prandtl number
$Re_{E}$
depends on the definition of the energy of the disturbance (2.22), and is therefore a function of the Prandtl number
![]() $Pr$
and the coupling parameter
$Pr$
and the coupling parameter
![]() $\unicode[STIX]{x1D706}$
. For given Prandtl number, an optimal critical Reynolds number for the energy stability can be further defined as the maximum of
$\unicode[STIX]{x1D706}$
. For given Prandtl number, an optimal critical Reynolds number for the energy stability can be further defined as the maximum of
![]() $Re_{E}(Pr,\unicode[STIX]{x1D706})$
for all
$Re_{E}(Pr,\unicode[STIX]{x1D706})$
for all
![]() $\unicode[STIX]{x1D706}>0$
(Joseph Reference Joseph1966).
$\unicode[STIX]{x1D706}>0$
(Joseph Reference Joseph1966).
3 The monotonicity of the positive eigenvalues
 $R_{n}\,(n\geqslant 1)$
in the wavenumber plane
$R_{n}\,(n\geqslant 1)$
in the wavenumber plane
3.1 The expressions for
 $\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}k$
and
$\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}k$
and
 $\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
$\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
To study the monotonicity of
![]() $R_{n}$
in the
$R_{n}$
in the
![]() $(k,\unicode[STIX]{x1D703})$
plane, we first derive the expressions of
$(k,\unicode[STIX]{x1D703})$
plane, we first derive the expressions of
![]() $\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}k$
and
$\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}k$
and
![]() $\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
.
Denote (2.36)–(2.40) as
![]() $\unicode[STIX]{x1D647}\hat{\boldsymbol{u}}=\mathbf{0}$
, where
$\unicode[STIX]{x1D647}\hat{\boldsymbol{u}}=\mathbf{0}$
, where
 $$\begin{eqnarray}\unicode[STIX]{x1D647}=\left[\begin{array}{@{}ccccc@{}}\text{D}^{2}-k^{2} & -{\textstyle \frac{1}{2}}R(\text{D}U_{0}) & 0 & 0 & -\text{i}k\cos \unicode[STIX]{x1D703}\\ -{\textstyle \frac{1}{2}}R(\text{D}U_{0}) & \text{D}^{2}-k^{2} & 0 & -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D706}PrR(\text{D}\tilde{T}_{0}) & -\text{D}\\ 0 & 0 & \text{D}^{2}-k^{2} & 0 & -\text{i}k\sin \unicode[STIX]{x1D703}\\ 0 & -{\textstyle \frac{1}{2}}PrR(\text{D}\tilde{T}_{0}) & 0 & \text{D}^{2}-k^{2} & 0\\ \text{i}k\cos \unicode[STIX]{x1D703} & \text{D} & \text{i}k\sin \unicode[STIX]{x1D703} & 0 & 0\end{array}\right],\quad \hat{\boldsymbol{u}}=\left[\begin{array}{@{}c@{}}\hat{u} \\ \hat{v}\\ {\hat{w}}\\ \hat{T}\\ \hat{q}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D647}=\left[\begin{array}{@{}ccccc@{}}\text{D}^{2}-k^{2} & -{\textstyle \frac{1}{2}}R(\text{D}U_{0}) & 0 & 0 & -\text{i}k\cos \unicode[STIX]{x1D703}\\ -{\textstyle \frac{1}{2}}R(\text{D}U_{0}) & \text{D}^{2}-k^{2} & 0 & -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D706}PrR(\text{D}\tilde{T}_{0}) & -\text{D}\\ 0 & 0 & \text{D}^{2}-k^{2} & 0 & -\text{i}k\sin \unicode[STIX]{x1D703}\\ 0 & -{\textstyle \frac{1}{2}}PrR(\text{D}\tilde{T}_{0}) & 0 & \text{D}^{2}-k^{2} & 0\\ \text{i}k\cos \unicode[STIX]{x1D703} & \text{D} & \text{i}k\sin \unicode[STIX]{x1D703} & 0 & 0\end{array}\right],\quad \hat{\boldsymbol{u}}=\left[\begin{array}{@{}c@{}}\hat{u} \\ \hat{v}\\ {\hat{w}}\\ \hat{T}\\ \hat{q}\end{array}\right].\end{eqnarray}$$
For any
![]() $\unicode[STIX]{x1D706}>0$
, assume the geometric multiplicity of the
$\unicode[STIX]{x1D706}>0$
, assume the geometric multiplicity of the
![]() $n$
th eigenvalue
$n$
th eigenvalue
![]() $R_{n}(k,\unicode[STIX]{x1D703},Pr)$
to be 1 in an open set
$R_{n}(k,\unicode[STIX]{x1D703},Pr)$
to be 1 in an open set
![]() $S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]\times [0,+\infty )$
. If the
$S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]\times [0,+\infty )$
. If the
![]() $n$
th positive eigenvalue and the corresponding eigenvector of (2.36)–(2.41) are
$n$
th positive eigenvalue and the corresponding eigenvector of (2.36)–(2.41) are
![]() $(R_{n},\hat{\boldsymbol{u}}_{n})$
for parameters
$(R_{n},\hat{\boldsymbol{u}}_{n})$
for parameters
![]() $(k,\unicode[STIX]{x1D703},Pr)\in S$
, and are
$(k,\unicode[STIX]{x1D703},Pr)\in S$
, and are
![]() $(R_{n}+\text{d}R_{n},\hat{\boldsymbol{u}}_{n}+\text{d}\hat{\boldsymbol{u}}_{n})$
for parameters
$(R_{n}+\text{d}R_{n},\hat{\boldsymbol{u}}_{n}+\text{d}\hat{\boldsymbol{u}}_{n})$
for parameters
![]() $(k+\text{d}k,\unicode[STIX]{x1D703}+\text{d}\unicode[STIX]{x1D703},Pr+\text{d}Pr)\in S$
, we can neglect the higher-order terms and obtain
$(k+\text{d}k,\unicode[STIX]{x1D703}+\text{d}\unicode[STIX]{x1D703},Pr+\text{d}Pr)\in S$
, we can neglect the higher-order terms and obtain
Define the inner product between two vectors
![]() $\hat{\boldsymbol{u}}^{\prime }$
and
$\hat{\boldsymbol{u}}^{\prime }$
and
![]() $\hat{\boldsymbol{u}}^{\prime \prime }$
as
$\hat{\boldsymbol{u}}^{\prime \prime }$
as
where the overlines denote the complex conjugates. Because
![]() $\unicode[STIX]{x1D647}$
is a self-adjoint operator with respect to the inner product (3.5) and the boundary conditions (2.41), (3.3) and (3.4), we have
$\unicode[STIX]{x1D647}$
is a self-adjoint operator with respect to the inner product (3.5) and the boundary conditions (2.41), (3.3) and (3.4), we have
and then it follows from (3.2) that
Therefore, we have
 $$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}}{\unicode[STIX]{x2202}k}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}k}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}R_{n}}}\hat{\boldsymbol{u}}_{n}\right\rangle }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}}{\unicode[STIX]{x2202}k}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}k}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}R_{n}}}\hat{\boldsymbol{u}}_{n}\right\rangle }}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}R_{n}}}\hat{\boldsymbol{u}}_{n}\right\rangle }}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}R_{n}}}\hat{\boldsymbol{u}}_{n}\right\rangle }}. & \displaystyle\end{eqnarray}$$
The inner products in (3.7)–(3.9) are
where
![]() $\hat{\unicode[STIX]{x1D702}}_{n}=\text{i}k\hat{u} _{n}\sin \unicode[STIX]{x1D703}-\text{i}k{\hat{w}}_{n}\cos \unicode[STIX]{x1D703}$
is the wall-normal component of the disturbance vorticity.
$\hat{\unicode[STIX]{x1D702}}_{n}=\text{i}k\hat{u} _{n}\sin \unicode[STIX]{x1D703}-\text{i}k{\hat{w}}_{n}\cos \unicode[STIX]{x1D703}$
is the wall-normal component of the disturbance vorticity.
Using (2.36)–(2.41) in (3.10)–(3.13), we have
where
3.2 The dependence of the positive eigenvalues
 $R_{n}$
$R_{n}$
 $(n\geqslant 1)$
on
$(n\geqslant 1)$
on
 $k$
$k$
Theorem 1. For any continuously differentiable real functions
![]() $\text{D}U_{0}$
and
$\text{D}U_{0}$
and
![]() $\text{D}\tilde{T}_{0}$
, and any
$\text{D}\tilde{T}_{0}$
, and any
![]() $\unicode[STIX]{x1D706}>0$
,
$\unicode[STIX]{x1D706}>0$
,
![]() $Pr\geqslant 0$
,
$Pr\geqslant 0$
,
![]() $l\geqslant 0$
,
$l\geqslant 0$
,
![]() $l_{T}\geqslant 0$
and
$l_{T}\geqslant 0$
and
![]() $\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}/2]$
,
$\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}/2]$
,
![]() $kR_{n}$
is an increasing function of
$kR_{n}$
is an increasing function of
![]() $k$
when
$k$
when
![]() $k>0$
, and
$k>0$
, and
![]() $R_{n}$
is a decreasing function of
$R_{n}$
is a decreasing function of
![]() $k$
when
$k$
when
![]() $0<k<k_{0}(l,l_{T})$
, where
$0<k<k_{0}(l,l_{T})$
, where
![]() $R_{n}$
is the
$R_{n}$
is the
![]() $n$
th positive eigenvalue of (2.36)–(2.41)
$n$
th positive eigenvalue of (2.36)–(2.41)
![]() $(n\geqslant 1)$
, and
$(n\geqslant 1)$
, and
![]() $k_{0}(l,l_{T})=\min \{k_{0}^{\prime }(l),\unicode[STIX]{x1D70E}(\max \{l,l_{T}\})\}$
. Here
$k_{0}(l,l_{T})=\min \{k_{0}^{\prime }(l),\unicode[STIX]{x1D70E}(\max \{l,l_{T}\})\}$
. Here
![]() $k_{0}^{\prime }(l)$
is the solution of the equation
$k_{0}^{\prime }(l)$
is the solution of the equation
in the interval
![]() $(\unicode[STIX]{x03C0}/\sqrt{12},\unicode[STIX]{x03C0}/\sqrt{3})$
;
$(\unicode[STIX]{x03C0}/\sqrt{12},\unicode[STIX]{x03C0}/\sqrt{3})$
;
![]() $\unicode[STIX]{x1D70E}(l)$
is the solution of the equation
$\unicode[STIX]{x1D70E}(l)$
is the solution of the equation
![]() $\unicode[STIX]{x1D70E}^{-1}\cot \unicode[STIX]{x1D70E}=l$
in the interval
$\unicode[STIX]{x1D70E}^{-1}\cot \unicode[STIX]{x1D70E}=l$
in the interval
![]() $(0,\unicode[STIX]{x03C0}/2]$
. Specifically, when
$(0,\unicode[STIX]{x03C0}/2]$
. Specifically, when
![]() $l=l_{T}=0$
and
$l=l_{T}=0$
and
![]() $0<k<k_{0}(0,0)=k_{0}^{\prime }(0)\approx 1.534$
,
$0<k<k_{0}(0,0)=k_{0}^{\prime }(0)\approx 1.534$
,
![]() $R_{n}$
is a decreasing function of
$R_{n}$
is a decreasing function of
![]() $k$
.
$k$
.
The following lemmas, which can be proved easily with the variational method, will be used in the proof of theorem 1.
Lemma 1. For any
![]() $l\geqslant 0$
and any complex-valued function
$l\geqslant 0$
and any complex-valued function
![]() $\hat{f}$
, if
$\hat{f}$
, if
![]() $(\hat{f}\pm l\text{D}\hat{f})(\pm 1)=0$
, then
$(\hat{f}\pm l\text{D}\hat{f})(\pm 1)=0$
, then
where
![]() $\unicode[STIX]{x1D70E}(l)$
is the solution of the equation
$\unicode[STIX]{x1D70E}(l)$
is the solution of the equation
![]() $\unicode[STIX]{x1D70E}^{-1}\cot \unicode[STIX]{x1D70E}=l$
in the interval
$\unicode[STIX]{x1D70E}^{-1}\cot \unicode[STIX]{x1D70E}=l$
in the interval
![]() $(0,\unicode[STIX]{x03C0}/2]$
. The equality in (3.22) holds when
$(0,\unicode[STIX]{x03C0}/2]$
. The equality in (3.22) holds when
![]() $\hat{f}=C\cos (\unicode[STIX]{x1D70E}y)$
, where
$\hat{f}=C\cos (\unicode[STIX]{x1D70E}y)$
, where
![]() $C$
is any complex constant.
$C$
is any complex constant.
Lemma 2. For any
![]() $l\geqslant 0$
and any complex-valued function
$l\geqslant 0$
and any complex-valued function
![]() ${\hat{g}}$
, if
${\hat{g}}$
, if
![]() ${\hat{g}}(\pm 1)=(\text{D}{\hat{g}}\pm l\text{D}^{2}{\hat{g}})(\pm 1)=0$
, then
${\hat{g}}(\pm 1)=(\text{D}{\hat{g}}\pm l\text{D}^{2}{\hat{g}})(\pm 1)=0$
, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-1}^{1}(|\text{D}^{2}{\hat{g}}|^{2}+k^{2}|\text{D}{\hat{g}}|^{2})\,\text{d}y+l[|(\text{D}^{2}{\hat{g}})(1)|^{2}+|(\text{D}^{2}{\hat{g}})(-1)|^{2}]\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant [\unicode[STIX]{x1D70E}^{\prime }(k,l)]^{2}\int _{-1}^{1}(|\text{D}{\hat{g}}|^{2}+k^{2}|{\hat{g}}|^{2})\,\text{d}y,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-1}^{1}(|\text{D}^{2}{\hat{g}}|^{2}+k^{2}|\text{D}{\hat{g}}|^{2})\,\text{d}y+l[|(\text{D}^{2}{\hat{g}})(1)|^{2}+|(\text{D}^{2}{\hat{g}})(-1)|^{2}]\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant [\unicode[STIX]{x1D70E}^{\prime }(k,l)]^{2}\int _{-1}^{1}(|\text{D}{\hat{g}}|^{2}+k^{2}|{\hat{g}}|^{2})\,\text{d}y,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}^{\prime }(k,l)$
is the solution of the equation
$\unicode[STIX]{x1D70E}^{\prime }(k,l)$
is the solution of the equation
![]() $\unicode[STIX]{x1D70E}^{\prime }\tan \unicode[STIX]{x1D70E}^{\prime }+k\tanh k+({\unicode[STIX]{x1D70E}^{\prime }}^{2}+k^{2})l=0$
in the interval
$\unicode[STIX]{x1D70E}^{\prime }\tan \unicode[STIX]{x1D70E}^{\prime }+k\tanh k+({\unicode[STIX]{x1D70E}^{\prime }}^{2}+k^{2})l=0$
in the interval
![]() $(\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0})$
. The equality in (3.23) holds when
$(\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0})$
. The equality in (3.23) holds when
![]() ${\hat{g}}=C^{\prime }[\cos (\unicode[STIX]{x1D70E}^{\prime })\cosh (ky)-\cosh (k)\cos (\unicode[STIX]{x1D70E}^{\prime }y)]$
, where
${\hat{g}}=C^{\prime }[\cos (\unicode[STIX]{x1D70E}^{\prime })\cosh (ky)-\cosh (k)\cos (\unicode[STIX]{x1D70E}^{\prime }y)]$
, where
![]() $C^{\prime }$
is any complex constant.
$C^{\prime }$
is any complex constant.
To prove theorem 1, it is sufficient to prove for any given
![]() $\unicode[STIX]{x1D706}>0$
,
$\unicode[STIX]{x1D706}>0$
,
![]() $l\geqslant 0$
and
$l\geqslant 0$
and
![]() $l_{T}\geqslant 0$
,
$l_{T}\geqslant 0$
,
in each subset
![]() $S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]\times [0,+\infty )$
where the geometric multiplicity of the
$S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]\times [0,+\infty )$
where the geometric multiplicity of the
![]() $n$
th eigenvalue
$n$
th eigenvalue
![]() $R_{n}(k,\unicode[STIX]{x1D703},Pr)$
is 1.
$R_{n}(k,\unicode[STIX]{x1D703},Pr)$
is 1.
Substituting (3.14) and (3.17) into (3.8), we have
![]() $\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}k\geqslant -R_{n}/k$
, and then (3.24) holds.
$\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}k\geqslant -R_{n}/k$
, and then (3.24) holds.
Using lemma 1 for
![]() $\hat{\unicode[STIX]{x1D702}}_{n}$
and
$\hat{\unicode[STIX]{x1D702}}_{n}$
and
![]() $\hat{T}_{n}$
, and using lemma 2 for
$\hat{T}_{n}$
, and using lemma 2 for
![]() $\hat{v}_{n}$
, we have
$\hat{v}_{n}$
, we have
Substituting (3.26)–(3.28) into (3.14), we have
 $$\begin{eqnarray}\displaystyle \left\langle \hat{\boldsymbol{u}}_{n},\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}k}\hat{\boldsymbol{u}}_{n}\right\rangle & {\geqslant} & \displaystyle \frac{(\unicode[STIX]{x1D70E}^{\prime }(k,l))^{2}-3k^{2}}{k^{3}}\int _{-1}^{1}(|\text{D}\hat{v}_{n}|^{2}+k^{2}|\hat{v}_{n}|^{2})\,\text{d}y+\frac{(\unicode[STIX]{x1D70E}(l))^{2}-k^{2}}{k^{3}}\int _{-1}^{1}|\hat{\unicode[STIX]{x1D702}}_{n}|^{2}\,\text{d}y\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D706}[(\unicode[STIX]{x1D70E}(l_{T}))^{2}-k^{2}]}{k}\int _{-1}^{1}|\hat{T}_{n}|^{2}\,\text{d}y.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\langle \hat{\boldsymbol{u}}_{n},\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}}{\unicode[STIX]{x2202}k}\hat{\boldsymbol{u}}_{n}\right\rangle & {\geqslant} & \displaystyle \frac{(\unicode[STIX]{x1D70E}^{\prime }(k,l))^{2}-3k^{2}}{k^{3}}\int _{-1}^{1}(|\text{D}\hat{v}_{n}|^{2}+k^{2}|\hat{v}_{n}|^{2})\,\text{d}y+\frac{(\unicode[STIX]{x1D70E}(l))^{2}-k^{2}}{k^{3}}\int _{-1}^{1}|\hat{\unicode[STIX]{x1D702}}_{n}|^{2}\,\text{d}y\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D706}[(\unicode[STIX]{x1D70E}(l_{T}))^{2}-k^{2}]}{k}\int _{-1}^{1}|\hat{T}_{n}|^{2}\,\text{d}y.\end{eqnarray}$$
When
![]() $0<k\leqslant k_{0}^{\prime }(l)$
, we have
$0<k\leqslant k_{0}^{\prime }(l)$
, we have
![]() $[\unicode[STIX]{x1D70E}^{\prime }(k,l)]^{2}-3k^{2}\geqslant [\unicode[STIX]{x1D70E}^{\prime }(k_{0}^{\prime }(l),l)]^{2}-3[k_{0}^{\prime }(l)]^{2}=0$
, because
$[\unicode[STIX]{x1D70E}^{\prime }(k,l)]^{2}-3k^{2}\geqslant [\unicode[STIX]{x1D70E}^{\prime }(k_{0}^{\prime }(l),l)]^{2}-3[k_{0}^{\prime }(l)]^{2}=0$
, because
![]() $\unicode[STIX]{x1D70E}^{\prime }(k,l)$
is a decreasing function of
$\unicode[STIX]{x1D70E}^{\prime }(k,l)$
is a decreasing function of
![]() $k$
for any given
$k$
for any given
![]() $l\geqslant 0$
. Noticing that
$l\geqslant 0$
. Noticing that
![]() $\unicode[STIX]{x1D70E}(l)$
is a decreasing function of
$\unicode[STIX]{x1D70E}(l)$
is a decreasing function of
![]() $l$
when
$l$
when
![]() $l\geqslant 0$
, we have
$l\geqslant 0$
, we have
![]() $[\unicode[STIX]{x1D70E}(l)]^{2}-k^{2}\geqslant 0$
and
$[\unicode[STIX]{x1D70E}(l)]^{2}-k^{2}\geqslant 0$
and
![]() $[\unicode[STIX]{x1D70E}(l_{T})]^{2}-k^{2}\geqslant 0$
when
$[\unicode[STIX]{x1D70E}(l_{T})]^{2}-k^{2}\geqslant 0$
when
![]() $0<k\leqslant \unicode[STIX]{x1D70E}(\max \{l,l_{T}\})$
. Therefore, we have
$0<k\leqslant \unicode[STIX]{x1D70E}(\max \{l,l_{T}\})$
. Therefore, we have
![]() $\langle \hat{\boldsymbol{u}}_{n},(\unicode[STIX]{x2202}\unicode[STIX]{x1D647}/\unicode[STIX]{x2202}k)\hat{\boldsymbol{u}}_{n}\rangle \geqslant 0$
when
$\langle \hat{\boldsymbol{u}}_{n},(\unicode[STIX]{x2202}\unicode[STIX]{x1D647}/\unicode[STIX]{x2202}k)\hat{\boldsymbol{u}}_{n}\rangle \geqslant 0$
when
![]() $0<k<k_{0}(l,l_{T})=\min \{k_{0}^{\prime }(l),\unicode[STIX]{x1D70E}(\max \{l,l_{T}\})\}$
, and then (3.25) holds because of (3.8) and (3.17).
$0<k<k_{0}(l,l_{T})=\min \{k_{0}^{\prime }(l),\unicode[STIX]{x1D70E}(\max \{l,l_{T}\})\}$
, and then (3.25) holds because of (3.8) and (3.17).
Specifically, when
![]() $l=l_{T}=0$
, we have
$l=l_{T}=0$
, we have
![]() $k_{0}(0,0)=k_{0}^{\prime }(0)$
because
$k_{0}(0,0)=k_{0}^{\prime }(0)$
because
![]() $k_{0}^{\prime }(0)\approx 1.534<\unicode[STIX]{x03C0}/2=\unicode[STIX]{x1D70E}(0)$
. Thus we have proved theorem 1.
$k_{0}^{\prime }(0)\approx 1.534<\unicode[STIX]{x03C0}/2=\unicode[STIX]{x1D70E}(0)$
. Thus we have proved theorem 1.
A direct corollary of theorem 1 is that
![]() $R_{n}=O(k^{-1})$
when
$R_{n}=O(k^{-1})$
when
![]() $k\rightarrow 0$
. Another corollary is that the least stable mode in the energy method must have
$k\rightarrow 0$
. Another corollary is that the least stable mode in the energy method must have
![]() $k\geqslant k_{0}(l,l_{T})$
. The contours of
$k\geqslant k_{0}(l,l_{T})$
. The contours of
![]() $k_{0}$
in the
$k_{0}$
in the
![]() $(l,l_{T})$
plane are plotted in figure 2.
$(l,l_{T})$
plane are plotted in figure 2.

Figure 2. The contours of
![]() $k_{0}$
in the
$k_{0}$
in the
![]() $(l,l_{T})$
plane.
$(l,l_{T})$
plane.
3.3 The dependence of the positive eigenvalues
 $R_{n}$
$R_{n}$
 $(n\geqslant 1)$
on
$(n\geqslant 1)$
on
 $\unicode[STIX]{x1D703}$
$\unicode[STIX]{x1D703}$
Theorem 2. For any continuously differentiable real functions
![]() $\text{D}U_{0}$
and
$\text{D}U_{0}$
and
![]() $\text{D}\tilde{T}_{0}$
, and any
$\text{D}\tilde{T}_{0}$
, and any
![]() $\unicode[STIX]{x1D706}>0$
,
$\unicode[STIX]{x1D706}>0$
,
![]() $Pr\geqslant 0$
,
$Pr\geqslant 0$
,
![]() $l\geqslant 0$
,
$l\geqslant 0$
,
![]() $l_{T}\geqslant 0$
and
$l_{T}\geqslant 0$
and
![]() $k>0$
,
$k>0$
,
![]() $(\cos \unicode[STIX]{x1D703}\pm 1)R_{n}$
are decreasing functions of
$(\cos \unicode[STIX]{x1D703}\pm 1)R_{n}$
are decreasing functions of
![]() $\unicode[STIX]{x1D703}$
when
$\unicode[STIX]{x1D703}$
when
![]() $0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
, where
$0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
, where
![]() $R_{n}$
is the
$R_{n}$
is the
![]() $n$
th positive eigenvalue of (2.36)–(2.41)
$n$
th positive eigenvalue of (2.36)–(2.41)
![]() $(n\geqslant 1)$
.
$(n\geqslant 1)$
.
To prove theorem 2, it is sufficient to prove for any given
![]() $\unicode[STIX]{x1D706}>0$
,
$\unicode[STIX]{x1D706}>0$
,
![]() $l\geqslant 0$
and
$l\geqslant 0$
and
![]() $l_{T}\geqslant 0$
,
$l_{T}\geqslant 0$
,
in each subset
![]() $S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]\times [0,+\infty )$
where the geometric multiplicity of the
$S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]\times [0,+\infty )$
where the geometric multiplicity of the
![]() $n$
th eigenvalue
$n$
th eigenvalue
![]() $R_{n}(k,\unicode[STIX]{x1D703},Pr)$
is 1.
$R_{n}(k,\unicode[STIX]{x1D703},Pr)$
is 1.
Substituting (3.13) and (3.15) into (3.9), we have
 $$\begin{eqnarray}\frac{1}{R_{n}}\frac{\unicode[STIX]{x2202}R_{n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}=\frac{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{v}}_{n}{\hat{w}}_{n}+\hat{v}_{n}\bar{{\hat{w}}}_{n})\,\text{d}y}{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{u} }_{n}\hat{v}_{n}+\hat{u} _{n}\bar{\hat{v}}_{n})\,\text{d}y+\unicode[STIX]{x1D706}Pr\int _{-1}^{1}(\text{D}\tilde{T}_{0})(\bar{\hat{v}}_{n}\hat{T}_{n}+\hat{v}_{n}\bar{\hat{T}}_{n})\,\text{d}y}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{R_{n}}\frac{\unicode[STIX]{x2202}R_{n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}=\frac{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{v}}_{n}{\hat{w}}_{n}+\hat{v}_{n}\bar{{\hat{w}}}_{n})\,\text{d}y}{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{u} }_{n}\hat{v}_{n}+\hat{u} _{n}\bar{\hat{v}}_{n})\,\text{d}y+\unicode[STIX]{x1D706}Pr\int _{-1}^{1}(\text{D}\tilde{T}_{0})(\bar{\hat{v}}_{n}\hat{T}_{n}+\hat{v}_{n}\bar{\hat{T}}_{n})\,\text{d}y}.\end{eqnarray}$$
(i) When
![]() $\unicode[STIX]{x1D703}=0$
, we have
$\unicode[STIX]{x1D703}=0$
, we have
![]() ${\hat{w}}_{n}=0$
from (2.38) and (2.41), and then
${\hat{w}}_{n}=0$
from (2.38) and (2.41), and then
![]() $\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
follows from (3.31). As a result,
$\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
follows from (3.31). As a result,
(ii) When
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, if
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, if
![]() $(\hat{u} _{n},\hat{v}_{n},{\hat{w}}_{n},\hat{T}_{n},\hat{q}_{n})$
is an eigenvector corresponding to the eigenvalue
$(\hat{u} _{n},\hat{v}_{n},{\hat{w}}_{n},\hat{T}_{n},\hat{q}_{n})$
is an eigenvector corresponding to the eigenvalue
![]() $R_{n}$
, then
$R_{n}$
, then
![]() $(\bar{\hat{u} }_{n},\bar{\hat{v}}_{n},-\bar{{\hat{w}}}_{n},\bar{\hat{T}}_{n},\bar{\hat{q}}_{n})$
is also an eigenvector corresponding to the same eigenvalue. In each subset
$(\bar{\hat{u} }_{n},\bar{\hat{v}}_{n},-\bar{{\hat{w}}}_{n},\bar{\hat{T}}_{n},\bar{\hat{q}}_{n})$
is also an eigenvector corresponding to the same eigenvalue. In each subset
![]() $S$
where the geometric multiplicity of the eigenvalue
$S$
where the geometric multiplicity of the eigenvalue
![]() $R_{n}$
is 1, there exists a complex constant
$R_{n}$
is 1, there exists a complex constant
![]() $C$
such that
$C$
such that
![]() $(\bar{\hat{u} }_{n},\bar{\hat{v}}_{n},-\bar{{\hat{w}}}_{n},\bar{\hat{T}}_{n},\bar{\hat{q}}_{n})=C(\hat{u} _{n},\hat{v}_{n},{\hat{w}}_{n},\hat{T}_{n},\hat{q}_{n})$
, and then
$(\bar{\hat{u} }_{n},\bar{\hat{v}}_{n},-\bar{{\hat{w}}}_{n},\bar{\hat{T}}_{n},\bar{\hat{q}}_{n})=C(\hat{u} _{n},\hat{v}_{n},{\hat{w}}_{n},\hat{T}_{n},\hat{q}_{n})$
, and then
![]() $\bar{\hat{v}}_{n}{\hat{w}}_{n}+\hat{v}_{n}\bar{{\hat{w}}}_{n}=0$
. Therefore, we have
$\bar{\hat{v}}_{n}{\hat{w}}_{n}+\hat{v}_{n}\bar{{\hat{w}}}_{n}=0$
. Therefore, we have
![]() $\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
from (3.31), and then
$\unicode[STIX]{x2202}R_{n}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
from (3.31), and then
(iii) When
![]() $0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2$
, using (2.36)–(2.41) in (3.15), we have
$0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2$
, using (2.36)–(2.41) in (3.15), we have
Define
for
![]() $\unicode[STIX]{x1D707}\in \mathbb{R}$
, where
$\unicode[STIX]{x1D707}\in \mathbb{R}$
, where
Using (2.36)–(2.41) in (3.35), we have
Substituting (3.17) and (3.34) into (3.9), we have
and then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{R_{n}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}[(\cos \unicode[STIX]{x1D703}\pm 1)R_{n}]\nonumber\\ \displaystyle & & \displaystyle \quad =\pm \frac{(\sin ^{2}\unicode[STIX]{x1D703})I_{v}-(1\pm \cos \unicode[STIX]{x1D703})^{2}I_{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D706}k^{2}(\sin ^{2}\unicode[STIX]{x1D703})(1\pm 2\cos \unicode[STIX]{x1D703})I_{T}}{(\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D703})(I_{v}+I_{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D706}k^{2}I_{T})}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{(\sin ^{2}\unicode[STIX]{x1D703})I\left({\displaystyle \frac{\cos \unicode[STIX]{x1D703}\pm 1}{\sin \unicode[STIX]{x1D703}}}\right)+\unicode[STIX]{x1D706}k^{2}(\sin ^{2}\unicode[STIX]{x1D703})I_{T}+k^{2}(1\pm \cos \unicode[STIX]{x1D703})^{2}\displaystyle \int _{-1}^{1}|\hat{\unicode[STIX]{x1D702}}_{n}|^{2}\,\text{d}y}{(\sin \unicode[STIX]{x1D703})(I_{v}+I_{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D706}k^{2}I_{T})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{R_{n}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}[(\cos \unicode[STIX]{x1D703}\pm 1)R_{n}]\nonumber\\ \displaystyle & & \displaystyle \quad =\pm \frac{(\sin ^{2}\unicode[STIX]{x1D703})I_{v}-(1\pm \cos \unicode[STIX]{x1D703})^{2}I_{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D706}k^{2}(\sin ^{2}\unicode[STIX]{x1D703})(1\pm 2\cos \unicode[STIX]{x1D703})I_{T}}{(\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D703})(I_{v}+I_{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D706}k^{2}I_{T})}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{(\sin ^{2}\unicode[STIX]{x1D703})I\left({\displaystyle \frac{\cos \unicode[STIX]{x1D703}\pm 1}{\sin \unicode[STIX]{x1D703}}}\right)+\unicode[STIX]{x1D706}k^{2}(\sin ^{2}\unicode[STIX]{x1D703})I_{T}+k^{2}(1\pm \cos \unicode[STIX]{x1D703})^{2}\displaystyle \int _{-1}^{1}|\hat{\unicode[STIX]{x1D702}}_{n}|^{2}\,\text{d}y}{(\sin \unicode[STIX]{x1D703})(I_{v}+I_{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D706}k^{2}I_{T})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 0,\end{eqnarray}$$
where we have used (3.37) for
![]() $\unicode[STIX]{x1D707}=(\cos \unicode[STIX]{x1D703}\pm 1)/\sin \unicode[STIX]{x1D703}$
. Noticing that
$\unicode[STIX]{x1D707}=(\cos \unicode[STIX]{x1D703}\pm 1)/\sin \unicode[STIX]{x1D703}$
. Noticing that
![]() $R_{n}>0$
, we have proved theorem 2.
$R_{n}>0$
, we have proved theorem 2.
According to theorem 2, we have
 $$\begin{eqnarray}\frac{R_{n}\left(k,{\displaystyle \frac{\unicode[STIX]{x03C0}}{2}},Pr,\unicode[STIX]{x1D706}\right)}{1+\cos \unicode[STIX]{x1D703}}\leqslant R_{n}(k,\unicode[STIX]{x1D703},Pr,\unicode[STIX]{x1D706})\leqslant \min \left\{\frac{R_{n}\left(k,{\displaystyle \frac{\unicode[STIX]{x03C0}}{2}},Pr,\unicode[STIX]{x1D706}\right)}{1-\cos \unicode[STIX]{x1D703}},\frac{2R_{n}(k,0,Pr,\unicode[STIX]{x1D706})}{1+\cos \unicode[STIX]{x1D703}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\frac{R_{n}\left(k,{\displaystyle \frac{\unicode[STIX]{x03C0}}{2}},Pr,\unicode[STIX]{x1D706}\right)}{1+\cos \unicode[STIX]{x1D703}}\leqslant R_{n}(k,\unicode[STIX]{x1D703},Pr,\unicode[STIX]{x1D706})\leqslant \min \left\{\frac{R_{n}\left(k,{\displaystyle \frac{\unicode[STIX]{x03C0}}{2}},Pr,\unicode[STIX]{x1D706}\right)}{1-\cos \unicode[STIX]{x1D703}},\frac{2R_{n}(k,0,Pr,\unicode[STIX]{x1D706})}{1+\cos \unicode[STIX]{x1D703}}\right\},\end{eqnarray}$$
for any
![]() $k>0$
,
$k>0$
,
![]() $0<\unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
,
$0<\unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
,
![]() $Pr\geqslant 0$
,
$Pr\geqslant 0$
,
![]() $\unicode[STIX]{x1D706}>0$
,
$\unicode[STIX]{x1D706}>0$
,
![]() $l\geqslant 0$
,
$l\geqslant 0$
,
![]() $l_{T}\geqslant 0$
and
$l_{T}\geqslant 0$
and
![]() $n\geqslant 1$
. From (2.42) and (3.40), we have
$n\geqslant 1$
. From (2.42) and (3.40), we have
Calculating the critical Reynolds number for the energy stability
![]() $Re_{E}$
according to (2.42) requires solving the eigenvalue equation (2.36)–(2.41) for all wavenumber pairs
$Re_{E}$
according to (2.42) requires solving the eigenvalue equation (2.36)–(2.41) for all wavenumber pairs
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
or
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
or
![]() $(k,\unicode[STIX]{x1D703})$
. However, the critical Reynolds number can be estimated by only solving the eigenvalue equation for the streamwise vortices with
$(k,\unicode[STIX]{x1D703})$
. However, the critical Reynolds number can be estimated by only solving the eigenvalue equation for the streamwise vortices with
![]() $\unicode[STIX]{x1D6FC}=k\cos \unicode[STIX]{x1D703}=0$
according to (3.41).
$\unicode[STIX]{x1D6FC}=k\cos \unicode[STIX]{x1D703}=0$
according to (3.41).
As a direct result of (3.41), the minimum
![]() $R_{1}$
for all two-dimensional waves is also bounded from below by a half of the minimum
$R_{1}$
for all two-dimensional waves is also bounded from below by a half of the minimum
![]() $R_{1}$
for all streamwise vortices, i.e.
$R_{1}$
for all streamwise vortices, i.e.
for any
![]() $Pr\geqslant 0$
,
$Pr\geqslant 0$
,
![]() $\unicode[STIX]{x1D706}>0$
,
$\unicode[STIX]{x1D706}>0$
,
![]() $l\geqslant 0$
and
$l\geqslant 0$
and
![]() $l_{T}\geqslant 0$
. Kaiser & Schmitt (Reference Kaiser and Schmitt2001) have proved an inequality stronger than (3.42),
$l_{T}\geqslant 0$
. Kaiser & Schmitt (Reference Kaiser and Schmitt2001) have proved an inequality stronger than (3.42),
for
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
and
$Pr\,\text{D}\tilde{T}_{0}=0$
and
![]() $l=l_{T}=0$
.
$l=l_{T}=0$
.
4 Numerical results
In order to calculate the first positive eigenvalue
![]() $R_{1}$
of the eigenvalue equation (2.36)–(2.41) for various base flows, we first discretise the equation using 129 Chebyshev–Gauss–Lobatto collocation points, and then solve it with the QZ function in MATLAB (Dongarra, Straughan & Walker Reference Dongarra, Straughan and Walker1996). The first positive eigenvalue
$R_{1}$
of the eigenvalue equation (2.36)–(2.41) for various base flows, we first discretise the equation using 129 Chebyshev–Gauss–Lobatto collocation points, and then solve it with the QZ function in MATLAB (Dongarra, Straughan & Walker Reference Dongarra, Straughan and Walker1996). The first positive eigenvalue
![]() $R_{1}$
is found to decrease with increasing
$R_{1}$
is found to decrease with increasing
![]() $\unicode[STIX]{x1D703}$
for any given
$\unicode[STIX]{x1D703}$
for any given
![]() $k$
in the energy stability analysis of the plane Couette flow, the plane Poiseuille flow, the shear flow with a cubic velocity profile and the inclined buoyancy layer when
$k$
in the energy stability analysis of the plane Couette flow, the plane Poiseuille flow, the shear flow with a cubic velocity profile and the inclined buoyancy layer when
![]() $\unicode[STIX]{x1D706}=1$
(figure 3). In figure 3, we plot the contours of
$\unicode[STIX]{x1D706}=1$
(figure 3). In figure 3, we plot the contours of
![]() $R_{1}$
in the
$R_{1}$
in the
![]() $(k,\unicode[STIX]{x1D703})$
plane, instead of plotting them in the usual wavenumber plane
$(k,\unicode[STIX]{x1D703})$
plane, instead of plotting them in the usual wavenumber plane
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
as in the previous works (Reddy & Henningson Reference Reddy and Henningson1993; Xiong & Tao Reference Xiong and Tao2017). Although Sagalakov & Shtern (Reference Sagalakov and Shtern1971) also plotted their figure 2 in the
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
as in the previous works (Reddy & Henningson Reference Reddy and Henningson1993; Xiong & Tao Reference Xiong and Tao2017). Although Sagalakov & Shtern (Reference Sagalakov and Shtern1971) also plotted their figure 2 in the
![]() $(k,\unicode[STIX]{x1D703})$
plane, the contour
$(k,\unicode[STIX]{x1D703})$
plane, the contour
![]() $R_{1}=35$
in their figure is slightly different from that in our figure 3(c), implying that
$R_{1}=35$
in their figure is slightly different from that in our figure 3(c), implying that
![]() $R_{1}$
increases with increasing
$R_{1}$
increases with increasing
![]() $\unicode[STIX]{x1D703}$
at
$\unicode[STIX]{x1D703}$
at
![]() $(k,\unicode[STIX]{x1D703})\approx (1.9,\unicode[STIX]{x03C0}/2)$
. Noticing that their contour
$(k,\unicode[STIX]{x1D703})\approx (1.9,\unicode[STIX]{x03C0}/2)$
. Noticing that their contour
![]() $R_{1}=35$
and the boundary
$R_{1}=35$
and the boundary
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
do not intersect at a right angle at
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
do not intersect at a right angle at
![]() $(k,\unicode[STIX]{x1D703})\approx (1.9,\unicode[STIX]{x03C0}/2)$
, we believe our result is more accurate. Actually, we have shown
$(k,\unicode[STIX]{x1D703})\approx (1.9,\unicode[STIX]{x03C0}/2)$
, we believe our result is more accurate. Actually, we have shown
![]() $\unicode[STIX]{x2202}R_{1}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
at the boundaries
$\unicode[STIX]{x2202}R_{1}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
at the boundaries
![]() $\unicode[STIX]{x1D703}=0$
and
$\unicode[STIX]{x1D703}=0$
and
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
in the proof of theorem 2.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
in the proof of theorem 2.

Figure 3. The contours of the first positive eigenvalue
![]() $R_{1}$
for the energy stability of various base flows. (a) The plane Couette flow with the no-slip boundary condition (
$R_{1}$
for the energy stability of various base flows. (a) The plane Couette flow with the no-slip boundary condition (
![]() $\text{D}U_{0}=1$
,
$\text{D}U_{0}=1$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
and
$Pr\,\text{D}\tilde{T}_{0}=0$
and
![]() $l=0$
) (Reddy & Henningson Reference Reddy and Henningson1993). (b) The plane Poiseuille flow with the no-slip boundary condition (
$l=0$
) (Reddy & Henningson Reference Reddy and Henningson1993). (b) The plane Poiseuille flow with the no-slip boundary condition (
![]() $\text{D}U_{0}=-2y$
,
$\text{D}U_{0}=-2y$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
and
$Pr\,\text{D}\tilde{T}_{0}=0$
and
![]() $l=0$
) (Reddy & Henningson Reference Reddy and Henningson1993). (c) The plane Couette flow with the slip boundary condition (
$l=0$
) (Reddy & Henningson Reference Reddy and Henningson1993). (c) The plane Couette flow with the slip boundary condition (
![]() $\text{D}U_{0}=(1+l)^{-1}$
,
$\text{D}U_{0}=(1+l)^{-1}$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
and
$Pr\,\text{D}\tilde{T}_{0}=0$
and
![]() $l=0.1$
). (d) The plane Poiseuille flow with the slip boundary condition (
$l=0.1$
). (d) The plane Poiseuille flow with the slip boundary condition (
![]() $\text{D}U_{0}=-2(1+3l)^{-1}y$
,
$\text{D}U_{0}=-2(1+3l)^{-1}y$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
and
$Pr\,\text{D}\tilde{T}_{0}=0$
and
![]() $l=0.1$
). (e) The shear flow with a cubic velocity profile (
$l=0.1$
). (e) The shear flow with a cubic velocity profile (
![]() $\text{D}U_{0}=1-3y^{2}$
,
$\text{D}U_{0}=1-3y^{2}$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
and
$Pr\,\text{D}\tilde{T}_{0}=0$
and
![]() $l=0$
) (Sagalakov & Shtern Reference Sagalakov and Shtern1971). (f) The inclined buoyancy layer (
$l=0$
) (Sagalakov & Shtern Reference Sagalakov and Shtern1971). (f) The inclined buoyancy layer (
![]() $\text{D}U_{0}=-0.5L^{2}\text{e}^{-y^{\prime }}(\sin y^{\prime }-\cos y^{\prime })$
,
$\text{D}U_{0}=-0.5L^{2}\text{e}^{-y^{\prime }}(\sin y^{\prime }-\cos y^{\prime })$
,
![]() $Pr=0.72$
,
$Pr=0.72$
,
![]() $\text{D}\tilde{T}_{0}=-0.5L^{2}\text{e}^{-y^{\prime }}(\sin y^{\prime }+\cos y^{\prime })$
,
$\text{D}\tilde{T}_{0}=-0.5L^{2}\text{e}^{-y^{\prime }}(\sin y^{\prime }+\cos y^{\prime })$
,
![]() $\unicode[STIX]{x1D706}=1$
and
$\unicode[STIX]{x1D706}=1$
and
![]() $l=l_{T}=0$
, where
$l=l_{T}=0$
, where
![]() $y^{\prime }=L(y+1)$
and
$y^{\prime }=L(y+1)$
and
![]() $L=20$
) (Xiong & Tao Reference Xiong and Tao2017).
$L=20$
) (Xiong & Tao Reference Xiong and Tao2017).
Under the no-slip boundary condition and the slip boundary condition with the slip length
![]() $l=0.1$
, the least stable modes in the energy stability analysis of the plane Couette flow have
$l=0.1$
, the least stable modes in the energy stability analysis of the plane Couette flow have
![]() $(k,\unicode[STIX]{x1D703})=(1.558,\unicode[STIX]{x03C0}/2)$
(figure 3
a) and
$(k,\unicode[STIX]{x1D703})=(1.558,\unicode[STIX]{x03C0}/2)$
(figure 3
a) and
![]() $(k,\unicode[STIX]{x1D703})=(1.426,\unicode[STIX]{x03C0}/2)$
(figure 3
c), respectively. These wavenumbers
$(k,\unicode[STIX]{x1D703})=(1.426,\unicode[STIX]{x03C0}/2)$
(figure 3
c), respectively. These wavenumbers
![]() $k$
are close to the corresponding lower bounds
$k$
are close to the corresponding lower bounds
![]() $k_{0}(0,0)=1.534$
and
$k_{0}(0,0)=1.534$
and
![]() $k_{0}(0.1,0)=1.411$
given in theorem 1 (figure 2).
$k_{0}(0.1,0)=1.411$
given in theorem 1 (figure 2).
When there is temperature variation in the base flow (
![]() $Pr\,\text{D}\tilde{T}_{0}\neq 0$
), the first positive eigenvalue
$Pr\,\text{D}\tilde{T}_{0}\neq 0$
), the first positive eigenvalue
![]() $R_{1}$
may increase with
$R_{1}$
may increase with
![]() $\unicode[STIX]{x1D703}$
, e.g. when
$\unicode[STIX]{x1D703}$
, e.g. when
![]() $\text{D}U_{0}=\cos (\unicode[STIX]{x03C0}y)+\cos (3\unicode[STIX]{x03C0}y)$
,
$\text{D}U_{0}=\cos (\unicode[STIX]{x03C0}y)+\cos (3\unicode[STIX]{x03C0}y)$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=10\sin (\unicode[STIX]{x03C0}y)$
,
$Pr\,\text{D}\tilde{T}_{0}=10\sin (\unicode[STIX]{x03C0}y)$
,
![]() $\unicode[STIX]{x1D706}=1$
and
$\unicode[STIX]{x1D706}=1$
and
![]() $l=l_{T}=0$
(figure 4
a). Figure 4(b) shows that theorem 2 still holds for this base flow.
$l=l_{T}=0$
(figure 4
a). Figure 4(b) shows that theorem 2 still holds for this base flow.

Figure 4. The contours of
![]() $R_{1}$
(a) and
$R_{1}$
(a) and
![]() $(1+\cos \unicode[STIX]{x1D703})R_{1}$
(b) for the energy stability of the mixed convection with
$(1+\cos \unicode[STIX]{x1D703})R_{1}$
(b) for the energy stability of the mixed convection with
![]() $\text{D}U_{0}=\cos (\unicode[STIX]{x03C0}y)+\cos (3\unicode[STIX]{x03C0}y)$
,
$\text{D}U_{0}=\cos (\unicode[STIX]{x03C0}y)+\cos (3\unicode[STIX]{x03C0}y)$
,
![]() $Pr\,\text{D}\tilde{T}_{0}=10\sin (\unicode[STIX]{x03C0}y)$
,
$Pr\,\text{D}\tilde{T}_{0}=10\sin (\unicode[STIX]{x03C0}y)$
,
![]() $\unicode[STIX]{x1D706}=1$
and
$\unicode[STIX]{x1D706}=1$
and
![]() $l=l_{T}=0$
.
$l=l_{T}=0$
.
For shear flows under the no-slip boundary condition (
![]() $l=0$
) and without variations in temperature (
$l=0$
) and without variations in temperature (
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
), we define
$Pr\,\text{D}\tilde{T}_{0}=0$
), we define
 $$\begin{eqnarray}J(k,\unicode[STIX]{x1D703},\boldsymbol{a})=-\frac{1}{R_{1}}\frac{\text{d}R_{1}}{\text{d}\unicode[STIX]{x1D703}}=-\frac{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{v}}_{1}{\hat{w}}_{1}+\hat{v}_{1}\bar{{\hat{w}}}_{1})\,\text{d}y}{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{u} }_{1}\hat{v}_{1}+\hat{u} _{1}\bar{\hat{v}}_{1})\,\text{d}y},\end{eqnarray}$$
$$\begin{eqnarray}J(k,\unicode[STIX]{x1D703},\boldsymbol{a})=-\frac{1}{R_{1}}\frac{\text{d}R_{1}}{\text{d}\unicode[STIX]{x1D703}}=-\frac{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{v}}_{1}{\hat{w}}_{1}+\hat{v}_{1}\bar{{\hat{w}}}_{1})\,\text{d}y}{\displaystyle \int _{-1}^{1}(\text{D}U_{0})(\bar{\hat{u} }_{1}\hat{v}_{1}+\hat{u} _{1}\bar{\hat{v}}_{1})\,\text{d}y},\end{eqnarray}$$
where we have used (3.31). Here
![]() $\text{D}U_{0}=\sum _{m\geqslant 0}a_{m}T_{m}(y)$
,
$\text{D}U_{0}=\sum _{m\geqslant 0}a_{m}T_{m}(y)$
,
![]() $T_{m}$
is the Chebyshev polynomial of degree
$T_{m}$
is the Chebyshev polynomial of degree
![]() $m$
, and
$m$
, and
![]() $\boldsymbol{a}=(a_{0},a_{1},\ldots )$
is the coefficient. We also define
$\boldsymbol{a}=(a_{0},a_{1},\ldots )$
is the coefficient. We also define
Note that
![]() $R_{1}$
and
$R_{1}$
and
![]() $\text{D}U_{0}$
only appear in the form of
$\text{D}U_{0}$
only appear in the form of
![]() $R_{1}\text{D}U_{0}$
in (2.36)–(2.41), provided that
$R_{1}\text{D}U_{0}$
in (2.36)–(2.41), provided that
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
. The eigenvector
$Pr\,\text{D}\tilde{T}_{0}=0$
. The eigenvector
![]() $\hat{\boldsymbol{u}}_{1}$
therefore does not change when
$\hat{\boldsymbol{u}}_{1}$
therefore does not change when
![]() $\text{D}U_{0}$
is multiplied by a non-zero real constant, and then
$\text{D}U_{0}$
is multiplied by a non-zero real constant, and then
![]() $J(k,\unicode[STIX]{x1D703},C\boldsymbol{a})=J(k,\unicode[STIX]{x1D703},\boldsymbol{a})$
for any real constant
$J(k,\unicode[STIX]{x1D703},C\boldsymbol{a})=J(k,\unicode[STIX]{x1D703},\boldsymbol{a})$
for any real constant
![]() $C\neq 0$
.
$C\neq 0$
.
We use two methods to approximate
![]() $J_{min}$
at
$J_{min}$
at
![]() $(k_{j},\unicode[STIX]{x1D703}_{s})$
, where
$(k_{j},\unicode[STIX]{x1D703}_{s})$
, where
![]() $k_{j}=10^{-1+(j-1)/5}$
$k_{j}=10^{-1+(j-1)/5}$
![]() $(1\leqslant j\leqslant 11)$
and
$(1\leqslant j\leqslant 11)$
and
![]() $\unicode[STIX]{x1D703}_{s}=(s/20)\unicode[STIX]{x03C0}$
$\unicode[STIX]{x1D703}_{s}=(s/20)\unicode[STIX]{x03C0}$
![]() $(1\leqslant s\leqslant 9)$
. In the following calculations, 65 Chebyshev–Gauss–Lobatto collocation points are used. In the first calculation, for given wavenumber pair
$(1\leqslant s\leqslant 9)$
. In the following calculations, 65 Chebyshev–Gauss–Lobatto collocation points are used. In the first calculation, for given wavenumber pair
![]() $(k_{j},\unicode[STIX]{x1D703}_{s})$
,
$(k_{j},\unicode[STIX]{x1D703}_{s})$
,
![]() $J_{min}$
is approximated by the minimum of
$J_{min}$
is approximated by the minimum of
![]() $J(k_{j},\unicode[STIX]{x1D703}_{s},\boldsymbol{a})$
among all
$J(k_{j},\unicode[STIX]{x1D703}_{s},\boldsymbol{a})$
among all
![]() $\boldsymbol{a}$
such that
$\boldsymbol{a}$
such that
![]() $|a_{m}|\leqslant 5$
$|a_{m}|\leqslant 5$
![]() $(0\leqslant m\leqslant 5)$
are integers and
$(0\leqslant m\leqslant 5)$
are integers and
![]() $a_{m}=0$
for
$a_{m}=0$
for
![]() $m\geqslant 6$
(figure 5
a). In the second calculation,
$m\geqslant 6$
(figure 5
a). In the second calculation,
![]() $J_{min}$
is approximated with a gradient descent method among all
$J_{min}$
is approximated with a gradient descent method among all
![]() $\boldsymbol{a}$
such that
$\boldsymbol{a}$
such that
![]() $a_{m}$
$a_{m}$
![]() $(0\leqslant m\leqslant 15)$
are real numbers and
$(0\leqslant m\leqslant 15)$
are real numbers and
![]() $a_{m}=0$
for
$a_{m}=0$
for
![]() $m\geqslant 16$
. The minimum found with the gradient descent method is generally a local minimum, and depends on the initial value of the coefficient
$m\geqslant 16$
. The minimum found with the gradient descent method is generally a local minimum, and depends on the initial value of the coefficient
![]() $\boldsymbol{a}$
. The result shown in figure 5(b) is the minimum of
$\boldsymbol{a}$
. The result shown in figure 5(b) is the minimum of
![]() $J$
calculated from 100 sets of initial
$J$
calculated from 100 sets of initial
![]() $\boldsymbol{a}$
that are randomly chosen. The detail of the gradient descent algorithm will be introduced in appendix B. In both calculations, we did not find
$\boldsymbol{a}$
that are randomly chosen. The detail of the gradient descent algorithm will be introduced in appendix B. In both calculations, we did not find
![]() $J<0$
for any base flow at any
$J<0$
for any base flow at any
![]() $(k_{j},\unicode[STIX]{x1D703}_{s})$
(
$(k_{j},\unicode[STIX]{x1D703}_{s})$
(
![]() $1\leqslant j\leqslant 11$
and
$1\leqslant j\leqslant 11$
and
![]() $1\leqslant s\leqslant 9$
), which means
$1\leqslant s\leqslant 9$
), which means
![]() $R_{1}$
is probably a decreasing function of
$R_{1}$
is probably a decreasing function of
![]() $\unicode[STIX]{x1D703}$
for the base flows that we have examined. Note that
$\unicode[STIX]{x1D703}$
for the base flows that we have examined. Note that
![]() $J=0$
when
$J=0$
when
![]() $\unicode[STIX]{x1D703}=0$
or
$\unicode[STIX]{x1D703}=0$
or
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, according to the proof of theorem 2.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
, according to the proof of theorem 2.

Figure 5. The contours of
![]() $J_{min}$
in the wavenumber plane approximated with two methods: (a)
$J_{min}$
in the wavenumber plane approximated with two methods: (a)
![]() $J_{min}$
is approximated by the minimum of
$J_{min}$
is approximated by the minimum of
![]() $J$
for all
$J$
for all
![]() $\text{D}U_{0}=\sum _{0\leqslant m\leqslant 5}a_{m}T_{m}(y)$
, where
$\text{D}U_{0}=\sum _{0\leqslant m\leqslant 5}a_{m}T_{m}(y)$
, where
![]() $T_{m}$
is the Chebyshev polynomial of degree
$T_{m}$
is the Chebyshev polynomial of degree
![]() $m$
, and
$m$
, and
![]() $|a_{m}|\leqslant 5$
$|a_{m}|\leqslant 5$
![]() $(0\leqslant m\leqslant 5)$
are integers; (b)
$(0\leqslant m\leqslant 5)$
are integers; (b)
![]() $J_{min}$
is approximated by the local minimum of
$J_{min}$
is approximated by the local minimum of
![]() $J$
among all
$J$
among all
![]() $\text{D}U_{0}=\sum _{0\leqslant m\leqslant 15}a_{m}T_{m}(y)$
with a gradient descent method.
$\text{D}U_{0}=\sum _{0\leqslant m\leqslant 15}a_{m}T_{m}(y)$
with a gradient descent method.
5 Conjecture
In the parallel shear flows without variations in temperature, we have
![]() $\text{D}T_{0}=0$
and
$\text{D}T_{0}=0$
and
![]() $Gr=0$
, and then
$Gr=0$
, and then
![]() $\text{D}\tilde{T}_{0}=0$
due to (2.24). Under this circumstance,
$\text{D}\tilde{T}_{0}=0$
due to (2.24). Under this circumstance,
![]() $Pr$
,
$Pr$
,
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $l_{T}$
have no influence on the eigenvalue equation (2.36)–(2.41). According to the numerical results in § 4, we propose the following conjecture:
$l_{T}$
have no influence on the eigenvalue equation (2.36)–(2.41). According to the numerical results in § 4, we propose the following conjecture:
Conjecture 1. For any continuously differentiable real function
![]() $\text{D}U_{0}$
, if
$\text{D}U_{0}$
, if
![]() $\text{D}\tilde{T}_{0}=0$
and
$\text{D}\tilde{T}_{0}=0$
and
![]() $l=0$
, then the first positive eigenvalue of (2.36)–(2.41)
$l=0$
, then the first positive eigenvalue of (2.36)–(2.41)
![]() $R_{1}(k,\unicode[STIX]{x1D703})$
is a decreasing function of
$R_{1}(k,\unicode[STIX]{x1D703})$
is a decreasing function of
![]() $\unicode[STIX]{x1D703}$
when
$\unicode[STIX]{x1D703}$
when
![]() $0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
for any
$0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
for any
![]() $k>0$
.
$k>0$
.
If conjecture 1 is correct, the least stable mode for the energy stability of any parallel shear flow between no-slip walls without variations in temperature will be a streamwise vortex, because
follows from (2.42), and
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
implies the streamwise wavenumber
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
implies the streamwise wavenumber
![]() $\unicode[STIX]{x1D6FC}=k\cos \unicode[STIX]{x1D703}=0$
.
$\unicode[STIX]{x1D6FC}=k\cos \unicode[STIX]{x1D703}=0$
.
Conjecture 1 implies that
in each subset
![]() $S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]$
where the geometric multiplicity of the first eigenvalue
$S\subset (0,+\infty )\times [0,\unicode[STIX]{x03C0}/2]$
where the geometric multiplicity of the first eigenvalue
![]() $R_{1}(k,\unicode[STIX]{x1D703})$
is 1.
$R_{1}(k,\unicode[STIX]{x1D703})$
is 1.
According to (3.9), (3.11) and (3.17), conjecture 1 is equivalent to the following conjecture:
Conjecture 2 (A conjecture equivalent to conjecture 1).
For any continuously differentiable real function
![]() $\text{D}U_{0}$
, if
$\text{D}U_{0}$
, if
![]() $\text{D}\tilde{T}_{0}=0$
,
$\text{D}\tilde{T}_{0}=0$
,
![]() $l=0$
,
$l=0$
,
![]() $k>0$
and
$k>0$
and
![]() $0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
, then the eigenvector corresponding to the first positive eigenvalue of (2.36)–(2.41) satisfies
$0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
, then the eigenvector corresponding to the first positive eigenvalue of (2.36)–(2.41) satisfies
Now the monotonicity of the eigenvalue in conjecture 1 has been transformed to a more tractable inequality of the eigenvector in conjecture 2, where more mathematical tools can be used in the proof, such as the lemmas used in the proof of theorem 1.
Using (3.15) instead of (3.11), we have another condition which is equivalent to (5.3),
When
![]() $\text{D}\tilde{T}_{0}=0$
, we have
$\text{D}\tilde{T}_{0}=0$
, we have
![]() $\hat{T}_{1}=0$
from (2.39) and (2.41), and then
$\hat{T}_{1}=0$
from (2.39) and (2.41), and then
![]() $I_{T}=0$
. The condition (5.3) is therefore also equivalent to
$I_{T}=0$
. The condition (5.3) is therefore also equivalent to
6 Conclusion
In this paper, we explore the monotonicity of the positive eigenvalues of the eigenvalue equation for the energy stability of plane parallel flows in the
![]() $(k,\unicode[STIX]{x1D703})$
plane, where
$(k,\unicode[STIX]{x1D703})$
plane, where
![]() $k=(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})^{1/2}$
and
$k=(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})^{1/2}$
and
![]() $\unicode[STIX]{x1D703}=\arctan (\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC})$
, and
$\unicode[STIX]{x1D703}=\arctan (\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC})$
, and
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are the streamwise and spanwise wavenumbers of the normal mode. We prove that the
$\unicode[STIX]{x1D6FD}$
are the streamwise and spanwise wavenumbers of the normal mode. We prove that the
![]() $n$
th positive eigenvalue
$n$
th positive eigenvalue
![]() $R_{n}$
decreases with increasing
$R_{n}$
decreases with increasing
![]() $k$
when
$k$
when
![]() $0<k<k_{0}(l,l_{T})$
, and
$0<k<k_{0}(l,l_{T})$
, and
![]() $kR_{n}$
increases with
$kR_{n}$
increases with
![]() $k$
when
$k$
when
![]() $k>0$
. We also prove that
$k>0$
. We also prove that
![]() $(\cos \unicode[STIX]{x1D703}\pm 1)R_{n}$
are decreasing functions of
$(\cos \unicode[STIX]{x1D703}\pm 1)R_{n}$
are decreasing functions of
![]() $\unicode[STIX]{x1D703}$
when
$\unicode[STIX]{x1D703}$
when
![]() $0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
. The above results apply to all parallel base flows between no-slip or slip parallel plates with or without variations in temperature, including the plane Couette flow, the plane Poiseuille flow and the inclined buoyancy layer. When there is temperature variation in the base flow, the difference between
$0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
. The above results apply to all parallel base flows between no-slip or slip parallel plates with or without variations in temperature, including the plane Couette flow, the plane Poiseuille flow and the inclined buoyancy layer. When there is temperature variation in the base flow, the difference between
![]() $T_{0}$
and
$T_{0}$
and
![]() $\tilde{T}_{0}$
should be noted, i.e. (2.24). If
$\tilde{T}_{0}$
should be noted, i.e. (2.24). If
![]() $T_{0}$
instead of
$T_{0}$
instead of
![]() $\tilde{T}_{0}$
is given, the above results hold for any given
$\tilde{T}_{0}$
is given, the above results hold for any given
![]() $Gr/(\unicode[STIX]{x1D706}PrRe^{2})$
.
$Gr/(\unicode[STIX]{x1D706}PrRe^{2})$
.
Our theorems are also illustrated with the computations of the energy stability of various basic flows when the coupling parameter
![]() $\unicode[STIX]{x1D706}=1$
. The first positive eigenvalue
$\unicode[STIX]{x1D706}=1$
. The first positive eigenvalue
![]() $R_{1}$
is found to decrease with increasing
$R_{1}$
is found to decrease with increasing
![]() $\unicode[STIX]{x1D703}$
in the computations for many parallel shear flows under the no-slip boundary condition and without variations in temperature. Therefore, we conjecture that
$\unicode[STIX]{x1D703}$
in the computations for many parallel shear flows under the no-slip boundary condition and without variations in temperature. Therefore, we conjecture that
![]() $R_{1}$
is a decreasing function of
$R_{1}$
is a decreasing function of
![]() $\unicode[STIX]{x1D703}$
for all parallel shear flows between no-slip walls without variations in temperature. We also propose an equivalent conjecture to relate the monotonicity of the eigenvalue to an inequality of the eigenvector (5.3), and derive two equivalent expressions of (5.3), which are (5.4) and (5.5).
$\unicode[STIX]{x1D703}$
for all parallel shear flows between no-slip walls without variations in temperature. We also propose an equivalent conjecture to relate the monotonicity of the eigenvalue to an inequality of the eigenvector (5.3), and derive two equivalent expressions of (5.3), which are (5.4) and (5.5).
If our conjecture is correct, then the least stable mode for the energy stability of any parallel shear flow under the no-slip boundary condition and without variations in temperature must be a streamwise vortex. The importance of this conjecture to the energy stability theory is similar to the importance of Squire’s theorem to the linear stability theory. Actually, Squire’s theorem implies that the neutral stable Reynolds number for the linear stability always increases with
![]() $\unicode[STIX]{x1D703}$
for given
$\unicode[STIX]{x1D703}$
for given
![]() $k>0$
; our conjecture anticipates the opposite for the energy stability.
$k>0$
; our conjecture anticipates the opposite for the energy stability.
In the special case with
![]() $\text{D}\tilde{T}_{0}=\text{D}U_{0}$
,
$\text{D}\tilde{T}_{0}=\text{D}U_{0}$
,
![]() $l=l_{T}\geqslant 0$
and
$l=l_{T}\geqslant 0$
and
![]() $\unicode[STIX]{x1D706}=1$
, we prove that
$\unicode[STIX]{x1D706}=1$
, we prove that
![]() $(1+Pr^{2})^{1/2}R_{n}(k,\unicode[STIX]{x1D703},Pr)$
only depends on
$(1+Pr^{2})^{1/2}R_{n}(k,\unicode[STIX]{x1D703},Pr)$
only depends on
![]() $k$
and
$k$
and
![]() $(1+Pr^{2})^{-1/2}\cos \unicode[STIX]{x1D703}$
in appendix A, and explain why the proof by Joseph (Reference Joseph1966) is not completed to prove that the least stable mode for the energy stability of the plane Couette flow is a streamwise vortex.
$(1+Pr^{2})^{-1/2}\cos \unicode[STIX]{x1D703}$
in appendix A, and explain why the proof by Joseph (Reference Joseph1966) is not completed to prove that the least stable mode for the energy stability of the plane Couette flow is a streamwise vortex.
Acknowledgements
This work has been supported by the National Natural Science Foundation of China (grant nos 11602148 and 11571240). The authors thank W. Su and X. Wang for inspiring discussions.
Appendix A. A special case with
 $\text{D}\tilde{T}_{0}=\text{D}U_{0}$
,
$\text{D}\tilde{T}_{0}=\text{D}U_{0}$
,
 $l=l_{T}\geqslant 0$
and
$l=l_{T}\geqslant 0$
and
 $\unicode[STIX]{x1D706}=1$
$\unicode[STIX]{x1D706}=1$
Theorem 3. For any continuously differentiable real function
![]() $\text{D}U_{0}$
and any
$\text{D}U_{0}$
and any
![]() $l=l_{T}\geqslant 0$
, if
$l=l_{T}\geqslant 0$
, if
![]() $\text{D}\tilde{T}_{0}=\text{D}U_{0}$
and
$\text{D}\tilde{T}_{0}=\text{D}U_{0}$
and
![]() $\unicode[STIX]{x1D706}=1$
, then there exist functions
$\unicode[STIX]{x1D706}=1$
, then there exist functions
![]() $\{{f_{n}\}}_{n\geqslant 1}$
of
$\{{f_{n}\}}_{n\geqslant 1}$
of
![]() $k$
and
$k$
and
![]() $(1+Pr^{2})^{-1/2}\cos \unicode[STIX]{x1D703}$
such that
$(1+Pr^{2})^{-1/2}\cos \unicode[STIX]{x1D703}$
such that
where
![]() $R_{n}$
is the
$R_{n}$
is the
![]() $n$
th positive eigenvalue of (2.36)–(2.41)
$n$
th positive eigenvalue of (2.36)–(2.41)
![]() $(n\geqslant 1)$
.
$(n\geqslant 1)$
.
To prove theorem 3, we rewrite the eigenvalue equation (2.36)–(2.41) by introducing
![]() $\unicode[STIX]{x1D719}=\arctan (Pr)$
and
$\unicode[STIX]{x1D719}=\arctan (Pr)$
and
![]() $R_{n}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})=(1+Pr^{2})^{1/2}R_{n}(k,\unicode[STIX]{x1D703},Pr)$
.
$R_{n}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})=(1+Pr^{2})^{1/2}R_{n}(k,\unicode[STIX]{x1D703},Pr)$
.
When
![]() $\text{D}\tilde{T}_{0}=\text{D}U_{0}$
,
$\text{D}\tilde{T}_{0}=\text{D}U_{0}$
,
![]() $l=l_{T}\geqslant 0$
and
$l=l_{T}\geqslant 0$
and
![]() $\unicode[STIX]{x1D706}=1$
, we have
$\unicode[STIX]{x1D706}=1$
, we have
where
 $$\begin{eqnarray}\unicode[STIX]{x1D647}^{\prime }=\left[\begin{array}{@{}ccccc@{}}\text{D}^{2}-k^{2} & -{\displaystyle \frac{\cos \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & 0 & 0 & -\text{i}k\cos \unicode[STIX]{x1D703}\\ -{\displaystyle \frac{\cos \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & \text{D}^{2}-k^{2} & 0 & -{\displaystyle \frac{\sin \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & -\text{D}\\ 0 & 0 & \text{D}^{2}-k^{2} & 0 & -\text{i}k\sin \unicode[STIX]{x1D703}\\ 0 & -{\displaystyle \frac{\sin \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & 0 & \text{D}^{2}-k^{2} & 0\\ \text{i}k\cos \unicode[STIX]{x1D703} & \text{D} & \text{i}k\sin \unicode[STIX]{x1D703} & 0 & 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D647}^{\prime }=\left[\begin{array}{@{}ccccc@{}}\text{D}^{2}-k^{2} & -{\displaystyle \frac{\cos \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & 0 & 0 & -\text{i}k\cos \unicode[STIX]{x1D703}\\ -{\displaystyle \frac{\cos \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & \text{D}^{2}-k^{2} & 0 & -{\displaystyle \frac{\sin \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & -\text{D}\\ 0 & 0 & \text{D}^{2}-k^{2} & 0 & -\text{i}k\sin \unicode[STIX]{x1D703}\\ 0 & -{\displaystyle \frac{\sin \unicode[STIX]{x1D719}}{2}}R_{n}^{\prime }(\text{D}U_{0}) & 0 & \text{D}^{2}-k^{2} & 0\\ \text{i}k\cos \unicode[STIX]{x1D703} & \text{D} & \text{i}k\sin \unicode[STIX]{x1D703} & 0 & 0\end{array}\right].\end{eqnarray}$$
After a similar discussion as in § 2, we have
and then
 $$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}R_{n}^{\prime }}}\hat{\boldsymbol{u}}_{n}\right\rangle }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}R_{n}^{\prime }}}\hat{\boldsymbol{u}}_{n}\right\rangle }}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}R_{n}^{\prime }}}\hat{\boldsymbol{u}}_{n}\right\rangle }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}R_{n}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}}=-{\displaystyle \frac{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}}\hat{\boldsymbol{u}}_{n}\right\rangle }{\left\langle \hat{\boldsymbol{u}}_{n},{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D647}^{\prime }}{\unicode[STIX]{x2202}R_{n}^{\prime }}}\hat{\boldsymbol{u}}_{n}\right\rangle }}, & \displaystyle\end{eqnarray}$$
where
where
![]() ${\hat{g}}_{n}=(\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719})\hat{u} _{n}-(\cos \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719}){\hat{w}}_{n}-(\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719})\hat{T}_{n}$
. Then we have
${\hat{g}}_{n}=(\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719})\hat{u} _{n}-(\cos \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719}){\hat{w}}_{n}-(\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719})\hat{T}_{n}$
. Then we have
![]() ${\hat{g}}_{n}=0$
, which leads to
${\hat{g}}_{n}=0$
, which leads to
because of (A 8) and (A 9), and then
where we have used (A 6), (A 7) and (A 12).
For given
![]() $k>0$
, the tangent direction of the contour of
$k>0$
, the tangent direction of the contour of
![]() $R_{n}^{\prime }$
at any point
$R_{n}^{\prime }$
at any point
![]() $(\unicode[STIX]{x1D703}_{0},\unicode[STIX]{x1D719}_{0})$
in the
$(\unicode[STIX]{x1D703}_{0},\unicode[STIX]{x1D719}_{0})$
in the
![]() $(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
plane is therefore parallel to
$(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
plane is therefore parallel to
![]() $(\cos \unicode[STIX]{x1D703}_{0}\sin \unicode[STIX]{x1D719}_{0},-\sin \unicode[STIX]{x1D703}_{0}\cos \unicode[STIX]{x1D719}_{0})$
, which is just the tangent direction of the contour of
$(\cos \unicode[STIX]{x1D703}_{0}\sin \unicode[STIX]{x1D719}_{0},-\sin \unicode[STIX]{x1D703}_{0}\cos \unicode[STIX]{x1D719}_{0})$
, which is just the tangent direction of the contour of
![]() $\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
at the same point. Consequently,
$\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
at the same point. Consequently,
![]() $R_{n}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
only depends on
$R_{n}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
only depends on
![]() $k$
and
$k$
and
![]() $\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
, which means that
$\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}$
, which means that
![]() $(1+Pr^{2})^{1/2}R_{n}(k,\unicode[STIX]{x1D703},Pr)$
only depends on
$(1+Pr^{2})^{1/2}R_{n}(k,\unicode[STIX]{x1D703},Pr)$
only depends on
![]() $k$
and
$k$
and
![]() $(1+Pr^{2})^{-1/2}\cos \unicode[STIX]{x1D703}$
. Theorem 3 is therefore proved.
$(1+Pr^{2})^{-1/2}\cos \unicode[STIX]{x1D703}$
. Theorem 3 is therefore proved.
According to the proof of theorem 3, we have
for any
![]() $0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
and
$0\leqslant \unicode[STIX]{x1D703}\leqslant \unicode[STIX]{x03C0}/2$
and
![]() $0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}/2$
. Note that there is no singularity in (A 2)–(A 3) when
$0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}/2$
. Note that there is no singularity in (A 2)–(A 3) when
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/2$
(
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/2$
(
![]() $Pr\rightarrow +\infty$
).
$Pr\rightarrow +\infty$
).
Theorem 3 is an extension of the work by Joseph (Reference Joseph1966), who studied the case with
![]() $\text{D}U_{0}=\text{D}\tilde{T}_{0}=1$
and
$\text{D}U_{0}=\text{D}\tilde{T}_{0}=1$
and
![]() $l=l_{T}=0$
. He implicitly used an expression similar to (A 13) to declare that
$l=l_{T}=0$
. He implicitly used an expression similar to (A 13) to declare that
![]() $R_{1}^{\prime }$
is independent of
$R_{1}^{\prime }$
is independent of
![]() $\unicode[STIX]{x1D719}$
along the line
$\unicode[STIX]{x1D719}$
along the line
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}(k,\unicode[STIX]{x1D719})$
, where
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}(k,\unicode[STIX]{x1D719})$
, where
![]() $\unicode[STIX]{x1D703}_{0}(k,\unicode[STIX]{x1D719})$
satisfies
$\unicode[STIX]{x1D703}_{0}(k,\unicode[STIX]{x1D719})$
satisfies
![]() $R_{1}^{\prime }(k,\unicode[STIX]{x1D703}_{0},\unicode[STIX]{x1D719})=\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
.
$R_{1}^{\prime }(k,\unicode[STIX]{x1D703}_{0},\unicode[STIX]{x1D719})=\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
.
![]() $\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
is therefore independent of
$\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
is therefore independent of
![]() $\unicode[STIX]{x1D719}$
, and then
$\unicode[STIX]{x1D719}$
, and then
![]() $\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},0)=\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x03C0}/2)=R_{1}^{\prime }(k,\unicode[STIX]{x03C0}/2,0)$
, where (A 14) has been used. He concluded from
$\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},0)=\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},\unicode[STIX]{x03C0}/2)=R_{1}^{\prime }(k,\unicode[STIX]{x03C0}/2,0)$
, where (A 14) has been used. He concluded from
![]() $\unicode[STIX]{x1D703}_{0}(k,0)=\unicode[STIX]{x03C0}/2$
that the minimum
$\unicode[STIX]{x1D703}_{0}(k,0)=\unicode[STIX]{x03C0}/2$
that the minimum
![]() $R_{1}^{\prime }$
is achieved by a streamwise vortex in the case of the plane Couette flow (
$R_{1}^{\prime }$
is achieved by a streamwise vortex in the case of the plane Couette flow (
![]() $\unicode[STIX]{x1D719}=0$
).
$\unicode[STIX]{x1D719}=0$
).
Although the conclusion of Joseph (Reference Joseph1966) has been verified by previous computation (Reddy & Henningson Reference Reddy and Henningson1993) and our computation (figure 6), there is a gap in his proof: equation (A 13) cannot guarantee
![]() $\unicode[STIX]{x2202}R_{1}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D719}=0$
if
$\unicode[STIX]{x2202}R_{1}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D719}=0$
if
![]() $\unicode[STIX]{x2202}R_{1}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
at
$\unicode[STIX]{x2202}R_{1}^{\prime }/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}=0$
at
![]() $\unicode[STIX]{x1D703}=0$
(Busse Reference Busse1972). Actually, theorem 2 and theorem 3 cannot rule out the possibility that
$\unicode[STIX]{x1D703}=0$
(Busse Reference Busse1972). Actually, theorem 2 and theorem 3 cannot rule out the possibility that
![]() $R_{1}^{\prime }$
may be
$R_{1}^{\prime }$
may be
![]() $(1+\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719})^{-1}$
or
$(1+\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719})^{-1}$
or
![]() $1-\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}+\cos ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}$
, and
$1-\cos \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}+\cos ^{2}\unicode[STIX]{x1D703}\cos ^{2}\unicode[STIX]{x1D719}$
, and
![]() $\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},0)$
may be achieved at
$\min _{\unicode[STIX]{x1D703}}R_{1}^{\prime }(k,\unicode[STIX]{x1D703},0)$
may be achieved at
![]() $\unicode[STIX]{x1D703}=0$
or
$\unicode[STIX]{x1D703}=0$
or
![]() $0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2$
.
$0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2$
.

Figure 6. The contours of
![]() $R_{1}^{\prime }$
for
$R_{1}^{\prime }$
for
![]() $\text{D}U_{0}=\text{D}\tilde{T}_{0}=1$
,
$\text{D}U_{0}=\text{D}\tilde{T}_{0}=1$
,
![]() $k=1$
,
$k=1$
,
![]() $\unicode[STIX]{x1D706}=1$
and
$\unicode[STIX]{x1D706}=1$
and
![]() $l=l_{T}=0$
. The boundaries
$l=l_{T}=0$
. The boundaries
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
and
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/2$
constitute the contour
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/2$
constitute the contour
![]() $R_{1}^{\prime }\approx 23.33$
.
$R_{1}^{\prime }\approx 23.33$
.
Appendix B. The gradient descent algorithm for
 $J_{min}$
$J_{min}$
When
![]() $Pr\,\text{D}\tilde{T}_{0}=0$
,
$Pr\,\text{D}\tilde{T}_{0}=0$
,
![]() $l=0$
and
$l=0$
and
![]() $\text{D}U_{0}=\sum _{0\leqslant m\leqslant M}a_{m}T_{m}(y)$
, where
$\text{D}U_{0}=\sum _{0\leqslant m\leqslant M}a_{m}T_{m}(y)$
, where
![]() $T_{m}$
is the Chebyshev polynomial of degree
$T_{m}$
is the Chebyshev polynomial of degree
![]() $m$
, and
$m$
, and
![]() $\boldsymbol{a}=(a_{0},a_{1},\ldots ,a_{M})$
is the coefficient, we have
$\boldsymbol{a}=(a_{0},a_{1},\ldots ,a_{M})$
is the coefficient, we have
where
 $$\begin{eqnarray}\unicode[STIX]{x1D647}^{\prime \prime }=\left[\begin{array}{@{}cccc@{}}\text{D}^{2}-k^{2} & -\frac{1}{2}R_{1}(\text{D}U_{0}) & 0 & -\text{i}k\cos \unicode[STIX]{x1D703}\\ -\frac{1}{2}R_{1}(\text{D}U_{0}) & \text{D}^{2}-k^{2} & 0 & -\text{D}\\ 0 & 0 & \text{D}^{2}-k^{2} & -\text{i}k\sin \unicode[STIX]{x1D703}\\ \text{i}k\cos \unicode[STIX]{x1D703} & \text{D} & \text{i}k\sin \unicode[STIX]{x1D703} & 0\end{array}\right],\quad \hat{\boldsymbol{u}}_{1}=\left[\begin{array}{@{}c@{}}\hat{u} _{1}\\ \hat{v}_{1}\\ {\hat{w}}_{1}\\ \hat{q}_{1}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D647}^{\prime \prime }=\left[\begin{array}{@{}cccc@{}}\text{D}^{2}-k^{2} & -\frac{1}{2}R_{1}(\text{D}U_{0}) & 0 & -\text{i}k\cos \unicode[STIX]{x1D703}\\ -\frac{1}{2}R_{1}(\text{D}U_{0}) & \text{D}^{2}-k^{2} & 0 & -\text{D}\\ 0 & 0 & \text{D}^{2}-k^{2} & -\text{i}k\sin \unicode[STIX]{x1D703}\\ \text{i}k\cos \unicode[STIX]{x1D703} & \text{D} & \text{i}k\sin \unicode[STIX]{x1D703} & 0\end{array}\right],\quad \hat{\boldsymbol{u}}_{1}=\left[\begin{array}{@{}c@{}}\hat{u} _{1}\\ \hat{v}_{1}\\ {\hat{w}}_{1}\\ \hat{q}_{1}\end{array}\right],\end{eqnarray}$$
and then
at given
![]() $(k,\unicode[STIX]{x1D703})$
.
$(k,\unicode[STIX]{x1D703})$
.
Define the inner product between two vectors
![]() $\hat{\boldsymbol{u}}^{\prime }$
and
$\hat{\boldsymbol{u}}^{\prime }$
and
![]() $\hat{\boldsymbol{u}}^{\prime \prime }$
as
$\hat{\boldsymbol{u}}^{\prime \prime }$
as
It is straightforward to examine that
![]() $\unicode[STIX]{x1D647}^{\prime \prime }$
is a self-adjoint operator with respect to this inner product and the boundary conditions, and then we have
$\unicode[STIX]{x1D647}^{\prime \prime }$
is a self-adjoint operator with respect to this inner product and the boundary conditions, and then we have
and then it follows from (B 4) that
The inner products in (B 8) are
where
and
![]() $\hat{\unicode[STIX]{x1D702}}_{1}=\text{i}k\hat{u} _{1}\sin \unicode[STIX]{x1D703}-\text{i}k{\hat{w}}_{1}\cos \unicode[STIX]{x1D703}$
.
$\hat{\unicode[STIX]{x1D702}}_{1}=\text{i}k\hat{u} _{1}\sin \unicode[STIX]{x1D703}-\text{i}k{\hat{w}}_{1}\cos \unicode[STIX]{x1D703}$
.
Without loss of generality, we assume
For
![]() $0\leqslant m\leqslant M$
, from (B 8), (B 9) and (B 13), we have
$0\leqslant m\leqslant M$
, from (B 8), (B 9) and (B 13), we have
From (B 4), (B 5) and (B 14), we have
Equation (B 13) also requires
Substituting (B 13) into (4.1), we have
and then
Noticing that
![]() $J(k,\unicode[STIX]{x1D703},C\boldsymbol{a})=J(k,\unicode[STIX]{x1D703},\boldsymbol{a})$
for any real constant
$J(k,\unicode[STIX]{x1D703},C\boldsymbol{a})=J(k,\unicode[STIX]{x1D703},\boldsymbol{a})$
for any real constant
![]() $C\neq 0$
, instead of searching for the minimum of
$C\neq 0$
, instead of searching for the minimum of
![]() $J$
, we search the minimum of
$J$
, we search the minimum of
to avoid the potential blow-up of
![]() $\Vert \boldsymbol{a}\Vert$
. Therefore, we have
$\Vert \boldsymbol{a}\Vert$
. Therefore, we have
The minimum of
![]() $J$
is calculated with the AdaMax algorithm (Kingma & Ba Reference Kingma and Ba2017), which is a gradient-based optimisation algorithm. The detailed algorithm is as follows:
$J$
is calculated with the AdaMax algorithm (Kingma & Ba Reference Kingma and Ba2017), which is a gradient-based optimisation algorithm. The detailed algorithm is as follows:
(i) For given wavenumber pair
![]() $(k,\unicode[STIX]{x1D703})$
, randomly choose initial
$(k,\unicode[STIX]{x1D703})$
, randomly choose initial
![]() $\boldsymbol{a}$
such that
$\boldsymbol{a}$
such that
![]() $\Vert \boldsymbol{a}\Vert =1$
. Set
$\Vert \boldsymbol{a}\Vert =1$
. Set
![]() $t=0$
,
$t=0$
,
![]() $\boldsymbol{s}=(s_{0},s_{1},\ldots ,s_{M})=\mathbf{0}$
and
$\boldsymbol{s}=(s_{0},s_{1},\ldots ,s_{M})=\mathbf{0}$
and
![]() $\boldsymbol{r}=(r_{0},r_{1},\ldots ,r_{M})=\mathbf{0}$
.
$\boldsymbol{r}=(r_{0},r_{1},\ldots ,r_{M})=\mathbf{0}$
.
(ii) Solve the eigenvalue equation (B 1)–(B 2) for the first positive eigenvalue
![]() $R_{1}$
and the corresponding eigenvector
$R_{1}$
and the corresponding eigenvector
![]() $\hat{\boldsymbol{u}}_{1}$
. Equation (B 13) is satisfied by scaling
$\hat{\boldsymbol{u}}_{1}$
. Equation (B 13) is satisfied by scaling
![]() $\hat{\boldsymbol{u}}_{1}$
.
$\hat{\boldsymbol{u}}_{1}$
.
(iii) Solve (B 15)–(B 16) for a particular solution
![]() $\unicode[STIX]{x2202}\hat{\boldsymbol{u}}_{1}/\unicode[STIX]{x2202}a_{m}\;(0\leqslant m\leqslant M)$
. Noticing that
$\unicode[STIX]{x2202}\hat{\boldsymbol{u}}_{1}/\unicode[STIX]{x2202}a_{m}\;(0\leqslant m\leqslant M)$
. Noticing that
![]() $(\unicode[STIX]{x2202}\hat{\boldsymbol{u}}_{1}/\unicode[STIX]{x2202}a_{m})+C\hat{\boldsymbol{u}}_{1}$
is also a solution of (B 15)–(B 16) for any complex constant
$(\unicode[STIX]{x2202}\hat{\boldsymbol{u}}_{1}/\unicode[STIX]{x2202}a_{m})+C\hat{\boldsymbol{u}}_{1}$
is also a solution of (B 15)–(B 16) for any complex constant
![]() $C$
, we require
$C$
, we require
and then (B 17) holds naturally.
(iv) For
![]() $0\leqslant m\leqslant M$
, calculate
$0\leqslant m\leqslant M$
, calculate
![]() $\unicode[STIX]{x2202}J^{\prime }/\unicode[STIX]{x2202}a_{m}$
from (B 19) and (B 21).
$\unicode[STIX]{x2202}J^{\prime }/\unicode[STIX]{x2202}a_{m}$
from (B 19) and (B 21).
(v) Set
![]() $t+1$
to be the new
$t+1$
to be the new
![]() $t$
. For
$t$
. For
![]() $0\leqslant m\leqslant M$
, set
$0\leqslant m\leqslant M$
, set
![]() $0.9s_{m}+0.1\unicode[STIX]{x2202}J^{\prime }/\unicode[STIX]{x2202}a_{m}$
as the new
$0.9s_{m}+0.1\unicode[STIX]{x2202}J^{\prime }/\unicode[STIX]{x2202}a_{m}$
as the new
![]() $s_{m}$
; set
$s_{m}$
; set
![]() $\max \{0.999r_{m},|\unicode[STIX]{x2202}J^{\prime }/\unicode[STIX]{x2202}a_{m}|\}$
as the new
$\max \{0.999r_{m},|\unicode[STIX]{x2202}J^{\prime }/\unicode[STIX]{x2202}a_{m}|\}$
as the new
![]() $r_{m}$
; set
$r_{m}$
; set
![]() $a_{m}-0.002s_{m}/((1-0.9^{t})r_{m})$
as the new
$a_{m}-0.002s_{m}/((1-0.9^{t})r_{m})$
as the new
![]() $a_{m}$
. Repeat (ii)–(v) until
$a_{m}$
. Repeat (ii)–(v) until
![]() $t=10\,000$
or until
$t=10\,000$
or until
![]() $J$
cannot be decreased in the last 1000 steps. The parameters here are recommended by Kingma & Ba (Reference Kingma and Ba2017).
$J$
cannot be decreased in the last 1000 steps. The parameters here are recommended by Kingma & Ba (Reference Kingma and Ba2017).