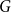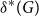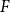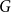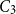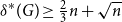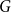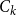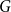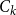1. Introduction
For a graph
![]() $F$
on
$F$
on
![]() $[k] \,:\!=\, \{1, \dotsc, k\}$
, we say that
$[k] \,:\!=\, \{1, \dotsc, k\}$
, we say that
![]() $B$
is the
$B$
is the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $F$
if there exists an ordered partition
$F$
if there exists an ordered partition
![]() $(V_1, \dotsc, V_k)$
of
$(V_1, \dotsc, V_k)$
of
![]() $V(B)$
such that
$V(B)$
such that
![]() $|V_1| = \dotsm = |V_k| = n$
and we have that
$|V_1| = \dotsm = |V_k| = n$
and we have that
![]() $uu^{\prime} \in E(B)$
if and only if
$uu^{\prime} \in E(B)$
if and only if
![]() $u \in V_i$
and
$u \in V_i$
and
![]() $u^{\prime} \in V_{j}$
for some
$u^{\prime} \in V_{j}$
for some
![]() $ij \in E(F)$
. For
$ij \in E(F)$
. For
![]() $G$
a spanning subgraph of
$G$
a spanning subgraph of
![]() $B$
, we call the sequence
$B$
, we call the sequence
![]() $V_1, \dotsc, V_k$
the parts of
$V_1, \dotsc, V_k$
the parts of
![]() $G$
and we define
$G$
and we define
where
![]() $G[V_i, V_j]$
is the bipartite subgraph of
$G[V_i, V_j]$
is the bipartite subgraph of
![]() $G$
induced by the parts
$G$
induced by the parts
![]() $V_i$
and
$V_i$
and
![]() $V_j$
. We often drop the subscript
$V_j$
. We often drop the subscript
![]() $F$
when it is clear from the context. For a graph
$F$
when it is clear from the context. For a graph
![]() $H$
, we call
$H$
, we call
![]() $\mathcal{T}$
an
$\mathcal{T}$
an
![]() $H$
-tiling of
$H$
-tiling of
![]() $G$
if
$G$
if
![]() $\mathcal{T}$
consists of vertex disjoint copies of
$\mathcal{T}$
consists of vertex disjoint copies of
![]() $H$
in
$H$
in
![]() $G$
. We say that
$G$
. We say that
![]() $\mathcal{T}$
covers
$\mathcal{T}$
covers
![]() $V(\mathcal{T}) \,:\!=\, \bigcup \{ V(H^{\prime}) \,:\, H^{\prime} \in \mathcal{T} \}$
and say that
$V(\mathcal{T}) \,:\!=\, \bigcup \{ V(H^{\prime}) \,:\, H^{\prime} \in \mathcal{T} \}$
and say that
![]() $\mathcal{T}$
is perfect or an
$\mathcal{T}$
is perfect or an
![]() $H$
-factor if it covers every vertex of
$H$
-factor if it covers every vertex of
![]() $G$
. Call a subset of
$G$
. Call a subset of
![]() $V(G)$
or a subgraph of
$V(G)$
or a subgraph of
![]() $G$
a transversal if it intersects each part in exactly one vertex and a partial transversal if it intersects each part in at most one vertex. An
$G$
a transversal if it intersects each part in exactly one vertex and a partial transversal if it intersects each part in at most one vertex. An
![]() $H$
-tiling is a transversal
$H$
-tiling is a transversal
![]() $H$
-tiling if each copy of
$H$
-tiling if each copy of
![]() $H$
in
$H$
in
![]() $\mathcal{T}$
is a transversal. We call a perfect transversal
$\mathcal{T}$
is a transversal. We call a perfect transversal
![]() $H$
-tiling a transversal
$H$
-tiling a transversal
![]() $H$
-factor.
$H$
-factor.
Fischer [Reference Fischer3] conjectured the following multipartite version of the Hajnal–Szemerédi Theorem: If
![]() $G$
is the
$G$
is the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $K_k$
, and
$K_k$
, and
![]() $\delta ^*(G) \ge \left (1 - \frac{1}{k}\right )n$
, then
$\delta ^*(G) \ge \left (1 - \frac{1}{k}\right )n$
, then
![]() $G$
has a
$G$
has a
![]() $K_k$
-factor. In the same paper, Fischer proved that, when
$K_k$
-factor. In the same paper, Fischer proved that, when
![]() $k\in \{3, 4\}$
, such a graph
$k\in \{3, 4\}$
, such a graph
![]() $G$
contains a
$G$
contains a
![]() $K_k$
-tiling of size at least
$K_k$
-tiling of size at least
![]() $n-C$
, where
$n-C$
, where
![]() $C$
is a constant that depends only on
$C$
is a constant that depends only on
![]() $k$
. Johansson [Reference Johansson4] proved that, for every
$k$
. Johansson [Reference Johansson4] proved that, for every
![]() $n$
, if
$n$
, if
![]() $G$
is a spanning subgraph of the
$G$
is a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $K_3$
and
$K_3$
and
![]() $\delta ^*(G) \ge 2n/3 + \sqrt{n}$
, then
$\delta ^*(G) \ge 2n/3 + \sqrt{n}$
, then
![]() $G$
contains a
$G$
contains a
![]() $K_3$
-factor, so Johansson proved the triangle case of the conjecture asymptotically. Later, Lo & Märkstrom [Reference Lo and Markström8] and, independently, Keevash & Mycroft [Reference Keevash and Mycroft5] proved the conjecture asymptotically for every
$K_3$
-factor, so Johansson proved the triangle case of the conjecture asymptotically. Later, Lo & Märkstrom [Reference Lo and Markström8] and, independently, Keevash & Mycroft [Reference Keevash and Mycroft5] proved the conjecture asymptotically for every
![]() $k \ge 4$
. The following theorem, which was proved for
$k \ge 4$
. The following theorem, which was proved for
![]() $k=3$
by Magyar & Martin [Reference Magyar and Martin9], for
$k=3$
by Magyar & Martin [Reference Magyar and Martin9], for
![]() $k=4$
by Martin & Szemerédi [Reference Martin and Szemerédi10] and for
$k=4$
by Martin & Szemerédi [Reference Martin and Szemerédi10] and for
![]() $k \ge 5$
by Keevash & Mycroft [Reference Keevash and Mycroft5], shows that Fischer’s original conjecture was nearly true for
$k \ge 5$
by Keevash & Mycroft [Reference Keevash and Mycroft5], shows that Fischer’s original conjecture was nearly true for
![]() $n$
sufficiently large. (Keevash & Mycroft actually proved more, see Theorem 1.1 in [Reference Keevash and Mycroft5] for details.)
$n$
sufficiently large. (Keevash & Mycroft actually proved more, see Theorem 1.1 in [Reference Keevash and Mycroft5] for details.)
Theorem 1.
For every
![]() $k$
there exists
$k$
there exists
![]() $n_0 \,:\!=\, n_0(k)$
such that whenever
$n_0 \,:\!=\, n_0(k)$
such that whenever
![]() $n \ge n_0$
the following holds for every spanning subgraph
$n \ge n_0$
the following holds for every spanning subgraph
![]() $G$
of the
$G$
of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $K_k$
where
$K_k$
where
The graph
![]() $G$
does not contain a
$G$
does not contain a
![]() $K_k$
-factor if and only if both
$K_k$
-factor if and only if both
![]() $n$
and
$n$
and
![]() $k$
are odd,
$k$
are odd,
![]() $k$
divides
$k$
divides
![]() $n$
and
$n$
and
![]() $G$
is isomorphic to a specific spanning subgraph
$G$
is isomorphic to a specific spanning subgraph
![]() $\Gamma _{n,k}$
of the
$\Gamma _{n,k}$
of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $K_k$
where
$K_k$
where
![]() $\delta ^*(\Gamma _{n,k}) = \left (1 - \frac{1}{k}\right )n$
.
$\delta ^*(\Gamma _{n,k}) = \left (1 - \frac{1}{k}\right )n$
.
The following conjecture of Häggkvist, which appeared in [Reference Johansson4], can be seen as a different generalisation of the
![]() $k=3$
case of Theorem 1. Independently, Fischer made a similar conjecture in [Reference Fischer3].
$k=3$
case of Theorem 1. Independently, Fischer made a similar conjecture in [Reference Fischer3].
Conjecture 2. For every
![]() $k \ge 3$
, if
$k \ge 3$
, if
![]() $G$
is a spanning subgraph of the
$G$
is a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
and
$C_k$
and
then
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
Our first result establishes an asymptotic version of Conjecture 2.
Theorem 3.
For every
![]() $\varepsilon \gt 0$
and positive integer
$\varepsilon \gt 0$
and positive integer
![]() $k \ge 4$
there exists
$k \ge 4$
there exists
![]() $n_0 \,:\!=\, n_0(k,\varepsilon )$
such that for every
$n_0 \,:\!=\, n_0(k,\varepsilon )$
such that for every
![]() $n \ge n_0$
the following holds. If
$n \ge n_0$
the following holds. If
![]() $G$
is a spanning subgraph of the
$G$
is a spanning subgraph of the
![]() $n$
-blowup of
$n$
-blowup of
![]() $C_k$
and
$C_k$
and
then
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
Note that Theorem 1 shows that Conjecture 2 is tight when
![]() $k = 3$
. The following example from [Reference Johansson4] shows that, for
$k = 3$
. The following example from [Reference Johansson4] shows that, for
![]() $k \ge 4$
, the minimum degree condition (1) in Conjecture 2 cannot be decreased by more than
$k \ge 4$
, the minimum degree condition (1) in Conjecture 2 cannot be decreased by more than
![]() $1$
. Call
$1$
. Call
![]() $Z \subseteq V(G)$
a transversal
$Z \subseteq V(G)$
a transversal
![]() $C_k$
-cover if every transversal
$C_k$
-cover if every transversal
![]() $C_k$
in
$C_k$
in
![]() $G$
intersects
$G$
intersects
![]() $Z$
and let the transversal
$Z$
and let the transversal
![]() $C_k$
-cover number of
$C_k$
-cover number of
![]() $G$
be the order of a smallest transversal
$G$
be the order of a smallest transversal
![]() $C_k$
-cover. This example relies on the observation that, because every transversal
$C_k$
-cover. This example relies on the observation that, because every transversal
![]() $C_k$
has at least one vertex in a transversal
$C_k$
has at least one vertex in a transversal
![]() $C_k$
-cover, the maximum size of a transversal
$C_k$
-cover, the maximum size of a transversal
![]() $C_k$
-tiling is bounded above by the transversal
$C_k$
-tiling is bounded above by the transversal
![]() $C_k$
-cover number. (Note that we always view arithmetic on elements of
$C_k$
-cover number. (Note that we always view arithmetic on elements of
![]() $[k] \,:\!=\, \{1, \dotsc, k\}$
modulo
$[k] \,:\!=\, \{1, \dotsc, k\}$
modulo
![]() $k$
.)
$k$
.)
Example 4. For
![]() $k \ge 3$
and
$k \ge 3$
and
![]() $m \ge 1$
, let
$m \ge 1$
, let
![]() $n \,:\!=\, 2km$
and
$n \,:\!=\, 2km$
and
![]() $V_1, \dotsc, V_k$
be disjoint sets each of size
$V_1, \dotsc, V_k$
be disjoint sets each of size
![]() $n$
. For
$n$
. For
![]() $i \in [k-1]$
, let
$i \in [k-1]$
, let
![]() $\left\{U_i, W_i, Z_i\right\}$
be a partition of
$\left\{U_i, W_i, Z_i\right\}$
be a partition of
![]() $V_i$
such that
$V_i$
such that
![]() $|U_i| = (k-1)m$
,
$|U_i| = (k-1)m$
,
![]() $|W_i| = (k-1)m$
and
$|W_i| = (k-1)m$
and
![]() $|Z_i| = 2m$
, and let
$|Z_i| = 2m$
, and let
![]() $\{U_k, W_k, Z_k\}$
be a partition of
$\{U_k, W_k, Z_k\}$
be a partition of
![]() $V_k$
such that
$V_k$
such that
![]() $|U_k| = (k-1)m$
,
$|U_k| = (k-1)m$
,
![]() $|W_k| =$
$|W_k| =$
![]() $ (k-1)m+1$
and
$ (k-1)m+1$
and
![]() $|Z_k| = 2m-1$
. Let
$|Z_k| = 2m-1$
. Let
![]() $G$
be the spanning subgraph of the
$G$
be the spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts
$C_k$
with parts
![]() $V_1,\dotsc,V_k$
where
$V_1,\dotsc,V_k$
where
![]() $E(G)$
consists of the union of the edges in the following graphs:
$E(G)$
consists of the union of the edges in the following graphs:
-
the complete bipartite graphs with parts
 $Z_i, V_{i-1}$
and
$Z_i, V_{i-1}$
and
 $Z_i, V_{i+1}$
for each
$Z_i, V_{i+1}$
for each
 $i \in [k]$
,
$i \in [k]$
, -
the complete bipartite graphs with parts
 $U_i,U_{i+1}$
and
$U_i,U_{i+1}$
and
 $W_i,W_{i+1}$
for each
$W_i,W_{i+1}$
for each
 $i \in [k-1]$
,
$i \in [k-1]$
, -
the complete bipartite graphs with parts
 $U_k,W_1$
and
$U_k,W_1$
and
 $W_k,U_1$
.
$W_k,U_1$
.
Note that
![]() $\delta ^*(G) = (k+1)m - 1 = \left (1 + \frac{1}{k}\right )\frac{n}{2} - 1$
, and that every transversal
$\delta ^*(G) = (k+1)m - 1 = \left (1 + \frac{1}{k}\right )\frac{n}{2} - 1$
, and that every transversal
![]() $C_k$
has at least one vertex in
$C_k$
has at least one vertex in
![]() $Z \,:\!=\, Z_1 \cup \dotsm \cup Z_k$
, that is.,
$Z \,:\!=\, Z_1 \cup \dotsm \cup Z_k$
, that is.,
![]() $Z$
is a transversal
$Z$
is a transversal
![]() $C_k$
-cover of
$C_k$
-cover of
![]() $G$
. The fact that
$G$
. The fact that
![]() $|Z| = 2mk - 1 \lt n$
then implies that
$|Z| = 2mk - 1 \lt n$
then implies that
![]() $G$
does not contain a transversal
$G$
does not contain a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
We make the following conjecture which, if true, would be a strengthening of Theorem 3.
Conjecture 5. For every
![]() $k \ge 3$
and
$k \ge 3$
and
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $n_0 \,:\!=\, n_0(k,\varepsilon )$
such that for every
$n_0 \,:\!=\, n_0(k,\varepsilon )$
such that for every
![]() $n \ge n_0$
the following holds. Let
$n \ge n_0$
the following holds. Let
![]() $G$
be a spanning subgraph of the
$G$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts
$C_k$
with parts
![]() $V_1, \dotsc, V_k$
. If there exist
$V_1, \dotsc, V_k$
. If there exist
![]() $\delta _1,\delta _2, \ldots, \delta _k\ge n/2$
such that
$\delta _1,\delta _2, \ldots, \delta _k\ge n/2$
such that
![]() $\delta (G[V_i,V_{i+1}])\geq \delta _i$
, for every
$\delta (G[V_i,V_{i+1}])\geq \delta _i$
, for every
![]() $i\in [k]$
, and
$i\in [k]$
, and
then
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
Note that Theorem 3 is a special, uniform case of Conjecture 5, namely the case when
![]() $\delta _1=\delta _2=\ldots =\delta _k$
. Also, note that the condition
$\delta _1=\delta _2=\ldots =\delta _k$
. Also, note that the condition
![]() $\delta _1, \dotsc, \delta _k \ge n/2$
is necessary because a transversal
$\delta _1, \dotsc, \delta _k \ge n/2$
is necessary because a transversal
![]() $C_k$
-factor in
$C_k$
-factor in
![]() $G$
defines a perfect matching in
$G$
defines a perfect matching in
![]() $G[V_i, V_{i+1}]$
for every
$G[V_i, V_{i+1}]$
for every
![]() $i \in [k]$
and
$i \in [k]$
and
![]() $n/2$
is the smallest minimum degree condition necessary to guarantee a perfect matching in a bipartite graph with parts of size
$n/2$
is the smallest minimum degree condition necessary to guarantee a perfect matching in a bipartite graph with parts of size
![]() $n$
.
$n$
.
Our second result shows that Conjecture 5 holds for
![]() $k=3$
. Note that this result can also be seen as a strengthening of an asymptotic version of the
$k=3$
. Note that this result can also be seen as a strengthening of an asymptotic version of the
![]() $k=3$
case of Theorem 1.
$k=3$
case of Theorem 1.
Theorem 6.
For every
![]() $\varepsilon \gt 0$
there exists
$\varepsilon \gt 0$
there exists
![]() $n_0 \,:\!=\, n_0(\varepsilon )$
such that for every
$n_0 \,:\!=\, n_0(\varepsilon )$
such that for every
![]() $n \ge n_0$
the following holds. Let
$n \ge n_0$
the following holds. Let
![]() $G$
be a spanning subgraph of the
$G$
be a spanning subgraph of the
![]() $n$
-blow-up of a triangle with parts
$n$
-blow-up of a triangle with parts
![]() $V_1,V_2,V_3$
. If there exist
$V_1,V_2,V_3$
. If there exist
![]() $\delta _1,\delta _2,\delta _3\ge n/2$
such that
$\delta _1,\delta _2,\delta _3\ge n/2$
such that
![]() $\delta (G[V_i,V_{i+1}])\geq \delta _i$
, for every
$\delta (G[V_i,V_{i+1}])\geq \delta _i$
, for every
![]() $i\in [3]$
, and
$i\in [3]$
, and
then
![]() $G$
has a triangle factor.
$G$
has a triangle factor.
Because of Example 4, the condition on the average of the minimum degrees in Conjecture 5 is asymptotically sharp. However, it might be possible to weaken the degree condition by only placing a lower bound on the average of some proper subset of the minimum degrees. For example, in the triangle case, we do not have an example of a graph without a triangle factor in which all of the minimum degrees are at least
![]() $n/2$
and the average of only the two largest minimum degrees is at least
$n/2$
and the average of only the two largest minimum degrees is at least
![]() $2n/3$
. Often one tries to find such examples that either have an independent set which is larger than
$2n/3$
. Often one tries to find such examples that either have an independent set which is larger than
![]() $n$
or have a triangle cover of size less than
$n$
or have a triangle cover of size less than
![]() $n$
, since either one of these two conditions imply that the graph cannot contain
$n$
, since either one of these two conditions imply that the graph cannot contain
![]() $n$
vertex disjoint triangles. It is a straightforward exercise to show that, under these conditions, the independence number must be
$n$
vertex disjoint triangles. It is a straightforward exercise to show that, under these conditions, the independence number must be
![]() $n$
. The following theorem proves that the triangle cover number must be
$n$
. The following theorem proves that the triangle cover number must be
![]() $n$
as well.
$n$
as well.
Theorem 7.
For every
![]() $n \in \mathbb{N}$
, the following holds for every spanning subgraph
$n \in \mathbb{N}$
, the following holds for every spanning subgraph
![]() $G$
of the
$G$
of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_3$
with parts
$C_3$
with parts
![]() $V_1,V_2,V_3$
. If
$V_1,V_2,V_3$
. If
![]() $\delta _1 \ge \delta _2 \ge \delta _3 \ge n/2$
,
$\delta _1 \ge \delta _2 \ge \delta _3 \ge n/2$
,
![]() $\delta (G[V_i, V_{i+1}]) \ge \delta _i$
for
$\delta (G[V_i, V_{i+1}]) \ge \delta _i$
for
![]() $i \in [3]$
, and
$i \in [3]$
, and
then the triangle cover number of
![]() $G$
is
$G$
is
![]() $n$
.
$n$
.
Moreover, for every rational
![]() $\gamma \in \big(\frac 34,\frac 79\big] \cup \big\{\frac 23\big\}$
there are infinitely many
$\gamma \in \big(\frac 34,\frac 79\big] \cup \big\{\frac 23\big\}$
there are infinitely many
![]() $n \in \mathbb{N}$
such that when
$n \in \mathbb{N}$
such that when
![]() $\beta = 4/3 - \gamma$
there exists a spanning subgraph
$\beta = 4/3 - \gamma$
there exists a spanning subgraph
![]() $G$
of the
$G$
of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_3$
with parts
$C_3$
with parts
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
such that
$C$
such that
![]() $\delta (G[A,B]) \ge \gamma n -1$
,
$\delta (G[A,B]) \ge \gamma n -1$
,
![]() $\delta (G[A,C]) \ge \beta n$
and
$\delta (G[A,C]) \ge \beta n$
and
![]() $\delta (G[B,C]) \ge n/2$
that has a triangle cover of order less than
$\delta (G[B,C]) \ge n/2$
that has a triangle cover of order less than
![]() $n$
.
$n$
.
Suppose that for every sufficiently small
![]() $\varepsilon \gt 0$
there exists
$\varepsilon \gt 0$
there exists
![]() $n_0$
such that for every
$n_0$
such that for every
![]() $n \ge n_0$
there exists a subgraph of the
$n \ge n_0$
there exists a subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_3$
with parts
$C_3$
with parts
![]() $V_1,V_2,V_3$
that meets the stronger degree conditions
$V_1,V_2,V_3$
that meets the stronger degree conditions
![]() $\delta _1 \ge \delta _2 \ge \delta _3 \ge (1 + \varepsilon )n/2$
and
$\delta _1 \ge \delta _2 \ge \delta _3 \ge (1 + \varepsilon )n/2$
and
![]() $(\delta _1 + \delta _2)/2 \ge (2/3 + \varepsilon )n$
yet does not have a triangle factor. In Section 2 (Lemma 13 and Proposition 15), we will show that, under these conditions, we can apply the absorbing method. This would therefore mean that, for some
$(\delta _1 + \delta _2)/2 \ge (2/3 + \varepsilon )n$
yet does not have a triangle factor. In Section 2 (Lemma 13 and Proposition 15), we will show that, under these conditions, we can apply the absorbing method. This would therefore mean that, for some
![]() $\sigma \gt 0$
and for every sufficiently large
$\sigma \gt 0$
and for every sufficiently large
![]() $n$
, there would exist a subgraph of the
$n$
, there would exist a subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_3$
that meets the degree conditions of first part of Theorem 7 in which every triangle factor has order at most
$C_3$
that meets the degree conditions of first part of Theorem 7 in which every triangle factor has order at most
![]() $(1 - \sigma )n$
, but has triangle cover number
$(1 - \sigma )n$
, but has triangle cover number
![]() $n$
and independence number
$n$
and independence number
![]() $n$
.Footnote
1
$n$
.Footnote
1
1.1 Additional observations and remarks related to Conjecture 5
Let
![]() $k$
,
$k$
,
![]() $\delta _1, \dotsc, \delta _k$
,
$\delta _1, \dotsc, \delta _k$
,
![]() $n$
and
$n$
and
![]() $G$
be as in Conjecture 5.
$G$
be as in Conjecture 5.
Observation 8. In the case of
![]() $\delta _i\le (1 + \varepsilon )\frac n2$
for some
$\delta _i\le (1 + \varepsilon )\frac n2$
for some
![]() $i\in [k]$
, the problem in Conjecture 5 for
$i\in [k]$
, the problem in Conjecture 5 for
![]() $k$
can be reduced to
$k$
can be reduced to
![]() $k-1$
. To see this, assume
$k-1$
. To see this, assume
![]() $i = k$
(for convenience) and first note that
$i = k$
(for convenience) and first note that
Because
![]() $\delta (G[V_1, V_k]) \ge \frac n2$
, Hall’s Theorem implies that we can match every
$\delta (G[V_1, V_k]) \ge \frac n2$
, Hall’s Theorem implies that we can match every
![]() $v \in V_{1}$
to a unique
$v \in V_{1}$
to a unique
![]() $f_v \in V_{k}$
that is adjacent to
$f_v \in V_{k}$
that is adjacent to
![]() $v$
. Let
$v$
. Let
![]() $G^{\prime}$
be the graph derived from
$G^{\prime}$
be the graph derived from
![]() $G$
by collapsing each edge
$G$
by collapsing each edge
![]() $vf_v$
into
$vf_v$
into
![]() $v$
for each
$v$
for each
![]() $v\in V_1$
, that is,
$v\in V_1$
, that is,
![]() $G^{\prime}$
is
$G^{\prime}$
is
![]() $G - V_k$
with an edge between
$G - V_k$
with an edge between
![]() $v \in V_1$
and
$v \in V_1$
and
![]() $u \in V_{k-1}$
if and only if
$u \in V_{k-1}$
if and only if
![]() $f_v$
is adjacent to
$f_v$
is adjacent to
![]() $u$
in
$u$
in
![]() $G$
. It is easy to see that
$G$
. It is easy to see that
![]() $G^{\prime}$
is a spanning subgraph of the
$G^{\prime}$
is a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_{k-1}$
with parts
$C_{k-1}$
with parts
![]() $V_1, \dotsc, V_{k-1}$
such that
$V_1, \dotsc, V_{k-1}$
such that
![]() $\delta (G[V_i,V_{i+1}]) \ge \delta _i$
for each
$\delta (G[V_i,V_{i+1}]) \ge \delta _i$
for each
![]() $i\in [k-1]$
, and that any transversal
$i\in [k-1]$
, and that any transversal
![]() $C_{k-1}$
-factor in
$C_{k-1}$
-factor in
![]() $G^{\prime}$
can be extended to a transversal
$G^{\prime}$
can be extended to a transversal
![]() $C_{k}$
-factor in
$C_{k}$
-factor in
![]() $G$
. So, by (4), if the
$G$
. So, by (4), if the
![]() $k-1$
case of Conjecture 5 holds, then
$k-1$
case of Conjecture 5 holds, then
![]() $G$
has a
$G$
has a
![]() $C_k$
-factor.
$C_k$
-factor.
Repeated applications of Observation 8 and Theorem 6 imply the following.
Remark 9. For every
![]() $k \ge 3$
and sufficiently large
$k \ge 3$
and sufficiently large
![]() $n$
, Conjecture 5 holds if
$n$
, Conjecture 5 holds if
that is, Conjecture 5 holds in the case when all the excess values of
![]() $\delta _i$
compared to
$\delta _i$
compared to
![]() $n/2$
are concentrated in at most
$n/2$
are concentrated in at most
![]() $3$
members of
$3$
members of
![]() $\delta _1,\delta _2,\ldots \delta _k$
.
$\delta _1,\delta _2,\ldots \delta _k$
.
To further support Conjecture 5 we now mention a natural extension of Conjecture 5 for the case when
![]() $k=2$
which is easily proved with Hall’s Theorem. To motivate this extension, first consider a spanning subgraph
$k=2$
which is easily proved with Hall’s Theorem. To motivate this extension, first consider a spanning subgraph
![]() $G$
of the
$G$
of the
![]() $n$
-blow-up of a triangle with parts
$n$
-blow-up of a triangle with parts
![]() $V_1, V_2, V_3$
that meets the conditions of the
$V_1, V_2, V_3$
that meets the conditions of the
![]() $k=3$
case of the conjecture. Since
$k=3$
case of the conjecture. Since
![]() $G[V_1, V_3] \ge n/2$
, Hall’s Theorem implies that we can match every
$G[V_1, V_3] \ge n/2$
, Hall’s Theorem implies that we can match every
![]() $v \in V_1$
to some
$v \in V_1$
to some
![]() $f_v \in V_3$
. Similarly to Observation 8, we note that a perfect matching in the bipartite graph
$f_v \in V_3$
. Similarly to Observation 8, we note that a perfect matching in the bipartite graph
![]() $G[V_1, V_2]$
that is simultaneously a perfect matching in the bipartite graph
$G[V_1, V_2]$
that is simultaneously a perfect matching in the bipartite graph
![]() $H$
with parts
$H$
with parts
![]() $V_1$
and
$V_1$
and
![]() $V_2$
in which
$V_2$
in which
![]() $v \in V_1$
is adjacent to
$v \in V_1$
is adjacent to
![]() $u \in V_2$
in
$u \in V_2$
in
![]() $H$
if and only if
$H$
if and only if
![]() $u$
is adjacent to
$u$
is adjacent to
![]() $f_{v}$
in
$f_{v}$
in
![]() $G[V_2, V_3]$
corresponds to a triangle factor of
$G[V_2, V_3]$
corresponds to a triangle factor of
![]() $G$
.
$G$
.
This leads to the aforementioned extension of Conjecture 5 for
![]() $k=2$
: Suppose that
$k=2$
: Suppose that
![]() $H$
and
$H$
and
![]() $H^{\prime}$
are two balanced bipartite graphs both with the same partite sets
$H^{\prime}$
are two balanced bipartite graphs both with the same partite sets
![]() $V_1$
and
$V_1$
and
![]() $V_2$
where
$V_2$
where
![]() $|V_1| = |V_2| = n$
and that
$|V_1| = |V_2| = n$
and that
![]() $\frac 12\!\left (\delta (H) + \delta (H^{\prime})\right ) \ge \frac{3n}{4}$
. Then there exists
$\frac 12\!\left (\delta (H) + \delta (H^{\prime})\right ) \ge \frac{3n}{4}$
. Then there exists
![]() $M \subseteq E(H) \cap E(H^{\prime})$
that is simultaneously a perfect matching of both
$M \subseteq E(H) \cap E(H^{\prime})$
that is simultaneously a perfect matching of both
![]() $H$
and
$H$
and
![]() $H^{\prime}$
. Indeed, every vertex in
$H^{\prime}$
. Indeed, every vertex in
![]() $v \in V_1 \cup V_2$
is incident to at least
$v \in V_1 \cup V_2$
is incident to at least
![]() $d_H(v) + d_{H^{\prime}}(v) - n \ge n/2$
edges in
$d_H(v) + d_{H^{\prime}}(v) - n \ge n/2$
edges in
![]() $E(H) \cap E(H^{\prime})$
, so Hall’s Theorem implies the desired matching exists.
$E(H) \cap E(H^{\prime})$
, so Hall’s Theorem implies the desired matching exists.
This with Observation 8, implies the following.
Remark 10. For every
![]() $k \ge 3$
and
$k \ge 3$
and
![]() $n$
, Conjecture 5 holds whenever
$n$
, Conjecture 5 holds whenever
![]() $\frac{\delta _i + \delta _j}{2} \ge \left (1 + \frac{1}{2}\right )\frac{n}{2} = \frac{3n}{4}$
for distinct
$\frac{\delta _i + \delta _j}{2} \ge \left (1 + \frac{1}{2}\right )\frac{n}{2} = \frac{3n}{4}$
for distinct
![]() $i,j \in [k]$
.
$i,j \in [k]$
.
Using Remark 10, Observation 8, and a straightforward application of the absorbing method of Rödl, Ruciński and Szemerédi we will show (see Lemma 16 of Section 2) that one only needs to prove the following weaker conjecture to establish Conjecture 5. We use this reduction in our proof of Theorem 6.
Conjecture 11. For every
![]() $k \ge 3$
,
$k \ge 3$
,
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $\sigma \gt 0$
, there exists
$\sigma \gt 0$
, there exists
![]() $n_0 \,:\!=\, n_0(k,\varepsilon, \sigma )$
such that for every
$n_0 \,:\!=\, n_0(k,\varepsilon, \sigma )$
such that for every
![]() $n \ge n_0$
the following holds. Let
$n \ge n_0$
the following holds. Let
![]() $G$
be a spanning subgraph of the
$G$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts
$C_k$
with parts
![]() $V_1, \dotsc, V_k$
. If there exist
$V_1, \dotsc, V_k$
. If there exist
![]() $\delta _1,\delta _2, \ldots, \delta _k\ge (1 + \varepsilon ) n/2$
such that
$\delta _1,\delta _2, \ldots, \delta _k\ge (1 + \varepsilon ) n/2$
such that
![]() $\delta (G[V_i,V_{i+1}])\geq \delta _i$
, for every
$\delta (G[V_i,V_{i+1}])\geq \delta _i$
, for every
![]() $i\in [k]$
, and
$i\in [k]$
, and
then
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_k$
-tiling of size at least
$C_k$
-tiling of size at least
![]() $(1-\sigma )n$
.
$(1-\sigma )n$
.
1.2 Notation
For a graph
![]() $G$
,
$G$
,
![]() $e(G)$
denotes the number of edges in
$e(G)$
denotes the number of edges in
![]() $G$
. For
$G$
. For
![]() $S, T \subseteq V(G)$
, we let
$S, T \subseteq V(G)$
, we let
![]() $N_G(S, T) \,:\!=\, T \cap \left (\bigcap \{N_G(v) \,:\, v \in S \}\right )$
be the common neighbourhood of
$N_G(S, T) \,:\!=\, T \cap \left (\bigcap \{N_G(v) \,:\, v \in S \}\right )$
be the common neighbourhood of
![]() $S$
in
$S$
in
![]() $T$
and we let
$T$
and we let
![]() $d_G(S, T) \,:\!=\, |N_G(S, T)|$
. For
$d_G(S, T) \,:\!=\, |N_G(S, T)|$
. For
![]() $v \in V(G)$
, we define
$v \in V(G)$
, we define
![]() $N_G(v, T) \,:\!=\, N_G(\{v\}, T)$
and
$N_G(v, T) \,:\!=\, N_G(\{v\}, T)$
and
![]() $d_G(v, T) = d_G(\{v\}, T)$
. We typically drop the subscript from this notation when it is clear from the context. For a tiling
$d_G(v, T) = d_G(\{v\}, T)$
. We typically drop the subscript from this notation when it is clear from the context. For a tiling
![]() $\mathcal{T}$
, we let
$\mathcal{T}$
, we let
![]() $U(\mathcal{T}) \,:\!=\, V(G) \setminus V(\mathcal{T})$
be the vertices uncovered by
$U(\mathcal{T}) \,:\!=\, V(G) \setminus V(\mathcal{T})$
be the vertices uncovered by
![]() $\mathcal{T}$
and if
$\mathcal{T}$
and if
![]() $v \in U(\mathcal{T})$
we say that
$v \in U(\mathcal{T})$
we say that
![]() $v$
is uncovered by
$v$
is uncovered by
![]() $\mathcal{T}$
. Similarly, if
$\mathcal{T}$
. Similarly, if
![]() $e \in E(G)$
, and both endpoints of
$e \in E(G)$
, and both endpoints of
![]() $e$
are uncovered by
$e$
are uncovered by
![]() $\mathcal{T}$
, we say that
$\mathcal{T}$
, we say that
![]() $e$
is uncovered by
$e$
is uncovered by
![]() $\mathcal{T}$
.
$\mathcal{T}$
.
2. The absorbing method
We use a straightforward application of the absorbing method of Rödl, Ruciński and Szemerédi [Reference Rödl, Ruciński and Szemerédi11]. Propositions 14 and 15 are essentially all that is necessary to derive appropriate absorbing lemmas in this setting.
Definition 12. For
![]() $k \ge 3$
, let
$k \ge 3$
, let
![]() $G$
be a subgraph of the
$G$
be a subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts
$C_k$
with parts
![]() $V_1, \dotsc, V_k$
. For vertices
$V_1, \dotsc, V_k$
. For vertices
![]() $v,v^{\prime}$
in the same part, we call a
$v,v^{\prime}$
in the same part, we call a
![]() $t$
-tuple of distinct vertices
$t$
-tuple of distinct vertices
![]() $(v_1,\ldots v_{t})$
a
$(v_1,\ldots v_{t})$
a
![]() $(v,v^{\prime}, t)$
-linking sequence if both
$(v,v^{\prime}, t)$
-linking sequence if both
![]() $G[\{v,v_1,\dotsc v_t\}]$
and
$G[\{v,v_1,\dotsc v_t\}]$
and
![]() $G[\{v^{\prime},v_1,\dotsc,v_{t}\}]$
have a transversal
$G[\{v^{\prime},v_1,\dotsc,v_{t}\}]$
have a transversal
![]() $C_k$
-factor. We allow
$C_k$
-factor. We allow
![]() $v = v^{\prime}$
in this definition. We say that
$v = v^{\prime}$
in this definition. We say that
![]() $G$
is
$G$
is
![]() $(\eta,t)$
-linked if, for every
$(\eta,t)$
-linked if, for every
![]() $i \in [k]$
and
$i \in [k]$
and
![]() $v,v^{\prime} \in V_i$
, the number of
$v,v^{\prime} \in V_i$
, the number of
![]() $(v,v^{\prime},t)$
-linking sequences is at least
$(v,v^{\prime},t)$
-linking sequences is at least
![]() $\eta n^{t}$
.
$\eta n^{t}$
.
The proof of the following lemma is standard (e.g., it is very similar to Lemma 1.1 in [Reference Lo and Markström7]), but we include a proof in the appendix for completeness.
Lemma 13.
The Absorbing Lemma For
![]() $k \ge 3$
,
$k \ge 3$
,
![]() $t \ge k-1$
,
$t \ge k-1$
,
![]() $\eta \gt 0$
and
$\eta \gt 0$
and
![]() $0 \lt \sigma \le \frac{0.1 \eta ^{k+1}}{(k(t+1))^2 + 1}$
, there exists
$0 \lt \sigma \le \frac{0.1 \eta ^{k+1}}{(k(t+1))^2 + 1}$
, there exists
![]() $n_0(k, t, \eta, \sigma )$
such that for every
$n_0(k, t, \eta, \sigma )$
such that for every
![]() $n \ge n_0$
the following holds. Suppose that
$n \ge n_0$
the following holds. Suppose that
![]() $G$
is a subgraph of the
$G$
is a subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts
$C_k$
with parts
![]() $V_1, \dotsc, V_k$
that is
$V_1, \dotsc, V_k$
that is
![]() $(2\eta,t)$
-linked. For some
$(2\eta,t)$
-linked. For some
![]() $z \le \sigma n$
, there exists
$z \le \sigma n$
, there exists
![]() $A \subseteq V(G)$
where
$A \subseteq V(G)$
where
![]() $|A \cap V_i| = z$
for every
$|A \cap V_i| = z$
for every
![]() $i \in [k]$
such that if
$i \in [k]$
such that if
![]() $G - A$
has a transversal
$G - A$
has a transversal
![]() $C_k$
-tiling of size at least
$C_k$
-tiling of size at least
![]() $n - z - \sigma ^2 n$
, then
$n - z - \sigma ^2 n$
, then
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
Note that the degree condition in the following proposition is weaker than the degree condition in Conjecture 2.
Proposition 14.
For
![]() $k \ge 4$
and
$k \ge 4$
and
![]() $\varepsilon \gt 0$
, if
$\varepsilon \gt 0$
, if
![]() $G$
is a subgraph of the
$G$
is a subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
and
$C_k$
and
![]() $\delta ^*(G) \ge (1 + \varepsilon )n/2$
, then
$\delta ^*(G) \ge (1 + \varepsilon )n/2$
, then
![]() $G$
is
$G$
is
![]() $(\varepsilon ^3/2^{k},k-1)$
-linked.
$(\varepsilon ^3/2^{k},k-1)$
-linked.
Proof. Let
![]() $V_1, \dotsc, V_k$
be the parts of
$V_1, \dotsc, V_k$
be the parts of
![]() $G$
. Without loss of generality we can assume that
$G$
. Without loss of generality we can assume that
![]() $v,v^{\prime} \in V_1$
. We can construct
$v,v^{\prime} \in V_1$
. We can construct
![]() $(v_2, \dotsc, v_k)$
a
$(v_2, \dotsc, v_k)$
a
![]() $(v,v^{\prime})$
-linking sequence by first selecting
$(v,v^{\prime})$
-linking sequence by first selecting
![]() $v_2 \in N(\{v, v^{\prime}\}, V_2)$
and then
$v_2 \in N(\{v, v^{\prime}\}, V_2)$
and then
![]() $v_k \in N(\{v, v^{\prime}\}, V_k)$
each in at least
$v_k \in N(\{v, v^{\prime}\}, V_k)$
each in at least
![]() $2 \delta ^*(G) - n \ge \varepsilon n$
ways. Iteratively, for
$2 \delta ^*(G) - n \ge \varepsilon n$
ways. Iteratively, for
![]() $i$
from
$i$
from
![]() $3$
to
$3$
to
![]() $k-2$
we can select
$k-2$
we can select
![]() $v_i \in N(v_{i-1}, V_i)$
in at least
$v_i \in N(v_{i-1}, V_i)$
in at least
![]() $\delta ^*(G) \ge n/2$
ways. Finally, we can select
$\delta ^*(G) \ge n/2$
ways. Finally, we can select
![]() $v_{k-1} \in N(\{v_{k-2}, v_k\}, V_{k-1})$
in at least
$v_{k-1} \in N(\{v_{k-2}, v_k\}, V_{k-1})$
in at least
![]() $2 \delta ^*(G) - n \ge \varepsilon n$
ways.
$2 \delta ^*(G) - n \ge \varepsilon n$
ways.
Proposition 15.
For every
![]() $\varepsilon \gt 0$
there exists
$\varepsilon \gt 0$
there exists
![]() $n_0(\varepsilon )$
such that for every
$n_0(\varepsilon )$
such that for every
![]() $n \ge n_0$
the following holds. Let
$n \ge n_0$
the following holds. Let
![]() $G$
be a subgraph of the
$G$
be a subgraph of the
![]() $n$
-blow-up of a triangle with parts
$n$
-blow-up of a triangle with parts
![]() $V_1,V_2, V_3$
. If
$V_1,V_2, V_3$
. If
![]() $\delta _1 \ge \delta _2 \ge \delta _3\geq (1+\varepsilon )n/2$
are such that
$\delta _1 \ge \delta _2 \ge \delta _3\geq (1+\varepsilon )n/2$
are such that
![]() $\delta (G[V_i,V_{i+1}])\ge \delta _i$
for every
$\delta (G[V_i,V_{i+1}])\ge \delta _i$
for every
![]() $i \in [3]$
, and
$i \in [3]$
, and
then
![]() $G$
is
$G$
is
![]() $(\varepsilon ^3/100,5)$
-linked.
$(\varepsilon ^3/100,5)$
-linked.
Proof. There are at least
![]() $n \cdot \delta _3 \cdot (\delta _1 + \delta _2 - n) \ge n^3/6$
triangles in
$n \cdot \delta _3 \cdot (\delta _1 + \delta _2 - n) \ge n^3/6$
triangles in
![]() $G$
, because we can pick any
$G$
, because we can pick any
![]() $w_3 \in V_3$
, then any
$w_3 \in V_3$
, then any
![]() $w_1 \in N(w_3, V_1)$
and then any
$w_1 \in N(w_3, V_1)$
and then any
![]() $w_2 \in N(w_1) \cap N(w_3) \cap V_2$
to form a triangle. We will also need the following fact:
$w_2 \in N(w_1) \cap N(w_3) \cap V_2$
to form a triangle. We will also need the following fact:
To see (5), note that there are at least
![]() $2 \delta _3 - n \ge 2 \varepsilon n$
ways to pick a vertex
$2 \delta _3 - n \ge 2 \varepsilon n$
ways to pick a vertex
![]() $u_3 \in V_3$
adjacent to both
$u_3 \in V_3$
adjacent to both
![]() $u_1$
and
$u_1$
and
![]() $u^{\prime}_1$
and that then there are at least
$u^{\prime}_1$
and that then there are at least
![]() $2\delta _1 + \delta _2 - 2n \ge 3 (\delta _1 + \delta _2)/2 - 2n \ge 3 \varepsilon n$
ways to select a vertex
$2\delta _1 + \delta _2 - 2n \ge 3 (\delta _1 + \delta _2)/2 - 2n \ge 3 \varepsilon n$
ways to select a vertex
![]() $u_2 \in V_2$
that is adjacent to
$u_2 \in V_2$
that is adjacent to
![]() $u_1$
,
$u_1$
,
![]() $u^{\prime}_1$
and
$u^{\prime}_1$
and
![]() $u_3$
.
$u_3$
.
The fact that there are at least
![]() $n^3/6$
triangles and (5) immediately implies that, for every
$n^3/6$
triangles and (5) immediately implies that, for every
![]() $v,v^{\prime} \in V_1$
, the number of
$v,v^{\prime} \in V_1$
, the number of
![]() $(v,v^{\prime},5)$
-linking sequences is at least
$(v,v^{\prime},5)$
-linking sequences is at least
![]() $\frac{\varepsilon ^3 n^5}{100}$
, because the sequence
$\frac{\varepsilon ^3 n^5}{100}$
, because the sequence
![]() $(u_2,u_3,w_1,w_2,w_3)$
is a
$(u_2,u_3,w_1,w_2,w_3)$
is a
![]() $(v,v^{\prime},5)$
-linking sequence whenever
$(v,v^{\prime},5)$
-linking sequence whenever
![]() $vu_2u_3$
and
$vu_2u_3$
and
![]() $v^{\prime}u_2u_3$
are both triangles and
$v^{\prime}u_2u_3$
are both triangles and
![]() $w_1w_2w_3$
is a triangle disjoint from
$w_1w_2w_3$
is a triangle disjoint from
![]() $\{v,v^{\prime},u_2,u_3\}$
.
$\{v,v^{\prime},u_2,u_3\}$
.
So we are left to consider the case when
![]() $v,v^{\prime} \in V_i$
for
$v,v^{\prime} \in V_i$
for
![]() $i \in \{2, 3\}$
. Let
$i \in \{2, 3\}$
. Let
![]() $j \in \{2, 3\}$
so
$j \in \{2, 3\}$
so
![]() $i \neq j$
. We can pick
$i \neq j$
. We can pick
![]() $u_j \in N(v) \cap N(v^{\prime}) \cap V_j$
in at least
$u_j \in N(v) \cap N(v^{\prime}) \cap V_j$
in at least
![]() $2\delta _2 - n \ge 2 \varepsilon n$
ways. Then we can pick
$2\delta _2 - n \ge 2 \varepsilon n$
ways. Then we can pick
![]() $u_1 \in N(v) \cap N(u_j) \cap V_1$
in at least
$u_1 \in N(v) \cap N(u_j) \cap V_1$
in at least
![]() $\delta _1 + \delta _3 - n \ge n/6$
ways. Similarly, we can now pick
$\delta _1 + \delta _3 - n \ge n/6$
ways. Similarly, we can now pick
![]() $u^{\prime}_1 \in N(v^{\prime}) \cap N(u_j) \cap V_1$
distinct from
$u^{\prime}_1 \in N(v^{\prime}) \cap N(u_j) \cap V_1$
distinct from
![]() $u_1$
in at least
$u_1$
in at least
![]() $\delta _1 + \delta _3 - n - 1 \ge n/6$
ways. Observe that
$\delta _1 + \delta _3 - n - 1 \ge n/6$
ways. Observe that
![]() $vu_ju_1$
and
$vu_ju_1$
and
![]() $v^{\prime}u_ju^{\prime}_1$
are both triangles. By (5), there are at least
$v^{\prime}u_ju^{\prime}_1$
are both triangles. By (5), there are at least
![]() $\frac 12 \cdot 6 \varepsilon ^2 n^2$
ways to now pick
$\frac 12 \cdot 6 \varepsilon ^2 n^2$
ways to now pick
![]() $u_2$
and
$u_2$
and
![]() $u_3$
such that
$u_3$
such that
![]() $u_1u_2u_3$
and
$u_1u_2u_3$
and
![]() $u^{\prime}_1u_2u_3$
are both triangles and such that
$u^{\prime}_1u_2u_3$
are both triangles and such that
![]() $u_2$
and
$u_2$
and
![]() $u_3$
are disjoint from
$u_3$
are disjoint from
![]() $\left\{v, v^{\prime}, u_j\right\}$
. All together there are at least
$\left\{v, v^{\prime}, u_j\right\}$
. All together there are at least
ways to make these selection. To complete the proof, we observe that every such selection
![]() $\left(u_j, u_1, u_2, u_3, u^{\prime}_1\right)$
is a
$\left(u_j, u_1, u_2, u_3, u^{\prime}_1\right)$
is a
![]() $(v,v^{\prime},5)$
-linking sequence, because
$(v,v^{\prime},5)$
-linking sequence, because
![]() $vu_ju_1$
and
$vu_ju_1$
and
![]() $u^{\prime}_1u_2u_3$
are both triangles and
$u^{\prime}_1u_2u_3$
are both triangles and
![]() $v^{\prime}u_ju^{\prime}_1$
and
$v^{\prime}u_ju^{\prime}_1$
and
![]() $u_1u_2u_3$
are both triangles.
$u_1u_2u_3$
are both triangles.
Proof. We can assume
![]() $\sigma$
is small enough and
$\sigma$
is small enough and
![]() $n$
is large enough so that the following holds:
$n$
is large enough so that the following holds:
-
 $\sigma ^{1/2} \lt \varepsilon$
and, because Observation 8 implies that if Conjecture 11 holds for
$\sigma ^{1/2} \lt \varepsilon$
and, because Observation 8 implies that if Conjecture 11 holds for
 $k$
, then Conjecture 11 holds for every
$k$
, then Conjecture 11 holds for every
 $\ell$
less than
$\ell$
less than
 $k$
, we can assume that for every
$k$
, we can assume that for every
 $n^{\prime} \ge \left(1-\sigma ^{1/2}\right)n$
and for every
$n^{\prime} \ge \left(1-\sigma ^{1/2}\right)n$
and for every
 $3 \le \ell \le k$
, we can apply Conjecture 11 with
$3 \le \ell \le k$
, we can apply Conjecture 11 with
 $\ell$
,
$\ell$
,
 $\sigma$
,
$\sigma$
,
 $n^{\prime}$
and
$n^{\prime}$
and
 $\varepsilon - \sigma ^{1/2}$
playing the roles of
$\varepsilon - \sigma ^{1/2}$
playing the roles of
 $k$
,
$k$
,
 $\sigma$
,
$\sigma$
,
 $n$
and
$n$
and
 $\varepsilon$
, respectively;
$\varepsilon$
, respectively; -
for every
 $4 \le \ell \le k$
, we can apply Lemma 13 with
$4 \le \ell \le k$
, we can apply Lemma 13 with
 $\ell$
,
$\ell$
,
 $\ell -1$
,
$\ell -1$
,
 $\varepsilon ^3/2^\ell$
and
$\varepsilon ^3/2^\ell$
and
 $\sigma ^{1/2}$
playing the roles of
$\sigma ^{1/2}$
playing the roles of
 $k$
,
$k$
,
 $t$
,
$t$
,
 $\eta$
and
$\eta$
and
 $\sigma$
, respectively; and
$\sigma$
, respectively; and -
we can apply Lemma 13 with
 $3$
,
$3$
,
 $5$
,
$5$
,
 $\varepsilon ^3/100$
and
$\varepsilon ^3/100$
and
 $\sigma ^{1/2}$
playing the roles of
$\sigma ^{1/2}$
playing the roles of
 $k$
,
$k$
,
 $t$
,
$t$
,
 $\eta$
and
$\eta$
and
 $\sigma$
, respectively.
$\sigma$
, respectively.
Let
![]() $G$
and
$G$
and
![]() $\delta _1, \dotsc, \delta _k$
be as in the statement of Conjecture 5. Let
$\delta _1, \dotsc, \delta _k$
be as in the statement of Conjecture 5. Let
![]() $I \,:\!=\, \left\{i \in [k] \,:\, \delta _i \lt (1 + \varepsilon ) \frac n2\right\}$
, let
$I \,:\!=\, \left\{i \in [k] \,:\, \delta _i \lt (1 + \varepsilon ) \frac n2\right\}$
, let
![]() $\ell = k - |I|$
and let
$\ell = k - |I|$
and let
![]() $i_1 \lt \dotsm \lt i_{|I|}$
be an ordering of the elements of
$i_1 \lt \dotsm \lt i_{|I|}$
be an ordering of the elements of
![]() $I$
. In the manner described after the statement of Theorem 6, iteratively, for
$I$
. In the manner described after the statement of Theorem 6, iteratively, for
![]() $j$
from
$j$
from
![]() $1$
to
$1$
to
![]() $|I|$
, we can match every
$|I|$
, we can match every
![]() $v \in V_{i_j}$
to a unique
$v \in V_{i_j}$
to a unique
![]() $f_v \in V_{i_j+1}$
and then collapse the edge
$f_v \in V_{i_j+1}$
and then collapse the edge
![]() $vf_v$
into
$vf_v$
into
![]() $f_v$
. Let
$f_v$
. Let
![]() $G^{\prime}$
be the resulting graph, so
$G^{\prime}$
be the resulting graph, so
![]() $G^{\prime}$
will be a subgraph of the
$G^{\prime}$
will be a subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_\ell$
such that a transversal
$C_\ell$
such that a transversal
![]() $C_\ell$
factor of
$C_\ell$
factor of
![]() $G^{\prime}$
corresponds to a transversal
$G^{\prime}$
corresponds to a transversal
![]() $C_k$
factor of
$C_k$
factor of
![]() $G$
. For convenience, we relabel the parts of
$G$
. For convenience, we relabel the parts of
![]() $G^{\prime}$
as
$G^{\prime}$
as
![]() $V^{\prime}_1,\dotsc,V^{\prime}_\ell$
so that, for
$V^{\prime}_1,\dotsc,V^{\prime}_\ell$
so that, for
![]() $i \in [\ell ]$
, we have
$i \in [\ell ]$
, we have
![]() $G^{\prime}[V^{\prime}_i, V^{\prime}_{i+1}] \ge \delta ^{\prime}_i$
. Note that
$G^{\prime}[V^{\prime}_i, V^{\prime}_{i+1}] \ge \delta ^{\prime}_i$
. Note that
![]() $\delta ^{\prime}_i \ge (1 + \varepsilon ) \frac n2$
for
$\delta ^{\prime}_i \ge (1 + \varepsilon ) \frac n2$
for
![]() $i \in [\ell ]$
and
$i \in [\ell ]$
and
 \begin{equation} \sum _{i=1}^{\ell } \delta ^{\prime}_i = \sum _{i=1}^{k} \delta _i - \sum _{j=1}^{k-\ell }\delta _{i_j} \gt k\!\left (1 + \frac 1k + \varepsilon \right )\frac n2 - (k - \ell )(1 + \varepsilon ) \frac n2 = \ell \left (1 + \frac 1\ell + \varepsilon \right ) \frac n2. \end{equation}
\begin{equation} \sum _{i=1}^{\ell } \delta ^{\prime}_i = \sum _{i=1}^{k} \delta _i - \sum _{j=1}^{k-\ell }\delta _{i_j} \gt k\!\left (1 + \frac 1k + \varepsilon \right )\frac n2 - (k - \ell )(1 + \varepsilon ) \frac n2 = \ell \left (1 + \frac 1\ell + \varepsilon \right ) \frac n2. \end{equation}
Clearly (6) implies
![]() $\ell \ge 2$
and that we can assume
$\ell \ge 2$
and that we can assume
![]() $\ell \ge 3$
by Remark 10. If
$\ell \ge 3$
by Remark 10. If
![]() $\ell =3$
, then Proposition 15 implies that
$\ell =3$
, then Proposition 15 implies that
![]() $G$
is
$G$
is
![]() $\left(\varepsilon ^3/100,5\right)$
-linked and if
$\left(\varepsilon ^3/100,5\right)$
-linked and if
![]() $\ell \ge 4$
, Proposition 14 implies that
$\ell \ge 4$
, Proposition 14 implies that
![]() $G$
is
$G$
is
![]() $(\varepsilon ^3/2^\ell, \ell - 1)$
-linked. So by the selection of
$(\varepsilon ^3/2^\ell, \ell - 1)$
-linked. So by the selection of
![]() $\sigma$
and
$\sigma$
and
![]() $n$
, we can apply Lemma 13 with
$n$
, we can apply Lemma 13 with
![]() $G^{\prime}$
and
$G^{\prime}$
and
![]() $\sigma ^{1/2}$
playing the roles of
$\sigma ^{1/2}$
playing the roles of
![]() $G$
and
$G$
and
![]() $\sigma$
to find a set
$\sigma$
to find a set
![]() $A \subseteq V(G^{\prime})$
with
$A \subseteq V(G^{\prime})$
with
![]() $z = |V^{\prime}_i \cap A| \le \sigma ^{1/2}$
for
$z = |V^{\prime}_i \cap A| \le \sigma ^{1/2}$
for
![]() $i \in [\ell ]$
guaranteed by Lemma 13. Conjecture 11 then implies that
$i \in [\ell ]$
guaranteed by Lemma 13. Conjecture 11 then implies that
![]() $G^{\prime} - A$
has a transversal
$G^{\prime} - A$
has a transversal
![]() $C_\ell$
-tiling of size at least
$C_\ell$
-tiling of size at least
![]() $n - z - \sigma n$
which implies that
$n - z - \sigma n$
which implies that
![]() $G^{\prime}$
has a transversal
$G^{\prime}$
has a transversal
![]() $C_\ell$
-factor. This in turn implies that
$C_\ell$
-factor. This in turn implies that
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
3. Proof of Theorem 3
Informally the proof of Theorem 3 proceeds as follows: Given a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts
$C_k$
with parts
![]() $V_1, \dotsc, V_k$
that satisfies the degree condition (2), we independently select, for every
$V_1, \dotsc, V_k$
that satisfies the degree condition (2), we independently select, for every
![]() $i \in k$
and for large
$i \in k$
and for large
![]() $T \,:\!=\, T(k, \varepsilon )$
, a partition of almost all of
$T \,:\!=\, T(k, \varepsilon )$
, a partition of almost all of
![]() $V_i$
into
$V_i$
into
![]() $T+1$
parts
$T+1$
parts
![]() $U_{i,1}, W_{i,1}, W_{i,2}, \dotsc, W_{i,T}$
each of size
$U_{i,1}, W_{i,1}, W_{i,2}, \dotsc, W_{i,T}$
each of size
![]() $mk$
. The Chernoff and union bounds imply that, if
$mk$
. The Chernoff and union bounds imply that, if
![]() $n$
is sufficiently large, there exists an outcome where, for every
$n$
is sufficiently large, there exists an outcome where, for every
![]() $i \in [k]$
and every
$i \in [k]$
and every
![]() $v \in V_{i-1} \cup V_{i+1}$
, the vertex
$v \in V_{i-1} \cup V_{i+1}$
, the vertex
![]() $v$
has at least
$v$
has at least
![]() $(1 + 1/k + \varepsilon/2)\!mk/2$
neighbours in each of the
$(1 + 1/k + \varepsilon/2)\!mk/2$
neighbours in each of the
![]() $T+1$
parts of
$T+1$
parts of
![]() $V_i$
. Therefore, for
$V_i$
. Therefore, for
![]() $t$
from
$t$
from
![]() $1$
to
$1$
to
![]() $T$
, we can iteratively apply the following lemma (Lemma 17) to find a transversal
$T$
, we can iteratively apply the following lemma (Lemma 17) to find a transversal
![]() $C_k$
-tiling
$C_k$
-tiling
![]() $\mathcal{T}_t$
of size
$\mathcal{T}_t$
of size
![]() $mk$
contained in
$mk$
contained in
![]() $\bigcup _{i \in k}\! \left (U_{i,t} \cup W_{i,t}\right )$
so that, if, for
$\bigcup _{i \in k}\! \left (U_{i,t} \cup W_{i,t}\right )$
so that, if, for
![]() $i \in [k]$
, we let
$i \in [k]$
, we let
![]() $U_{i,{t+1}}$
be the vertices in
$U_{i,{t+1}}$
be the vertices in
![]() $U_{i,t} \cup W_{i,t}$
uncovered by
$U_{i,t} \cup W_{i,t}$
uncovered by
![]() $\mathcal{T}_t$
, we can continue with the next iteration. In this way, we can cover almost all of the vertices, so with absorbing (i.e., Proposition 14 and Lemma 13) we can find a transversal
$\mathcal{T}_t$
, we can continue with the next iteration. In this way, we can cover almost all of the vertices, so with absorbing (i.e., Proposition 14 and Lemma 13) we can find a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
Lemma 17.
For
![]() $\varepsilon \gt 0$
and integer
$\varepsilon \gt 0$
and integer
![]() $k \ge 3$
, there exists
$k \ge 3$
, there exists
![]() $m_0 \,:\!=\, m_0(k,\varepsilon )$
such that for every
$m_0 \,:\!=\, m_0(k,\varepsilon )$
such that for every
![]() $m \ge m_0$
the following holds for
$m \ge m_0$
the following holds for
![]() $n \ge 2mk$
. Suppose that
$n \ge 2mk$
. Suppose that
![]() $G$
is a subgraph of the
$G$
is a subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts
$C_k$
with parts
![]() $V_1, \dotsc, V_k$
, and that, for every
$V_1, \dotsc, V_k$
, and that, for every
![]() $i \in [k]$
, there exist disjoint
$i \in [k]$
, there exist disjoint
![]() $U_i, W_i \subseteq V_i$
where
$U_i, W_i \subseteq V_i$
where
![]() $|U_i| = |W_i| = mk$
and the following conditions hold for every
$|U_i| = |W_i| = mk$
and the following conditions hold for every
![]() $v \in V_{i-1} \cup V_{i+1}$
:
$v \in V_{i-1} \cup V_{i+1}$
:
-
(A)
 $d(v, U_i) \ge \left (1 + \sigma \right )\!mk/2$
, and
$d(v, U_i) \ge \left (1 + \sigma \right )\!mk/2$
, and
-
(B)
 $d(v, W_i) \ge \left (1 + 1/k + \sigma \right )\!mk/2$
.
$d(v, W_i) \ge \left (1 + 1/k + \sigma \right )\!mk/2$
.
Then
![]() $G$
contains a transversal
$G$
contains a transversal
![]() $C_k$
-tiling
$C_k$
-tiling
![]() $\mathcal{T}$
of size
$\mathcal{T}$
of size
![]() $mk$
contained in
$mk$
contained in
![]() $\bigcup _{i \in [k]} U_i \cup W_i$
such that for every
$\bigcup _{i \in [k]} U_i \cup W_i$
such that for every
![]() $i \in [k]$
and every
$i \in [k]$
and every
![]() $v \in V_{i-1} \cup V_{i+1}$
with
$v \in V_{i-1} \cup V_{i+1}$
with
![]() $U^{\prime}_i \,:\!=\, \left (U_i \cup W_i\right ) \setminus V(\mathcal{T})$
we have
$U^{\prime}_i \,:\!=\, \left (U_i \cup W_i\right ) \setminus V(\mathcal{T})$
we have
Proof. For every
![]() $i \in [k]$
, independently and uniformly at random select a partition of
$i \in [k]$
, independently and uniformly at random select a partition of
![]() $U_i$
into parts
$U_i$
into parts
![]() $U_{i,1}, \dotsc, U_{i,k}$
each of size
$U_{i,1}, \dotsc, U_{i,k}$
each of size
![]() $m$
. For every
$m$
. For every
![]() $i,j \in [k]$
and every
$i,j \in [k]$
and every
![]() $v \in V_{i-1} \cup V_{i+1}$
, the random variable
$v \in V_{i-1} \cup V_{i+1}$
, the random variable
![]() $d\!\left(v, U_{i,j}\right)$
is hypergeometrically distributed with expected value
$d\!\left(v, U_{i,j}\right)$
is hypergeometrically distributed with expected value
![]() $d(v, U_i) \frac{|U_{i,j}|}{|U_i|} = \frac{d(v, U_i)}{k}$
. Therefore, by (C1) and the Chernoff and union bounds, there exists an outcome such that for every
$d(v, U_i) \frac{|U_{i,j}|}{|U_i|} = \frac{d(v, U_i)}{k}$
. Therefore, by (C1) and the Chernoff and union bounds, there exists an outcome such that for every
![]() $i,j \in [k]$
and every
$i,j \in [k]$
and every
![]() $v \in V_{i-1} \cup V_{i+1}$
we have
$v \in V_{i-1} \cup V_{i+1}$
we have
This implies that for every
![]() $i,j\in [k]$
, the bipartite graph
$i,j\in [k]$
, the bipartite graph
![]() $G[U_{i,j}, U_{i+1,j}]$
is balanced with parts of size
$G[U_{i,j}, U_{i+1,j}]$
is balanced with parts of size
![]() $m$
and minimum degree at least
$m$
and minimum degree at least
![]() $m/2$
, so, by Hall’s Theorem, it contains a perfect matching
$m/2$
, so, by Hall’s Theorem, it contains a perfect matching
![]() $M_{i,j}$
. For
$M_{i,j}$
. For
![]() $j \in [k]$
, let
$j \in [k]$
, let
![]() $H_j$
be the graph with vertex set
$H_j$
be the graph with vertex set
![]() $U_{1,j} \cup \dotsm \cup U_{k,j}$
such that
$U_{1,j} \cup \dotsm \cup U_{k,j}$
such that
 \begin{equation*} E(H_j)\,:\!=\,\bigcup _{i=1}^{k} M_{i,j} \setminus \left (M_{j-1,j} \cup M_{j,j}\right). \end{equation*}
\begin{equation*} E(H_j)\,:\!=\,\bigcup _{i=1}^{k} M_{i,j} \setminus \left (M_{j-1,j} \cup M_{j,j}\right). \end{equation*}
Note that
![]() $H_j$
consists of a collection
$H_j$
consists of a collection
![]() $\mathcal{P}_{j}$
of
$\mathcal{P}_{j}$
of
![]() $m$
vertex disjoint paths each on
$m$
vertex disjoint paths each on
![]() $k-1$
vertices such that
$k-1$
vertices such that
-
 $V(\mathcal{P}_j) = V(H_j) \setminus U_{j,j}$
;
$V(\mathcal{P}_j) = V(H_j) \setminus U_{j,j}$
; -
every
 $P \in \mathcal{P}_j$
has exactly one vertex in each of the sets
$P \in \mathcal{P}_j$
has exactly one vertex in each of the sets
 $U_{1,j}, \dotsc, U_{k,j}$
except
$U_{1,j}, \dotsc, U_{k,j}$
except
 $U_{j,j}$
; and
$U_{j,j}$
; and -
every
 $P \in \mathcal{P}_j$
has one end-vertex in
$P \in \mathcal{P}_j$
has one end-vertex in
 $U_{j-1,j}$
and the other end-vertex in
$U_{j-1,j}$
and the other end-vertex in
 $U_{j+1,j}$
.
$U_{j+1,j}$
.
By (C2), the number of common neighbours in
![]() $W_j$
of the endpoints of every path in
$W_j$
of the endpoints of every path in
![]() $\mathcal{P}_j$
is at least
$\mathcal{P}_j$
is at least
Therefore, we can greedily select such a common neighbour for every path in
![]() $\mathcal{P}_j$
to form
$\mathcal{P}_j$
to form
![]() $\mathcal{T}_j$
, a transversal
$\mathcal{T}_j$
, a transversal
![]() $C_k$
-tiling of size
$C_k$
-tiling of size
![]() $m$
. The union
$m$
. The union
![]() $\mathcal{T} \,:\!=\, \mathcal{T}_1 \cup \dotsm \cup \mathcal{T}_k$
is a transversal
$\mathcal{T} \,:\!=\, \mathcal{T}_1 \cup \dotsm \cup \mathcal{T}_k$
is a transversal
![]() $C_k$
-tiling of
$C_k$
-tiling of
![]() $G$
of size
$G$
of size
![]() $mk$
. For every
$mk$
. For every
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $U^{\prime}_i \,:\!=\, \left (U_i \cup W_i\right ) \setminus V(\mathcal{T}) = U_{i,i} \cup \left (W_i \setminus V(\mathcal{T})\right )$
, so
$U^{\prime}_i \,:\!=\, \left (U_i \cup W_i\right ) \setminus V(\mathcal{T}) = U_{i,i} \cup \left (W_i \setminus V(\mathcal{T})\right )$
, so
With (C2) and (7), for every
![]() $v \in V_{i-1} \cup V_{i+1}$
, we have that
$v \in V_{i-1} \cup V_{i+1}$
, we have that
Proof of Theorem 3. Define
![]() $\eta \,:\!=\, k^{-3} \cdot 2^{-k}$
and
$\eta \,:\!=\, k^{-3} \cdot 2^{-k}$
and
![]() $\sigma \,:\!=\, \min \{\varepsilon/4, 0.1 \eta ^{k+1}/(k^4 + 1)\}$
. By Proposition 14,
$\sigma \,:\!=\, \min \{\varepsilon/4, 0.1 \eta ^{k+1}/(k^4 + 1)\}$
. By Proposition 14,
![]() $G$
is
$G$
is
![]() $(\eta, k-1)$
-linked. Let
$(\eta, k-1)$
-linked. Let
![]() $A$
be the set guaranteed by Lemma 13, so there exists
$A$
be the set guaranteed by Lemma 13, so there exists
![]() $z \le \sigma n$
such that
$z \le \sigma n$
such that
![]() $|A \cap V_i| = z$
for every
$|A \cap V_i| = z$
for every
![]() $i \in [k]$
. Let
$i \in [k]$
. Let
![]() $m \,:\!=\, \left \lfloor \frac{\sigma ^2 n}{2k} \right \rfloor$
and let
$m \,:\!=\, \left \lfloor \frac{\sigma ^2 n}{2k} \right \rfloor$
and let
![]() $T \,:\!=\, \left \lfloor \frac{n - z}{mk} \right \rfloor -1$
and note that
$T \,:\!=\, \left \lfloor \frac{n - z}{mk} \right \rfloor -1$
and note that
![]() $(T+1)\!mk \le n - z \le (T+2)\!mk$
and that
$(T+1)\!mk \le n - z \le (T+2)\!mk$
and that
![]() $T$
is bounded above by a constant that depends only on
$T$
is bounded above by a constant that depends only on
![]() $k$
and
$k$
and
![]() $\varepsilon$
. For every
$\varepsilon$
. For every
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $V^{\prime}_i \subseteq V_i \setminus A$
where
$V^{\prime}_i \subseteq V_i \setminus A$
where
![]() $|V^{\prime}_i| = (T+1)\!mk$
. We will construct
$|V^{\prime}_i| = (T+1)\!mk$
. We will construct
![]() $T$
disjoint transversal
$T$
disjoint transversal
![]() $C_k$
-tilings each of size
$C_k$
-tilings each of size
![]() $mk$
that each avoid
$mk$
that each avoid
![]() $A$
. Because
$A$
. Because
this will imply the theorem by the properties of
![]() $A$
from Lemma 13.
$A$
from Lemma 13.
Note that, by (2), for every
![]() $i \in [k]$
and
$i \in [k]$
and
![]() $v \in V_{i-1} \cup V_{i+1}$
, we have
$v \in V_{i-1} \cup V_{i+1}$
, we have
For every
![]() $i \in [k]$
, independently and uniformly at random select a partition of
$i \in [k]$
, independently and uniformly at random select a partition of
![]() $V^{\prime}_i$
into
$V^{\prime}_i$
into
![]() $T+1$
parts
$T+1$
parts
![]() $W_{i,0}, \dotsc, W_{i,T}$
each of size
$W_{i,0}, \dotsc, W_{i,T}$
each of size
![]() $mk$
. For every
$mk$
. For every
![]() $i \in [k]$
, every
$i \in [k]$
, every
![]() $0 \le t \le T$
and every
$0 \le t \le T$
and every
![]() $v \in V_{i-1} \cup V_{i+1}$
, the random variable
$v \in V_{i-1} \cup V_{i+1}$
, the random variable
![]() $d(v, W_{i, t})$
is hypergeometrically distributed with expected value
$d(v, W_{i, t})$
is hypergeometrically distributed with expected value
![]() $d\!\left(v, V^{\prime}_i\right) \frac{|W_{i,t}|}{|V^{\prime}_i|}$
. Therefore, by (8) and the Chernoff and union bounds, there exists an outcome such that for every
$d\!\left(v, V^{\prime}_i\right) \frac{|W_{i,t}|}{|V^{\prime}_i|}$
. Therefore, by (8) and the Chernoff and union bounds, there exists an outcome such that for every
![]() $i \in [k]$
,
$i \in [k]$
,
![]() $0 \le t \le T$
and
$0 \le t \le T$
and
![]() $v \in V_{i-1} \cup V_{i+1}$
we have
$v \in V_{i-1} \cup V_{i+1}$
we have
We will now show by induction on
![]() $t$
from
$t$
from
![]() $1$
to
$1$
to
![]() $T+1$
that there exist
$T+1$
that there exist
![]() $t-1$
disjoint transversal
$t-1$
disjoint transversal
![]() $C_k$
-tilings
$C_k$
-tilings
![]() $\mathcal{T}_1, \dotsc, \mathcal{T}_{t-1}$
each of size
$\mathcal{T}_1, \dotsc, \mathcal{T}_{t-1}$
each of size
![]() $mk$
that are contained in
$mk$
that are contained in
![]() $\bigcup _{i \in k} \bigcup _{s = 0}^{t-1} W_{i,s}$
, and that, for every
$\bigcup _{i \in k} \bigcup _{s = 0}^{t-1} W_{i,s}$
, and that, for every
![]() $i \in [k]$
, if we let
$i \in [k]$
, if we let
![]() $U_{i, t} \,:\!=\, \left (\bigcup _{s=0}^{t-1} W_{i,s}\right ) \setminus \left (\bigcup _{s = 1}^{t-1} V(\mathcal{T}_s)\right )$
, then the following holds:
$U_{i, t} \,:\!=\, \left (\bigcup _{s=0}^{t-1} W_{i,s}\right ) \setminus \left (\bigcup _{s = 1}^{t-1} V(\mathcal{T}_s)\right )$
, then the following holds:
This will prove the theorem.
For the base case, note that when
![]() $t = 1$
we have that
$t = 1$
we have that
![]() $U_{i,t} = U_{i,1} = W_{i,0}$
for every
$U_{i,t} = U_{i,1} = W_{i,0}$
for every
![]() $i \in [k]$
so (10) holds by (9). Now assume the induction hypothesis holds for some
$i \in [k]$
so (10) holds by (9). Now assume the induction hypothesis holds for some
![]() $1 \le t \le T$
. With (9) and (10) we can apply Lemma 17 to find a tiling
$1 \le t \le T$
. With (9) and (10) we can apply Lemma 17 to find a tiling
![]() $\mathcal{T}_t$
of size
$\mathcal{T}_t$
of size
![]() $mk$
contained in
$mk$
contained in
![]() $\bigcup _{i \in [k]} U_{i, t} \cup W_{i, t}$
such that, for every
$\bigcup _{i \in [k]} U_{i, t} \cup W_{i, t}$
such that, for every
![]() $i \in [k]$
, we have that
$i \in [k]$
, we have that
 \begin{equation*} U_{i,t+1} = \left (\bigcup _{s=0}^{t} W_{i,s}\right ) \setminus \left (\bigcup _{s = 1}^{t} V(\mathcal {T}_s)\right ) = \left (U_{i, t} \cup W_{i, t}\right )\setminus V(\mathcal {T}_t) \end{equation*}
\begin{equation*} U_{i,t+1} = \left (\bigcup _{s=0}^{t} W_{i,s}\right ) \setminus \left (\bigcup _{s = 1}^{t} V(\mathcal {T}_s)\right ) = \left (U_{i, t} \cup W_{i, t}\right )\setminus V(\mathcal {T}_t) \end{equation*}
satisfies (10) with
![]() $t$
set to
$t$
set to
![]() $t+1$
. Therefore, the induction hypothesis holds for
$t+1$
. Therefore, the induction hypothesis holds for
![]() $t+1$
.
$t+1$
.
4. Proof of Theorem 6
Because Theorem 18 works for every
![]() $n$
and the degree condition is weaker than Theorem 6, it might have independent interest. Note that Theorem 18 is stronger than the
$n$
and the degree condition is weaker than Theorem 6, it might have independent interest. Note that Theorem 18 is stronger than the
![]() $k=3$
case of Conjecture 11, so Lemma 16 and Theorem 18 together imply Theorem 6.
$k=3$
case of Conjecture 11, so Lemma 16 and Theorem 18 together imply Theorem 6.
Theorem 18.
The following holds for every
![]() $n \in \mathbb{N}$
and every subgraph
$n \in \mathbb{N}$
and every subgraph
![]() $G$
of the
$G$
of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_3$
with parts
$C_3$
with parts
![]() $V_1, V_2, V_3$
. If there exist
$V_1, V_2, V_3$
. If there exist
![]() $\delta _1, \delta _2,\delta _3\ge n/2$
such that
$\delta _1, \delta _2,\delta _3\ge n/2$
such that
![]() $\delta _1 + \delta _2 + \delta _3 \ge 2n$
and
$\delta _1 + \delta _2 + \delta _3 \ge 2n$
and
then
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_3$
-tiling of size at least
$C_3$
-tiling of size at least
![]() $n-1$
.
$n-1$
.
Proof. For brevity, in this proof we call a transversal
![]() $C_3$
-tiling a tiling. Let the size of a maximum tiling of
$C_3$
-tiling a tiling. Let the size of a maximum tiling of
![]() $G$
be
$G$
be
![]() $m$
and let us assume for a contradiction that
$m$
and let us assume for a contradiction that
![]() $m \le n-2$
. Call a pair of edges
$m \le n-2$
. Call a pair of edges
![]() $e$
and
$e$
and
![]() $f$
dissimilar if
$f$
dissimilar if
![]() $e \in E(G[V_i, V_{i+1}])$
and
$e \in E(G[V_i, V_{i+1}])$
and
![]() $f \in E\big(G\big[V_j, V_{j+1}\big]\big)$
for distinct
$f \in E\big(G\big[V_j, V_{j+1}\big]\big)$
for distinct
![]() $i,j \in [3]$
. Call a set
$i,j \in [3]$
. Call a set
![]() $F \subseteq E(G)$
a dissimilar matching if the edges in
$F \subseteq E(G)$
a dissimilar matching if the edges in
![]() $F$
are disjoint and the edges in
$F$
are disjoint and the edges in
![]() $F$
are pairwise dissimilar. For every maximum tiling
$F$
are pairwise dissimilar. For every maximum tiling
![]() $\mathcal{T}$
, let
$\mathcal{T}$
, let
![]() $h(\mathcal{T})$
be the maximum size of a dissimilar matching
$h(\mathcal{T})$
be the maximum size of a dissimilar matching
![]() $F \subseteq E(G[U(\mathcal{T})])$
such that every edge in
$F \subseteq E(G[U(\mathcal{T})])$
such that every edge in
![]() $F$
is uncovered by
$F$
is uncovered by
![]() $\mathcal{T}$
. Recall that an edge
$\mathcal{T}$
. Recall that an edge
![]() $e$
is uncovered by
$e$
is uncovered by
![]() $\mathcal{T}$
if both endpoints of
$\mathcal{T}$
if both endpoints of
![]() $e$
are disjoint from
$e$
are disjoint from
![]() $V(\mathcal{T})$
. Let
$V(\mathcal{T})$
. Let
![]() $\{\alpha, \beta, \gamma \} = \{\delta _1/n, \delta _2/n, \delta _3/n\}$
and
$\{\alpha, \beta, \gamma \} = \{\delta _1/n, \delta _2/n, \delta _3/n\}$
and
![]() $\{A, B, C\} = \{V_1, V_2, V_3\}$
be labellings such that
$\{A, B, C\} = \{V_1, V_2, V_3\}$
be labellings such that
![]() $\alpha \le \beta \le \gamma$
and
$\alpha \le \beta \le \gamma$
and
Claim 18.1.
Let
![]() $\mathcal{T}$
be a maximum tiling. If
$\mathcal{T}$
be a maximum tiling. If
![]() $e \in E(G)$
is uncovered by
$e \in E(G)$
is uncovered by
![]() $\mathcal{T}$
, then
$\mathcal{T}$
, then
![]() $d(e, U(\mathcal{T})) = 0$
. Furthermore, if
$d(e, U(\mathcal{T})) = 0$
. Furthermore, if
![]() $e$
and
$e$
and
![]() $f$
are disjoint dissimilar edges that are uncovered by
$f$
are disjoint dissimilar edges that are uncovered by
![]() $\mathcal{T}$
, then
$\mathcal{T}$
, then
![]() $d(e, T) + d(f, T) \le 1$
for every
$d(e, T) + d(f, T) \le 1$
for every
![]() $T \in \mathcal{T}$
.
$T \in \mathcal{T}$
.
Proof. If
![]() $e$
is an edge uncovered by
$e$
is an edge uncovered by
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $x \in U(\mathcal{T})$
is such that
$x \in U(\mathcal{T})$
is such that
![]() $d(e, \{x\}) = 1$
, then
$d(e, \{x\}) = 1$
, then
![]() $ex$
is triangle, and adding
$ex$
is triangle, and adding
![]() $ex$
to
$ex$
to
![]() $\mathcal{T}$
creates a tiling of size
$\mathcal{T}$
creates a tiling of size
![]() $m+1$
, a contradiction. Similarly, if
$m+1$
, a contradiction. Similarly, if
![]() $e$
and
$e$
and
![]() $f$
are disjoint and dissimilar edges that are uncovered by
$f$
are disjoint and dissimilar edges that are uncovered by
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $d(e, T) + d(f, T) \ge 2$
for some
$d(e, T) + d(f, T) \ge 2$
for some
![]() $T \in \mathcal{T}$
, then, because
$T \in \mathcal{T}$
, then, because
![]() $e$
and
$e$
and
![]() $f$
are dissimilar, there exist distinct
$f$
are dissimilar, there exist distinct
![]() $x,y \in T$
such that
$x,y \in T$
such that
![]() $ex$
and
$ex$
and
![]() $fy$
are both triangles, so if we replace
$fy$
are both triangles, so if we replace
![]() $T$
with
$T$
with
![]() $ex$
and
$ex$
and
![]() $fy$
in
$fy$
in
![]() $\mathcal{T}$
, then we have a tiling of size
$\mathcal{T}$
, then we have a tiling of size
![]() $m+1$
, a contradiction.
$m+1$
, a contradiction.
Claim 18.2.
Let
![]() $\mathcal{T}$
be a maximum tiling and let
$\mathcal{T}$
be a maximum tiling and let
![]() $F$
be a dissimilar matching with
$F$
be a dissimilar matching with
![]() $|F|=3$
. Then either there exists
$|F|=3$
. Then either there exists
![]() $e \in F$
such that
$e \in F$
such that
![]() $d(e, U(\mathcal{T})) \ge 1$
or there exists
$d(e, U(\mathcal{T})) \ge 1$
or there exists
![]() $T \in \mathcal{T}$
such that
$T \in \mathcal{T}$
such that
![]() $\sum _{e \in F} d(e, T) \ge 2$
. Consequently,
$\sum _{e \in F} d(e, T) \ge 2$
. Consequently,
![]() $h(\mathcal{T}) \le 2$
for every maximum tiling
$h(\mathcal{T}) \le 2$
for every maximum tiling
![]() $\mathcal{T}$
.
$\mathcal{T}$
.
Proof. Let
![]() $\{a_1, \dotsc, a_n\}$
,
$\{a_1, \dotsc, a_n\}$
,
![]() $\{b_1, \dotsc, b_n\}$
and
$\{b_1, \dotsc, b_n\}$
and
![]() $\{c_1, \dotsc, c_n\}$
be orderings of
$\{c_1, \dotsc, c_n\}$
be orderings of
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
, respectively, such that
$C$
, respectively, such that
![]() $a_ib_ic_i \in \mathcal{T}$
for every
$a_ib_ic_i \in \mathcal{T}$
for every
![]() $i \in [m]$
(so, when
$i \in [m]$
(so, when
![]() $m + 1 \le i \le n$
,
$m + 1 \le i \le n$
,
![]() $a_ib_ic_i$
is not a triangle). By (11), we have
$a_ib_ic_i$
is not a triangle). By (11), we have
Therefore, if
![]() $0=\sum _{e \in F} d(e, U(\mathcal{T})) = \sum _{i=m+1}^{n}\sum _{e \in F} d(e, a_ib_ic_i)$
, then there exists
$0=\sum _{e \in F} d(e, U(\mathcal{T})) = \sum _{i=m+1}^{n}\sum _{e \in F} d(e, a_ib_ic_i)$
, then there exists
![]() $1 \le i \le m$
such that
$1 \le i \le m$
such that
![]() $\sum _{e \in F} d(e, a_ib_ic_i) = 2$
. This proves the first statement.
$\sum _{e \in F} d(e, a_ib_ic_i) = 2$
. This proves the first statement.
To see the second statement, assume for a contradiction that there exists a maximum tiling
![]() $\mathcal{T}$
such that
$\mathcal{T}$
such that
![]() $h(\mathcal{T}) = 3$
. This means that there exists a dissimilar matching
$h(\mathcal{T}) = 3$
. This means that there exists a dissimilar matching
![]() $F$
such that
$F$
such that
![]() $|F| = 3$
and such that every edge in
$|F| = 3$
and such that every edge in
![]() $F$
is uncovered by
$F$
is uncovered by
![]() $\mathcal{T}$
. By the first part of the statement, there either exists
$\mathcal{T}$
. By the first part of the statement, there either exists
![]() $e \in F$
such
$e \in F$
such
![]() $d(e, U(\mathcal{T})) \ge 1$
, or there exist two edges
$d(e, U(\mathcal{T})) \ge 1$
, or there exist two edges
![]() $e,f \in F$
and
$e,f \in F$
and
![]() $T \in \mathcal{T}$
such that
$T \in \mathcal{T}$
such that
![]() $d(e, T) + d(f, T) \ge 1$
. Because every edge in
$d(e, T) + d(f, T) \ge 1$
. Because every edge in
![]() $F$
is uncovered by
$F$
is uncovered by
![]() $\mathcal{T}$
, this contradicts Claim 18.1.
$\mathcal{T}$
, this contradicts Claim 18.1.
Claim 18.3.
There exists a maximum tiling
![]() $\mathcal{T}$
such that
$\mathcal{T}$
such that
![]() $h(\mathcal{T}) = 2$
, and for every maximum tiling
$h(\mathcal{T}) = 2$
, and for every maximum tiling
![]() $\mathcal{T}$
there does not exist
$\mathcal{T}$
there does not exist
![]() $e\in E(G[B,C])$
which is uncovered by
$e\in E(G[B,C])$
which is uncovered by
![]() $\mathcal{T}$
.
$\mathcal{T}$
.
Proof. Suppose for a contradiction that the statement is false and assume
![]() $\mathcal{T}$
and a dissimilar matching
$\mathcal{T}$
and a dissimilar matching
![]() $F$
in
$F$
in
![]() $G[U(\mathcal{T})]$
have both been selected so that
$G[U(\mathcal{T})]$
have both been selected so that
-
(A) there exists
 $e \in F$
such that
$e \in F$
such that
 $e \in E(G[B,C])$
if possible, and,
$e \in E(G[B,C])$
if possible, and, -
(B) subject to (A),
 $|F|$
is as large as possible.
$|F|$
is as large as possible.
Note that Claim 18.2, implies that
![]() $|F| \le h(\mathcal{T}) \le 2$
, so if there exists
$|F| \le h(\mathcal{T}) \le 2$
, so if there exists
![]() $e \in F$
such that
$e \in F$
such that
![]() $e \in E(G[B,C])$
, then
$e \in E(G[B,C])$
, then
![]() $F$
has at most one edge that is contained in
$F$
has at most one edge that is contained in
![]() $E(G[A,B]) \cup E(G[A,C])$
. If there is no
$E(G[A,B]) \cup E(G[A,C])$
. If there is no
![]() $e \in F$
that is in
$e \in F$
that is in
![]() $E(G[B,C])$
, then by the selection of
$E(G[B,C])$
, then by the selection of
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $F$
(c.f. (A)), for every maximum tiling
$F$
(c.f. (A)), for every maximum tiling
![]() $\mathcal{T}$
there does not exist
$\mathcal{T}$
there does not exist
![]() $e \in E(G[B,C])$
, so our contrary assumption implies
$e \in E(G[B,C])$
, so our contrary assumption implies
![]() $|F| \le h(\mathcal{T}) \le 1$
. Therefore, in all cases,
$|F| \le h(\mathcal{T}) \le 1$
. Therefore, in all cases,
![]() $F$
has at most one edge that is contained in
$F$
has at most one edge that is contained in
![]() $E(G[A,B]) \cup E(G[A,C])$
. Let
$E(G[A,B]) \cup E(G[A,C])$
. Let
![]() $\{X, Y\} = \{B, C\}$
be a labelling such that
$\{X, Y\} = \{B, C\}$
be a labelling such that
![]() $F$
does not contain an edge in
$F$
does not contain an edge in
![]() $E(G[A,X])$
.
$E(G[A,X])$
.
Let
![]() $W \subseteq U$
be the set of vertices that are incident to an edge in
$W \subseteq U$
be the set of vertices that are incident to an edge in
![]() $F$
. The fact that
$F$
. The fact that
![]() $|\mathcal{T}| \le n -2$
, implies that there exist nonadjacent vertices
$|\mathcal{T}| \le n -2$
, implies that there exist nonadjacent vertices
![]() $a \in A \setminus W$
and
$a \in A \setminus W$
and
![]() $x \in X \setminus W$
that are uncovered by
$x \in X \setminus W$
that are uncovered by
![]() $\mathcal{T}$
. Let
$\mathcal{T}$
. Let
![]() $\{a_1, \dotsc, a_n\}$
,
$\{a_1, \dotsc, a_n\}$
,
![]() $\{x_1, \dotsc, x_n\}$
and
$\{x_1, \dotsc, x_n\}$
and
![]() $\{y_1, \dotsc, y_n\}$
be orderings of
$\{y_1, \dotsc, y_n\}$
be orderings of
![]() $A$
,
$A$
,
![]() $X$
and
$X$
and
![]() $Y$
, respectively such that
$Y$
, respectively such that
![]() $a_n = a$
,
$a_n = a$
,
![]() $x_n = x$
and
$x_n = x$
and
![]() $a_ix_iy_i \in \mathcal{T}$
for every
$a_ix_iy_i \in \mathcal{T}$
for every
![]() $i \in [m]$
. We can assume that the orderings are such that
$i \in [m]$
. We can assume that the orderings are such that
![]() $W$
is contained in the set
$W$
is contained in the set
![]() $\left\{a_{n-1}, x_{n-1}, y_{n-1}, y_n\right\}$
with
$\left\{a_{n-1}, x_{n-1}, y_{n-1}, y_n\right\}$
with
![]() $x_{n-1}y_{n-1} \in F$
if
$x_{n-1}y_{n-1} \in F$
if
![]() $F \cap E(G[X,Y]) = F \cap E(G[B,C]) \neq \emptyset$
.
$F \cap E(G[X,Y]) = F \cap E(G[B,C]) \neq \emptyset$
.
Since
![]() $a$
and
$a$
and
![]() $x$
are nonadjacent,
$x$
are nonadjacent,
![]() $d(x, a_n) + d(a, x_n) + d(a, y_n) = d(x, a) + d(a, x) + d(a, y_n) \le 1$
, and, by (11) and the fact that
$d(x, a_n) + d(a, x_n) + d(a, y_n) = d(x, a) + d(a, x) + d(a, y_n) \le 1$
, and, by (11) and the fact that
![]() $\alpha \le \beta \le \gamma$
, we have
$\alpha \le \beta \le \gamma$
, we have
so there must exist
![]() $i \in [n-1]$
such that
$i \in [n-1]$
such that
![]() $d(x, a_i) + d(a, x_i) + d(a, y_i) = 3$
. Note that
$d(x, a_i) + d(a, x_i) + d(a, y_i) = 3$
. Note that
![]() $i \neq n-1$
, because if
$i \neq n-1$
, because if
![]() $ax_{n-1}$
is an edge, then the fact that
$ax_{n-1}$
is an edge, then the fact that
![]() $F \cap E(G[A,X]) = \emptyset$
and the maximality of
$F \cap E(G[A,X]) = \emptyset$
and the maximality of
![]() $F$
imply that
$F$
imply that
![]() $x_{n-1}y_{n-1} \in F$
, but, because
$x_{n-1}y_{n-1} \in F$
, but, because
![]() $\mathcal{T}$
is a maximum tiling,
$\mathcal{T}$
is a maximum tiling,
![]() $ax_{n-1}y_{n-1}$
is not a triangle. Since
$ax_{n-1}y_{n-1}$
is not a triangle. Since
![]() $F \cap E(G[A,X]) = \emptyset$
, the maximality of
$F \cap E(G[A,X]) = \emptyset$
, the maximality of
![]() $F$
also implies that that
$F$
also implies that that
![]() $d(x, a_j) = 0$
for every
$d(x, a_j) = 0$
for every
![]() $m+1 \le j \le n-2$
, so it must be that
$m+1 \le j \le n-2$
, so it must be that
![]() $i \in [m]$
, that is, that
$i \in [m]$
, that is, that
![]() $T = a_ix_iy_i$
is a triangle in
$T = a_ix_iy_i$
is a triangle in
![]() $\mathcal{T}$
. Therefore, we can swap
$\mathcal{T}$
. Therefore, we can swap
![]() $T$
for the triangle
$T$
for the triangle
![]() $ax_iy_i$
in
$ax_iy_i$
in
![]() $\mathcal{T}$
to form the maximum tiling
$\mathcal{T}$
to form the maximum tiling
![]() $\mathcal{T}^{\prime}$
. Because the edge
$\mathcal{T}^{\prime}$
. Because the edge
![]() $a_ix$
is uncovered by
$a_ix$
is uncovered by
![]() $\mathcal{T}^{\prime}$
and
$\mathcal{T}^{\prime}$
and
![]() $W \subseteq U(\mathcal{T}^{\prime})$
, we have a contradiction to the selection of
$W \subseteq U(\mathcal{T}^{\prime})$
, we have a contradiction to the selection of
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $F$
(c.f. (B)).
$F$
(c.f. (B)).
Claim 18.3 implies that there exists a maximum tiling
![]() $\mathcal{T}$
such that
$\mathcal{T}$
such that
![]() $h(\mathcal{T}) = 2$
. By Claim 18.3, we can assume that
$h(\mathcal{T}) = 2$
. By Claim 18.3, we can assume that
![]() $\mathcal{T}$
leaves no edge in
$\mathcal{T}$
leaves no edge in
![]() $E(G[B,C])$
uncovered by
$E(G[B,C])$
uncovered by
![]() $\mathcal{T}$
. This means that there are disjoint edges
$\mathcal{T}$
. This means that there are disjoint edges
![]() $ab \in E(G[A, B])$
and
$ab \in E(G[A, B])$
and
![]() $a^{\prime}c \in E(G[A,C])$
with
$a^{\prime}c \in E(G[A,C])$
with
![]() $a, a^{\prime} \in A$
that are uncovered by
$a, a^{\prime} \in A$
that are uncovered by
![]() $\mathcal{T}$
. Since
$\mathcal{T}$
. Since
![]() $|\mathcal{T}| = m \le n - 2$
, there also exists
$|\mathcal{T}| = m \le n - 2$
, there also exists
![]() $b^{\prime} \in B \setminus \{b\}$
and
$b^{\prime} \in B \setminus \{b\}$
and
![]() $c^{\prime} \in C \setminus \{c\}$
that are uncovered by
$c^{\prime} \in C \setminus \{c\}$
that are uncovered by
![]() $\mathcal{T}$
. Furthermore, the fact that no edge in
$\mathcal{T}$
. Furthermore, the fact that no edge in
![]() $E(G[B,C])$
is uncovered implies that
$E(G[B,C])$
is uncovered implies that
so there exists
![]() $T \in \mathcal{T}$
such that
$T \in \mathcal{T}$
such that
![]() $d\!\left(b^{\prime}, T \cap C\right) + d\!\left(c^{\prime}, T \cap B\right) = 2$
. Let
$d\!\left(b^{\prime}, T \cap C\right) + d\!\left(c^{\prime}, T \cap B\right) = 2$
. Let
![]() $e$
be the edge incident to
$e$
be the edge incident to
![]() $c^{\prime}$
and
$c^{\prime}$
and
![]() $T \cap B$
and let
$T \cap B$
and let
![]() $e^{\prime}$
be the edge incident to
$e^{\prime}$
be the edge incident to
![]() $b^{\prime}$
and
$b^{\prime}$
and
![]() $T \cap C$
. If we define
$T \cap C$
. If we define
![]() $F \,:\!=\, \{ab, a^{\prime}c, e\}$
, then
$F \,:\!=\, \{ab, a^{\prime}c, e\}$
, then
![]() $F$
is a dissimilar matching, so Claim 18.2 implies that we are in one of the following two cases.
$F$
is a dissimilar matching, so Claim 18.2 implies that we are in one of the following two cases.
Case 1: There exists
![]() $f \in F$
such that
$f \in F$
such that
![]() $d(f, U(\mathcal{T})) \ge 1$
. By Claim 18.1, the fact that
$d(f, U(\mathcal{T})) \ge 1$
. By Claim 18.1, the fact that
![]() $ab$
and
$ab$
and
![]() $a^{\prime}c$
are uncovered by
$a^{\prime}c$
are uncovered by
![]() $\mathcal{T}$
implies that
$\mathcal{T}$
implies that
![]() $f = e$
. So, there exists a triangle
$f = e$
. So, there exists a triangle
![]() $T^{\prime}$
that contains
$T^{\prime}$
that contains
![]() $e$
and a vertex in
$e$
and a vertex in
![]() $U \cap A$
. This means that we can create a maximum tiling by replacing
$U \cap A$
. This means that we can create a maximum tiling by replacing
![]() $T$
with
$T$
with
![]() $T^{\prime}$
in
$T^{\prime}$
in
![]() $\mathcal{T}$
that leaves the edge
$\mathcal{T}$
that leaves the edge
![]() $e^{\prime} \in E(G[B,C])$
uncovered, contradicting Claim 18.3.
$e^{\prime} \in E(G[B,C])$
uncovered, contradicting Claim 18.3.
Case 2: There exists
![]() $T^{\prime} \in \mathcal{T}$
such that
$T^{\prime} \in \mathcal{T}$
such that
![]() $\sum _{f \in F} d(f,T^{\prime}) \ge 2$
. By Claim 18.1,
$\sum _{f \in F} d(f,T^{\prime}) \ge 2$
. By Claim 18.1,
![]() $d(ab, T^{\prime}) + d(a^{\prime}c, T^{\prime}) \le 1$
, so there is
$d(ab, T^{\prime}) + d(a^{\prime}c, T^{\prime}) \le 1$
, so there is
![]() $f \in \{ab, a^{\prime}c\}$
such that
$f \in \{ab, a^{\prime}c\}$
such that
![]() $d(e, T^{\prime}) + d(f, T^{\prime}) \ge 2$
. This means that there exist two triangles, say
$d(e, T^{\prime}) + d(f, T^{\prime}) \ge 2$
. This means that there exist two triangles, say
![]() $T^{\prime\prime}$
,
$T^{\prime\prime}$
,
![]() $T^{\prime\prime\prime}$
, in the graph induced by the vertices incident to
$T^{\prime\prime\prime}$
, in the graph induced by the vertices incident to
![]() $e$
,
$e$
,
![]() $f$
and
$f$
and
![]() $T^{\prime}$
. Therefore, we can create a new tiling, say
$T^{\prime}$
. Therefore, we can create a new tiling, say
![]() $\mathcal{T}^{\prime}$
, by removing
$\mathcal{T}^{\prime}$
, by removing
![]() $T$
and
$T$
and
![]() $T^{\prime}$
from
$T^{\prime}$
from
![]() $\mathcal{T}$
and replacing them with
$\mathcal{T}$
and replacing them with
![]() $T^{\prime\prime}$
and
$T^{\prime\prime}$
and
![]() $T^{\prime\prime\prime}$
. Since
$T^{\prime\prime\prime}$
. Since
![]() $\mathcal{T}$
is maximum tiling, we have that
$\mathcal{T}$
is maximum tiling, we have that
![]() $T \neq T^{\prime}$
and that
$T \neq T^{\prime}$
and that
![]() $\mathcal{T}^{\prime}$
is a maximum tiling. Because
$\mathcal{T}^{\prime}$
is a maximum tiling. Because
![]() $T \neq T^{\prime}$
, the edge
$T \neq T^{\prime}$
, the edge
![]() $e^{\prime} \in E(G[B,C])$
is uncovered by
$e^{\prime} \in E(G[B,C])$
is uncovered by
![]() $\mathcal{T}^{\prime}$
which contradicts Claim 18.3.
$\mathcal{T}^{\prime}$
which contradicts Claim 18.3.
5. Proof of Theorem 7
The following example proves the second part of the theorem
Example 19. For the case
![]() $\gamma =2/3$
, it can be checked that Example 4 for
$\gamma =2/3$
, it can be checked that Example 4 for
![]() $k=3$
satisfies the second claim of Theorem 7.
$k=3$
satisfies the second claim of Theorem 7.
For the case
![]() $\gamma \in \big(\frac 34,\frac 79\big]$
, we assume
$\gamma \in \big(\frac 34,\frac 79\big]$
, we assume
![]() $n$
satisfies the following:
$n$
satisfies the following:
![]() $\gamma \ge \frac 34+\frac 1n$
and
$\gamma \ge \frac 34+\frac 1n$
and
![]() $(1-\beta )n/2$
is an integer. Clearly, since
$(1-\beta )n/2$
is an integer. Clearly, since
![]() $\beta$
is rational and
$\beta$
is rational and
![]() $\gamma \gt 4/3$
, there are infinitely many choices for such
$\gamma \gt 4/3$
, there are infinitely many choices for such
![]() $n$
. Let us fix
$n$
. Let us fix
![]() $\varepsilon \in \big(0,\frac 1n\big]$
such that
$\varepsilon \in \big(0,\frac 1n\big]$
such that
![]() $(1-\gamma +\varepsilon )n$
is an integer.
$(1-\gamma +\varepsilon )n$
is an integer.
Take sets
![]() $A=A_0\cup A_1\cup A_2 \cup A_3$
,
$A=A_0\cup A_1\cup A_2 \cup A_3$
,
![]() $B=B_0\cup B_1\cup B_2 \cup B_3$
and
$B=B_0\cup B_1\cup B_2 \cup B_3$
and
![]() $C=C_0\cup C_1\cup C_2 \cup C_3$
, such that:
$C=C_0\cup C_1\cup C_2 \cup C_3$
, such that:
-
 $|B_i|=(1-\gamma +\varepsilon )n$
,
$|B_i|=(1-\gamma +\varepsilon )n$
,
 $|A_i|=|C_i|=(1-\beta )n/2$
, for
$|A_i|=|C_i|=(1-\beta )n/2$
, for
 $i\in [3]$
;
$i\in [3]$
; -
 $|B_0|=n-3(1-\gamma +\varepsilon )n=(3\gamma -2)n-3\varepsilon n$
; and
$|B_0|=n-3(1-\gamma +\varepsilon )n=(3\gamma -2)n-3\varepsilon n$
; and -
 $|A_0|=|C_0|=n-3(1-\beta )n/2=(3\beta -1)n/2$
.
$|A_0|=|C_0|=n-3(1-\beta )n/2=(3\beta -1)n/2$
.
Let
![]() $G$
be the
$G$
be the
![]() $3$
-partite graph with parts
$3$
-partite graph with parts
![]() $A,B$
and
$A,B$
and
![]() $C$
, where
$C$
, where
![]() $E(G)$
consists of the union of the edges in the following graphs:
$E(G)$
consists of the union of the edges in the following graphs:
-
the complete bipartite graphs with parts
 $A_0, B\cup C$
and
$A_0, B\cup C$
and
 $B_0, A\cup C$
and
$B_0, A\cup C$
and
 $C_0, A\cup B$
.
$C_0, A\cup B$
. -
the complete bipartite graphs with parts
 $A_1,B_2\cup B_3$
and
$A_1,B_2\cup B_3$
and
 $A_2,B_1\cup B_3$
and
$A_2,B_1\cup B_3$
and
 $A_3,B_1\cup B_2$
.
$A_3,B_1\cup B_2$
. -
the complete bipartite graphs with parts
 $B_i,C_i$
and
$B_i,C_i$
and
 $A_i,C_i$
for each
$A_i,C_i$
for each
 $i\in [3]$
.
$i\in [3]$
.
Since
![]() $\gamma \le \frac 79$
and
$\gamma \le \frac 79$
and
![]() $\varepsilon \gt 0$
, we have
$\varepsilon \gt 0$
, we have
![]() $(1-\gamma +\varepsilon )n \gt (\gamma - 1/3)n/2 =(1-\beta )n/2$
. So,
$(1-\gamma +\varepsilon )n \gt (\gamma - 1/3)n/2 =(1-\beta )n/2$
. So,
-
 $\delta (G[A,B])=n-(1-\gamma +\varepsilon )n= \gamma n-\varepsilon n$
,
$\delta (G[A,B])=n-(1-\gamma +\varepsilon )n= \gamma n-\varepsilon n$
, -
 $\delta (G[B,C])= n-2(1-\gamma +\varepsilon )n= (2\gamma -1) n-2\varepsilon n$
, and
$\delta (G[B,C])= n-2(1-\gamma +\varepsilon )n= (2\gamma -1) n-2\varepsilon n$
, and -
 $\delta (G[A,C])= n-2(1-\beta )n/2=\beta n$
.
$\delta (G[A,C])= n-2(1-\beta )n/2=\beta n$
.
Recall that
![]() $\varepsilon \le \frac 1n$
and
$\varepsilon \le \frac 1n$
and
![]() $\gamma \ge \frac 34+\frac 1n$
, so
$\gamma \ge \frac 34+\frac 1n$
, so
![]() $\delta (G[A,B]) \ge \gamma n -1$
and
$\delta (G[A,B]) \ge \gamma n -1$
and
![]() $\delta (G[B,C]) \ge (2\gamma - 1)n - 2 \ge n/2$
.
$\delta (G[B,C]) \ge (2\gamma - 1)n - 2 \ge n/2$
.
Note that
![]() $A_0 \cup B_0 \cup C_0$
is a triangle cover and
$A_0 \cup B_0 \cup C_0$
is a triangle cover and
We now proceed with the proof of the first part of the Theorem 7. We will use the following definition throughout the proof.
Definition 20. For
![]() $U, W, U^{\prime} \subseteq V(G)$
, let
$U, W, U^{\prime} \subseteq V(G)$
, let
![]() $P_{3}(U, W, U^{\prime})$
be the set of paths on
$P_{3}(U, W, U^{\prime})$
be the set of paths on
![]() $3$
vertices in which the middle vertex is in
$3$
vertices in which the middle vertex is in
![]() $W$
, one endpoint is in
$W$
, one endpoint is in
![]() $U$
and the other endpoint is in
$U$
and the other endpoint is in
![]() $U^{\prime}$
. When a set
$U^{\prime}$
. When a set
![]() $\{u\}$
is a singleton, we sometimes replace
$\{u\}$
is a singleton, we sometimes replace
![]() $\{u\}$
with
$\{u\}$
with
![]() $u$
in this notation.
$u$
in this notation.
Let
![]() $\{\alpha, \beta, \gamma \} = \{\delta _1/n, \delta _2/n, \delta _3/n\}$
and
$\{\alpha, \beta, \gamma \} = \{\delta _1/n, \delta _2/n, \delta _3/n\}$
and
![]() $\{A, B, C\} = \{V_1, V_2, V_3\}$
be labellings such that
$\{A, B, C\} = \{V_1, V_2, V_3\}$
be labellings such that
![]() $\alpha \le \beta \le \gamma$
and
$\alpha \le \beta \le \gamma$
and
We can assume
![]() $\gamma + \beta = 4/3$
and
$\gamma + \beta = 4/3$
and
![]() $\alpha = 1/2$
. Therefore,
$\alpha = 1/2$
. Therefore,
Let
![]() $U$
be a triangle cover and let
$U$
be a triangle cover and let
![]() $x = |A \cap U|/n$
,
$x = |A \cap U|/n$
,
![]() $y = |B \cap U|/n$
and
$y = |B \cap U|/n$
and
![]() $z = |C \cap U|/n$
. For a contradiction, assume that
$z = |C \cap U|/n$
. For a contradiction, assume that
Let
![]() $A^{\prime} = A \setminus U$
,
$A^{\prime} = A \setminus U$
,
![]() $B^{\prime} = B \setminus U$
and
$B^{\prime} = B \setminus U$
and
![]() $C^{\prime} = C \setminus U$
.
$C^{\prime} = C \setminus U$
.
Using this notation, we now give an informal sketch of the proof. We use the fact that
![]() $G[A^{\prime}, B^{\prime}, C^{\prime}]$
is triangle-free to iteratively improve bounds on
$G[A^{\prime}, B^{\prime}, C^{\prime}]$
is triangle-free to iteratively improve bounds on
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
until we derive a contradiction.
$z$
until we derive a contradiction.
We start with the simple observation that the common neighbourhood of the endpoints of every edge in
![]() $G[A^{\prime}, B^{\prime}, C^{\prime}]$
must be in
$G[A^{\prime}, B^{\prime}, C^{\prime}]$
must be in
![]() $U$
, so
$U$
, so
![]() $x \ge \gamma + \beta - 1 = 1/3$
,
$x \ge \gamma + \beta - 1 = 1/3$
,
![]() $y \ge \gamma + \alpha - 1 = \gamma - 1/2$
and
$y \ge \gamma + \alpha - 1 = \gamma - 1/2$
and
![]() $z \ge \beta + \alpha - 1 = \beta - 1/2$
(Claim 20.1). Since
$z \ge \beta + \alpha - 1 = \beta - 1/2$
(Claim 20.1). Since
![]() $1 \gt x + y + z$
and
$1 \gt x + y + z$
and
![]() $\gamma \ge 2/3$
, these lower bounds imply that
$\gamma \ge 2/3$
, these lower bounds imply that
![]() $x,y \lt \gamma$
and
$x,y \lt \gamma$
and
![]() $\beta \lt 1/2$
. We derive that
$\beta \lt 1/2$
. We derive that
![]() $y \lt 1/2$
by noting that if
$y \lt 1/2$
by noting that if
![]() $y \ge 1/2$
, then for every
$y \ge 1/2$
, then for every
![]() $b \in B^{\prime}$
and every
$b \in B^{\prime}$
and every
![]() $a \in N_{\overline{G}}(b, A^{\prime})$
there exists
$a \in N_{\overline{G}}(b, A^{\prime})$
there exists
![]() $b^{\prime} \in B^{\prime}$
and
$b^{\prime} \in B^{\prime}$
and
![]() $a^{\prime} \in A^{\prime}$
such that
$a^{\prime} \in A^{\prime}$
such that
![]() $ab^{\prime}a^{\prime}b$
is a
$ab^{\prime}a^{\prime}b$
is a
![]() $4$
-vertex path. This then implies that
$4$
-vertex path. This then implies that
![]() $|P_3(b, C^{\prime}, a)| \le |C^{\prime}| - d(a^{\prime}, C) - d\!\left(b^{\prime}, C\right)$
, which further implies an upper bound on
$|P_3(b, C^{\prime}, a)| \le |C^{\prime}| - d(a^{\prime}, C) - d\!\left(b^{\prime}, C\right)$
, which further implies an upper bound on
![]() $|P_3(b, C^{\prime}, A^{\prime})|$
that contradicts the fact that
$|P_3(b, C^{\prime}, A^{\prime})|$
that contradicts the fact that
So
![]() $y \lt 1/2$
(Claim 20.2). This means every vertex in
$y \lt 1/2$
(Claim 20.2). This means every vertex in
![]() $C^{\prime}$
has a neighbour in
$C^{\prime}$
has a neighbour in
![]() $B^{\prime}$
. We use this to get an upper bound on
$B^{\prime}$
. We use this to get an upper bound on
![]() $G[A^{\prime}, C^{\prime}]$
which we compare to the lower bound given by the minimum degree. This inequality is then used to prove that there is a
$G[A^{\prime}, C^{\prime}]$
which we compare to the lower bound given by the minimum degree. This inequality is then used to prove that there is a
![]() $4$
-vertex path in
$4$
-vertex path in
![]() $G[A^{\prime}, B^{\prime}]$
between every nonadjacent
$G[A^{\prime}, B^{\prime}]$
between every nonadjacent
![]() $a \in A^{\prime}$
and
$a \in A^{\prime}$
and
![]() $b \in B^{\prime}$
(Claim 20.3). Using these paths in the same manner as before, we derive upper and lower bounds on
$b \in B^{\prime}$
(Claim 20.3). Using these paths in the same manner as before, we derive upper and lower bounds on
![]() $|P_3(a, C^{\prime}, B^{\prime})|$
and
$|P_3(a, C^{\prime}, B^{\prime})|$
and
![]() $|P_3(A^{\prime}, B^{\prime}, b)|$
for every
$|P_3(A^{\prime}, B^{\prime}, b)|$
for every
![]() $a \in A^{\prime}$
and
$a \in A^{\prime}$
and
![]() $b \in B^{\prime}$
. These bounds and the previous inequality imply that
$b \in B^{\prime}$
. These bounds and the previous inequality imply that
![]() $y \lt 1/3$
and
$y \lt 1/3$
and
![]() $x \lt \beta$
(Claim 20.4). A similar argument implies that there exist non-adjacent
$x \lt \beta$
(Claim 20.4). A similar argument implies that there exist non-adjacent
![]() $a_1 \in A^{\prime}$
and
$a_1 \in A^{\prime}$
and
![]() $c_1 \in C^{\prime}$
such that there does not exist a
$c_1 \in C^{\prime}$
such that there does not exist a
![]() $4$
-vertex path between
$4$
-vertex path between
![]() $a_1$
and
$a_1$
and
![]() $c_1$
(Claim 20.5). We fix
$c_1$
(Claim 20.5). We fix
![]() $a_2 \in N(c_1, A^{\prime})$
and
$a_2 \in N(c_1, A^{\prime})$
and
![]() $c_2 \in N(a_1, C^{\prime})$
. We then observe that, by the selection of
$c_2 \in N(a_1, C^{\prime})$
. We then observe that, by the selection of
![]() $a_1$
and
$a_1$
and
![]() $c_1$
, the sets
$c_1$
, the sets
![]() $N(a_1, C^{\prime})$
and
$N(a_1, C^{\prime})$
and
![]() $N(a_2, C^{\prime})$
are disjoint and the sets
$N(a_2, C^{\prime})$
are disjoint and the sets
![]() $A_1 = N(c_1, A^{\prime})$
and
$A_1 = N(c_1, A^{\prime})$
and
![]() $A_2 = N(c_2, A^{\prime})$
are disjoint. Since
$A_2 = N(c_2, A^{\prime})$
are disjoint. Since
![]() $a_1$
and
$a_1$
and
![]() $a_2$
must have a common neighbour in
$a_2$
must have a common neighbour in
![]() $B^{\prime}$
, we get that
$B^{\prime}$
, we get that
![]() $z \ge \beta - 1/4$
(Claim 20.6). We can now deduce that, in
$z \ge \beta - 1/4$
(Claim 20.6). We can now deduce that, in
![]() $G[A^{\prime}, C^{\prime}]$
, every
$G[A^{\prime}, C^{\prime}]$
, every
![]() $a \in A^{\prime}$
has a
$a \in A^{\prime}$
has a
![]() $4$
-vertex path to either
$4$
-vertex path to either
![]() $c_1$
or
$c_1$
or
![]() $c_2$
(Claim 20.8). We let
$c_2$
(Claim 20.8). We let
![]() $B_1$
and
$B_1$
and
![]() $B_2$
be subsets of
$B_2$
be subsets of
![]() $N(c_1, B^{\prime})$
and
$N(c_1, B^{\prime})$
and
![]() $N(c_2, B^{\prime})$
with cardinality exactly
$N(c_2, B^{\prime})$
with cardinality exactly
![]() $\left \lceil (1/2 - y)n \right \rceil$
. Note that for every
$\left \lceil (1/2 - y)n \right \rceil$
. Note that for every
![]() $a \in A_i$
every vertex in
$a \in A_i$
every vertex in
![]() $B_i$
is a non-neighbour of
$B_i$
is a non-neighbour of
![]() $a$
and this yields an upper bound on the number of non-neighbours of
$a$
and this yields an upper bound on the number of non-neighbours of
![]() $a$
in
$a$
in
![]() $B \setminus (B_1 \cup B_2)$
. Using the fact that for every
$B \setminus (B_1 \cup B_2)$
. Using the fact that for every
![]() $a \in A \setminus (A_1 \cup A_2)$
there is
$a \in A \setminus (A_1 \cup A_2)$
there is
![]() $4$
-vertex path in
$4$
-vertex path in
![]() $G[A^{\prime}, C^{\prime}]$
from
$G[A^{\prime}, C^{\prime}]$
from
![]() $a$
to
$a$
to
![]() $c_i$
, we can get an upper bound on the number of non-neighbours of
$c_i$
, we can get an upper bound on the number of non-neighbours of
![]() $a$
in
$a$
in
![]() $B \setminus (B_1 \cup B_2)$
(Claim 20.9). There observations lead to a upper bound on the number of non-neighbours between
$B \setminus (B_1 \cup B_2)$
(Claim 20.9). There observations lead to a upper bound on the number of non-neighbours between
![]() $A^{\prime}$
and
$A^{\prime}$
and
![]() $B^{\prime} \setminus (B_1 \cup B_2)$
. To get a contradiction, we note that every vertex in
$B^{\prime} \setminus (B_1 \cup B_2)$
. To get a contradiction, we note that every vertex in
![]() $B^{\prime}$
has a neighbour in
$B^{\prime}$
has a neighbour in
![]() $C^{\prime}$
, which implies a lower bound on the number of non-neighbours between
$C^{\prime}$
, which implies a lower bound on the number of non-neighbours between
![]() $A^{\prime}$
and
$A^{\prime}$
and
![]() $B^{\prime} \setminus (B_1 \cup B_2)$
that is in conflict with the previous upper bound.
$B^{\prime} \setminus (B_1 \cup B_2)$
that is in conflict with the previous upper bound.
We now proceed with the formal proof.
Claim 20.1.
![]() $x \ge 1/3$
,
$x \ge 1/3$
,
![]() $y \ge \gamma - 1/2$
and
$y \ge \gamma - 1/2$
and
![]() $z \ge \beta - 1/2$
.
$z \ge \beta - 1/2$
.
Proof. Since
![]() $y + z \le x + y + z \lt 1$
, one of
$y + z \le x + y + z \lt 1$
, one of
![]() $y$
or
$y$
or
![]() $z$
is less than
$z$
is less than
![]() $1/2$
, so there exists an edge
$1/2$
, so there exists an edge
![]() $bc \in E(G[B^{\prime},C^{\prime}])$
. Because
$bc \in E(G[B^{\prime},C^{\prime}])$
. Because
![]() $G[A^{\prime}, B^{\prime}, C^{\prime}]$
is triangle-free,
$G[A^{\prime}, B^{\prime}, C^{\prime}]$
is triangle-free,
so
![]() $x \ge 1/3$
. By considering an edge in
$x \ge 1/3$
. By considering an edge in
![]() $E(G[A^{\prime},B^{\prime}])$
and an edge in
$E(G[A^{\prime},B^{\prime}])$
and an edge in
![]() $E(G[A^{\prime},C^{\prime}])$
the same argument yields
$E(G[A^{\prime},C^{\prime}])$
the same argument yields
![]() $z \ge \beta - 1/2$
and
$z \ge \beta - 1/2$
and
![]() $y \ge \gamma - 1/2$
, respectively.
$y \ge \gamma - 1/2$
, respectively.
Claim 20.2.
![]() $x \lt \gamma$
,
$x \lt \gamma$
,
![]() $y \lt 1/2$
and
$y \lt 1/2$
and
![]() $z \lt 1/2$
.
$z \lt 1/2$
.
Proof. We first show that both
![]() $x \lt \gamma$
and
$x \lt \gamma$
and
![]() $y \lt \gamma$
. To this end, note that if
$y \lt \gamma$
. To this end, note that if
![]() $x \ge \gamma$
, then
$x \ge \gamma$
, then
![]() $x + y \ge \gamma + \gamma - 1/2 = 2\gamma - 1/2$
. If
$x + y \ge \gamma + \gamma - 1/2 = 2\gamma - 1/2$
. If
![]() $y \ge \gamma$
, then, because
$y \ge \gamma$
, then, because
![]() $\gamma - 1/2 \le 5/6 - 1/2 = 1/3$
, we also have
$\gamma - 1/2 \le 5/6 - 1/2 = 1/3$
, we also have
![]() $x + y \ge 1/3 + \gamma \ge 2\gamma - 1/2$
. So, in either case, we have the following contradiction
$x + y \ge 1/3 + \gamma \ge 2\gamma - 1/2$
. So, in either case, we have the following contradiction
Similarly, it is clear that
![]() $z \lt 1/2$
, since otherwise
$z \lt 1/2$
, since otherwise
![]() $x + y + z \ge 1/3 + (\gamma - 1/2) + 1/2 \ge 1$
, a contradiction.
$x + y + z \ge 1/3 + (\gamma - 1/2) + 1/2 \ge 1$
, a contradiction.
Assume
![]() $y \ge 1/2$
and let
$y \ge 1/2$
and let
![]() $b \in B^{\prime}$
. Note that there are at most
$b \in B^{\prime}$
. Note that there are at most
![]() $(1-\gamma )n$
vertices
$(1-\gamma )n$
vertices
![]() $a \in N_{\overline{G}}(b, A^{\prime})$
. For every such
$a \in N_{\overline{G}}(b, A^{\prime})$
. For every such
![]() $a$
we can find a
$a$
we can find a
![]() $4$
-vertex path
$4$
-vertex path
![]() $ab^{\prime}a^{\prime}b$
in
$ab^{\prime}a^{\prime}b$
in
![]() $G[A^{\prime},B^{\prime}]$
. Indeed, since
$G[A^{\prime},B^{\prime}]$
. Indeed, since
![]() $y \lt \gamma$
, there exists
$y \lt \gamma$
, there exists
![]() $b^{\prime} \in N(a, B^{\prime})$
. Then, because
$b^{\prime} \in N(a, B^{\prime})$
. Then, because
![]() $2 \gamma + \beta \ge 2$
and
$2 \gamma + \beta \ge 2$
and
![]() $1 \gt x + y + z$
,
$1 \gt x + y + z$
,
Since
![]() $|N(b, A) \cap N(b^{\prime}, A)| \ge 2\gamma n - n\gt xn$
, there exists
$|N(b, A) \cap N(b^{\prime}, A)| \ge 2\gamma n - n\gt xn$
, there exists
![]() $a^{\prime} \in |N(b, A^{\prime}) \cap N(b^{\prime}, A^{\prime})|$
, giving us the
$a^{\prime} \in |N(b, A^{\prime}) \cap N(b^{\prime}, A^{\prime})|$
, giving us the
![]() $4$
-path
$4$
-path
![]() $ab^{\prime}a^{\prime}b$
. Note that
$ab^{\prime}a^{\prime}b$
. Note that
![]() $N(a^{\prime}, C^{\prime})$
and
$N(a^{\prime}, C^{\prime})$
and
![]() $N(b^{\prime}, C^{\prime})$
are disjoint and that every
$N(b^{\prime}, C^{\prime})$
are disjoint and that every
![]() $c \in C^{\prime}$
that is adjacent to both
$c \in C^{\prime}$
that is adjacent to both
![]() $a$
and
$a$
and
![]() $b$
is not adjacent to
$b$
is not adjacent to
![]() $a^{\prime}$
and not adjacent to
$a^{\prime}$
and not adjacent to
![]() $b^{\prime}$
. Therefore,
$b^{\prime}$
. Therefore,
![]() $|P_3( b, C^{\prime}, a)|$
is at most
$|P_3( b, C^{\prime}, a)|$
is at most
and
![]() $|P_3(b, C^{\prime}, A^{\prime})|/n^2 \le (1 - \gamma )(z - \beta + 1/2)$
. On the other hand,
$|P_3(b, C^{\prime}, A^{\prime})|/n^2 \le (1 - \gamma )(z - \beta + 1/2)$
. On the other hand,
The claim then follows because there are no solutions to
when
![]() $x \ge 1/3$
,
$x \ge 1/3$
,
![]() $y \ge 1/2$
and
$y \ge 1/2$
and
![]() $z \ge \beta - 1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.)
$z \ge \beta - 1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.)
Note that Claim 20.2 implies that
![]() $\delta (G[A^{\prime},B^{\prime}]) \ge 1$
,
$\delta (G[A^{\prime},B^{\prime}]) \ge 1$
,
![]() $\delta (G[B^{\prime},C^{\prime}]) \ge 1$
, and that every vertex in
$\delta (G[B^{\prime},C^{\prime}]) \ge 1$
, and that every vertex in
![]() $A^{\prime}$
has a neighbour in
$A^{\prime}$
has a neighbour in
![]() $C^{\prime}$
. (We do not yet know if every vertex in
$C^{\prime}$
. (We do not yet know if every vertex in
![]() $C^{\prime}$
has a neighbour in
$C^{\prime}$
has a neighbour in
![]() $A^{\prime}$
.) We will use these facts in the rest of the argument without comment.
$A^{\prime}$
.) We will use these facts in the rest of the argument without comment.
In particular, the fact that every
![]() $c \in C^{\prime}$
has a neighbour
$c \in C^{\prime}$
has a neighbour
![]() $b \in B^{\prime}$
implies that
$b \in B^{\prime}$
implies that
so
![]() $|E(A^{\prime}, C^{\prime})| = \sum _{c \in C^{\prime}}d(c, A^{\prime}) \le |C^{\prime}|(1 - \gamma )n = (1-z)(1-\gamma )n^2$
. On the other hand, we have that
$|E(A^{\prime}, C^{\prime})| = \sum _{c \in C^{\prime}}d(c, A^{\prime}) \le |C^{\prime}|(1 - \gamma )n = (1-z)(1-\gamma )n^2$
. On the other hand, we have that
![]() $|E(A^{\prime}, C^{\prime})| = \sum _{a \in A^{\prime}}d(a, C^{\prime}) \ge |A^{\prime}|(\beta - z)n = (1-x)(\beta -z)n^2$
. This yields the following useful inequality
$|E(A^{\prime}, C^{\prime})| = \sum _{a \in A^{\prime}}d(a, C^{\prime}) \ge |A^{\prime}|(\beta - z)n = (1-x)(\beta -z)n^2$
. This yields the following useful inequality
Claim 20.3.
For every
![]() $a \in A^{\prime}$
and
$a \in A^{\prime}$
and
![]() $b \in B^{\prime}$
, there is an
$b \in B^{\prime}$
, there is an
![]() $(a,b)$
-path in
$(a,b)$
-path in
![]() $G[A^{\prime}, B^{\prime}]$
with at most
$G[A^{\prime}, B^{\prime}]$
with at most
![]() $4$
vertices.
$4$
vertices.
Proof. Assume the contrary and let
![]() $a \in A^{\prime}$
and
$a \in A^{\prime}$
and
![]() $b \in B^{\prime}$
be such that there is no
$b \in B^{\prime}$
be such that there is no
![]() $(a,b)$
-path in
$(a,b)$
-path in
![]() $G[A^{\prime}, B^{\prime}]$
with at most
$G[A^{\prime}, B^{\prime}]$
with at most
![]() $4$
vertices. Let
$4$
vertices. Let
![]() $b^{\prime} \in N(a, B^{\prime})$
and
$b^{\prime} \in N(a, B^{\prime})$
and
![]() $a^{\prime} \in N(b, A^{\prime})$
. By our contrary assumption, we have that
$a^{\prime} \in N(b, A^{\prime})$
. By our contrary assumption, we have that
![]() $N(a, B^{\prime}) \cap N(a^{\prime}, B^{\prime}) = \emptyset$
so
$N(a, B^{\prime}) \cap N(a^{\prime}, B^{\prime}) = \emptyset$
so
![]() $y \ge |N(a, B) \cap N(a^{\prime}, B)|/n \ge 2\gamma - 1$
, By the same argument,
$y \ge |N(a, B) \cap N(a^{\prime}, B)|/n \ge 2\gamma - 1$
, By the same argument,
![]() $N(b, A^{\prime}) \cap N(b^{\prime}, A^{\prime}) = \emptyset$
and
$N(b, A^{\prime}) \cap N(b^{\prime}, A^{\prime}) = \emptyset$
and
![]() $x \ge 2\gamma - 1$
. Since
$x \ge 2\gamma - 1$
. Since
![]() $\beta \le 2/3$
, we have
$\beta \le 2/3$
, we have
![]() $2 \gamma - 1 = 2(4/3 - \beta ) - 1 = 5/3 - 2\beta \ge 1 - \beta$
, so
$2 \gamma - 1 = 2(4/3 - \beta ) - 1 = 5/3 - 2\beta \ge 1 - \beta$
, so
therefore there exists
![]() $c \in N(a, C^{\prime}) \cap N(a^{\prime}, C^{\prime})$
. But then
$c \in N(a, C^{\prime}) \cap N(a^{\prime}, C^{\prime})$
. But then
![]() $N(c, B^{\prime})$
cannot intersect
$N(c, B^{\prime})$
cannot intersect
![]() $N(a, B^{\prime}) \cup N(a^{\prime}, B^{\prime})$
, so
$N(a, B^{\prime}) \cup N(a^{\prime}, B^{\prime})$
, so
which implies that
![]() $y \ge \gamma - 1/4$
, therefore
$y \ge \gamma - 1/4$
, therefore
![]() $y\ge 5/12$
. But (14) has no solutions when
$y\ge 5/12$
. But (14) has no solutions when
![]() $y \ge 5/12$
,
$y \ge 5/12$
,
![]() $x \ge 1/3$
and
$x \ge 1/3$
and
![]() $z \ge \beta -1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.) This is a contradiction.
$z \ge \beta -1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.) This is a contradiction.
Claim 20.4.
![]() $y \lt 1/3$
and
$y \lt 1/3$
and
![]() $x\lt \beta$
.
$x\lt \beta$
.
Proof. Let
![]() $a \in A^{\prime}$
. We first get an upper bound on
$a \in A^{\prime}$
. We first get an upper bound on
![]() $|P_3(a, C^{\prime}, B^{\prime})|$
. Note that there are at most
$|P_3(a, C^{\prime}, B^{\prime})|$
. Note that there are at most
![]() $(1 - \gamma )n$
ways to select
$(1 - \gamma )n$
ways to select
![]() $b \in B^{\prime}$
that is not adjacent to
$b \in B^{\prime}$
that is not adjacent to
![]() $a$
. By Claim 20.3, there exists
$a$
. By Claim 20.3, there exists
![]() $a^{\prime} \in A^{\prime}$
and
$a^{\prime} \in A^{\prime}$
and
![]() $b^{\prime} \in B^{\prime}$
such that
$b^{\prime} \in B^{\prime}$
such that
![]() $ab^{\prime}a^{\prime}b$
is a path. Note that every vertex
$ab^{\prime}a^{\prime}b$
is a path. Note that every vertex
![]() $c \in C^{\prime}$
that is adjacent to both
$c \in C^{\prime}$
that is adjacent to both
![]() $a$
and
$a$
and
![]() $b$
cannot be in
$b$
cannot be in
![]() $N(a^{\prime}, C^{\prime}) \cup N(b^{\prime}, C^{\prime})$
. Since
$N(a^{\prime}, C^{\prime}) \cup N(b^{\prime}, C^{\prime})$
. Since
![]() $N(a^{\prime}, C^{\prime})$
and
$N(a^{\prime}, C^{\prime})$
and
![]() $N\!\left(b^{\prime}, C\right)$
are disjoint, we have the cardinality of
$N\!\left(b^{\prime}, C\right)$
are disjoint, we have the cardinality of
![]() $P_3(a, C^{\prime}, b)$
is at most
$P_3(a, C^{\prime}, b)$
is at most
Therefore,
![]() $|P_3(a,C^{\prime}, B^{\prime})|/n^2 \le (1 - \gamma )(z - \beta + 1/2)$
. We also have that
$|P_3(a,C^{\prime}, B^{\prime})|/n^2 \le (1 - \gamma )(z - \beta + 1/2)$
. We also have that
![]() $|P_3(a, C^{\prime}, B^{\prime})| \ge \sum _{c \in N(a, C^{\prime})}d(c, B^{\prime})\ge (\beta - z)n(1/2 - y)n$
, so
$|P_3(a, C^{\prime}, B^{\prime})| \ge \sum _{c \in N(a, C^{\prime})}d(c, B^{\prime})\ge (\beta - z)n(1/2 - y)n$
, so
By considering
![]() $b \in B^{\prime}$
and estimating
$b \in B^{\prime}$
and estimating
![]() $P_{3}(A^{\prime},C^{\prime}, b$
), the same arguments yield that
$P_{3}(A^{\prime},C^{\prime}, b$
), the same arguments yield that
But (15), (16) and (14) cannot hold simultaneously when
![]() $x \ge 1/3$
,
$x \ge 1/3$
,
![]() $y \ge 1/3$
and
$y \ge 1/3$
and
![]() $z \ge \beta - 1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.) Therefore
$z \ge \beta - 1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.) Therefore
![]() $y \lt 1/3$
.
$y \lt 1/3$
.
Now we will show that
![]() $x\lt \beta$
. Indeed, if
$x\lt \beta$
. Indeed, if
![]() $\beta \le x$
, we have
$\beta \le x$
, we have
so
![]() $z \lt 1/6$
. With (15) we get
$z \lt 1/6$
. With (15) we get
![]() $(\beta -1/3)(1/6 - \beta + 1/2) \ge (\beta - 1/6)(1/2 - y)$
. Plugging
$(\beta -1/3)(1/6 - \beta + 1/2) \ge (\beta - 1/6)(1/2 - y)$
. Plugging
![]() $y\lt 1/3$
we get that
$y\lt 1/3$
we get that
![]() $-\beta ^2+(5/6)\beta -1/4\gt 0$
which does not have a solution, a contradiction.
$-\beta ^2+(5/6)\beta -1/4\gt 0$
which does not have a solution, a contradiction.
Note that Claims 20.2 and 20.4 together imply
![]() $\delta (G[A^{\prime},B^{\prime}]), \delta (G[B^{\prime},C^{\prime}]), \delta (G[C^{\prime},A^{\prime}]) \ge 1$
.
$\delta (G[A^{\prime},B^{\prime}]), \delta (G[B^{\prime},C^{\prime}]), \delta (G[C^{\prime},A^{\prime}]) \ge 1$
.
Claim 20.5.
There exists
![]() $a_1 \in A^{\prime}$
and
$a_1 \in A^{\prime}$
and
![]() $c_1 \in C^{\prime}$
such that there is no
$c_1 \in C^{\prime}$
such that there is no
![]() $(a_1, c_1)$
-path in
$(a_1, c_1)$
-path in
![]() $G[A^{\prime}, C^{\prime}]$
with at most
$G[A^{\prime}, C^{\prime}]$
with at most
![]() $4$
-vertices.
$4$
-vertices.
Proof. Assume the contrary and let
![]() $a_1 \in A^{\prime}$
. Then, for every
$a_1 \in A^{\prime}$
. Then, for every
![]() $c_1 \in C^{\prime}\setminus N(a^{\prime},C^{\prime})$
, there exists
$c_1 \in C^{\prime}\setminus N(a^{\prime},C^{\prime})$
, there exists
![]() $a_2 \in A^{\prime}$
and
$a_2 \in A^{\prime}$
and
![]() $c_2 \in C^{\prime}$
such that
$c_2 \in C^{\prime}$
such that
![]() $a_1c_2a_2c_1$
is a path, so, since
$a_1c_2a_2c_1$
is a path, so, since
![]() $G[A^{\prime},B^{\prime},C^{\prime}]$
is triangle-free,
$G[A^{\prime},B^{\prime},C^{\prime}]$
is triangle-free,
![]() $|P_3(a_1, B^{\prime}, c_1)|$
is at most
$|P_3(a_1, B^{\prime}, c_1)|$
is at most
Since
![]() $a_1$
has at most
$a_1$
has at most
![]() $(1 - \beta )n$
non-neighbours in
$(1 - \beta )n$
non-neighbours in
![]() $C^{\prime}$
, we have that
$C^{\prime}$
, we have that
which is impossible when
![]() $x \ge 1/3$
,
$x \ge 1/3$
,
![]() $1/3 \gt y \ge \gamma - 1/2$
and
$1/3 \gt y \ge \gamma - 1/2$
and
![]() $z \ge \beta - 1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.)
$z \ge \beta - 1/2$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.)
By Claim 20.5, there exists
![]() $a_1 \in A^{\prime}$
and
$a_1 \in A^{\prime}$
and
![]() $c_1 \in C^{\prime}$
such that there is no
$c_1 \in C^{\prime}$
such that there is no
![]() $(a_1,c_1)$
-path in
$(a_1,c_1)$
-path in
![]() $G[A^{\prime}, C^{\prime}]$
with at most
$G[A^{\prime}, C^{\prime}]$
with at most
![]() $4$
-vertices. Fix such vertices
$4$
-vertices. Fix such vertices
![]() $a_1$
and
$a_1$
and
![]() $c_1$
. By Claims 20.2 and 20.4, we can also fix
$c_1$
. By Claims 20.2 and 20.4, we can also fix
![]() $c_2 \in N(a_1, C^{\prime})$
and
$c_2 \in N(a_1, C^{\prime})$
and
![]() $a_2 \in N(c_1, A^{\prime})$
. Note that, by the selection of
$a_2 \in N(c_1, A^{\prime})$
. Note that, by the selection of
![]() $a_1$
and
$a_1$
and
![]() $c_1$
,
$c_1$
,
Claim 20.6.
![]() $z \ge \beta - 1/4$
.
$z \ge \beta - 1/4$
.
Proof. Since
![]() $|N(a_1, B) \cap N(a_2, B)|/n \ge 2 \gamma - 1 \ge 1/3 \gt y$
, there exists
$|N(a_1, B) \cap N(a_2, B)|/n \ge 2 \gamma - 1 \ge 1/3 \gt y$
, there exists
![]() $b \in B^{\prime}$
that is adjacent to both
$b \in B^{\prime}$
that is adjacent to both
![]() $a_1$
and
$a_1$
and
![]() $a_2$
. Since
$a_2$
. Since
![]() $G[A^{\prime},B^{\prime},C^{\prime}]$
is triangle-free (17) implies that
$G[A^{\prime},B^{\prime},C^{\prime}]$
is triangle-free (17) implies that
so
![]() $z \ge \beta - 1/4$
.
$z \ge \beta - 1/4$
.
Claim 20.7. At least one of the following statements is true.
-
• For every
 $a \in A^{\prime}$
, we have that
$a \in A^{\prime}$
, we have that
 $N(a, C^{\prime})$
intersects
$N(a, C^{\prime})$
intersects
 $N(a_1, C^{\prime}) \cup N(a_2, C^{\prime})$
.
$N(a_1, C^{\prime}) \cup N(a_2, C^{\prime})$
. -
• For every
 $c \in C^{\prime}$
, we have that
$c \in C^{\prime}$
, we have that
 $N(c, A^{\prime})$
intersects
$N(c, A^{\prime})$
intersects
 $N(c_1, A^{\prime}) \cup N(c_2, A^{\prime})$
.
$N(c_1, A^{\prime}) \cup N(c_2, A^{\prime})$
.
Proof. Assume the contrary, so there exists
![]() $a_3 \in A^{\prime}$
such that
$a_3 \in A^{\prime}$
such that
![]() $N(a_1,C^{\prime})$
,
$N(a_1,C^{\prime})$
,
![]() $N(a_2, C^{\prime})$
and
$N(a_2, C^{\prime})$
and
![]() $N(a_3, C^{\prime})$
are pairwise disjoint and that there exists
$N(a_3, C^{\prime})$
are pairwise disjoint and that there exists
![]() $c_3 \in C^{\prime}$
such that
$c_3 \in C^{\prime}$
such that
![]() $N(c_1,A^{\prime})$
,
$N(c_1,A^{\prime})$
,
![]() $N(c_2, A^{\prime})$
and
$N(c_2, A^{\prime})$
and
![]() $N(c_3, A^{\prime})$
are pairwise disjoint. This implies that
$N(c_3, A^{\prime})$
are pairwise disjoint. This implies that
so
![]() $x \ge (3 \beta - 1)/2$
, and, by considering the sets
$x \ge (3 \beta - 1)/2$
, and, by considering the sets
![]() $N(a_1, C^{\prime})$
,
$N(a_1, C^{\prime})$
,
![]() $N(a_2, C^{\prime})$
and
$N(a_2, C^{\prime})$
and
![]() $N(a_3, C^{\prime})$
, we similarly have that
$N(a_3, C^{\prime})$
, we similarly have that
![]() $z \ge (3\beta - 1)/2$
. This implies that
$z \ge (3\beta - 1)/2$
. This implies that
Note that
![]() $|N(a_1, B) \cap N(a_2, B) \cap N(a_3, B)| \ge 3 \gamma n - 2|B| = (3 \gamma - 2)n \gt y n$
, so there exists
$|N(a_1, B) \cap N(a_2, B) \cap N(a_3, B)| \ge 3 \gamma n - 2|B| = (3 \gamma - 2)n \gt y n$
, so there exists
![]() $b \in N(a_1, B^{\prime}) \cap N(a_2, B^{\prime}) \cap N(a_3, B^{\prime})$
. Note that
$b \in N(a_1, B^{\prime}) \cap N(a_2, B^{\prime}) \cap N(a_3, B^{\prime})$
. Note that
![]() $N(b, C^{\prime})$
must be disjoint from
$N(b, C^{\prime})$
must be disjoint from
![]() $N(a_1, C^{\prime}) \cup N(a_2, C^{\prime}) \cup N(a_3, C^{\prime})$
so, since
$N(a_1, C^{\prime}) \cup N(a_2, C^{\prime}) \cup N(a_3, C^{\prime})$
so, since
![]() $N(a_1, C^{\prime})$
,
$N(a_1, C^{\prime})$
,
![]() $N(a_2, C^{\prime})$
and
$N(a_2, C^{\prime})$
and
![]() $N(a_3, C^{\prime})$
are pairwise disjoint,
$N(a_3, C^{\prime})$
are pairwise disjoint,
so
![]() $z \ge \beta - 1/6$
. But then
$z \ge \beta - 1/6$
. But then
![]() $1 \gt x + y + z \ge 1/3 + \gamma - 1/2 + \beta - 1/6 = 1$
, a contradiction.
$1 \gt x + y + z \ge 1/3 + \gamma - 1/2 + \beta - 1/6 = 1$
, a contradiction.
Claim 20.8.
For every
![]() $a \in A^{\prime}$
there exists
$a \in A^{\prime}$
there exists
![]() $i \in \{1, 2\}$
such that there is an
$i \in \{1, 2\}$
such that there is an
![]() $(a, c_i)$
-path in
$(a, c_i)$
-path in
![]() $G[A^{\prime},C^{\prime}]$
with at most
$G[A^{\prime},C^{\prime}]$
with at most
![]() $4$
vertices.
$4$
vertices.
Proof. Since
![]() $c_1a_2$
and
$c_1a_2$
and
![]() $c_2a_1$
are edges, we have the desired path if
$c_2a_1$
are edges, we have the desired path if
![]() $N(a, C^{\prime})$
intersects either
$N(a, C^{\prime})$
intersects either
![]() $N(a_1, C^{\prime})$
or
$N(a_1, C^{\prime})$
or
![]() $N(a_2, C^{\prime})$
. So assume otherwise, that is, assume that the sets
$N(a_2, C^{\prime})$
. So assume otherwise, that is, assume that the sets
![]() $N(a, C^{\prime})$
,
$N(a, C^{\prime})$
,
![]() $N(a_1, C^{\prime})$
and
$N(a_1, C^{\prime})$
and
![]() $N(a_2, C^{\prime})$
are pairwise disjoint. By Claim 20.2, there exists
$N(a_2, C^{\prime})$
are pairwise disjoint. By Claim 20.2, there exists
![]() $c \in N(a, C^{\prime})$
. Because
$c \in N(a, C^{\prime})$
. Because
![]() $N(c_1, A^{\prime})$
and
$N(c_1, A^{\prime})$
and
![]() $N(c_2, A^{\prime})$
are disjoint, Claim 20.7 implies that
$N(c_2, A^{\prime})$
are disjoint, Claim 20.7 implies that
![]() $N(c, A^{\prime})$
must intersect one of
$N(c, A^{\prime})$
must intersect one of
![]() $N(c_1, A^{\prime})$
or
$N(c_1, A^{\prime})$
or
![]() $N(c_2, A^{\prime})$
and this gives us the desired path.
$N(c_2, A^{\prime})$
and this gives us the desired path.
For
![]() $i \in \{1,2\}$
, let
$i \in \{1,2\}$
, let
![]() $A_i = N(c_i, A^{\prime})$
, let
$A_i = N(c_i, A^{\prime})$
, let
![]() $B_i \subseteq N(c_i, B^{\prime})$
such that
$B_i \subseteq N(c_i, B^{\prime})$
such that
![]() $|B_i| = \left \lceil (1/2 - y)n \right \rceil$
, and let
$|B_i| = \left \lceil (1/2 - y)n \right \rceil$
, and let
![]() $B_0 = B^{\prime} \setminus (B_1 \cup B_2)$
. Define
$B_0 = B^{\prime} \setminus (B_1 \cup B_2)$
. Define
![]() $\zeta = |B_1|/n = |B_2|/n$
, so
$\zeta = |B_1|/n = |B_2|/n$
, so
![]() $|B_0| \ge (1 - y - 2\zeta )n$
.
$|B_0| \ge (1 - y - 2\zeta )n$
.
Claim 20.9.
Every
![]() $a \in A_1 \cup A_2$
has at most
$a \in A_1 \cup A_2$
has at most
![]() $(1 - \gamma - \zeta )n$
non-neighbours in
$(1 - \gamma - \zeta )n$
non-neighbours in
![]() $B_0$
. Every
$B_0$
. Every
![]() $a \in A^{\prime} \setminus (A_1 \cup A_2)$
has at most
$a \in A^{\prime} \setminus (A_1 \cup A_2)$
has at most
![]() $2(1 - \gamma - \zeta )n$
non-neighbours in
$2(1 - \gamma - \zeta )n$
non-neighbours in
![]() $B_0$
.
$B_0$
.
Proof. Let
![]() $a \in A^{\prime}$
. First suppose
$a \in A^{\prime}$
. First suppose
![]() $a \in A_i = N(c_i, A^{\prime})$
for some
$a \in A_i = N(c_i, A^{\prime})$
for some
![]() $i \in \{1, 2\}$
, then
$i \in \{1, 2\}$
, then
![]() $a$
has no neighbours in
$a$
has no neighbours in
![]() $B_i$
, so
$B_i$
, so
Now assume that
![]() $a \in A^{\prime} \setminus (A_1 \cup A_2)$
. By Claim 20.8, there exists
$a \in A^{\prime} \setminus (A_1 \cup A_2)$
. By Claim 20.8, there exists
![]() $i \in \{1, 2\}$
,
$i \in \{1, 2\}$
,
![]() $c^{\prime} \in C^{\prime}$
and
$c^{\prime} \in C^{\prime}$
and
![]() $a^{\prime} \in A^{\prime}$
such that
$a^{\prime} \in A^{\prime}$
such that
![]() $ac^{\prime}a^{\prime}c_i$
is a path. Because
$ac^{\prime}a^{\prime}c_i$
is a path. Because
![]() $ac^{\prime}$
is an edge,
$ac^{\prime}$
is an edge,
![]() $a$
has no neighbours in
$a$
has no neighbours in
![]() $N_G(c^{\prime}, B^{\prime})$
, thus the number of non-neighbours of
$N_G(c^{\prime}, B^{\prime})$
, thus the number of non-neighbours of
![]() $a$
in
$a$
in
![]() $B\setminus N_G(c^{\prime}, B^{\prime})$
is at most
$B\setminus N_G(c^{\prime}, B^{\prime})$
is at most
so the number of non-neighbours of
![]() $a$
in
$a$
in
![]() $B_0 \setminus N_G(c^{\prime}, B_0) \subseteq B \setminus N_G\!\left(c^{\prime}, B\right)$
is at most
$B_0 \setminus N_G(c^{\prime}, B_0) \subseteq B \setminus N_G\!\left(c^{\prime}, B\right)$
is at most
![]() $(1 - \gamma - \zeta )n$
. To see that the number of non-neighbours of
$(1 - \gamma - \zeta )n$
. To see that the number of non-neighbours of
![]() $a$
in
$a$
in
![]() $N_G(c^{\prime}, B_0)$
is at most
$N_G(c^{\prime}, B_0)$
is at most
![]() $(1 - \gamma - \zeta )n$
(which proves the claim), note that
$(1 - \gamma - \zeta )n$
(which proves the claim), note that
![]() $N_G(c^{\prime}, B_0) \subseteq N_{\overline{G}}(a^{\prime}, B_0)$
(because
$N_G(c^{\prime}, B_0) \subseteq N_{\overline{G}}(a^{\prime}, B_0)$
(because
![]() $G$
is triangle-free) and, by the first part of the claim, the fact that
$G$
is triangle-free) and, by the first part of the claim, the fact that
![]() $a^{\prime} \in N(c_i, A^{\prime}) = A_i$
implies that
$a^{\prime} \in N(c_i, A^{\prime}) = A_i$
implies that
![]() $|N_{\overline{G}}(a^{\prime}, B_0)| \le (1 - \gamma - \zeta )n$
.
$|N_{\overline{G}}(a^{\prime}, B_0)| \le (1 - \gamma - \zeta )n$
.
Now we will estimate
![]() $e\!\left(\overline{G}[A^{\prime}, B_0]\right)$
from both sides. Recall that
$e\!\left(\overline{G}[A^{\prime}, B_0]\right)$
from both sides. Recall that
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are disjoint, so
$A_2$
are disjoint, so
![]() $|A_1 \cup A_2| \ge 2(\beta - x)n$
. This with Claim 20.9 implies
$|A_1 \cup A_2| \ge 2(\beta - x)n$
. This with Claim 20.9 implies
 \begin{align} \begin{split} e\!\left(\overline{G}[A^{\prime}, B_0]\right) &\le |A_1 \cup A_2|\cdot (1 - \gamma - \zeta )n + |A^{\prime} \setminus (A_1 \cup A_2)| \cdot 2(1 - \gamma - \zeta )n \\ & \le 2(\beta - x)(1 - \gamma - \zeta )n^2 + (1 - 2\beta + x) \cdot 2(1 - \gamma - \zeta )n^2 \\ &= 2(1 - \beta )(1 - \gamma - \zeta )n^2. \end{split} \end{align}
\begin{align} \begin{split} e\!\left(\overline{G}[A^{\prime}, B_0]\right) &\le |A_1 \cup A_2|\cdot (1 - \gamma - \zeta )n + |A^{\prime} \setminus (A_1 \cup A_2)| \cdot 2(1 - \gamma - \zeta )n \\ & \le 2(\beta - x)(1 - \gamma - \zeta )n^2 + (1 - 2\beta + x) \cdot 2(1 - \gamma - \zeta )n^2 \\ &= 2(1 - \beta )(1 - \gamma - \zeta )n^2. \end{split} \end{align}
(In (18), we used that
![]() $1 - \gamma - \zeta \ge 0$
, which is implied by Claim 20.9.) By Claim 20.2, for every
$1 - \gamma - \zeta \ge 0$
, which is implied by Claim 20.9.) By Claim 20.2, for every
![]() $b \in B_0$
there exists
$b \in B_0$
there exists
![]() $c \in N(b, C^{\prime})$
. Since
$c \in N(b, C^{\prime})$
. Since
![]() $N_{\overline{G}}(b, A^{\prime}) \supseteq N(c, A^{\prime})$
,
$N_{\overline{G}}(b, A^{\prime}) \supseteq N(c, A^{\prime})$
,
The conclusion then follows because (18) and (19) together yield
which has no solutions when
![]() $x \ge 1/3$
,
$x \ge 1/3$
,
![]() $1/3 \gt y \ge \gamma - 1/2$
,
$1/3 \gt y \ge \gamma - 1/2$
,
![]() $z \ge \beta - 1/4$
and
$z \ge \beta - 1/4$
and
![]() $\zeta \ge 1/2 - y$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.)
$\zeta \ge 1/2 - y$
. (See Appendix B in [Reference Ergemlidze and Molla2] for a proof of this fact.)
Acknowledgement
We thank the anonymous referee for their careful reading of the paper and their helpful comments which improved the presentation of this paper.
A. Proof of Lemma 13
Let
![]() $V_1, \dotsc, V_k$
be the parts of
$V_1, \dotsc, V_k$
be the parts of
![]() $G$
, let
$G$
, let
![]() $\ell \,:\!=\, k(t+1)$
, and let
$\ell \,:\!=\, k(t+1)$
, and let
![]() $\mathcal{A}$
be the set of all
$\mathcal{A}$
be the set of all
![]() $n^{\ell }$
sequences
$n^{\ell }$
sequences
![]() $a_1,\dotsc, a_{\ell }$
such that
$a_1,\dotsc, a_{\ell }$
such that
![]() $a_j \in V_i$
if
$a_j \in V_i$
if
![]() $j$
is equivalent to
$j$
is equivalent to
![]() $i$
modulo
$i$
modulo
![]() $k$
. Note that we do not require the vertices
$k$
. Note that we do not require the vertices
![]() $a_1, \dotsc,a_{\ell }$
to be distinct in this definition, so
$a_1, \dotsc,a_{\ell }$
to be distinct in this definition, so
![]() $|\mathcal{A}| = n^\ell$
.
$|\mathcal{A}| = n^\ell$
.
For every transversal
![]() $U$
, define
$U$
, define
![]() $\mathcal{A}_U$
to be the set of sequences in
$\mathcal{A}_U$
to be the set of sequences in
![]() $\mathcal{A}$
such that if
$\mathcal{A}$
such that if
![]() $A$
is the set of vertices in
$A$
is the set of vertices in
![]() $\mathcal{A}_U$
, the graph induced by
$\mathcal{A}_U$
, the graph induced by
![]() $A$
and the graph induced by
$A$
and the graph induced by
![]() $A \cup U$
both have a transversal
$A \cup U$
both have a transversal
![]() $C_k$
-factor. The probabilistic argument below relies critically on the fact that, for every transversal
$C_k$
-factor. The probabilistic argument below relies critically on the fact that, for every transversal
![]() $U$
, the set
$U$
, the set
![]() $\mathcal{A}_U$
is sufficiently large, and this follows from the fact that
$\mathcal{A}_U$
is sufficiently large, and this follows from the fact that
![]() $G$
is
$G$
is
![]() $(2 \eta, t)$
-linked. To see this, first label the vertices in
$(2 \eta, t)$
-linked. To see this, first label the vertices in
![]() $U$
as
$U$
as
![]() $u_1, \dotsc, u_k$
so that
$u_1, \dotsc, u_k$
so that
![]() $u_i \in V_i$
for
$u_i \in V_i$
for
![]() $i \in [k]$
. Because
$i \in [k]$
. Because
![]() $G$
is
$G$
is
![]() $(2\eta,t)$
-linked we easily have that there are at least
$(2\eta,t)$
-linked we easily have that there are at least
![]() $\eta n^k$
ways to select vertices
$\eta n^k$
ways to select vertices
![]() $c_1, \dotsc, c_k$
where
$c_1, \dotsc, c_k$
where
![]() $c_i \in V_i \setminus \{u_i\}$
for
$c_i \in V_i \setminus \{u_i\}$
for
![]() $i \in [k]$
that induce a transversal
$i \in [k]$
that induce a transversal
![]() $C_k$
in
$C_k$
in
![]() $G$
. Because
$G$
. Because
![]() $G$
is
$G$
is
![]() $(2\eta, t)$
-linked, iteratively, for
$(2\eta, t)$
-linked, iteratively, for
![]() $i$
from
$i$
from
![]() $1$
to
$1$
to
![]() $k$
, we can select a
$k$
, we can select a
![]() $(c_i, u_i, t)$
-linking sequence
$(c_i, u_i, t)$
-linking sequence
![]() $L_i$
that avoids all previously selected vertices in at least
$L_i$
that avoids all previously selected vertices in at least
![]() $\eta n^t$
ways. Since the graph induced by
$\eta n^t$
ways. Since the graph induced by
![]() $c_i$
and the vertices in
$c_i$
and the vertices in
![]() $L_i$
contains a transversal
$L_i$
contains a transversal
![]() $C_k$
-factor we have that
$C_k$
-factor we have that
![]() $(t+1)$
is divisible by
$(t+1)$
is divisible by
![]() $k$
and that there exists
$k$
and that there exists
![]() $S_i$
an ordering of these
$S_i$
an ordering of these
![]() $(t+1)$
vertices so that the
$(t+1)$
vertices so that the
![]() $j$
th vertex is in
$j$
th vertex is in
![]() $V_i$
if
$V_i$
if
![]() $j$
is equivalent to
$j$
is equivalent to
![]() $i$
modulo
$i$
modulo
![]() $k$
. Finally, because each
$k$
. Finally, because each
![]() $L_i$
is a
$L_i$
is a
![]() $(c_i, u_i, t)$
-linking sequence, the concatenation of the sequences
$(c_i, u_i, t)$
-linking sequence, the concatenation of the sequences
![]() $S_1, \dotsc, S_k$
is in
$S_1, \dotsc, S_k$
is in
![]() $\mathcal{A}_U$
, and we have that
$\mathcal{A}_U$
, and we have that
![]() $|\mathcal{A}_U| \ge \eta n^k \cdot \left(\eta n^t\right)^k = \eta ^{k+1} n^{\ell }$
.
$|\mathcal{A}_U| \ge \eta n^k \cdot \left(\eta n^t\right)^k = \eta ^{k+1} n^{\ell }$
.
Let
![]() $p \,:\!=\, 0.2 \cdot \sigma \cdot n^{-\ell + 1}$
and select the elements of
$p \,:\!=\, 0.2 \cdot \sigma \cdot n^{-\ell + 1}$
and select the elements of
![]() $\mathcal{A}$
independently with probability
$\mathcal{A}$
independently with probability
![]() $p$
to form the random set
$p$
to form the random set
![]() $\mathcal{A}_{\textrm{rand}}$
. The Chernoff and union bounds imply that with high probability
$\mathcal{A}_{\textrm{rand}}$
. The Chernoff and union bounds imply that with high probability
for every transversal
![]() $U \subseteq V(G)$
. Note that the number of pairs of sequences in
$U \subseteq V(G)$
. Note that the number of pairs of sequences in
![]() $\mathcal{A}$
in which a vertex is repeated is less than
$\mathcal{A}$
in which a vertex is repeated is less than
![]() $n \cdot \binom{2 \ell }{2} \cdot n^{2\ell - 2} = \binom{2 \ell }{2} n^{2\ell - 1}$
, so the expected number of pairs of sequences in
$n \cdot \binom{2 \ell }{2} \cdot n^{2\ell - 2} = \binom{2 \ell }{2} n^{2\ell - 1}$
, so the expected number of pairs of sequences in
![]() $\mathcal{A}_{\textrm{rand}}$
in which a vertex is repeated is less than
$\mathcal{A}_{\textrm{rand}}$
in which a vertex is repeated is less than
![]() $p^2 \cdot \binom{2 \ell }{2} n^{2\ell - 1} \le (\ell ^2 \sigma ^2 n)/4$
. So, by Markov’s inequality, with probability at least
$p^2 \cdot \binom{2 \ell }{2} n^{2\ell - 1} \le (\ell ^2 \sigma ^2 n)/4$
. So, by Markov’s inequality, with probability at least
![]() $1/2$
, if we add both elements from every such pair to form the set
$1/2$
, if we add both elements from every such pair to form the set
![]() $\mathcal{A}_{\textrm{rep}}$
we have that
$\mathcal{A}_{\textrm{rep}}$
we have that
Therefore, there exists an outcome in which both (20) and (21) hold. We form the collection
![]() $\mathcal{A}'$
from
$\mathcal{A}'$
from
![]() $\mathcal{A}_{\textrm{rand}}$
by removing all sequences that are in
$\mathcal{A}_{\textrm{rand}}$
by removing all sequences that are in
![]() $\mathcal{A}_{\textrm{rep}}$
and all sequences for which there does not exists a transversal
$\mathcal{A}_{\textrm{rep}}$
and all sequences for which there does not exists a transversal
![]() $U$
for which it is a linking sequence. Note that, by (20),
$U$
for which it is a linking sequence. Note that, by (20),
![]() $z: = |\mathcal{A}'| \le \sigma n$
and, by (20) and (21),
$z: = |\mathcal{A}'| \le \sigma n$
and, by (20) and (21),
![]() $|\mathcal{A}' \cap \mathcal{A}_U| \ge \sigma ^2 n$
for every transversal
$|\mathcal{A}' \cap \mathcal{A}_U| \ge \sigma ^2 n$
for every transversal
![]() $U \subseteq V(G)$
. Let
$U \subseteq V(G)$
. Let
![]() $A$
be the vertices that appear in a sequence of
$A$
be the vertices that appear in a sequence of
![]() $\mathcal{A}'$
. Because no vertex is repeated in
$\mathcal{A}'$
. Because no vertex is repeated in
![]() $\mathcal{A}'$
we have that
$\mathcal{A}'$
we have that
![]() $|A \cap V_i| = z$
for every
$|A \cap V_i| = z$
for every
![]() $i \in [k]$
, nd, because every sequence in
$i \in [k]$
, nd, because every sequence in
![]() $\mathcal{A}'$
is a linking sequence for some transversal
$\mathcal{A}'$
is a linking sequence for some transversal
![]() $U$
, for every sequence in
$U$
, for every sequence in
![]() $\mathcal{A}'$
the graph induced by the vertices in the sequence has a transversal
$\mathcal{A}'$
the graph induced by the vertices in the sequence has a transversal
![]() $C_k$
-factor.
$C_k$
-factor.
Suppose that there exists a transversal
![]() $C_k$
-tiling of
$C_k$
-tiling of
![]() $G - A$
that covers all of the vertices in
$G - A$
that covers all of the vertices in
![]() $V(G - A)$
except a set
$V(G - A)$
except a set
![]() $W$
such that
$W$
such that
![]() $|W| \le k \sigma ^2 n$
. We can arbitrarily partition
$|W| \le k \sigma ^2 n$
. We can arbitrarily partition
![]() $W$
into transversals
$W$
into transversals
![]() $U_1, \dotsc, U_m$
where
$U_1, \dotsc, U_m$
where
![]() $m = |W|/k \le \sigma ^2 n$
. Since for every
$m = |W|/k \le \sigma ^2 n$
. Since for every
![]() $i \in [m]$
, we have that
$i \in [m]$
, we have that
![]() $|\mathcal{A}_{U_i} \cap \mathcal{A}'| \ge \sigma ^2 n \ge m$
, we can greedily select distinct sequences
$|\mathcal{A}_{U_i} \cap \mathcal{A}'| \ge \sigma ^2 n \ge m$
, we can greedily select distinct sequences
![]() $A_1, \dotsc, A_m$
such that
$A_1, \dotsc, A_m$
such that
![]() $A_i \in \mathcal{A}_{U_i} \cap \mathcal{A}'$
for every
$A_i \in \mathcal{A}_{U_i} \cap \mathcal{A}'$
for every
![]() $i \in [m]$
. This implies that there is a transversal
$i \in [m]$
. This implies that there is a transversal
![]() $C_k$
-factor of
$C_k$
-factor of
![]() $G[W \cup A]$
and, therefore, a transversal
$G[W \cup A]$
and, therefore, a transversal
![]() $C_k$
-factor of
$C_k$
-factor of
![]() $G$
.
$G$
.