Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-11T07:17:13.803Z Has data issue: false hasContentIssue false
  • English
  • Français

Star Versus Two Stripes Ramsey Numbers and a Conjecture of Schelp

Published online by Cambridge University Press:  02 February 2012

ANDRÁS GYÁRFÁS  and
GÁBOR N. SÁRKÖZY
ANDRÁS GYÁRFÁS
Affiliation:
Computer and Automation Research Institute, Hungarian Academy of Sciences, PO Box 63, Budapest, H-1518Hungary (e-mail: gyarfas2@gmail.com)
GÁBOR N. SÁRKÖZY
Affiliation:
Computer and Automation Research Institute, Hungarian Academy of Sciences, PO Box 63, Budapest, H-1518Hungary (e-mail: gyarfas2@gmail.com) Computer Science Department, Worcester Polytechnic Institute, Worcester, MA 01609, USA (e-mail: gsarkozy@cs.wpi.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

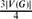R. H. Schelp conjectured that if G is a graph with |V(G)| = R(Pn, Pn) such that δ(G) > , then in every 2-colouring of the edges of G there is a monochromatic Pn. In other words, the Ramsey number of a path does not change if the graph to be coloured is not complete but has large minimum degree.

Here we prove Ramsey-type results that imply the conjecture in a weakened form, first replacing the path by a matching, showing that the star-matching–matching Ramsey number satisfying R(Sn, nK2, nK2) = 3n − 1. This extends R(nK2, nK2) = 3n − 1, an old result of Cockayne and Lorimer. Then we extend this further from matchings to connected matchings, and outline how this implies Schelp's conjecture in an asymptotic sense through a standard application of the Regularity Lemma.

It is sad that we are unable to hear Dick Schelp's reaction to our work generated by his conjecture.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 179 - 186
Copyright
Copyright © Cambridge University Press 2012

References

[1]Benevides, F. S., Łuczak, T., Scott, A., Skokan, J. and White, M. (2012) Monochromatic cycles in 2-coloured graphs. Combin. Probab. Comput. 21 57–87.Google Scholar
[2]Benevides, F. S. and Skokan, J. (2009) The 3-colored Ramsey number of even cycles. J. Combin. Theory Ser. B 99 690–708.CrossRefGoogle Scholar
[3]Cockayne, E. J. and Lorimer, P. J. (1975) The Ramsey number for stripes. J. Austral. Math. Soc. 19 252–256.CrossRefGoogle Scholar
[4]Cockayne, E. J. and Lorimer, P. J. (1975) On Ramsey graph numbers for stars and stripes. Canadian Math. Bull. 18 31–34.CrossRefGoogle Scholar
[5]Erdős, P. and Pósa, L. (1962) On the maximal number of disjoint circuits of a graph. Publ. Math. Debrecen 9 3–13.CrossRefGoogle Scholar
[6]Figaj, A. and Łuczak, T. (2007) The Ramsey number for a triple of long even cycles. J. Combin. Theory Ser. B 97 584–596.CrossRefGoogle Scholar
[7]Gerencsér, L. and Gyárfás, A. (1967) On Ramsey type problems. Ann. Univ. Sci. Eötvös, Budapest 10 167–170.Google Scholar
[8]Gyárfás, A. (2010) Large monochromatic components in edge colorings of graphs: A survey. In Ramsey Theory: Yesterday, Today and Tomorrow (Soifer, A., ed.), Birkhäuser, pp. 77–96.Google Scholar
[9]Gyárfás, A., Lehel, J., Sárközy, G. N. and Schelp, R. H. (2008) Monochromatic Hamiltonian Berge cycles in colored complete hypergraphs. J. Combin. Theory Ser. B 98 342–358.CrossRefGoogle Scholar
[10]Gyárfás, A., Ruszinkó, M., Sárközy, G. N. and Szemerédi, E. (2007) Tripartite Ramsey numbers for paths. J. Graph Theory 55 164–170.CrossRefGoogle Scholar
[11]Gyárfás, A., Ruszinkó, M., Sárközy, G. N. and Szemerédi, E. (2007) Three-color Ramsey numbers for paths. Combinatorica 27 35–69.CrossRefGoogle Scholar
[12]Komlós, J. and Simonovits, M. (1996) Szemerédi's Regularity Lemma and its applications in Graph Theory. In Combinatorics: Paul Erdős is Eighty (Miklós, D., Sós, V. T. and Szőnyi, T., eds), Vol. 2 of Bolyai Society Mathematical Studies, pp. 295–352.Google Scholar
[13]Łuczak, T. (1999) R(Cn, Cn, Cn) ≤ (4 + o(1))n. J. Combin. Theory Ser. B 75 174–187.CrossRefGoogle Scholar
[14]Sárközy, G. N. (2008) On 2-factors with k components. Discrete Math. 308 1962–1972.CrossRefGoogle Scholar
[15]Schelp, R. H. Some Ramsey–Turán type problems and related questions. Manuscript, to appear in a special volume of Discrete Math.Google Scholar
[16]Schelp, R. H. A minimum degree condition on a Ramsey graph which arrows a path. Unpublished.Google Scholar
[17]Szemerédi, E. (1978) Regular partitions of graphs. In Problèmes Combinatoires et Théorie des Graphes: Orsay 1976, Vol. 260 of Colloques Internationaux CNRS, pp. 399–401.Google Scholar