Published online by Cambridge University Press: 19 September 2016
We say a graph is (Qn,Qm)-saturated if it is a maximal Qm-free subgraph of the n-dimensional hypercube Qn. A graph is said to be (Qn,Qm)-semi-saturated if it is a subgraph of Qn and adding any edge forms a new copy of Qm. The minimum number of edges a (Qn,Qm)-saturated graph (respectively (Qn,Qm)-semi-saturated graph) can have is denoted by sat(Qn,Qm) (respectively s-sat(Qn,Qm)). We prove that
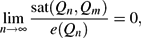 $$
\begin{linenomath}
\lim_{n\to\infty}\ffrac{\sat(Q_n,Q_m)}{e(Q_n)}=0,
\end{linenomath}$$
$$
\begin{linenomath}
\lim_{n\to\infty}\ffrac{\sat(Q_n,Q_m)}{e(Q_n)}=0,
\end{linenomath}$$
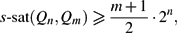 $$
\begin{linenomath}
\ssat(Q_n,Q_m)\geq \ffrac{m+1}{2}\cdot 2^n,
\end{linenomath}$$
$$
\begin{linenomath}
\ssat(Q_n,Q_m)\geq \ffrac{m+1}{2}\cdot 2^n,
\end{linenomath}$$