Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T19:02:03.733Z Has data issue: false hasContentIssue false
  • English
  • Français

Planting Colourings Silently

Part of: Graph theory

Published online by Cambridge University Press:  07 December 2016

VICTOR BAPST ,
AMIN COJA-OGHLAN  and
CHARILAOS EFTHYMIOU
VICTOR BAPST
Affiliation:
Mathematics Institute, Goethe University, 10 Robert Mayer St, Frankfurt 60325, Germany (e-mail: bapst@math.uni-frankfurt.de, acoghlan@math.uni-frankfurt.de, efthymiou@math.uni-frankfurt.de)
AMIN COJA-OGHLAN
Affiliation:
Mathematics Institute, Goethe University, 10 Robert Mayer St, Frankfurt 60325, Germany (e-mail: bapst@math.uni-frankfurt.de, acoghlan@math.uni-frankfurt.de, efthymiou@math.uni-frankfurt.de)
CHARILAOS EFTHYMIOU
Affiliation:
Mathematics Institute, Goethe University, 10 Robert Mayer St, Frankfurt 60325, Germany (e-mail: bapst@math.uni-frankfurt.de, acoghlan@math.uni-frankfurt.de, efthymiou@math.uni-frankfurt.de)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k ⩾ 3 be a fixed integer and let Zk(G) be the number of k-colourings of the graph G. For certain values of the average degree, the random variable Zk(G(n, m)) is known to be concentrated in the sense that 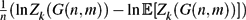$\tfrac{1}{n}(\ln Z_k(G(n,m))-\ln\Erw[Z_k(G(n,m))])$ converges to 0 in probability (Achlioptas and Coja-Oghlan, Proc. FOCS 2008). In the present paper we prove a significantly stronger concentration result. Namely, we show that for a wide range of average degrees, 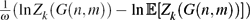$\tfrac{1}{\omega}(\ln Z_k(G(n,m))-\ln\Erw[Z_k(G(n,m))])$ converges to 0 in probability for any diverging function 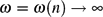$\omega=\omega(n)\ra\infty$. For k exceeding a certain constant k0 this result covers all average degrees up to the so-called condensation phase transitiondk,con, and this is best possible. As an application, we show that the experiment of choosing a k-colouring of the random graph G(n,m) uniformly at random is contiguous with respect to the so-called ‘planted model’.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C15: Coloring of graphs and hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 3 , May 2017 , pp. 338 - 366
Copyright
Copyright © Cambridge University Press 2016 

References

[1] Achlioptas, D. and Coja-Oghlan, A. (2008) Algorithmic barriers from phase transitions. In Proc. 49th FOCS, pp. 793–802.Google Scholar
[2] Achlioptas, D. and Friedgut, E. (1999) A sharp threshold for k-colorability. Random Struct. Alg. 14 63–70.3.0.CO;2-7>CrossRefGoogle Scholar
[3] Achlioptas, D. and Molloy, M. (1997) The analysis of a list-coloring algorithm on a random graph. In Proc. 38th FOCS, pp. 204–212.CrossRefGoogle Scholar
[4] Achlioptas, D. and Moore, C. (2004) The chromatic number of random regular graphs. In Proc. 8th RANDOM, pp. 219–228.Google Scholar
[5] Achlioptas, D. and Naor, A. (2005) The two possible values of the chromatic number of a random graph. Ann. of Math. 162 1333–1349.Google Scholar
[6] Alon, N. and Krivelevich, M. (1997) The concentration of the chromatic number of random graphs. Combinatorica 17 303–313.Google Scholar
[7] Banks, J. and Moore, C. Information-theoretic thresholds for community detection in sparse networks. arXiv:1601.02658 Google Scholar
[8] Bapst, V., Coja-Oghlan, A., Hetterich, S., Raßmann, F. and Vilenchik, D. (2016) The condensation phase transition in random graph coloring. Comm. Math. Phys. 341 543–606.Google Scholar
[9] Bollobás, B. (1988) The chromatic number of random graphs. Combinatorica 8 49–55 CrossRefGoogle Scholar
[10] Bollobás, B. (2001) Random Graphs, second edition, Cambridge University Press.Google Scholar
[11] Coja-Oghlan, A. (2013) Upper-bounding the k-colorability threshold by counting covers. Electron. J. Combin. 20 P32.CrossRefGoogle Scholar
[12] Coja-Oghlan, A., Efthymiou, C. and Hetterich, S. (2016) On the chromatic number of random regular graphs. J. Combin. Theory Ser. B 116 367–439.Google Scholar
[13] Coja-Oghlan, A. and Pachon-Pinzon, A. Y. (2012) The decimation process in random k-SAT. SIAM J. Discrete Math. 26 1471–1509.Google Scholar
[14] Coja-Oghlan, A. and Panagiotou, K. (2016) Going after the k-SAT threshold. In Proc. 45th STOC 2013, pp. 705–714, and Adv. Math. 288 985–1068.Google Scholar
[15] Coja-Oghlan, A. and Vilenchik, D. (2013) Chasing the k-colorability threshold. In Proc. 54th FOCS, pp. 380–389. A full version is available as arXiv:1304.1063 Google Scholar
[16] Efthymiou, C. (2014) Switching colouring of G(n, d/n) for sampling up to Gibbs uniqueness threshold. In Proc. 22nd ESA, pp. 371–281.Google Scholar
[17] Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5 17–61.Google Scholar
[18] Grimmett, G. and McDiarmid, C. (1975) On colouring random graphs. Math. Proc. Cambridge Phil. Soc. 77 313–324 Google Scholar
[19] Janson, S. (1995) Random regular graphs: Asymptotic distributions and contiguity. Combin. Probab. Comput. 4 369–405.CrossRefGoogle Scholar
[20] Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.Google Scholar
[21] Kemkes, G., Perez-Gimenez, X. and Wormald, N. (2010) On the chromatic number of random d-regular graphs. Adv. Math. 223 300–328.Google Scholar
[22] Krivelevich, M. and Sudakov, B. (1998) Coloring random graphs. Inform. Process. Lett. 67 71–74 Google Scholar
[23] Krzakala, F., Montanari, A., Ricci-Tersenghi, F., Semerjian, G. and Zdeborova, L. (2007) Gibbs states and the set of solutions of random constraint satisfaction problems. Proc. Nat. Acad. Sci. 104 10318–10323.Google Scholar
[24] Krzakala, F., Pagnani, A. and Weigt, M. (2004) Threshold values, stability analysis and high-q asymptotics for the coloring problem on random graphs. Phys. Rev. E 70 046705.Google Scholar
[25] Krzakala, F. and Zdeborová, L. (2009) Hiding quiet solutions in random constraint satisfaction problems. Phys. Rev. Lett. 102 238701.CrossRefGoogle ScholarPubMed
[26] Łuczak, T. (1991) The chromatic number of random graphs. Combinatorica 11 45–54 Google Scholar
[27] Łuczak, T. (1991) A note on the sharp concentration of the chromatic number of random graphs. Combinatorica 11 295–297 CrossRefGoogle Scholar
[28] Matula, D. (1987) Expose-and-merge exploration and the chromatic number of a random graph. Combinatorica 7 275–284.Google Scholar
[29] McDiarmid, C. (1998) Concentration. In Probabilistic Methods for Algorithmic Discrete Mathematics (Habib, M. et al., eds), Springer, pp. 195–248.Google Scholar
[30] Mézard, M. and Montanari, A. (2009) Information, Physics and Computation, Oxford University Press.Google Scholar
[31] Molloy, M. (2012) The freezing threshold for k-colourings of a random graph. In Proc. 43rd STOC, pp. 921–930.Google Scholar
[32] Molloy, M. and Restrepo, R. (2013) Frozen variables in random boolean constraint satisfaction problems. In Proc. 24th SODA, pp. 1306–1318.Google Scholar
[33] Montanari, A., Restrepo, R. and Tetali, P. (2011) Reconstruction and clustering in random constraint satisfaction problems. SIAM J. Discrete Math. 25 771–808.Google Scholar
[34] Mulet, R., Pagnani, A., Weigt, M. and Zecchina, R. (2002) Coloring random graphs. Phys. Rev. Lett. 89 268701.Google Scholar
[35] Neeman, J. and Netrapalli, P. Non-reconstructability in the stochastic block model. arXiv:1404.6304 Google Scholar
[36] Robinson, R. and Wormald, N. (1994) Almost all regular graphs are Hamiltonian. Random Struct. Alg. 5 363–374.Google Scholar
[37] Shamir, E. and Spencer, J. (1987) Sharp concentration of the chromatic number of random graphs G(n, p). Combinatorica 7 121–129 Google Scholar
[38] Zdeborová, L. and Krzakala, F. (2007) Phase transition in the coloring of random graphs. Phys. Rev. E 76 031131.Google Scholar