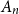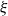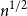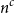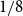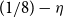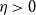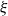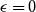1. Introduction
Let
![]() $M_{n}$
denote an
$M_{n}$
denote an
![]() $n\times n$
random matrix, each of whose entries is an independent copy of a sub-Gaussian random variable
$n\times n$
random matrix, each of whose entries is an independent copy of a sub-Gaussian random variable
![]() $\xi$
with mean 0 and variance 1. Prominent well-studied examples include the Ginibre ensemble (corresponding to
$\xi$
with mean 0 and variance 1. Prominent well-studied examples include the Ginibre ensemble (corresponding to
![]() $\xi = \mathcal{N}(0,1)$
) and i.i.d. Rademacher matrices (corresponding to the Rademacher random variable
$\xi = \mathcal{N}(0,1)$
) and i.i.d. Rademacher matrices (corresponding to the Rademacher random variable
![]() $\xi = \pm 1$
with probability
$\xi = \pm 1$
with probability
![]() $1/2$
each).
$1/2$
each).
A landmark result of Rudelson and Vershynin [Reference Rudelson and Vershynin26] shows that there are absolute constants
![]() $C, c > 0$
, depending only on the sub-Gaussian norm of
$C, c > 0$
, depending only on the sub-Gaussian norm of
![]() $\xi$
, for which
$\xi$
, for which
where
![]() $s_n(M_n) = \inf_{v \in \mathbb{S}^{n-1}}\lVert{Mv}_2\rVert$
denotes the smallest singular value of
$s_n(M_n) = \inf_{v \in \mathbb{S}^{n-1}}\lVert{Mv}_2\rVert$
denotes the smallest singular value of
![]() $M_n$
. Up to the constants
$M_n$
. Up to the constants
![]() $C, c > 0$
, the above result is optimal, as can be seen by considering the two examples mentioned above. In particular, this result shows that the probability that an i.i.d. Rademacher matrix is singular is at most
$C, c > 0$
, the above result is optimal, as can be seen by considering the two examples mentioned above. In particular, this result shows that the probability that an i.i.d. Rademacher matrix is singular is at most
![]() $2\exp(\!-\!cn)$
(for some
$2\exp(\!-\!cn)$
(for some
![]() $c > 0$
), thereby recovering (and substantially generalising) a well-known result of Kahn, Komlós, and Szemerédi [Reference Kahn, Komlós and Szemerédi13]. We remark that after a series of intermediate works [Reference Bourgain, Vu and Wood2, Reference Tao and Vu27, Reference Tao and Vu28], a breakthrough result of Tikhomirov [Reference Tikhomirov29] established that the probability of singularity of an i.i.d. Rademacher matrix is at most
$c > 0$
), thereby recovering (and substantially generalising) a well-known result of Kahn, Komlós, and Szemerédi [Reference Kahn, Komlós and Szemerédi13]. We remark that after a series of intermediate works [Reference Bourgain, Vu and Wood2, Reference Tao and Vu27, Reference Tao and Vu28], a breakthrough result of Tikhomirov [Reference Tikhomirov29] established that the probability of singularity of an i.i.d. Rademacher matrix is at most
![]() $(1/2 + o_n(1))^{n}$
, which is optimal up to the
$(1/2 + o_n(1))^{n}$
, which is optimal up to the
![]() $o_n(1)$
term.
$o_n(1)$
term.
In this paper, we will be concerned with
![]() $n\times n$
symmetric random matrices
$n\times n$
symmetric random matrices
![]() $A_{n}$
i.e.
$A_{n}$
i.e.
![]() $(A_{n})_{ij} = (A_{n})_{ji}$
, each of whose entries on and above the diagonal is an independent copy of a sub-Gaussian random variable
$(A_{n})_{ij} = (A_{n})_{ji}$
, each of whose entries on and above the diagonal is an independent copy of a sub-Gaussian random variable
![]() $\xi$
with mean 0 and variance 1. We note that the identical distribution assumption may be significantly relaxed (in particular, allowing for the diagonal entries to have a different distribution), although for the sake of simplicity, we do not deal with this modification here; the interested reader is referred to [Reference Livshyts, Tikhomirov and Vershynin16, Reference Vershynin30].
$\xi$
with mean 0 and variance 1. We note that the identical distribution assumption may be significantly relaxed (in particular, allowing for the diagonal entries to have a different distribution), although for the sake of simplicity, we do not deal with this modification here; the interested reader is referred to [Reference Livshyts, Tikhomirov and Vershynin16, Reference Vershynin30].
While symmetric matrices are especially convenient to work with linear algebraically, the lack of independence between the entries of
![]() $A_{n}$
makes the non-asymptotic study of its smallest singular value considerably more challenging than that of
$A_{n}$
makes the non-asymptotic study of its smallest singular value considerably more challenging than that of
![]() $M_{n}$
. In the early 1990s, it was conjectured by Weiss that
$M_{n}$
. In the early 1990s, it was conjectured by Weiss that
![]() $A_n(\!\operatorname{Rad}\!)$
(i.e.
$A_n(\!\operatorname{Rad}\!)$
(i.e.
![]() $A_n$
where
$A_n$
where
![]() $\xi$
is a Rademacher random variable) is invertible with probability
$\xi$
is a Rademacher random variable) is invertible with probability
![]() $1-o_n(1)$
. This was only resolved in 2005 by Costello, Tao, and Vu [Reference Costello, Tao and Vu6], despite the corresponding statement for
$1-o_n(1)$
. This was only resolved in 2005 by Costello, Tao, and Vu [Reference Costello, Tao and Vu6], despite the corresponding statement for
![]() $M_n$
(due to Komlós [Reference Komlós14]) having been established almost 40 years prior (see also [Reference Ferber8] for a recent simple proof).
$M_n$
(due to Komlós [Reference Komlós14]) having been established almost 40 years prior (see also [Reference Ferber8] for a recent simple proof).
Vershynin [Reference Vershynin30] showed that for any sub-Gaussian random variable
![]() $\xi$
with mean 0 and variance 1, there are constants
$\xi$
with mean 0 and variance 1, there are constants
![]() $c, C_\eta$
depending only on the sub-Gaussian norm of
$c, C_\eta$
depending only on the sub-Gaussian norm of
![]() $\xi$
such that
$\xi$
such that
This improves (and generalizes) the nearly concurrent estimate of
![]() $O_{C}(n^{-C})$
on the singularity probability of
$O_{C}(n^{-C})$
on the singularity probability of
![]() $A_n(\!\operatorname{Rad}\!)$
obtained by Nguyen [Reference Nguyen21] using a novel quadratic variant of the inverse Littlewood–Offord theory. We note that in a subsequent work [Reference Nguyen22], Nguyen obtained estimates on the lower tail of
$A_n(\!\operatorname{Rad}\!)$
obtained by Nguyen [Reference Nguyen21] using a novel quadratic variant of the inverse Littlewood–Offord theory. We note that in a subsequent work [Reference Nguyen22], Nguyen obtained estimates on the lower tail of
![]() $s_n(A_n)$
for a large class of random variables
$s_n(A_n)$
for a large class of random variables
![]() $\xi$
, including those not covered by [Reference Vershynin30], although the quantitative bounds in this work are much weaker than (2).
$\xi$
, including those not covered by [Reference Vershynin30], although the quantitative bounds in this work are much weaker than (2).
Recently, the upper bound on the singularity probability of
![]() $A_n(\!\operatorname{Rad}\!)$
has been improved in a couple of works. Building on novel combinatorial techniques in [Reference Ferber, Jain, Luh and Samotij10], it was shown by Ferber and Jain [Reference Ferber and Jain9] that this probability is at most
$A_n(\!\operatorname{Rad}\!)$
has been improved in a couple of works. Building on novel combinatorial techniques in [Reference Ferber, Jain, Luh and Samotij10], it was shown by Ferber and Jain [Reference Ferber and Jain9] that this probability is at most
![]() $\exp(\!-\Omega(n^{1/4}\sqrt{\log{n}}))$
. Subsequently, using a different combinatorial method inspired by the method of hypergraph containers [Reference Balogh, Morris and Samotij1], Campos, Mattos, Morris, and Morrison improved the bound to
$\exp(\!-\Omega(n^{1/4}\sqrt{\log{n}}))$
. Subsequently, using a different combinatorial method inspired by the method of hypergraph containers [Reference Balogh, Morris and Samotij1], Campos, Mattos, Morris, and Morrison improved the bound to
![]() $\exp(\!-\Omega(\sqrt{n}))$
. We note that both of these works deal only with
$\exp(\!-\Omega(\sqrt{n}))$
. We note that both of these works deal only with
![]() $A_n(\!\operatorname{Rad}\!)$
, and only with the singularity probability as opposed to quantitative estimates on
$A_n(\!\operatorname{Rad}\!)$
, and only with the singularity probability as opposed to quantitative estimates on
![]() $s_n(A_n(\!\operatorname{Rad}\!))$
.
$s_n(A_n(\!\operatorname{Rad}\!))$
.
The first main result of this paper is a strengthening of (2); the quantitative bounds are sufficiently powerful to generalize the aforementioned result of Campos et al. to all sub-Gaussian random variables.
Theorem 1.1 Let
![]() $A_n$
denote an
$A_n$
denote an
![]() $n\times n$
random symmetric matrix, each of whose entries on and above the diagonal is an independent copy of a sub-Gaussian random variable
$n\times n$
random symmetric matrix, each of whose entries on and above the diagonal is an independent copy of a sub-Gaussian random variable
![]() $\xi$
with mean 0 and variance 1. Then, there are constants
$\xi$
with mean 0 and variance 1. Then, there are constants
![]() $C_{1.1}, c_{1.1}$
depending only on the sub-Gaussian norm of
$C_{1.1}, c_{1.1}$
depending only on the sub-Gaussian norm of
![]() $\xi$
such that, for all
$\xi$
such that, for all
![]() $\epsilon \ge 0$
,
$\epsilon \ge 0$
,
Next, we consider the particularly well-studied case
![]() $\xi = \operatorname{Rad}$
; setting
$\xi = \operatorname{Rad}$
; setting
![]() $\epsilon = 0$
in the theorem below improves the result of Campos et al. (see (3) in the Remark below).
$\epsilon = 0$
in the theorem below improves the result of Campos et al. (see (3) in the Remark below).
Theorem 1.2 Let
![]() $A_n$
denote an
$A_n$
denote an
![]() $n\times n$
random symmetric matrix, each of whose entries on and above the diagonal is an independent Rademacher random variable. Then, there are absolute constants
$n\times n$
random symmetric matrix, each of whose entries on and above the diagonal is an independent Rademacher random variable. Then, there are absolute constants
![]() $C_{1.2}, c_{1.2}$
such that, for all
$C_{1.2}, c_{1.2}$
such that, for all
![]() $\epsilon \ge 0$
,
$\epsilon \ge 0$
,
Remark
-
1. We note that Theorem 1.2 can be extended to the setting of discrete random variables covered in recent work of the authors [Reference Jain, Sah and Sawhney11]. We leave the details to an interested reader.
-
2. The
 $\epsilon^{1/8}$
term on the right-hand side in Theorem 1.1 improves on the
$\epsilon^{1/8}$
term on the right-hand side in Theorem 1.1 improves on the
 $\epsilon^{1/8 + \eta}$
in [Reference Vershynin30]. It is believed that the correct dependence on
$\epsilon^{1/8 + \eta}$
in [Reference Vershynin30]. It is believed that the correct dependence on
 $\epsilon$
is
$\epsilon$
is
 $O(\epsilon)$
, which would be optimal in light of the Gaussian example.
$O(\epsilon)$
, which would be optimal in light of the Gaussian example. -
3. The term
 $\exp(\!-\Omega(n^{1/2}))$
on the right-hand side in Theorem 1.1 extends the result of Campos, Mattos, Morris, and Morrison to general sub-Gaussian random variables, whereas Theorem 1.2 improves this result by a factor of
$\exp(\!-\Omega(n^{1/2}))$
on the right-hand side in Theorem 1.1 extends the result of Campos, Mattos, Morris, and Morrison to general sub-Gaussian random variables, whereas Theorem 1.2 improves this result by a factor of
 $(\!\log n)^{1/4}$
in the exponent, in the special case when
$(\!\log n)^{1/4}$
in the exponent, in the special case when
 $\xi = \operatorname{Rad}$
. A well-known conjecture is that one should be able to replace this with
$\xi = \operatorname{Rad}$
. A well-known conjecture is that one should be able to replace this with
 $\exp(\!-\Omega(n))$
, although this will likely require significant new ideas.
$\exp(\!-\Omega(n))$
, although this will likely require significant new ideas.
Our proof follows the geometric framework for studying the smallest singular value of random matrices, pioneered by Rudelson and Vershynin [Reference Rudelson and Vershynin26] for random matrices with i.i.d. entries (see the notes [Reference Rudelson25] for a highly readable introduction) and adapted for random symmetric matrices by Vershynin [Reference Vershynin30]. For the purpose of studying the singularity probability, the key ingredient in this framework is to identify an appropriate quantitative notion of arithmetic structure of vectors on the unit sphere, which on the one hand controls the anti-concentration properties of the vector and on the other hand permits the construction of sufficiently small epsilon-nets for its sub-level sets. In the seminal work of Rudelson and Vershynin [Reference Rudelson and Vershynin26], the (essential) Least Common Denominator (LCD) plays this role, crucially relying on the independence of the rows of the matrix in order to ‘tensorize’ the corresponding anti-concentration estimates. For the study of random symmetric matrices, where the rows are highly dependent, the LCD proves to be insufficient. Consequently, Vershynin [Reference Vershynin30] introduced the notion of the RLCD, which allows a limited amount of tensorization of the corresponding anti-concentration estimates, but at the cost of being able to take advantage of only a very small amount of randomness in the matrix.
The main innovation in our work are new notions of arithmetic structure of vectors, which we call the MRLCD (see Section 3) and the Median Threshold (see Section 4). Compared to the RLCD and its natural threshold analogue, the MRLCD and median threshold are able to exploit the information that many different coordinate projections (i.e. subvectors) of a vector are arithmetically unstructured in a simple and transparent manner, thereby allowing us to take advantage of substantially more randomness in the matrix compared to [Reference Vershynin30]. Moreover, we are able to show that level sets of the MRLCD and median threshold admit sufficiently small nets at the appropriate scale – for the MRLCD, this follows by suitably adapting by-now standard bounds due to Rudelson and Vershynin [Reference Rudelson and Vershynin26], whereas for the median threshold, we adapt work of Tikhomirov [Reference Tikhomirov29] on the singularity of i.i.d Bernoulli random matrices. As the details are anyway short, we defer further discussion to Sections 3 and 4.
We note that since its first appearance in [Reference Vershynin30], the RLCD has been used in many works (see, e.g., [Reference Lopatto and Luh17, Reference Luh and Vu18, Reference Nguyen, Tao and Vu20, Reference O’Rourke and Touri23, Reference Wei31]); the MRLCD (and median threshold, for discrete distributions) can replace these applications in a black-box manner, and likely lead to improved quantitative estimates. We also note that a related use of combinatorially incorporating arithmetic unstructure of different projections of a vector appeared in recent work of the authors [Reference Jain, Sah and Sawhney12] on the probability of singularity of the adjacency matrix of random regular digraphs; however, the interaction with both the net and anticoncentration estimates is more delicate here.
1.1 Notation
We will drop the dimension in the subscript, henceforth denoting
![]() $A_n$
by A, and denoting its rows by
$A_n$
by A, and denoting its rows by
![]() $A_1,\dots,A_n$
. For an integer N,
$A_1,\dots,A_n$
. For an integer N,
![]() $\mathbb{S}^{N-1}$
denotes the set of unit vectors in
$\mathbb{S}^{N-1}$
denotes the set of unit vectors in
![]() $\mathbb{R}^{N}$
, and
$\mathbb{R}^{N}$
, and
![]() $\mathbb{B}_2^N$
denotes the unit ball in
$\mathbb{B}_2^N$
denotes the unit ball in
![]() $\mathbb{R}^{N}$
(i.e., the set of vectors of Euclidean norm at most 1).
$\mathbb{R}^{N}$
(i.e., the set of vectors of Euclidean norm at most 1).
![]() $\lVert{\cdot}_2\rVert$
denotes the standard Euclidean norm of a vector, and for a matrix
$\lVert{\cdot}_2\rVert$
denotes the standard Euclidean norm of a vector, and for a matrix
![]() $A = (a_{ij})$
,
$A = (a_{ij})$
,
![]() $\lVert{A}\rVert$
is its spectral norm (i.e.,
$\lVert{A}\rVert$
is its spectral norm (i.e.,
![]() $\ell^{2} \to \ell^{2}$
operator norm), and
$\ell^{2} \to \ell^{2}$
operator norm), and
![]() $\lVert{A}_{\operatorname{HS}}\rVert$
is its Hilbert-Schmidt norm, defined by
$\lVert{A}_{\operatorname{HS}}\rVert$
is its Hilbert-Schmidt norm, defined by
![]() $\lVert{A}_{\operatorname{HS}}^{2}\rVert = \sum_{i,j}a_{ij}^{2}$
.
$\lVert{A}_{\operatorname{HS}}^{2}\rVert = \sum_{i,j}a_{ij}^{2}$
.
We will let [N] denote the interval
![]() $\{1,\dots, N\}$
,
$\{1,\dots, N\}$
,
![]() $\mathfrak{S}_{[N]}$
denote the set of permutations of [N], and
$\mathfrak{S}_{[N]}$
denote the set of permutations of [N], and
![]() $\binom{[N]}{k}$
denote the set of subsets of [N] of size exactly k. We will denote multisets by
$\binom{[N]}{k}$
denote the set of subsets of [N] of size exactly k. We will denote multisets by
![]() $\{\{\}\}$
, so that
$\{\{\}\}$
, so that
![]() $\{\{a_1,\dots, a_{n}\}\}$
, with the
$\{\{a_1,\dots, a_{n}\}\}$
, with the
![]() $a_i$
’s possibly repeated, is a multi-set of size n. For a vector
$a_i$
’s possibly repeated, is a multi-set of size n. For a vector
![]() $v \in \mathbb{R}^{N}$
and
$v \in \mathbb{R}^{N}$
and
![]() $T\subseteq [N]$
,
$T\subseteq [N]$
,
![]() $v|_{T}$
denotes the
$v|_{T}$
denotes the
![]() $|T|$
-dimensional vector obtained by only retaining the coordinates of v in T. We write
$|T|$
-dimensional vector obtained by only retaining the coordinates of v in T. We write
![]() $u\parallel v$
for
$u\parallel v$
for
![]() $u,v\in\mathbb{R}^N$
if there is
$u,v\in\mathbb{R}^N$
if there is
![]() $t\in\mathbb{R}$
such that
$t\in\mathbb{R}$
such that
![]() $u = tv$
or
$u = tv$
or
![]() $tu = v$
.
$tu = v$
.
We will also make use of asymptotic notation. For functions f,g,
![]() $f = O_{\alpha}(g)$
(or
$f = O_{\alpha}(g)$
(or
![]() $f\lesssim_{\alpha} g$
means that
$f\lesssim_{\alpha} g$
means that
![]() $f \le C_\alpha g$
, where
$f \le C_\alpha g$
, where
![]() $C_\alpha$
is some constant depending on
$C_\alpha$
is some constant depending on
![]() $\alpha$
;
$\alpha$
;
![]() $f = \Omega_{\alpha}(g)$
(or
$f = \Omega_{\alpha}(g)$
(or
![]() $f \gtrsim_{\alpha} g$
) means that
$f \gtrsim_{\alpha} g$
) means that
![]() $f \ge c_{\alpha} g$
, where
$f \ge c_{\alpha} g$
, where
![]() $c_\alpha > 0$
is some constant depending on
$c_\alpha > 0$
is some constant depending on
![]() $\alpha$
, and
$\alpha$
, and
![]() $f = \Theta_{\alpha}(g)$
means that both
$f = \Theta_{\alpha}(g)$
means that both
![]() $f = O_{\alpha}(g)$
and
$f = O_{\alpha}(g)$
and
![]() $f = \Omega_{\alpha}(g)$
hold.
$f = \Omega_{\alpha}(g)$
hold.
All logarithms are natural, unless indicated otherwise, and floors and ceilings are omitted when they make no essential difference.
1.2 Concurrent work
After uploading the first version of this manuscript, we learned of concurrent and independent work of Campos et al. [Reference Campos, Jenssen, Michelen and Sahasrabudhe3] which, building on the techniques of [Reference Campos, Mattos, Morris and Morrison5], proved a singularity bound of
![]() $\exp(\!-\Omega(\sqrt{n\log n}))$
for symmetric Bernoulli matrices, a slightly improved bound over the
$\exp(\!-\Omega(\sqrt{n\log n}))$
for symmetric Bernoulli matrices, a slightly improved bound over the
![]() $\epsilon = 0$
case of Theorem 1.2. However, the combinatorial methods used there do not provide quantitative information on the least singular value, and their results do not apply in as general a setting.
$\epsilon = 0$
case of Theorem 1.2. However, the combinatorial methods used there do not provide quantitative information on the least singular value, and their results do not apply in as general a setting.
1.3 Subsequent work
Several months after the appearance of this article on the arXiv, a remarkable breakthrough work of Campos et al. [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] obtained an upper bound of the form
![]() $O(\exp(\!-\!cn))$
on the probability of singularity of
$O(\exp(\!-\!cn))$
on the probability of singularity of
![]() $n\times n$
symmetric Rademacher matrices, also using geometric techniques.
$n\times n$
symmetric Rademacher matrices, also using geometric techniques.
2. Preliminaries
We will need the decomposition of the unit sphere into compressible and incompressible vectors, as formalized by Rudelson and Vershynin [Reference Rudelson and Vershynin26].
Definition 2.1 (Compressible and incompressible vectors) For
![]() $c_0, c_1 \in (0,1)$
,
$c_0, c_1 \in (0,1)$
,
![]() $\operatorname{Comp}(c_0, c_1)$
consists of all vectors
$\operatorname{Comp}(c_0, c_1)$
consists of all vectors
![]() $v\in \mathbb{S}^{n-1}$
which are within Euclidean distance
$v\in \mathbb{S}^{n-1}$
which are within Euclidean distance
![]() $c_1$
of some vector
$c_1$
of some vector
![]() $w \in \mathbb{R}^{n}$
satisfying
$w \in \mathbb{R}^{n}$
satisfying
![]() $|\operatorname{Supp}(w)| \le c_0 n$
. Moreover,
$|\operatorname{Supp}(w)| \le c_0 n$
. Moreover,
![]() $\operatorname{Incomp}(c_0, c_1)\,{:\!=}\, \mathbb{S}^{n-1}\setminus \operatorname{Comp}(c_0, c_1)$
.
$\operatorname{Incomp}(c_0, c_1)\,{:\!=}\, \mathbb{S}^{n-1}\setminus \operatorname{Comp}(c_0, c_1)$
.
In order to prove Theorem 1.1, it suffices to analyze
![]() $\inf_{x \in \operatorname{Incomp(c_0,c_1)}}\lVert{Ax}_{2}\rVert$
due to the following.
$\inf_{x \in \operatorname{Incomp(c_0,c_1)}}\lVert{Ax}_{2}\rVert$
due to the following.
Lemma 2.2 There exist
![]() $c_0,c_1,c\in(0,1)$
depending only on the sub-Gaussian moment of
$c_0,c_1,c\in(0,1)$
depending only on the sub-Gaussian moment of
![]() $\xi$
so that for any vector
$\xi$
so that for any vector
![]() $u\in\mathbb{R}^n$
, we have
$u\in\mathbb{R}^n$
, we have
Proof. This follows immediately by combining [Reference Vershynin30, Proposition 4.2] with the concentration of the operator norm of random matrices with independent, uniformly sub-Gaussian centred entries (cf. [Reference Vershynin30, Lemma 2.3]).
Lemma 2.3 (Incompressible vectors are spread, cf. [Reference Vershynin30, Lemma 3.8]) For every
![]() $c_0, c_1 \in (0,1)$
, we can choose
$c_0, c_1 \in (0,1)$
, we can choose
![]() $c_{2.3} \,{:\!=}\, c_{2.3}(c_0, c_1) \in (0,1/5)$
depending only on
$c_{2.3} \,{:\!=}\, c_{2.3}(c_0, c_1) \in (0,1/5)$
depending only on
![]() $c_0, c_1$
such that the following holds. For every
$c_0, c_1$
such that the following holds. For every
![]() $v \in \operatorname{Incomp}(c_0, c_1)$
, there are at least
$v \in \operatorname{Incomp}(c_0, c_1)$
, there are at least
![]() $2\lceil c_{2.3}n \rceil $
indices
$2\lceil c_{2.3}n \rceil $
indices
![]() $k \in [n]$
such that
$k \in [n]$
such that
Definition 2.4 (Spread set) For every
![]() $c_0, c_1 \in (0,1)$
, and for every
$c_0, c_1 \in (0,1)$
, and for every
![]() $v \in \operatorname{Incomp}(c_0, c_1)$
, we assign a subset
$v \in \operatorname{Incomp}(c_0, c_1)$
, we assign a subset
![]() $\operatorname{Spread}(v) \subseteq [n]$
such that
$\operatorname{Spread}(v) \subseteq [n]$
such that
Definition 2.5 For every
![]() $c_0, c_1 \in (0,1)$
and for
$c_0, c_1 \in (0,1)$
and for
![]() $\lambda\in(0,c_{2.3}/2)$
, let
$\lambda\in(0,c_{2.3}/2)$
, let
![]() $c_{2.5}(\lambda)n$
be the largest multiple of
$c_{2.5}(\lambda)n$
be the largest multiple of
![]() $\lceil\lambda n\rceil$
less than or equal to
$\lceil\lambda n\rceil$
less than or equal to
![]() $\lceil c_{2.3}n\rceil$
. Note that
$\lceil c_{2.3}n\rceil$
. Note that
![]() $c_{2.5}(\lambda)\ge\frac{c_{2.3}}{2}$
.
$c_{2.5}(\lambda)\ge\frac{c_{2.3}}{2}$
.
To every
![]() $v \in \operatorname{Incomp}(c_0, c_1)$
, we assign
$v \in \operatorname{Incomp}(c_0, c_1)$
, we assign
![]() $\operatorname{Spread}_\lambda(v)\subseteq\operatorname{Spread}(v)$
such that
$\operatorname{Spread}_\lambda(v)\subseteq\operatorname{Spread}(v)$
such that
and choose a partition
 \begin{equation*}\operatorname{Spread}_\lambda(v) = \bigsqcup_{j=1}^k\operatorname{Spread}_\lambda^j(v)\end{equation*}
\begin{equation*}\operatorname{Spread}_\lambda(v) = \bigsqcup_{j=1}^k\operatorname{Spread}_\lambda^j(v)\end{equation*}
into
![]() $k = c_{2.3}(\lambda)n/\lfloor\lambda n\rfloor$
disjoint subsets of size
$k = c_{2.3}(\lambda)n/\lfloor\lambda n\rfloor$
disjoint subsets of size
![]() $\lfloor\lambda n\rfloor$
. We further assume that the choice of
$\lfloor\lambda n\rfloor$
. We further assume that the choice of
![]() $\operatorname{Spread}_{\lambda}(v)$
and
$\operatorname{Spread}_{\lambda}(v)$
and
![]() $\operatorname{Spread}_{\lambda}^{j}(v)$
is uniform for a given choice of
$\operatorname{Spread}_{\lambda}^{j}(v)$
is uniform for a given choice of
![]() $\lambda$
and
$\lambda$
and
![]() $\operatorname{Spread}(v)$
(in particular, these choices do not depend directly on v).
$\operatorname{Spread}(v)$
(in particular, these choices do not depend directly on v).
In the above definition, we will ultimately choose
![]() $\lambda = \Theta(1/\sqrt{n})$
for Theorem 1.1 and
$\lambda = \Theta(1/\sqrt{n})$
for Theorem 1.1 and
![]() $\lambda = \Theta((\!\log n)^{1/4}/\sqrt{n})$
for Theorem 1.2. We recall the definition of the Lévy concentration function.
$\lambda = \Theta((\!\log n)^{1/4}/\sqrt{n})$
for Theorem 1.2. We recall the definition of the Lévy concentration function.
Definition 2.6 For a random variable X and
![]() $\epsilon \ge 0$
, the Lévy concentration of X of width
$\epsilon \ge 0$
, the Lévy concentration of X of width
![]() $\epsilon$
is
$\epsilon$
is
We will also need a slight variant of the standard tensorization lemma, whose proof follows from the usual argument (cf. [Reference Rudelson and Vershynin26, Lemma 2.2]). We include the details for completeness.
Lemma 2.7 (Tensorization) Let
![]() $X = (X_1,\dots,X_N)$
be a random vector in
$X = (X_1,\dots,X_N)$
be a random vector in
![]() $\mathbb{R}^{N}$
with independent coordinates. Suppose that for all
$\mathbb{R}^{N}$
with independent coordinates. Suppose that for all
![]() $k \in [N]$
, there exist
$k \in [N]$
, there exist
![]() $a_k,b_k \ge 0$
such that
$a_k,b_k \ge 0$
such that
Then
 \begin{equation*}\mathcal{L}(X,\epsilon\sqrt{N}) \le e^N\prod_{k=1}^N(a_k\epsilon + b_k).\end{equation*}
\begin{equation*}\mathcal{L}(X,\epsilon\sqrt{N}) \le e^N\prod_{k=1}^N(a_k\epsilon + b_k).\end{equation*}
Proof. We have
 \begin{align*}\mathbb{P}[|X|\le\epsilon\sqrt{N}]&=\mathbb{P}\bigg[\sum_{j=1}^NX_j^2\le\epsilon^2N\bigg] = \mathbb{P}\bigg[N-\frac{1}{\epsilon^2}\sum_{j=1}^NX_j^2\ge 0\bigg]\\ &\le\mathbb{E}\exp\left(N-\frac{1}{\epsilon^2}\sum_{j=1}^NX_j^2\right)\\ &\le e^N\prod_{j=1}^N\sup_{X_1,\ldots,X_{j-1}}\mathbb{E}\exp(\!-X_j^2/\epsilon^2|X_1,\ldots,X_{j-1}).\end{align*}
\begin{align*}\mathbb{P}[|X|\le\epsilon\sqrt{N}]&=\mathbb{P}\bigg[\sum_{j=1}^NX_j^2\le\epsilon^2N\bigg] = \mathbb{P}\bigg[N-\frac{1}{\epsilon^2}\sum_{j=1}^NX_j^2\ge 0\bigg]\\ &\le\mathbb{E}\exp\left(N-\frac{1}{\epsilon^2}\sum_{j=1}^NX_j^2\right)\\ &\le e^N\prod_{j=1}^N\sup_{X_1,\ldots,X_{j-1}}\mathbb{E}\exp(\!-X_j^2/\epsilon^2|X_1,\ldots,X_{j-1}).\end{align*}
We finish by noting that for any realization of
![]() $X_1,\ldots,X_{j-1}$
,
$X_1,\ldots,X_{j-1}$
,
 \begin{align*}\mathbb{E}\exp(\!-X_j^2/\epsilon^2|X_1,\ldots,X_{j-1})&= \int_0^\infty 2ue^{-u^2}\mathbb{P}[|X_k| < \epsilon u|X_1,\ldots,X_{j-1}]\,du\\[3pt] &\le\int_0^\infty 2ue^{-u^2}(a_j\epsilon u+b_j)\,du\le a_j\epsilon+b_j.\\[-36pt]\end{align*}
\begin{align*}\mathbb{E}\exp(\!-X_j^2/\epsilon^2|X_1,\ldots,X_{j-1})&= \int_0^\infty 2ue^{-u^2}\mathbb{P}[|X_k| < \epsilon u|X_1,\ldots,X_{j-1}]\,du\\[3pt] &\le\int_0^\infty 2ue^{-u^2}(a_j\epsilon u+b_j)\,du\le a_j\epsilon+b_j.\\[-36pt]\end{align*}
We also recall the definition of essential least common denominator (LCD). We use a log-normalized version due to Rudelson (unpublished), which also appears in [Reference Vershynin30].
Definition 2.8 (LCD). For
![]() $L \ge 1$
and
$L \ge 1$
and
![]() $v \in \mathbb{S}^{N-1}$
, the least common denominator (LCD)
$v \in \mathbb{S}^{N-1}$
, the least common denominator (LCD)
![]() $D_{L}(v)$
is defined as
$D_{L}(v)$
is defined as
Finally we will require the following anticoncentration inequality of Miroshnikov and Rogozin [Reference Mirošnikov and Rogozin19]; this generalizes a well-known inequality of Lévy-Kolmogorov-Rogozin [Reference Rogozin24], which is itself an extension of Erdös’s solution [Reference Erdös7] to the Littlewood-Offord problem.
Lemma 2.9 ([Reference Mirošnikov and Rogozin19, Corollary 1]). Let
![]() $\xi_1,\dots, \xi_{N}$
be independent random variables. Then, for any real numbers
$\xi_1,\dots, \xi_{N}$
be independent random variables. Then, for any real numbers
![]() $r_1,\dots,r_N > 0$
and any real
$r_1,\dots,r_N > 0$
and any real
![]() $r \ge \max_{i \in [N]}r_N$
, we have
$r \ge \max_{i \in [N]}r_N$
, we have
 \begin{align*} \mathcal{L}\left(\sum_{i=1}^{N}\xi_i, r\right) \le C_{2.9}r \left(\sum_{i=1}^{N}\frac{r_i^2(1-\mathcal{L}(\xi_i,r_i))}{\mathcal{L}(\xi_i,r_i)^2}\right)^{-1/2},\end{align*}
\begin{align*} \mathcal{L}\left(\sum_{i=1}^{N}\xi_i, r\right) \le C_{2.9}r \left(\sum_{i=1}^{N}\frac{r_i^2(1-\mathcal{L}(\xi_i,r_i))}{\mathcal{L}(\xi_i,r_i)^2}\right)^{-1/2},\end{align*}
where
![]() $C_{2.9}>0$
is an absolute constant.
$C_{2.9}>0$
is an absolute constant.
3. Median regularized LCD (MRLCD)
In this section, we introduce the median regularized LCD (MRLCD), which is the notion of arithmetic structure that we will use in the proof of Theorem 1.1. As opposed to the regularized LCD (RLCD) (introduced in [Reference Vershynin30]) which guarantees only one arithmetically unstructured projection of the vector, a large MRLCD guarantees many arithmetically unstructured projections of the vector. This simple change allows the MRLCD to piece together various unstructured parts of the vector to obtain significantly better small-ball probability estimates (Proposition 3.5), while at the same time not significantly impacting the size of nets of level sets (Proposition 3.3).
Definition 3.1 (Median Regularized LCD). For
![]() $v \in \operatorname{Incomp}(c_0, c_1)$
,
$v \in \operatorname{Incomp}(c_0, c_1)$
,
![]() $\lambda \in (0,c_{2.3})$
, and
$\lambda \in (0,c_{2.3})$
, and
![]() $L \ge 1$
, the median regularized LCD, denoted
$L \ge 1$
, the median regularized LCD, denoted
![]() $\widehat{MD}_{L}(v,\lambda)$
, is defined as
$\widehat{MD}_{L}(v,\lambda)$
, is defined as
Here, the median of an even number of elements is not an average, but instead the value of the upper half. We denote by
![]() $I_M(v)$
the set
$I_M(v)$
the set
![]() $\operatorname{Spread}_\lambda^j(v)$
achieving the median (arbitrarily chosen from among all such sets), and
$\operatorname{Spread}_\lambda^j(v)$
achieving the median (arbitrarily chosen from among all such sets), and
![]() $\mathcal{I}_M(v)$
the collection of sets attaining values at least that of the median. We let
$\mathcal{I}_M(v)$
the collection of sets attaining values at least that of the median. We let
![]() $\mathcal{J}_M(v)$
be the collection of sets attaining values at most that of the median.
$\mathcal{J}_M(v)$
be the collection of sets attaining values at most that of the median.
We will consider level sets obtained by dyadically chopping the range of the MRLCD.
Definition 3.2 (Level sets of MRLCD) For
![]() $\lambda \in (0, c_{2.3})$
,
$\lambda \in (0, c_{2.3})$
,
![]() $L \ge 1$
, and
$L \ge 1$
, and
![]() $D \ge 1$
, we define the set
$D \ge 1$
, we define the set
3.1 Nets for level sets of MRLCD
The main result of this subsection is the following.
Proposition 3.3 Let
![]() $c_0, c_1 \in (0,1)$
. There exists
$c_0, c_1 \in (0,1)$
. There exists
![]() $C_{3.3} = C_{3.3}(c_0,c_1) > 0$
for which the following holds. Let
$C_{3.3} = C_{3.3}(c_0,c_1) > 0$
for which the following holds. Let
![]() $\lambda \in (C_{3.3}/n, c_{2.3}/2)$
and
$\lambda \in (C_{3.3}/n, c_{2.3}/2)$
and
![]() $L \ge 1$
. For every
$L \ge 1$
. For every
![]() $D \ge 1$
,
$D \ge 1$
,
![]() $S_{D}$
has a
$S_{D}$
has a
![]() $\beta$
-net
$\beta$
-net
![]() $\mathcal{N}$
such that
$\mathcal{N}$
such that
 \begin{equation*}\beta = \frac{L\sqrt{\log(2D)}}{D}, \quad |\mathcal{N}| \le D^{1/\lambda}\left(\frac{C_{3.3}D}{\sqrt{\log(2D)}}\right)^n\cdot\left(\frac{\sqrt{\log(2D)}}{\sqrt{\lambda n}}\right)^{c_{2.3}n/8}.\end{equation*}
\begin{equation*}\beta = \frac{L\sqrt{\log(2D)}}{D}, \quad |\mathcal{N}| \le D^{1/\lambda}\left(\frac{C_{3.3}D}{\sqrt{\log(2D)}}\right)^n\cdot\left(\frac{\sqrt{\log(2D)}}{\sqrt{\lambda n}}\right)^{c_{2.3}n/8}.\end{equation*}
Remark By changing
![]() $C_{3.3}$
by a constant factor, we can further assume that
$C_{3.3}$
by a constant factor, we can further assume that
![]() $\mathcal{N}\subseteq S_D$
. Also, the L dependence here is not optimal – one can save a factor of
$\mathcal{N}\subseteq S_D$
. Also, the L dependence here is not optimal – one can save a factor of
![]() $L^{n(1-c_{2.3}/8)}$
by being more careful, although this does not affect the overall bounds if L is of constant order as in our application.
$L^{n(1-c_{2.3}/8)}$
by being more careful, although this does not affect the overall bounds if L is of constant order as in our application.
The proof of Proposition 3.3 relies on a bound on the size of nets for level sets of the LCD.
Lemma 3.4 (Corollary of Lemma 7.8 in [Reference Vershynin30]) Let
![]() $m \in \mathbb{N}$
,
$m \in \mathbb{N}$
,
![]() $D \ge 1$
, and
$D \ge 1$
, and
![]() $c\in(0,1)$
be such that
$c\in(0,1)$
be such that
![]() $D > c\sqrt{m}\ge 2$
. There exists a constant C depending only on c for which the following holds. Let
$D > c\sqrt{m}\ge 2$
. There exists a constant C depending only on c for which the following holds. Let
![]() $\chi > 1$
,
$\chi > 1$
,
![]() $L \ge 1$
, and
$L \ge 1$
, and
![]() $\lambda > 0$
. Then the set
$\lambda > 0$
. Then the set
has a
![]() $\beta\sqrt{\chi\lambda}$
-net
$\beta\sqrt{\chi\lambda}$
-net
![]() $\mathcal{N}$
such that
$\mathcal{N}$
such that
Now we conclude the result.
Proof of Proposition 3.3. Let
![]() $r = \lceil \lambda n \rceil$
and
$r = \lceil \lambda n \rceil$
and
![]() $k = c_{2.5}(\lambda)n$
, so that
$k = c_{2.5}(\lambda)n$
, so that
![]() $r | k$
by definition.
$r | k$
by definition.
Let
![]() $v \in S_D$
. By paying a factor of at most
$v \in S_D$
. By paying a factor of at most
![]() $2^n$
in the size of our net, we may fix a realization of
$2^n$
in the size of our net, we may fix a realization of
![]() $\operatorname{Spread}(v)$
, which determines
$\operatorname{Spread}(v)$
, which determines
![]() $\operatorname{Spread}_\lambda(v)$
and
$\operatorname{Spread}_\lambda(v)$
and
![]() $\operatorname{Spread}_\lambda^j(v)$
for
$\operatorname{Spread}_\lambda^j(v)$
for
![]() $1\le j\le k/r$
. We pay an additional factor of at most
$1\le j\le k/r$
. We pay an additional factor of at most
![]() $2^n$
to reveal which sets
$2^n$
to reveal which sets
![]() $\operatorname{Spread}_\lambda^j(v)$
are in
$\operatorname{Spread}_\lambda^j(v)$
are in
![]() $\mathcal{J}_M(v)$
. Let
$\mathcal{J}_M(v)$
. Let
![]() $J\subseteq[k/r]$
be the collection of corresponding indices j. We see that
$J\subseteq[k/r]$
be the collection of corresponding indices j. We see that
![]() $t \,{:\!=}\, |J|\ge k/(2r)$
by definition of median. Write
$t \,{:\!=}\, |J|\ge k/(2r)$
by definition of median. Write
![]() $J = \{j_1,\ldots,j_t\}$
and let
$J = \{j_1,\ldots,j_t\}$
and let
![]() $I_i = \operatorname{Spread}_\lambda^{j_i}(v)$
.
$I_i = \operatorname{Spread}_\lambda^{j_i}(v)$
.
Note that, given
![]() $I_1,\ldots,I_t$
, we know that
$I_1,\ldots,I_t$
, we know that
![]() $D_L(v_{I_i}/\lVert{v_{I_i}}_2\rVert)\le 2D$
for all
$D_L(v_{I_i}/\lVert{v_{I_i}}_2\rVert)\le 2D$
for all
![]() $1\le i\le t$
. Moreover, since
$1\le i\le t$
. Moreover, since
![]() $I_i \subseteq \operatorname{Spread}_{\lambda}(v)$
, it follows that
$I_i \subseteq \operatorname{Spread}_{\lambda}(v)$
, it follows that
![]() $\lVert{v_{I_i}}_2\rVert\le\sqrt{\chi\lambda}$
for some
$\lVert{v_{I_i}}_2\rVert\le\sqrt{\chi\lambda}$
for some
![]() $\chi$
depending only on
$\chi$
depending only on
![]() $c_0$
. Further, by [Reference Vershynin30, Lemma 6.2], it follows (again, since
$c_0$
. Further, by [Reference Vershynin30, Lemma 6.2], it follows (again, since
![]() $I_i \subseteq \operatorname{Spread}_{\lambda}(v)$
) that
$I_i \subseteq \operatorname{Spread}_{\lambda}(v)$
) that
![]() $D_L(v_{I_i}/\lVert{v_{I_i}}\rVert_2) \ge c\sqrt{\lceil \lambda n \rceil}$
for some c depending only on
$D_L(v_{I_i}/\lVert{v_{I_i}}\rVert_2) \ge c\sqrt{\lceil \lambda n \rceil}$
for some c depending only on
![]() $c_0, c_1$
. Hence, by Lemma 3.4, we have a
$c_0, c_1$
. Hence, by Lemma 3.4, we have a
![]() $\beta\sqrt{\chi\lambda}$
-net for
$\beta\sqrt{\chi\lambda}$
-net for
![]() $\{v_{I_i}\}_{v\in S_D}$
where
$\{v_{I_i}\}_{v\in S_D}$
where
of size at most
Finally, we take a product of these nets over
![]() $1\le i\le t$
, along with a standard
$1\le i\le t$
, along with a standard
![]() $\beta$
-net of
$\beta$
-net of
![]() $\mathbb{B}_2^{I_0}$
(this net has size at most
$\mathbb{B}_2^{I_0}$
(this net has size at most
![]() $(1+3/\beta)^{|I_0|}$
), where we let
$(1+3/\beta)^{|I_0|}$
), where we let
![]() $I_0 = [n]\setminus(I_1\cup\cdots\cup I_t)$
, to obtain the desired conclusion upon adjusting the value of
$I_0 = [n]\setminus(I_1\cup\cdots\cup I_t)$
, to obtain the desired conclusion upon adjusting the value of
![]() $\beta$
by standard arguments.
$\beta$
by standard arguments.
3.2 Anticoncentration via MRLCD
We derive anticoncentration for a fixed vector with respect to MRLCD; the key idea is to patch together anticoncentration estimates on different segments of the vector through the use of Lemma 2.9.
Proposition 3.5 (Anticoncentration via the MRLCD). Let
![]() $\xi_1,\dots,\xi_{n}$
be i.i.d. random variables. Suppose that there exist
$\xi_1,\dots,\xi_{n}$
be i.i.d. random variables. Suppose that there exist
![]() $\epsilon_0, p_0, M_0 > 0$
such that
$\epsilon_0, p_0, M_0 > 0$
such that
![]() $\mathcal{L}(\xi_k, \epsilon_0) \le 1-p_0$
and
$\mathcal{L}(\xi_k, \epsilon_0) \le 1-p_0$
and
![]() $\mathbb{E}[|\xi_k|]\le M_0$
for all k. Finally, let
$\mathbb{E}[|\xi_k|]\le M_0$
for all k. Finally, let
![]() $c_0, c_1 \in (0,1)$
. Then, there exist
$c_0, c_1 \in (0,1)$
. Then, there exist
![]() $C_{3.5}$
, depending only on
$C_{3.5}$
, depending only on
![]() $\epsilon_0, p_0, M_0$
and
$\epsilon_0, p_0, M_0$
and
![]() $C^{\prime}_{3.5}$
depending on
$C^{\prime}_{3.5}$
depending on
![]() $\epsilon_0, p_0, M_0, c_0, c_1$
such that the following holds.
$\epsilon_0, p_0, M_0, c_0, c_1$
such that the following holds.
Let
![]() $L\ge p_0^{-1/2}$
,
$L\ge p_0^{-1/2}$
,
![]() $\lambda \in (C^{\prime}_{3.5}L^2/n,c_{2.3})$
,
$\lambda \in (C^{\prime}_{3.5}L^2/n,c_{2.3})$
,
![]() $v \in \operatorname{Incomp}(c_0, c_1)$
,
$v \in \operatorname{Incomp}(c_0, c_1)$
,
![]() $J\subseteq\operatorname{Spread}_\lambda(v)$
, and
$J\subseteq\operatorname{Spread}_\lambda(v)$
, and
![]() $S_J = \sum_{k \in J}v_k \xi_k$
. Suppose that J is a union of sets in
$S_J = \sum_{k \in J}v_k \xi_k$
. Suppose that J is a union of sets in
![]() $\mathcal{I}_M(v)$
. Then for every
$\mathcal{I}_M(v)$
. Then for every
![]() $\epsilon \ge 0$
, we have for sufficiently large n (depending on
$\epsilon \ge 0$
, we have for sufficiently large n (depending on
![]() $\epsilon_0, p_0, M_0, c_0, c_1$
) that
$\epsilon_0, p_0, M_0, c_0, c_1$
) that
Remark The above proposition should be compared with [Reference Vershynin30, Proposition 6.9], which bounds the Lévy concentration function in terms of the regularized LCD. The key difference is that the term
![]() $\sqrt{|J|/n}$
in the denominator of our bound is replaced by
$\sqrt{|J|/n}$
in the denominator of our bound is replaced by
![]() $\sqrt{\lambda}$
, which is always smaller. In fact, in the application considered here,
$\sqrt{\lambda}$
, which is always smaller. In fact, in the application considered here,
![]() $\lambda$
must be chosen to be
$\lambda$
must be chosen to be
![]() $O (1/\sqrt{n})$
, which makes the above proposition significantly more efficient than the corresponding proposition in [Reference Vershynin30] for most of the matrix row-vector products (which satisfy
$O (1/\sqrt{n})$
, which makes the above proposition significantly more efficient than the corresponding proposition in [Reference Vershynin30] for most of the matrix row-vector products (which satisfy
![]() $|J|/n = \Theta(1)$
).
$|J|/n = \Theta(1)$
).
Proof. Since
![]() $v\in\operatorname{Incomp}(c_0,c_1)$
, we have
$v\in\operatorname{Incomp}(c_0,c_1)$
, we have
![]() $\widehat{MD}_L(v,\lambda)\ge c\sqrt{\lceil\lambda n\rceil}$
for some c depending only on
$\widehat{MD}_L(v,\lambda)\ge c\sqrt{\lceil\lambda n\rceil}$
for some c depending only on
![]() $c_0,c_1$
([Reference Vershynin30, Lemma 6.2]).
$c_0,c_1$
([Reference Vershynin30, Lemma 6.2]).
First, assume that
![]() $\epsilon \le 1/(c\sqrt{n})$
. Let
$\epsilon \le 1/(c\sqrt{n})$
. Let
![]() $r = \lceil \lambda n \rceil$
and
$r = \lceil \lambda n \rceil$
and
![]() $k = c_{2.5}(\lambda)n$
, so that
$k = c_{2.5}(\lambda)n$
, so that
![]() $r | k$
by definition. For
$r | k$
by definition. For
![]() $i\in[k/r]$
, let
$i\in[k/r]$
, let
Let I be such that
![]() $J = \cup_{i\in I}\operatorname{Spread}_\lambda^i(v)$
. Since J is a union of sets in
$J = \cup_{i\in I}\operatorname{Spread}_\lambda^i(v)$
. Since J is a union of sets in
![]() $\mathcal{I}_M(v)$
, and
$\mathcal{I}_M(v)$
, and
![]() $D_L(v_I/\lVert{v_I}\rVert_2) \ge \widehat{MD}_L(v,\lambda)$
for each
$D_L(v_I/\lVert{v_I}\rVert_2) \ge \widehat{MD}_L(v,\lambda)$
for each
![]() $I \in \mathcal{I}_M(v)$
, it follows by standard anticoncentration estimates based on the LCD (see [Reference Vershynin30, Proposition 6.9] for the logarithmic version), that there exists an absolute constant
$I \in \mathcal{I}_M(v)$
, it follows by standard anticoncentration estimates based on the LCD (see [Reference Vershynin30, Proposition 6.9] for the logarithmic version), that there exists an absolute constant
![]() $C > 0$
such that
$C > 0$
such that
for all
![]() $i\in I$
, where the latter inequality follows from the assumption that
$i\in I$
, where the latter inequality follows from the assumption that
![]() $\epsilon \le 1/(c\sqrt{n})$
, along with the lower bound on
$\epsilon \le 1/(c\sqrt{n})$
, along with the lower bound on
![]() $\lambda$
(by taking
$\lambda$
(by taking
![]() $C^{\prime}_{3.5}$
sufficiently large depending on various parameters).
$C^{\prime}_{3.5}$
sufficiently large depending on various parameters).
Now note that
and that the
![]() $S_i$
are independent. Also, note that
$S_i$
are independent. Also, note that
![]() $|I| = |J|/\lceil\lambda n\rceil$
. Therefore, by Lemma 2.9, we have
$|I| = |J|/\lceil\lambda n\rceil$
. Therefore, by Lemma 2.9, we have
 \begin{align*}\mathcal{L}(S_J,\epsilon)&\le C_{2.9}\epsilon\left(\sum_{i\in I}\frac{\epsilon^2(1-\mathcal{L}(S_i,\epsilon))}{\mathcal{L}(S_i,\epsilon)^2}\right)^{-1/2}\\[3pt] &\le\frac{C_{2.9}\sqrt{2}}{\sqrt{|I|}}\max_{i\in I}\mathcal{L}(S_i,\epsilon)\le\frac{2C_{2.9}}{\sqrt{|J|/n}}\cdot CL\left(\epsilon+\frac{\sqrt{\lambda}}{\widehat{MD}_L(v,\lambda)}\right),\end{align*}
\begin{align*}\mathcal{L}(S_J,\epsilon)&\le C_{2.9}\epsilon\left(\sum_{i\in I}\frac{\epsilon^2(1-\mathcal{L}(S_i,\epsilon))}{\mathcal{L}(S_i,\epsilon)^2}\right)^{-1/2}\\[3pt] &\le\frac{C_{2.9}\sqrt{2}}{\sqrt{|I|}}\max_{i\in I}\mathcal{L}(S_i,\epsilon)\le\frac{2C_{2.9}}{\sqrt{|J|/n}}\cdot CL\left(\epsilon+\frac{\sqrt{\lambda}}{\widehat{MD}_L(v,\lambda)}\right),\end{align*}
which proves the desired conclusion for
![]() $\epsilon \le 1/c\sqrt{n}$
.
$\epsilon \le 1/c\sqrt{n}$
.
Finally, for
![]() $\epsilon > 1/(c\sqrt{n})$
, we note that any interval of length
$\epsilon > 1/(c\sqrt{n})$
, we note that any interval of length
![]() $2\epsilon$
can be tiled by at most
$2\epsilon$
can be tiled by at most
![]() $2\epsilon/\epsilon_0$
intervals of length
$2\epsilon/\epsilon_0$
intervals of length
![]() $2\epsilon_0$
, where
$2\epsilon_0$
, where
![]() $\epsilon_0 = 1/(2c\sqrt{n})$
. Moreover, for such
$\epsilon_0 = 1/(2c\sqrt{n})$
. Moreover, for such
![]() $\epsilon_0$
, we have
$\epsilon_0$
, we have
Hence, we have that for all
![]() $\epsilon > 1/(c\sqrt{n})$
,
$\epsilon > 1/(c\sqrt{n})$
,
 \begin{align*} \mathcal{L}(S_J, \epsilon) &\le \frac{2\epsilon}{\epsilon_0}\cdot\mathcal{L}(S_J, \epsilon_0)\\[3pt] &\le \frac{2\epsilon}{\epsilon_0}\cdot\frac{2C_{2.9}CL}{\sqrt{|J|/n}}\cdot 4\epsilon_0 \le {16C_{2.9}CL}\cdot \frac{\epsilon}{\sqrt{\lambda}},\end{align*}
\begin{align*} \mathcal{L}(S_J, \epsilon) &\le \frac{2\epsilon}{\epsilon_0}\cdot\mathcal{L}(S_J, \epsilon_0)\\[3pt] &\le \frac{2\epsilon}{\epsilon_0}\cdot\frac{2C_{2.9}CL}{\sqrt{|J|/n}}\cdot 4\epsilon_0 \le {16C_{2.9}CL}\cdot \frac{\epsilon}{\sqrt{\lambda}},\end{align*}
as desired.
Next, we derive a small-ball result for (symmetric) matrix-vector products.
Lemma 3.6 Fix
![]() $K\ge 1$
,
$K\ge 1$
,
![]() $c_0, c_1 \in (0,1)$
and
$c_0, c_1 \in (0,1)$
and
![]() $v \in \operatorname{Incomp}(c_0, c_1)$
. There exists L depending only on the sub-Gaussian norm of
$v \in \operatorname{Incomp}(c_0, c_1)$
. There exists L depending only on the sub-Gaussian norm of
![]() $\xi$
, and
$\xi$
, and
![]() $c_{3.6}, C_{3.6}$
depending on the sub-Gaussian norm of
$c_{3.6}, C_{3.6}$
depending on the sub-Gaussian norm of
![]() $\xi$
and on
$\xi$
and on
![]() $c_0, c_1$
such that the following holds.
$c_0, c_1$
such that the following holds.
Let
![]() $\lambda \in (C_{3.6}/n, c_{3.6})$
and suppose that
$\lambda \in (C_{3.6}/n, c_{3.6})$
and suppose that
![]() $v\in S_D$
(with MRLCD defined with respect to
$v\in S_D$
(with MRLCD defined with respect to
![]() $\lambda, L$
). Then, for any
$\lambda, L$
). Then, for any
![]() $u \in \mathbb{R}^{n}$
, we have
$u \in \mathbb{R}^{n}$
, we have
 \begin{equation*}\mathbb{P}[\lVert{Av-u}\rVert_2\le K\beta\sqrt{n}]\le\left(\frac{C_{3.6}L^2\sqrt{\log(2D)}}{D}\right)^{n-\lceil\lambda n\rceil},\end{equation*}
\begin{equation*}\mathbb{P}[\lVert{Av-u}\rVert_2\le K\beta\sqrt{n}]\le\left(\frac{C_{3.6}L^2\sqrt{\log(2D)}}{D}\right)^{n-\lceil\lambda n\rceil},\end{equation*}
where
Proof. Fix
![]() $u \in \mathbb{R}^{n}$
and
$u \in \mathbb{R}^{n}$
and
![]() $v \in S_D$
. Note that for any permutation matrix P,
$v \in S_D$
. Note that for any permutation matrix P,
![]() $\lVert{Av-u}\rVert_2\le K\beta\sqrt{n}$
occurs if and only if
$\lVert{Av-u}\rVert_2\le K\beta\sqrt{n}$
occurs if and only if
Furthermore,
![]() $PAP^{-1} = PAP^\intercal$
has the same distribution as A. Therefore, we will be able to permute the indices of [n] at our convenience (depending on v).
$PAP^{-1} = PAP^\intercal$
has the same distribution as A. Therefore, we will be able to permute the indices of [n] at our convenience (depending on v).
In particular, we may assume that
![]() $\operatorname{Spread}_\lambda(v) = [c_{2.5}(\lambda)n]$
. Let
$\operatorname{Spread}_\lambda(v) = [c_{2.5}(\lambda)n]$
. Let
![]() $A_t = \{k\in[n]\,{:}\, t\lceil\lambda n\rceil < k\le (t+1)\lceil\lambda n\rceil\}$
(defined for
$A_t = \{k\in[n]\,{:}\, t\lceil\lambda n\rceil < k\le (t+1)\lceil\lambda n\rceil\}$
(defined for
![]() $0\le t\le T-1$
), where
$0\le t\le T-1$
), where
We may also assume that
![]() $A_{t} \in \mathcal{I}_M(v)$
for all
$A_{t} \in \mathcal{I}_M(v)$
for all
![]() $t\le \lceil T/2 \rceil - 1$
. Then, for all
$t\le \lceil T/2 \rceil - 1$
. Then, for all
![]() $\lceil\lambda n\rceil\le j\le c_{2.5}(\lambda)n$
, the set
$\lceil\lambda n\rceil\le j\le c_{2.5}(\lambda)n$
, the set
![]() $J = [j]$
has a subset of at least half the size which satisfies the assumptions of Proposition 3.5 (namely, the union of the first
$J = [j]$
has a subset of at least half the size which satisfies the assumptions of Proposition 3.5 (namely, the union of the first
![]() $\lfloor j/\lceil\lambda n\rceil\rfloor$
sets
$\lfloor j/\lceil\lambda n\rceil\rfloor$
sets
![]() $A_t$
).
$A_t$
).
Therefore, Proposition 3.5 implies that for all L sufficiently large depending on the sub-Gaussian norm of
![]() $\xi$
, if
$\xi$
, if
![]() $j\ge\lceil\lambda n\rceil$
and
$j\ge\lceil\lambda n\rceil$
and
![]() $\epsilon\ge 0$
, then
$\epsilon\ge 0$
, then
 \begin{equation*}\mathcal{L}((Av-u)_j|(Av-u)_{j+1,\ldots,n},\epsilon)\le CC_{3.5}L\left(\frac{\epsilon}{\sqrt{j/n}}+\frac{\sqrt{\lambda n/j}}{D}\right),\end{equation*}
\begin{equation*}\mathcal{L}((Av-u)_j|(Av-u)_{j+1,\ldots,n},\epsilon)\le CC_{3.5}L\left(\frac{\epsilon}{\sqrt{j/n}}+\frac{\sqrt{\lambda n/j}}{D}\right),\end{equation*}
where C depends only on
![]() $c_0,c_1$
. Here, we have used that the first j elements of the
$c_0,c_1$
. Here, we have used that the first j elements of the
![]() $j\textrm{th}$
row are independent of rows
$j\textrm{th}$
row are independent of rows
![]() $j+1,\dots,n$
, and that the Lévy concentration is monotone under removing independent random variables from a sum.
$j+1,\dots,n$
, and that the Lévy concentration is monotone under removing independent random variables from a sum.
Let
![]() $j' = \min(j, c_{2.5}(\lambda)n)$
. Then, by Lemma 2.7, we deduce
$j' = \min(j, c_{2.5}(\lambda)n)$
. Then, by Lemma 2.7, we deduce
 \begin{align*}\mathbb{P}[\lVert{Av-u}\rVert_2\le K\beta\sqrt{n}]&\le\mathbb{P}\left[\sum_{j = \lceil \lambda n \rceil}^{n} (Av-u)_{j}^{2} \le K^{2}\beta^{2} n\right]\\[3pt] &\le (CL)^n\prod_{j=\lceil\lambda n\rceil}^n\left(\frac{K\beta\sqrt{n/(n-\lceil\lambda n\rceil)}}{\sqrt{j'/n}}+\frac{\sqrt{\lambda n/j'}}{D}\right)\\[3pt] &\le (CL)^n\prod_{j=\lceil\lambda n\rceil}^n\left(\frac{KL\sqrt{n\log(2D)}}{D\sqrt{j'}}\right)\\[3pt] &\le\left(\frac{CL^2\sqrt{\log(2D)}}{D}\right)^{n-\lceil\lambda n\rceil},\end{align*}
\begin{align*}\mathbb{P}[\lVert{Av-u}\rVert_2\le K\beta\sqrt{n}]&\le\mathbb{P}\left[\sum_{j = \lceil \lambda n \rceil}^{n} (Av-u)_{j}^{2} \le K^{2}\beta^{2} n\right]\\[3pt] &\le (CL)^n\prod_{j=\lceil\lambda n\rceil}^n\left(\frac{K\beta\sqrt{n/(n-\lceil\lambda n\rceil)}}{\sqrt{j'/n}}+\frac{\sqrt{\lambda n/j'}}{D}\right)\\[3pt] &\le (CL)^n\prod_{j=\lceil\lambda n\rceil}^n\left(\frac{KL\sqrt{n\log(2D)}}{D\sqrt{j'}}\right)\\[3pt] &\le\left(\frac{CL^2\sqrt{\log(2D)}}{D}\right)^{n-\lceil\lambda n\rceil},\end{align*}
where the last inequality uses
![]() $\prod_{j=1}^n(n/j)\le e^n$
.
$\prod_{j=1}^n(n/j)\le e^n$
.
3.3 Structure theorem
We will need the following structure theorem, which shows that, except with exponentially small probability, the preimage under A of any fixed vector is highly unstructured. This is our replacement for the key [Reference Vershynin30, Theorem 7.1]. As usual, A denotes a random
![]() $n\times n$
symmetric matrix with independent
$n\times n$
symmetric matrix with independent
![]() $\xi$
entries on and above the diagonal.
$\xi$
entries on and above the diagonal.
Theorem 3.7 Fix
![]() $K\ge 1$
. Depending on the sub-Gaussian norm of
$K\ge 1$
. Depending on the sub-Gaussian norm of
![]() $\xi$
, we can choose L, c, C so that the following holds. For all
$\xi$
, we can choose L, c, C so that the following holds. For all
![]() $\lambda\in (C/n,1/\sqrt{n})$
, we have for any
$\lambda\in (C/n,1/\sqrt{n})$
, we have for any
![]() $u \in \mathbb{R}^{n}$
that
$u \in \mathbb{R}^{n}$
that
Proof. This is an immediate consequence of Proposition 3.3, Lemmas 3.2 and 3.6. Note that if
![]() $Av = tu$
for
$Av = tu$
for
![]() $t\in\mathbb{R}$
, then
$t\in\mathbb{R}$
, then
![]() $\lVert{A}\rVert\le K\sqrt{n}$
implies
$\lVert{A}\rVert\le K\sqrt{n}$
implies
![]() $\lVert{tu}\rVert_2\le K\sqrt{n}$
. For compressible vectors v, we use Lemma 2.2 on a constant amount of target vectors parallel to u so as to cover the full range. For the rest, if the MRLCD is between D and 2D (for some
$\lVert{tu}\rVert_2\le K\sqrt{n}$
. For compressible vectors v, we use Lemma 2.2 on a constant amount of target vectors parallel to u so as to cover the full range. For the rest, if the MRLCD is between D and 2D (for some
![]() $D\le 2^{\lambda n/C}$
), we take a net constructed in Lemma 3.4 along with a
$D\le 2^{\lambda n/C}$
), we take a net constructed in Lemma 3.4 along with a
![]() $1/D$
-net for
$1/D$
-net for
![]() $\{tu\,{:}\, \lVert{tu}\rVert_2 \le K\sqrt{n}\}$
, which adds an additional (unimportant) factor of
$\{tu\,{:}\, \lVert{tu}\rVert_2 \le K\sqrt{n}\}$
, which adds an additional (unimportant) factor of
![]() $KD\sqrt{n}$
to the size of our nets. Since
$KD\sqrt{n}$
to the size of our nets. Since
 \begin{align*}KD\sqrt{n}\cdot D^{1/\lambda}\left(\frac{C_{3.3}D}{\sqrt{\log(2D)}}\right)^n\cdot&\left(\frac{\sqrt{\log(2D)}}{\sqrt{\lambda n}}\right)^{c_{2.3}n/8}\times\left(\frac{C_{3.6}L^2\sqrt{\log(2D)}}{D}\right)^{n-\lceil\lambda n\rceil}\\[2pt] &= KD\sqrt{n}\cdot D^{1/\lambda}\left(\frac{C'D}{\sqrt{\log(2D)}}\right)^{\lceil\lambda n\rceil}\left(\frac{\sqrt{\log(2D)}}{\sqrt{\lambda n}}\right)^{c_{2.3}n/8}\\[2pt] &\le C'^n\cdot 2^{\lambda^2n^2/C}\cdot (1/C)^{c_{2.3}n/16}\\[2pt] &\le C'^n2^{n/C}(1/C)^{c_{2.3}n/16},\end{align*}
\begin{align*}KD\sqrt{n}\cdot D^{1/\lambda}\left(\frac{C_{3.3}D}{\sqrt{\log(2D)}}\right)^n\cdot&\left(\frac{\sqrt{\log(2D)}}{\sqrt{\lambda n}}\right)^{c_{2.3}n/8}\times\left(\frac{C_{3.6}L^2\sqrt{\log(2D)}}{D}\right)^{n-\lceil\lambda n\rceil}\\[2pt] &= KD\sqrt{n}\cdot D^{1/\lambda}\left(\frac{C'D}{\sqrt{\log(2D)}}\right)^{\lceil\lambda n\rceil}\left(\frac{\sqrt{\log(2D)}}{\sqrt{\lambda n}}\right)^{c_{2.3}n/8}\\[2pt] &\le C'^n\cdot 2^{\lambda^2n^2/C}\cdot (1/C)^{c_{2.3}n/16}\\[2pt] &\le C'^n2^{n/C}(1/C)^{c_{2.3}n/16},\end{align*}
the result follows by a union bound upon taking C sufficiently large. We omit the standard details, referring the reader to the proof of [Reference Vershynin30, Theorem 7.1] for a more detailed calculation.
4. Median threshold
We begin by defining an alternate notion of structure, based on the so-called threshold function (Definition 4.1), which will allow us to use results of Tikhomirov [Reference Tikhomirov29] to obtain a stronger bound for the probability of singularity Rademacher random symmetric matrices. We note that, although we have chosen to focus on the Rademacher case, our analysis can be extended to general real discrete distributions using recent results of the authors [Reference Jain, Sah and Sawhney11].
For a technical reason that will become clear later, we fix a sufficiently small absolute constant
![]() $p\in(0,1/2]$
throughout this section; for the case of Rademacher random variables, which is our focus, one can take
$p\in(0,1/2]$
throughout this section; for the case of Rademacher random variables, which is our focus, one can take
![]() $p = 1/10$
.
$p = 1/10$
.
Definition 4.1 For
![]() $p\in(0,1)$
,
$p\in(0,1)$
,
![]() $L\ge 1$
, and
$L\ge 1$
, and
![]() $v\in\mathbb{S}^{N-1}$
, the threshold
$v\in\mathbb{S}^{N-1}$
, the threshold
![]() $\mathcal{T}_{p,L}(v)$
is defined as
$\mathcal{T}_{p,L}(v)$
is defined as
 \begin{equation*}\mathcal{T}_{p,L}(v) = \sup\bigg\{t\in(0,1)\,{:}\, \mathcal{L}\left(\sum_{i=1}^Nb_i'v_i,t\right) > Lt\bigg\},\end{equation*}
\begin{equation*}\mathcal{T}_{p,L}(v) = \sup\bigg\{t\in(0,1)\,{:}\, \mathcal{L}\left(\sum_{i=1}^Nb_i'v_i,t\right) > Lt\bigg\},\end{equation*}
where the
![]() $b_i'$
are i.i.d. random variables distributed as
$b_i'$
are i.i.d. random variables distributed as
![]() $\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
.
$\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
.
Definition 4.2 For
![]() $p\in(0,1)$
,
$p\in(0,1)$
,
![]() $v\in\operatorname{Incomp}(c_0,c_1)$
,
$v\in\operatorname{Incomp}(c_0,c_1)$
,
![]() $\lambda\in(0,c_{2.3})$
, and
$\lambda\in(0,c_{2.3})$
, and
![]() $L\ge 1$
, the median threshold, denoted
$L\ge 1$
, the median threshold, denoted
![]() $\widehat{\mathcal{T}}_{p,L}(v,\lambda)$
, is defined as
$\widehat{\mathcal{T}}_{p,L}(v,\lambda)$
, is defined as
4.1. Threshold of random lattice points
We next recall the key technical result of Tikhomirov [Reference Tikhomirov29], which upper bounds the number of vectors with “large” threshold within a lattice of appropriate size. The important fact is that the number of such vectors is superexponentially small compared to the size of the lattice, which is the key difference with the results coming from the MRLCD. First, we must establish some notation.
Definition 4.3 Choose
![]() $N,n\ge 1$
and
$N,n\ge 1$
and
![]() $\delta\in(0,1]$
, as well as
$\delta\in(0,1]$
, as well as
![]() $K\ge 1$
. We say that
$K\ge 1$
. We say that
![]() $\mathcal{A}\subseteq\mathbb{Z}^n$
is
$\mathcal{A}\subseteq\mathbb{Z}^n$
is
![]() $(N,n,K,\delta)$
-admissible if the following hold:
$(N,n,K,\delta)$
-admissible if the following hold:
-
•
 $\mathcal{A} = A_1\times\cdots\times A_n$
, where each
$\mathcal{A} = A_1\times\cdots\times A_n$
, where each
 $A_i$
is an origin-symmetric subset of
$A_i$
is an origin-symmetric subset of
 $\mathbb{Z}\cap(\!-nN,nN)$
,
$\mathbb{Z}\cap(\!-nN,nN)$
, -
•
 $A_i$
is an integer interval of size at least
$A_i$
is an integer interval of size at least
 $2N+1$
for all
$2N+1$
for all
 $i > \delta n$
,
$i > \delta n$
, -
•
 $A_i$
is a union of two integer intervals of total size at least 2N and
$A_i$
is a union of two integer intervals of total size at least 2N and
 $A_i\cap[\!-N,N] = \emptyset$
for all
$A_i\cap[\!-N,N] = \emptyset$
for all
 $i\le\delta n$
, and
$i\le\delta n$
, and -
•
 $|\mathcal{A}|\le (KN)^n$
.
$|\mathcal{A}|\le (KN)^n$
.
Theorem 4.4 (From [Reference Tikhomirov29, Corollary 4.3]). Let
![]() $\delta,\epsilon\in(0,1]$
,
$\delta,\epsilon\in(0,1]$
,
![]() $p\in (0,1/2]$
, and
$p\in (0,1/2]$
, and
![]() $K,M\ge 1$
. There exist
$K,M\ge 1$
. There exist
![]() $n_{4.4} = n_{4.4}(\delta,\epsilon,K,M)\ge 1$
and
$n_{4.4} = n_{4.4}(\delta,\epsilon,K,M)\ge 1$
and
![]() $L_{4.4} = L_{4.4}(\delta,\epsilon,K) > 0$
such that the following holds. If
$L_{4.4} = L_{4.4}(\delta,\epsilon,K) > 0$
such that the following holds. If
![]() $n\ge n_{4.4}$
,
$n\ge n_{4.4}$
,
![]() $1\le N\le (1-p+\epsilon)^{-n}$
, and
$1\le N\le (1-p+\epsilon)^{-n}$
, and
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $(N,n,K,\delta)$
-admissible, then
$(N,n,K,\delta)$
-admissible, then
 \begin{equation*}\bigg|\bigg\{x\in\mathcal{A}\,{:}\, \mathcal{L}\left(\sum_{i=1}^nb_ix_i,\sqrt{n}\right)\ge L_{4.4}N^{-1}\bigg\}\bigg|\le\exp(\!-\!Mn)|\mathcal{A}|,\end{equation*}
\begin{equation*}\bigg|\bigg\{x\in\mathcal{A}\,{:}\, \mathcal{L}\left(\sum_{i=1}^nb_ix_i,\sqrt{n}\right)\ge L_{4.4}N^{-1}\bigg\}\bigg|\le\exp(\!-\!Mn)|\mathcal{A}|,\end{equation*}
where the
![]() $b_i$
are i.i.d.
$b_i$
are i.i.d.
![]() $\operatorname{Ber}(p)$
random variables. Furthermore,
$\operatorname{Ber}(p)$
random variables. Furthermore,
![]() $n_{4.4} = \exp(C_{4.4}(\delta,\epsilon,K)M^2)$
is allowable.
$n_{4.4} = \exp(C_{4.4}(\delta,\epsilon,K)M^2)$
is allowable.
Remark. This is the same as [Reference Tikhomirov29, Corollary 4.3], except that we have claimed an explicit dependence between n and M, namely that one can take M growing as
![]() $(\!\log n)^{1/2}$
(all other parameters fixed). This is an immediate consequence of unraveling the parameter dependencies in [Reference Tikhomirov29, Theorem 4.2]. We give a brief sketch, using the notation of [Reference Tikhomirov29, Theorem 4.2]. In the proof of [Reference Tikhomirov29, Theorem 4.2], one sets
$(\!\log n)^{1/2}$
(all other parameters fixed). This is an immediate consequence of unraveling the parameter dependencies in [Reference Tikhomirov29, Theorem 4.2]. We give a brief sketch, using the notation of [Reference Tikhomirov29, Theorem 4.2]. In the proof of [Reference Tikhomirov29, Theorem 4.2], one sets
![]() $L = L_{4.5}(2M,p,\delta,\epsilon/2)$
, which can be checked to grow exponentially in M by examining the last line of the proof of [Reference Tikhomirov29, Proposition 4.5]. This shows that the parameter q in the proof of [Reference Tikhomirov29, Theorem 4.2] is chosen to be linear in M, and hence, the parameter
$L = L_{4.5}(2M,p,\delta,\epsilon/2)$
, which can be checked to grow exponentially in M by examining the last line of the proof of [Reference Tikhomirov29, Proposition 4.5]. This shows that the parameter q in the proof of [Reference Tikhomirov29, Theorem 4.2] is chosen to be linear in M, and hence, the parameter
![]() $\widetilde{\epsilon}$
grows as
$\widetilde{\epsilon}$
grows as
![]() $M^{-1}$
. Next, it is required that
$M^{-1}$
. Next, it is required that
![]() $n\ge n_{4.10}(p,\widetilde{\epsilon},\max(16\widetilde{R},L),\widetilde{R},2M)$
and
$n\ge n_{4.10}(p,\widetilde{\epsilon},\max(16\widetilde{R},L),\widetilde{R},2M)$
and
![]() $n \ge n_{4.5}(2M, p, \delta, \epsilon/2)$
. The more restrictive condition comes from [Reference Tikhomirov29, Proposition 4.10], and indeed, an examination of the first few lines of the proof of this proposition reveals that it suffices to have n growing as
$n \ge n_{4.5}(2M, p, \delta, \epsilon/2)$
. The more restrictive condition comes from [Reference Tikhomirov29, Proposition 4.10], and indeed, an examination of the first few lines of the proof of this proposition reveals that it suffices to have n growing as
![]() $\exp(\Theta(M^{2}))$
. One also sees that
$\exp(\Theta(M^{2}))$
. One also sees that
![]() $\eta_{4.2} = \eta_{4.10}(p,\widetilde{\epsilon},\max(16\widetilde{R},L),\widetilde{R},2M)$
decays as
$\eta_{4.2} = \eta_{4.10}(p,\widetilde{\epsilon},\max(16\widetilde{R},L),\widetilde{R},2M)$
decays as
![]() $\exp(\!-\Theta(M^{2}))$
. Finally, the deduction of [Reference Tikhomirov29, Corollary 4.3] from [Reference Tikhomirov29, Theorem 4.2] requires
$\exp(\!-\Theta(M^{2}))$
. Finally, the deduction of [Reference Tikhomirov29, Corollary 4.3] from [Reference Tikhomirov29, Theorem 4.2] requires
![]() $n^{-1/2}\le\eta$
, for which n growing as
$n^{-1/2}\le\eta$
, for which n growing as
![]() $\exp(\Theta(M^{2}))$
is sufficient in light of the decay of
$\exp(\Theta(M^{2}))$
is sufficient in light of the decay of
![]() $\eta$
discussed above.
$\eta$
discussed above.
4.2. Replacement
In order to relate the anticoncentration of a vector with respect to Rademacher random variables to Definition 4.1 and 4.2, we will require the following inequality. This is closely related to the replacement trick employed by Kahn et al. [Reference Kahn, Komlós and Szemerédi13] and later by Tao and Vu [Reference Tao and Vu28] (although the application here is substantially simpler).
Lemma 4.5 There exists an absolute constant
![]() $C_{4.5}$
for which the following holds. Let
$C_{4.5}$
for which the following holds. Let
![]() $v\in \mathbb{R}^n$
and
$v\in \mathbb{R}^n$
and
![]() $r> 0$
. Then, for any
$r> 0$
. Then, for any
![]() $0 < p \le (2-\sqrt{2})/4$
,
$0 < p \le (2-\sqrt{2})/4$
,
 \begin{equation*}\mathcal{L}\left(\sum_{i=1}^{n}b_iv_i,r\right)\le C_{4.5} \mathcal{L}\left(\sum_{i=1}^{n}b_i'v_i,r\right),\end{equation*}
\begin{equation*}\mathcal{L}\left(\sum_{i=1}^{n}b_iv_i,r\right)\le C_{4.5} \mathcal{L}\left(\sum_{i=1}^{n}b_i'v_i,r\right),\end{equation*}
where
![]() $b_i$
are independent Rademacher random variables and
$b_i$
are independent Rademacher random variables and
![]() $b_i'$
are distributed as
$b_i'$
are distributed as
![]() $\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
.
$\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
.
Proof. Note that by scaling v, we may assume without loss of generality that
![]() $r = 1$
. Let
$r = 1$
. Let
![]() $X = \sum_{i=1}^nb_i'v_i$
. By Esseen’s inequality and
$X = \sum_{i=1}^nb_i'v_i$
. By Esseen’s inequality and
![]() $|\cos t|\le (3+\cos(2t))/4$
, we find
$|\cos t|\le (3+\cos(2t))/4$
, we find
 \begin{align*}\mathcal{L}\left(\sum_{i=1}^nb_iv_i,1\right)&\le C\int_{-2}^2\prod_{i=1}^n|\cos(v_i\theta)|d\theta\le C\int_{-2}^2\prod_{i=1}^n\left(\frac{3}{4}+\frac{1}{4}\cos(2v_i\theta)\right)d\theta\\[3pt] &\le C\int_{-2}^2 \prod_{i=1}^{n}\mathbb{E}\exp\left(i\theta \cdot 2b_i'v_i\right)d\theta\le 2C\int_{\mathbb{R}}{1}_{[\!-2,2]}\ast{1}_{[\!-2,2]}(\theta)\mathbb{E}\exp(i\theta(2X))d\theta\\\end{align*}
\begin{align*}\mathcal{L}\left(\sum_{i=1}^nb_iv_i,1\right)&\le C\int_{-2}^2\prod_{i=1}^n|\cos(v_i\theta)|d\theta\le C\int_{-2}^2\prod_{i=1}^n\left(\frac{3}{4}+\frac{1}{4}\cos(2v_i\theta)\right)d\theta\\[3pt] &\le C\int_{-2}^2 \prod_{i=1}^{n}\mathbb{E}\exp\left(i\theta \cdot 2b_i'v_i\right)d\theta\le 2C\int_{\mathbb{R}}{1}_{[\!-2,2]}\ast{1}_{[\!-2,2]}(\theta)\mathbb{E}\exp(i\theta(2X))d\theta\\\end{align*}
 \begin{align*} &= 4C\mathbb{E}\left(\frac{\sin(4X)}{2X}\right)^2\\[2pt] &\le 4C\mathbb{E}\left(\frac{\sin(4X)}{2X}\cdot {1}_{X\in [\!-1,1]}\right)^2 + \sum_{k=1}^{\infty}4C\mathbb{E}\left(\frac{\sin(4X)}{2X}\cdot {1}_{\pm X\in [2k-1, 2k+1]} \right)^2\\[2pt] &\le 16C\mathcal{L}(X,1) + C\sum_{k=1}^{\infty}\frac{\mathcal{L}(X,1)}{(2k-1)^{2}} \le C'\mathcal{L}(X,1).\end{align*}
\begin{align*} &= 4C\mathbb{E}\left(\frac{\sin(4X)}{2X}\right)^2\\[2pt] &\le 4C\mathbb{E}\left(\frac{\sin(4X)}{2X}\cdot {1}_{X\in [\!-1,1]}\right)^2 + \sum_{k=1}^{\infty}4C\mathbb{E}\left(\frac{\sin(4X)}{2X}\cdot {1}_{\pm X\in [2k-1, 2k+1]} \right)^2\\[2pt] &\le 16C\mathcal{L}(X,1) + C\sum_{k=1}^{\infty}\frac{\mathcal{L}(X,1)}{(2k-1)^{2}} \le C'\mathcal{L}(X,1).\end{align*}
The third inequality uses
![]() $p\le (2-\sqrt{2})/4$
, and the penultimate inequality uses
$p\le (2-\sqrt{2})/4$
, and the penultimate inequality uses
![]() $\sin(4x)/(2x) \le 2$
for
$\sin(4x)/(2x) \le 2$
for
![]() $x \in [\!-1,1]$
.
$x \in [\!-1,1]$
.
4.3 Randomized rounding
We will make use of a slight modification of [Reference Tikhomirov29, Lemma 5.3], proved using randomized rounding (cf. [Reference Livshyts15]). As the proof is identical we omit the details.
Lemma 4.6 Let
![]() $y = (y_1,\ldots,y_n)\in \mathbb{R}^n$
be a vector,
$y = (y_1,\ldots,y_n)\in \mathbb{R}^n$
be a vector,
![]() $\Delta$
be a fixed distribution supported in
$\Delta$
be a fixed distribution supported in
![]() $[\!-1,1]^n$
, and let
$[\!-1,1]^n$
, and let
![]() $\mu>0$
,
$\mu>0$
,
![]() $\psi\in \mathbb{R}$
be fixed. There exist absolute constants
$\psi\in \mathbb{R}$
be fixed. There exist absolute constants
![]() $c_{4.6}$
and
$c_{4.6}$
and
![]() $C_{4.6}$
for which the following holds.
$C_{4.6}$
for which the following holds.
Suppose that for all
![]() $t\ge \sqrt{n}$
,
$t\ge \sqrt{n}$
,
where
![]() $(b_1,\dots, b_n)$
are independent and distributed as
$(b_1,\dots, b_n)$
are independent and distributed as
![]() $\Delta$
. Then, there exists a vector
$\Delta$
. Then, there exists a vector
![]() $y' \in \mathbb{Z}^{n}$
satisfying
$y' \in \mathbb{Z}^{n}$
satisfying
-
(R1)
 $\lVert{y-y'}\rVert_\infty\le 1$
,
$\lVert{y-y'}\rVert_\infty\le 1$
, -
(R2)
 $\mathbb{P}[|\sum_{i=1}^nb_iy_i'-\psi|\le t]\le C_{4.6}\mu t$
for all
$\mathbb{P}[|\sum_{i=1}^nb_iy_i'-\psi|\le t]\le C_{4.6}\mu t$
for all
 $t\ge \sqrt{n}$
, and
$t\ge \sqrt{n}$
, and -
(R3)
 $\mathcal{L}(\sum_{i=1}^nb_iy_i',\sqrt{n})\ge c_{4.6}\mathcal{L}(\sum_{i=1}^nb_iy_i,\sqrt{n})$
.
$\mathcal{L}(\sum_{i=1}^nb_iy_i',\sqrt{n})\ge c_{4.6}\mathcal{L}(\sum_{i=1}^nb_iy_i,\sqrt{n})$
.
Next, we prove a version of the above proposition for the case when
![]() $\Delta = \operatorname{Ber}(p) - \operatorname{Ber}'(p)$
with p sufficiently small. The main difference is that the left hand side in (R2) above can be replaced by the Lévy concentration at width t; this can be done since for a distribution with non-negative characteristic function, the maximum concentration of given width is essentially obtained around
$\Delta = \operatorname{Ber}(p) - \operatorname{Ber}'(p)$
with p sufficiently small. The main difference is that the left hand side in (R2) above can be replaced by the Lévy concentration at width t; this can be done since for a distribution with non-negative characteristic function, the maximum concentration of given width is essentially obtained around
![]() $\psi = 0$
.
$\psi = 0$
.
Lemma 4.7 Let
![]() $y = (y_1,\ldots,y_n)\in \mathbb{R}^n$
be a vector,
$y = (y_1,\ldots,y_n)\in \mathbb{R}^n$
be a vector,
![]() $p\in(0,1)$
, and let
$p\in(0,1)$
, and let
![]() $\mu>0$
,
$\mu>0$
,
![]() $\psi\in \mathbb{R}$
be fixed. There exist absolute constants
$\psi\in \mathbb{R}$
be fixed. There exist absolute constants
![]() $c_{4.7}$
and
$c_{4.7}$
and
![]() $C_{4.7}$
for which the following holds.
$C_{4.7}$
for which the following holds.
Suppose that for all
![]() $t\ge \sqrt{n}$
,
$t\ge \sqrt{n}$
,
 \begin{equation*}\mathcal{L}\left(\sum_{i=1}^nb_i'y_i,t\right)\le\mu t,\end{equation*}
\begin{equation*}\mathcal{L}\left(\sum_{i=1}^nb_i'y_i,t\right)\le\mu t,\end{equation*}
where the
![]() $b_i'$
are independent and distributed as
$b_i'$
are independent and distributed as
![]() $\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
. Then, there exists a vector
$\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
. Then, there exists a vector
![]() $y' = (y_1',\dots,y_n') \in \mathbb{Z}^{n}$
satisfying
$y' = (y_1',\dots,y_n') \in \mathbb{Z}^{n}$
satisfying
-
(R1)
 $\lVert{y-y'}\rVert_\infty\le 1$
,
$\lVert{y-y'}\rVert_\infty\le 1$
, -
(R2)
 $\mathcal{L}(\sum_{i=1}^nb_i'y_i',t)\le C_{4.7}\mu t$
for all
$\mathcal{L}(\sum_{i=1}^nb_i'y_i',t)\le C_{4.7}\mu t$
for all
 $t\ge \sqrt{n}$
, and
$t\ge \sqrt{n}$
, and -
(R3)
 $\mathcal{L}(\sum_{i=1}^nb_i'y_i',\sqrt{n})\ge c_{4.7}\mathcal{L}(\sum_{i=1}^nb_i'y_i,\sqrt{n})$
.
$\mathcal{L}(\sum_{i=1}^nb_i'y_i',\sqrt{n})\ge c_{4.7}\mathcal{L}(\sum_{i=1}^nb_i'y_i,\sqrt{n})$
.
Proof. We apply Lemma 4.6 to the distribution
![]() $\Delta = \operatorname{Ber}(p)- \operatorname{Ber}'(p)$
and
$\Delta = \operatorname{Ber}(p)- \operatorname{Ber}'(p)$
and
![]() $\psi = 0$
. From (R2),
$\psi = 0$
. From (R2),
for all
![]() $t\ge\sqrt{n}$
. Now let
$t\ge\sqrt{n}$
. Now let
![]() $t\ge\sqrt{n}$
and
$t\ge\sqrt{n}$
and
![]() $X = (\sum_{i=1}^nb_i'y_i')/t$
, and note that X has nonnegative characteristic function since
$X = (\sum_{i=1}^nb_i'y_i')/t$
, and note that X has nonnegative characteristic function since
![]() $b_i'$
does. Thus, for all
$b_i'$
does. Thus, for all
![]() $\psi\in\mathbb{R}$
,
$\psi\in\mathbb{R}$
,
 \begin{align*}\mathbb{P}[|X-\psi|\le 1]&=\mathbb{E}[{1}_{[\!-1,1]}(X-\psi)]\le\mathbb{E}[{1}_{[\!-1,1]}\ast{1}_{[\!-1,1]}(X-\psi)]\\[3pt]&=\int_{\mathbb{R}}\left(\frac{2\sin\theta}{\theta}\right)^2\mathbb{E}\exp(i\theta(X-\psi))d\theta\\[3pt]&\le\int_{\mathbb{R}}\left(\frac{2\sin\theta}{\theta}\right)^2|\mathbb{E}\exp(i\theta X)|d\theta\\[3pt] &=\int_{\mathbb{R}}\left(\frac{2\sin\theta}{\theta}\right)^2\mathbb{E}\exp(i\theta X)d\theta\\[3pt] &= \mathbb{E}[{1}_{[\!-1,1]}\ast{1}_{[\!-1,1]}(X)]\le 2\mathbb{P}[|X|\le 2]\le 4C_{4.6}\mu t.\\[-35pt]\end{align*}
\begin{align*}\mathbb{P}[|X-\psi|\le 1]&=\mathbb{E}[{1}_{[\!-1,1]}(X-\psi)]\le\mathbb{E}[{1}_{[\!-1,1]}\ast{1}_{[\!-1,1]}(X-\psi)]\\[3pt]&=\int_{\mathbb{R}}\left(\frac{2\sin\theta}{\theta}\right)^2\mathbb{E}\exp(i\theta(X-\psi))d\theta\\[3pt]&\le\int_{\mathbb{R}}\left(\frac{2\sin\theta}{\theta}\right)^2|\mathbb{E}\exp(i\theta X)|d\theta\\[3pt] &=\int_{\mathbb{R}}\left(\frac{2\sin\theta}{\theta}\right)^2\mathbb{E}\exp(i\theta X)d\theta\\[3pt] &= \mathbb{E}[{1}_{[\!-1,1]}\ast{1}_{[\!-1,1]}(X)]\le 2\mathbb{P}[|X|\le 2]\le 4C_{4.6}\mu t.\\[-35pt]\end{align*}
4.4 Threshold structure theorem
We now prove the following improved version of Theorem 3.7.
Theorem 4.8 Fix
![]() $K\ge 1$
and
$K\ge 1$
and
![]() $0 < p\le (2-\sqrt{2})/4$
. We can choose
$0 < p\le (2-\sqrt{2})/4$
. We can choose
![]() $L, c > 0$
and
$L, c > 0$
and
![]() $c' = c'(p)$
so that the following holds for sufficiently large n. For all
$c' = c'(p)$
so that the following holds for sufficiently large n. For all
![]() $\lambda\in (n^{-2/3},c(\!\log n)^{1/4}n^{-1/2})$
, we have for any
$\lambda\in (n^{-2/3},c(\!\log n)^{1/4}n^{-1/2})$
, we have for any
![]() $u \in \mathbb{R}^{n}$
that
$u \in \mathbb{R}^{n}$
that
where A is a symmetric matrix with entries on and above the diagonal i.i.d. and distributed as the sum of a Rademacher random variable, and a Gaussian random variable of mean 0 and variance
![]() $n^{-2n}$
.
$n^{-2n}$
.
Remark The Gaussian perturbation of the entries of A is not important here and will only be used later, where it will be convenient to assume that various sub-matrices of A are invertible almost surely. Moreover, the variance of the Gaussian is chosen sufficiently small so that all anticoncentration claims that we need are essentially unaffected by this perturbation.
Proof. As in the proof of Theorem 3.7, we can deal with compressible vectors using Lemma 2.2. Therefore, it remains to deal with incompressible vectors with ‘large’ median threshold.
By standard small-ball estimates for incompressible vectors using a quantitative central limit theorem (see [Reference Tikhomirov29, Lemma 5.1]), for
![]() $v\in\operatorname{Incomp}(c_0,c_1)$
, there is
$v\in\operatorname{Incomp}(c_0,c_1)$
, there is
![]() $C_0 = C_0(p,c_0,c_1)$
such that
$C_0 = C_0(p,c_0,c_1)$
such that
![]() $\widehat{\mathcal{T}}_{p,L}(v,\lambda)\le C_0(\lambda n)^{-1/2}$
. We let
$\widehat{\mathcal{T}}_{p,L}(v,\lambda)\le C_0(\lambda n)^{-1/2}$
. We let
![]() $r = \lceil\lambda n\rceil$
and
$r = \lceil\lambda n\rceil$
and
![]() $k = c_{2.5}(\lambda)n$
, so that
$k = c_{2.5}(\lambda)n$
, so that
![]() $r|k$
by definition, and let
$r|k$
by definition, and let
![]() $m = \lfloor k/(2r)\rfloor$
.
$m = \lfloor k/(2r)\rfloor$
.
Step 1: Randomized rounding. We consider the case
![]() $\widehat{\mathcal{T}}_{p,L}(v,\lambda)\in[1/T,2/T]$
, where
$\widehat{\mathcal{T}}_{p,L}(v,\lambda)\in[1/T,2/T]$
, where
![]() $T\in[C_0^{-1}\sqrt{\lambda n},2^{c'\lambda n}]$
. Then, by definition, there exist intervals
$T\in[C_0^{-1}\sqrt{\lambda n},2^{c'\lambda n}]$
. Then, by definition, there exist intervals
![]() $I_1,\ldots,I_m$
of the form
$I_1,\ldots,I_m$
of the form
![]() $\operatorname{Spread}_\lambda^j(v)$
with
$\operatorname{Spread}_\lambda^j(v)$
with
for all
![]() $i\in[m]$
.
$i\in[m]$
.
Let
![]() $D = C_1\sqrt{n}T$
, where
$D = C_1\sqrt{n}T$
, where
![]() $C_1 = C_1(p,c_0,c_1)\ge 1$
will be an integer chosen later. Let
$C_1 = C_1(p,c_0,c_1)\ge 1$
will be an integer chosen later. Let
![]() $y = Dv$
. By the definition of the threshold, for all
$y = Dv$
. By the definition of the threshold, for all
![]() $t\ge\sqrt{\lceil\lambda n\rceil}$
we have
$t\ge\sqrt{\lceil\lambda n\rceil}$
we have
 \begin{align*}\mathcal{L}\left(\sum_{j\in I_i}b_j'y_j,t\right) &= \mathcal{L}\left(\sum_{j\in I_i}b_j'v_j,\frac{t}{D}\right) = \mathcal{L}\left(\sum_{j\in I_i}b_j'\frac{v_j}{\lVert{v_{I_i}}\rVert_{2}},\frac{t}{D\lVert{v_{I_i}}\rVert_{2} }\right)\\[3pt] &\le\mathcal{L}\left(\sum_{j\in I_i}b_j'\frac{v_j}{\lVert{v_{I_i}}\rVert_2},\frac{\sqrt{2}t}{c_1C_1\sqrt{\lceil\lambda n\rceil}T}\right)\le\frac{L}{T}\cdot\frac{2t}{\sqrt{\lceil\lambda n\rceil}},\end{align*}
\begin{align*}\mathcal{L}\left(\sum_{j\in I_i}b_j'y_j,t\right) &= \mathcal{L}\left(\sum_{j\in I_i}b_j'v_j,\frac{t}{D}\right) = \mathcal{L}\left(\sum_{j\in I_i}b_j'\frac{v_j}{\lVert{v_{I_i}}\rVert_{2}},\frac{t}{D\lVert{v_{I_i}}\rVert_{2} }\right)\\[3pt] &\le\mathcal{L}\left(\sum_{j\in I_i}b_j'\frac{v_j}{\lVert{v_{I_i}}\rVert_2},\frac{\sqrt{2}t}{c_1C_1\sqrt{\lceil\lambda n\rceil}T}\right)\le\frac{L}{T}\cdot\frac{2t}{\sqrt{\lceil\lambda n\rceil}},\end{align*}
as long as we chose
![]() $C_1 > \sqrt{2}/c_1$
, where the
$C_1 > \sqrt{2}/c_1$
, where the
![]() $b_i'$
are independent random variables distributed as
$b_i'$
are independent random variables distributed as
![]() $\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
. Applying Lemma 4.7 to the
$\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
. Applying Lemma 4.7 to the
![]() $\lceil\lambda n\rceil$
-dimension vector
$\lceil\lambda n\rceil$
-dimension vector
![]() $y_{I_i}$
, we see that there is
$y_{I_i}$
, we see that there is
![]() $y_{I_i}^{\prime}\in\mathbb{Z}^{\lceil\lambda n\rceil}$
satisfying the conclusions of Lemma 4.7 (with n replaced by
$y_{I_i}^{\prime}\in\mathbb{Z}^{\lceil\lambda n\rceil}$
satisfying the conclusions of Lemma 4.7 (with n replaced by
![]() $\lceil\lambda n\rceil$
). In particular, by (R3), we see that
$\lceil\lambda n\rceil$
). In particular, by (R3), we see that
 \begin{align} \mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}y_j^{\prime}, \sqrt{\lceil\lambda n\rceil}\right) &\ge c_{4.7}\mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}v_j, \sqrt{\lambda}/(C_1T)\right) \nonumber\\ & \ge c_{4.7}\mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}\frac{v_j}{\lVert{v_{I_i}}\rVert_{2}}, \frac{2\sqrt{\lambda}}{C_1T\cdot \sqrt{\lambda/c_0}}\right) \nonumber\\ &\ge C_1^{-1}\sqrt{c_0}\cdot c_{4.7}\mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}\frac{v_j}{\lVert{v_{I_i}}\rVert_2}, 2/T\right) \nonumber\\ &\ge C_1^{-1}\sqrt{c_0}\cdot c_{4.7}\cdot 2LT^{-1}.\end{align}
\begin{align} \mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}y_j^{\prime}, \sqrt{\lceil\lambda n\rceil}\right) &\ge c_{4.7}\mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}v_j, \sqrt{\lambda}/(C_1T)\right) \nonumber\\ & \ge c_{4.7}\mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}\frac{v_j}{\lVert{v_{I_i}}\rVert_{2}}, \frac{2\sqrt{\lambda}}{C_1T\cdot \sqrt{\lambda/c_0}}\right) \nonumber\\ &\ge C_1^{-1}\sqrt{c_0}\cdot c_{4.7}\mathcal{L}\left(\sum_{j\in I_i}b_j^{\prime}\frac{v_j}{\lVert{v_{I_i}}\rVert_2}, 2/T\right) \nonumber\\ &\ge C_1^{-1}\sqrt{c_0}\cdot c_{4.7}\cdot 2LT^{-1}.\end{align}
Let
![]() $I_0 = [n]\setminus (I_1 \cup \dots \cup I_m)$
. Then, by approximating each coordinate of
$I_0 = [n]\setminus (I_1 \cup \dots \cup I_m)$
. Then, by approximating each coordinate of
![]() $y_{I_0}$
by the nearest integer, and combining with the above integer approximations of
$y_{I_0}$
by the nearest integer, and combining with the above integer approximations of
![]() $y_{I_1},\dots, y_{I_m}$
, we obtain an integer vector
$y_{I_1},\dots, y_{I_m}$
, we obtain an integer vector
![]() $y'\in\mathbb{Z}^n$
such that for all
$y'\in\mathbb{Z}^n$
such that for all
![]() $1\leq i \leq m$
, the
$1\leq i \leq m$
, the
![]() $\lceil \lambda n \rceil$
-dimensional integer vector
$\lceil \lambda n \rceil$
-dimensional integer vector
![]() $y^{\prime}_{I_i}$
satisfies
$y^{\prime}_{I_i}$
satisfies
![]() $\|y_{I_i} - y^{\prime}_{I_i}\|_{\infty} \leq 1$
, (3), and
$\|y_{I_i} - y^{\prime}_{I_i}\|_{\infty} \leq 1$
, (3), and
 \begin{equation*}\mathcal{L}\left(\sum_{j \in I_i} b_j^{\prime}y_j^{\prime}, t \right) \leq C_{4.7}\frac{2L}{T\sqrt{\lceil \lambda n \rceil}} t, \quad \text{for all }t\geq \sqrt{\lceil \lambda n \rceil}.\end{equation*}
\begin{equation*}\mathcal{L}\left(\sum_{j \in I_i} b_j^{\prime}y_j^{\prime}, t \right) \leq C_{4.7}\frac{2L}{T\sqrt{\lceil \lambda n \rceil}} t, \quad \text{for all }t\geq \sqrt{\lceil \lambda n \rceil}.\end{equation*}
Step 2: Size of nets of level sets. We now estimate the number of possible realizations y’. This is the analogue of Proposition 3.3 in the present context. By paying an overall factor of at most
![]() $6^n$
, we may fix
$6^n$
, we may fix
![]() $\operatorname{Spread}(v)$
(hence all the
$\operatorname{Spread}(v)$
(hence all the
![]() $\operatorname{Spread}_\lambda^j(v)$
), as well as which
$\operatorname{Spread}_\lambda^j(v)$
), as well as which
![]() $\operatorname{Spread}_\lambda^j(v)$
are in
$\operatorname{Spread}_\lambda^j(v)$
are in
![]() $\mathcal{I}_M(v)$
and
$\mathcal{I}_M(v)$
and
![]() $\mathcal{J}_M(v)$
. As above, let us denote the intervals
$\mathcal{J}_M(v)$
. As above, let us denote the intervals
![]() $\operatorname{Spread}_\lambda^j(v)$
in
$\operatorname{Spread}_\lambda^j(v)$
in
![]() $\mathcal{I}_M(v)$
by
$\mathcal{I}_M(v)$
by
![]() $I_1,\dots, I_m$
, and let
$I_1,\dots, I_m$
, and let
![]() $I_0 = [n]\setminus (I_1\cup \dots \cup I_m)$
.
$I_0 = [n]\setminus (I_1\cup \dots \cup I_m)$
.
First, note that the number of choices for
![]() $y^{\prime}_{I_0}$
is at most
$y^{\prime}_{I_0}$
is at most
![]() $(CD/\sqrt{n})^{|I_0|}$
for an absolute constant C – this follows since
$(CD/\sqrt{n})^{|I_0|}$
for an absolute constant C – this follows since
![]() $y^{\prime}_{I_0}$
is an integer point in a ball of radius
$y^{\prime}_{I_0}$
is an integer point in a ball of radius
![]() $D \ge \sqrt{n} \ge \sqrt{|I_0|}$
(provided that
$D \ge \sqrt{n} \ge \sqrt{|I_0|}$
(provided that
![]() $C_1$
is chosen sufficiently large), at which point, we can use a standard volumetric estimate for the number of integer points in
$C_1$
is chosen sufficiently large), at which point, we can use a standard volumetric estimate for the number of integer points in
![]() $\mathbb{R}^{I_0}$
in a ball of radius
$\mathbb{R}^{I_0}$
in a ball of radius
![]() $R \ge \sqrt{|I_0|}$
, together with the bound
$R \ge \sqrt{|I_0|}$
, together with the bound
![]() $|I_0| \ge n/2$
.
$|I_0| \ge n/2$
.
Next, we fix
![]() $i \in [m]$
, and bound the number of choices for
$i \in [m]$
, and bound the number of choices for
![]() $y^{\prime}_{I_i}$
. Note that for any
$y^{\prime}_{I_i}$
. Note that for any
![]() $r \ge 0$
,
$r \ge 0$
,
 \begin{equation*}\mathcal{L}\left(\sum_{j \in I_i}b_j y^{\prime}_j, r\right) \ge \mathcal{L}\left(\sum_{j \in I_i}(b_j - \widetilde{b}_j) y^{\prime}_j, r\right),\end{equation*}
\begin{equation*}\mathcal{L}\left(\sum_{j \in I_i}b_j y^{\prime}_j, r\right) \ge \mathcal{L}\left(\sum_{j \in I_i}(b_j - \widetilde{b}_j) y^{\prime}_j, r\right),\end{equation*}
where
![]() $b_i, \widetilde{b}_i$
are independent copies of
$b_i, \widetilde{b}_i$
are independent copies of
![]() $\operatorname{Ber}(p)$
. Since
$\operatorname{Ber}(p)$
. Since
![]() $b^{\prime}_j$
is distributed as
$b^{\prime}_j$
is distributed as
![]() $b_j - \widetilde{b}_j$
, it follows from (3) that
$b_j - \widetilde{b}_j$
, it follows from (3) that
 \begin{equation*}\mathcal{L}\left(\sum_{j\in I_i}b_jy_j^{\prime},\sqrt{\lceil\lambda n\rceil}\right)\ge c_2LN^{-1},\end{equation*}
\begin{equation*}\mathcal{L}\left(\sum_{j\in I_i}b_jy_j^{\prime},\sqrt{\lceil\lambda n\rceil}\right)\ge c_2LN^{-1},\end{equation*}
where
![]() $b_j$
are i.i.d.
$b_j$
are i.i.d.
![]() $\operatorname{Ber}(p)$
random variables. From the definition of
$\operatorname{Ber}(p)$
random variables. From the definition of
![]() $\operatorname{Spread}_{\lambda}(v)$
and (R1), we see that
$\operatorname{Spread}_{\lambda}(v)$
and (R1), we see that
![]() $y_{I_i}^{\prime}$
lies within a
$y_{I_i}^{\prime}$
lies within a
![]() $(D/(C_2\sqrt{n}),\lceil\lambda n\rceil,K',1)$
-admissible set
$(D/(C_2\sqrt{n}),\lceil\lambda n\rceil,K',1)$
-admissible set
![]() $\mathcal{A}$
for
$\mathcal{A}$
for
![]() $C_2$
and K’ sufficiently large depending on
$C_2$
and K’ sufficiently large depending on
![]() $c_0, c_1$
. Then, for L sufficiently large depending on
$c_0, c_1$
. Then, for L sufficiently large depending on
![]() $c_0, c_1, p$
, by Theorem 4.4 (noting that D is bounded by
$c_0, c_1, p$
, by Theorem 4.4 (noting that D is bounded by
![]() $n2^{c'\lambda n}$
for all sufficiently large n, and that we can take c’ to be sufficiently small depending on p), we deduce that the number of potential
$n2^{c'\lambda n}$
for all sufficiently large n, and that we can take c’ to be sufficiently small depending on p), we deduce that the number of potential
![]() $y_{I_i}^{\prime}\in\mathbb{Z}^{I_i}$
is bounded by
$y_{I_i}^{\prime}\in\mathbb{Z}^{I_i}$
is bounded by
where C depends on
![]() $c_0, c_1$
, and M grows as
$c_0, c_1$
, and M grows as
![]() $\sqrt{\log\lceil\lambda n\rceil}$
, hence as
$\sqrt{\log\lceil\lambda n\rceil}$
, hence as
![]() $\sqrt{\log n}$
. Explicitly, we can pick
$\sqrt{\log n}$
. Explicitly, we can pick
![]() $M\ge c_3\sqrt{\log n}$
for some small
$M\ge c_3\sqrt{\log n}$
for some small
![]() $c_3 > 0$
depending only on
$c_3 > 0$
depending only on
![]() $c_0, c_1, p$
. Multiplying the total number of possibilities for
$c_0, c_1, p$
. Multiplying the total number of possibilities for
![]() $y^{\prime}_0,y^{\prime}_1,\dots, y^{\prime}_m$
, we see that the total number of possibilities for
$y^{\prime}_0,y^{\prime}_1,\dots, y^{\prime}_m$
, we see that the total number of possibilities for
![]() $y' \in \mathbb{Z}^{n}$
is at most
$y' \in \mathbb{Z}^{n}$
is at most
for C depending on
![]() $c_0, c_1$
and
$c_0, c_1$
and
![]() $M \ge c_3 \sqrt{\log{n}}$
with
$M \ge c_3 \sqrt{\log{n}}$
with
![]() $c_3$
depending on
$c_3$
depending on
![]() $c_0, c_1, p$
.
$c_0, c_1, p$
.
Step 3: Small-ball probability for net points. Fix
![]() $y' \in \mathbb{Z}^{n}$
resulting from the randomized rounding process and
$y' \in \mathbb{Z}^{n}$
resulting from the randomized rounding process and
![]() $u \in \mathbb{R}^{n}$
. Our goal is to bound
$u \in \mathbb{R}^{n}$
. Our goal is to bound
![]() $\mathbb{P}[\lVert{Ay'-u}\rVert_{2} \le Kn]$
. As in the proof of Lemma 3.6, we can without loss of generality permute the coordinates of y’ so that
$\mathbb{P}[\lVert{Ay'-u}\rVert_{2} \le Kn]$
. As in the proof of Lemma 3.6, we can without loss of generality permute the coordinates of y’ so that
![]() $I_1,\ldots,I_m$
are the first m blocks of size
$I_1,\ldots,I_m$
are the first m blocks of size
![]() $\lceil\lambda n\rceil$
within [n]. Then, for all
$\lceil\lambda n\rceil$
within [n]. Then, for all
![]() $\lceil\lambda n\rceil\le j\le c_{2.5}(\lambda)n$
, we have for all
$\lceil\lambda n\rceil\le j\le c_{2.5}(\lambda)n$
, we have for all
![]() $\epsilon \ge 0$
that
$\epsilon \ge 0$
that
 \begin{equation*}\mathcal{L}((Ay'-u)_j|(Ay'-u)_{j+1,\ldots,n},D\epsilon)\le CL\left(\frac{\epsilon}{\sqrt{j/n}}+\frac{\sqrt{\lambda n/j}}{{T}}\right),\end{equation*}
\begin{equation*}\mathcal{L}((Ay'-u)_j|(Ay'-u)_{j+1,\ldots,n},D\epsilon)\le CL\left(\frac{\epsilon}{\sqrt{j/n}}+\frac{\sqrt{\lambda n/j}}{{T}}\right),\end{equation*}
where C is an absolute constant. To deduce this, we use that the first j elements of row j are independent of rows
![]() $j+1,\dots, n$
, then use Lemma 4.5 to replace the Rademacher entries of A (plus the small Gaussian perturbation, which has variance so small that it can be disregarded) by
$j+1,\dots, n$
, then use Lemma 4.5 to replace the Rademacher entries of A (plus the small Gaussian perturbation, which has variance so small that it can be disregarded) by
![]() $\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
, and finally use Lemma 2.9 (as in the proof of Proposition 3.5) to stitch together the Lévy concentration properties of each
$\operatorname{Ber}(p)-\operatorname{Ber}'(p)$
, and finally use Lemma 2.9 (as in the proof of Proposition 3.5) to stitch together the Lévy concentration properties of each
![]() $y_{I_i}^{\prime}$
(guaranteed by (R3) of Lemma 4.7). Combining this with Lemma 2.7, we see that for y’, u as above,
$y_{I_i}^{\prime}$
(guaranteed by (R3) of Lemma 4.7). Combining this with Lemma 2.7, we see that for y’, u as above,
where C
![]() $^{\prime\prime}$
depends only on
$^{\prime\prime}$
depends only on
![]() $c_0, c_1, p$
.
$c_0, c_1, p$
.
Step 4: Union bound. On the event
![]() $\lVert{A}\rVert\le K\sqrt{n}$
,
$\lVert{A}\rVert\le K\sqrt{n}$
,
![]() $Av = tu$
with
$Av = tu$
with
![]() $\lVert{tu}\rVert_{2} \le K\sqrt{n}$
. By splitting the range
$\lVert{tu}\rVert_{2} \le K\sqrt{n}$
. By splitting the range
![]() $\{tu\}$
into
$\{tu\}$
into
![]() $(4D/\sqrt{n})^{2}$
intervals, and rounding v as in Step 2, we see that the probability of the event in question is bounded above by
$(4D/\sqrt{n})^{2}$
intervals, and rounding v as in Step 2, we see that the probability of the event in question is bounded above by
where the supremum is over
![]() $u \in \mathbb{R}^{n}$
and
$u \in \mathbb{R}^{n}$
and
![]() $y' \in \mathbb{Z}^{n}$
such that each
$y' \in \mathbb{Z}^{n}$
such that each
![]() $y_{I_i}^{\prime}$
for
$y_{I_i}^{\prime}$
for
![]() $i\in[m]$
satisfies the conclusions of Lemma 4.7 (with n replaced by
$i\in[m]$
satisfies the conclusions of Lemma 4.7 (with n replaced by
![]() $\lceil\lambda n\rceil$
). Controlling the final factor by Step 3, we see that the probability is bounded above by
$\lceil\lambda n\rceil$
). Controlling the final factor by Step 3, we see that the probability is bounded above by
where C depends on
![]() $c_0, c_1, p$
. Finally, since
$c_0, c_1, p$
. Finally, since
![]() $D\le 2^{2c'\lambda n}$
for all n sufficiently large (depending on
$D\le 2^{2c'\lambda n}$
for all n sufficiently large (depending on
![]() $c_0, c_1, p$
), we obtain an overall upper bound of
$c_0, c_1, p$
), we obtain an overall upper bound of
Since
![]() $M \ge c_3 \sqrt{\log{n}}$
, for
$M \ge c_3 \sqrt{\log{n}}$
, for
![]() $c_3$
depending on
$c_3$
depending on
![]() $c_0, c_1, p$
, the desired result follows by choosing
$c_0, c_1, p$
, the desired result follows by choosing
![]() $\lambda < c(\!\log n)^{1/4}n^{-1/2}$
for c sufficiently small depending on
$\lambda < c(\!\log n)^{1/4}n^{-1/2}$
for c sufficiently small depending on
![]() $c_0, c_1, p$
, so that the quantity above is bounded by
$c_0, c_1, p$
, so that the quantity above is bounded by
![]() $\exp(\!-\Omega(n(\!\log n)^{1/2}))$
.
$\exp(\!-\Omega(n(\!\log n)^{1/2}))$
.
5. Proof of Theorem 1.1
In this section (along with Appendix A), we complete the proof of Theorem 1.1 by closely following [Reference Vershynin30] with appropriate modifications. Since the smallest singular value is a continuous function of the entries of the matrix, by perturbing each entry of the random matrix by a Gaussian variable with arbitrarily small variance, one may assume that
![]() $\xi$
is absolutely continuous with respect to the Lebesgue measure; in particular, one may freely assume that various square matrices whose entries are independent copies of
$\xi$
is absolutely continuous with respect to the Lebesgue measure; in particular, one may freely assume that various square matrices whose entries are independent copies of
![]() $\xi$
are invertible.
$\xi$
are invertible.
5.1 Quadratic small-ball probabilities
To prove Theorem 1.1 and 1.2, we need the following small-ball inequalities for quadratic forms. The derivation is almost identical to the approach in [Reference Vershynin30, Theorem 8.1], with improvements coming from Theorem 3.7 and Proposition 3.5 (respectively Theorem 4.8). We include details in the appendix for the reader’s convenience.
Theorem 5.1 Let A be an
![]() $n\times n$
symmetric random matrix whose independent entries are identical copies of a sub-Gaussian random variable
$n\times n$
symmetric random matrix whose independent entries are identical copies of a sub-Gaussian random variable
![]() $\xi$
with variance 1. Suppose X is a random vector (independent of A) whose entries are independent copies of
$\xi$
with variance 1. Suppose X is a random vector (independent of A) whose entries are independent copies of
![]() $\xi$
. Then, for every
$\xi$
. Then, for every
![]() $\epsilon\ge 0$
and
$\epsilon\ge 0$
and
![]() $u\in\mathbb{R}$
, we have
$u\in\mathbb{R}$
, we have
 \begin{equation*}\mathbb{P}\bigg[\frac{|\langle {A^{-1}X,X} \rangle-u|}{\sqrt{1+\lVert{A^{-1}X}\rVert_2^2}}\le\epsilon\wedge\lVert{A}\rVert\le K\sqrt{n}\bigg]\le C_{5.1}\epsilon^{1/8}+2\exp(\!-\!c_{5.1}n^{1/2}).\end{equation*}
\begin{equation*}\mathbb{P}\bigg[\frac{|\langle {A^{-1}X,X} \rangle-u|}{\sqrt{1+\lVert{A^{-1}X}\rVert_2^2}}\le\epsilon\wedge\lVert{A}\rVert\le K\sqrt{n}\bigg]\le C_{5.1}\epsilon^{1/8}+2\exp(\!-\!c_{5.1}n^{1/2}).\end{equation*}
We similarly derive the following strengthening for Rademacher entries.
Theorem 5.2 Let A be an
![]() $n\times n$
symmetric random matrix whose independent entries are distributed as the sum of a Rademacher random variable and a centred Gaussian with variance
$n\times n$
symmetric random matrix whose independent entries are distributed as the sum of a Rademacher random variable and a centred Gaussian with variance
![]() $n^{-2n}$
. Suppose X is a random vector (independent of A) whose entries are independent Rademachers. Then, for all sufficiently large n, and for every
$n^{-2n}$
. Suppose X is a random vector (independent of A) whose entries are independent Rademachers. Then, for all sufficiently large n, and for every
![]() $\epsilon\ge 0$
and
$\epsilon\ge 0$
and
![]() $u\in\mathbb{R}$
, we have
$u\in\mathbb{R}$
, we have
 \begin{equation*}\mathbb{P}\bigg[\frac{|\langle {A^{-1}X,X} \rangle-u|}{\sqrt{1+\lVert{A^{-1}X}\rVert_2^2}}\le\epsilon\wedge\lVert{A}\rVert\le K\sqrt{n}\bigg]\le C_{5.1}\epsilon^{1/8}+2\exp(\!-\!c_{5.1}n^{1/2}(\!\log n)^{1/4}).\end{equation*}
\begin{equation*}\mathbb{P}\bigg[\frac{|\langle {A^{-1}X,X} \rangle-u|}{\sqrt{1+\lVert{A^{-1}X}\rVert_2^2}}\le\epsilon\wedge\lVert{A}\rVert\le K\sqrt{n}\bigg]\le C_{5.1}\epsilon^{1/8}+2\exp(\!-\!c_{5.1}n^{1/2}(\!\log n)^{1/4}).\end{equation*}
5.2 Putting it together
Given the above, the proofs of Theorems 1.1 and 1.2 follows from a modification (due to Vershynin) of the invertibility-via-distance paradigm due to Rudelson and Vershynin. We reproduce the details from [Reference Vershynin30] for the reader’s convenience
Proof of Theorems 1.1 and 1.2. Fix
![]() $c_0, c_1,c \in (0,1)$
, as guaranteed by Lemma 2.2. We can clearly assume that
$c_0, c_1,c \in (0,1)$
, as guaranteed by Lemma 2.2. We can clearly assume that
![]() $\epsilon \le c$
. Then, by the union bound and Lemma 2.2, we have
$\epsilon \le c$
. Then, by the union bound and Lemma 2.2, we have
Let
![]() $A_1,\dots, A_n$
denote the rows of A, and note that, by symmetry,
$A_1,\dots, A_n$
denote the rows of A, and note that, by symmetry,
In particular,
where
![]() $H_i$
is the span of the rows
$H_i$
is the span of the rows
![]() $A_j$
for
$A_j$
for
![]() $j\neq i$
. Since
$j\neq i$
. Since
![]() $|v_i| \ge c_1/2\sqrt{n}$
for all
$|v_i| \ge c_1/2\sqrt{n}$
for all
![]() $i \in \operatorname{Spread}(v)$
, it follows that if
$i \in \operatorname{Spread}(v)$
, it follows that if
![]() $\lVert{Av}\rVert_2 \le \epsilon/\sqrt{n}$
for some
$\lVert{Av}\rVert_2 \le \epsilon/\sqrt{n}$
for some
![]() $v \in \operatorname{Incomp}(c_0, c_1)$
, then we must necessarily have
$v \in \operatorname{Incomp}(c_0, c_1)$
, then we must necessarily have
for at least
![]() $c_{2.3}n$
indices
$c_{2.3}n$
indices
![]() $i \in [n]$
. Thus, we see that the probability that
$i \in [n]$
. Thus, we see that the probability that
![]() $s_n(A) \le \epsilon/\sqrt{n}$
is at most
$s_n(A) \le \epsilon/\sqrt{n}$
is at most
Therefore, for Theorem 1.1 it suffices to show that
A direct computation ([Reference Vershynin30, Proposition 5.1]) shows that
 \begin{equation*}\operatorname{dist}(A_1,H_1) = \frac{|\langle {(A')^{-1}X,X} \rangle-a_{11}|}{\sqrt{1+\lVert{(A')^{-1}X}\rVert_2^2}},\end{equation*}
\begin{equation*}\operatorname{dist}(A_1,H_1) = \frac{|\langle {(A')^{-1}X,X} \rangle-a_{11}|}{\sqrt{1+\lVert{(A')^{-1}X}\rVert_2^2}},\end{equation*}
where A
![]() $^{\prime}$
is the bottom right
$^{\prime}$
is the bottom right
![]() $(n-1)\times(n-1)$
block of A, and X is the first column of A with the top element removed. At this point, we can apply Theorem 5.1 to conclude. If A has Rademacher entries, by continuity we can transfer the singular value estimate to the model where the distribution is perturbed by a centred Gaussian with sufficiently small variance, at which point, an application of Theorem 5.2 allows us to conclude.
$(n-1)\times(n-1)$
block of A, and X is the first column of A with the top element removed. At this point, we can apply Theorem 5.1 to conclude. If A has Rademacher entries, by continuity we can transfer the singular value estimate to the model where the distribution is perturbed by a centred Gaussian with sufficiently small variance, at which point, an application of Theorem 5.2 allows us to conclude.
Acknowledgements
We thank Asaf Ferber and Roman Vershynin for comments on the manuscript. We also thank Dhruv Rohatgi for pointing out some typographical errors in a previous version. We are grateful to an anonymous referee for their careful reading of the manuscript and valuable comments. The last two authors were supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1745302. This work was done while the first author was participating in a program at the Simons Institute for the Theory of Computing.
Appendix A: Quadratic small-ball probabilities
The purpose of this appendix is to prove Theorem 5.1 for completeness. We will also briefly note the necessary modifications to deduce Theorem 5.2.
We essentially replicate the argument in [Reference Vershynin30, Section 8] with the obvious modifications. In brief, our improved anticoncentration estimate Proposition 3.5 will allow us to replace the
![]() $\epsilon^{1/8+\eta}$
dependence in [Reference Vershynin30] with
$\epsilon^{1/8+\eta}$
dependence in [Reference Vershynin30] with
![]() $\epsilon^{1/8}$
, and the improved range of arithmetic structure derived in Theorem 3.7 will allow us to achieve an error term of
$\epsilon^{1/8}$
, and the improved range of arithmetic structure derived in Theorem 3.7 will allow us to achieve an error term of
![]() $\exp(\!-\Omega(\sqrt{n}))$
. For the sake of simplicity, we define the event
$\exp(\!-\Omega(\sqrt{n}))$
. For the sake of simplicity, we define the event
Proposition A.1 (Analogue of [Reference Vershynin30, Proposition 8.2]) Let A be a symmetric random matrix whose independent entries are identical copies of a sub-Gaussian random variable with mean 0 and variance 1. Let X be a random vector (independent of A) whose coordinates are i.i.d. copies of
![]() $\xi$
. There exist constants
$\xi$
. There exist constants
![]() $C, c > 0$
depending only on the sub-Gaussian moment of
$C, c > 0$
depending only on the sub-Gaussian moment of
![]() $\xi$
for which the following holds.
$\xi$
for which the following holds.
For
![]() $\lambda\in(C/n,1/\sqrt{n})$
, A satisfies the following with probability at least
$\lambda\in(C/n,1/\sqrt{n})$
, A satisfies the following with probability at least
![]() $1-2e^{-cn}$
: if
$1-2e^{-cn}$
: if
![]() $\mathcal{E}_K$
holds, then for every
$\mathcal{E}_K$
holds, then for every
![]() $\epsilon > 0$
:
$\epsilon > 0$
:
-
•
 $\lVert{A^{-1}X}\rVert_2\ge c$
with probability at least
$\lVert{A^{-1}X}\rVert_2\ge c$
with probability at least
 $1-e^{-cn}$
in the randomness of X.
$1-e^{-cn}$
in the randomness of X. -
•
 $\lVert{A^{-1}X}\rVert_2\le\epsilon^{-1/2}\lVert{A^{-1}}\rVert_{\operatorname{HS}}$
with probability at least
$\lVert{A^{-1}X}\rVert_2\le\epsilon^{-1/2}\lVert{A^{-1}}\rVert_{\operatorname{HS}}$
with probability at least
 $1-\epsilon$
in the randomness of X.
$1-\epsilon$
in the randomness of X. -
•
 $\lVert{A^{-1}X}\rVert_2\ge\epsilon\lVert{A^{-1}}\rVert_{\operatorname{HS}}$
with probability at least
$\lVert{A^{-1}X}\rVert_2\ge\epsilon\lVert{A^{-1}}\rVert_{\operatorname{HS}}$
with probability at least
 $1-C\epsilon-2e^{-c\lambda n}$
in the randomness of X.
$1-C\epsilon-2e^{-c\lambda n}$
in the randomness of X.
Proof. The first two parts have the same proof as in [Reference Vershynin30, Proposition 8.2]. The last part also has essentially the same proof, except that we use Proposition 3.5 in place of [Reference Vershynin30, Proposition 6.9] and use Theorem 3.7 in place of [Reference Vershynin30, Theorem 7.1].
Remark For Theorem 5.2, we note that if A has entries that are Rademacher plus a centred Gaussian with sufficiently small variance, we can prove the same statement with
![]() $n^{-2/3} < \lambda < c(\!\log n)^{1/4}n^{-1/2}$
. We use Theorem 4.8 instead of Theorem 3.7 and the analogue of Proposition 3.5 for the threshold. The remaining part of the proof is exactly the same.
$n^{-2/3} < \lambda < c(\!\log n)^{1/4}n^{-1/2}$
. We use Theorem 4.8 instead of Theorem 3.7 and the analogue of Proposition 3.5 for the threshold. The remaining part of the proof is exactly the same.
Next, we require the following decoupling lemma from [Reference Vershynin30]; this use of decoupling to establish singularity for symmetric random matrices originates in work of Costello et al. [Reference Costello, Tao and Vu6] and has been used in essentially all follow-up works.
Lemma A.2 ([Reference Vershynin30, Lemma 8.4]) Let G be an arbitrary symmetric
![]() $n\times n$
matrix, and let X,X
$n\times n$
matrix, and let X,X
![]() $^{\prime}$
be independent samples of a random vector in
$^{\prime}$
be independent samples of a random vector in
![]() $\mathbb{R}^n$
with independent coordinates. Let
$\mathbb{R}^n$
with independent coordinates. Let
![]() $J\subseteq[n]$
. Then, for every
$J\subseteq[n]$
. Then, for every
![]() $\epsilon\ge 0$
we have
$\epsilon\ge 0$
we have
for some random variable v determined by
![]() $G|_{J^c\times J^c}$
and
$G|_{J^c\times J^c}$
and
![]() $P_{J^c}X, P_{J^c}X'$
.
$P_{J^c}X, P_{J^c}X'$
.
We can now prove Theorem 5.1; we refer the reader to [Reference Vershynin30] for a more detailed exposition.
Proof of Theorem 5.1. We randomly choose
![]() $J\subseteq[n]$
by sampling elements independently with probability
$J\subseteq[n]$
by sampling elements independently with probability
![]() $1-c_{2.3}/2$
. We trivially see by the Chernoff bound that if
$1-c_{2.3}/2$
. We trivially see by the Chernoff bound that if
![]() $\mathcal{E}_J = \{|J^c|\le c_{2.3}n\}$
, then
$\mathcal{E}_J = \{|J^c|\le c_{2.3}n\}$
, then
For J satisfying
![]() $\mathcal{E}_J$
, let us assign the set
$\mathcal{E}_J$
, let us assign the set
![]() $\operatorname{Spread}(v)$
for
$\operatorname{Spread}(v)$
for
![]() $v\in\operatorname{Incomp}(c_0,c_1)$
in a way such that
$v\in\operatorname{Incomp}(c_0,c_1)$
in a way such that
![]() $\operatorname{Spread}(x)\subseteq |J|$
. We can do this since, in Lemma 2.3, we chose
$\operatorname{Spread}(x)\subseteq |J|$
. We can do this since, in Lemma 2.3, we chose
![]() $c_{2.3}$
so as to have at least
$c_{2.3}$
so as to have at least
![]() $2c_{2.3}n$
spread coordinates. We will then use this assignment to obtain the median regularized LCDs that are used.
$2c_{2.3}n$
spread coordinates. We will then use this assignment to obtain the median regularized LCDs that are used.
Next, consider the event
![]() $\mathcal{E}_D$
given by
$\mathcal{E}_D$
given by
Applying Proposition A.1 to X and
![]() $Y_i = \delta_i(X_i-X_i')$
, where
$Y_i = \delta_i(X_i-X_i')$
, where
![]() $\delta_i$
is the indicator of
$\delta_i$
is the indicator of
![]() $i\in J^c$
, and adjusting constants appropriately, we find that
$i\in J^c$
, and adjusting constants appropriately, we find that
where the constants depend only on the sub-Gaussian norm of
![]() $\xi$
. Now define
$\xi$
. Now define
which is a random vector. If the denominator is 0, we can use an arbitrary fixed vector. Let
![]() $\mathcal{E}_U$
be the event (analogue of [Reference Vershynin30, Equation 8.11]) that
$\mathcal{E}_U$
be the event (analogue of [Reference Vershynin30, Equation 8.11]) that
where we choose L as in Theorem 3.7.
Now condition on some J satisfying
![]() $\mathcal{E}_J$
and some X,X’. By Theorem 3.7, we deduce that
$\mathcal{E}_J$
and some X,X’. By Theorem 3.7, we deduce that
Thus (analogue of [Reference Vershynin30, Equation 8.12])
where
![]() $p_0 = C\max(\epsilon_0,2^{-\lambda n/C})$
. Hence, there is a realization of J such that
$p_0 = C\max(\epsilon_0,2^{-\lambda n/C})$
. Hence, there is a realization of J such that
![]() $\mathcal{E}_J$
holds and
$\mathcal{E}_J$
holds and
We fix this choice of J for the remainder of the proof. Now let
![]() $\mathcal{E}_A$
be the event, dependent only on A, that simultaneously
$\mathcal{E}_A$
be the event, dependent only on A, that simultaneously
![]() $\mathcal{E}_K$
and
$\mathcal{E}_K$
and
By Fubini’s theorem, Markov’s inequality, and the fact that
![]() $\mathcal{E}_K$
depends only on A, we see from the above that (analogue of [Reference Vershynin30, Equation 8.13])
$\mathcal{E}_K$
depends only on A, we see from the above that (analogue of [Reference Vershynin30, Equation 8.13])
Now, if
![]() $\mathcal{E}$
is the desired event
$\mathcal{E}$
is the desired event
 \begin{equation*}\frac{|\langle {A^{-1}X,X} \rangle-u|}{\sqrt{1+\lVert{A^{-1}X}\rVert_2^2}}\le\epsilon,\end{equation*}
\begin{equation*}\frac{|\langle {A^{-1}X,X} \rangle-u|}{\sqrt{1+\lVert{A^{-1}X}\rVert_2^2}}\le\epsilon,\end{equation*}
then
Fix some
![]() $A\in\mathcal{E}_A$
for the remainder of the proof. We need to bound
$A\in\mathcal{E}_A$
for the remainder of the proof. We need to bound
Using
![]() $\mathcal{E}_D$
along with
$\mathcal{E}_D$
along with
![]() $\mathcal{E}$
, we see that
$\mathcal{E}$
, we see that
Then by Lemma A.2, we find that this satisfies
where
![]() $v = v(A^{-1},P_{J^c}X,P_{J^c}X')$
is some random variable depending on these parameters only. This last probability is at most
$v = v(A^{-1},P_{J^c}X,P_{J^c}X')$
is some random variable depending on these parameters only. This last probability is at most
Now by using
![]() $\mathcal{E}_D$
again, and dividing the inequality in question by
$\mathcal{E}_D$
again, and dividing the inequality in question by
![]() $\lVert{A^{-1}P_{J^c}(X-X')}\rVert_2$
, we see that (analogue of [Reference Vershynin30, Equation 8.15])
$\lVert{A^{-1}P_{J^c}(X-X')}\rVert_2$
, we see that (analogue of [Reference Vershynin30, Equation 8.15])
Finally, we can apply Proposition 3.5 to this random variable. Note that
![]() $x_0,w$
do not depend on
$x_0,w$
do not depend on
![]() $P_JX$
. Also, we know from
$P_JX$
. Also, we know from
![]() $\mathcal{E}_U$
that
$\mathcal{E}_U$
that
![]() $\widehat{MD}_L(x_0,\lambda)\ge 2^{\lambda n/C}$
. It suffices to check that
$\widehat{MD}_L(x_0,\lambda)\ge 2^{\lambda n/C}$
. It suffices to check that
![]() $\operatorname{Spread}_\lambda(x_0)\subseteq J$
by the definitions chosen at the beginning; hence, we can drop the randomness in
$\operatorname{Spread}_\lambda(x_0)\subseteq J$
by the definitions chosen at the beginning; hence, we can drop the randomness in
![]() $P_JX$
of all coordinates except for those in the spread set and apply the result. We again technically need to check that
$P_JX$
of all coordinates except for those in the spread set and apply the result. We again technically need to check that
![]() $\operatorname{Spread}_\lambda(x_0)$
satisfies the conditions on Proposition 3.5, which we have already implicitly verified before. Overall, we deduce
$\operatorname{Spread}_\lambda(x_0)$
satisfies the conditions on Proposition 3.5, which we have already implicitly verified before. Overall, we deduce
Finally, tracing it all back, we have
by sub-Gaussian concentration of the operator norm of A ([Reference Vershynin30, Lemma 2.3]). Now choosing
![]() $\epsilon_0 = \epsilon^{1/2}$
and
$\epsilon_0 = \epsilon^{1/2}$
and
![]() $\lambda = 1/\sqrt{n}$
, which is the biggest permitted by Theorem 3.7, we are done.
$\lambda = 1/\sqrt{n}$
, which is the biggest permitted by Theorem 3.7, we are done.