Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-11T21:38:16.975Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Independence Number of Steiner Systems

Published online by Cambridge University Press:  30 January 2013

ALEX EUSTIS  and
JACQUES VERSTRAËTE
ALEX EUSTIS
Affiliation:
Department of Mathematics, UCSD, 9500 Gilman Drive, La Jolla, CA 92093-0112, USA (e-mail: jbaverstraete@gmail.com)
JACQUES VERSTRAËTE
Affiliation:
Department of Mathematics, UCSD, 9500 Gilman Drive, La Jolla, CA 92093-0112, USA (e-mail: jbaverstraete@gmail.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

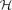A partial Steiner (n,r,l)-system is an r-uniform hypergraph on n vertices in which every set of l vertices is contained in at most one edge. A partial Steiner (n,r,l)-system is complete if every set of l vertices is contained in exactly one edge. In a hypergraph , the independence number α(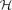) denotes the maximum size of a set of vertices in 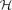containing no edge. In this article we prove the following. Given integers r,l such that r ≥ 2l − 1 ≥ 3, we prove that there exists a partial Steiner (n,r,l)-system 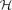such that

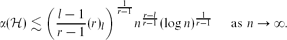$$\alpha(\HH) \lesssim \biggl(\frac{l-1}{r-1}(r)_l\biggr)^{\frac{1}{r-1}}n^{\frac{r-l}{r-1}} (\log n)^{\frac{1}{r-1}} \quad \mbox{ as }n \rightarrow \infty.$$
This improves earlier results of Phelps and Rödl, and Rödl and Ŝinajová. We conjecture that it is best possible as it matches the independence number of a random r-uniform hypergraph of the same density. If l = 2 or l = 3, then for infinitely many r the partial Steiner systems constructed are complete for infinitely many n.

Keywords

Primary 05B05Secondary 05B0705B2005B2505D40
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 2 , March 2013 , pp. 241 - 252
Copyright
Copyright © Cambridge University Press 2013

References

[1]Ajtai, M., Komlós, J., Pintz, J., Spencer, J. and Szemerédi, E. (1982) Extremal uncrowded hypergraphs. J. Combin. Theory Ser. A 32 321–335.CrossRefGoogle Scholar
[2]Alon, N., Mellinger, K., Mubayi, D. and Verstraëte, J. (2011) The de Bruijn–Erdős theorem for hypergraphs. Submitted.Google Scholar
[3]Alon, N. and Spencer, J. (2000) The Probabilistic Method, second edition, Wiley.Google Scholar
[4]Caro, Y. and Tuza, Z. (1991) Improved lower bounds on $k$-independence. J. Graph Theory 15 99–107.Google Scholar
[5]Colbourn, C. and Dinitz, J., eds (1996) The CRC Handbook of Combinatorial Designs, CRC Press.Google Scholar
[6]Dembowski, P. (1996) Finite Geometries, Springer. Reprint of 1968 edition.Google Scholar
[7]Duke, R., Lefmann, H. and Rödl, V. (1995) On uncrowded hypergraphs. Random Struct. Alg. 6 209–212.CrossRefGoogle Scholar
[8]Eustis, A. and Verstraëte, J. (2012) Independent sets in randomized construction of Steiner (n,r,r-1)-systems. Preprint.Google Scholar
[9]Erdős, P. and Hanani, H. (1963) On a limit theorem in combinatorial analysis. Publ. Math. Debrecen 10 10–13.CrossRefGoogle Scholar
[10]Frieze, A. and Mubayi, D. (2008) On the chromatic number of simple triangle-free triple systems. Electron. J. Combin. 15 R121.Google Scholar
[11]Frieze, A. and Mubayi, D. (2008) Coloring simple hypergraphs. Preprint.Google Scholar
[12]Füredi, Z. (1991) Maximal independent subsets in Steiner systems and in planar sets. SIAM J. Discrete Math. 4 196–199Google Scholar
[13]Haemers, W. (1980) Eigenvalue techniques in design and graph theory. PhD thesis, Technical University Eindhoven. Math. Centre Tract 121, Mathematical Centre, Amsterdam.Google Scholar
[14]Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of Erdős. Combin. Theory Appl. 2 601–623.Google Scholar
[15]Keevash, P., Sudakov, B. and Verstraëte, J. (2011) On a conjecture of Erdős and Simonovits: Even Cycles. Combinatorica. (accepted).Google Scholar
[16]Kirkman, T. (1847) On a problem in combinations. The Cambridge and Dublin Mathematical Journal (Macmillan, Barclay, and Macmillan) II 191–204.Google Scholar
[17]Komlós, J., Pintz, J. and Szemerédi, E. (1982) A lower bound for Heilbronn's problem. J. London Math. Soc. (2) 25 13–24.Google Scholar
[18]Kostochka, A., Mubayi, D. and Verstraëte, J. (2011) On independent sets in hypergraphs. Random Struct. Alg. (accepted).Google Scholar
[19]Krivelevich, M. and Sudakov, B. (1998) The chromatic numbers of random hypergraphs. Random Struct. Alg. 12 381–403.Google Scholar
[20]Phelps, K. and Rödl, V. (1986) Steiner triple systems with minimum independence number. Ars Combin. 21 167–172.Google Scholar
[21]Rödl, V. (1985) On a packing and covering problem. Europ. J. Combin. 6 69–78.Google Scholar
[22]Rödl, V. and Ŝinajová, V. (1994) Note on independent sets in Steiner systems. Random Struct. Alg. 5 183–190.Google Scholar
[23]Shearer, J. (1983) A note on the independence number of triangle-free graphs. Discrete Math. 46 83–87.Google Scholar
[24]Wilson, R. (1975) An existence theorem for pairwise balanced designs III: Proof of the existence conjecture. J. Combin. Theory Ser. A 18 71–79.Google Scholar