Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-06T19:52:33.376Z Has data issue: false hasContentIssue false
  • English
  • Français

On n-Sums in an Abelian Group

Part of: Abelian groups Sequences and sets Additive number theory; partitions

Published online by Cambridge University Press:  03 November 2015

WEIDONG GAO ,
DAVID J. GRYNKIEWICZ  and
XINGWU XIA
WEIDONG GAO
Affiliation:
Center for Combinatorics, LPMC-TJKLC, Nankai University, Tianjin 300071, PR China (e-mail: wdgao1963@aliyun.com)
DAVID J. GRYNKIEWICZ
Affiliation:
University of Memphis, Memphis, TN 38152, USA (e-mail: diambri@hotmail.com)
XINGWU XIA
Affiliation:
Department of Mathematics, Luoyang Normal University, Luoyang 471022, PR China (e-mail: xxwsjtu@aliyun.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be an additive abelian group, let n ⩾ 1 be an integer, let S be a sequence over G of length |S| ⩾ n + 1, and let 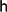${\mathsf h}$(S) denote the maximum multiplicity of a term in S. Let Σn(S) denote the set consisting of all elements in G which can be expressed as the sum of terms from a subsequence of S having length n. In this paper, we prove that either ng ∈ Σn(S) for every term g in S whose multiplicity is at least 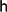${\mathsf h}$(S) − 1 or |Σn(S)| ⩾ min{n + 1, |S| − n + | supp (S)| − 1}, where |supp(S)| denotes the number of distinct terms that occur in S. When G is finite cyclic and n = |G|, this confirms a conjecture of Y. O. Hamidoune from 2003.

MSC classification

Primary: 11B75: Other combinatorial number theory
Secondary: 11P99: None of the above, but in this section 20K01: Finite abelian groups
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 3 , May 2016 , pp. 419 - 435
Copyright
Copyright © Cambridge University Press 2015 

References

[1] Bialostocki, A., Grynkiewicz, D. and Lotspeich, M. (2003) On some developments of the Erdős–Ginzburg–Ziv theorem II. Acta Arith. 110 173–184.Google Scholar
[2] Bialostocki, A. and Lotspeich, M. (1992) Some developments of the Erdős–Ginzburg–Ziv theorem. In Sets, Graphs and Numbers, Vol. 60 of Coll. Math. Soc. J. Bolyai, pp. 97–117.Google Scholar
[3] Bollobás, B. and Leader, I. (1999) The number of k-sums modulo k. J. Number Theory 78 27–35.CrossRefGoogle Scholar
[4] Bovey, J. D., Erdős, P. and Niven, I. (1975) Conditions for zero sum modulo n. Canad. Math. Bull. 18 27–29.CrossRefGoogle Scholar
[5] Caro, Y. (1996) Zero-sum problems: A survey. Discrete Math. 152 93–113.Google Scholar
[6] DeVos, M., Goddyn, L. and Mohar, B. (2009) A generalization of Kneser's Addition Theorem. Adv. Math. 220 1531–1548.Google Scholar
[7] Eggleton, R. B. and Erdős, P. (1972) Two combinatorial problems in group theory. Acta Arith. 21 111–116.CrossRefGoogle Scholar
[8] Gallardo, L., Grekos, G. and Pinko, J. (1999) On a variant of the Erdős–Ginzburg–Ziv problem. Acta Arith. 89 331–336.Google Scholar
[9] Gao, W. D. (1995) Addition theorems for finite abelian groups. J. Number Theory 53 241–246.CrossRefGoogle Scholar
[10] Gao, W. D. (1996) A combinatorial problem on finite abelian groups. J. Number Theory 58 100–103.CrossRefGoogle Scholar
[11] Gao, W. D. (1999) On the number of subsequences with given sum. Discrete Math. 195 127–138.CrossRefGoogle Scholar
[12] Gao, W. D. and Leader, I. (2006) Sums and k-sums in abelian groups of order k. J. Number Theory 120 26–32.Google Scholar
[13] Gao, W. D., Li, Y. L., Peng, J. T. and Sun, F. (2008) On subsequence sums of a zero-sum free sequence II. Electron. J. Combin. 15 R117.CrossRefGoogle Scholar
[14] Geroldinger, A. and Halter-Koch, F. (2006) Non-Unique Factorizations: Algebraic, Combinatorial and Analytic Theory, Vol. 278 of Pure and Applied Mathematics, Chapman & Hall/CRC.Google Scholar
[15] Grynkiewicz, D. (2005) On a conjecture of Hamidoune for subsequence sums. Integers 5 A7.Google Scholar
[16] Grynkiewicz, D. (2013) Structural Additive Theory, Developments in Mathematics, Springer.Google Scholar
[17] Grynkiewicz, D. J., Marchan, E. and Ordaz, O. (2009) Representation of finite abelian group elements by subsequence sums. J. Théor. Nombres Bordeaux 21 559–587.CrossRefGoogle Scholar
[18] Hamidoune, Y. O. (2003) Subsequence sums. Combin. Probab. Comput. 12 413–425.Google Scholar
[19] Mann, H. B. (1967) Two addition theorems. J. Combin. Theory 3 233–235.CrossRefGoogle Scholar
[20] Nathanson, M. B. (1996) Additive Number Theory: Inverse Problems and the Geometry of Sumsets, Vol. 165 of Graduate Texts in Mathematics, Springer.Google Scholar
[21] Olson, J. E. (1977) An addition theorem for finite abelian groups. J. Number Theory 9 63–70.Google Scholar
[22] Olson, J. E. and White, E. T. (1977) Sums from a sequence of group elements. In Number Theory and Algebra, Academic Press, pp. 215–222.Google Scholar
[23] Pixton, A. (2009) Sequences with small subsum sets. J. Number Theory 129 806–817.Google Scholar
[24] Savchev, S. and Chen, F. (2008) Long n-zero-free sequences in finite cyclic groups. Discrete Math. 308 1–8.Google Scholar
[25] Scherk, P. (1955) Distinct elements in a set of sums. Amer. Math. Monthly 62 46–47.Google Scholar
[26] Sun, F. (2007) On subsequence sums of a zero-sum free sequence. Electron. J. Combin. 14 R52.CrossRefGoogle Scholar