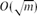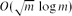Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ackerman, Eyal
and
Schaefer, Marcus
2014.
Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications.
Vol. 8827,
Issue. ,
p.
222.
Matoušek, Jiří
2014.
Geometry, Structure and Randomness in Combinatorics.
p.
61.
Har-Peled, Sariel
and
Quanrud, Kent
2015.
Algorithms - ESA 2015.
Vol. 9294,
Issue. ,
p.
717.
Har-Peled, Sariel
and
Quanrud, Kent
2017.
Approximation Algorithms for Polynomial-Expansion and Low-Density Graphs.
SIAM Journal on Computing,
Vol. 46,
Issue. 6,
p.
1712.
Carmi, Paz
Chiu, Man Kwun
Katz, Matthew J.
Korman, Matias
Okamoto, Yoshio
van Renssen, André
Roeloffzen, Marcel
Shiitada, Taichi
and
Smorodinsky, Shakhar
2017.
Algorithms and Data Structures.
Vol. 10389,
Issue. ,
p.
241.
Janson, Svante
and
Uzzell, Andrew J.
2017.
On String Graph Limits and the Structure of a Typical String Graph.
Journal of Graph Theory,
Vol. 84,
Issue. 4,
p.
386.
Pach, János
Rubin, Natan
and
Tardos, Gábor
2018.
A Crossing Lemma for Jordan curves.
Advances in Mathematics,
Vol. 331,
Issue. ,
p.
908.
Bonnet, Édouard
and
Rzążewski, Paweł
2018.
Graph-Theoretic Concepts in Computer Science.
Vol. 11159,
Issue. ,
p.
79.
Dujmović, Vida
Joret, Gwenaël
Morin, Pat
Norin, Sergey
and
Wood, David R.
2018.
Orthogonal Tree Decompositions of Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 2,
p.
839.
Rok, Alexandre
and
Walczak, Bartosz
2019.
Outerstring Graphs are $\chi$-Bounded.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 4,
p.
2181.
Rok, Alexandre
and
Walczak, Bartosz
2019.
Coloring Curves that Cross a Fixed Curve.
Discrete & Computational Geometry,
Vol. 61,
Issue. 4,
p.
830.
Adamaszek, Anna
Har-Peled, Sariel
and
Wiese, Andreas
2019.
Approximation Schemes for Independent Set and Sparse Subsets of Polygons.
Journal of the ACM,
Vol. 66,
Issue. 4,
p.
1.
Bonnet, Édouard
and
Rzążewski, Paweł
2019.
Optimality Program in Segment and String Graphs.
Algorithmica,
Vol. 81,
Issue. 7,
p.
3047.
OLIVEIRA, Farley Soares
HIRAISHI, Hidefumi
and
IMAI, Hiroshi
2019.
Revisiting the Top-Down Computation of BDD of Spanning Trees of a Graph and Its Tutte Polynomial.
IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences,
Vol. E102.A,
Issue. 9,
p.
1022.
Okrasa, Karolina
and
Rzążewski, Paweł
2019.
Graph-Theoretic Concepts in Computer Science.
Vol. 11789,
Issue. ,
p.
1.
Okrasa, Karolina
and
Rzążewski, Paweł
2020.
Subexponential algorithms for variants of the homomorphism problem in string graphs.
Journal of Computer and System Sciences,
Vol. 109,
Issue. ,
p.
126.
Carmi, Paz
Chiu, Man Kwun
Katz, Matthew J.
Korman, Matias
Okamoto, Yoshio
van Renssen, André
Roeloffzen, Marcel
Shiitada, Taichi
and
Smorodinsky, Shakhar
2020.
Balanced line separators of unit disk graphs.
Computational Geometry,
Vol. 86,
Issue. ,
p.
101575.
Keller, Chaya
Rok, Alexandre
and
Smorodinsky, Shakhar
2021.
Conflict-Free Coloring of String Graphs.
Discrete & Computational Geometry,
Vol. 65,
Issue. 4,
p.
1337.
Tomon, István
2022.
A Sharp Threshold Phenomenon in String Graphs.
Discrete & Computational Geometry,
Vol. 67,
Issue. 1,
p.
338.
Bonamy, Marthe
Bousquet, Nicolas
Pilipczuk, Michał
Rzążewski, Paweł
Thomassé, Stéphan
and
Walczak, Bartosz
2022.
Degeneracy of P-free and C⩾-free graphs with no large complete bipartite subgraphs.
Journal of Combinatorial Theory, Series B,
Vol. 152,
Issue. ,
p.
353.