Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T19:41:15.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Judicious Partitioning of Hypergraphs with Edges of Size at Most 2†

Part of: Graph theory

Published online by Cambridge University Press:  16 August 2016

JIANFENG HOU  and
QINGHOU ZENG
JIANFENG HOU
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian, P. R. China350003 (e-mail: jfhou@fzu.edu.cn, qinghouzeng@hotmail.com)
QINGHOU ZENG*
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian, P. R. China350003 (e-mail: jfhou@fzu.edu.cn, qinghouzeng@hotmail.com)
*
‡Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Judicious partitioning problems on graphs and hypergraphs ask for partitions that optimize several quantities simultaneously. Let k ≥ 2 be an integer and let G be a hypergraph with mi edges of size i for i=1,2. Bollobás and Scott conjectured that G has a partition into k classes, each of which contains at most 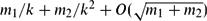$m_1/k+m_2/k^2+O(\sqrt{m_1+m_2})$ edges. In this paper, we confirm the conjecture affirmatively by showing that G has a partition into k classes, each of which contains at most

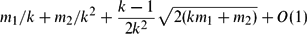$$m_1/k+m_2/k^2+\ffrac{k-1}{2k^2}\sqrt{2(km_1+m_2)}+O(1)$$.
edges. This bound is tight up to O(1).

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C75: Structural characterization of families of graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 2 , March 2017 , pp. 267 - 284
Copyright
Copyright © Cambridge University Press 2016 

Footnotes

†

This work is supported by research grant NSFC.

References

[1] Alon, N. (1996) Bipartite subgraphs. Combinatorica 16 301–311.CrossRefGoogle Scholar
[2] Alon, N., Bollobás, B., Krivelevich, M. and Sudakov, B. (2003) Maximum cuts and judicious partitions in graphs without short cycles. J. Combin. Theory Ser. B 88 329–346.Google Scholar
[3] Bollobás, B. and Scott, A. D. (1997) Judicious partitions of hypergraphs. J. Combin. Theory Ser. A 78 15–31.Google Scholar
[4] Bollobás, B. and Scott, A. D. (1999) Exact bounds for judicious partitions of graphs. Combinatorica 19 473–486.Google Scholar
[5] Bollobás, B. and Scott, A. D. (2000) Judicious partitions of 3-uniform hypergraphs. European J. Combin. 21 289–300.Google Scholar
[6] Bollobás, B. and Scott, A. D. (2002) Better bounds for Max Cut. In Contemporary Combinatorics, Vol. 10 of Bolyai Society Mathematical Studies, pp. 185–246.Google Scholar
[7] Bollobás, B. and Scott, A. D. (2002) Problems and results on judicious partitions. Random Struct. Alg. 21 414–430.CrossRefGoogle Scholar
[8] Bollobás, B. and Scott, A. D. (2010) Max k-cut and judicious k-partitions. Discrete Math. 310 2126–2139.Google Scholar
[9] Edwards, C. S. (1973) Some extremal properties of bipartite graphs. Canad. J. Math. 3 475–485.CrossRefGoogle Scholar
[10] Edwards, C. S. (1975) An improved lower bound for the number of edges in a largest bipartite subgraph. In Proc. 2nd Czechoslovak Symposium on Graph Theory, pp. 167–181.Google Scholar
[11] Fan, G. and Hou, J. Bounds for pairs in judicious partitions of graphs. Random Struct. Alg. doi:10.1002/rsa.20642 CrossRefGoogle Scholar
[12] Fan, G., Hou, J. and Zeng, Q. (2014) A bound for judicious k-partitions of graphs. Discrete Appl. Math. 179 86–99.Google Scholar
[13] Haslegrave, J. (2012) The Bollobás–Thomason conjecture for 3-uniform hypergraphs. Combinatorica 32 451–471.Google Scholar
[14] Haslegrave, J. (2014) Judicious partitions of uniform hypergraphs. Combinatorica 34 561–572.CrossRefGoogle Scholar
[15] Hou, J., Wu, S. and Yan, G. (2016) On judicious partitions of uniform hypergraphs. J. Combin. Theory Ser. A 141 16–32.CrossRefGoogle Scholar
[16] Lee, C., Loh, P. and Sudakov, B. (2013) Bisections of graphs. J. Combin. Theory Ser. B 103 599–629.Google Scholar
[17] Ma, J., Yen, P. and Yu, X. (2010) On several partitioning problems of Bollobás and Scott. J. Combin. Theory Ser. B 100 631–649.CrossRefGoogle Scholar
[18] Ma, J. and Yu, X. (2012) Partitioning 3-uniform hypergraphs. J. Combin. Theory Ser. B 102 212–232.Google Scholar
[19] Scott, A. D. (2005) Judicious partitions and related problems. In Surveys in Combinatorics, Vol. 327 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 95–117.Google Scholar
[20] Xu, B. and Yu, X. (2008) Triangle-free subcubic graphs with minimum bipartite density. J. Combin. Theory Ser. B 98 516–537.CrossRefGoogle Scholar
[21] Xu, B. and Yu, X. (2014) On judicious bisections of graphs. J. Combin. Theory Ser. B 106 30–69.CrossRefGoogle Scholar
[22] Yannakakis, M. (1978) Node- and edge-deletion NP-complete problems. In STOC '78: Proc. 10th Annual ACM Symposium on Theory of Computing, pp. 253–264.Google Scholar
[23] Zhu, X. (2009) Bipartite density of triangle-free subcubic graphs. Discrete Appl. Math. 157 710–714.Google Scholar