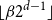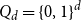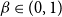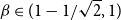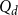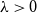1. Introduction
Let
![]() $Q_d$
be the discrete hypercube: the graph with vertex set
$Q_d$
be the discrete hypercube: the graph with vertex set
![]() $\{0,1\}^d$
in which two vectors are joined by an edge if they differ in exactly one coordinate. An independent set is a set of vertices that contains no edge. Let
$\{0,1\}^d$
in which two vectors are joined by an edge if they differ in exactly one coordinate. An independent set is a set of vertices that contains no edge. Let
![]() $\mathcal {I}(Q_d)$
be the set of independent sets of
$\mathcal {I}(Q_d)$
be the set of independent sets of
![]() $Q_d$
and let
$Q_d$
and let
![]() $i(Q_d)= | \mathcal {I}(Q_d)|$
be the number of independent sets of the hypercube. The vertices of
$i(Q_d)= | \mathcal {I}(Q_d)|$
be the number of independent sets of the hypercube. The vertices of
![]() $Q_d$
can be divided into two sets, those whose coordinates sum to an even number and those whose coordinates sum to an odd number. This partition shows that
$Q_d$
can be divided into two sets, those whose coordinates sum to an even number and those whose coordinates sum to an odd number. This partition shows that
![]() $Q_d$
is a bipartite graph. We let
$Q_d$
is a bipartite graph. We let
![]() $N := 2^{d-1}$
be the number of even (or odd) vertices of
$N := 2^{d-1}$
be the number of even (or odd) vertices of
![]() $Q_d$
. A trivial lower bound on
$Q_d$
. A trivial lower bound on
![]() $i(Q_d)$
is
$i(Q_d)$
is
![]() $2 \cdot 2^{N} -1$
obtained by considering independent sets of only even or only odd vertices. A better lower bound is obtained by considering independent sets with an arbitrary (but constant) number of ‘defect’ vertices on one side of the bipartition. This increases the lower bound by a factor
$2 \cdot 2^{N} -1$
obtained by considering independent sets of only even or only odd vertices. A better lower bound is obtained by considering independent sets with an arbitrary (but constant) number of ‘defect’ vertices on one side of the bipartition. This increases the lower bound by a factor
![]() $\sqrt{e}$
. Korshunov and Sapozhenko showed that this gives the correct asymptotics for
$\sqrt{e}$
. Korshunov and Sapozhenko showed that this gives the correct asymptotics for
![]() $i(Q_d)$
as
$i(Q_d)$
as
![]() $d \to \infty$
[Reference Korshunov and Sapozhenko16].
$d \to \infty$
[Reference Korshunov and Sapozhenko16].
Theorem 1 (Korshunov and Sapozhenko). As
![]() $d \to \infty$
,
$d \to \infty$
,
Galvin later studied weighted independent sets in the hypercube. For
![]() $\lambda\ge 0$
, define the independence polynomial of
$\lambda\ge 0$
, define the independence polynomial of
![]() $Q_d$
,
$Q_d$
,
Taking
![]() $\lambda=1$
recovers
$\lambda=1$
recovers
![]() $i(Q_d)$
. In what follows we will drop
$i(Q_d)$
. In what follows we will drop
![]() $Q_d$
from the notation, writing
$Q_d$
from the notation, writing
![]() $Z(\lambda)$
and
$Z(\lambda)$
and
![]() $\mathcal {I}$
for
$\mathcal {I}$
for
![]() $Z_{Q_d}(\lambda)$
and
$Z_{Q_d}(\lambda)$
and
![]() $\mathcal {I}(Q_d)$
.
$\mathcal {I}(Q_d)$
.
The independence polynomial
![]() $Z(\lambda)$
is also the partition function of the hard-core model on
$Z(\lambda)$
is also the partition function of the hard-core model on
![]() $Q_d$
: the probability distribution
$Q_d$
: the probability distribution
![]() $\mu_\lambda$
on
$\mu_\lambda$
on
![]() $\mathcal {I}$
defined by
$\mathcal {I}$
defined by
![]() $\mu_\lambda(I) = \lambda^{|I|}/Z(\lambda)$
. By generalising Sapozhenko’s alternative proof of Theorem 1 in [Reference Sapozhenko20], Galvin found the asymptotics for
$\mu_\lambda(I) = \lambda^{|I|}/Z(\lambda)$
. By generalising Sapozhenko’s alternative proof of Theorem 1 in [Reference Sapozhenko20], Galvin found the asymptotics for
![]() $Z(\lambda)$
for
$Z(\lambda)$
for
![]() $\lambda> \sqrt{2}-1$
[Reference Galvin10] (as well as the asymptotics of
$\lambda> \sqrt{2}-1$
[Reference Galvin10] (as well as the asymptotics of
![]() $\log Z(\lambda)$
for
$\log Z(\lambda)$
for
![]() $\lambda= \Omega(\log d/d^{1/3})$
).
$\lambda= \Omega(\log d/d^{1/3})$
).
Theorem 2 (Galvin) For
![]() $\lambda> \sqrt{2}- 1$
,
$\lambda> \sqrt{2}- 1$
,
 \begin{align*} Z(\lambda) = (2+o(1)) (1+\lambda)^{N} \exp \left[ \lambda N \left( \frac{1}{1+\lambda} \right)^d \right ] \end{align*}
\begin{align*} Z(\lambda) = (2+o(1)) (1+\lambda)^{N} \exp \left[ \lambda N \left( \frac{1}{1+\lambda} \right)^d \right ] \end{align*}
as
![]() $d \to \infty$
.
$d \to \infty$
.
Analogously to Theorem 1, the trivial lower bound for
![]() $Z(\lambda)$
is
$Z(\lambda)$
is
![]() $2 (1+\lambda)^N -1$
, and the asymptotic formula in Theorem 2 includes the contribution from independent sets with a constant number of defect vertices, captured by the exponential factor.
$2 (1+\lambda)^N -1$
, and the asymptotic formula in Theorem 2 includes the contribution from independent sets with a constant number of defect vertices, captured by the exponential factor.
Galvin also studied the typical structure of the defect vertices under the probability distribution
![]() $\mu_{\lambda}$
. Formally, given an independent set
$\mu_{\lambda}$
. Formally, given an independent set
![]() $I\in \mathcal {I}$
, if
$I\in \mathcal {I}$
, if
![]() $|I\cap\mathcal {O}|\leq |I\cap\mathcal {E}|$
, we refer to the elements of
$|I\cap\mathcal {O}|\leq |I\cap\mathcal {E}|$
, we refer to the elements of
![]() $I\cap\mathcal {O}$
as the defect vertices of I; otherwise we say that
$I\cap\mathcal {O}$
as the defect vertices of I; otherwise we say that
![]() $I\cap\mathcal {E}$
is the set of defect vertices. A natural way to describe the structure of a set
$I\cap\mathcal {E}$
is the set of defect vertices. A natural way to describe the structure of a set
![]() $S\subset\mathcal {O}, \mathcal {E}$
is to describe the graph
$S\subset\mathcal {O}, \mathcal {E}$
is to describe the graph
![]() $Q_d^2[S]$
where
$Q_d^2[S]$
where
![]() $Q_d^2$
denotes the square of
$Q_d^2$
denotes the square of
![]() $Q_d$
. Given an independent set I with defect vertices S, we refer to the connected components of
$Q_d$
. Given an independent set I with defect vertices S, we refer to the connected components of
![]() $Q_d^2[S]$
as the defects of I. Galvin showed that for
$Q_d^2[S]$
as the defects of I. Galvin showed that for
![]() $\lambda>\sqrt{2}-1$
, all but a vanishing fraction of
$\lambda>\sqrt{2}-1$
, all but a vanishing fraction of
![]() $Z(\lambda)$
comes from independent sets with defects of size at most 1.
$Z(\lambda)$
comes from independent sets with defects of size at most 1.
Recently, the first two authors found the asymptotics of
![]() $Z(\lambda)$
for all fixed
$Z(\lambda)$
for all fixed
![]() $\lambda>0$
[Reference Jenssen and Perkins15]. The asymptotic formula takes into account defects of arbitrary, but constant size. The smaller
$\lambda>0$
[Reference Jenssen and Perkins15]. The asymptotic formula takes into account defects of arbitrary, but constant size. The smaller
![]() $\lambda$
is, the larger the size of defects that must be considered.
$\lambda$
is, the larger the size of defects that must be considered.
Theorem 3 (Jenssen and Perkins) There is a sequence of polynomials
![]() $R_j(d,\lambda)$
,
$R_j(d,\lambda)$
,
![]() $j\in \mathbb N$
, such that for any fixed
$j\in \mathbb N$
, such that for any fixed
![]() $t\ge 1$
and
$t\ge 1$
and
![]() $\lambda> 2^{1/t} -1$
,
$\lambda> 2^{1/t} -1$
,
 \begin{align*} Z(\lambda) = (2+o(1)) (1+\lambda)^N \exp \left[ N \sum_{j=1}^{t-1} R_j(d,\lambda) (1+\lambda)^{-dj} \right ] \end{align*}
\begin{align*} Z(\lambda) = (2+o(1)) (1+\lambda)^N \exp \left[ N \sum_{j=1}^{t-1} R_j(d,\lambda) (1+\lambda)^{-dj} \right ] \end{align*}
as
![]() $d \to \infty$
. Moreover the coefficients of the polynomial
$d \to \infty$
. Moreover the coefficients of the polynomial
![]() $R_j$
can be computed in time
$R_j$
can be computed in time
![]() $e^{O( j \log j)}$
.
$e^{O( j \log j)}$
.
In particular,
![]() $R_1 =\lambda$
, recovering the formula in Theorem 2.
$R_1 =\lambda$
, recovering the formula in Theorem 2.
Given these results it is natural to ask for the asymptotics of
![]() $i_m(Q_d)$
, the number of independent sets of size m in
$i_m(Q_d)$
, the number of independent sets of size m in
![]() $Q_d$
. There is a trivial lower bound of
$Q_d$
. There is a trivial lower bound of
![]() $i_m(Q_d) \ge 2 \binom{N}{m}$
, obtained by considering independent sets composed entirely of even or odd vertices, but depending on how large m is, we may need to take into account independent sets of size m with defects up to a given size.
$i_m(Q_d) \ge 2 \binom{N}{m}$
, obtained by considering independent sets composed entirely of even or odd vertices, but depending on how large m is, we may need to take into account independent sets of size m with defects up to a given size.
Galvin [Reference Galvin11] gave the asymptotics of
![]() $i_m(Q_d)$
in the range for which almost all independent sets of size m contain defects of size at most 1.
$i_m(Q_d)$
in the range for which almost all independent sets of size m contain defects of size at most 1.
Theorem 4. (Galvin) Fix
![]() $\beta \in (1-1/\sqrt{2}, 1)$
and let
$\beta \in (1-1/\sqrt{2}, 1)$
and let
![]() $\lambda= \frac{\beta}{1-\beta}$
. Then
$\lambda= \frac{\beta}{1-\beta}$
. Then
 \begin{align} i_{\lfloor \beta N \rfloor}(Q_d) &= (2+o(1)) \binom{N}{ \lfloor \beta N \rfloor} \exp \left [ \lambda N \left(\frac{1}{1+\lambda} \right)^{d} \right] \,.\end{align}
\begin{align} i_{\lfloor \beta N \rfloor}(Q_d) &= (2+o(1)) \binom{N}{ \lfloor \beta N \rfloor} \exp \left [ \lambda N \left(\frac{1}{1+\lambda} \right)^{d} \right] \,.\end{align}
as
![]() $d \to \infty$
.
$d \to \infty$
.
Note that the asymptotic formula (1) consists of the trivial lower bound
![]() $2 \binom{N}{ \lfloor \beta N \rfloor}$
multiplied by the same exponential correction factor in the asymptotic formula for
$2 \binom{N}{ \lfloor \beta N \rfloor}$
multiplied by the same exponential correction factor in the asymptotic formula for
![]() $Z(\lambda)$
in the range
$Z(\lambda)$
in the range
![]() $\lambda> \sqrt{2}-1$
.
$\lambda> \sqrt{2}-1$
.
We show that a similar, but more complicated, formula holds for all
![]() $\beta >0$
. In particular, when
$\beta >0$
. In particular, when
![]() $\beta< 1- 1/\sqrt{2}$
the formula is not simply the trivial bound multiplied by the appropriate exponential correction factor from Theorem 3. We explain below where the extra complexity arises.
$\beta< 1- 1/\sqrt{2}$
the formula is not simply the trivial bound multiplied by the appropriate exponential correction factor from Theorem 3. We explain below where the extra complexity arises.
Theorem 5. There is a sequence of rational functions
![]() $P_j(d,\beta)$
,
$P_j(d,\beta)$
,
![]() $j\in\mathbb N$
, such that so that for any fixed
$j\in\mathbb N$
, such that so that for any fixed
![]() $t\ge 1$
and
$t\ge 1$
and
![]() $\beta \in (1-2^{-1/t},1)$
,
$\beta \in (1-2^{-1/t},1)$
,
 \begin{align} i_{\lfloor \beta N \rfloor}(Q_d) &= (2+o(1)) \binom{N}{ \lfloor \beta N \rfloor} \exp \left[ N \sum_{j=1}^{t-1} P_j (d,\beta) \cdot (1-\beta)^{jd} \right] \end{align}
\begin{align} i_{\lfloor \beta N \rfloor}(Q_d) &= (2+o(1)) \binom{N}{ \lfloor \beta N \rfloor} \exp \left[ N \sum_{j=1}^{t-1} P_j (d,\beta) \cdot (1-\beta)^{jd} \right] \end{align}
as
![]() $d \to \infty$
. Moreover the coefficients of
$d \to \infty$
. Moreover the coefficients of
![]() $P_j$
can be computed in time
$P_j$
can be computed in time
![]() $e^{O( j \log j)}$
.
$e^{O( j \log j)}$
.
For small values of j the functions
![]() $P_j$
can be computed by hand. For example,
$P_j$
can be computed by hand. For example,
![]() $P_1 = \frac{\beta}{1-\beta}$
, and taking
$P_1 = \frac{\beta}{1-\beta}$
, and taking
![]() $t=2$
in Theorem 5 recovers Galvin’s Theorem 4. A more involved calculation carried out in Section 3 yields
$t=2$
in Theorem 5 recovers Galvin’s Theorem 4. A more involved calculation carried out in Section 3 yields
By Theorem 5 this gives an explicit asymptotic formula for
![]() $i_{\lfloor \beta N \rfloor}(Q_d)$
for
$i_{\lfloor \beta N \rfloor}(Q_d)$
for
![]() $\beta>1-2^{-1/3}$
:
$\beta>1-2^{-1/3}$
:
 \begin{align*} &i_{\lfloor \beta N \rfloor}(Q_d) \sim 2 \binom{N}{ \lfloor \beta N \rfloor} \exp \left[ N \frac{\beta}{1-\beta} (1-\beta)^d\right.\\ &\quad \left.+ N \left( \frac{2(\beta - 1)^3 \beta - d(d - 1) (\beta - 2) \beta^3}{4(1-\beta)^4}-\frac{\beta(1-d\beta)^2}{2(1-\beta)^3} \right) (1-\beta)^{2d} \right ] \,.\end{align*}
\begin{align*} &i_{\lfloor \beta N \rfloor}(Q_d) \sim 2 \binom{N}{ \lfloor \beta N \rfloor} \exp \left[ N \frac{\beta}{1-\beta} (1-\beta)^d\right.\\ &\quad \left.+ N \left( \frac{2(\beta - 1)^3 \beta - d(d - 1) (\beta - 2) \beta^3}{4(1-\beta)^4}-\frac{\beta(1-d\beta)^2}{2(1-\beta)^3} \right) (1-\beta)^{2d} \right ] \,.\end{align*}
In principle, one can continue to compute
![]() $P_3, P_4, \dots$
and obtain explicit asymptotics for any fixed
$P_3, P_4, \dots$
and obtain explicit asymptotics for any fixed
![]() $\beta$
. More generally, the results of [Reference Jenssen and Perkins15] and of this paper hold for much smaller
$\beta$
. More generally, the results of [Reference Jenssen and Perkins15] and of this paper hold for much smaller
![]() $\lambda$
and
$\lambda$
and
![]() $\beta$
, tending to 0 as
$\beta$
, tending to 0 as
![]() $d \to \infty$
, as long as
$d \to \infty$
, as long as
![]() $\lambda\ge C \log d/d^{1/3}$
and
$\lambda\ge C \log d/d^{1/3}$
and
![]() $\beta > C \log d /d^{1/3}$
for an absolute constant C. In this case, however, the asymptotic formulas in Theorems 3 and 5 become series with a number of terms that grows with d. These series can be used to give an algorithm to approximate
$\beta > C \log d /d^{1/3}$
for an absolute constant C. In this case, however, the asymptotic formulas in Theorems 3 and 5 become series with a number of terms that grows with d. These series can be used to give an algorithm to approximate
![]() $Z(\lambda)$
and
$Z(\lambda)$
and
![]() $i_{\lfloor \beta N \rfloor}(Q_d)$
up to a
$i_{\lfloor \beta N \rfloor}(Q_d)$
up to a
![]() $(1+\varepsilon)$
multiplicative factor in time polynomial in
$(1+\varepsilon)$
multiplicative factor in time polynomial in
![]() $1/\varepsilon $
and N (an FPTAS in the language of approximate counting; see e.g. [Reference Jenssen, Keevash and Perkins14] for such an algorithm for independent sets in expander graphs). This raises an interesting question of what it means to determine the asymptotics of a sequence f(d) as
$1/\varepsilon $
and N (an FPTAS in the language of approximate counting; see e.g. [Reference Jenssen, Keevash and Perkins14] for such an algorithm for independent sets in expander graphs). This raises an interesting question of what it means to determine the asymptotics of a sequence f(d) as
![]() $d \to \infty$
. Evaluating a closed-form expression involving, say, exponentials or logarithms, might also involve truncating a power series, and so in a sense an algorithmic definition is natural. We do not pursue this further here and instead stick with
$d \to \infty$
. Evaluating a closed-form expression involving, say, exponentials or logarithms, might also involve truncating a power series, and so in a sense an algorithmic definition is natural. We do not pursue this further here and instead stick with
![]() $\beta$
constant.
$\beta$
constant.
The proof of Theorem 5 makes use of the following simple yet useful identity. Let
![]() $\mathcal {I}_m = \{ I \in \mathcal {I} : | I | = m\}$
so that
$\mathcal {I}_m = \{ I \in \mathcal {I} : | I | = m\}$
so that
![]() $i_m(Q_d) = | \mathcal {I}_m|$
. For
$i_m(Q_d) = | \mathcal {I}_m|$
. For
![]() $m\in\mathbb N$
and
$m\in\mathbb N$
and
![]() $\lambda>0$
,
$\lambda>0$
,
In fact this formula follows from the definition of
![]() $\mu_\lambda$
and so holds for any graph, not just
$\mu_\lambda$
and so holds for any graph, not just
![]() $Q_d$
. To use (3) along with Theorem 3 to derive asymptotics for
$Q_d$
. To use (3) along with Theorem 3 to derive asymptotics for
![]() $i_m(Q_d)$
, we must compute the asymptotics of
$i_m(Q_d)$
, we must compute the asymptotics of
![]() $ \mu_\lambda( \mathcal {I}_m)$
. The feasibility of doing this depends very much on m and the choice of
$ \mu_\lambda( \mathcal {I}_m)$
. The feasibility of doing this depends very much on m and the choice of
![]() $\lambda$
. By choosing
$\lambda$
. By choosing
![]() $\lambda$
so that the expected size of an independent set drawn from
$\lambda$
so that the expected size of an independent set drawn from
![]() $\mu_{\lambda}$
is approximately m, we can compute the asymptotics of
$\mu_{\lambda}$
is approximately m, we can compute the asymptotics of
![]() $ \mu_\lambda( \mathcal {I}_m)$
using a local central limit theorem. In practice, we do not work with the hard-core model directly, but with an approximating measure derived from a polymer model which describes the distribution on defects in an independent set from the hard-core model (see Section 2). This polymer model was introduced in [Reference Jenssen and Perkins15].
$ \mu_\lambda( \mathcal {I}_m)$
using a local central limit theorem. In practice, we do not work with the hard-core model directly, but with an approximating measure derived from a polymer model which describes the distribution on defects in an independent set from the hard-core model (see Section 2). This polymer model was introduced in [Reference Jenssen and Perkins15].
In the next theorem we give an expansion in
![]() $(1-\beta)^d$
for a value of the fugacity
$(1-\beta)^d$
for a value of the fugacity
![]() $\lambda$
for which the expected size of
$\lambda$
for which the expected size of
![]() $\mathbf I$
, a random sample from the hard-core model, is close to
$\mathbf I$
, a random sample from the hard-core model, is close to
![]() $\lfloor \beta N \rfloor$
. By expanding the formula (5) below and combining this with (4) we obtain Theorem 5.
$\lfloor \beta N \rfloor$
. By expanding the formula (5) below and combining this with (4) we obtain Theorem 5.
Theorem 6 There exists a sequence of rational functions
![]() $B_j(d,\beta)$
,
$B_j(d,\beta)$
,
![]() $j\in \mathbb N$
, such that the coefficients of
$j\in \mathbb N$
, such that the coefficients of
![]() $B_j$
can be computed in time
$B_j$
can be computed in time
![]() $e^{O( j \log j)}$
and the following holds. Fix
$e^{O( j \log j)}$
and the following holds. Fix
![]() $\beta \in (0,1)$
and let
$\beta \in (0,1)$
and let
![]() $t\ge 1$
be such that
$t\ge 1$
be such that
![]() $\beta> 1-2^{-1/t}$
. Then with
$\beta> 1-2^{-1/t}$
. Then with
 \begin{align}\lambda_{\beta} &= \frac{\beta}{1-\beta} + \sum_{j=1}^{t-1} B_j (d,\beta) \cdot (1-\beta)^{jd}\end{align}
\begin{align}\lambda_{\beta} &= \frac{\beta}{1-\beta} + \sum_{j=1}^{t-1} B_j (d,\beta) \cdot (1-\beta)^{jd}\end{align}
we have
 \begin{align} i_{\lfloor \beta N \rfloor}(Q_d)= \frac{ 1+o(1)}{ \sqrt{2\pi N \beta (1-\beta)} } \frac{Z(\lambda_{\beta})}{\lambda_{\beta}^{\lfloor \beta N \rfloor } } \end{align}
\begin{align} i_{\lfloor \beta N \rfloor}(Q_d)= \frac{ 1+o(1)}{ \sqrt{2\pi N \beta (1-\beta)} } \frac{Z(\lambda_{\beta})}{\lambda_{\beta}^{\lfloor \beta N \rfloor } } \end{align}
as
![]() $d \to \infty$
. Moreover,
$d \to \infty$
. Moreover,
In [Reference Jenssen and Perkins15] the authors prove a multivariate central limit theorem for the number of defects of different types in the polymer model. In Section 4, we establish a multivariate local central limit theorem for this polymer model which allows us to refine Theorems 5 and 6 further still. Given a defect S, we define the type of S to be the isomorphism class of the graph
![]() $Q_d^2[S]$
. For a given defect type T, we let
$Q_d^2[S]$
. For a given defect type T, we let
![]() $X_{T}$
be the random variable that counts the number of defects of type T in a sample from the hard-core model on
$X_{T}$
be the random variable that counts the number of defects of type T in a sample from the hard-core model on
![]() $Q_d$
. We let
$Q_d$
. We let
![]() $m_{T} = \mathbb{E}_{\lambda} X_{T}$
.
$m_{T} = \mathbb{E}_{\lambda} X_{T}$
.
Given a collection
![]() $\mathcal {T}$
of types and vector of non-negative integers
$\mathcal {T}$
of types and vector of non-negative integers
![]() $ \mathbf k=(k_T )_{T \in \mathcal T}$
, let
$ \mathbf k=(k_T )_{T \in \mathcal T}$
, let
![]() $ i_{m, \mathbf x}(Q_d) $
denote the number of independent sets in
$ i_{m, \mathbf x}(Q_d) $
denote the number of independent sets in
![]() $Q_d$
of size m with exactly
$Q_d$
of size m with exactly
![]() $ k_T $
defects of type T for all
$ k_T $
defects of type T for all
![]() $T \in \mathcal T$
.
$T \in \mathcal T$
.
Theorem 7 Fix
![]() $\beta \in (0,1)$
and let
$\beta \in (0,1)$
and let
![]() $\lambda=\lambda_\beta$
be as in Theorem 6. Let
$\lambda=\lambda_\beta$
be as in Theorem 6. Let
![]() $\mathcal {T}_1$
be the set of defect types T such that
$\mathcal {T}_1$
be the set of defect types T such that
![]() $m_T \to \rho_T$
for some constant
$m_T \to \rho_T$
for some constant
![]() $\rho_T >0$
as
$\rho_T >0$
as
![]() $d \to \infty$
and
$d \to \infty$
and
![]() $\mathcal {T}_2$
the set of defect types T so that
$\mathcal {T}_2$
the set of defect types T so that
![]() $m_T\to\infty$
. Let
$m_T\to\infty$
. Let
![]() $ ( k_T )_{T \in \mathcal T_1}$
be a vector of fixed non-negative integers and let
$ ( k_T )_{T \in \mathcal T_1}$
be a vector of fixed non-negative integers and let
![]() $ ( k_T )_{T \in \mathcal T_2}$
be such that
$ ( k_T )_{T \in \mathcal T_2}$
be such that
![]() $k_T= \lfloor m_T +s_T \rfloor$
where
$k_T= \lfloor m_T +s_T \rfloor$
where
![]() $| s_T| = O(\sqrt{ m_T})$
for all
$| s_T| = O(\sqrt{ m_T})$
for all
![]() $T \in \mathcal T_2$
. Let
$T \in \mathcal T_2$
. Let
![]() $\mathbf k= (k_T)_{T\in \mathcal {T}_1\cup\mathcal {T}_2}$
. Then
$\mathbf k= (k_T)_{T\in \mathcal {T}_1\cup\mathcal {T}_2}$
. Then
 \begin{align} i_{\lfloor \beta N \rfloor, \mathbf k}(Q_d)= \frac{ 1 +o(1) }{ \sqrt{2\pi N \beta (1-\beta)} } \frac{Z(\lambda_{\beta})}{\lambda_{\beta}^{\lfloor \beta N \rfloor } } \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!} \prod_{T \in \mathcal T_{2}} \frac{e^{ - \frac{ s_T^2}{2 m_T}}}{\sqrt{2 \pi m_T}}\, \end{align}
\begin{align} i_{\lfloor \beta N \rfloor, \mathbf k}(Q_d)= \frac{ 1 +o(1) }{ \sqrt{2\pi N \beta (1-\beta)} } \frac{Z(\lambda_{\beta})}{\lambda_{\beta}^{\lfloor \beta N \rfloor } } \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!} \prod_{T \in \mathcal T_{2}} \frac{e^{ - \frac{ s_T^2}{2 m_T}}}{\sqrt{2 \pi m_T}}\, \end{align}
as
![]() $d \to \infty$
.
$d \to \infty$
.
This formula matches that of (5) with additional factors corresponding to Poisson probabilities (for
![]() $T \in \mathcal {T}_1$
) and local central limit theorem probabilities (for
$T \in \mathcal {T}_1$
) and local central limit theorem probabilities (for
![]() $T \in \mathcal {T}_2$
).
$T \in \mathcal {T}_2$
).
1.1 Methods: maximum entropy, statistical mechanics and local central limit theorems
The methods we use here combine several different probabilistic tools, including abstract polymer models and the cluster expansion, large deviations and local central limit theorems. Counting independent sets in the hypercube is a canonical combinatorial enumeration problem, and so we hope this provides a template for using this combination of tools in other combinatorial problems.
There is a long history of using local central limit theorems in combinatorics, with many examples in analytic combinatorics and the study of integer partitions (see e.g. [Reference DeSalvo and Menz7,Reference McKinley, Michelen and Perkins17–Reference Romik19]) as well as the enumeration of contingency tables [Reference Barvinok and Hartigan4] and graphs with prescribed degree sequences (e.g. [Reference Barvinok and Hartigan5,Reference Isaev and McKay12]). Here we show that local central limit theorems work very well in combination with two tools from statistical physics, polymer models and the cluster expansion, which have been used recently in combinatorial enumeration [Reference Balogh, Garcia and Li2,Reference Jenssen and Keevash13,Reference Jenssen and Perkins15].
The connection between these methods starts with a general approach to counting via probability and the principle of maximum entropy which is laid out explicitly by Barvinok and Hartigan in [Reference Barvinok and Hartigan3] (and later discussed in [Reference McKinley, Michelen and Perkins17]), but appears implicitly in other enumerations methods, such as the circle method (see [Reference Isaev and McKay12] for an explanation of these connections). The main idea is that to count a subset of objects defined by a number of constraints, one considers the maximum entropy distribution on the larger set that satisfies the constraints in expectation. The size of the subset can then be expressed as the exponential of the entropy of this distribution times the probability that a random object drawn from this distribution satisfies the constraints. In the example of enumerating integer partitions, these maximum entropy distributions take the form of sequences of independent geometric random variables with different means [Reference Arratia and Tavaré1,Reference Fristedt9], and asymptotic enumeration can be accomplished by solving a convex optimisation problem to find these means and then proving a local central limit theorem for linear combinations of independent geometric random variables [Reference DeSalvo and Menz7,Reference McKinley, Michelen and Perkins17–Reference Romik19].
This approach naturally leads to considering statistical physics models. For example, the maximum entropy distribution over independent sets in a graph with a given mean size is the hard-core model. The entropy of the hard-core model is the log partition function minus the expected size of an independent set:
![]() $H(\mu_\lambda) = \log Z(\lambda) - \log \lambda\cdot \mathbb{E}_{\mu} | \mathbf I|$
, and so the enumeration problem for independent sets of a given size reduces to computing
$H(\mu_\lambda) = \log Z(\lambda) - \log \lambda\cdot \mathbb{E}_{\mu} | \mathbf I|$
, and so the enumeration problem for independent sets of a given size reduces to computing
![]() $\log Z$
and computing
$\log Z$
and computing
![]() $\mu_{\lambda}(\mathcal {I}_k)$
(via, say, a local central limit theorem) as described above.
$\mu_{\lambda}(\mathcal {I}_k)$
(via, say, a local central limit theorem) as described above.
The complication is that the quantities of interest (say, the size of an independent set from the hard-core model) can no longer be written as the sum of independent random variables. When interactions are weak enough (or density small enough) correlations between vertices decay exponentially in distance and methods like the cluster expansion can be used to prove both central limit theorems and local central limit theorem. This type of result is closely related to the concept of equivalence of ensembles between the grand canonical ensemble (fixed mean energy) and the canonical ensemble (fixed energy). For instance, Dobrushin and Tirozzi showed that for spin models with finite-range interactions on
![]() $\mathbb{Z}^d$
, a central limit theorem implies a local central limit theorem [Reference Dobrushin and Tirozzi8] (see also [Reference Campanino, Capocaccia and Tirozzi6] for an extension to long-range interactions).
$\mathbb{Z}^d$
, a central limit theorem implies a local central limit theorem [Reference Dobrushin and Tirozzi8] (see also [Reference Campanino, Capocaccia and Tirozzi6] for an extension to long-range interactions).
What we do here is prove local central limit theorems conditioned on a phase in the strong interaction, phase coexistence regime. This, in combination with using polymer models and the cluster expansion to find the asymptotics of
![]() $Z(\lambda)$
, allows us to enumerate independent sets of a given size and structure.
$Z(\lambda)$
, allows us to enumerate independent sets of a given size and structure.
In Section 2, we recall the even and odd polymer models introduced in [Reference Jenssen and Perkins15], and state and extend some of the probabilistic estimates proved there.
In Section 3 we prove Theorems 5 and 6, finding an expansion for a fugacity
![]() $\lambda_\beta$
so that the expected size of an independent set is sufficiently close to
$\lambda_\beta$
so that the expected size of an independent set is sufficiently close to
![]() $\lfloor \beta N \rfloor$
that a local central limit theorem will allow us to compute asymptotics.
$\lfloor \beta N \rfloor$
that a local central limit theorem will allow us to compute asymptotics.
In Section 4 we show how local central limit theorems for polymer models follow from sufficiently fast convergence of the cluster expansion.
Finally in Section 5 we combine the above results to prove Theorem 7.
2. The even and odd polymer models
Let
![]() $\mathcal {E} \subset V(Q_d)$
be the set of even vertices of the hypercube, those whose coordinates sum to an even number, and let
$\mathcal {E} \subset V(Q_d)$
be the set of even vertices of the hypercube, those whose coordinates sum to an even number, and let
![]() $\mathcal {O} \subset V(Q_d)$
be the odd vertices. Note that
$\mathcal {O} \subset V(Q_d)$
be the odd vertices. Note that
![]() $Q_d$
is a bipartite graph with bipartition
$Q_d$
is a bipartite graph with bipartition
![]() $(\mathcal {E}, \mathcal {O})$
and that
$(\mathcal {E}, \mathcal {O})$
and that
![]() $|\mathcal {E}| = | \mathcal {O} | =N:=2^{d-1}$
. A key insight of [Reference Jenssen and Perkins15] is that, for
$|\mathcal {E}| = | \mathcal {O} | =N:=2^{d-1}$
. A key insight of [Reference Jenssen and Perkins15] is that, for
![]() $\lambda$
not too small, the hard-core measure
$\lambda$
not too small, the hard-core measure
![]() $\mu_{Q_d, \lambda}$
can be closely approximated by a random perturbation of a random subset of either
$\mu_{Q_d, \lambda}$
can be closely approximated by a random perturbation of a random subset of either
![]() $\mathcal {O}$
or
$\mathcal {O}$
or
![]() $\mathcal {E}$
. The random perturbation takes the form of a polymer model with convergent cluster expansion, two notions that we introduce now.
$\mathcal {E}$
. The random perturbation takes the form of a polymer model with convergent cluster expansion, two notions that we introduce now.
For a set
![]() $S \subseteq \mathcal {O}$
(and analogously for
$S \subseteq \mathcal {O}$
(and analogously for
![]() $S \subseteq \mathcal {E}$
), let
$S \subseteq \mathcal {E}$
), let
![]() $|S|$
denote the number of vertices of S, N(S) be the set of neighbours of S and
$|S|$
denote the number of vertices of S, N(S) be the set of neighbours of S and
![]() $[S]= \{ v \in \mathcal {O} \,{:}\, N(v) \subseteq N(S) \}$
the bipartite closure of S. We call a set
$[S]= \{ v \in \mathcal {O} \,{:}\, N(v) \subseteq N(S) \}$
the bipartite closure of S. We call a set
![]() $S\subseteq \mathcal {O}$
an odd polymer if (i) the subgraph of
$S\subseteq \mathcal {O}$
an odd polymer if (i) the subgraph of
![]() $Q_d$
induced by the vertex set
$Q_d$
induced by the vertex set
![]() $S\cup N(S)$
is connected and (ii)
$S\cup N(S)$
is connected and (ii)
![]() $ |[ S]| \le N/2$
. We let
$ |[ S]| \le N/2$
. We let
![]() $\mathcal {P}_\mathcal {O}$
denote the set of all odd polymers. The weight of an odd polymer S is
$\mathcal {P}_\mathcal {O}$
denote the set of all odd polymers. The weight of an odd polymer S is
We say that two odd polymers
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are compatible and write
$S_2$
are compatible and write
![]() $S_1\sim S_2$
, if the graph distance between
$S_1\sim S_2$
, if the graph distance between
![]() $S_1, S_2$
is
$S_1, S_2$
is
![]() $Q_d$
is
$Q_d$
is
![]() $>2$
. We let
$>2$
. We let
![]() $\Omega_\mathcal {O}$
denote the set of all collections of mutually compatible odd polymers and define the following Gibbs measure on
$\Omega_\mathcal {O}$
denote the set of all collections of mutually compatible odd polymers and define the following Gibbs measure on
![]() $\Omega_\mathcal {O}$
: for
$\Omega_\mathcal {O}$
: for
![]() $\Gamma\in \Omega_\mathcal {O}$
,
$\Gamma\in \Omega_\mathcal {O}$
,
is the odd polymer model partition function. Using
![]() $\nu_\mathcal {O}$
we define a measure
$\nu_\mathcal {O}$
we define a measure
![]() $\mu_{\mathcal {O}, \lambda}$
on independent sets in
$\mu_{\mathcal {O}, \lambda}$
on independent sets in
![]() $Q_d$
.
$Q_d$
.
Definition 8 Let
![]() $\mu_{\mathcal {O}, \lambda}$
be the measure on
$\mu_{\mathcal {O}, \lambda}$
be the measure on
![]() $\mathcal {I}$
defined by the following two-step process:
$\mathcal {I}$
defined by the following two-step process:
-
1. Choose a polymer configuration
 $\Gamma \in \Omega_{\mathcal {O}} $
from
$\Gamma \in \Omega_{\mathcal {O}} $
from
 $\nu_\mathcal {O}$
and assign all vertices of
$\nu_\mathcal {O}$
and assign all vertices of
 $\cup_{S\in \Gamma} S$
to be occupied.
$\cup_{S\in \Gamma} S$
to be occupied. -
2. For each vertex v in
 $\mathcal {E}$
that is not blocked by an occupied vertex in
$\mathcal {E}$
that is not blocked by an occupied vertex in
 $\mathcal {O}$
, include v in the independent set independently with probability
$\mathcal {O}$
, include v in the independent set independently with probability
 $\frac{\lambda}{1+\lambda}$
.
$\frac{\lambda}{1+\lambda}$
.
Let
![]() $Z_{\mathcal {O}}(\lambda) = (1+\lambda)^N \Xi_{\mathcal {O}}$
, the independence polynomial of
$Z_{\mathcal {O}}(\lambda) = (1+\lambda)^N \Xi_{\mathcal {O}}$
, the independence polynomial of
![]() $Q_d$
restricted to independent sets achievable in the odd polymer model; that is, those for which
$Q_d$
restricted to independent sets achievable in the odd polymer model; that is, those for which
![]() $\mu_{\mathcal {O}, \lambda}$
assigns positive probability.
$\mu_{\mathcal {O}, \lambda}$
assigns positive probability.
We think of Step 1 in Definition 8 as a perturbation of the ‘ground state’ measure that simply selects a p-random subset of
![]() $\mathcal {E}$
with
$\mathcal {E}$
with
![]() $p=\lambda/(1+\lambda)$
. The polymer configuration chosen in Step 1 will be typically small and so this process typically returns an independent set that is highly unbalanced with the majority of vertices even. We define even polymers, the even polymer model partition function
$p=\lambda/(1+\lambda)$
. The polymer configuration chosen in Step 1 will be typically small and so this process typically returns an independent set that is highly unbalanced with the majority of vertices even. We define even polymers, the even polymer model partition function
![]() $\Xi_\mathcal {E}$
, and measures
$\Xi_\mathcal {E}$
, and measures
![]() $\nu_\mathcal {E}$
,
$\nu_\mathcal {E}$
,
![]() $\mu_{\mathcal {E}, \lambda}$
analogously. It was shown in [Reference Jenssen and Perkins15] that for
$\mu_{\mathcal {E}, \lambda}$
analogously. It was shown in [Reference Jenssen and Perkins15] that for
![]() $\lambda>C\log d/d^{1/3}$
, the hard-core measure
$\lambda>C\log d/d^{1/3}$
, the hard-core measure
![]() $\mu_{Q_d, \lambda}$
can be closely approximated by the mixture
$\mu_{Q_d, \lambda}$
can be closely approximated by the mixture
![]() $\tfrac{1}{2}\mu_{\mathcal {O}, \lambda} + \tfrac{1}{2}\mu_{\mathcal {E}, \lambda}$
.
$\tfrac{1}{2}\mu_{\mathcal {O}, \lambda} + \tfrac{1}{2}\mu_{\mathcal {E}, \lambda}$
.
Theorem 9 ([Reference Jenssen and Perkins15]) For
![]() $\lambda\ge C \log d/d^{1/3}$
, we have
$\lambda\ge C \log d/d^{1/3}$
, we have
Moreover, letting
![]() $\hat\mu_{\lambda}=\tfrac{1}{2}\mu_{\mathcal {O}, \lambda} + \tfrac{1}{2}\mu_{\mathcal {E}, \lambda}$
, we have
$\hat\mu_{\lambda}=\tfrac{1}{2}\mu_{\mathcal {O}, \lambda} + \tfrac{1}{2}\mu_{\mathcal {E}, \lambda}$
, we have
Finally, with probability at least
![]() $1- O(\exp(\!-N/d^4))$
any defect vertices of I drawn from
$1- O(\exp(\!-N/d^4))$
any defect vertices of I drawn from
![]() $\mu_{\mathcal {O}, \lambda} $
are on the odd side of the bipartition; that is, the defects are the polymers of the polymer configuration.
$\mu_{\mathcal {O}, \lambda} $
are on the odd side of the bipartition; that is, the defects are the polymers of the polymer configuration.
The lower bound on
![]() $\lambda$
in Theorem 9 is an artefact of Sapozhenko’s graph container method as implemented by Galvin [Reference Galvin10]. Theorem 9 quite possibly remains true for
$\lambda$
in Theorem 9 is an artefact of Sapozhenko’s graph container method as implemented by Galvin [Reference Galvin10]. Theorem 9 quite possibly remains true for
![]() $\lambda=\tilde\Omega(1/d)$
though proving this would require significant new ideas.
$\lambda=\tilde\Omega(1/d)$
though proving this would require significant new ideas.
The power of Theorem 9 stems from the fact that the even and odd polymer models admit convergent cluster expansions allowing for a detailed understanding of the measures
![]() $\mu_{\mathcal {O}, \lambda}, \mu_{\mathcal {E}, \lambda}$
. Let us now introduce the cluster expansion formally.
$\mu_{\mathcal {O}, \lambda}, \mu_{\mathcal {E}, \lambda}$
. Let us now introduce the cluster expansion formally.
For a tuple
![]() $\Gamma$
of odd polymers, the incompatibility graph,
$\Gamma$
of odd polymers, the incompatibility graph,
![]() $H(\Gamma)$
, is the graph with vertex set
$H(\Gamma)$
, is the graph with vertex set
![]() $\Gamma$
and an edge between any two incompatible polymers. An odd cluster
$\Gamma$
and an edge between any two incompatible polymers. An odd cluster
![]() $\Gamma$
is an ordered tuple of even polymers so that
$\Gamma$
is an ordered tuple of even polymers so that
![]() $H(\Gamma)$
is connected. The size of a cluster
$H(\Gamma)$
is connected. The size of a cluster
![]() $\Gamma$
is
$\Gamma$
is
![]() $\|\Gamma \| = \sum_{S \in \Gamma} |S|$
. Let
$\|\Gamma \| = \sum_{S \in \Gamma} |S|$
. Let
![]() $\mathcal {C}$
be the set of all odd clusters. For a cluster
$\mathcal {C}$
be the set of all odd clusters. For a cluster
![]() $\Gamma$
we define
$\Gamma$
we define
where
![]() $\phi(H)$
is the Ursell function of a graph H, defined by
$\phi(H)$
is the Ursell function of a graph H, defined by
 \begin{align}\phi(H) &= \frac{1}{|V(H)|!} \sum_{\substack{A \subseteq E(H)\\ \text{spanning, connected}}} (\!-1)^{|A|} \, .\end{align}
\begin{align}\phi(H) &= \frac{1}{|V(H)|!} \sum_{\substack{A \subseteq E(H)\\ \text{spanning, connected}}} (\!-1)^{|A|} \, .\end{align}
The cluster expansion is the formal infinite series
We define the cluster expansion of
![]() $\log \Xi_\mathcal {E}$
analogously and note that by symmetry the expansions are identical.
$\log \Xi_\mathcal {E}$
analogously and note that by symmetry the expansions are identical.
In light of Theorem 9, throughout this section will we assume that
![]() $ \lambda\ge C \log d/d^{1/3}$
. We will also assume that
$ \lambda\ge C \log d/d^{1/3}$
. We will also assume that
![]() $\lambda=O(1)$
as
$\lambda=O(1)$
as
![]() $d\to\infty$
. The following result from [Reference Jenssen and Perkins15] shows that for such
$d\to\infty$
. The following result from [Reference Jenssen and Perkins15] shows that for such
![]() $\lambda$
the cluster expansion converges, we have good tail bounds on the expansion, and the terms of the cluster expansion can be efficiently computed. We say that a polynomial is computable in time t, if its coefficients can be computed in time t.
$\lambda$
the cluster expansion converges, we have good tail bounds on the expansion, and the terms of the cluster expansion can be efficiently computed. We say that a polynomial is computable in time t, if its coefficients can be computed in time t.
Theorem 10 For fixed
![]() $k \ge 1$
,
$k \ge 1$
,
 \begin{align*} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq k}}|w(\Gamma)|= O \left ( \frac{2^d d^{2(k-1)}}{(1+ \lambda)^{dk} }\right )\end{align*}
\begin{align*} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq k}}|w(\Gamma)|= O \left ( \frac{2^d d^{2(k-1)}}{(1+ \lambda)^{dk} }\right )\end{align*}
and
 \begin{align} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\|= k}} w(\Gamma) = N\cdot R_k(\lambda,d) (1+\lambda)^{-kd}\end{align}
\begin{align} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\|= k}} w(\Gamma) = N\cdot R_k(\lambda,d) (1+\lambda)^{-kd}\end{align}
where
![]() $R_k$
is a polynomial in d and
$R_k$
is a polynomial in d and
![]() $\lambda$
of degree at most 2k in d and of degree at most
$\lambda$
of degree at most 2k in d and of degree at most
![]() $3k^2$
in
$3k^2$
in
![]() $\lambda$
. Moreover
$\lambda$
. Moreover
![]() $R_k$
is computable in time
$R_k$
is computable in time
![]() $e^{O(k \log k)}$
. In particular,
$e^{O(k \log k)}$
. In particular,
 \begin{align*}\log \Xi_\mathcal {O}&= N \sum_{j=1}^k R_j(\lambda,d) (1+\lambda)^{-jd} + O \left ( \frac{2^d d^{2k}}{(1+ \lambda)^{d(k+1)} }\right ) \, .\end{align*}
\begin{align*}\log \Xi_\mathcal {O}&= N \sum_{j=1}^k R_j(\lambda,d) (1+\lambda)^{-jd} + O \left ( \frac{2^d d^{2k}}{(1+ \lambda)^{d(k+1)} }\right ) \, .\end{align*}
We note that Theorem 3 follows in [Reference Jenssen and Perkins15] from Theorems 9 and 10.
It will also be useful to record the following slightly strengthened tail bound on the cluster expansion. The following lemma is essentially contained in [Reference Jenssen and Perkins15], though it does not appear explicitly and so we provide the details.
Lemma 11 For
![]() $t, \ell\geq 1$
fixed,
$t, \ell\geq 1$
fixed,
 \begin{align*} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq t}}|w(\Gamma)| \|\Gamma\|^\ell = O \left ( \frac{2^d d^{2(t-1)}}{(1+ \lambda)^{dt} }\right )\, .\end{align*}
\begin{align*} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq t}}|w(\Gamma)| \|\Gamma\|^\ell = O \left ( \frac{2^d d^{2(t-1)}}{(1+ \lambda)^{dt} }\right )\, .\end{align*}
Proof. In [Reference Jenssen and Perkins15] (see Lemma 15) it is shown that
where
 \begin{align*}\gamma(d,k) &= \begin{cases}\log(1+\lambda) (dk - 3 k^2)- 7 k\log d \text{ if } k \le \dfrac{d}{10} \\ \\[-7pt] \dfrac{d \log(1+\lambda) k}{20} \text{ if } \dfrac{d}{10} < k \le d^4\\ \\[-7pt] \dfrac{k}{d^{3/2}} \text{ if } k > d^4 \,.\end{cases}\end{align*}
\begin{align*}\gamma(d,k) &= \begin{cases}\log(1+\lambda) (dk - 3 k^2)- 7 k\log d \text{ if } k \le \dfrac{d}{10} \\ \\[-7pt] \dfrac{d \log(1+\lambda) k}{20} \text{ if } \dfrac{d}{10} < k \le d^4\\ \\[-7pt] \dfrac{k}{d^{3/2}} \text{ if } k > d^4 \,.\end{cases}\end{align*}
Since
![]() $e^{\gamma(d,k)/2}\geq k^\ell$
for all k and d sufficiently large, it follows that
$e^{\gamma(d,k)/2}\geq k^\ell$
for all k and d sufficiently large, it follows that
Keeping only terms in the above inequality corresponding to clusters of size at least k we have
 \begin{align} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq k}} |w(\Gamma)|\|\Gamma\|^\ell & \le O(2^{d} d^{-3/2}e^{-\gamma(d,k)/2}) \,.\end{align}
\begin{align} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq k}} |w(\Gamma)|\|\Gamma\|^\ell & \le O(2^{d} d^{-3/2}e^{-\gamma(d,k)/2}) \,.\end{align}
With
![]() $t\geq0$
fixed we have by Theorem 10 and (12) that
$t\geq0$
fixed we have by Theorem 10 and (12) that
 \begin{align*}\sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq t}} |w(\Gamma)|\|\Gamma\|^\ell &= \sum_{\substack{\Gamma \in \mathcal{C} \\ t\leq\|\Gamma\| < 3t}} |w(\Gamma)|\|\Gamma\|^\ell + \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq 3t}} |w(\Gamma)|\|\Gamma\|^\ell \\[3pt] &= O \left ( \frac{2^d d^{2(t-1)}}{(1+ \lambda)^{dt} }\right ) + O\left(\frac{2^{d}d^{11t}}{(1+\lambda)^{3dt/2}}\right)\\[3pt] &= O \left ( \frac{2^d d^{2(t-1)}}{(1+ \lambda)^{dt} }\right ) \, .\end{align*}
\begin{align*}\sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq t}} |w(\Gamma)|\|\Gamma\|^\ell &= \sum_{\substack{\Gamma \in \mathcal{C} \\ t\leq\|\Gamma\| < 3t}} |w(\Gamma)|\|\Gamma\|^\ell + \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \geq 3t}} |w(\Gamma)|\|\Gamma\|^\ell \\[3pt] &= O \left ( \frac{2^d d^{2(t-1)}}{(1+ \lambda)^{dt} }\right ) + O\left(\frac{2^{d}d^{11t}}{(1+\lambda)^{3dt/2}}\right)\\[3pt] &= O \left ( \frac{2^d d^{2(t-1)}}{(1+ \lambda)^{dt} }\right ) \, .\end{align*}
Let
![]() $\boldsymbol\Gamma$
be a collection of compatible polymers sampled according to
$\boldsymbol\Gamma$
be a collection of compatible polymers sampled according to
![]() $\nu_{\mathcal {O}}$
(the polymer measure at Step 1 of Definition 8, the definition of
$\nu_{\mathcal {O}}$
(the polymer measure at Step 1 of Definition 8, the definition of
![]() $\mu_{\mathcal {O}, \lambda}$
). We will use the above lemma to show that
$\mu_{\mathcal {O}, \lambda}$
). We will use the above lemma to show that
![]() $\|\boldsymbol\Gamma\|$
and
$\|\boldsymbol\Gamma\|$
and
![]() $|N(\boldsymbol\Gamma)|$
obey a central limit theorem. Formally, we say a sequence of random variables
$|N(\boldsymbol\Gamma)|$
obey a central limit theorem. Formally, we say a sequence of random variables
![]() $(X_d)$
obeys a central limit theorem if
$(X_d)$
obeys a central limit theorem if
![]() $(X_d - \mathbb{E} X_d)/\sqrt{\text{var}(X_d)}$
converges to N(0,1) in distribution as
$(X_d - \mathbb{E} X_d)/\sqrt{\text{var}(X_d)}$
converges to N(0,1) in distribution as
![]() $d\to\infty$
. To prove this central limit theorem we will make use of a connection between the cluster expansion and cumulant generating functions.
$d\to\infty$
. To prove this central limit theorem we will make use of a connection between the cluster expansion and cumulant generating functions.
Recall the cumulant generating function of a random variable X, is
![]() $h_t(X) = \log \mathbb{E} e^{tX}$
. The
$h_t(X) = \log \mathbb{E} e^{tX}$
. The
![]() $\ell$
th cumulant of X is defined by taking derivatives of
$\ell$
th cumulant of X is defined by taking derivatives of
![]() $h_t(X)$
and evaluating at 0:
$h_t(X)$
and evaluating at 0:
 \begin{align*}\kappa_\ell(X) &= \frac{ \partial^\ell h_t(X)}{\partial t^\ell} \Bigg|_{t=0} \,.\end{align*}
\begin{align*}\kappa_\ell(X) &= \frac{ \partial^\ell h_t(X)}{\partial t^\ell} \Bigg|_{t=0} \,.\end{align*}
In particular,
![]() $\kappa_1(X)=\mathbb{E} (X)$
and
$\kappa_1(X)=\mathbb{E} (X)$
and
![]() $\kappa_2(X)=\text{var}(X)$
. The cumulants of
$\kappa_2(X)=\text{var}(X)$
. The cumulants of
![]() $|N(\mathbf\Gamma)|$
can be expressed in terms of the cluster expansion as follows. Consider the odd polymer model with modified weights
$|N(\mathbf\Gamma)|$
can be expressed in terms of the cluster expansion as follows. Consider the odd polymer model with modified weights
![]() $w_t(S)=w(S)e^{t|N(S)|}$
for
$w_t(S)=w(S)e^{t|N(S)|}$
for
![]() $t>0$
and let
$t>0$
and let
![]() $\Xi_t$
denote the corresponding partition function. We then have
$\Xi_t$
denote the corresponding partition function. We then have
Applying the cluster expansion to
![]() $\log \Xi_t$
, taking derivatives, and evaluating at
$\log \Xi_t$
, taking derivatives, and evaluating at
![]() $t=0$
shows that
$t=0$
shows that
Similarly
![]() $\kappa_\ell(\|\boldsymbol\Gamma\|)= \sum_{\Gamma\in\mathcal {C}}w(\Gamma)\|\Gamma\|^{\ell}$
.
$\kappa_\ell(\|\boldsymbol\Gamma\|)= \sum_{\Gamma\in\mathcal {C}}w(\Gamma)\|\Gamma\|^{\ell}$
.
Lemma 12 Let
![]() $\boldsymbol\Gamma$
be a collection of compatible polymers sampled according to
$\boldsymbol\Gamma$
be a collection of compatible polymers sampled according to
![]() $\nu_{\mathcal {O}}$
. Then
$\nu_{\mathcal {O}}$
. Then
![]() $\|\boldsymbol\Gamma\|$
and
$\|\boldsymbol\Gamma\|$
and
![]() $|N(\boldsymbol\Gamma)|$
both obey a central limit theorem.
$|N(\boldsymbol\Gamma)|$
both obey a central limit theorem.
Proof. We show that
![]() $|N(\boldsymbol\Gamma)|$
obeys a central limit theorem and the proof for
$|N(\boldsymbol\Gamma)|$
obeys a central limit theorem and the proof for
![]() $\|\boldsymbol\Gamma\|$
is identical. Let
$\|\boldsymbol\Gamma\|$
is identical. Let
![]() $Z=(|N(\boldsymbol\Gamma)| - \mathbb{E} |N(\boldsymbol\Gamma)|)/\sqrt{\text{var}(|N(\boldsymbol\Gamma)|)}$
. To show that Z converges to N(0,1) in distribution, it suffices to show that the cumulants of Z converge to the cumulants of a standard normal i.e. it suffices to show that
$Z=(|N(\boldsymbol\Gamma)| - \mathbb{E} |N(\boldsymbol\Gamma)|)/\sqrt{\text{var}(|N(\boldsymbol\Gamma)|)}$
. To show that Z converges to N(0,1) in distribution, it suffices to show that the cumulants of Z converge to the cumulants of a standard normal i.e. it suffices to show that
![]() $\kappa_\ell(Z)\to 0$
for
$\kappa_\ell(Z)\to 0$
for
![]() $\ell \geq 3$
. Now by (13) and Lemma 11,
$\ell \geq 3$
. Now by (13) and Lemma 11,
 \begin{align*}\kappa_\ell(|N(\boldsymbol\Gamma)|)= \sum_{\Gamma\in \mathcal {C}}w(\Gamma)|N(\Gamma)|^{\ell}\leq d^\ell \sum_{\Gamma\in \mathcal {C}}w(\Gamma)\|\Gamma\|^{\ell}= O \left ( \frac{2^d d^\ell }{(1+ \lambda)^{d} }\right )\, .\end{align*}
\begin{align*}\kappa_\ell(|N(\boldsymbol\Gamma)|)= \sum_{\Gamma\in \mathcal {C}}w(\Gamma)|N(\Gamma)|^{\ell}\leq d^\ell \sum_{\Gamma\in \mathcal {C}}w(\Gamma)\|\Gamma\|^{\ell}= O \left ( \frac{2^d d^\ell }{(1+ \lambda)^{d} }\right )\, .\end{align*}
On the other hand, by (13) and Lemma 11 again we have
 \begin{align*}\text{var}(|N(\boldsymbol\Gamma)|)= \sum_{\Gamma\in \mathcal {C}}w(\Gamma)|N(\Gamma)|^{2}\geq \sum_{\Gamma\in \mathcal {C}}w(\Gamma)\|\Gamma\|^2= 2^{d-1}\frac{\lambda}{(1+\lambda)^d}+ O \left ( \frac{2^d d^2}{(1+ \lambda)^{2d} }\right )\, .\end{align*}
\begin{align*}\text{var}(|N(\boldsymbol\Gamma)|)= \sum_{\Gamma\in \mathcal {C}}w(\Gamma)|N(\Gamma)|^{2}\geq \sum_{\Gamma\in \mathcal {C}}w(\Gamma)\|\Gamma\|^2= 2^{d-1}\frac{\lambda}{(1+\lambda)^d}+ O \left ( \frac{2^d d^2}{(1+ \lambda)^{2d} }\right )\, .\end{align*}
It follows that if
![]() $\ell\geq 3$
then
$\ell\geq 3$
then
as desired.
Next we will use the cluster expansion to give bounds on
![]() $\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)$
, the expected size of an independent set sampled according to
$\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)$
, the expected size of an independent set sampled according to
![]() $\mu_{\mathcal {O}, \lambda}$
. We begin by recording a useful expression for
$\mu_{\mathcal {O}, \lambda}$
. We begin by recording a useful expression for
![]() $\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)$
in terms of the cluster expansion.
$\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)$
in terms of the cluster expansion.
Lemma 13
Proof. Note that for an independent set I such that
![]() $\mu_{\mathcal {O},\lambda}(I)>0$
, we have
$\mu_{\mathcal {O},\lambda}(I)>0$
, we have
It follows that
We expand
![]() $\log \Xi_\mathcal {O}$
via the cluster expansion as in (10) (which converges absolutely by Theorem 10). Recalling that
$\log \Xi_\mathcal {O}$
via the cluster expansion as in (10) (which converges absolutely by Theorem 10). Recalling that
![]() $w(\Gamma)= \phi(H(\Gamma))\lambda^{\|\Gamma\|}(1+\lambda)^{-|N(\Gamma)|}$
for a cluster
$w(\Gamma)= \phi(H(\Gamma))\lambda^{\|\Gamma\|}(1+\lambda)^{-|N(\Gamma)|}$
for a cluster
![]() $\Gamma$
, we have
$\Gamma$
, we have
 \begin{align*}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)&=\frac{\lambda}{1+ \lambda} N + \sum_{\Gamma\in\mathcal {C}} \phi(H(\Gamma)) \frac{ \lambda^{|\Gamma|} ( (1+\lambda)\|\Gamma\| - \lambda|N(\Gamma)| ) }{ (1+\lambda)^{|N(\Gamma)|+1} } \\&= \frac{\lambda}{1+ \lambda} N + \sum_{\Gamma\in\mathcal {C}} w(\Gamma)\left(\|\Gamma\|- \frac{\lambda}{1+\lambda}|N(\Gamma)|\right)\, .\\[-45pt]\end{align*}
\begin{align*}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)&=\frac{\lambda}{1+ \lambda} N + \sum_{\Gamma\in\mathcal {C}} \phi(H(\Gamma)) \frac{ \lambda^{|\Gamma|} ( (1+\lambda)\|\Gamma\| - \lambda|N(\Gamma)| ) }{ (1+\lambda)^{|N(\Gamma)|+1} } \\&= \frac{\lambda}{1+ \lambda} N + \sum_{\Gamma\in\mathcal {C}} w(\Gamma)\left(\|\Gamma\|- \frac{\lambda}{1+\lambda}|N(\Gamma)|\right)\, .\\[-45pt]\end{align*}
Corollary 14 For fixed
![]() $k\geq 0$
,
$k\geq 0$
,
 \begin{align*}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |) &= \frac{\lambda}{1+ \lambda} N + \lambda N \sum_{j=1}^k \frac{ \frac{\partial}{\partial \lambda}R_j(\lambda,d) }{ (1+\lambda)^{jd} } - \frac{ jd R_j(\lambda,d) }{ (1+\lambda)^{jd+1} } + O\left( \frac{2^d d^{2k+1}}{ (1+\lambda)^{d(k+1)}} \right)\, .\end{align*}
\begin{align*}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |) &= \frac{\lambda}{1+ \lambda} N + \lambda N \sum_{j=1}^k \frac{ \frac{\partial}{\partial \lambda}R_j(\lambda,d) }{ (1+\lambda)^{jd} } - \frac{ jd R_j(\lambda,d) }{ (1+\lambda)^{jd+1} } + O\left( \frac{2^d d^{2k+1}}{ (1+\lambda)^{d(k+1)}} \right)\, .\end{align*}
Where the
![]() $R_j(\lambda, d)$
are as in Theorem 10.
$R_j(\lambda, d)$
are as in Theorem 10.
Proof. By Lemmas 11 and 13, noting that
![]() $|N(\Gamma)|\leq d\|\Gamma\|$
for any cluster
$|N(\Gamma)|\leq d\|\Gamma\|$
for any cluster
![]() $\Gamma$
, we have
$\Gamma$
, we have
 \begin{align*}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)= \frac{\lambda}{1+ \lambda} N + \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \leq k}} w(\Gamma)\left(\|\Gamma\|- \frac{\lambda}{1+\lambda}|N(\Gamma)|\right) + O \left ( \frac{2^d d^{2k+1}}{(1+ \lambda)^{d(k+1)} }\right )\, .\end{align*}
\begin{align*}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)= \frac{\lambda}{1+ \lambda} N + \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| \leq k}} w(\Gamma)\left(\|\Gamma\|- \frac{\lambda}{1+\lambda}|N(\Gamma)|\right) + O \left ( \frac{2^d d^{2k+1}}{(1+ \lambda)^{d(k+1)} }\right )\, .\end{align*}
The result follows by recalling the definition of
![]() $R_j(\lambda, d)$
at (11) .
$R_j(\lambda, d)$
at (11) .
3. Independent sets of a given size
Theorem 6 will follow from several lemmas. The first says that almost all independent sets of size
![]() $m = \lfloor \beta N \rfloor$
are accounted for by exactly one of the two polymer distributions. The second says that if we find
$m = \lfloor \beta N \rfloor$
are accounted for by exactly one of the two polymer distributions. The second says that if we find
![]() $\lambda_\beta$
so that the expected size of the independent set drawn from
$\lambda_\beta$
so that the expected size of the independent set drawn from
![]() $\mu_{\mathcal {O}, \lambda_\beta}$
(as in Definition 8) is close to m then we have an asymptotic formula for the number of independent sets of size m in terms of
$\mu_{\mathcal {O}, \lambda_\beta}$
(as in Definition 8) is close to m then we have an asymptotic formula for the number of independent sets of size m in terms of
![]() $\lambda_\beta$
and
$\lambda_\beta$
and
![]() $Z_{\mathcal {O}}(\lambda_{\beta})$
. The third lemma gives an efficiently computable formula for a suitable such
$Z_{\mathcal {O}}(\lambda_{\beta})$
. The third lemma gives an efficiently computable formula for a suitable such
![]() $\lambda_\beta$
. We will then prove Theorem 5 by analysing expansions of
$\lambda_\beta$
. We will then prove Theorem 5 by analysing expansions of
![]() $\log Z_{\mathcal {O}}(\lambda_{\beta})$
and
$\log Z_{\mathcal {O}}(\lambda_{\beta})$
and
![]() $\log \lambda_\beta$
in powers of
$\log \lambda_\beta$
in powers of
![]() $(1-\beta)^d$
.
$(1-\beta)^d$
.
Let
![]() $i_m(\mathcal {O}) $
be the number of independent sets I of size m in
$i_m(\mathcal {O}) $
be the number of independent sets I of size m in
![]() $Q_d$
that are achievable in the odd polymer model (i.e.
$Q_d$
that are achievable in the odd polymer model (i.e.
![]() $\mu_{\mathcal {O},\lambda}(I)>0$
).
$\mu_{\mathcal {O},\lambda}(I)>0$
).
Lemma 15 For any
![]() $\beta >0$
,
$\beta >0$
,
as
![]() $d \to \infty$
.
$d \to \infty$
.
Lemma 16 Fix
![]() $\beta>0$
. Suppose
$\beta>0$
. Suppose
![]() $\lambda= \lambda(\beta, d)$
is such that
$\lambda= \lambda(\beta, d)$
is such that
Then
Lemma 17 There exists a sequence of rational functions
![]() $B_j(d,\beta)$
,
$B_j(d,\beta)$
,
![]() $j\in \mathbb N$
, such that
$j\in \mathbb N$
, such that
![]() $B_j$
can be computed in time
$B_j$
can be computed in time
![]() $e^{O( j \log j)}$
and the following holds. Fix
$e^{O( j \log j)}$
and the following holds. Fix
![]() $t \ge 1$
and let
$t \ge 1$
and let
![]() $r=\lceil t/2 \rceil-1$
. Suppose that
$r=\lceil t/2 \rceil-1$
. Suppose that
![]() $m = \lfloor \beta N \rfloor$
with
$m = \lfloor \beta N \rfloor$
with
![]() $\beta > 1- 2^{-1/t} $
, then if
$\beta > 1- 2^{-1/t} $
, then if
 \begin{equation}\lambda_{\beta} = \frac{\beta}{1-\beta} + \sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd}\, ,\end{equation}
\begin{equation}\lambda_{\beta} = \frac{\beta}{1-\beta} + \sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd}\, ,\end{equation}
then
We prove Lemma 16 first, for which we need the following basic binomial local central limit result.
Lemma 18 Fix
![]() $p \in (0,1)$
and suppose
$p \in (0,1)$
and suppose
![]() $X \sim \text{Bin}(n,p)$
. Suppose
$X \sim \text{Bin}(n,p)$
. Suppose
![]() $n \to \infty$
and
$n \to \infty$
and
![]() $k=o(\sqrt{n})$
, then
$k=o(\sqrt{n})$
, then
Proof of Lemma 16. Let
![]() $m = \lfloor \beta N\rfloor$
. For any
$m = \lfloor \beta N\rfloor$
. For any
![]() $\lambda>0$
, we have
$\lambda>0$
, we have
where the probability is with respect to the measure
![]() $\mu_{\mathcal {O}, \lambda}$
. We therefore need to show that if
$\mu_{\mathcal {O}, \lambda}$
. We therefore need to show that if
![]() $\lambda$
satisfies (14), then
$\lambda$
satisfies (14), then
By considering first the collection of polymers
![]() $\boldsymbol\Gamma$
chosen at Step 1 in the definition of
$\boldsymbol\Gamma$
chosen at Step 1 in the definition of
![]() $\mu_{\mathcal {O}, \lambda}$
(Definition 8), and then the probability that the correct number of additional vertices are chosen at Step 2, we see that
$\mu_{\mathcal {O}, \lambda}$
(Definition 8), and then the probability that the correct number of additional vertices are chosen at Step 2, we see that
where we recall that
![]() $\Omega_\mathcal {O}$
denotes the set of all collections of mutually compatible odd polymers. By the large deviation bound [Reference Jenssen and Perkins15, Lemma 16] we have
$\Omega_\mathcal {O}$
denotes the set of all collections of mutually compatible odd polymers. By the large deviation bound [Reference Jenssen and Perkins15, Lemma 16] we have
and so we can condition on the event
![]() $|N(\boldsymbol\Gamma)|\leq \frac{2N}{d}$
throughout (17) and only change the resulting probability by an additive factor of
$|N(\boldsymbol\Gamma)|\leq \frac{2N}{d}$
throughout (17) and only change the resulting probability by an additive factor of
![]() $O( \exp(\!-N/d^4))=o(N^{-1/2})$
. Under this conditioning, the binomial probabilities in (17) are uniformly bounded by
$O( \exp(\!-N/d^4))=o(N^{-1/2})$
. Under this conditioning, the binomial probabilities in (17) are uniformly bounded by
![]() $O(1/\sqrt{N})$
. To establish (16), it therefore suffices to show that with high probability in the choice of
$O(1/\sqrt{N})$
. To establish (16), it therefore suffices to show that with high probability in the choice of
![]() $\boldsymbol\Gamma$
, the binomial probabilities in (17) are in fact equal to
$\boldsymbol\Gamma$
, the binomial probabilities in (17) are in fact equal to
![]() $(1+o(1)) \frac{1+ \lambda}{ \sqrt{2 \pi N \lambda} }$
. By Lemma 18, it suffices to show that with high probability in the choice of
$(1+o(1)) \frac{1+ \lambda}{ \sqrt{2 \pi N \lambda} }$
. By Lemma 18, it suffices to show that with high probability in the choice of
![]() $\boldsymbol\Gamma$
we have
$\boldsymbol\Gamma$
we have
Now, by our assumption on
![]() $\lambda$
, (13) and Lemma 13,
$\lambda$
, (13) and Lemma 13,
It follows that to show (18) holds whp with respect to
![]() $\boldsymbol\Gamma$
, it suffices to show that
$\boldsymbol\Gamma$
, it suffices to show that
and similarly for
![]() $|N(\boldsymbol\Gamma)|$
. This is an immediate consequence of Lemma 12 and the fact that
$|N(\boldsymbol\Gamma)|$
. This is an immediate consequence of Lemma 12 and the fact that
where we have used (13) and Lemma 11.
Next we prove Lemma 15.
Proof of Lemma 15. Let
![]() $\mathcal I_m$
denote the set of all independent sets of size m in
$\mathcal I_m$
denote the set of all independent sets of size m in
![]() $Q_d$
. Then by Theorem 9 (and the symmetry between even and odd) we have
$Q_d$
. Then by Theorem 9 (and the symmetry between even and odd) we have
By Theorem 9 again it follows that
It therefore suffices to show that there is a choice of
![]() $\lambda$
such that
$\lambda$
such that
![]() $\frac{i_m(\mathcal {O})\lambda^m}{ Z_{\mathcal {O}}(\lambda)}$
is much larger than
$\frac{i_m(\mathcal {O})\lambda^m}{ Z_{\mathcal {O}}(\lambda)}$
is much larger than
![]() $\exp (\!-N/d^4)$
. This follows from Lemma 16 by choosing
$\exp (\!-N/d^4)$
. This follows from Lemma 16 by choosing
![]() $\lambda$
satisfying (14).
$\lambda$
satisfying (14).
Next we prove Lemma 17. In the following, if P(x, y) is a polynomial in x, y, we write
![]() ${\textrm{deg}}_x(P)$
for the degree of P in x.
${\textrm{deg}}_x(P)$
for the degree of P in x.
Proof of Lemma 17. Let
![]() $r=\lceil t/2 \rceil - 1$
and set
$r=\lceil t/2 \rceil - 1$
and set
 \begin{align*}\lambda=\lambda_{\beta} = \frac{\beta}{1-\beta} + \sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd}\, ,\end{align*}
\begin{align*}\lambda=\lambda_{\beta} = \frac{\beta}{1-\beta} + \sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd}\, ,\end{align*}
where the functions
![]() $B_j$
are rational polynomials in
$B_j$
are rational polynomials in
![]() $\beta, d$
of constant degree (independent of d) to be determined later. Let
$\beta, d$
of constant degree (independent of d) to be determined later. Let
![]() $X:=\sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd+1}$
and note that
$X:=\sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd+1}$
and note that
![]() $X=o(1)$
. It will be useful to note that for
$X=o(1)$
. It will be useful to note that for
![]() $k=O(d)$
,
$k=O(d)$
,
In particular, since
![]() $\beta > 1-2^{-1/t}$
,
$\beta > 1-2^{-1/t}$
,
for some constant
![]() $c>0$
.
$c>0$
.
By Corollary 14 and Theorem 10,
 \begin{align}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)&= N \frac{\lambda}{1+ \lambda} + \lambda N \sum_{j=1}^r \frac{ \frac{\partial}{\partial \lambda}R_j(\lambda,d) }{ (1+\lambda)^{jd} } - \frac{ jd R_j(\lambda,d) }{ (1+\lambda)^{jd+1} } + O\left(N \frac{d^{2r+1}}{ (1+\lambda)^{d(r+1)}} \right)\nonumber \\&=\frac{\lambda}{1+ \lambda} N + N \sum_{j=1}^r F_j(\lambda, d)(1+\lambda)^{-jd-1} + o\left(N^{1/2} \right)\, , \end{align}
\begin{align}\mathbb{E}_{\mathcal {O},\lambda} ( | \mathbf I |)&= N \frac{\lambda}{1+ \lambda} + \lambda N \sum_{j=1}^r \frac{ \frac{\partial}{\partial \lambda}R_j(\lambda,d) }{ (1+\lambda)^{jd} } - \frac{ jd R_j(\lambda,d) }{ (1+\lambda)^{jd+1} } + O\left(N \frac{d^{2r+1}}{ (1+\lambda)^{d(r+1)}} \right)\nonumber \\&=\frac{\lambda}{1+ \lambda} N + N \sum_{j=1}^r F_j(\lambda, d)(1+\lambda)^{-jd-1} + o\left(N^{1/2} \right)\, , \end{align}
where the
![]() $F_j$
are polynomials in
$F_j$
are polynomials in
![]() $\lambda, d$
with
$\lambda, d$
with
![]() ${\textrm{deg}}_d(F_j)\leq 2j+1$
and
${\textrm{deg}}_d(F_j)\leq 2j+1$
and
![]() ${\textrm{deg}}_\lambda(F_j)\leq 3j^2$
. Our goal is to show that there exists an appropriate choice of
${\textrm{deg}}_\lambda(F_j)\leq 3j^2$
. Our goal is to show that there exists an appropriate choice of
![]() $B_1, \ldots, B_r$
that makes this final expression (23) equal to
$B_1, \ldots, B_r$
that makes this final expression (23) equal to
![]() $m+o\left(N^{1/2} \right)$
.
$m+o\left(N^{1/2} \right)$
.
Since
![]() ${\textrm{deg}}_\lambda(F_j)\leq 3j^2$
, and
${\textrm{deg}}_\lambda(F_j)\leq 3j^2$
, and
![]() $\lambda=(\beta+X)/(1-\beta)$
we may write
$\lambda=(\beta+X)/(1-\beta)$
we may write
for some non-negative integer
![]() $c_j\leq 3j^2$
and
$c_j\leq 3j^2$
and
![]() $G_j$
a polynomial in
$G_j$
a polynomial in
![]() $\beta, d, X$
such that
$\beta, d, X$
such that
![]() ${\textrm{deg}}_d(G_j)\leq 2j+1$
. It follows by (21) that
${\textrm{deg}}_d(G_j)\leq 2j+1$
. It follows by (21) that
 \begin{align}\nonumber &\frac{\lambda}{1+\lambda} + \sum_{j=1}^r F_j(\lambda, d) (1+\lambda)^{-jd-1}=(\beta+X)\sum_{i=0}^{r}(\!-X)^i \\&\quad + \sum_{j=1}^rG_j(\beta, d, X) (1-\beta)^{jd+1-c_j}\sum_{i=0}^{r}\binom{-jd-1}{i}X^i + O(d^{3r}X^{r+1})\, .\end{align}
\begin{align}\nonumber &\frac{\lambda}{1+\lambda} + \sum_{j=1}^r F_j(\lambda, d) (1+\lambda)^{-jd-1}=(\beta+X)\sum_{i=0}^{r}(\!-X)^i \\&\quad + \sum_{j=1}^rG_j(\beta, d, X) (1-\beta)^{jd+1-c_j}\sum_{i=0}^{r}\binom{-jd-1}{i}X^i + O(d^{3r}X^{r+1})\, .\end{align}
We now recall that
![]() $X=\sum_{j=1}^r B_j (1-\beta)^{jd+1}$
and we expand this final expression as a polynomial in
$X=\sum_{j=1}^r B_j (1-\beta)^{jd+1}$
and we expand this final expression as a polynomial in
![]() $(1-\beta)^d$
. This yields
$(1-\beta)^d$
. This yields
 \begin{align}\frac{\lambda}{1+\lambda} + \sum_{j=1}^r F_j(\lambda, d) (1+\lambda)^{-jd-1}&=\beta + \sum_{j=1}^{r} Q_j(\beta, d, B_1,\ldots, B_r)\cdot (1-\beta)^{jd} + O(d^{3r}X^{r+1})\end{align}
\begin{align}\frac{\lambda}{1+\lambda} + \sum_{j=1}^r F_j(\lambda, d) (1+\lambda)^{-jd-1}&=\beta + \sum_{j=1}^{r} Q_j(\beta, d, B_1,\ldots, B_r)\cdot (1-\beta)^{jd} + O(d^{3r}X^{r+1})\end{align}
where
![]() $Q_j=Q_j(\beta, d, B_1,\ldots, B_r)$
is a rational function
$Q_j=Q_j(\beta, d, B_1,\ldots, B_r)$
is a rational function
![]() $\beta, d, B_1, \ldots, B_r$
with denominator
$\beta, d, B_1, \ldots, B_r$
with denominator
![]() $(1-\beta)^{b_j}$
for some
$(1-\beta)^{b_j}$
for some
![]() $b_j\leq 3j^2$
and with
$b_j\leq 3j^2$
and with
![]() ${\textrm{deg}}_d(Q_j)\leq 2j+1$
. Moreover, by examining the expansion (24), we see that
${\textrm{deg}}_d(Q_j)\leq 2j+1$
. Moreover, by examining the expansion (24), we see that
![]() $Q_j$
is linear in
$Q_j$
is linear in
![]() $B_j$
where the coefficient of
$B_j$
where the coefficient of
![]() $B_j$
is
$B_j$
is
![]() $(1-\beta)^2$
(in particular the coefficient is non-zero). It follows inductively that there is a choice of
$(1-\beta)^2$
(in particular the coefficient is non-zero). It follows inductively that there is a choice of
![]() $B_1, \ldots, B_r$
such that
$B_1, \ldots, B_r$
such that
![]() $Q_1=\ldots=Q_r=0$
where
$Q_1=\ldots=Q_r=0$
where
![]() $B_j$
is a rational function of
$B_j$
is a rational function of
![]() $\beta, d$
of constant degree (depending on j but not d). With this choice of
$\beta, d$
of constant degree (depending on j but not d). With this choice of
![]() $B_1, \ldots, B_r$
it follows from (23) and (25) that
$B_1, \ldots, B_r$
it follows from (23) and (25) that
where for the last bound we used that
![]() $d^{3r}X^{r+1}=d^{O_r(1)}(1-\beta)^{d(r+1)}=o(N^{-1/2})$
by (22).
$d^{3r}X^{r+1}=d^{O_r(1)}(1-\beta)^{d(r+1)}=o(N^{-1/2})$
by (22).
Finally we note that the above argument gives an algorithm for computing the
![]() $B_j$
. Since the
$B_j$
. Since the
![]() $R_j$
, and so also the
$R_j$
, and so also the
![]() $F_j$
and
$F_j$
and
![]() $G_j$
, can be computed in
$G_j$
, can be computed in
![]() $e^{O(j \log j)}$
time, we see that the
$e^{O(j \log j)}$
time, we see that the
![]() $Q_j$
can be computed in
$Q_j$
can be computed in
![]() $e^{O(j \log j)}$
time. The
$e^{O(j \log j)}$
time. The
![]() $B_j$
can then be computed by solving j successive linear equations.
$B_j$
can then be computed by solving j successive linear equations.
To give a concrete example of the algorithm above in action, we pause for a moment to calculate the rational function
![]() $B_1$
. Using the definition of
$B_1$
. Using the definition of
![]() $R_1$
at (11), we see that
$R_1$
at (11), we see that
![]() $R_1=\lambda$
. In the notation of the proof of Theorem 17, it follows that
$R_1=\lambda$
. In the notation of the proof of Theorem 17, it follows that
![]() $F_1=\lambda+(1-d)\lambda^2$
. Noting that
$F_1=\lambda+(1-d)\lambda^2$
. Noting that
![]() $\lambda=(\beta+X)/(1-\beta)$
we have
$\lambda=(\beta+X)/(1-\beta)$
we have
and so
![]() $G_1= (1-\beta)(\beta+X) + (1-d)(\beta+X)^2$
and
$G_1= (1-\beta)(\beta+X) + (1-d)(\beta+X)^2$
and
![]() $c_1=2$
. Recalling that
$c_1=2$
. Recalling that
![]() $X:=\sum_{j=1}^r B_j (1-\beta)^{jd+1}$
and examining the coefficient of
$X:=\sum_{j=1}^r B_j (1-\beta)^{jd+1}$
and examining the coefficient of
![]() $(1-\beta)^d$
in (24), we see that
$(1-\beta)^d$
in (24), we see that
Solving
![]() $Q_1=0$
yields
$Q_1=0$
yields
3.2 Proof of Theorem 5
We now prove Theorem 5. Given the formula (5) from Theorem 6, we need to extract the binomial coefficient
![]() $\binom{N}{ \lfloor \beta N \rfloor}$
and expand the logarithm of what remains.
$\binom{N}{ \lfloor \beta N \rfloor}$
and expand the logarithm of what remains.
Lemma 19 Fix
![]() $\beta \in (0,1)$
. With
$\beta \in (0,1)$
. With
![]() $\lambda_0 = \frac{\beta}{1 - \beta}$
,
$\lambda_0 = \frac{\beta}{1 - \beta}$
,
as
![]() $N \to \infty$
.
$N \to \infty$
.
The proof follows from Stirling’s formula.
Proof of Theorem 5. Given Lemma 19, Theorems 3 and 6, we are left to compute coefficients
![]() $P_j = P_j(\beta, d)$
,
$P_j = P_j(\beta, d)$
,
![]() $j \ge 1$
, so that for
$j \ge 1$
, so that for
![]() $t \ge 1 $
and
$t \ge 1 $
and
![]() $\beta > 1- 2^{-1/t}$
we have
$\beta > 1- 2^{-1/t}$
we have
 \begin{align} \log \left( \frac{1+\lambda_\beta}{1+\lambda_0} \right) - \beta \log \frac{\lambda_\beta}{\lambda_0} + \sum_{j=1}^{t-1} R_j(d,\lambda_\beta) (1+\lambda_\beta)^{-dj} &= \sum_{j=1}^{t-1} P_j \cdot (1-\beta)^{jd} +o(N^{-1})\end{align}
\begin{align} \log \left( \frac{1+\lambda_\beta}{1+\lambda_0} \right) - \beta \log \frac{\lambda_\beta}{\lambda_0} + \sum_{j=1}^{t-1} R_j(d,\lambda_\beta) (1+\lambda_\beta)^{-dj} &= \sum_{j=1}^{t-1} P_j \cdot (1-\beta)^{jd} +o(N^{-1})\end{align}
where
![]() $\lambda_\beta$
is given by (4). We proceed by expanding each term on the left-hand side of (27) as a power series in
$\lambda_\beta$
is given by (4). We proceed by expanding each term on the left-hand side of (27) as a power series in
![]() $(1-\beta)^d$
. As in the proof of Lemma 17 we set
$(1-\beta)^d$
. As in the proof of Lemma 17 we set
![]() $X:=\sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd+1}$
and note that
$X:=\sum_{j=1}^r B_j(\beta, d) (1-\beta)^{jd+1}$
and note that
![]() $X^t=o(N^{-1})$
since
$X^t=o(N^{-1})$
since
![]() $\beta > 1- 2^{-1/t}$
. It follows by Taylor expansion that
$\beta > 1- 2^{-1/t}$
. It follows by Taylor expansion that
 \begin{align}\nonumber \log \left( \frac{1+\lambda_\beta}{1+\lambda_0} \right) - \beta \log \frac{\lambda_\beta}{\lambda_0} &= \log(1+X)-\beta \log(1+X/\beta)\\ &= \sum_{i=1}^{t-1}\frac{(\!-1)^{1+i}}{i}(1-\beta^{1-i})X^i + o(N^{-1})\, .\end{align}
\begin{align}\nonumber \log \left( \frac{1+\lambda_\beta}{1+\lambda_0} \right) - \beta \log \frac{\lambda_\beta}{\lambda_0} &= \log(1+X)-\beta \log(1+X/\beta)\\ &= \sum_{i=1}^{t-1}\frac{(\!-1)^{1+i}}{i}(1-\beta^{1-i})X^i + o(N^{-1})\, .\end{align}
We now turn to the sum on the left-hand side of (27). Since
![]() $R_j$
is a polynomial in
$R_j$
is a polynomial in
![]() $\lambda_\beta, d$
such that
$\lambda_\beta, d$
such that
![]() ${\textrm{deg}}_{\lambda_\beta}(R_j)\leq 3j^2$
and
${\textrm{deg}}_{\lambda_\beta}(R_j)\leq 3j^2$
and
![]() ${\textrm{deg}}_d(R_j)\leq 2j$
and the fact that
${\textrm{deg}}_d(R_j)\leq 2j$
and the fact that
![]() $\lambda_\beta=(\beta+X)/(1-\beta)$
, we may write
$\lambda_\beta=(\beta+X)/(1-\beta)$
, we may write
for some non-negative integer
![]() $c_j\leq 3j^2$
and
$c_j\leq 3j^2$
and
![]() $S_j$
a polynomial in
$S_j$
a polynomial in
![]() $\beta, d, X$
such that
$\beta, d, X$
such that
![]() ${\textrm{deg}}_d(S_j)\leq 2j$
. It follows by (21) that
${\textrm{deg}}_d(S_j)\leq 2j$
. It follows by (21) that
 \begin{align}\sum_{j=1}^t R_j(\lambda_\beta, d) (1+\lambda_\beta)^{-dj}&=\sum_{j=1}^{t-1}S_j(\beta, d, X) (1-\beta)^{jd-c_j}\sum_{i=0}^{t-1}\binom{-jd}{i}X^i + O(d^{2t}X^t)\, .\end{align}
\begin{align}\sum_{j=1}^t R_j(\lambda_\beta, d) (1+\lambda_\beta)^{-dj}&=\sum_{j=1}^{t-1}S_j(\beta, d, X) (1-\beta)^{jd-c_j}\sum_{i=0}^{t-1}\binom{-jd}{i}X^i + O(d^{2t}X^t)\, .\end{align}
We note that
![]() $O(d^{2t}X^t)=O(d^{3t}(1-\beta)^{td})=o(N^{-1})$
. To compute the
$O(d^{2t}X^t)=O(d^{3t}(1-\beta)^{td})=o(N^{-1})$
. To compute the
![]() $P_j$
we simply sum (28) and (29), expand the powers of X and collect the coefficients of
$P_j$
we simply sum (28) and (29), expand the powers of X and collect the coefficients of
![]() $(1-\beta)^d, \ldots, (1-\beta)^{(t-1)d}$
. Finally we note that since
$(1-\beta)^d, \ldots, (1-\beta)^{(t-1)d}$
. Finally we note that since
![]() $R_j, S_j$
and
$R_j, S_j$
and
![]() $B_j$
can each be computed in time
$B_j$
can each be computed in time
![]() $e^{O(j\log j)}$
,
$e^{O(j\log j)}$
,
![]() $P_j$
can be computed in time
$P_j$
can be computed in time
![]() $e^{O(j\log j)}$
.
$e^{O(j\log j)}$
.
3.2.1 Computation of
 $P_1, P_2$
$P_1, P_2$
To illustrate the algorithm for computing the
![]() $P_j$
in Theorem 5, we use it to compute
$P_j$
in Theorem 5, we use it to compute
![]() $P_1$
and
$P_1$
and
![]() $P_2$
. First we note that in [Reference Jenssen and Perkins15] it was shown that
$P_2$
. First we note that in [Reference Jenssen and Perkins15] it was shown that
It follows that (using the notation of the proof of Theorem 5)
and
![]() $c_1=1$
,
$c_1=1$
,
![]() $c_2=4$
. Now, to compute
$c_2=4$
. Now, to compute
![]() $P_1, P_2$
we compute the coefficients of
$P_1, P_2$
we compute the coefficients of
![]() $(1-\beta)^d, (1-\beta)^{2d}$
in the sum of (28) and (29). The coefficient of
$(1-\beta)^d, (1-\beta)^{2d}$
in the sum of (28) and (29). The coefficient of
![]() $(1-\beta)^d$
in (28) is 0 and in (29) it is
$(1-\beta)^d$
in (28) is 0 and in (29) it is
![]() $\beta/(1-\beta)$
and so
$\beta/(1-\beta)$
and so
The coefficient of
![]() $(1-\beta)^{2d}$
in (28) is
$(1-\beta)^{2d}$
in (28) is
The coefficient of
![]() $(1-\beta)^{2d}$
in (29) is
$(1-\beta)^{2d}$
in (29) is
Recalling (26), the formula for
![]() $B_1$
, and summing the above two expressions yields
$B_1$
, and summing the above two expressions yields
4. Local central limit theorems for polymer models
In the odd polymer model, let T be a defect type and
![]() $X_T$
be the random variable counting the number of defects of type T in a sample from
$X_T$
be the random variable counting the number of defects of type T in a sample from
![]() $\mu_{\mathcal {O}, \lambda}$
. Recall that
$\mu_{\mathcal {O}, \lambda}$
. Recall that
![]() $m_T = \mathbb{E} X_T$
and let
$m_T = \mathbb{E} X_T$
and let
![]() $\sigma^2_T = \text{var}(X_T)$
. Moreover, let
$\sigma^2_T = \text{var}(X_T)$
. Moreover, let
![]() $n_T$
denote the number of polymers of type T and let
$n_T$
denote the number of polymers of type T and let
![]() $w_T$
denote the weight w(S) (defined at (7)) of a representative polymer S of type T.
$w_T$
denote the weight w(S) (defined at (7)) of a representative polymer S of type T.
Throughout this section we assume that
![]() $\lambda\ge C\log d /d^{1/3}$
as in Theorem 9 and probabilities and expectations are with respect to the odd polymer model. The main result of this section is a multivariate local central limit theorem for the number of polymers of different types, extending the multivariate central limit theorem of [Reference Jenssen and Perkins15, Theorem 6].
$\lambda\ge C\log d /d^{1/3}$
as in Theorem 9 and probabilities and expectations are with respect to the odd polymer model. The main result of this section is a multivariate local central limit theorem for the number of polymers of different types, extending the multivariate central limit theorem of [Reference Jenssen and Perkins15, Theorem 6].
Theorem 20 Let
![]() $\mathcal {T}_1$
and
$\mathcal {T}_1$
and
![]() $\mathcal {T}_2$
be two fixed sets of defect types so that for each
$\mathcal {T}_2$
be two fixed sets of defect types so that for each
![]() $T \in \mathcal {T}_1$
,
$T \in \mathcal {T}_1$
,
![]() $m_T \to \rho_T$
for some constant
$m_T \to \rho_T$
for some constant
![]() $\rho_T>0$
, and for each
$\rho_T>0$
, and for each
![]() $T \in \mathcal {T}_2$
,
$T \in \mathcal {T}_2$
,
![]() $m_T \to \infty$
as
$m_T \to \infty$
as
![]() $d \to \infty$
. Let
$d \to \infty$
. Let
![]() $ \{ k_T \}_{T \in \mathcal T_1}$
be a collection of non-negative integers and let
$ \{ k_T \}_{T \in \mathcal T_1}$
be a collection of non-negative integers and let
![]() $ \{ k_T \}_{T \in \mathcal T_2}$
be such that
$ \{ k_T \}_{T \in \mathcal T_2}$
be such that
![]() $k_T= \lfloor m_T +s_T \rfloor$
where
$k_T= \lfloor m_T +s_T \rfloor$
where
![]() $| s_T| = O(\sqrt{ m_T})$
for all
$| s_T| = O(\sqrt{ m_T})$
for all
![]() $T \in \mathcal T_2$
. Then
$T \in \mathcal T_2$
. Then
 \begin{align*}\mathbb{P} \left( \bigcap_{T \in \mathcal {T}_1\cup \mathcal {T}_2} X_T=k_T\right )&= (1+o(1)) \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!}\prod_{T \in \mathcal T_2} \frac{e^{ - \frac{ s_T^2}{2 m_T}}}{\sqrt{2 \pi m_T}} \,.\end{align*}
\begin{align*}\mathbb{P} \left( \bigcap_{T \in \mathcal {T}_1\cup \mathcal {T}_2} X_T=k_T\right )&= (1+o(1)) \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!}\prod_{T \in \mathcal T_2} \frac{e^{ - \frac{ s_T^2}{2 m_T}}}{\sqrt{2 \pi m_T}} \,.\end{align*}
The probability in the theorem statement is with respect to the odd polymer model, but the statement also holds for defects of an independent set drawn from the hard-core model on
![]() $Q_d$
via Theorem 9.
$Q_d$
via Theorem 9.
Before we proceed it will be useful to recall a result from [Reference Jenssen and Perkins15] on the cumulants of the random variables
![]() $X_T$
. Recall that for a random variable X we use
$X_T$
. Recall that for a random variable X we use
![]() $\kappa_k(X)$
to denote the kth cumulant of X. The following result appears as Lemma 20 in [Reference Jenssen and Perkins15].
$\kappa_k(X)$
to denote the kth cumulant of X. The following result appears as Lemma 20 in [Reference Jenssen and Perkins15].
Lemma 21 For a defect type T, let
![]() $Y_T(\Gamma)$
denote the number of polymers of type T in the cluster
$Y_T(\Gamma)$
denote the number of polymers of type T in the cluster
![]() $\Gamma$
. Then for any fixed
$\Gamma$
. Then for any fixed
![]() $k \ge 1$
,
$k \ge 1$
,
and
 \begin{equation} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| > |T|}} \left | w(\Gamma) Y_T(\Gamma)^k \right| = o( n_T w_T) \,.\end{equation}
\begin{equation} \sum_{\substack{\Gamma \in \mathcal{C} \\ \|\Gamma\| > |T|}} \left | w(\Gamma) Y_T(\Gamma)^k \right| = o( n_T w_T) \,.\end{equation}
Given a random vector
![]() $X=(X_1, \ldots, X_q)\in\mathbb{R}^q$
its characteristic function is
$X=(X_1, \ldots, X_q)\in\mathbb{R}^q$
its characteristic function is
for
![]() $t \in \mathbb{R}^q$
.
$t \in \mathbb{R}^q$
.
Lemma 22 Fix
![]() $q\in\mathbb N$
and a list
$q\in\mathbb N$
and a list
![]() $T_1, \ldots, T_q$
of defect types. Let
$T_1, \ldots, T_q$
of defect types. Let
![]() $X=(X_{T_1}, \ldots, X_{T_q})$
. There exists
$X=(X_{T_1}, \ldots, X_{T_q})$
. There exists
![]() $c>0$
such that
$c>0$
such that
 \begin{align*} |\varphi_{X}(t) | \le \exp\left\{- c \sum_{i=1}^q t_i^2 n_{T_i}w_{T_i}\right\} \, , \end{align*}
\begin{align*} |\varphi_{X}(t) | \le \exp\left\{- c \sum_{i=1}^q t_i^2 n_{T_i}w_{T_i}\right\} \, , \end{align*}
for all
![]() $t\in[\!-\pi,\pi]^q$
.
$t\in[\!-\pi,\pi]^q$
.
Proof. Given a cluster
![]() $\Gamma\in \mathcal {C}$
, let
$\Gamma\in \mathcal {C}$
, let
![]() $Y(\Gamma)=(Y_{T_1}(\Gamma),\ldots, Y_{T_q}(\Gamma))$
. Using the cluster expansion we write
$Y(\Gamma)=(Y_{T_1}(\Gamma),\ldots, Y_{T_q}(\Gamma))$
. Using the cluster expansion we write
 \begin{align*}\log \mathbb{E} e^{i\langle t, X\rangle} &= \sum_{\Gamma\in \mathcal {C}} w(\Gamma) e^{i \langle t, Y(\Gamma)\rangle} - \sum_{\Gamma\in\mathcal {C}} w(\Gamma) \\[3pt] &= \sum_{\Gamma\in \mathcal {C}} w(\Gamma) (e^{i \langle t, Y(\Gamma)\rangle}-1) \,.\end{align*}
\begin{align*}\log \mathbb{E} e^{i\langle t, X\rangle} &= \sum_{\Gamma\in \mathcal {C}} w(\Gamma) e^{i \langle t, Y(\Gamma)\rangle} - \sum_{\Gamma\in\mathcal {C}} w(\Gamma) \\[3pt] &= \sum_{\Gamma\in \mathcal {C}} w(\Gamma) (e^{i \langle t, Y(\Gamma)\rangle}-1) \,.\end{align*}
Let
 \begin{align*}\mathcal{M}_j=\left\{\Gamma\in \mathcal {C}: j=\max\{i: Y_{T_i}(\Gamma)>0\}, \sum_{i=1}^q Y_{T_i}(\Gamma)>1 \right\}\, .\end{align*}
\begin{align*}\mathcal{M}_j=\left\{\Gamma\in \mathcal {C}: j=\max\{i: Y_{T_i}(\Gamma)>0\}, \sum_{i=1}^q Y_{T_i}(\Gamma)>1 \right\}\, .\end{align*}
Then,
 \begin{align*}\textrm {Re} \log \mathbb{E} e^{i\langle t, X\rangle} &= \sum_{\Gamma\in \mathcal {C}} w(\Gamma) (\cos( \langle t, Y(\Gamma)\rangle)-1) \\[2pt] &=\sum_{i=1}^q n_{T_i} w_{T_i} (\cos (t_i) -1) +\sum_{j=1}^q\sum_{\Gamma\in \mathcal{M}_j} w(\Gamma) (\cos( \langle t, Y(\Gamma)\rangle)-1) \\[2pt] &\le-\frac{1}{5}\sum_{i=1}^q t_i^2 n_{T_i} w_{T_i} +\sum_{j=1}^q\sum_{\Gamma\in \mathcal{M}_j} |w(\Gamma)| \langle t, Y(\Gamma)\rangle^2 \\[2pt] &\le-\frac{1}{5}\sum_{i=1}^q t_i^2 n_{T_i} w_{T_i} +\sum_{j=1}^q\sum_{\Gamma\in \mathcal{M}_j} |w(\Gamma)|j\sum_{i=1}^jt_i^2Y_{T_i}(\Gamma)^2 \\[2pt] &\le -\frac{1}{5}\sum_{i=1}^q t_i^2 n_{T_i} w_{T_i} +\sum_{i=1}^qt_i^2o(n_{T_i}w_{T_i}) \\\end{align*}
\begin{align*}\textrm {Re} \log \mathbb{E} e^{i\langle t, X\rangle} &= \sum_{\Gamma\in \mathcal {C}} w(\Gamma) (\cos( \langle t, Y(\Gamma)\rangle)-1) \\[2pt] &=\sum_{i=1}^q n_{T_i} w_{T_i} (\cos (t_i) -1) +\sum_{j=1}^q\sum_{\Gamma\in \mathcal{M}_j} w(\Gamma) (\cos( \langle t, Y(\Gamma)\rangle)-1) \\[2pt] &\le-\frac{1}{5}\sum_{i=1}^q t_i^2 n_{T_i} w_{T_i} +\sum_{j=1}^q\sum_{\Gamma\in \mathcal{M}_j} |w(\Gamma)| \langle t, Y(\Gamma)\rangle^2 \\[2pt] &\le-\frac{1}{5}\sum_{i=1}^q t_i^2 n_{T_i} w_{T_i} +\sum_{j=1}^q\sum_{\Gamma\in \mathcal{M}_j} |w(\Gamma)|j\sum_{i=1}^jt_i^2Y_{T_i}(\Gamma)^2 \\[2pt] &\le -\frac{1}{5}\sum_{i=1}^q t_i^2 n_{T_i} w_{T_i} +\sum_{i=1}^qt_i^2o(n_{T_i}w_{T_i}) \\\end{align*}
where for the first inequality we used that
![]() $-t^2\leq\cos(t)-1\leq -t^2/5$
for
$-t^2\leq\cos(t)-1\leq -t^2/5$
for
![]() $t\in[\!-\pi,\pi]$
. For the next inequality we used Cauchy–Schwarz, and for the final inequality we used Lemma 21.
$t\in[\!-\pi,\pi]$
. For the next inequality we used Cauchy–Schwarz, and for the final inequality we used Lemma 21.
Proof of Theorem 20. Let
![]() $\mathcal {T}_1=\{T_1,\ldots, T_p\}$
,
$\mathcal {T}_1=\{T_1,\ldots, T_p\}$
,
![]() $\mathcal {T}_2=\{T_{p+1},\ldots, T_q\}$
and
$\mathcal {T}_2=\{T_{p+1},\ldots, T_q\}$
and
![]() $\mathcal {T}=\mathcal {T}_1\cup\mathcal {T}_2$
. Let
$\mathcal {T}=\mathcal {T}_1\cup\mathcal {T}_2$
. Let
![]() $X_i=X_{T_i}$
,
$X_i=X_{T_i}$
,
![]() $m_i=m_{T_i}$
,
$m_i=m_{T_i}$
,
![]() $\sigma_i=\sigma_{T_i}$
,
$\sigma_i=\sigma_{T_i}$
,
![]() $k_i=k_{T_i}$
for
$k_i=k_{T_i}$
for
![]() $i\in [q]$
. Let
$i\in [q]$
. Let
![]() $X=(X_1,\ldots, X_q)$
and let
$X=(X_1,\ldots, X_q)$
and let
By Fourier inversion,
 \begin{align*}\mathbb{P}\left( \bigcap_{T \in \mathcal T} X_T=k_T\right) &= \frac{1}{(2 \pi)^q} \int_{[\!-\pi,\pi]^q} \varphi_X(t) \cdot e^{-i\langle t, k \rangle } \, dt\, .\end{align*}
\begin{align*}\mathbb{P}\left( \bigcap_{T \in \mathcal T} X_T=k_T\right) &= \frac{1}{(2 \pi)^q} \int_{[\!-\pi,\pi]^q} \varphi_X(t) \cdot e^{-i\langle t, k \rangle } \, dt\, .\end{align*}
Making the substitution
![]() $t_i=x_i$
for
$t_i=x_i$
for
![]() $i\in[p]$
and
$i\in[p]$
and
![]() $t_i=x_i/\sigma_i$
for
$t_i=x_i/\sigma_i$
for
![]() $i>p$
, we have
$i>p$
, we have
 \begin{align}\mathbb{P}\left( \bigcap_{T \in \mathcal T} X_T=k_T\right) = \frac{1}{(2 \pi)^q} \prod_{i>p}\sigma_i^{-1} \int_{B_1} \int_{B_2} \varphi_{\tilde X}(x)g(x)dx_q\ldots dx_1\end{align}
\begin{align}\mathbb{P}\left( \bigcap_{T \in \mathcal T} X_T=k_T\right) = \frac{1}{(2 \pi)^q} \prod_{i>p}\sigma_i^{-1} \int_{B_1} \int_{B_2} \varphi_{\tilde X}(x)g(x)dx_q\ldots dx_1\end{align}
where
![]() $B_1=[\!-\pi,\pi]^p$
,
$B_1=[\!-\pi,\pi]^p$
,
![]() $B_2=[\!-\pi\sigma_{p+1}, \pi\sigma_{p+1}]\times\ldots\times [\!-\pi\sigma_{q}, \pi\sigma_{q}]$
and
$B_2=[\!-\pi\sigma_{p+1}, \pi\sigma_{p+1}]\times\ldots\times [\!-\pi\sigma_{q}, \pi\sigma_{q}]$
and
 \begin{align*}g(x)=\exp\left\{i\sum_{j>p}x_j\frac{m_j-k_j}{\sigma_j}-i\sum_{j\leq p}x_jk_j\right\}\, .\end{align*}
\begin{align*}g(x)=\exp\left\{i\sum_{j>p}x_j\frac{m_j-k_j}{\sigma_j}-i\sum_{j\leq p}x_jk_j\right\}\, .\end{align*}
Let
![]() $Y=(Y_1, \ldots, Y_q)$
where
$Y=(Y_1, \ldots, Y_q)$
where
![]() $Y_{i}\sim {\textrm{Po}}(\rho_i)$
for
$Y_{i}\sim {\textrm{Po}}(\rho_i)$
for
![]() $i\in [p]$
,
$i\in [p]$
,
![]() $Y_{i} \sim N(0,1)$
for
$Y_{i} \sim N(0,1)$
for
![]() $i>p$
, and
$i>p$
, and
![]() $Y_1,\ldots,Y_q$
are jointly independent. Then by Fourier inversion, we have the identity:
$Y_1,\ldots,Y_q$
are jointly independent. Then by Fourier inversion, we have the identity:
 \begin{align*}\frac{1}{(2 \pi)^q} \int_{B_1} \int_{\mathbb R^{q-p}} \varphi_{Y}(x)g(x)dx_q\ldots dx_1 &= \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!}\prod_{T \in \mathcal T_2} \frac{e^{- \frac{(k_T-m_T)^2}{2\sigma_T^2}}}{\sqrt{2\pi}}\, . \\\end{align*}
\begin{align*}\frac{1}{(2 \pi)^q} \int_{B_1} \int_{\mathbb R^{q-p}} \varphi_{Y}(x)g(x)dx_q\ldots dx_1 &= \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!}\prod_{T \in \mathcal T_2} \frac{e^{- \frac{(k_T-m_T)^2}{2\sigma_T^2}}}{\sqrt{2\pi}}\, . \\\end{align*}
By (32) (noting that
![]() $m_i=(1+o(1))\sigma^2_i$
by Lemma 21), it therefore suffices to show that
$m_i=(1+o(1))\sigma^2_i$
by Lemma 21), it therefore suffices to show that
Since,
![]() $m_i\to\infty$
for
$m_i\to\infty$
for
![]() $i>p$
, Lemma 21 implies that
$i>p$
, Lemma 21 implies that
![]() $\sigma_i\to\infty$
for
$\sigma_i\to\infty$
for
![]() $i>p$
also. It follows that
$i>p$
also. It follows that
and so it suffices to show that
In [Reference Jenssen and Perkins15, Theorem 6] it was shown that
![]() $\tilde X$
converges to Y in distribution and so
$\tilde X$
converges to Y in distribution and so
![]() $\varphi_{\tilde X}\to \varphi_Y$
pointwise. It therefore suffices, by dominated convergence, to show that
$\varphi_{\tilde X}\to \varphi_Y$
pointwise. It therefore suffices, by dominated convergence, to show that
![]() $|\varphi_{\tilde X}(x)-\varphi_Y(x)|$
is bounded by an integrable function. By Lemmas 21 and 22,
$|\varphi_{\tilde X}(x)-\varphi_Y(x)|$
is bounded by an integrable function. By Lemmas 21 and 22,
We have a similar bound for
![]() $|\varphi_Y(x)|$
and so we are done.
$|\varphi_Y(x)|$
and so we are done.
5. Independent sets of a given size and structure
Here we prove Theorem 7. Recall that for a set of defect types
![]() $\mathcal {T}$
and a vector of integers
$\mathcal {T}$
and a vector of integers
![]() $ \mathbf x=( x_T )_{T \in \mathcal T}$
, we let
$ \mathbf x=( x_T )_{T \in \mathcal T}$
, we let
![]() $ i_{m, \mathbf x}(Q_d) $
denote the number of independent sets in
$ i_{m, \mathbf x}(Q_d) $
denote the number of independent sets in
![]() $Q_d$
of size m with exactly
$Q_d$
of size m with exactly
![]() $ x_T $
defects of type T for each
$ x_T $
defects of type T for each
![]() $T \in \mathcal T$
.
$T \in \mathcal T$
.
We use the following identity, an easy extension of (3). For any
![]() $\lambda>0$
,
$\lambda>0$
,
where
![]() $X_T$
be the random variable counting the number of defects of type T in a sample from
$X_T$
be the random variable counting the number of defects of type T in a sample from
![]() $\mu_{\lambda}$
. Theorem 7 follows immediately from (33), Theorem 6 and the following lemma.
$\mu_{\lambda}$
. Theorem 7 follows immediately from (33), Theorem 6 and the following lemma.
Lemma 23 Fix
![]() $\lambda>0$
and let
$\lambda>0$
and let
![]() $m = m(d)$
be such that that
$m = m(d)$
be such that that
![]() $|\mathbb{E}_{\lambda} | \mathbf I| -m | = o(N^{1/2})$
. Let
$|\mathbb{E}_{\lambda} | \mathbf I| -m | = o(N^{1/2})$
. Let
![]() $\mathcal {T}_1, \mathcal {T}_2$
be the sets of defect types such that
$\mathcal {T}_1, \mathcal {T}_2$
be the sets of defect types such that
![]() $m_T \to \rho_T$
for some fixed
$m_T \to \rho_T$
for some fixed
![]() $\rho_T > 0$
as
$\rho_T > 0$
as
![]() $d \to \infty$
for all
$d \to \infty$
for all
![]() $T\in \mathcal {T}_1$
and
$T\in \mathcal {T}_1$
and
![]() $m_T\to\infty$
for all
$m_T\to\infty$
for all
![]() $T\in \mathcal {T}_2$
. Let
$T\in \mathcal {T}_2$
. Let
![]() $ ( k_T )_{T \in \mathcal T_1}$
be a vector of fixed non-negative integers and let
$ ( k_T )_{T \in \mathcal T_1}$
be a vector of fixed non-negative integers and let
![]() $ ( k_T )_{T \in \mathcal T_2}$
be such that
$ ( k_T )_{T \in \mathcal T_2}$
be such that
![]() $k_T= \lfloor m_T +s_T \rfloor$
where
$k_T= \lfloor m_T +s_T \rfloor$
where
![]() $| s_T| = O(\sqrt{ m_T})$
for all
$| s_T| = O(\sqrt{ m_T})$
for all
![]() $T \in \mathcal T_2$
. Let
$T \in \mathcal T_2$
. Let
![]() $\mathbf x= (k_T)_{T\in \mathcal {T}_1\cup\mathcal {T}_2}$
. Then
$\mathbf x= (k_T)_{T\in \mathcal {T}_1\cup\mathcal {T}_2}$
. Then
 \begin{align*}\mathbb{P}_{\lambda} \left [ |\mathbf I | =m, (X_T)_{T \in \mathcal {T}_1 \cup \mathcal {T}_2} = \mathbf x \right ] &= (1+o(1)) \mathbb{P}_{\lambda} [ |\mathbf I | =m] \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!} \prod_{T \in \mathcal T_{2}} \frac{e^{ - \frac{ s_T^2}{2 m_T}}}{\sqrt{2 \pi m_T}} \,.\end{align*}
\begin{align*}\mathbb{P}_{\lambda} \left [ |\mathbf I | =m, (X_T)_{T \in \mathcal {T}_1 \cup \mathcal {T}_2} = \mathbf x \right ] &= (1+o(1)) \mathbb{P}_{\lambda} [ |\mathbf I | =m] \prod_{T \in \mathcal {T}_1} \frac{\rho_T^{k_T} e^{-\rho_T}}{(k_T)!} \prod_{T \in \mathcal T_{2}} \frac{e^{ - \frac{ s_T^2}{2 m_T}}}{\sqrt{2 \pi m_T}} \,.\end{align*}
Proof. Using Theorems 9 and 20, it is enough to show that
where the above probabilities are with respect to
![]() $\mu_{\mathcal {O}, \lambda}$
and
$\mu_{\mathcal {O}, \lambda}$
and
![]() $X_T$
is now the random variable counting the number of defects of type T in a sample from
$X_T$
is now the random variable counting the number of defects of type T in a sample from
![]() $\mu_{\mathcal {O}, \lambda}$
. Let
$\mu_{\mathcal {O}, \lambda}$
. Let
![]() $\boldsymbol\Gamma$
be the random collection of compatible polymers chosen at Step 1 in the definition of
$\boldsymbol\Gamma$
be the random collection of compatible polymers chosen at Step 1 in the definition of
![]() $\mu_{\mathcal {O}, \lambda}$
(Definition 8) and let
$\mu_{\mathcal {O}, \lambda}$
(Definition 8) and let
![]() $\Gamma$
be a fixed collection of compatible polymers such that
$\Gamma$
be a fixed collection of compatible polymers such that
and
Then the proof of Lemma 16 gives us that
and so in particular, if
![]() $\Gamma$
is also consistent with
$\Gamma$
is also consistent with
![]() $\mathbf x$
(i.e.
$\mathbf x$
(i.e.
![]() $\Gamma$
has precisely
$\Gamma$
has precisely
![]() $k_T$
polymers of type T for all
$k_T$
polymers of type T for all
![]() $T\in \mathcal {T}_1 \cup \mathcal {T}_2$
),
$T\in \mathcal {T}_1 \cup \mathcal {T}_2$
),
Finally, Lemma 12 gives us that (34) and (35) both hold with probability
![]() $1 - o(1)$
, completing the proof.
$1 - o(1)$
, completing the proof.
Acknowledgements
The authors thank Catherine Greenhill for helpful remarks about maximum entropy in combinatorial enumeration. WP is supported in part by NSF grant DMS-1847451. AP is supported in part by NSF grant CCF-1934915.