Published online by Cambridge University Press: 08 March 2016
The 3-uniform tight cycle Cs3 has vertex set 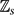 ${\mathbb Z}_s$ and edge set {{i, i + 1, i + 2}: i ∈
${\mathbb Z}_s$ and edge set {{i, i + 1, i + 2}: i ∈ 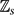 ${\mathbb Z}_s$}. We prove that for every s ≢ 0 (mod 3) with s ⩾ 16 or s ∈ {8, 11, 14} there is a cs > 0 such that the 3-uniform hypergraph Ramsey number r(Cs3, Kn3) satisfies
This answers in a strong form a question of the author and Rödl, who asked for an upper bound of the form
${\mathbb Z}_s$}. We prove that for every s ≢ 0 (mod 3) with s ⩾ 16 or s ∈ {8, 11, 14} there is a cs > 0 such that the 3-uniform hypergraph Ramsey number r(Cs3, Kn3) satisfies
This answers in a strong form a question of the author and Rödl, who asked for an upper bound of the form 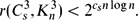 $$\begin{equation*}
r(C_s^3, K_n^3)< 2^{c_s n \log n}.\
\end{equation*}$$
$$\begin{equation*}
r(C_s^3, K_n^3)< 2^{c_s n \log n}.\
\end{equation*}$$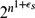 $2^{n^{1+\epsilon_s}}$ for each fixed s ⩾ 4, where εs → 0 as s → ∞ and n is sufficiently large. The result is nearly tight as the lower bound is known to be exponential in n.
$2^{n^{1+\epsilon_s}}$ for each fixed s ⩾ 4, where εs → 0 as s → ∞ and n is sufficiently large. The result is nearly tight as the lower bound is known to be exponential in n.