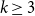1. Introduction
A hypergraph
![]() $G = (V, E)$
is a set of vertices
$G = (V, E)$
is a set of vertices
![]() $V$
together with a set of edges
$V$
together with a set of edges
![]() $E \subset 2^V$
. A hypergraph is
$E \subset 2^V$
. A hypergraph is
![]() $k$
-uniform if every edge has size
$k$
-uniform if every edge has size
![]() $k$
. The degree of a vertex
$k$
. The degree of a vertex
![]() $v \in V$
, denoted by
$v \in V$
, denoted by
![]() $d(v)$
, is the number of edges it appears in; in a hypergraph with maximum degree
$d(v)$
, is the number of edges it appears in; in a hypergraph with maximum degree
![]() $\Delta$
, each vertex appears in at most
$\Delta$
, each vertex appears in at most
![]() $\Delta$
edges.
$\Delta$
edges.
An independent set in
![]() $G$
is a set of vertices
$G$
is a set of vertices
![]() $I \subset V$
such that
$I \subset V$
such that
![]() $I$
contains no edge. Let
$I$
contains no edge. Let
![]() $\mathcal {I}(G)$
denote the family of all independent sets in
$\mathcal {I}(G)$
denote the family of all independent sets in
![]() $G$
. The independence polynomial of
$G$
. The independence polynomial of
![]() $G$
is defined by
$G$
is defined by
This polynomial plays an important role in mathematics, physics and computer science [Reference Davies and Perkins1, Reference Heilmann and Lieb3, Reference Jain, Perkins, Sah and Sawhney4, Reference Scott and Sokal7–Reference Weitz10]. A key property for understanding this polynomial is the largest radius of a disk-shaped zero-free region(ZFR), a region in
![]() $\mathbb {C}$
where
$\mathbb {C}$
where
![]() $Z_G$
has no zero. We refer the reader to the introduction of [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2] for a survey of how knowledge of the zeros of
$Z_G$
has no zero. We refer the reader to the introduction of [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2] for a survey of how knowledge of the zeros of
![]() $Z_G$
can lead to interesting results about independent set.
$Z_G$
can lead to interesting results about independent set.
When
![]() $G$
is a graph with maximum degree
$G$
is a graph with maximum degree
![]() $\Delta$
, the ZFRs for
$\Delta$
, the ZFRs for
![]() $Z_G$
are well-understood [Reference Peters and Regts6, Reference Shearer8]. Specifically, Shearer [Reference Shearer8] showed that
$Z_G$
are well-understood [Reference Peters and Regts6, Reference Shearer8]. Specifically, Shearer [Reference Shearer8] showed that
![]() $Z_G$
has no zero inside the disk
$Z_G$
has no zero inside the disk
![]() $\left \vert \lambda \right \vert \lt \frac {(\Delta - 1)^{\Delta - 1}}{\Delta ^{\Delta }}$
, and this bound is the best possible.
$\left \vert \lambda \right \vert \lt \frac {(\Delta - 1)^{\Delta - 1}}{\Delta ^{\Delta }}$
, and this bound is the best possible.
In a recent paper [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2], Galvin, McKinley, Perkins, Sarantis and Tetali studied the zeros of
![]() $Z_G$
when
$Z_G$
when
![]() $G$
is a general hypergraph with given maximum degree
$G$
is a general hypergraph with given maximum degree
![]() $\Delta$
. They showed that
$\Delta$
. They showed that
![]() $Z_G$
has no zero inside the disk
$Z_G$
has no zero inside the disk
![]() $\left \vert \lambda \right \vert \lt \frac {\Delta ^\Delta }{(\Delta + 1)^{(\Delta + 1)}}$
. Furthermore, for each uniformity
$\left \vert \lambda \right \vert \lt \frac {\Delta ^\Delta }{(\Delta + 1)^{(\Delta + 1)}}$
. Furthermore, for each uniformity
![]() $k \geq 2$
, they constructed a family of
$k \geq 2$
, they constructed a family of
![]() $k$
-uniform hypergraphs with arbitrarily large maximum degree
$k$
-uniform hypergraphs with arbitrarily large maximum degree
![]() $\Delta$
such that
$\Delta$
such that
![]() $Z_G$
has a zero
$Z_G$
has a zero
![]() $\lambda$
with
$\lambda$
with
![]() $\left \vert \lambda \right \vert \lt O_k\left (\frac {\log \Delta }{\Delta }\right )$
, thereby showing that their bound is tight up to a logarithmic factor if we place no additional assumption on
$\left \vert \lambda \right \vert \lt O_k\left (\frac {\log \Delta }{\Delta }\right )$
, thereby showing that their bound is tight up to a logarithmic factor if we place no additional assumption on
![]() $G$
.
$G$
.
A hypergraph is linear if each pair of edges intersect in at most one vertex. The aforementioned constructions in [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2, Section 4] are far from linear, since they contain edges that intersect in
![]() $(k - 1)$
vertices. In [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2, Conjecture 3], Galvin, McKinley, Perkins, Sarantis and Tetali conjectured that their lower bound on the maximum radius of the zero-free disk for
$(k - 1)$
vertices. In [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2, Conjecture 3], Galvin, McKinley, Perkins, Sarantis and Tetali conjectured that their lower bound on the maximum radius of the zero-free disk for
![]() $Z_G$
can be improved under the additional assumption that
$Z_G$
can be improved under the additional assumption that
![]() $G$
is linear.
$G$
is linear.
Conjecture 1.1.
For each
![]() $k \geq 2$
, there exists a constant
$k \geq 2$
, there exists a constant
![]() $C_k \gt 0$
such that the following is true. If
$C_k \gt 0$
such that the following is true. If
![]() $G$
is a
$G$
is a
![]() $k$
-uniform, linear hypergraph with maximum degree
$k$
-uniform, linear hypergraph with maximum degree
![]() $\Delta$
and if
$\Delta$
and if
then
![]() $Z_G(\lambda ) \neq 0$
.
$Z_G(\lambda ) \neq 0$
.
This conjecture is motivated by results on asymptotic enumeration in [Reference Mousset, Noever, Panagiotou and Samotij5]. Galvin, McKinley, Perkins, Sarantis and Tetali verified this conjecture when
![]() $G$
is a hypertree [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2, Theorem 4],
$G$
is a hypertree [Reference Galvin, McKinley, Perkins, Sarantis and Tetali2, Theorem 4],
In this note, we disprove Conjecture1.1 in any uniformity
![]() $k \geq 3$
. Our counterexample shows that the radius of the disk-shaped ZFR
$k \geq 3$
. Our counterexample shows that the radius of the disk-shaped ZFR
![]() $\left \vert \lambda \right \vert \lt \frac {\Delta ^\Delta }{(\Delta + 1)^{(\Delta + 1)}}$
is tight up to a logarithmic factor even if we assume that
$\left \vert \lambda \right \vert \lt \frac {\Delta ^\Delta }{(\Delta + 1)^{(\Delta + 1)}}$
is tight up to a logarithmic factor even if we assume that
![]() $G$
is a
$G$
is a
![]() $k$
-uniform linear hypergraph.
$k$
-uniform linear hypergraph.
Theorem 1.2.
For each uniformity
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $\Delta \gt 100k^2$
, there exists a
$\Delta \gt 100k^2$
, there exists a
![]() $k$
-uniform linear hypergraph
$k$
-uniform linear hypergraph
![]() $G$
with maximum degree
$G$
with maximum degree
![]() $\Delta$
, such that
$\Delta$
, such that
![]() $Z_{G}$
has a negative real zero
$Z_{G}$
has a negative real zero
![]() $\lambda$
with
$\lambda$
with
![]() $\lambda \in [-\frac {6k \log \Delta }{\Delta }, 0]$
.
$\lambda \in [-\frac {6k \log \Delta }{\Delta }, 0]$
.
2. The counterexample
We begin by describing a general construction.
Definition 2.1.
Let
![]() $G = (V, E)$
be a hypergraph. We define
$G = (V, E)$
be a hypergraph. We define
![]() $S_G$
as the hypergraph whose vertex set is
$S_G$
as the hypergraph whose vertex set is
![]() $V \sqcup E$
, and whose edge set is
$V \sqcup E$
, and whose edge set is
![]() $\{e \cup \{e\}\,:\, e \in E\}$
.
$\{e \cup \{e\}\,:\, e \in E\}$
.

We begin by showing a basic property of
![]() $S_G$
.
$S_G$
.
Proposition 2.2.
If
![]() $G = (V, E)$
is a
$G = (V, E)$
is a
![]() $(k - 1)$
uniform linear hypergraph with maximum degree
$(k - 1)$
uniform linear hypergraph with maximum degree
![]() $\Delta$
, then
$\Delta$
, then
![]() $S_G$
is a
$S_G$
is a
![]() $k$
uniform linear hypergraph with maximum degree
$k$
uniform linear hypergraph with maximum degree
![]() $\Delta$
.
$\Delta$
.
Proof. Each edge in
![]() $S_G$
has the form
$S_G$
has the form
![]() $e \cup \{e\}$
for some
$e \cup \{e\}$
for some
![]() $e \in E$
, and
$e \in E$
, and
![]() $\left \vert e \cup \{e\} \right \vert = \left \vert e \right \vert + 1 = k$
. So
$\left \vert e \cup \{e\} \right \vert = \left \vert e \right \vert + 1 = k$
. So
![]() $S_G$
is
$S_G$
is
![]() $k$
uniform.
$k$
uniform.
For any pair of distinct edges
![]() $e_1 \cup \{e_1\}$
and
$e_1 \cup \{e_1\}$
and
![]() $e_2 \cup \{e_2\}$
in
$e_2 \cup \{e_2\}$
in
![]() $S_G$
, we have
$S_G$
, we have
Thus
![]() $S_G$
is linear.
$S_G$
is linear.
Finally, each vertex in
![]() $V$
has the same degree in
$V$
has the same degree in
![]() $G$
and
$G$
and
![]() $S_G$
, while each element in
$S_G$
, while each element in
![]() $E$
has degree
$E$
has degree
![]() $1$
in
$1$
in
![]() $S_G$
. Therefore, the maximum degree of
$S_G$
. Therefore, the maximum degree of
![]() $S_G$
is the same as the maximum degree of
$S_G$
is the same as the maximum degree of
![]() $G$
.
$G$
.
In the next two lemmas, we give an explicit formula for the independence polynomial
![]() $Z_{S_G}$
of
$Z_{S_G}$
of
![]() $S_G$
and prove that it has a zero close to the origin whenever
$S_G$
and prove that it has a zero close to the origin whenever
![]() $G$
satisfies a mild expansion property.
$G$
satisfies a mild expansion property.
Lemma 2.3.
Let
![]() $G = (V, E)$
be a hypergraph. For each set of vertices
$G = (V, E)$
be a hypergraph. For each set of vertices
![]() $S \subset V$
, let
$S \subset V$
, let
![]() $E(S)$
denote the edges of
$E(S)$
denote the edges of
![]() $G$
with at least one vertex in
$G$
with at least one vertex in
![]() $S$
, and write
$S$
, and write
![]() $e(S) = \left \vert E(S) \right \vert$
. Then we have
$e(S) = \left \vert E(S) \right \vert$
. Then we have
Proof. Classifying the independence sets of
![]() $S_G$
based on their intersections with
$S_G$
based on their intersections with
![]() $V \subset V(S_G)$
, we have
$V \subset V(S_G)$
, we have
A set of vertices
![]() $I \subset V \sqcup E$
with
$I \subset V \sqcup E$
with
![]() $I \cap V = V \backslash S$
is independent in
$I \cap V = V \backslash S$
is independent in
![]() $S_G$
if and only if
$S_G$
if and only if
![]() $J \,:\!=\, I \cap E$
is contained in
$J \,:\!=\, I \cap E$
is contained in
![]() $E(S)$
. So we have
$E(S)$
. So we have
and the lemma follows.
Lemma 2.4.
Let
![]() $G = (V, E)$
be a hypergraph with
$G = (V, E)$
be a hypergraph with
![]() $n \geq 3$
vertices. Assume that
$n \geq 3$
vertices. Assume that
![]() $n$
is odd. Furthermore, assume that for some
$n$
is odd. Furthermore, assume that for some
![]() $\alpha \in [3\log n, n]$
, we have
$\alpha \in [3\log n, n]$
, we have
![]() $e(S) \geq \alpha \left \vert S \right \vert$
for any
$e(S) \geq \alpha \left \vert S \right \vert$
for any
![]() $S \subset V$
. Then
$S \subset V$
. Then
![]() $Z_{S_G}$
has a negative real zero in the interval
$Z_{S_G}$
has a negative real zero in the interval
Proof. Set
![]() $\lambda _0 = -\frac {3\log n}{\alpha }$
. As
$\lambda _0 = -\frac {3\log n}{\alpha }$
. As
![]() $Z_{S_G}(0) = 1$
, it suffices to show that
$Z_{S_G}(0) = 1$
, it suffices to show that
![]() $Z_{S_G}(\lambda _0) \lt 0$
.
$Z_{S_G}(\lambda _0) \lt 0$
.
By Lemma2.3, we have the identity
We isolate the term with
![]() $S = \emptyset$
and obtain
$S = \emptyset$
and obtain
 \begin{equation*}Z_{S_G}(\lambda _0) = \lambda _0^{\left \vert V \right \vert } \left (1 + \sum _{S \subset V, S \neq \emptyset } \lambda _0^{-\left \vert S \right \vert } (1 + \lambda _0)^{e(S)}\right )\end{equation*}
\begin{equation*}Z_{S_G}(\lambda _0) = \lambda _0^{\left \vert V \right \vert } \left (1 + \sum _{S \subset V, S \neq \emptyset } \lambda _0^{-\left \vert S \right \vert } (1 + \lambda _0)^{e(S)}\right )\end{equation*}
Since
![]() $0 \leq 1 + \lambda _0 \leq e^{\lambda _0}$
, for each
$0 \leq 1 + \lambda _0 \leq e^{\lambda _0}$
, for each
![]() $S \subset V$
we can estimate
$S \subset V$
we can estimate
Thus we have
 \begin{equation*}\left \vert \sum _{S \subset V, S \neq \emptyset } \lambda _0^{-\left \vert S \right \vert } (1 + \lambda _0)^{e(S)} \right \vert \leq \sum _{k = 1}^n \binom {n}{k} \alpha ^{k} e^{-3 \log n \cdot k} \leq \sum _{k = 1}^n \frac {1}{k!} \left (\frac {\alpha }{n^2}\right )^k.\end{equation*}
\begin{equation*}\left \vert \sum _{S \subset V, S \neq \emptyset } \lambda _0^{-\left \vert S \right \vert } (1 + \lambda _0)^{e(S)} \right \vert \leq \sum _{k = 1}^n \binom {n}{k} \alpha ^{k} e^{-3 \log n \cdot k} \leq \sum _{k = 1}^n \frac {1}{k!} \left (\frac {\alpha }{n^2}\right )^k.\end{equation*}
where the second inequality uses the estimate
![]() $\binom {n}{k} \leq \frac {n^k}{k!}$
.
$\binom {n}{k} \leq \frac {n^k}{k!}$
.
We assume that
![]() $\alpha \leq n$
, so
$\alpha \leq n$
, so
![]() $\left (\frac {\alpha }{n^2}\right )^k \lt \frac {1}{n}$
for each
$\left (\frac {\alpha }{n^2}\right )^k \lt \frac {1}{n}$
for each
![]() $k \geq 1$
. This leads to
$k \geq 1$
. This leads to
 \begin{equation*}\left \vert \sum _{S \subset V, S \neq \emptyset } \lambda _0^{-\left \vert S \right \vert } (1 + \lambda _0)^{e(S)} \right \vert \leq \frac {1}{n}\sum _{k = 1}^n \frac {1}{k!} \lt \frac {e}{n} \lt 1.\end{equation*}
\begin{equation*}\left \vert \sum _{S \subset V, S \neq \emptyset } \lambda _0^{-\left \vert S \right \vert } (1 + \lambda _0)^{e(S)} \right \vert \leq \frac {1}{n}\sum _{k = 1}^n \frac {1}{k!} \lt \frac {e}{n} \lt 1.\end{equation*}
Thus we conclude that
so
![]() $Z_{S_G}(\lambda _0) \lt 0$
, as desired.
$Z_{S_G}(\lambda _0) \lt 0$
, as desired.
Our main theorem is an easy corollary of this result. Indeed, for any
![]() $(k - 1)$
uniform hypergraph
$(k - 1)$
uniform hypergraph
![]() $G$
we can show that
$G$
we can show that
![]() $e(S) \geq \frac {\delta (G) \left \vert S \right \vert }{k - 1}$
for any
$e(S) \geq \frac {\delta (G) \left \vert S \right \vert }{k - 1}$
for any
![]() $S \subset V$
. So when
$S \subset V$
. So when
![]() $\delta (G) \geq \Delta (G) - 1$
, one can take
$\delta (G) \geq \Delta (G) - 1$
, one can take
![]() $\alpha = \frac {\Delta (G) - 1}{k - 1}$
in Lemma2.4. We give an explicit construction of such a hypergraph.
$\alpha = \frac {\Delta (G) - 1}{k - 1}$
in Lemma2.4. We give an explicit construction of such a hypergraph.
Lemma 2.5.
For any uniformity
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $\Delta \geq k$
, there exists a
$\Delta \geq k$
, there exists a
![]() $k$
uniform,
$k$
uniform,
![]() $\Delta$
regular linear hypergraph
$\Delta$
regular linear hypergraph
![]() $H_{k, \Delta }$
on at most
$H_{k, \Delta }$
on at most
![]() $2k \Delta$
vertices.
$2k \Delta$
vertices.
Proof. We take a prime
![]() $p$
in
$p$
in
![]() $[\Delta, 2\Delta ]$
, which exists by Chebyshev’s theorem. Let
$[\Delta, 2\Delta ]$
, which exists by Chebyshev’s theorem. Let
![]() $H_{k, \Delta }$
be the hypergraph on the vertex set
$H_{k, \Delta }$
be the hypergraph on the vertex set
![]() $V = [k] \times \mathbb {Z}_p$
with an edge
$V = [k] \times \mathbb {Z}_p$
with an edge
![]() $\{(i, a + id)\,:\, i \in [k]\}$
for each pair
$\{(i, a + id)\,:\, i \in [k]\}$
for each pair
![]() $(a, d) \in \mathbb {Z}_p \times [\Delta ]$
. The number of vertices in
$(a, d) \in \mathbb {Z}_p \times [\Delta ]$
. The number of vertices in
![]() $H_{k, \Delta }$
is
$H_{k, \Delta }$
is
![]() $\left \vert V \right \vert = kp \leq 2 \Delta k$
.
$\left \vert V \right \vert = kp \leq 2 \Delta k$
.
Any vertex
![]() $(i, x) \in V$
is contained precisely in the edges corresponding to
$(i, x) \in V$
is contained precisely in the edges corresponding to
![]() $(a, d) \in \mathbb {Z}_p \times [\Delta ]$
with
$(a, d) \in \mathbb {Z}_p \times [\Delta ]$
with
![]() $a \equiv x - id \pmod {p}$
. As there is exactly one
$a \equiv x - id \pmod {p}$
. As there is exactly one
![]() $a \in \mathbb {Z}_p$
corresponding to each
$a \in \mathbb {Z}_p$
corresponding to each
![]() $d \in [\Delta ]$
,
$d \in [\Delta ]$
,
![]() $H_{k, \Delta }$
is
$H_{k, \Delta }$
is
![]() $\Delta$
regular.
$\Delta$
regular.
The size of the intersection between two distinct edges corresponding to
![]() $(a, d)$
and
$(a, d)$
and
![]() $(a', d')$
is the number of solutions
$(a', d')$
is the number of solutions
![]() $i \in [k]$
to the linear congruence equation
$i \in [k]$
to the linear congruence equation
![]() $a + id \equiv a' + id' \pmod {p}$
. As
$a + id \equiv a' + id' \pmod {p}$
. As
![]() $k \leq \Delta \leq p$
, there is at most one solution
$k \leq \Delta \leq p$
, there is at most one solution
![]() $i \in [k]$
to this linear congruence equation, so every pair of hyperedges in
$i \in [k]$
to this linear congruence equation, so every pair of hyperedges in
![]() $H_{k, \Delta }$
intersect in at most one vertex. Therefore,
$H_{k, \Delta }$
intersect in at most one vertex. Therefore,
![]() $H_{k, \Delta }$
is a linear hypergraph.
$H_{k, \Delta }$
is a linear hypergraph.
Proof of Theorem
1.2. Let
![]() $H = H_{(k - 1), \Delta }$
be the
$H = H_{(k - 1), \Delta }$
be the
![]() $(k - 1)$
uniform linear hypergraph constructed in Lemma2.5. If
$(k - 1)$
uniform linear hypergraph constructed in Lemma2.5. If
![]() $H$
has an even number of vertices, we remove an arbitrary vertex
$H$
has an even number of vertices, we remove an arbitrary vertex
![]() $v$
of
$v$
of
![]() $H$
together with any edge containing the vertex. Thus, we obtain a
$H$
together with any edge containing the vertex. Thus, we obtain a
![]() $(k - 1)$
uniform linear hypergraph
$(k - 1)$
uniform linear hypergraph
![]() $H$
with an odd number of vertices, maximum degree
$H$
with an odd number of vertices, maximum degree
![]() $\Delta$
, and minimum degree at least
$\Delta$
, and minimum degree at least
![]() $(\Delta - 1)$
. By Proposition2.2,
$(\Delta - 1)$
. By Proposition2.2,
![]() $G = S_H$
is a
$G = S_H$
is a
![]() $k$
uniform linear hypergraph with maximum degree
$k$
uniform linear hypergraph with maximum degree
![]() $\Delta$
.
$\Delta$
.
Let
![]() $n \leq 2k \Delta$
be the number of vertices in
$n \leq 2k \Delta$
be the number of vertices in
![]() $H$
. For any vertex subset
$H$
. For any vertex subset
![]() $S$
of
$S$
of
![]() $H$
, the
$H$
, the
![]() $(k - 1)$
uniformity of
$(k - 1)$
uniformity of
![]() $H$
implies that the number of edges in
$H$
implies that the number of edges in
![]() $G$
with at least one vertex in
$G$
with at least one vertex in
![]() $S$
is lower bounded by
$S$
is lower bounded by
By our assumptions
![]() $\Delta \gt 100k^2$
and
$\Delta \gt 100k^2$
and
![]() $n \leq 2k \Delta$
, we can check that
$n \leq 2k \Delta$
, we can check that
Furthermore, we have
![]() $\frac {\Delta - 1}{k - 1} \leq \Delta - 1 \lt n$
. So we can apply Lemma2.4 with
$\frac {\Delta - 1}{k - 1} \leq \Delta - 1 \lt n$
. So we can apply Lemma2.4 with
![]() $\alpha = \frac {\Delta - 1}{k - 1}$
. We conclude that
$\alpha = \frac {\Delta - 1}{k - 1}$
. We conclude that
![]() $Z_{G}$
has a negative real zero
$Z_{G}$
has a negative real zero
![]() $\lambda$
with
$\lambda$
with
where the last two inequalities follow from
![]() $\Delta \gt 100k^2$
. So
$\Delta \gt 100k^2$
. So
![]() $G$
satisfies the requirements of Theorem 1.2.
$G$
satisfies the requirements of Theorem 1.2.
Acknowledgements
I am supported by the Craig Franklin Fellowship in Mathematics at Stanford University. I thank Professor Nima Anari and Professor Will Perkins for many helpful discussions and comments. I also thank the anonymous referee for valuable feedbacks on the manuscript.