Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-06T20:21:50.781Z Has data issue: false hasContentIssue false
  • English
  • Français

Forbidden Subgraphs Generating Almost the Same Sets

Published online by Cambridge University Press:  11 July 2013

SHINYA FUJITA ,
MICHITAKA FURUYA  and
KENTA OZEKI
SHINYA FUJITA
Affiliation:
Department of Integrated Design Engineering, Maebashi Institute of Technology, 460-1 Kamisadori, Maebashi, Gunma 371-0816, Japan (e-mail: shinya.fujita.ph.d@gmail.com)
MICHITAKA FURUYA
Affiliation:
Department of Mathematical Information Science, Tokyo University of Science, 1-3 Kagurazaka, Shinjuku-ku, Tokyo 162-8601, Japan (e-mail: michitaka.furuya@gmail.com)
KENTA OZEKI
Affiliation:
National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan JST, ERATO, Kawarabayashi Large Graph Project, Japan (e-mail: ozeki@nii.ac.jp)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 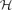$\mathcal{H}$ be a set of connected graphs. A graph G is said to be 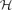$\mathcal{H}$-free if G does not contain any element of 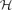$\mathcal{H}$ as an induced subgraph. Let 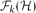$\mathcal{F}_{k}(\mathcal{H})$ be the set of k-connected 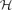$\mathcal{H}$-free graphs. When we study the relationship between forbidden subgraphs and a certain graph property, we often allow a finite exceptional set of graphs. But if the symmetric difference of 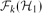$\mathcal{F}_{k}(\mathcal{H}_{1})$ and 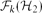$\mathcal{F}_{k}(\mathcal{H}_{2})$ is finite and we allow a finite number of exceptions, no graph property can distinguish them. Motivated by this observation, we study when we obtain a finite symmetric difference. In this paper, our main aim is the following. If 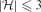$|\mathcal{H}|\leq 3$ and the symmetric difference of $\mathcal{F}_{1}(\{H\})$ and 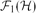$\mathcal{F}_{1}(\mathcal{H})$ is finite, then either 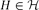$H\in \mathcal{H}$ or 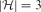$|\mathcal{H}|=3$ and H=C3. Furthermore, we prove that if the symmetric difference of 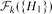$\mathcal{F}_{k}(\{H_{1}\})$ and $\mathcal{F}_{k}(\{H_{2}\})$ is finite, then H1=H2.

Keywords

05C75
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 5 , September 2013 , pp. 733 - 748
Copyright
Copyright © Cambridge University Press 2013 

References

[1]Aldred, R. E. L., Fujisawa, J. and Saito, A. (2010) Forbidden subgraphs and the existence of 2-factor. J. Graph Theory 64 250–266.Google Scholar
[2]Barrus, M. D., Kumbhat, M. and Hartke, S. G. (2008) Graph classes characterized both by forbidden subgraphs and degree sequences. J. Graph Theory 57 131–148.Google Scholar
[3]Bedrossian, P. (1991) Forbidden subgraphs and minimum degree conditions for Hamiltonicity. PhD thesis, University of Memphis.Google Scholar
[4]Broersma, H., Faudree, R. J., Huck, A., Trommel, H. and Veldman, H. J. (2002) Forbidden subgraphs that imply Hamiltonian-connectedness. J. Graph Theory 40 104–119.CrossRefGoogle Scholar
[5]Chartrand, G. and Lesniak, L. (2005) Graphs and Digraphs, fourth edition, Chapman & Hall/CRC.Google Scholar
[6]Cockayne, E. J., Ko, C. W. and Shepherd, F. B. (1985) Inequalities concerning dominating sets in graphs. Technical report DM-370-IR, Department of Mathematics, University of Victoria.Google Scholar
[7]Duffus, D., Gould, R. J. and Jacobson, M. S. (1981) Forbidden subgraphs and the Hamiltonian theme. In The Theory and Applications of Graphs (Chartrand, G.et al., eds), Wiley, pp. 297–316.Google Scholar
[8]Faudree, R. J. and Gould, R. J. (1997) Characterizing forbidden pairs for Hamiltonian properties. Discrete Math. 173 45–60.Google Scholar
[9]Faudree, R. J., Gould, R. J., Ryjáček, Z. and Schiermeyer, I. (1995) Forbidden subgraphs and pancyclicity. Congress Numer. 109 13–32.Google Scholar
[10]Fujisawa, J. and Saito, A. (2012) A pair of forbidden subgraphs and 2-factors. Combin. Probab. Comput. 21 149–158.Google Scholar
[11]Fujisawa, J., Fujita, S., Plummer, M. D., Saito, A. and Schiermeyer, I. (2011) A pair of forbidden subgraphs and perfect matchings in graphs of high connectivity. Combinatorica 31 703–723.Google Scholar
[12]Fujisawa, J., Ota, K., Ozeki, K. and Sueiro, G. (2011) Forbidden induced subgraphs for star-free graphs. Discrete Math. 311 2475–2484.Google Scholar
[13]Fujita, S., Kawarabayashi, K., Lucchesi, C. L., Ota, K., Plummer, M. and Saito, A. (2006) A pair of forbidden subgraphs and perfect matchings. J. Combin. Theory Ser. B 96 315–324.CrossRefGoogle Scholar
[14]Randerath, B. and Schiermeyer, I. (2004) Vertex colouring and forbidden subgraphs: A survey. Graphs Combin. 20 1–40.Google Scholar
[15]Xu, J. M. and Yang, C. (2006) Connectivity of Cartesian product graphs. Discrete Math. 306 159–165.Google Scholar