Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T15:43:19.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Finding Hidden Cliques in Linear Time with High Probability

Published online by Cambridge University Press:  14 November 2013

YAEL DEKEL ,
ORI GUREL-GUREVICH  and
YUVAL PERES
YAEL DEKEL
Affiliation:
The Selim and Rachel Benin School of Computer Science and Engineering, The Hebrew University of Jerusalem, Edmond J. Safra Campus, Jerusalem 91904, Israel (e-mail: yaelvin@cs.huji.ac.il)
ORI GUREL-GUREVICH
Affiliation:
Department of Mathematics, University of British Columbia, 121-1984 Mathematics Road, Vancouver, BC, V6T 1Z2Canada (e-mail: origurel@math.ucb.ca)
YUVAL PERES
Affiliation:
Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA (e-mail: peres@microsoft.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are given a graph G with n vertices, where a random subset of k vertices has been made into a clique, and the remaining edges are chosen independently with probability $\frac12$. This random graph model is denoted 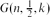$G(n,\frac12,k)$. The hidden clique problem is to design an algorithm that finds the k-clique in polynomial time with high probability. An algorithm due to Alon, Krivelevich and Sudakov [3] uses spectral techniques to find the hidden clique with high probability when 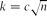$k = c \sqrt{n}$ for a sufficiently large constant c > 0. Recently, an algorithm that solves the same problem was proposed by Feige and Ron [12]. It has the advantages of being simpler and more intuitive, and of an improved running time of O(n2). However, the analysis in [12] gives a success probability of only 2/3. In this paper we present a new algorithm for finding hidden cliques that both runs in time O(n2) (that is, linear in the size of the input) and has a failure probability that tends to 0 as n tends to ∞. We develop this algorithm in the more general setting where the clique is replaced by a dense random graph.

Keywords

Primary 05C80Secondary 05C8568W20
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 1 , January 2014 , pp. 29 - 49
Copyright
Copyright © Cambridge University Press 2013 

References

[1]Abramowitz, M. and Stegun, I. A., eds (1964) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover.Google Scholar
[2]Alon, N., Andoni, A., Kaufman, T., Matulef, K., Rubinfeld, R. and Xie, N. (2007) Testing k-wise and almost k-wise independence. In STOC, ACM, pp. 496–505.Google Scholar
[3]Alon, N., Krivelevich, M. and Sudakov, B. (1998) Finding a large hidden clique in a random graph. Random Struct. Alg. 13 457–466.Google Scholar
[4]Arora, S. and Safra, S. (1998) Probabilistic checking of proofs: A new characterization of NP. J. Assoc. Comput. Mach. 45 70–122.Google Scholar
[5]Arora, S., Lund, C., Motwani, R., Sudan, M. and Szegedy, M. (1992) Proof verification and hardness of approximation problems. In FOCS, ACM, pp. 14–23.Google Scholar
[6]Azuma, K. (1967) Weighted sums of certain dependent random variables. Tohoku Math. J. 19 357–367.Google Scholar
[7]Ben-Dor, A., Shamir, R. and Yakhini, Z. (1999) Clustering gene expression patterns. J. Comput. Biol. 6 281–297.Google Scholar
[8]Ben Sasson, E., Bilu, Y. and Gutfreund, D. (2002) Finding a randomly planted assignment in a random 3CNF. Manuscript.Google Scholar
[9]Berry, A. C. (1941) The accuracy of the Gaussian approximation to the sum of independent variates. Trans. Amer. Math. Soc. 49 122–136.CrossRefGoogle Scholar
[10]Durrett, R. (2010) Probability: Theory and Examples, fourth edition, Cambridge University Press.Google Scholar
[11]Esseen, C. G. (1942) On the Liapunoff limit of error in the theory of probability. Arkiv för Matematik, Astronomi och Fysik A28 1–19.Google Scholar
[12]Feige, U. and Ron, D. (2010) Finding hidden cliques in linear time. In AOFA, DMTCS.Google Scholar
[13]Feige, U., Goldwasser, S., Lovász, L., Safra, S. and Szegedy, M. (1991) Approximating clique is almost NP-complete (preliminary version). In FOCS, IEEE Computer Society, pp. 2–12.Google Scholar
[14]Feige, U. and Krauthgamer, R. (2000) Finding and certifying a large hidden clique in a semirandom graph. Random Struct. Alg. 16 195–208.Google Scholar
[15]Feige, U. and Krauthgamer, R. (2003) The probable value of the Lovász–Schrijver relaxations for maximum independent set. SIAM J. Comput. 32 345–370.Google Scholar
[16]Frieze, A. M. and Kannan, R. (2008) A new approach to the planted clique problem. In FSTTCS, Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, pp. 187–198.Google Scholar
[17]Grimmett, G. and McDiarmid, C. (1975) On colouring random graphs. Math. Proc. Cam. Phil. Soc. 77 313–324.Google Scholar
[18]Hazan, E. and Krauthgamer, R. (2009) How hard is it to approximate the best Nash equilibrium? In SODA, Society for Industrial and Applied Mathematics, pp. 720–727.Google Scholar
[19]Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58 13–30.Google Scholar
[20]Jerrum, M. (1992) Large cliques elude the metropolis process. Random Struct. Alg. 3 347–359.Google Scholar
[21]Juels, A. and Peinado, M. (2000) Hiding cliques for cryptographic security. Des. Codes Cryptography 20 269–280.Google Scholar
[22]Karp, R. M. (1972) Reducibility among combinatorial problems. In Complexity of Computer Computations (Miller, R. E. and Thatcher, J. W., eds), Plenum, pp. 85–103.Google Scholar
[23]Krivelevich, M. and Vilenchik, D. (2006) Solving random satisfiable 3CNF formulas in expected polynomial time. In SODA, ACM, pp. 454–463.Google Scholar
[24]Kučera, L. (1991) A generalized encryption scheme based on random graphs. In Graph-Theoretic Concepts in Computer Science (Schmidt, G. and Berghammer, R., eds), Vol. 570 of Lecture Notes in Computer Science, Springer, pp. 180–186.Google Scholar
[25]Kučera, L. (1995) Expected complexity of graph partitioning problems. Discrete Applied Math. 57 193–212.Google Scholar
[26]McSherry, F. (2001) Spectral partitioning of random graphs. In FOCS, IEEE Computer Society, pp. 529–537.Google Scholar