Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T22:49:34.799Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansion of Percolation Critical Points for Hamming Graphs

Part of: Equilibrium statistical mechanics Special processes

Published online by Cambridge University Press:  05 August 2019

Lorenzo Federico ,
Remco Van Der Hofstad ,
Frank Den Hollander  and
Tim Hulshof
Lorenzo Federico*
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, UK
Remco Van Der Hofstad
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands (e-mails: r.w.v.d.hofstad@tue.nl, w.j.t.hulshof@tue.nl)
Frank Den Hollander
Affiliation:
Mathematisch Instituut, Leiden University, 2333 CA Leiden, The Netherlands (e-mail: denholla@math.leidenuniv.nl)
Tim Hulshof
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands (e-mails: r.w.v.d.hofstad@tue.nl, w.j.t.hulshof@tue.nl)
*
*Corresponding author. Email: Lorenzo.Federico@warwick.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Hamming graph H(d, n) is the Cartesian product of d complete graphs on n vertices. Let 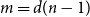${m=d(n-1)}$ be the degree and 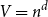$V = n^d$ be the number of vertices of H(d, n). Let 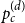$p_c^{(d)}$ be the critical point for bond percolation on H(d, n). We show that, for 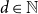$d \in \mathbb{N}$ fixed and 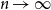$n \to \infty$,

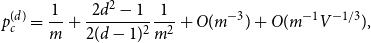$$p_c^{(d)} = {1 \over m} + {{2{d^2} - 1} \over {2{{(d - 1)}^2}}}{1 \over {{m^2}}} + O({m^{ - 3}}) + O({m^{ - 1}}{V^{ - 1/3}}),$$
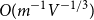which extends the asymptotics found in [10] by one order. The term $O(m^{-1}V^{-1/3})$ is the width of the critical window. For 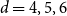$d=4,5,6$ we have 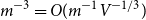$m^{-3} = O(m^{-1}V^{-1/3})$, and so the above formula represents the full asymptotic expansion of 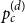$p_c^{(d)}$. In [16] we show that this formula is a crucial ingredient in the study of critical bond percolation on H(d, n) for 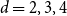$d=2,3,4$. The proof uses a lace expansion for the upper bound and a novel comparison with a branching random walk for the lower bound. The proof of the lower bound also yields a refined asymptotics for the susceptibility of a subcritical Erdös–Rényi random graph.

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60K37: Processes in random environments 82B43: Percolation
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 1 , January 2020 , pp. 68 - 100
Copyright
© Cambridge University Press 2019 

References

Aizenman, M. and Barsky, D. J. (1987) Sharpness of the phase transition in percolation models. Comm. Math. Phys. 108 489–526.CrossRefGoogle Scholar
Aizenman, M. and Newman, C. M. (1984) Tree graph inequalities and critical behavior in percolation models. J. Statist. Phys. 36 107–143.CrossRefGoogle Scholar
Aldous, D. (1997) Brownian excursions, critical random graphs and the multiplicative coalescent. Ann. Probab. 25 812–854.CrossRefGoogle Scholar
van den Berg, J. and Kesten, H. (1985) Inequalities with applications to percolation and reliability. J. Appl. Probab. 22 556–569.CrossRefGoogle Scholar
Bhamidi, S., van der Hofstad, R. and van Leeuwaarden, J. S. H. (2010) Scaling limits for critical inhomogeneous random graphs with finite third moments. Electron. J. Probab. 15 1682–1703.CrossRefGoogle Scholar
Bhamidi, S., van der Hofstad, R. and van Leeuwaarden, J. S. H. (2012) Novel scaling limits for critical inhomogeneous random graphs. Ann. Probab. 40 2299–2361.CrossRefGoogle Scholar
Bollobás, B. (1984) The evolution of random graphs. Trans. Amer. Math. Soc. 286 257–274.CrossRefGoogle Scholar
Bollobás, B. (2001) Random Graphs, second edition, Vol. 73 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.CrossRefGoogle Scholar
Borgs, C., Chayes, J., van der Hofstad, R., Slade, G. and Spencer, J. (2005) Random subgraphs of finite graphs, I: The scaling window under the triangle condition. Random Struct. Alg. 27 137–184.CrossRefGoogle Scholar
Borgs, C., Chayes, J., van der Hofstad, R., Slade, G. and Spencer, J. (2005) Random subgraphs of finite graphs, II: The lace expansion and the triangle condition. Ann. Probab. 33 1886–1944.CrossRefGoogle Scholar
Borgs, C., Chayes, J., van der Hofstad, R., Slade, G. and Spencer, J. (2006) Random subgraphs of finite graphs, III: The phase transition for the n-cube. Combinatorica 26 395–410.CrossRefGoogle Scholar
Brydges, D. and Spencer, T. (1985) Self-avoiding walk in 5 or more dimensions. Comm. Math. Phys. 97 125–148.CrossRefGoogle Scholar
Durrett, R. (2007) Random Graph Dynamics, Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press.Google Scholar
Erdős, P. and Rényi, A. (1959) On random graphs, I. Publ. Math. Debrecen 6 290–297.Google Scholar
Erdős, P. and Spencer, J. (1979) Evolution of the n-cube. Comput. Math. Appl. 5 33–39.CrossRefGoogle Scholar
Federico, L., van der Hofstad, R., den Hollander, F. and Hulshof, T. (2019) The scaling limit for critical percolation on the Hamming graph. In preparation.Google Scholar
Federico, L., van der Hofstad, R. and Hulshof, T. (2016) Connectivity threshold for random subgraphs of the Hamming graph. Electron. Commun. Probab., 21 #27.CrossRefGoogle Scholar
Fitzner, R. and van der Hofstad, R. (2013) Non-backtracking random walk. J. Statist. Phys. 150 264–284.CrossRefGoogle Scholar
Grimmett, G. (1999) Percolation, second edition, Springer.CrossRefGoogle Scholar
Grimmett, G. (2012) Percolation and disordered systems. In Percolation Theory at Saint-Flour, Springer, pp. 141–303.Google Scholar
Hara, T. and Slade, G. (1990) Mean-field critical behaviour for percolation in high dimensions. Commun. Math. Phys. 128 333–391.CrossRefGoogle Scholar
Heydenreich, M. and van der Hofstad, R. (2017) Progress in High-Dimensional Percolation and Random Graphs, CMR Short Courses, Springer.CrossRefGoogle Scholar
van der Hofstad, R. (2017) Random Graphs and Complex Networks, Vol. 1, Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press.CrossRefGoogle Scholar
van der Hofstad, R. and Luczak, M. J. (2010) Random subgraphs of the 2D Hamming graph: The supercritical phase. Probab. Theory Related Fields 147 1–41.CrossRefGoogle Scholar
van der Hofstad, R., Luczak, M. J. and Spencer, J. (2010) The second largest component in the supercritical 2D Hamming graph. Random Struct. Alg. 36 80–89.CrossRefGoogle Scholar
van der Hofstad, R. and Nachmias, A. (2014) Unlacing hypercube percolation: A survey. Metrika 77 23–50.CrossRefGoogle Scholar
van der Hofstad, R. and Nachmias, A. (2017) Hypercube percolation. J. Eur. Math. Soc. 19 725–814.CrossRefGoogle Scholar
van der Hofstad, R. and Slade, G. (2005) Asymptotic expansions in $n^{-1}$ for percolation critical values on the n-cube and ${\mathbb Z}^n$. Random Struct. Alg. 27 331–357.CrossRefGoogle Scholar
van der Hofstad, R. and Slade, G. (2006) Expansion in $n^{-1}$ for percolation critical values on the n-cube and ${\mathbb Z}^n$: The first three terms. Combin. Probab. Comput. 15 695–713.CrossRefGoogle Scholar
Janson, S., Knuth, D., Łuczak, T. and Pittel, B. (1993) The birth of the giant component. Random Struct. Alg. 4 231–358.CrossRefGoogle Scholar
Janson, S. and Warnke, L. (2018) On the critical probability in percolation. Electron. J. Probab. 23 #1.CrossRefGoogle Scholar
Joseph, A. (2014) The component sizes of a critical random graph with given degree sequence. Ann. Appl. Probab. 24 2560–2594.CrossRefGoogle Scholar
Łuczak, T., Pittel, B. and Wierman, J. C. (1994) The structure of a random graph at the point of the phase transition. Trans. Amer. Math. Soc. 341 721–748.CrossRefGoogle Scholar
Menshikov, M. V. (1986) Coincidence of critical points in percolation problems. Soviet Math. Doklady 33 856–859.Google Scholar
Miłoś, P. and Şengül, B. (2019) Existence of a phase transition of the interchange process on the Hamming graph. Electronic J. Probab. 24 64.CrossRefGoogle Scholar
Nachmias, A. and Peres, Y. (2007) Component sizes of the random graph outside the scaling window. ALEA Lat. Am. J. Probab. Math. Stat. 3 133–142.Google Scholar
Nachmias, A. and Peres, Y. (2008) Critical random graphs: Diameter and mixing time. Ann. Probab. 36 1267–1286.CrossRefGoogle Scholar
Nachmias, A. and Peres, Y. (2010) Critical percolation on random regular graphs. Random Struct. Alg. 36 111–148.CrossRefGoogle Scholar
Pakes, A. G. (1971) Some limit theorems for the total progeny of a branching process. Adv. Appl. Probab. 3 176–192.CrossRefGoogle Scholar
Pittel, B. (2001) On the largest component of the random graph at a nearcritical stage. J. Combin. Theory Ser. B 82 237–269.CrossRefGoogle Scholar
Ráth, B. (2018) A moment-generating formula for Erdős–Rényi component sizes. Electron. Commun. Probab. 23 #24.CrossRefGoogle Scholar
Russo, L. (1981) On the critical percolation probabilities. Z. Wahrsch. Verw. Gebiete 56 229–237.CrossRefGoogle Scholar