Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-12T04:13:37.463Z Has data issue: false hasContentIssue false
  • English
  • Français

The Dual BKR Inequality and Rudich's Conjecture

Published online by Cambridge University Press:  02 December 2010

JEFF KAHN ,
MICHAEL SAKS  and
CLIFFORD SMYTH
JEFF KAHN
Affiliation:
Mathematics Department, Rutgers University, Piscataway, NJ, USA (e-mail: jkahn@math.rutgers.edu, saks@math.rutgers.edu)
MICHAEL SAKS
Affiliation:
Mathematics Department, Rutgers University, Piscataway, NJ, USA (e-mail: jkahn@math.rutgers.edu, saks@math.rutgers.edu)
CLIFFORD SMYTH
Affiliation:
Mathematics Department, University of North Carolina Greensboro, Greensboro, NC, USA (e-mail: cdsmyth@uncg.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let be a set of terms over an arbitrary (but finite) number of Boolean variables. Let U() be the set of truth assignments that satisfy exactly one term in . Motivated by questions in computational complexity, Rudich conjectured that there exist ∊, δ > 0 such that, if is any set of terms for which U() contains at least a (1−∊)-fraction of all truth assignments, then there exists a term t ∈ such that at least a δ-fraction of assignments satisfy some term of sharing a variable with t [8].

We prove a stronger version: for any independent assignment of the variables (not necessarily the uniform one), if the measure of U() is at least 1 − ∊, there exists a t ∈ such that the measure of the set of assignments satisfying either t or some term incompatible with t (i.e., having no satisfying assignments in common with t) is at least 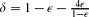. (A key part of the proof is a correlation-like inequality on events in a finite product probability space that is in some sense dual to Reimer's inequality [11], a.k.a. the BKR inequality [5], or the van den Berg–Kesten conjecture [3].)

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 2 , March 2011 , pp. 257 - 266
Copyright
Copyright © Cambridge University Press 2010

References

[1]Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, third edition, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley.CrossRefGoogle Scholar
[2]van den Berg, J. and Fiebig, U. (1987) On a combinatorial conjecture concerning disjoint occurrences of events. Ann. Probab. 15 354–374.Google Scholar
[3]van den Berg, J. and Kesten, H. (1985) Inequalities with applications to percolation and reliability. J. Appl. Probab. 22 556–569.CrossRefGoogle Scholar
[4]Erdős, P. and Lovász, L. (1975) Problems and results on 3-chromatic hypergraphs and some related questions. In Infinite and Finite Sets: Colloq., Keszthely, 1973; Dedicated to P. Erdős on his 60th Birthday, Vol. II, János Bolyai, Vol.10, North-Holland, pp. 609–627.Google Scholar
[5]Goldstein, L. and Rinott, Y. (2007) Functional BKR inequalities, and their duals, with applications. J. Theoret. Probab. 20 275–293.CrossRefGoogle Scholar
[6]Harris, T. E. (1960) A lower bound for the critical probability in a certain percolation process. Proc. Cambridge Philos. Soc. 56 13–20.CrossRefGoogle Scholar
[7]Impagliazzo, R. and Rudich, S. Personal communication.Google Scholar
[8]Impagliazzo, R. and Rudich, S. (1990) Limits on the provable consequences of one-way permutations. In Advances in Cryptology: CRYPTO '88 (Santa Barbara), Vol. 403 of Lecture Notes in Computer Science, Springer, pp. 8–26.CrossRefGoogle Scholar
[9]Kahn, J., Saks, M. and Smyth, C. (2000) A dual version of Reimer's inequality and a proof of Rudich's conjecture. In 15th Annual IEEE Conference on Computational Complexity (Florence), IEEE Computer Society, pp. 98–103.Google Scholar
[10]Kleitman, D. J. (1966) Families of non-disjoint subsets. J. Combin. Theory 1 153–155.CrossRefGoogle Scholar
[11]Reimer, D. (2000) Proof of the van den Berg–Kesten conjecture. Combin. Probab. Comput. 9 27–32.CrossRefGoogle Scholar
[12]Rudich, S. (ca. 1990) Unpublished.Google Scholar
[13]Smyth, C. (2002) Reimer's inequality and Tardos' conjecture. In Proc. 34th Annual ACM Symposium on Theory of Computing (New York), ACM, pp. 218–221.Google Scholar
[14]Szegedy, M. (ca. 1990) Unpublished.Google Scholar
[15]Tardos, G. (1989) Query complexity, or why is it difficult to separate NPA ∩ co-NPA from PA by random oracles A? Combinatorica 9 385–392.CrossRefGoogle Scholar
[16]Tardos, G. (ca. 1990) Unpublished.Google Scholar