Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T22:18:07.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting Intersecting and Pairs of Cross-Intersecting Families

Part of: Extremal combinatorics

Published online by Cambridge University Press:  16 October 2017

PETER FRANKL  and
ANDREY KUPAVSKII
PETER FRANKL
Affiliation:
Department of Discrete Mathematics, Moscow Institute of Physics and Technology, Moscow, Russia and Ecole Polytechnique Fédérale de Lausanne, Switzerland (e-mail: kupavskii@yandex.ru)
ANDREY KUPAVSKII
Affiliation:
Department of Discrete Mathematics, Moscow Institute of Physics and Technology, Moscow, Russia and Ecole Polytechnique Fédérale de Lausanne, Switzerland (e-mail: kupavskii@yandex.ru)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A family of subsets of {1,. . .,n} is called intersecting if any two of its sets intersect. A classical result in extremal combinatorics due to Erdős, Ko and Rado determines the maximum size of an intersecting family of k-subsets of {1,. . .,n}. In this paper we study the following problem: How many intersecting families of k-subsets of {1,. . .,n} are there? Improving a result of Balogh, Das, Delcourt, Liu and Sharifzadeh, we determine this quantity asymptotically for n ≥ 2k+2+2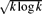$\sqrt{k\log k}$ and k → ∞. Moreover, under the same assumptions we also determine asymptotically the number of non-trivial intersecting families, that is, intersecting families for which the intersection of all sets is empty. We obtain analogous results for pairs of cross-intersecting families.

MSC classification

Primary: 05D05: Extremal set theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Issue 1 , January 2018 , pp. 60 - 68
Copyright
Copyright © Cambridge University Press 2017 

References

[1] Balogh, J., Das, S. A., Delcourt, M., Liu, H. and Sharifzadeh, M. (2015) Intersecting families of discrete structures are typically trivial. J. Combin. Theory Ser. A 132 224–245.Google Scholar
[2] Bollobás, B. (1965) On generalized graphs. Acta Math. Acad. Sci. Hungar. 16 447–452.Google Scholar
[3] Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. 12 313–320.Google Scholar
[4] Frankl, P. (1987) Erdős–Ko–Rado theorem with conditions on the maximal degree. J. Combin. Theory Ser. A 46 252–263.CrossRefGoogle Scholar
[5] Frankl, P. and Tokushige, N. (1992) Some best possible inequalities concerning cross-intersecting families. J. Combin. Theory Ser. A 61 87–97.Google Scholar
[6] Hilton, A. J. W. (1976) The Erdős–Ko–Rado theorem with valency conditions. Unpublished manuscript.Google Scholar
[7] Hilton, A. J. W. and Milner, E. C. (1967) Some intersection theorems for systems of finite sets. Quart. J. Math. Oxford 18 369–384.Google Scholar
[8] Jaeger, F. and Payan, C. (1971) Nombre maximal d'arêtes d'un hypergraphe critique de rang h. CR Acad. Sci. Paris 273 221–223.Google Scholar
[9] Katona, G. O. H. (1974) Solution of a problem of A. Ehrenfeucht and J. Mycielski. J. Combin. Theory Ser. A 17 265–266.Google Scholar
[10] Katona, G. O. H. (1987) A theorem of finite sets. In Classic Papers in Combinatorics (Gessel, I. and Rota, G.-C., eds), Birkhäuser, pp. 381–401.Google Scholar
[11] Kruskal, J. B. (1963) The number of simplices in a complex. In Mathematical Optimization Techniques (Bellman, R., ed.), University of California Press, pp. 251–278.Google Scholar
[12] Kupavskii, A. and Zakharov, D. Regular bipartite graphs and intersecting families. Accepted at J. Combin. Theory Ser. A arXiv:1611.03129 Google Scholar
[13] Lovász, L. (1979) Combinatorial Problems and Exercises, North-Holland.Google Scholar