Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T19:16:29.304Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting Independent Sets in Hypergraphs

Published online by Cambridge University Press:  08 April 2014

JEFF COOPER ,
KUNAL DUTTA  and
DHRUV MUBAYI
JEFF COOPER
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, IL 60607, USA (e-mail: jcoope8@uic.edu, mubayi@uic.edu)
KUNAL DUTTA
Affiliation:
Algorithms and Complexity Department, Max Planck Institute for Informatics, Saarbrücken, Germany (e-mail: kdutta@mpi-inf.mpg.de)
DHRUV MUBAYI
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, IL 60607, USA (e-mail: jcoope8@uic.edu, mubayi@uic.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a triangle-free graph with n vertices and average degree t. We show that G contains at least

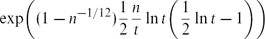${\exp\biggl({1-n^{-1/12})\frac{1}{2}\frac{n}{t}\ln t} \biggl(\frac{1}{2}\ln t-1\biggr)\biggr)}$
independent sets. This improves a recent result of the first and third authors [8]. In particular, it implies that as n → ∞, every triangle-free graph on n vertices has at least ${e^{(c_1-o(1)) \sqrt{n} \ln n}}$ independent sets, where 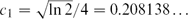$c_1 = \sqrt{\ln 2}/4 = 0.208138 \ldots$. Further, we show that for all n, there exists a triangle-free graph with n vertices which has at most 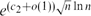${e^{(c_2+o(1))\sqrt{n}\ln n}}$ independent sets, where 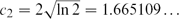$c_2 = 2\sqrt{\ln 2} = 1.665109 \ldots$. This disproves a conjecture from [8].

Let H be a (k+1)-uniform linear hypergraph with n vertices and average degree t. We also show that there exists a constant ck such that the number of independent sets in H is at least

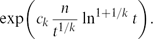${\exp\biggl({c_{k} \frac{n}{t^{1/k}}\ln^{1+1/k}{t}\biggr})}.$
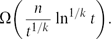This is tight apart from the constant ck and generalizes a result of Duke, Lefmann and Rödl [9], which guarantees the existence of an independent set of size
$\Omega\biggl(\frac{n}{t^{1/k}} \ln^{1/k}t\biggr).$
 Both of our lower bounds follow from a more general statement, which applies to hereditary properties of hypergraphs.

Keywords

Primary 05D40Secondary 05C6505D05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 4 , July 2014 , pp. 539 - 550
Copyright
Copyright © Cambridge University Press 2014 

References

[1]Ajtai, M., Erdős, P., Komlós, J. and Szemerédi, E. (1981), On Turán's theorem for sparse graphs. Combinatorica 1 313–317.Google Scholar
[2]Ajtai, M., Komlós, J., Pintz, J., Spencer, J. and Szemerédi, E. (1982) Extremal uncrowded hypergraphs. J. Combin. Theory Ser. A 32 321–335.Google Scholar
[3]Ajtai, M., Komlós, J. and Szemerédi, E. (1981) A dense infinite Sidon sequence. Europ. J. Combin. 2 1–11.Google Scholar
[4]Alon, N., Kim, J.-H. and Spencer, J. (1997) Nearly perfect matchings in regular simple hypergraphs. Israel J. Math. 100 171–187.Google Scholar
[5]Asratian, A. S. and Kuzjurin, N. N. (2000) On the number of partial Steiner systems. J. Combin. Des. 8 347–352.Google Scholar
[6]Bohman, T. and Keevash, P. (2013) Dynamic concentration of the triangle-free process. arXiv.1302.5963Google Scholar
[7]Colbourn, C. J., Hoffman, D. G., Phelps, K. T., Rödl, V. and Winkler, P. M. (1991) The number of t-wise balanced designs. Combinatorica 11 207–218.CrossRefGoogle Scholar
[8]Cooper, J. and Mubayi, D. Counting independent sets in triangle-free graphs. Proc. Amer. Math. Soc., to appear.Google Scholar
[9]Duke, R. A., Lefmann, H. and Rödl, V. (1995) On uncrowded hypergraphs. Random Struct. Alg. 6 209–212.Google Scholar
[10]Fiz Pontiveros, G., Griffiths, S. and Morris, R. (2013) The triangle-free process and r(3,k). arXiv.1302.6279Google Scholar
[11]Grable, D. A. and Phelps, K. T. (1996) Random methods in design theory: A survey. J. Combin. Des. 4 255–273.3.0.CO;2-E>CrossRefGoogle Scholar
[12]Kim, J. H. (1995) The Ramsey number R(3,t) has order of magnitude t 2/log t. Random Struct. Alg. 7 173–207.Google Scholar
[13]Kim, J. H. and Vu, V. H. (2000) Concentration of multivariate polynomials and its applications. Combinatorica 20 417–434.CrossRefGoogle Scholar
[14]Molloy, M. and Reed, B. (2002) Graph Colouring and the Probabilistic Method, Vol. 23 of Algorithms and Combinatorics, Springer.Google Scholar
[15]Shearer, J. B. (1983) A note on the independence number of triangle-free graphs. Discrete Math. 46 83–87.CrossRefGoogle Scholar
[16]Shearer, J. B. (1995) On the independence number of sparse graphs. Random Struct. Alg. 7 269–271.Google Scholar