No CrossRef data available.
Published online by Cambridge University Press: 06 June 2017
Let G be a finite D-quasirandom group and A ⊂ Gk a δ-dense subset. Then the density of the set of side lengths g of corners
converges to 1 as D → ∞.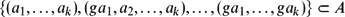 $$
\{(a_{1},\dotsc,a_{k}),(ga_{1},a_{2},\dotsc,a_{k}),\dotsc,(ga_{1},\dotsc,ga_{k})\} \subset A
$$
$$
\{(a_{1},\dotsc,a_{k}),(ga_{1},a_{2},\dotsc,a_{k}),\dotsc,(ga_{1},\dotsc,ga_{k})\} \subset A
$$